A Gimballed Control Moment Gyroscope Cluster Design for Spacecraft Attitude Control
Abstract
:1. Introduction
2. Mathematical Modeling
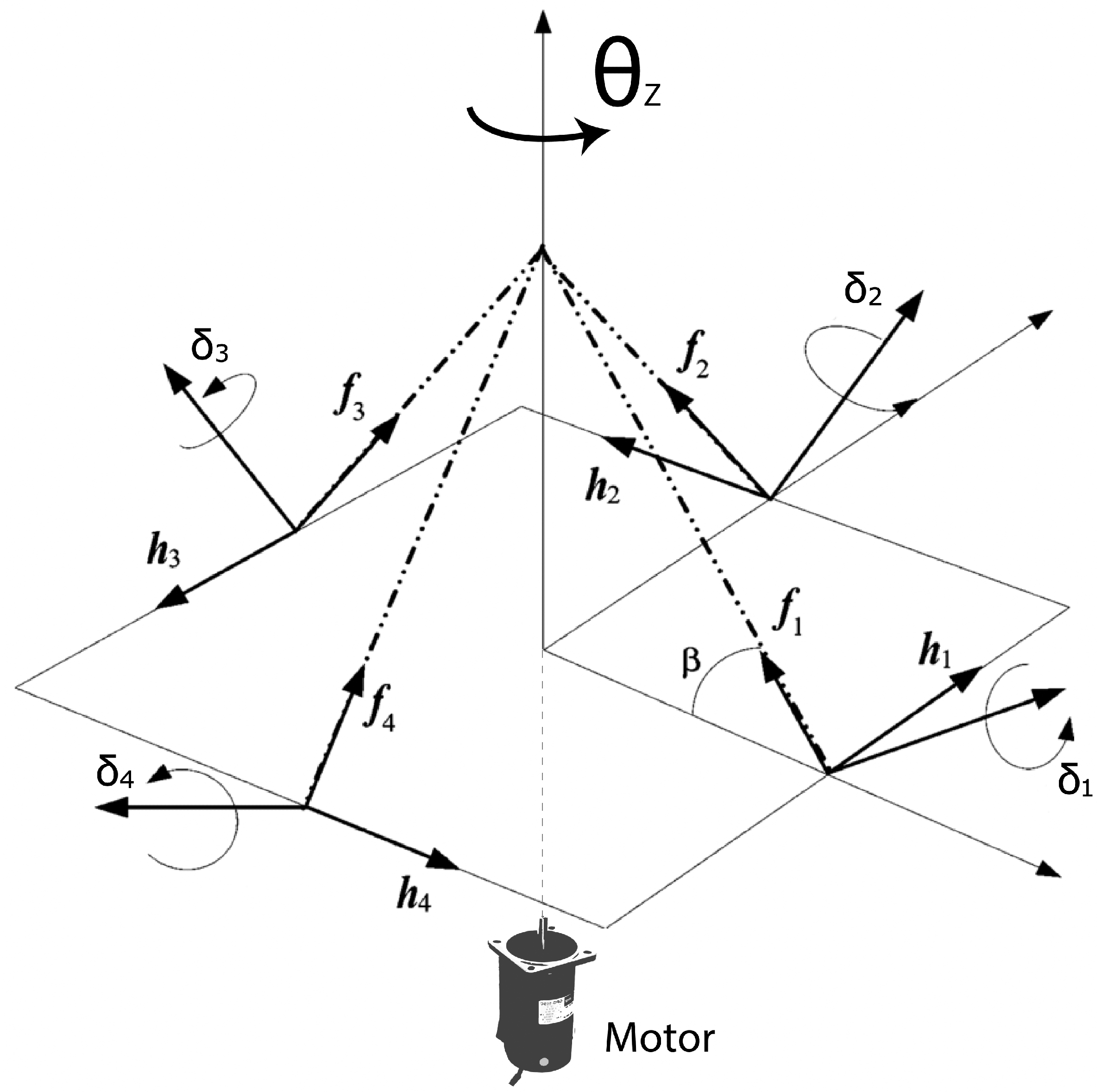
2.1. VSCMG Equations of Motion
2.2. GCMG Equations of Motion
Linearized Model
3. Singularities—Preliminaries
4. Simulation Set-Up
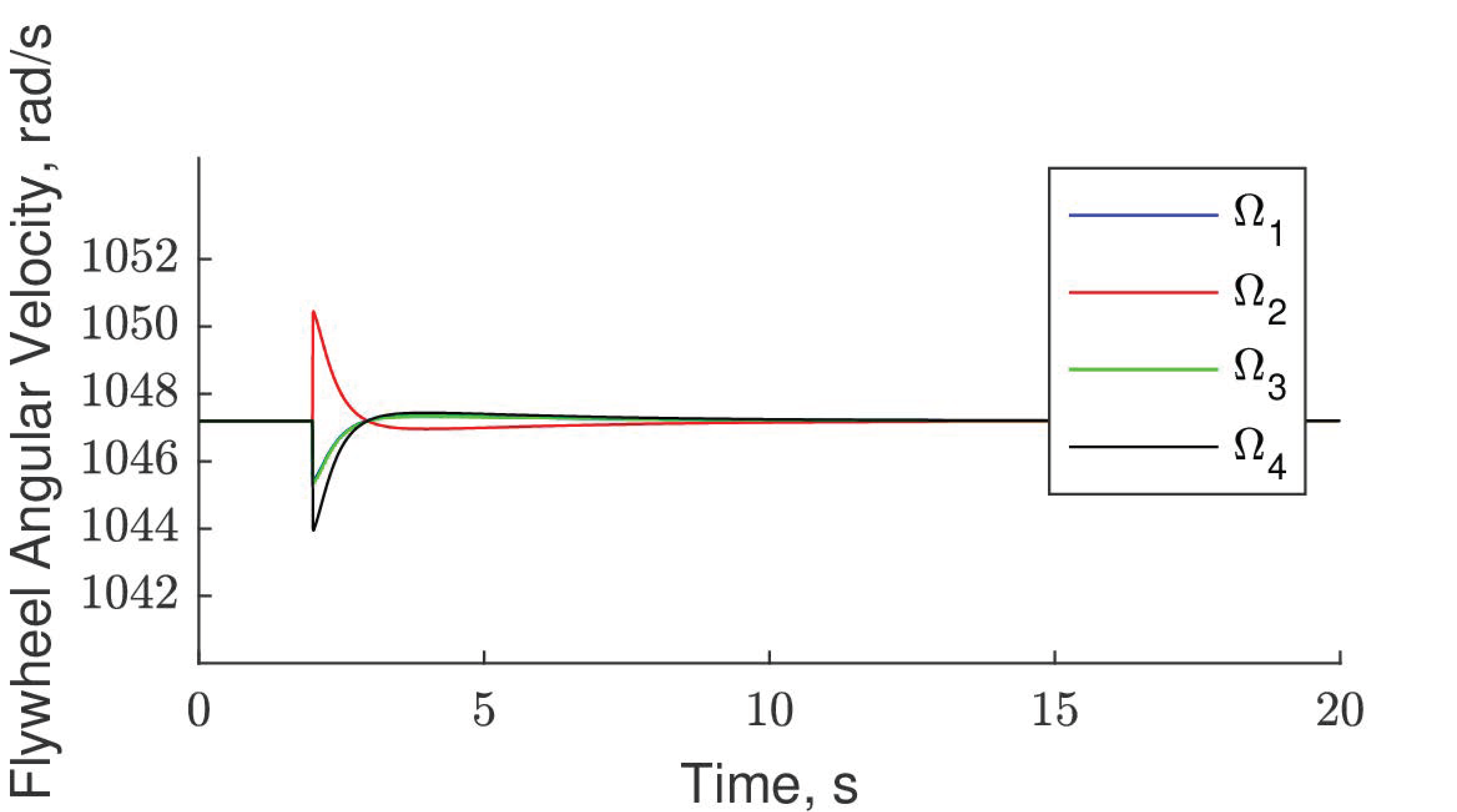
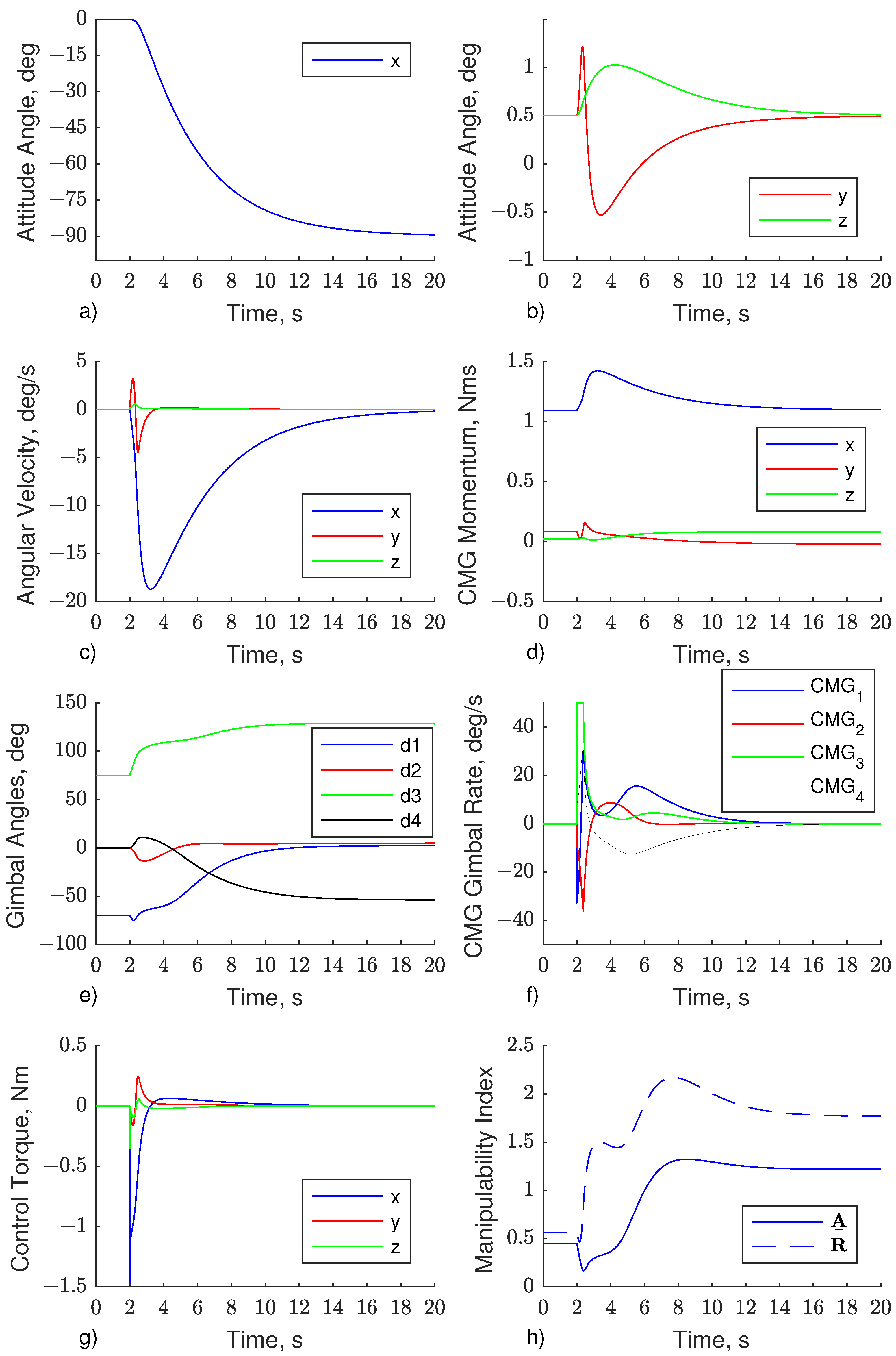
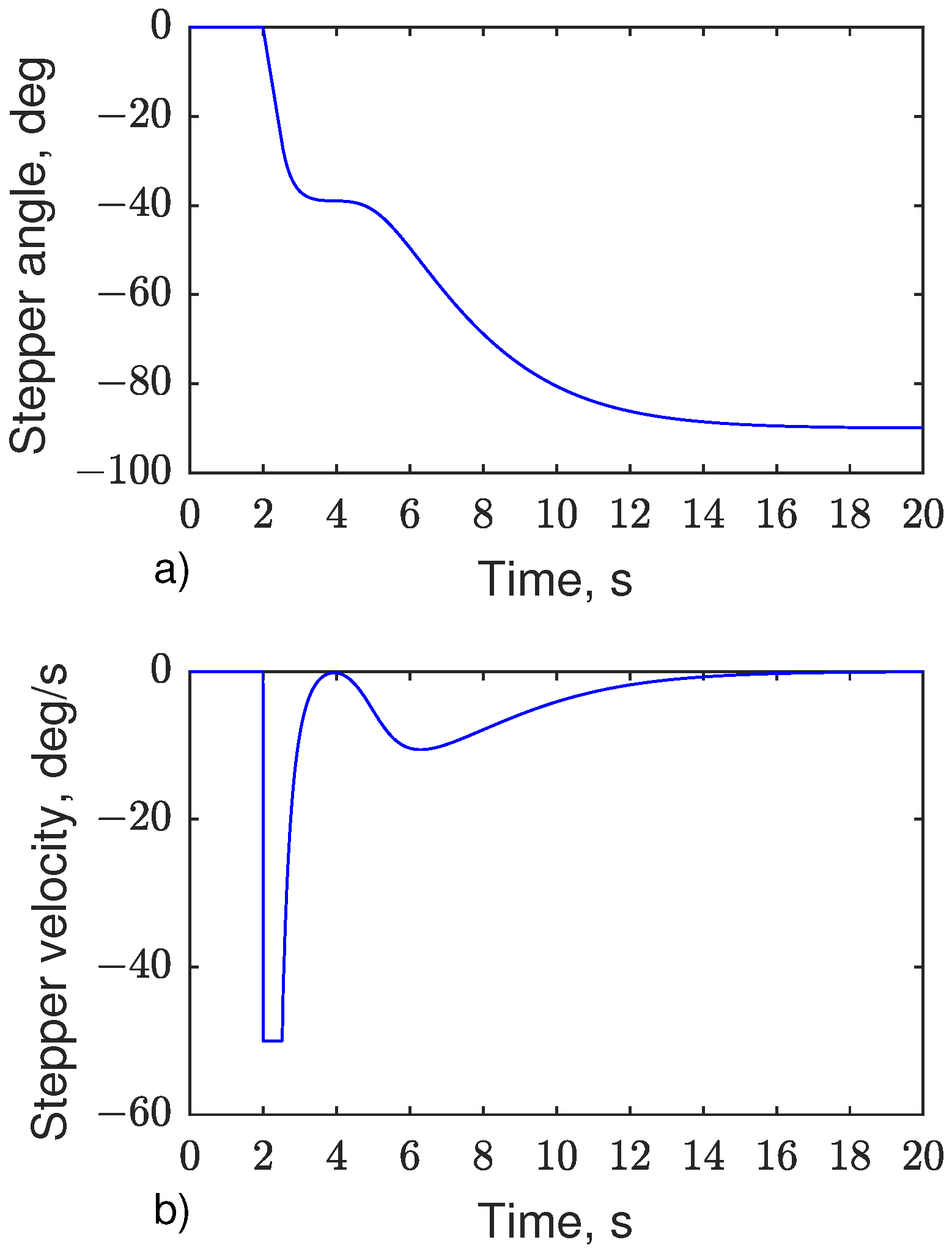
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wie, B. New Singularity Escape/Avoidance Steering Logic for Control Moment Gyro Systems. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Boston, MA, USA, 10–12 August 2003; American Institute of Aeronautics and Astronautics: Austin, TX, USA, 2003. [Google Scholar] [CrossRef]
- Margulies, G. Geometric Theory of Single-Gimbal Control Moment Gyro Systems. J. Astronaut. Sci. 1978, 26, 159–191. [Google Scholar]
- Roser, X.; Sghedoni, M. Control Moment Gyroscopes (CMG’s) and their Application in Future Scientific Missions. In Spacecraft Guidance, Navigation and Control Systems; Kaldeich-Schuermann, B., Ed.; European Space Agency (ESA) Special Publication: Noordwijk, The Netherlands, 1997; Volume 381, p. 523. [Google Scholar]
- Defendini, A.; Lagadec, K.; Guay, P.; Blais, T.; Griseri, G. Low Cost CMG-Based AOCS Designs. In Spacecraft Guidance, Navigation and Control Systems; Schürmann, B., Ed.; ESA Special Publication: Noordwijk, The Netherlands, 2000; Volume 425, p. 393. [Google Scholar]
- Wie, B. Space Vehicle Dynamics and Control; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Leve, F.A.; Hamilton, B.J.; Peck, M.A. Spacecraft Momentum Control Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 1–247. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Manipulator Performance Measures—A Comprehensive Literature Survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef] [Green Version]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Wie, B.; Bailey, D.; Heiberg, C. Singularity Robust Steering Logic for Redundant Single-Gimbal Control Moment Gyros. J. Guid. Control Dyn. 2001, 24, 865–872. [Google Scholar] [CrossRef]
- Paradiso, J. A Search-Based Approach to Steering Single Gimballed CMGs; Draper Laboratory: Cambridge, MA, USA, 1991. [Google Scholar]
- Paradiso, J. Global steering of single gimballed control moment gyroscopes using a directed search. J. Guid. Control Dyn. 1992, 15, 1236–1244. [Google Scholar] [CrossRef]
- Vadali, S.R.; Walker, S.R.; OH, H.S. Preferred gimbal angles for single gimbal control moment gyros. J. Guid. Control Dyn. 1990, 13, 1090–1095. [Google Scholar] [CrossRef]
- Geshnizjani, R.; Kornienko, A.; Ziegler, T.; Loehr, J.; Fichter, W. Optimal Initial Gimbal Angles for Agile Slew Maneuvers with Control Moment Gyroscopes. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Nanamori, Y.; Takahashi, M. Steering law of control moment gyros using optimization of initial gimbal angles for satellite attitude control. Nihon Kikai Gakkai Ronbunshu C Hen/Trans. Jpn. Soc. Mech. Eng. Part C 2008, 74, 2698–2704. [Google Scholar] [CrossRef]
- Qian, Z.; Guojin, T. Technical Note: Space Station Zero Propellant Maneuver Path Planning Considering SGCMG Saturation and Singularity. J. Astronaut. Sci. 2014, 61, 305–318. [Google Scholar] [CrossRef]
- Cui, P.; He, J.; Cui, J.; Li, H. Improved Path Planning and Attitude Control Method for Agile Maneuver Satellite with Double-Gimbal Control Moment Gyros. Math. Probl. Eng. 2015, 2015, 878724. [Google Scholar] [CrossRef]
- Geng, Y.; Hou, Z.; Huang, S. Global Singularity Avoidance Steering Law for Single-Gimbal Control Moment Gyroscopes. J. Guid. Control Dyn. 2017, 40, 3027–3036. [Google Scholar] [CrossRef]
- Jia, Y.; Misra, A.K. Trajectory Planning for a Space Robot Actuated by Control Moment Gyroscopes. J. Guid. Control Dyn. 2018, 41, 1838–1842. [Google Scholar] [CrossRef]
- Leeghim, H.; Lee, C.Y.; Jin, J.; Kim, D. A Singularity-free Steering Law of Roof Array of Control Moment Gyros for Agile Spacecraft Maneuver. Int. J. Control. Autom. Syst. 2020, 18, 1679–1690. [Google Scholar] [CrossRef]
- Currie, B.J. Control of a Spacecraft Using Mixed Momentum Exchange Devices. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2014. [Google Scholar]
- Ye, D.; Sun, Z.; Wu, S. Hybrid thrusters and reaction wheels strategy for large angle rapid reorientation with high precision. Acta Astronaut. 2012, 77, 149–155. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, B.U.; Oh, H.S.; Lee, S.H.; Rhee, S.W. Time optimal attitude maneuver strategies for the agile spacecraft with reaction wheels and thrusters. J. Mech. Sci. Technol. 2005, 19, 1695–1705. [Google Scholar] [CrossRef]
- Hall, C.D.; Tsiotras, P.; Shen, H. Tracking Rigid Body Motion Using Thrusters and Momentum Wheels. J. Astronaut. Sci. 2002, 50, 311–323. [Google Scholar] [CrossRef]
- Skelton, C.E. Mixed Control Moment Gyro and Momentum Wheel Attitude Control Strategies. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2003. [Google Scholar]
- Richie, D.J.; Lappas, V.J.; Palmer, P.L. Sizing/Optimization of a Small Satellite Energy Storage and Attitude Control System. J. Spacecr. Rocket. 2007, 44, 940–952. [Google Scholar] [CrossRef] [Green Version]
- Richie, D.J.; Lappas, V.J.; Asghar, S. Constrained singularity avoidance using VSCMGs for combined attitude and power tracking. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 3500–3506. [Google Scholar] [CrossRef]
- Richie, D.J.; Lappas, V.J.; Prassinos, G. A practical small satellite variable-speed control moment gyroscope for combined energy storage and attitude control. Acta Astronaut. 2009, 65, 1745–1764. [Google Scholar] [CrossRef]
- Yoon, H.; Tsiotras, P. Spacecraft Adaptive Attitude and Power Tracking with Variable Speed Control Moment Gyroscopes. J. Guid. Control Dyn. 2002, 25, 1081–1090. [Google Scholar] [CrossRef] [Green Version]
- Yoshihara, H.; Takahashi, M. Optimal Power Management Considering Attitude Control and Battery Deterioration Control for Spacecraft with VSCMG/IPACS. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, 2020; pp. 1–13. [Google Scholar] [CrossRef]
- Sasaki, T.; Alcorn, J.; Schaub, H.; Shimomura, T. Convex Optimization for Power Tracking of Double-Gimbal Variable-Speed Control Moment Gyroscopes. J. Spacecr. Rocket. 2018, 55, 541–551. [Google Scholar] [CrossRef]
- Sasaki, T.; Shimomura, T.; Schaub, H. Robust Attitude Control Using a Double-Gimbal Variable-Speed Control Moment Gyroscope. J. Spacecr. Rocket. 2018, 55, 1235–1247. [Google Scholar] [CrossRef]
- Stevenson, D.; Schaub, H. Nonlinear Control Analysis of a Double-Gimbal Variable-Speed Control Moment Gyroscope. J. Guid. Control Dyn. 2012, 35, 787–793. [Google Scholar] [CrossRef]
- Gaude, A.; Lappas, V. Design and Structural Analysis of a Control Moment Gyroscope (CMG) Actuator for CubeSats. Aerospace 2020, 7, 55. [Google Scholar] [CrossRef]
- Lappas, V.J. A Control Moment Gyro (CMG) Based Attitude Control System (ACS) for Agile Small Satellites. Ph.D. Dissertation, School of Electronics and Physical Sciences, University of Surrey, Guildford, UK, 2002. [Google Scholar]
- Lappas, V.; Steyn, W.H.; Underwood, C. Design and Testing of a Control Moment Gyroscope Cluster for Small Satellites. J. Spacecr. Rocket. 2005, 42, 729–739. [Google Scholar] [CrossRef]
- Schaub, H.; Junkins, J. CMG singularity avoidance using VSCMG null motion. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Boston, MA, USA, 10–12 August 1998; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998. [Google Scholar] [CrossRef]
- Schaub, H.; Vadali, S.R.; Junkins, J.L. Feedback Control Law for Variable Speed Control Moment Gyros. J. Astronaut. Sci. 1998, 46, 307–328. [Google Scholar] [CrossRef]
- Wie, B.; Weiss, H.; Arapostathis, A. Quarternion feedback regulator for spacecraft eigenaxis rotations. J. Guid. Control Dyn. 1989, 12, 375–380. [Google Scholar] [CrossRef]
- Junkins, J.L.; Schaub, H. Analytical Mechanics of Space Systems, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar] [CrossRef]
- Xue-qin, C.; Yun-hai, G.; Yu-hai, M.; Feng, W.; Xi-bin, C. Integrated attitude control algorithm and steering law for agile small satellites. In Proceedings of the 2011 6th Institute of Electrical and Electronics Engineers IEEE Conference on Industrial Electronics and Applications, Melbourne, VIC, Australia, 7–10 November 2011; pp. 139–142. [Google Scholar] [CrossRef]
- Kalman, R.; Bertram, J. Control system analysis and design via the second method of lyapunov: (I) continuous-time systems (II) discrete time systems. Inst. Electr. Electron. Eng. Trans. Autom. Control 1959, 4, 112. [Google Scholar] [CrossRef]
- Bedrossian, N.S.; Paradiso, J.; Bergmann, E.V.; Rowell, D. Redundant single gimbal control moment gyroscope singularity analysis. J. Guid. Control Dyn. 1990, 13, 1096–1101. [Google Scholar] [CrossRef]
- Cornick, D. Singularity avoidance control laws for single gimbal control moment gyros. In Proceedings of the Guidance and Control Conference, Boulder, CO, USA, 6–8 August 1979; Guidance, Navigation, and Control and Co-Located Conferences. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1979. [Google Scholar] [CrossRef]
- Kurokawa, H.; Yajima, N.; Usui, S. A study of single gimbal CMG systems. In Proceedings of the 15th International Symposium on Space Technology and Science, Tokyo, Japan, 19–23 May 1986; Volume 2, pp. 1219–1224. [Google Scholar]
- Tokar, E.N.; Platonov, V.N. Singular surfaces in unsupported gyrodyne systems. Cosm. Res. 1979, 16, 547–555. [Google Scholar]
- Wie, B. Singularity Analysis and Visualization of Single-Gimbal Control Moment Gyro Systems. J. Guid. Control Dyn. 2004, 27, 271–282. [Google Scholar] [CrossRef]
- Bedrossian, N.; Paradiso, J.; Bergmann, E.V.; Rowell, D. Steering law design for redundant single-gimbal control moment gyroscopes. J. Guid. Control Dyn. 1991, 13, 1083–1089. [Google Scholar] [CrossRef]
- Wie, B. Singularity Escape/Avoidance Steering Logic for Control Moment Gyro Systems. J. Guid. Control Dyn. 2005, 28, 1872–1873. [Google Scholar] [CrossRef]




| Parameter | VSCMG | GCMG |
|---|---|---|
| Manoeuvre | 0 to −90 deg | 0 to −90 deg |
| Moment of Inertia J | ||
| ----- | ||
| ----- | 38 | |
| Time-step dt | 0.01 s | 0.01 s |
| Simulation time | 20 s | 20 s |
| PD, , | 1.6, 3 | 1.6, 3 |
| Skew angle | 54.73 deg | 54.73 deg |
| 50 deg/s | 50 deg/s | |
| deg | deg | |
| ----- | 50 deg/s | |
| ----- | deg | |
| rad/s | rad/s |
| Parameter | Value |
|---|---|
| 1, 0 | |
| 1 | |
| rad/s | |
| ----- | |
| 1 | |
| 0 |
| Parameter | Value |
|---|---|
| 1 | |
| −90 deg |
| Parameter | Value |
|---|---|
| Max attitude error in y | 455% |
| Max attitude error in z | −41% |
| Max velocity in x | −1% |
| Min manipulability | 11% |
| Steady state manipulability | 160% |
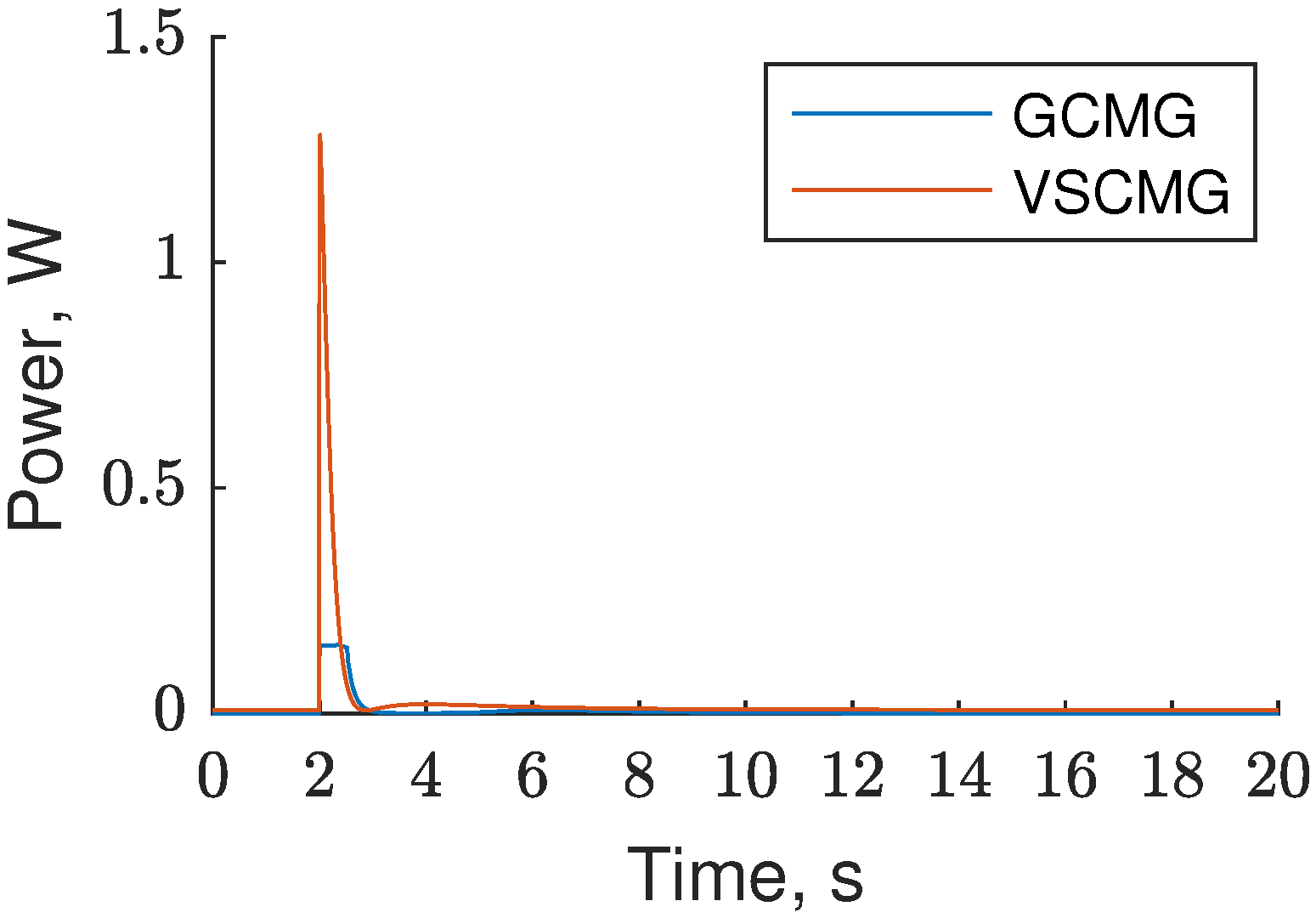
| Power | GCMG | VSCMG |
|---|---|---|
| Maximum | 0.153 W | 1.28 W |
| Mean | 0.006 W | 0.023 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papakonstantinou, C.; Lappas, V.; Kostopoulos, V. A Gimballed Control Moment Gyroscope Cluster Design for Spacecraft Attitude Control. Aerospace 2021, 8, 273. https://doi.org/10.3390/aerospace8090273
Papakonstantinou C, Lappas V, Kostopoulos V. A Gimballed Control Moment Gyroscope Cluster Design for Spacecraft Attitude Control. Aerospace. 2021; 8(9):273. https://doi.org/10.3390/aerospace8090273
Chicago/Turabian StylePapakonstantinou, Charalampos, Vaios Lappas, and Vassilis Kostopoulos. 2021. "A Gimballed Control Moment Gyroscope Cluster Design for Spacecraft Attitude Control" Aerospace 8, no. 9: 273. https://doi.org/10.3390/aerospace8090273
APA StylePapakonstantinou, C., Lappas, V., & Kostopoulos, V. (2021). A Gimballed Control Moment Gyroscope Cluster Design for Spacecraft Attitude Control. Aerospace, 8(9), 273. https://doi.org/10.3390/aerospace8090273








