An Effective Form Analysis Approach for Designing and Optimizing a Cable-Net Structure of a Giant Active Reflector
Abstract
1. Introduction
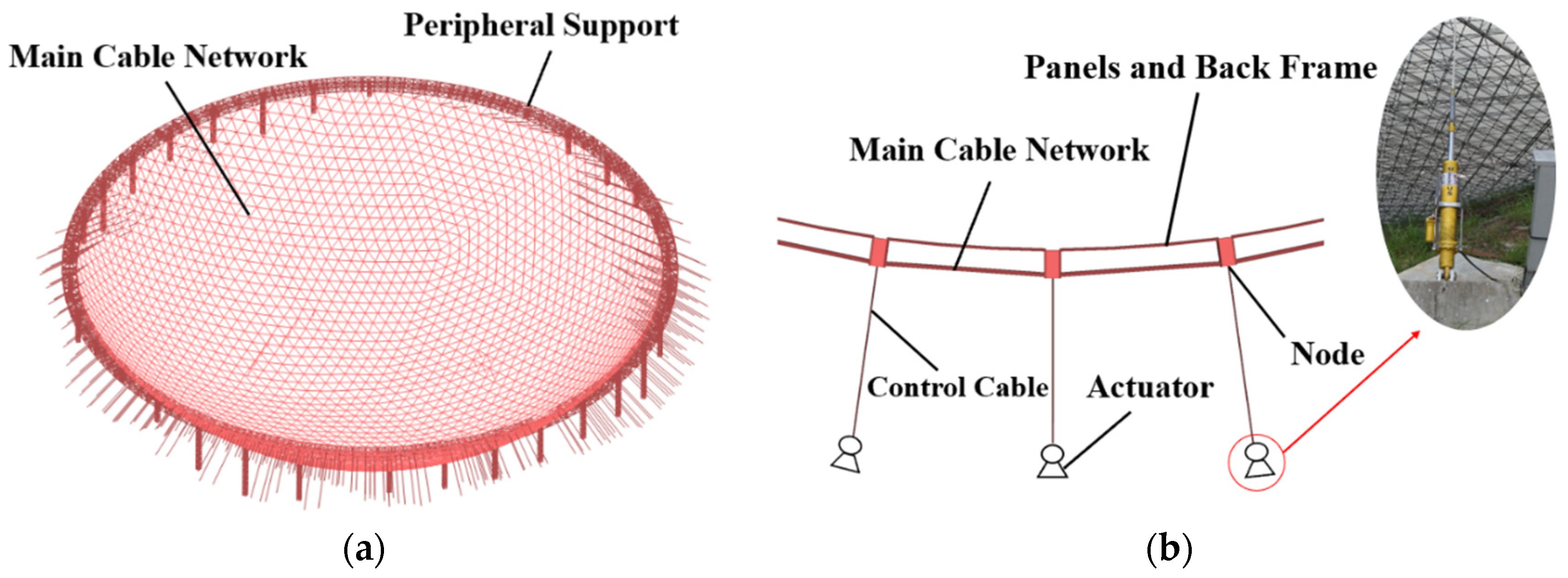
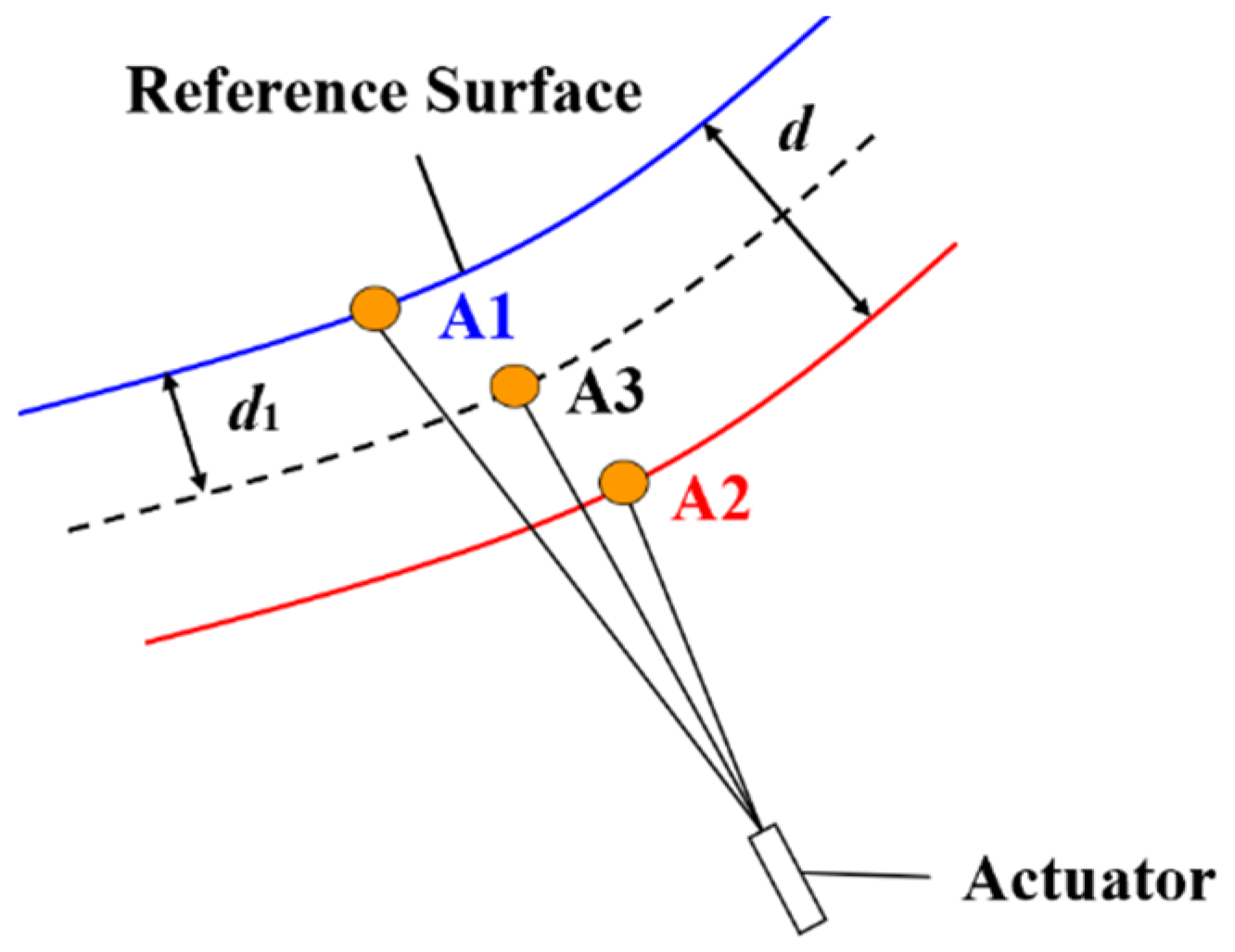
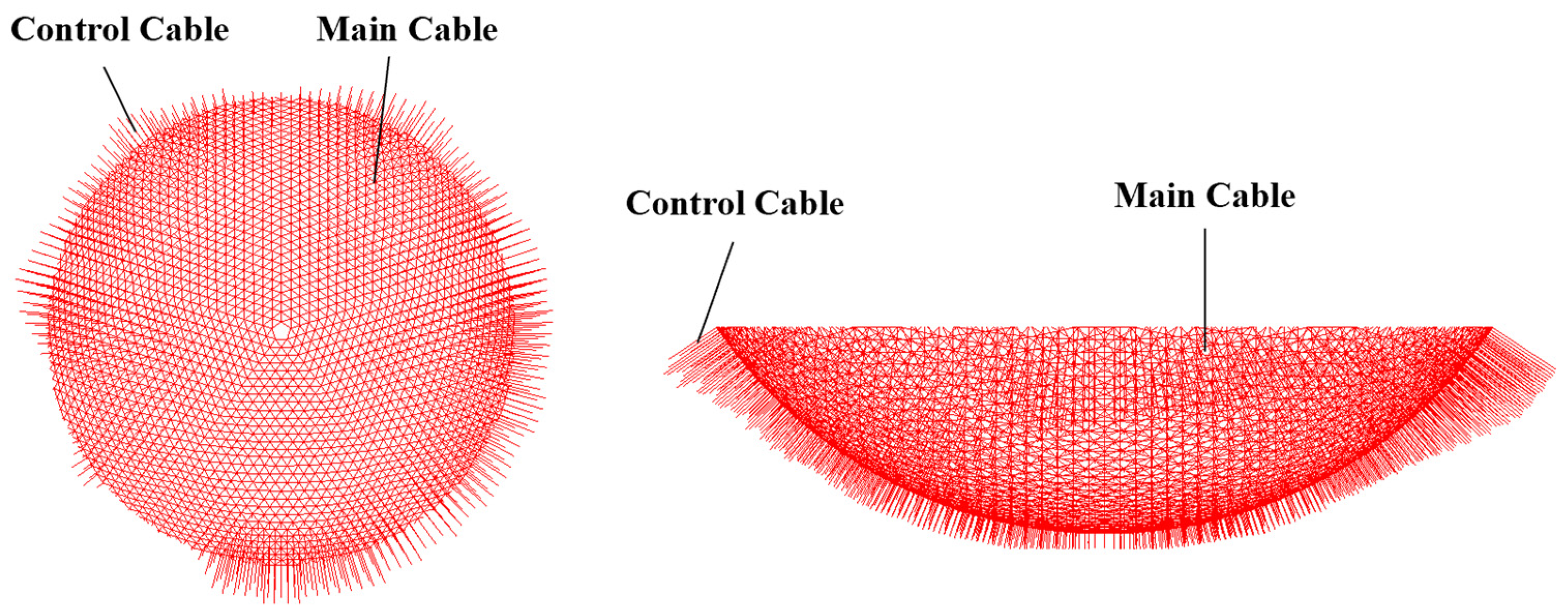
2. Cable-Net Structure of the Active Reflector
3. Basic Form Analysis Principles of the Reflector Cable-Net Structure
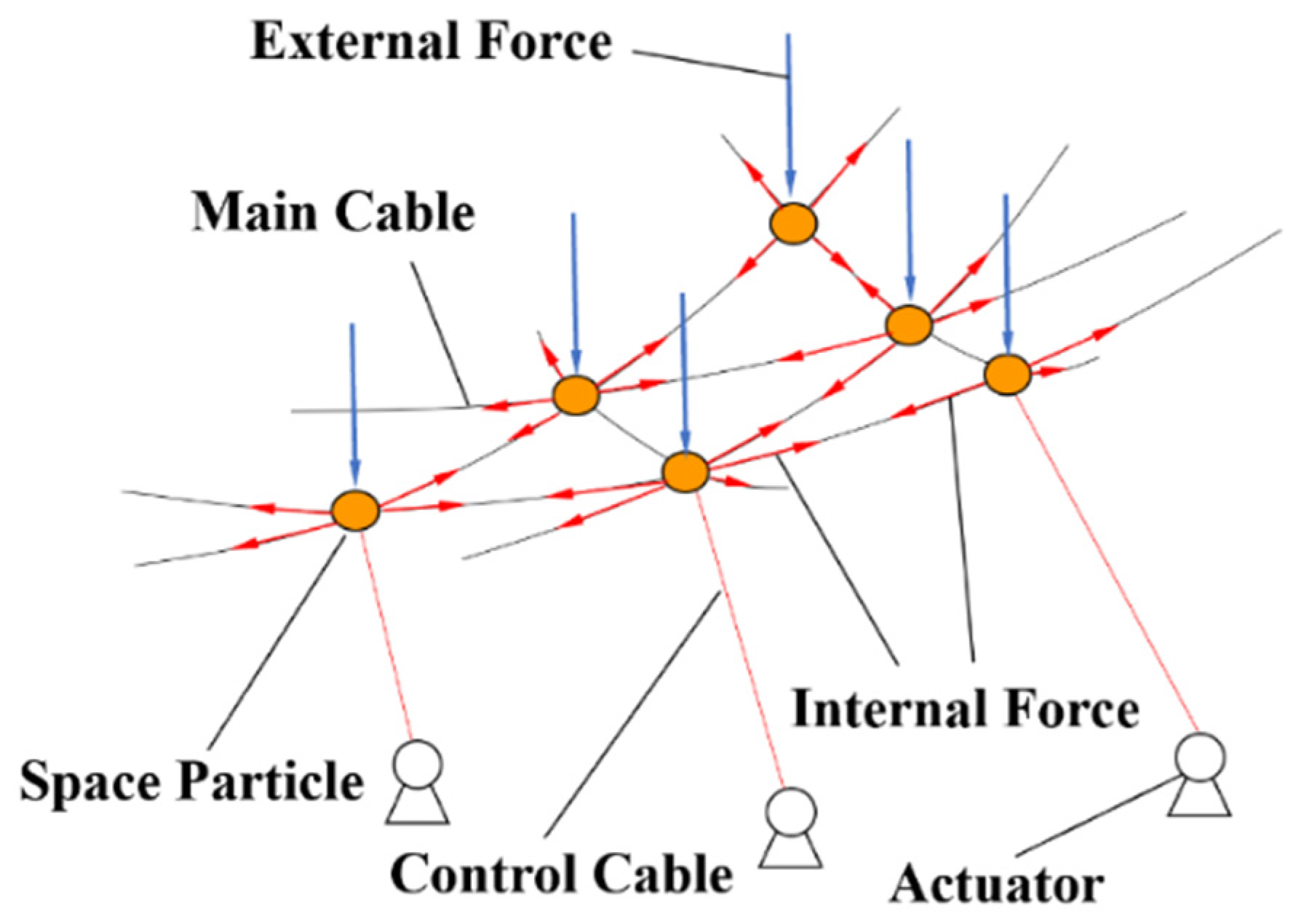
3.1. Structural Discretization and Motion Description
3.2. Principles for Solving Static Equilibrium
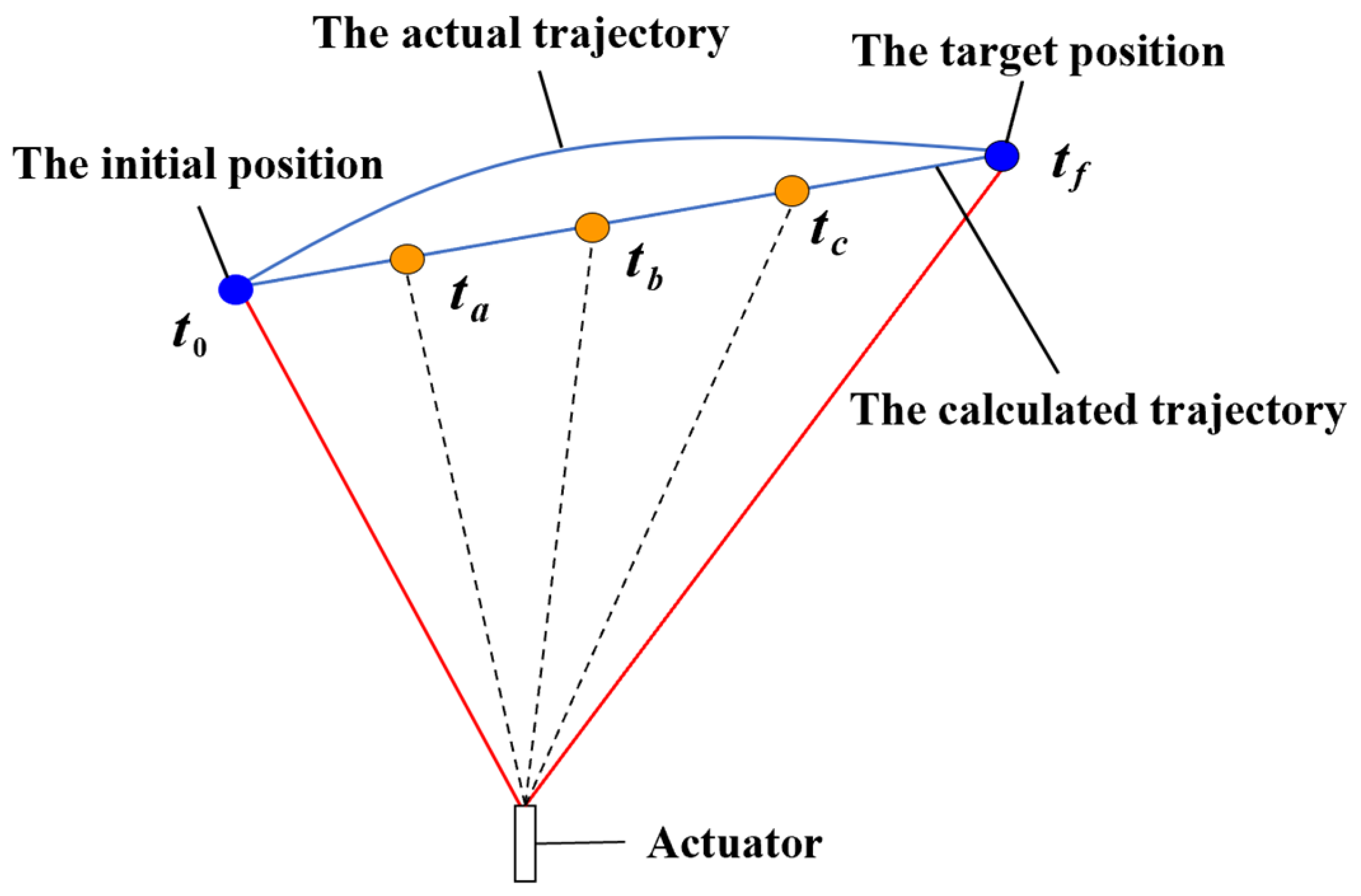
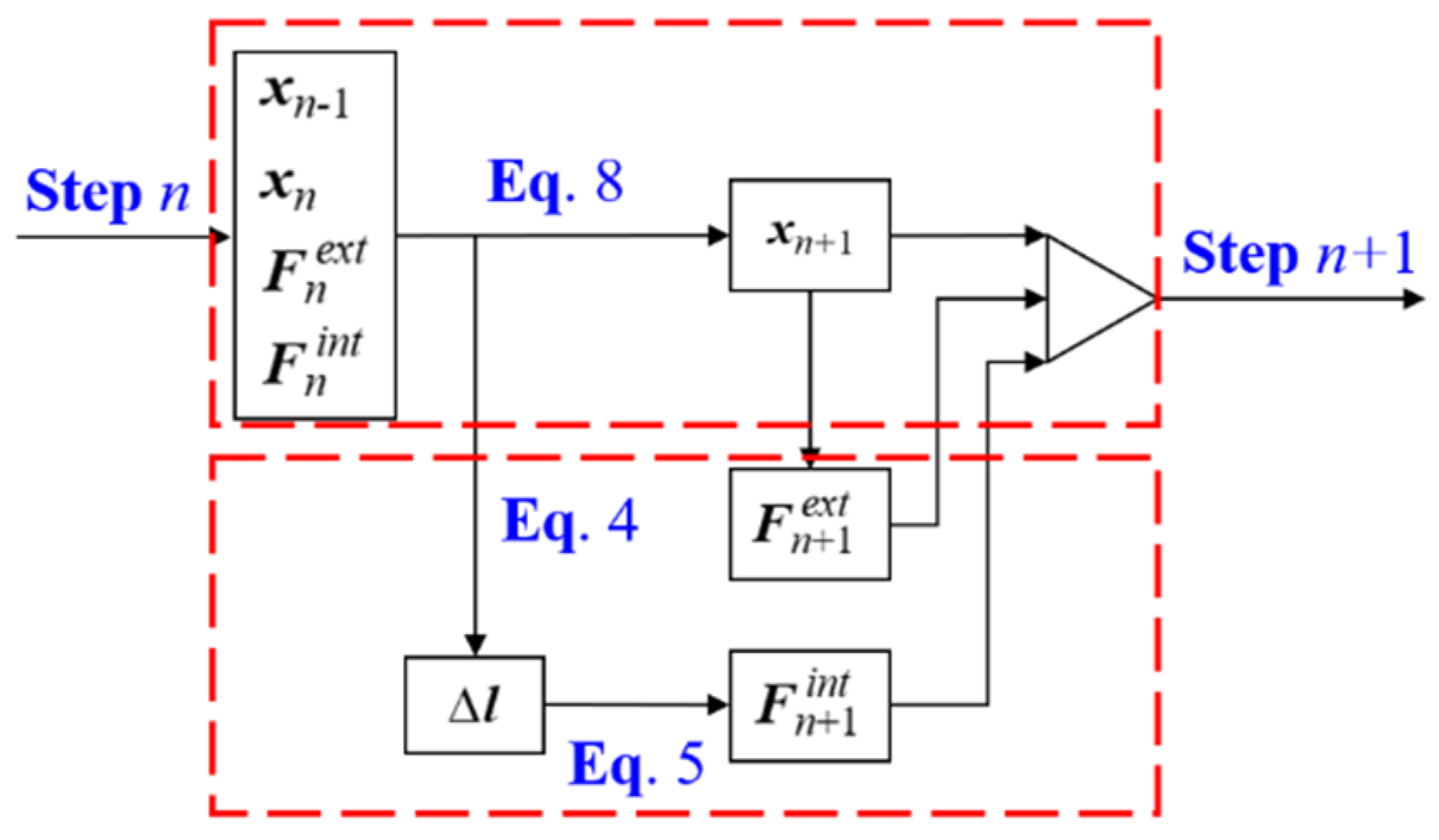
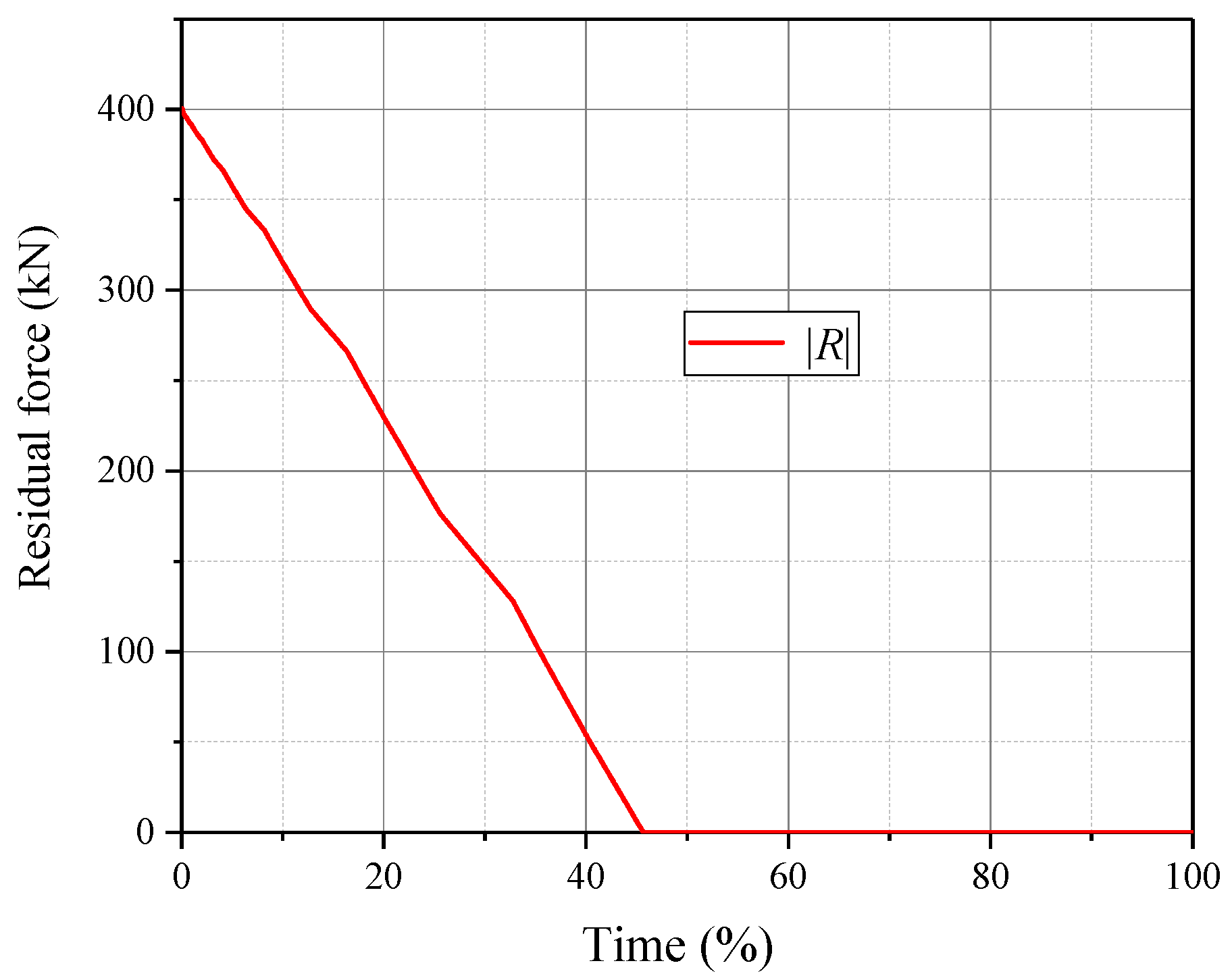
3.3. Iterative Principle and Basic Flow of Form Analysis
4. Form Analysis Results of the FAST Active Reflector Cable-Net Structure
4.1. Numerical Model of the Cable-Net Structure
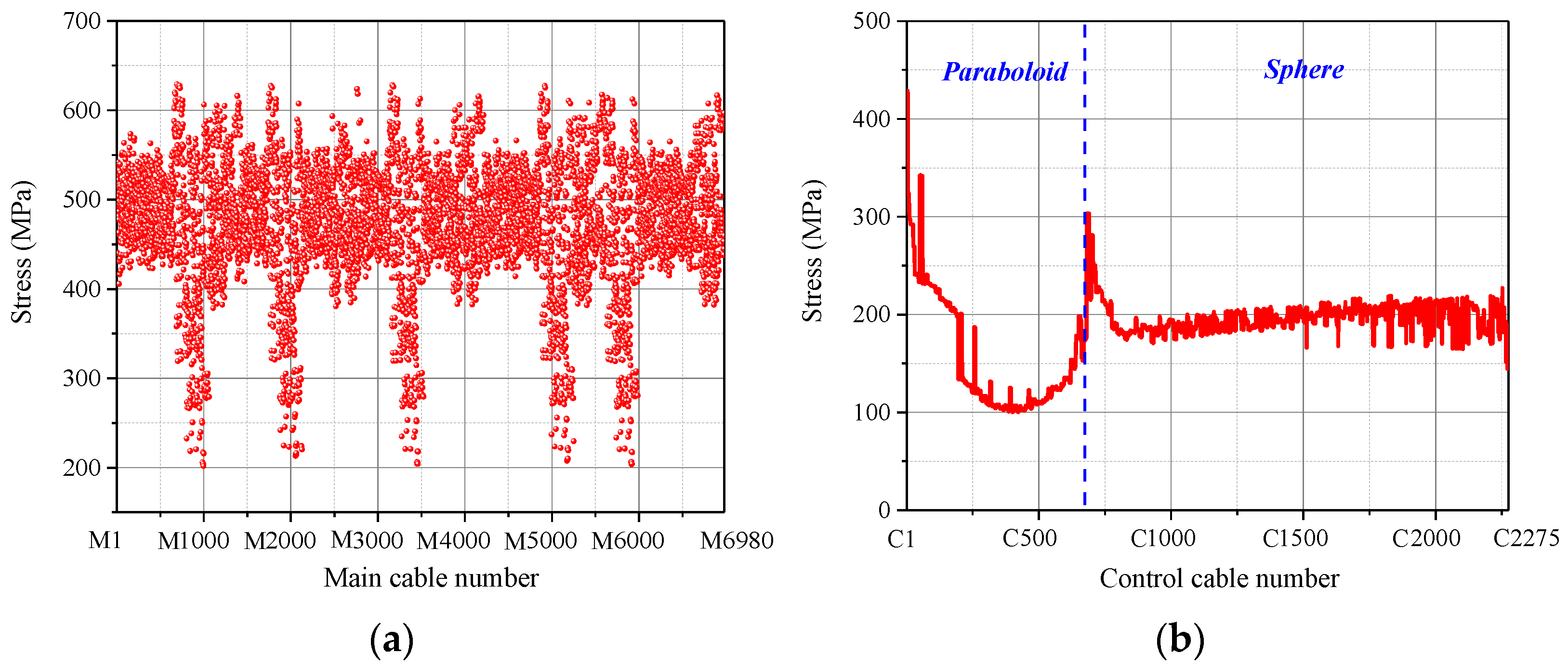
4.2. Form-Finding Analysis Results
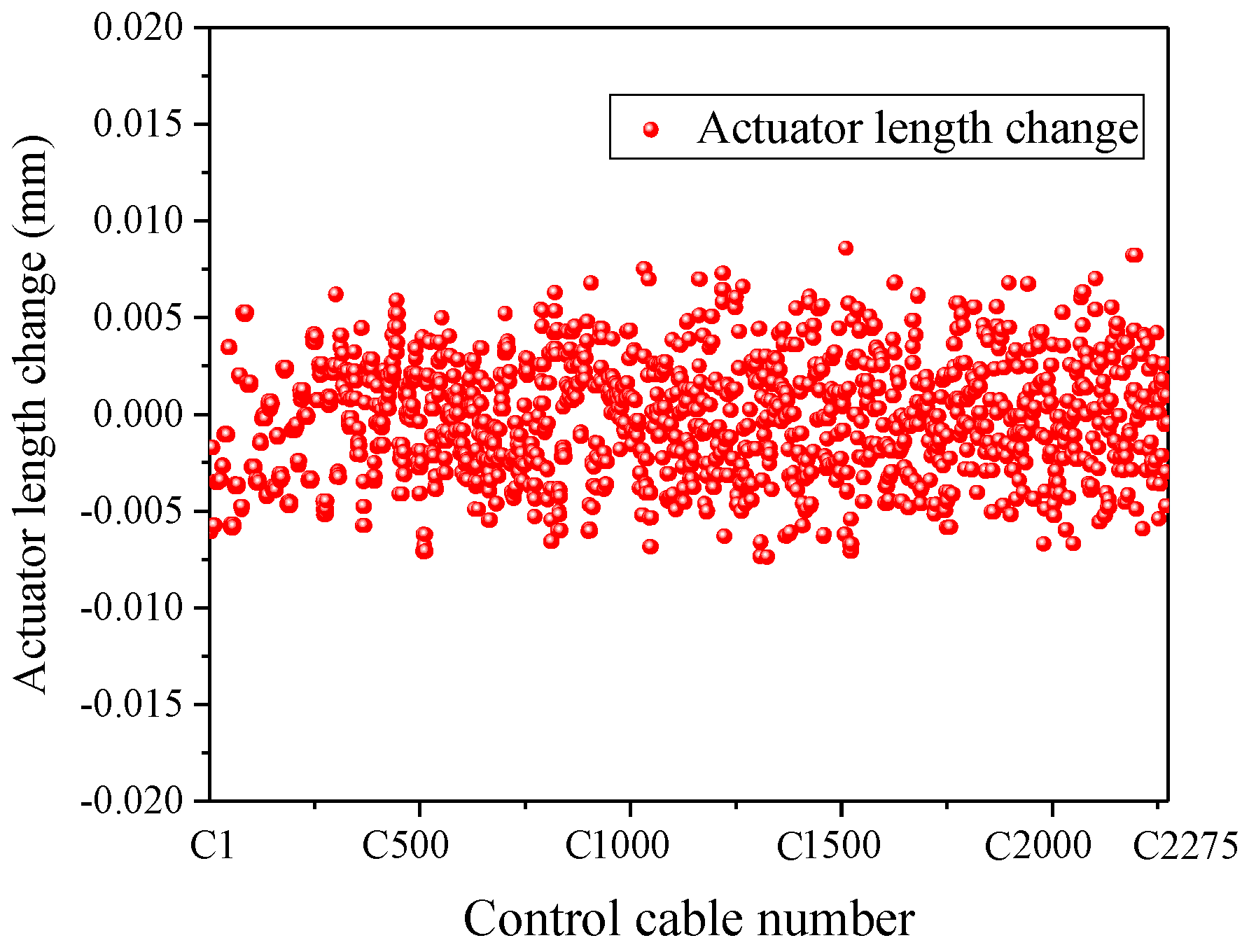
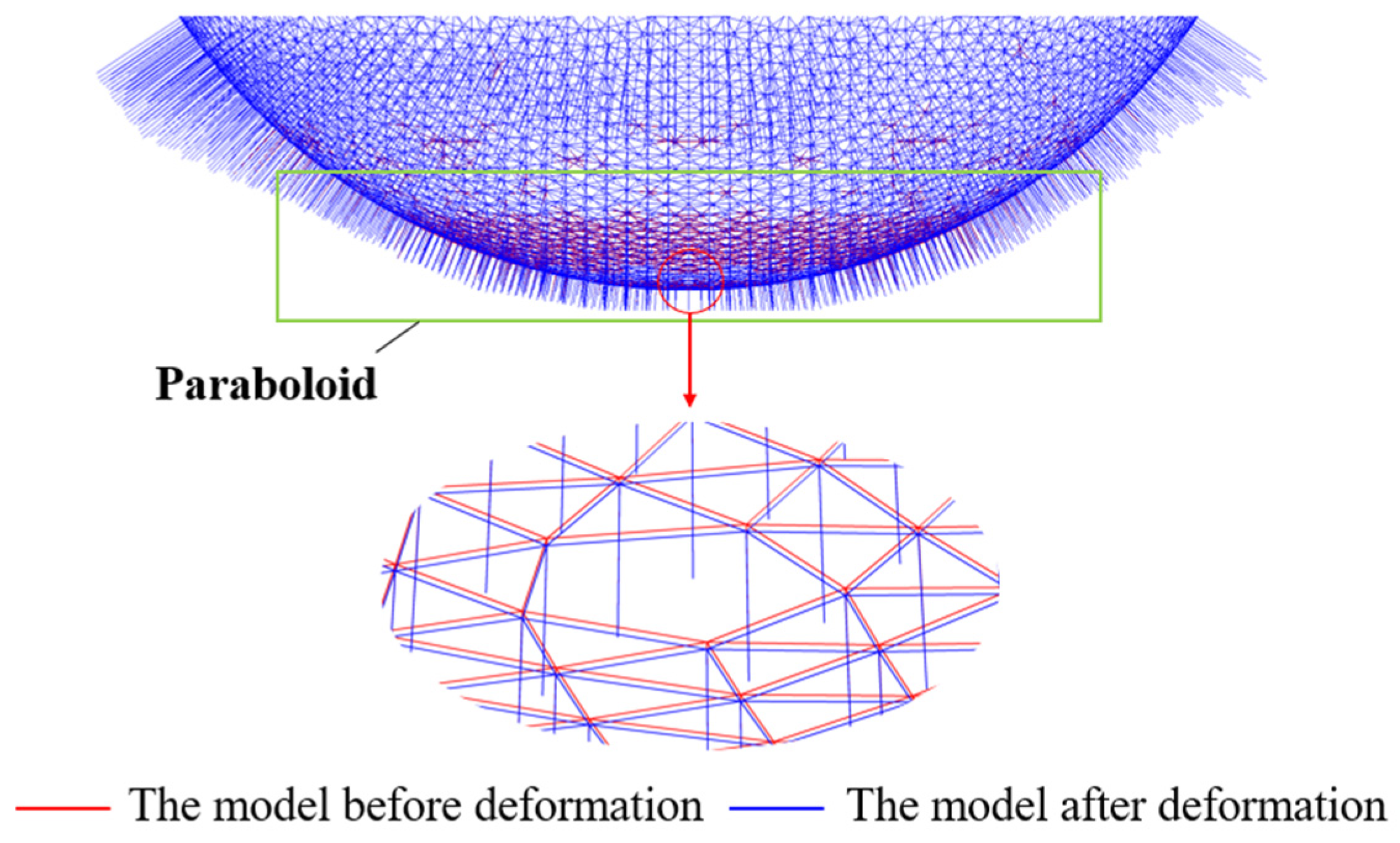
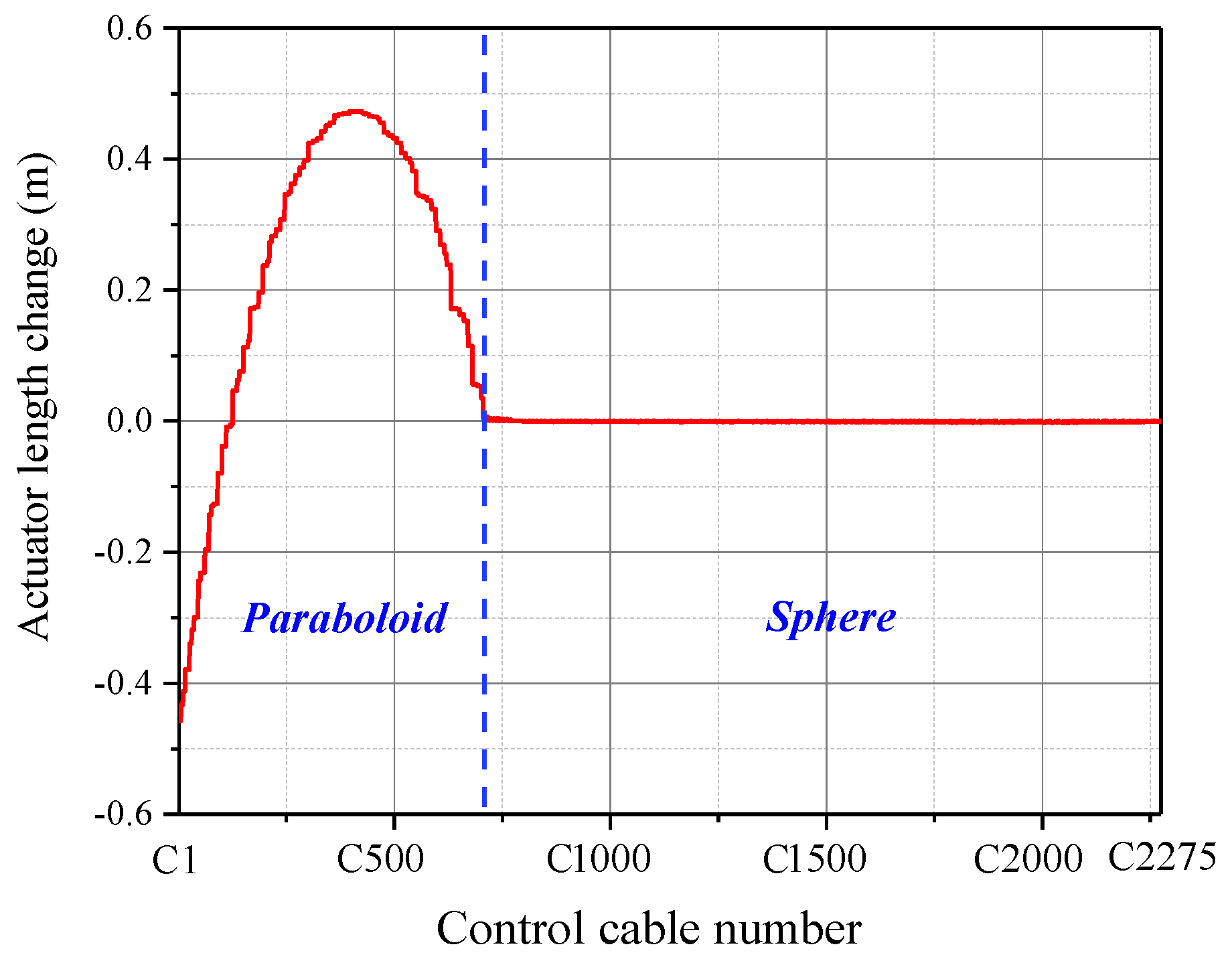
4.3. Form Deformation Analysis Results
5. Conclusions
- (1)
- The basic principle and flow for solving the static equilibrium of the active reflector cable-net structure based on VFIFE were proposed. The core idea was to dissipate energy by applying virtual damping. Through the combined effect of forced displacement and actuator length changes, the cable-net structure can achieve the target form and the equilibrium state can be also obtained.
- (2)
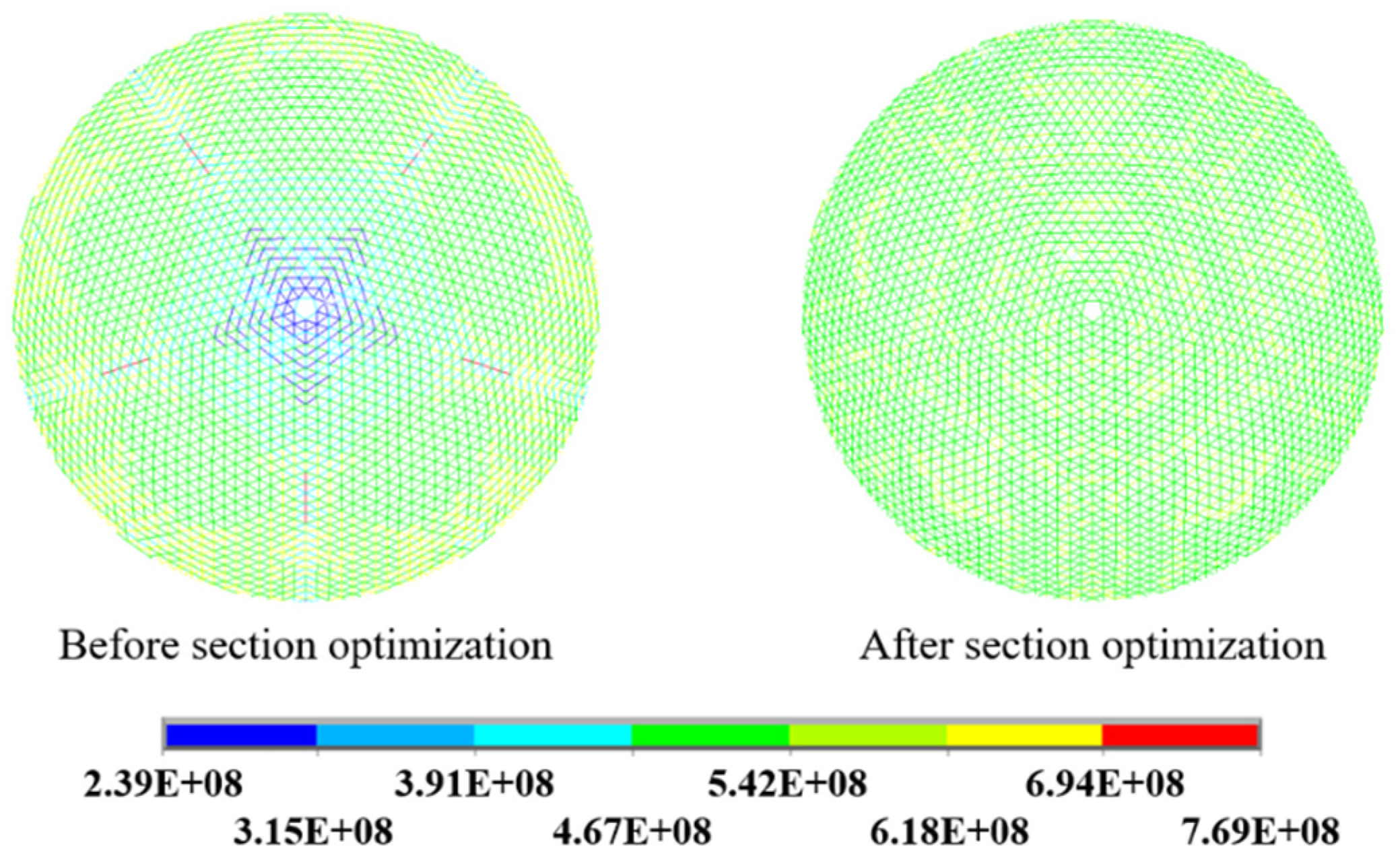
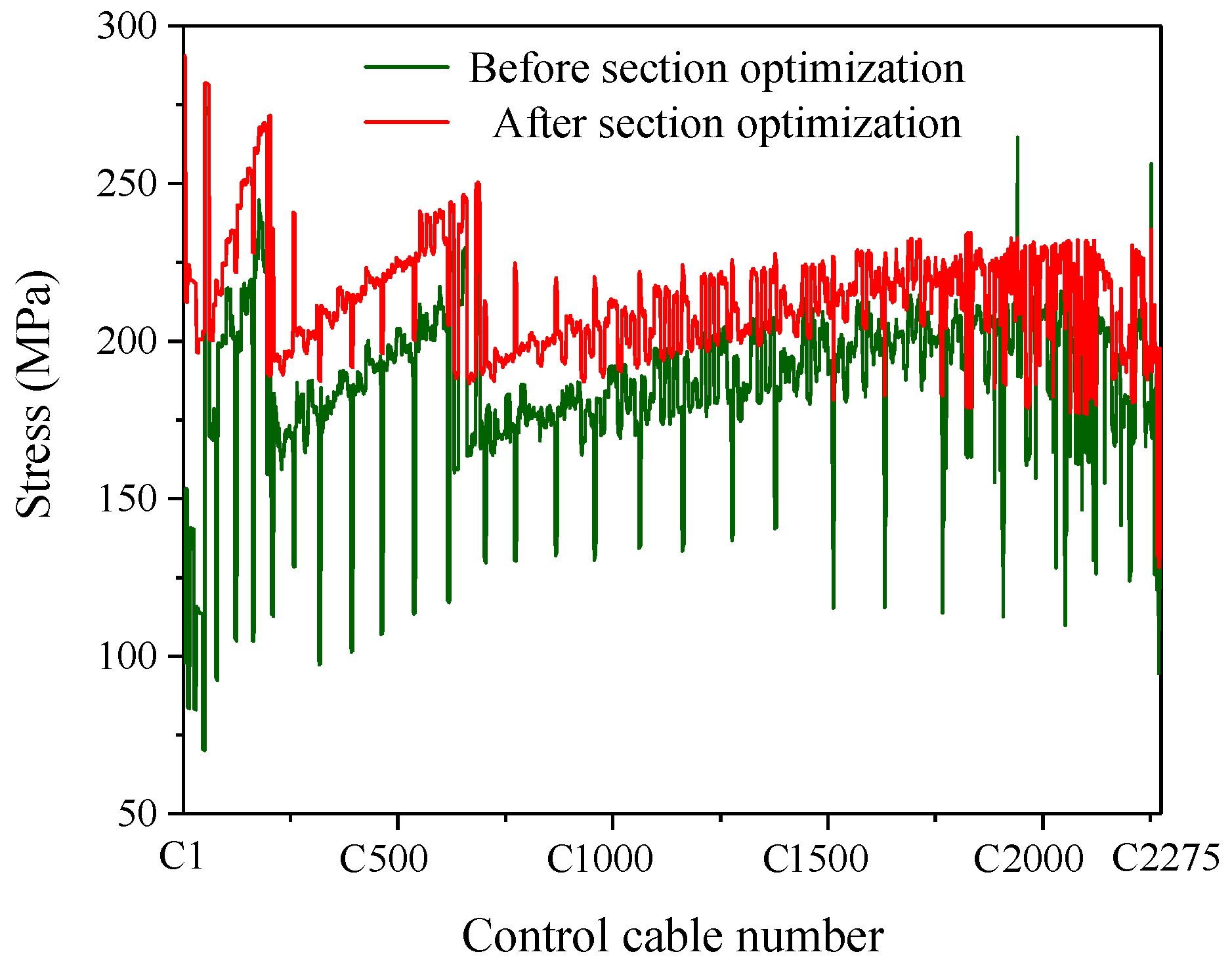
- The approach proposed can help achieve a uniform cable tension design based on the idea of “equal-tension replacement” in the form-finding analysis. The RMS error between the final form and the theoretical form was only 0.0097 mm. In addition, the stress of both main cables and control stress was optimized to be uniform. While grasping the stress distribution of various cables through the form-finding analysis, the length change of the actuators was also obtained.
- (3)
- For the form deformation analysis, the change process from the reference state to the target working state was successfully simulated by the proposed approach. The final form obtained conforms to the designated working paraboloid. The RMS error between the final form and the theoretical paraboloid was only 0.0133 mm. Moreover, the stress of various cables and the length change of the actuators were also obtained. The above conclusions provide an important basis for the actual operation and the control optimization of the active reflector. This approach is also applicable to the form analysis of similar cable-net structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nan, R.; Peng, B. A Chinese concept for the 1 km2 radio telescope. Acta Astronaut. 2000, 46, 667–675. [Google Scholar] [CrossRef]
- Linkwitz, K.; Schek, H.J. Einige bemerkungenzur berechnung von vorgespannten seilnetzkon struktionen. Arch. Appl. Mech. 1974, 40, 145–158. [Google Scholar]
- Schek, H.J. The force density method for form finding and computation of general networks. Comput. Methods Appl. Mech. Eng. 1974, 3, 115–134. [Google Scholar] [CrossRef]
- Zhang, J.; Ohsaki, M. Adaptive force density method for form-finding problem of tensegrity structures. Int. J. Solids Struct. 2006, 43, 5658–5673. [Google Scholar] [CrossRef]
- Tanaka, H.; Shimozono, N.; Natori, M.C. A design method for cable network structures considering the flexibility of supporting structures. Trans. Jpn. Soc. Aeronaut. Space Sci. 2007, 50, 267–273. [Google Scholar] [CrossRef]
- Morterolle, S.; Maurin, B.; Quirant, J.; Dupuy, C. Numerical form-finding of geotensoid tension truss for mesh reflector. Acta Astronaut. 2012, 76, 154–163. [Google Scholar] [CrossRef]
- Maddio, P.D.; Meschini, A.; Sinatra, R.; Cammarata, A. An optimized form-finding method of an asymmetric large deployable reflector. Eng. Struct. 2019, 181, 27–34. [Google Scholar] [CrossRef]
- Yang, D.; Liu, J.; Zhang, Y.; Zhang, S. Optimal surface profile design of deployable mesh reflectors via a force density strategy. Acta Astronaut. 2016, 130, 137–146. [Google Scholar] [CrossRef]
- Thomson, M.W. The astromesh deployable reflector. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Carpinteria, CA, USA, 11–16 July 1999. [Google Scholar]
- Wang, X.; Cai, J.; Yang, R.; Feng, J. Form-finding of deployable mesh reflectors using dynamic relaxation method. Acta Astronaut. 2018, 151, 380–388. [Google Scholar] [CrossRef]
- Yang, G.; Yang, D.; Zhang, Y.; Du, J. Form-finding design of cable-mesh reflector antennas with minimal length configuration. Aerosp. Sci. Technol. 2017, 63, 9–17. [Google Scholar] [CrossRef]
- Day, A.S. An introduction to dynamic relaxation. Engineer 1965, 219, 218–221. [Google Scholar]
- Barnes, M.R. Form finding and analysis of tension structures by dynamic relaxation. Int. J. Space Struct. 1999, 14, 89–104. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Arabi, E.; Masoodi, A.R. Nonlinear analysis of FG-sandwich plates and shells. Aerosp. Sci. Technol. 2019, 87, 178–189. [Google Scholar] [CrossRef]
- Ma, X.; Song, Y.; Li, Z.; Li, T.; Wang, Z.; Deng, H. Mesh reflector antennas: Form-finding analysis review. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar]
- Li, T.; Jiang, J.; Deng, H.; Lin, Z.; Wang, Z. Form-finding methods for deployable mesh reflector antennas. Chin. J. Aeronaut. 2013, 26, 1276–1282. [Google Scholar] [CrossRef]
- Yuan, S.; Yang, B. The fixed nodal position method for form finding of high-precision lightweight truss structures. Int. J. Solids Struct. 2019, 161, 82–95. [Google Scholar] [CrossRef]
- Shi, H.; Yuan, S.; Yang, B. New methodology of surface mesh geometry design for deployable mesh reflectors. J. Spacecr. Rockets 2018, 55, 266–281. [Google Scholar] [CrossRef]
- Yuan, S.; Yang, B.; Fang, H. The projecting surface method for improvement of surface accuracy of large deployable mesh reflectors. Acta Astronaut. 2018, 151, 678–690. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Tian, Q.; Hu, H.; Song, Y. Dynamics of a deployable mesh reflector of satellite antenna: Form-finding and modal analysis. J. Comput. Nonlinear Dyn. 2016, 11, 041017. [Google Scholar] [CrossRef]
- Nie, R.; He, B.; Zhang, L.; Fang, Y. Deployment analysis for space cable net structures with varying topologies and parameters. Aerosp. Sci. Technol. 2017, 68, 1–10. [Google Scholar] [CrossRef]
- Nie, R.; He, B.; Hodges, D.H.; Ma, X. Integrated form finding method for mesh reflector antennas considering the flexible truss and hinges. Aerosp. Sci. Technol. 2019, 84, 926–937. [Google Scholar] [CrossRef]
- Ting, E.C.; Shi, C.; Wang, Y.K. Fundamentals of a vector form intrinsic finite element: Part I. Basic procedure and a planar frame element. J. Mech. 2004, 20, 113–122. [Google Scholar] [CrossRef]
- Ting, E.C.; Shi, C.; Wang, Y.K. Fundamentals of a vector form intrinsic finite element: Part II. Plane solid element. J. Mech. 2004, 20, 123–132. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y.K.; Ting, E.C. Fundamentals of a vector form intrinsic finite element: Part III. Convected material frame and examples. J. Mech. 2004, 20, 133–143. [Google Scholar] [CrossRef]
- Wu, T.Y.; Wang, C.Y.; Chuang, C.C.; Ting, E.C. Motion analysis of 3D membrane structures by a vector form intrinsic finite element. J. Chin. Inst. Eng. 2007, 30, 961–976. [Google Scholar] [CrossRef]
- Wu, T.Y.; Ting, E.C. Large deflection analysis of 3D membrane structures by a 4-node quadrilateral intrinsic element. Thin-Walled Struct. 2008, 46, 261–275. [Google Scholar] [CrossRef]
- Hou, X.; Fang, Z.; Zhang, X. Static contact analysis of spiral bevel gear based on modified VFIFE (vector form intrinsic finite element) method. Appl. Math. Model. 2018, 60, 192–207. [Google Scholar] [CrossRef]
- Lien, K.H.; Chiou, Y.J.; Wang, R.Z.; Hsiao, P.A. Vector form intrinsic finite element analysis of nonlinear behavior of steel structures exposed to fire. Eng. Struct. 2010, 32, 80–92. [Google Scholar] [CrossRef]
- Lien, K.H.; Chiou, Y.J.; Wang, R.Z.; Hsiao, P.A. Nonlinear behavior of steel structures considering the cooling phase of a fire. J. Constr. Steel Res. 2009, 65, 1776–1786. [Google Scholar] [CrossRef]
- Duan, Y.F.; Wang, S.M.; Wang, R.Z.; Wang, C.Y.; Ting, E.C. Vector form intrinsic finite element based approach to simulate crack propagation. J. Mech. 2017, 33, 797–812. [Google Scholar] [CrossRef]
- Xu, L.; Lin, M. Numerical study on critical axial forces of upheaval buckling for initially stressed submarine pipelines on uneven seabed. Ocean Eng. 2017, 145, 344–358. [Google Scholar] [CrossRef][Green Version]
- Xu, L.; Lin, M. On the critical axial forces of upheaval buckling for imperfect submarine pipelines. Eng. Struct. 2017, 147, 692–704. [Google Scholar] [CrossRef]
- China Academy of Building Research. Technical Specification for Cable Structures; China Academy of Building Research: Beijing, China, 2012; JGJ 257-2012. [Google Scholar]
- Qian, H. Theoretical and Experimental Research on Supporting Structure of FAST Reflector. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China, 2007. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Zhang, Y.; Qian, H.; Zhang, K.; Wang, H. An Effective Form Analysis Approach for Designing and Optimizing a Cable-Net Structure of a Giant Active Reflector. Aerospace 2021, 8, 269. https://doi.org/10.3390/aerospace8090269
Chen D, Zhang Y, Qian H, Zhang K, Wang H. An Effective Form Analysis Approach for Designing and Optimizing a Cable-Net Structure of a Giant Active Reflector. Aerospace. 2021; 8(9):269. https://doi.org/10.3390/aerospace8090269
Chicago/Turabian StyleChen, Deshen, Yan Zhang, Hongliang Qian, Kai Zhang, and Huajie Wang. 2021. "An Effective Form Analysis Approach for Designing and Optimizing a Cable-Net Structure of a Giant Active Reflector" Aerospace 8, no. 9: 269. https://doi.org/10.3390/aerospace8090269
APA StyleChen, D., Zhang, Y., Qian, H., Zhang, K., & Wang, H. (2021). An Effective Form Analysis Approach for Designing and Optimizing a Cable-Net Structure of a Giant Active Reflector. Aerospace, 8(9), 269. https://doi.org/10.3390/aerospace8090269




