Hybrid Rockets as Post-Boost Stages and Kick Motors
Abstract
:1. Introduction
1.1. State of Hybrid Rocket Development
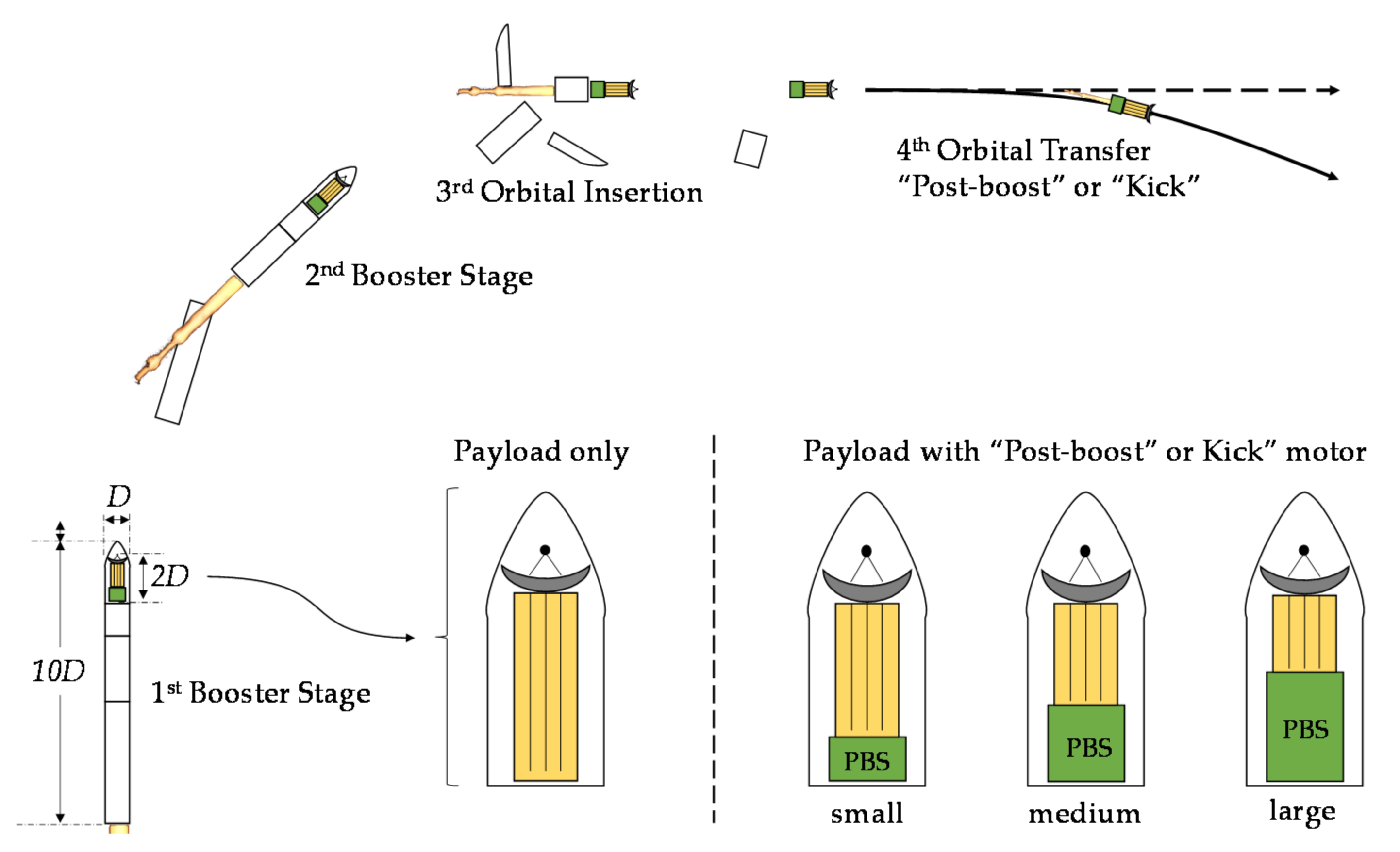
1.2. Post-Boost Stages and Kick Motors
1.3. Considerations for Hybrid Rocket-Based Post-Boost Stages and Kick Motors
2. Materials and Methods
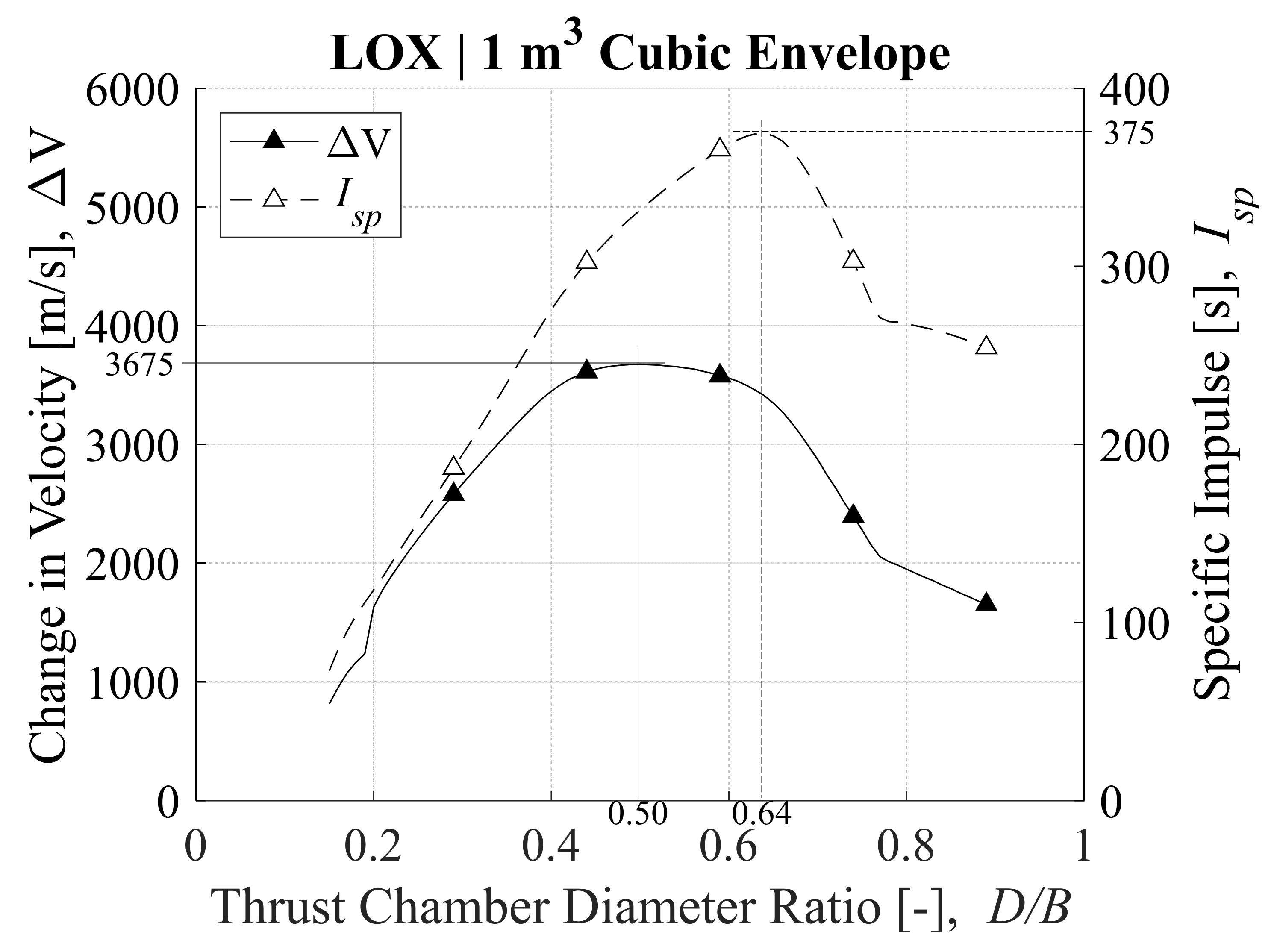
2.1. Maximizing the Change in Velocity, ΔV
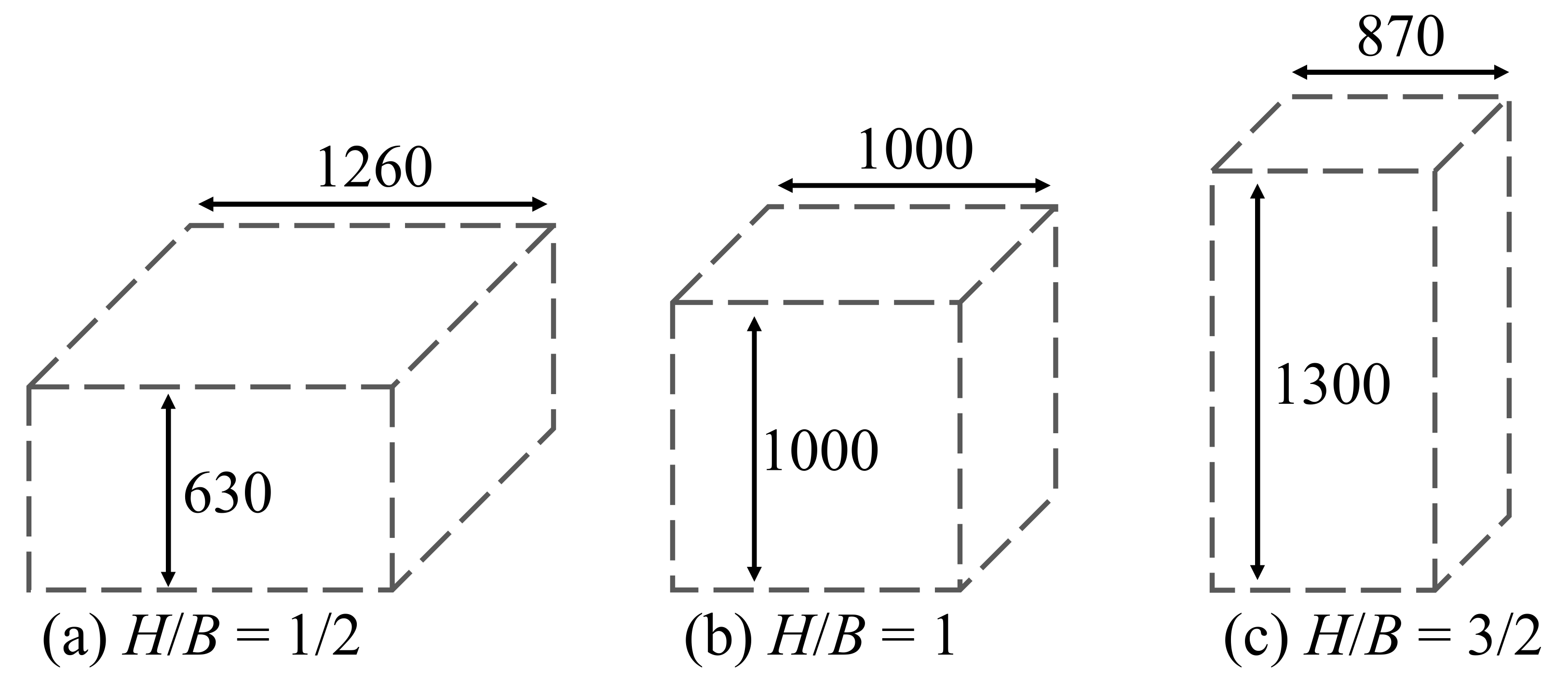
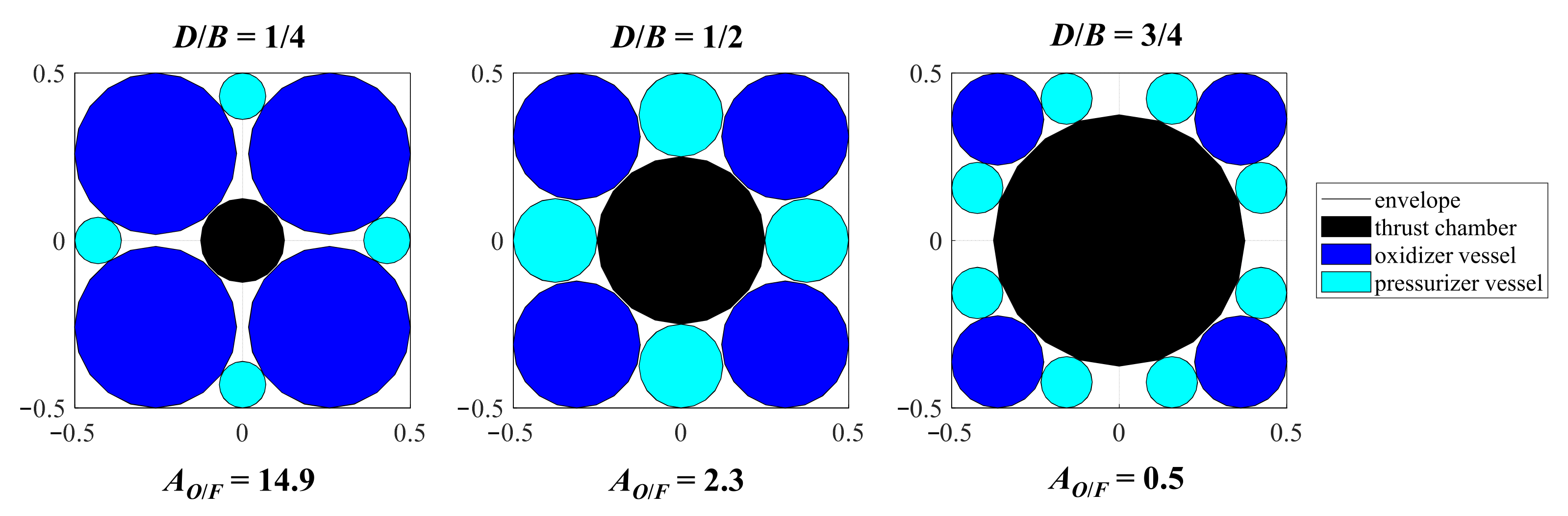
2.2. The Envelopes and Their Parametrization
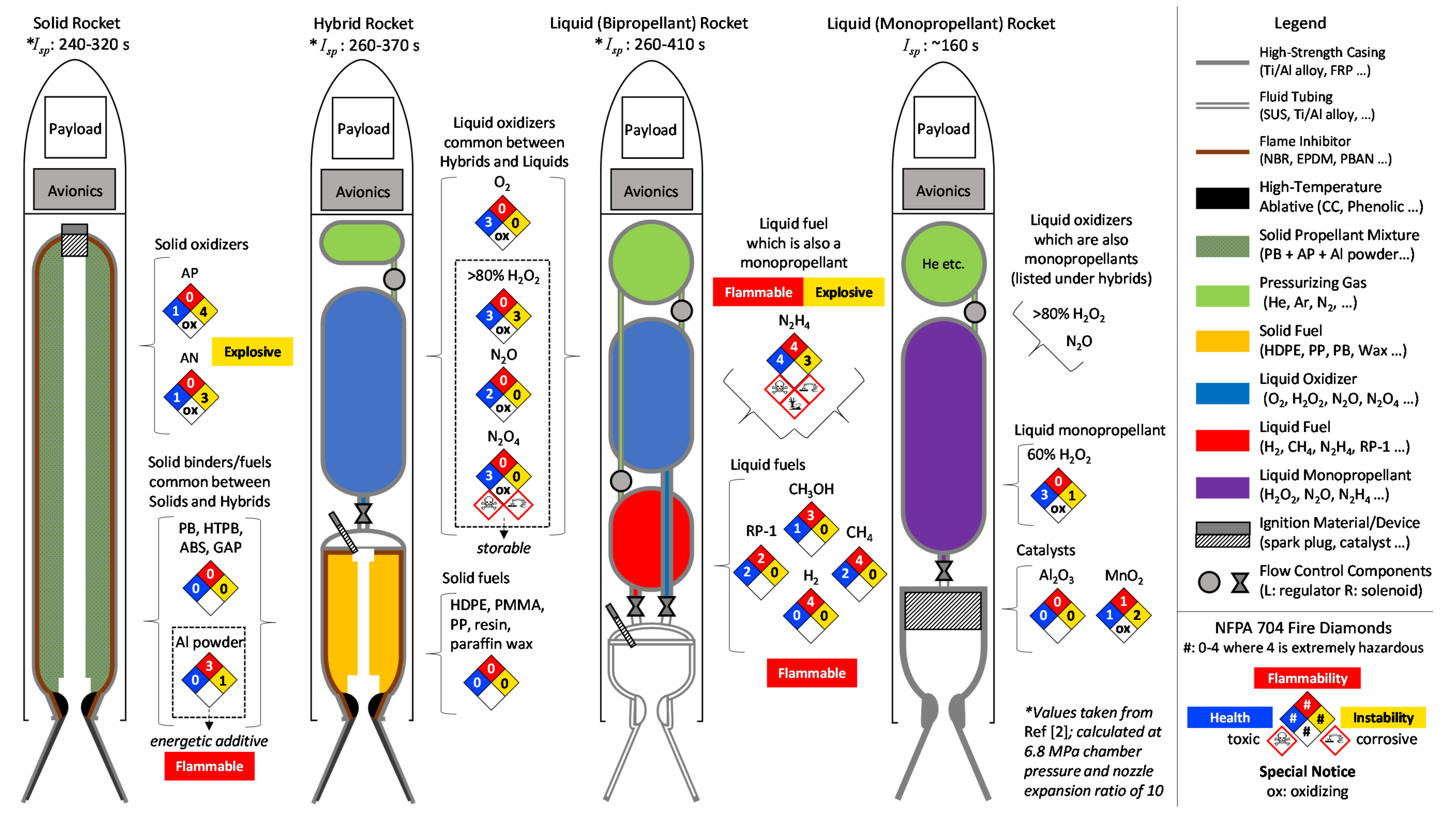
2.3. The Oxidizers, Their Theoretical Isp, and Effect on Motor Configuration
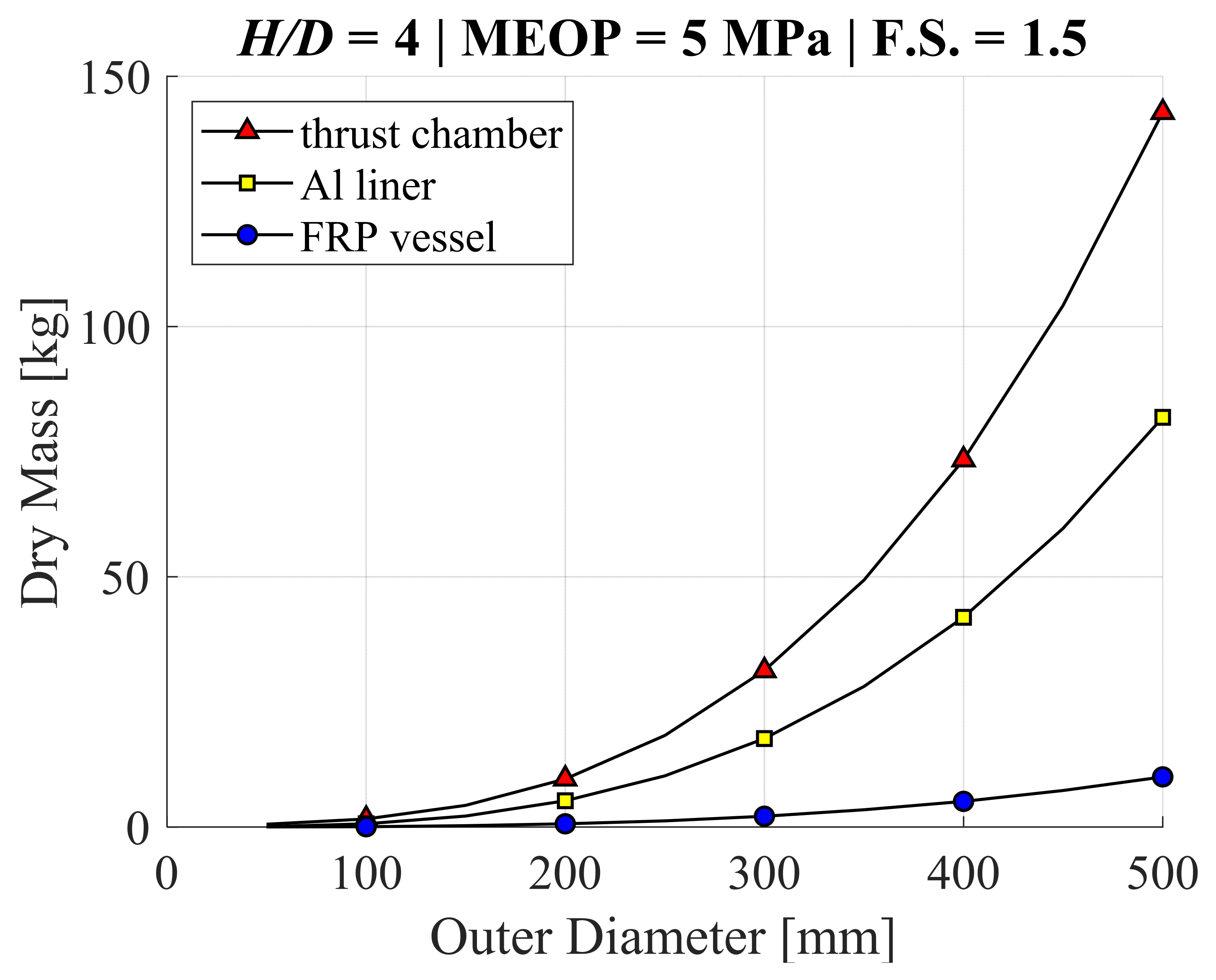
2.4. Standardized Formulation of Motor Component Size and Mass
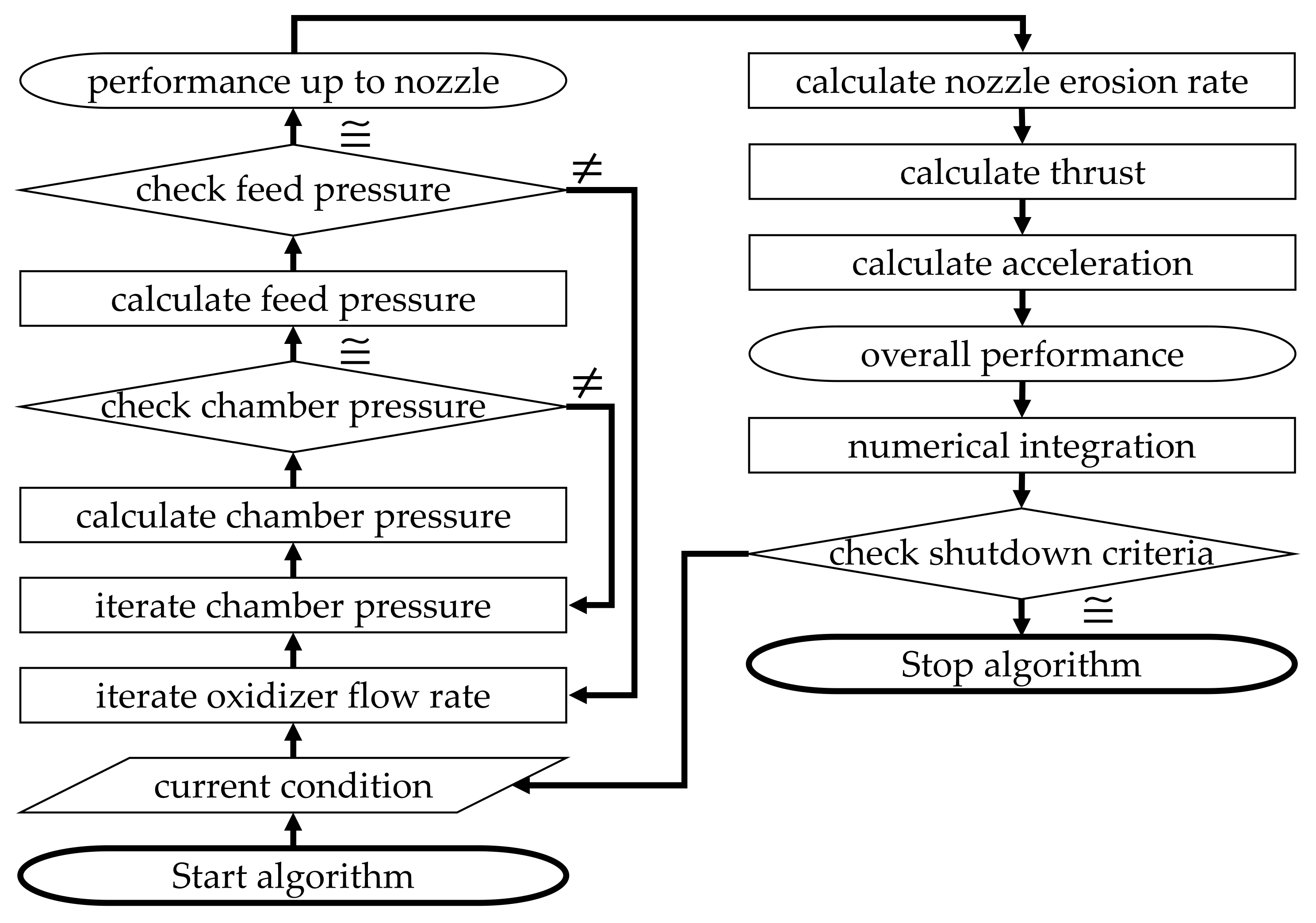
2.5. Internal Ballistics Simulation Algorithm
3. Results
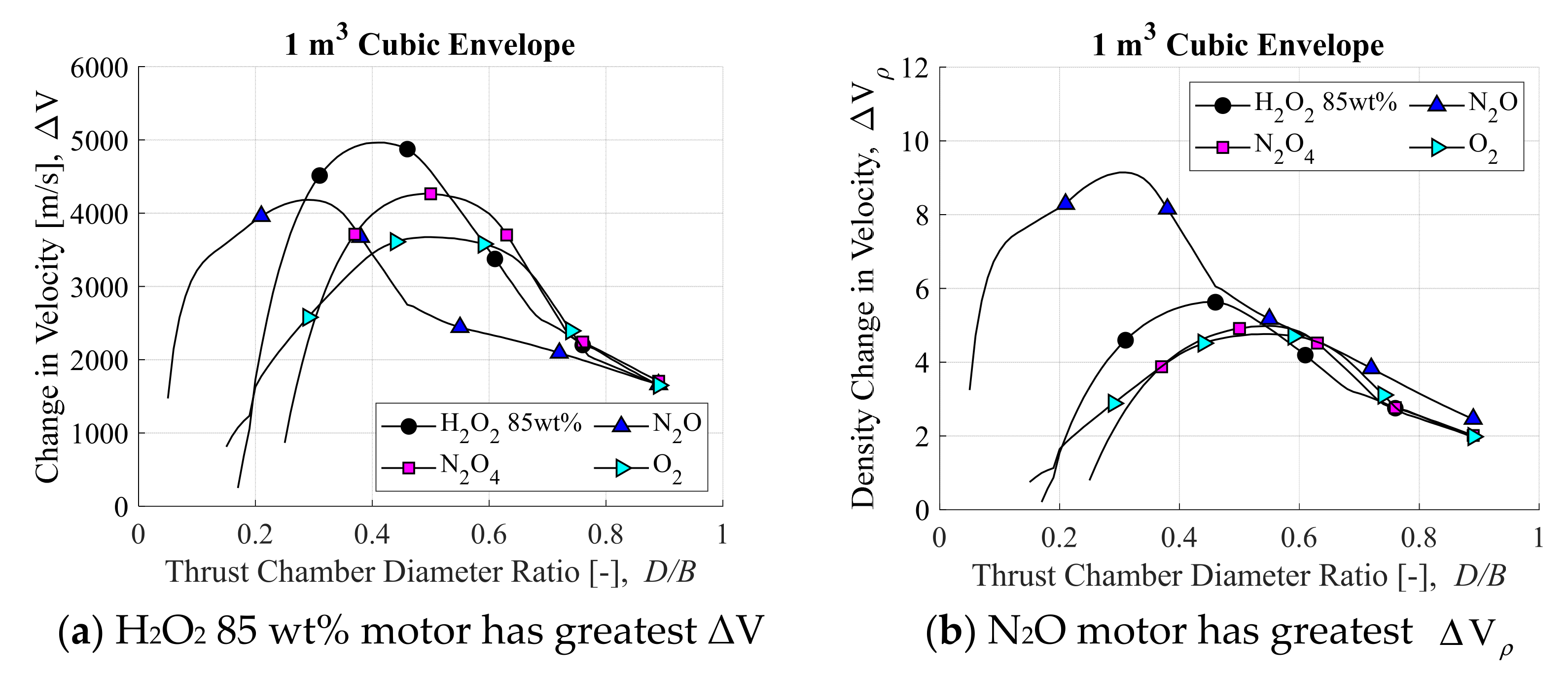
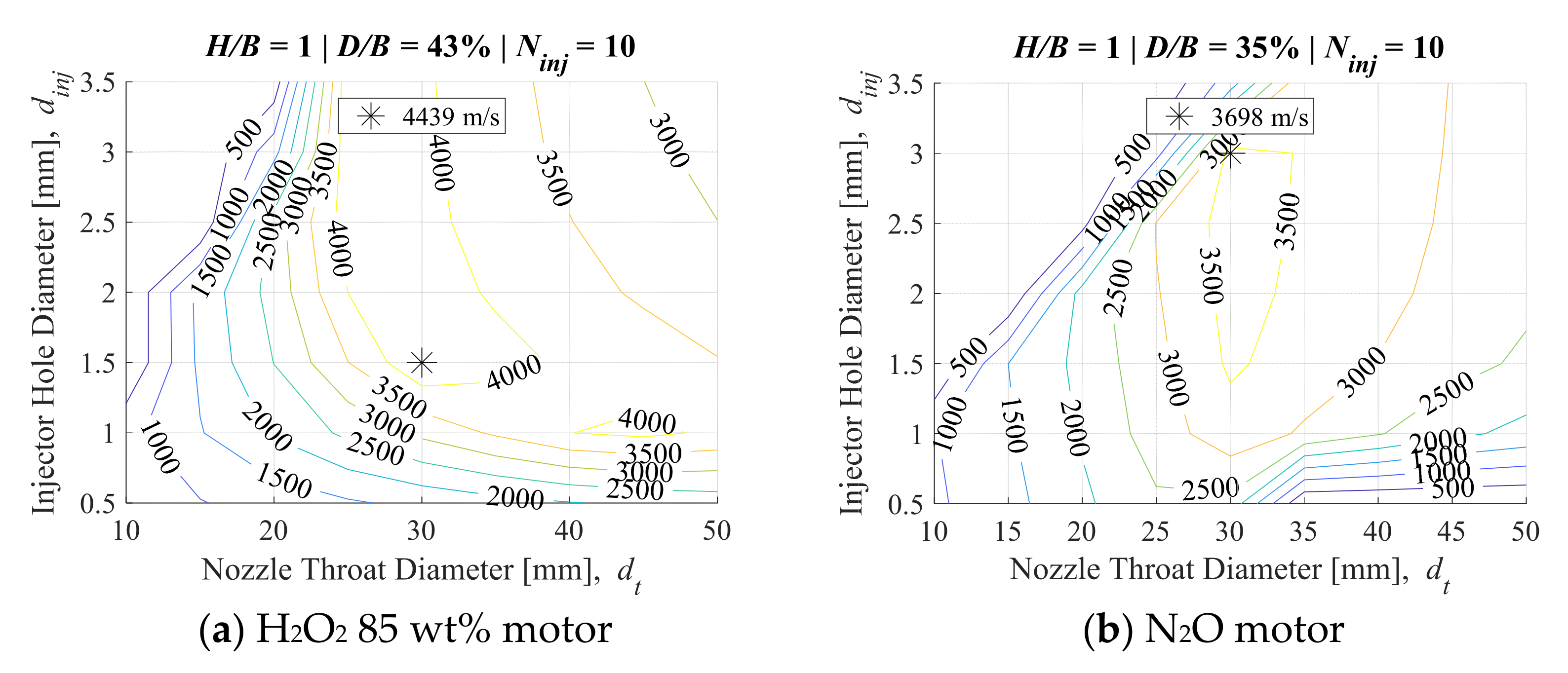
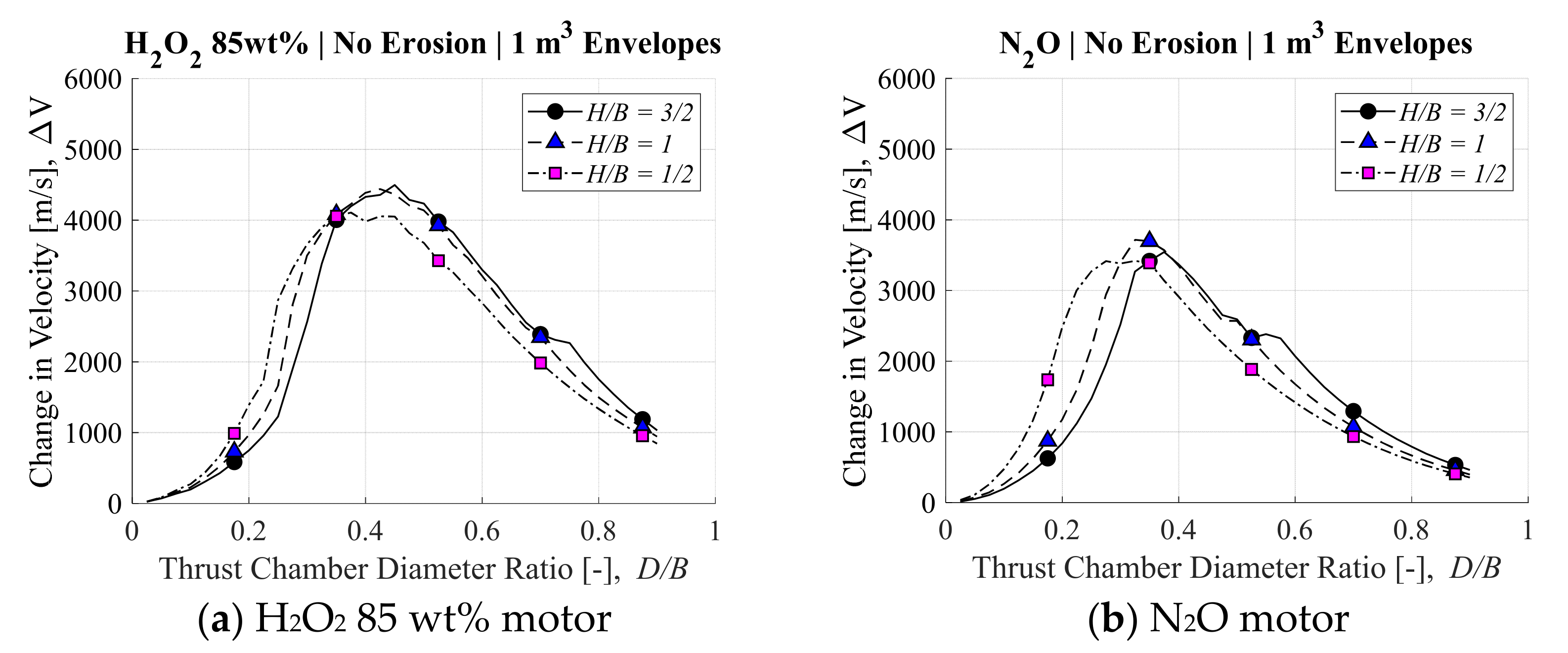
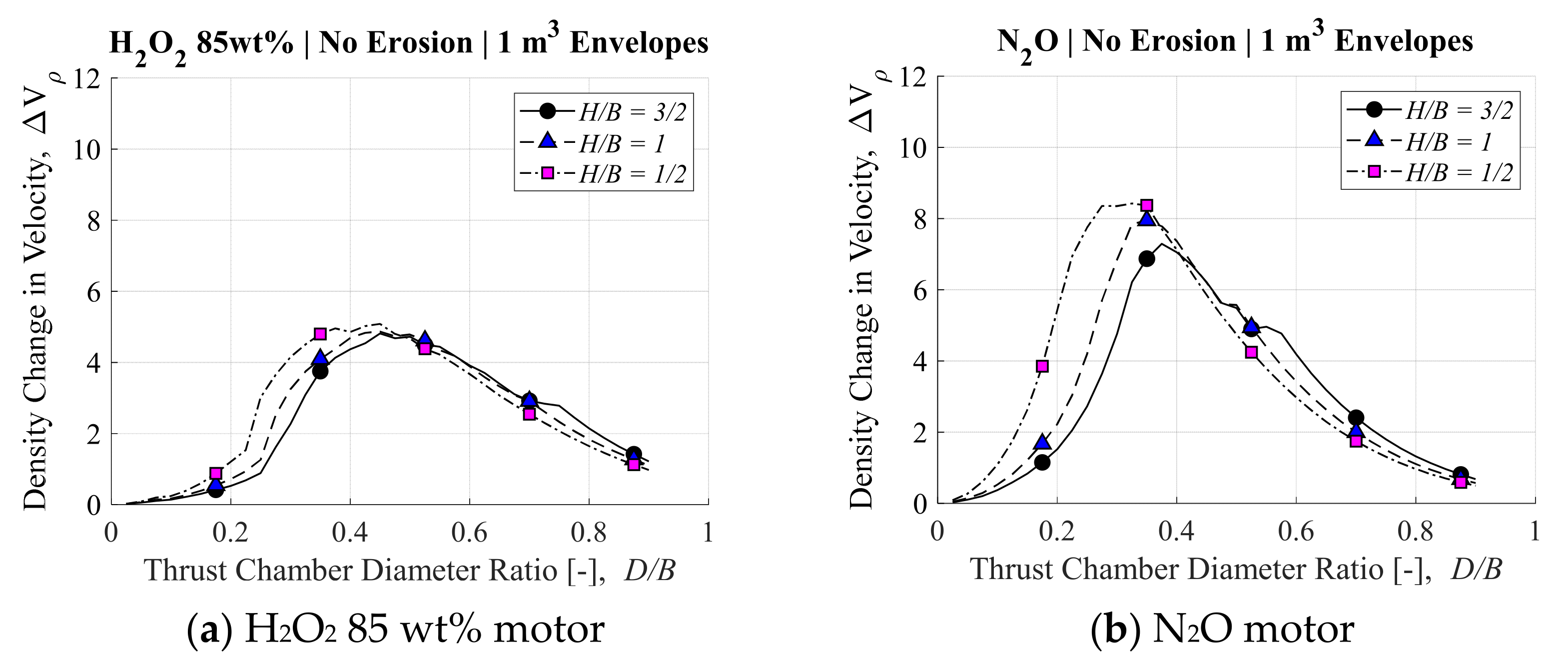
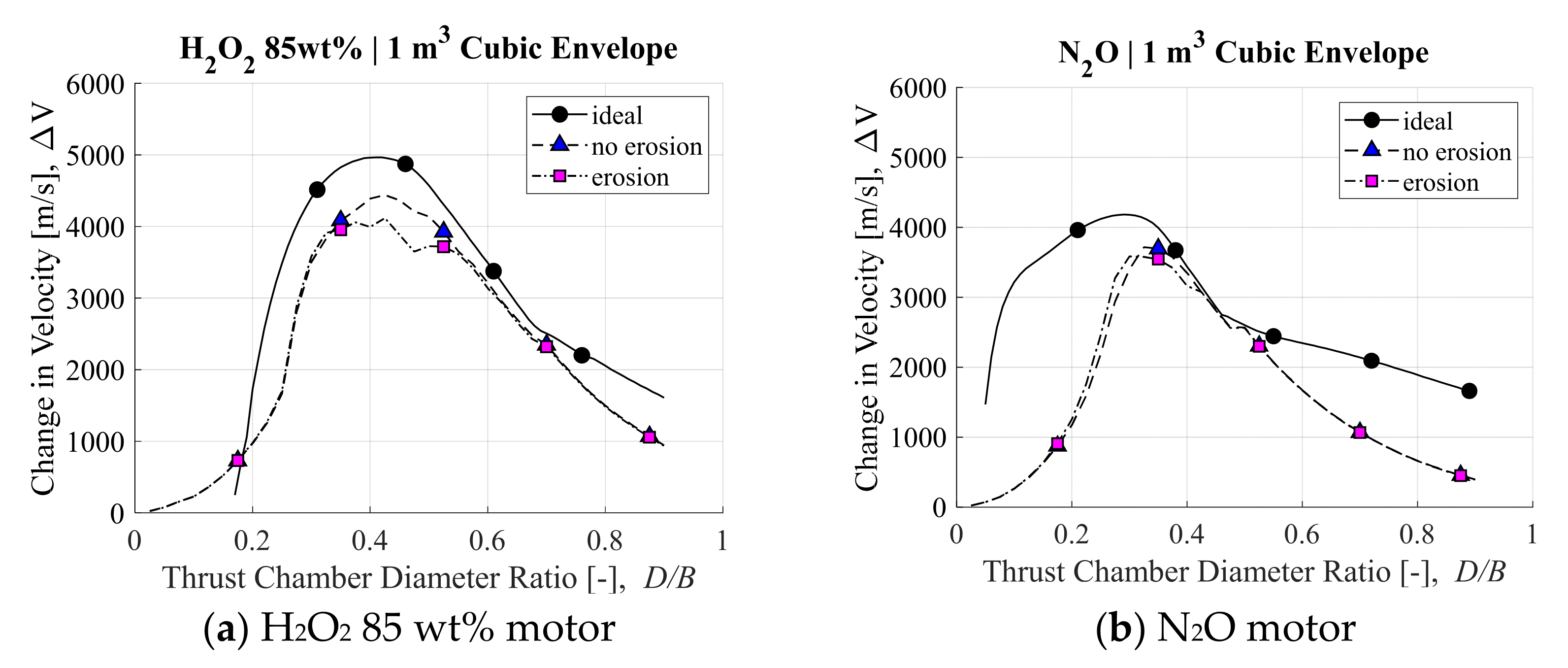
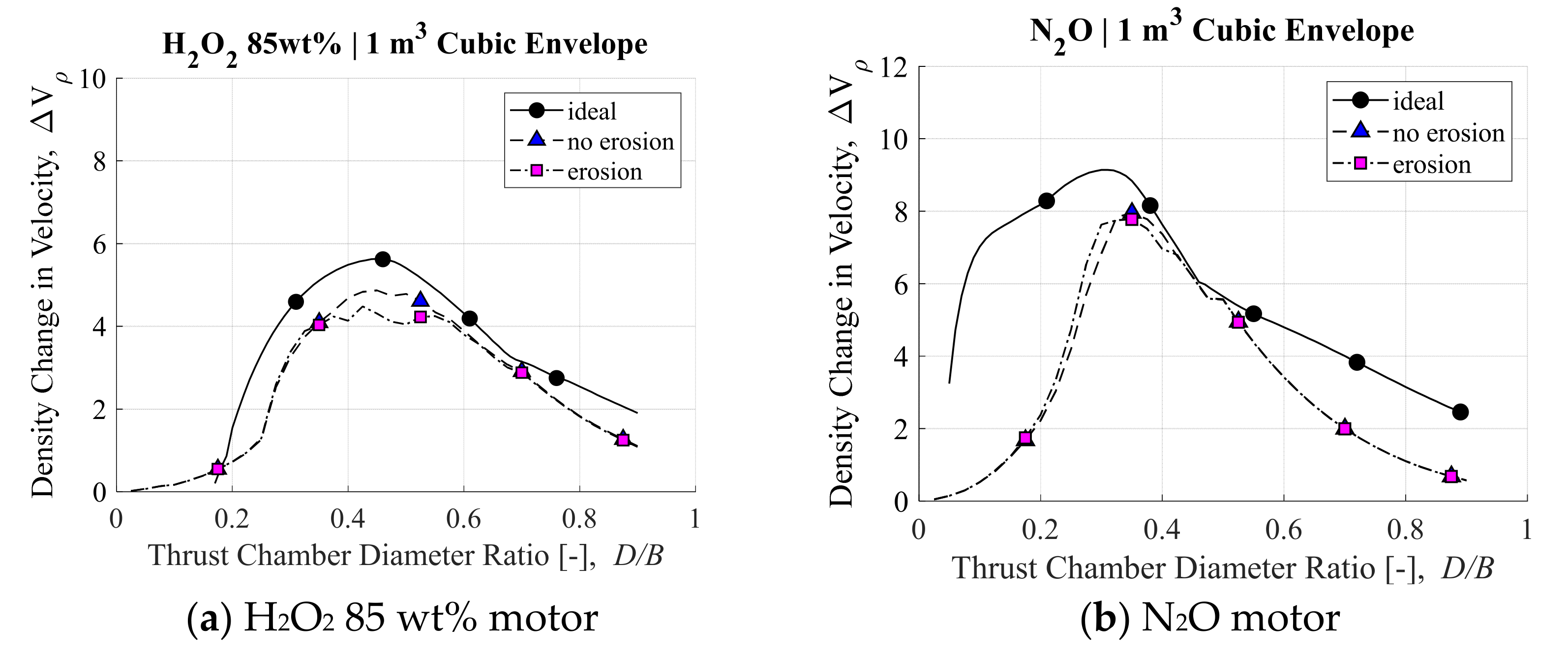
3.1. Ideal Post-Boost Stage and Kick Motor Results
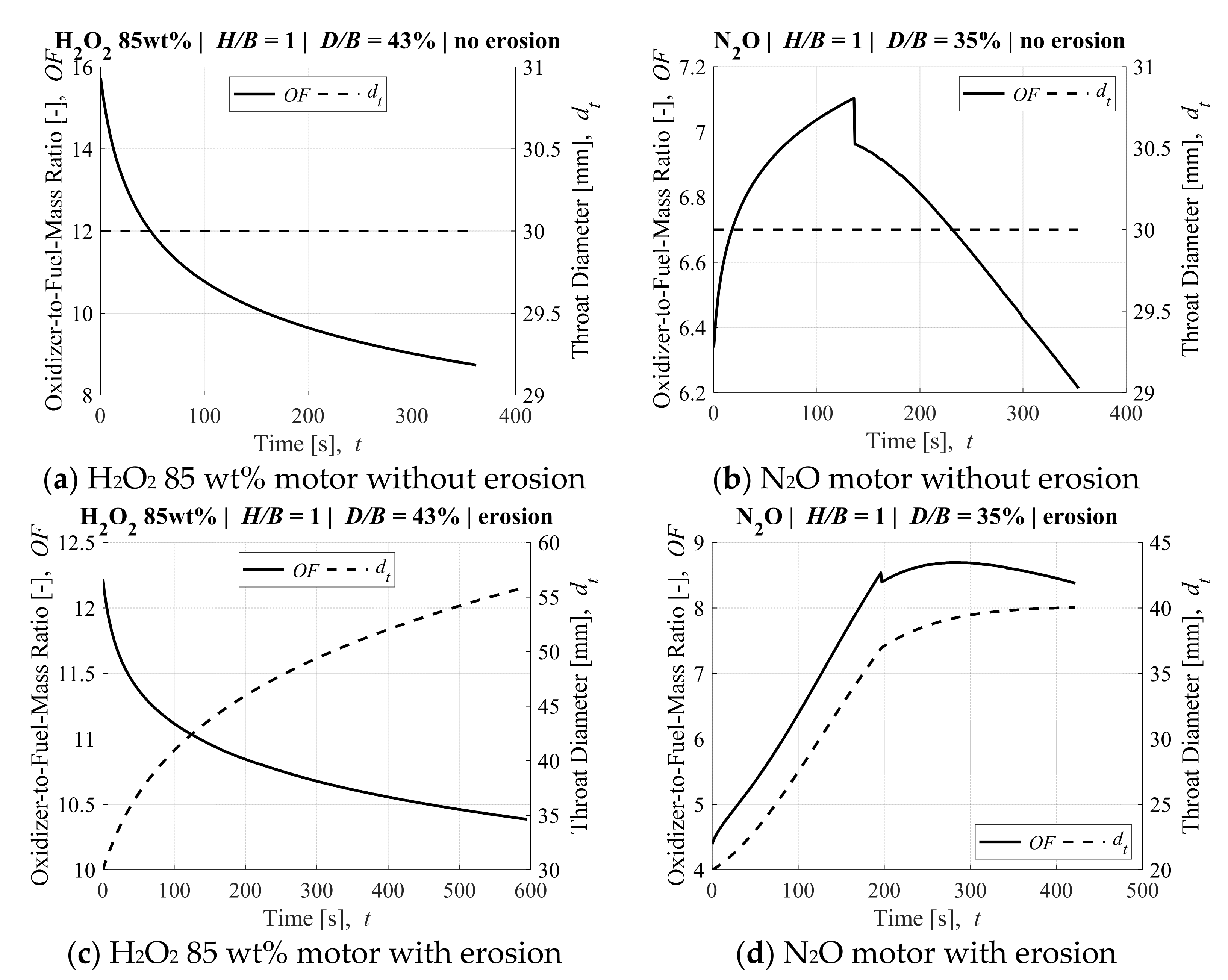
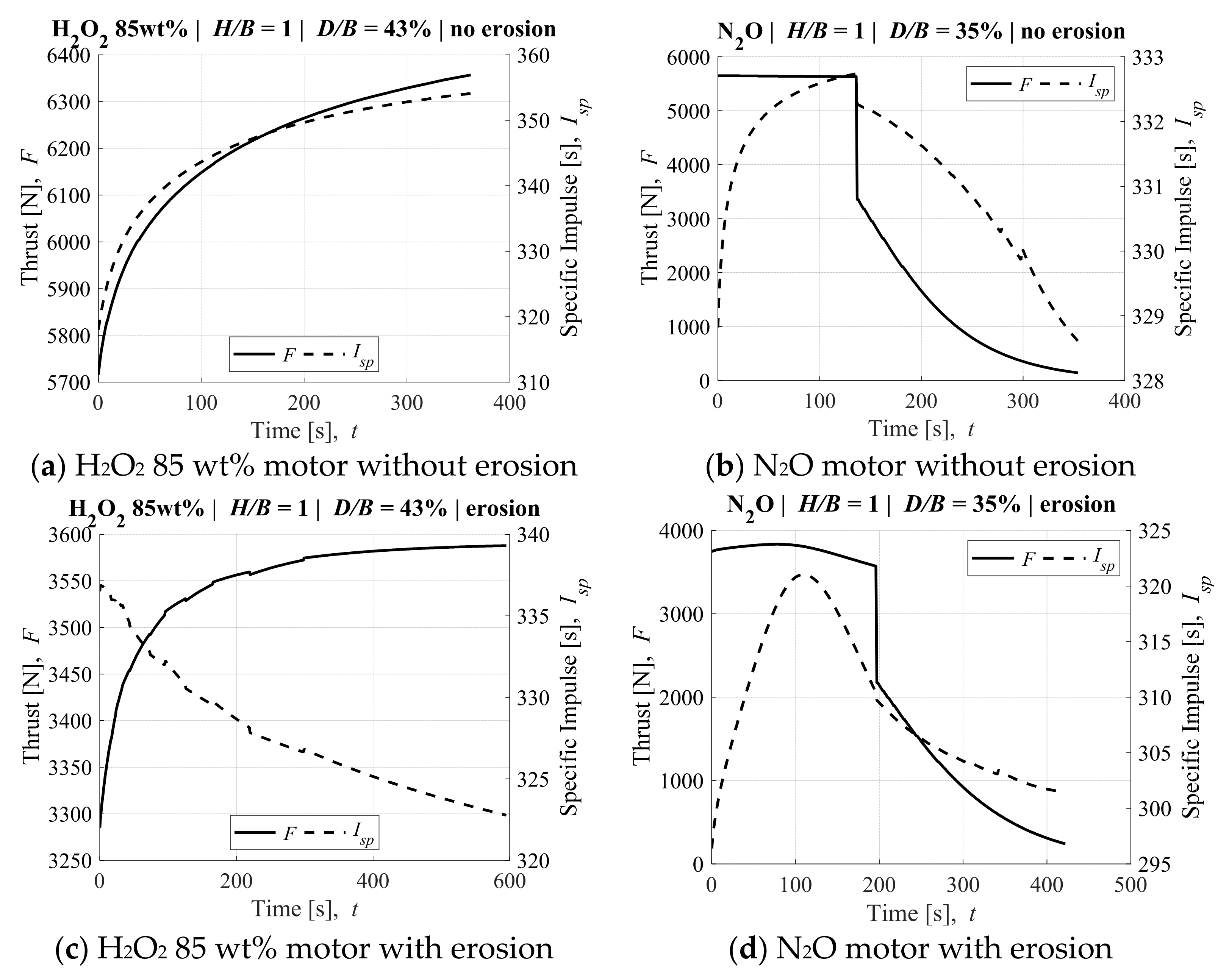
3.2. Impact of O/F Shift and Nozzle Erosion on Ideal Performance
4. Discussion
4.1. Technologies for Reducing O/F Shift and Nozzle Erosion
4.2. Nonintuitive Nature of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a, m, n | fuel regression rate constants, Equation (5) |
| A | area, m2 |
| AO/F | oxidizer-to-fuel cross-sectional area ratio |
| b, E, n, β1, β2,β3 | nozzle erosion rate constants, Equation (7) |
| c* | characteristic exhaust velocity, m/s |
| CD, CG | dimensionless flow coefficients |
| d | inner diameter, m |
| D | outer diameter, m or binary mass diffusivity, m2/s |
| D/B | (thrust chamber) diameter-to-base ratio |
| F | thrust, N |
| F.S. | factor of safety |
| g | (Earth) gravitational acceleration, ≅9.8 m/s2 |
| H/B | (envelope) height-to-base ratio |
| H/D | (envelope) height-to-(thrust chamber) diameter ratio |
| Isp | specific impulse, s |
| MEOP | maximum expected operation pressure, Pa |
| mass flow rate, kg/s | |
| M | (initial) propellant mass, kg |
| M | (initial) wet mass, kg |
| O/F | oxidizer-to-fuel-mass ratio |
| P | pressure, Pa |
| r | nozzle throat or fuel port radius, m |
| Re | Reynolds number |
| Sc | Schmidt number |
| t | (wall) thickness, m |
| T | temperature, K |
| ΔV | change in velocity, m/s |
| ΔVρ | density change in velocity, m4/kg-s |
| ε | nozzle expansion ratio |
| γ | specific heat ratio |
| Φ | equivalence ratio, Φ > 1 is fuel-rich |
| ρ | Density, kg/m3 |
| σ | tensile strength, Pa |
| Subscripts | |
| bs | burning surface |
| c | thrust chamber (position) |
| dw, up | (orifice) downstream, upstream (position) |
| e, t, w | (nozzle) exit, throat, wall (position) |
| fu, n, ox | fuel, nozzle, oxidizer |
| inj | injector |
Appendix A
References
- Altman, D.; Holzman, A. Overview and History of Hybrid Rocket Propulsion. In Fundamentals of Hybrid Rocket Combustion and Propulsion, 1st ed.; Chiaverini, M.J., Kuo, K.K., Eds.; American Institute of Aeronautics and Astronautics: Renton, VA, USA, 2007; Progress in Aeronautics and Astronautics; Volume 218, pp. 1–36. [Google Scholar]
- Chiaverini, M. Review of Solid-Fuel Regression Rate in Classical and Nonclassical Hybrid Rocket Motors. In Fundamentals of Hybrid Rocket Combustion and Propulsion, 1st ed.; Chiaverini, M.J., Kuo, K.K., Eds.; American Institute of Aeronautics and Astronautics: Renton, VA, USA, 2007; Progress in Aeronautics and Astronautics; Volume 218, pp. 37–125. [Google Scholar]
- Story, G.; Arves, J. Flight Testing of Hybrid-Powered Vehicles. In Fundamentals of Hybrid Rocket Combustion and Propulsion, 1st ed.; Chiaverini, M.J., Kuo, K.K., Eds.; American Institute of Aeronautics and Astronautics: Renton, VA, USA, 2007; Progress in Aeronautics and Astronautics; Volume 218, pp. 553–591. [Google Scholar]
- Ansari X-Prize. Available online: https://www.xprize.org/prizes/ansari (accessed on 25 July 2021).
- Brinkmann, P. Rocket Crafters Pivots with New Patents for 3D-Printed Fuel. Available online: https://www.spacedaily.com/reports/Florida_space_startup_Rocket_Crafters_pivots_with_new_patents_for_3D_printed_fuel_999.html (accessed on 25 July 2021).
- Vaya Space. Available online: https://www.vayaspace.com (accessed on 25 July 2021).
- Gilmour Space. Available online: https://www.gspacetech.com (accessed on 25 July 2021).
- Cecil, O.; Majdalani, J. Several Hybrid Rocket Technologies Hit Advanced Test Stages. Aerospace America. Available online: https://aerospaceamerica.aiaa.org/year-in-review/several-hybrid-rocket-technologies-hit-advanced-test-stages (accessed on 25 July 2021).
- Chen, Y.S.; Wu, B. Development of a Small Launch Vehicle with Hybrid Rocket Propulsion. In Proceedings of the AIAA Propulsion and Energy 2018 Forum, Cincinnati, OH, USA, 9–11 July 2018. AIAA-Paper 2018-4835. [Google Scholar]
- Chen, Y.S. Development of Hapith Small Launch Vehicle Based on Hybrid Rocket Propulsion. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IND, USA, 19–22 August 2019. AIAA-Paper 2019-3837. [Google Scholar]
- Faenza, M.G.; Boiron, A.; Haemmerli, B.; Verberne, O. Development of Nucleus Hybrid Propulsion System: Enabling a Successful Flight Demonstration. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IND, USA, 19–22 August 2019. AIAA-Paper 2019-3839. [Google Scholar]
- Schmierer, C.; Kobald, M.; Tomilin, K.; Fischer, U. Low Cost Small-Satellite Access to Space Using Hybrid Rocket Propulsion. Acta Astronaut. 2019, 159, 578–583. [Google Scholar] [CrossRef]
- Henry, C. DLR Spinoff HyImpulse Plans Small Launcher Debut. Available online: https://spacenews.com/dlr-spinoff-hyimpulse-plans-small-launcher-debut-in-2022 (accessed on 25 July 2021).
- Firehawk. Available online: https://www.firehawkaerospace.com (accessed on 25 July 2021).
- Gamal, H.; Matusiewicz, A.; Magiera, R.; Hubert, D.; Karolewski, L.; Zielinski, K. Design, Analysis and Testing of a Hybrid Rocket Engine with a Multi-port Nozzle. In Proceedings of the AIAA Propulsion and Energy 2018 Forum, Cincinnati, OH, USA, 9–11 July 2018. AIAA-Paper 2018-4666. [Google Scholar]
- Space Forest. Available online: https://spaceforest.pl/sir-suborbital-inexpensive-rocket/ (accessed on 25 July 2021).
- T4i Hybrid Propellant. Available online: https://www.t4innovation.com/hybrid-propellant (accessed on 25 July 2021).
- Eilers, S.D.; Whitmore, S.; Peterson, Z. Multiple Use Hybrid Rocket Motor. U.S. Patent US20140026537A1, 30 January 2014. [Google Scholar]
- Whitmore, S.A. Nytrox as “Drop-in” Replacement for Gaseous Oxygen in SmallSat Hybrid Propulsion Systems. Aerospace 2020, 7, 43. [Google Scholar] [CrossRef] [Green Version]
- Jens, E.T.; Cantwell, B.J.; Hubbard, G.S. Hybrid Rocket Propulsion Systems for Outer Planet Exploration Missions. Acta Astronaut. 2016, 128, 119–130. [Google Scholar] [CrossRef]
- Jens, E.T.; Karp, A.C.; Rabinovitch, J.; Nakazono, B. Hybrid Propulsion System Enabling Orbit Insertion Delta-Vs within a 12 U Spacecraft. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019. [Google Scholar]
- Kamps, L.; Molas-Roca, P.; Uchiyama, E.; Takanashi, T.; Nagata, H. Development of N2O/HDPE Hybrid Rocket for Microsatellite Propulsion. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Kamps, L.; Sakurai, K.; Saito, Y.; Nagata, H. Comprehensive Data Reduction for N2O/HDPE Hybrid Rocket Motor Performance Evaluation. Aerospace 2019, 6, 45. [Google Scholar] [CrossRef] [Green Version]
- Karp, A.C.; Nakazono, B.; Shotwell, R.; Benito, J.; Vaughan, D. Technology Development Plan and Preliminary Results for a Low Temperature Hybrid Mars Ascent Vehicle Concept. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. AIAA Paper 2017-4900. [Google Scholar]
- Story, G.; Karp, A.; Nakazono, B.; Evans, B.; Whittinghill, G. Mars Ascent Vehicle Hybrid Propulsion Effort. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–28 August 2020. AIAA Paper 2020-3727. [Google Scholar]
- Process for Limiting Orbital Debris. NASA-STD-8719.14A. 2011. Available online: https://explorers.larc.nasa.gov/HPMIDEX/pdf_files/10_nasa-std-8719.14a_with_change_1.pdf (accessed on 1 July 2021).
- Marks, P. Dodging Debris. Aerospace America. Available online: https://aerospaceamerica.aiaa.org/features/dodging-debris (accessed on 25 July 2021).
- Molas-Roca, P. Design of Scalable Hybrid Rocket Motor for Space Propulsion Applications. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Gordon, S.; McBride, B. Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications; National Aeronautics and Space Administration: Lewis Research Center, OH, USA, 1994; NASA RP-1311. [Google Scholar]
- Kamps, L.; Hirai, S.; Sakurai, K.; Viscor, T.; Saito, Y.; Guan, R.; Isochi, H.; Adachi, N.; Itoh, M.; Nagata, H. Investigation of Graphite Nozzle Erosion in Hybrid Rockets Using Oxygen/High-Density Polyethylene. J. Propuls. Power 2020, 36, 423–434. [Google Scholar] [CrossRef]
- Kamps, L.; Sakurai, K.; Ozawa, K.; Nagata, H. Investigation of Graphite Nozzle Erosion in Hybrid Rockets Using N2O/HDPE. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. AIAA Paper 2019-4264. [Google Scholar]
- Ito, S.; Kamps, L.; Nagata, H. Fuel Regression Characteristics in Hybrid Rockets Using Nitrous Oxide/High-Density Polyethylene. J. Propuls. Power 2020, 37, 342–348. [Google Scholar] [CrossRef]
- Carmicino, C.; Sorge, A.R. Role of Injection in Hybrid Rockets Regression Rate Behavior. J. Propuls. Power 2005, 21, 606–612. [Google Scholar] [CrossRef]
- Zimmerman, J.E.; Waxman, B.S.; Cantwell, B.J.; Zilliac, G.G. Review and Evaluation of Models for Self-Pressurizing Propellant Tank Dynamics. In Proceedings of the 49th AIAA/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013. AIAA Paper 2013-4045. [Google Scholar]
- Nagata, H.; Teraki, H.; Saito, Y.; Kanai, R.; Yasukochi, H.; Wakita, M.; Totani, T. Verification Firings of End-Burning Type Hybrid Rockets. J. Propuls. Power 2017, 33, 1473–1477. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Yokoi, T.; Yasukochi, H.; Soeda, K.; Totani, T.; Wakita, M.; Nagata, H. Fuel Regression Characteristics of a Novel Axial-Injection End-Burning Hybrid Rocket. J. Propuls. Power 2018, 34, 247–259. [Google Scholar] [CrossRef]
- Hitt, M.; Frederick, R. Testing and Modeling of a Porous Axial-Injection, End-Burning Hybrid Motor. J. Propuls. Power 2016, 32, 834–843. [Google Scholar] [CrossRef] [Green Version]
- Hitt, M.; Frederick, R. Experimental Evaluation of a Nitrous-Oxide Axial-Injection, End-Burning Hybrid Motor. J. Propuls. Power 2017, 33, 1555–1560. [Google Scholar] [CrossRef]
- Saito, Y.; Kimino, M.; Tsuji, A.; Okutani, Y.; Soeda, K.; Nagata, H. High Pressure Fuel Regression Characteristics of Axial-Injection End-Burning Hybrid Rockets. J. Propuls. Power 2019, 35, 328–341. [Google Scholar] [CrossRef]
- Suzuki, S.; Tsuji, A.; Soeda, K.; Kamps, L.; Nagata, H. Influence of Port Manufacturing Accuracy on Backfiring in Axial-Injection End-Burning Hybrid Rocket. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. AIAA Paper 2021-3516. [Google Scholar]
- Nakagawa, I.; Kishizato, D.; Koinuma, Y.; Tanaka, S. Demonstration of an Alternating-intensity Swirling Oxidizer Flow Type Hybrid Rocket Function. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IND, USA, 19–22 August 2019. AIAA-Paper 2019-4093. [Google Scholar]
- Ozawa, K.; Kitagawa, K.; Aso, S.; Shimada, T. Hybrid Rocket Firing Experiments at Various Axial-Tangential Oxidizer-Flow-Rate Ratios. J. Propuls. Power 2019, 35, 94–108. [Google Scholar] [CrossRef]
- Kamps, L.; Saito, Y.; Kawabata, R.; Wakita, M.; Totani, T.; Takahashi, Y.; Nagata, H. Method for Determining Nozzle-Throat-Erosion History in Hybrid Rockets. J. Propuls. Power 2017, 33, 1369–1377. [Google Scholar] [CrossRef] [Green Version]
- D’Elia, R.; Bernhart, G.; Hijlkema, J.; Cutard, T. Experimental Analysis of SiC-based Refractory Concrete in Hybrid Rocket Nozzles. Acta Astronaut. 2016, 126, 168–177. [Google Scholar] [CrossRef] [Green Version]
- Whitmore, S.; Babb, R.; Stephens, J.; Horlacher, J. Further Development of Low-Erosion Nozzle Materials for Long-Duration Hybrid Rocket Burns. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. AIAA Paper 2021-3514. [Google Scholar]
- Ito, S.; Kamps, L.; Yoshimaru, S.; Nagata, H. Evaluation of the Thermal Onset of Graphite Nozzle Erosion. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–28 August 2020. AIAA Paper 2020-3755. [Google Scholar]
- Bianchi, D.; Nasuti, F. Numerical Analysis of Nozzle Material Thermochemical Erosion in Hybrid Rockets. J. Propuls. Power 2013, 29, 547–558. [Google Scholar] [CrossRef]
- Chandler, A.; Cantwell, B.; Hubbard, S. Hybrid Propulsion for Solar System Exploration. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Diego, CA, USA, 31 July–3 August 2011. AIAA Paper 2011-6103. [Google Scholar]

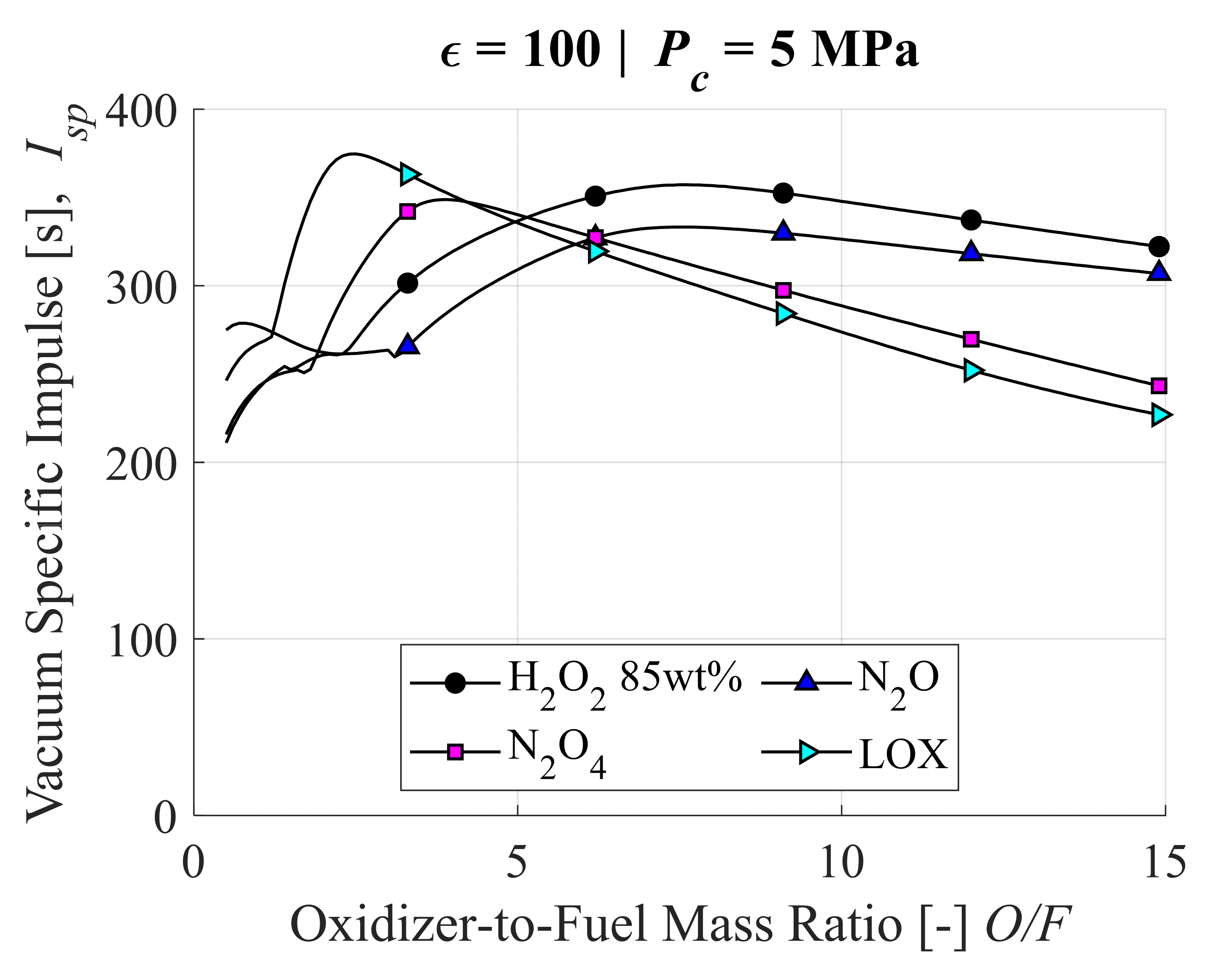



| Oxidizer | Density, kg/m3 | Positive Attributes | Negative Attributes |
|---|---|---|---|
| H2O2 85wt% | 1380 | catalytic ignition possible | unstable, dilutes in time |
| N2O | 550 1 | safe, self-pressurizing | high ignition threshold |
| N2O4 | 1440 | space heritage, stable | highly toxic |
| LOX | 1140 | nontoxic, easy ignition | cryogenic storage required |
| Category | Material | Density, kg/m3 | Yield Stress, MPa | Components, # 1 |
|---|---|---|---|---|
| case | aluminum | 2700 | 260 | 1–6, 12, 13, 16, 17 |
| fuel | HDPE | 955 | not considered | 10 |
| insulator | laminate | 1300 | not considered | 7, 8, 11, 14, 18 |
| liner, mixing | graphite | 1850 | not considered | 9, 15, 19 |
| vessel (wall) | FRP | 1370 | 800 | 21, 23 |
| Component | Reference | Mass Estimation | Quantity |
|---|---|---|---|
| valve | Marotta CoRe | 1.6 kg/valve 1 | 2 (self-fed), 4 (gas-fed) |
| tube | Swagelok ½” | 0.25 kg/m | 4B (self-fed), 8B (gas-fed) |
| structure | [28] | 60 × B2H (self-fed), 90 × B2H (gas-fed) | 1 |
| Propellants 1 | a, m, n of Equation (5) | β1, β2, β3, b, E, n of Equation (7) |
|---|---|---|
| N2O | 8.1 × 10−8, 0.43, 0.53 [32] | 0.10, 2.09, 3.77, −0.07, 2996, 0.15 [31] |
| LOX a | 1.5 × 10−6,0.26,0.36 [33] | 4.6 × 10−5, 5.43, 6.36, −0.02, 6436, 1.02 [30] |
| Independent Variable | Increment | Lower Value | Upper Value |
|---|---|---|---|
| Thrust chamber diameter ratio, D/B | 1/40 | 1/40 | 36/40 |
| Injector hole diameter, dinj 1 | 0.5 mm | 0.5 mm | 3.5 mm |
| Nozzle throat diameter, dt | 5 mm | 10 mm | 50 mm |
| Solution | H2O2 85wt% No Erosion | Erosion | N2O No Erosion | Erosion |
|---|---|---|
| Thrust chamber diameter ratio, D/B | 43% | 43% | 35% | 35% |
| Injector hole diameter, dinj 1 | 1.5 mm | 1.0 mm | 3.0 mm | 2.5 mm |
| Nozzle throat diameter, dt | 30 mm | 30 mm | 30 mm | 20 mm |
| Change of velocity, ΔV | 4379 m/s | 4053 m/s | 3698 m/s | 3545 m/s |
| Wet Mass, Mwet | 916 kg | 916 kg | 465 kg | 456 kg |
| Density-ΔV, | 4.8 m4/kg-s | 4.4 m4/kg-s | 8.0 m4/kg-s | 7.8 m4/kg-s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamps, L.; Hirai, S.; Nagata, H. Hybrid Rockets as Post-Boost Stages and Kick Motors. Aerospace 2021, 8, 253. https://doi.org/10.3390/aerospace8090253
Kamps L, Hirai S, Nagata H. Hybrid Rockets as Post-Boost Stages and Kick Motors. Aerospace. 2021; 8(9):253. https://doi.org/10.3390/aerospace8090253
Chicago/Turabian StyleKamps, Landon, Shota Hirai, and Harunori Nagata. 2021. "Hybrid Rockets as Post-Boost Stages and Kick Motors" Aerospace 8, no. 9: 253. https://doi.org/10.3390/aerospace8090253
APA StyleKamps, L., Hirai, S., & Nagata, H. (2021). Hybrid Rockets as Post-Boost Stages and Kick Motors. Aerospace, 8(9), 253. https://doi.org/10.3390/aerospace8090253







