A Review of Computational Methods and Reduced Order Models for Flutter Prediction in Turbomachinery
Abstract
1. Introduction
2. CFD Methods for Unsteady Flows in Turbomachinery
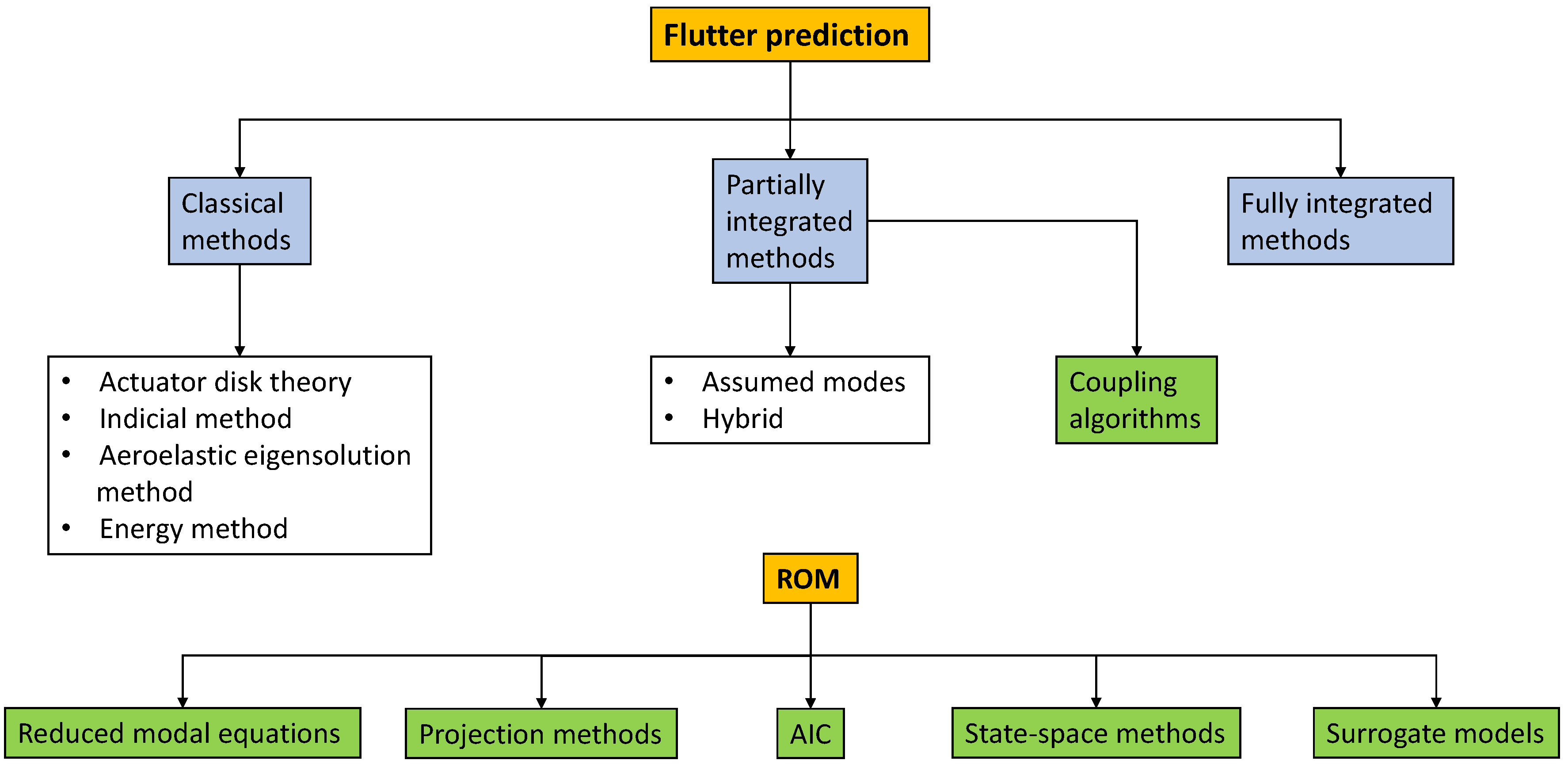
3. Aeroelasticity Methods in Turbomachinery
3.1. Classical Methods
- Simplicity of models and relatively low computational costs, due to lack of interexchanging information between the two domains at each substep.
- The assumption of uncoupling between the fluid and structural domain is usually realistic for many situations, especially at low speeds, so that the motion of the structure is well defined by a certain mode shape and frequency, which are substantially unaffected by the unsteady flow.
- The information regarding asymptotic stability of given modes and IBPAs, though conservative, is sufficient in many cases, especially for preliminary design purposes.
3.1.1. Actuator Disk Theory
3.1.2. Indicial Method
3.1.3. Aeroelastic Eigensolution Method
3.1.4. Energy Method
3.2. Integrated Aeroelasticity Methods
3.2.1. Partially Integrated Method
3.2.2. Periodic Mode Updating Method
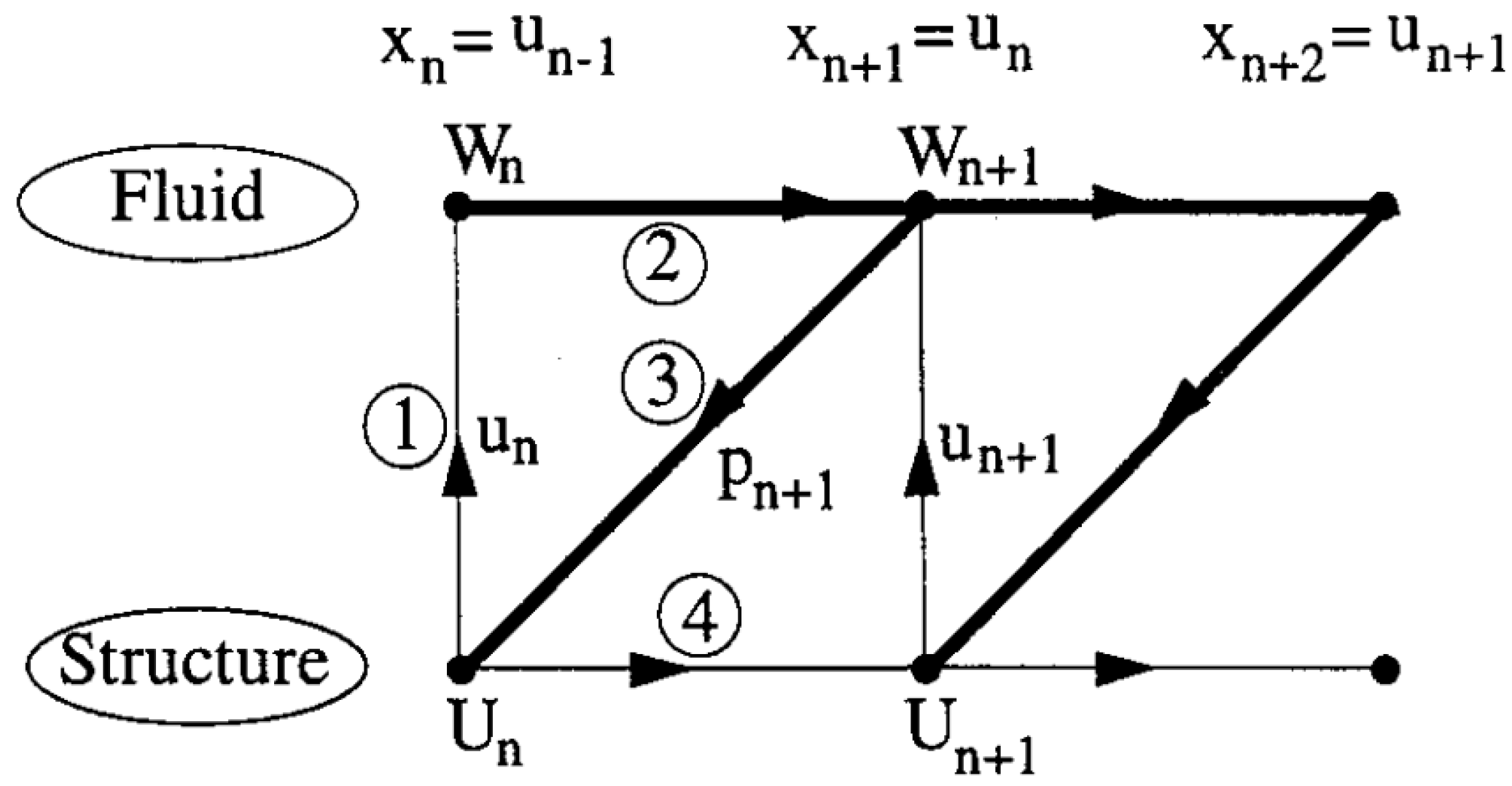
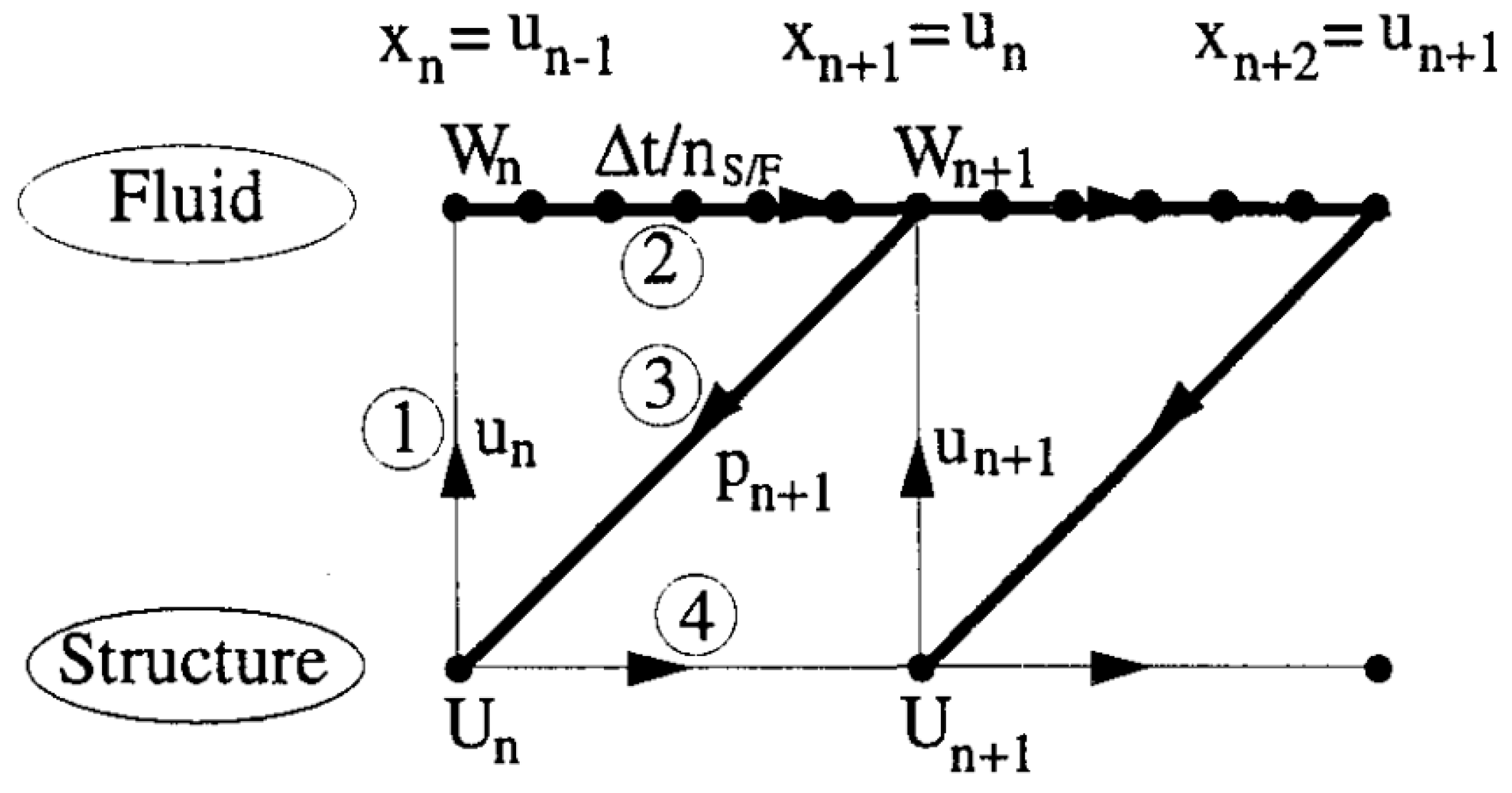
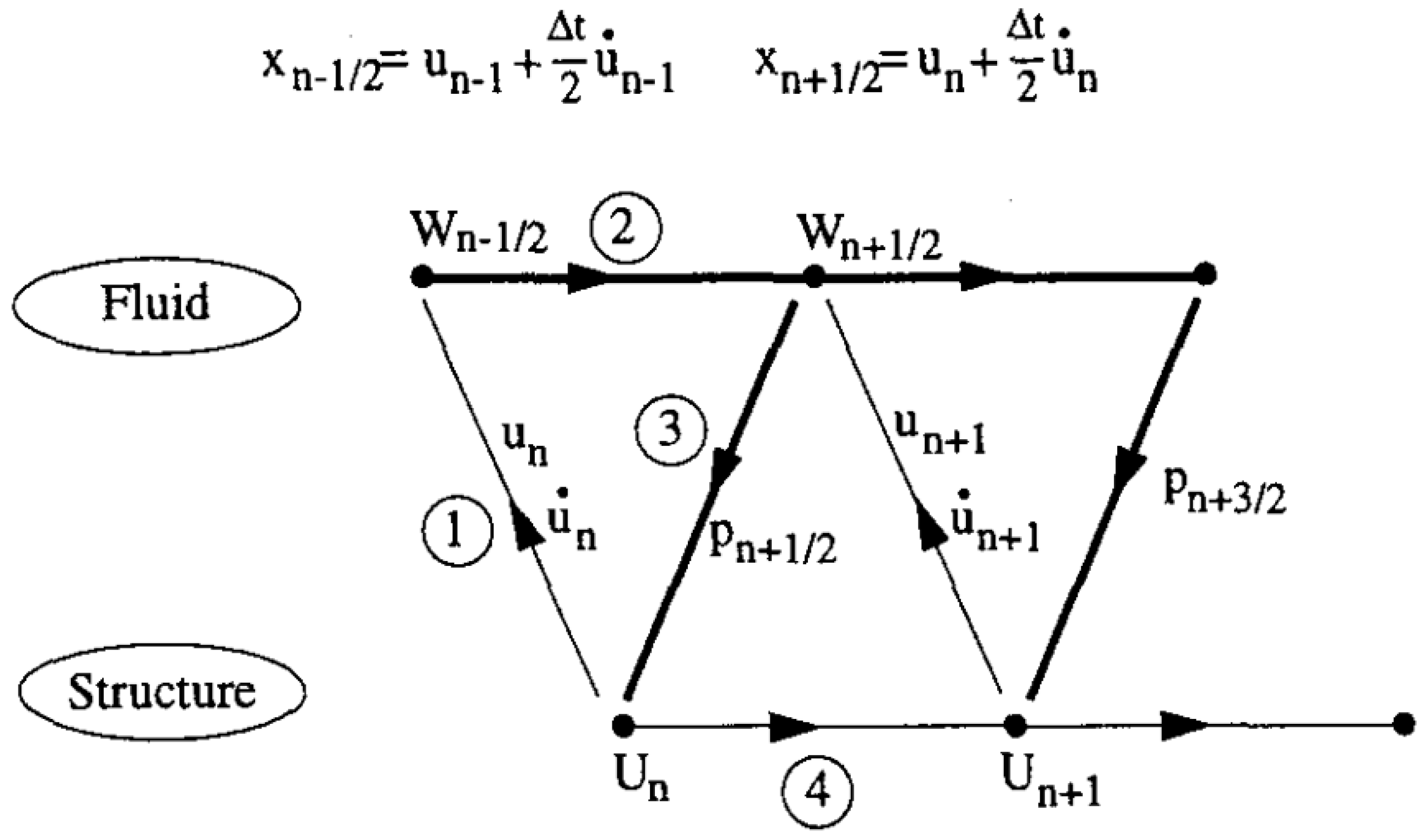
3.2.3. Fluid–Structure Coupling Algorithms
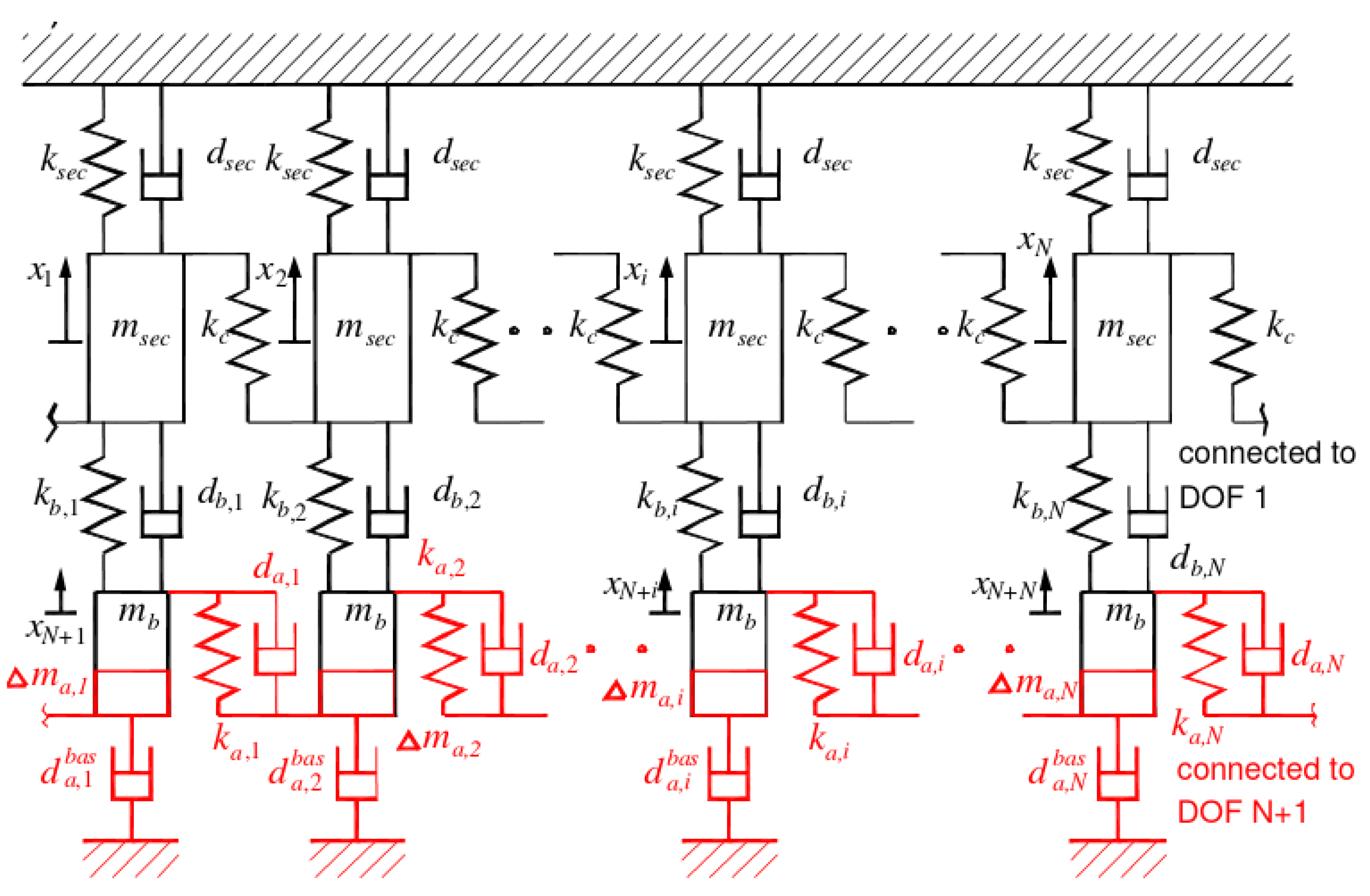
3.3. Fully Integrated Methods
4. ROMs for Flutter Prediction
4.1. Reduced Modal Equations
4.2. Projection Methods
- A small number of solutions using the full model are computed. The conditions for these full solutions or “snapshots” are chosen to span the operating range over which fidelity to the CFD results is desired.
- A set of basis vectors which capture the behaviour in the solutions is created. “Behaviour” can be quantified by spatial patterns in the flow, snapshots of the unsteady response (frequency domain) or the input–output transfer functions. The number of basis vectors required depends on the problem and the desired degree of fit.
- The original equations are projected onto the space represented by the basis vectors. The result is a set of ordinary differential equations (ODEs) for the time-varying coefficients of the basis vectors. The low-order system is completely defined by these coefficients or “states”; an approximate reconstruction of the entire flow field can be accomplished by multiplying the states by the basis vectors. Thus, any output quantity (blade pressure distribution, downstream disturbances, forces and moments) can be approximated.
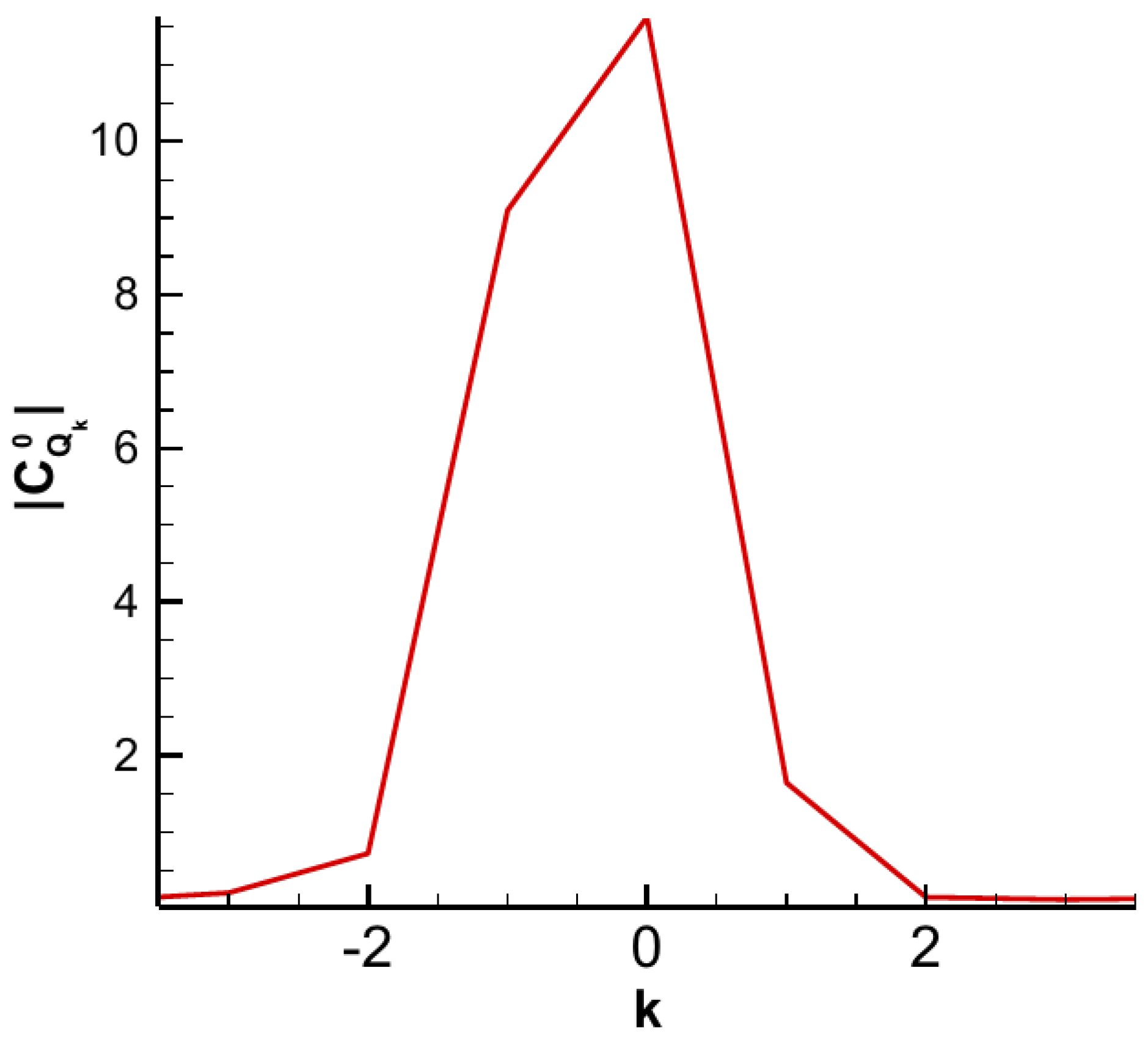
4.3. Aerodynamic Influence Coefficients
4.4. State-Space Representation
4.5. Surrogate Models for Aeroelastic Calculations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AIC | Aerodynamic Influence Coefficient |
| ALE | Arbitrary Lagrangian–Eulerian |
| ANN | Artificial Neural Network |
| ASA | Adaptive Simulated Annealing |
| CFD | Computational Fluid Dynamics |
| DES | Detached Eddie Simulation |
| d.o.f. | Degree of Freedom |
| EBM | Equivalent Blisk Model |
| EAE | Equivalent Aerodynamic Element |
| FEM | Finite Element Method |
| GAF | Generalised Aerodynamic Forces |
| HB | Harmonic Balance |
| IBPA | Interblade Phase Angle |
| I/O | Input/Output |
| LES | Large Eddie Simulation |
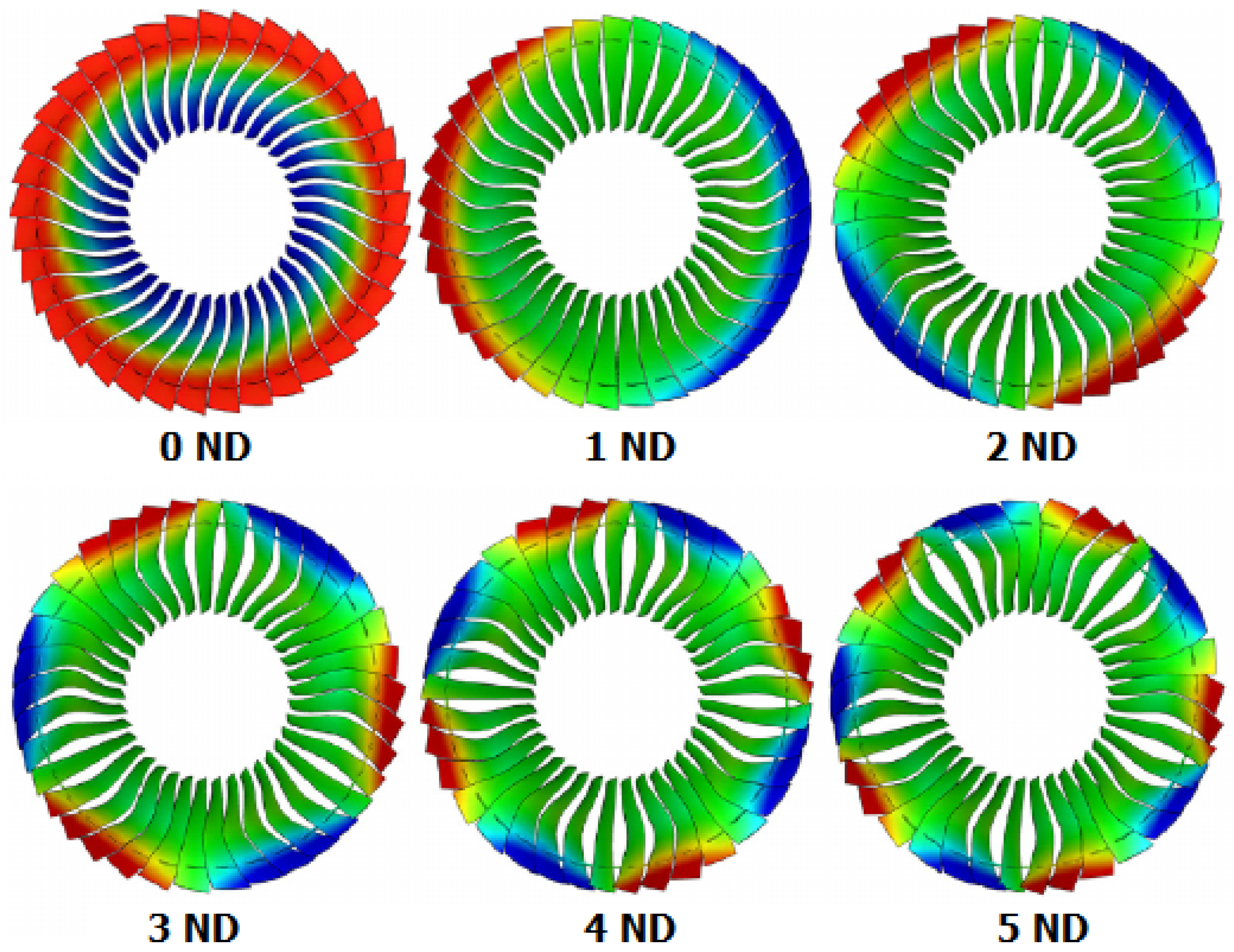
| ND | Nodal Diameter |
| NSV | Non-Synchronous Vibrations |
| ODE | Ordinary Differential Equations |
| POD | Proper Orthogonal Decomposition |
| RANS | Reynolds-Averaged Navier–Stokes |
| ROM | Reduced Order Model |
| RRBF | Recursive Radial Basis Function |
| SEREP | System Equivalent Reduction Expansion Process |
| SIMO | Single Input Multiple Output |
| TSD | Transonic Small Disturbance |
| Symbols | |
| Aerodynamic damping coefficient | |
| POD eigenvalue | |
| Structural damping coefficient | |
| Normalized mode shapes vector | |
| POD eigenvector | |
| Natural pulsation | |
| a | POD temporal coefficient |
| D | Structural damping matrix |
| Aerodynamic forces vector | |
| I | Identity matrix |
| K | Stiffness matrix |
| Vibrating blade mechanical energy | |
| M | Mass matrix |
| q | Principal coordinate |
| R | Autocorrelation matrix |
| t | Time |
| u | Generic oscillating scalar field |
| W | Aerodynamic work per cycle on blade |
| x | Physical displacement / Spatial coordinate |
References
- Collar, A.R. The expanding domain of aeroelasticity. J. R. Aeronaut. Soc. 1947, 51, 1–34. [Google Scholar] [CrossRef]
- Marshall, J.G.; Imregun, M. A review of aeroelasticity methods with emphasis on turbomachinery. J. Fluids Struct. 1996, 10, 237–267. [Google Scholar] [CrossRef]
- He, L. An Euler Solution for Unsteady Flows Around Oscillating Blades. Trans. ASME 1990, 112, 714–722. [Google Scholar] [CrossRef]
- Kahl, G.; Klose, A. Computation of time-linearized transonic flow in oscillating cascades. In Proceedings of the ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, OH, USA, 24–27 May 1993; pp. 1–9. [Google Scholar]
- He, L.; Denton, J.D. Inviscid-Viscous Coupled Solution for Unsteady Flows through Vibrating Blades: Parts 1 and 2; ASME Papers 91-GT-125 and 126; ASME: New York, NY, USA, 1991. [Google Scholar]
- He, L. Three-Dimensional Time-Marching Inviscid and Viscous Solutions for Unsteady flOws around Vibrating Blades; ASME Paper 93-GT-92; ASME: New York, NY, USA, 1993. [Google Scholar]
- Ekici, K.; Hall, K.C. Time-linearized Navier—Stokes analysis of flutter in multistage turbomachines. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 10–13 January 2005; AIAA: Reston, VA, USA; Volume 836, pp. 1–19. [Google Scholar]
- Breard, C.; Vahdati, M.; Sayma, A.I.; Imregun, M. An Integrated Time-Domain Aeroelasticity Model for the Prediction of Fan Forced Response due to Inlet Distortion. Trans. ASME J. Eng. Gas Turbines Power 2002, 124, 196–208. [Google Scholar] [CrossRef]
- Placzek, A.; Dugeai, A. Numerical prediction of the aeroelastic damping using multi-modal dynamically coupled simulations on a 360° fan configuration. In Proceedings of the International Forum of Aeroelasticity and Structural Dynamics (IFASD), Orlando, FL, USA, 4–7 January 2011; Volume 84. [Google Scholar]
- Im, H.; Chen, X.; Zha, G. Detached Eddy Simulation of Transonic Rotor Stall Flutter Using a Fully Coupled Fluid-Structure Interaction. In Proceedings of the ASME Turbo Expo 2011 GT2011, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- He, L.; Ning, W. Efficient Approach for Analysis of Unsteady Viscous Flows in Turbomachines. AIAA J. 1998, 36, 2005–2012. [Google Scholar] [CrossRef]
- Hall, K.C. Computation of Unsteady Nonlinear Flows in Cascades Using a Harmonic Balance Technique. In Kerrebrock Symposium, A Symposium in Honor of Professor Jack L. Kerrebrock’s 70th Birthday; Massachusetts Institute of Technology: Cambridge, MA, USA, 1998. [Google Scholar]
- Hall, K.C.; Thomas, J.P.; Clark, W.S. Computation of Unsteady Nonlinear Flows in Cascades Using a Harmonic Balance Technique. AIAA J. 2002, 40, 879–886. [Google Scholar] [CrossRef]
- Ekici, K.; Hall, K.C. Nonlinear Analysis of Unsteady Flows in Multistage Turbomachines Using Harmonic Balance. AIAA J. 2007, 45, 1047–1057. [Google Scholar] [CrossRef]
- Aschcroft, G.; Frey, C.; Kersken, H.P. On the development of a harmonic balance method for aeroelastic analysis. In Proceedings of the 6th European Conference on Computational Fluid Dynamics—ECFD VI, Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Sicot, F.; Gomar, A.; Dufour, G.; Dugeai, A. Time-Domain Harmonic Balance Method for Turbomachinery Aeroelasticity. AIAA J. 2014, 52, 62–71. [Google Scholar] [CrossRef]
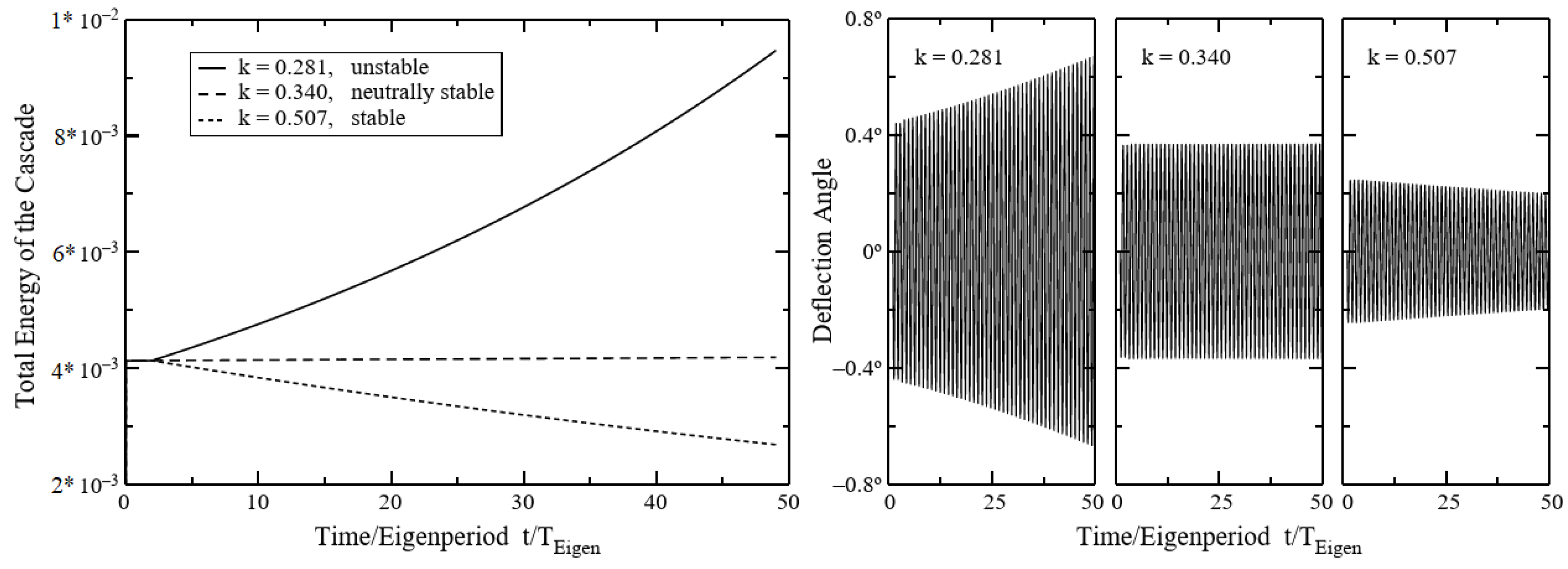
- Berthold, C.; Gross, J.; Frey, C.; Krack, M. Development of a fully-coupled harmonic balance method and a refined energy method for the computation of flutter-induced Limit Cycle Oscillations of bladed disks with nonlinear friction contacts. J. Fluids Struct. 2021, 102, 103233. [Google Scholar] [CrossRef]
- Lane, F. System mode shapes in the flutter of compressor blade rows. J. Aeronaut. Sci. 1956, 23, 54–66. [Google Scholar] [CrossRef]
- Whitehead, D.S. The vibration of cascade blades treated by actuator disk methods. Proc. Inst. Mech. Eng. 1959, 173, 555–557. [Google Scholar] [CrossRef]
- Tanida, Y.; Okazaki, T. Translatory vibration of cascade blades as treated by semi-actuator disk methods—Parts 1 and 2. Trans. JSME 1963, 6, 744–758. [Google Scholar] [CrossRef]
- Adamczyk, J.J. Analysis of Supersonic Stall Bending Flutter in Axial-Flow Compressor by Actuator Disk Theory; NASA Technical Paper No. NASA-TP-1345; NASA: Washington, DC, USA, 1978. [Google Scholar]
- Ballhaus, W.F.; Goorjian, P.M. Computation of unsteady transonic flows by the indicial method. AIAA J. 1978, 16, 117–124. [Google Scholar] [CrossRef]
- Ueda, T.; Dowell, E.H. Flutter analysis using nonlinear aerodynamic forces. AIAA J. Aircr. 1984, 21, 101–109. [Google Scholar] [CrossRef]
- Stark, V.J.E. General equations of motion for an elastic wing and methods of solution. AIAA J. 1984, 22, 1146–1153. [Google Scholar] [CrossRef]
- Klose, A.H. Advanced Ducted Engines: Impact of Unsteady Aerodynamics on Fan Vibration Properties; ASME: New York, NY, USA, 1992. [Google Scholar]
- Mahler, A.; Placzec, A. Efficient coupling strategies for the numerical prediction of the aeroelastic stability of bladed disks. In Proceedings of the International Symposium on Unsteady Aerodynamics, Aeroacoustics and Aeroelasticity of Turbomachines, Tokyo, Japan, 8–11 September 2012. [Google Scholar]
- Tateishi, A.; Watanabe, T.; Himeno, T.; Aotsuka, M.; Murooka, T. Verification and Application of Fluid-Structure Interaction and a Modal Identification Technique to Cascade Flutter Simulations. Int. J. Gas Turbine Propuls. Power Syst. 2016, 8, 20–28. [Google Scholar] [CrossRef]
- Carta, F.O. Coupled blade-disc-shroud flutter instabilities in turbojet engine rotors. ASME J. Eng. Power 1967, 89, 419–426. [Google Scholar] [CrossRef]
- Clark, W.S.; Hall, K.C. A time-linearized Navier-Stokes analysis of flutter. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar]
- Nowinski, M.; Panowsky, J. Flutter Mechanisms in Low Pressure Turbine Blades. Trans. ASME J. Eng. Gas Turbines Power 2000, 122, 82–88. [Google Scholar] [CrossRef]
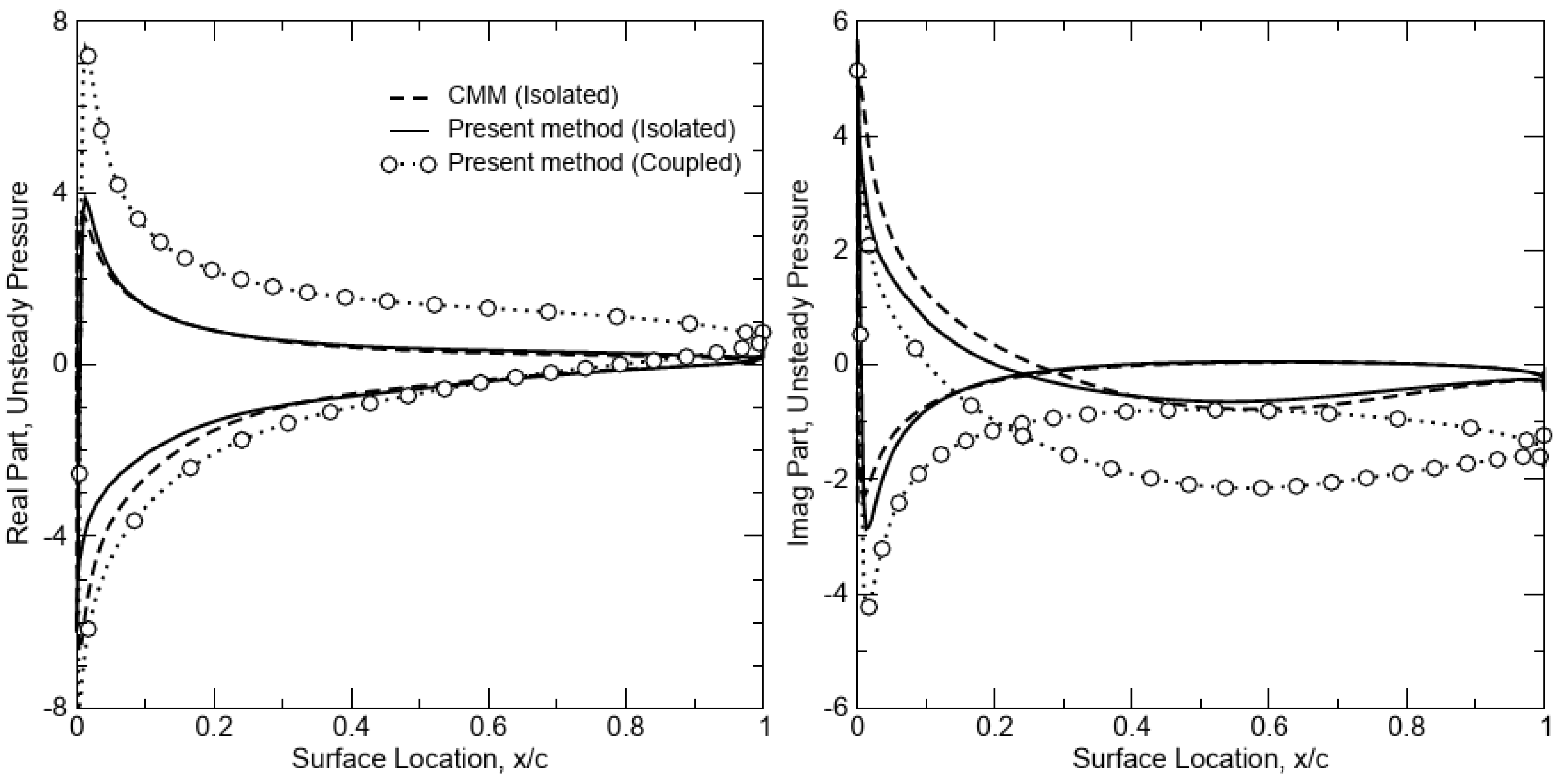
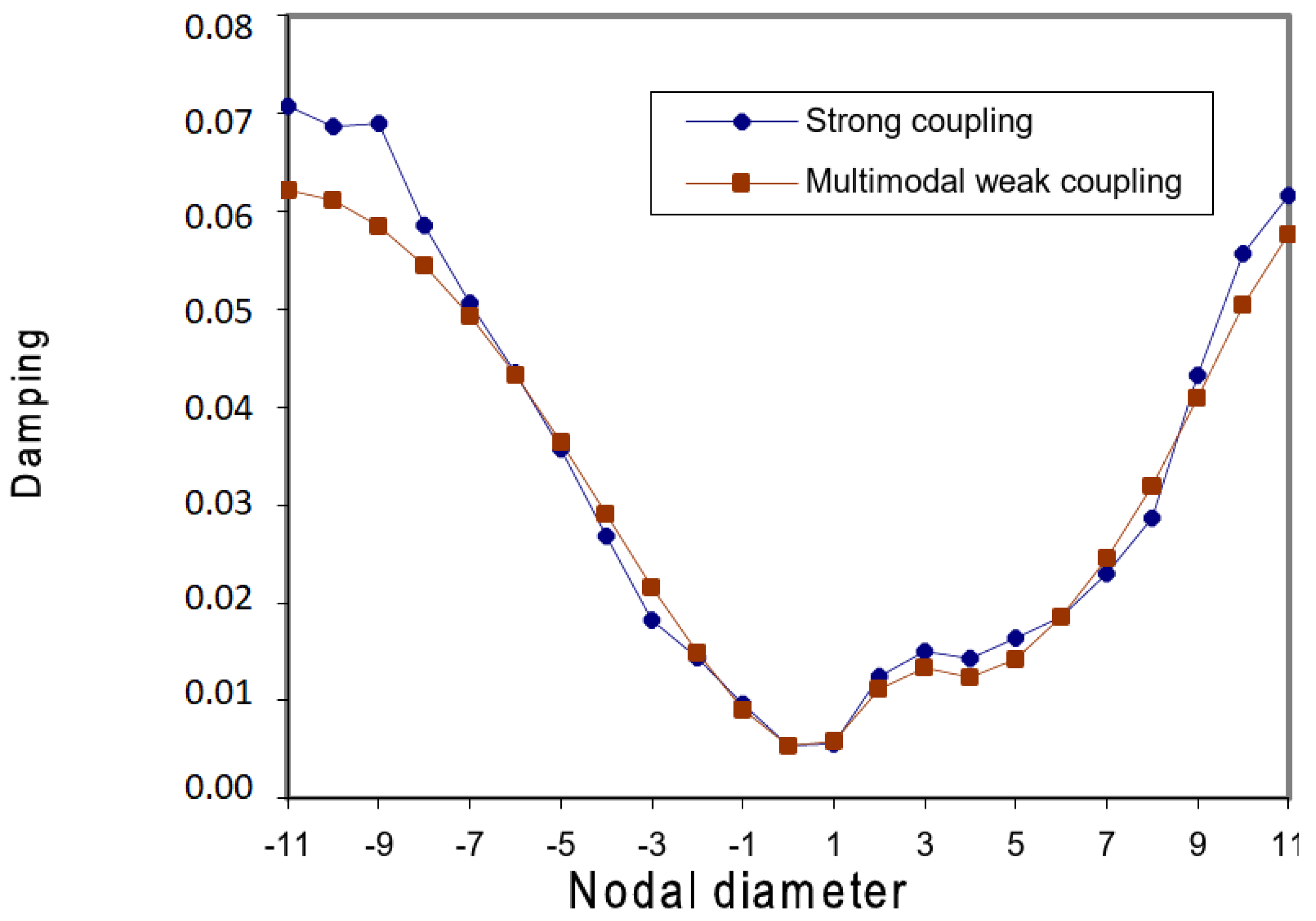
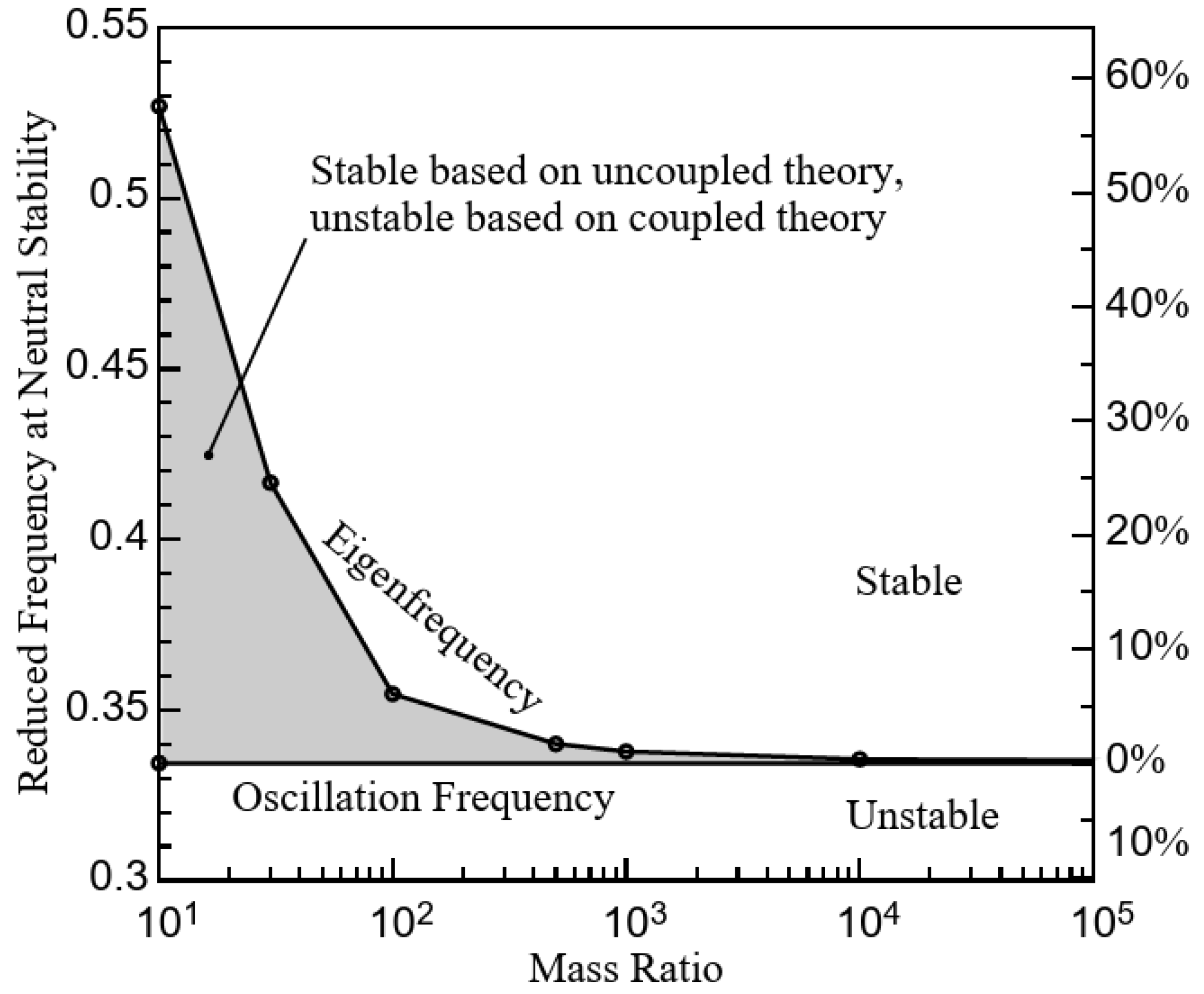
- Sadeghi, M.; Liu, F. Computation of cascade flutter by uncoupled and coupled methods. Int. J. Comput. Fluid Dyn. 2005, 19, 559–569. [Google Scholar] [CrossRef]
- Su, D.; Zhang, W.; Ye, Z. A reduced order model for uncoupled and coupled cascade flutter analysis. J. Fluids Struct. 2016, 61, 410–430. [Google Scholar] [CrossRef]
- Lian, B.; Hu, P.; Chen, Y.; Zhu, X.; Du, Z. Insight on aerodynamic damping of the civil transonic fan blade. In Proceedings of the ASME Turbo Expo 2021 Turbomachinery Technical Conference and Exposition GT2021, Virtual, 7–11 June 2021. [Google Scholar]
- Sayma, A.I.; Vahdati, M.; Imregun, M. An integrated nonlinear approach for turbomachinery forced response prediction. Part I: Formulation. J. Fluids Struct. 2000, 14, 87–101. [Google Scholar] [CrossRef]
- Debrabandere, F.; Tartinville, B.; Hirsch, C.; Coussement, G. Fluid—Structure interaction using a modal approach. J. Turbomachinery-Trans. ASME 2012, 134, 051043. [Google Scholar] [CrossRef]
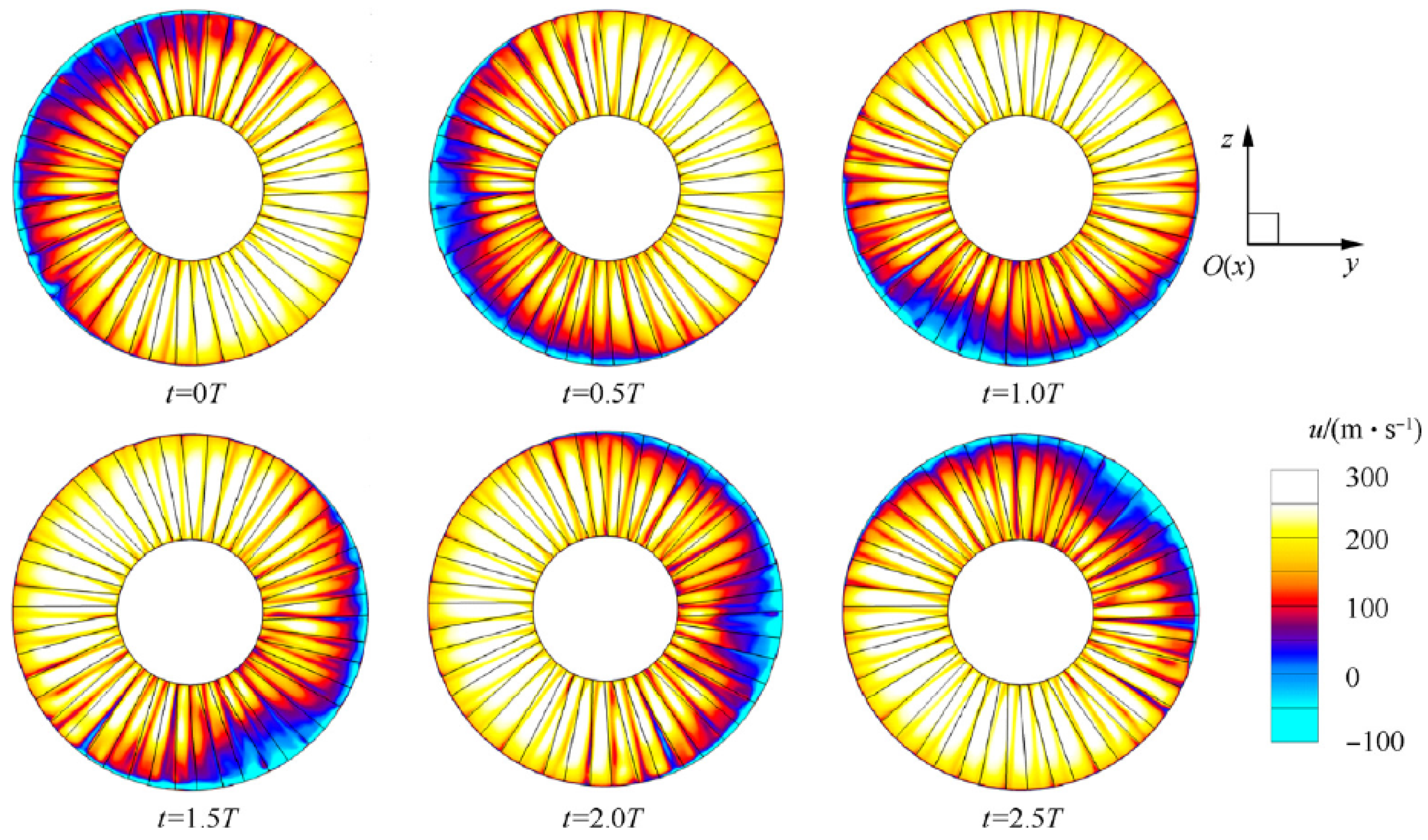
- Zheng, Y.; Yang, H. Coupled Fluid-structure Flutter Analysis of a Transonic Fan. Chin. J. Aeronaut. 2011, 24, 258–264. [Google Scholar] [CrossRef]
- Li, J.; Yang, X.; Hou, A.; Chen, Y.; Li, M. Aerodynamic Damping Prediction for Turbomachinery Based on Fluid-Structure Interaction with Modal Excitation. Appl. Sci. 2019, 9, 4411. [Google Scholar] [CrossRef]
- Liang, F.; Xie, Z.; Xia, A.; Zhou, M. Aeroelastic simulation of the first 1.5-stage aeroengine fan at rotating stall. Chin. J. Aeronaut. 2020, 33, 529–549. [Google Scholar] [CrossRef]
- Zhang, M.; Hou, A.; Zhou, S.; Yang, X. Analysis on Flutter Characteristics of Transonic Compressor Blade Row by a Fluid-Structure Coupled Method. In Proceedings of the ASME Turbo Expo 2012 GT2012, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Gerolymos, G.A. Coupled 3-D Aeroelastic Stability Analysis of Bladed Disks; ASME paper 92-GT-171; ASME: New York, NY, USA, 1992. [Google Scholar]
- Farhat, C.; Lesoinne, M. Higher-Order Staggered and Subiteration Free Algorithms for Coupled Dynamic Aeroelasticity Problems. In Proceedings of the 36th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Carstens, V.; Kemme, R.; Schmitt, S. Coupled simulation of flow-structure interaction in turbomachinery. Aerosp. Sci. Technol. 2003, 7, 298–306. [Google Scholar] [CrossRef]
- Bendiksen, O.O. A New approach to computational aeroelasticity. In Proceedings of the 31st Structural Dynamics and Materials Conference, Long Beach, CA, USA, 2–4 April 1991. AIAA Paper 91-0939. [Google Scholar]
- Willcox, K.; Perarire, J.; Paduano, J.D. Application of model order reduction to compressor aeroelastic models. In Proceedings of the ASME TURBO EXPO 2000, International Gas Turbine and Aeroengine Congress and Exhibition, Munich, Germany, 8–11 May 2000. [Google Scholar]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K. Aerodynamic Data Reconstruction and Inverse Design using Proper Orthogonal Decomposition. AIAA J. 2004, 42, 1505–1516. [Google Scholar] [CrossRef]
- Zhang, L.; Mi, D.; Yan, C.; Tang, F. Multidisciplinary Design Optimization for a Centrifugal Compressor Based on Proper Orthogonal Decomposition and an Adaptive Sampling Method. Appl. Sci. 2018, 8, 2608. [Google Scholar] [CrossRef]
- Epureanu, B.I.; Hall, K.C.; Dowell, E.H. Reduced order models of unsteady viscous flows in turbomachinery using viscous-inviscid coupling. J. Fluids Struct. 2001, 15, 255–273. [Google Scholar] [CrossRef]
- Epureanu, B.I. A parametric analysis of reduced order models of viscous flows in turbomachinery. J. Fluids Struct. 2003, 17, 971–982. [Google Scholar] [CrossRef]
- Willcox, K.; Perarire, J.; Paduano, J.D. Low order aerodynamic models for aeroelastic control of turbomachinery. In Proceedings of the 40th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials (SDM) Conference, St. Louis, MO, USA, 12–15 April 1999. [Google Scholar]
- Willcox, K.; Perarire, J.; White, J. An Arnoldi approach for generation of reduced-order models for turbomachinery. Comput. Fluids 2002, 31, 369–389. [Google Scholar] [CrossRef][Green Version]
- Clark, S.T.; Besem, F.M.; Kielb, R.E.; Thomas, J.P. Developing a Reduced-Order Model of Nonsynchronous Vibration in Turbomachinery Using Proper Orthogonal Decomposition Methods. J. Eng. Gas Turbines Power 2015, 137, 052501. [Google Scholar] [CrossRef]
- Sarkar, S.; Venkatraman, K. Model order reduction of unsteady flow past oscillating airfoil cascades. J. Fluids Struct. 2004, 19, 239–247. [Google Scholar] [CrossRef]
- Hanamura, Y.; Tanaka, H.; Yamaguchi, Y. A simplified method to measure unsteady forces acting on the vibrating blades in cascade. Bull. JSME 1980, 23, 880–887. [Google Scholar] [CrossRef]
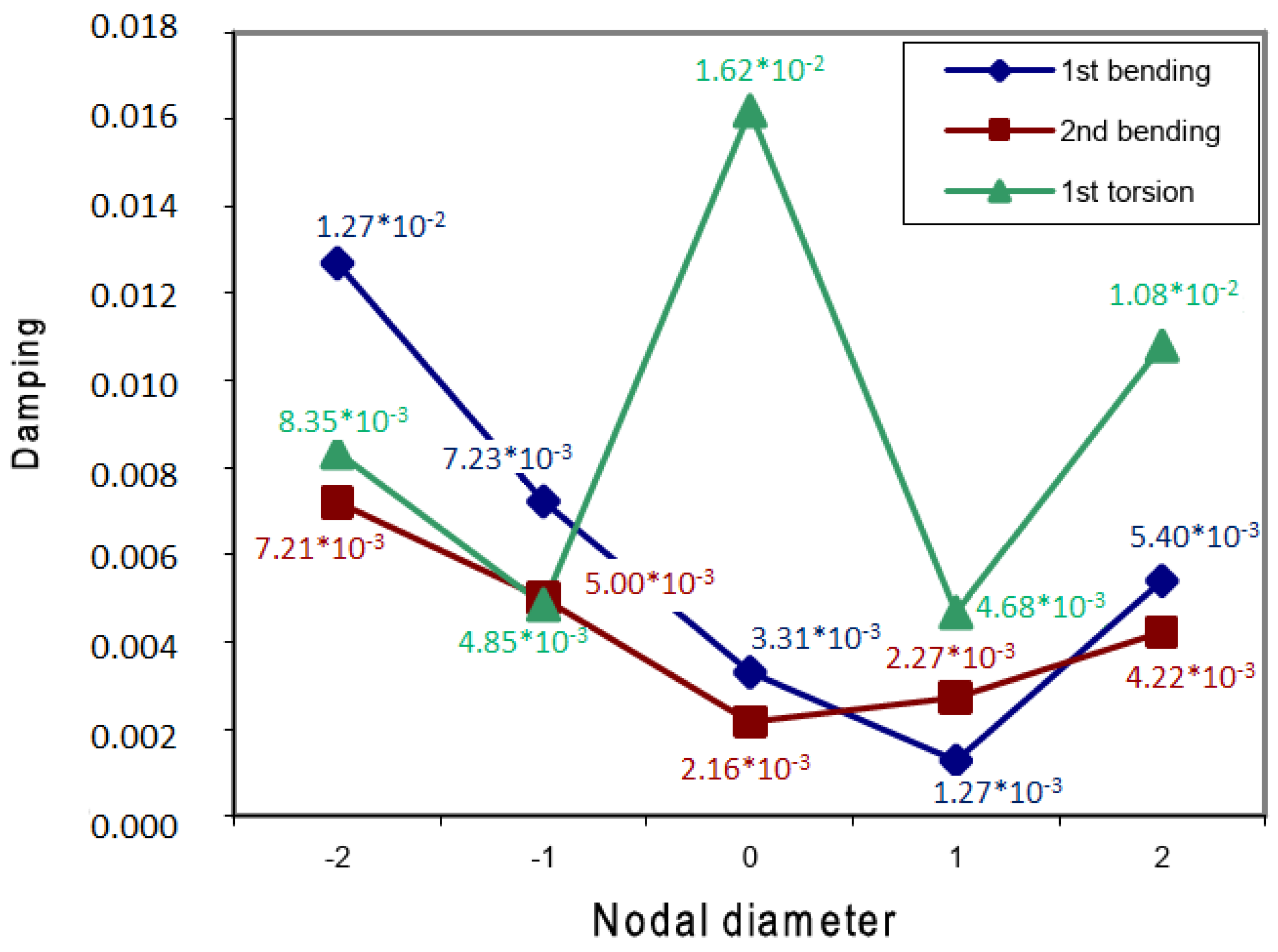
- Nipkau, J.; Kühhorn, A.; Beirow, B. Modal and aeroelastic analysis of a compressor blisk considering mistuning. In Proceedings of the ASME Turbo Expo 2011 GT2011, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Stapelfeldt, S.; Brandstetter, C. Suppression of non-synchronous-vibration through intentional aerodynamic and structural mistuning. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, GT2021, Virtual, 7–11 June 2021. [Google Scholar]
- Karpel, M. Design for active flutter suppression and gust alleviation using state-space aeroelastic modelling. J. Aircr. 1982, 19, 221–229. [Google Scholar] [CrossRef]
- Moore, B.C. Principal component analysis in linear systems: Controllability, observability, and model reduction. Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Tran, D.M. Multi-parameter aerodynamic modelling for aeroelastic coupling in turbomachinery. J. Fluids Struct. 2009, 25, 519–534. [Google Scholar] [CrossRef]
- Rodriguez, S.; Martel, C. Analysis of experimental results of turbomachinery flutter using an asymptotic reduced order model. J. Sound Vib. 2021, 509, 116225. [Google Scholar] [CrossRef]
- Stel’makh, A.L.; Zinkovskii, A.P.; Kabannik, S.N. Rapid method of predicting the subsonic flutter stability of AGTE axial-flow compressor blade cascades. Part 1. Physical backgrounds of the method. Strength Mater. 2019, 51, 175–182. [Google Scholar] [CrossRef]
- Hu, J.; Liu, H.; Wang, Y.; Chen, W.; Ma, Y. Reduced order model for unsteady aerodynamic performance of compressor cascade based on recursive RBF. Chin. J. Aeronaut. 2021, 34, 341–351. [Google Scholar] [CrossRef]
- Massoud, T.; Sabour, M.H. Reduced-order modeling of dynamic stall using neuro-fuzzy inference system and orthogonal functions. Phys. Fluids 2020, 32, 45101. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casoni, M.; Benini, E. A Review of Computational Methods and Reduced Order Models for Flutter Prediction in Turbomachinery. Aerospace 2021, 8, 242. https://doi.org/10.3390/aerospace8090242
Casoni M, Benini E. A Review of Computational Methods and Reduced Order Models for Flutter Prediction in Turbomachinery. Aerospace. 2021; 8(9):242. https://doi.org/10.3390/aerospace8090242
Chicago/Turabian StyleCasoni, Marco, and Ernesto Benini. 2021. "A Review of Computational Methods and Reduced Order Models for Flutter Prediction in Turbomachinery" Aerospace 8, no. 9: 242. https://doi.org/10.3390/aerospace8090242
APA StyleCasoni, M., & Benini, E. (2021). A Review of Computational Methods and Reduced Order Models for Flutter Prediction in Turbomachinery. Aerospace, 8(9), 242. https://doi.org/10.3390/aerospace8090242






