Leaf Vein-Inspired Bionic Design Method for Heat Exchanger Infilled with Graded Lattice Structure
Abstract
:1. Introduction
2. Models and Methods
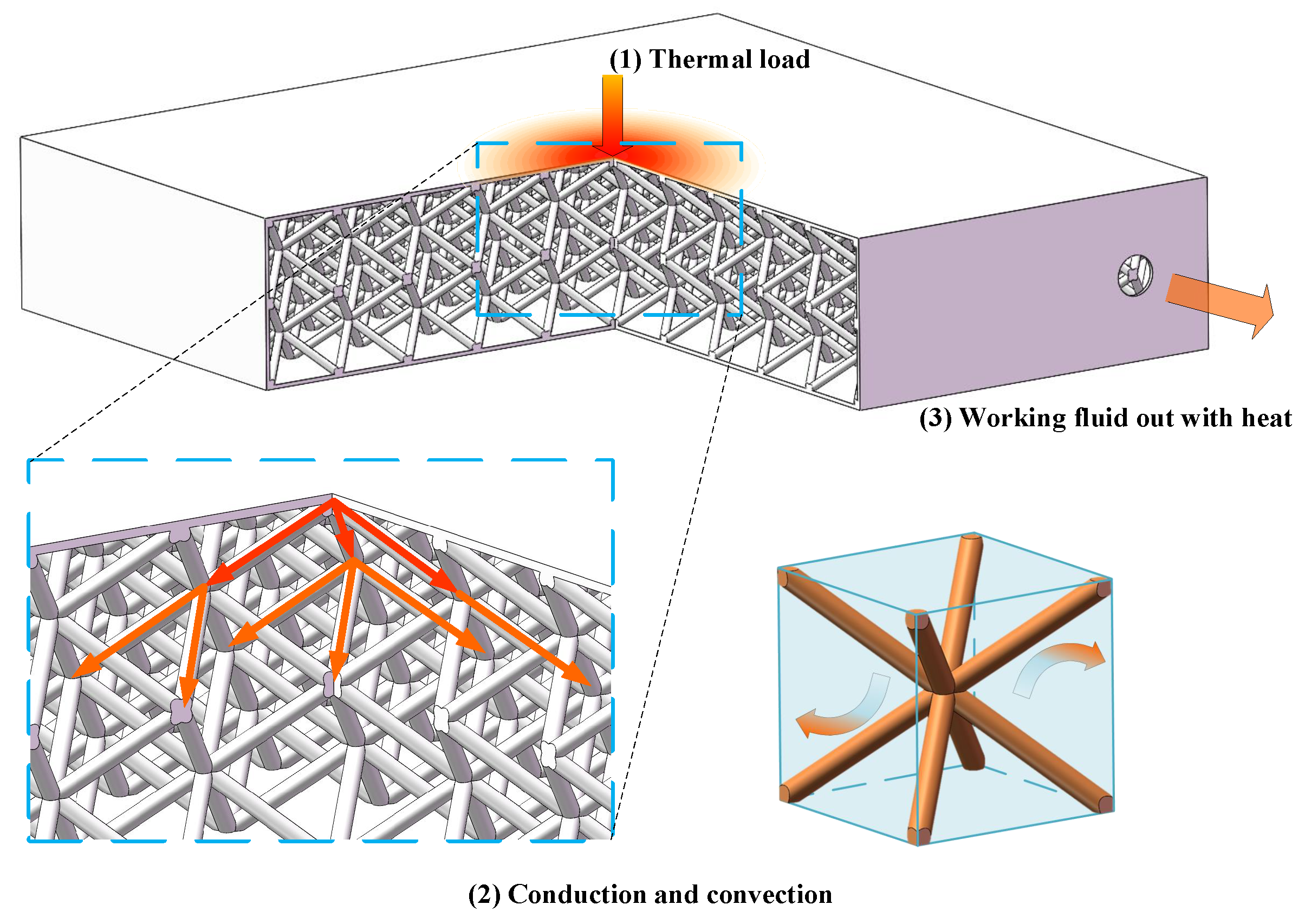
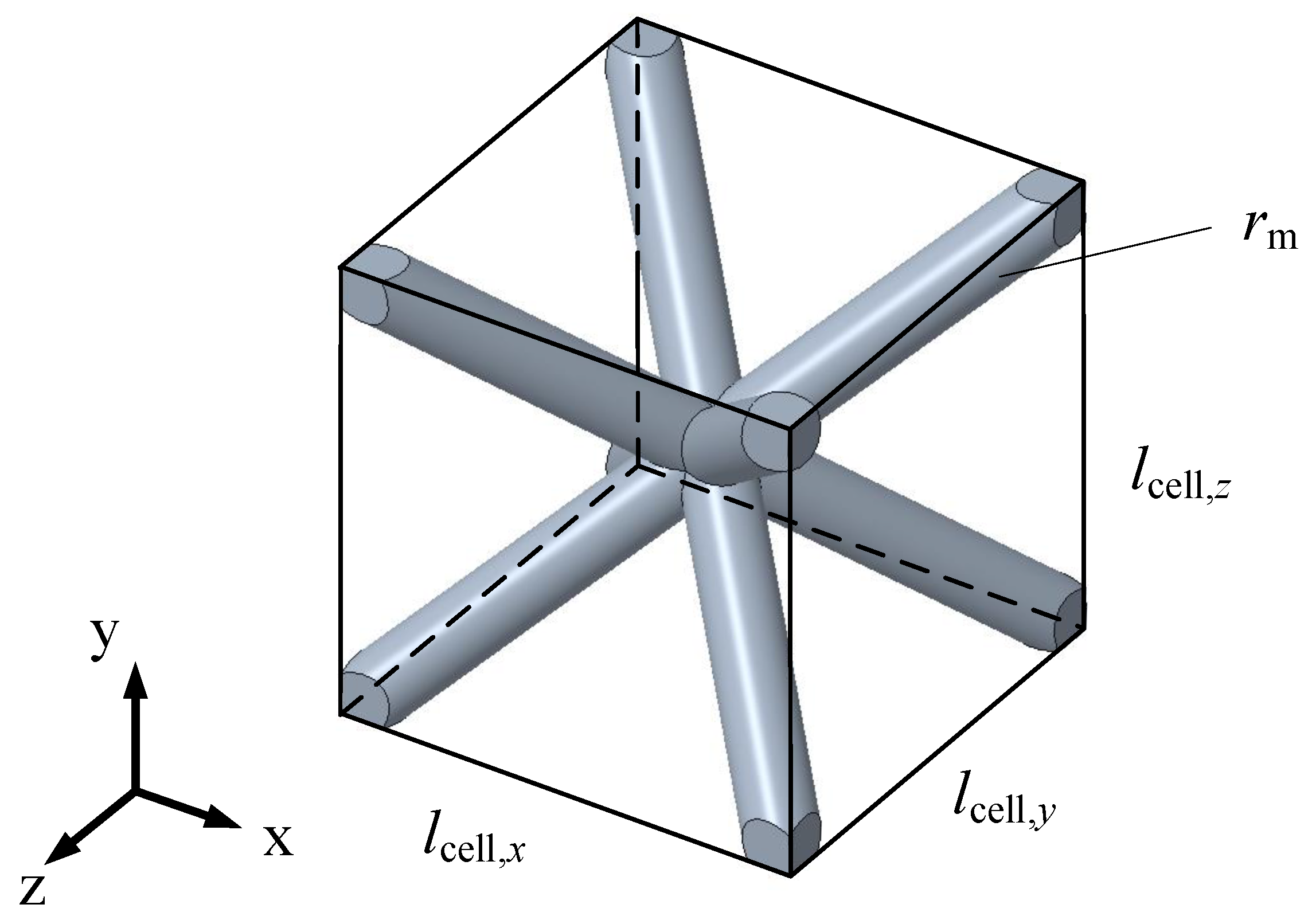
2.1. Mathematical Model of Heat Transfer
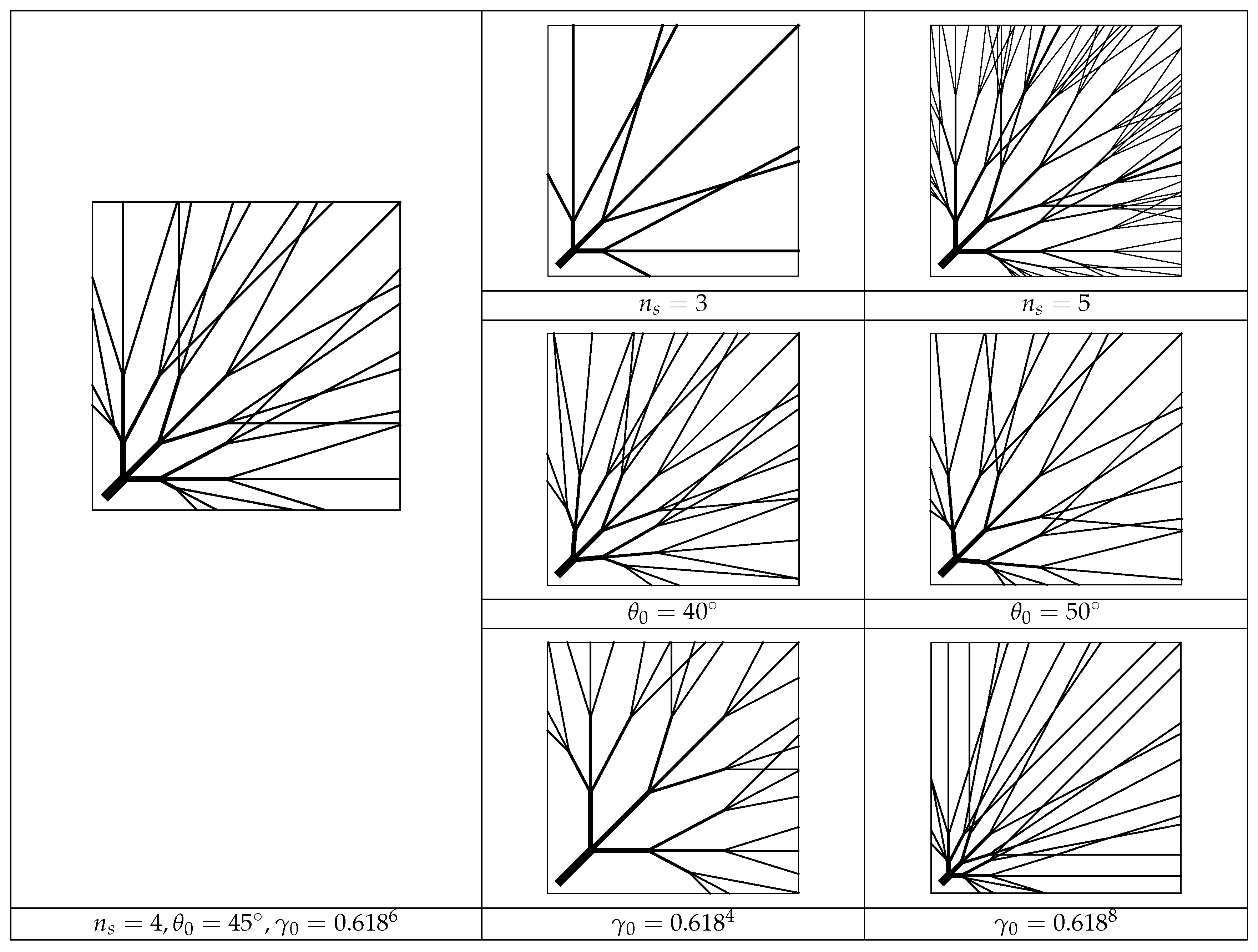
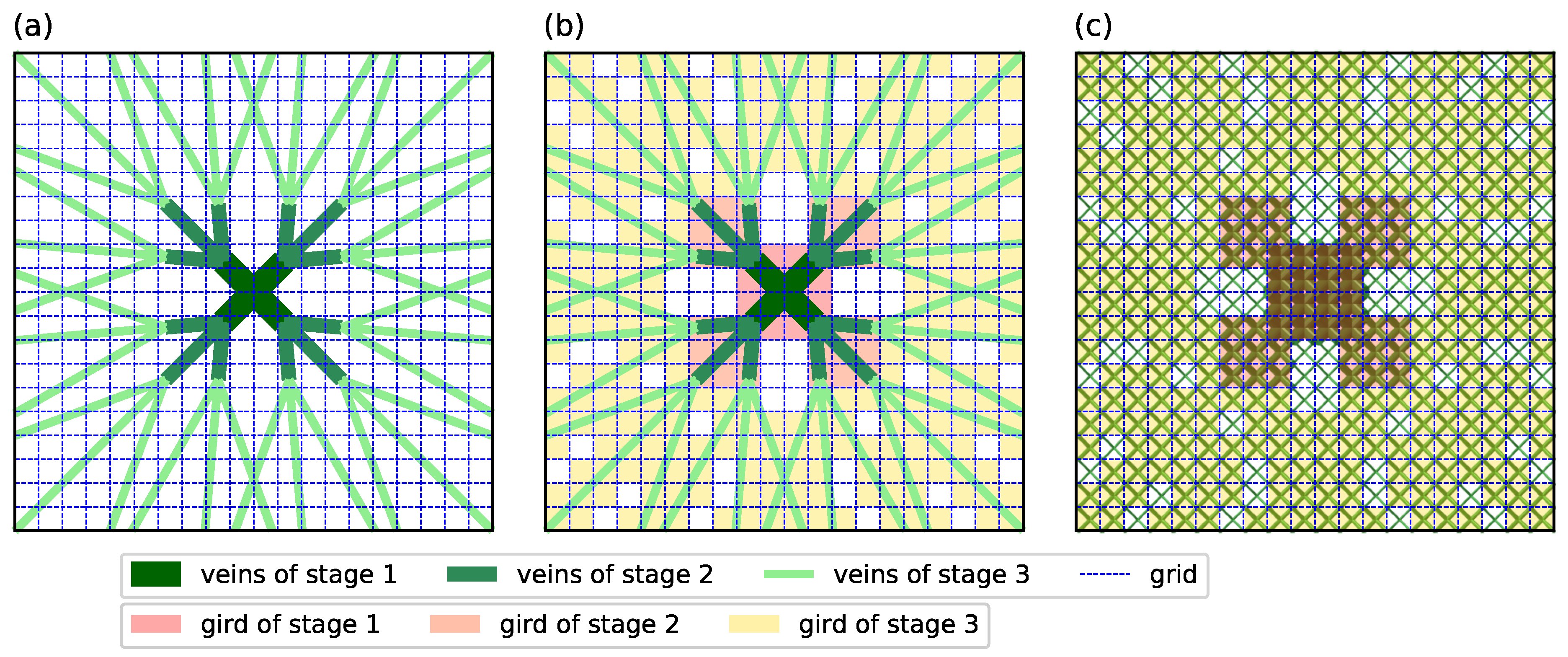
2.2. Leaf Vein Model
2.3. Mapping Method
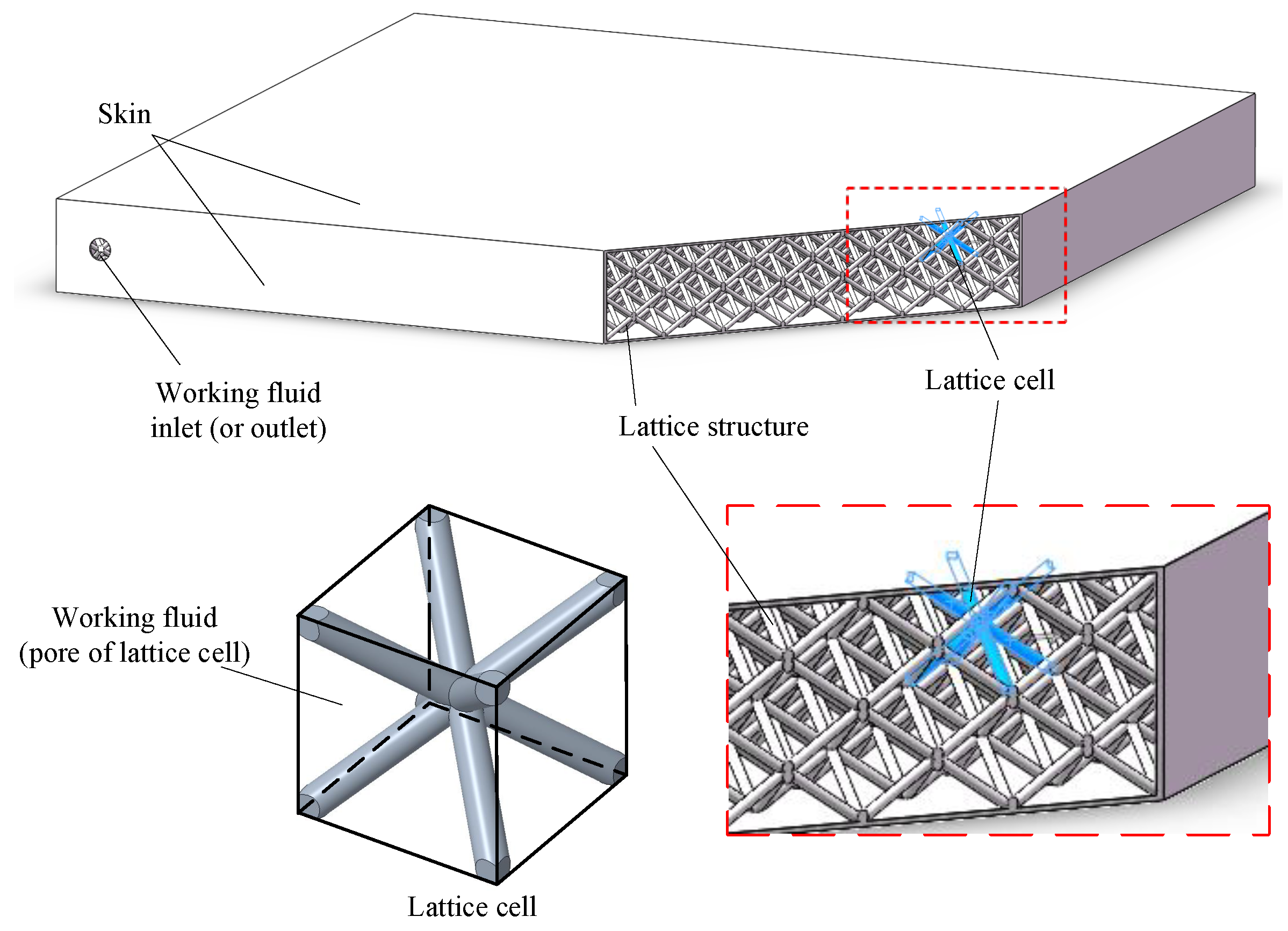
3. Uniform and Bionic Designs
3.1. Working Conditions and Uniform Design
3.2. Bionic Design Inspired by Leaf Veins
4. Results and Discussion
4.1. Finite Element Model
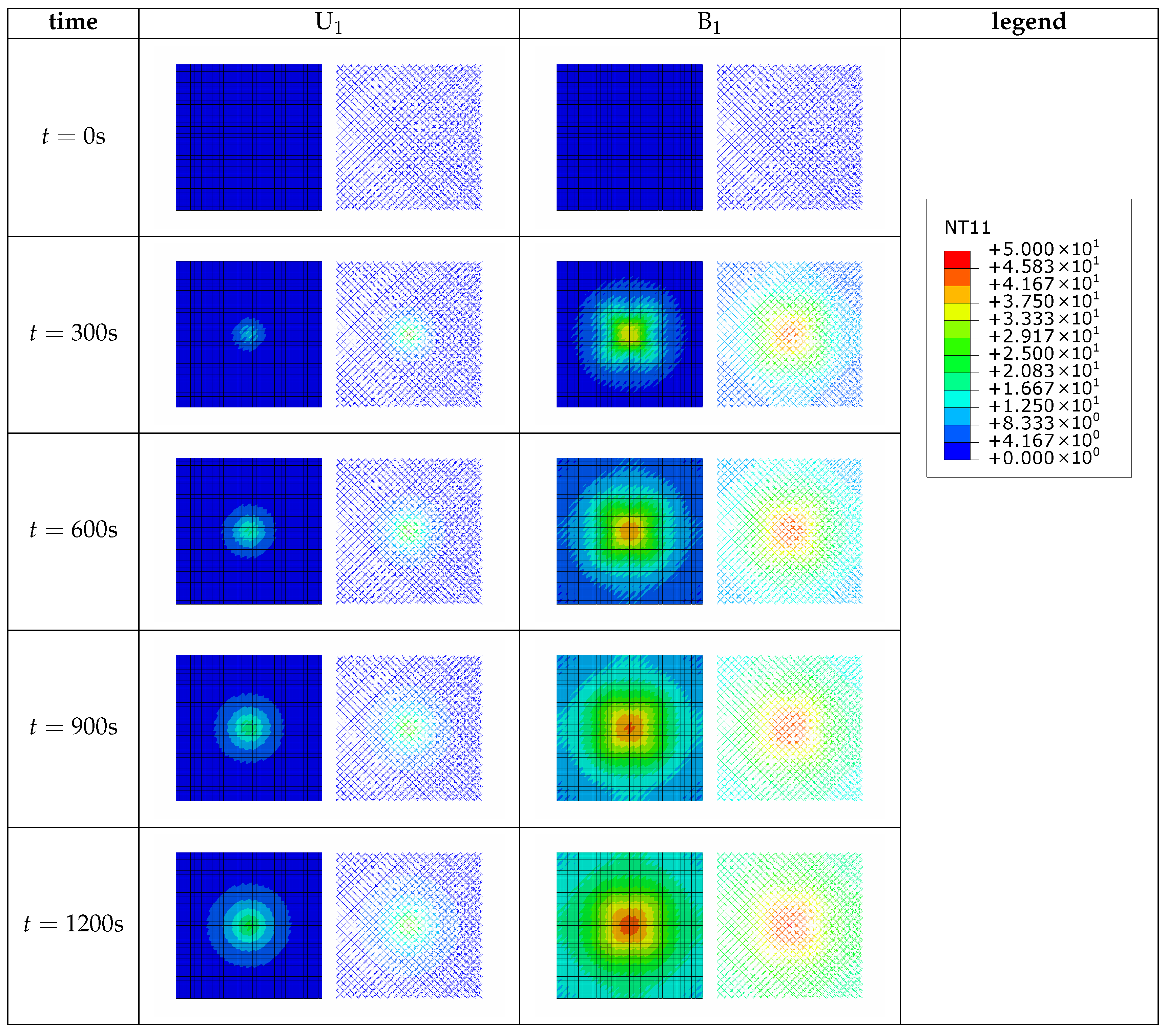
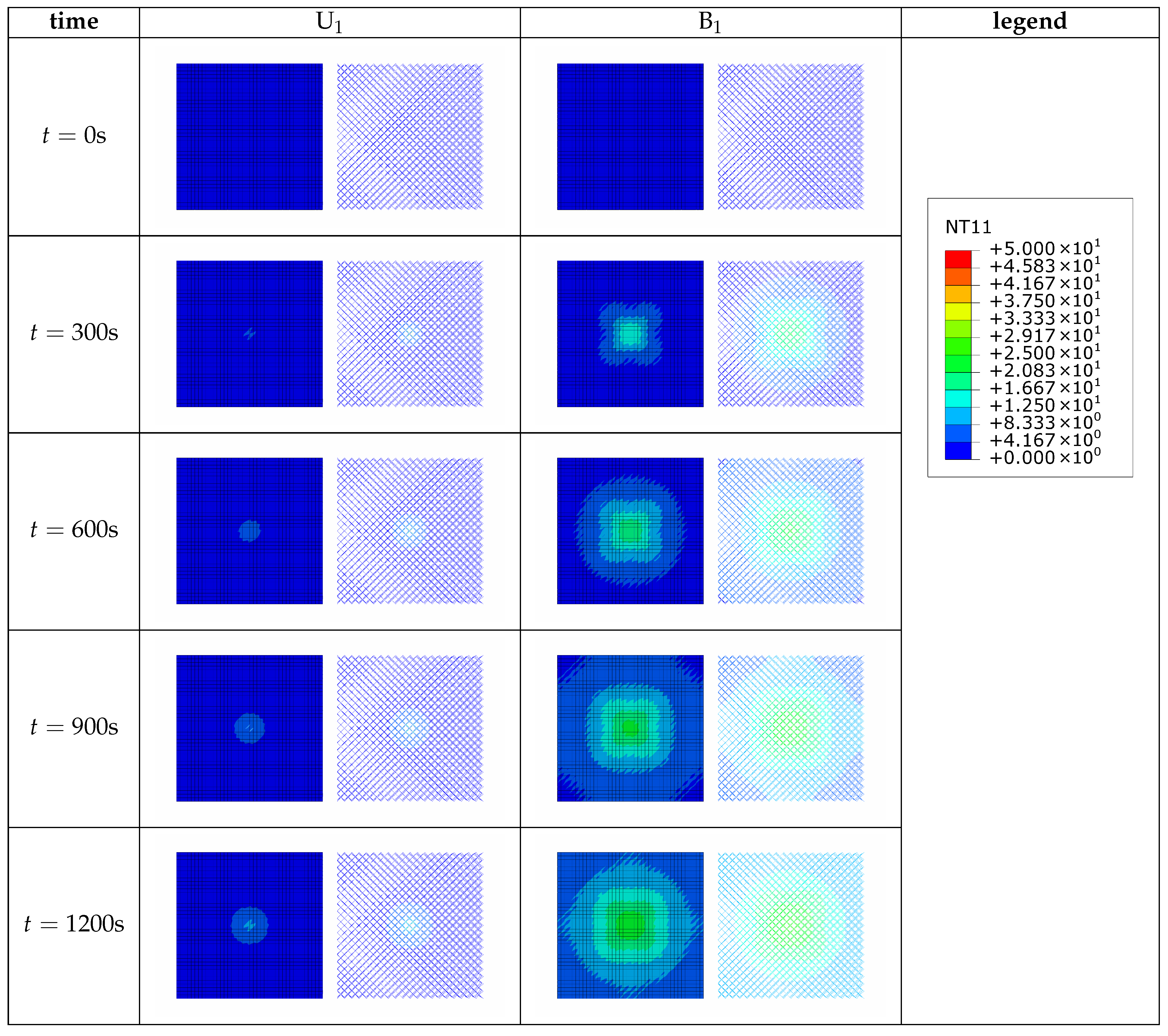
4.2. Working Condition 1
4.3. Working Condition 2
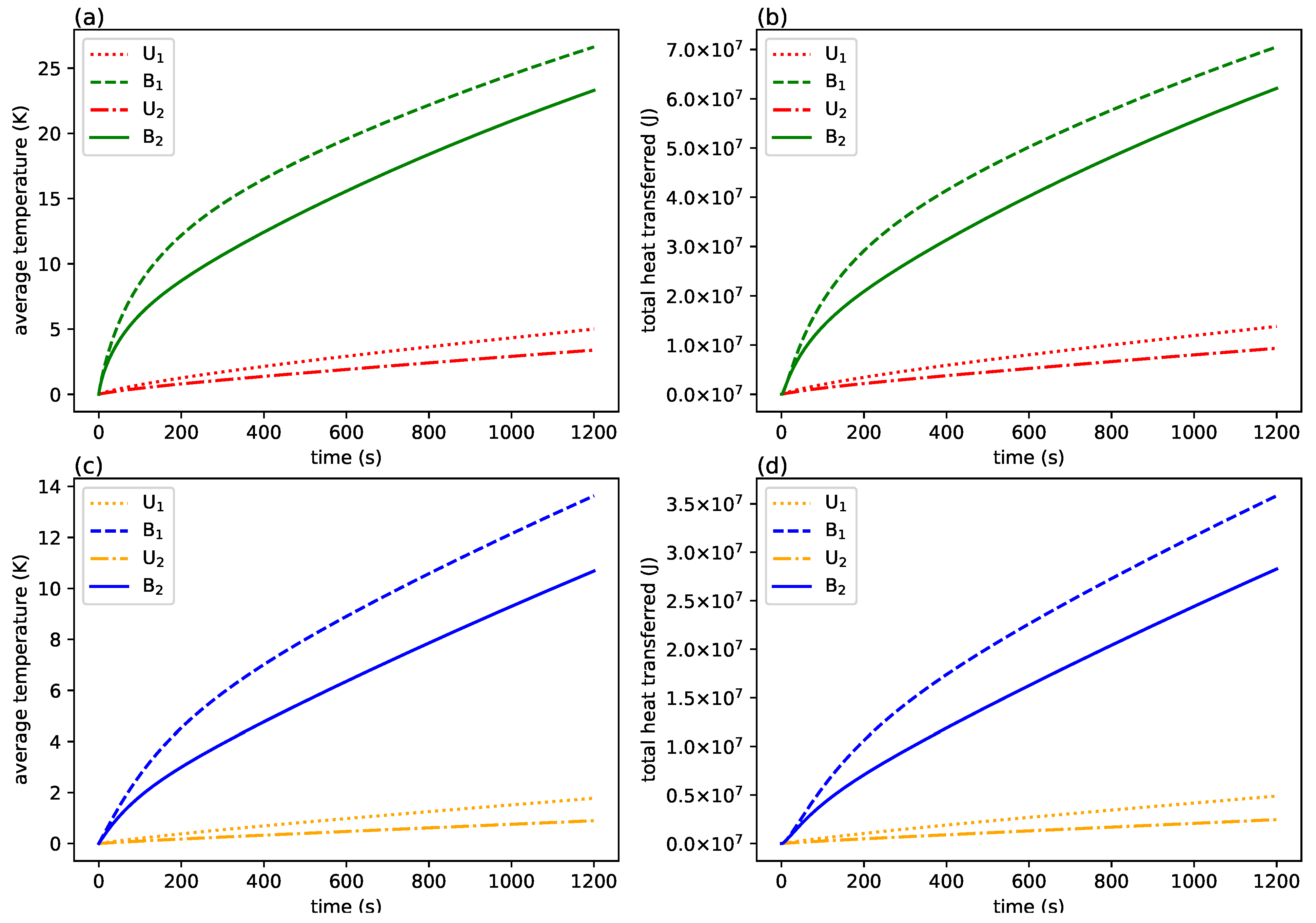
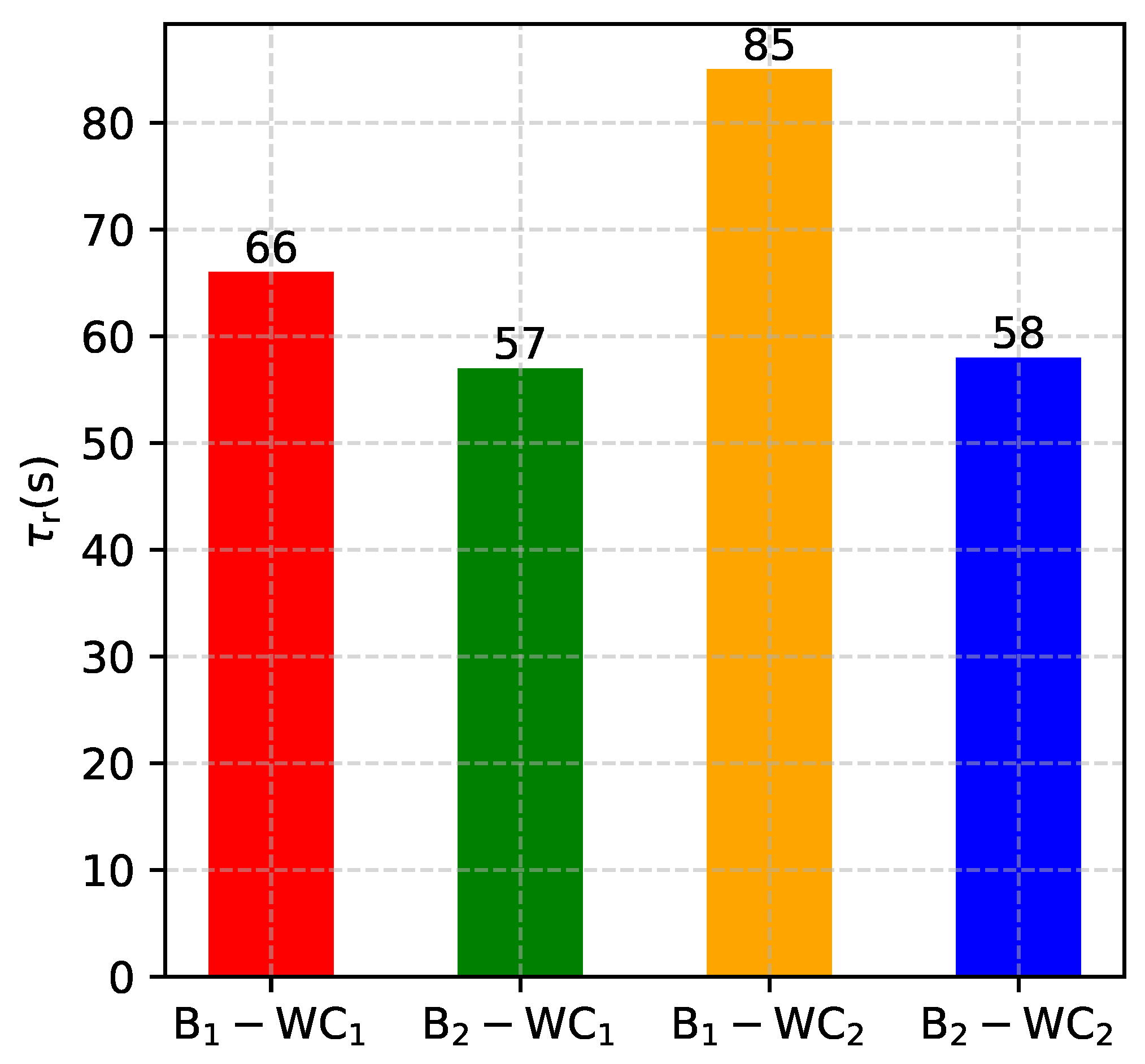
4.4. Comparison of Heat Transfer Efficiency
4.5. Comparison between and
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ashby, M.; Cebon, D. Materials Selection in Mechanical Design. J. Phys. IV Proc. 1993, 3, C7-1–C7-9. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.S.; Li, M.Z.; Joo, J.H.; Kang, K.J.; Kim, T.; Lu, T.J. Thermomechanical Properties of Brazed Wire-Woven Bulk Kagome Cellular Metals for Multifunctional Applications. J. Thermophys. Heat Transf. 2012, 26, 66–74. [Google Scholar] [CrossRef]
- Yan, H.B.; Zhang, Q.C.; Lu, T.J.; Kim, T. A Lightweight X-Type Metallic Lattice in Single-Phase Forced Convection. Int. J. Heat Mass Transf. 2015, 83, 273–283. [Google Scholar] [CrossRef]
- Joo, J.H.; Kang, K.J.; Kim, T.; Lu, T.J. Forced Convective Heat Transfer in All Metallic Wire-Woven Bulk Kagome Sandwich Panels. Int. J. Heat Mass Transf. 2011, 54, 5658–5662. [Google Scholar] [CrossRef]
- Kim, T.; Zhao, C.Y.; Lu, T.J.; Hodson, H.P. Convective Heat Dissipation with Lattice-Frame Materials. Mech. Mater. 2004, 36, 767–780. [Google Scholar] [CrossRef]
- Maloney, K.J.; Fink, K.D.; Schaedler, T.A.; Kolodziejska, J.A.; Jacobsen, A.J.; Roper, C.S. Multifunctional Heat Exchangers Derived from Three-Dimensional Micro-Lattice Structures. Int. J. Heat Mass Transf. 2012, 55, 2486–2493. [Google Scholar] [CrossRef]
- Ranut, P. On the Effective Thermal Conductivity of Aluminum Metal Foams: Review and Improvement of the Available Empirical and Analytical Models. Appl. Therm. Eng. 2016, 101, 496–524. [Google Scholar] [CrossRef]
- Dai, Z.; Nawaz, K.; Park, Y.G.; Bock, J.; Jacobi, A.M. Correcting and Extending the Boomsma–Poulikakos Effective Thermal Conductivity Model for Three-Dimensional, Fluid-Saturated Metal Foams. Int. Commun. Heat Mass Transf. 2010, 37, 575–580. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D. On the Effective Thermal Conductivity of a Three-Dimensionally Structured Fluid-Saturated Metal Foam. Int. J. Heat Mass Transf. 2001, 44, 827–836. [Google Scholar] [CrossRef]
- Haack, D.; Butcher, K.; Kim, T.; Lu, T. Novel Lightweight Metal Foam Heat Exchangers. Am. Soc. Mech. Eng. Process. Ind. Div. (Publ.) PID 2001, 6, 1–7. [Google Scholar]
- Wang, N.; Kaur, I.; Singh, P.; Li, L. Prediction of Effective Thermal Conductivity of Porous Lattice Structures and Validation with Additively Manufactured Metal Foams. Appl. Therm. Eng. 2021, 187, 116558. [Google Scholar] [CrossRef]
- Ho, J.; Leong, K. Cylindrical Porous Inserts for Enhancing the Thermal and Hydraulic Performance of Water-Cooled Cold Plates. Appl. Therm. Eng. 2017, 121, 863–878. [Google Scholar] [CrossRef]
- Ho, J.Y.; Leong, K.C.; Wong, T.N. Experimental and Numerical Investigation of Forced Convection Heat Transfer in Porous Lattice Structures Produced by Selective Laser Melting. Int. J. Therm. Sci. 2019, 137, 276–287. [Google Scholar] [CrossRef]
- Shen, B.; Li, Y.; Yan, H.; Boetcher, S.K.S.; Xie, G. Heat Transfer Enhancement of Wedge-Shaped Channels by Replacing Pin Fins with Kagome Lattice Structures. Int. J. Heat Mass Transf. 2019, 141, 88–101. [Google Scholar] [CrossRef]
- Deng, H.; Wang, C. Equivalent thermal analysis and optimization method for three-dimensional lattice structure. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1122–1128. [Google Scholar]
- Sypeck, D.J. Cellular Truss Core Sandwich Structures. Appl. Compos. Mater. 2005, 12, 229–246. [Google Scholar] [CrossRef]
- Yan, H.B.; Zhang, Q.C.; Lu, T.J. An X-Type Lattice Cored Ventilated Brake Disc with Enhanced Cooling Performance. Int. J. Heat Mass Transf. 2015, 80, 458–468. [Google Scholar] [CrossRef]
- Qi, C.; Wang, Y.; Tang, J. Effect of Squid Fin Bionic Surface and Magnetic Nanofluids on CPU Cooling Performance under Magnetic Field. Asia-Pac. J. Chem. Eng. 2020, 15, e2482. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, P.; Zheng, N.; Shan, F.; Liu, Z.; Liu, W. Numerical Investigation of Heat Transfer and Flow Characteristics of Laminar Flow in a Tube with Center-Tapered Wavy-Tape Insert. Appl. Therm. Eng. 2019, 148, 557–567. [Google Scholar] [CrossRef]
- Dey, P.; Hedau, G.; Saha, S.K. Experimental and Numerical Investigations of Fluid Flow and Heat Transfer in a Bioinspired Surface Enriched Microchannel. Int. J. Therm. Sci. 2019, 135, 44–60. [Google Scholar] [CrossRef]
- Huang, P.; Dong, G.; Zhong, X.; Pan, M. Numerical Investigation of the Fluid Flow and Heat Transfer Characteristics of Tree-Shaped Microchannel Heat Sink with Variable Cross-Section. Chem. Eng. Process.—Process. Intensif. 2020, 147, 107769. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Hu, X.; Yang, L. Characteristics of Heat Transfer and Fluid Flow in a Fractal Multilayer Silicon Microchannel. Int. Commun. Heat Mass Transf. 2016, 71, 86–95. [Google Scholar] [CrossRef]
- Xu, S.; Wang, W.; Fang, K.; Wong, C.N. Heat Transfer Performance of a Fractal Silicon Microchannel Heat Sink Subjected to Pulsation Flow. Int. J. Heat Mass Transf. 2015, 81, 33–40. [Google Scholar] [CrossRef]
- Zhang, D.y.; Luo, Y.h.; Li, X.; Chen, H.w. Numerical Simulation and Experimental Study of Drag-Reducing Surface of a Real Shark Skin. J. Hydrodyn. Ser. B 2011, 23, 204–211. [Google Scholar] [CrossRef]
- Žemaitis, A.; Mikšys, J.; Gaidys, M.; Gečys, P.; Gedvilas, M. High-Efficiency Laser Fabrication of Drag Reducing Riblet Surfaces on Pre-Heated Teflon. Mater. Res. Express 2019, 6, 065309. [Google Scholar] [CrossRef]
- Bai, Q.; Bai, J.; Meng, X.; Ji, C.; Liang, Y. Drag Reduction Characteristics and Flow Field Analysis of Textured Surface. Friction 2016, 4, 165–175. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Wang, C.; Huang, H.; Ma, R. Heat transfer performance of flat-plate heat pipe with bionic vein microstructure surface. J. Therm. Sci. Technol. 2019, 18, 471–475. [Google Scholar]
- Zhang, Q.; Han, Y.; Chen, C.; Lu, T. Ultralight X-Type Lattice Sandwich Structure (I): Concept, Fabrication and Experimental Characterization. Sci. China Ser. E Technol. Sci. 2009, 52, 2147–2154. [Google Scholar] [CrossRef]
- Sun, Z.; Cui, T.; Zhu, Y.; Zhang, W.; Shi, S.; Tang, S.; Du, Z.; Liu, C.; Cui, R.; Chen, H.; et al. The Mechanical Principles behind the Golden Ratio Distribution of Veins in Plant Leaves. Sci. Rep. 2018, 8, 13859. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, H.; Zhang, X.; Zeng, H.; Yang, H.; Lei, H.; Li, X.; Wang, Y. Lightweight Structure of a Phase-Change Thermal Controller Based on Lattice Cells Manufactured by SLM. Chin. J. Aeronaut. 2019, 32, 1727–1732. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, H.; Fu, W.; Bai, L.; Miao, J. Temperature Control of Star Sensor Baffle Using 3D Printing and PCM Thermal Energy Storage Technology. Int. J. Heat Mass Transf. 2021, 165, 120644. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, H.; Lin, G.; Jin, H.; Shen, X.; He, J.; Miao, J. Thermal Performance of a 3D Printed Lattice-Structure Heat Sink Packaging Phase Change Material. Chin. J. Aeronaut. 2021, 34, 373–385. [Google Scholar] [CrossRef]




| Parameters | Uniform Design 1 (U1) | Uniform Design 2 (U2) |
|---|---|---|
| N | 800 | 2700 |
| Parameters | Bionic Design 1 (B1) | Bionic Design 2 (B1) |
|---|---|---|
| 0.5 | 0.4 | |
| 1.793 | 1.746 | |
| Designs | WC1 | WC2 | ||
|---|---|---|---|---|
| 4897 | ||||
| ratio | 5.32 | 5.12 | 7.67 | 7.31 |
| 3.390 | 9344 | 0.896 | 2469 | |
| 23.298 | 62,106 | 10.683 | 28,275 | |
| ratio | 6.87 | 6.65 | 11.91 | 11.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Zhao, J.; Wang, C. Leaf Vein-Inspired Bionic Design Method for Heat Exchanger Infilled with Graded Lattice Structure. Aerospace 2021, 8, 237. https://doi.org/10.3390/aerospace8090237
Deng H, Zhao J, Wang C. Leaf Vein-Inspired Bionic Design Method for Heat Exchanger Infilled with Graded Lattice Structure. Aerospace. 2021; 8(9):237. https://doi.org/10.3390/aerospace8090237
Chicago/Turabian StyleDeng, Haoyu, Junpeng Zhao, and Chunjie Wang. 2021. "Leaf Vein-Inspired Bionic Design Method for Heat Exchanger Infilled with Graded Lattice Structure" Aerospace 8, no. 9: 237. https://doi.org/10.3390/aerospace8090237
APA StyleDeng, H., Zhao, J., & Wang, C. (2021). Leaf Vein-Inspired Bionic Design Method for Heat Exchanger Infilled with Graded Lattice Structure. Aerospace, 8(9), 237. https://doi.org/10.3390/aerospace8090237






