Impact Time Control Cooperative Guidance Law Design Based on Modified Proportional Navigation
Abstract
:1. Introduction
- (1)
- A more accurate time-to-go method compared to the time-to-go estimation methods designed in [32,33] is proposed, and based on which, the MPNG law is designed. The MPNG law is also effective when the initial leading angle is zero, while some existing impact time control guidance laws cannot start in [7,12,13,26].
- (2)
- The cooperative guidance architecture with centralized coordination is adopted, using the MPNG law as the local guidance, and the desired impact time as the coordination variables, a two-dimensional impact time control cooperative guidance law under constant velocity is designed, numerical simulation results verify the feasibility and applicability of the method.
- (3)
- The analytic function of velocity with respect to time is derived, and a three-dimensional impact time control cooperative guidance law under time-varying velocity based on desired impact time is designed.
2. Problem Statement
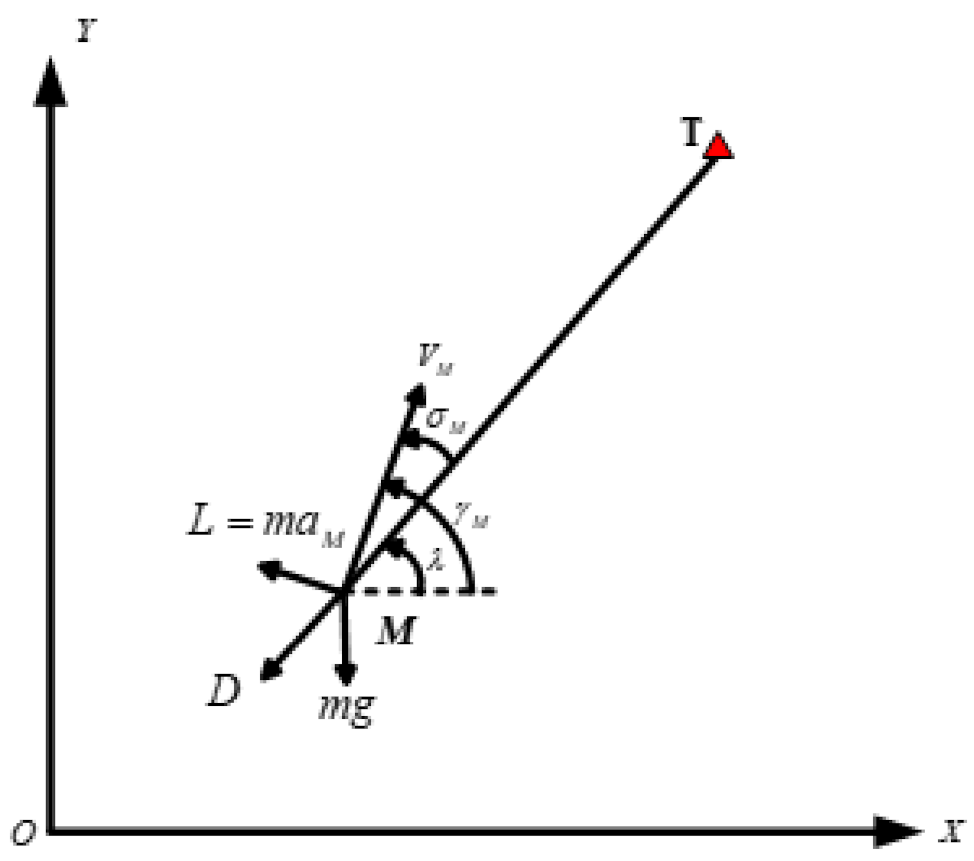
2.1. Mathematical Model of Missile on Two-Dimensional Plan
2.1.1. The Velocity of Missile Is Constant
2.1.2. The Velocity of Missile Is Time-Varying
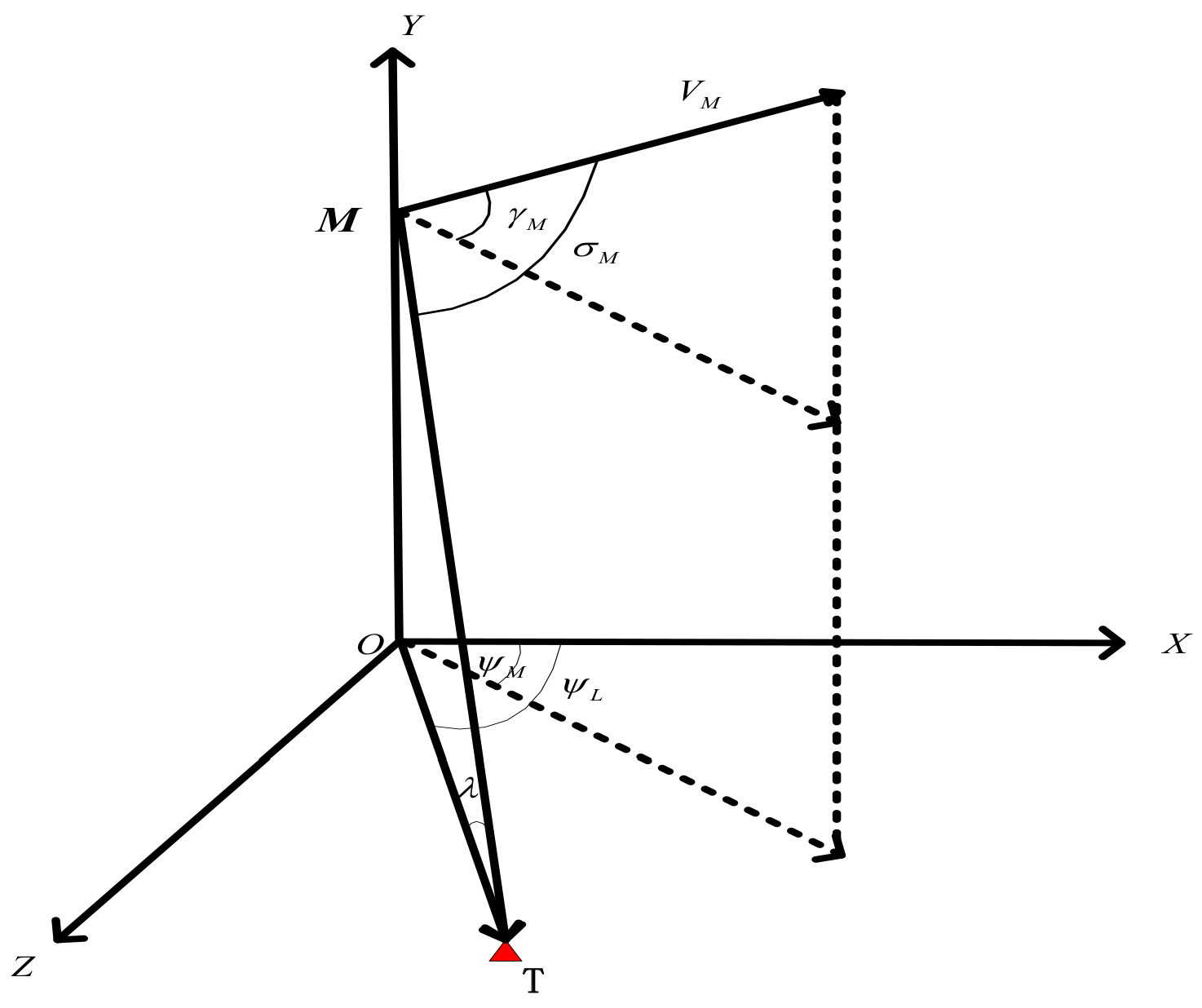
2.2. Mathematical Model of Missile in Three-Dimensional Space
3. Time-to-Go Estimation of PNG Law
3.1. Time-to-Go Estimation When Velocity Is Constant
3.2. Time-to-Go Estimation under Time-Varying Velocity
4. The Design of Impact Time Control Cooperative Guidance Law
4.1. Two-Dimensional Impact Time Control Cooperative Guidance Law under Constant Velocity
4.1.1. MPNG Law
4.1.2. Impact Time Control Cooperative Guidance Law Based on Coordination Variables
4.2. Three-Dimensional Impact Time Control Cooperative Guidance Law under Time-Varying Velocity
5. Numerical Simulation
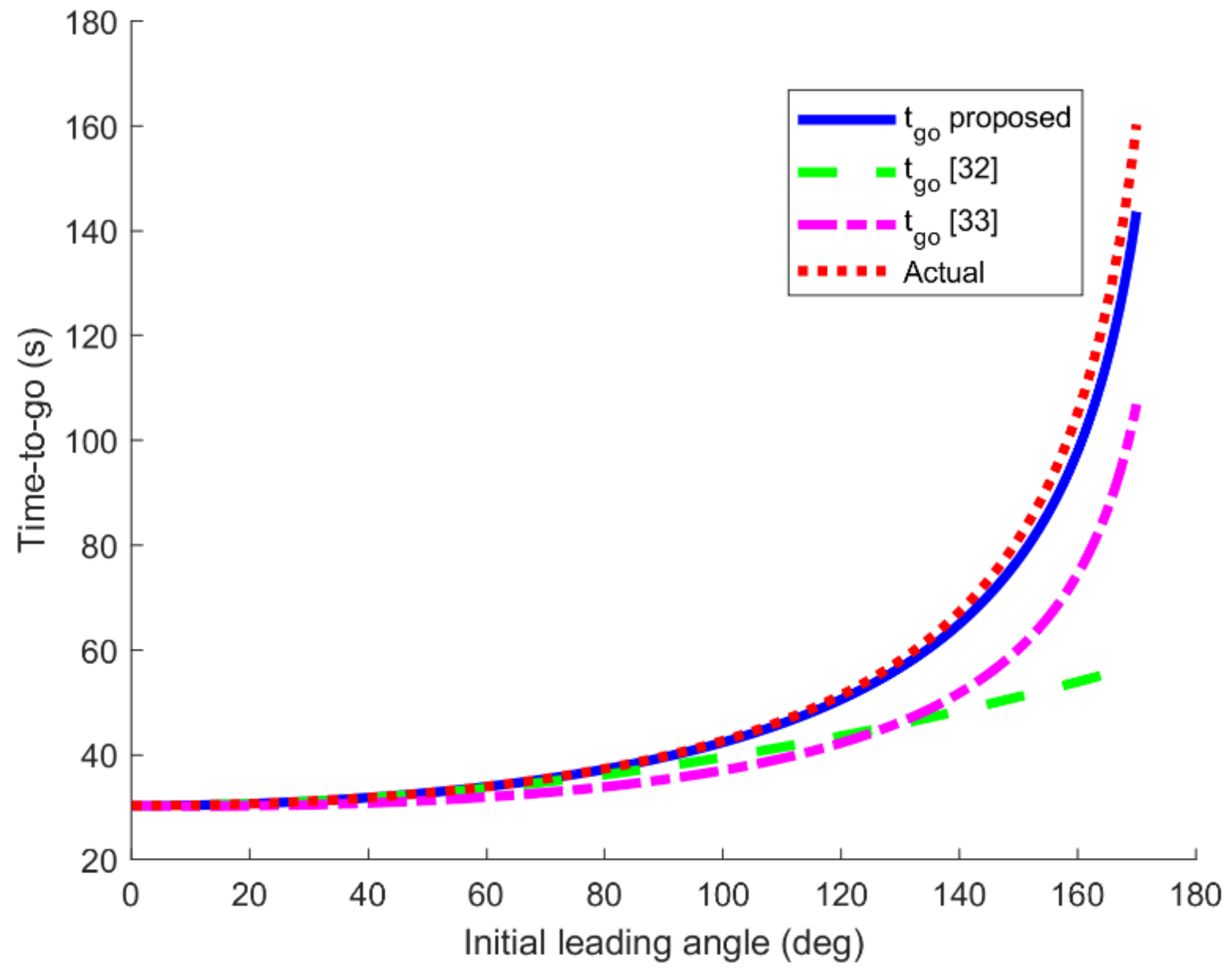
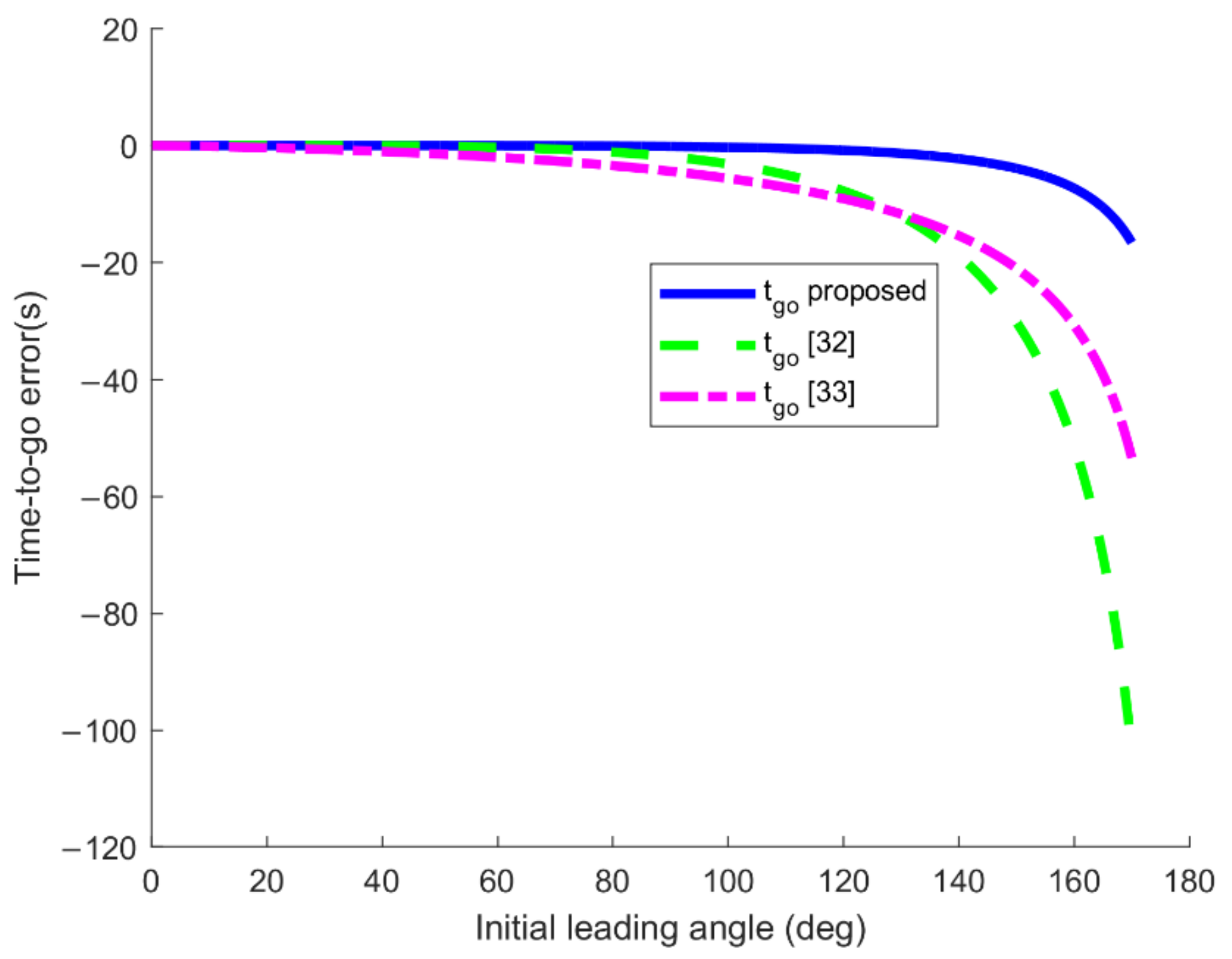
5.1. Comparison of Methods for Time-to-Go Estimation
5.2. Performance of MPNG Law
5.2.1. Comparison of the MPNG Law and the SMC Law
5.2.2. Salvo Attack with the MPNG Law
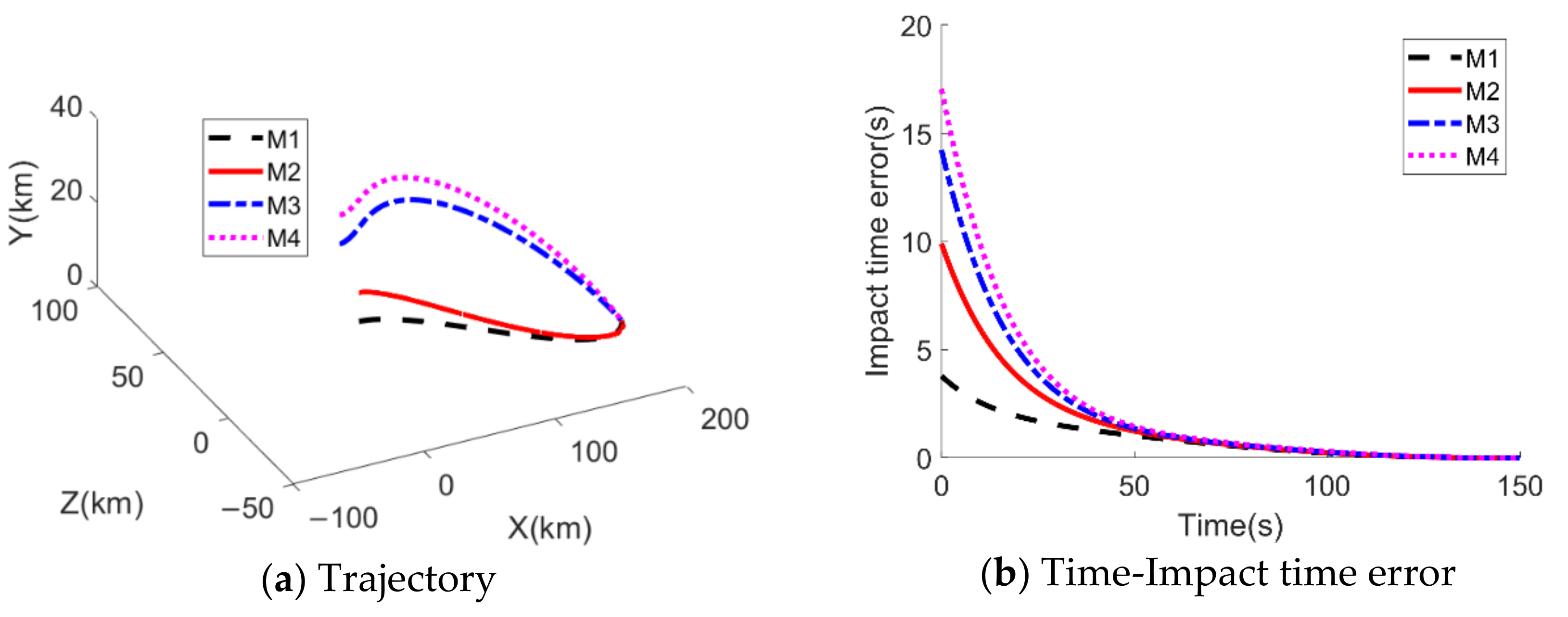
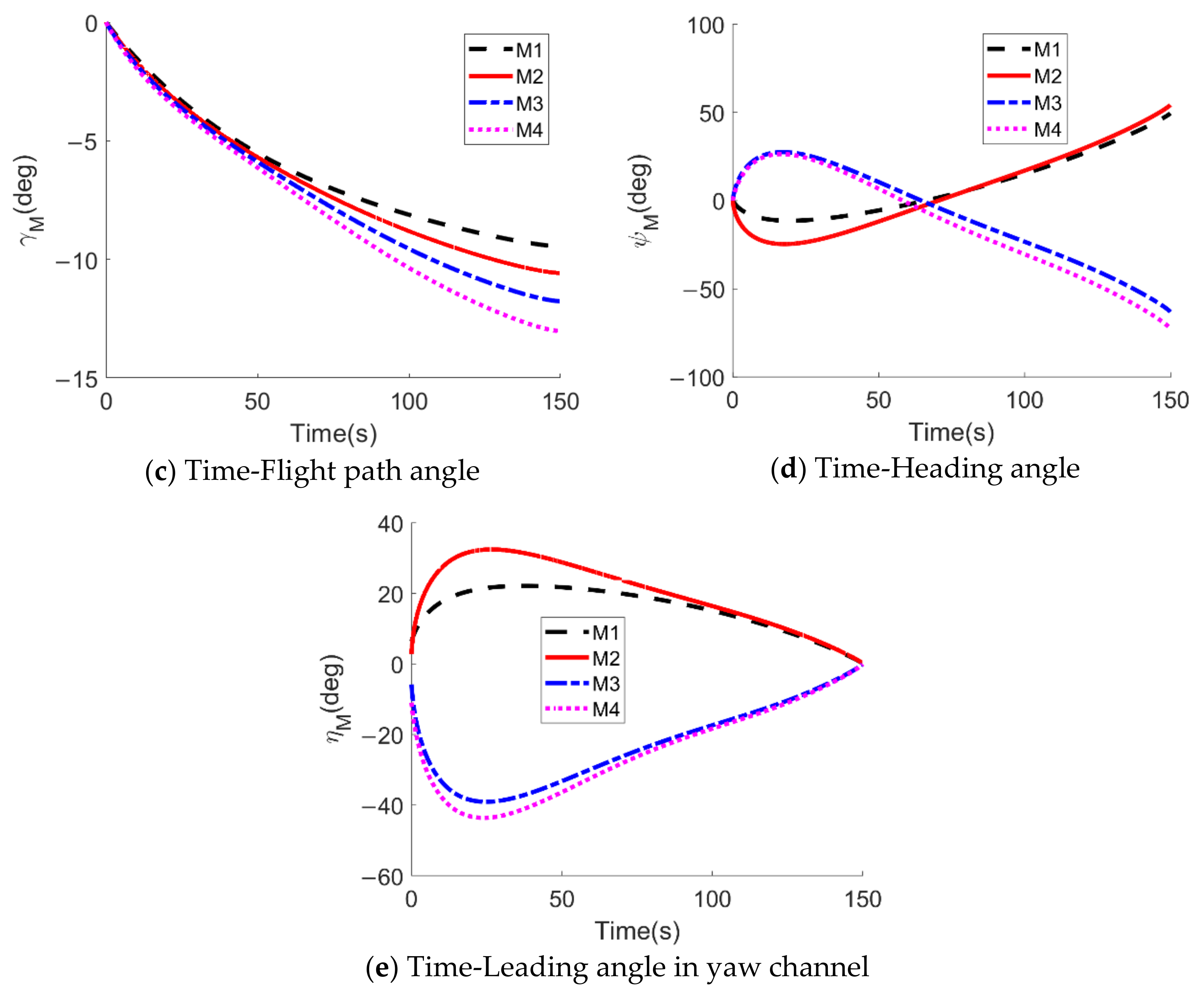
5.3. Performance of Two-Dimensional Impact Time Control Cooperative Guidance Law under Constant Velocity
5.4. Performance of Three-Dimensional Impact Time Control Cooperative Guidance Law under Time-Varying Velocity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lyu, T.; Guo, Y.; Li, C.; Ma, G.; Zhang, H. Multiple missiles cooperative guidance with simultaneous attack requirement under directed topologies. Aerosp. Sci. Technol. 2019, 89, 100–110. [Google Scholar] [CrossRef]
- Jiang, H.; An, Z.; Chen, S.; Xiong, F. Cooperative guidance with multiple constraints using convex optimization. Aerosp. Sci. Technol. 2018, 79, 426–440. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation. J. Guid. Control Dyn. 2016, 39, 1887–1892. [Google Scholar] [CrossRef]
- Tahk, M.J.; Sang, D.K. Guidance Law Switching Logic Considering the Seeker’s Field-of-view Limits. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 1049–1058. [Google Scholar]
- Zhang, Y.; Wang, X.; Ma, G. Impact time control guidance law with large impact angle constraint. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 2119–2131. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wu, H. Impact time control guidance law with field of view constraint. Aerosp. Sci. Technol. 2014, 39, 361–369. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, Y. Impact time control guidance law with seeker field of view limitation. J. Ballist. 2013, 25, 6–11. [Google Scholar]
- Cho, N.; Kim, Y. Modified Pure Proportional Navigation Guidance Law for Impact Time Control. J. Guid. Control Dyn. 2016, 39, 1–21. [Google Scholar] [CrossRef]
- He, S.; Lin, D. Three-Dimensional Optimal Impact Time Guidance for Antiship Missiles. J. Guid. Control Dyn. 2019, 42, 941–948. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Ghose, D.; Raha, S. Three dimensional PN based impact angle control for higher speed nonmaneuvering targets. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Kumar, S.R.; Ghose, D. Sliding mode control based guidance law with impact time constraints. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Kumar, S.R.; Ghose, D. Impact time guidance for large heading errors using sliding mode control. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3123–3138. [Google Scholar] [CrossRef]
- Cho, D.; Kim, H.J.; Tahk, M.J. Nonsingular Sliding Mode Guidance for Impact Time Control. J. Guid. Control Dyn. 2016, 39, 61–68. [Google Scholar] [CrossRef]
- Harl, N.; Balakrishnan, S.N. Impact Time and Angle Guidance With Sliding Mode Control. IEEE Trans. Control Syst. Technol. 2012, 20, 1436–1449. [Google Scholar] [CrossRef]
- Talole, S.E.; Phadke, S.B. Robust Input-Ouput Linearisation Using Uncertainly and Disturbance Estimation. Int. J. Control 2009, 82, 1794–1803. [Google Scholar] [CrossRef]
- Saleem, A.; Ratnoo, A. Lyapunov-Based Guidance Law for Impact Time Control and Simultaneous Arrival. J. Guid. Control Dyn. 2016, 39, 164–173. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y.; Li, P.; Guo, H.; Wu, W. Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry. Aerospace 2020, 8, 6. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, B.; Liu, L.; Wang, Y. A composite impact-time-control guidance law and simultaneous arrival. Aerosp. Sci. Technol. 2018, 80, 403–412. [Google Scholar] [CrossRef]
- Wang, P.; Guo, Y.; Ma, G.; Wie, B. New Differential Geometric Guidance Strategies for Impact-Time Control Problem. J. Guid. Control Dyn. 2019, 42, 1982–1992. [Google Scholar] [CrossRef]
- Hu, Q.; Han, T.; Xin, M. Sliding-Mode Impact Time Guidance Law Design for Various Target Motions. J. Guid. Control Dyn. 2019, 42, 136–148. [Google Scholar] [CrossRef]
- Kumar, S.R.; Ghose, D. Impact time and angle control guidance. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Kumar, S.R.; Ghose, D. Sliding mode guidance for impact time and angle constraints. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 232, 2961–2977. [Google Scholar] [CrossRef]
- Ryoo, C.K.; Cho, H.; Tahk, M.J. Optimal guidance laws with terminal impact angle constrain. J. Guid. Control Dyn. 2005, 28, 724–732. [Google Scholar] [CrossRef]
- Hou, Z.; Yang, Y.; Liu, L.; Wang, Y. Terminal sliding mode control based impact time and angle constrained guidance. Aerosp. Sci. Technol. 2019, 93, 105142. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, G.; Liu, A. Guidance law with impact time and impact angle constraints. Chin. J. Aeronaut. 2013, 26, 960–966. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Wang, J. Optimal control based guidance law to control both impact time and impact angle. Aerosp. Sci. Technol. 2019, 84, 454–463. [Google Scholar] [CrossRef]
- Zhao, S.; Rui, Z. Multi-missile Cooperative Guidance Using Coordination Variables. Acta Aeronaut. Astronaut. Sin. 2008, 29, 1605–1611. [Google Scholar]
- Kumar, S.R.; Ghose, D. Cooperative Rendezvous Guidance using Sliding Mode Control for Interception of Stationary Targets. IFAC Proc. Vol. 2014, 47, 477–483. [Google Scholar] [CrossRef]
- Zhang, B.; Song, J.; Song, S. Research on multi-missile coordinated guidance with angle constraints. J. Proj. Rocket. Missiles Guid. 2014, 34, 13–15. [Google Scholar]
- Zhao, E.; Wang, S.; Chao, T.; Yang, M. Multiple missiles cooperative guidance based on leader-follower strategy. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014. [Google Scholar]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Homing guidance law for cooperative attack of multiple missiles. J. Guid. Control Dyn. 2010, 33, 275–280. [Google Scholar] [CrossRef]
- Dhananjay, N.; Ghose, D. Accurate Time-to-Go Estimation for Proportional Navigation Guidance. J. Guid. Control Dyn. 2014, 37, 1378–1383. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, G.; Wei, C.; Cai, D.; Yu, Y. Impact-Time-Control Guidance Law for Hypersonic Missiles in Terminal Phase. IEEE Access 2020, 8, 44611–44621. [Google Scholar] [CrossRef]

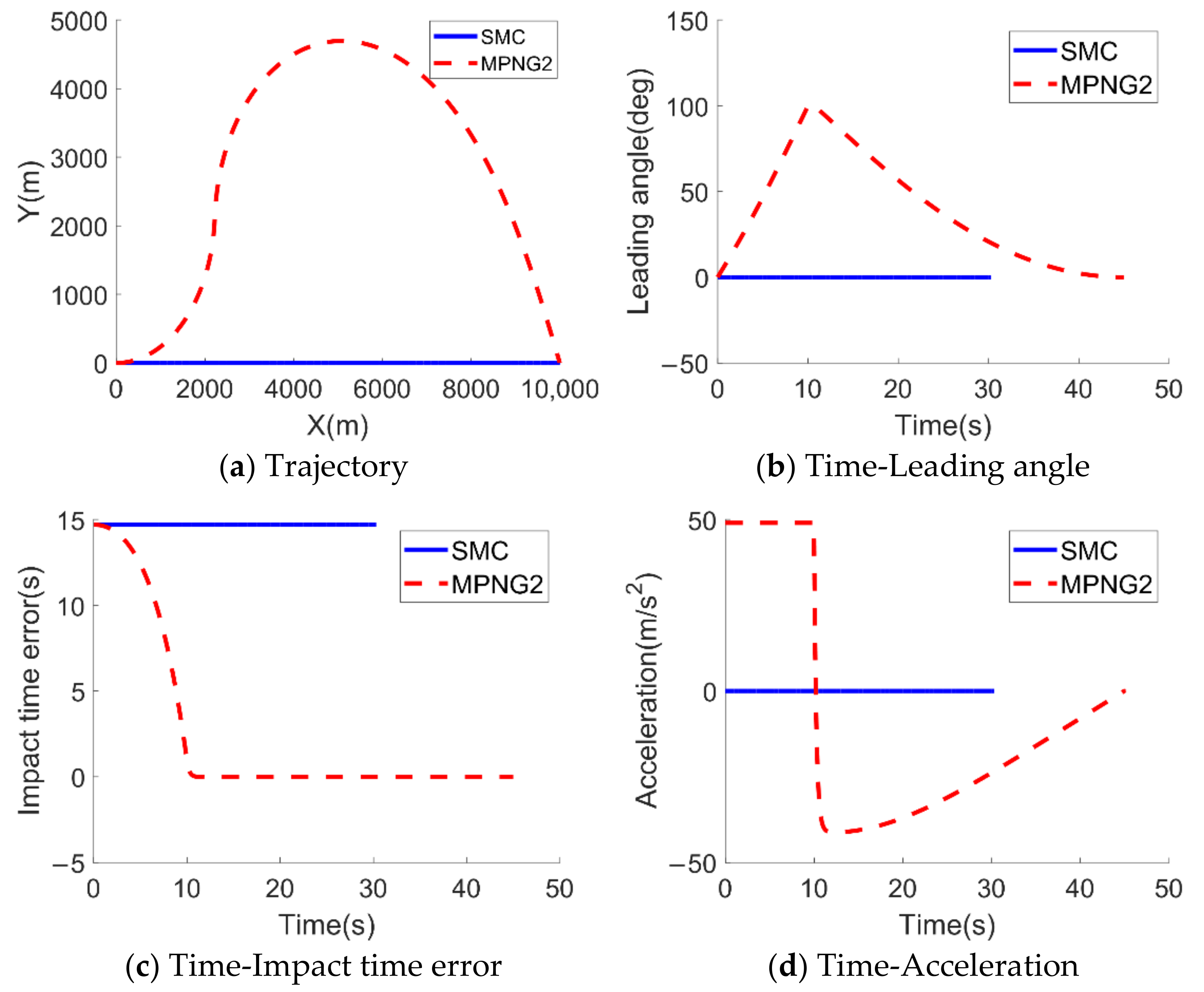
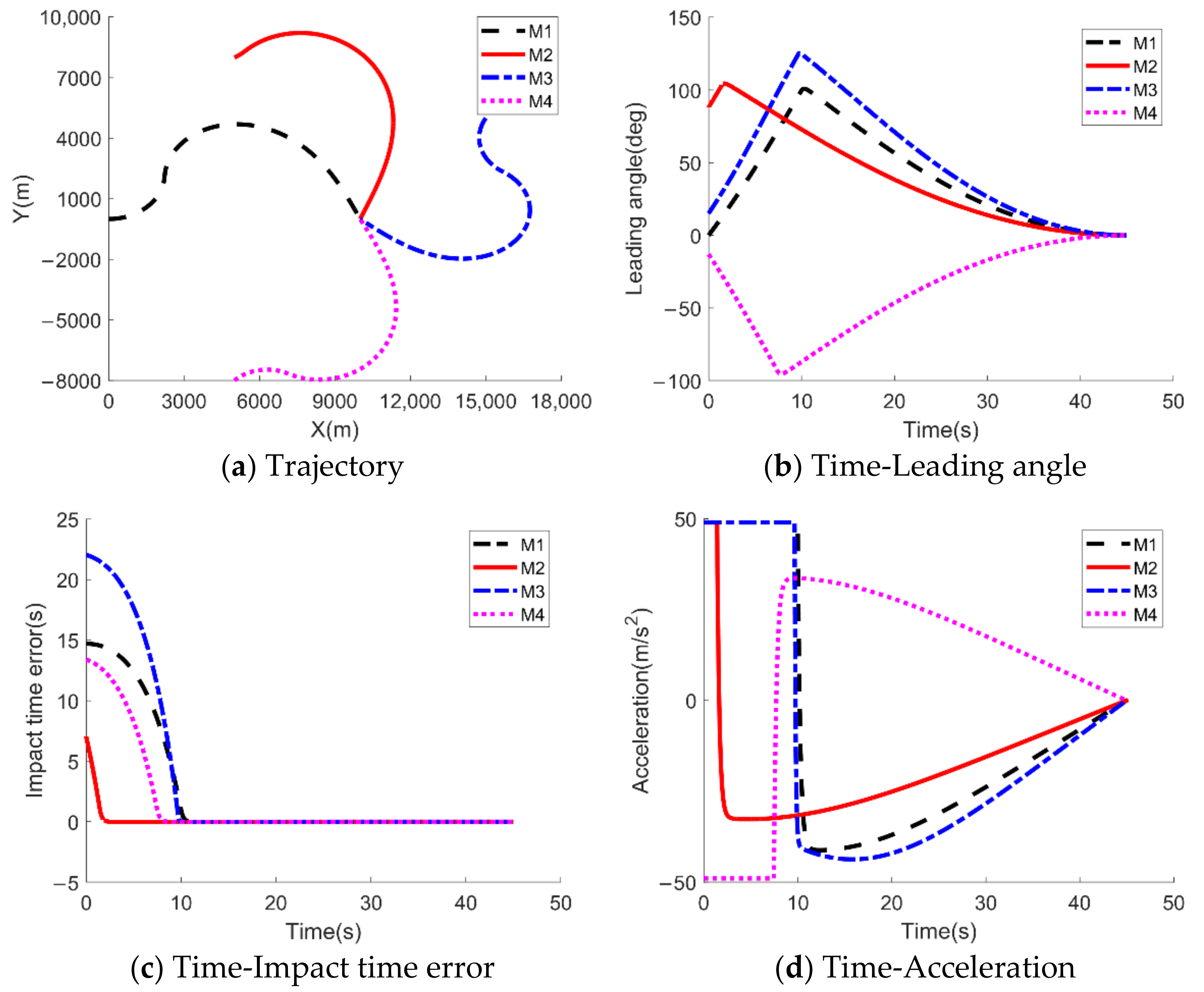
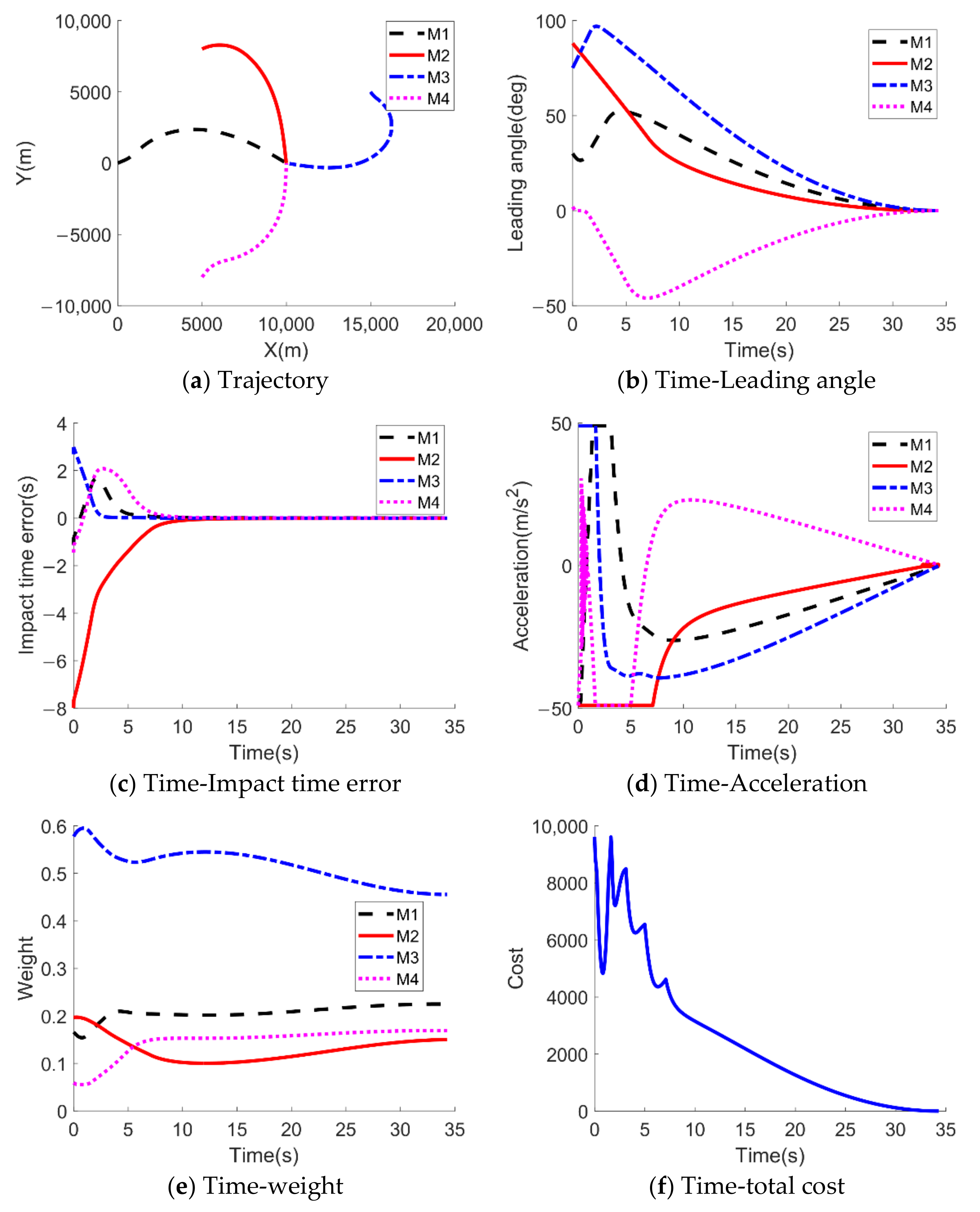
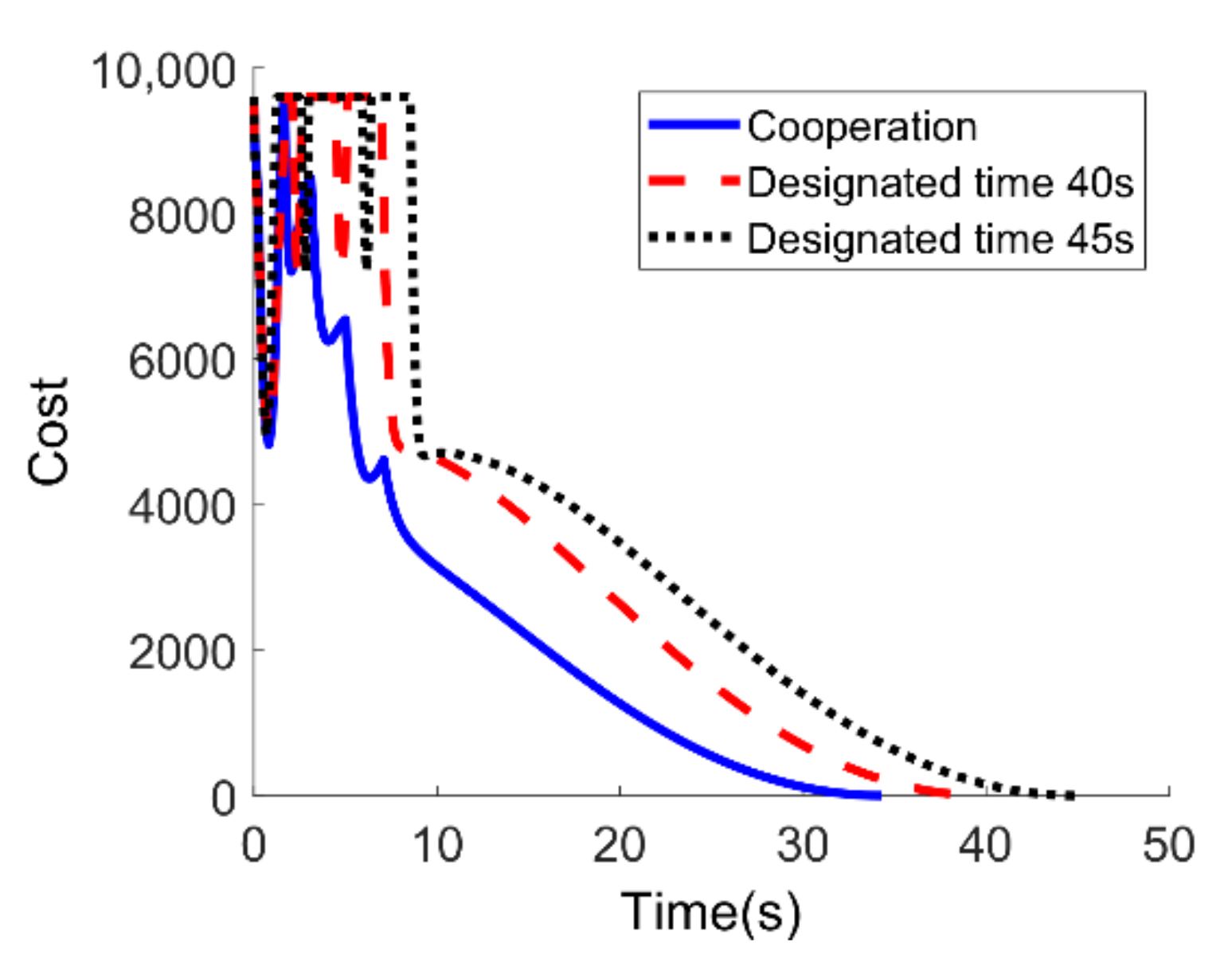
| (0,0) km | |
|---|---|
| Target position | (10,0) km |
| Velocity of the missile | 330 m/s |
| Initial flight path angle | 0 deg |
| Missiles | Initial Position (km) | Target Position (km) | Velocity (m/s) | Initial Flight Path Angle (Deg) | Designated Impact Time (s) |
|---|---|---|---|---|---|
| M1 | (0,0) | (10,0) | 330 | 0 | 45 |
| M2 | (5,8) | 320 | 30 | ||
| M3 | (15,5) | 310 | −120 | ||
| M4 | (5,−8) | 300 | 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Ge, J.; Xu, Q.; Yang, T. Impact Time Control Cooperative Guidance Law Design Based on Modified Proportional Navigation. Aerospace 2021, 8, 231. https://doi.org/10.3390/aerospace8080231
Jiang Z, Ge J, Xu Q, Yang T. Impact Time Control Cooperative Guidance Law Design Based on Modified Proportional Navigation. Aerospace. 2021; 8(8):231. https://doi.org/10.3390/aerospace8080231
Chicago/Turabian StyleJiang, Zhanyuan, Jianquan Ge, Qiangqiang Xu, and Tao Yang. 2021. "Impact Time Control Cooperative Guidance Law Design Based on Modified Proportional Navigation" Aerospace 8, no. 8: 231. https://doi.org/10.3390/aerospace8080231
APA StyleJiang, Z., Ge, J., Xu, Q., & Yang, T. (2021). Impact Time Control Cooperative Guidance Law Design Based on Modified Proportional Navigation. Aerospace, 8(8), 231. https://doi.org/10.3390/aerospace8080231





