Hybrid Rocket Engine Design Optimization at Politecnico di Torino: A Review

Abstract

Optimization of Hybrid Rocket Engines at Politecnico di Torino began in the 1990s. A comprehensive review of the related research activities carried out in the last three decades is here presented. After a brief introduction that retraces driving motivations and the most significant steps of the research path, the more relevant aspects of analysis, modeling and achieved results are illustrated. First, criteria for the propulsion system preliminary design choices (namely the propellant combination, the feed system and the grain design) are summarized and the engine modeling is presented. Then, the authors describe the in-house tools that have been developed and used for coupled trajectory and propulsion system design optimization. Both deterministic and robust-based approaches are presented. The applications that the authors analyzed over the years, starting from simpler hybrid powered sounding rocket to more complex multi-stage launchers, are then presented. Finally, authors’ conclusive remarks on the work done and their future perspective in the context of the optimization of hybrid rocket propulsion systems are reported.

1. Introduction

The history of trajectory and propulsion system optimization at the Politecnico di Torino (POLITO) begins thanks to the efforts of two brilliant Professors, Giuseppe Bussi and Guido Colasurdo. Two of the authors (L. Casalino and D. Pastrone) had the privilege to have them as mentors, colleagues and friends. With an in-depth study, Giuseppe Bussi reworked the Theory of Optimal Control to obtain a synthetic formulation suitable for an engineering approach. His colleague and friend Guido Colasurdo, inspired by this work, started the development of an in-house indirect approach method for trajectory optimization. This procedure and its improved versions become the backbone of a great numbers of optimization analysis carried out at POLITO, being able to deal with both impulsive and finite thrust, ascent trajectories, orbit tranfers, rendez-vous, unpowered/powered/aero-assisted flybys, interplanetary missions and debris removal.

The capabilities of this indirect optimization procedure was tested during the participation to different editions of Global Trajectory Optimization Competition (GTOC). This competition was initiated by ESA in 2005, with the purpose of comparing and developing methods for space trajectory optimization. The POLITO team was the winner of the GTOC2, (https://sophia.estec.esa.int/gtoc_portal/?page_id=15, accessed on 24 May 2021) organized by NASA Jet Propulsion Laboratory (JPL) in 2006, and GTOC6 [1] (in team with the Università di Roma Sapienza) organized by JPL in 2012, and obtained several additional good placements. The outstanding results obtained proved the validity of the procedure and the excellent level of know-how and skills reached at POLITO in such field. In parallel, due to the strong interdependence of propulsion system performance and specific application, the same approach has been used to carry out coupled optimization of trajectory, propulsion systems design and control [2,3]. In this fertile environment, starting from the early 90’s, Hybrid Rocket Engines drew attention of the researchers at POLITO [4].

In that period chemical rockets were (and still remain) the most common propulsion systems option for space transportation and exploration. Despite their lower technological maturity, Hybrid Rocket Engines (HREs) were promising propulsion alternative to Liquid Rocket Engines (LREs) and Solid Rocket Motors (SRMs). In fact, HREs result in being safer and lower-cost with performance close to semi-cryo LREs. The physical separation of oxidizer and fuel, stored in two different phases, gives interesting advantages to HREs: the solid grain contains only fuel, resulting in safer and simpler production process and operation with respect to SRM grains, while the flow of liquid oxidizer can be controlled, allowing for fine throttling, shut-down and restart of the engine, such as in LREs. Last, but not the least, HREs propellants are in general more environmentally friendly than storable-liquid and solid counterparts, characteristic which becomes more and more relevant as ecological consciousness grows in the public community. On the other hand some issues, together with lack of substantial funding, delayed the HREs development. Main challenges are related to their peculiar combustion process, which usually determines a low regression rate [5], and the time-dependent coupling of thrust level and mixture ratio through the evolution of grain geometry, which makes the mixture ratio a variable parameter even if the oxidizer mass flow is kept constant (i.e., the so-called mixture-ratio shifting).

Researchers at POLITO were fascinated by the great growth margin of HREs and were intrigued by their peculiar control behavior, envisaging that their in-house optimization methods could have been used to make the most of HREs performance while preserving their simple one-lever control architecture. In the meanwhile, the historical flight of Space Ship One in 2004 gave a significant impulse to HREs development and, since then, dedicated research programs flourished all over the world. Networking started in Italy [6], while membership in American Institution of Aeronautics and Astronautics (AIAA) gave to POLITO researchers the opportunity to be part of an international, lively, friendly and inspiring community of rocket scientists. Different applications were considered and optimization procedures were improved. In this contest, the authors become more and more aware that the regression rate, one of the most important value to be determined for HREs design and performance prediction, is difficult to measure, has a high degree of scatter, is strongly test-dependent and suffers from scale effects [7,8,9]. Specifically, a lecture held by Professor Brian Cantwell during a AIAA Hybrid Rocket Technical Committee meeting [10], inspired the authors to analyze the effects of regression rate uncertainties, driving them towards robust design [11]. Since then, the authors have developed in-house robust-based procedures aiming at an optimal design which is less sensitive to the presence of uncertainties and able to grant mission accomplishment.

The present work represents a comprehensive review of the research carried out at POLITO, from the early 1990s to the present day, concerning the design and optimization of HREs. In Section 2 the engine modeling is presented highlighting the main options to choose from. Section 3 is devoted to the approaches developed by the authors concerning the optimization of engine and trajectory. Special attention is paid to the robust-based optimization. In Section 4, the main application considered by the authors are collected and the most important results summarized. In the end, concluding remarks and future perspective are presented in Section 5.

2. Hybrid Rocket Engine Modeling

The engine performance must be evaluated many times during the optimization process, and the engine model must be able to guarantee a suitable accuracy while having a low computational cost. In this section the models used for engine design and operation are described (Section 2.4) including the main sub-system options to choose from, namely the propellant combination (Section 2.1), the feed system (Section 2.2) and the grain geometry (Section 2.3).

2.1. Propellant Combination

The selection of propellants combination strongly affects design, performance and operation of the engine. As outlined by [12], practical known propellants do not have all the desired properties and present some drawbacks. Therefore, propellant combination is usually chosen as a compromise of different factors such as performance, availability, handling/storability, hazards, physical properties of unreacted propellants and combustion properties. Among the others, density of stored propellants, characteristic velocity $c^{*}$ and regression correlation parameters are the most relevant properties for HREs.

For the oxidizer, a few options are viable for HRE, and the following oxidizers have been considered: Liquid OXygen (LOX), Hydrogen Peroxide (HP), and Nitrous OXide (NOX). Oxygen is stored in liquid phase at cryogenic temperature and can be injected in the combustion chamber directly as a liquid or can be gasified before ignition in order to enhance its stability. The vaporization process of LOX adds costs and weight, reducing at the same time the system safety. Among selected oxidizers, LOX gives the highest characteristic velocities, even if maximum values of $c^{*}$ are obtained at a quite low mixture ratio $\alpha$, making the low regression rate a pressing issue. Unlike LOX, which is completely non-toxic, HP (in water solutions) and NOX are slightly toxic and may decompose in their tank. The use of HP usually requires a catalytic bed, which is an expensive component (due to the rare metal employed in the decomposition reaction) and introduces complexity to the feeding system. NOX does not require any additional subsystem and is directly injected in the combustion chamber due to its slower decomposition rate. Uncontrolled decomposition may still lead to tank over-pressure; nonetheless, NOX is assessed as fairly safe. Despite its low performance, NOX is currently considered to be appealing for different applications thank to its low cost and its self-pressurizing behavior when stored at ambient temperature.

For the fuel selection, the regression rate value represents an important driver: the fuel mass flow is proportional to the product of burning surface by regression rate and low regression rates lead to excessively long fuel grains or multi-port fuel grains (as will be discussed in the following). A mitigation strategy consists in the use of propellant combinations which are characterized by a maximum value of $c^{*}$ at high values of the mixture ratio, thus reducing the relative contribution of fuel flow to the overall propellant flow exhausted by the engine. Unfortunately, this behavior is typical of oxidizers which contain also non-oxidizing species, which have a detrimental effect on propellant combination performance. Most straightforward solutions are based on the improvement of the regression rate value. Paraffin-based fuels form a melting layer on the grain surface which may be unstable, under proper conditions, and a new mass transfer mechanism, called entrainment, enhances regression rate: liquid droplets, coming from the melting layer, enter the boundary layer without enhancing the negative effect of surface blowing on the convective heat flux [13,14]. Similar effects may be obtained by freezing propellants (solid cryogenic hybrids), and using fuel additives, unconventional injectors or geometries. Please note that all of these approaches have some drawbacks, such as higher cost, safety, and environmental issues, and costs vs. benefits have to be evaluated for any given mission/application.

In their works, the authors considered and compared a few different propellant combinations [15,16,17]. An interesting and comprehensive comparison of propellants for hybrids applications can be found in [18]. Six propellant combinations were taken into account in order to find the optimal design of a hybrid-powered sounding rocket. The cost function to be optimized was the time spent above 100 km (i.e., in micro-gravity conditions) for given initial and payload masses. The regression rate correlation coefficients a and exponent n are reported in

Table 1. HREs propellant combinations. PE and HTPB stand for PolyEthylene and Hydroxyl-Terminated PolyButadiene, respectively.

Propellants	a	n	Ref.
	${\mathbf{m}}^{1+2\mathbf{n}}$${\mathbf{kg}}^{-\mathbf{n}}{\mathbf{s}}^{\mathbf{n}-1}$	-	-
HP/PE	$7.00\times {10}^{-6}$	$0.800$	[19,20]
HP 90%/HTPB	$2.47\times {10}^{-5}$	$0.666$	[21]
LOX/HTPB	$9.29\times {10}^{-6}$	$0.852$	[22]
LOX/Wax	$9.10\times {10}^{-5}$	$0.690$	[13]
NOX/PE	$1.04\times {10}^{-4}$	$0.352$	[23]
NOX/HTPB	$1.87\times {10}^{-4}$	$0.347$	[24]

. LOX/paraffin-based wax resulted in being the best propellant combination due to its large regression rate, allowing for the use of simpler grain designs and mixture ratios really close to the optimal values which maximize the characteristic velocity $c^{*}$.

2.2. Feed System

As outlined in Section 1, a time-dependent link exists between thrust level and specific impulse: the fuel mass flow ${\dot{m}}_F$ is a function of oxidizer mass flow ${\dot{m}}_O$, burning area $A_b$ and port area $A_p$. Thus, the choice of the feeding system and control is even more crucial than in LREs, since it has a stronger impact on performance. Some researchers proposed approaches to control mixture ratio at cost of increased engine architecture complexity [25]. At the moment, researchers at POLITO analyzed the potential of the more classical one-lever control architecture.

The simplest feeding system available for HREs is the pressure-feed blow down type, which is particularly suited for applications where a low $\Delta v$ gain (i.e., a low total impulse) is required. In this case, the propellant flow is not controlled but a proper blow down ratio is to be selected to obtain acceptable thrust level variations while keeping the mixture ratio in a proper range. Due to its high vapor pressure (50.4 bar at 293 K, 58.9 bar at 300 K), NOX has an appealing self-pressurizing behavior, reducing tank pressure decrease and improving performance. In fact, when NOX is stored at ambient temperature as a saturated liquid, the pressure decrease due to liquid outflow during engine operation induces evaporation of a portion of liquid NOX. The benefit is limited by the fact that phase change lowers the temperatures of the liquid, thus lowering the actual vapor pressure. In this case, in order to evaluate HREs performance, a proper model of NOX behavior is required to evaluate tank pressure history. The simplest homogeneous model may be not sufficiently accurate. The authors [26] developed a two-phase lumped model based on the spinodal line which is able to give an approximated but still quite accurate evaluation of tank pressure at a low computational cost (see Figure 1). Further details may be found in Appendix A.

For liquid propellants without self-pressurizing capabilities, performance may be enhanced by actively restoring the tank pressure among blow down phases, by means of rapid recharges from auxiliary pressurizing tanks. A single-shot repressurization was considered in Ref. [28], as depicted in Figure 2. This technique was used in the liquid mono-propellant blow down system of Magellan spacecraft and guarantees a lower thrust level variation at cost of a slightly increased system complexity.

Better performance and control capabilities can be obtained with continuously regulated feed system which, however, introduces additional components and weight. The following examples show that the optimal solution privileges the reduction of the aforementioned additional weight by means of a partially regulated feed system, in which a constant tank pressure phase is followed by a blow down phase.

All the above-mentioned gas pressure feed systems are not well suited for high $\Delta v$ applications, when high pressure levels are needed in the tank to keep high thrust levels and regression rates. In this case, the oxidizer and auxiliary tanks are may be excessively heavy and the use of turbo pump feed systems can improve rocket performance in a substantial way: propellant tank mass is reduced since both tank pressure and pressurizing gas requirements are low. However, in HREs there is only one liquid propellant, thus it is quite hard to produce an high-energy working fluid to feed a turbine to drive the pump. Possible solutions, such as decomposing mono propellants (e.g., HP) or auxiliary liquid propellants, introduce additional complexity to the feeding system (i.e., higher costs). For this reasons, the use of batteries to power an electrically driven turbo pump is really promising. Details about the models developed to describe such feed systems are reported in Appendix B.

In Ref. [29] a HRE powered upper-stage of a Vega-like launcher was optimized comparing blow down, partially regulated and electric pump feed systems. The chosen propellant combination was HP/PE and, due to the low regression rate, a multi-port grain was adopted (see the following Section 2.3 and Appendix C). The initial mass of the third stage was given (14,522 kg) and the mission target was the insertion of the payload into a 700-km circular polar orbit.

In Figure 3, trends of thrust and mixture ratio are shown. The thrust range variation is reduced when passing from blow down to turbo pump. On the contrary, a larger variation of mixture ratio occurs and specific impulse penalties are expected. Nevertheless, dry mass reductions prevails: the regulated case has a 200 kg gain (more than 10%) with respect to the blow down case and further 200 kg are gained by the turbo pump case. Similar results are found for different applications and propellants. For instance, in Ref. [30], the same problem was analyzed with a robust-based approach, but with LOX and paraffin-based wax as propellants and with a single port grain (thanks to the higher regression rate). In this case the gain of the turbo pump solutions with respect to a regulated case was 250–400 kg depending on the considered technological level of batteries and electric motor, as reported in

Table 2. Mass budget comparison. The first column reports the feed system employed: regulated (R) or turbo-pump (TP). (A) and (B) refer to the electrical properties used in the mass evaluation (see Table A1).

Case	$\mathit{\mu }$	${\mathit{m}}_{\mathit{p}}$	${\mathit{m}}_{\mathit{c}\mathit{c}}$	${\mathit{m}}_{\mathit{t}}$	${\mathit{m}}_{\mathit{n}\mathit{z}}$	${\mathit{m}}_{\mathit{c}\mathit{a}\mathit{s}\mathit{e}}$	${\mathit{m}}_{\mathit{g}}$	${\mathit{m}}_{\mathit{a}}$	${\mathit{m}}_{\mathit{b}}$	${\mathit{m}}_{\mathit{e}\mathit{p}}$
	kg	kg	kg	kg	kg	kg	kg	kg	kg	kg
R	2070	10,768	160	299	351	166	24	150	-	-
TP${}_A$	2322	10,800	147	12	310	164	0.032	-	98	134
TP${}_B$	2468	10,795	162	12	240	158	0.031	-	77	74

.

2.3. Grain Geometry

In HREs the initial grain geometry, i.e., the initial port area ${\left(A_p\right)}_i$ and initial burning area ${\left(A_b\right)}_i$, determines the initial propellant flow rate, which in turn gives the initial thrust. During engine burn these areas change as a function of time. Thus, the evaluation of HRE operation and performance requires the knowledge of the grain geometry evolution as a function of time. Namely, relations are more easily written as a function of burnt distance $y\left(t\right)$.

The simplest grain design adopts a single-port geometry, with axial symmetry and a circular port. A uniform regression rate is assumed along the grain and the port area $A_p$ and burning area $A_b$ can be computed by means of Equations (1) and (2),

$$A_p=\pi {\left[{\left(R_c\right)}_i+y\left(t\right)\right]}^2$$

(1)

$$A_b=2\pi \left[{\left(R_c\right)}_i+y\left(t\right)\right]L_b$$

(2)

where ${\left(R_c\right)}_i$ is the initial cylindrical port radius and $L_b$ is the length of the fuel grain. Single-port fuel grains require a large value of $L_b$ in order to ensure consistent values of $A_b$ and thrust because of the typical low regression rate of hybrid fuels. For this reason, multi-port grains are usually employed.

In Ref. [31], the authors compared two types of multi-port grain, namely triangular port and quadrangular port design. Details about the multi-port grain design can be found in Appendix C. Six and eight ports were considered for both triangular and quadrangular geometry, whereas HP/PE was the propellant combination. Both a blow down feed system and a partially regulated feed system were taken into account for the liquid propellant. The case study was the maximization of the payload inserted into a 700-km circular polar orbit by the hybrid powered upper stage of a Vega-like launch system. In this specific application, the difference in the optimal design between triangular and quadrangular port design are relevant when $N=8$ was considered. Nevertheless, the quadrangular wagon-wheel design always showed better performance than the triangular grain geometry. Quadrangular ports required a smaller initial thrust and a larger tank pressure, allowing for a lighter nozzle and a shorter engine, but also an heavier propellant tank. Quadrangular ports showed a slightly longer burning time, due to the lower thrust level during the whole engine burn. Moreover, they had a lower sliver, thanks to the presence of the central additional port, which resulted in a mass saving from around 10 kg to 30 kg (i.e., around 23% to 44% of the sliver mass), depending on the feeding system and the choice of N. Concerning the mixture ratio, the quadrangular ports exhibited a smaller shifting during engine operation, allowing for operations close to the value that provide the maximum specific impulse (about 6.5). In this way, a further mass saving due to propellant mass reduction, was obtained, which resulted in a payload improvement ranging from about 20 kg ($N=6$, blow down) to more than 40 kg ($N=8$, regulated). Optimal designs and performance are compared in

Table 3. Optimal design and performance for different port shapes (PS): triangular ports (TP) and quadrangular ports (QP). The second column reports the feed system option (FO): blow down (BD) and regulated (R). The design variables are $F_i$, ${\alpha }_i$, ${\left(p_t\right)}_i$ and E. $R_g$, w, $R_t$ and L stand for grain outer radius, web thickness, throat radius and engine length, respectively. $F/m$ is the maximum longitudinal acceleration imparted to the payload $\mu$.

PS	FO	N	${\mathit{F}}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$	${\left({\mathit{p}}_{\mathit{t}}\right)}_{\mathit{i}}$	E	${\mathit{R}}_{\mathit{g}}$	w	${\mathit{R}}_{\mathit{t}}$	L	$\mathit{F}/\mathit{m}$	$\mathit{\mu }$
			$\mathrm{kN}$	−	$\mathrm{bar}$	−	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{g}$	$\mathrm{kg}$
TP	BD	6	365	7.08	20.2	11.8	0.520	0.039	0.288	12.3	5.77	1796
QP	BD	6	359	7.09	20.7	12.1	0.515	0.040	0.281	12.2	5.67	1814
TP	BD	8	414	7.02	19.8	11.3	0.558	0.034	0.310	12.0	6.64	1775
QP	BD	8	388	7.01	20.8	11.9	0.537	0.037	0.293	11.9	6.18	1811
TP	R	6	209	6.22	13.0	11.9	0.508	0.042	0.271	9.8	5.49	1989
QP	R	6	203	6.21	13.5	12.4	0.501	0.044	0.262	9.6	5.35	2012
TP	R	8	231	6.16	12.3	11.2	0.546	0.037	0.293	9.4	6.33	1971
QP	R	8	213	6.11	13.3	12.1	0.522	0.041	0.271	9.3	5.82	2013

and

Table 4. Mass budget for different port shapes (PS): triangular ports (TP) and quadrangular ports (QP). The second column reports the feed system option (FO): blow down (BD) and regulated (R). The average mixture ratio and specific impulse are reported as ${\alpha }_{avg}$ and ${\left(I_{SP}\right)}_{avg}$, respectively. $m_{res}$ is the residual propellant mass, $m_g$ is the pressurizing gas mass, $m_t$ is the tank mass, $m_{gt}$ is the pressurizing gas tank mass, $m_{nz}$ is the nozzle mass, $m_{cc}$ is the combustion chamber mass and $m_{hc}$ is the engine casing mass.

PS	FO	N	$\mathit{\mu }$	${\mathit{m}}_{\mathit{p}}$	${\mathit{m}}_{\mathit{r}\mathit{e}\mathit{s}}$	${\mathit{m}}_{\mathit{g}}$	${\mathit{m}}_{\mathit{t}}$	${\mathit{m}}_{\mathit{g}\mathit{t}}$	${\mathit{m}}_{\mathit{n}\mathit{z}}$	${\mathit{m}}_{\mathit{c}\mathit{c}}$	${\mathit{m}}_{\mathit{h}\mathit{c}}$
			$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$
TP	BD	6	1796	10,966	43.6	22.4	445.0	-	330.4	125.1	207.0
QP	BD	6	1814	10,925	31.0	23.0	456.3	-	328.5	121.6	204.9
TP	BD	8	1775	10,984	57.2	22.3	440.3	-	333.8	121.5	201.5
QP	BD	8	1811	10,931	31.8	23.3	459.3	-	329.8	117.6	200.2
TP	R	6	1989	10,971	51.7	21.7	164.8	139.4	329.7	104.1	163.7
QP	R	6	2012	10,921	37.3	22.7	170.4	146.1	327.2	100.2	161.1
TP	R	8	1971	10,990	67.6	21.3	156.4	136.8	335.5	100.1	157.3
QP	R	8	2013	10,926	38.6	23.0	167.5	148.0	329.8	95.6	155.5

.

2.4. Engine Modeling

Engine design is defined by a limited number of design parameters, and a proper selection of the design variables may help the design process. A convenient set comprises the initial thrust $F_i$, the initial mixture ratio ${\alpha }_i$, the initial throat-to-port area J and nozzle expansion ratio E. From these variables the initial propellant mass flow ${\left({\dot{m}}_P\right)}_i$ can be computed:

$${\left({\dot{m}}_P\right)}_i=\frac{F_i}{c_i^{*}{\left(C_F\right)}_i}=(1+{\alpha }_i){\left({\dot{m}}_F\right)}_i=\frac{1+{\alpha }_i}{{\alpha }_i}{\left({\dot{m}}_O\right)}_i$$

(3)

where the initial values of the characteristic velocity $c_i^{*}$ and thrust coefficient ${\left(C_F\right)}_i$ are calculated as described in Appendix D. The hydraulic resistance Z can then be computed by means of Equation (A35). The initial throat area ${\left(A_{th}\right)}_i$ is given by Equation (4), once the initial chamber pressure ${\left(p_c\right)}_i$ is assigned as will be discussed later.

$${\left(A_{th}\right)}_i=\frac{{\left({\dot{m}}_P\right)}_i}{{\left(p_c\right)}_i{c}_i^{*}}$$

(4)

The initial throat-to-port area ratio J gives the initial port area ${\left(A_p\right)}_i={\left(A_{th}\right)}_i/J$ and the mass conservation principle provides the initial burning area as described by Equation (5).

$${\left(A_b\right)}_i=\frac{{\left(A_p\right)}_i^n}{a{\rho }_F}\frac{{\left({\dot{m}}_F\right)}_i}{{\left({\dot{m}}_O\right)}_i}$$

(5)

Once the required ${\left(A_b\right)}_i$ is know, one can determine grain geometry directly, when a single circular port is used, or iteratively, when more complex geometries are employed.

After designing the engine, the relations recalled in the Appendixes can be used to define the HRE behavior during operations. When throat erosion effects can be neglected, the throat area remains constant during operations, i.e., $A_{th}={\left(A_{th}\right)}_i=\mathrm{constant}$. Appendix D shows how throat erosion can be taken into account, when required. At each instant t, known the feeding pressure and the engine geometry, one can calculate fuel and oxidizer mass flow rates, their ratio $\alpha$, chamber pressure $p_c$ and head-end pressure $p_1$ by means of the equations described in Appendix D. The thrust level can then be evaluated as $F=p_c{A}_{th}{C}_F$ once the value of $C_F$ has been computed at the actual altitude by means of Equation (A32). In the deterministic approach (see next Section) the time integration is carried out till contemporary burn out of solid fuel and depletion of liquid oxidizer occurs: the overall propellant mass (exhausted and sliver) can be evaluated, which allows for an estimation of the structural masses of the HRE. On the contrary, in the robust case, additional design parameters are used to define residual fuel and residual oxidizer.

3. Optimization

The optimization process can be regarded as the seek for a particular set of design variables or parameters which, at the same time, satisfy imposed constraints and maximize (or minimize) some assigned performance index. In the particular case of propulsion system, the optimization has usually to do with mass. For example the problem can be posed in the form of the maximization of payload mass for given initial mass or the minimization of engine dry mass for given mission performance. Obviously, the specific performance index, complexity of the problem, design issues and other aspects are strongly related to the considered applications and test cases.

HREs typically are characterized by variable thrust magnitude, mixture ratio and overall performance during operation due to evolving grain geometry and non-constant oxidizer flow rate. Moreover, the optimization problem can be even more tricky, for example when upper stages are considered, since the performance of the whole launcher have to be taken into account, and the optimization of the hybrid propulsion system cannot be detached from the ascent trajectory optimization. For these reason, the authors developed and refined over the years a coupled optimization procedure of engine design and trajectory.

Once grain geometry, propellant combination and feed system have been chosen, HRE performance at ignition and during operation are determined by a small set of parameters; the most commonly employed are: initial thrust magnitude $F_i$, initial mixture ratio ${\alpha }_i$, initial nozzle-expansion ratio $E_i$, initial chamber pressure value ${\left(p_c\right)}_i$, initial feeding pressure value ${\left(p_{fs}\right)}_i$, initial port to initial throat area J. Some of these latter are free and optimized by some sort of algorithm, which will be described in the followings, whereas others are constrained by safety or operation limits. For instance, the authors typically assign the initial chamber pressure by imposing a certain ratio between initial chamber pressure and initial feeding pressure, in order to avoid the coupling of oxidizer feed system and combustion chamber dynamics. In particular, ${\left(p_c\right)}_i=0.4{\left(p_{fs}\right)}_i$ is sufficient to guarantee $p_{fs}/p_c\ge 1.5$ for the whole engine burn, despite the drop in $p_{fs}$ which can eventually occur when blow down or partially regulated system are employed. Some other variables may be implicitly given by imposed constraints related to the trajectory, such as maximum acceleration level or minimum regression rate. In this case, the relevant variables are dropped from the engine optimization process and added to the variables of the trajectory optimization, in order to grant the fulfillment of the related constraints. As a result, usually less than five design parameters have to be optimized, allowing for the use of efficient procedures. On the other hand, once engine design is assigned, an indirect method is employed for the trajectory in order to compute the optimization merit function.

The authors mainly employed two approaches to deal with engine design optimization: a direct method and evolutionary algorithms. The direct method involves the computation of the numeric derivatives of the performance index with respect to each design parameter, as prescribed by a forward-finite-difference scheme. Then, an iterative procedure based on Newton’s method is used to obtain corrections of the tentative values of the design parameters in order to nullify the partial derivatives of the performance index [32]. The evolutionary algorithms, on the other hand, select a random initial population of individuals (i.e., a group of tentative engine designs) and evaluate their performance index. Then, biological-inspired processes are applied to the starting population which evolves towards improved individuals leading the optimization to the optimal design. Details about several evolutionary algorithms developed by the authors can be found in References [33,34,35].

A direct or evolutionary algorithm drives the choice of the set of the design parameters which gives the engine configuration and performance. For each engine design, an indirect method optimizes the trajectory. The authors take advantage of an indirect method developed at Politecnico di Torino in the early 1990s. The details of such procedure have been presented in detail in Refs. [4,36] and are here only summarized. A point mass rocket is considered. The state equations, written in non-dimensional form, in order to improve the accuracy of the numerical integration, provide the derivative of position r (radius, latitude and longitude), velocity v (radial, eastward and northward components) and rocket mass M, as reported in a vectorial form by Equation (6):

$$\left\{\begin{array}{c}\frac{\mathrm{d}\mathit{r}}{\mathrm{d}t}=\mathit{v}\hfill \\ \frac{\mathrm{d}\mathit{v}}{\mathrm{d}t}=\mathit{g}+\frac{\mathit{F}-\mathit{D}}{M}\hfill \\ \frac{\mathrm{d}M}{\mathrm{d}t}=-\frac{\left|\mathit{F}\right|}{c^{*}{C}_F}\hfill \end{array}\right.$$

(6)

where F and D are the non-dimensional thrust and drag vector, respectively. Equation (7) presents the inverse-square gravity field assumed for g, where G is the gravitational constant and $M_{*}$ is the planet mass.

$$\mathit{g}=-\frac{G{M}_{*}}{\left|\right|{\mathit{r}}^3\left|\right|}\mathit{r}$$

(7)

The trajectory is split into phases, which depend on the particular problem considered. Examples of phases are vertical ascent, kick phase, zero-lift gravity turn ascent, coast arcs etc. Some time length are usually assigned (e.g., stage separation, fairing jettisoning, thrust rotation) whereas the others are determined during the trajectory optimization (e.g., engine burns and coast arcs). Thrust magnitude and propellant flow rate as functions of time are provided by the selected engine design. The mission to be performed is defined by a set of boundary conditions, such as initial or payload mass (or both), initial position, initial velocity, flight direction, maximum heat flux and target orbit in terms of altitude, eccentricity and inclination.

At this point, an adjoint variable is associated to each equation and the theory of optimal control [37] is able to provide Euler-Lagrange equations, alongside with algebraic equations, which give the control variables (i.e., the thrust direction) and with boundary conditions for optimality, which implicitly define the engine switching times. The multi-point boundary value problem that arises is solved by means of a numerical procedure based on Newton’s method. A tentative value is initially assigned to each problem unknown and progressively modified aiming at the fulfillment of the problem boundary conditions. Such unknowns are usually the time length of some trajectory phases, the initial value of the adjoint variables and/or some design parameters that cannot be assigned “a priori” but only checked “a posteriori” after the optimal trajectory has been computed. Examples of the settings of the indirect trajectory optimization methods can be found in the references cited in Section 4. Alternative methods for trajectory optimization have been proposed by the authors in Ref. [38], employing an approximate control law for the thrust angles, and in Ref. [18], using a purely evolutionary algorithm.

3.1. Robustness

HRE design and optimization require a complex multidisciplinary optimization approach due to their one-lever control feature and their unique combustion mechanism. Furthermore, mission goal attainment could be jeopardized by severe deviation of the engine performance from nominal ones due to the presence of even small uncertainties in particularly sensible design aspects. In this context, a robust-based design and optimization approach is mandatory in order to reduce the sensitivity of the engine performance to such uncertainties. The definitions of robust design are various, here we summarize the basic concept of “robustness” as “the capability of the system to grant a fixed level of performance” (i.e., to match mission goals), “minimizing the effect of uncertainties in the design parameters without eliminating their causes” [39]. The computational cost of robust-based procedures is consistent because its growth is exponential depending on the number of uncertain parameters which are present in the specific problem. Thus, a preliminary selection of the uncertain quantities which exhibit the largest negative influences on the system performance should be carried out.

In Ref. [40] the authors proposed a sensitivity analysis procedure, based on Morris method [41]. First, the model parameters have to be split between design and input parameters. Design parameters, contained in vector b, are the quantities that can be freely set by the designer and their relative design space is discretized in a certain number of finite levels. Then a pool of starting design points are selected, e.g., by means of random search. An acceptance criterion should be included, in order to evaluate the sensitivity of the system to uncertainties for feasible (and interesting) solutions. For HRE design and optimization, possible criteria are a minimum insertion altitude, minimum payload mass or other performance index limitations. On the contrary, input parameters are all the other problem parameters, contained in vector X that, at this point of the procedure, are all regarded as uncertain and discretized in three levels (higher than nominal, nominal and lower than nominal values). In the specific case of HRE, examples of input parameters are nozzle throat erosion reference values, regression rate correlation coefficient and exponent, structural materials densities, propellant densities, initial tank pressure, trajectory parameters and efficiency related to characteristic velocity and thrust coefficient. The sensitivity analysis prescribes the computation of incremental ratios, called Elementary Effects (EEs), for each of the selected starting point. Once at a time, a variation of each input parameter is imposed, while all the others are fixed, in order to obtain a so called Morris trajectory inside the input parameters space. The process is repeated many times for each starting point. The direction of such variations and their sequence are both random. An EEs is obtained from each trajectory for each input parameter. Morris indices are then calculated as the mean of the absolute value and the standard deviation of these EEs. The mean value measures the influence of an input parameter on model output (i.e., on system performance), whereas the deviation measures its non-linear effects or interactions with other input parameters. Based on their indices, the input parameters, which have a strong effect on model output can be identified, and regarded as uncertain parameters in the subsequent robust-based optimization. On the other hand, input parameters which show a negligible effect on system performance are regarded as constant and their value is fixed on the nominal one.

In the literature, robust optimization problems are formally expressed as reported by Equation (8), where ${\mathit{z}}^p$ is the noise vector of the design parameters vector p, $g_j$ is the j-th inequality constraint, ${\mathit{b}}_L$ and ${\mathit{b}}_U$ are, in the general case, the lower and upper boundary of the design parameters, respectively.

$$\begin{array}{cccc}\hfill & \mathrm{find}\hfill & \hfill & \mathit{b}\in {\mathbb{R}}^n\hfill \\ \hfill & \mathrm{to}\mathrm{maximize}\hfill & \hfill & \Phi \left(\mathit{b},\mathit{p}\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & g_j\left(\mathit{b},\mathit{p}+{\mathit{z}}^p\right)⩽0,j=1,...,r\hfill \\ \hfill & \mathrm{and}\mathrm{to}\hfill & \hfill & {\mathit{b}}_L⩽\mathit{b}⩽{\mathit{b}}_U\hfill \end{array}$$

(8)

In the present approach, the authors take into account uncertainties by means of three different levels for each uncertain variables, analogously to the discretization employed in the sensitivity analysis. The performance index, which depends on both design and uncertain parameters, is evaluated for each combination of the uncertain parameters prescribed by a suitable design of the experiments techniques keeping, on the contrary, the design parameters fixed. The corresponding optimization merit function $\Phi$ can be computed in several ways, e.g., as the average of the performance index for the prescribed uncertainties combinations or considering the worst-case scenario. An examples of design of experiments techniques is reported in

Table 5. Example of design of experiment techniques: Taguchi’s $L_{18}$ orthogonal array. Each row reports a combination of uncertain parameters to be evaluated. The 1, 2 and 3 are the discrete levels that represent respectively lower than nominal, nominal and higher than nominal values. Each column corresponds to one of the uncertain parameters and shows its value expressed by the aforementioned levels.

1	1	1	1	1	1
1	2	2	2	2	2
1	3	3	3	3	3
2	1	1	2	3	3
2	2	2	3	1	1
2	3	3	1	2	2
3	1	2	3	2	3
3	2	3	1	3	1
3	3	1	2	1	2
1	1	3	2	2	1
1	2	1	3	3	2
1	3	2	1	1	3
2	1	2	1	3	2
2	2	3	2	1	3
2	3	1	3	2	1
3	1	3	3	1	2
3	2	1	1	2	3
3	3	2	2	3	1

for six uncertain parameters. One can notice that the rows of the example table is equal to eighteen when the number of uncertain parameters (i.e., the columns) are six. A precise relation between the number of parameters, the number of levels and the number of combinations does not exist and strongly depends on the type of design of experiment technique considered. However, the computational effort of a robust-based optimization is many times the one required by the corresponding deterministic optimization, because no matter what technique is employed, the number of combinations required to obtain one merit function value is far greater than one (which can be regarded as the number of uncertain combinations in the deterministic optimization). Further details about sensitivity analysis and robust-based approach are provided in Appendix E.

4. Applications

4.1. Sounding Rocket for Micro-Gravity Platform

One of the key features of HREs is their relatively low cost when compared to the achievable performance, making a hybrid powered sounding rocket a viable option to transport small payloads to high altitudes, where the absence of the atmosphere allows for micro-gravity conditions that can be experienced in free flight. In such kind of application, a suitable optimization merit function to be maximized is the time spent above 100 km (later called $t_{\mu g}$), when the initial and payload mass, $m_i$ and $\mu$ respectively, are given. In this context, the authors considered a 500-kg sounding rocket as a case study [16]. The initial mass includes a 100-kg payload, fixed masses, propulsion system and propellants. The optimal mass split between propellants and propulsion, the optimal grain geometry and the corresponding optimal trajectory are sought in order to maximize $t_{\mu g}$. A single-port grain design and blow down feed system are adopted to reduce the complexity and the cost of the propulsion system. Several options are taken into consideration as propellant combination, namely HP/PE, LOX/HTPB and NOX/HTPB. The design variables are three when self pressurizing NOX is employed as oxidizer: the initial thrust level $F_i$, the initial mixture ratio ${\alpha }_i$ and the nozzle expansion area ratio E. Erosion effects are here neglected, thus $E=\mathrm{constant}$. On the other hand, a total of five design parameters are required when HP and LOX are used: the initial tank pressure ${\left(p_t\right)}_i$ and the ullage volume $V_u$ alongside with the aforementioned $F_i$, ${\alpha }_i$ and E. The use of NOX fixes the initial tank pressure due to the liquid-vapor equilibrium (see Appendix A.1 for the details), whereas the ullage volume is fixed at 3% of the tank volume.

The results are reported in

Table 6. Optimal design and performance for the considered propellant combinations. $m_p$, $R_t$, D and L are the propellants mass boarded, the nozzle throat radius, the engine overall diameter and length, respectively. ${\left(V_g\right)}_i$ and ${\left(p_t\right)}_i$ are optimization variables only for HP/PE and LOX/HTPB combinations.

Propellants	${\mathit{F}}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$	E	${\left({\mathit{p}}_{\mathit{t}}\right)}_{\mathit{i}}$	${\left({\mathit{V}}_{\mathit{g}}\right)}_{\mathit{i}}$	${\mathit{m}}_{\mathit{p}}$	${\mathit{R}}_{\mathit{t}}$	D	L	${\mathit{t}}_{\mathit{\mu }\mathit{g}}$
	$\mathrm{kN}$	−	−	$\mathrm{bar}$	${\mathrm{m}}^3$	$\mathrm{kg}$	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{s}$
HP/PE	24.8	8.57	4.98	60.1	0.094	339	0.048	0.42	5.01	299
LOX/HTPB	23.5	3.20	4.53	59.9	0.097	328	0.047	0.46	5.52	219
NOX/HTPB	16.2	10.92	4.14	45.0	–	340	0.046	0.40	4.75	177

, showing the higher performance of the HP/PE combination. The LOX solution exhibits a low initial mixture ratio, requiring a larger and heavier grain which increases propulsion system mass at the expense of the propellant mass on board. On the contrary, the use of the NOX combination results in worst performance due to its lower specific impulse, albeit interesting features in terms of overall rocket length and diameter are obtained thanks to the larger mixture ratio. Moreover, looking at Figure 4, one can notice that the optimal initial thrust and thrust history are quite different depending on the propellants employed.

The complex influence of the design parameters on the thrust history (i.e., on the optimal trajectory) is well exemplified switching the initial thrust of HP/PE and NOX/HTPB. In these cases, $t_{\mu g}$ presents a relevant reduction to 150 s for NOX/HTPB ($-15\%$) and to 267 s for HP/PE ($-10\%$). Concerning the tank pressure histories, the NOX solution is able to maintain an high pressure level longer than HP and LOX, due to its self-pressurization capability, resulting in a more regular thrust level. Such behavior holds until the liquid phase exist inside the oxidizer tank ($t<50$ s); later the thrust drops and one can observe a change in tank pressure derivative due to the residual gas phase which is fed into the combustion chamber acting as a propellant.

4.2. Hypersonic Accelerator

Hypersonic propulsion and the development of hypersonic-capable vehicles is a growing trend in recent years. The test conditions of such systems, subsystems and devices require Mach number greater than five at an altitude in the range 25–50 km. Thus, one more time, a HRE is a viable option for this kind of missions for the same reasons explained in Section 4.1. Ref. [42] considered the following test case: initial mass $m_i$ fixed and equal to 1000 kg, payload mass $\mu$ equal to either 100 kg or 200 kg and 30-km target altitude. HP/PE, single circular port and blow down are the considered propellants, grain design and feed system, respectively. The optimization aims at the maximization of the Mach number $M_f$ at the target altitude. Despite the high altitude operation considered as target, the rocket spends a relevant amount of time at lower altitude, thus requiring an accurate modeling of its aerodynamic interactions (i.e., drag) in order to obtain significant results. A single stage design has been considered, which employs a single HRE, alongside with two different two stage designs: the first uses a single HRE in the first and second stage (1+1 configuration), whereas the second design employs two HRE in the first stage and a single engine in the second stage (2+1 configuration). To reduce development cost and system complexity, the same HRE is used for each multi-engine configuration. In this context, the design parameters are the initial thrust $F_i$, the initial mixture ratio ${\alpha }_i$, the initial tank pressure ${\left(p_t\right)}_i$, the initial volume of pressurizing gas ${\left(V_g\right)}_i$ and the nozzle expansion area ratio E. The value of ${\left(V_g\right)}_i$ is evaluated in order to grant a sufficient regression rate at burnout (i.e., avoid grain cooking), despite the blow down operation.

Table 7. Optimal design and performance of the hybrid-powered accelerator. D and L are the engine diameter and length. In the first column (Cfg.) the configurations are reported as: (1) single stage, (1+1) two stage/single engine per stage, (2+1) two stage/two engines in the first stage.

Cfg.	$\mathit{\mu }$	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{F}}_{\mathit{i}}$	${\left({\mathit{p}}_{\mathit{t}}\right)}_{\mathit{i}}$	${\left({\mathit{V}}_{\mathit{g}}\right)}_{\mathit{i}}$	E	D	L	${\mathit{M}}_{\mathit{f}}$
	$\mathrm{kg}$	−	$\mathrm{kN}$	$\mathrm{bar}$	${\mathrm{m}}^3$	−	$\mathrm{m}$	$\mathrm{m}$	−
1	100	7.43	26.64	58.20	0.265	5.89	0.431	8.62	7.51
1	200	7.39	29.57	70.86	0.191	5.88	0.407	8.15	5.34
1+1	100	8.62	34.73	86.27	0.082	4.67	0.468	4.68	7.50
1+1	200	8.96	37.10	93.77	0.079	5.11	0.454	4.54	4.80
2+1	100	9.10	18.10	64.41	0.076	6.71	0.408	4.08	7.68
2+1	200	8.49	18.02	75.64	0.058	6.35	0.390	3.90	5.32

reports the optimal design and performance of the HRE.

To reduce propulsion system mass, small thrust-low tank pressure designs should be preferred; however such optimization strategy fails in the 100-kg single stage case and in the 2+1 case (both payload) because the resulting thrust level tends to become too small and unfeasible solutions with negative coast arcs would be obtained. Thus, the initial thrust is dropped from the set of design parameters for such cases and determined by the trajectory optimization procedure itself, allowing for a feasible solution. The results show that a hybrid powered rocket can effectively accelerate a payload in the range 100–200 kg to the hypersonic corridor. Looking at the last column of Table 7, one can notice that, counter intuitively, the two stage design does not result in Mach number $M_f$ higher than the single stage configuration (first two rows), with the exception of the 2+1 configuration when the lowest payload is taken into account (second-to-last row).

4.3. Mars Ascent Vehicle

HREs are particularly well suited for missions which require shut down and restart capabilities and are less sensitive to low temperature, with respect to liquid rocket engines. These characteristics make a hybrid powered Mars Ascent Vehicle (MAV) a viable alternative to the heritage options for such application. In particular, the use of LOX/Wax propellant combination is really promising, since the oxidizer could be produced in situ from CO2 in Mars atmosphere. In Ref. [43] the authors analyzed a two-stage vehicle for the return of samples from Mars’ surface and for a manned mission. A cluster of engines is used in the first stage, whereas a single HRE powers the second stage. The same engine is used in both stages, in order to limit the development costs of the MAV. Both a simple blow down feed system and a more complex regulated system are taken into account as possible architectures. The number of engine design parameters is four, three of them being in common between the two feed system alternatives, namely initial mixture ratio ${\alpha }_i$, initial tank pressure ${\left(p_t\right)}_i$ and nozzle area ratio E. The fourth parameter is the initial volume of pressurizing gas ${\left(V_g\right)}_i$, when the blow down feed system is employed, or the exhausted oxidizer mass during regulated operation $m_O^{*}$, when the regulated system is considered. The number of engines used in the first stage must also be selected, since different configuration are possible, in particular $N_1=2,3,4$ are analyzed. The optimization aims at the maximization of the MAV payload $\mu$ at given initial mass, namely 500 kg in the sample return mission and 60 tons in the manned mission. A reference target orbit of 170-km altitude is taken into consideration for both the test cases. The most significant results are reported in

Table 8. Hybrid engine design and performance: sample return mission. The first column (Cfg.) reports the launcher configuration, e.g., 2+1 stands for two engines in the first stage and one engine in the second stage. The second column reports the feed system, blow down (BD) or regulated (R). $V_{He}$ is the volume of pressurizing gas D and L are engine diameter and length. $m_d$ is the engine dry mass and $m_p$ is the propellant mass.

Cfg.	FO	${\mathit{\alpha }}_{\mathit{i}}$	${\left({\mathit{p}}_{\mathit{t}}\right)}_{\mathit{i}}$	${\left({\mathit{V}}_{\mathit{g}}\right)}_{\mathit{i}}$	${\mathit{V}}_{\mathit{H}\mathit{e}}$	E	D	L	${\mathit{m}}_{\mathit{d}}$	${\mathit{m}}_{\mathit{p}}$	$\mathit{\mu }$
		−	$\mathrm{bar}$	${\mathrm{m}}^3$	${\mathrm{m}}^3$	−	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$
2+1	BD	1.53	21.38	0.071	-	17.6	0.31	2.98	79.2	345.8	75.0
3+1	BD	1.44	21.51	0.055	-	18.8	0.36	2.63	85.4	339.8	74.8
4+1	BD	1.39	20.86	0.044	-	18.1	0.33	2.39	89.2	337.8	72.3
2+1	R	1.47	16.90	-	0.0097	17.2	0.24	2.77	67.8	346.0	86.3
3+1	R	1.38	17.92	-	0.0074	18.6	0.22	2.37	71.9	340.6	86.7
4+1	R	1.32	19.00	-	0.0058	19.5	0.21	2.13	76.2	338.2	84.8

and

Table 9. Hybrid engine design and performance: manned mission. The first column (Cfg.) reports the launcher configuration, e.g., 2+1 stands for two engines in the first stage and one engine in the second stage. The second column reports the feed system, blow down (BD) or regulated (R). D and L are engine diameter and length. $m_d$ is the engine dry mass and $m_p$ is the propellant mass.

Cfg.	FO	${\mathit{\alpha }}_{\mathit{i}}$	${\left({\mathit{p}}_{\mathit{t}}\right)}_{\mathit{i}}$	${\left({\mathit{V}}_{\mathit{g}}\right)}_{\mathit{i}}$	${\mathit{V}}_{\mathit{H}\mathit{e}}$	E	D	L	${\mathit{m}}_{\mathit{d}}$	${\mathit{m}}_{\mathit{p}}$	$\mathit{\mu }$
		−	$\mathrm{bar}$	${\mathrm{m}}^3$	${\mathrm{m}}^3$	−	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{tons}$	$\mathrm{tons}$	$\mathrm{tons}$
2+1	BD	2.11	18.29	10.05	-	16.2	1.37	21.27	4.80	43.15	12.05
3+1	BD	2.05	17.06	7.76	-	15.2	1.25	18.94	4.83	42.89	12.38
4+1	BD	2.03	15.76	6.01	-	13.1	1.17	16.84	4.55	43.03	12.42
2+1	R	1.98	16.03	-	0.79	16.6	1.15	17.62	4.44	42.61	12.95
3+1	R	1.93	15.74	-	0.56	16.6	1.03	15.61	4.40	42.25	13.35
4+1	R	1.89	15.54	-	0.43	16.4	0.94	14.32	4.40	42.14	13.46

for the sample return and manned mission, respectively.

Concerning the sample return mission, the maximum payloads are obtained with the use of two and three engines, when the simple blow down feed or the regulated system are respectively used. The use of a regulated system always improves the resulting payload mass. On the other hand, in the manned mission, the greatest payload is achieved when four engines are used in the first stage since the larger and sustained thrust allows for a more efficient trajectory and, alongside with the dry mass reduction, increases the payload mass. For the same reasons, the payloads of the regulated optimal solutions are always greater than the corresponding blow down ones, analogously to the sample return mission optimal solutions.

These results are comparable, in terms of payload, to those provided by traditional liquid rocket eninges envisaged for a Mars return mission. However, the low cost and simplicity of HREs makes the described launcher options worth of consideration.

4.4. Small Launcher

Since the early 2000s, the demand for small launch vehicles is constantly growing due to the spread of the small satellite market. Until recently, operative launcher especially designed for such application are an exception and HREs, due to their features, are a promising propulsion system for a small satellite launcher. For these reasons, in Refs. [44,45,46] the authors investigated the optimal design of a hybrid-powered 5000-kg small launcher. LOX/paraffin-based wax is considered as propellant combination for its high regression rate, which allows for a simpler single port grain design. Concerning the feed system, a blow down type is taken into account. The launcher employs the same HRE in different number in each stage: six, three and one in the first, second and third stage, respectively. An airborne launch is considered at given altitude and speed (e.g., Pegasus Launcher).

The optimization is carried out from both a deterministic and a robust point of view, and the number of design parameters are respectively two (${\left(V_g\right)}_i$ and ${\alpha }_i$) and five (${\left(V_g\right)}_i$, ${\alpha }_i$, E, total oxidizer mass boarded $m_{O,tot}$ and $R_g$). Different trajectory setups are taken into consideration, namely given initial thrust (called design A) and free initial thrust/fixed maximum acceleration (called design B). In the latter cases $F_i$ is an additional design parameters which is optimized. Only the regression rate is regarded as uncertain in the robust-based optimization. The optimization aims at the maximization of the payload inserted in a given-altitude, circular and polar orbit. The optimal designs for the deterministic optimization are reported in

Table 10. Performance and design summary: deterministic optimization (800 km altitude). $R_f$ stands for the final grain burning distance, $m_F$ is the total fuel mass burned and $m_d$ is the engine dry mass.

Des.	${\mathit{F}}_{\mathit{i}}$	${\left({\mathit{V}}_{\mathit{g}}\right)}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$	w	${\mathit{R}}_{\mathit{f}}$	D	E	${\mathit{m}}_{\mathit{O}}$	${\mathit{m}}_{\mathit{F}}$	${\mathit{m}}_{\mathit{d}}$	$\mathit{\mu }$
	$\mathrm{kN}$	${\mathrm{m}}^3$	−	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{m}$	−	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$
A	11.5	0.253	1.86	0.140	0.211	0.481	14.0	291.5	134.2	61.0	48.0
B	27.2	0.108	2.58	0.105	0.213	0.549	12.5	297.2	129.1	57.8	73.6

, whereas the time histories of their key performance indexes are shown in Figure 5.

In this application, the optimal ascent trajectory prescribes a large acceleration for a suitably long time, in order to reduce gravitation and aerodynamic losses. Thus, the deterministic design A exhibits a large value of ${\left(V_g\right)}_i$ because its initial thrust is fixed, whereas the deterministic design B is free to follow a steep trajectory by means of a larger initial thrust $F_i$ despite a smaller volume of pressurizing gas. This behavior allows for an engine dry mass reduction, albeit a greater propellant load is required due to the less efficient trajectory and lower nozzle expansion area ratio E (i.e., lower specific impulse $I_{SP}$), with respect to the deterministic design A. Thus, the deterministic design B is capable of inserting a 73.6-kg payload into the target orbit, i.e., a 25-kg increase with respect to the deterministic design A.

In the context of the robust-based optimization, the authors decided to maintain the same design philosophy, first seeking for a fixed initial thrust solution (here called robust design A) and then trying to find out an optimized thrust solution (here called robust design B). The hope was to obtain a performance improvement, analogously at what happened in the deterministic optimization. In the context of the robust-based optimization, the performance index to be maximized was ${\Phi }_{avg}$, a linear combination of the payload $\mu$ inserted in the target orbit and the average altitude violation ${\Delta }_{avg}$ due to uncertainty with respect to such orbit. A large value is here used for the linear combination coefficient in order to force the altitude violation to zero. A detailed definition of the robust-based merit function can be found in Ref. [46]. The number of design parameters grows up to four when robust-based procedure is employed, namely the initial mixture ratio ${\alpha }_i$, the grain outer radius $R_g$, the initial pressurizing gas volume ${\left(V_g\right)}_i$ and the total oxidizer mass boarded. The optimal robust design A is reported in

Table 11. Performance and design comparison: deterministic design A (DET${}_A$) vs. robust design A (ROB${}_A$) (800 km altitude). ${\Delta }_{avg}$ is the average altitude violation with respect to the target altitude, whereas ${\Phi }_{avg}$ is the optimization merit function.

Des.	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{R}}_{\mathit{g}}$	${\left({\mathit{V}}_{\mathit{g}}\right)}_{\mathit{i}}$	${\mathit{m}}_{\mathit{O},\mathit{t}\mathit{o}\mathit{t}}$	E	${\mathit{m}}_{\mathit{F}}$	${\mathit{m}}_{\mathit{d}}$	$\mathit{\mu }$	${\mathbf{\Delta }}_{\mathit{a}\mathit{v}\mathit{g}}$	${\mathbf{\Phi }}_{\mathit{a}\mathit{v}\mathit{g}}$
	−	$\mathrm{m}$	${\mathrm{m}}^3$	$\mathrm{kg}$	−	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{kg}$	$\mathrm{km}$	$\mathrm{kg}$
DET${}_A$	1.86	0.211	0.253	291.5	14.00	134.2	61.0	48.0	500.75	−9967.1
ROB${}_A$	1.87	0.212	0.261	291.8	14.00	133.3	63.0	34.3	0.00	34.3

and compared to the optimal deterministic design A. One can observe that ${\Delta }_{avg}$ is equal to 500 km for the deterministic solution in the face of a 800-km target orbit, i.e., more than half of the considered uncertain parameters combinations lead to a rocket crash (insertion altitude null) when a proper robust-based design is not carried out. On the contrary, the ROB${}_A$ solution exhibits a null altitude violation, granting robustness in the design, at the cost of a relevant payload reduction (−28% with respect to deterministic design A). To improve this result, a robust design B (ROB${}_B$) is sough, by freeing the initial thrust, which become an additional trajectory unknown, and adding a constraint on the final acceleration, as previously done in the deterministic procedure. This approach results in payload increases, with respect to ROB${}_A$ optimal solution, of 10 kg and 20 kg, when maximum accelerations of 6 g and 5 g are imposed in the indirect trajectory optimization. However, the average altitude violation of these solution is not passably close to zero (131 km and 50 km when 6 g and 5 g are respectively used) and unacceptable in a robust-based optimization.

4.5. Upper Stage

In the context of small and low-cost launchers, SRMs have been used extensively used: one can consider the Pegasus launcher and the European Vega launcher as an example for two different payload class. In Pegasus all the stages are powered by SRMs. However, the lack of shut down/restart capability of SRMs imposes the use of at least one stage for each burn required by the ascent trajectory, whereas the absence of throttling determines relevant scattering in the target orbit insertion parameters (e.g., the altitude). Moreover, SRMs are characterized by a lower specific impulse than their liquid counterparts, which results in penalties in the final part of the ascent. These issues are solved in Vega by employing an additional small liquid-powered stage, which is devoted to the final orbital maneuvers but results in higher costs and worse structural efficiency. HREs represents an alternative and viable solution for an upper stage in this context, because they are able to deliver the high performance of a SRM and the fine control features of the aforementioned additional small LRE, but at a lower cost. Furthermore, the use of typical hybrid propellant combinations avoids safety issues related to the chemicals used in the LRE final stage, such as Nitrogen TetrOxide (NTO) and MonoMethylHydrazine (MMH).

For these reasons, the authors focused on the design and optimization of a hybrid powered upper stage suitable for the replacement of the third and fourth stages of a launcher based on the characteristic of the European Vega Launch Vehicle (VLV). The optimization aims at the maximization of the payload inserted into a 700-km polar orbit with a launch from Kourou. A baseline value for the payload mass using three solid-propellant stage and a liquid-powered upper stage is 1430 kg, consistent with the performance of the Vega [47]. The initial mass of the launcher is given and the lower stages are unmodified.

Back in 2010 the authors approached to this topic for the first time [48]. The trajectory is optimized from lift-off to orbit insertion and the same constraints of the reference launch are taken into account, such as heat flux limitation after fairing jettisoning. The considered propellant combination is HP/PE, which requires a multiple-port grain design in order to deliver the required high thrust levels. Several options for grain geometry and feed system are compared. The engine design parameters are four, namely the initial thrust $F_i$, the initial mixture ratio ${\alpha }_i$, the initial tank pressure ${\left(p_t\right)}_i$ and the nozzle area ratio E (erosion effect are neglected). The initial ullage volume ${\left(V_g\right)}_i$ (blow down case only), the oxidizer mass at the start of the blow down and its final value (regulated case only), and the grain outer radius $R_g$ are additional unknowns of the ascent trajectory optimization. 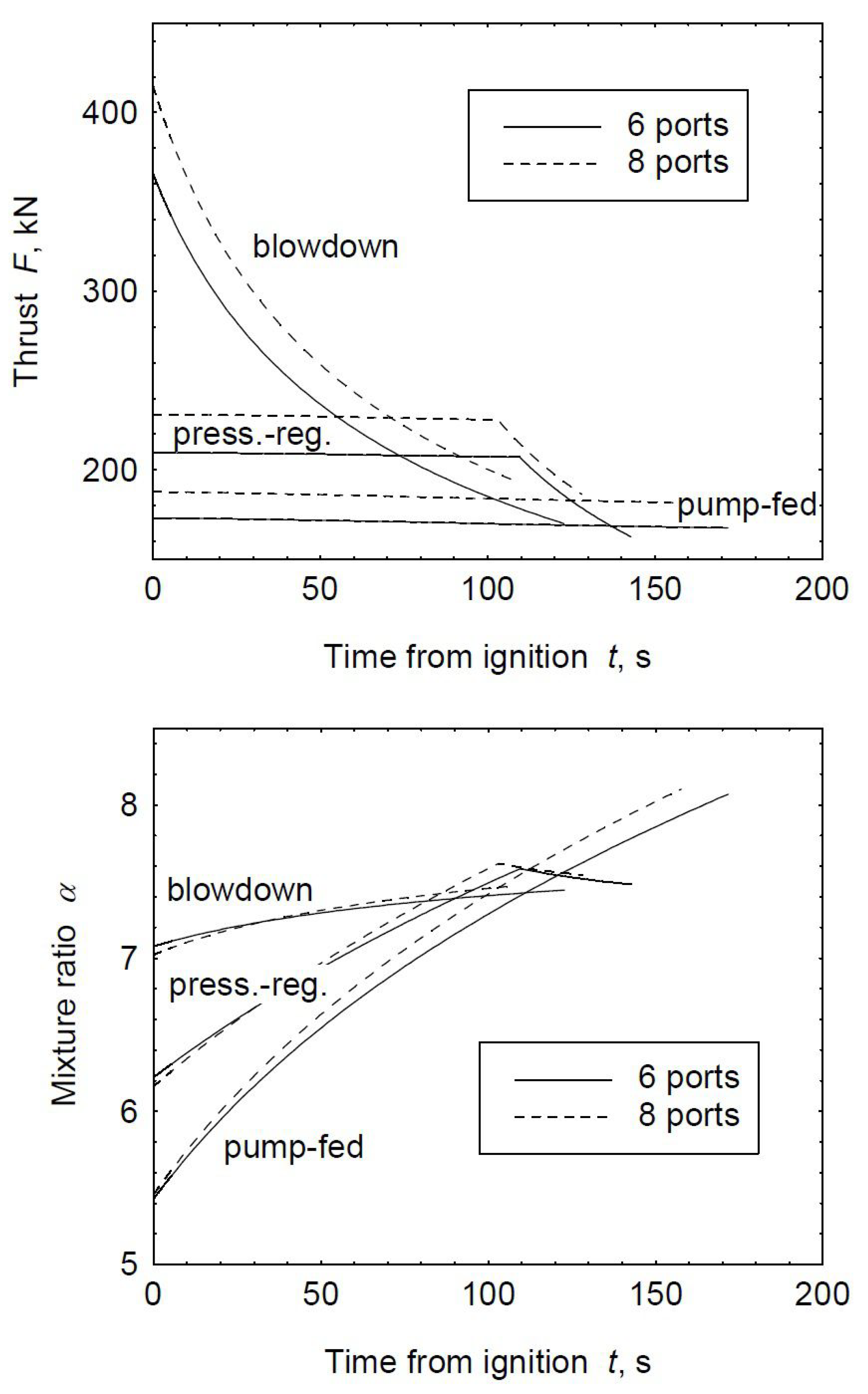Figure 6 depicts tank pressure, thrust and mixture ratio histories for a blow down and a partially regulated feed system. These results are obtained assuming eight quadrilateral ports for the fuel grain.

The use of the blow down feed system results in a large thrust level variation during engine burn. Thus, a really high initial tank pressure is mandatory, in order to maintain a sufficient thrust until the end of the engine burn, also avoiding an increase in pressurizing gas mass. A performance improvement is obtained employing a partially regulated feed system: the introduction of an auxiliary pressurizing gas tank is balanced, in terms of engine dry mass, by the reduction of the oxidizer tank mass due to the lower pressurization. However, a stronger mixture ratio shifting penalizes the performance of the HRE during the constant pressure operation, with respect to the blow down optimal solution. Further performance improvement are achievable employing an electrically driven turbo-pump feed system [29]. The effect of grain geometry (number of ports and shapes) on launcher performance has been already described at the end of Section 2.3.

In 2014, the authors considered alternative propellant combinations for the same upper stage application, namely HP90%/HTPB, LOX/HTPB and LOX/paraffin-based wax [33]. Moreover, the authors took into account nozzle throat erosion effects by means of the Bartz method (see Appendix D). The use of paraffin-based wax allows for a single port grain design, thanks to its relatively high regression rate value. The optimal solution presents a payload increase of about 350 kg with respect to the best performing conventional propellant combination, as shown in

Table 12. Hybrid upper stage design and performance. The first column reports the propellant combination. E column reports the initial nozzle area ratio when erosion effects are considered.

PC	${\mathit{F}}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$	${\left({\mathit{p}}_{\mathit{t}}\right)}_{\mathit{i}}$	E	${\mathit{R}}_{\mathit{g}}$	w	L	${\mathit{m}}_{\mathit{p}}$	$\frac{{\mathit{m}}_{\mathit{p}}}{{\mathit{m}}_{\mathit{p}}+{\mathit{m}}_{\mathit{d}}}$	$\mathit{\mu }$
	$\mathrm{kN}$	−	$\mathrm{bar}$	${\mathrm{m}}^3$	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{m}$	$\mathrm{kg}$	−	$\mathrm{kg}$
HP/PE	231	6.16	12.3	11.2	0.546	0.037	9.4	10,989	0.924	1971
LOX/Wax	185	1.98	13.3	10.8	0.619	0.258	9.7	10,699	0.933	2311

, being at the same time only slightly affected by performance deterioration due to throat erosion.

In 2015 the authors started to shift their attention from design trade-off between different HRE configuration, regarded strictly from a deterministic point of view, to uncertainty based approaches in the context of the optimization of the aforementioned upper stage. The first attempt to perform a robust-based optimization is presented in Ref. [11]. Regression rate correlation coefficient a and exponent n are varied around their nominal values for the optimal solutions and off-design launcher performance are evaluated. The results show that the mission is unfeasible when the actual regression rate is greater than the nominal one, because a relevant amount of unburned oxidizer remains as an inert mass after fuel grain burn out. On the other hand, off-nominal launcher performance of the optimal design are satisfying when a regression rate larger than nominal is assumed during the optimization procedure. In this case the average altitude is increased and the standard deviation reduced (from 250 km to 12 km).

This management of the intrinsic uncertainties represents a preliminary approach to robust design, which the authors improved in Ref. [49] embedding uncertain parameters variations inside the optimization procedure, in place of an “a posteriori” check of optimal solutions off-design performance. Thus, a new optimization merit function is introduced, combining linearly the payload mass, which is unaffected by the uncertainties, with the average altitude violation with respect to target altitude, which, on the contrary, is affected by uncertainty because the actual insertion orbit depends on the actual value of the regression rate. The number of design parameters rises due to the robust-based formulation of the optimization problem. In the deterministic approach oxidizer and fuel masses are such that they end at the same moment at burnout and are optimized (i.e., minimized) by the indirect procedure to reach exactly the target orbit. On the other hand, in the robust-based optimization, the actual value of regression rate varies resulting in three possible situations:

• the regression rate is higher than nominal; in this case all the fuel burns whereas a certain amount of unburned oxidizer remains in the tank;
• the regression rate is lower than nominal; in this case all the oxidizer is exhausted whereas a fuel sliver is present in the combustion chamber;
• the regression rate is the nominal one; in this case fuel and oxidizer end at the same time.

The surplus in fuel/oxidizer mass required to reach (at least) target orbit, even in the higher/lower than nominal operation, have to be fixed before trajectory optimization, in order to compute launcher payload and define its design. Thus, the fuel mass $m_F$ (given by grain outer radius $R_g$ only for circular port grain, $R_g$ and web thickness w for multiport grain design), and the total oxidizer mass boarded are no longer trajectory unknowns but become engine design parameters. These surplus in propellant masses result in payload penalties for the robust optimal solutions with respect to deterministic one. Obviously the robust designs are able to reach higher altitude than the target when nominal regression rate occurs. The results prove that robustness in the design can be achieved at the expense of a small payload reduction of 82 kg, i.e., less than 5% of the launcher payload, with respect to the deterministic optimal solution for the same grain geometry, propellants and feed system. Figure 7 reports the thrust and mixture ratio histories for the deterministic and optimal design. The robust design shows a slightly larger thrust magnitude variation and mixture ratio shifting during engine burn, due to the different grain geometry which causes enhanced changes of port and burning area. The obtained robust optimal solution is able to grant the fulfillment of launcher mission goals (i.e., 100% target orbit reaching) despite the presence of regression rate uncertainties. In Ref. [30] this robust-based approach is applied to a slightly different upper stage architecture, which employs electrically driven pump to feed the oxidizer into the combustion chamber. Mission goals and all the other aspects of the problem are unmodified. The results show that this feed system option is viable, even when uncertainties in the design are taken into account. The use of electric systems is able to grant a relevant performance boost with respect to conventional gas pressurized feed system, which in terms of payload provides a 12% increase (+250 kg).

In the robust-based optimization new core aspects become more relevant, namely the number of uncertain parameters and the algorithm to be used to lead the engine design optimization. The first determines the number of uncertain parameters combination that have to be considered in the robust-based procedure, i.e., the number of trajectory integration required to compute one value of the optimization merit function. The latter is devoted to the choice of the engine designs to be evaluated during the optimization in order to reach an optimal solution. Thus, both this aspects have a huge impact on the computational effort of the whole robust-based optimization method. For these reasons, the authors in Ref. [35] proposed a comparison of the performance of different optimization algorithm, namely a Genetic Algorithm (GA), a Particle Swarm Optimization algorithm (PSO), a hybrid genetic-Taguchi algorithm and an Iterated Local Search (ILS). The optimization of the hybrid powered upper stage is the test case, one more time. PSO and ILS outperformed the other methods, showing similar performance, despite their completely different nature: the first is a population-based algorithm, whereas the second employs a meta-heuristic approach.

In Ref. [40] the authors described an approach, which takes advantage of a sensitivity analysis performed by means of Morris Method, to select the model parameters to be regarded as uncertain [41]. Details about this technique are reported in Section 3.1. The results show that even small variations of six model parameter (regression rate correlation coefficient a and exponent n, throat erosion synthetic parameter $K_{ero}$, fuel density ${\rho }_F$, initial tank pressure ${\left(p_t\right)}_i$ and initial throat to port area ratio J) have a relevant impact on system performance and thus have to be considered as uncertain in the upper stage test case. In terms of payload, this uncertainty model determines a 12% payload reduction, with respect to the deterministic optimal solution obtained for the same grain geometry and propellants. This reduction is more than twice the one imposed by the simpler uncertain model, which considered only the regression rate uncertainties, mentioned in the previous paragraph, but it is worth taking the robustness gain into account. For the sake of comparison,

Table 13. Normalized ratios for the reference (VLV) and robust optimized solutions. GP2 and EP2 are the solutions for gas pressurized and electric turbo pump feed system employing simpler 2-parameter robust-based approach. GP6 reports the mass ratios for the 6-parameter robust-based approach.

Case	$\mathit{\mu }$	$\frac{\mathit{\mu }}{{\mathit{m}}_{\mathit{i}}}$	$\frac{{\mathit{m}}_{\mathit{p}}}{{\mathit{m}}_{\mathit{i}}}$	$\frac{{\mathit{m}}_{\mathit{p}}}{{\mathit{m}}_{\mathit{p}}+{\mathit{m}}_{\mathit{d}\mathit{r}\mathit{y}}}$
	-	-	-
VLV	1430	0.094	0.731	0.840
GP2	2070	0.143	0.741	0.904
EP2	2322	0.160	0.744	0.926
GP6	2001	0.140	0.746	0.905

reports the normalized mass ratios for the reference and the robust optimized solutions.

5. Conclusions

The present overview of the activities on HRE at Politecnico di Torino has been structured in three main parts. First, the preliminary design options, (i.e., propellant combination, feed system and grain design) have been presented and investigated by means of references to specific works which faced one of these fundamental choices at a time. Then, in the second part of the review, the focus of the writers shifted on the description of the mathematical model, which underlies the description of HREs performance and operation, and the developed optimization approaches, concerning engine and trajectory. In this context, special attention has been devoted to the robustness issue, which is the authors’ most investigated topic in their recent works. In the last part of the manuscript, relevant examples of HREs applications, analyzed by the authors during the years, have been collected.

This rundown of examples underlined the complex interactions between problem input parameters and system performance. The optimal designs are the results of a trade-off process between conflicting requirements. In general, high initial thrust levels and sustained thrust are beneficial for the trajectory, reducing gravitational and aerodynamic losses. On the other hand, such level of performance comes together with an increase in the propulsion system mass, because heavier and/or additional components are required, reducing the available payload mass. Moreover, this scenario is further complicated by both the coupling between thrust and mixture ratio, typical of hybrids, and the sensitivity of the system to the ineluctable presence of uncertainties in the design. For these reasons, the true advantages attainable by the use of HREs can be highlighted solely through the employment of proper tools, which are able to couple engine design and trajectory optimization, embedding uncertainty management inside the procedure. In this context, the procedure developed at the Politecnico di Torino and here presented, proved to be flexible and reliable thanks to a well-reasoned use of the most suitable direct/evolutionary/indirect methods.

Nevertheless, issues are still present in the proposed approaches. The seek of more robust solutions struggles against the huge computational costs due to the growth of the number of uncertain parameters and approximated methods may not be suitable, because the introduced simplifications could override the complex parameters interaction intrinsic in HREs design and operation. However, the use of innovative propellants and feed system, such as paraffin-based wax and electric turbo-pump, proved to be able to overcome hybrids performance reduction and methods limitations due to a rigorous robust-based approach.

In the near future, the authors will point their attention upon the generalization of their robust-based coupled engine/trajectory optimization method to even more diverse HREs applications and the improvements in the models for the engine description (dry masses and thermal control), paying special attention to the upcoming technological development in the field of hybrid propulsion systems.