1. Introduction
Despite continued research efforts, numerical simulation of high-Mach flows remains a significant challenge in computational fluid dynamics (CFD). From a design standpoint, accurate prediction of the nonequilibrium aerothermodynamic environment is necessary for the development and optimization of vehicle systems to sustain the large aerodynamic and thermal loads experienced during hypersonic flight. This prediction is made challenging by the presence of finite-rate processes that arise due to highly-energetic molecular collisions, affecting both fluid bulk and transport properties. The development of efficient and robust computational models that effectively capture the coupling between fluid bulk motion, chemical kinetics, and thermodynamic processes remains an active area of research within the CFD community.
The hypersonic regime is characterized by high-temperature effects associated with high-flow kinetic energy relative to the static thermal enthalpy. This can give rise to finite-rate kinetic processes when the flow is rapidly decelerated, such as across a strong shock. When the relaxation time of these processes is on the order of the fluid mechanical residence time, a state of thermochemical nonequilibrium is established. In this state, the thermodynamic properties and species concentrations must be spatially resolved to accurately model the flow. High fluid-specific energy densities make recreating the mission-relevant time and length scales difficult and costly, particularly in ground-based experimental facilities [
1,
2]. The inability to completely capture these physical phenomena can lead to catastrophic failure, such as the case of the NASA X-15 [
3], where an unanticipated shock impingement and the associated localized heating caused structural failure. Numerical simulation provides an additional, and often necessary, method to predict the flow environment. It is commonly employed for test planning and data reduction in ground-based test facilities [
4], as well as in analyses during the vehicle design process. As flow enthalpy increases, nonequilibrium effects become increasingly significant and complex, requiring additional models to capture the underlying physics. The addition of these models to CFD codes gives rise to new challenges in solver stability, robustness, and efficiency that have been documented in the literature.
Design of vehicles for atmospheric entry has provided a major historical impetus for the development of nonequilibrium modeling capabilities. An early effort to incorporate chemical nonequilibrium effects into numerical methods using upwinding schemes was carried out by Gnoffo and McCandless [
5], who implemented loose coupling of chemical source terms that provided accurate predictions of the chemical species concentrations for high-speed flows around spheres. Increased computational power and improved numerical methods have allowed for higher-fidelity solutions, including the implementation of individual conservation equations for each species present in the flow and each molecular energy mode. The LAURA solver [
6] developed at the NASA Langley Research Center represents a well-validated solver incorporating these reacting Navier–Stokes equations.
The DPLR solver [
7], developed at the NASA Ames Research Center, takes advantage of the uniform geometry of blunt body entry vehicles for simulation on structured grids. Unlike LAURA, DPLR employs a modified Gauss–Seidel line relaxation method to efficiently solve along lines perpendicular to the surface, which shows rapid convergence even in the presence of large gradients [
7]. The primary challenge in these cases is efficiently generating structured grids, particularly for complex geometries.
US3D [
8,
9] is a solver developed as an extension of the DPLR algorithm for unstructured grids. US3D uses a hybrid grid approach with line relaxation in the structured region of the grid, and point relaxation everywhere else. US3D represents the state-of-the-art in hypersonic simulation capabilities, including a full suite of physical models for nonequilibrium effects, turbulence, wall-modeled large eddy simulation, grid alignment, and material thermal response and shape change [
10].
Several open-source codes for modeling flows in thermochemical nonequilibrium have also been developed. Within the widely used OpenFOAM CFD framework, a coupled DSMC-CFD solver, hy2Foam [
11], has been deployed. The hy2Foam solver utilizes a two-temperature model and has been validated for a range of operating conditions employing a five-species air model. Another open-source code suite for simulating hypersonic flows is COOLFluiD [
12], developed at the Von Karman Institute for Fluid Dynamics and at the KU Leuven Center for mathematical Plasma Astrophysics. COOLFluiD leverages state-of-the-art numerical methods to solve multi-physics problems on unstructured methods, and has been applied to problems in re-entry aerothermodynamics, aeroacoustics, turbulence modeling, and plasma dynamics.
Recent interest in sustainable spaceflight has motivated the design of reusable space systems capable of accommodating the entry environment many times over. These developments highlight the need for design and optimization software capable of modeling the complex physics of nonequilibrium flows across a wide range of mission profiles and vehicle geometries. One such design-optimization-focused code is SU2. SU2 [
13,
14] is an open-source software suite developed to solve partial differential equations (PDEs) and PDE-constrained optimization problems. While SU2 was developed primarily for computational fluid dynamics, it has also been applied to problems in heat conduction and radiation. In order to capture the complex physics of nonequilibrium flows [
15], an effort has been undertaken to enhance the nonequilibrium modeling capabilities in SU2, culminating in the NonEquilibrium MOdeling (NEMO) code base within the SU2 framework. This effort has extended the SU2 base code to include additional conservation equations to capture the physics of multi-component reacting flows in thermodynamic and chemical nonequilibrium.
Past work in SU2 has included implementation of a continuous adjoint formulation for design sensitivity analysis in hypersonic flows [
15] and study of shock interaction mechanisms in other-than-air gases [
16,
17]. Other developments include integration of anisotropic mesh adaptation using the discrete adjoint for nonequilibrium flows [
18]. Because of its modular design, SU2 is an excellent framework for the test and development of simulation and physical modeling capabilities for hypersonic, reacting flows. Recent efforts have focused on coupling SU2-NEMO with the Mutation++ thermochemical library [
19,
20] to provide an alternative to the set of chemistry models included in the code. Moreover, SU2 is built with design optimization in mind, utilizing the discrete adjoint methodology to efficiently extract design sensitivities. This will allow SU2-NEMO to not only study the complex flow physics, but to also be used to aid the design of hypersonic systems. This paper discusses the implementation of SU2-NEMO, including the code structure, constitutive physical models, and the numerical implementation. Verification and validation (V&V) test cases are presented, demonstrating the code’s capability of modeling a variety of flow physics in comparison to numerical and experimental results. Numerical results are presented for complex and realistic vehicle geometry, demonstrating a direction for future application and continued development of the code base.
2. Code Architecture and Design
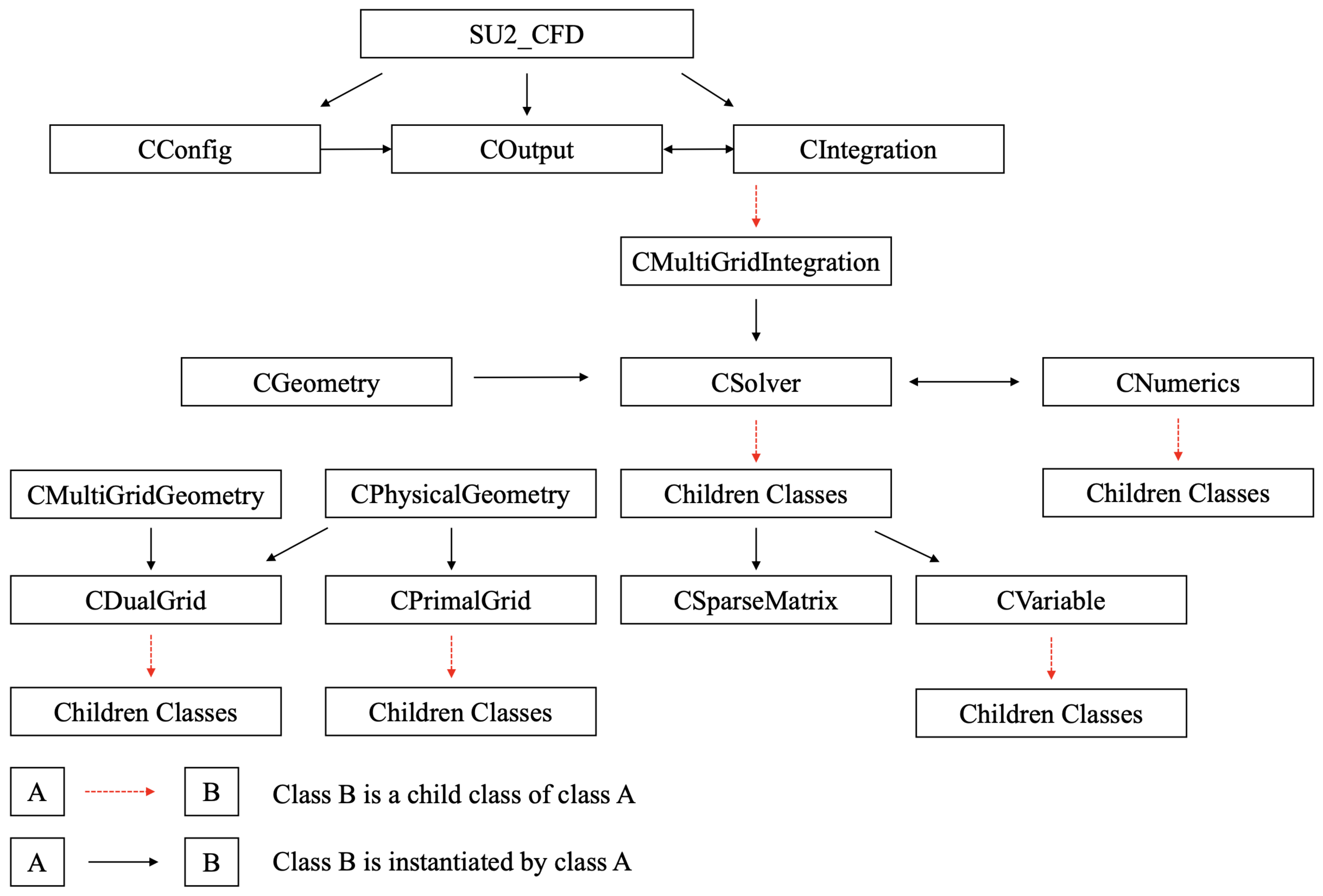
SU2-NEMO is built upon the existing open-source, multiphysics code suite, SU2. SU2 was designed for the analysis of PDE-based problems using state-of-the-art numerical methods [
13]. The primary code base is written in C++ and includes Python scripts for analysis, design, and optimization tasks. SU2 utilizes the object-oriented nature of the C++ programming language to efficiently implement new capabilities within its class structure. The overarching themes within the software are polymorphism and modularity; functions can be adapted or added without impacting the rest of the code. SU2-NEMO relies on the higher-level functions provided by the SU2 framework (geometry, integration, and output class structures), but has added numerical methods (convective schemes, viscous fluxes, and source terms) unique to the modeling of the nonequilibrium hypersonic environment.
The modularity of the SU2-NEMO architecture facilitates the rapid implementation of new models, providing an efficient framework for the test and development of new schemes and thermochemical libraries without having to significantly alter existing codes [
15]. Additional advantages of creating SU2-NEMO within the class structure of the SU2 framework include the ability to utilize and modify a variety of different implicit solvers and the ability to leverage the mature discrete adjoint infrastructure already available in SU2 for nonequilibrium flows. An overview of the general SU2 class architecture is given in
Figure 1. The authors invite the readers to see the original SU2 paper [
13] for a more in-depth discussion of the code architecture and philosophy.
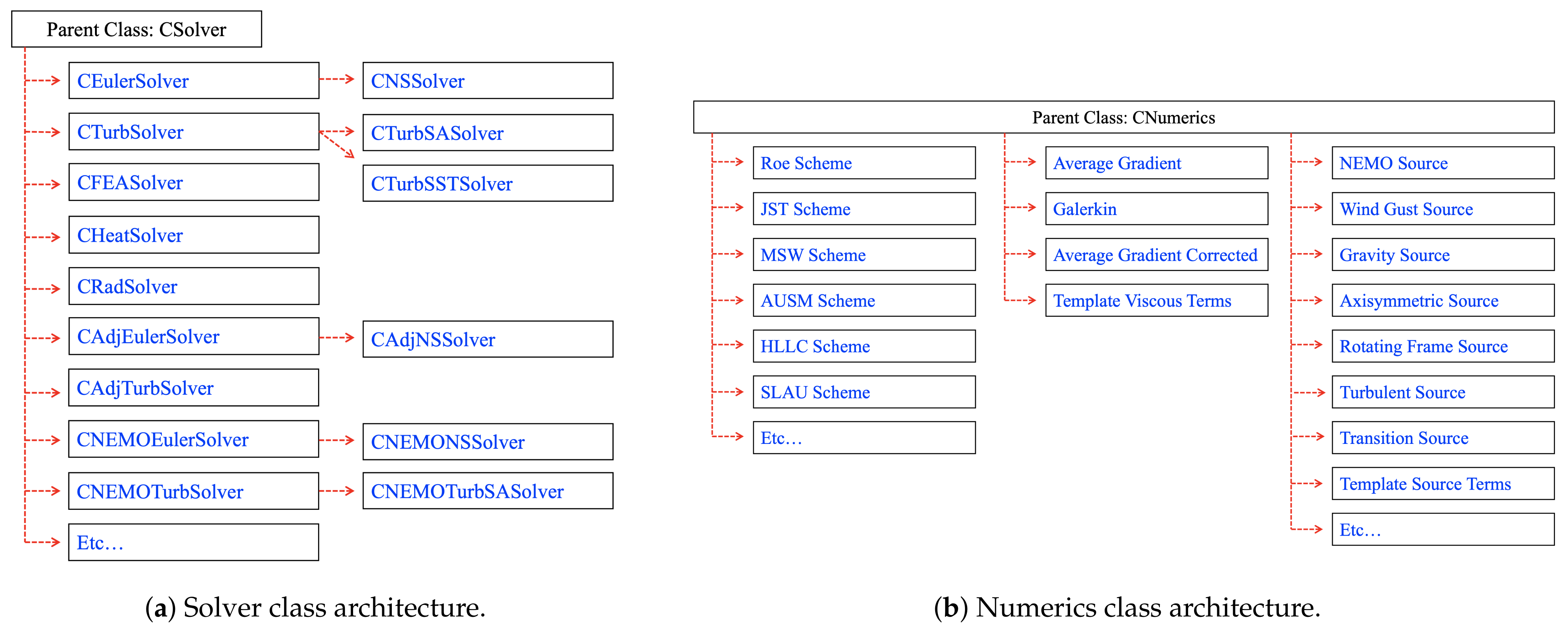
The main extensions of the code for SU2-NEMO occur within the CSolver, CFluidModel, and CNumerics classes. Like the SU2 framework, SU2-NEMO includes solver classes that define the physical phenomena being modeled: Euler Equations, Navier–Stokes, RANS, and so forth. To account for the additional conservation equations and differing data structures required to model the flow physics, the solver classes are extended with NEMO-specific functions. Similarly, this logic is extended to the numerics classes to include NEMO-specific convective schemes, such as MSW and AUSM. These extensions to the solver and numerics classes can be seen in
Figure 2a,b. The NEMO-specific classes have been generalized for any nonequilibrium flow. The additions to the framework allow for an arbitrary gas model to be simulated without further changes to the CNumerics, CVariable, or CSolver structures.
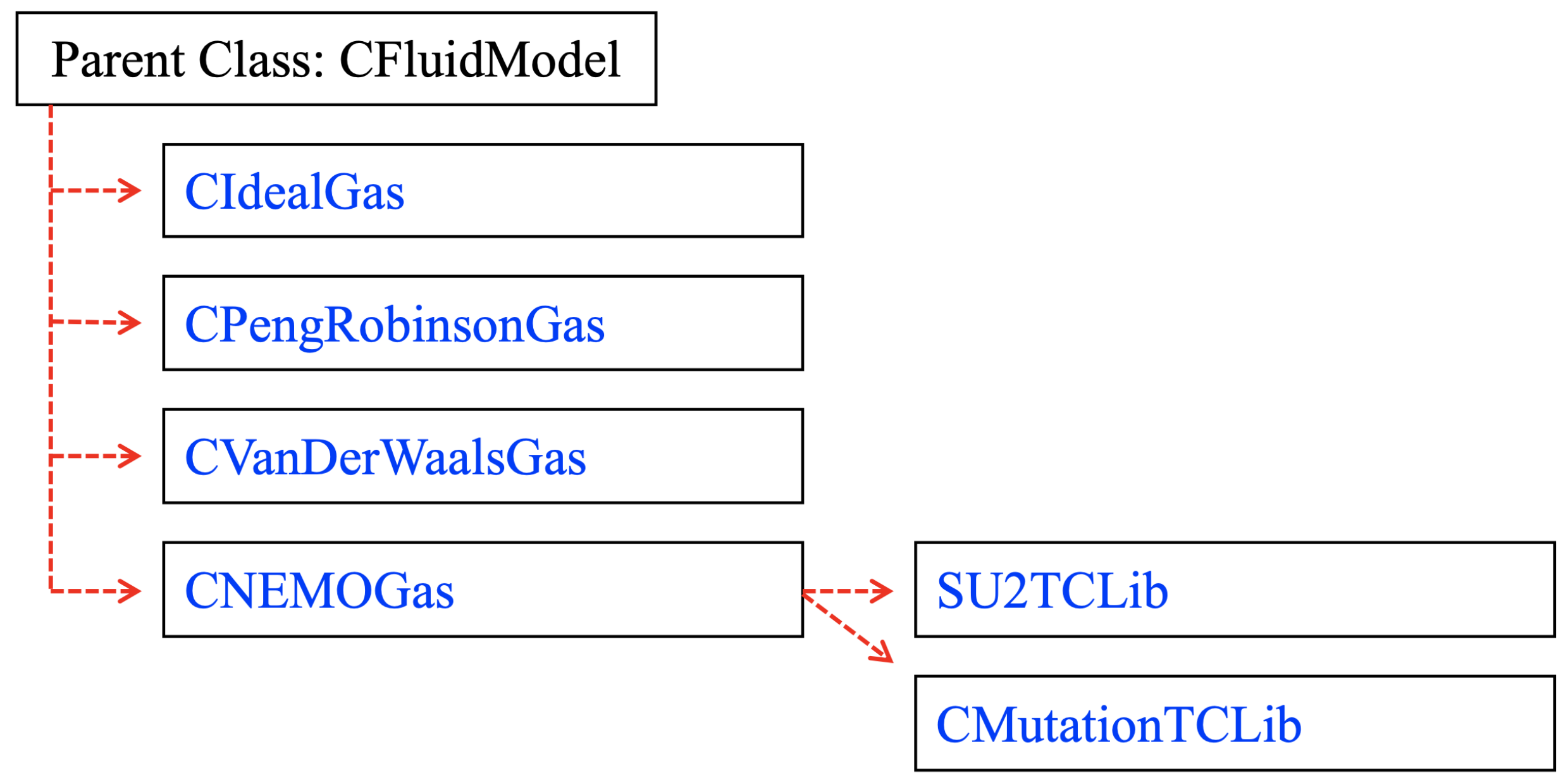
Gas-specific properties are computed using the CFluidModel class. A major benefit of the SU2-NEMO framework is the ability to alter or add different thermochemical models using the CNEMOGas child class within the CFluidModel, as seen in
Figure 3. The CNEMOGas class contains all data and functions necessary to compute flow thermochemical and transport properties. Currently, CNEMOGas has two additional child classes: CSU2TCLib, the native thermochemical library, and CMutationTCLib, a class implementing a connection with Mutation++.
2.1. Mutation++
Due to the modular implementation of SU2, the code suite is amenable to interfacing with external libraries. SU2-NEMO takes advantage of this through an abstraction of thermochemical source terms using the CMutationTCLib class. SU2-NEMO is linked to the MUlticomponent Thermodynamic And Transport properties for IONized gases library in C++ (Mutation++) [
19], a well-validated physio-chemical library. CMutationTCLib implements calls to Mutation++ for computation of mixture thermodynamic, chemical kinetic, and transport properties. Mutation++ is developed, updated, and configuration-managed by the von Karman Institute, utilizing high-fidelity models for nonequilibrium processes in reacting mixtures. Mutation++ provides the capability to simulate a wide array of different gas compositions.
2.2. SU2 Native Thermochemical Library
SU2-NEMO also contains a native thermochemical library, CSU2TCLib. The native SU2 library includes three standard gas models: Air-5, N2, and Argon. CSU2TCLib demonstrates similar robustness and convergence behavior to CMutationTCLib, and permits easier integration with other SU2 capabilities, but has been shown to be less computationally efficient than CMutationTCLib on benchmark test cases.
3. Physical Modeling
Continuum hypersonic flows are modeled in SU2-NEMO with the Navier–Stokes equations extended for reacting flows in thermochemical nonequilibrium. These are a set of coupled nonlinear partial differential equations, given below in their conservation form in Equation (
1).
where the conservative variables, convective flux, viscous flux, and source terms are given using standard notation for a number of species
by
where the details of the notation will be described in subsequent sections. The thermochemical nonequilibrium closure terms (
Q), transport properties, and mixture energies introduced in the next section are provided by the CFluidModel class, either through the CMutationTCLib class linked to the Mutation++ library or CSU2TCLib class containing the native SU2 library.
3.1. Two-Temperature Model
Energy carried within polyatomic molecules in a gas-phase species is partitioned among translational, rotational, vibrational, and electronic degrees of freedom. The energy stored in each mode is quantized, and the allowable energy levels are given by eigenstates of the time-independent Schrödinger equation [
21].
A complete description of the interaction among energy modes is too complex for implementation in a CFD code, so simplifying assumptions are used. In the models implemented in SU2-NEMO, rotational energy is determined assuming rigid body dynamics (fixed bond length) for polyatomic molecules, and vibrational energy is approximated as a simple harmonic oscillator. Inter-mode coupling between the energy modes, such as coupling between the rotational and vibrational modes due to bond length variation, is neglected and the energy modes are assumed to be independent.
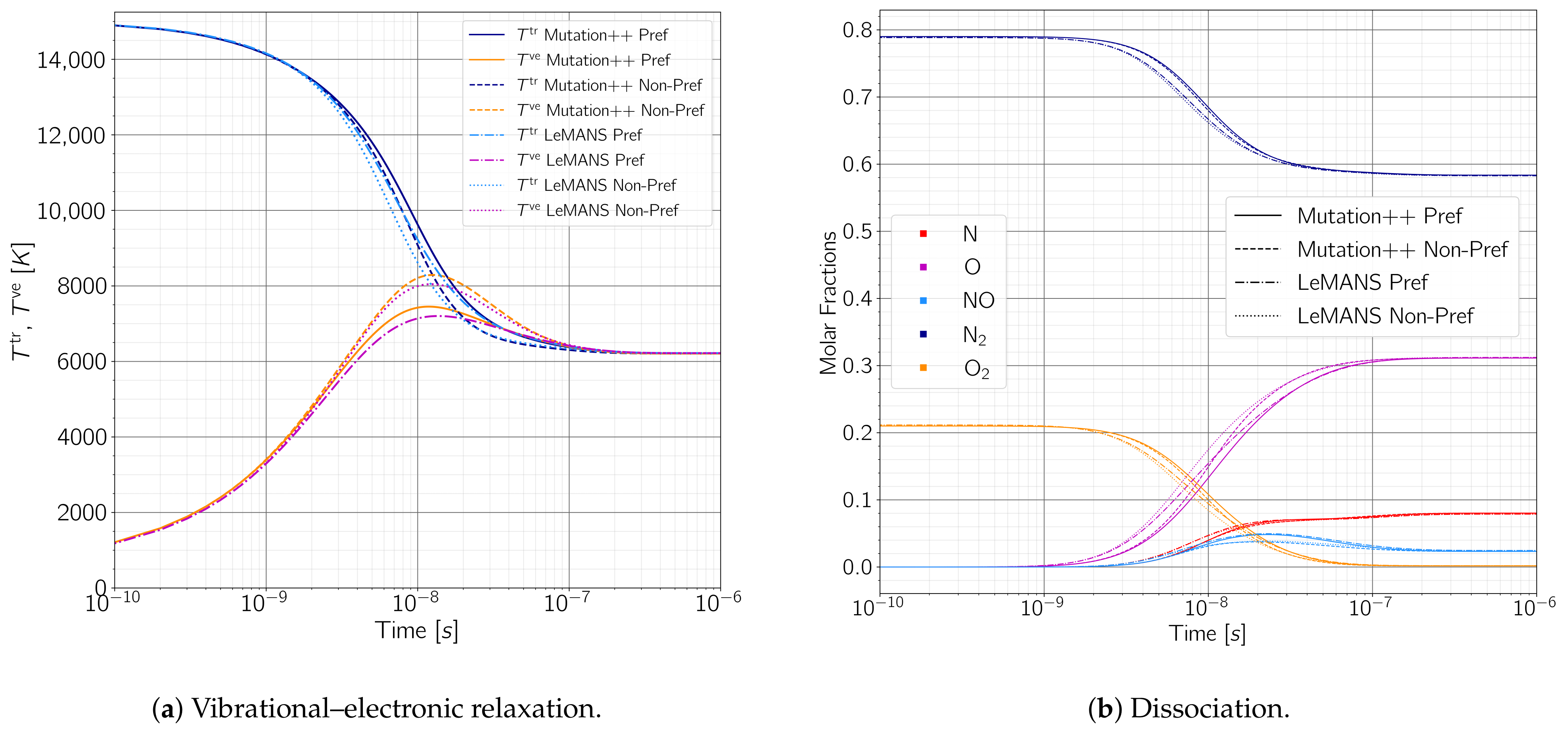
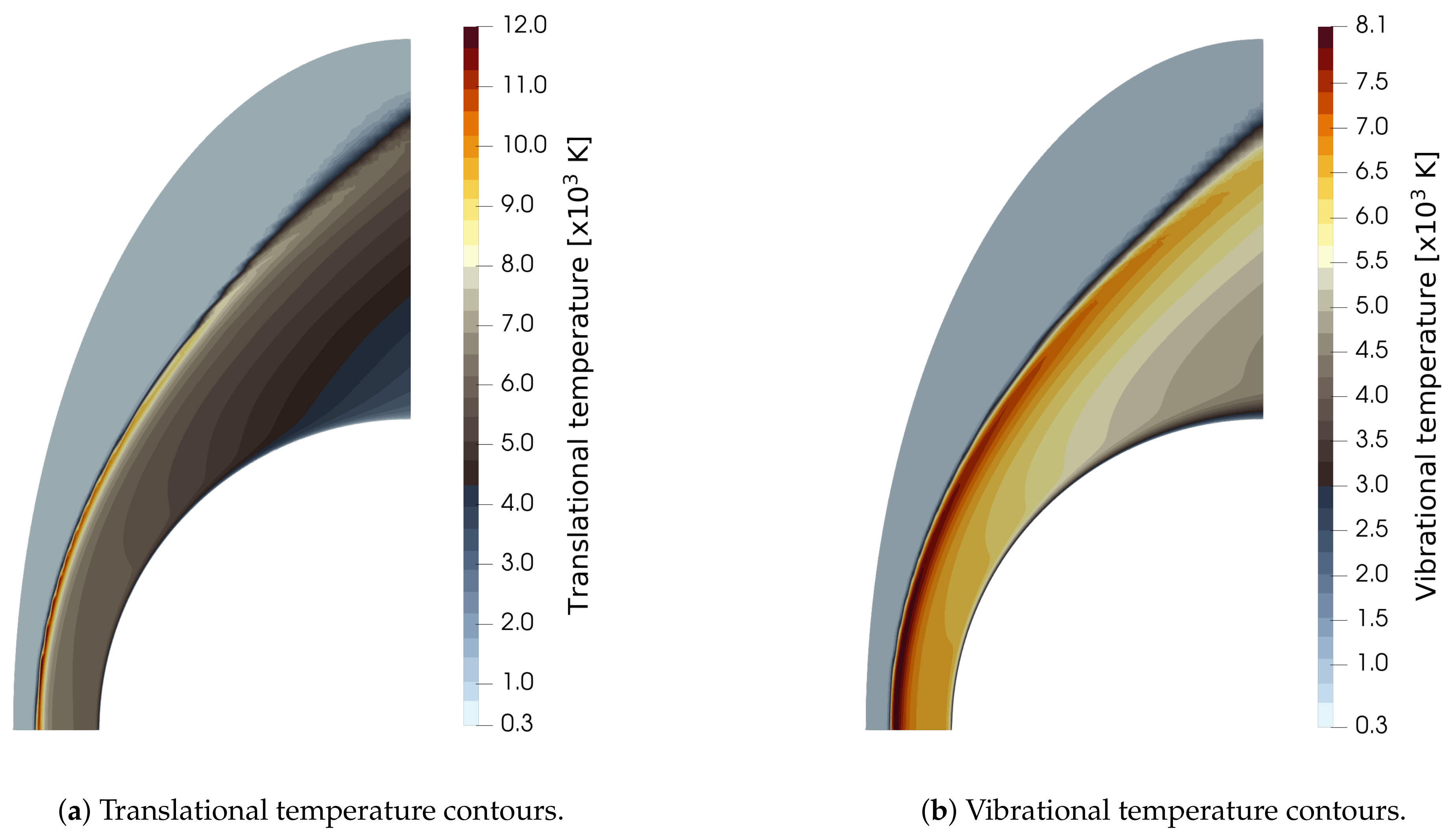
To accommodate differences in the number of collisions required to reach equilibrium, separate temperatures are used to track the translational–rotational energy modes and vibrational–electronic energy modes. This two-temperature model assumes equilibrium between the translational and rotational energy modes, and between the vibrational and electronic modes, but also assumes that these two sets are not necessarily in equilibrium with each other. The rigid-rotor harmonic oscillator (RRHO) two-temperature model has been shown to accurately predict flow and transport properties from high supersonic to atmospheric entry conditions [
15]. More sophisticated correction terms can be used where modes are excited sufficiently far from their ground state, such that non-ideal and anharmonic behavior becomes significant to solution accuracy.
Through the independence of the energy levels, the total energy and vibrational–electronic energy per unit volume can be expressed as
and
Considering a general gas mixture consisting of polyatomic, monatomic, and free electron species, expressions for the energy stored in the translational, rotational, vibrational, and electronic modes are given as
where
is an integer specifying the number of axes of rotation,
where
is the characteristic vibrational temperature of the species, and
where
is the characteristic electronic temperature of the species and
is the degeneracy of the
state.
Vibrational–Electronic Relaxation
Vibrational relaxation is computed using a standard Landau–Teller [
22] relaxation time with Park high-temperature correction
where
is computed using a combination of the Landau–Teller relaxation time,
, and a limiting relaxation time from Park,
using
and
The interspecies relaxation times are taken from experimental data from Millikan and White [
23], expressed as
A limiting relaxation time,
, is used to correct for under-prediction of the Millikan–White model at high temperatures [
23].
is defined as
where
is the effective collision cross-section.
3.2. Finite-Rate Chemical Kinetics
Energetic collisions also result in chemical reactions taking place in the flow. The source terms in the species conservation equations described in Equation (
2) are the species’ volumetric mass production rates which are governed by the forward and backward reaction rates,
and
, for a given reaction
r, and can be expressed as
From kinetic theory, the forward and backward reaction rates are dependent on the molar concentrations of the reactants and products, as well as the forward and backward reaction rate coefficients,
and
, respectively [
21], and can be expressed as
and
For an Arrhenius reaction, the forward reaction rate coefficient can be computed as
where
is the pre-factor,
is the rate-controlling temperature for the reaction,
is an empirical exponent, and
is the activation energy per molecule. A list of these values can be seen in
Table A1.
The rate-controlling temperature of the reaction is calculated as a geometric average of the translation–rotational and vibrational–electronic temperatures,
where the constants
and
, shown in
Table A2, are dependent on the nature of the reaction. The forward and backward rate coefficients are related by the reaction equilibrium constant which is determined using curve fits from the Park 1990 model [
24], shown in
Table A3.
3.3. Transport Properties
Mass, momentum, and energy transport in fluids are all governed by molecular collisions, and expressions for these transport properties can be derived from the kinetic theory. The mass diffusion fluxes,
, are computed using Fick’s Law of Diffusion:
where
is the species mass fraction and
is the species multi-component diffusion coefficient. The values of
are computed as a weighted sum of binary diffusion coefficients between all species in the mixture. These are obtained by solving the Stefan–Maxwell equations under the Ramshaw approximations [
25]. The viscous stress tensor is written as
where
is the mixture viscosity coefficient. The conduction heat flux for each thermal energy mode,
, is assumed to be given by Fourier’s Law of heat conduction:
where
is the temperature and
is the thermal conductivity coefficient of the
kth energy mode. Viscosity and thermal conductivity are computed using Wilke’s mixing rule [
26]. The species viscosity model is calculated using either Blottner’s three-parameter curve fits for high-temperature air [
27], or Gupta–Yos [
28]. Thermal conductivity is calculated using Eucken’s formula [
29].
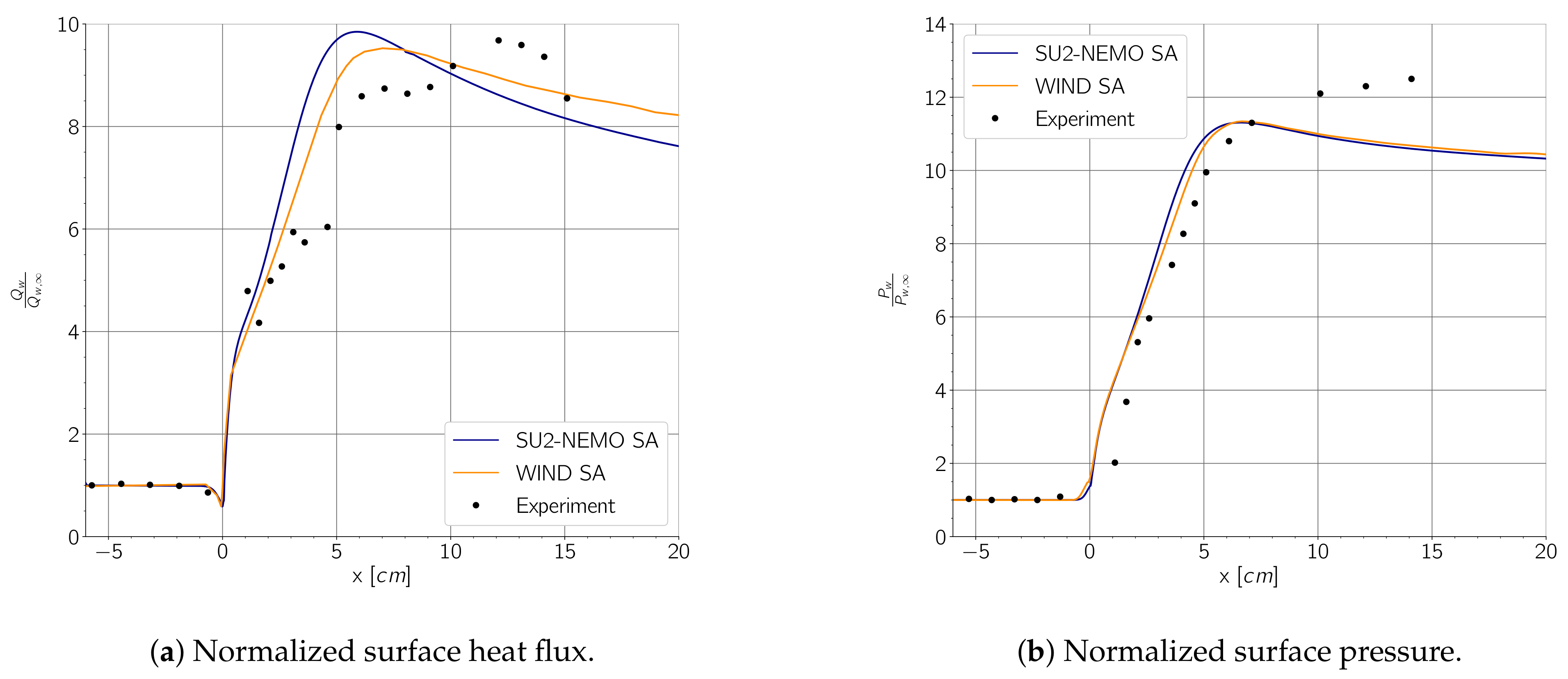
3.4. Turbulence Modeling
One of the core features in the SU2 suite is a Reynolds-Averaged-Navier–Stokes (RANS) solver to solve compressible turbulent flow [
30]. The RANS equations are solved in SU2 using two main models: the one-equation Spallart-Allmaras (SA) model [
31] and the two-equation Menter k-omega SST model [
32]. Within the SU2-NEMO framework, the SA model has been implemented. The turbulent eddy viscosity is computed as
where
is solved for using
The SA model was not designed for multiple species being present in a given flow, and as such, does not account for the multiple species’ densities. This work takes the total density of the flow as
Hypersonic turbulence modeling remains a challenge in the community, and work is being done to improve and validate models within the NEMO framework.
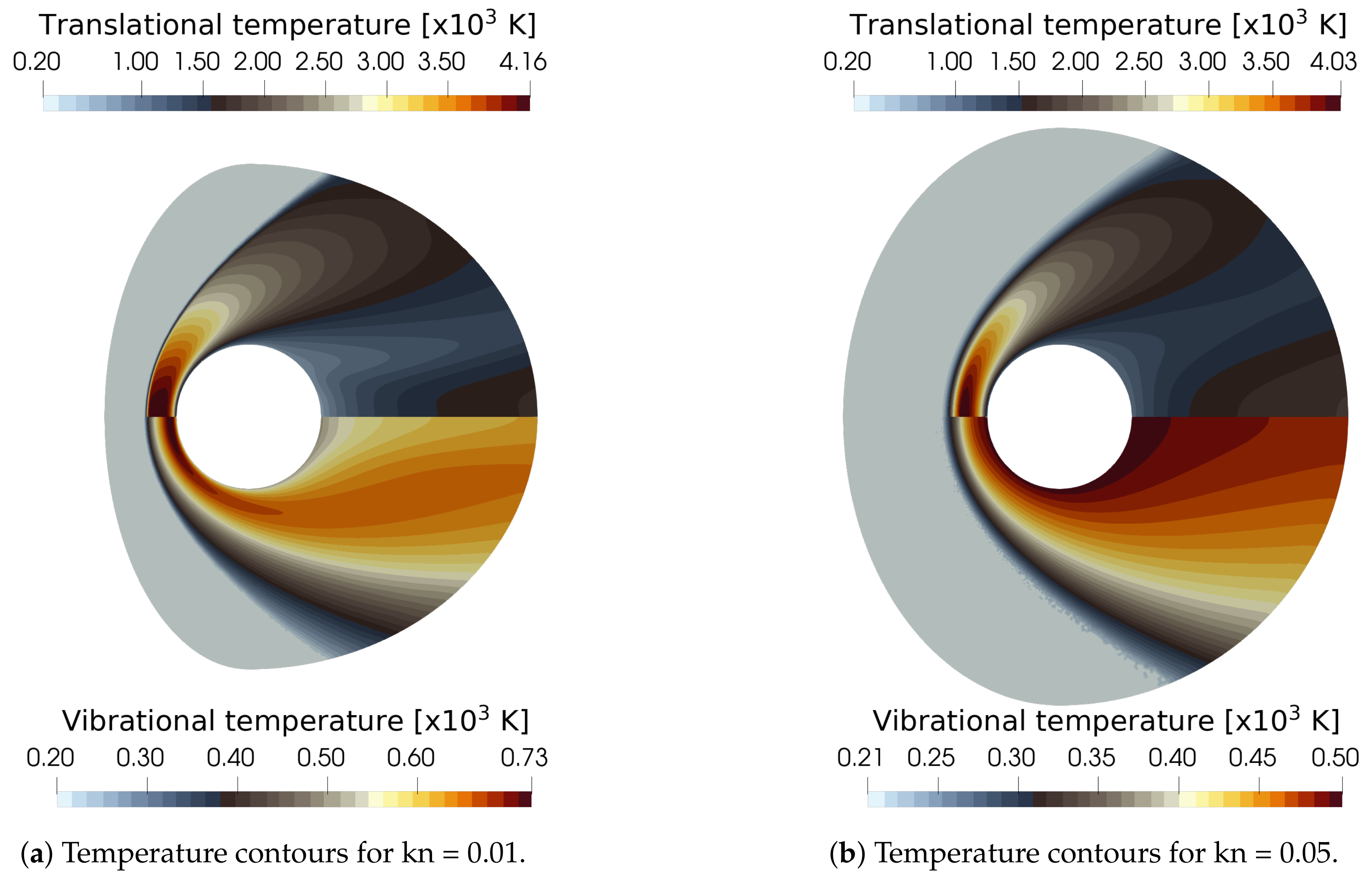
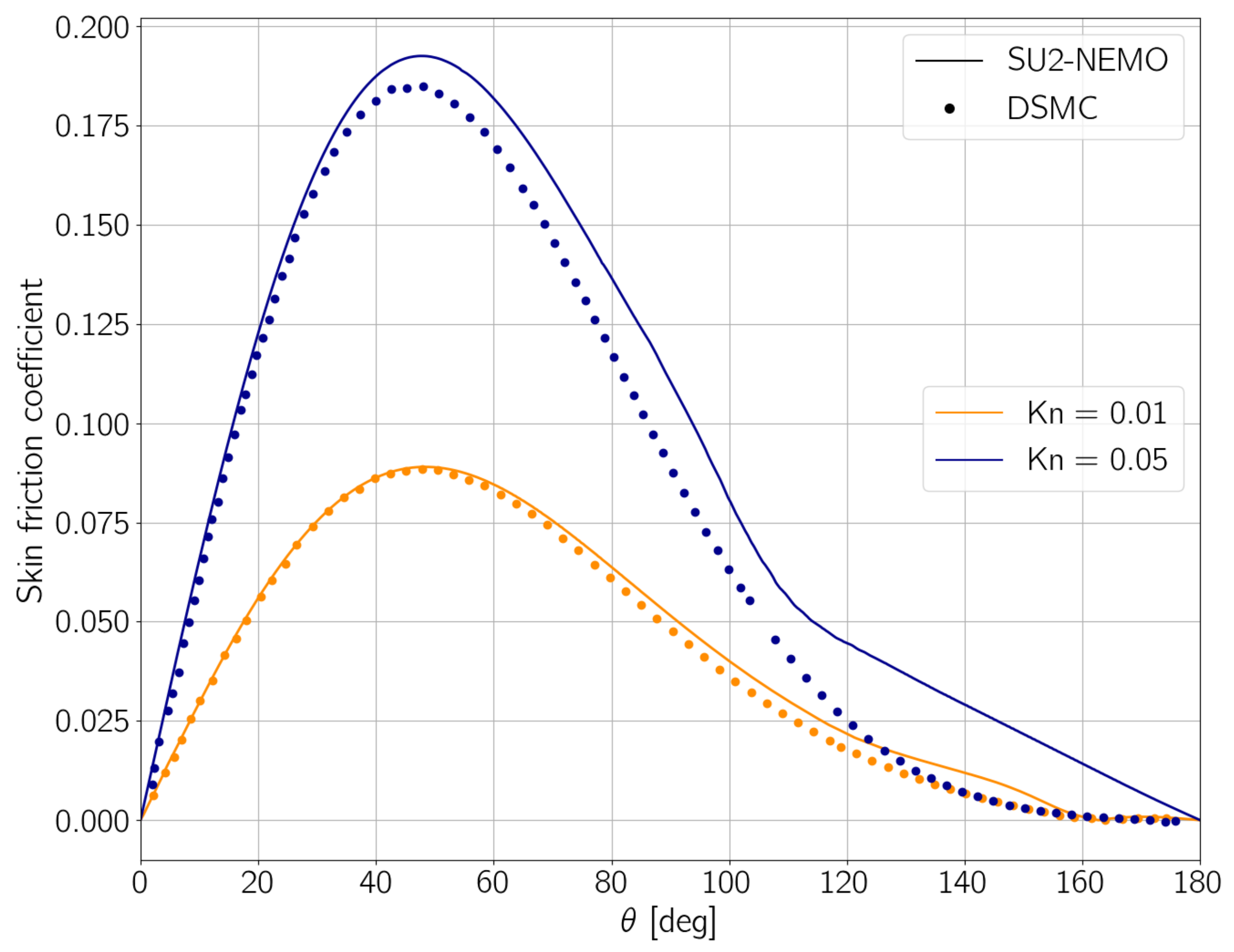
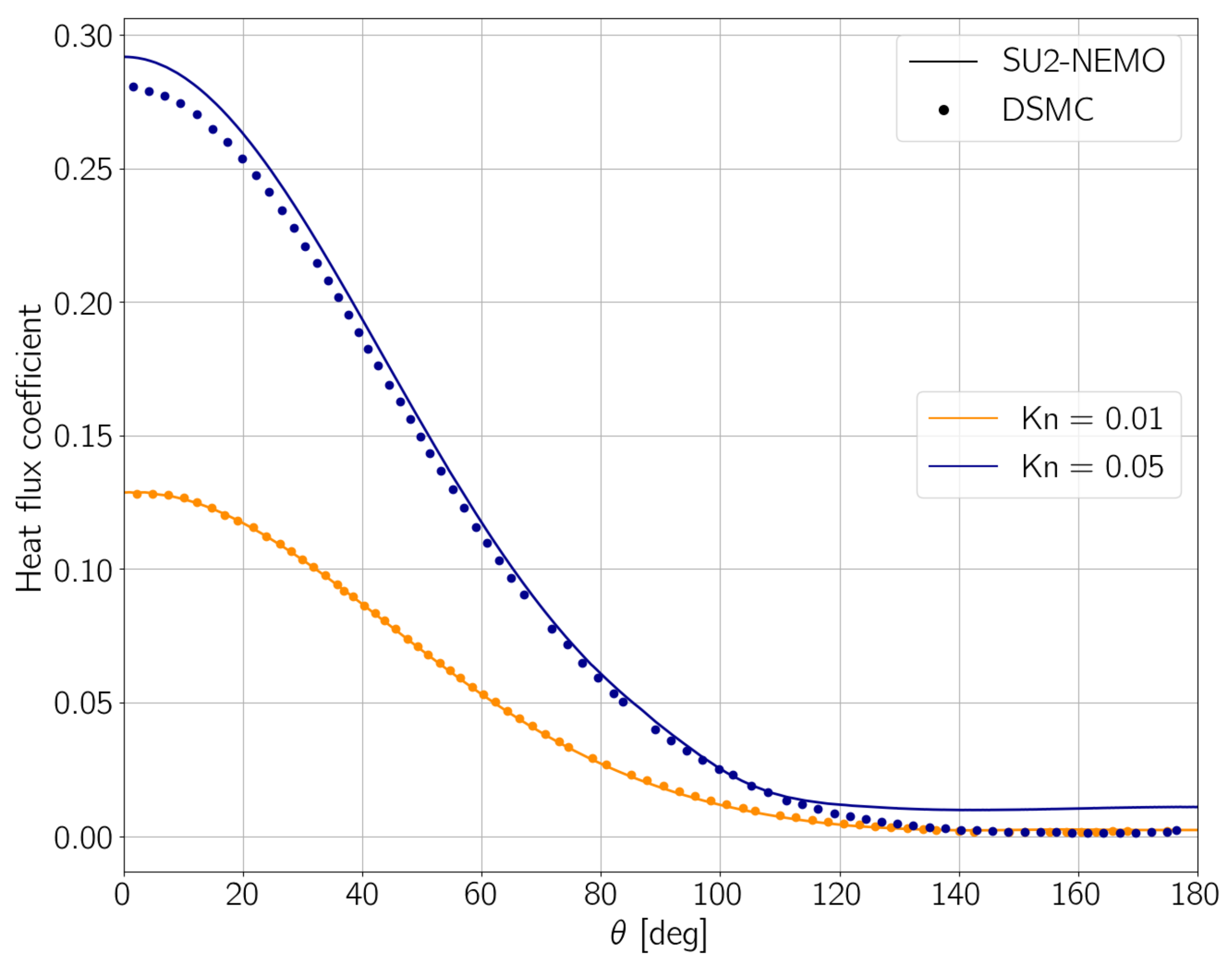
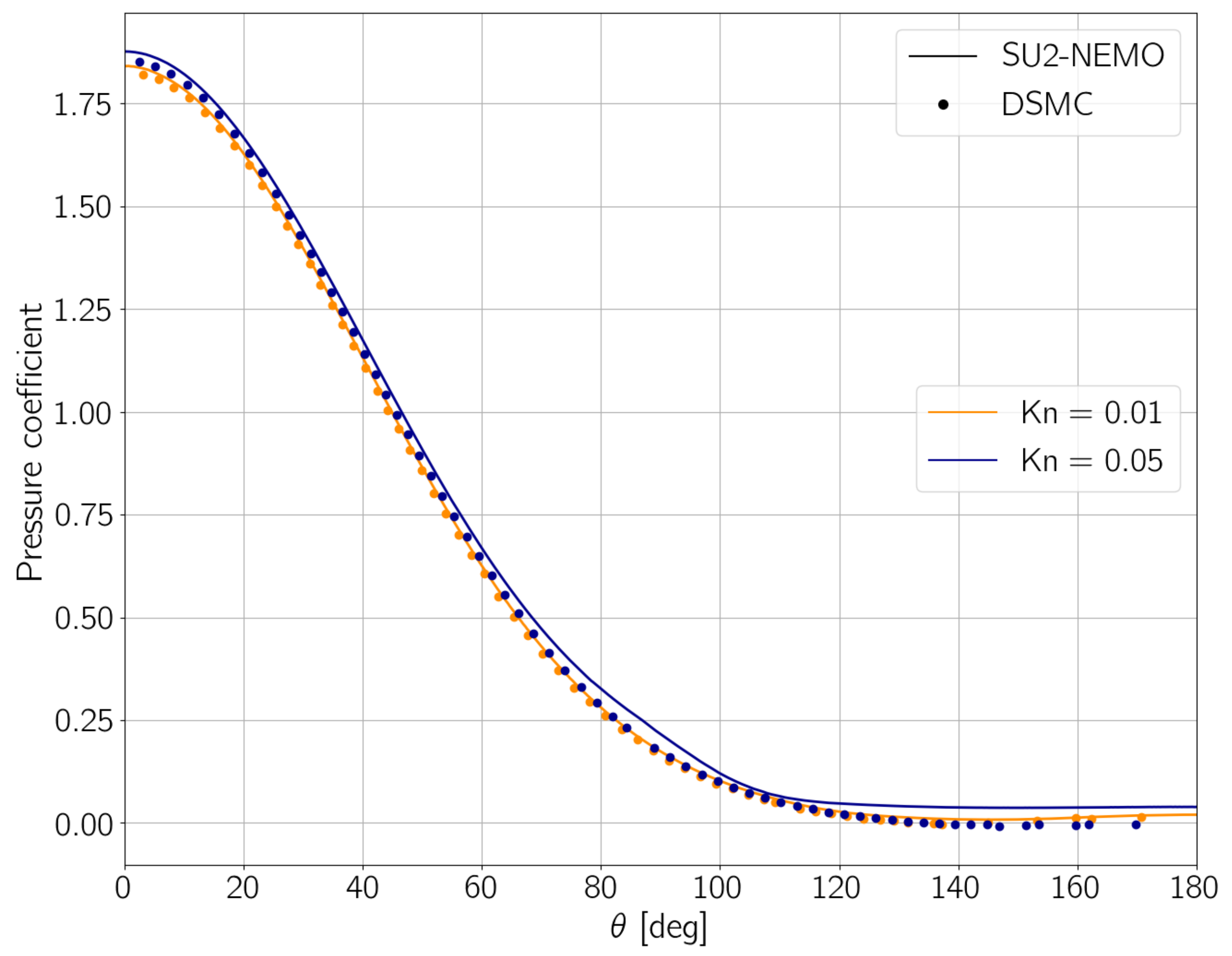
3.5. Modeling of the Slip Regime
One of the most recent implementations in SU2-NEMO is the capability of simulating flows with moderate rarefaction, for which the Navier–Stokes continuum equations hold for the whole domain except at the vicinity of solid surfaces. Near the wall, due to the lack of collisions, the gas flow will not have the same properties as the surface, that is, wall temperature and velocity. Thus, there is the need to account for the molecular slippage. SU2-NEMO uses the Maxwell velocity slip [
33] and Smoluchowski temperature jump [
34] equations to compute the velocity and temperature of the gas in contact with the surface. The equations are given as
and
respectively, where
is the flow viscosity,
is the mixture density,
is the Prandtl number,
is the specific heat ratio,
T is the temperature of the gas,
is the temperature of the surface, and
is the mean free path, calculated as [
35]
The coefficients
and
are referred to as the Tangential Momentum Accommodation Coefficient (TMAC) and the Thermal Accommodation Coefficient (TAC), respectively. The values of the accommodation coefficients depend on the physical characteristics of the surface, and are usually determined empirically [
36].
4. Numerical Implementation
This section highlights the numerical implementation of models within SU2-NEMO. This includes both the discretization of the governing equations and time-integration strategies. The basic numerical procedures are consistent with those implemented in the base SU2 software, and more details can be found in the Reference [
13]. However, SU2-NEMO employs some specific convective schemes well-suited to high-speed flows, which are described in more detail.
4.1. Spatial Integration
SU2 utilizes the Finite Volume Method to solve the discretized governing equations on an edge-based median dual-grid numerical mesh. The discretized conservation equations can be written for a control volume
as
where
is the vector of conservative variables and
is the residual representing the integration of all spatial terms at node
i.
and
are the numerical approximations of the convective and viscous fluxes, and
is a vector of source terms.
is the area of the face associated with the edge
,
is the volume of the dual control volume, and
is the set of neighboring nodes to node
i. The fluxes are computed at the midpoint of each edge and added/subtracted to the residual for each of the two nodes making up a particular edge.
4.1.1. Convective Flux
SU2-NEMO, like the base SU2, can be discretized using both upwind and central convective schemes. This section will not discuss each scheme at length, but will focus on two schemes implemented specifically for high-speed flow simulation: the Modified Steger-Warming (MSW) and Advection Upstream Splitting Method (AUSM) flux-vector splitting schemes.
The original Steger-Warming flux-vector splitting scheme is an upwinding numerical method for resolving flows in the presence of large shocks. The scheme involves splitting the flux vector based on the direction of information propagation in the flow [
37]. MSW is widely used due to its highly dissipative nature, mitigating convergence issues due to the stiffness of nonequilibrium equations. The approximated flux between nodes
i and
j is given by
The flux Jacobian can be diagonalized through a similarity transformation, as
To address accuracy concerns of the Steger-Warming scheme, Modified Steger-Warming adds a weighting factor to reduce the numerical dissipation in the presence of large pressure gradients, such as near-shocks and in boundary layers, to ensure greater accuracy without impacting flow stability. The weighting factor is calculated as
where
is a tunable parameter, taken as 5 by default in SU2-NEMO. The weighting factor is used to compute the corrected primal state vectors as
and
AUSM is another flux-vector splitting method commonly used for high-speed flows. The standard AUSM scheme [
38] is described in detail below. The scheme separates the flux vector into convective terms propagated at the local flow velocity and pressure terms propagated at the local speed of sound, expressed as
where the Mach number can be split as
and
are defined by using Van Leer splitting [
39]. Pressure is similarly discretized as
such that
The flux approximation is given by
The resulting scheme is accurate and robust, with lower numerical dissipation than MSW. In addition to the scheme described above, several extensions of AUSM have also been implemented in SU2-NEMO. These include the AUSM+M [
40] and AUSM
+ up2 [
41] schemes, which contain improvements on the stability characteristics and accuracy of the original AUSM scheme. The AUSM family of schemes offer superior shock-capturing and avoid the presence of carbuncles observed in stagnation regions around blunt bodies. SU2-NEMO, like the base SU2 code, has slope-limiters for higher-order accuracy solutions.
4.1.2. Viscous Flux
Viscous flux values are computed at the median dual-grid interfaces. Gradient information required for the viscous fluxes can be evaluated by either the Gauss-Green Theorem or Weighted Least-Squares approach, with appropriate corrections in areas of high cell skewness.
4.2. Boundary Conditions
SU2-NEMO employs several wall boundary conditions similar to those in the base SU2 code. These include non-catalytic isothermal and heat flux wall boundaries for viscous flow simulation, as well as the inviscid Euler wall. The Smoluchowski–Maxwell boundary condition, as described in [
42], is also implemented for modeling rarefied flows. A more detailed description of the slip boundary condition implementation is done in
Section 3.5.
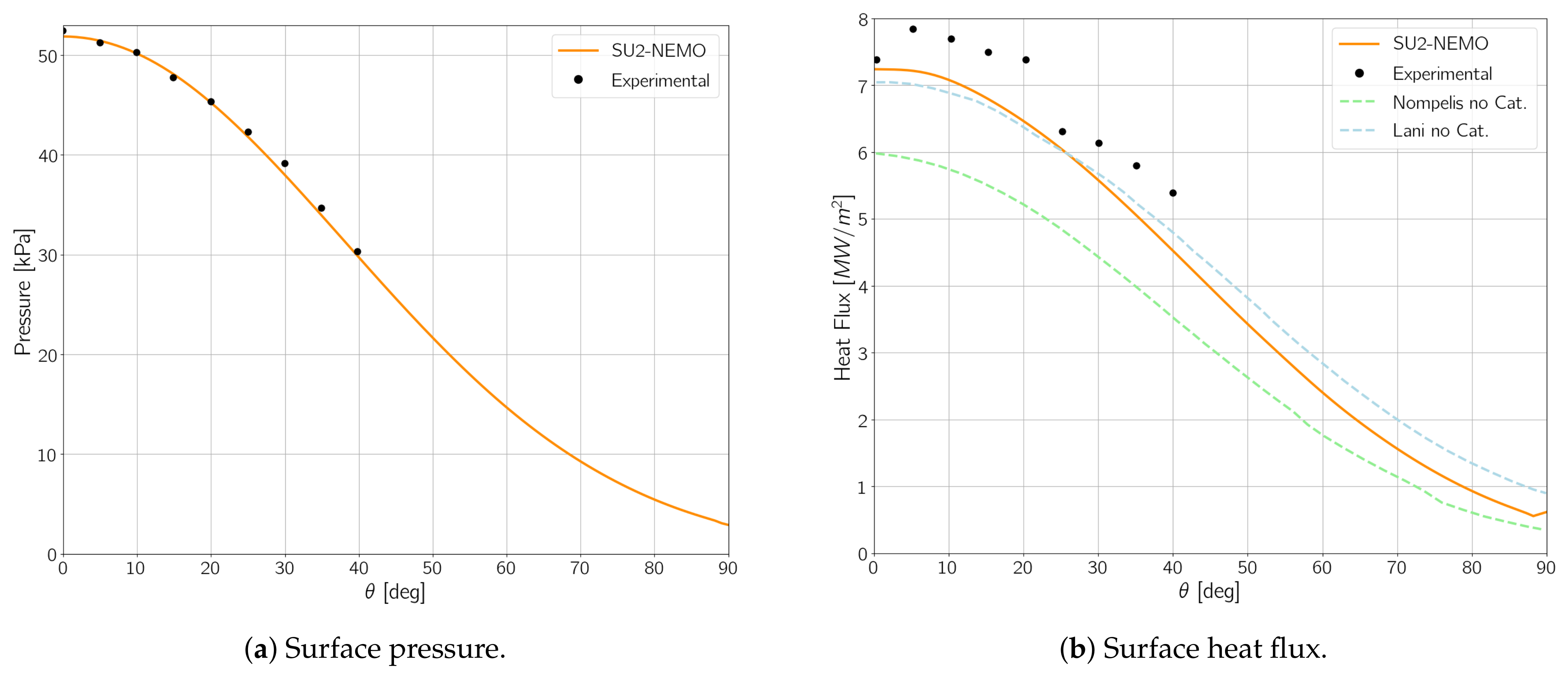
Surface-catalyzed chemical reactions can have a significant impact in high-speed flows, and current efforts focusing on the development and validation of more complex gas–surface models in SU2-NEMO are ongoing.
4.3. Time Integration
SU2-NEMO takes advantage of the time integration available in the general SU2 framework, utilizing both explicit time integration (explicit forward Euler and Runge–Kutta explicit), and implicit time integration (implicit backward Euler).
Explicit time integration schemes are easily parallelizable, since they involve a local update at each cell. The drawback is that explicit schemes place requirements on the allowable Courant–Friedrichs–Lewy (CFL) number of the local time-step based on wave speed. The CFL number must be sufficiently small, which can result in a large number of iterations to converge, especially in regions of large gradients.
Implicit methods incorporate information at the next time-step, so they do not suffer from the same stability concerns as explicit methods. However, they require the simultaneous solution of all residual equations by means of a linear system, resulting in a higher computational cost per time-step. Several linear solvers are implemented in SU2, as well as a suite of preconditioners to reduce the computational cost of the solution.
6. Conclusions
This paper presented the SU2-NEMO framework, detailing the multiphysics extensions to SU2 for applications in high-temperature and high-Mach flows. This paper outlined the SU2-NEMO framework design, which provides the flexibility to rapidly modify existing thermochemical models, or to couple external software suites like Mutation++ with the addition of the CNEMOGas CFluidModel class. This paper also provided details on the numerical models implemented to account for nonequilibrium and chemical phenomena required to accurately model the hypersonic flight regime.
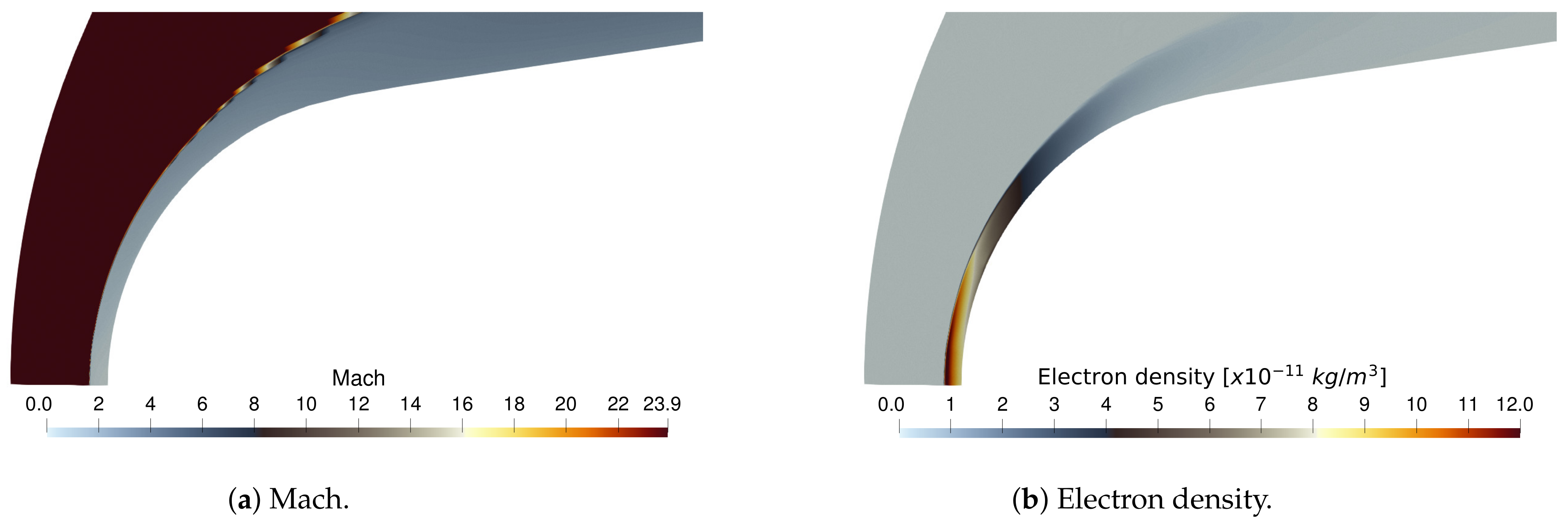
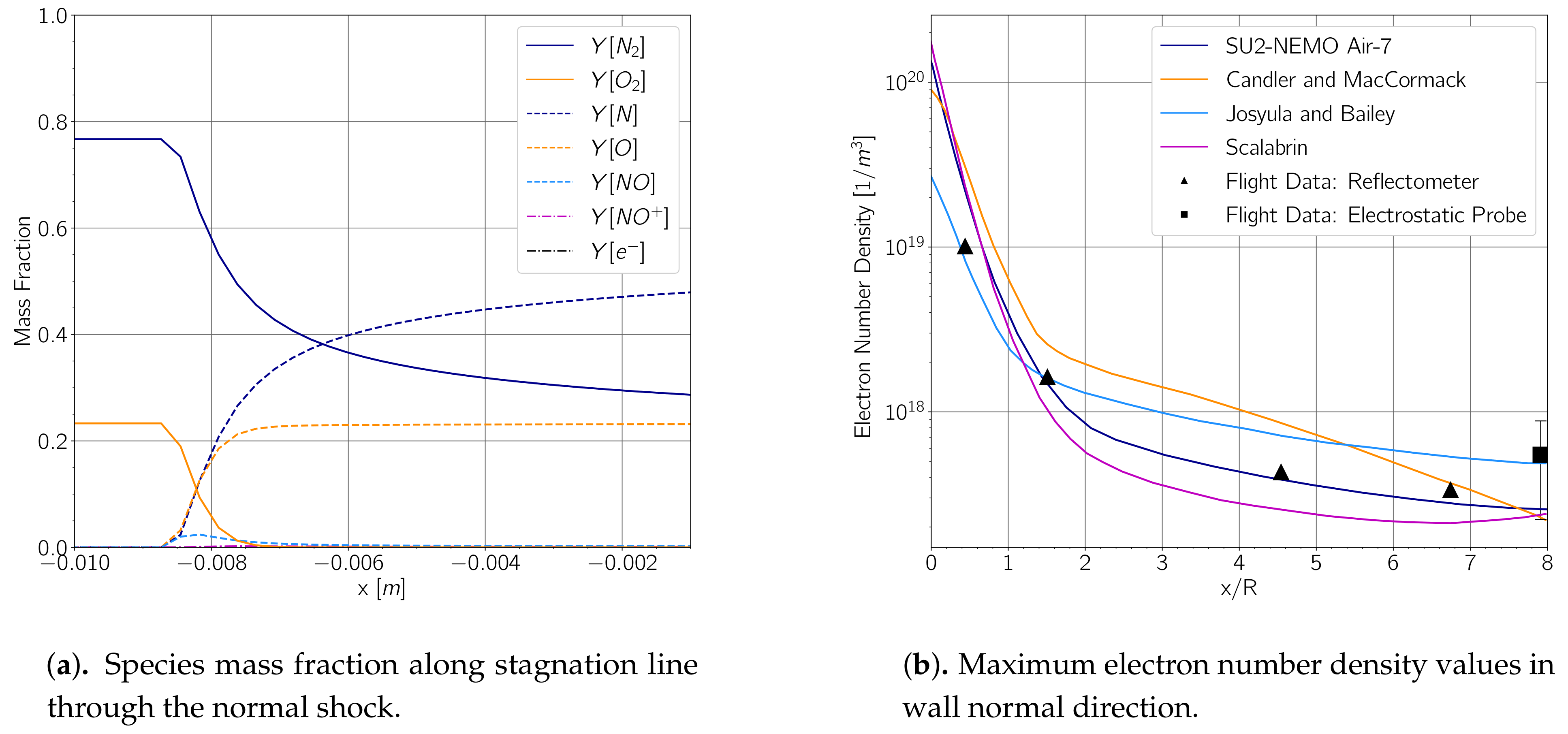
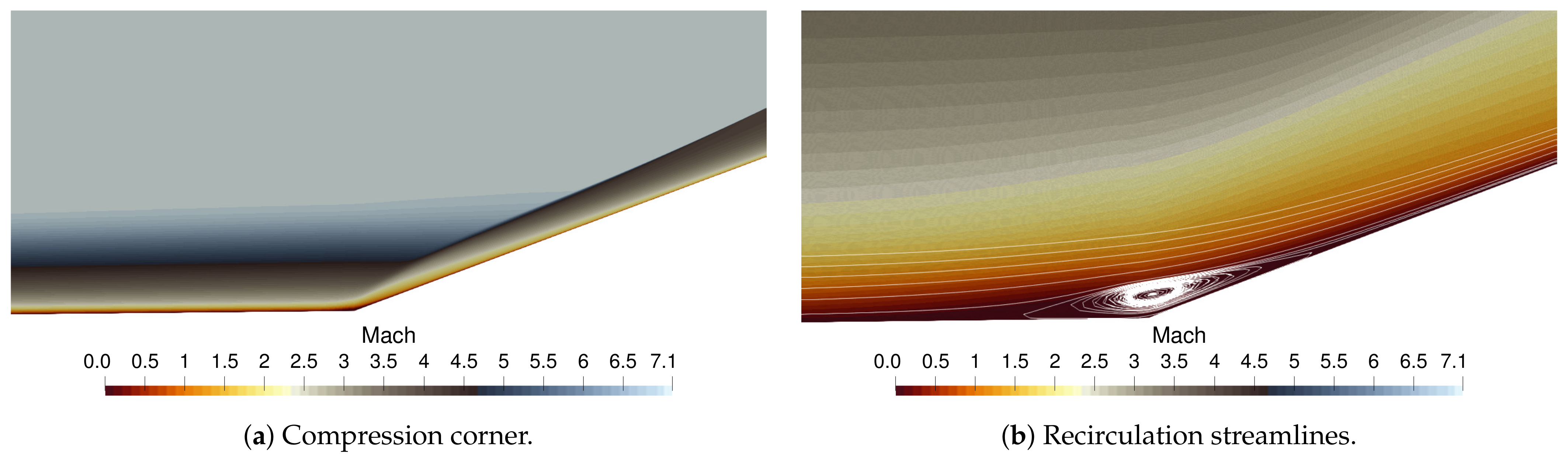
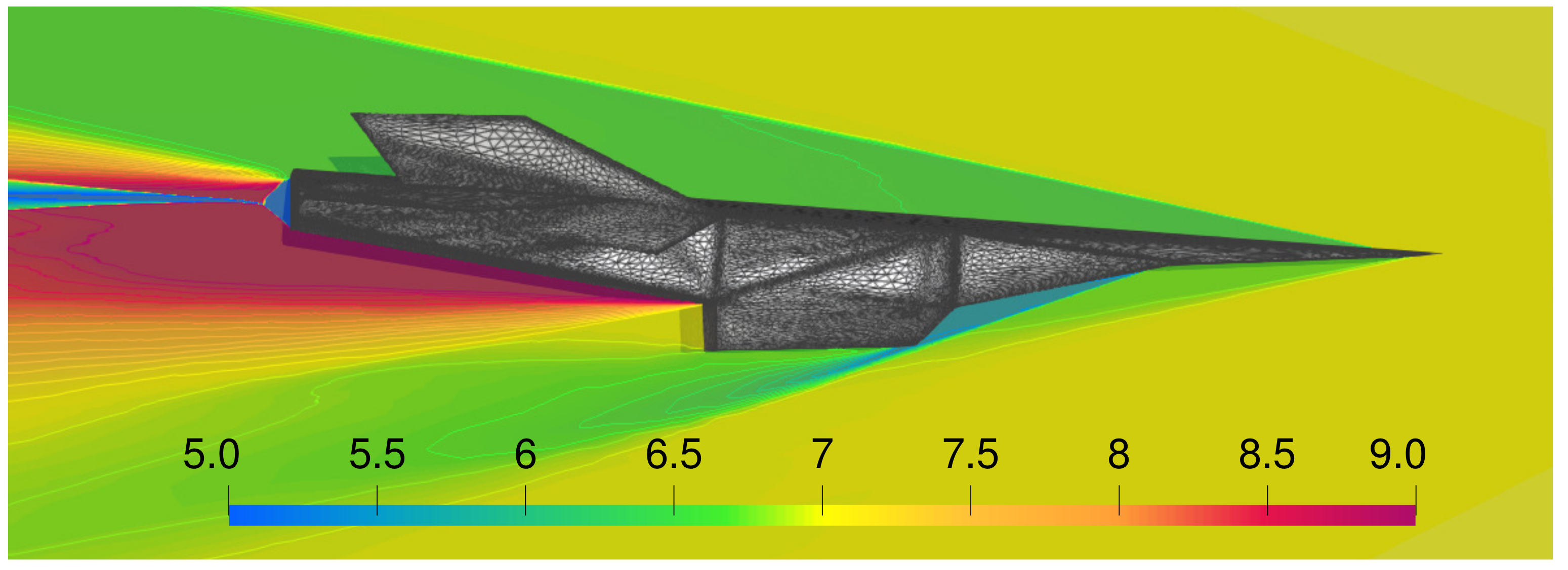
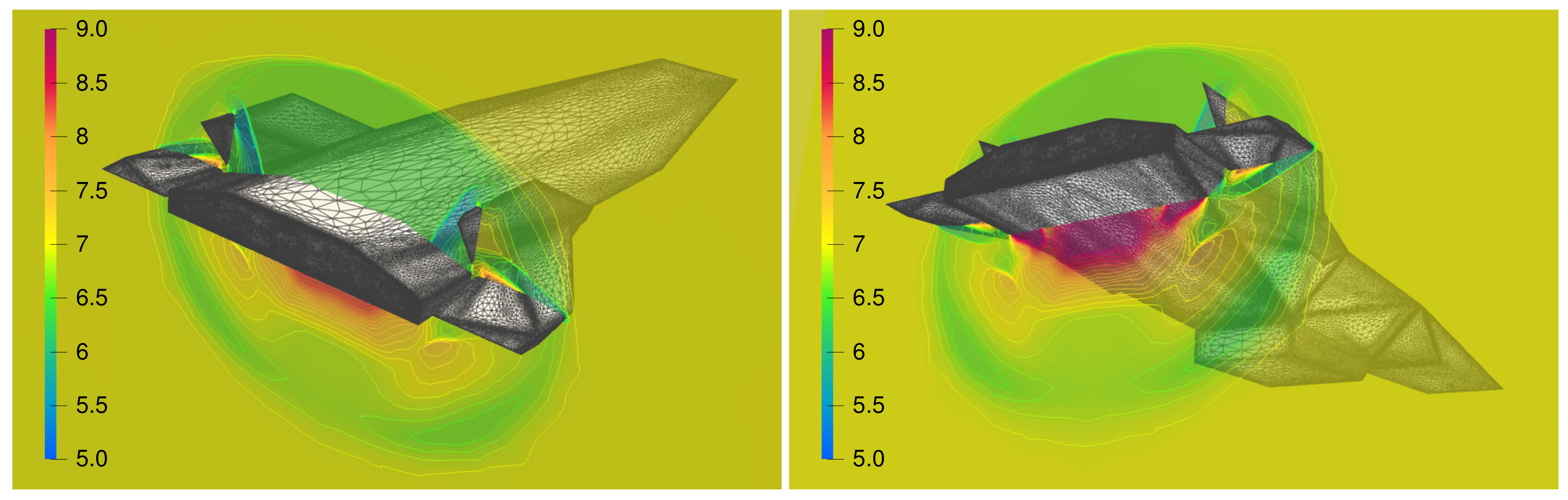
Additionally, the SU2-NEMO thermochemical models were verified and validated using several canonical hypersonic test cases, including a zero-dimensional heat bath, the HEG hypersonic cylinder, and the weakly ionized RAM-C vehicle. A low Knudsen number cylinder has been presented, verifying the slip flow regime boundary conditions. An axisymmetric turbulent cone-flare geometry has also been simulated to demonstrate the implementation of the RANS SA turbulence model in SU2-NEMO. Finally, SU2-NEMO was used to simulate an X-43a-like vehicle, capturing the shock–surface interactions on a complex body using anisotropically adapted unstructured meshes.
SU2-NEMO has been developed to take advantage of the capabilities present in the rapidly evolving SU2 mulitphysics suite. While this paper discussed the fundamental capabilities of SU2-NEMO, future work will include expanding the framework to incorporate the use of the adjoint solver for sensitivity analysis and design optimization applications, more complex gas–surface interaction boundary conditions, and improved turbulence models.