Effect of Two-Head Flared Hole on Film Cooling Performance over a Flat Plate
Abstract
1. Introduction
2. Numerical Analysis
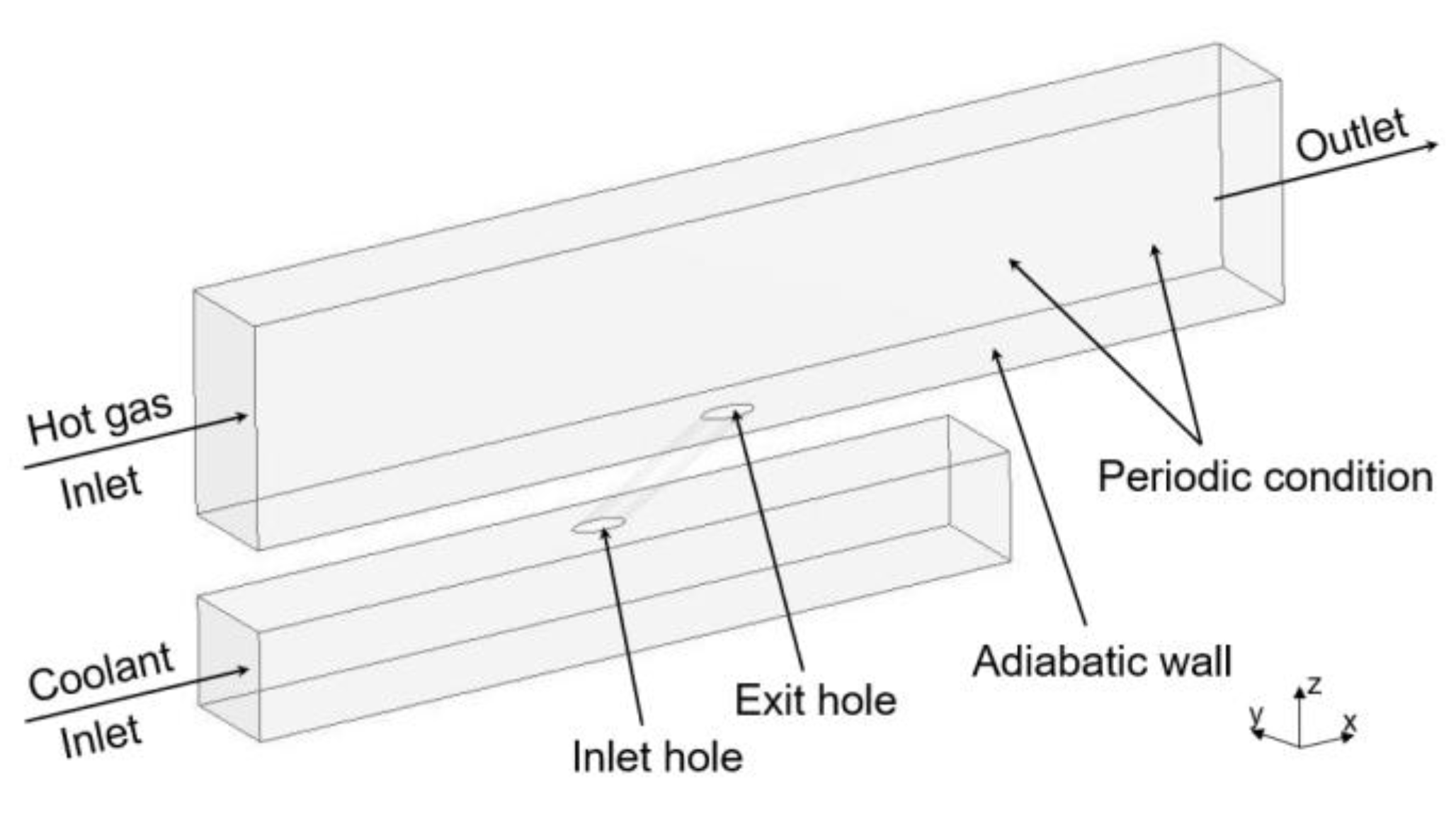
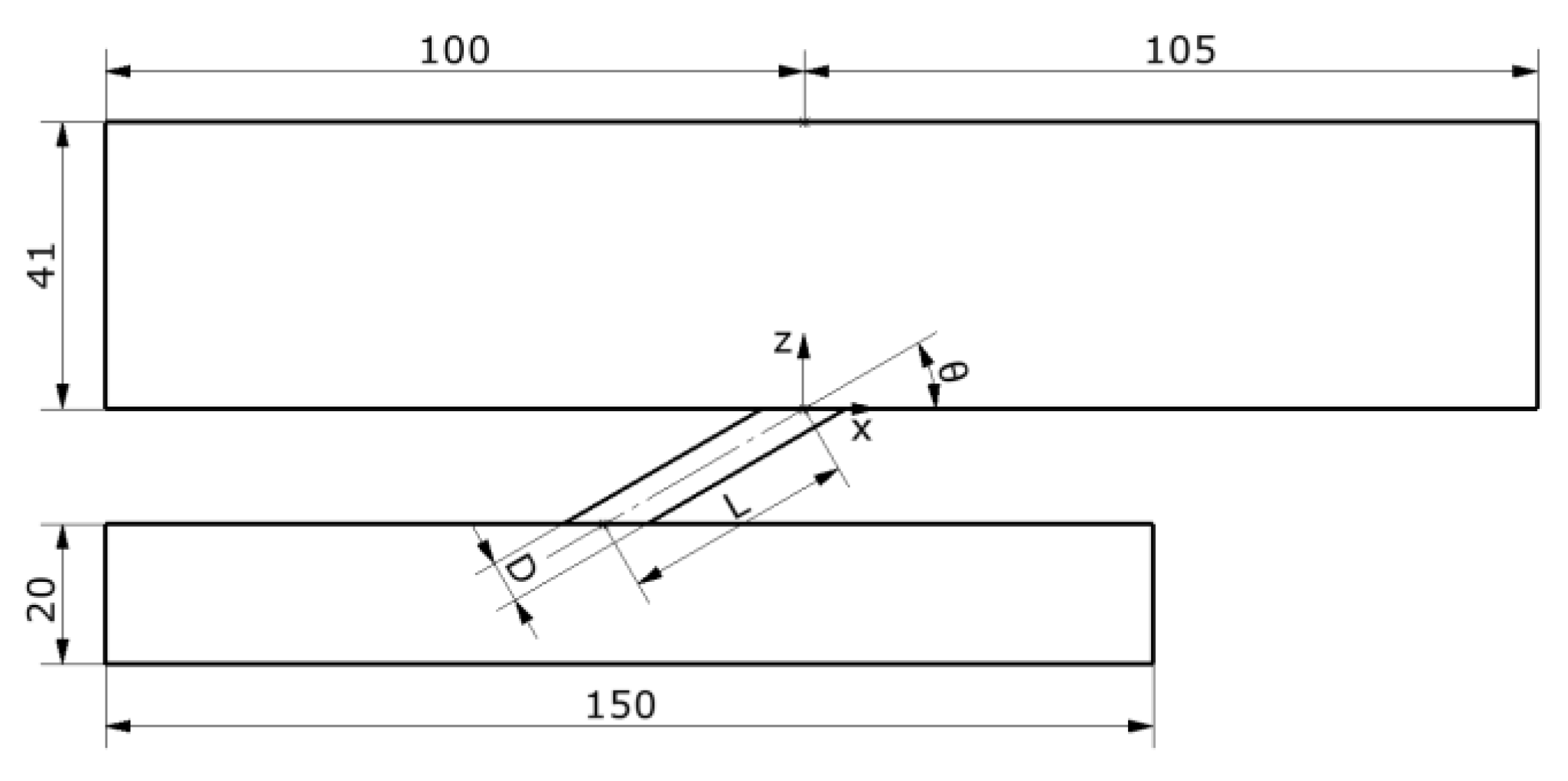
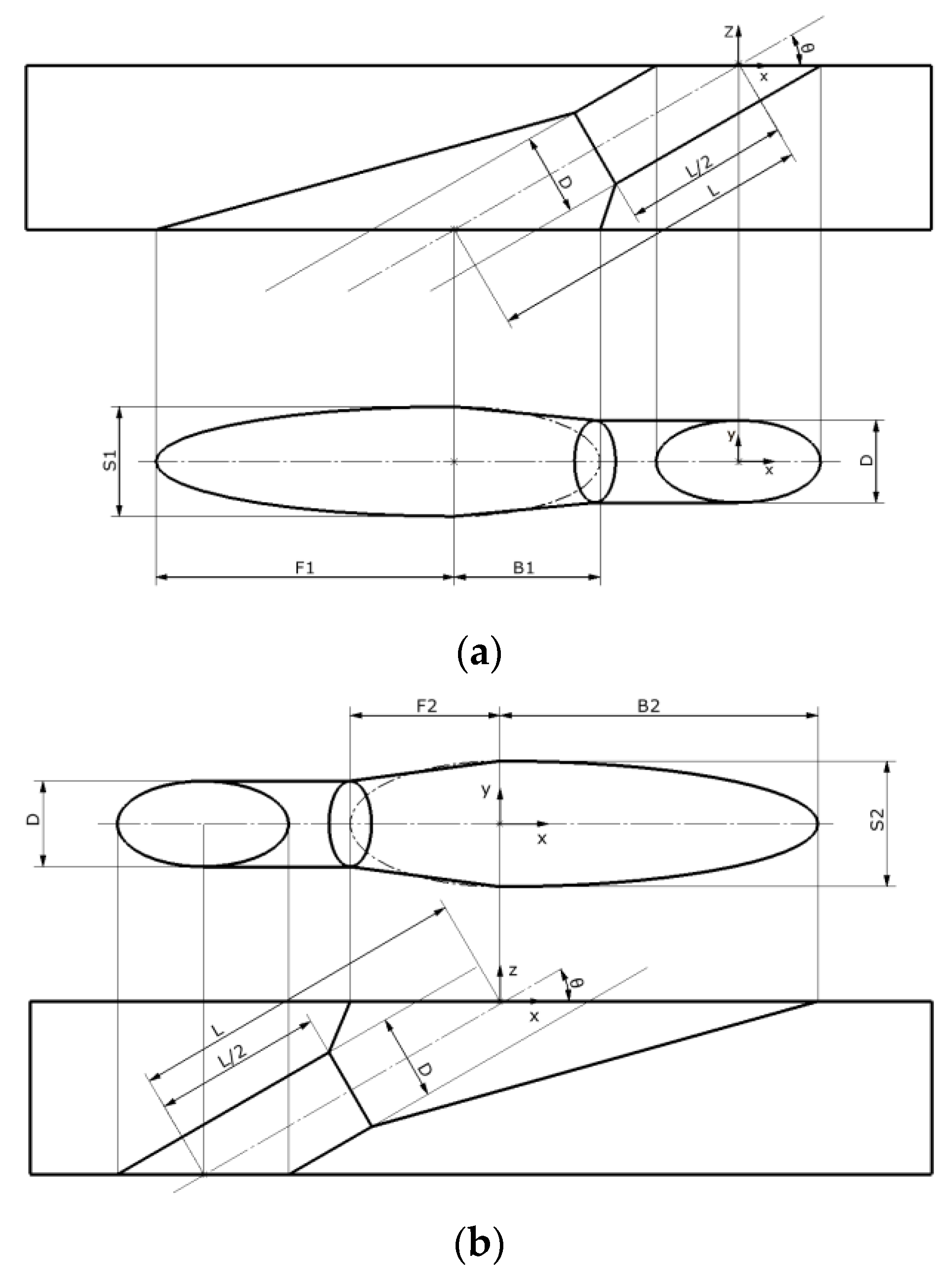
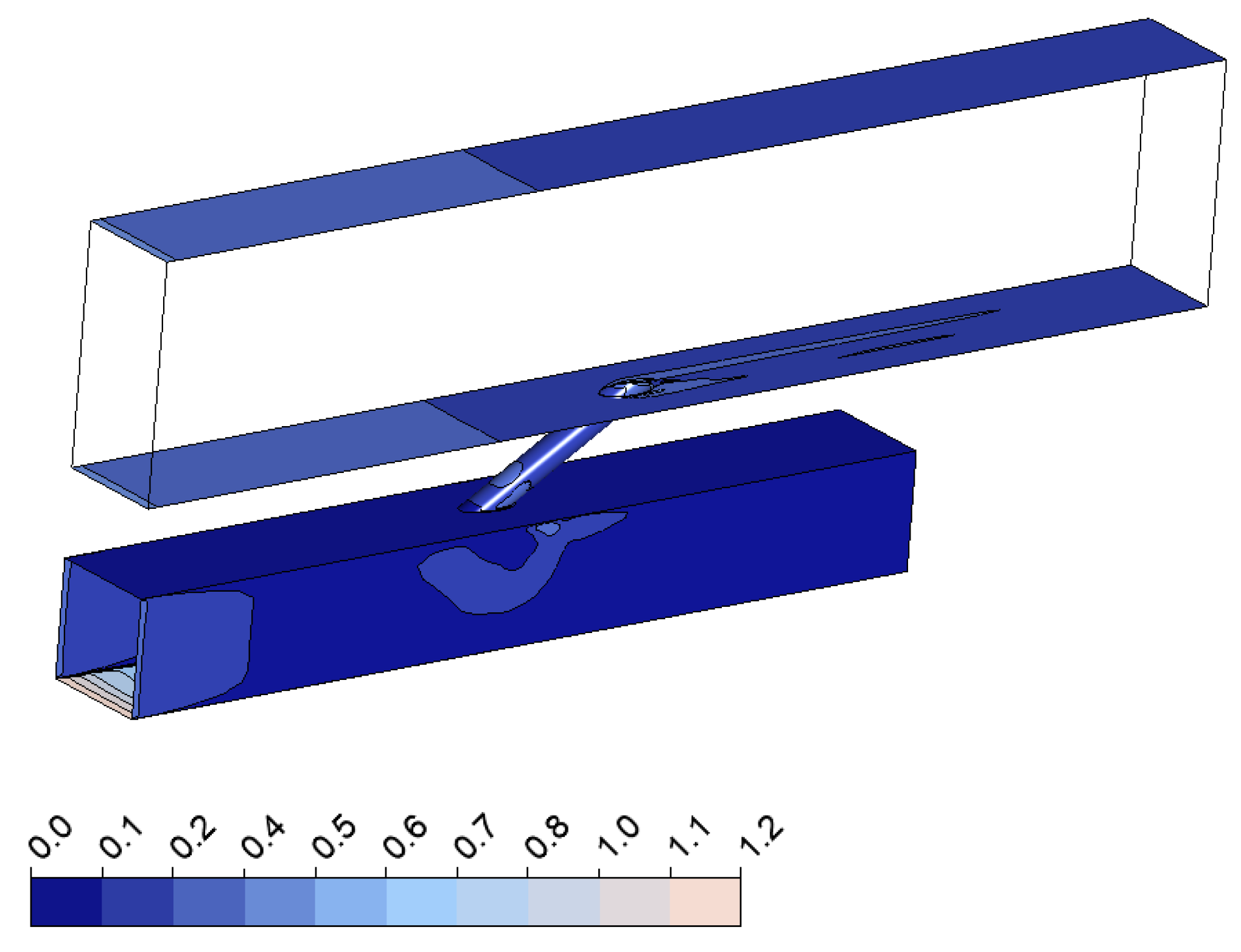
2.1. Description of Geometry
2.2. Numerical Method
3. Results
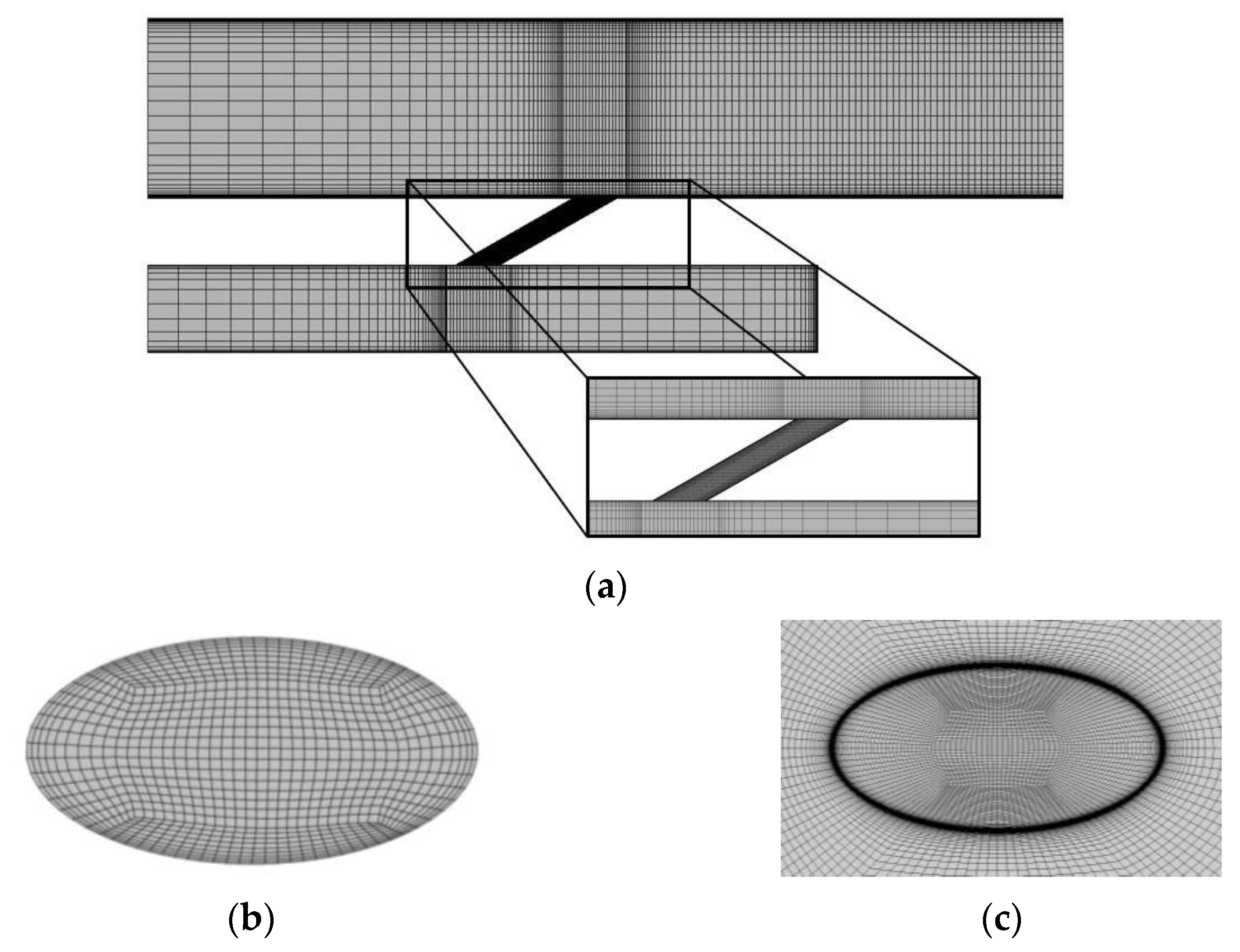
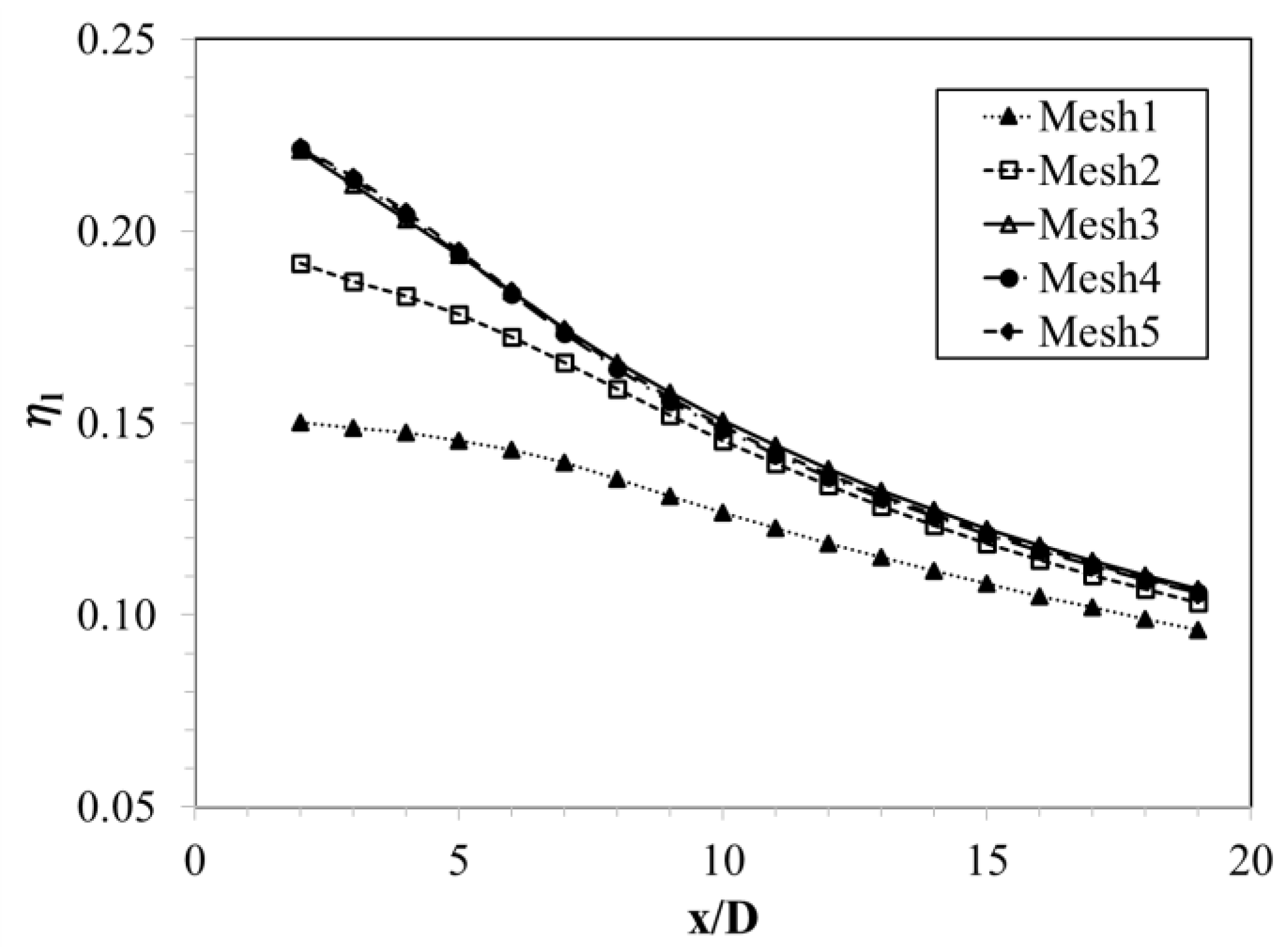
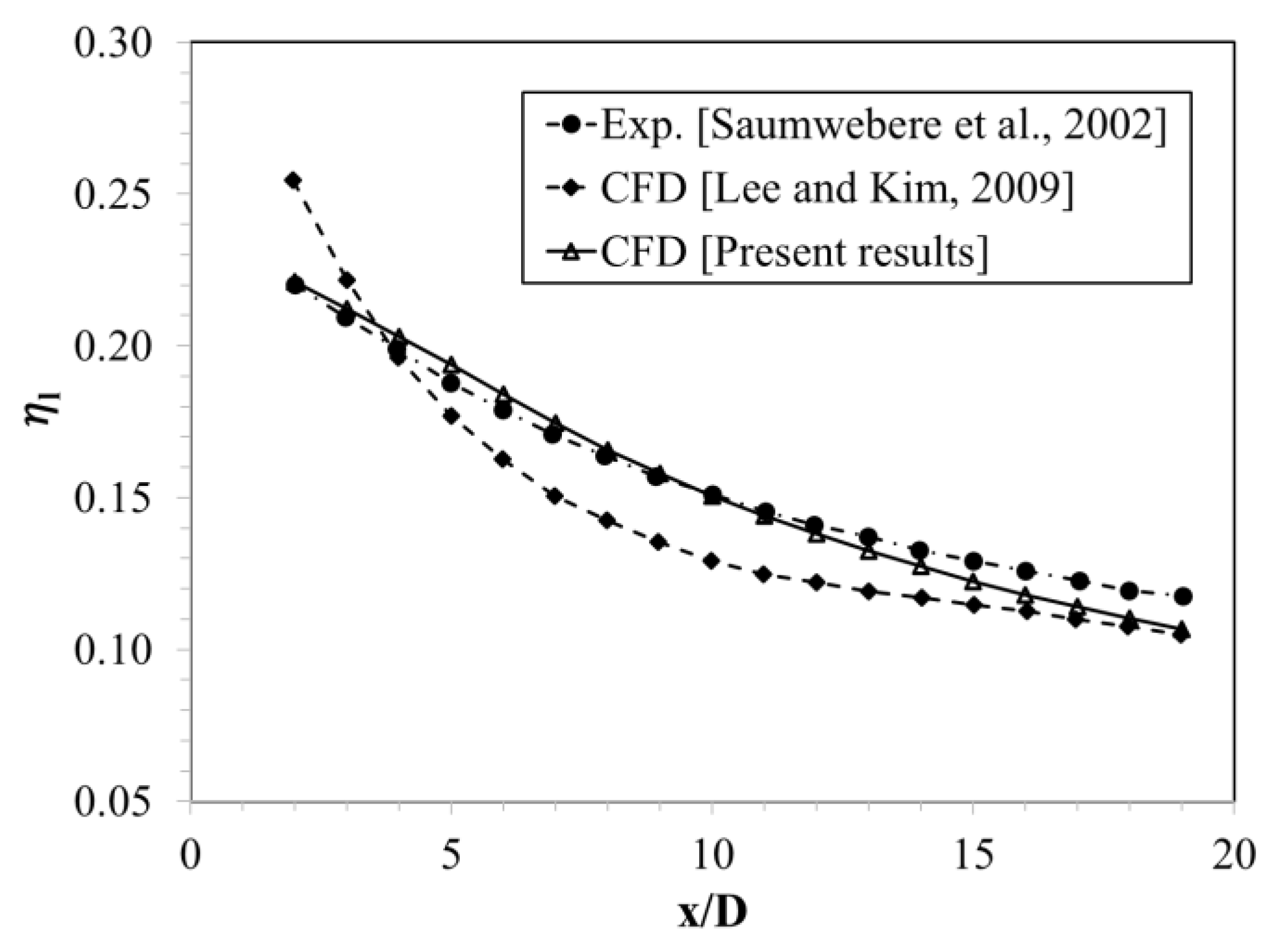
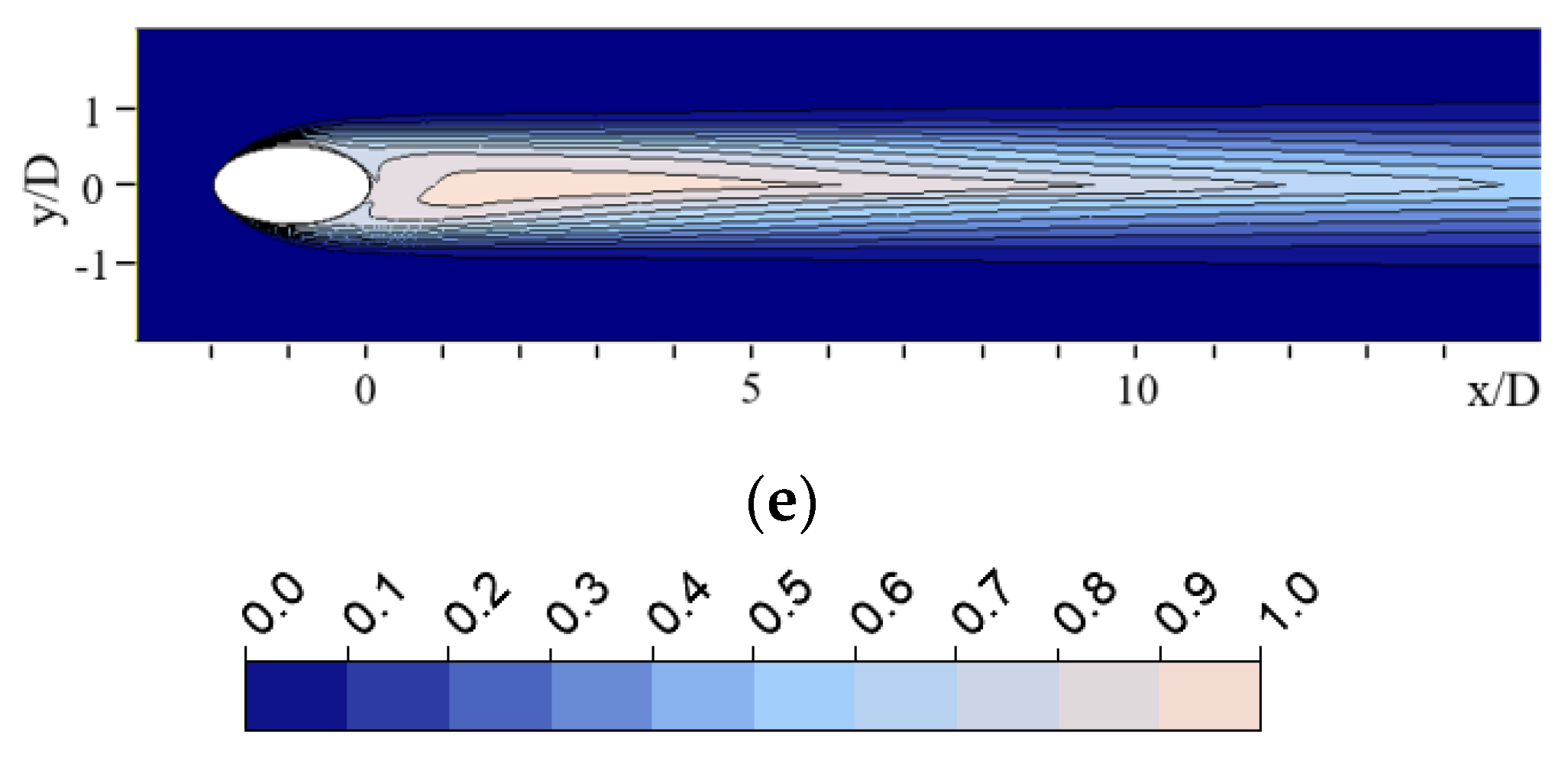
3.1. Grid Independency Test and Validation
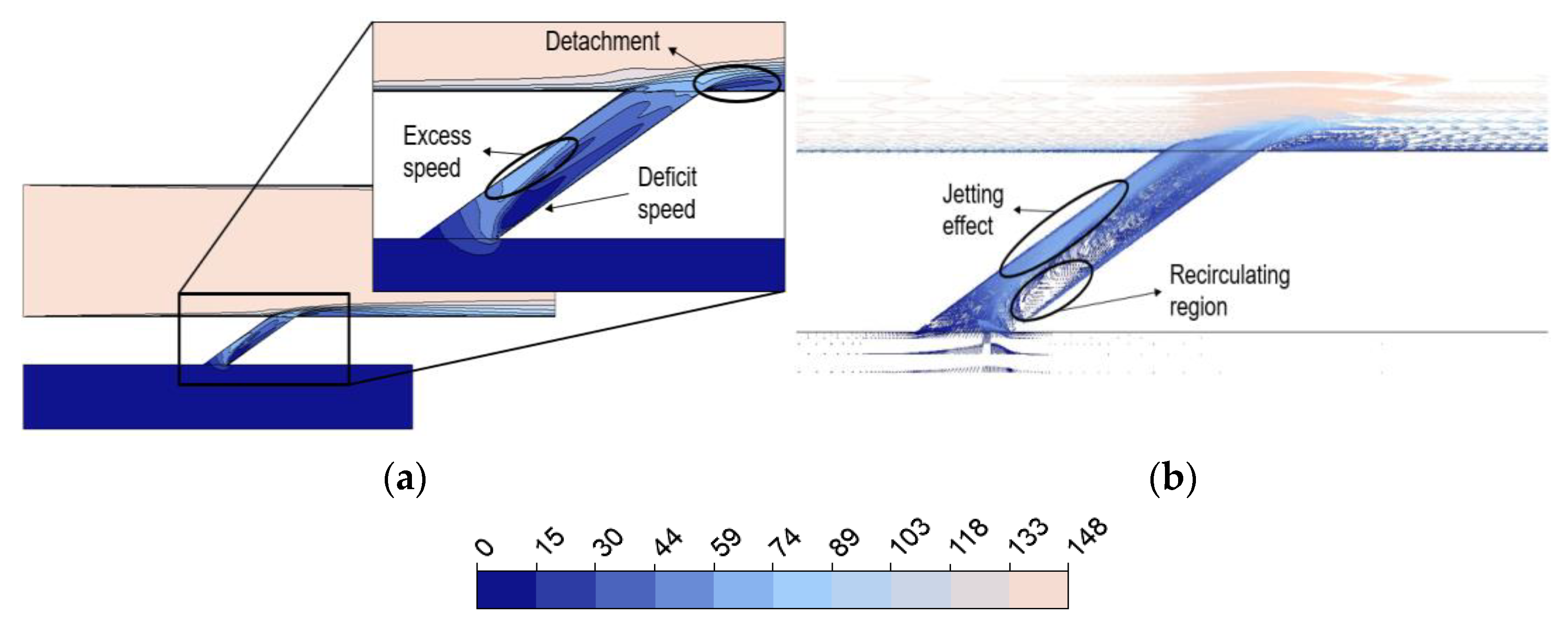
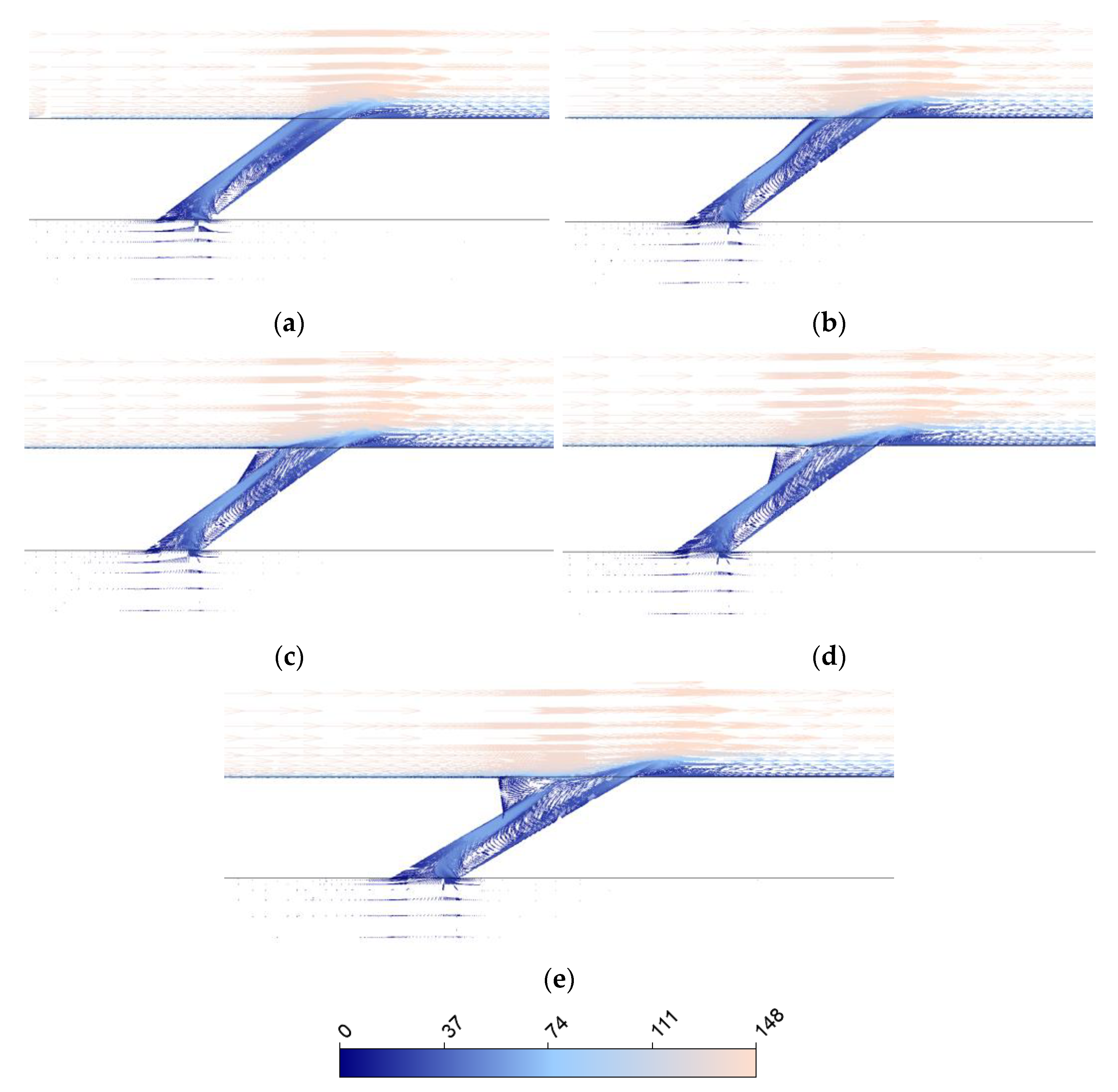
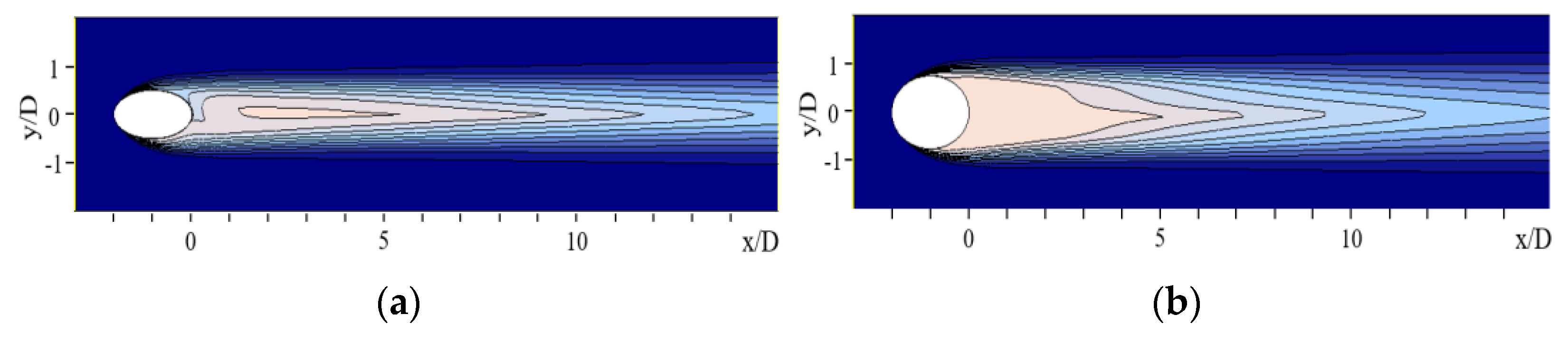
3.2. Expansion behind the Inlet Hole
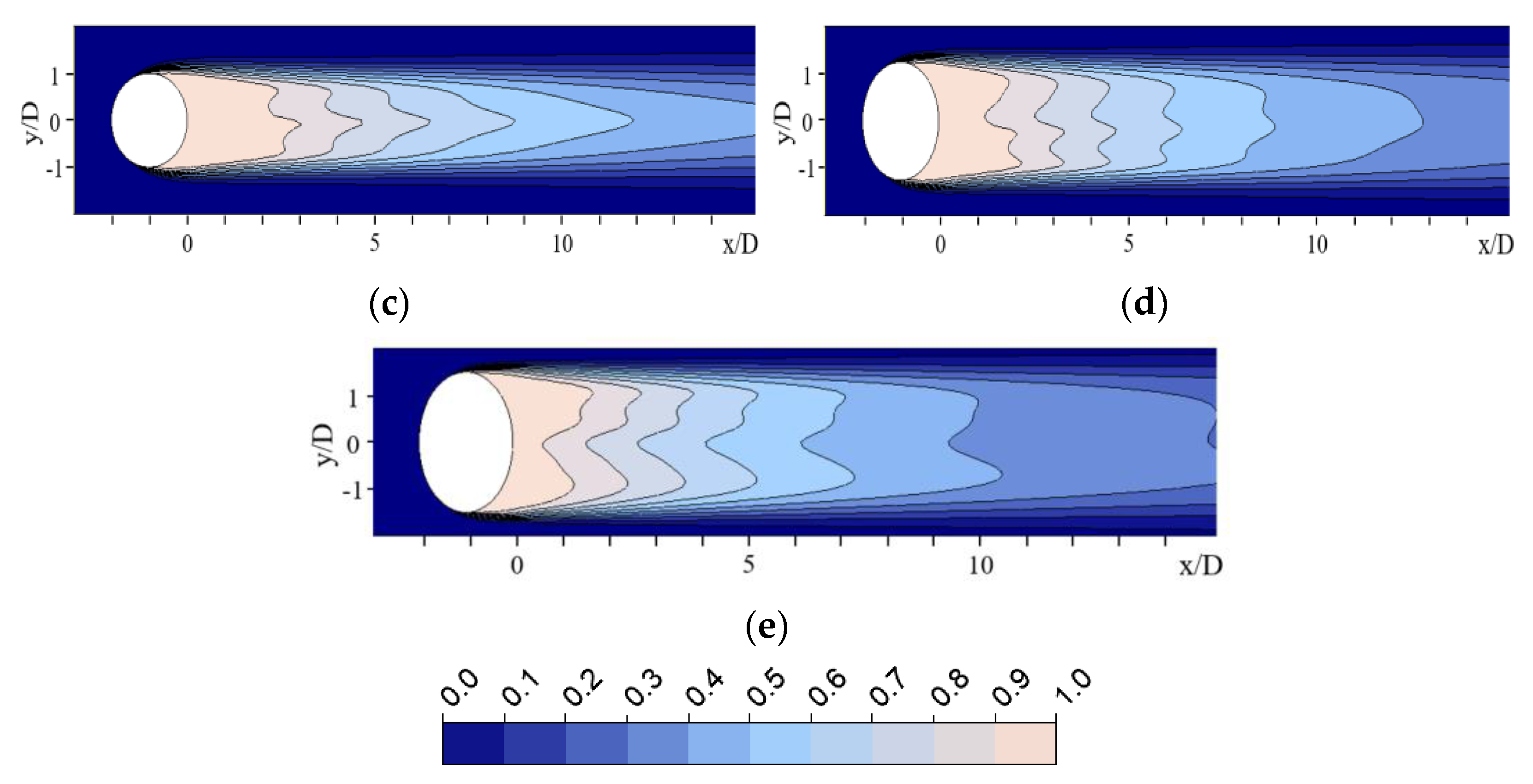
3.3. Expansion in Front of the Inlet Hole
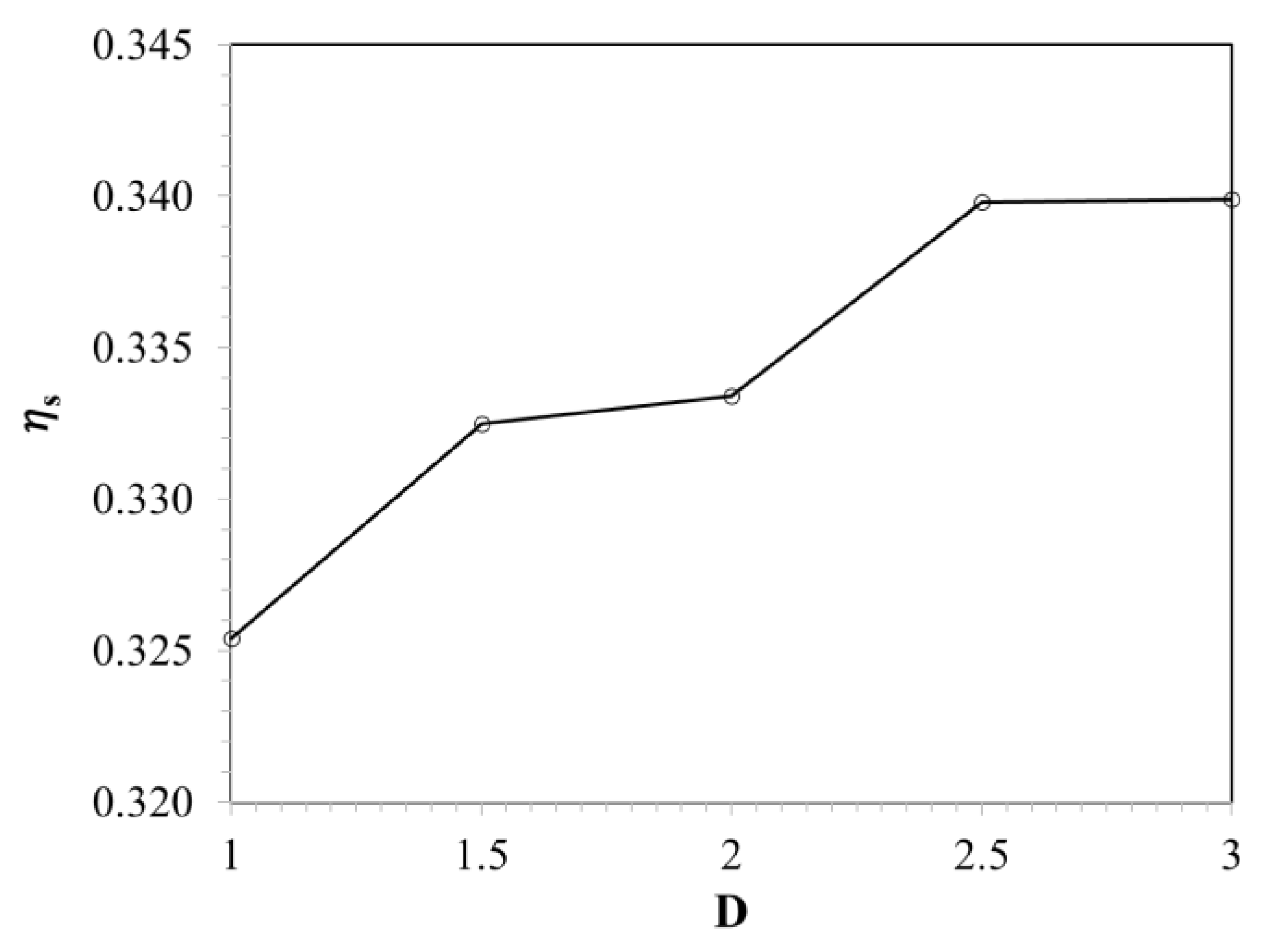
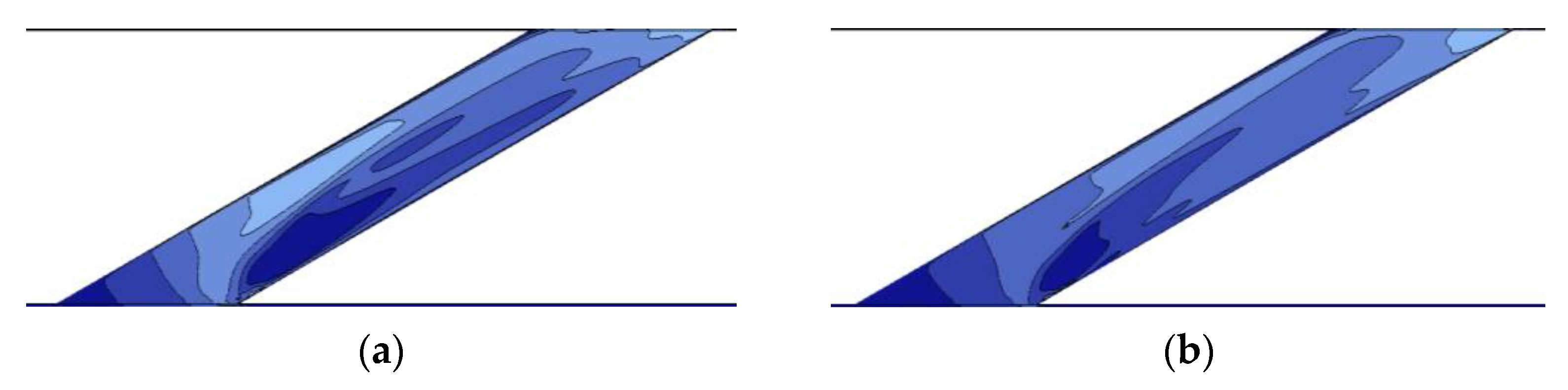
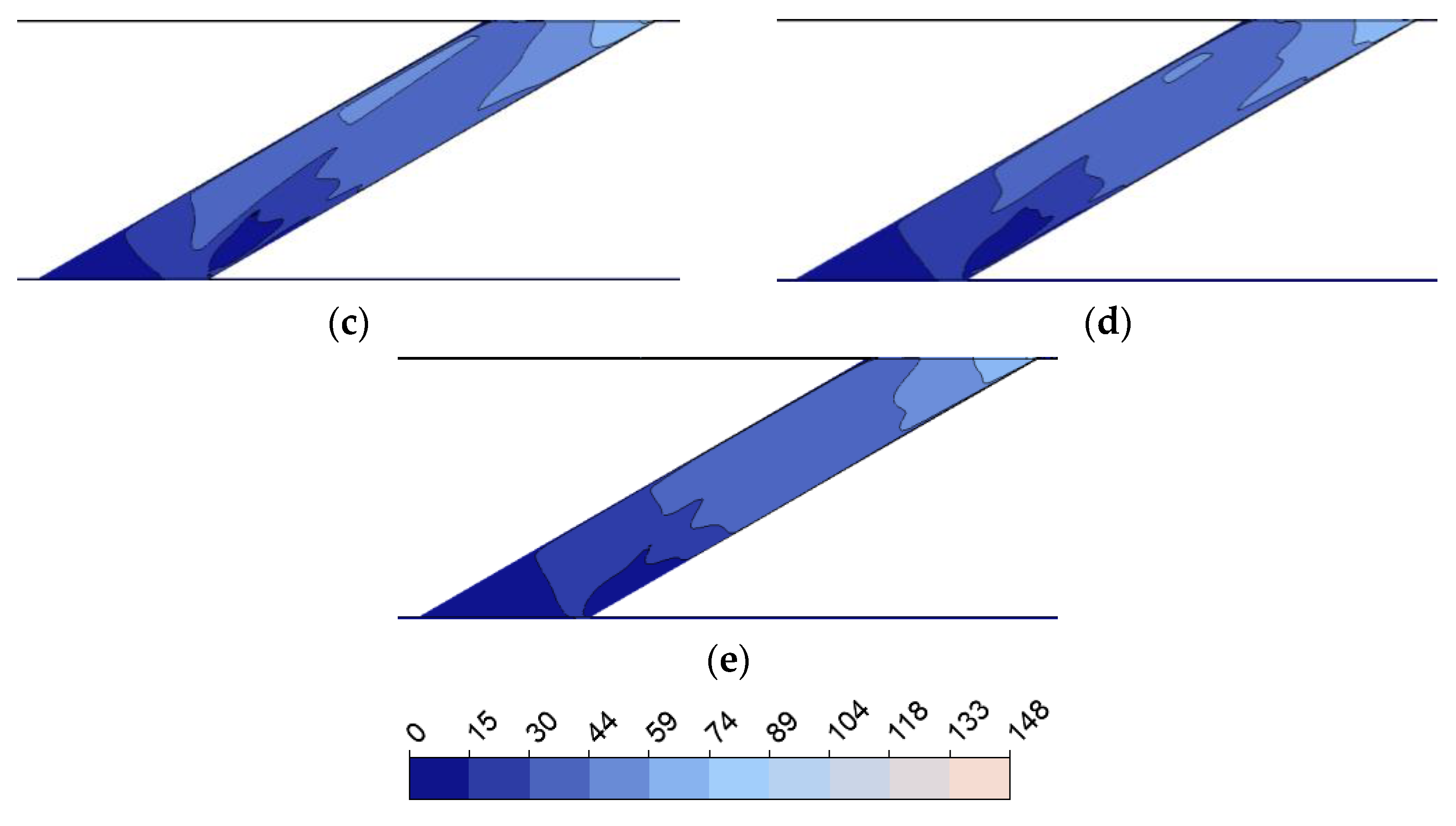
3.4. Expansion to the Sides of the Inlet Hole
3.5. Expansion behind the Exit Hole
3.6. Expansion in Front of the Exit Hole
3.7. Expansion to the Sides of the Exit Hole
4. Conclusions
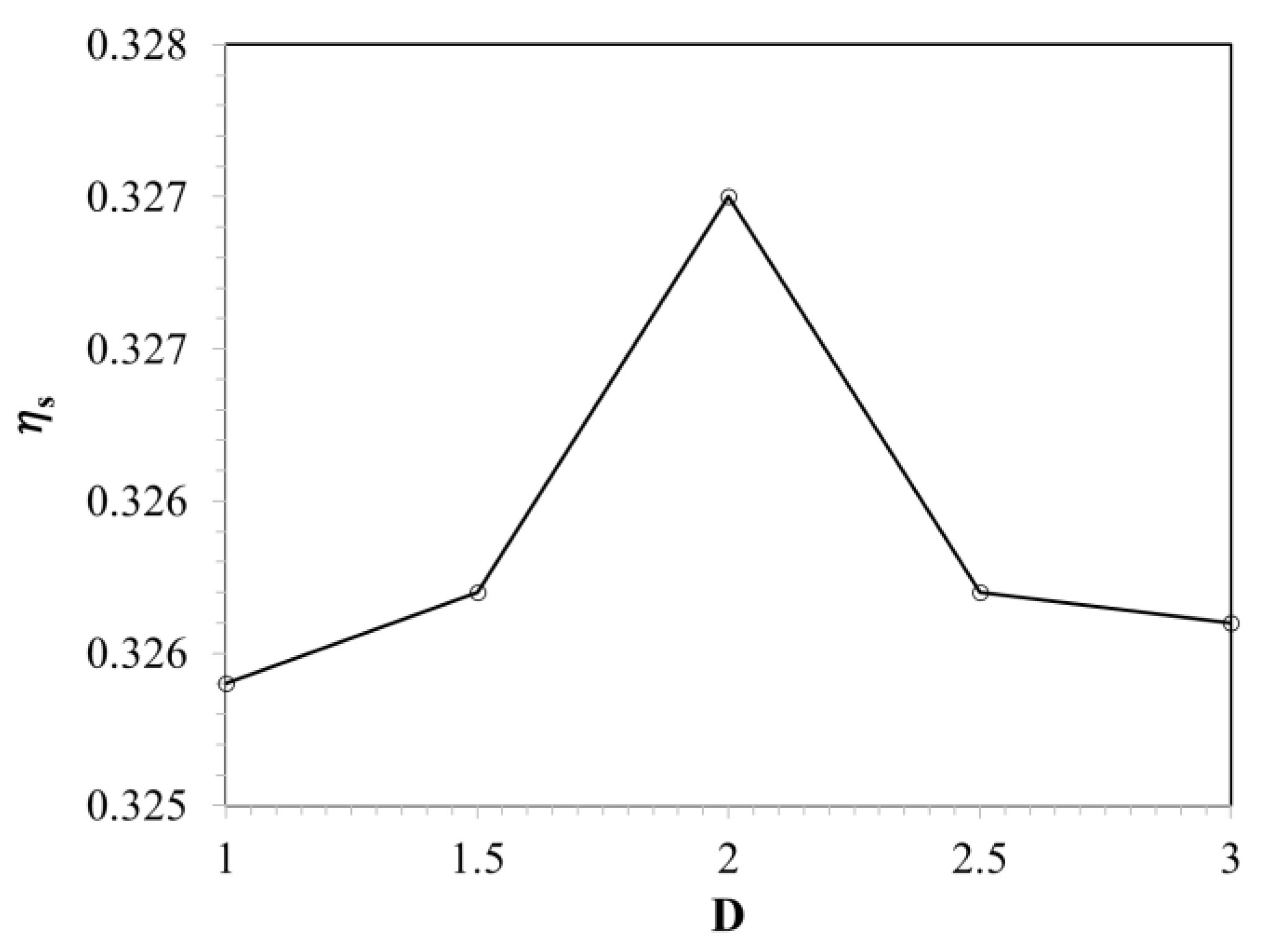
- For the expansion behind the inlet hole, the highest increased by 0.5% at the 2D expanded position. This converged design increased the film cooling’s performance by subduing the recirculating region and reducing the jetting effect in the cooling hole.
- For the expansion in front of the inlet hole, the maximum FE occurred at the 2.5D expanded position, which was 1.045% higher than that of the CH design.
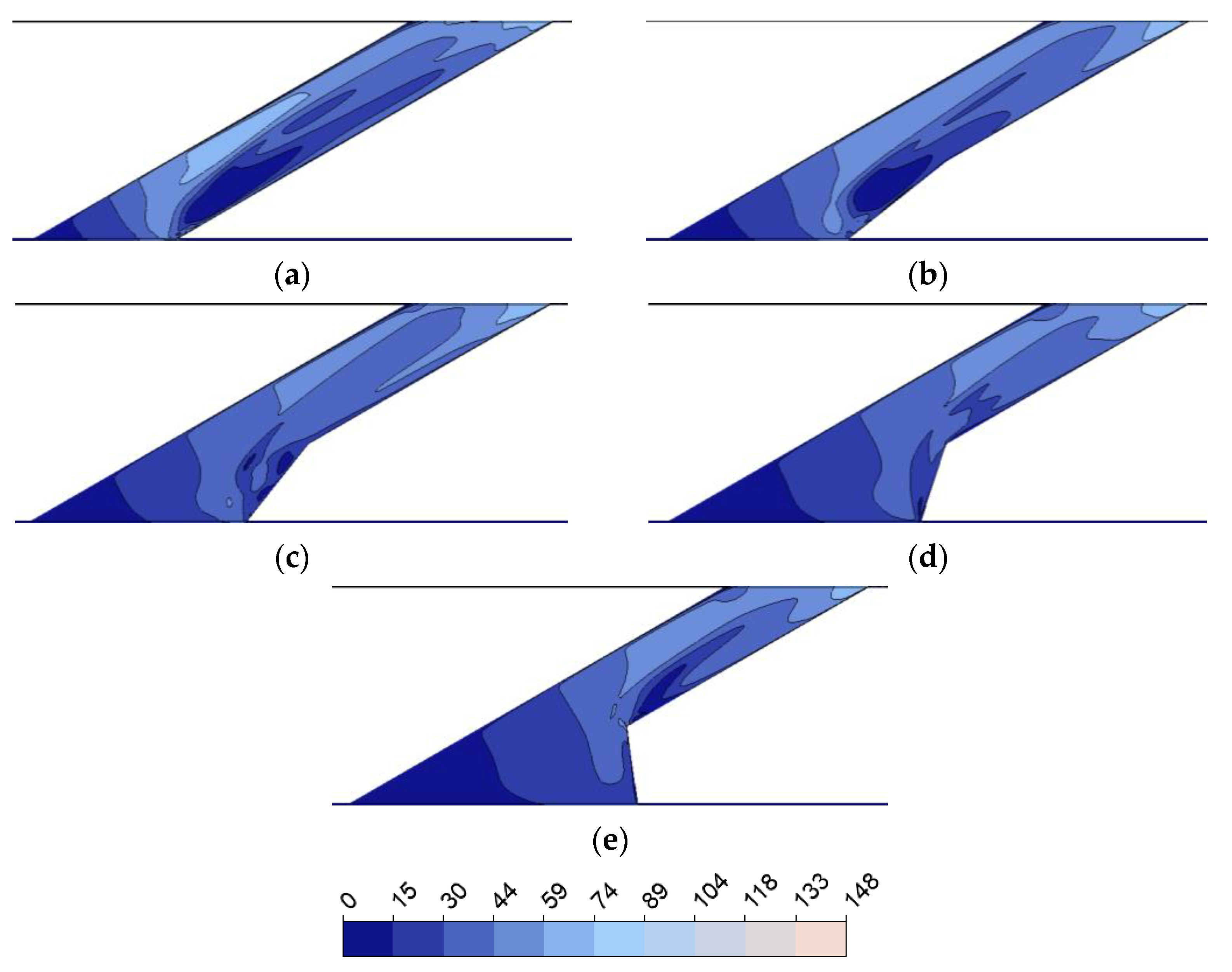
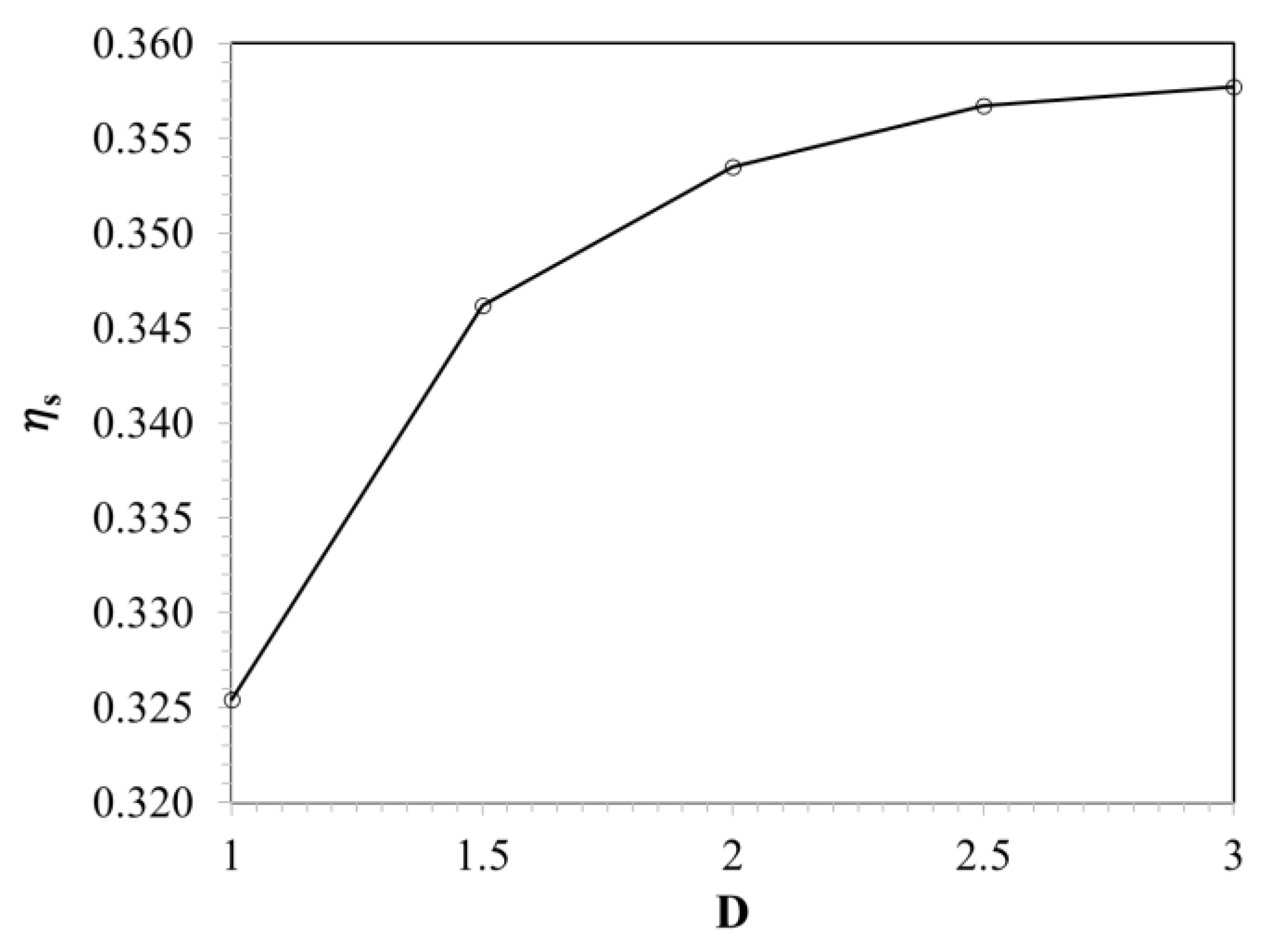
- In the case of the expansion to the sides of the inlet hole, the highest cooling performance gain was 4.456% at the 3D expanded position. In this case, the velocity field in the pipe became smoother and less turbulent.
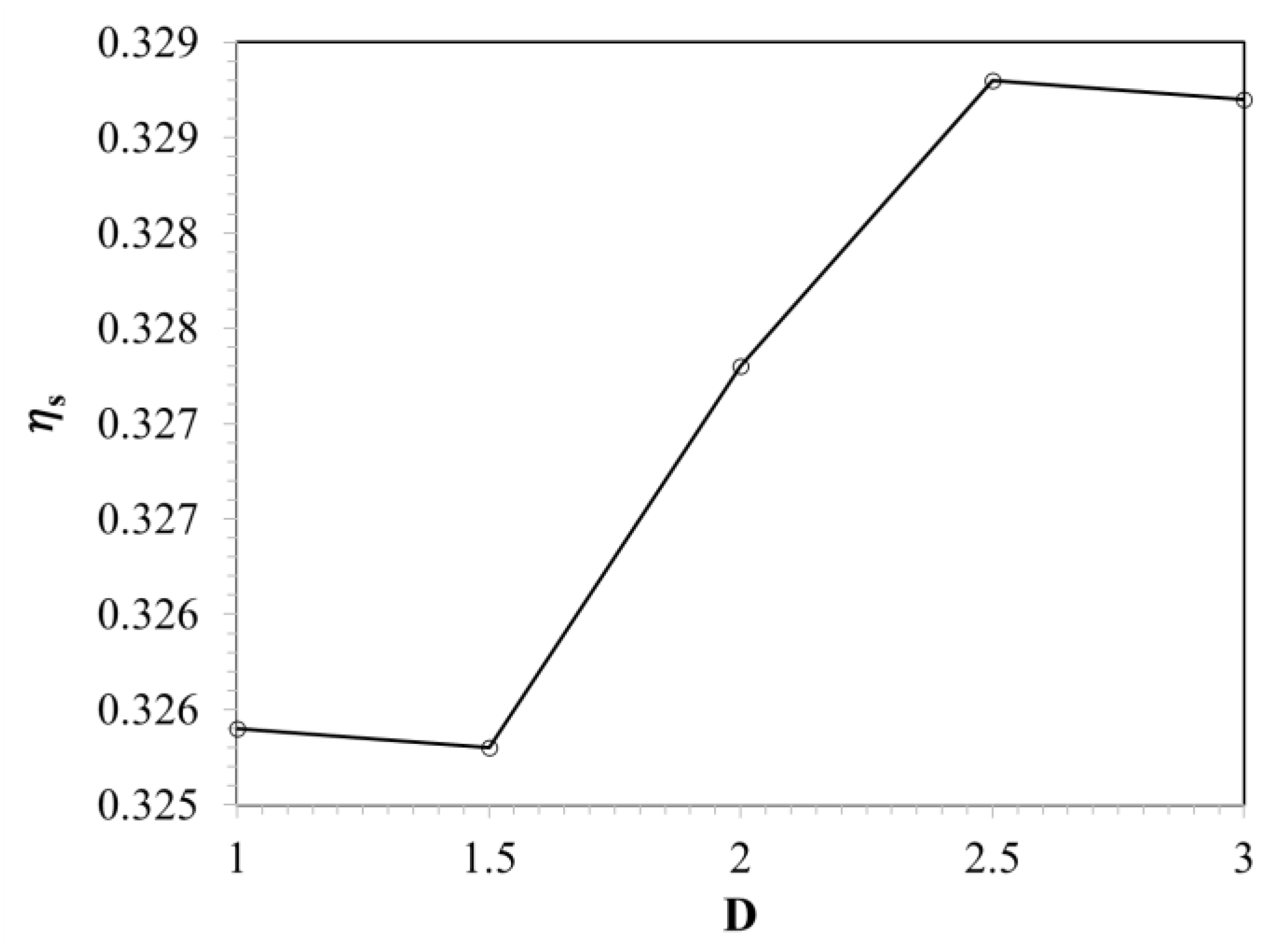
- The expansion behind the exit hole significantly increased the performance. At the 1.5D expanded position, the FE increased by 6.669%, and the highest FE enhanced by 9.926% at the 3D expanded position.
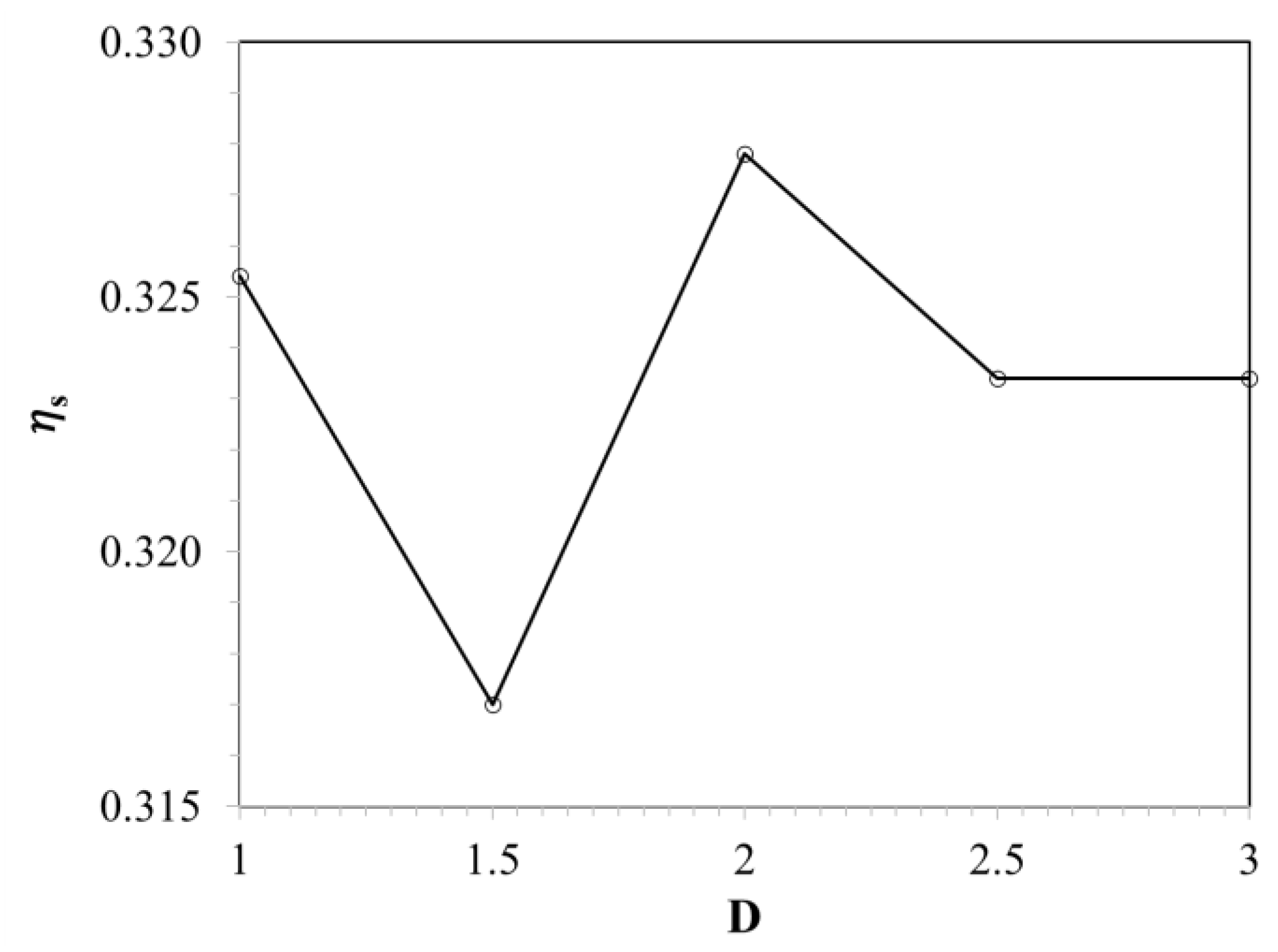
- A slight increase in performance is also obtained at the forward expansion of the exit hole. The highest FE improved by 0.738% at the 2D expanded position. However, in this way, the cooling performance is not stable.
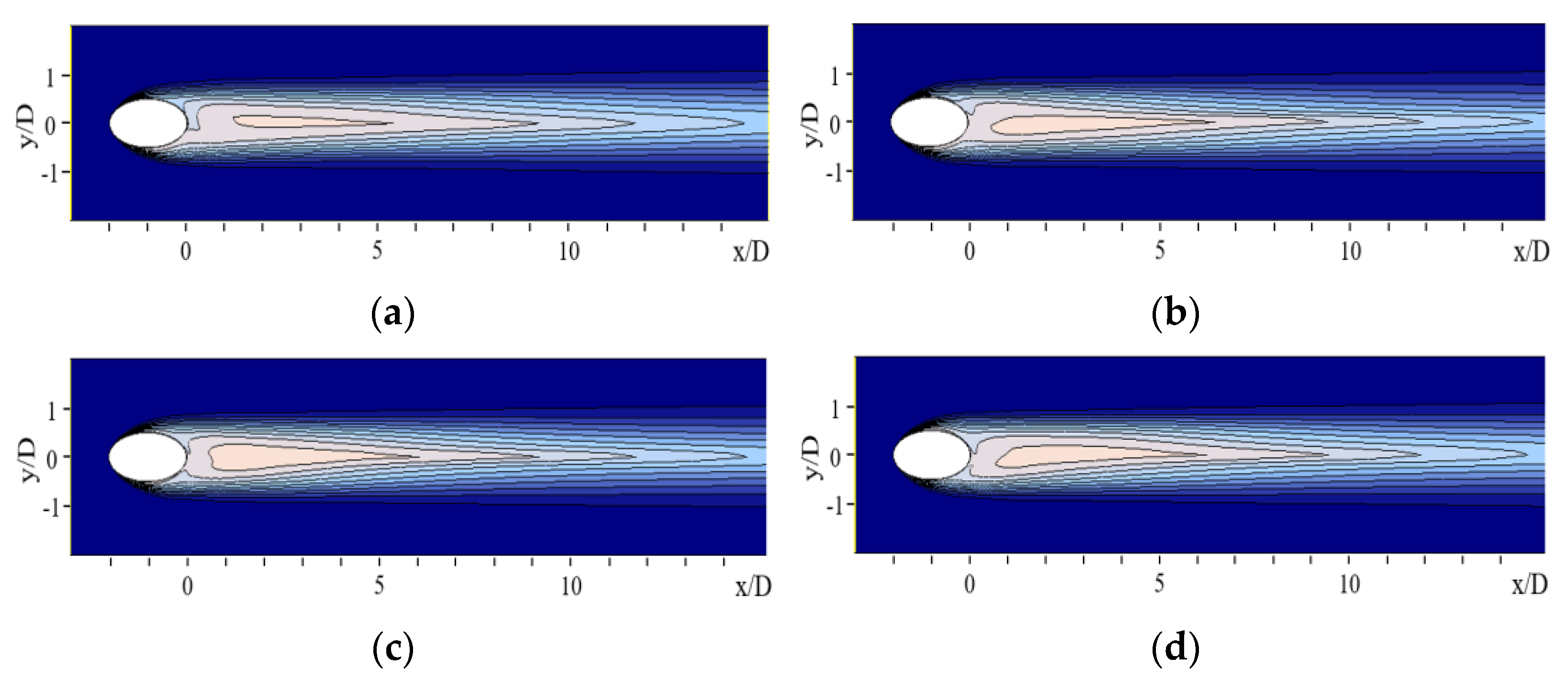
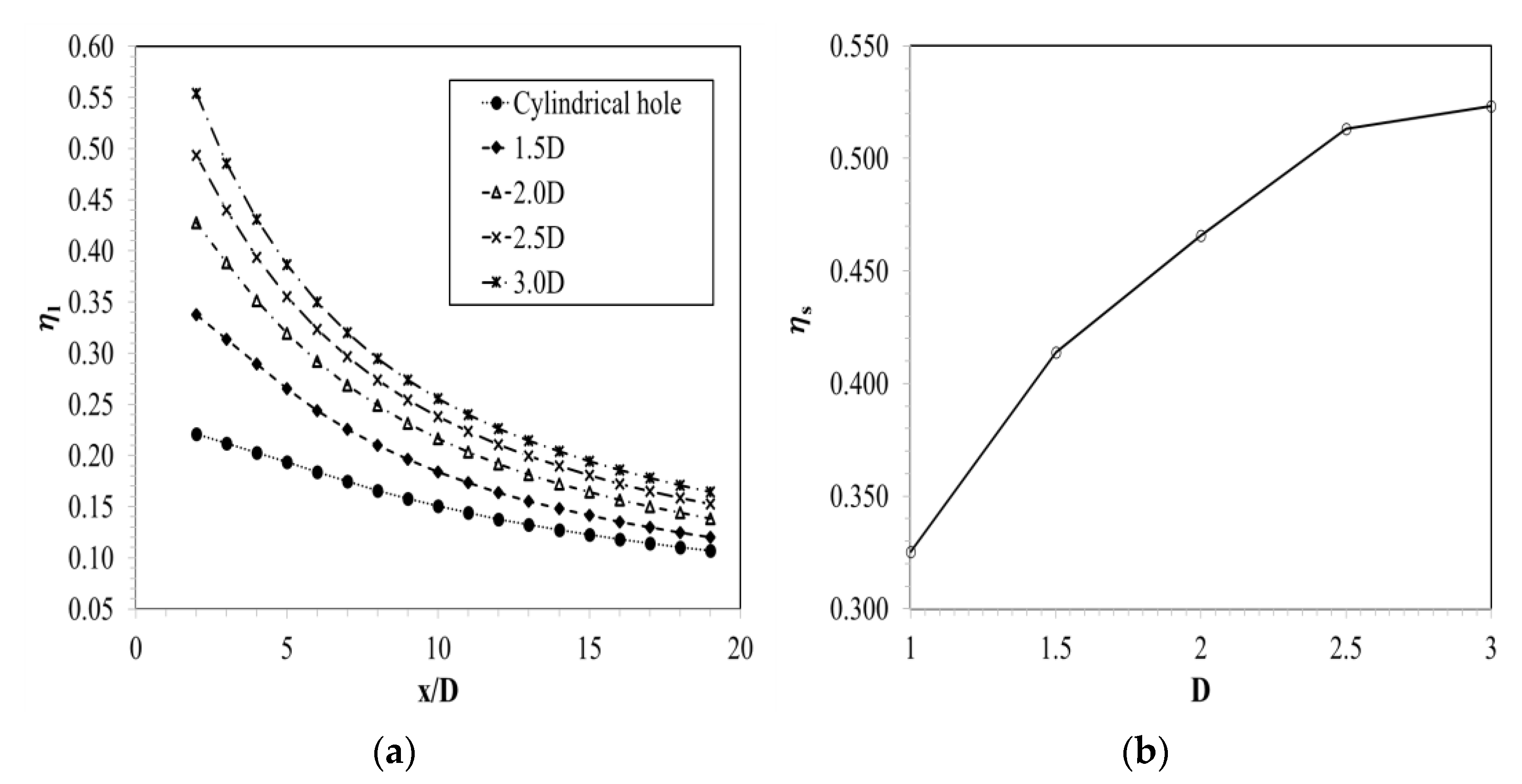
- The expansion to the sides of the exit hole provided the best film cooling performance in all six cases of the expanded holes investigated. The FE increased in the range of 27.197% to 60.787%, with expanded positions increasing from 1.5D to 3D, respectively. This is also the optimal film cooling method that many researchers are investigating.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| B | expand to the front of hole center | (mm) |
| D | diameter of the film-cooling hole | (mm) |
| DR | density ratio, (/) | (-) |
| F | expand to behind hole center | (mm) |
| M | blowing ratio, ()/() | (-) |
| S | expand to the sides of hole center | (mm) |
| adiabatic wall temperature | () | |
| hot gas temperature in the main channel | () | |
| coolant jet temperature | () | |
| velocity of coolant at the hole exit | (m/s) | |
| velocity at the main-stream inlet | (m/s) | |
| dimensionless distance | (-) | |
| Greek | ||
| density of steam | (kg/m3) | |
| spatially averaged film cooling effectiveness | (-) | |
| laterally averaged film cooling effectiveness | (-) | |
| θ | injection angle | (°) |
| Subcripts | ||
| aw | adiabatic wall | |
| c | coolant | |
| h | hot gas | |
| l | laterally averaged | |
| 1 | at the surface of inlet hole | |
| 2 | at the surface of outlet hole | |
| ∞ | main-stream | |
| Acronyms | ||
| CH | cylindrical hole | |
| FE | film cooling effectiveness | |
| RANS | Reynolds-averaged Navier–Stokes | |
| SST | shear stress transport | |
References
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, Chapter 4, 6th ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Lutum, E.; Johnson, B.V. Influence of the Hole Length-to-Diameter Ratio on Film Cooling With Cylindrical Holes. J. Turbomach. 1999, 121, 209–216. [Google Scholar] [CrossRef]
- Burd, S.W.; Kaszeta, R.W.; Simon, T.W. Measurements in Film Cooling Flows: Hole L/D and Turbulence Intensity Effects. J. Turbomach. 1998, 120, 791–798. [Google Scholar] [CrossRef]
- Lee, K.-D.; Kim, K.-Y. Optimization of a Cylindrical Film Cooling Hole using Surrogate Modeling. Numer. Heat Transf. Part A Appl. 2009, 55, 362–380. [Google Scholar] [CrossRef]
- Yuen, C.; Martinez-Botas, R. Film cooling characteristics of a single round hole at various streamwise angles in a crossflow: Part II: Heat transfer coefficients. Int. J. Heat Mass Transf. 2003, 46, 237–249. [Google Scholar] [CrossRef]
- Park, S.; Chung, H.; Choi, S.M.; Kim, S.H.; Cho, H.H. Design of sister hole arrangements to reduce kidney vortex for film cooling enhancement. J. Mech. Sci. Technol. 2017, 31, 3981–3992. [Google Scholar] [CrossRef]
- Li, G.-C.; Zhang, W. Improving film cooling performance by using one -inlet and double-outlet hole. J. Therm. Sci. 2010, 19, 430–437. [Google Scholar] [CrossRef]
- Li, M.; He, Y.; Li, R.; Yang, T. Effects of Injection Angles and Aperture Ratios on Film Cooling Performance of Sister Holes. J. Therm. Sci. 2020, 30, 716–728. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, J. Investigation on film cooling characteristics from a row of converging slot-holes on flat plate. Sci. China Ser. E Technol. Sci. 2011, 54, 1793–1800. [Google Scholar] [CrossRef]
- Hyams, D.G.; Leylek, J.H. A Detailed Analysis of Film Cooling Physics Part III: Streamwise Injection With Shaped Holes. J. Turbomach. 2000, 122, 122–132. [Google Scholar] [CrossRef]
- Saumweber, C.; Schulz, A.; Wittig, S. Free-Stream Turbulence Effects on Film Cooling With Shaped Holes. J. Turbomach. 2003, 125, 65–73. [Google Scholar] [CrossRef]
- Silieti, M.; Kassab, A.J.; Divo, E. Film Cooling Effectiveness From a Single Scaled-Up Fan-Shaped Hole: A CFD Simulation of Adiabatic and Conjugate Heat Transfer Models. ASME Turbo Expo 2005, 47268, 431–441. [Google Scholar] [CrossRef]
- Gritsch, M.; Colban, W.; Schär, H.; Döbbeling, K. Effect of Hole Geometry on the Thermal Performance of Fan-Shaped Film Cooling Holes. J. Turbomach. 2005, 127, 718–725. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eckert, E.R.G.; Burggraf, F. Effects of hole geometry and density on three-dimensional film cooling. Int. J. Heat Mass Transf. 1974, 17, 595–607. [Google Scholar] [CrossRef]
- Liu, C.-L.; Zhu, H.-R.; Bai, J.-T.; Xu, D.-C. Film Cooling Performance of Waist-Shaped Slot Holes. ASME Turbo Expo 2010, 43994, 1359–1370. [Google Scholar] [CrossRef]
- Yu, Y.; Yen, C.-H.; Shih, T.I.-P.; Chyu, M.K.; Gogineni, S. Film Cooling Effectiveness and Heat Transfer Coefficient Distributions Around Diffusion Shaped Holes. J. Heat Transf. 2002, 124, 820–827. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, S.-M. Influence of shaped injection holes on turbine blade leading edge film cooling. Int. J. Heat Mass Transf. 2004, 47, 245–256. [Google Scholar] [CrossRef]
- Fu, Z.; Zhu, H.; Liu, C.; Wei, J.; Zhang, B. Investigation of the Influence of Inclination Angle and Diffusion Angle on the Film Cooling Performance of Chevron Shaped Hole. J. Therm. Sci. 2018, 27, 580–591. [Google Scholar] [CrossRef]
- Liu, J.; An, B.; Liu, J.; Zhan, W. Leading Edge Film Cooling Enhancement for an Inlet Guide Vane with Fan-Shaped Holes. J. Therm. Sci. 2010, 19, 514–518. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, K.-Y. Film-cooling performance of converged-inlet hole shapes. Int. J. Therm. Sci. 2018, 124, 196–211. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, K.-Y. Performance evaluation of a converging-diverging film-cooling hole. Int. J. Therm. Sci. 2019, 142, 295–304. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, K.Y. Design Optimization of Rib-roughened Channel to Enhance Turbulent Heat Transfer. Int. J. Heat Mass Transf. 2004, 47, 5159–5168. [Google Scholar] [CrossRef]
- Kohli, A.; Thole, K.A. Entrance effects on diffused film cooling holes. ASME Turbo Expo 1998, 78651, V004T09A070. [Google Scholar]
- Gritsch, M.; Schulz, A.; Wittig, S. Adiabatic Wall Effectiveness Measurements of Film-Cooling Holes with Expanded Exits. J. Turbomach. 1998, 120, 549–556. [Google Scholar] [CrossRef]
- Hay, N.; Lampard, D.; Khaldi, A. The Coefficient of Discharge of 30° Inclined Film Cooling Holes with Rounded Entries or Exits. ASME Turbo Expo 1994, 78866, V004T09A030. [Google Scholar]
- Afzal, A.; Samee, A.D.M.; Razak, R.K.A.; Khan, S.A.; Khan, H. Optimum spacing between grooved tubes: An experimental study. J. Mech. Sci. Technol. 2019, 34, 469–475. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, H.-R.; Yu, Q.-P.; Li, G.-C. Numerical study on unsteady film cooling performance under the mainstream swing condition. J. Mech. Sci. Technol. 2019, 33, 5527–5536. [Google Scholar] [CrossRef]
- Du, K.; Li, Z.; Li, J. Effects of Trenched Film Hole Configurations on the Endwall Film Cooling and Suction Side Phantom Cooling. J. Therm. Sci. 2019, 28, 905–914. [Google Scholar] [CrossRef]
- ANSYS CFX-19.1; ANSYS Inc.: Hanoi, Vietnam, 2018.

| Geometric Parameter | Ref. Value | Lower Bound | Upper Bound | Step |
|---|---|---|---|---|
| S | 1D | 1.5D | 3D | 0.5D |
| B | 1D | 1.5D | 3D | 0.5D |
| F | 1D | 1.5D | 3D | 0.5D |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, X.-T.; Nguyen, D.-A.; Dinh, C.-T.; Nguyen, Q.-H. Effect of Two-Head Flared Hole on Film Cooling Performance over a Flat Plate. Aerospace 2021, 8, 128. https://doi.org/10.3390/aerospace8050128
Le X-T, Nguyen D-A, Dinh C-T, Nguyen Q-H. Effect of Two-Head Flared Hole on Film Cooling Performance over a Flat Plate. Aerospace. 2021; 8(5):128. https://doi.org/10.3390/aerospace8050128
Chicago/Turabian StyleLe, Xuan-Truong, Duc-Anh Nguyen, Cong-Truong Dinh, and Quang-Hai Nguyen. 2021. "Effect of Two-Head Flared Hole on Film Cooling Performance over a Flat Plate" Aerospace 8, no. 5: 128. https://doi.org/10.3390/aerospace8050128
APA StyleLe, X.-T., Nguyen, D.-A., Dinh, C.-T., & Nguyen, Q.-H. (2021). Effect of Two-Head Flared Hole on Film Cooling Performance over a Flat Plate. Aerospace, 8(5), 128. https://doi.org/10.3390/aerospace8050128






