Investigation of the Film-Cooling Performance of 2.5D Braided Ceramic Matrix Composite Plates with Preformed Hole
Abstract
1. Introduction
2. Numerical Methodology
2.1. Numerical Models
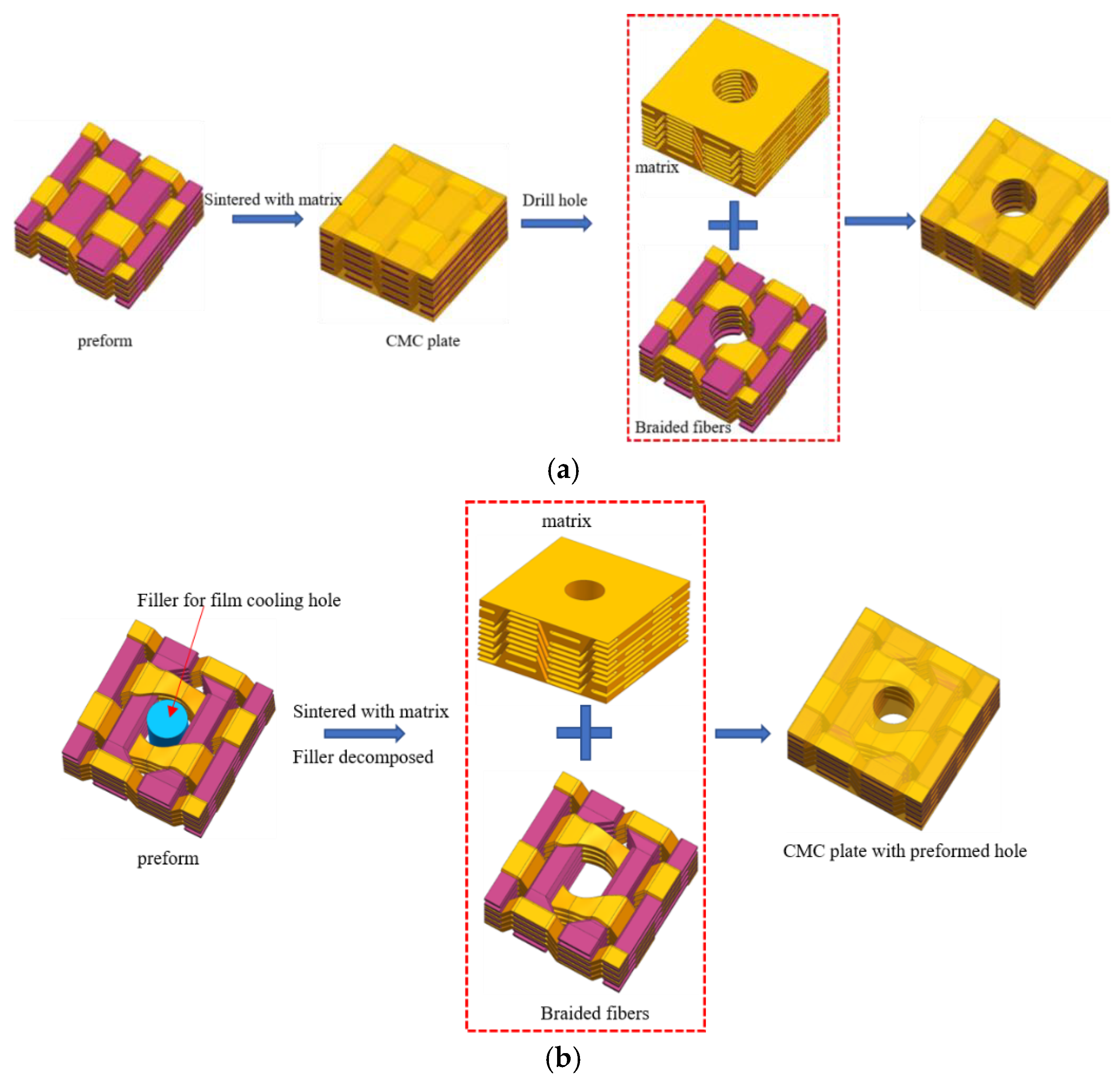
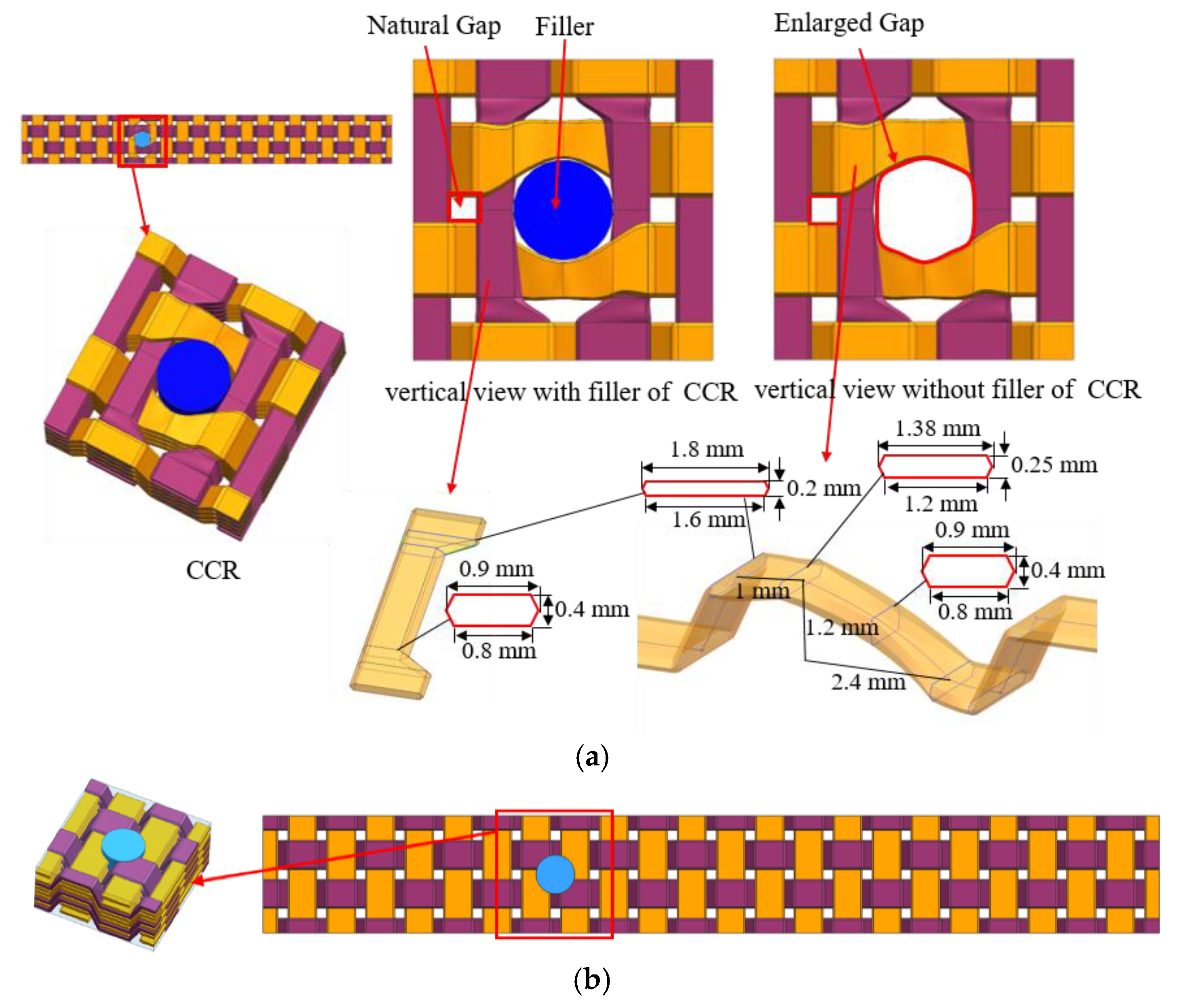
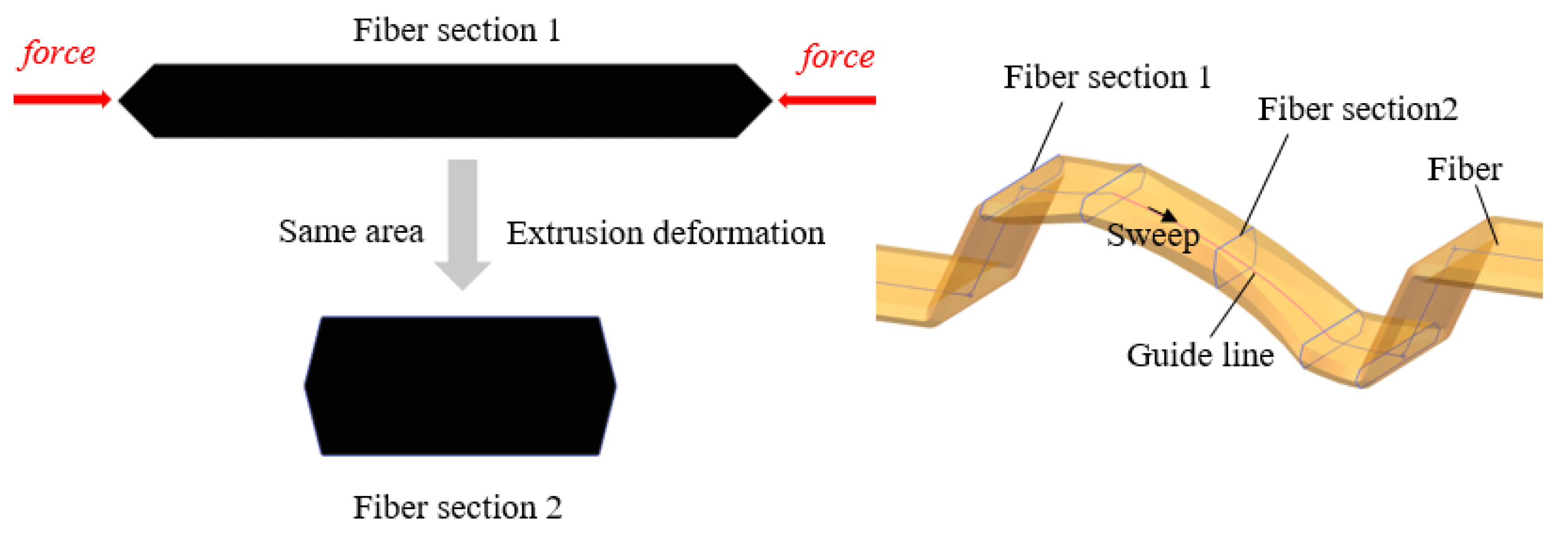
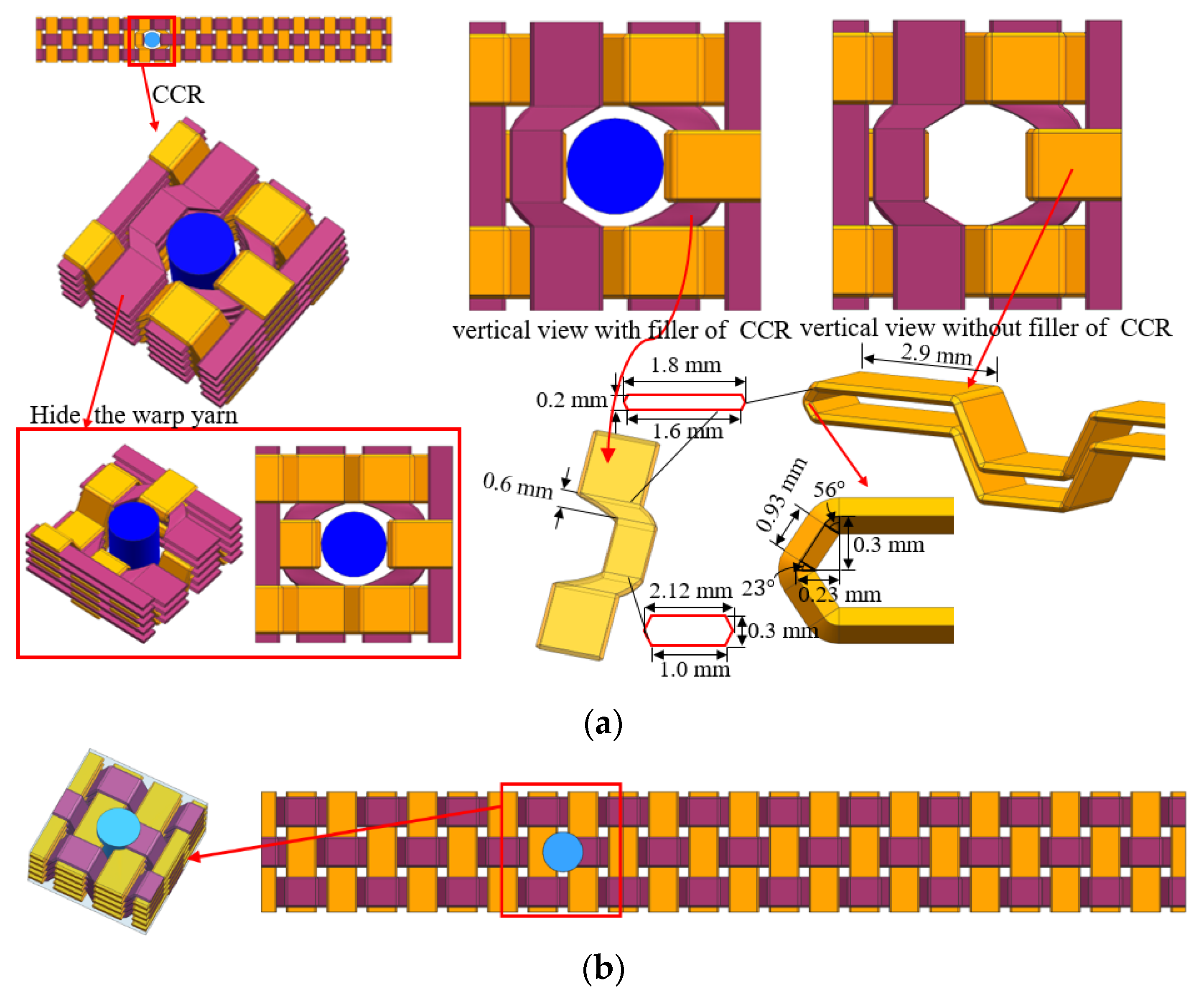
2.1.1. Numerical Models with EP-Hole and DR-Hole 1
2.1.2. Numerical Models with BP-Hole and DR-Hole 2
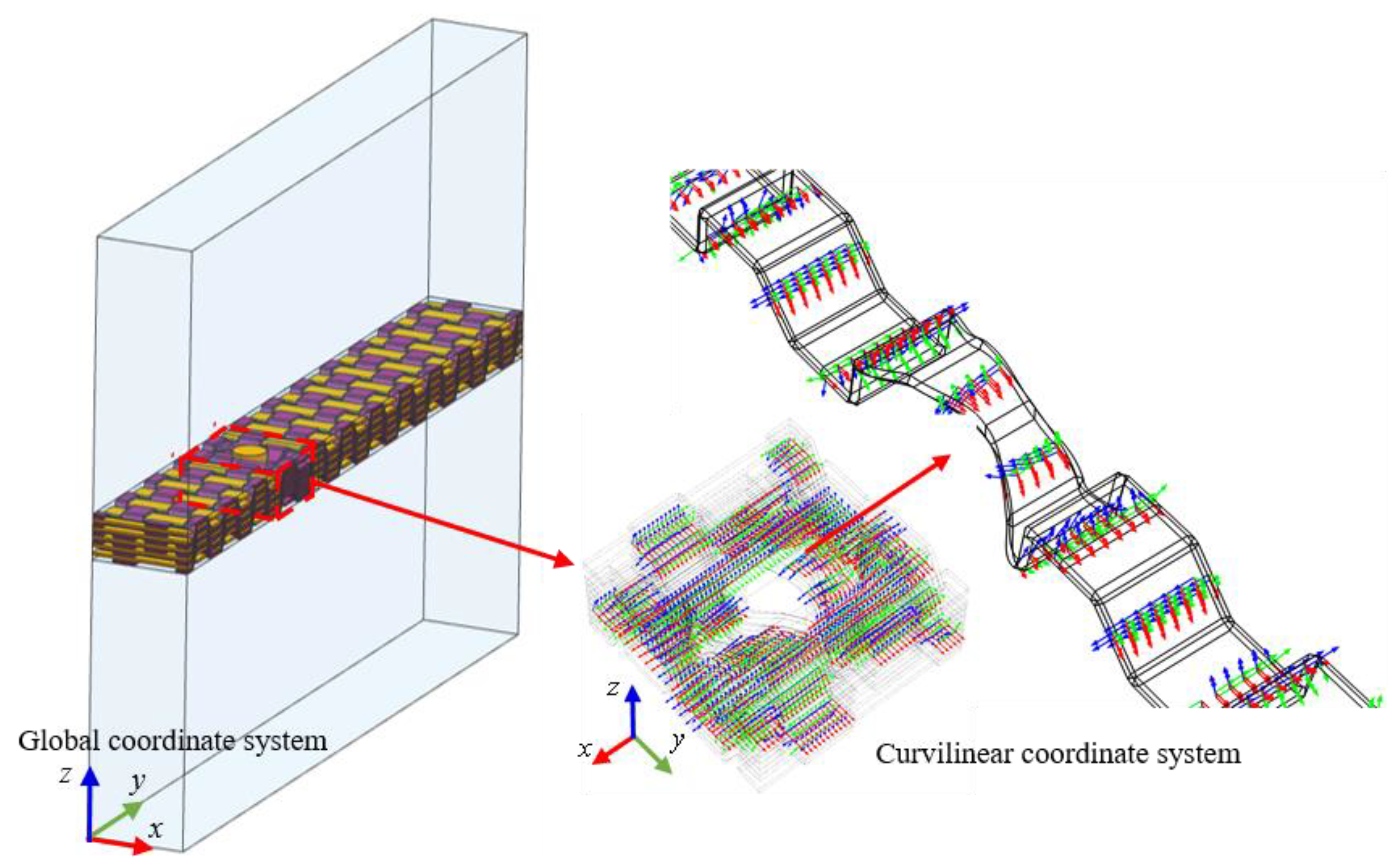
2.2. Calculation Coordinates for Anisotropic Thermal Conductivity
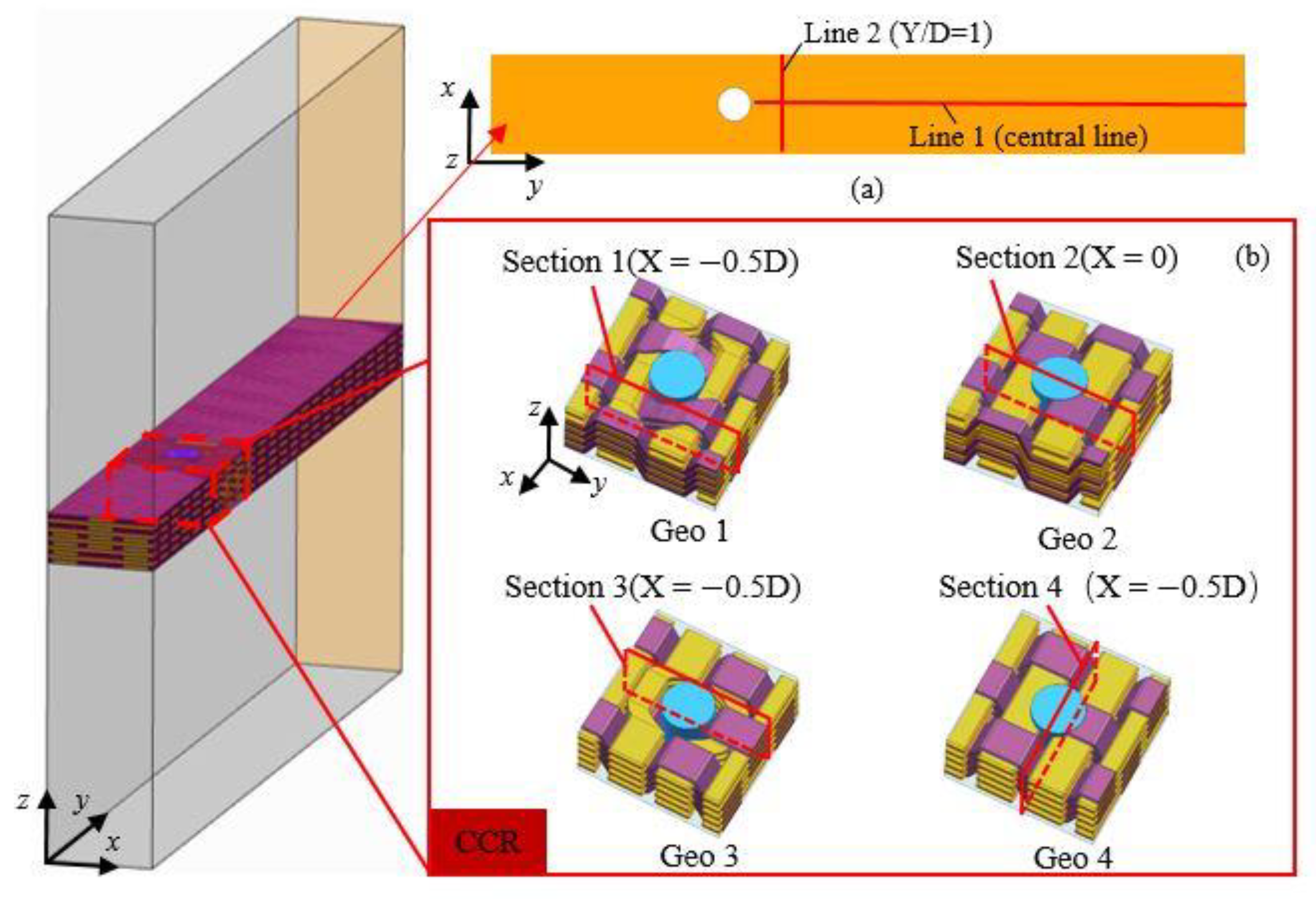
2.3. Boundary Conditions and Parameter Definitions
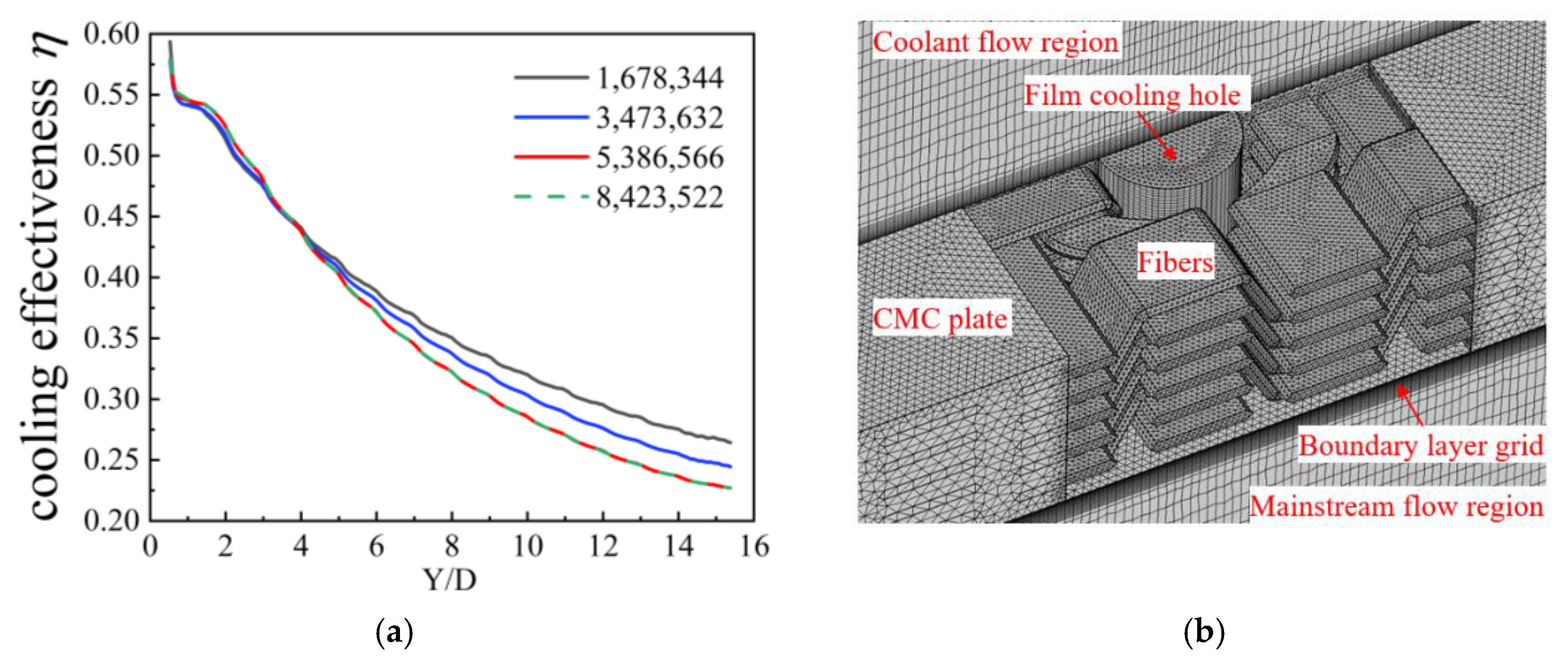
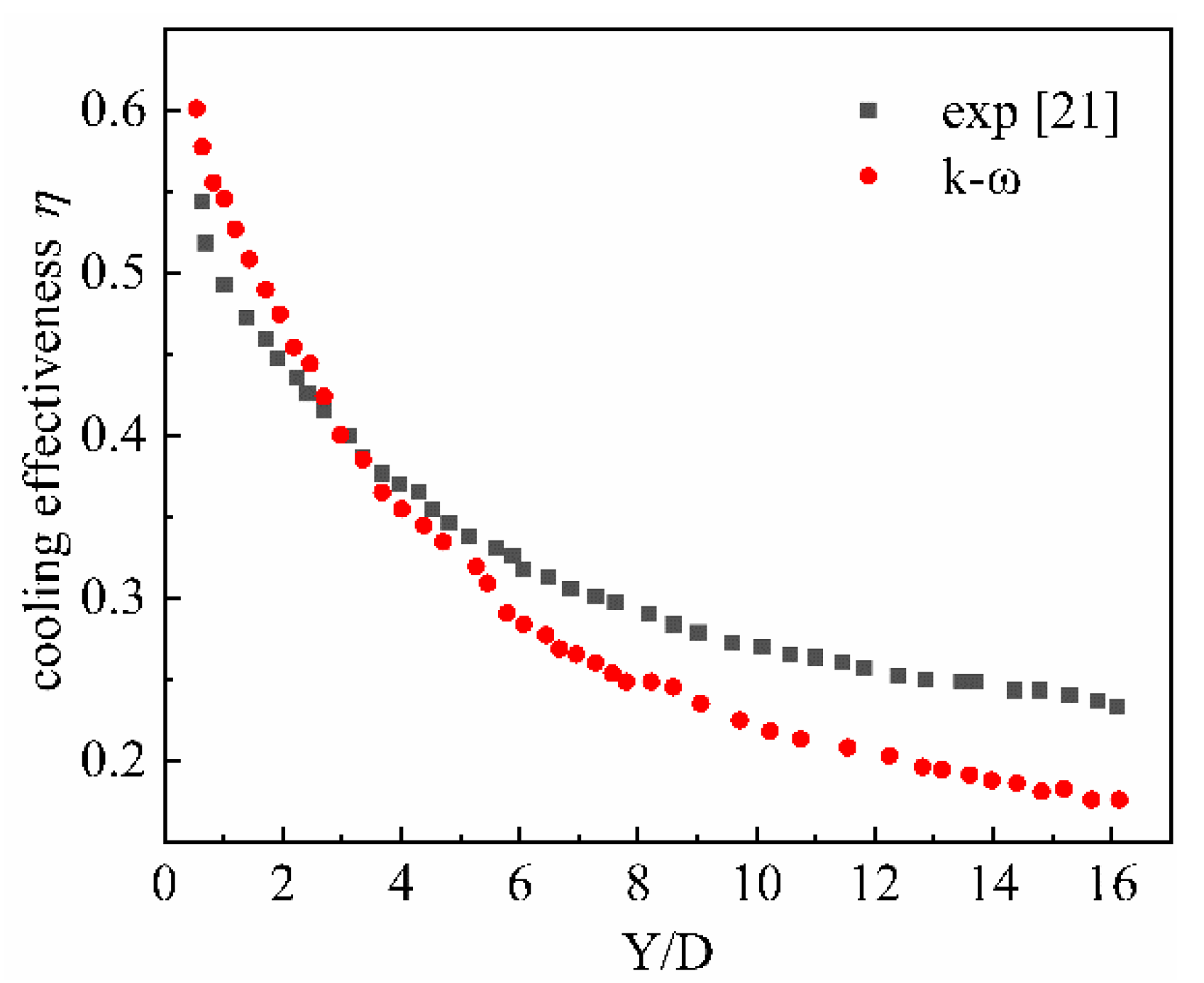
2.4. Grid System
2.5. Grid System
2.6. Operating Conditions
3. Results and Discussions
3.1. Influence of Different Film-Cooling Holes on Film-Cooling Performance
3.1.1. Influence on the Overall Cooling Effectiveness of the Hot-Side Wall
3.1.2. Temperature Gradient Distribution of CCR
3.1.3. Thermal Gradient Distribution of CCR
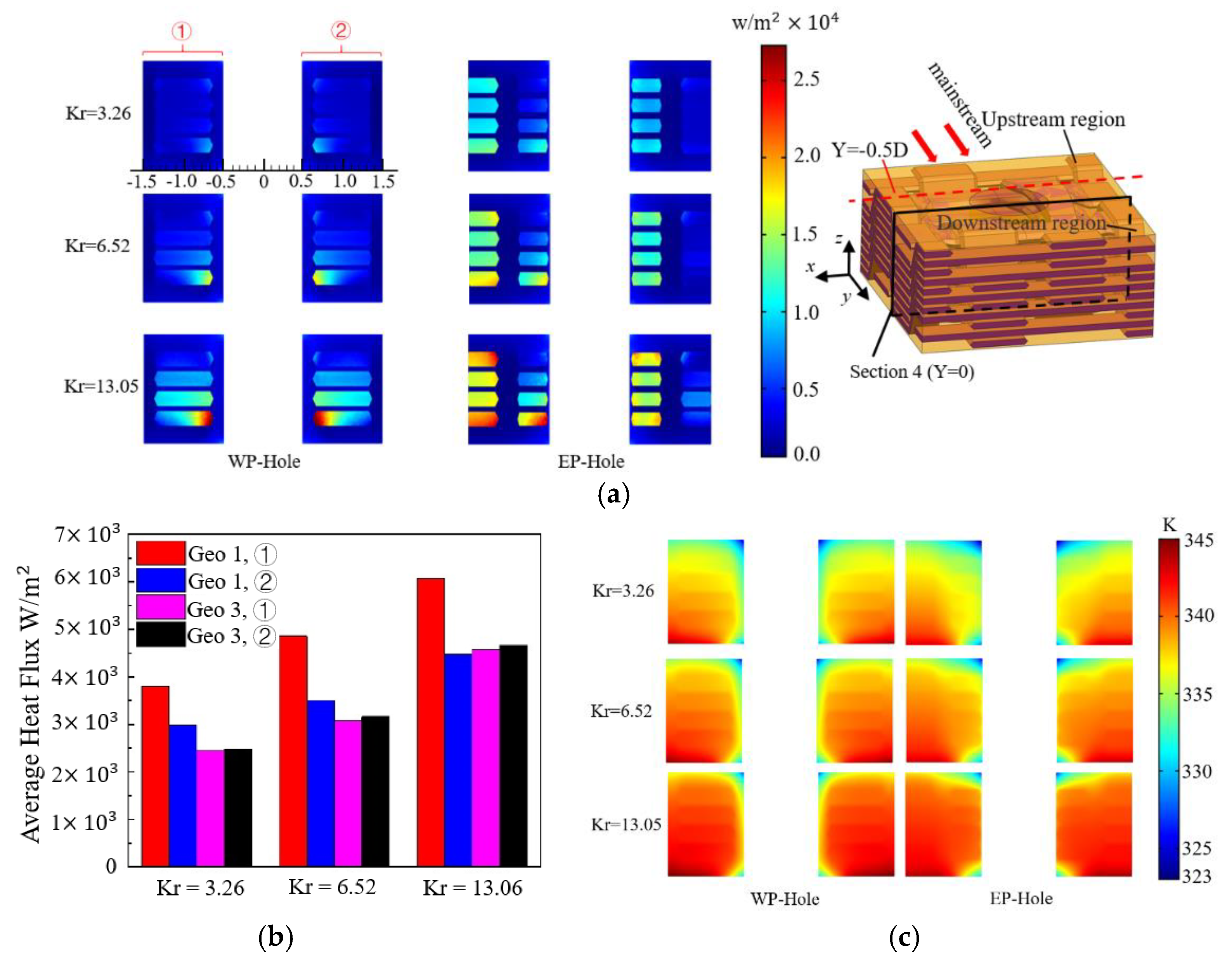
3.2. Influence of Kr
4. Conclusions
- 1.
- Different preformed holes have a significant impact on the temperature distribution inside the plate around the film-cooling hole; the change of dimensionless temperature inside the plate for the four models is up to 12%. The temperature of CCR in the models with EP-Hole and WP-Hole is lower than that of the model with the drilled hole. Furthermore, the WP-Hole forms a connected low-temperature area around the film-cooling hole. Compared with the drilled hole, the preformed holes can effectively reduce the maximum thermal gradient inside the plate. The maximum thermal gradient around the DP-Hole is significantly higher than that of WP-Hole and EP-Hole (DP-Hole 1 is 55.3% higher than EP-Hole and DP-Hole 2 is 123.3% higher than WP-Hole).
- 2.
- With Kr increasing, the overall cooling effectiveness of the 2.5D braided plate decreases. With the increase of Kr, the variation trend of the overall cooling efficiency of the plate brought by the four kinds of film holes is consistent. When Kr increases from 3.26 to 13.05, the average overall cooling effectiveness dropped by about 10%. The difference in overall cooling efficiency caused by different preformed holes will not change much with the change of Kr.
- 3.
- With the increase of Kr, the advantages of the two preformed hole structures in controlling the temperature gradient of the CMC plate with film-cooling holes are further expanded. The increase of Kr has a little effect on the maximum thermal gradient of the preformed hole structure. The maximum thermal gradient change is less than 3% for the EP-Hole structure and WP-hole structure caused by the increase of Kr. However, the increase of Kr has a significant effect on the maximum thermal gradient of the drilled structure. The increase of Kr will increase the maximum thermal gradient. The maximum thermal gradients for DP-Hole 1 and DP-Hole 2 increase by 10.7% and 18.8%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, C.D. Development Research of Aero Engine; Aviation Industry Press: Beijing, China, 2009; pp. 57–80. [Google Scholar]
- Stephan, S.W. Evaluation of ultra-high temperature ceramics and coating systems for their application in orbital and air-breathing propulsion. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012. [Google Scholar]
- Dicarlo, J.A.; Morscher, G.N.; Bhatt, R.T. Progress in SiC/SiC ceramic composite development for gas turbine hot section components under NASA EPM and UEET programs. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air Conference, Amsterdam, The Netherlands, 3–6 June 2002; Volume 36096, pp. 39–45. [Google Scholar]
- Gao, T.; Hong, Z.L.; Yang, J. Application and prospect of ceramic matrix composite components for commercial aircraft engine. Aeronaut. Manuf. Technol. 2014, 6, 14–21. [Google Scholar]
- Verrilli, M.; Calomino, A.; Robinson, R.C.; Thomas, D.J. Ceramic matrix composite vane sub-element testing in a gas turbine environment. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air Conference, Vienna, Austria, 14–17 June 2004; Volume 41677, pp. 393–399. [Google Scholar]
- He, Z.; Dong, C.; Liang, D.; Mao, J. A weighted-sum-of-gray soot-fractal-aggregates model for nongray heat radiation in the high temperature gas-soot mixture. J. Quant. Spectrosc. Radiat. Transf. 2021, 260, 107431. [Google Scholar] [CrossRef]
- Singh, M. Advanced Ceramic Matrix Composites for High Temperature Applications; NASA Technical Reports Server: Cleveland, OH, USA, 2005. [Google Scholar]
- Murthy, P.L.N.; Nemeth, N.N.; Brewer, D.N. Probabilistic analysis of a SiC/SiC ceramic matrix composite turbine vane. Compos. Part B Eng. 2008, 39, 694–703. [Google Scholar] [CrossRef]
- Beyer, S.; Schmidt, W.S.; Quering, K. Technology status of fuel cooled ceramic matrix composites for dual-mode ramjet and liquid rocket engine applications. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012; p. 5877. [Google Scholar]
- Wen, S.Q.; He, A.J. Application of CMC on thermal parts of aero engine. Aeronaut. Manuf. Technol. 2009, z1, 4–7. [Google Scholar]
- Jacobson, N.S.; Fox, D.S.; Opila, E.J. High temperature oxidation of ceramic matrix composites. Pure Appl. Chem. 1998, 70, 493–500. [Google Scholar] [CrossRef]
- Ryo, I.; Yuraro, A.; Yuki, K. Development of short and continuous carbon fiber-reinforced zrb2-sic-zrc matrix composites for thermal protection systems. Ceram. Int. 2018, 44, 15858–15867. [Google Scholar]
- Lu, G.F.; Qiao, S.R.; Gong, M.F. Fabrication and oxidation behavior of C/Si-C-N composite. J. Mater. Eng. 2010, 3, 17–21. [Google Scholar]
- Wei, Y.Q.; Yang, Y.; Liu, M. Oxidation mechanism and kinetics of SiBCN/HfC ceramic composites at high temperatures. J. Mater. Res. Technol. 2020, 9, 2289–2298. [Google Scholar] [CrossRef]
- Corman, G.; Upadhyay, R.; Sinha, S. Materials Research for Manufacturing; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 59–91. [Google Scholar]
- Unal, O.; Eckel, A.J.; Laabs, F.C. The 1400 °C oxidation effect on microstructure strength and cyclic life of SiC/SiC composites. Scr. Metall. 1995, 33, 983–988. [Google Scholar] [CrossRef]
- Schmidt, A.S.; Beyer, S.A.; Knabe, H.B.; Immich, H.; Meistring, R.; Gessler, A. Advanced ceramic matrix composite materials for current and future propulsion technology applications. Acta Astronautica. 2004, 55, 409–420. [Google Scholar] [CrossRef]
- Tu, Z.C.; Mao, J.K.; Han, X.S. Numerical study of film cooling over a flat plate with anisotropic thermal conductivity. Appl. Therm. Eng. 2017, 111, 968–980. [Google Scholar] [CrossRef]
- Tu, Z.C.; Mao, J.K.; Han, X.S. Experimental study of film cooling over a fiber-reinforced composite plate with anisotropic thermal conductivity. Appl. Therm. Eng. 2019, 148, 447–456. [Google Scholar] [CrossRef]
- Zhang, D.X.; Hayhurst, D.R. Influence of applied in-plane strain on transverse thermal conductivity of 0°/90° and plain weave ceramic matrix composites. Int. J. Solids Struct. 2011, 48, 828–842. [Google Scholar] [CrossRef][Green Version]
- Zhao, X. Investigation on Film Cooling of Braided Composites Considering Film Hole and Braided Structure Interference. Master Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, Jiangsu, 2018. [Google Scholar]
- Yang, X.; Zhao, Q.; Liu, Z.; Liu, Z.; Feng, Z. Film Cooling Patterns over an Aircraft Engine Turbine Endwall with Slot Leakage and Discrete Hole Injection. Int. J. Heat Mass Transf. 2021, 165, 120565. [Google Scholar] [CrossRef]
- Khalatov, A.; Shi-Ju, E.; Wang, D.; Borisov, I. Film cooling evaluation of a single array of triangular craters. Int. J. Heat Mass Transf. 2020, 159, 120055. [Google Scholar] [CrossRef]
- Xie, C.H.; Xue, P. Optimization and analysis of stress concentration in composite laminates with different cutouts. J. Shaanxi Norm. Univ. (Nat. Sci. Ed.) 2014, 4, 27–32. [Google Scholar]
- Gruber, B.; Hufenbach, W. Stress concentration analysis of fiber-reinforced multilayered composites with pin-loaded holes. Compos. Sci. Technol. 2007, 67, 1439–1450. [Google Scholar] [CrossRef]
- Liu, Z.G.; Lin, Q.; Ya, J.X. Experimental research on mechanical properties of 3D full 5-direactional braided composites lugs. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2225–2233. [Google Scholar]
- Zitoune, R.; Crouzeix, L.; Collombet, F.; Tamine, T.; Grunevald, Y.H. Behaviour of composite plates with drilled and moulded hole under tensile load. Compos. Struct. 2011, 93, 2384–2391. [Google Scholar] [CrossRef]
- Yamada, R.; Igawa, N.; Taguchi, T. Thermal diffusivity/conductivity of Tyranno SA fiber- and Hi-Nicalon Type S fiber-reinforced 3-D SiC/SiC composites. J. Nucl. Mater. 2004, 329, 497–501. [Google Scholar] [CrossRef]
- Rüdiger, B.; Martin, F.; Günther, N. Thermal conductivity, specific heat capacity, and emissivity of ceramic matrix composites at high temperatures. High Temp. High Press. 2003, 3536, 169–177. [Google Scholar]
- Chen, J.; Long, Y.; Xiong, X. Microstructure and thermal conductivity of carbon/carbon composites made with different kinds of carbon fibers. J. Cent. South Univ. 2012, 19, 1780–1784. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, L.T.; Liu, Y.S. Increasing the thermal conductivity of 2D SiC/SiC composites by heat-treatment. Fusion Eng. Des. 2015, 90, 110–118. [Google Scholar] [CrossRef]
- COMSOL. Inc. COMSOL Multiphysics Help—Theory for the Heat Transfer; COMSOL. Inc.: Stockholm, Sweden, 2011. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Cañada Flintridge, CA, USA, 1998. [Google Scholar]
- Bianchini, C.; Andrei, L.; Andreini, A.; Facchini, B. Numerical benchmark of nonconventional RANS turbulence models for film and effusion cooling. ASME J. Turbomach. 2013, 135, 041026. [Google Scholar] [CrossRef]
- Sinha, A.K.; Bogard, D.G.; Crawford, M.E. Film-cooling effectiveness downstream of a single row of holes with variable density ratio. ASME J. Turbomach. 1991, 113, 442–449. [Google Scholar] [CrossRef]
- Dong, P. Research on Conjugate Heat Transfer Simulation of Aero Turbine Engine Air-Cooled Vane; Harbin Institute of Technology: Harbin, China, 2009. [Google Scholar]


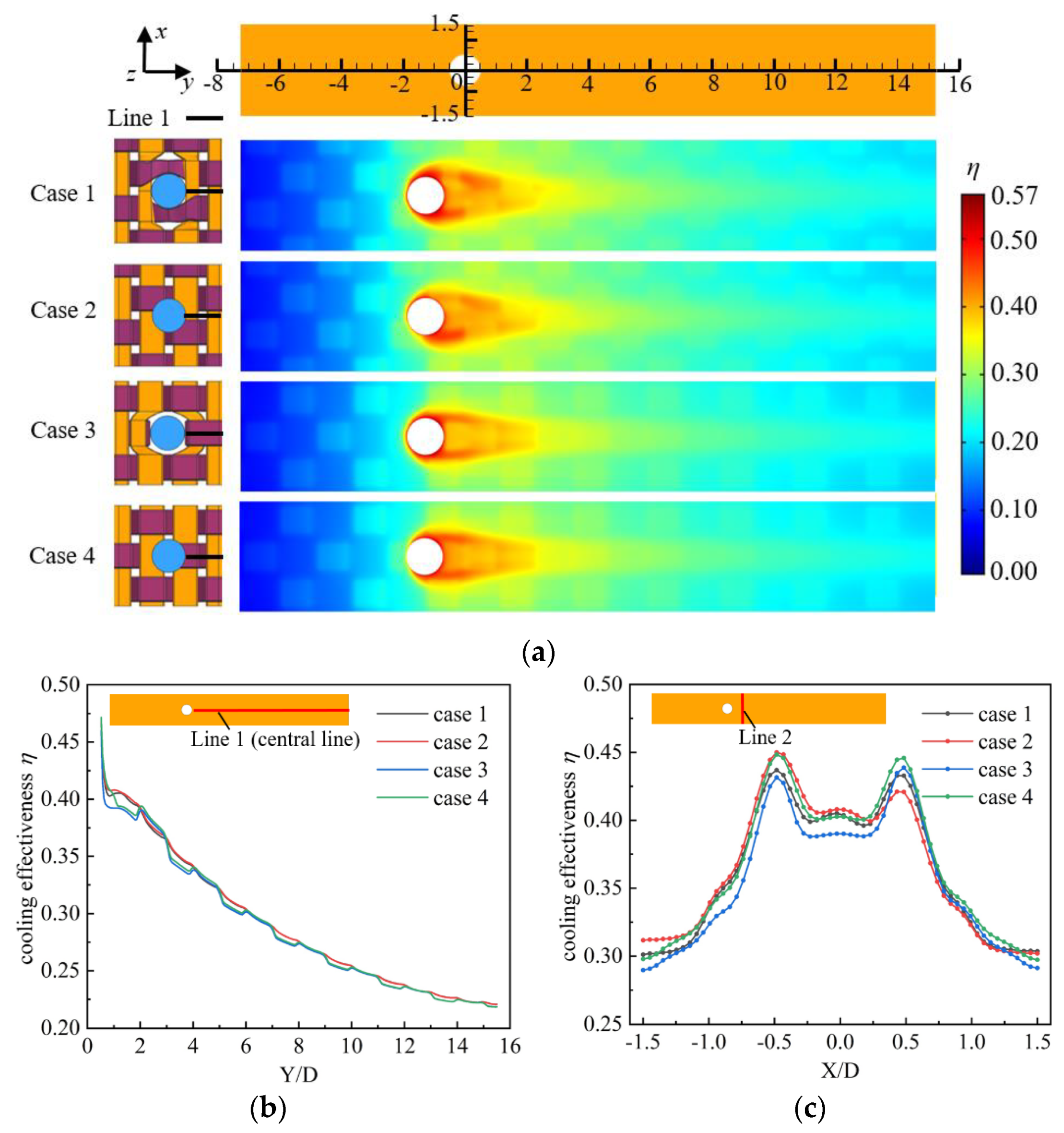
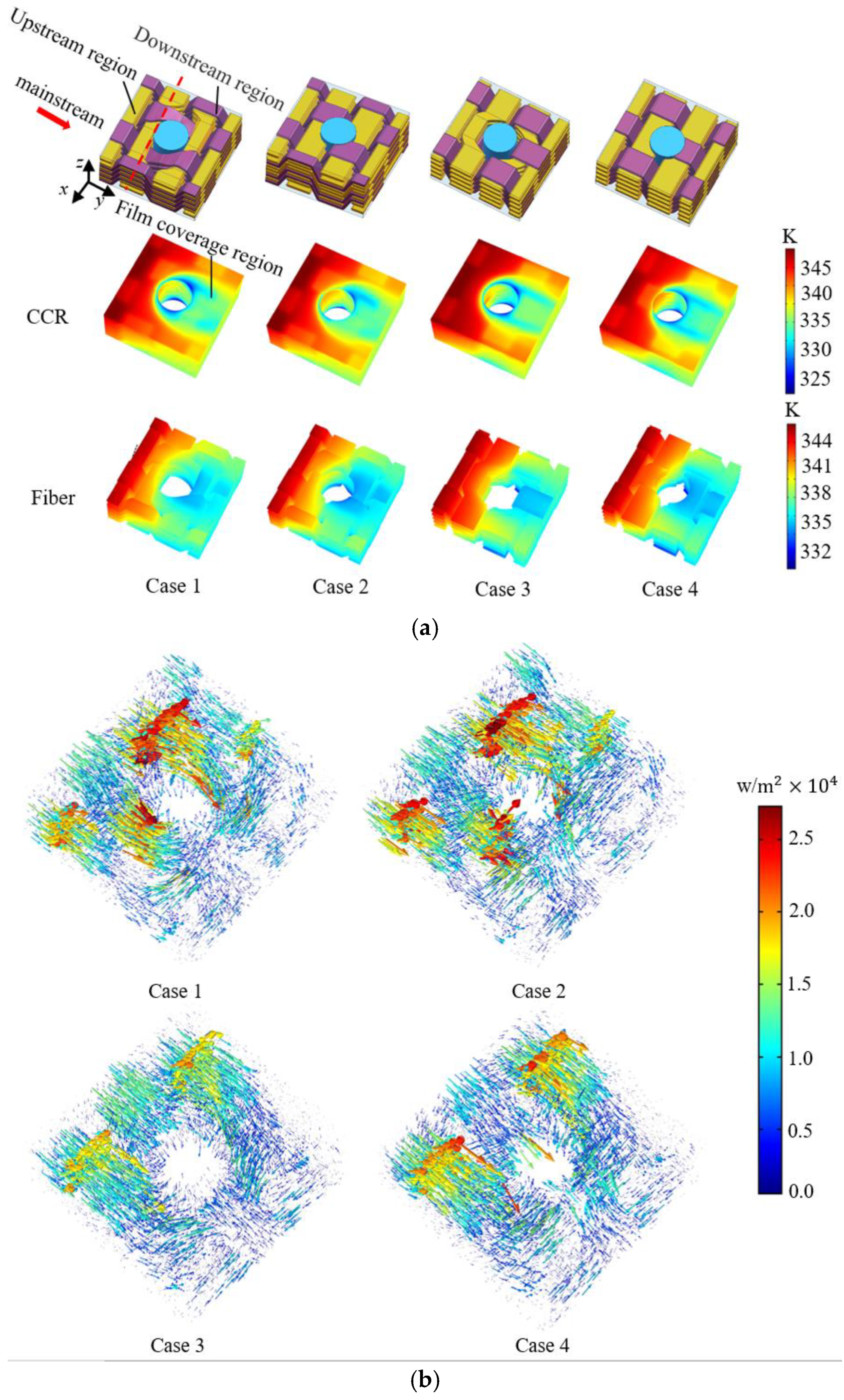

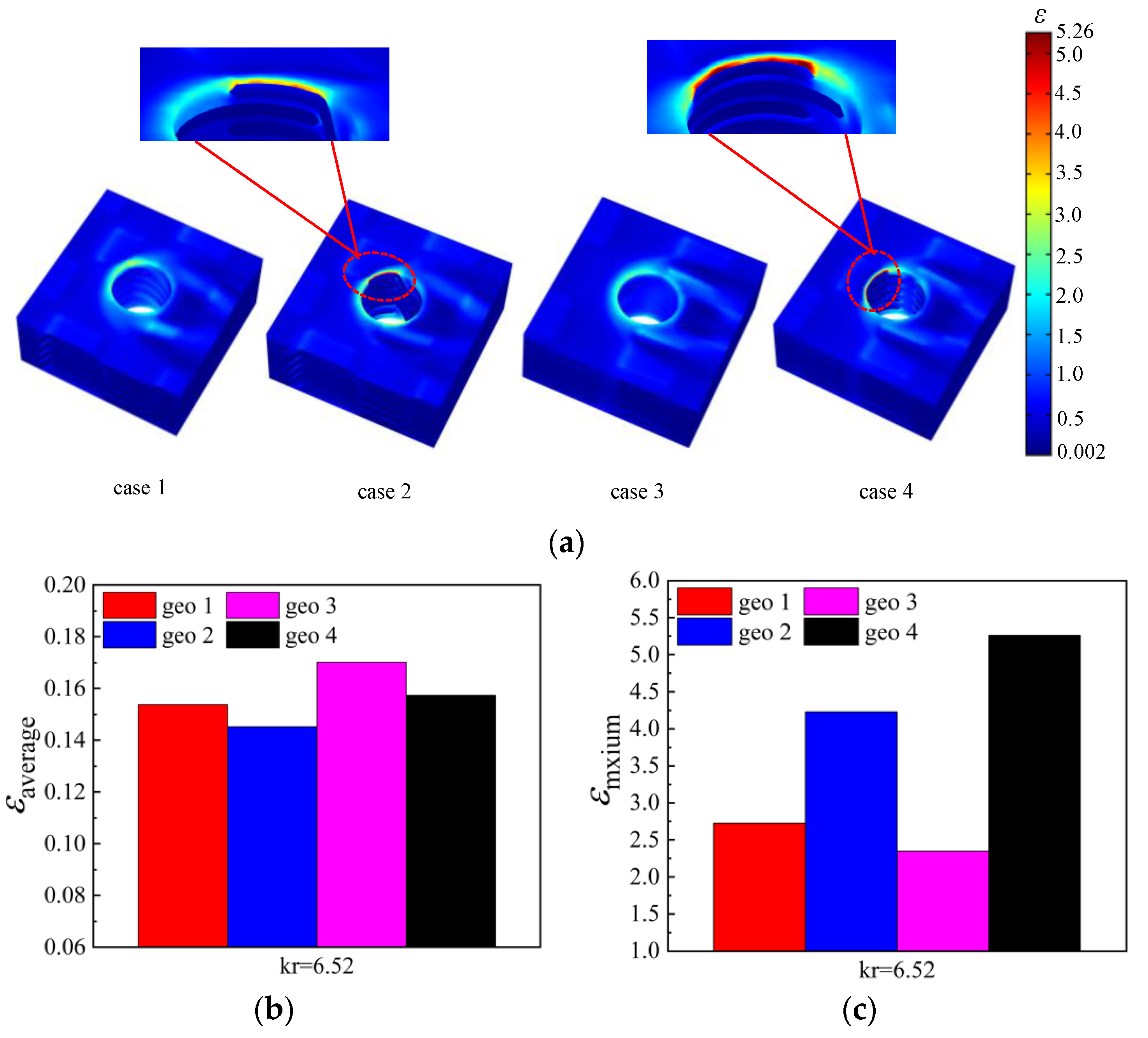
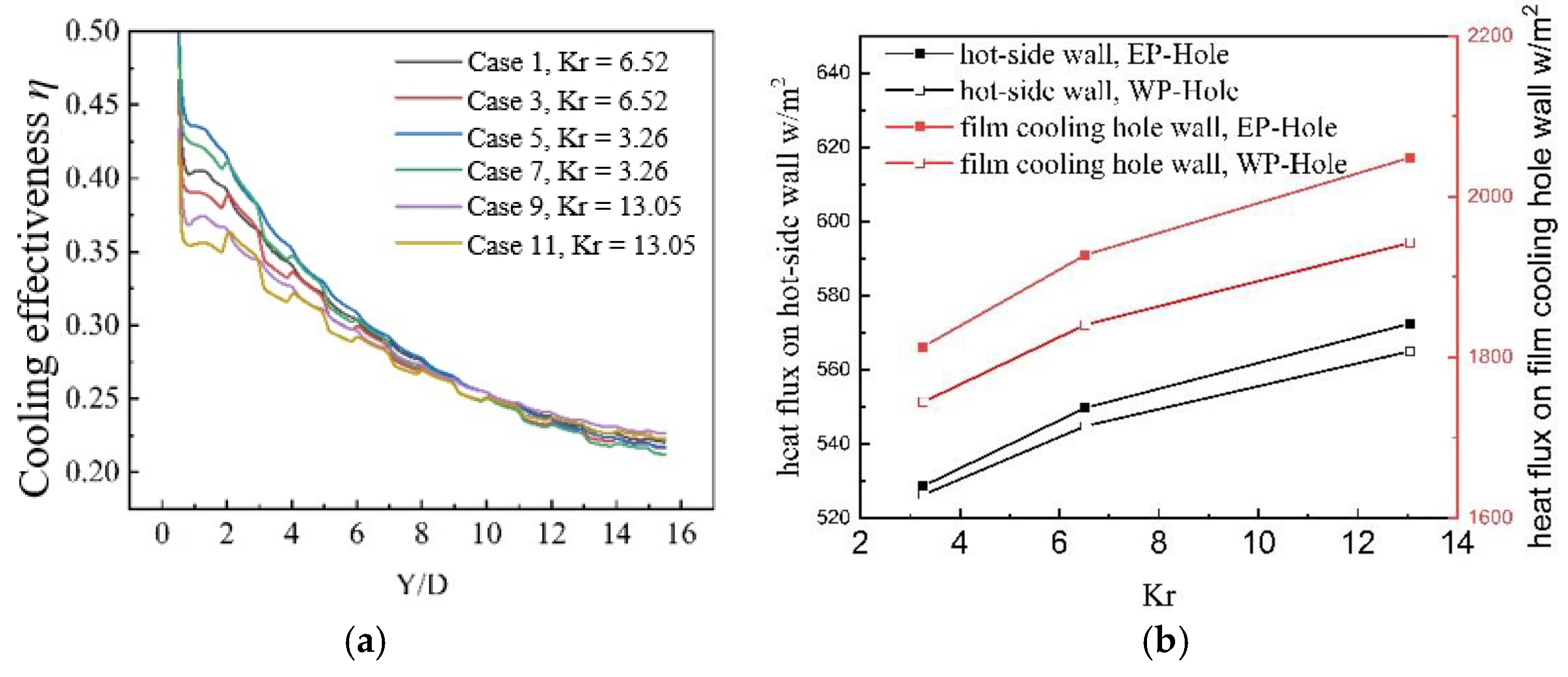

| Serial | Thermal Conductivity in Axial of the Fiber Bundles (kxx)/W/(m·K) | Thermal Conductivity in Radial of the Fiber Bundles (kyy and kzz)/W/(m·K) | Thermal Conductivity of Matrix (km)/W/(m·K) | Kr |
|---|---|---|---|---|
| 1 | 4.83 | 1.48 | 0.2 | 3.26 |
| 2 | 9.66 | 1.48 | 0.2 | 6.52 |
| 3 | 19.32 | 1.48 | 0.2 | 13.05 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kr | 6.52 | 3.26 | 13.05 | |||||||||
| Geo | Geo1 | Geo2 | Geo3 | Geo4 | Geo1 | Geo2 | Geo3 | Geo4 | Geo1 | Geo2 | Geo3 | Geo4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Tu, Z.; Mao, J. Investigation of the Film-Cooling Performance of 2.5D Braided Ceramic Matrix Composite Plates with Preformed Hole. Aerospace 2021, 8, 116. https://doi.org/10.3390/aerospace8040116
Zhao C, Tu Z, Mao J. Investigation of the Film-Cooling Performance of 2.5D Braided Ceramic Matrix Composite Plates with Preformed Hole. Aerospace. 2021; 8(4):116. https://doi.org/10.3390/aerospace8040116
Chicago/Turabian StyleZhao, Chenwei, Zecan Tu, and Junkui Mao. 2021. "Investigation of the Film-Cooling Performance of 2.5D Braided Ceramic Matrix Composite Plates with Preformed Hole" Aerospace 8, no. 4: 116. https://doi.org/10.3390/aerospace8040116
APA StyleZhao, C., Tu, Z., & Mao, J. (2021). Investigation of the Film-Cooling Performance of 2.5D Braided Ceramic Matrix Composite Plates with Preformed Hole. Aerospace, 8(4), 116. https://doi.org/10.3390/aerospace8040116





