On-Orbit Pulse Phase Estimation Based on CE-Adam Algorithm
Abstract
1. Introduction
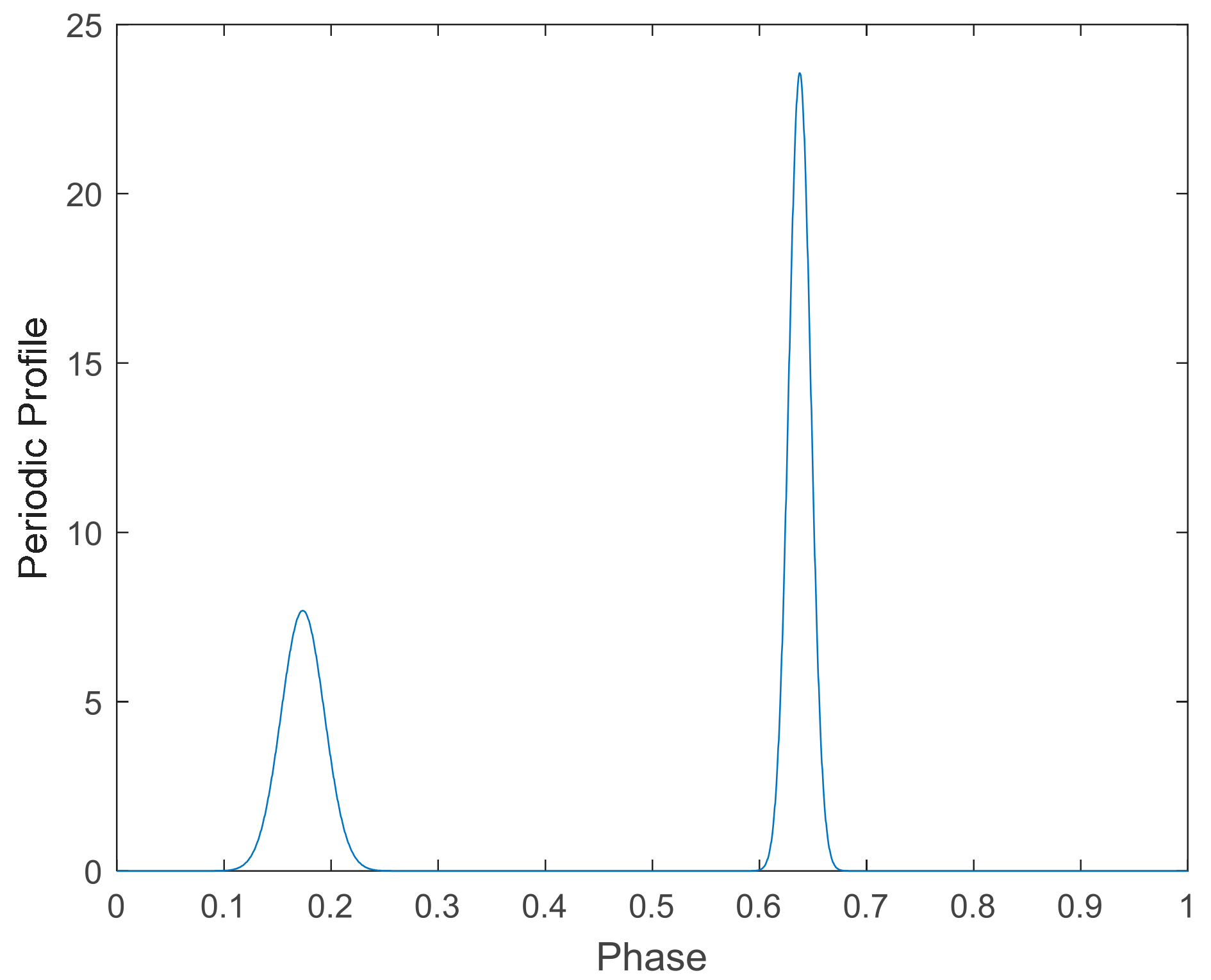
2. Principle of Pulse Phase Estimation
3. Related Algorithm
3.1. Cross-Entropy (CE) Algorithm
- Chose , , the elite sampling rate , and the sample size . Let the number of iterations and the elite sample size be:
- Generate samples from the , calculate and sort the objective function .
- Choose the best samples as the elite samples.
- Update the distribution parameters with the collected elite samples, calculate the and
- Smoothing and
- If ( is the standard deviation threshold), the algorithm returns , otherwise, lets and returns to step 2.
3.2. Adam Algorithm
4. Cross-Entropy Adaptive Moment Estimation (CE-Adam) Algorithm
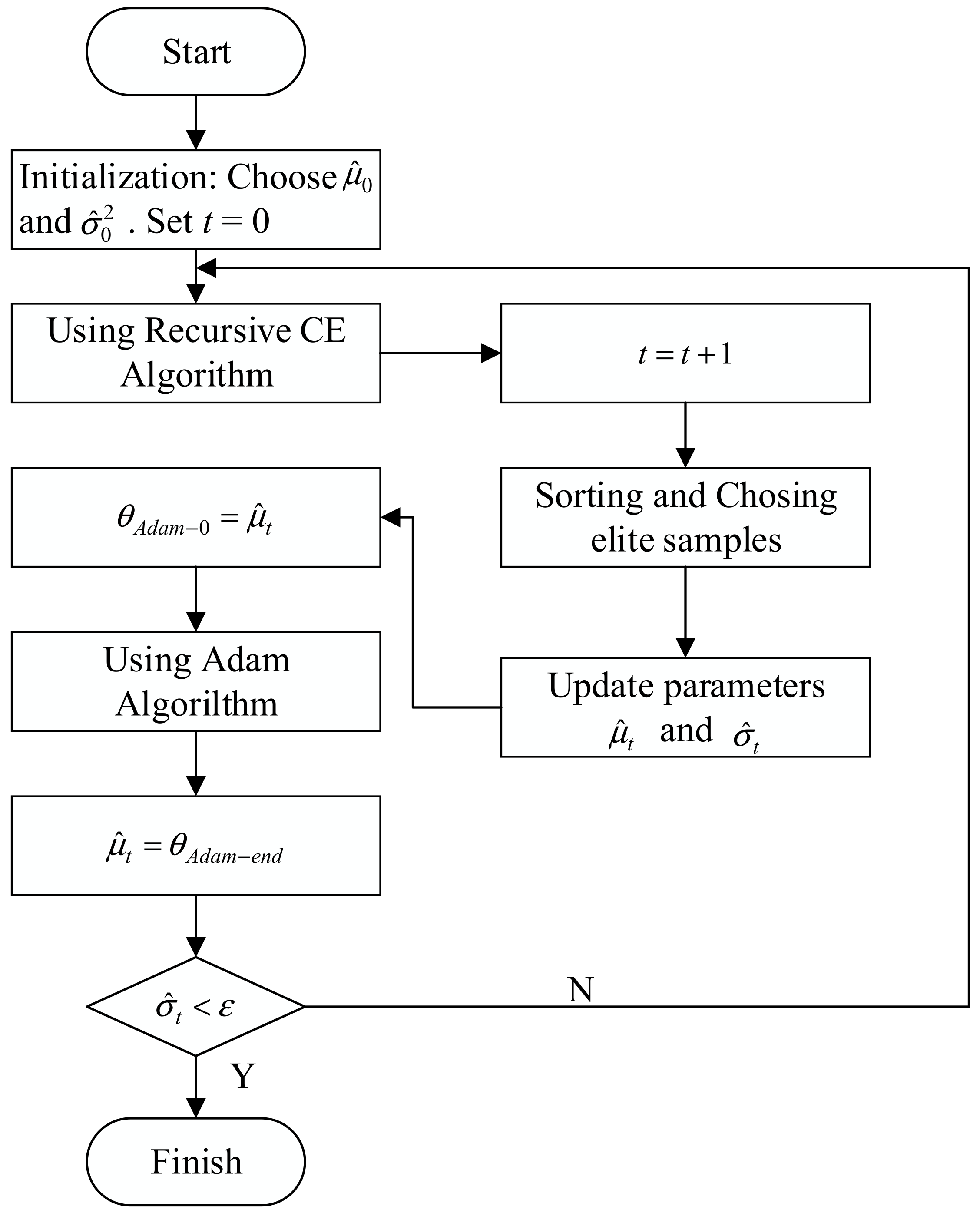
4.1. Recursive CE Algorithm
4.2. Proposal of CE-Adam Algorithm
5. Experiments
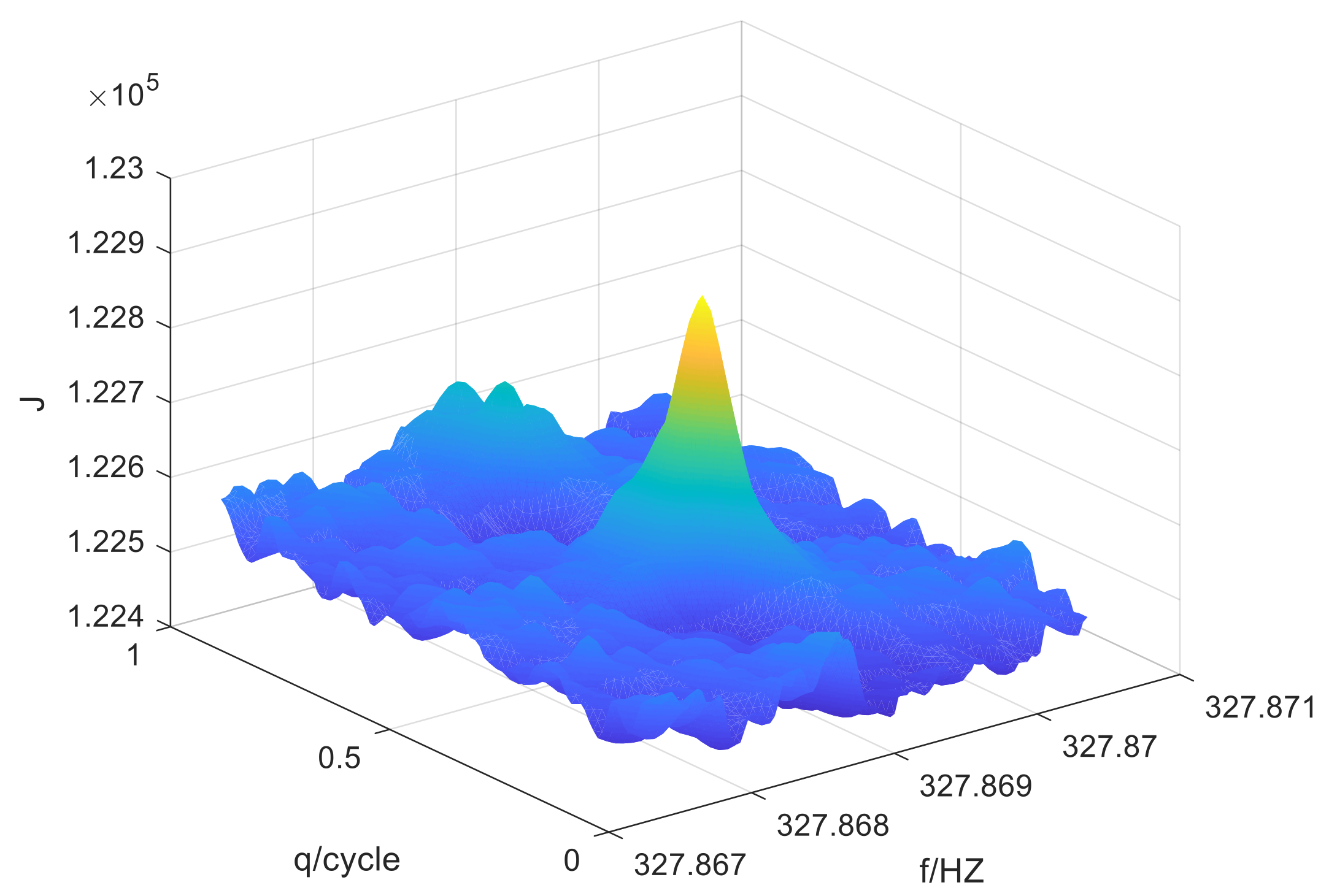
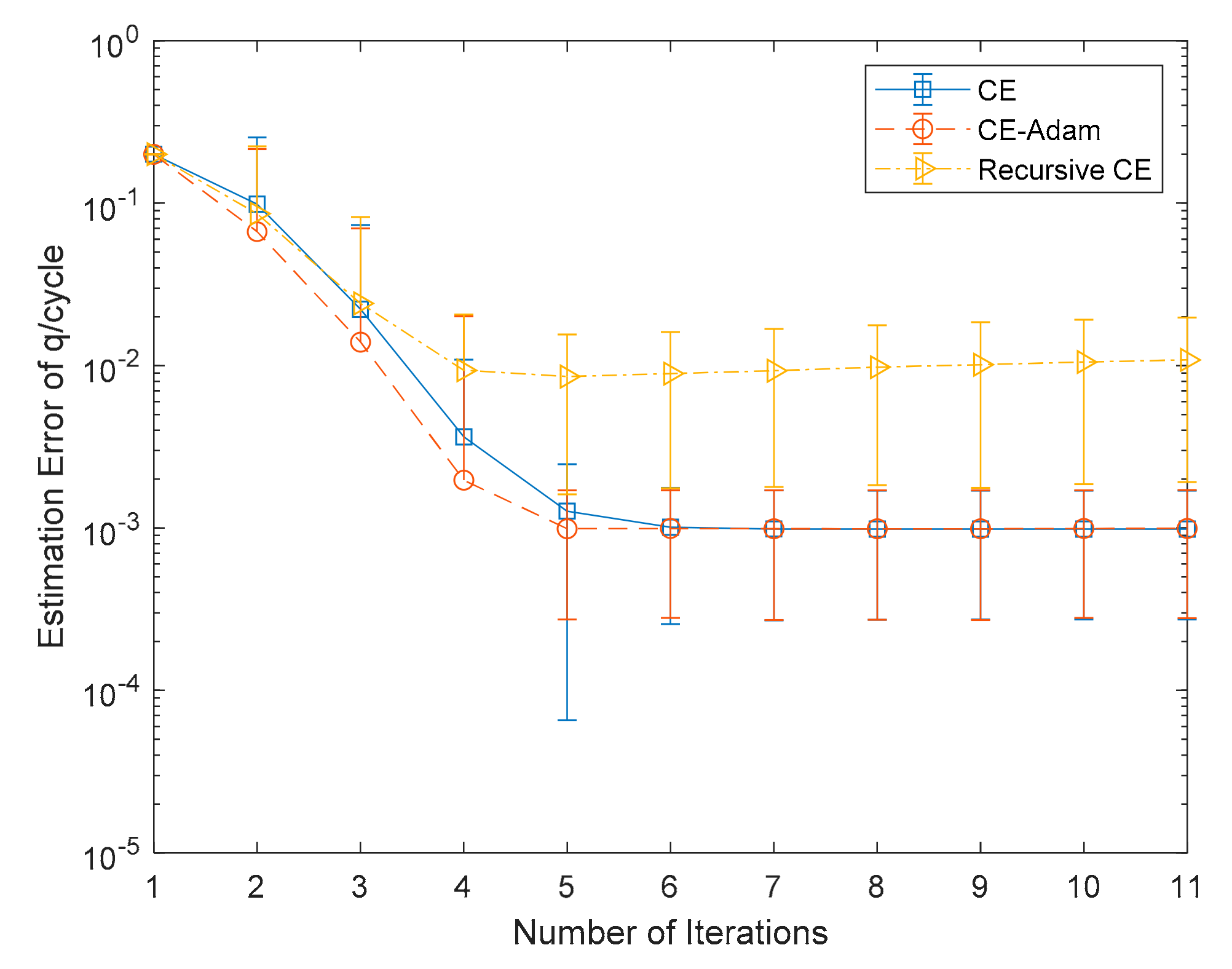
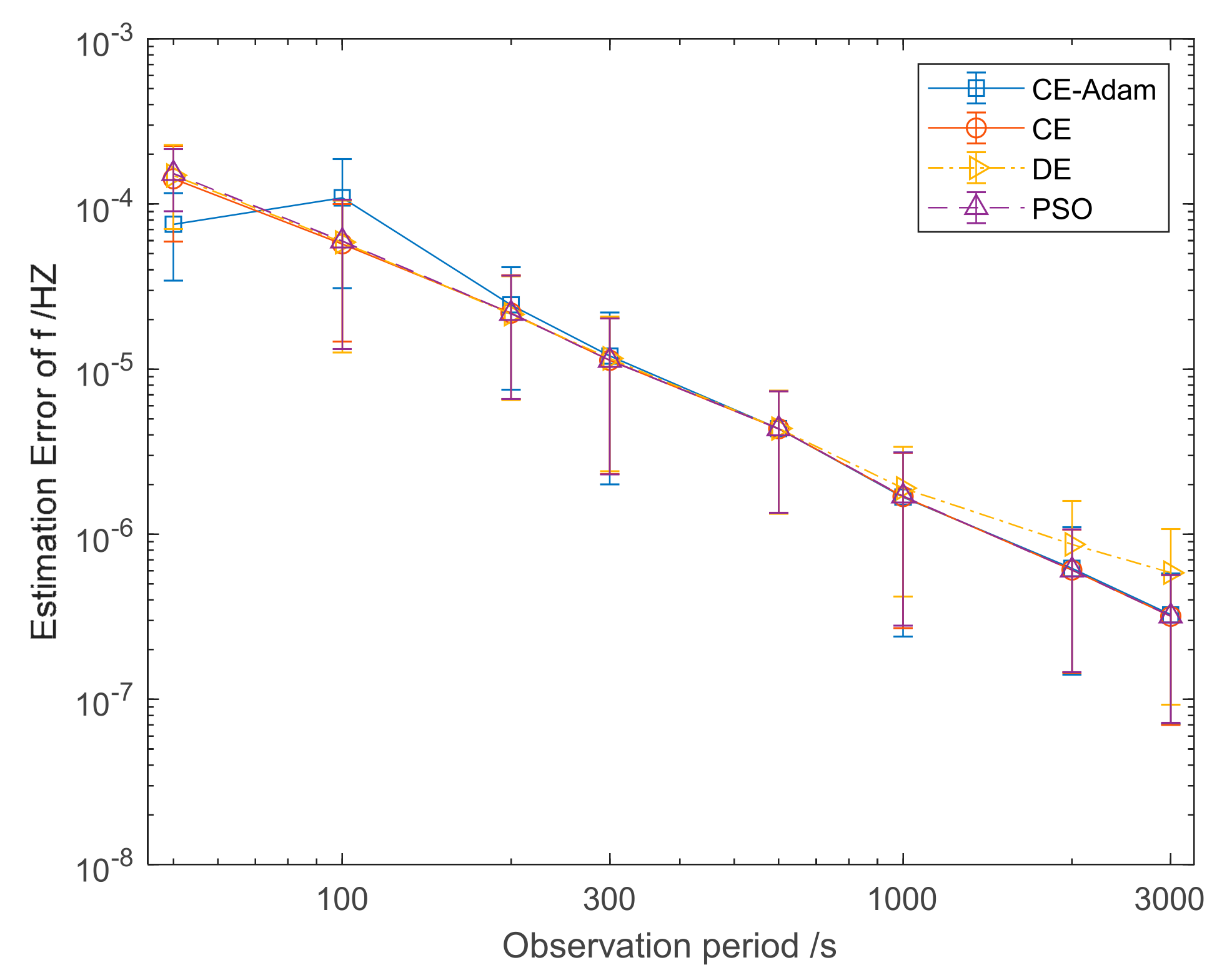
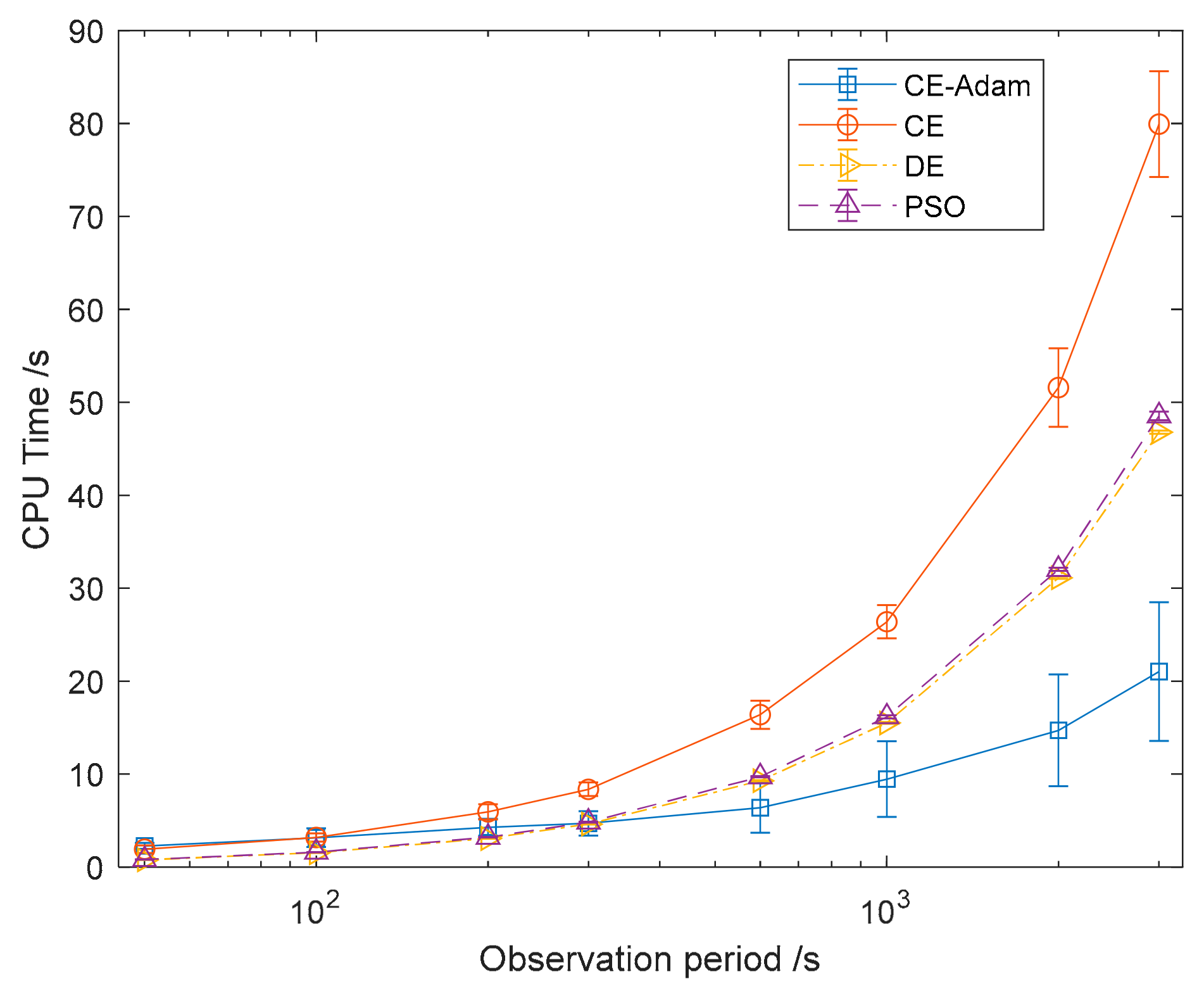
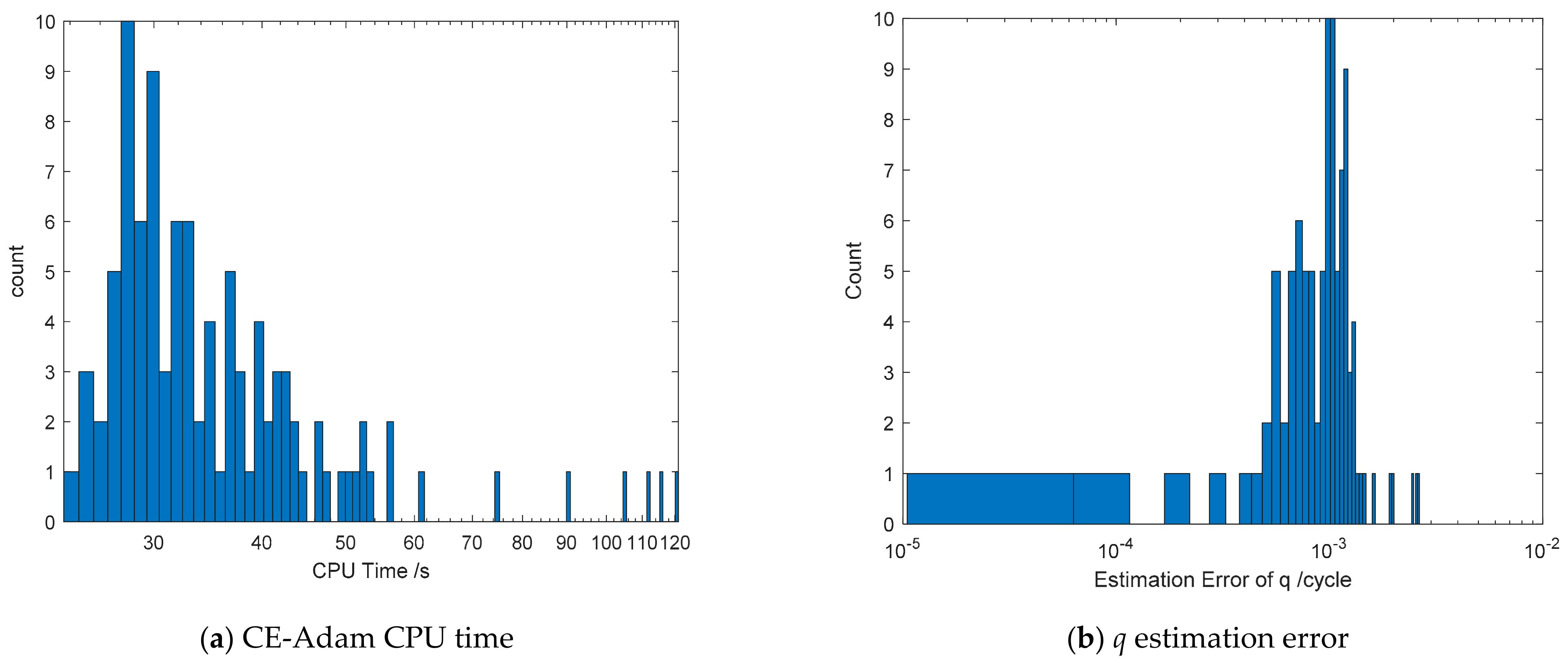
5.1. Experiments with Simulation Data
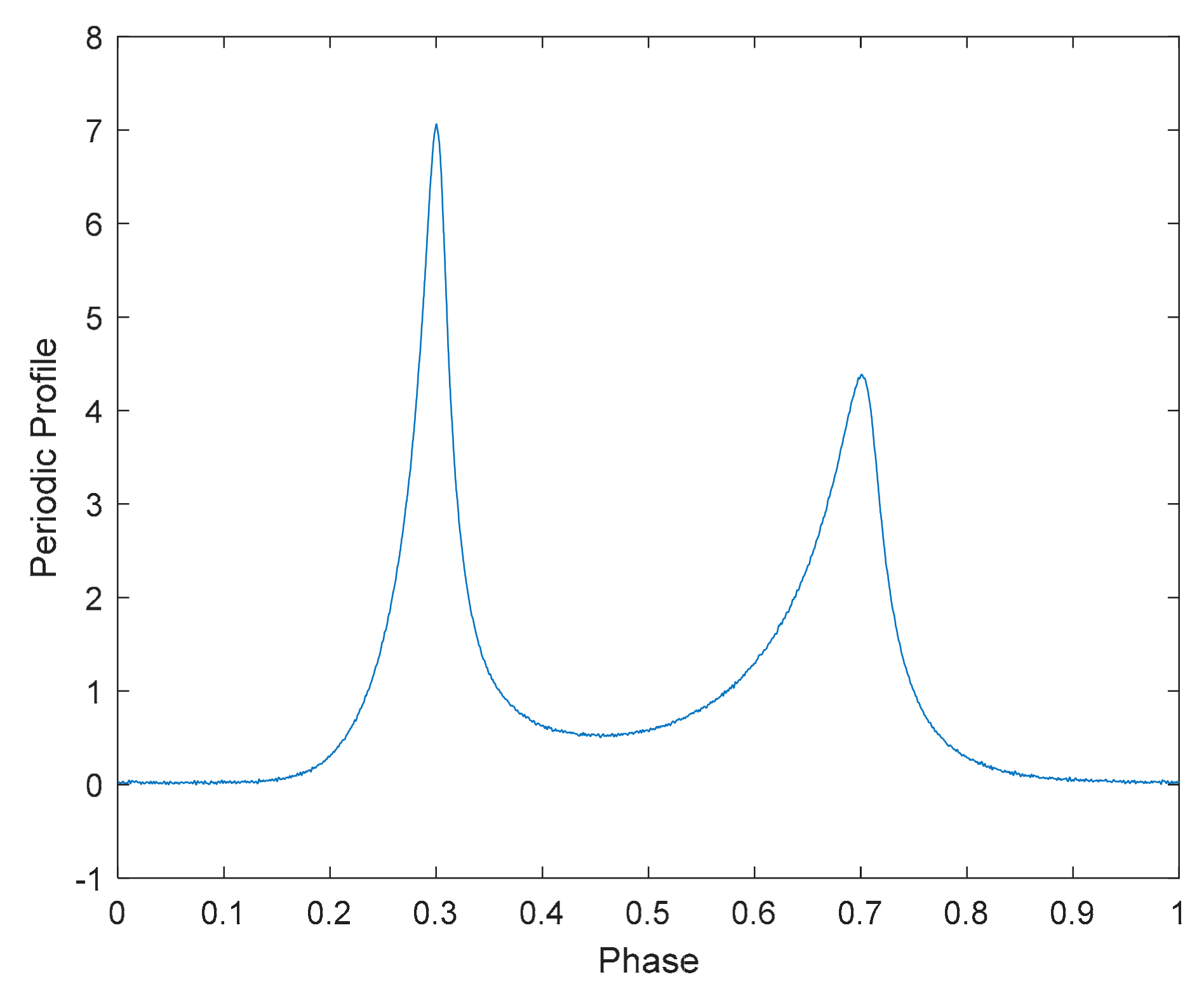
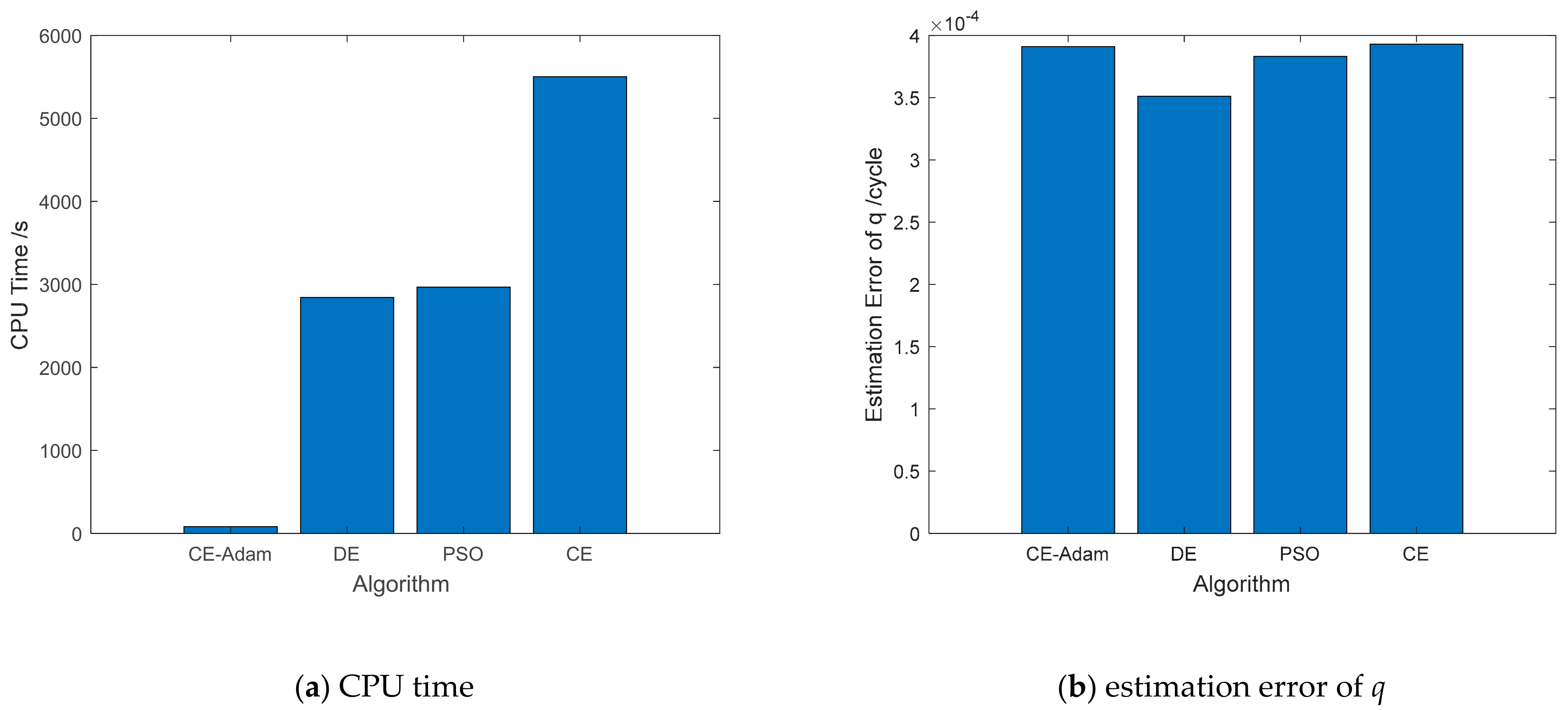
5.2. Experiments with Real Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, W.; Wang, Y. Introduction. In X-ray Pulsar–Based Navigation: Theory and Applications; Springer: Singapore, 2020; pp. 1–24. [Google Scholar] [CrossRef]
- Chester, T.J.; Butman, S.A. Navigation Using X-Ray Pulsars. Telecommun. Data Acquis. Prog. Rep. 1981, 63, 22. [Google Scholar]
- Mitchell, J.W.; Winternitz, L.B.; Hassouneh, M.A.; Price, S.R.; Semper, S.R.; Yu, W.H.; Ray, P.S.; Wolff, M.T.; Kerr, M.; Wood, K.S.; et al. Sextant x-ray pulsar navigation demonstration: Initial on-orbit results. In Proceedings of the 2018 SpaceOps Conference, Marseille, France, 28 May–1 June 2018. [Google Scholar]
- Zheng, S.J.; Ge, M.Y.; Han, D.W. Test of pulsar navigation with POLAR on TG-2 spacelab. Sci. Sin. Phys. Mech. Astron. 2017, 47, 120–128. [Google Scholar] [CrossRef]
- Zheng, S.J.; Zhang, S.N.; Lu, F.J.; Wang, W.B.; Gao, Y.; Li, T.P.; Song, L.M.; Ge, M.Y.; Han, D.W.; Chen, Y.; et al. In-orbit Demonstration of X-Ray Pulsar Navigation with the Insight-HXMT Satellite. Astrophys. J. Suppl. Ser. 2019, 244. [Google Scholar] [CrossRef]
- Emadzadeh, A.A.; Speyer, J.L. X-Ray Pulsar-Based Relative Navigation using Epoch Folding. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2317–2328. [Google Scholar] [CrossRef]
- Emadzadeh, A.; Speyer, J.; Golshan, A. Asymptotically Efficient Estimation of Pulse Time Delay for X-Ray Pulsar Based Relative Navigation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.; Kang, Z.; Liu, J. A fast pulse time-delay estimation method for X-ray pulsars based on wavelet-bispectrum. J. Opt. 2020, 207, 1–11. [Google Scholar] [CrossRef]
- Liu, L.; Liu, J.; Ning, X.; Kang, Z. Real-time and accurate pulsar time-of-arrival estimation using GA-optimized EMD-CS. J. Opt. 2021, 225, 1–11. [Google Scholar] [CrossRef]
- Song, G.; Kang, Z.W. Fast Pulse Time Delay Estimation Algorithm Based on Variable Step Size Iteration. In Proceedings of the 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 1505–1509. [Google Scholar] [CrossRef]
- Golshan, A.R.; Sheikh, S.I. On Pulse Phase Estimation and Tracking of Variable Celestial X-Ray Sources. In Proceedings of the 63rd Annual Meeting of the Institute of Navigation, Cambridge, MA, USA, 23–25 April 2007. [Google Scholar]
- Huang, L.; Liang, B.; Zhang, T. Pulse phase and doppler frequency estimation of X-ray pulsars under conditions of spacecraft and binary motion and its application in navigation. Sci. China-Phys. Mech. Astron. 2013, 56, 848–858. [Google Scholar] [CrossRef]
- Anderson, K.D.; Pines, D.J.; Sheikh, S.I. Validation of Pulsar Phase Tracking for Spacecraft Navigation. J. Guid. Control. Dyn. 2015, 38, 1885–1897. [Google Scholar] [CrossRef]
- Winternitz, L.M.B.; Hassouneh, M.A.; Mitchell, J.W.; Valdez, J.E.; Price, S.R.; Semper, S.R.; Yu, W.H.; Ray, P.S.; Wood, K.S.; Arzoumanian, Z.; et al. X-ray Pulsar Navigation Algorithms and Testbed for SEXTANT. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Wang, Y.; Zheng, W. Pulse Phase Estimation of X-ray Pulsar with the Aid of Vehicle Orbital Dynamics. J. Navig. 2016, 69, 414–432. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W. Pulse Phase and Doppler Frequency Estimation for XNAV Using On-orbit Epoch Folding. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2210–2219. [Google Scholar] [CrossRef]
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by direct search: New perspectives on some classical and modern methods. SIAM Rev. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Xue, M.; Li, X.; Fu, L.; Fang, H.; Sun, H.; Shen, L. X-ray pulsar-based navigation using pulse phase and Doppler frequency measurements. Sci. China Inf. Sci. 2015, 58, 1–14. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, W.; Li, W.; Wang, J.; Xu, Y.; Lu, F.; Wang, Y.; Chen, T.; Han, D.; Hu, W.; et al. The Low Energy X-ray telescope (LE) onboard the Insight-HXMT astronomy satellite. Sci. China Phys., Mech. Astron. 2020, 63, 249–505. [Google Scholar] [CrossRef]
- Bogdanov, S.; Guillot, S.; Ray, P.S.; Wolff, M.T.; Chakrabarty, D.; Ho, W.C.G.; Kerr, M.; Lamb, F.K.; Lommen, A.; Ludlam, R.M.; et al. Constraining the Neutron Star Mass–Radius Relation and Dense Matter Equation of State with NICER. I. Astrophys. J. 2019, 887, L25. [Google Scholar] [CrossRef]
- Emadzadeh, A.A.; Speyer, J.L. Pulse Delay Estimation. In Navigation in Space by X-ray Pulsars; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- De Boer, P.T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Kroese, D.P.; Porotsky, S.; Rubinstein, R.Y. The cross-entropy method for continuous multi-extremal optimization. Methodol. Comput. Appl. Probab. 2006, 8, 383–407. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, C.; Tang, Q. CEGA: Research on Improved Multi-objective CE Optimization Algorithm. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018; pp. 2463–2467. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Zhou, J.; Wang, H.D.; Wei, J.L.; Liu, L.; Huang, X.C.; Gao, S.C.; Liu, W.P.; Li, J.P.; Yu, C.Y.; Li, Z.H. Adaptive moment estimation for polynomial nonlinear equalizer in PAM8-based optical interconnects. Opt. Express 2019, 27, 32210–32216. [Google Scholar] [CrossRef] [PubMed]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J. Particle Swarm Optimization. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; pp. 760–766. [Google Scholar] [CrossRef]
- Emadzadeh, A.A.; Speyer, J.L. On Modeling and Pulse Phase Estimation of X-Ray Pulsars. IEEE Trans. Signal Process. 2010, 58, 4484–4495. [Google Scholar] [CrossRef]
- Gendreau, K.; Arzoumanian, Z.; Adkins, P.; Albert, C.; Anders, J.; Aylward, A.; Baker, C.; Balsamo, E.; Bamford, W.; Benegalrao, S.; et al. The Neutron star Interior Composition Explorer (NICER): Design and Development; SPIE: Bellingham, WA, USA, 2016; Volume 9905. [Google Scholar]


| Parameters | Value |
|---|---|
| period/ms | 3.05 |
| /ph·s−1 | 1.93 |
| /ph·s−1 | 50 |
| Observation Period/s | Estimation Error of q/1 × 10−3 Cycle | Estimation Error of f/1 × 10−6 HZ | ||||||
|---|---|---|---|---|---|---|---|---|
| PSO | DE | CE | CE-Adam | PSO | DE | CE | CE-Adam | |
| 1000 | 0.958 | 1.04 | 0.957 | 0.94 | 1.7 | 1.90 | 1.69 | 1.68 |
| 2000 | 0.727 | 1.08 | 0.726 | 0.721 | 0.607 | 0.868 | 0.606 | 0.621 |
| 3000 | 0.567 | 1.04 | 0.565 | 0.567 | 0.319 | 0.585 | 0.318 | 0.325 |
| Methods | Estimation Error of q/1 × 10−3 Cycle | CPU Time/s |
|---|---|---|
| Proposed method | 0.95 | 26.4 |
| Linearized method | 1.2 | 8203.1 |
| Parameters | Value |
|---|---|
| period/ms | 33.4 |
| /ph·s−1 | 660 |
| /ph·s−1 | 13,860.2 |
| Parameters | Value |
| Epoch | 2018/12/26 00:31:03 |
| Semi-major axis/km | 677.0809 |
| Eccentricity | 0.0015 |
| Inclination/° | 51.6775 |
| Ascending node ascension/° | 142.3733 |
| Perigee auxiliary angle/° | 101.7365 |
| True anomaly/° | 161.7955 |
| Data | Duration | |
| data 1 | 07:58:39–08:34:35 | |
| data 2 | 09:31:20–10:07:16 | |
| data 3 | 11:04:01–11:40:14 | |
| data 4 | 12:36:41–13:12:44 | |
| data 5 | 14:09:20–14:45:27 | |
| data 6 | 15:42:00–16:18:11 | |
| data 7 | 17:14:41–17:50:53 | |
| data 8 | 18:47:20–19:23:35 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Y.; Zheng, W. On-Orbit Pulse Phase Estimation Based on CE-Adam Algorithm. Aerospace 2021, 8, 95. https://doi.org/10.3390/aerospace8040095
Wang Y, Wang Y, Zheng W. On-Orbit Pulse Phase Estimation Based on CE-Adam Algorithm. Aerospace. 2021; 8(4):95. https://doi.org/10.3390/aerospace8040095
Chicago/Turabian StyleWang, Yusong, Yidi Wang, and Wei Zheng. 2021. "On-Orbit Pulse Phase Estimation Based on CE-Adam Algorithm" Aerospace 8, no. 4: 95. https://doi.org/10.3390/aerospace8040095
APA StyleWang, Y., Wang, Y., & Zheng, W. (2021). On-Orbit Pulse Phase Estimation Based on CE-Adam Algorithm. Aerospace, 8(4), 95. https://doi.org/10.3390/aerospace8040095






