Rope-Hook Recovery Controller Designed for a Flying-Wing UAV

Abstract

Due to the complexity of landing environments, precision guidance and high-precision control technology have become key to the rope-hook recovery of shipborne unmanned aerial vehicles (UAVs). The recovery process was divided into three stages and a reasonable guidance strategy had been designed for them, respectively. This study separated the guidance and control issues into an outer guidance loop and an inner control loop. The inner loop (attitude control loop) controled the UAV to follow the acceleration commands generated by the outer loop (trajectory tracking loop). The inner loop of the longitudinal controller and the lateral controller were designed based on active disturbance rejection control (ADRC), which has strong anti-interference ability. In the last phase, the outer loop of the longitudinal controller switched from a total energy control system (TECS), which greatly decoupled the altitude channel and speed channel, to the proportional navigation (PN) guidance law, while the outer loop of lateral controller switches from the proportional control law based on the L₁ guidance law, which can reduce the tracking error and deviation, to the PN guidance law, which considerably enhances the tracking precision. Finally, the simulation data and flight test data show that the controller has strong robustness and good tracking precision, which ensures safe rope-hook recovery.

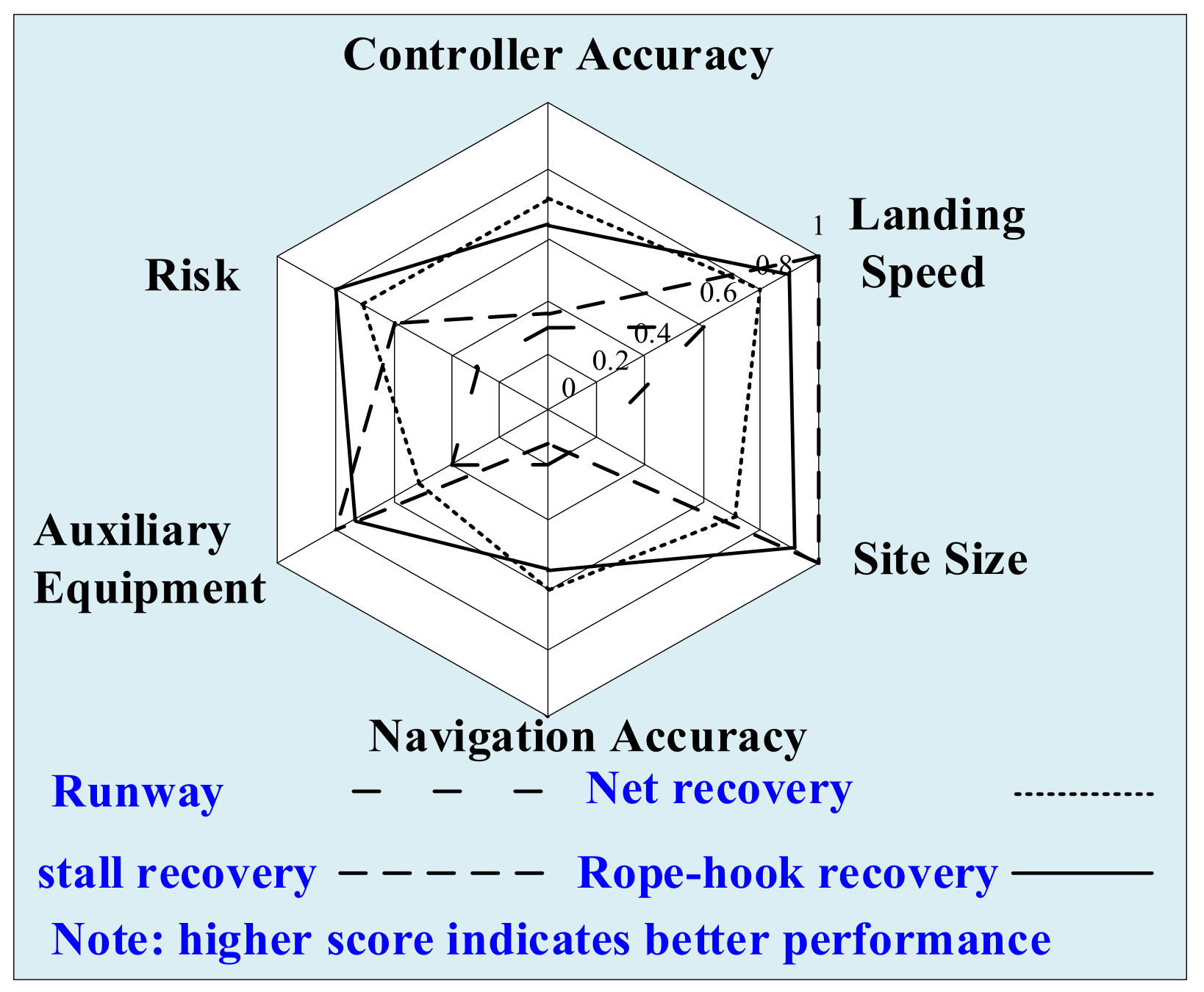
1. Introduction

Small shipborne fixed-wing unmanned aerial vehicles (UAVs) can be recovered in a variety of ways, and the reliability, flexibility and accuracy of these methods have become important indicators for evaluating the performance of UAVs [1,2,3,4]. Runway and barrier arrested recovery is mainly used for medium and large UAVs landing on large ships, requiring the UAV to have a high precision trajectory tracking ability and a strong anti-interference ability to vessel movement and wake flow. For UAVs that adopt the stall recovery mode, the angle of attack is considerably increased, resulting in a significant increase in resistance and a rapid decrease in speed. When the air speed falls below the stall speed, the UAV falls onto an elastic recovery net. The Osprey V22 and other fixed-wing UAVs with vertical take-off and landing (VTOL) capability activate the rotor system and switch to VTOL mode for landing, which is similar to the helicopter landing mode. The net recovery method requires UAV to fly into the center area of the net and hit the arresting net at the lowest speed through high precision navigation and positioning. The arresting rope of the vertical rope-hook recovery system is fixed to the side of the deck by the boom. When one wing of the UAV hits the arresting rope, the arresting rope slides into the self-locking device of the wing tip along the leading edge of the wing and is locked. The UAV performed rotational deceleration movement in a decreasing radius around the arresting rope, and finally hang stationary on the arresting rope. Figure 1 shows the characteristics of several typical recovery methods for small and medium-sized shipborne UAVs.

Figure 1 shows that vertical rope-hook recovery (Figure 2) is most suitable for small fixed-wing UAV [5]. Bornebusch presents a novel recovery method using two multirotor UAVs with a line suspended between them. Limited by the weight and length of the rope, this method is only suitable for fixed-wing UAVs with tiny take-off weights [6].

The shipborne recovery of miniature fixed-wing UAVs requires not only a high precision navigation system and guidance strategy, but also accurate control technology. Rope-hook recovery technology has evolved from net recovery technology. The mechanical design of the skyhook system has been researched by domestic and international scholars. The control technology is less publicized; however, the research on net recovery is fairly advanced. The authors of [7,8] established a multi-body dynamics simulation model of the rope hook recovery system, simulated the recovery arresting process, compared it with the experimental results, and verified the rationality of the model [7,8]. In another study, the authors adopted a multi-variable state feedback output tracking model reference adaptive control (MRAC) method to achieve the high-precision tracking control of UAVs in the shipborne landing stage [9,10]. A height controller based on the rate of height change, and a trajectory tracking controller based on track angle and lateral deviation, were proposed in [11,12,13]. At the same time, in order to enhance tracking accuracy, Li, K. designed the vessel motion compensation network [11]. The authors designed the inner loop angular rate control law and the outer loop height control law, respectively, by using the robust linear quadratic regulators (RLQRs) method. Zhang, M.X. proposed a position and attitude compensation control strategy combining an adaptive fast Fourier transform (FFT) disturbance prediction algorithm and fuzzy proportional integral differential (PID) control [14]. The work presented in Refs. [15,16,17] designed pseudo pursuit guidance law, angle of sight proportional guidance law and open-loop proportional navigation law to guide the UAV to the recovery net respectively, showing excellent engineering application feasibility.

In addition, the TECS and H∞ control theories were proposed to design the controller of the longitudinal carrier landing system in [18]. The authors adopted ADRC to design the longitudinal altitude and pitch attitude controllers in [19]. Zhao, D.H. applied the control method combining dynamic inverse and adaptive law to suppress the disturbance of vessel motion [20]. Sashank presented an approach angle constrained guidance law based on sliding mode control (SMC) for autonomous landing [21]. Liu, H.Y. designed the constant angle of attack power compensation control for the engine channel [22]. The authors proposed an aircraft carrier landing control law based on adaptive dynamic inversion, and modified the adaptive law using the Lyapunov stability principle in [23].

In this study, the rope-hook recovery scheme includes navigation, guidance and control, which are interdependent and must be highly coordinated to complete the high-precision recovery of UAVs. The global positioning system (GPS) was used for navigation, and guidance strategies were designed for each phase of recovery. Longitudinal and lateral trajectory tracking control laws for the first two stages were designed based on the TECS and L₁ guidance. In the last phase, the trajectory error was converted into the inner loop attitude control instruction using the proportional guidance control law used in missile pursuit.

2. Navigation and Guidance

The flying wing UAV (see Figure 3) studied in this paper is a miniature fixed-wing UAV with a low cruising speed, light mass and a large aspect ratio swept wing. The detailed parameters are shown in

Table 1. Specification of fixed-wing unmanned aerial vehicle (UAV).

Specification	Value
Wingspan	4.9 m
Wing area Maximum takeoff weight Mean aerodynamic chord	2.9 m2
	60 kg
	0.49 m
Cruising speed	30 m/s

.

The rope-hook recovery system moves with the vessel and with environmental disturbances, such as gusts, so the guidance strategy shown in Figure 4 was adopted in this paper. After receiving the landing instruction, the UAV returns to the airspace near the vessel under the guidance law, spirals down, and consumes potential energy. When the UAV descends to the approach altitude, it further adjusts the lateral position and heading, while following the height command. The UAV crashes into the impact point area of the rope-hook in the final phase to achieve high precision recovery.

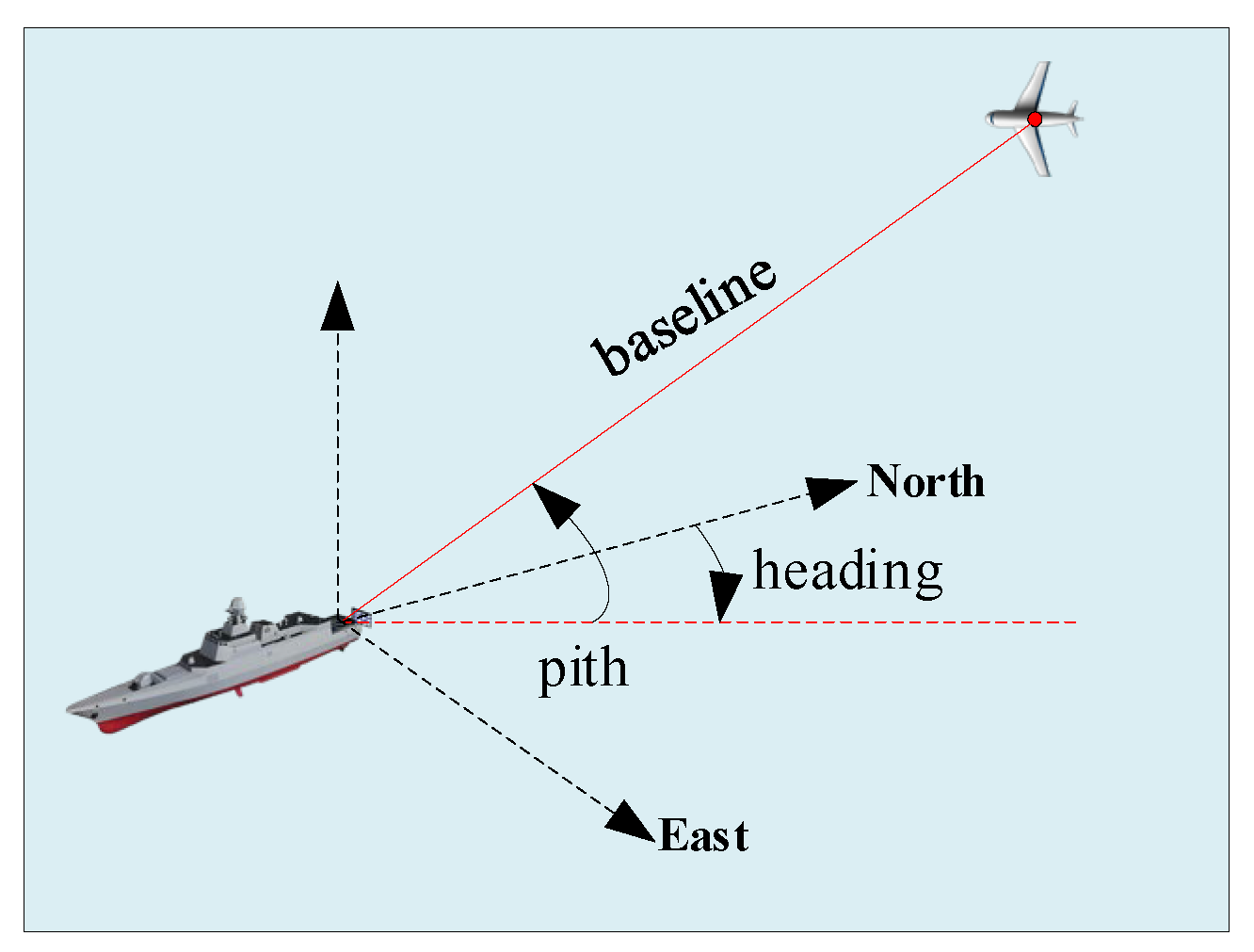
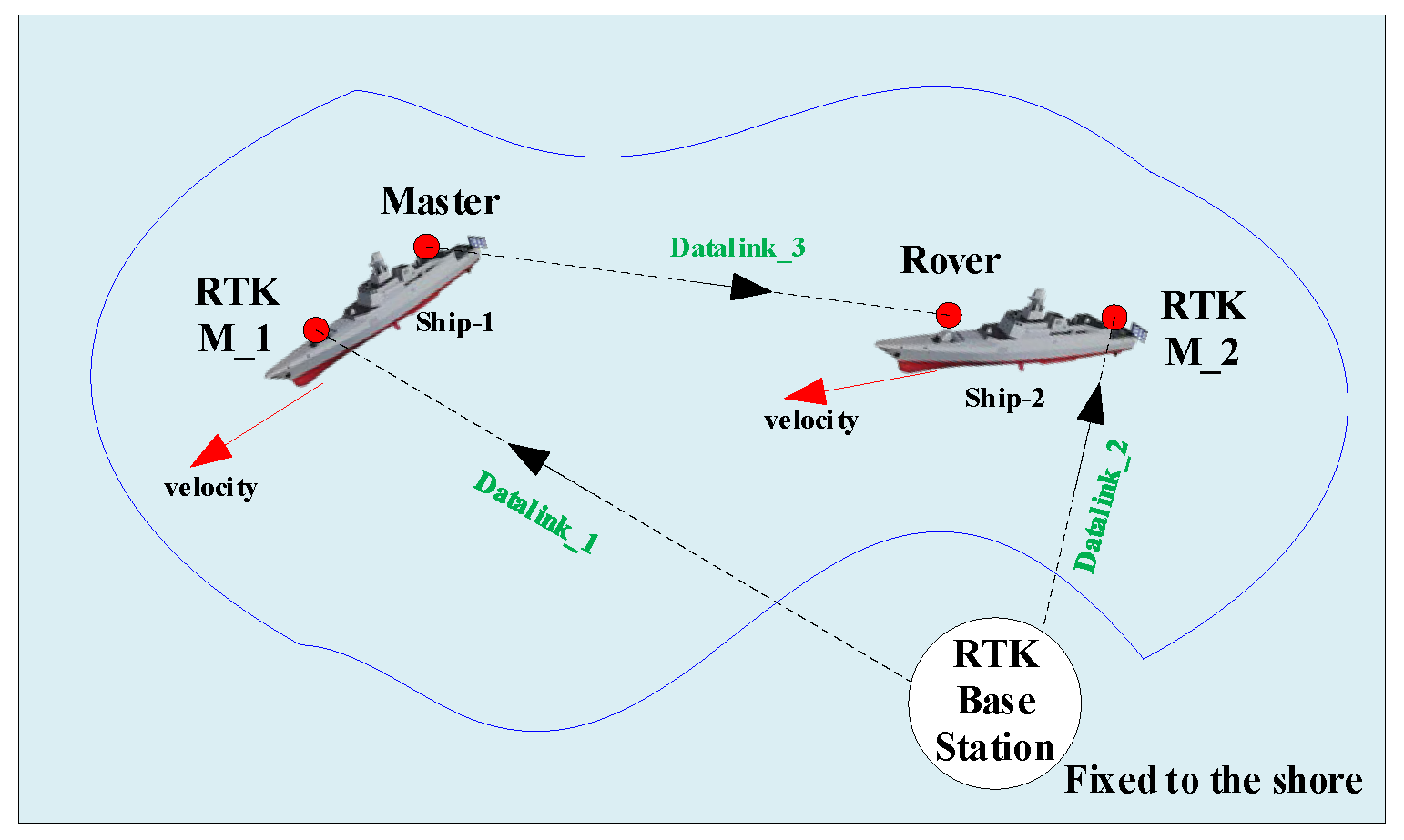
2.1. Navigation

The high-precision rope-hook recovery of UAVs is premised on high-precision navigation data. The purpose of the navigation is to obtain the relative position and attitude information between the UAV and the rope-hook in real time. The global positioning system (GPS) is not limited by weather or the environment, and can achieve all-weather, high-precision, continuous, real-time navigation. In particular, Novatel’s high-performance, miniaturized GPS navigation equipment is particularly suitable for small-sized UAVs with limited load capacity; therefore, this study used the GPS for navigation, including for ground and airborne equipment.

According to the position model, the GPS is divided into single-point positioning and differential GPS.

(1)

Single-point positioning

A GPS receiver was installed on the moving UAV and the ship to obtain their absolute position information, respectively. Next, the UAV calculated the relative position information by receiving the longitude, latitude and altitude information from the ship through datalink. Single-point GPS is not limited by distance; however, due to errors from sources such as satellite clocks and ephemerides, as well as ionospheric and tropospheric delays, its positioning accuracy is poor, usually in the order of meters.

(2)

Differential GPS

A GPS mobile station was positioned on the UAV, and a GPS base station was installed on the ship. The mobile station received differential correction data from the reference station to correct its GPS positioning information in real time, weakening the impact of relevant errors, and accurately measuring the relative heading and baseline between them, as shown in Figure 5. The typical applications of this technology are RTK mode and ALIGN mode; however, the former base station can only be fixed on stationary objects, while the latter can be applied to moving objects. The data update frequency of ALIGN mode is up to 20 Hz, the heading direction accuracy of the 2 m baseline is 0.1° and the relative positioning accuracy can be up to the centimeter level; however, the effective range is within 30 km.

In this study, considering the mission characteristics, accuracy requirements and feasibility of each recovery stage, the single-point mode was used for the guided capture stage, while the ALIGN mode was used for the last two phases.

(3)

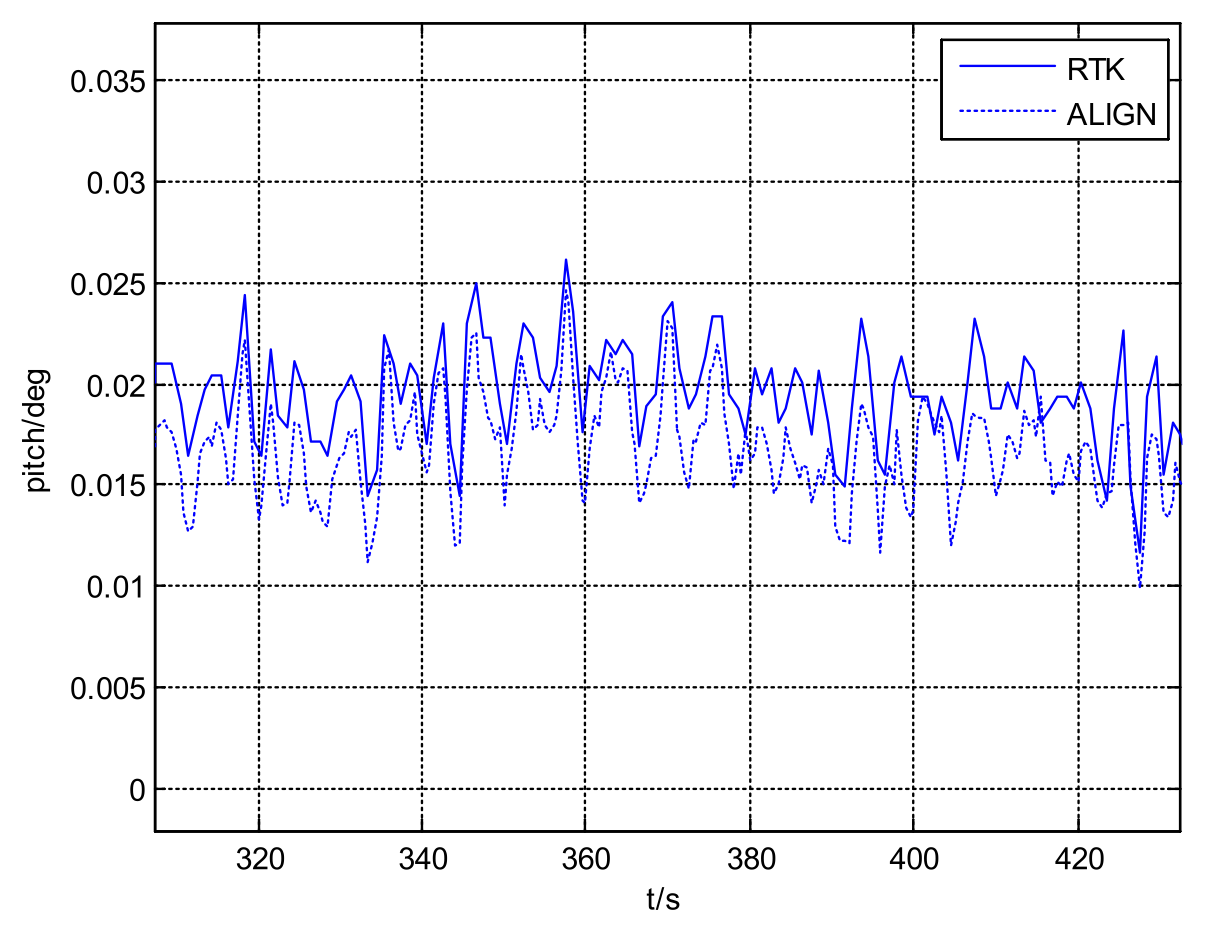
ALIGN Precision test

The positioning accuracy of RTK (real-time kinematic) can be up to the centimeter level, and can be used as standard data. Ship No. 1 was equipped with an ALIGN base station (Master) and an RTK mobile station M_1, while an ALIGN mobile station (Rover) and an RTK mobile station M_2 were installed on Ship No. 2. A RTK base station was fixed on the shore. The schematic diagram is represented in Figure 6.

The master corrected data was transmitted to rover through datalink 3. We could receive the pitch, heading and baseline of the two ships directly. RTK mobile stations received the correction data from the base station through datalink 1 and datalink 2 to correct their positioning data, respectively. By processing the positioning data of the two ships, the relative position information could be obtained indirectly.

Figure 7 and Figure 8 show the positioning data comparison obtained in the two modes. The heading difference between the ALIGN mode and the RTK mode was within 0.1°, and the baseline difference was within 0.1 m. The ALIGN mode has high positioning accuracy and its base station can be moved, which is highly suitable for rope-hook recovery on the moving ship.

2.2. Guidance

(1) Guided capture phase: the initial position and heading of the UAV were arbitrary. The UAV maintained the current flight altitude, tracked the real-time trajectory based on the planned Dubins curve, and returned to the vicinity of the spiral circle as soon as possible with the shortest distance. The heading command is the tangential heading between the current position and the spiral circle. As the vessel moves, the center of the spiral circle moves with it, so the heading instructions need to be updated in real time. Figure 9 presents the return trajectories of a UAV with different initial positions and headings.

(2) Spiral descent phase: the UAV followed a circular trajectory with a fixed radius and made heading adjustments while spiraling down. The relative position of the spiral circle and the vessel in the x-y plane was fixed (see Figure 10), so the circular trajectory needed to be updated in real time according to the location of the vessel. The position of the center of the circle (C) can be calculated using Equation (1):

$$\begin{array}{l}{x}_c=x_0-\sqrt{R^2+L_3{}^2}\cos \left({\zeta }_1+{\zeta }_2\right)\\ y_c=y_0+\sqrt{R^2+L_3{}^2}\sin \left({\zeta }_1+{\zeta }_2\right)\\ {\zeta }_1=\arctan \frac{R}{L_3}\end{array}$$

(1)

where $\left(x_c,y_c\right)$ is the position of the center of the circle; $\left(x_0,y_0\right)$ is the position of the rope-hook; R is the spiral radius; L₃ is the length of PN phase; and ${\zeta }_2$ is the angle between the rope-hook velocity vector and the x axis.

The spiral radius R can be obtained using Equation (2):

$$R=\frac{V^2}{g\tan {\varphi }_c}$$

(2)

where V is the cruising speed of the UAV and ${\varphi }_c$ is the roll command when turning. If this value is too large, the UAV will tilt at a large angle, the lateral and longitudinal coupling will be strengthened, and the nonlinear characteristics will be enhanced, which will lead to a decrease in trajectory tracking accuracy. On the other hand, the required radius will be large and not suitable in various narrow recovery environments. In this study, the rope-hook recovery was implemented at sea with sufficient airspace. In addition, in order to reduce the coupling and improve the trajectory tracking accuracy, the roll command was selected as 15 degrees, and the radius was approximately 330 m according to Equation (2). When the height of the UAV reached the designed height (60 m relative to the impact point) and the heading was consistent with the vessel’s heading, or the deviation was within a certain threshold, it flew away from the spiral circle in the tangential direction. If the height was satisfied but the heading was not, the UAV continued to hover at that height until the heading requirements were met and the UAV cut out.

(3) Proportional guidance phase: the distance to go (DTG, L₃) for the PN phase was a fixed value, which needed to be designed. Combined with the aerodynamic characteristics of the UAV, the glide state was balanced at the current flight altitude and cruising speed. The flight path angle was critical. If this value is too small, the projected area of the rope-hook system in the vertical plane will be reduced and the recovery difficulty will be increased. On the other hand, the height will drop very slowly and the recovery time will be increased. World-renowned UAVs, such as the Global Hawk and Israel’s “Heron”, typically track a straight path with a glide slope angle of −2~−5° when landing [24,25]. Considering the long period of convergence time for the UAV system, the PN phase guidance time must be at least 10 times the maximum time constant of each dynamic link in guidance systems. In this study, the parameters of the PN phase were designed as follows: the air speed was the cruising speed (30 m/s), the flight path angle was −2.865°, and the duration was 40 s. After calculation, the initial height of the UAV in the PN phase relative to the rope-hook system was +60 m, and the baseline was L₃ = 1200 m. The UAV maintained speed and made further heading adjustments, perpendicular to the plane of the rope-hook and boom. If the rope-hook was stationary, the ideal flight path was a straight line with a fixed glide angle of −2.865°; otherwise, it is a curve with an increasing radius of curvature. If the UAV does not hit the rope, it goes around as planned.

3. Controller Design

In this study, we make the following assumptions:

(1)

The UAV is rigid and its mass is constant;

(2)

The earth-surface inertial reference frame is an inertial coordinate system;

(3)

The curvature of the earth is ignored and the earth is flat;

(4)

The acceleration of gravity does not change with flight altitude;

(5)

The UAV is not only symmetrical in geometry, but also in internal mass distribution, that is, the product of inertia I_xy = I_zy = 0;

(6)

Ignoring the longitudinal and lateral motion coupling, the motion of the UAV is divided into independent longitudinal motion and lateral motion.

According to these assumptions, it was possible to design the controller. In most actual flight applications, the separate inner and outer loop approach is more commonly taken. The longitudinal and lateral controller structures designed in this study are shown in Figure 11a,b, respectively.

The inner loop of the longitudinal controller is the pitch angle control controller based on ADRC [26], which can increase the stability and realize the tracking of the pitch angle. The outer loop adopts the TECS to realize the decoupling of the altitude channel and the velocity channel in the first two phases, then it switches to PN law when the DTG is less than 1200 m.

The control law of the inner loop consists of the Dutch roll damper, which increases the Dutch roll stability, and the roll angle control loop based on ADRC. The outer loop is the flight path control loop based on L₁ guidance law. In the last phase, it switches to PN law.

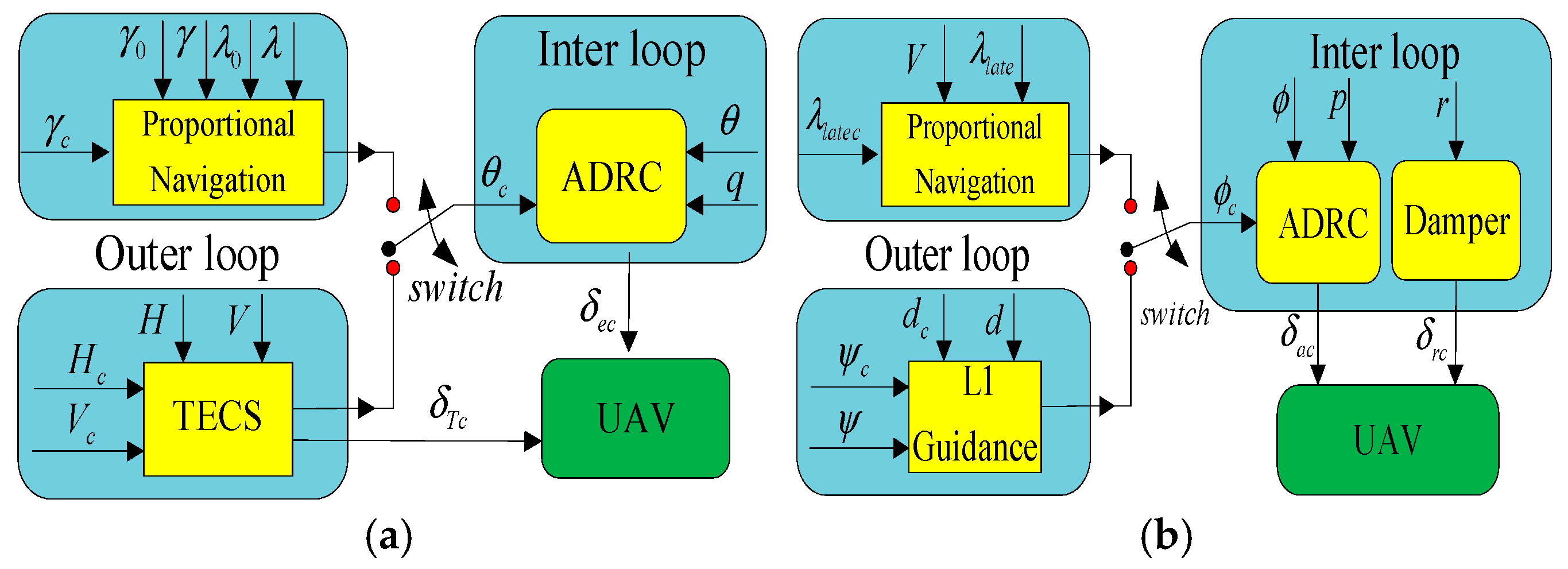
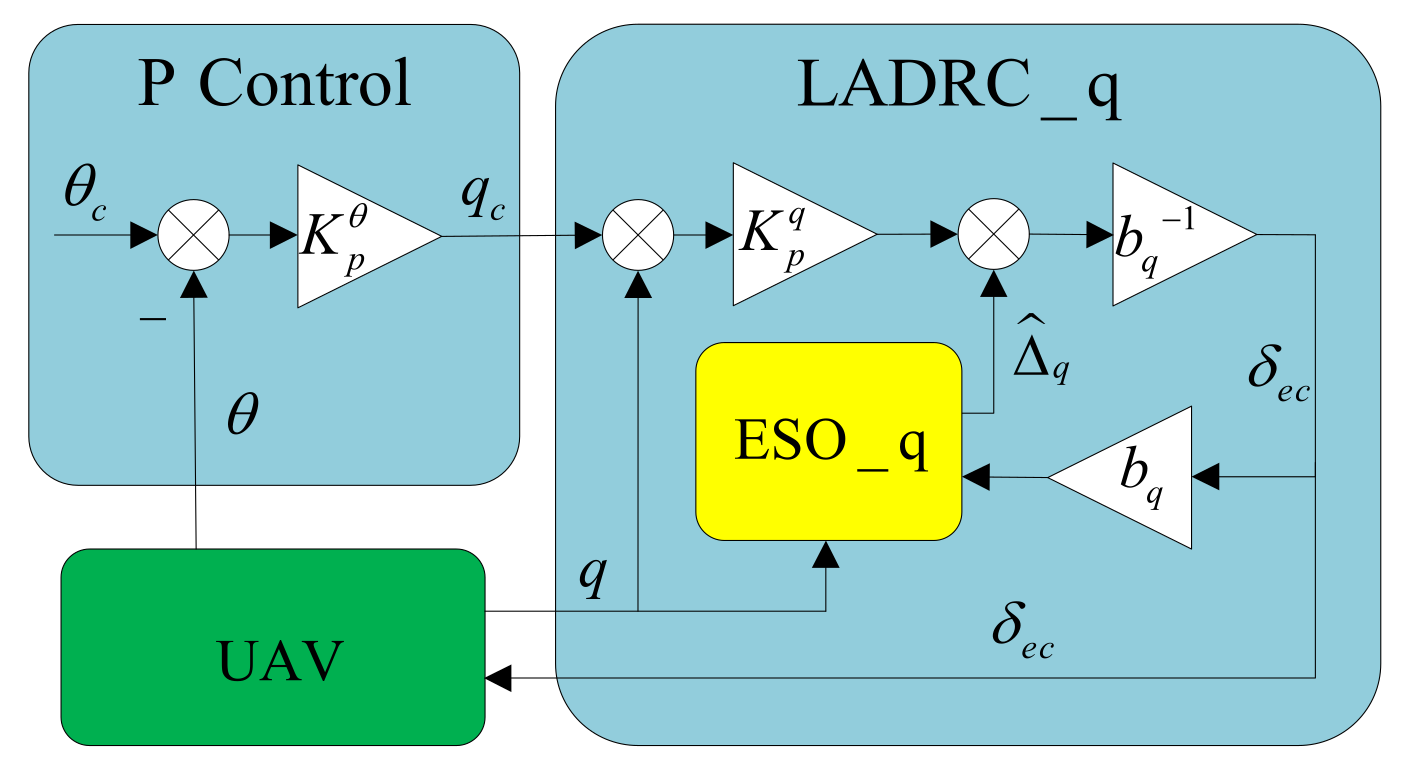
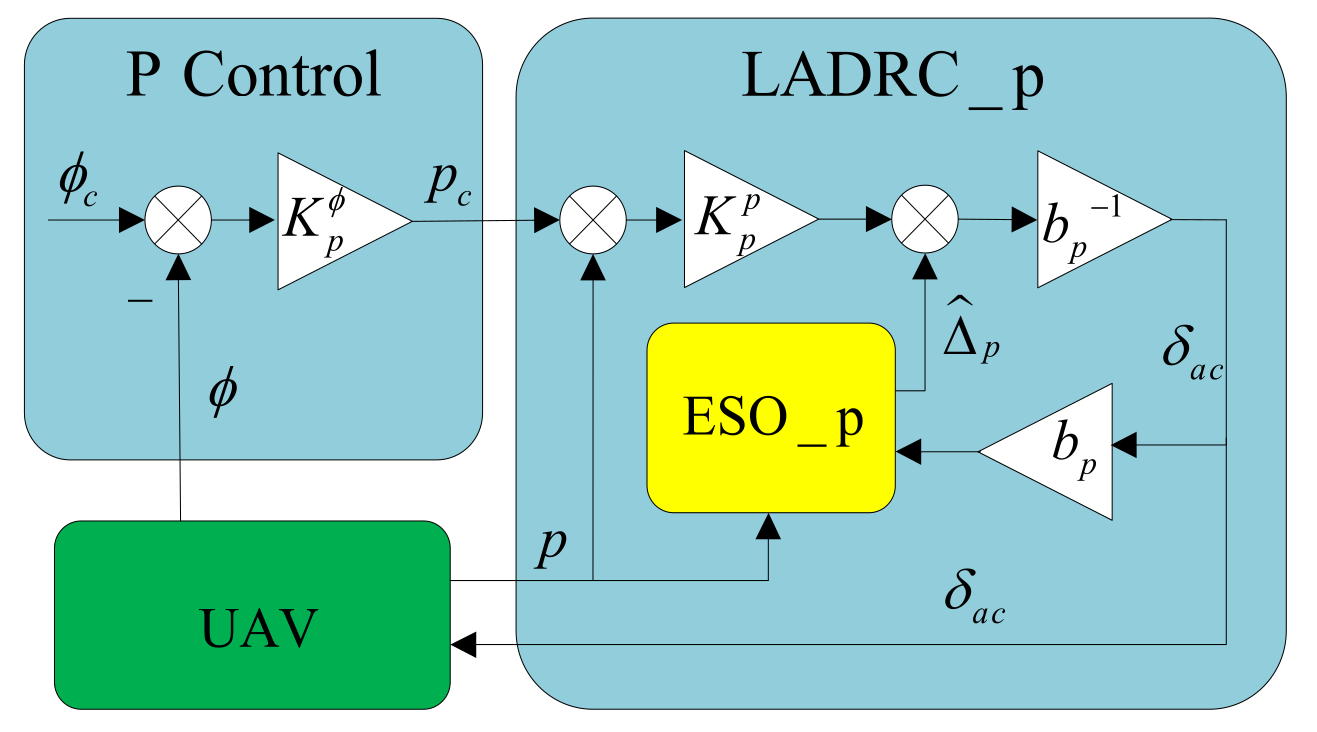
3.1. Attitude Controller Design

According to the principle of time-scale separation, the pitch angle controller is a dual-loop control structure (attitude angle control loop and angular rate control loop) (see Figure 12). The control law of the pitch angle loop adopts a proportional controller and outputs the pitch angular rate command, which can be designed as per Equation (3):

$$q_c=k_{p\theta }^{}({\theta }_c-\theta )$$

(3)

where $k_{p\theta }$ is the proportional gain, and $\theta$ and ${\theta }_c$ are pitch and pitch command, respectively.

The output of the pitch angular rate control loop is the elevator command ${\delta }_{ec}$, in the form of Equation (4):

$${\delta }_{ec}=b_q{}^{-1}(k_{pq}^{}(q_c-q)-{\widehat{\Delta }}_q)$$

(4)

where ${\widehat{\Delta }}_q$ is the estimation of the unmodeled dynamic system, including external interference, modeling error and other factors of the angular rate loop by the second-order extended state observer (ESO); $k_{pq}$ is the proportional gain; and $b_q$ is the control input gain from the elevator to pitch angular rate, the expression of which is as follows:

$$b_q=I_y^{-1}{q}_{s}S{c}_A{C}_M^{{\delta }_e}$$

(5)

where $I_y$ is the moment of inertia about the y axis; $q_s$ is the dynamic pressure; $S{c}_A$ is the effective elevator surface; and $C_M^{{\delta }_e}$ the coefficient of pitching moment.

A second-order ESO is designed to observe the total disturbance ${\Delta }_q$, see Equation (6) for details:

$$\begin{array}{l}\dot{\widehat{q}}={\widehat{\Delta }}_q-{\beta }_{1q}\left(\widehat{q}-q\right)+b_q{\delta }_{ec}\\ {\dot{\widehat{\Delta }}}_q=-{\beta }_{2q}\left(\widehat{q}-q\right)\end{array}$$

(6)

where ${\beta }_{1q}$ and ${\beta }_{2q}$ are the parameters of the ESO, which are usually a function of the observer bandwidth ${\omega }_q$:${\beta }_{1q}=2{\omega }_q$, ${\beta }_{2q}={\omega }_q{}^2$; and $\widehat{q}$ is the estimation of $q$.

Similar to the longitudinal attitude controller, one of the laterals is also designed based on ADRC (see Figure 13).

The control law of the roll angle loop adopts proportional control and outputs the roll angular rate command $p_c$, which can be designed as per Equation (7):

$$p_c=k_{p\varphi }^{}({\varphi }_c-\varphi )$$

(7)

where $k_{p\varphi }$ is the proportional gain; and $\varphi$ and ${\varphi }_c$ are roll and roll command, respectively.

The output of the roll angular rate control loop is the aileron command ${\delta }_{ac}$; see Equation (8):

$${\delta }_{ac}=b_p{}^{-1}(k_{pp}^{}(p_c-p)-{\widehat{\Delta }}_p)$$

(8)

where ${\widehat{\Delta }}_p$ is the estimation of the unmodeled dynamic system of the angular rate loop by the second-order ESO; $k_{pp}$ is the proportional gain; and $b_p$ is the control input gain from the aileron to the roll angular rate, the expression of which is as follows:

$$b_p=I_x^{-1}{q}_{s}S{c}_A{C}_R^{{\delta }_a}$$

(9)

where $I_x$ is the moment of inertia about the x axis; and $C_R^{{\delta }_a}$ is the coefficient of rolling moment. A second-order ESO is designed to observe the total disturbance ${\Delta }_p$:

$$\begin{array}{l}\dot{\widehat{p}}={\widehat{\Delta }}_p-{\beta }_{1p}\left(\widehat{p}-p\right)+b_p{\delta }_{ac}\\ {\dot{\widehat{\Delta }}}_p=-{\beta }_{2p}\left(\widehat{p}-p\right)\end{array}$$

(10)

where ${\beta }_{1p}$ and ${\beta }_{2p}$ are the parameters of the ESO, which are usually a function of the observer bandwidth ${\omega }_p$:${\beta }_{1p}=2{\omega }_p$, ${\beta }_{2p}={\omega }_p{}^2$; and $\widehat{p}$ is the estimation of $p$.

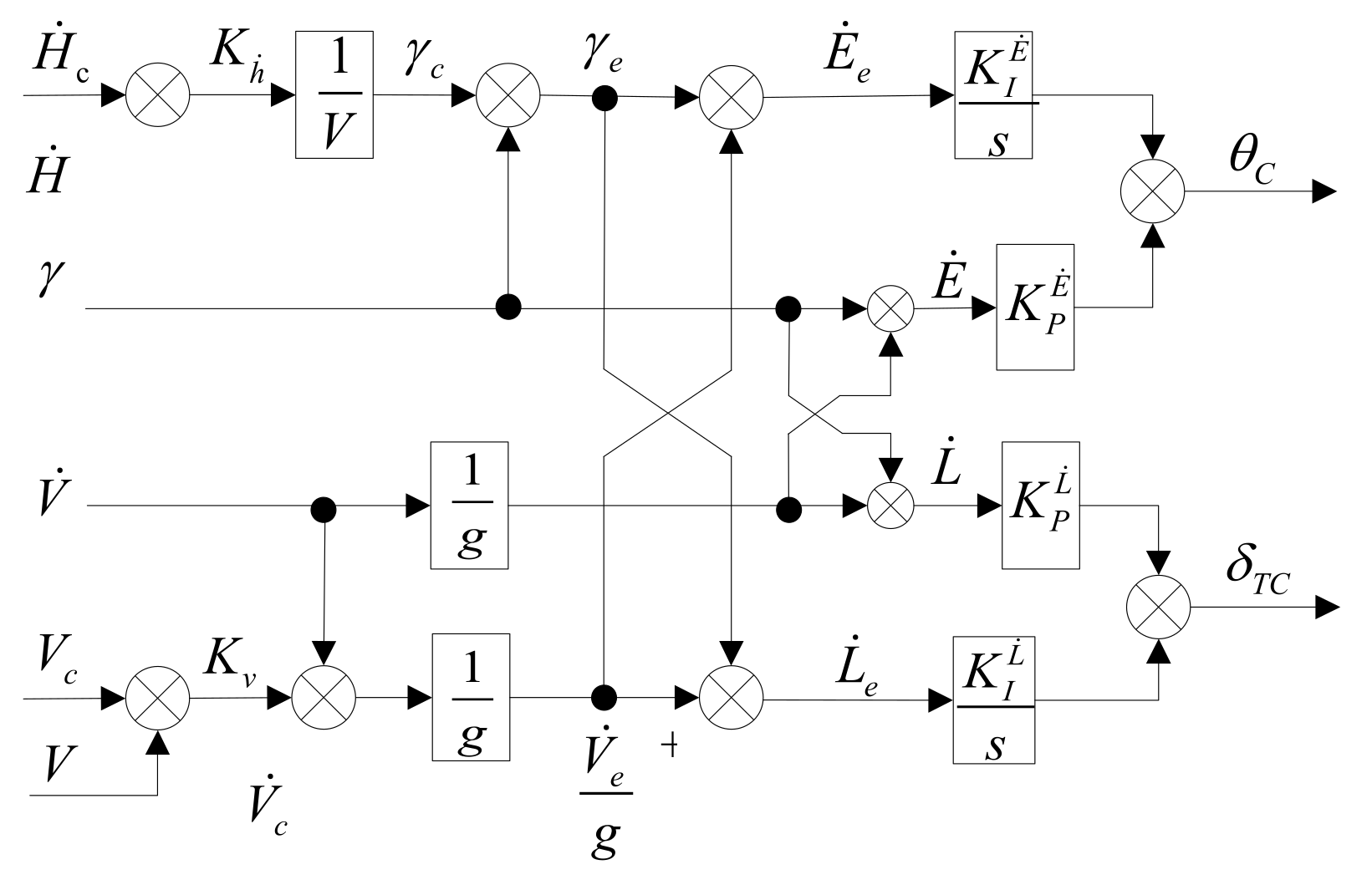
3.2. Height Controller Based on TECS

In 1987, the TECS was tested on a highly modified Boeing B737 by Boeing commercial airplane company. The TECS adopts the coordinated control of the throttle and the elevator: the throttle controls the total energy, and the elevator distributes the kinetic energy and the potential energy. Thus, the control channels of the flight path angle and speed are decoupled [27]. In 2013, Lambregts improved the traditional TECS by changing the control output of the energy distribution loop from the elevator to the pitch angle to increase damping against pitch oscillations generated by the TECS system, which was applied in the commercial open source flight control PX4 [28,29].

To ensure the same response to both speed and flight path angle $\gamma$ changes, the proportional and integral gains of throttle and pitch angle control law should be identical. The TECS formulas are shown in Equation (11) and the schematic diagram is shown in Figure 14:

$$\begin{array}{c}{\delta }_{Tc}=K_P^{\dot{E}}\dot{E}+K_I^{\dot{E}}{\displaystyle \int {\dot{E}}_e}dt\\ {\theta }_c=K_P^{\dot{L}}\dot{L}+K_I^{\dot{L}}{\displaystyle \int {\dot{L}}_e}dt\\ \dot{E}=\frac{\dot{V}}{\mathrm{g}}+\gamma ,\dot{L}=\frac{\dot{V}}{\mathrm{g}}-\gamma \\ {\dot{E}}_e=\left(\frac{K_V\left(V_c-V\right)}{\mathrm{g}}-\dot{V}\right)+\left(\frac{K_{\dot{h}}\left({\dot{H}}_c-\dot{H}\right)}{V}-\gamma \right)\\ {\dot{L}}_e=\left(\frac{K_V\left(V_c-V\right)}{\mathrm{g}}-\dot{V}\right)-\left(\frac{K_{\dot{h}}\left({\dot{H}}_c-\dot{H}\right)}{V}-\gamma \right)\end{array}$$

(11)

where $\dot{E}$ and ${\dot{E}}_e$ are the total energy rate and the total energy rate error, respectively; $\dot{L}$ and ${\dot{L}}_e$ are the energy rate distribution and the energy rate distribution error, respectively, $K_P^{\dot{E}}$ and $K_I^{\dot{E}}$ are the throttle proportional and integral gains, respectively; $K_P^{\dot{L}}$ and $K_I^{\dot{L}}$ are the pitch angle proportional and integral gains, respectively; $\dot{V}$ is the rate of change of velocity; $K_V$ is the proportional gain; and $K_{\dot{h}}$ is the proportional gain of the rate of change in height.

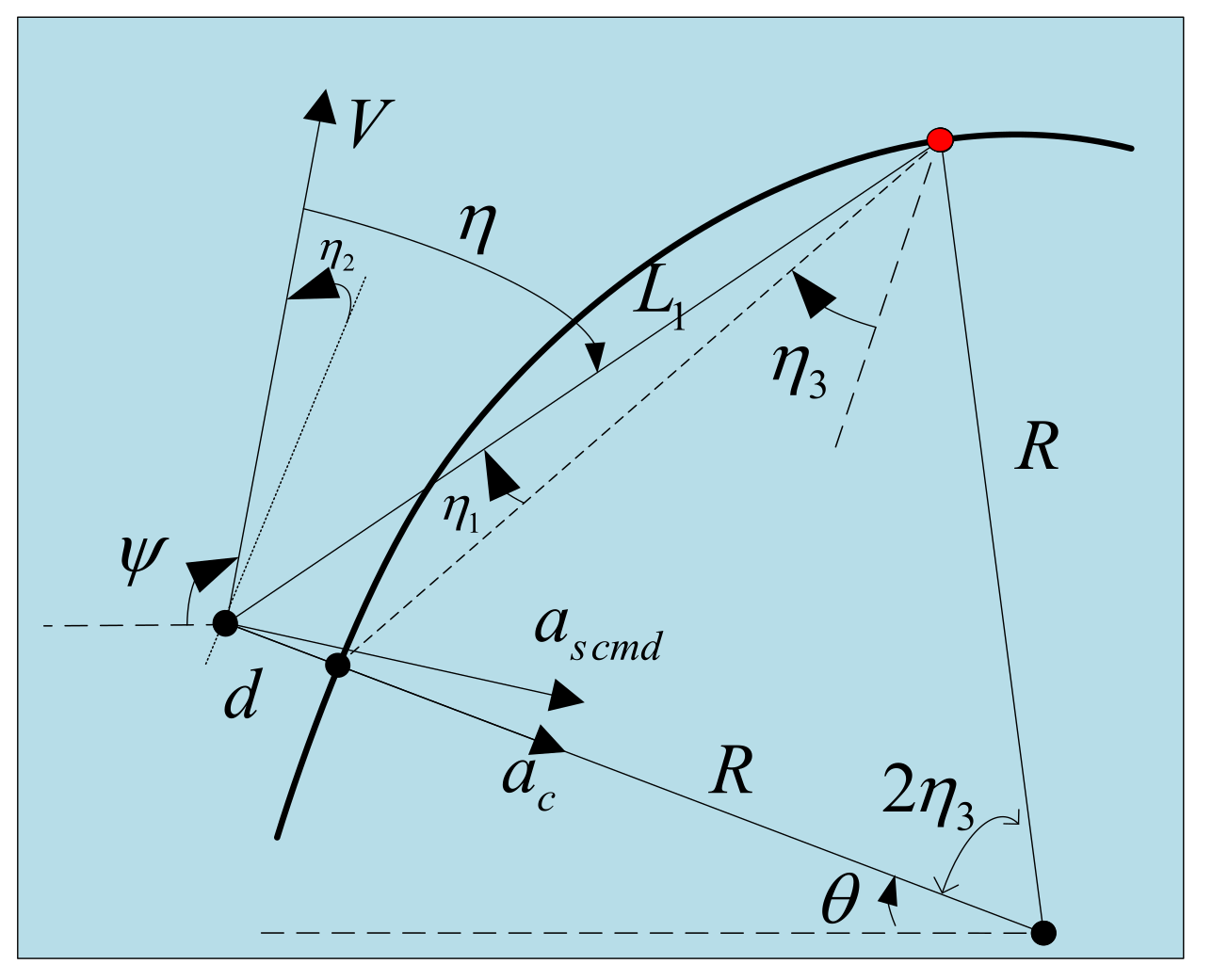
3.3. L₁ Guidance Law for Lateral

The lateral trajectory tracking control loop, a nonlinear guidance logic, is a proportional-derivative controller of lateral deviation and an element of anticipatory control, enabling tight tracking when following curved paths [30] (see Figure 15).

Where L₁ is the distance from the UAV position to a reference point on a desired trajectory; η is the angle from V to the line L₁; a_scmd is the acceleration command sideways; d is the cross-track error; and R is the radius of the circular segment.

Assuming that ${\eta }_1\approx 0,{\eta }_2\approx 0,{\eta }_3\gg 0$, then the lateral acceleration command is approximately equal to the centripetal acceleration to follow the circle with radius R at speed V:

$$\begin{array}{l}{a}_{scmd}=2\frac{V^2}{L_1}\sin \left({\eta }_1+{\eta }_2+{\eta }_3\right)\\ \approx 2\frac{V^2{c}^2}{L_1{}^2}d+2\frac{Vc}{L_1}\dot{d}+\frac{V^2}{R}\end{array}$$

(12)

where $c=\cos {\eta }_3=\sqrt{1-{\left(\frac{L_1}{2R}\right)}^2}$.

The lateral acceleration is expressed as:

$$a_{scmd}\approx V\dot{\psi }\approx V\left(\dot{\theta }-{\dot{\eta }}_2\right)=\frac{V^2}{R}-\ddot{d}$$

(13)

Combining Equations (12) and (13):

$$\ddot{d}+2\xi \varpi \dot{d}+{\varpi }^{2}d=0$$

(14)

where the damping ratio is $\xi =0.707$ and the natural frequency is $\varpi =\sqrt{2}\frac{Vc}{L_1}$, which is determined by V and L₁. As time approaches infinity, the lateral deviation converges to 0.

The desired lateral deviation adjustment time with an error margin of 2% is as follows:

$$t_s=\frac{\sqrt{2}\pi }{\xi \varpi }=\frac{\sqrt{2}\pi L_1}{Vc}$$

(15)

On the other hand, the lateral acceleration generated by the lateral force during roll action can be expressed as:

$$a=g\tan \varphi$$

(16)

The expression of the track control law is as follows:

$${\varphi }_c=\arctan \left(\frac{4{\pi }^2}{g{t}_s{}^2}d+\frac{2\sqrt{2}\pi }{g{t}_s}\dot{d}+\frac{V^2}{gR}\right)$$

(17)

The proportional and differential gains for cross-track error are variable gains, which are related not only to the distance L₁, but also to the flight speed, adding adaptive capability to the change in speed due to external disturbances, such as wind. At the same time, there is a compensation element of anticipation for the forthcoming local desired flight path.

In the Dutch roll damping loop, the yaw angular rate signal first passes through a high-pass filter to eliminate the low-frequency signal generated by the rolling motion during turning, and then adopts proportional control to act on the aileron. The control law is as follows:

$${\delta }_{rc}=K_P^r r$$

(18)

where $K_P^r$ is the damping loop gain and $r$ is the yaw angular rate.

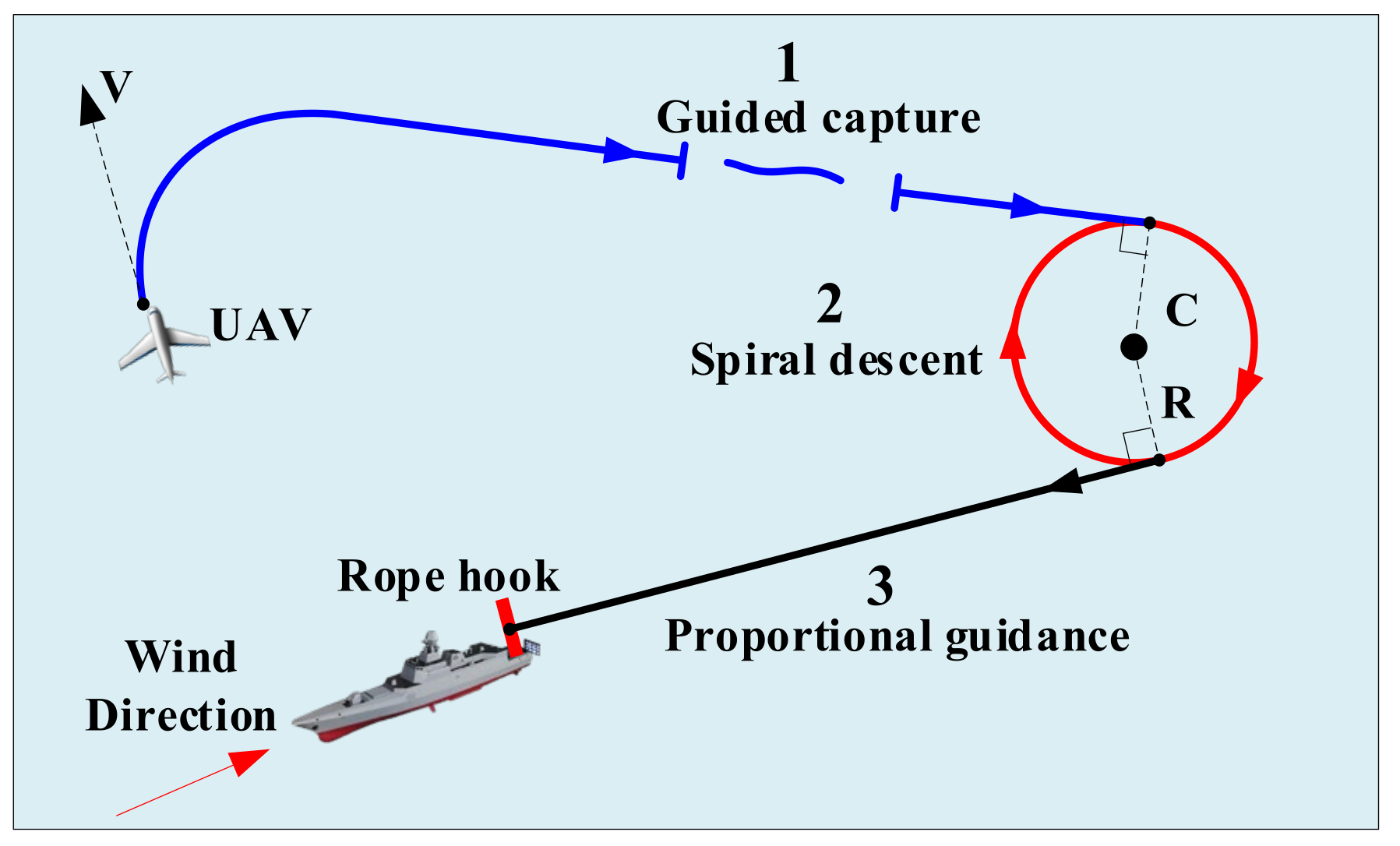
3.4. Terminal PN Law

Proportional navigation generally provides the best performance, with less control effort, in constant velocity intercepts, and it is widely accepted as the preferred method of guidance. Rope-hook recovery involves a constant velocity moving target tracking problem, so proportional navigation law is recommended, which has the advantages of a straight trajectory, a slight overload, good robustness and high guidance accuracy.

Proportional navigation is a guidance method where the rotational angular rate of missile velocity vector is proportional to the rotational angular rate of target line of sight (LOS):

$$\dot{\sigma }=K_{PN}\dot{q}$$

(19)

where $\dot{q}$ is the angular rate of LOS; $\dot{\sigma }$ is the angular rate of UAV velocity vector V; V_R is the target velocity vector; r is the distance between the UAV and the target; and K_PN is the guidance ratio, as shown in Figure 16 [17].

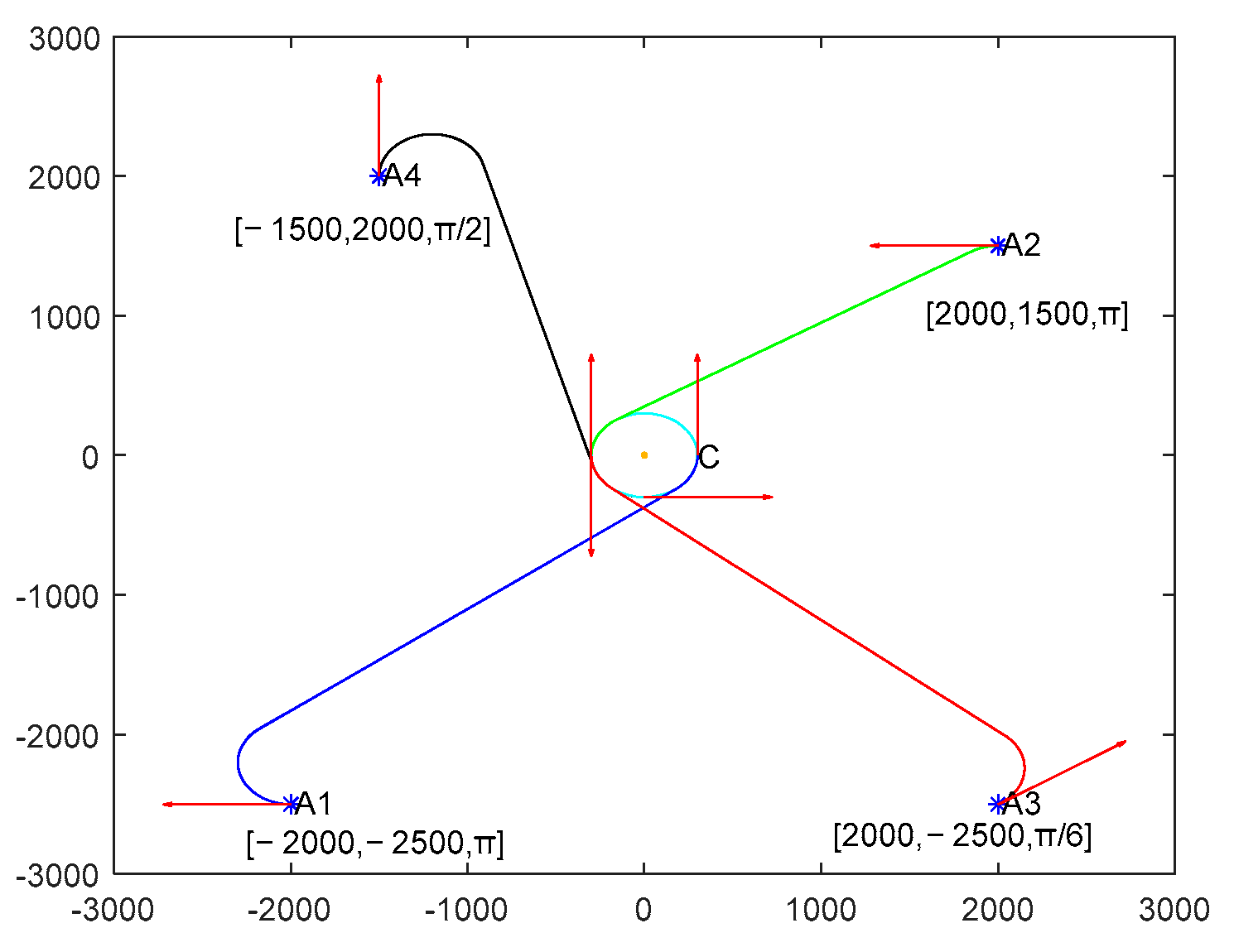
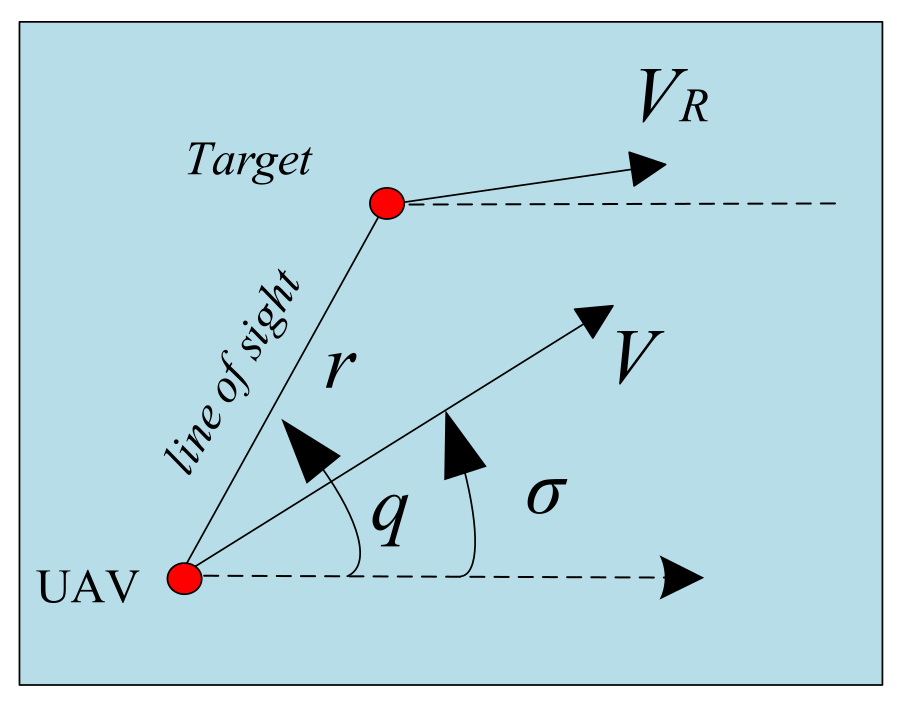
3.4.1. PN Law Based on Overload Control

PN law based on overload control consists of an overload feedback loop and an angle rate damping loop, driving the elevator and rudder deflection according to the pitch rate and the heading rate of LOS between the missile and the target, changing the angle of attack and sideslip angle, and generating in the normal force and the lateral force. The normal overload command is as follows:

$$n_c=\frac{a_n}{g}=\frac{V\dot{\sigma }}{g}=\frac{V{K}_{PN}}{g}\dot{q}$$

(20)

The longitudinal closed-loop PN law based on overload control is as follows:

$${\delta }_{ec}=K_e^n(n_c-n)+K_e^{q}q+{\delta }_{ectrim}$$

(21)

where $n$ is normal overload; $K_e^n$ is the gain from the normal overload to elevator; and ${\delta }_{ectrim}$ is the trim elevator deflection in a stable gliding state. However, in practical engineering applications, engine vibration brings great noise to the acceleration signal, which makes the sensor error larger, and directly affects the guidance accuracy. If the data is filtered, there will be a large phase delay. The normal and lateral overload data of the PN phase obtained by the sensors are shown in Figure 17.

Dynamic hook-recovery is similar to missile target tracking, so the PN law can be used for reference. However, due to the different characteristics of UAVs and missiles, the constraints of UAVs in attitude, trajectory, available overload and other conditions are much stricter than those of missiles. Therefore, it is necessary to comprehensively consider UAV performance, operating environment, sensors, external interference and other factors to obtain an improved control law suitable for UAVs. In this study, the PN law based on overload control was improved to be based on attitude control: the output of the guidance loop was input to the inner loop attitude angular rate loop, and then the deflection control quantity of the elevator and the rudder were generated (see Section 3.4.1 and Section 3.4.2).

Due to the limitation of the wing span length and the vertical length of the arresting cable, the impact point accuracy of rope-hook recovery was strictly required. The vertical error and horizontal error must be within ±2 m, so the miss distance of the terminal was taken as the control performance index. The smaller the absolute value of miss distance, the higher the terminal recovery accuracy.

In this section, we make the subsequent assumptions:

(1)

The guidance law is based on the basic assumption of biplane decoupling. After heading correction, the UAV and the ship are in the same longitudinal motion plane. When conducting lateral guidance, the UAV and the ship are in the same lateral motion plane;

(2)

The motion of the UAV and the ship are particle motion in a two-dimensional plane;

(3)

Both the UAV and the ship move at a constant speed, and the ship moves in a straight line;

(4)

The response delay of the flight control system and the actuator is ignored.

According to these assumptions, it is possible to design the proportional guidance law for longitudinal and lateral parts.

3.4.2. Longitudinal PN Law

In the vertical motion plane, the motion and location relationship between the UAV and the rope-hook is shown in Figure 18.

Equation (22) can be obtained from the proportional navigation law.

$$\dot{\gamma }=K_{PN}\dot{\lambda }$$

(22)

where $\dot{\lambda }$ is the angular rate of the LOS; $\dot{\gamma }$ is the flight path angular rate; V_R is the target velocity vector; and r is the distance between the UAV and the rope-hook. The line of sight angle can be obtained from the geometry of the UAV and the rope-hook system, as shown in Equation (23):

$$\lambda =\arctan \left(\frac{z-z_r}{x-x_r}\right)$$

(23)

where $\left(x,z\right)$ is the position of the UAV in the vertical plane, while $\left(x_r,z_r\right)$ is the position of the rope-hook. The relative motion relationship between them is shown in Equation (24):

$$\begin{array}{l}\dot{r}=V\cos \left(\lambda -\gamma \right)-V_R\cos \lambda \\ r\dot{\lambda }=V\sin \left(\lambda -\gamma \right)-V_R\sin \lambda \end{array}$$

(24)

where r is the relative distance between the UAV and the rope-hook.

The longitudinal control law structure in the terminal guidance phase consists of the outer control loop based on flight path angle control and the inner control loop based on pitch angle control. The outer loop is a proportional integral controller, as shown in Equation (25).

$${\theta }_c=k_p^{\theta }\left({\gamma }_c-\gamma \right)+k_i^{\theta }{\displaystyle \int \left({\gamma }_c-\gamma \right)dt}$$

(25)

where $K_p^{\theta }$ and $K_i^{\theta }$ are the flight path angle proportional and integral gains, respectively; and ${\gamma }_c$ is the flight path angle command.

Integrate both sides of Equation (26):

$${\gamma }_c=K_{PN}\left(\lambda -{\lambda }_0\right)+{\gamma }_0$$

(26)

where ${\lambda }_0$ is the initial sight angle, which can be obtained from the initial position of the UAV and the rope-hook, and ${\gamma }_0$ is the initial flight path angle.

As long as the UAV can track the sight angle command in time, the straightness of the trajectory can be guaranteed, the trajectory can be tracked with a little normal overload and the saturation of the control surface can also be avoided.

3.4.3. Lateral PN Law

The missile or aircraft turns in two ways: skid to turn (STT) and bank to turn (BTT). In the former mode, the aircraft does not roll, only generating a sideslip angle by rudder deflection, providing side force as turning centripetal force; the latter mode uses ailerons to steer the aircraft around, creating a lift tilt, and then uses the horizontal component of the lift to provide the turning centripetal force. The UAV was symmetrical about the xoz plane and asymmetrical about the xoy plane. When the UAV was rolling, the horizontal component of the lift force was greater than the lateral force caused by the sideslip angle, so BTT has high turning efficiency and high maneuverability. Therefore, in this study, the lateral control law adopted the traditional BTT; that is, the outer loop generated the roll angle command and sent it to the inner loop for trajectory tracking control.

Lateral overload can be obtained from the dynamics of the rolling action:

$$n_y=\tan \varphi =\frac{K_{PN}V}{g}{\dot{\lambda }}_l$$

(27)

where ${\dot{\lambda }}_l$ is the lateral angular rate of the LOS, which can be obtained by the proportional gain and the integration of the line-of-sight angle error, as shown in Equation (28):

$${\dot{\lambda }}_l=k_p^{\varphi }\left({\lambda }_{lc}-{\lambda }_l\right)+k_i^{\varphi }{\displaystyle \int \left({\lambda }_{lc}-{\lambda }_l\right)dt}$$

(28)

where $k_p^{\varphi }$ and $k_i^{\varphi }$ are the line of sight angle proportional and integral gains, respectively, and ${\lambda }_{lc}$ is the flight path angle command.

Combining Equations (27) and (28), the roll angle command can be obtained:

$${\varphi }_c={\tan }^{-1}\left(\frac{VK}{g}\left(k_p^{\varphi }\left({\lambda }_c-\lambda \right)+k_i^{\varphi }{\displaystyle \int \left({\lambda }_c-\lambda \right)dt}\right)\right)$$

(29)

In addition, the Dutch roll damping loop is also required to coordinate turns and reduce the sideslip angle.

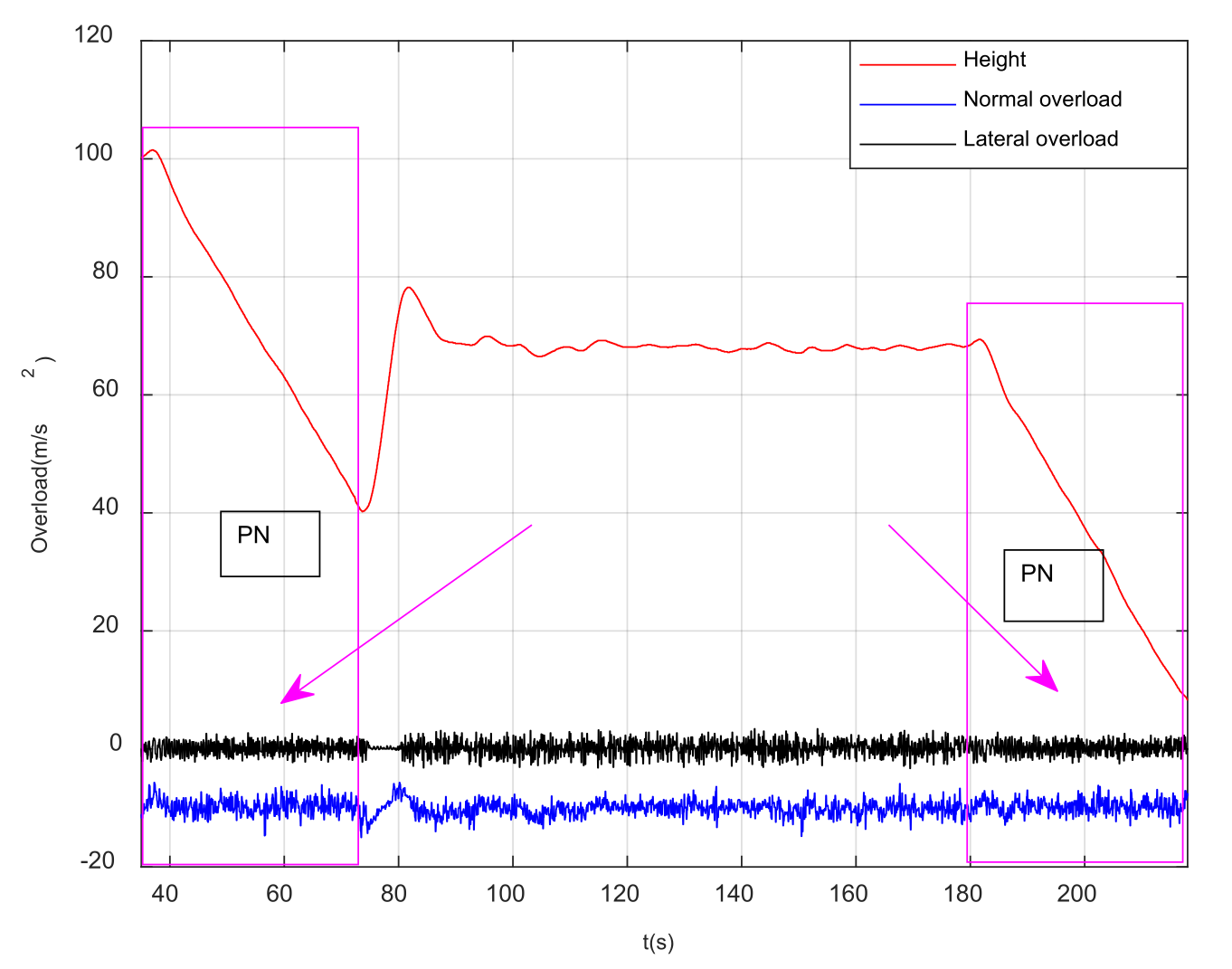
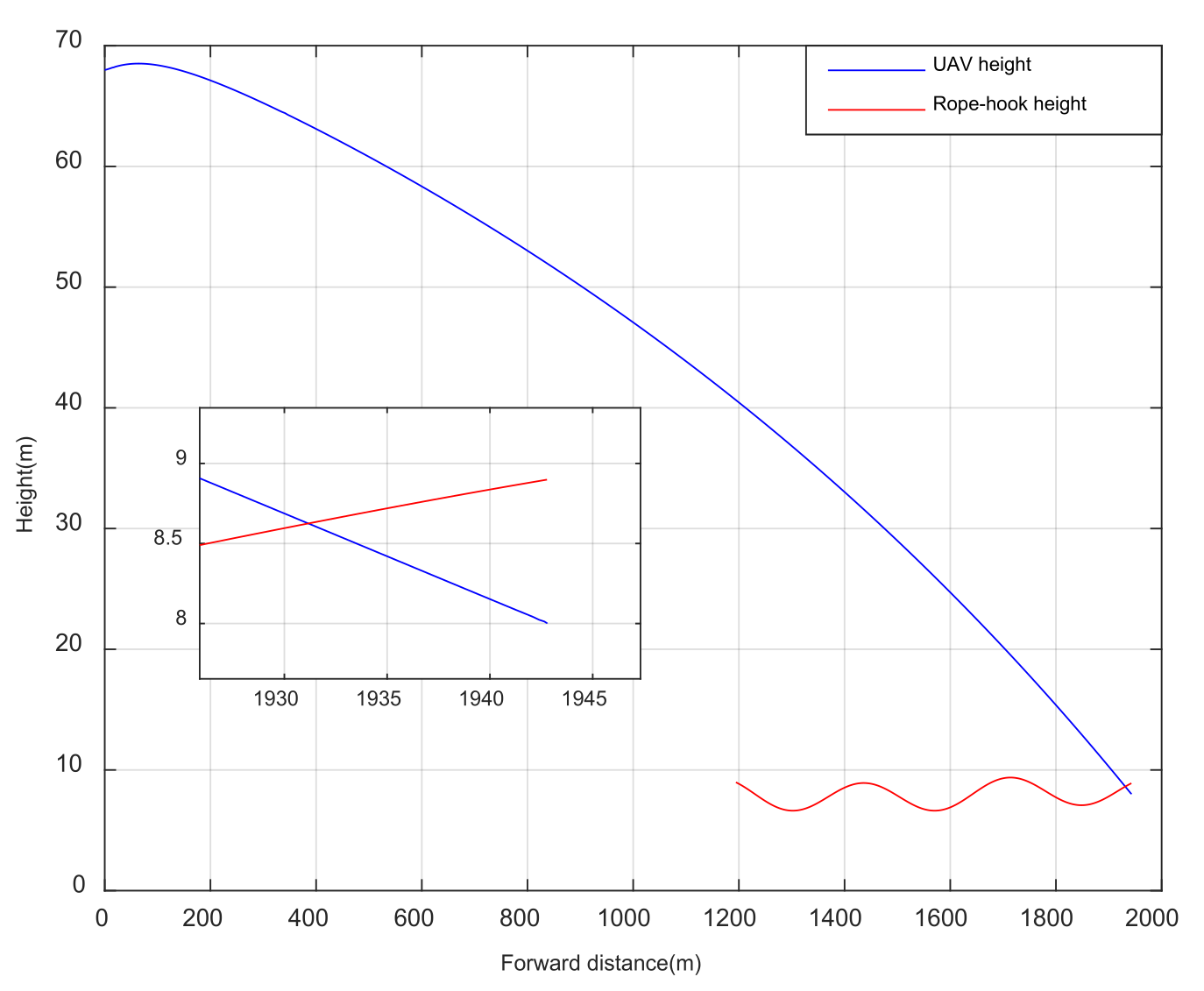
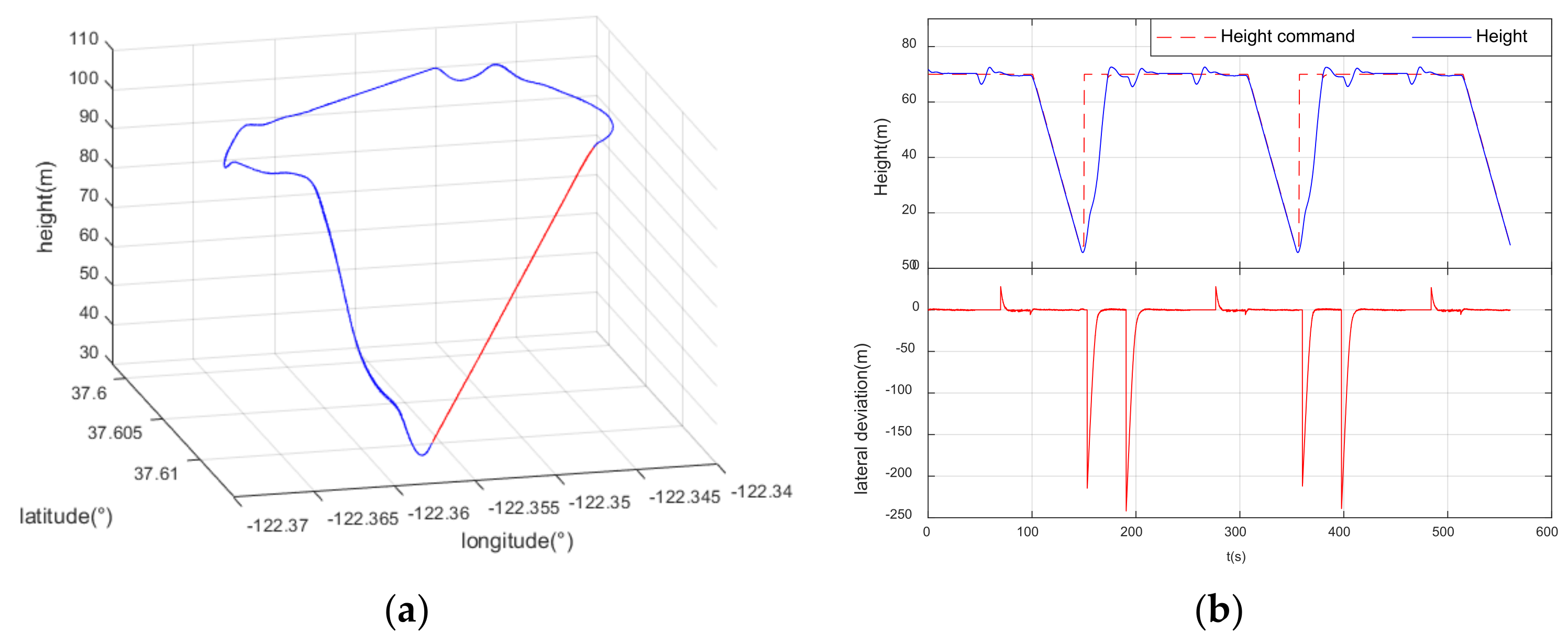
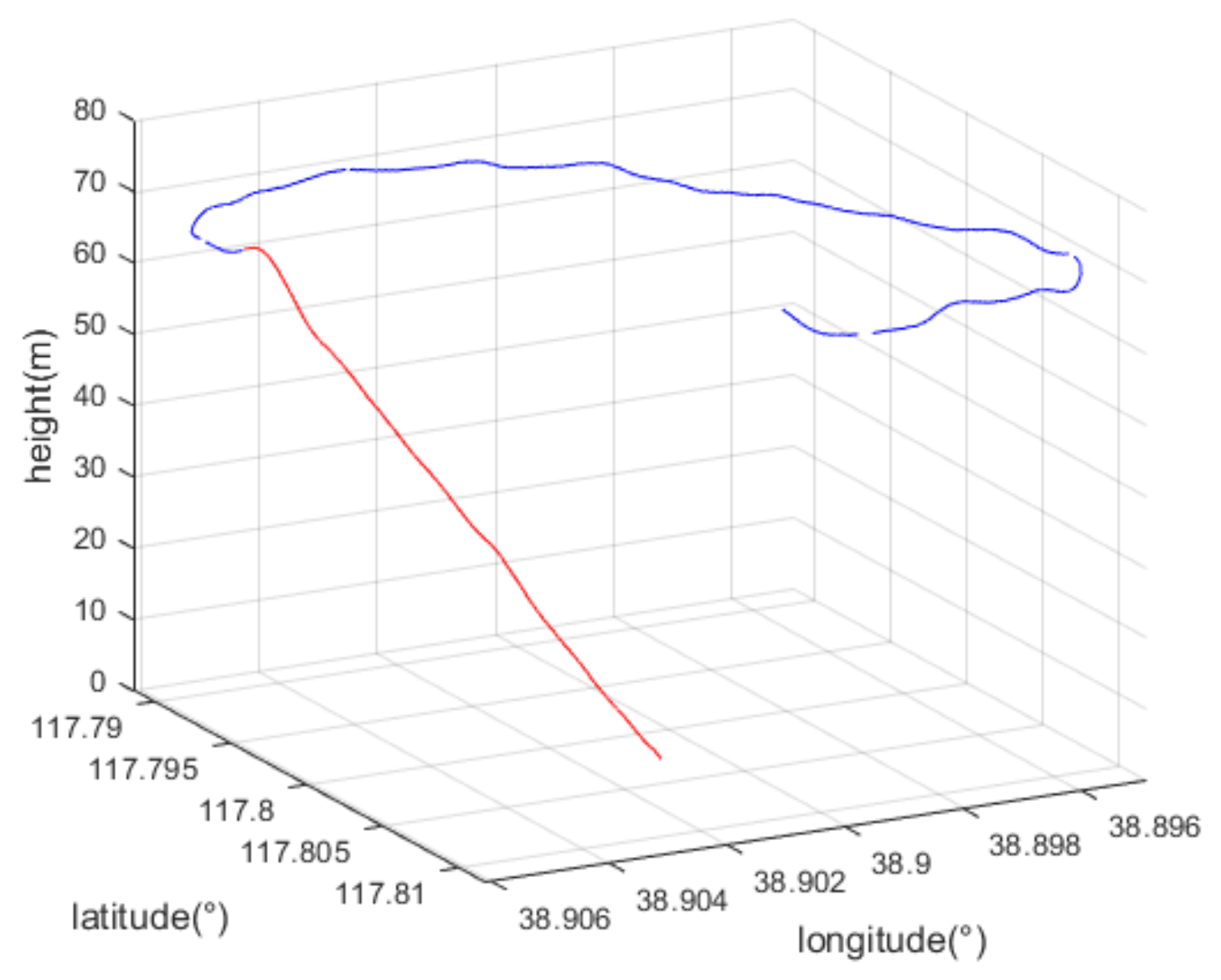
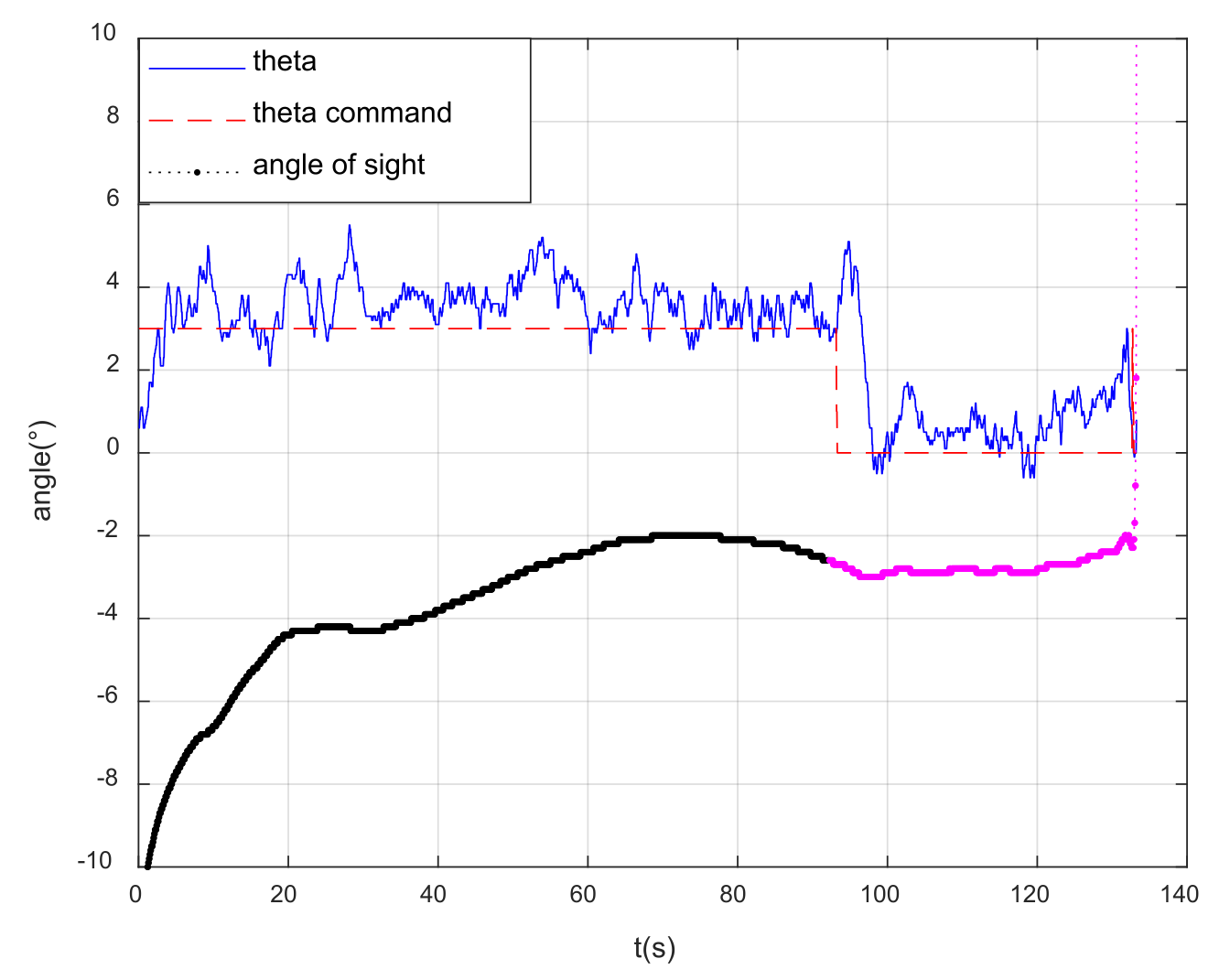
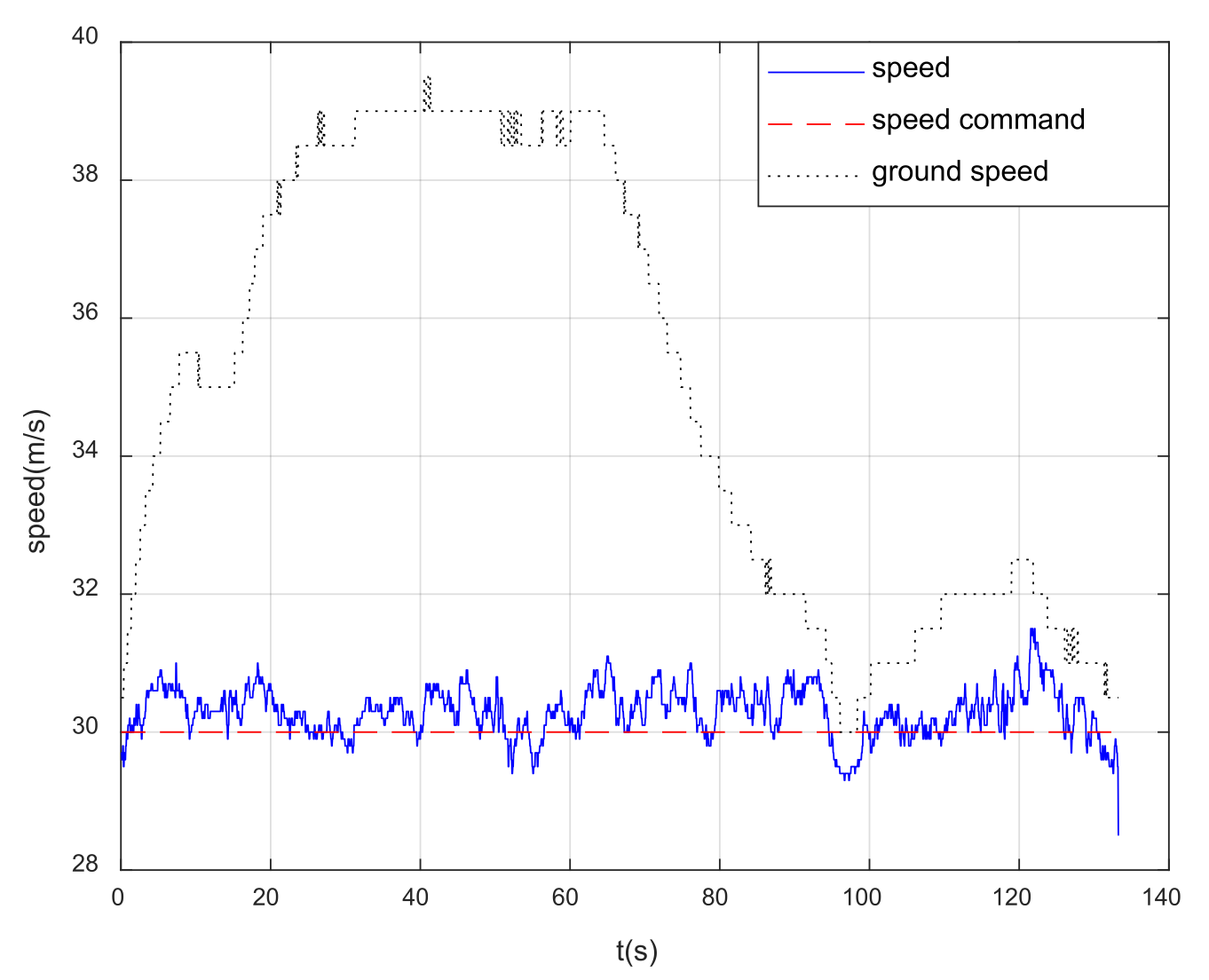
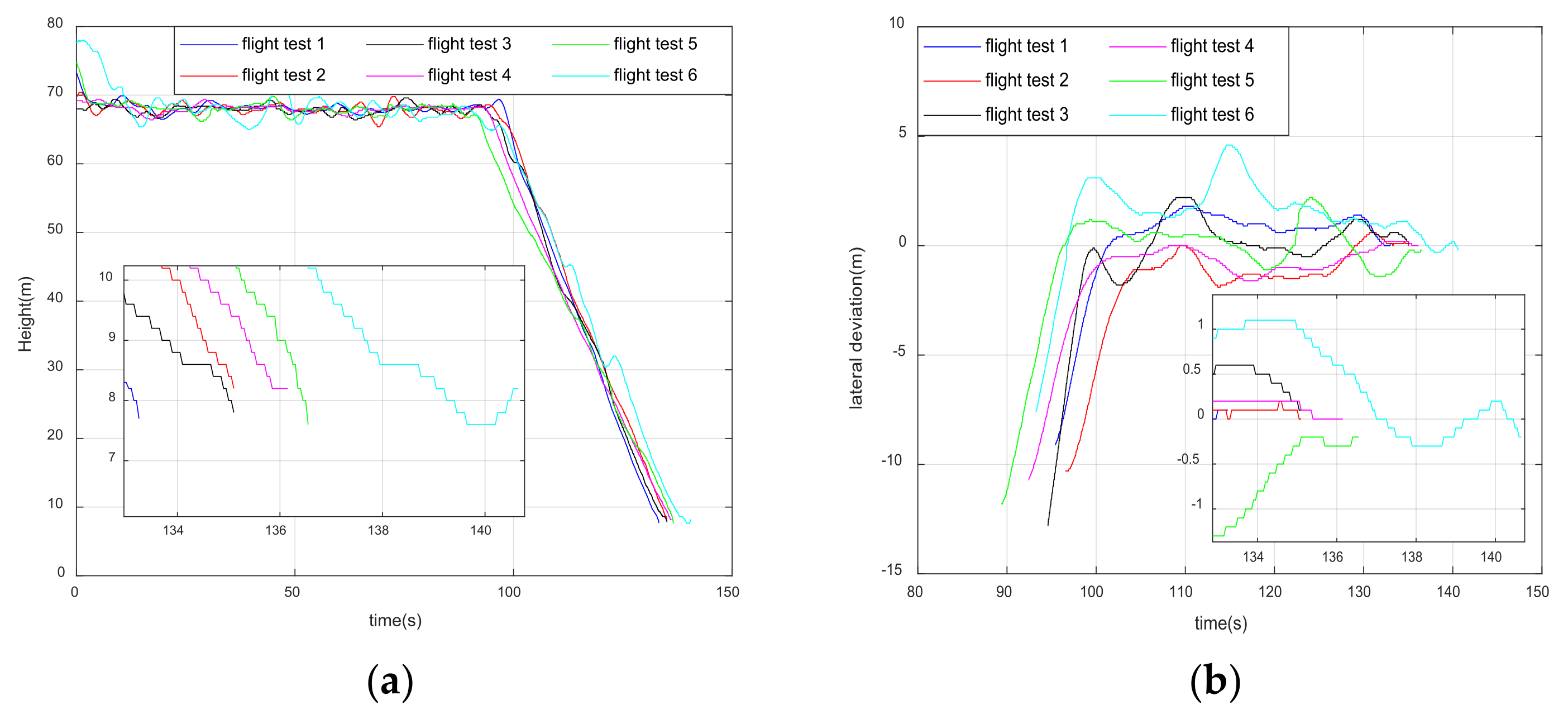
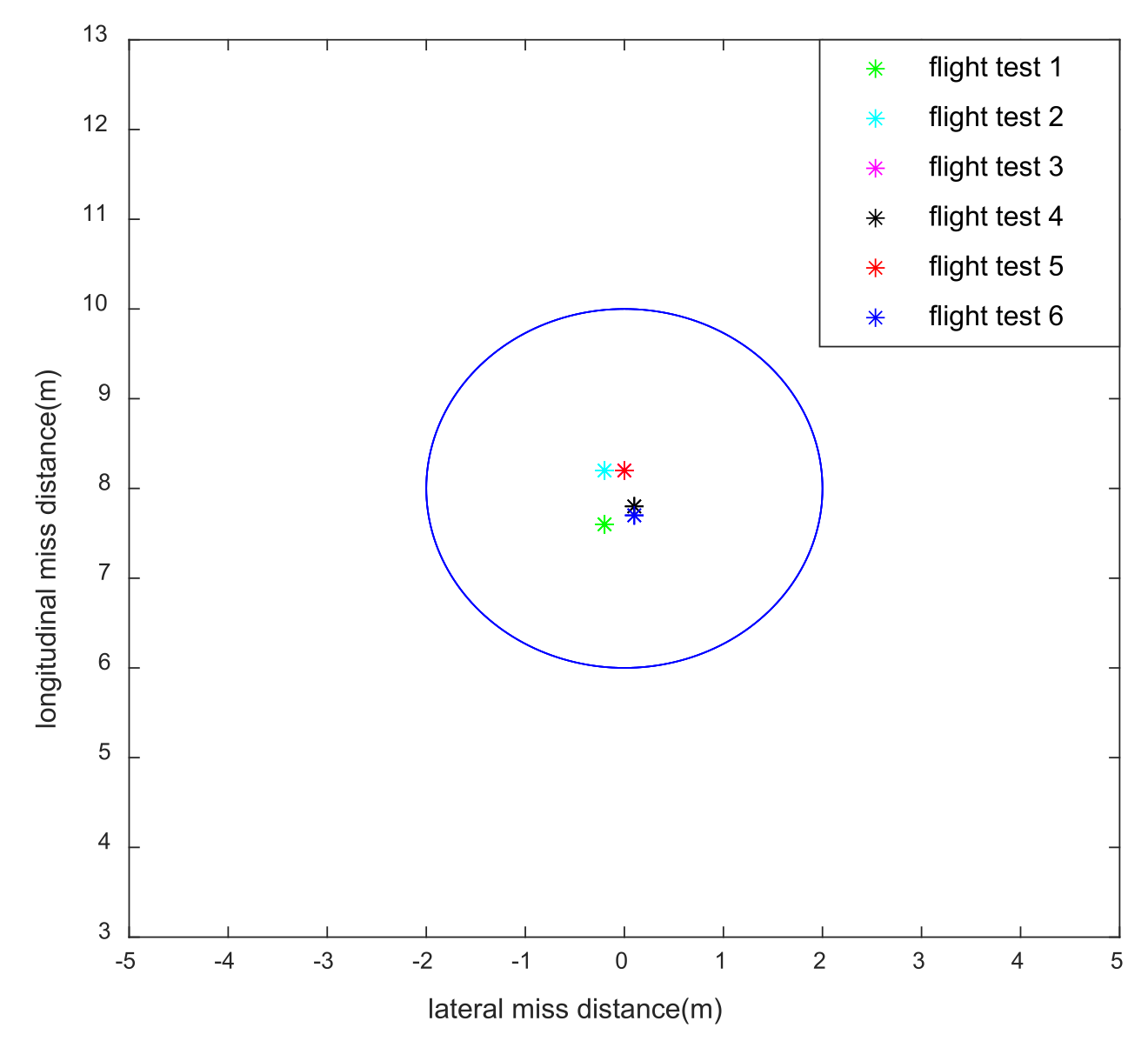
4. Results: Simulation and Flight Test

The six degrees of freedom nonlinear system was simulated in the Matlab/Simulink environment [31]. The simulation model used the simplified and typical vessel ups and downs motion model proposed in [4] to describe the rope-hook motion [32]:

$$z_r=1.22\sin \left(0.6t\right)+0.3\sin \left(0.2t\right)$$

(30)

(1) Assume that the initial flight height of the UAV was 68 m, the flight speed was 30 m/s, the vessel moved at a constant speed of 10 m/s and the heading was due north and remaind unchanged. The ideal impact point of the rope-hook was 8 m above the ground. Figure 19 shows the height trajectory of the UAV in pursuit of the moving rope-hook. The height error of impact point was 0.9 m, Hence, we can conclude that the landing controller was capable of steering the UAV to the target point with high accuracy.

(2) Simulation of collision with stationary rope-hook: after each flight test, the UAV climbed to a height of 68 m and conducted the next rope-hook impact test on the final approach of the traffic pattern, which was repeated three times. Figure 20a shows the 3D trajectory of the UAV and the average value of the height tracking error was 0.17 m, while the average value of lateral deviation was 0.3 m (see Figure 20b).

(3) Flight test with stationary rope-hook (8 m above ground): the UAV launch and recovery system are set up in an open field (see Figure 21).

The UAV took off by catapulting from waypoint 1, and then flew clockwise along waypoint 2, waypoint 3, waypoint 4 and waypoint 5 (as shown in Figure 22). Waypoint 4 to 5 was an arc with a radius of 300 m, which was mainly used to calibrate the heading. The distance from waypoint 5 to 1 was 1200 m, which is the PN phase. The flight path altitude was 68 m, +60 m relative to the ideal impact point of the rope-hook.

The UAV executed a traffic pattern as per Figure 22 and descended at the 5th side (final approach) to hit the rope-hook (see Figure 23). Figure 24 shows the 3D trajectory. The glide flight path angle was set to −2.865°.

The tracking error of the height trajectory was within ±1 m, and the final error of the impact point (longitudinal miss distance) was −0.3 m, which is of high accuracy (shown in Figure 25a). At the beginning of the proportional guidance phase, the lateral deviation was −9 the deviation rapidly converged to within +2 m, and the error of final impact point was +0.1 m (see the red curve in Figure 25b).

The pitch angle command of the flat flight stage was +3°, while that of the proportional guidance section was 0°. The UAV tracked instructions with high precision (see Figure 26). The angle of sight of the proportional guidance section was approximately −2.8°, which is basically consistent with the designed flight path angle, and also shows that the UAV essentially flew straight to the impact point. The desired airspeed was set to 30 m/s. The accuracy of airspeed control was high, and the error could be guaranteed within ±1 m, even under the condition of 9 m/s downwind (as shown in Figure 27).

The above test was repeated six times. As can be seen in Figure 28a,b, there was perfect trajectory tracking. The terminal height error was controlled within ±0.5 m, while the terminal lateral deviation was controlled within ±0.2 m. The longitudinal and lateral miss distances were much higher than the design value (see Figure 29). The proportional guidance controller had high trajectory tracking accuracy and fully met the safety recovery requirements of flying-wing UAVs.

5. Discussion

The designed controller in this study can safely recover UAVs with high control accuracy. The inner loop controller, based on ADRC, showed a strong anti-interference ability. The ESO estimated and compensated real disturbances (including external interference, modeling errors and other factors) in the control process so as to achieve anti-interference and good robustness, and to reduce dependence on the model. In addition, the strongly coupled angular rate loop could be decoupled by estimating the coupling term as disturbance. L₁ guidance law used ground velocity information toconsiders the impact of flight velocity changes caused by external disturbances, such as wind; therefore, it had excellent wind resistance. When the target was stationary, the lateral acceleration command was equivalent to PN law with a guidance coefficient of 2 (K_PN = 2), but this is only instantaneous equivalence. The terminal guidance law based on the PN law greatly improved the accuracy of the impact point, and the deflection angle of the control surface was small. The simulation data and flight test data show that the controller has strong robustness and good tracking precision. The next step is to deploy the rope-hook recovery system on a mobile vessel at sea to test the rope-hook recovery controller.