Abstract
Micro aerial vehicles (MAVs) usually suffer from several challenges, not least of which are unsatisfactory hover efficiency and limited fly time. This paper discusses the aerodynamic characteristics of a novel Hex-rotor MAV with a coaxial rotor capable of providing higher thrust in a compact structure. To extend the endurance during hover, flow field analysis and aerodynamic performance optimization are conducted by both experiments and numerical simulations with different rotor spacing ratios (i = 0.56, 0.59, 0.63, 0.67, 0.71, 0.77, 0.83, 0.91). The measured parameters are thrust, power, and hover efficiency during the experiments. Retip ranged from 0.7 × 105 to 1.3 × 105 is also studied by Spalart–Allmaras simulations. The test results show that the MAV has the optimum aerodynamic performance at i = 0.56 with Retip = 0.85 × 105. Compared to the MAV with i = 0.98 for Retip = 0.85 × 105, thrust is increased by 5.18% with a reduced power of 3.8%, and hover efficiency is also improved by 12.14%. The simulated results indicate a weakness in inter-rotor interference with the increased rotor spacing. Additionally, the enlarged pressure difference, reduced turbulence, and weakened vortices are responsible for the aerodynamic improvement. This provides an alternative method for increasing the MAV fly time and offers inspiration for future structural design.
1. Introduction
Micro aerial vehicles (MAVs) have attracted widespread interest in society due to the flexibility in performing flight missions in complex environments. The extensive applications of quad-rotor MAVs, in particular, have promoted innovation in the fields of film shooting, express delivery, military surveillance, and so forth [1,2,3,4,5]. However, further applications are restricted on account of the load capacity limitation. A novel hex-rotor MAV is presented with better stability and payload capacity compared to conventional quad-rotor MAV of the same vehicle size. Nevertheless, the flows within the multi-rotor system become more unsteady and complicated with an additional coaxial rotor. To make matters worse, the hover performance of the MAV will be severely affected if rotor spacing is too close, resulting in reduced flight time. Consequently, it is critically essential to figure out an optimal rotor spacing to improve the aerodynamic performance of the vehicle.
Bohorquez [6] conducted an aerodynamic study of four different rotors for small-sized multi-rotor aircraft by experiments. A numerical simulation was carried out to investigate rotor–rotor aerodynamic disturbances by Riccardo [7]. Hidemasa [8] et al. investigated, by means of motion-coupled flow simulations, the aerodynamic performance and flow details for the quadrotor in hover. Moreover, Tytus [9] performed a computational fluid dynamics study on rotors at an average Reynolds number of 1.5 × 105. Results proved that the hover performance of the rotor could be improved by a low Re setup. The thrust and torque coefficients were measured by Sang and Oh [10] to assess the interaction effect between two different co-axial rotors. By combining simulation findings with experimental data, Lei [11] et al. characterized the aerodynamics of a single rotor.
As can be seen above, most prior studies have been devoted to optimizing the aerodynamic performance of single rotor and coaxial rotors. Others have given priority to algorithmic development, flight control, path planning, etc., for MAVs. Although numerous results have been achieved, few have attached importance to the aerodynamic arrangement of MAVs. In the present article, we optimize the aerodynamics of a novel hex-rotor MAV by adjusting rotor spacing, aiming to minimize power consumption of the rotor system, thereby extending the endurance.
The rest of the paper is organized, as follows. A sketch of the hex-rotor MAV is presented in Section 2 with an aerodynamic analysis. Section 3 describes the experiment equipment and results, concluding with optimal spacing for the MAV. Section 4 shows the simulation results, which visualize the experiment. Finally, conclusions are drawn in Section 5.
2. Aerodynamic Analyses
Sketch of the hex-rotor MAV with a novel structure is indicated in Figure 1. D is the diameter of the rotor, and L is the distance between the rotation centers of adjacent single rotors. Ω is the rotor rotational speed per minute. As shown in Figure 1b, when the rotor rotates, the pressure difference on the blade surfaces generates thrust and induces downward air movement. This airflow is known as downwash flow. However, the slipstream field and downwash flows are complicated by the additional coaxial rotor and should be appropriately analyzed.
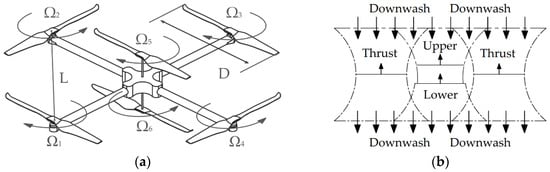
Figure 1.
Sketch of the coaxial hex-rotor MAV. (a) Vehicle Structure; (b) flowfield model.
There are three primary forms of aerodynamic interference in the hex-rotor MAV (1) interference between adjacent single rotors. The hover performance for the quad-rotor system is mainly affected by the behaviors of wakes. (2) Interference between the upper rotor and lower rotor of the coaxial rotor. The swinging blades and wandering vortexes make the aerodynamic optimization for coaxial rotors a real challenge. The lower rotor usually suffers a higher aerodynamic degradation by the influence of the upper rotor wake. (3) Interference between the single rotor and the coaxial rotor. Clearly, for the coaxial rotors, the downwash of the upper rotor imposed on the bottom rotor will definitely decrease the whole efficiency for certain spacing where the coaxial rotors is still domain the whole flowfield. Additionally, the downwash velocity and induced velocity are considered to be equivalent in hover, it may cause vibration, which is also a disadvantage for the MAV as a whole.
Figure 2 shows the slipstream model of the hex-rotor MAV. As shown in Figure 2, the induced power losses and flow turbulence are aggravated by the mutual coupling of slipstream fields for a small rotor spacing. With the rotor spacing increasing, the interaction between adjacent single rotors diminishes, and interference between the single rotor and the coaxial rotor weakens. Finally, interference between the upper rotor and lower rotor of the coaxial rotor dominates the whole flowfield.
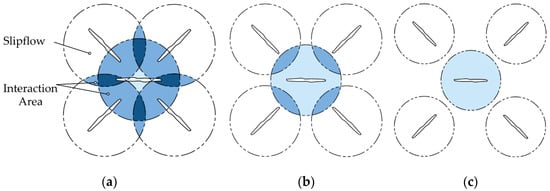
Figure 2.
Interaction area of the hex-rotor MAV with increased rotor spacing. (a) Small spacing; (b) mid spacing; and (c) large spacing. (The deeper the blue, the stronger the interaction).
To study the effect of the rotor spacing on the aerodynamic performance of the MAVs, rotor spacing ration i is defined as:
where D is the rotor diameter, 400 mm; L is the length between the center of the adjacent quadrotors. The minimum L = 1D is set to avoid the collision of adjacent rotors, and the maximum L = 2D is set to avoid oversize of the MAV since a large rotor spacing will lead to a long rotor arm with extra weight, which is proved not beneficial to improving maneuverability. Therefore, the spacing ratio i is 0.98, 0.91, 0.83, 0.77, 0.71, 0.67, 0.63, 0.59, and 0.56, respectively.
Airflow conditions around the rotor can be characterized by the dimensionless Reynolds number on the rotor tip as follows:
where:
- —air density at the height of rotor [Kg/m3].
- —rotor-tip speed [m/s].
- —average chord length of rotor [m].
- —dynamic viscosity of the air [Pa·s].
The speed of rotor-tip in Equation (2) can be achieved by
to characterize the aerodynamic performance for multi-rotor MAV in detail, figure of merit (FM, or), thrust coefficients and power coefficients are given by
where:
- P—power consumption of the rotor system [W].
- A—rotor disc area [m2].
In a steady hover, the downwash velocity and induced velocity are considered to be equivalent. The ideal induced velocity (or downwash velocity) for an isolated rotor in hover can be expressed by
The intensity of mutual interference for a multi-rotor system can be expressed by writing the induced velocity for the mth rotor as [12]
where:
- m, n—mth and nth rotor for the rotor system., —ideal induced velocity for the isolated mth and nth rotor [m/s].
- —correction for the additional induced loss of a real rotor.
- —interference factor.
3. Experiments
3.1. Setup
The experimental setup is shown in Figure 3, and the parameters of the rotor can be found in Table 1. To minimize the complexity, the spacing between the upper rotor and lower rotor of the coaxial rotors is optimally determined by 77 mm (0.18D) for the coaxial rotor [13]. The rotors are mounted inversely at a height of 2 m (5 times the rotor diameter) from the ground to avoid the impact of reversed flow on the measurement.
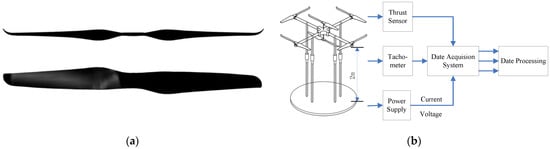
Figure 3.
Experimental setup (a) rotor configuration; and (b) sketch of setup.

Table 1.
Parameters of rotor.
As illustrated in Figure 4, rotors are powered by a BLDC motor (Model: MSYS-LRK 195.03) and are controlled through PCB. The speed of the propeller is monitored by an optical tachometer (Model: TM-5010K, accuracy: ±0.01%). Thrust is measured by a highly sensitive thrust transducer (Model: PLD204D-19, accuracy: 0.5% F.S) with a precision of ±0.005 N (±0.005% of the full range). Power, voltage, and current values are captured by a direct current supply (Model: ABF-SS-L303SPV accuracy: ±0.1 mV, ±0.1 μA). In anticipation of a large amount of data to be generated, we link the sensors with a PC to facilitate real-time recording and processing by a data acquisition system. Typical values of the standard deviations of thrust are about 1% of the mean values.
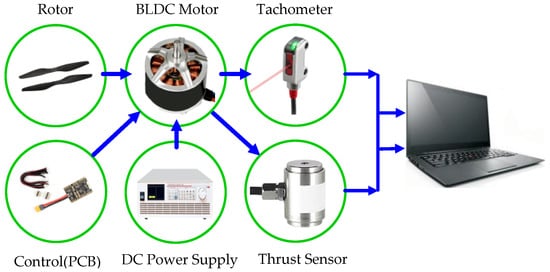
Figure 4.
Test section.
3.2. Results
Figure 5 shows the thrust variation compared with i = 0.98. Larger thrusts are obtained for almost all rotor spacing ratios. For Re = 0.89 × 105 at i = 0.56, there is a most significant increase of 5.18%. However, a maximum drop of 2.94% can be also noticed at Re = 0.84 × 105 for i = 0.56. This may be caused by the vibration of the rotor system for a specific Reynolds number. A similar fluctuation can be noted at Re = 0.84 × 105 for i = 0.59. In the case of Re = 0.84 × 105 for i = 0.91, the strong rotor interaction may lead to the decline in thrust.
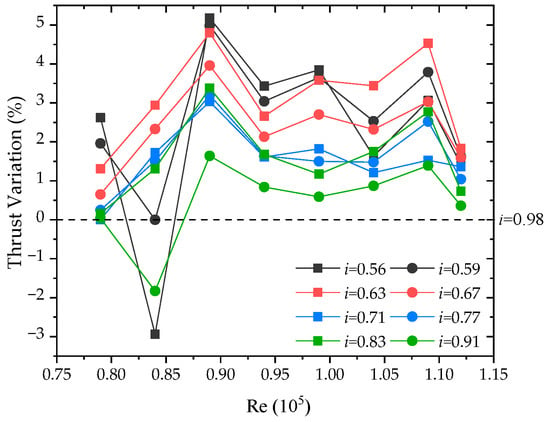
Figure 5.
Thrust variation in hover (compared with i = 0.98).
Power variation in hover is shown in Figure 6. It is interesting to notice that power consumption is sensitive to the change in Re numbers. Lower power consumption is observed with increasing Re. In particular, there is a reduction in power of 9.83% at Re = 1.12 × 105 for i = 0.71, while thrust is increased by 1.36%. The coupling of wakes at a proper rotor spacing may be responsible for the aerodynamic improvement. Similar curve behavior can be found in the case of Re = 1.12 × 105 for i = 0.77.
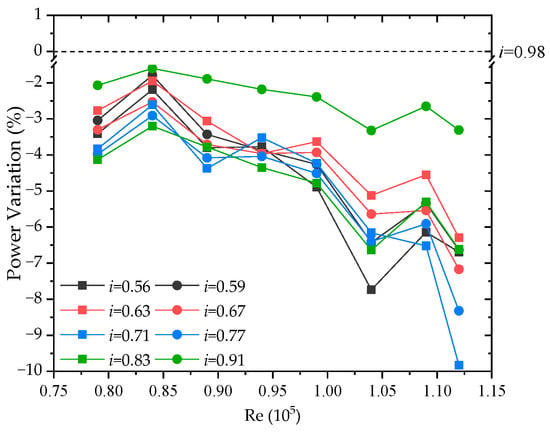
Figure 6.
Power Variation in hover (compared with i = 0.98).
Figure 7 shows FM variation compared with i = 0.98. It is observed that the FM decreased 2.51% and 1.15% at Re = 0.84 × 105 for i = 0.56 and i = 0.91, respectively. Based on Figure 5 and Equation (4), it can be caused by the thrust drop. From an aerodynamic perspective, the generated rotor tip-vortices are induced by each other and are impinged by the propellers, which causes very complicated blade–vortex interaction and vortex–vortex interaction [14,15,16,17]. For i = 0.56 at Re = 0.89 × 105, the FM (or hover efficiency) has a remarkable improvement of 12.14%. In this case, the MAV achieved a better aerodynamic characteristics at i = 0.56 with a higher Re.
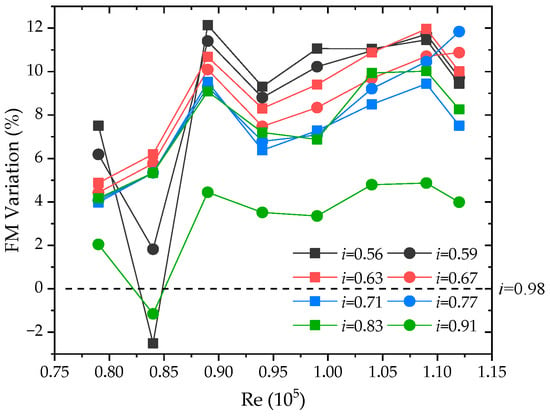
Figure 7.
FM variation in hover (compared with i = 0.98).
4. Simulations
4.1. Setup
Figure 8 illustrates the computational grid. The multi-rotor system is 2.5 m from the upper surface and 5 m over the lower surface to avoid the ground effect as well as the reversed flow. The Spalart–Allmaras (S–A) turbulence model is adopted for the low Reynolds number flows in the field. Rotational curvature correction is applied in the S–A model to enhance the accuracy of the prediction for tip vortexes. The boundaries within the rotation domains and the field domain are handled successfully by the utilized sliding mesh. The polyhedral meshes are applied to build flow fields and rotational domains, saving computational resources and minimizing mesh errors. To capture the rotor-tip flow, the mesh for the multi-rotor system is refined adaptively. Additionally, the total cells number used is approximately 23.6 million.

Figure 8.
Computational grid.
4.2. Results
Figure 9 shows pressure distribution with different spacing ratios. The interference between coaxial and single rotors severely affects the real-time pressure performance for the coaxial rotor at i = 0.71 and i = 0.63. In Figure 9a,b, we can see the inter-rotor vortices symmetrically distributed along the axis of the quadrotor, which is resulted from a strong interaction. By comparing the size of the positive and negative pressure regions around rotors, it can be verified that the maximum thrust is obtained at i = 0.56.
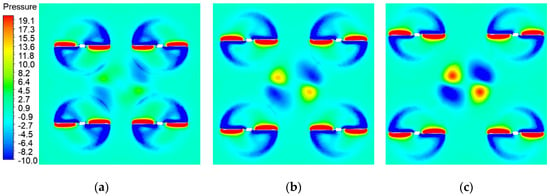
Figure 9.
Pressure distribution at Re = 0.89 × 105 (a) i = 0.71; (b) i = 0.63; (c) i = 0.56.
The velocity contours can be observed in Figure 10. The disk plane of the lower rotor encounters the accelerated wake from the upper rotor by the slipstream of the quad-rotor. Additionally, the geometry of wake boundaries is affected by the tip vortices in Figure 10a,b. Clearly, the maximum downwash areas are obtained at i = 0.56 since the interference between the rotors is relatively weak.
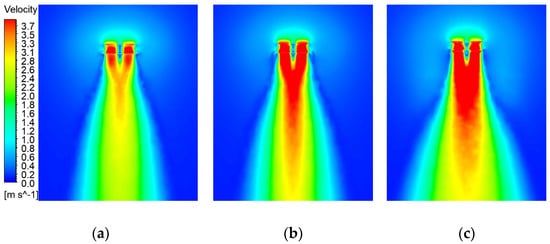
Figure 10.
Velocity contours at Re = 0.89 × 105. (a) i = 0.71; (b) i = 0.63; (c) i = 0.56.
Figure 11 shows vectors distribution with different spacing ratios. In Figure 11a,b, the sharp change in vector orientations indicates high flow resistance, which is characterized with the power consumption. The turbulence is aggravated by the interference between the coaxial rotor and quad-rotor, moving in the horizontal direction. As the rotor spacing ratio decreases, the turbulence flow weakens significantly, and therefore it has better aerodynamic performance for i = 0.56.
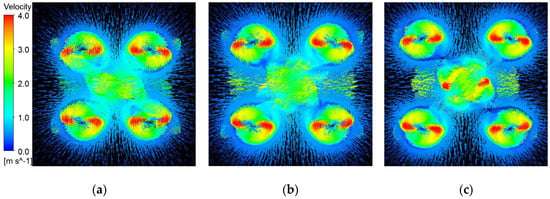
Figure 11.
Vectors distribution at Re = 0.89 × 105. (a) i = 0.71; (b) i = 0.63; (c) i = 0.56.
Figure 12 shows the velocity and pressure distribution for the MAV compared with corresponding isolated rotors without interference, where X is the distance from the center of the MAV. Obviously, the downwash velocity for all rotor tips increases from 8.43% to 23.22% because of the accelerated inflow by the slipstream. The rotor-tip pressure difference for the quadrotor increases by about 1.4%, while that of the coaxial rotor decreases by approximately 8%. This is because tip-vortices generated by the quad-rotor dissipate faster and get lesser time to be affected in the slipstream of the coaxial rotor, while the coaxial rotor is subject to stronger blade–vortex interactions due to the different structure. This result agrees well with previous research [18]. The overall thrust of the MAV drops slightly by 2.03% compared to the isolated rotor system. Further decrease in the rotor spacing ratio gives a slight aerodynamic enhancement for the MAV. Therefore, i = 0.56 is ultimately identified as the optimal spacing ratio for the MAV.
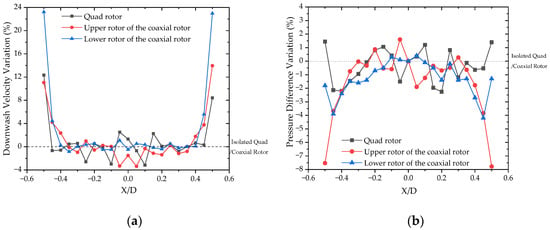
Figure 12.
Velocity and pressure distribution of MAV compared with isolated quad/coaxial rotors at Re = 0.89 × 105 for i = 0.56. (a) velocity variation; and (b) pressure variation.
5. Conclusions
In this paper, we proposed a hex-rotor MAV with a novel structure consisting of a coaxial rotor which showed a better payload capacity with a compact airframe. With the aim of optimizing the hover performance for the MAV, we analyzed the experimental and simulation results from an aerodynamic point of view and came to the following conclusions:
- The experimental results showed that the aerodynamic characteristics and hover performance of MAVs can be improved notably by adjusting the horizontal distance between rotors.
- The data presented exhibited a weak tendency of inter-rotor interference with the decreased rotor spacing ratio. The multi-rotor system has the optimized thrust, power, and hover performance with rotor rotational speed ranging from 1600 RPM to 2300 RPM at i = 0.56.
- The numerical simulation showed that the presence of the strong inter-rotor vortices led to a significant degradation in aerodynamic performance at a small rotor spacing, resulting in unsteady wake behaviors.
- Inter-rotor vortices and turbulence flows in the horizontal direction were the major manifestations of the interference between adjacent single and coaxial rotors.
- As the rotor spacing ratio decreases, the pressure difference on the rotor surface enlarged, and the velocity of the downwash increased. The aerodynamic disturbance is expected to be the weakest at the spacing ratio i = 0.56.
- The novel multi-rotor layout provides larger thrusts compared to conventional MAVs of the same size while exacerbating inter-rotor aerodynamic interference. Although a slight reduction (2.03%) in overall thrust was measured compared to an isolated rotor system, the wind resistance is improved by the accelerated rotor-tip downwash.
Future work will consider the effect of unsteady wind on the vehicle and focus on optimizing the MAV performance.
Author Contributions
Investigation, Y.L.; writing—review and editing, J.W.; software, W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51505087 and Fujian Provincial Industrial Robot Basic Components Technology Research and Development Center (2014H2004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are already included in the manuscript.
Acknowledgments
The authors thankfully acknowledge the Fuzhou University Jinjiang Science and Education Park, and Key Laboratory of Fluid Power and Intelligent Electro-Hydraulic Control (Fuzhou University) for providing experimental equipment and venues.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hein, B.R.; Chopra, I. Hover Performance of a Micro Air Vehicle: Rotors at Low Reynolds Number. J. Am. Helicopter Soc. 2007, 52, 254–262. [Google Scholar] [CrossRef]
- Lakshminarayan, V.K.; Baeder, J.D. Computational Investigation of Microscale Coaxial-Rotor Aerodynamics in Hover. J. Aircr. 2010, 47, 940–955. [Google Scholar] [CrossRef]
- Hassanalian, M.; Rice, D.; Abdelkefi, A. Aerodynamic performance analysis of fixed wing space drones in different solar system bodies. Acta Astronautica 2018, 152, 27–48. [Google Scholar] [CrossRef]
- Herrero, A.D.E.; Percin, M.; Karasek, M.; Van Oudheusden, B. Flow Visualization around a Flapping-Wing Micro Air Vehicle in Free Flight Using Large-Scale PIV. Aerospace 2018, 5, 99. [Google Scholar] [CrossRef]
- Sibilski, K.; Nowakowski, M.; Rykaczewski, D.; Szczepaniak, P.; Żyluk, A.; Sibilska-Mroziewicz, A.; Garbowski, M.; Wróblewski, W. Identification of Fixed-Wing Micro Aerial Vehicle Aerodynamic Derivatives from Dynamic Water Tunnel Tests. Aerospace 2020, 7, 116. [Google Scholar] [CrossRef]
- Bohorquez, F.; Pines, D. Hover Performance of Rotor Blades at Low Reynolds Numbers for Rotary Wing Micro Air Vehicles. In Proceedings of the 2nd AIAA Unmanned Unlimited Conference and Workshop & Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Piccinini, R.; Tugnoli, M.; Zanotti, A. Numerical Investigation of the Rotor-Rotor Aerodynamic Interaction for eVTOL Aircraft Configurations. Energies 2020, 13, 5995. [Google Scholar] [CrossRef]
- Hidemasa, Y.; Keiichi, K.; Yoshiaki, N. Numerical analysis of flow field and aerodynamic characteristics of a quadrotor. Trans. Jpn. Soc. Aeronaut. Space Sci. 2013, 11, 61–70. [Google Scholar]
- Tulwin, T. Low Reynolds Number Rotor Blade Aerodynamic Analysis. MATEC Web Conf. 2019, 252, 04006. [Google Scholar] [CrossRef]
- Sang, H.P.; Kwon, O.J. Numerical study about aerodynamic interaction for coaxial rotor blades. Int. J. Aeronaut. Space Sci. 2021, 22, 277–286. [Google Scholar]
- Lei, Y.; Ji, Y.; Wang, C. Numerical Simulation and Experimental Validation of Small-rotor Aerodynamic Characteristics. In Proceedings of the International Conference on Mechatronics Engineering & Information Technology, Xi’an China, 27–28 August 2016. [Google Scholar] [CrossRef][Green Version]
- Johnson, W. Twin Rotor Interference in Forward Flight. In Helicopter Theory; Dover: New York, NY, USA, 1994; p. 142. [Google Scholar]
- Lei, Y.; Bai, Y.; Xu, Z.; Gao, Q.; Zhao, C. An experimental investigation on aerodynamic performance of a coaxial rotor system with different rotor spacing and wind speed. Exp. Therm. Fluid Sci. 2013, 44, 779–785. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.J. Rotor interactional effects on aerodynamic and noise characteristics of a small multirotor un-manned aerial vehicle. Phys. Fluids 2020, 32, 47107. [Google Scholar]
- Lee, S.; Chae, S.; Woo, S.Y.; Jang, J.; Kim, J. Effects of Rotor-Rotor Interaction on the Wake Structure and Thrust Generation of a Quadrotor Unmanned Aerial Vehicle. IEEE Access 2021, 9, 85995–86016. [Google Scholar] [CrossRef]
- Zhou, W.; Ning, Z.; Li, H.; Hu, H. An Experimental Investigation on Rotor-to-Rotor Interactions of Small UAV Propellers. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3744. [Google Scholar] [CrossRef]
- Singh, P.; Friedmann, P.P. Application of Vortex Methods to Coaxial Rotor Wake and Load Calculations in Hover. J. Aircr. 2018, 55, 373–381. [Google Scholar] [CrossRef]
- Shukla, D.; Komerath, N. Multirotor Drone Aerodynamic Interaction Investigation. Drones 2018, 2, 43. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).