Abstract
The global control volume-based energy utilization balance for an aerospace vehicle is extended to allow for the analysis of jet-propelled vehicles. The methodology is first developed for analyzing the energy utilization and entropy generation characteristics of jet engines without airframe considerations. This methodology, when combined with separate energy utilization analysis for an unpowered airframe, allows for the assessment of a powered vehicle. Wake entropy generation for a powered vehicle is shown to be the summation of the wake entropy generation associated with the propulsion system (no airframe) and the unpowered airframe. The fundamental relationship between overall entropy generation and the flight conditions required for maximum range and endurance of a powered vehicle are also derived. Example energy utilization results obtained for a modeled turbojet engine in off-design operation are provided; wake and engine component entropy generation characteristics are directly related to engine operation and flight conditions. This engine model is then integrated with a legacy (twin-engine) Northrop F-5E Tiger II airframe. The overall entropy generation temporal rate for the vehicle is minimized, as predicted by our analysis, at flight conditions corresponding to maximum endurance. For flight conditions corresponding to maximum range, the overall entropy spatial rate is minimized.
1. Introduction
The effective utilization of available energy for an aerospace vehicle in flight is necessary in order to satisfy performance and mission requirements. These requirements are met primarily by generating suitable thrust and lift forces from available energy, as well as by the proper management of aerodynamic drag. While in some flight systems there are stored or acquired sources of available energy other than the propellant, the propellant is generally the only significant source of available energy for most powered aerospace vehicles. Furthermore, while there may be some usage of available energy in subsystems other than the propulsive and aerodynamic subsystems, such subsystems are usually thermodynamically tied into the propulsive and/or aerodynamic flow paths. Propulsive and aerodynamic flows ultimately, then, serve as thermal sinks for energy not explicitly associated with thrust/lift production and/or drag mitigation.
The analytical development of the fundamental rate-based energy utilization balance for powered aerospace flight vehicles, based on the global control volume approach, has enabled the direct assessment of the impact of available energy losses on vehicle performance at discrete flight conditions [1]. In addition, the energy utilization rate balance has been combined with vehicle equations of motion to provide time-integrated energy utilization balances, allowing for the assessment of energy utilization across vehicle missions and mission segments in terms of vehicle kinetic and potential energy changes [2]. Energy utilization formulations that are based on the global control volume approach have been used and validated for a wide range of applications and flow regimes, including multi-dimensional flows and chemically reacting flows [3]. Most applications have focused on hypersonic air-breathing vehicles with ram/scramjet propulsion systems [4] and rocket-powered vehicles [5,6].
Exergy analysis, and systematic application of entropy generation minimization techniques for performance improvements and optimization, are very well-established and widely utilized for ground-based systems; less so for aerospace flight vehicles, due in part to the lack of direct (analytical) linkage between exergy losses and classic vehicle performance characteristics and design objectives. Although energy utilization analysis based on the global control volume approach is a form of exergy analysis, the balance that results is specifically based on traditional vehicle performance (i.e., net propulsive and aerodynamic forces, changes in vehicle kinetic and potential energies, etc.). It (analytically) links losses in traditional performance metrics to entropy generation in the global control volume in which the vehicle is embedded at the specific flight condition of the vehicle. Nevertheless, both traditional exergy methods and the global control volume-based energy utilization balance are linked by their respective assessment of losses in terms of entropy generation. Entropy generation is the most fundamental measure of losses for all physical processes and hence provides the common (single) currency of losses for all sub-systems and processes associated with aerospace vehicles.
The earliest development of the global control volume-based approach for relating forces on aerodynamic shapes to entropy generation was by Ostawitch [7], who characterized the drag of an unpowered shape in fluid flow in terms of overall entropy generation. Subsequent developments of the approach are essentially extensions and refinements, applied to increasingly complex aerospace systems. The approach is also used by Giles and Cummings [8], who characterized the energy availability balance for a vehicle using a simple heating model for fuel energy release. The present work is also related to previous investigations ([9,10]) that sought to characterize gas turbine (turbojet and ramjet) transient behavior by employing energy utilization/entropy generation analysis. Abbas and Riggins [11] in prior work investigated energy utilization and entropy generation for a turbojet engine model without airframe considerations; focusing primarily on presenting uninstalled performance and providing related energy utilization information.
The earliest work in the area of performance assessment of jet engines includes that of Foa [12], Builder [13], and Lewis [14]; the latter reference provides a basic description of the framework of exergy methods applicable to jet engines, and hence is a precursor to later exergy-based investigations of aerospace propulsion systems. Clarke and Horlock [15] provided a pioneering treatment of availability and thrust power losses for aerospace jet engines, including a single operation point application of the method for a modeled turbojet engine. Their work, in terms of control volume-based analysis of stand-alone engines, is closely related to the global control volume-based energy utilization approach used in the present work, especially as applied to jet engines without airframe considerations. Subsequent interest in applying exergy methodology to aerospace propulsion systems, including airbreathing scramjet engines during the 1990s, led to work such as that by Czysz and Murthy [16], Murthy [17], and Brilliant [18]. A parallel effort (again with an initial emphasis on high-speed systems) focused on analysis and optimization based on the minimization of engine thrust losses. This engineering performance-based approach was first pioneered by Curran and Craig [19], who provided the basis of the thrust-potential methodology later developed by Riggins et al. (see, for example, [20,21,22]). In these and related investigations, the thrust for a high-speed engine was explicitly linked to entropy production occurring inside the engine. A parallel and related methodology was developed using work potential methods as applied to engines (see, for example, Roth [23,24]). Unlike exergy-based analyses, both thrust potential and work potential methods avoid wake entropy generation (wake exergy destruction) issues due to their direct assessment of forces and work potential specific to an engine flow-field itself. In more recent work using traditional exergy analysis, Ehyaei et al. [25] performed an exergy analysis of an afterburning turbojet engine at two altitudes and identified the exergetic efficiencies of the various engine components. Etele and Rosen [26] explored the important issue of the sensitivity of exergy analysis for aerospace systems to the choice of reference state. A discussion on and examples of the benefits of exergy-based analysis when applied to general (and specific) aerospace applications are reported by Doty et al. [27]. A recent detailed and comprehensive description of the exergy-based formulation for aircraft aerodynamic-propulsive performance assessment is provided by Arntz, Atinault, and Merlen [28]. Additional work analyzing exergetic aspects of gas turbine engines is done in [29,30,31,32,33].
There are three main objectives of the present work: the first objective is to extend the global control volume-based energy utilization balance to enable the analysis of aerospace vehicles with gas turbine (jet) engines, operating at either subsonic or supersonic flight Mach numbers. The second objective is to use the control-volume based energy utilization balance to analytically investigate the overall entropy generation characteristics of a jet-powered vehicle in cruise. The third objective is to provide performance and energy utilization results for specific applications (i.e., first for a specified engine without an airframe and then for a powered vehicle with a specified airframe, with a focus on cruise flight, range, and endurance).
The approach taken in this work to accomplish these objectives is to develop a turbojet engine model that correctly accounts for (hardware-specific) engine off-design operation; this requires the identification or use of component performance maps and loss models, and the implementation of component matching. The component-matched engine model then allows for the assessment of performance and energy utilization for a specific engine for all fuel throttle settings, flight Mach numbers, and altitudes across the off-design flight envelope. Most previous studies using conventional exergy techniques do not fully account for off-design engine operation but rely on traditional cycle analysis approximations and assumptions. The specific engine used in the application example for this work is selected and sized based on nominal on-design operation at a flight Mach of 0.85, altitude of 9 km, and a thrust requirement of 9.3 kN; off-design operation and performance for this engine is then calculated appropriately from the engine operating line information as obtained through the component matching process.
In conjunction with the installed thrust and additive drag models for this turbojet engine, a drag model for a legacy airframe with known aerodynamic and weight characteristics is defined; the Northrop F-5E Tiger II airframe (with twin turbojet engines) has been selected in this work. This airframe provides a good match in terms of its drag envelope to the modeled installed engine thrust performance envelope. Finally, a combination of the airframe and the modeled engines provides a complete (powered) vehicle model, thus allowing for the quantitative assessment of cruise flight in terms of energy utilization characteristics (and in terms of conventional principles).
This work (along with earlier complementary work described in [11]) is unique in employing a control volume/energy utilization analysis that explicitly includes the wake (and the entropy generation occurring therein) for the analysis of a gas turbine engine from a second-law/exergetic perspective. It is also the first exergy analysis of a turbojet engine utilizing that approach that analyzes a given engine over a range of ‘off-design’ conditions, as opposed to employing cycle analysis assumptions and limitations. In addition, the work is believed to provide the first fundamental derivation and case study showing the direct relation between overall entropy generation and maximum range and endurance conditions for an aircraft; this derivation results from the comprehensive nature of the global control volume/energy utilization approach.
Section 2 of this paper provides a brief summary and discussion of the global control volume-derived energy utilization balance for an aerospace vehicle in flight. Subsequent sections of this paper develop the analytical basis for using this energy availability balance in order to (1) assess conventional gas turbine engines without airframe considerations (Section 3), (2) assess integrated airframe and air-breathing (jet) propulsion systems, i.e., powered vehicles (Section 4 and Section 5), and (3) develop fundamental range and endurance considerations that result from the energy utilization balance (Section 6). Section 7 describes specifics of the gas turbine engine modeling (with an emphasis on correctly accounting for off-design performance using component matching) and the specific configuration for a modeled turbojet engine. Section 8 provides information regarding the airframe, the airframe drag model, and specifics of the selected airframe used in this study. Performance and energy utilization results are shown in Section 9 for both the stand-alone turbojet engine and for the integrated airframe and engines, with a focus on cruise implications for energy utilization and considerations related to flight for the maximum range and endurance of a jet-propelled vehicle.
2. Energy Utilization Analysis of Aerospace Vehicle Systems
The energy utilization rate balance for an air-breathing aerospace vehicle in flight is written as:
This fundamental relationship represents the combination of the first and second laws of thermodynamics, as well as momentum and continuity principles, applied to a global control volume containing fluid in which the vehicle is embedded (see Figure 1 for a 2-D representation). The boundary of the global control volume is defined to envelope all the fluid wetted solid surfaces of the vehicle. This includes both external and internal surfaces of the vehicle (i.e., all wetted surfaces associated with aerodynamic, propulsive, fuel feed, and tankage systems). The balance equation given by Equation (1) mandates that the vehicle (net) force power that is realized (the productive utilization of energy) is equal to the overall energy availability rate (primarily associated with fuel flow rate) minus all losses in available energy that occur within the global control volume.
Figure 1.
Global control volume for vehicle exergy analysis.
In the energy utilization balance (Equation (1)), is the vehicle flight velocity magnitude, and is the net resultant force component on all solid surfaces of the vehicle in the direction of flight (traditionally the ‘thrust minus drag’, or net accelerative force in the instantaneous flight direction). The first term on the right-hand side, , represents the (net) rate of energy interactions (heat and/or work) into the fluid in the global control volume. This is energy supplied to (or extracted from) the fluid within the global control volume from sources external to said control volume (e.g., batteries on board the vehicle). , however, will be assumed to be negligible in this work; all available energy will be strictly associated with the fuel. The second term on the right-hand side represents the overall energy availability rate associated with the fuel flow rate leaving the fuel tank(s). is the total thermochemical availability of the fuel (maximum chemical and thermal work potential as measured with respect to the ambient conditions) [1], and is the energy availability associated with the kinetic energy of the on-board fuel (this latter term, however, is negligible in comparison with for the conventional flight atmospheric systems/vehicles considered in the present work). The third term on the right-hand side of Equation (1) represents the rate of loss of available energy. is the freestream ambient temperature, and is the net rate of entropy change across the global control volume from to .
For analysis, the global control volume is divided into three sub-control volumes (see Figure 1). The first sub-control volume is that associated with the vehicle zone of influence (i.e., the flow field surrounding the vehicle and directly impacted or influenced by the vehicle, extending axially from to , and including the internal propulsion and propellant flow paths and all fluid in propellant feed systems and tankage). The second sub-control volume is that region defined by the side-bounding ‘far-field’ flow that is at freestream conditions (especially relevant for high-speed systems), theoretically extending to infinity in the lateral plane and extending axially from to . The third sub-control volume is that associated with the vehicle wake; it is downstream of the vehicle exit plane (extending from station to station ). The inflow to the global control volume at station is undisturbed and uniform at the freestream conditions. The outflow of the global control volume at is uniform (i.e., equilibrated) and the flow properties at are (for the very large lateral extent of the global control volume), by definition, infinitesimally displaced from those of the freestream.
There are two contributions to the total entropy flow rate change across the global control volume: (1) entropy generated in (and transferred to) the fluid associated with the sub-control volume encompassing the vehicle zone of influence (which can be further sub-divided into contributions from the propulsion system and from the external aerodynamic system) and (2) entropy generated in the unconstrained wake sub-control volume:
The entropy generated in the wake equilibration process generally significantly exceeds the total entropy generated in the vehicle zone of influence, including within the propulsive system. Entropy generation due to irreversibilities and non-ideal effects in other non-propulsive and non-aerodynamic subsystems on board the vehicle most generally result in the transfer of rejected heat to the fluid within the control volume, and hence the energy utilization balance is inclusive of such effects.
The energy availability balance mandates that if the total entropy generation rate can be quantified at a known fuel flow rate and for a known thermochemical availability, the net resultant force acting on the vehicle in the direction of flight can be determined using Equation (1). Conversely, if the net force power is known, the entropy generation rate is then necessarily fixed. Furthermore, the complete quantification and composition of expended energy associated with the fuel can be assessed in terms of both realized productive force power and the specific performance losses associated with entropy generation details (identifiable in terms of individual loss mechanisms, components, processes, and sub-systems). The level of detail available for such quantification depends on the level of modeling used.
In terms of the energy utilization balance, an energy utilization effectiveness, can be defined to assess the degree to which the overall energy availability associated with the fuel is realized as force-based power at any given flight condition for a powered vehicle:
3. Energy Availability Analysis of a Stand-Alone Gas Turbine Engine
The general energy availability balance for aerospace vehicles, as summarized in the previous section, can be readily adapted to a stand-alone gas turbine engine operating in either subsonic or supersonic flow. Here, the term stand-alone refers to an engine in flight without consideration of an airframe and with the constraint that all losses (entropy generation) occur only in the engine flow-path itself, as well as in the wake downstream of the engine. In such an application and reflective of the approach described in the last section, the global control volume is again divided into three sub-control volumes (see Figure 2): (1) the ‘outer’ or side-bounding sub-control volume (streamtube) from to that is of an asymptotically large (lateral) extent in which the fluid external to the engine is taken to be isentropically processed, (2) the sub-control volume (streamtube) associated with the air that is inducted into the engine, and (3) the downstream wake mixing sub-control volume in which the disparate flows at station are eventually equilibrated (at station ).
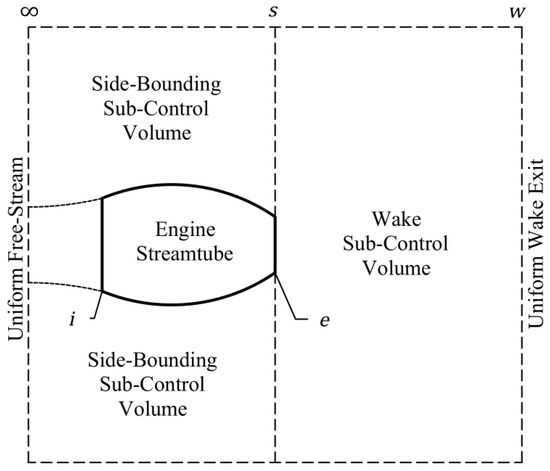
Figure 2.
Global control volume for stand-alone gas turbine engine exergy analysis.
Upstream of an engine, whether it is considered ‘stand-alone’ as defined above or attached to an airframe, external acceleration or deceleration of the captured airflow (for subsonic or subcritical engine operation) dictates that the propulsive flow path extends forward from the inlet face (station ) to the freestream (plane ). The actual (installed) thrust force delivered by an engine is the uninstalled thrust minus the sum of the additive and external cowl drags:
where:
From momentum considerations for the upstream captured streamtube entering an engine, the additive drag can be found as:
Furthermore, for a stand-alone engine configuration, with the requirement of isentropic flow in the side-bounding streamtube (mandating a frictionless external cowl) and the large lateral extent of this streamtube = , hence
Therefore:
For air-breathing (jet) engines, the thermochemical availability can be very closely approximated as the heating value of the fuel [1]. The installed thrust of the stand-alone jet engine in terms of heating value of fuel and total entropy generation rate (here subdivided between entropy generation in the engine streamtube from to , and entropy generation in the wake mixing zone from to , can then be determined with a known (or computed) wake entropy generation rate as:
Conversely, the entropy generation in the wake can be determined from a given (or computed) thrust using Equation (10). However, when it is desired to directly compute wake entropy generation from (upstream) flow rates at station (for instance to independently check the force obtained using the availability balance against the force obtained using engine flow-field modeling), a sufficiently large lateral dimension of the global streamtube must be used. The wake equilibration process (from plane to plane , where the flow is equilibrated and uniform) can then be modeled by enforcing conservation of mass flow rate, axial stream thrust, and total enthalpy flow rate between and , and solving for wake equilibrated conditions at station (thus allowing the computation of . With sufficiently large lateral extent of the global control volume, comparisons of the values of engine thrust obtained through momentum analysis (i.e., via classic cycle analysis) to values of engine thrust obtained independently from the energy availability balance have percent differences less than 10−6. In the current study, the ratio of cross-sectional area of the global control volume to the engine exit cross-sectional area is taken to be 109 for any direct computations of the wake entropy generation rate; this value is significantly larger than necessary but ensures asymptotic convergence (this corresponds to a square area of roughly 8 km for the modelled engine that has a nozzle exit diameter of about 0.3 m).
4. Energy Availability Analysis of an Unpowered Airframe
The overall energy availability balance can also be readily applied when considering the aerodynamics (drag characteristics) of an unpowered airframe; in fact, this situation corresponds to the first specific formulation and application of the global control volume approach with second law analysis by Oswatitsch [7]. The net axial force component developed on an unpowered airframe (colinear with the instantaneous flight direction) is the airframe drag, . In the absence of fuel usage, the energy availability balance for the unpowered airframe (with designating the entropy generation associated with the aerodynamics of the unpowered airframe from to ), simplifies to:
5. Vehicle Performance Model in Terms of Propulsive and Airframe Entropy Generation Rates
From the standpoint of flight performance, the dominant fluid dynamic force components experienced by a vehicle in atmospheric powered flight are associated with the airframe and with the propulsion system. For our purposes, conventional lift and drag are considered to be solely associated with the airframe, while the thrust is specifically associated with the defined propulsive flow path (the propulsion system), i.e., no consideration of thrust vectoring is made in the following development, although it can be incorporated readily. Note that the analysis is inclusive of airframe-engine integrated configurations as well, although care has to be taken to properly account for and allocate forces, based on the specifics of the performance accounting system being used and the exact delineations of engine and airframe boundaries and interfaces.
Consider the global control volume around a powered vehicle; the flow through the global control volume can be separated into a propulsive streamtube and an aerodynamic streamtube interacting with the airframe. These streamtubes can interact with each other but are separable in terms of both the mass flow rates of the air they process and their respective (exclusive) force interactions with either the engine solid surfaces or the airframe solid surfaces. The net instantaneous axial force developed on the vehicle in the flight direction is then written as:
or
The energy availability balance for the vehicle is written as:
The total entropy generation rate in the global control volume, , is composed of three contributions as follows:
If is considered small or, for convenience, is included in , a fundamental superposition principle for wake entropy generation can then be written as:
This wake entropy generation superposition principle states that the overall entropy generation in the wake of a powered vehicle is the summation of the entropy generation in the wake of the independently analyzed ‘stand-alone’ propulsion system and the entropy generation in the wake of the independently analyzed unpowered airframe.
6. Entropy Generation and Cruise; Range and Endurance
The performance of a powered vehicle in flight in terms of endurance, , and range, , are both related to the expenditure of fuel. The time traveled in cruise on a given amount of fuel is defined as the endurance, , of the vehicle. Endurance, by definition, is maximized when the time rate of fuel burned is minimized across the cruise leg. The distance traveled in cruise on a given amount of fuel is defined as the range, , of the vehicle. Range, by definition, is maximized when the fuel burned per unit distance travelled is minimized across the cruise leg. Flight conditions necessary for maximizing range and endurance for jet-propelled vehicles have traditionally been obtained in preliminary design by extension of the classic Breguet range and endurance methodology for propeller-driven vehicles based on cruise flight [34]. The range and endurance relationships that result are functions of thrust specific fuel consumption as well as specific aerodynamic flight characteristics of a jet-propelled vehicle in cruise. To an approximation, the time per unit mass of fuel burned in cruise is proportional to (the lift-to-drag ratio of the vehicle). Thus, when the vehicle is flown in cruise at an angle of attack and flight velocity corresponding to maximum , the endurance is approximately maximized. Likewise, the distance traveled per unit mass of fuel burned in cruise is approximately proportional to , such that range is maximized when this ratio is maximized, i.e., when the vehicle is flown in cruise at an angle of attack and flight velocity corresponding to this condition.
For a vehicle in cruise (i.e., neither accelerating nor decelerating in the flight direction), the net axial force developed on the vehicle is necessarily zero (). The energy availability balance then becomes:
This states that all availability associated with fuel usage (thermochemical and kinetic energy of the on-board stored fuel) is entirely lost. From Equation (17), flight at conditions corresponding to maximum endurance and maximum range, respectively, occur when the time rate of overall entropy generation is minimized and when the spatial rate of overall entropy generation is minimized, i.e.,:
In addition, Equation (17) can be rewritten based on the superposition principle in terms of separate contributions of the airframe and engine (evaluated at cruise flight conditions for the vehicle):
The total entropy generation rates on the right-hand side of Equation (20) are in turn composed of contributions occurring within the respective systems from to (again, evaluated at cruise flight conditions for the vehicle) and contributions occurring in the respective wake processes:
7. Turbojet Engine Specifications and Modeling Summary
This section provides the rationale and specifications for the fixed area single-spool turbojet engine modeled in this work, as well as a brief summary of the methodology used to characterize its performance across its operability envelope of allowable fuel throttle setting, flight Mach number, and altitude. Previous studies of availability and exergy in turbojet engines have generally performed cycle analysis (often simply assuming full mass capture without accounting for additive drag at all operational points). This effectively models the uninstalled performance of a family of engines as operating conditions are varied rather than the installed performance of a given engine. As an example, if compressor pressure ratio is kept constant as flight Mach number and altitude are varied, this is not reflective of the performance of a given engine, but rather actually models a family of engines with necessarily different compressors, since the performance of a given compressor (i.e., the compressor pressure ratio and efficiency) will necessarily change with flight Mach and/or altitude. Such analysis, then, does not account for individual engine component characteristics and the required matching of those components that is necessary to predict the performance of a given engine across the operational ranges of fuel throttle setting, flight Mach number, and altitude for that given engine. In addition, previous work on exergy/availability and gas turbine engine performance often make the assumption that the static pressure at the nozzle exit is equal to the ambient pressure at all operational points of interest. This assumption thus implicitly mandates a ‘flexible’ (non-constant) exit area of the engine rather than a given (specified) engine with fixed cross-sectional areas.
In addition, the specific values of , altitude, and flight Mach number at which a given engine is operated determine the mass flow rate of air inducted into the engine, i.e., the engine will accelerate or decelerate the upstream captured streamtube of air as necessary (determining the spillage characteristics and additive drag of that engine at those conditions). This information, for a given engine, must be obtained by a process of correctly matching components within the engine in order to correctly evaluate off-design performance. The component-matching methodology is applied in this work by utilizing a generic compressor performance map along with models for inlet, burner, turbine, and nozzle loss characteristics and a defined ‘on-design’ operating point in order to develop the full matched-component operating line for the engine. This in turn allows the analysis of the component-integrated engine performance (in terms of engine thrust, spillage, and RPM of the spool, as well as the energy availability characteristics) across the operational ranges of fuel throttle setting, flight Mach number, and altitude.
7.1. Turbojet Engine Selection and on-Design Point Specifications
The gas turbine engine modeled in this study is a single-spool turbojet engine with no afterburner, fixed geometry throughout, and a convergent nozzle with fixed exit area. The simplicity of such an engine selection when coupled with the appropriate component matching required for accurate off-design analysis facilitates the straightforward application and demonstration of the energy availability methodology discussed in earlier sections. Furthermore, the use of generic component performance maps and loss models in the analysis allows for the accurate generation of engine performance in terms of engine thrust, mass capture (spillage), and spool RPM across the allowable (off-design) ranges of fuel throttle setting, flight Mach number, and altitude. Engine component characteristics and (physical) sizing are chosen to be consistent with necessary required thrust requirements (for performance integration) for a specific airframe (vehicle airframe), to be described subsequently.
The on-design operational point for the defined turbojet corresponds to a flight Mach number of 0.85 at a standard altitude of 9 km and a fuel flow rate of 0.279 kg/s. For this defined on-design operational point, the compressor pressure ratio is 10 and compressor efficiency is 0.85; the engine produces 9.31 kN of thrust, the mass flow rate of air inducted is 14.49 kg/s, and the spool RPM is 15,000. The total temperature at burner exit is 1400 K. The inlet has a cross-sectional area of 0.1332 m2 (inlet area is sized to minimize spillage at the on-design point while avoiding excessive upstream acceleration at low-altitude low-speed operation) and the (convergent) nozzle exit has a cross-sectional area of 0.0666 m2 (with choked flow).
7.2. Turbojet Engine Control System Limits (Off-Design)
In calculation of off-design performance and losses, temperatures at turbine entrance greater than 1600 K were prohibited; this limit (along with the range on the generic compressor map that was utilized in this study) then led to limitations on the possible ranges of flight Mach number, fuel throttle setting, and altitude for the modeled engine.
7.3. Summary of Component Matching and Performance Evaluation Process for Off-Design Engine Operation
In order to be able to correctly predict the on and off-design performance of a specified engine, the coupling between integrated components (inlet, compressor, burner, turbine, and nozzle) must first be established, i.e., the individual components must be integrated (‘matched’) with each other. This drives the integrated-engine component operation lines on individual component performance maps. The information associated with this process then allows the correct prediction of the thrust, mass capture, and RPM across the off-design engine operational space of allowable flight Mach numbers, fuel throttle settings, and altitudes. The methodology of component matching and off-design performance evaluation is well-known and extensively documented in propulsion textbooks (see Refs. [35,36]). This section therefore provides only information relevant to specific modeling and component characterizations used in this particular work for the component matching for the defined turbojet engine.
7.3.1. Inlet
The adiabatic inlet total pressure loss model used for the turbojet engine is taken from [6]; this approximate model was developed by curve fitting over a wide representation of inlet data versus flight Mach number, as obtained from [35]. Captured streamtube characteristics, including spillage and additive drag, are determined by the specific fuel throttling, flight Mach number, and altitude operating point.
7.3.2. Compressor
The on and off-design component performance of the single-spool compressor integrated into the turbojet engine model is characterized, through component matching methodology as summarized in the previous section, by the development of a steady-state operating line on a selected generic compressor performance map. The modeled compressor allows for a wide operating range in terms of resulting component/engine performance. Specifically, for the selected compressor, the off-design variability in compressor pressure ratio ranges from 50% to 130% of the on-design value. Off-design corrected mass flow rates range from 55% to 115% of the on-design value and off-design corrected RPM range from 76% to 106% of the on-design RPM.
7.3.3. Burner
In order to simplify the analysis in this work (focused on demonstrating energy availability analysis for the overall engine), a burner map was not used; instead, the burner here is assumed to have negligible total pressure drop and no losses due to incomplete combustion or cooling of the flow.
7.3.4. Turbine
For the present work, the general turbine efficiency was assumed to be constant at 0.86 for both on-design and off-design performance; cooling of the turbine was also not considered. A more detailed analysis would incorporate an individual turbine performance map. This would allow for variations in the turbine efficiency as well as possible unchoking at the turbine entrance; however, turbine efficiency remains relatively constant and the flow at the turbine entrance usually remains choked across the engine on-off design operating envelope for a turbojet [36]. The inclusion of more detailed modeling of the turbine (i.e., utilization of the turbine performance map) is not necessary in the present work, which is focused on energy availability methodology and demonstration for a simple model of an engine.
7.3.5. Nozzle
Due to the relatively short length of the adiabatic nozzle required for the modeled turbojet and the lack of afterburning, the simplifying assumption is made in the current work that there is negligible total pressure loss through the nozzle.
7.3.6. Summary
Based on the engine operating line and loss information developed in the component matching methodology, as well as the fixed geometry (fixed cross-sectional areas throughout the engine) determined from on-design flight point requirements, flow properties at all engine stations are then readily computed for all possible fuel throttle settings, flight Mach numbers, and altitudes. This also allows for the computation of individual entropy generation rates for all individual engine components; energy availability losses for these individual engine components are then found by multiplying the specific entropy generation rate by the ambient temperature. Engine performance in terms of thrust (both uninstalled and installed), spool RPM, spillage, and overall entropy generation in the engine from to can then be computed as well (again, at all possible fuel throttle settings, flight Mach numbers, and altitudes, hence defining the performance-operability envelope for the given engine).
8. Airframe Specifications and Modeling Summary for Cruise Flight
Airframe and aerodynamic specifications in this work are based on the Northrop F-5E Tiger II. The F-5E is a legacy vehicle with well-documented aerodynamic characteristics; it was powered by two General Electric J85-GE-21 turbojet engines, each rated at 15.6 kN of dry thrust at sea-level (22.2 kN with afterburner), similar in terms of thrust performance to the turbojet engine modeled in this work. Specifically, thrust requirements and available thrust levels for cruise for this airframe are well matched using the respective engine model with this selected airframe. Specifications for the F-5E airframe [37] are given in Table 1 below.

Table 1.
Northrop F-5E Tiger II Specifications.
The airframe drag, , is calculated using the following classical airframe drag model [39]:
For cruising flight, aerodynamic lift () = vehicle weight () and airframe drag () = (). The thrust specific fuel consumption at a given fuel throttle setting, flight Mach number, and altitude is defined as:
Using the drag model given above and solving the energy availability balance for cruising flight (Equation (17)) in terms of , the following expression is obtained for in terms of airframe aerodynamic parameters, , vehicle weight , and freestream dynamic pressure :
From Equation (18), is minimized at the flight condition (flight velocity and vehicle angle of attack) corresponding to flight for maximum endurance. The thrust specific fuel consumption, , for a specific engine is, strictly speaking, a function of flight Mach number, altitude, and fuel throttle setting. At a flight/engine operational point, it can be estimated from simple engine cycle analysis or found using the higher-level methodology of component matching and subsequent off-design performance analysis for an engine (as described and applied in this paper). However, it is generally assumed to be approximately constant in basic range and endurance analysis, i.e., when finding the flight velocity required for maximum range and endurance. With this assumption, when is differentiated with respect to flight velocity and set to zero (and also noting that for gas turbine engines in general), the well-known requirement for flight for maximum endurance is obtained that parasite drag must be exactly balanced by the induced drag, i.e., .
Similarly, from Equation (17), can be written in terms of airframe aerodynamic parameters, , vehicle weight, and freestream dynamic pressure :
From Equation (19), this quantity must be minimized at the flight condition corresponding to maximum range. Furthermore, if this relationship is differentiated with respect to flight velocity and set to zero (again, ), the classic requirement for flight for maximum range is then obtained that the parasite drag is exactly three times the induced drag, i.e., . This analysis, along with the discussion in Section 6, therefore, provides the theoretical equivalence between the energy availability methodology (quantified in terms of entropy generation), classic range and endurance relationships, and flight conditions required to maximize range and endurance.
9. Results
This section of the paper provides quantitative results obtained using the energy utilization methodology as applied to specific engine and vehicle configurations. Selected details of the energy availability characteristics (and performance) of a defined turbojet engine in flight without airframe considerations are first presented. The modeling for this engine, and the resulting performance of the engine, has incorporated component matching (hence allowing the correct representation of actual on and off-design performance for a given engine, unlike most previous exergy studies which have not accounted for off-design engine behavior). This allows for the complete definition of the actual energy availability characteristics of a given engine across the complete range of off-design operational fuel throttle settings, flight Mach numbers, and altitudes for that engine. Representative results are then presented for the energy utilization characteristics (entropy generation) associated with a vehicle in cruise in terms of endurance and range. The airframe and propulsive models used in the range and endurance analysis are based on the aerodynamic and configurational characteristics of the F-5E Tiger II fighter and the defined turbojet engine, respectively, as discussed in previous sections.
9.1. Turbojet Engine Energy Utilization (No Airframe)
Table 2 provides a summary of five cases of engine-alone operation (each case representing operation at a specific fuel throttle setting, flight Mach number, and altitude). These cases were selected to provide representative results from the complete engine on/off-design performance/energy utilization study, with an emphasis on energy utilization and losses. Case 1 is the baseline nominal ‘on-design’ flight and engine operation condition (altitude 9 km, flight Mach number of 0.85, fuel flow rate of 0.279 kg/s, corresponding to a defined ‘100% on-design’ throttle setting, etc.). Cases 2 through 5 represent four distinct off-design operation points. Case 2 has the same flight Mach number and throttle setting as Case 1 but has an altitude of 4.5 km. Case 3 corresponds to the same altitude and fuel throttle setting as Case 1 but has a reduced flight Mach number of 0.6. Case 4 describes a flight Mach number of 1.25, while keeping altitude and fuel throttle at the on-design values. Case 5 denotes a 50% reduction in fuel throttle setting at on-design flight Mach number and altitude.

Table 2.
Comparative parameter values between the on-design case and the four off-design cases studied.
Figure 3 provides results for energy availability and losses for Cases 1 through 5. These results use relative values (as percent of overall energy availability) to facilitate comparisons and observations between the cases in subsequent discussions. In this figure, the far left-hand bar (in orange) represents the overall (initial) energy availability rate for all cases. This corresponds to 12.34 MW for Cases 1 through 4 and 6.17 MW for Case 5. The energy availability rate is decomposed for each case into contributions associated with individual engine component losses, wake loss, and the productive thrust power realized. Table 3 provides additional information for these five cases: including values of installed thrust, RPM, and spillage information, as well as compressor pressure ratios, fluid property ratios, etc. Examination of the information given in both Figure 3 and Table 3 allows for the comparative analysis of energy utilization and losses between these five cases. Because the data and information generated in these results are based on the operating line-determined performance of a specific engine (with integrated and matched components), a comparative analysis of the energy utilization increments between these cases can then be specifically related to changes in fuel throttle setting, altitude, and flight Mach number for that engine.
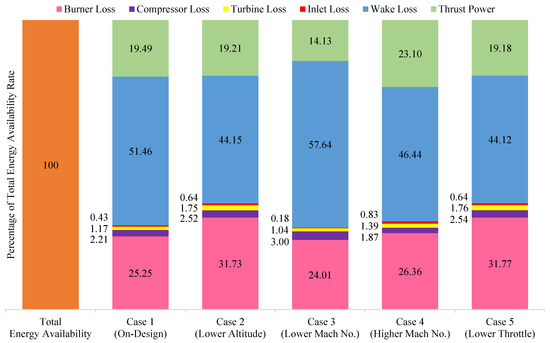
Figure 3.
Comparative energy availability breakdown for the different engine operating conditions.

Table 3.
Comparative parameter values for engine on- and off-design operations.
Figure 3 and Table 3 show that for Case 1, the on-design operating point, the wake mixing (equilibration) process is dominant in terms of entropy generation (losses). Wake loss represents approximately 64% of the total energy availability loss incurred by the engine at this condition. Wake entropy generation is driven by the degree of non-uniformity in the flow (the degree of non-equilibrium) between the propulsive and the side-bounding streamtubes at station (Section 2). The degree of this distortion entering the wake region for a given case is particularly indicated by the velocity ratio (nozzle exit to free stream) as provided in Table 3. Previous work has demonstrated the importance of the velocity ratio in terms of driving wake entropy generation behind powered aerospace vehicles in flight [15]. By the same token, the temperature and pressure ratios contribute as well to wake entropy generation.
For all individual engine component losses as well as the overall engine loss rate, loss rates in energy availability as given in Figure 3 (and Table 3) are directly proportional to the mass flow rate of air inducted into the engine (determined by flight and operating condition and resulting spillage characteristics upstream of the inlet face), as well as the individual component loss characteristics. Inlet energy availability losses are due to shocks, friction, etc.; inlet losses scale with flight Mach number via the inlet (diffuser) total pressure recovery model used. Compressor and turbine losses are functions of compressor and turbine efficiency, respectively, at a given operating point (in turn dependent on the operating line developed by the component matching for off-design performance analysis). Figure 3 shows that for Case 1, inlet and turbomachinery together account for only around 5% of the total lost availability rate; the compressor loss is larger than the turbine loss while the inlet loss is very small, as expected at a flight Mach of 0.85. Although significantly smaller than the wake loss, the burner generates the largest engine component loss (accounting for approximately 31% of overall lost energy availability) in comparison with all other engine components. As a consequence of all losses, only about 20% of the total initial available energy rate for the on-design point is realized as thrust power. This fraction represents the instantaneous energy availability utilization effectiveness .
The comparative (relative) values of the various losses in the individual components at the on-design condition (i.e., the burner clearly representing the largest engine component loss, followed by the compressor, etc.) are well-established by previous exergy and availability studies of gas turbine (jet) engines. However, because off-design engine performance is appropriately modeled using component matching in the present work, variations in individual component and wake energy availability loss rates can be directly associated with (and explained in terms of) changes in fuel throttle setting, flight Mach number, and altitude for a given engine. Hence, Case 2, which represents an off-design condition at the same fuel throttle setting and flight Mach as Case 1 (on-design), but at a lower altitude, has markedly larger respective burner losses (39%) and less wake losses (55%) than those same losses experienced in Case 1. This is due to the fact that Case 2, even with the increase in total temperature entering the compressor due to the lower altitude, represents engine operation at significantly lower RPM and lower compressor pressure ratio than Case 1 (i.e., it is operating lower on the engine operating line on the compressor map). The reduced compression results in a reduction in the thermal efficiency in the burner (, where is the total/stagnation temperature at compressor exit), therefore generating higher entropy in that component. Concurrently, wake losses decrease for Case 2 (relative to Case 1; on-design) since the nozzle exit conditions are closer to the freestream conditions for this spooled-down engine operation point. Due to the trade between wake loss and burner losses, thrust power contribution to the overall energy availability balance does not change appreciably between Case 1 and Case 2.
Case 3 (for a lower flight Mach number), in comparison to Case 1, demonstrates reduced burner losses and much greater wake loss (i.e., the increase in wake loss is significantly greater than the drop in burner losses). There are negligible inlet losses due to the low subsonic flight Mach number. The decreased burner losses as well as the increased wake loss are primarily because Case 3 represents a high RPM, high compressor pressure ratio condition for the engine (i.e., is higher on the operating line than the on-design operating point), see Table 3. The high compression results in increased thermal efficiency, hence lower losses in the burner. However, the larger gradients that then inherently exist at the nozzle exit (i.e., as seen in the velocity ratio between nozzle exit and freestream, etc.) and the increased mass flow rate of air generate increased entropy in the wake. Additionally, as flight Mach is reduced, the thrust power contribution necessarily drops (due to the lower flight velocity); thrust may increase marginally (as it does in this case) but thrust power drops overall, with the increased entropy generation necessarily appearing in the wake.
Case 4 (for a higher flight Mach number of 1.25) in comparison to Case 1 shows the expected increase in thrust power due to the increase in flight velocity; this occurs even though thrust has decreased. All loss increments in the energy availability balance are therefore necessarily reduced in part because of this effect (increased productive utilization of available energy, due to the higher flight velocity). However, this case represents a spooled-down operation point for this engine in terms of compressor pressure ratio, RPM, and inducted mass flow rate (high spillage). Wake loss is noticeably decreased; this is due again to the reduction in entropy generation associated with reduced fluid properties’ gradients between engine exit flow and the side-bounding flow at plane . Wake loss, however, still remains the largest loss contribution at 60%; burner losses represent 34% of total losses. Inlet loss increases markedly at this supersonic flight Mach number, as expected due to shock losses.
Case 5 (50% reduction in fuel throttling rate while maintaining on-design flight Mach number and altitude) in comparison to Case 1 inherently provides for loss rate reductions across the board of around a factor of two due to the proportional reduction in heat release in the burner. However, for this case, there is a relative increase in the burner loss as compared to the wake loss. This is driven by the fact that this low-throttle engine condition represents a very low RPM and a spooled down operating point (lower proportional mass flow rate of air inducted). This drives down the thermal efficiency (due to decreased pressure and temperature in the burner). This same effect, however, reduces gradients and the resulting entropy generation in the wake relative to the burner entropy generation and relative to the wake entropy generation contribution to losses seen for Case 1.
9.2. Selected Graphical Results of Engine Performance/Energy Availability Characteristics across the Operating Range
Previous results and analysis (Figure 3, Table 3 and associated discussion) give significant insight in terms of understanding (diagnosing) basic performance and corresponding energy availability losses for this engine. This was done by choosing five (discrete) off-design operation points, including the nominal on-design point. However, complete engine performance descriptions (i.e., thrust, RPM, mass capture, losses, and details of energy availability balances and relative loss contributions) are complex constructs defined at every point within the engine operational envelope of fuel throttle setting, flight Mach number, and altitude.
Figure 4 and Figure 5 illustrate selected energy availability information in terms of slices through the operational space of the engine. Specifically, Figure 4 provides contours of the ratio of entropy generation in the wake to the entropy generation in the engine for the modeled turbojet at 9 km altitude across ranges of flight Mach number and fuel throttle setting. Figure 5 provides contours of the same ratio for 100% (nominal) fuel flow rate across ranges of flight Mach number and altitude. Recall that the entropy generation in the engine is dominated by burner losses. These figures show that the ratio of wake entropy to engine entropy generation tends to increase with increasing throttle and altitude while tending to decrease with increasing flight Mach number. Within the entire envelope of engine operation, this quantity has a minimum that is close to unity (i.e., the wake and engine losses in availability are approximately the same) and has a maximum of around 2.5. As discussed at length in the more detailed analysis of specific off-design cases in the previous section, variance in this ratio (wake to engine loss) is mainly due to the effects of changing thermal efficiency, increased or decreased spooling of the engine and movement on the engine operating line, and changing fluid/thermodynamic gradients between engine exhaust flow and ambient.
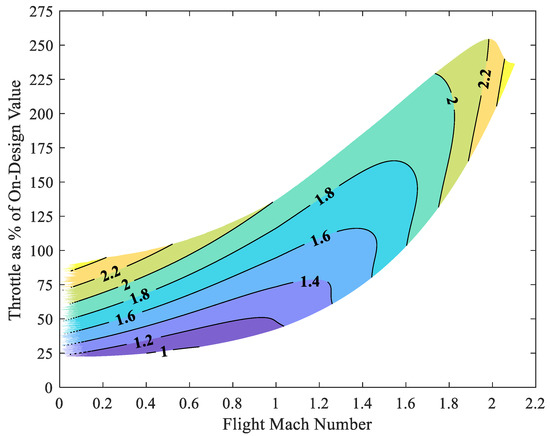
Figure 4.
Ratio of entropy generation rate in the wake to entropy generation rate in the engine at 9 km altitude.
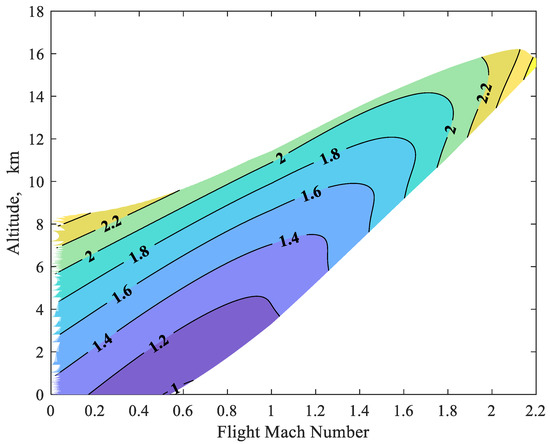
Figure 5.
Ratio of entropy generation rate in the wake to entropy generation rate in the engine at 100% on-design fuel throttle setting.
9.3. Endurance, Range, and Entropy Generation; A Case Study (Airframe-Engine Integration)
Previous Section 6 and Section 8 have developed and described the relationships between energy availability (entropy generation) and the endurance and range of a jet-powered vehicle in flight. Flight conditions for maximum endurance and range have been shown to correspond to the minimum time rate and the minimum spatial rate of overall entropy generation, respectively, within the global control volume in which a vehicle is embedded. In addition, classic maximum endurance and range parameters such as lift to drag relationships and the balances between parasite and induced drag have been shown to be directly related to energy availability considerations. The analysis developed in this paper also provides the methodology for separately assessing and then combining entropy generations and energy utilization for the airframe and for the propulsion system. A quantitative case study of energy utilization and range and endurance in cruise flight is now performed for a specific vehicle configuration for which a selected legacy airframe drag model (based on the twin-engine Northrop F-5E Tiger II, as described in Section 8) is integrated with the turbojet engine model developed in this work. Specifically, two turbojet engines are integrated with the F-5E airframe to provide a complete powered vehicle model for this study. Entropy generation characteristics for cruise flight are then assessed in conjunction with classic relationships and parameters for range and endurance.
The parabolic curve in Figure 6 shows the aerodynamic drag generated by the F-5E airframe at 9 km altitude versus flight velocity. This drag is based on the aerodynamic parameters for the F-5E airframe and the nominal vehicle gross weight as given in Section 8. The magnitude of drag at a given flight velocity is, by definition, the engine thrust required for the vehicle (consisting of both engine and airframe) to cruise; there is a minimum in thrust required (airframe drag) at a specific velocity, due to the trade between induced drag and parasite drag. In Figure 6, the line defining the thrust required for cruise is shown overlaid on a carpet plot of actual (available) thrusts provided by the two turbojet engines at this altitude for various fuel throttling rates, across the range of flight velocities. This underlying carpet plot of engine performance (shown as lines of constant ) is generated using the component-matched (off-design) turbojet analysis and methodology described earlier; the required thrust distribution for cruise across a wide range of flight velocities for the F-5E airframe is seen to lie within the envelope of the performance of the engine. The flight velocity associated with the minimum thrust required is also seen to be very close to the minimum fuel flow rate, as expected.
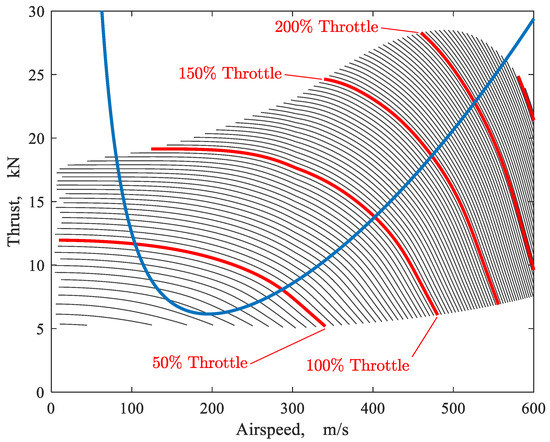
Figure 6.
Thrust required (blue line) for cruise for F-5E airframe overlaid on twin turbojets performance envelope (thrust versus fuel flow rate). Altitude = 9 km.
In Figure 7, four parameters associated with endurance in cruise for this aircraft configuration (integrated airframe and turbojet engines together) are plotted over a range of flight velocities at an altitude of 9 km. These parameters are mass flow rate of fuel required to cruise (obtained from the off-design engine analysis at the required thrust), overall entropy generation in the global control volume (also obtained from the off-design engine and airframe analysis), lift-to-drag ratio , and the required thrust (which is the airframe drag). Endurance for 1 gram of fuel consumed at the nominal gross weight is also plotted. All parameters are normalized by their respective extrema in order to clearly and easily compare characteristics. , , and thrust required are normalized by their minimum values of 174.4 g/s, 33.57 kW/K, and 6.15 kN, respectively. and endurance are normalized by their maximum values of 11.42 and 0.00573 s/g. It is seen that all four parameters, as expected from classic endurance relationships and from the energy availability analysis as developed and described in this work, give approximately similar results for the flight condition for maximum endurance. There is, however, as expected, a difference in terms of the flight velocity at which maximum lift-to-drag ratio and minimum thrust required occurs (as compared to the actual flight velocity required for maximum endurance, i.e., at minimum and minimum ). Whereas the flight velocity corresponding to maximum endurance is 168 m/s, the flight velocity corresponding to maximum lift-to-drag ratio is 195 m/s. This difference is due to the approximation in the classic endurance formulation that thrust specific fuel consumption () is constant with flight velocity. This approximation results in the condition that be maximized (and hence thrust required minimized) for flight conditions corresponding to maximum endurance (see the discussion in Section 8).
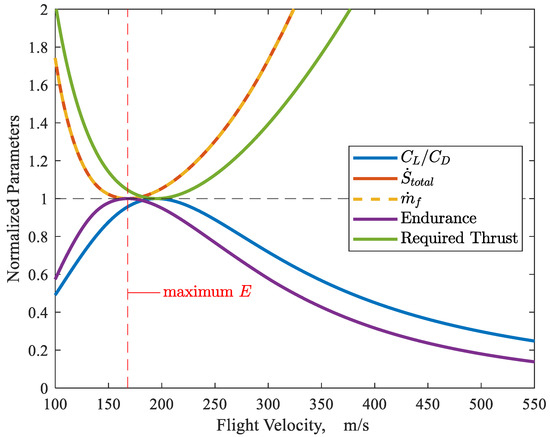
Figure 7.
Normalized endurance related parameters over range of flight velocities. F-5E airframe with modelled turbojet engines. Altitude = 9 km.
Figure 8 provides a plot of three parameters associated with range in cruise for the modeled vehicle (the F-5E airframe powered by a pair of the modeled turbojet) across the flight velocity range. These parameters are mass of fuel per distance traveled, (obtained from the off-design engine analysis at the required thrust), overall entropy generated per distance traveled (also obtained from the off-design engine analysis), and the ratio (obtained from the airframe model). The range for 1 gram of fuel consumed at the nominal gross weight is also plotted. These parameters are normalized by their respective extrema; and are normalized by their minimum values of 0.896 g/m and 172.5 N/K, respectively. and range are normalized by their maximum values of 19.3 and 1.116 m/g, respectively. For range (similar to observations regarding endurance in Figure 7), all four parameters in Figure 8, as expected from classic range relationships and from the energy availability analysis as developed and described in this work, yield approximately similar results for the flight condition required for maximum range. Referring to the discussion of Figure 7, however, and for the same reason that maximum is an approximate condition for maximum endurance, maximum also occurs at a somewhat different flight velocity (257 m/s) than that corresponding to a maximum range (226 m/s).
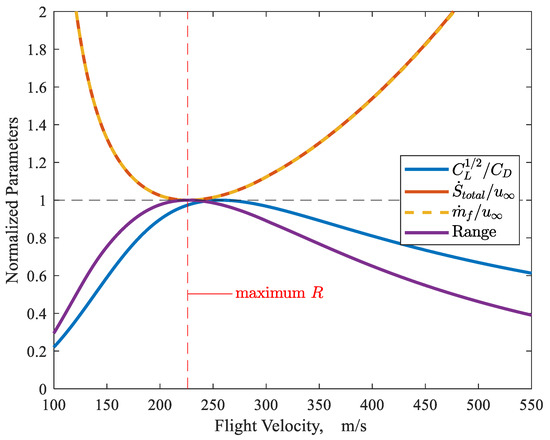
Figure 8.
Normalized range related parameters over range of flight velocities. F-5E airframe with modelled turbojet engines. Altitude = 9 km.
Figure 9 shows the total entropy generation rate versus flight velocity for the powered vehicle in cruise as the summation of the respective contributions associated with propulsion system and airframe, reflecting the superposition principle for losses described in Section 6. In Figure 9, the top (yellow) line represents the total entropy generation rate that occurs in the overall global control volume that encompasses the powered vehicle from freestream to wake exit plane (see Figure 2 for station designations). The bottom (blue) line represents the entropy generation rate within the propulsive flow paths (not including wake), i.e., from freestream to wake region entrance plane . The increment between the blue (bottom) line and the middle (orange) line represents the entropy generation that specifically occurs in the wake of the (twin-engine) propulsion system (analyzed without an airframe). Therefore, the middle (orange) line provides the total entropy generation rate associated with the propulsion system without airframe considerations, encompassing all losses: (1) in the upstream acceleration/deceleration captured streamtubes from to (inlet face), (2) inside the engines from to (engine exit), and (3) in the wakes of the stand-alone engines (from to ). Finally, the increment between the orange (middle) and yellow (top) lines represents the total entropy generation associated with the unpowered airframe. This increment includes losses upstream of the unpowered airframe wake, as well as losses within that wake. At a flight velocity of 168 m/s, corresponding to the minimum total entropy generation rate for the vehicle (which, as demonstrated in this work, also corresponds to maximum endurance), the propulsion system accounts for approximately 86% of the overall entropy generation (with the remaining 14% of losses associated with the airframe). Additionally, at this flight velocity, the propulsive system alone (no airframe) wake losses are seen to be approximately equal to the propulsive flow path losses occurring upstream of the wake. This relatively low ratio (approximately 1) of wake to engine entropy generations in the propulsive system analysis is entirely due to the low throttle operation of the engines at this point (i.e., at very near minimum thrust required, as described in previous discussion).
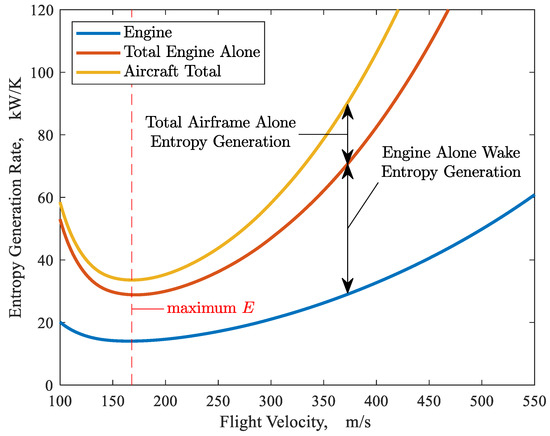
Figure 9.
Total aircraft entropy generation rate breakdown over range of flight velocities. F-5E airframe with modelled turbojet engines. Altitude = 9 km.
10. Discussion
The fundamental energy utilization balance for an air-breathing aerospace vehicle in flight represents the synthesis of both the first and second laws of thermodynamics and flight mechanics. This balance, as derived from the global control volume approach, directly (analytically) links classic vehicle force-based performance at a given flight condition to available energy associated with the propellant, and to losses in that available energy. While the global control volume approach and the resulting energy utilization balances (both rate-based and mission-integrated) have been previously described and applied in a number of works, including detailed analyses of scramjets and rockets, it has not been previously applied to the analysis of airframe/jet engine configurations in terms of cruise requirements.
In this paper, the energy availability balance is first specialized to allow the full analysis of the performance and energy utilization of a stand-alone gas turbine (jet) engine (without airframe considerations); this analysis accounts for additive drag effects and characterizes wake impacts as well as the contributions of individual engine components, in terms of entropy generation and resultant losses in installed engine thrust. Detailed results for five selected cases of engine-alone operation are obtained. These cases include the on-design point (defined by its specific fuel throttle rate, flight Mach number, and altitude) and four off-design points, each representing a variation in fuel throttle setting, flight Mach, and altitude from the design point values. Results obtained incorporate, for all five cases, both conventional off-design engine performance (installed thrust, spillage, additive drag, component performance, thermal efficiency, etc.) as well as significant parameters and information related to energy utilization and the energy utilization balance for the engine. For both on and off-design engine operation, the loss in overall energy availability (reflecting a reduction in delivered thrust) is dominated by the wake entropy generation. Within the engine itself, relative to other engine components, the burner is dominant in terms of entropy generation. Other component losses are generally very small in comparison to the burner loss. These results are expected, based on previous exergetic studies of similar gas turbines using, for instance, cycle analysis. However, because the results obtained in this study accurately reflect actual off-design performance of the (given) engine (rather than cycle analysis results), direct assessments of the linkage and drivers between energy utilization and entropy generation and the observed performance of the engine can be made in a consistent fashion between on and off-design points.
Specifically, by examining and comparing (stand-alone) engine conventional performance in conjunction with energy utilization results for the off-design cases, the two dominant influences on wake entropy generation are seen to be: (1) the degree of distortion at the (engine) exit plane and (2) the (related) engine operating point, RPM and spooling characteristics; these factors all determined by the specific fuel throttle setting, flight Mach number, and altitude for any particular case. In terms of the impact of the degree of distortion at engine exit plane, the wake entropy generation is observed to be (especially) correlated with the nozzle exit velocity to freestream velocity ratio, in line with previous energy availability studies for aerospace systems. The burner entropy generation, representing by far the largest loss within the engine itself, is driven (as expected) primarily by the thermal efficiency, which in turn is strongly related to the specific engine operating point, RPM, and spooling characteristics (as well as flight conditions).
In order to more comprehensively illustrate the actual envelope of off-design engine performance and energy utilization behavior obtained by the analysis in this paper, selected contour plots of the ratio of entropy generation in the wake to entropy generation in the engine are provided. These results are shown for varying flight Mach numbers and fuel flow rates at a given altitude and for varying flight Mach numbers and altitudes at a given fuel throttle setting and emphasize the dominant role of the losses in the wake in terms of overall utilization of available energy.
In addition to the employment of the energy availability balance to the study of a stand-alone engine, the balance is also applied to provide the energy utilization characteristics of an unpowered airframe in terms of drag of the airframe and resulting entropy generation. These engine-only and airframe-only energy utilization formulations are then combined analytically. This combination provides the capability to assess the overall performance of a jet-powered aircraft in terms of energy utilization. A superposition principal results from the analysis: the entropy generation that actually occurs in the wake of a powered vehicle is the summation of the entropy generations that (separately) occur in the modeled wake of its stand-alone (analyzed with no airframe) propulsion system and in the modeled wake of its airframe (analyzed with no propulsion system).
Entropy generation and energy utilization that are experienced by a vehicle in cruise are next formulated, utilizing the airframe drag model, with a focus on the flight conditions corresponding to maximum endurance and maximum range. The relationship of entropy generation and energy availability to classic range and endurance conditions is described. The theoretical requirement that overall entropy generation temporal rate in the global control volume must be minimized for a jet-powered vehicle at the flight condition for maximum endurance results from this analysis; similarly, the fundamental requirement that overall entropy generation spatial rate be minimized for maximum range is also shown. Additionally, energy utilization analysis in terms of entropy generation is shown to give the well-known (classic) balances between induced and parasite drag contributions required for maximum endurance and range, respectively. These characteristics of the entropy generation at cruise, as developed theoretically and then illustrated in this application, are fundamental requirements that emerge from the energy availability balance. Furthermore, the classic maximum endurance and range flight conditions involving the necessary balances of lift and drag are shown in this vehicle application to also correlate with the energy availability (entropy generation) results. These results also provide verification of theoretical derivations in this paper; the well-known lift and drag balances required for maximum endurance and maximum range, as well as the associated balances between parasite drag and induced drag, can be obtained directly from energy utilization analysis and global control volume-based considerations of entropy generation.
The work described in this paper provides the methodology necessary to apply the global control volume/energy utilization approach to both stand-alone gas turbine engines and to powered airframes with jet propulsion in the atmosphere. This methodology supplements (but does not replace) both traditional momentum-based analysis and conventional exergetic methods. Specifically, it allows new insight into the second-law aspects of powered flight. For instance, as shown in this paper, the approach uniquely enables the derivation of the necessary conditions for maximum range and endurance for cruise flight in terms of overall entropy generation. It is believed that the most promising use of this methodology undoubtably is in system-level analysis and optimization of aerospace flight systems. Entropy generation inherently provides a single universal metric of losses for all components, processes, and sub-systems associated with the flight of a vehicle. The methodology described in this paper enables the comprehensive and complete assessment of system-level performance losses and relationships in overall entropy generation, including wake effects, for the applications of interest.
Author Contributions
Conceptualization, M.A. and D.W.R.; methodology, M.A. and D.W.R.; software, M.A.; validation, M.A. and D.W.R.; formal analysis, M.A. and D.W.R.; investigation, M.A. and D.W.R.; resources, D.W.R.; data curation, M.A.; writing—original draft preparation, M.A.; writing—review and editing, M.A. and D.W.R.; visualization, M.A.; supervision, D.W.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| cross-sectional area, m2 | |
| aspect ratio | |
| aircraft drag coefficient | |
| induced drag coefficient | |
| parasitic (zero-lift) drag coefficient | |
| aircraft lift coefficient | |
| thrust specific fuel consumption, kg/N-s | |
| aerodynamic drag, N | |
| additive drag, N | |
| aircraft cruise endurance, sec | |
| net rate of energy transfer rate into a control volume (both heat and work), W | |
| Oswald efficiency factor | |
| net force in the direction of flight, N | |
| lower heating value of the fuel, J/kg | |
| total thermochemical availability, J/kg | |
| lift, N | |
| fuel mass, kg | |
| mass flow rate, kg/s | |
| fuel mass flow rate, kg/s | |
| unit vector in the direction of flight | |
| static pressure, N/m2 | |
| dynamic pressure, N/m2 | |
| aircraft cruise range, m | |
| planform area or control surface area, m2 | |
| time rate of change in entropy (generation for most cases) across a streamtube, W/K | |
| static temperature, K | |
| flow velocity, m/s | |
| flight/freestream velocity, m/s | |
| aircraft gross weight, N | |
| instantaneous energy utilization effectiveness | |
| mass density, kg/m3 | |
| shear stress | |
| Subscripts | |
| engine (nozzle) exit plane | |
| engine inlet plane | |
| exit plane of side-bounding sub-control volume | |
| exit plane of wake sub-control volume | |
| axial direction; direction of flight | |
| freestream conditions; upstream (entrance) plane of global control volume | |
References
- Riggins, D.W.; Taylor, T.; Moorhouse, D.J. Methodology for Performance Analysis of Aerospace Vehicles Using the Laws of Thermodynamics. J. Aircr. 2006, 43, 953–963. [Google Scholar] [CrossRef]
- Riggins, D.W.; Moorhouse, D.J.; Camberos, J.A. Characterization of Aerospace Vehicle Performance and Mission Analysis Using Thermodynamic Availability. J. Aircr. 2010, 47, 904–916. [Google Scholar] [CrossRef]
- Riggins, D.; Taylor, T.; Moorhouse, D.; Terhune, L. Methods for the Design of Energy Efficient High-Speed Aerospace Vehicles. Aeronaut. J. 2007, 111, 297–309. [Google Scholar] [CrossRef] [Green Version]
- Riggins, D.W.; Camberos, J.; Wolff, M.; Bowcutt, K. Mission-Integrated Exergy Analysis for Hypersonic Vehicles: Methodology and Application. J. Propuls. Power 2013, 29, 610–620. [Google Scholar] [CrossRef]
- Riggins, D.W.; Abbas, M.; Wainwright, M.; Camberos, J. Analysis of Energy Utilization for Chemical Rockets. J. Spacecr. Rocket. 2019, 56, 695–707. [Google Scholar] [CrossRef]
- Abbas, M.; Riggins, D.; Watson, M.D. Entropy-Based Performance Analysis of Chemical Rockets. In AIAA Scitech 2020 Forum; AIAA Paper 2020-0759; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2020. [Google Scholar] [CrossRef]
- Oswatitsch, K. General Equations and Theorems. In Gas Dynamics; Academic Press Inc.: New York, NY, USA, 1956; pp. 177–210. [Google Scholar]
- Giles, M.; Cummingst, R.M. Wake Integration for Three-Dimensional Flowfield Computations: Theoretical Development. J. Aircr. 1999, 36, 357–365. [Google Scholar] [CrossRef]
- Marley, C.; Riggins, D. The thermodynamics of Exergy Losses and Thrust Production in Gas Turbine engines. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, AIAA Paper 2011-6130, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar] [CrossRef]
- Marley, C.; Riggins, D. Exergy Analysis of a Turbojet Engine Modeled as a Lumped Parameter System. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA Paper 2012-1122, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Abbas, M.; Riggins, D.W. Exergy-Based Performance Analysis of a Turbojet Engine. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, AIAA Paper 2016-4638, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef]
- Foa, J. Efficiencies: Propulsive Cycles. In Elements of Flight Propulsion; Wiley: New York, NY, USA, 1960; pp. 274–287. [Google Scholar]
- Builder, C.H. On the Thermodynamic Spectrum of Air-Breathing Propulsion. In Proceedings of the 1st Annual Meeting, AIAA Paper 64-243, Washington, DC, USA, 29 June–2 July 1964. [Google Scholar] [CrossRef]
- Lewis, J.H., III. Propulsive Efficiency from an Energy Utilization Standpoint. J. Aircr. 1976, 13, 299–302. [Google Scholar] [CrossRef]
- Clarke, J.M.; Horlock, J.H. Availability and Propulsion. J. Mech. Eng. Sci. 1975, 17, 223–232. [Google Scholar] [CrossRef]
- Czysz, P.; Murthy, S.N.B. Energy Analysis of High-Speed Flight Systems, Chapter 3. In High-Speed Flight Propulsion Systems; Progress in Astronautics and Aeronautics Series; AIAA: Reston, VA, USA, 2012; Volume 137. [Google Scholar] [CrossRef]
- Murthy, S.N.B. Effectiveness of a Scram Engine. In Proceedings of the 30th Joint Propulsion Conference and Exhibit, AIAA Paper 94-3087, Indianapolis, IN, USA, 27–29 June 1994. [Google Scholar] [CrossRef]
- Brilliant, H.M. Analysis of Scramjet Engines Using Exergy Methods. In Proceedings of the 31th Joint Propulsion Conference and Exhibit, AIAA Paper 95-2767, San Diego, CA, USA, 10–12 July 1995. [Google Scholar] [CrossRef]
- Curran, E.T.; Craig, R.R. The Use of Stream Thrust Concepts for the Approximate Evaluation of Hypersonic Ramjet Engine Performance; Technical Report AFAPL-TR-73-38; Air Force Aero Propulsion Laboratory: Dayton, OH, USA, 1973. [Google Scholar]
- Riggins, D.W. The Thermodynamic Continuum of Jet Engine Performance; The Principle of Lost Work due to Irreversibility in Aerospace Systems. Int. J. Thermodyn. 2003, 6, 107–120. [Google Scholar] [CrossRef]
- Riggins, D.W.; McClinton, C.R.; Vitt, P.H. Thrust Losses in Hypersonic Engines Part 1: Methodology. J. Propuls. Power 1997, 13, 281–287. [Google Scholar] [CrossRef]
- Riggins, D.W. Thrust Losses in Hypersonic Engines Part 2: Applications. J. Propuls. Power 1997, 13, 288–295. [Google Scholar] [CrossRef]
- Roth, B.A.; Mavris, D.N. Comparison of Thermodynamic Loss Models Suitable for Gas Turbine Propulsion. J. Propuls. Power 2001, 17, 324–332. [Google Scholar] [CrossRef]
- Roth, B. Work Potential Perspective of Engine Component Performance. J. Propuls. Power 2002, 18, 1183–1190. [Google Scholar] [CrossRef]
- Ehyaei, M.; Anjiridezfuli, A.; Rosen, M. Exergetic analysis of an aircraft turbojet engine with an afterburner. Therm. Sci. 2013, 17, 1181–1194. [Google Scholar] [CrossRef] [Green Version]
- Etele, J.; Rosen, M.A. Sensitivity of exergy efficiencies of aerospace engines to reference environment selection. Exergy Int. J. 2001, 1, 91–99. [Google Scholar] [CrossRef]
- Doty, J.; Camberos, J.; Moorhouse, D. Benefits of Exergy-Based Analysis for Aerospace Engineering Applications: Part 1. In Proceedings of the 40th Thermophysics Conference, AIAA Paper 2008-4355, Seattle, WA, USA, 23–26 June 2008. [Google Scholar] [CrossRef]
- Arntz, A.; Atinault, O.; Merlen, A. Exergy-Based Formulation for Aircraft Aeropropulsive Performance Assessment: Theoretical Development. AIAA J. 2015, 53, 1627–1639. [Google Scholar] [CrossRef] [Green Version]
- Bastani, M.; Jafari, R.; Ghasemi, H. Exergy Analysis of an Aircraft Turbojet Engine. Int. J. Eng. Sci. Res. Technol. 2015, 4, 380–386. [Google Scholar]
- Karakoc, T.H.; Turan, O. Exergetic Destruction Effects of Operating Conditions on the Turbojet Engine Components. Appl. Mech. Mater. 2011, 110–116, 2390–2394. [Google Scholar] [CrossRef]
- Turan, O.; Karakoc, T.H. Exergetic and Energetic Response Surfaces for Small Turbojet Engine. Appl. Mech. Mater. 2011, 110–116, 1054–1058. [Google Scholar] [CrossRef]
- Yuksel, B.; Balli, O.; Gunerhan, H.; Hepbasli, A.; Atalay, H. Exergetic and Environmental Analyses of Turbojet Engine. In Proceedings of the 7th Global Conference on Global Warming (GCGW-2018), Izmir, Turkey, 24–28 June 2018. [Google Scholar]
- Grönstedt, T.; Irannezhad, M.; Lei, X.; Thulin, O.; Lundbladh, A. First and Second Law Analysis of Future Aircraft Engines. J. Eng. Gas Turbines Power 2014, 136, 031202. [Google Scholar] [CrossRef]
- Anderson, J.D. Introduction to Flight, 7th ed.; McGraw-Hill: New York, NY, USA, 2012; pp. 506–513. [Google Scholar]
- Mattingly, J.D. Elements of Propulsion: Gas Turbines and Rockets; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006; pp. 358–359, 437–769. [Google Scholar]
- Oates, G.C. Aerothermodynamics of Gas Turbine and Rocket Propulsion, 3rd ed.; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1997; pp. 277–322. [Google Scholar]
- Loftin, L.K. Quest for Performance: The Evolution of Modern Aircraft; National Aeronautics and Space Administration, History Office: Washington, DC, USA, 1985; pp. 488–492. [Google Scholar]
- Schaufele, R.D. The Elements of Aircraft Preliminary Design; Aries Publications: Santa Anna, CA, USA, 2000; p. 238. [Google Scholar]
- Anderson, J.D. Fundamentals of Aerodynamics, 5th ed.; McGraw-Hill: New York, NY, USA, 2011; pp. 502–503. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).