Weather Variability Induced Uncertainty of Contrail Radiative Forcing
Abstract
1. Introduction
2. Data and Methods
2.1. Data from Commercial Aircraft
2.2. Reanalysis Data
2.3. Methods
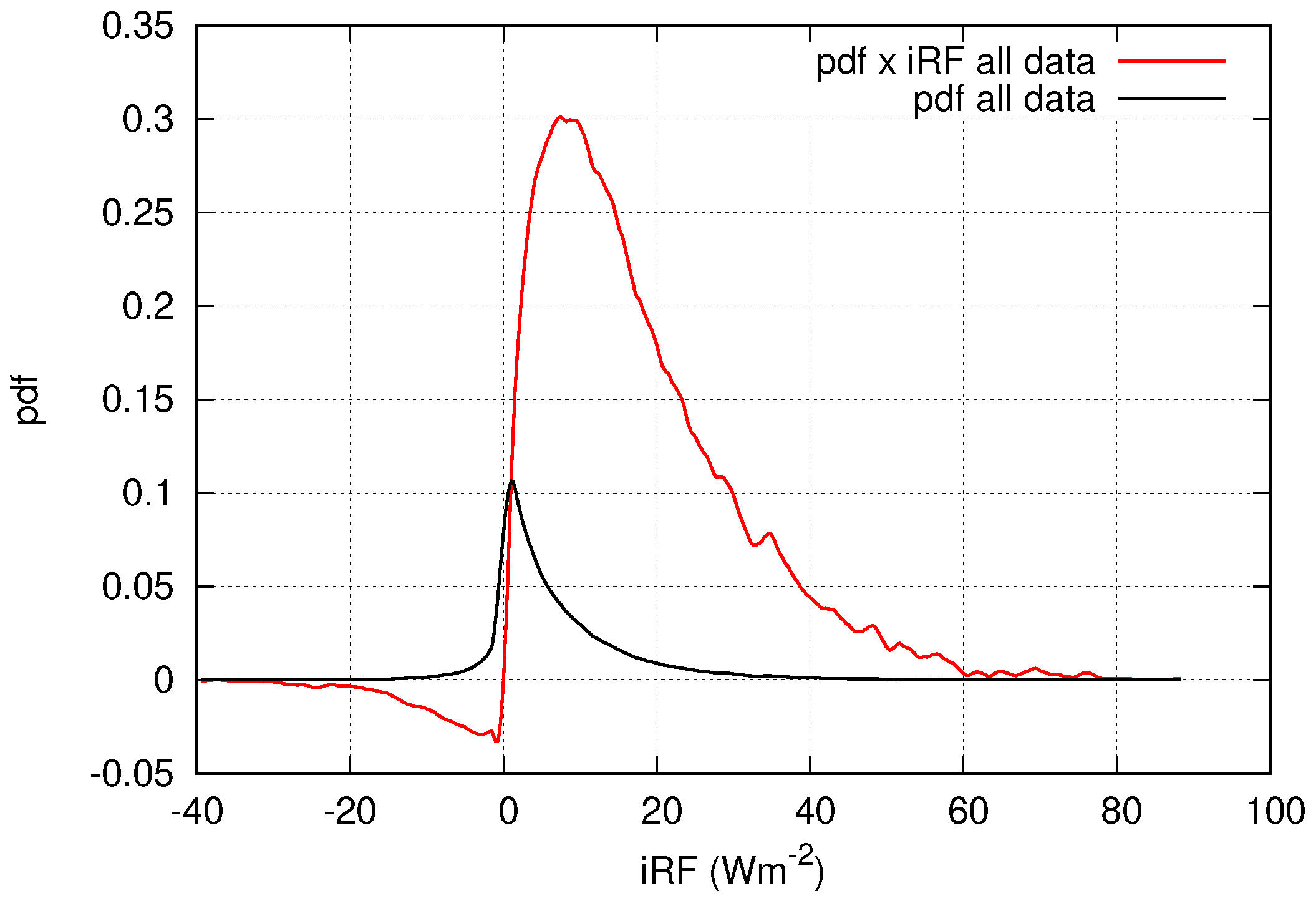
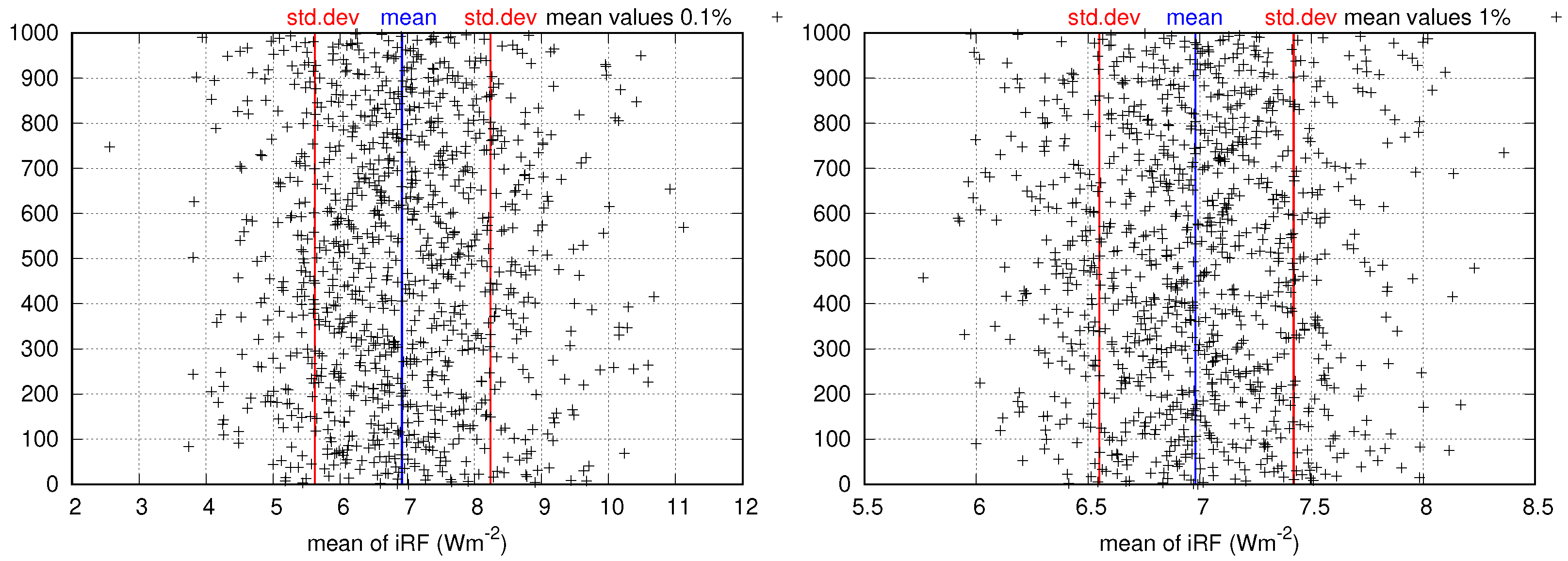
3. Results and Interpretation
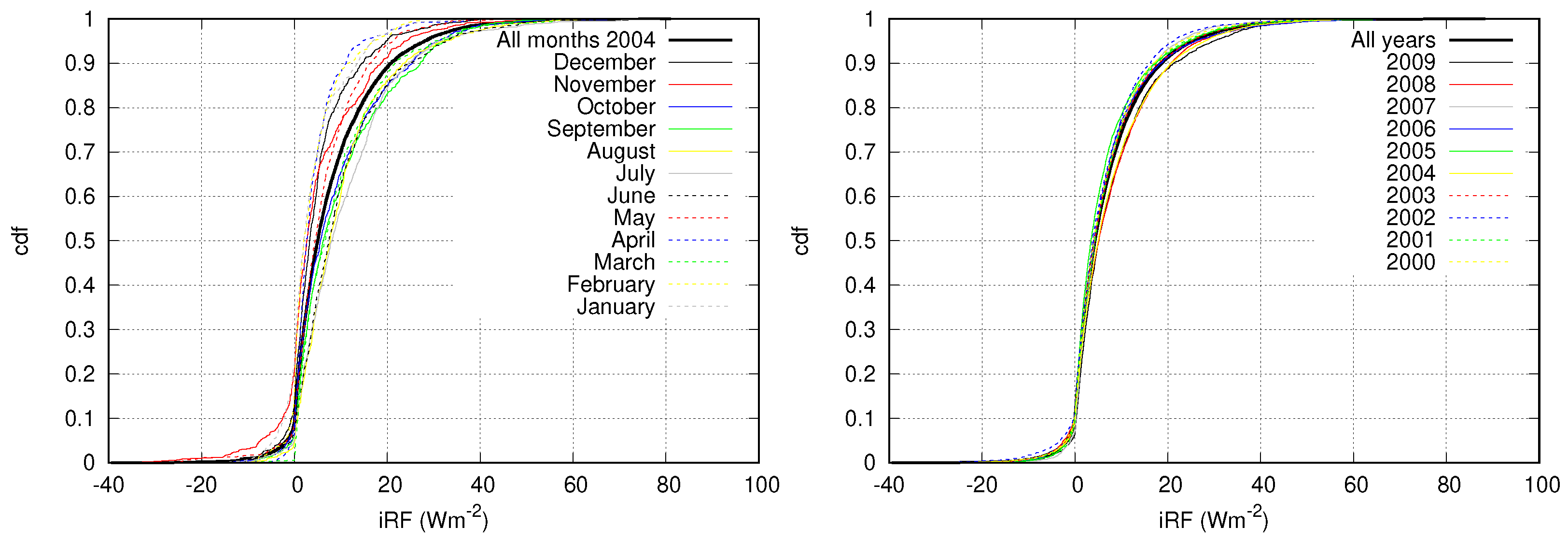
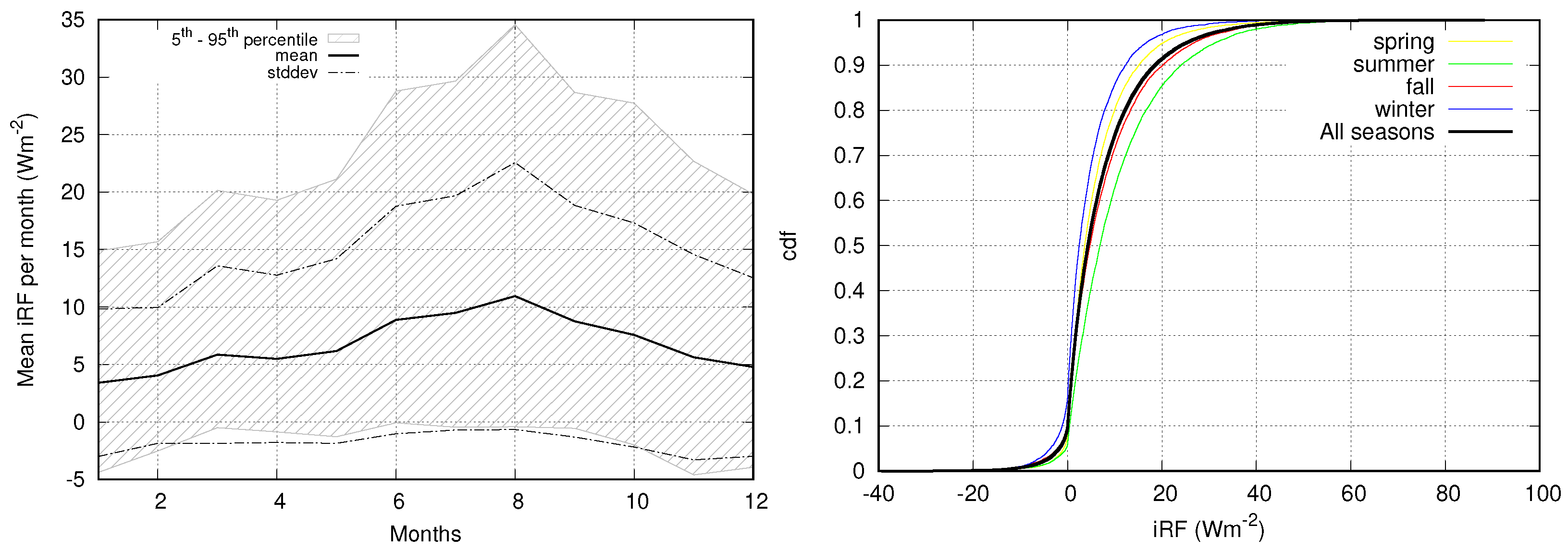
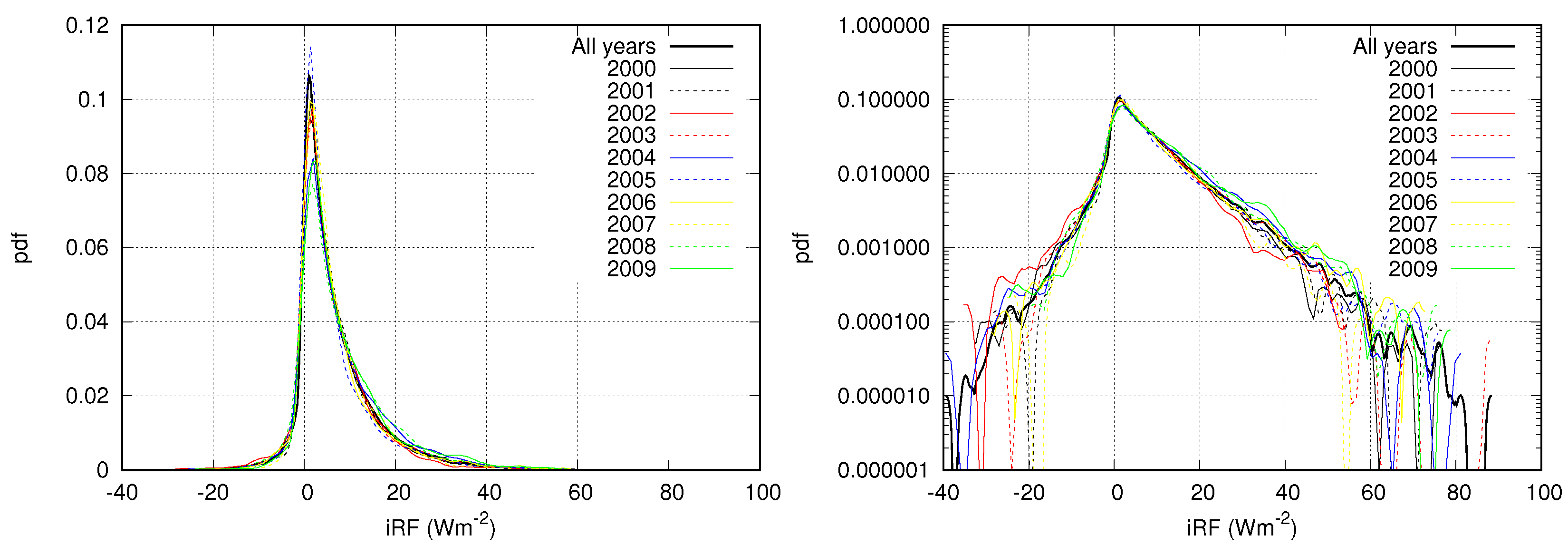
3.1. Statistics
3.2. Monte Carlo Experiments
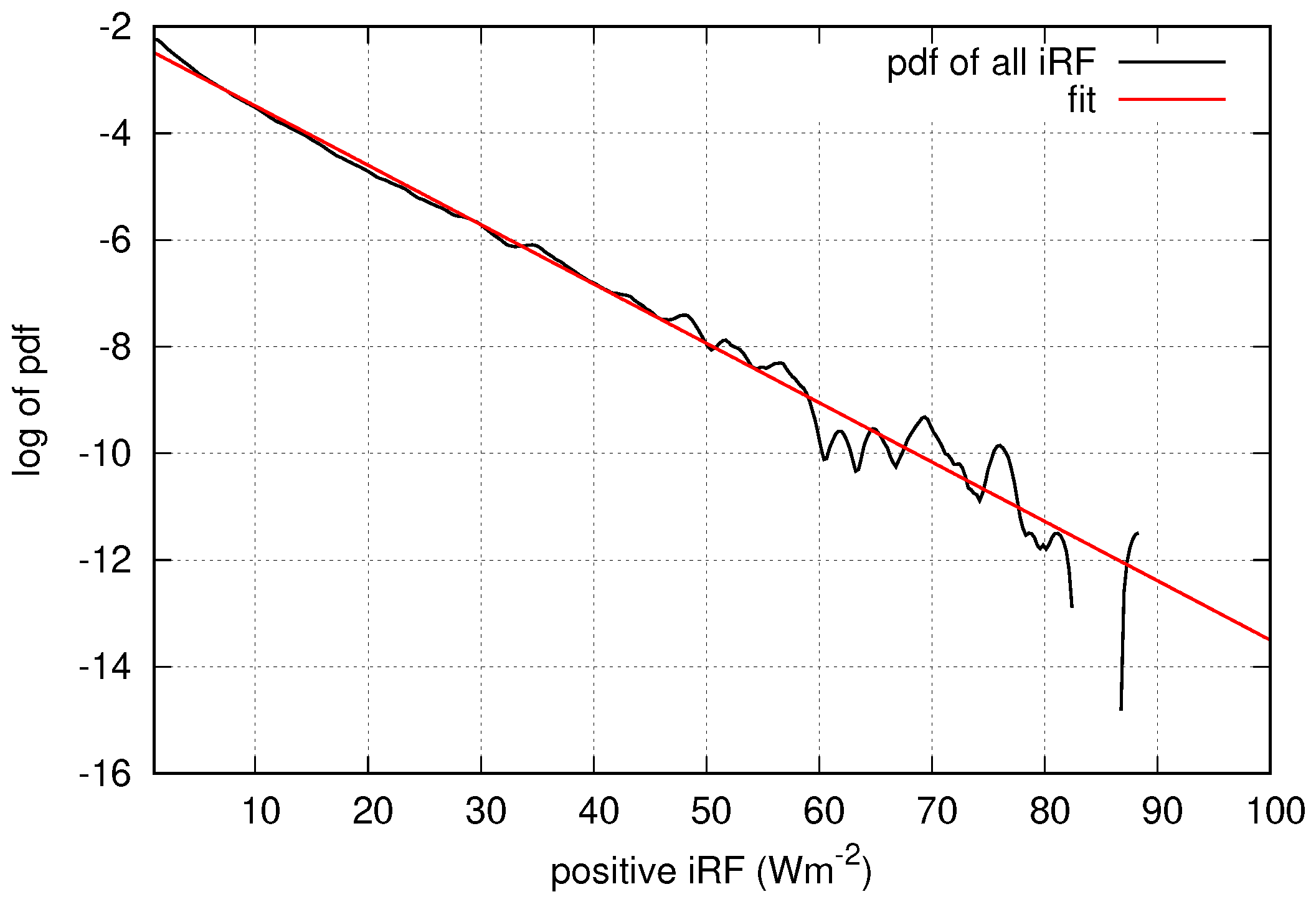
3.3. How Large Is the Maximum Instantaneous Radiative Forcing
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, D.; Fahey, D.; Skowron, A.; Allen, M.; Burkhardt, U.; Chen, Q.; Doherty, S.; Freeman, S.; Forster, P.; Fuglestvedt, J.; et al. The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018. Atmos. Environ. 2021, 244, 117834. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Fahey, D.; Forster, P.; Newton, P.; Wit, R.; Lim, L.; Owen, B.; Sausen, R. Aviation and global climate change in the 21st century. Atmos. Environ. 2009, 43, 3520–3537. [Google Scholar] [CrossRef]
- Penner, J.; Lister, D.; Griggs, D.; Dokken, D.; McFarland, M. (Eds.) Aviation and the Global Atmosphere; Cambridge University Press for the Intergovernmental Panel on Climate Change: Cambridge, UK, 1999; p. 373. [Google Scholar]
- Chauvigné, A.; Jourdan, O.; Schwarzenboeck, A.; Gourbeyre, C.; Gayet, J.F.; Voigt, C.; Schlager, H.; Kaufmann, S.; Borrmann, S.; Molleker, S.; et al. Statistical analysis of contrail to cirrus evolution during the Contrail and Cirrus Experiment (CONCERT). Atmos. Chem. Phys. ACP 2018, 18, 9803–9822. [Google Scholar] [CrossRef]
- Unterstrasser, S.; Sölch, I. Study of contrail microphysics in the vortex phase with a Lagrangian particle tracking model. Atmos. Chem. Phys. 2010, 10, 10003–10015. [Google Scholar] [CrossRef]
- Unterstrasser, S.; Görsch, N. Aircraft type dependency of contrail evolution. J. Geophys. Res. 2014, 119, 14015–14027. [Google Scholar] [CrossRef]
- Burkhardt, U.; Kärcher, B. Global radiative forcing from contrail cirrus. Nat. Clim. Chang. 2011, 1, 54–58. [Google Scholar] [CrossRef]
- Schumann, U. A contrail cirrus prediction model. Geosci. Model Dev. 2012, 5, 543–580. [Google Scholar] [CrossRef]
- Bock, L.; Burkhardt, U. Reassessing properties and radiative forcing of contrail cirrus using a climate model. J. Geophys. Res. 2016, 121, 97179736. [Google Scholar] [CrossRef]
- Yin, F.; Grewe, V.; Gierens, K. Impact of hybrid electric aircraft on contrail coverage. Aerospace 2020, 7, 147. [Google Scholar] [CrossRef]
- Gierens, K. Theory of Contrail Formation for Fuel Cells. Aerospace 2021, 8, 164. [Google Scholar] [CrossRef]
- Moore, R.H.; Thornhill, K.L.; Weinzierl, B.; Sauer, D.; D’Ascoli, E.; Kim, J.; Lichtenstern, M.; Scheibe, M.; Beaton, B.; Beyersdorf, A.J.; et al. Biofuel blending reduces particle emissions from aircraft engines at cruise conditions. Nature 2017, 543, 411–415. [Google Scholar] [CrossRef]
- Burkhardt, U.; Bock, L.; Bier, A. Mitigating the contrail cirrus climate impact by reducing aircraft soot number emissions. NPJ Clim. Atmos. Sci. 2018, 37, 1–7. [Google Scholar] [CrossRef]
- Unterstrasser, S. The contrail mitigation potential of aircraft formation flight derived from high-resolution simulations. Aerospace 2020, 7, 170. [Google Scholar] [CrossRef]
- Mannstein, H.; Meyer, R.; Wendling, P. Operational Detection of Contrails from NOAA–AVHRR-Data. Int. J. Remote Sens. 1999, 20, 1641–1660. [Google Scholar] [CrossRef]
- Vázquez-Navarro, M.; Mannstein, H.; Mayer, B. An automatic contrail tracking algorithm. Atmos. Meas. Tech. 2010, 3, 1089–1101. [Google Scholar] [CrossRef]
- Ramaswamy, V.; Collins, W.; Haywood, J.; Lean, J.; Mahowald, N.; Myhre, G.; Naik, V.; Shine, K.; Soden, B.; Stenchikov, G.; et al. Radiative forcing of climate: The historical evolution of the radiative forcing concept, the forcing agents and their quantification, and applications. Meteorol. Monogr. 2019, 59, 14.1–14.101. [Google Scholar] [CrossRef]
- Gettelman, A.; Chen, C.C.; Bardeen, C. The climate impact of COVID-19-induced contrail changes. Atmos. Chem. Phys. 2021, 21, 9405–9416. [Google Scholar] [CrossRef]
- Schumann, U.; Poll, D.; Teoh, R.; Koelle, R.; Spinielli, E.; Molly, J.; Koudis, G.; Baumann, R.; Bugliaro, L.; Stettler, M.; et al. Air traffic and contrail changes over Europe during COVID-19: A model study. Atmos. Chem. Phys. 2021, 21, 7429–7450. [Google Scholar] [CrossRef]
- Schumann, U.; Bugliaro, L.; Dörnbrack, A.; Baumann, R.; Voigt, C. Aviation contrail cirrus and radiative forcing over Europe during 6 months of COVID-19. Geophys. Res. Lett. 2021, 48, e2021GL092771. [Google Scholar] [CrossRef]
- Quaas, J.; Gryspeerdt, E.; Vautard, R.; Boucher, O. Climate impact of aircraft-induced cirrus assessed from satellite observations before and during COVID-19. Environ. Res. Lett. 2021, 16, 064051. [Google Scholar] [CrossRef]
- Marenco, A.; Thouret, V.; Nedelec, P.; Smit, H.; Helten, M.; Kley, D.; Karcher, F.; Simon, P.; Law, K.; Pyle, J.; et al. Measurement of ozone and water vapor by Airbus in-service aircraft: The MOZAIC airborne program, An overview. J. Geophys. Res. 1998, 103, 25631–25642. [Google Scholar] [CrossRef]
- Petzold, A.; Thouret, V.; Gerbig, C.; Zahn, A.; Brenninkmeijer, C.; Gallagher, M.; Hermann, M.; Pontaud, M.; Ziereis, H.; Boulanger, D.; et al. Global-scale atmosphere monitoring by in-service aircraft - current achievements and future prospects of the European Research Infrastructure IAGOS. Tellus B 2015, 67. [Google Scholar] [CrossRef]
- Petzold, A.; Krämer, M.; Neis, P.; Rolf, C.; Rohs, S.; Berkes, F.; Smit, H.; Gallagher, M.; Beswick, K.; Lloyd, G.; et al. Upper tropospheric water vapour and its interaction with cirrus clouds as seen from IAGOS long-term routine in-situ observations. Faraday Discuss. 2017, 200, 229–249. [Google Scholar] [CrossRef] [PubMed]
- Petzold, A.; Neis, P.; Rütimann, M.; Rohs, S.; Berkes, F.; Smit, H.; Krämer, M.; Spelten, N.; Spichtinger, P.; Nedelec, P.; et al. Ice-supersaturated air masses in the northern mid-latitudes from regular in situ observations by passenger aircraft: Vertical distribution, seasonality and tropospheric fingerprint. Atmos. Chem. Phys. 2020, 20, 8157–8179. [Google Scholar] [CrossRef]
- Neis, P.; Smit, H.; Rohs, S.; Bundke, U.; Krämer, M.; Spelten, N.; Ebert, V.; Buchholz, B.; Thomas, K.; Petzold, A. Quality assessment of MOZAIC and IAGOS capacitive hygrometers: Insights from airborne field studies. Tellus B Chem. Phys. Meteorol. 2015, 67, 1. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Hor’anyi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present. Technical Report, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 14 July 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Hor’anyi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Pressure Levels from 1979 to Present. Technical Report, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.bd0915c6?tab=form (accessed on 14 July 2021).
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Copernicus Climate Change Service Climate Data Store (CDS). 2017. Available online: https://cds.climate.copernicus.eu/cdsapp#!/search?type=dataset (accessed on 5 April 2020).
- Schumann, U. On conditions for contrail formation from aircraft exhausts. Meteorol. Z. 1996, 5, 4–23. [Google Scholar] [CrossRef]
- Ebert, E.; Curry, J. A parameterization of ice cloud optical properties for climate models. J. Geophys. Res. 1992, 97, 3831–3836. [Google Scholar] [CrossRef]
- Schumann, U.; Mayer, B.; Graf, K.; Mannstein, H. A parametric radiative forcing model for contrail cirrus. J. Appl. Meteorol. Climatol. 2012, 51, 1391–1406. [Google Scholar] [CrossRef]
- Myhre, G.; Kvalevag, M.; Rädel, G.; Cook, J.; Shine, K.P.; Clarke, H.; Karcher, F.; Markowicz, K.; Kardas, A.; Wolkenberg, P.; et al. Intercomparison of radiative forcing calculations of stratospheric water vapour and contrails. Meteorol. Z. 2009, 18, 585–596. [Google Scholar] [CrossRef]
- Gierens, K.; Matthes, S.; Rohs, S. How well can persistent contrails be predicted? Aerospace 2020, 7, 169. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Number 26 in Monographs on Statistics and Applied Probability; Chapman and Hall/CRC: Boca Raton, FL, USA, 1998. [Google Scholar]
- Meerkötter, R.; Schumann, U.; Doelling, D.; Minnis, P.; Nakajima, T.; Tsushima, Y. Radiative forcing by contrails. Ann. Geophys. 1999, 17, 1080–1094. [Google Scholar] [CrossRef]
- Stuber, N.; Forster, P.; Rädel, G.; Shine, K. The importance of the diurnal and annual cycle of air traffic for contrail radiative forcing. Nature 2006, 441, 864–867. [Google Scholar] [CrossRef] [PubMed]
- Gierens, K.; Schumann, U.; Helten, M.; Smit, H.; Marenco, A. A distribution law for relative humidity in the upper troposphere and lower stratosphere derived from three years of MOZAIC measurements. Ann. Geophys. 1999, 17, 1218–1226. [Google Scholar] [CrossRef][Green Version]
- Spichtinger, P.; Gierens, K.; Read, W. The statistical distribution law of relative humidity in the global tropopause region. Meteorol. Z. 2002, 11, 83–88. [Google Scholar] [CrossRef]
- Tompkins, A.; Gierens, K.; Rädel, G. Ice supersaturation in the ECMWF Integrated Forecast System. Quart. J. R. Met. Soc. 2007, 133, 53–63. [Google Scholar] [CrossRef]
- Teoh, R.; Schumann, U.; Majumdar, A.; Stettler, M. Mitigating the climate forcing of aircraft contrails by small-scale diversions and technology adoption. Environ. Sci. Technol. 2020, 54, 2941–2950. [Google Scholar] [CrossRef]
- Schumann, U.; Baumann, R.; Baumgardner, D.; Bedka, S.T.; Duda, D.P.; Freudenthaler, V.; Gayet, J.F.; Heymsfield, A.J.; Minnis, P.; Quante, M.; et al. Properties of individual contrails: A compilation of observations and some comparisons. Atmos. Chem. Phys. 2017, 17, 403–438. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences, 2nd ed.; Springer: Berlin, Germany, 2004; p. XIV+528. [Google Scholar]
- Atlas, D.; Wang, Z. Contrails of small and very large optical depth. J. Atmos. Sci. 2010, 67, 3065–3073. [Google Scholar] [CrossRef]
- Gayet, J.F.; Shcherbakov, V.; Voigt, C.; Schumann, U.; Schäuble, D.; Jeßberger, P.; Petzold, A.; Minikin, A.; Schlager, H.; Dubovik, O.; et al. The evolution of microphysical and optical properties of an A380 contrail in the vortex phase. Atmos. Chem. Phys. 2021, 12, 6629–6643. [Google Scholar] [CrossRef]
- Jeßberger, P.; Voigt, C.; Schumann, U.; Sölch, I.; Schlager, H.; Kaufmann, S.; Petzold, A.; Schäuble, D.; Gayet, J.F. Aircraft type influence on contrail properties. Atmos. Chem. Phys. 2013, 13, 11965–11984. [Google Scholar] [CrossRef]
- Gierens, K.; Ström, J. A numerical study of aircraft wake induced ice cloud formation. J. Atmos. Sci. 1998, 55, 3253–3263. [Google Scholar] [CrossRef]
- Sussmann, R.; Gierens, K. Differences in early contrail evolution of 2–engined versus 4–engined aircraft. Lidar measurements and numerical simulations. J. Geophys. Res. 2001, 106, 4899–4911. [Google Scholar] [CrossRef]
- Beyersdorf, A.J.; Timko, M.T.; Ziemba, L.D.; Bulzan, D.; Corporan, E.; Herndon, S.C.; Howard, R.; Miake-Lye, R.; Thornhill, K.L.; Winstead, E.; et al. Reductions in aircraft particulate emissions due to the use of FischerTropsch fuels. Atmos. Chem. Phys. 2014, 14, 11–23. [Google Scholar] [CrossRef]
- Dürbeck, T.; Gerz, T. Dispersion of aircraft exhausts in the free atmosphere. J. Geophys. Res. 1996, 101, 26007–26016. [Google Scholar] [CrossRef]
- Unterstrasser, S.; Gierens, K. Numerical simulations of contrail-to-cirrus transition—Part 2: Impact of initial ice crystal number, radiation, stratification, secondary nucleation and layer depth. Atmos. Chem. Phys. 2010, 10, 2037–2051. [Google Scholar] [CrossRef]
- Gierens, K. How the Sky Gets Covered with Condensation Trails. Meteorol. Z. 1998, 7, 181–187. [Google Scholar] [CrossRef]
- Dowling, D.; Radke, L. A summary of the physical properties of cirrus clouds. J. Appl. Meteorol. 1990, 29, 970–978. [Google Scholar] [CrossRef]
- Lynch, D.; Sassen, K.; Starr, D.; Stephens, G. (Eds.) Cirrus; Oxford University Press: Oxford, UK, 2002; p. 504. [Google Scholar]
- Schumann, U.; Graf, K.; Mannstein, H. Potential to reduce climate impact of aviation by flight level changes. In Proceedings of the 3rd AIAA Atmospheric Space Environments Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3376. [Google Scholar] [CrossRef]
- Gierens, K.; Vázquez-Navarro, M. Statistical analysis of contrail lifetimes from a satellite perspective. Meteorol. Z. 2018, 27, 183–193. [Google Scholar] [CrossRef]
- Bier, A.; Burkhardt, U.; Bock, L. Synoptic control of contrail cirrus lifecycles and their modification due to reduced soot number emissions. J. Geophys. Res. 2017, 122, 11584–11603. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Met. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilhelm, L.; Gierens, K.; Rohs, S. Weather Variability Induced Uncertainty of Contrail Radiative Forcing. Aerospace 2021, 8, 332. https://doi.org/10.3390/aerospace8110332
Wilhelm L, Gierens K, Rohs S. Weather Variability Induced Uncertainty of Contrail Radiative Forcing. Aerospace. 2021; 8(11):332. https://doi.org/10.3390/aerospace8110332
Chicago/Turabian StyleWilhelm, Lena, Klaus Gierens, and Susanne Rohs. 2021. "Weather Variability Induced Uncertainty of Contrail Radiative Forcing" Aerospace 8, no. 11: 332. https://doi.org/10.3390/aerospace8110332
APA StyleWilhelm, L., Gierens, K., & Rohs, S. (2021). Weather Variability Induced Uncertainty of Contrail Radiative Forcing. Aerospace, 8(11), 332. https://doi.org/10.3390/aerospace8110332






