Numerical Study of the Lift Enhancement Mechanism of Circulation Control in Transonic Flow
Abstract
:1. Introduction
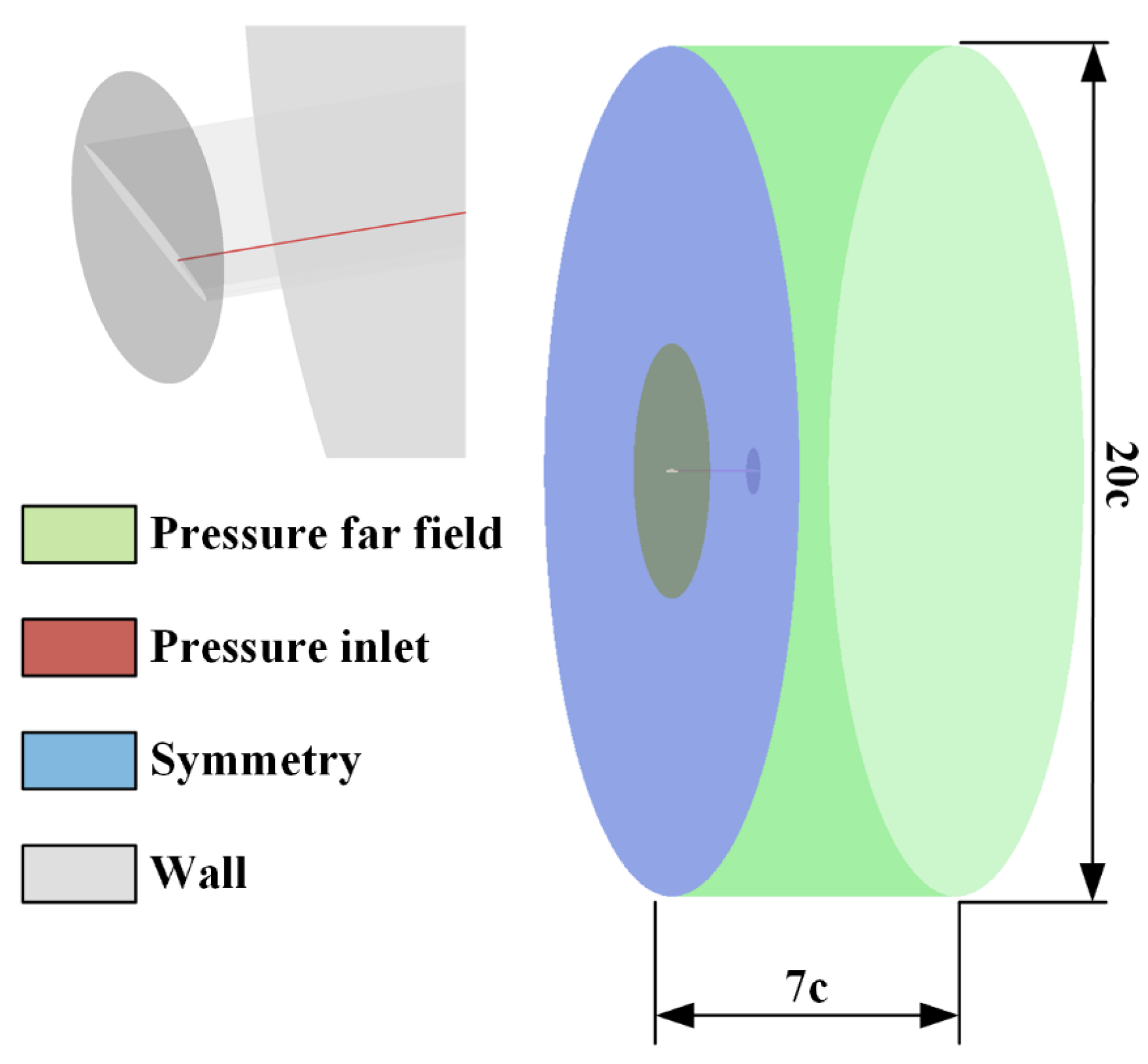
2. Numerical Methods
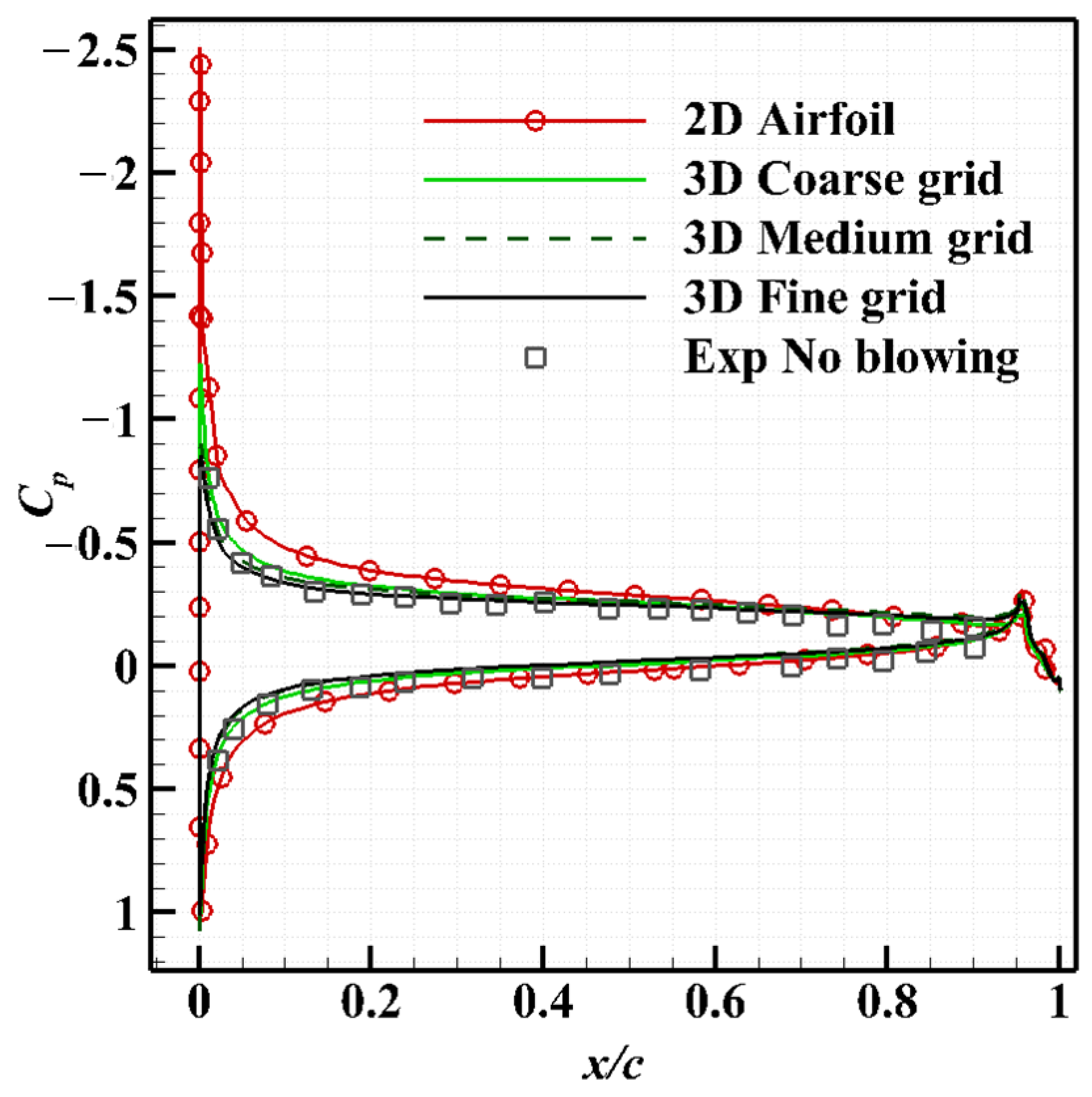
3. Validation of Trailing-Edge CC
4. Flow Physics of CC Jet in Transonic and Subsonic Incoming Flows
4.1. Numerical Model Setup of the RAE2822 Airfoil with CC
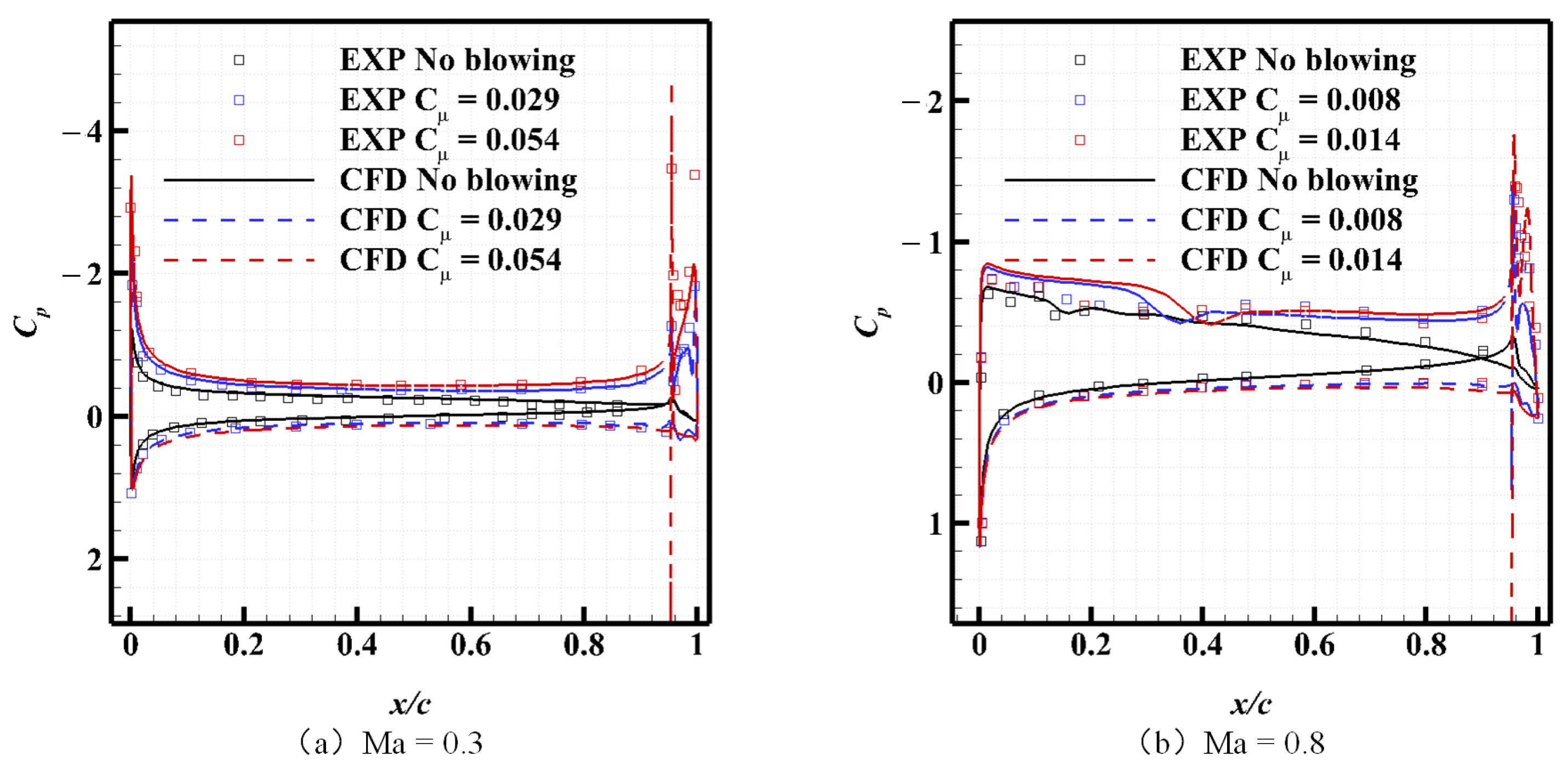
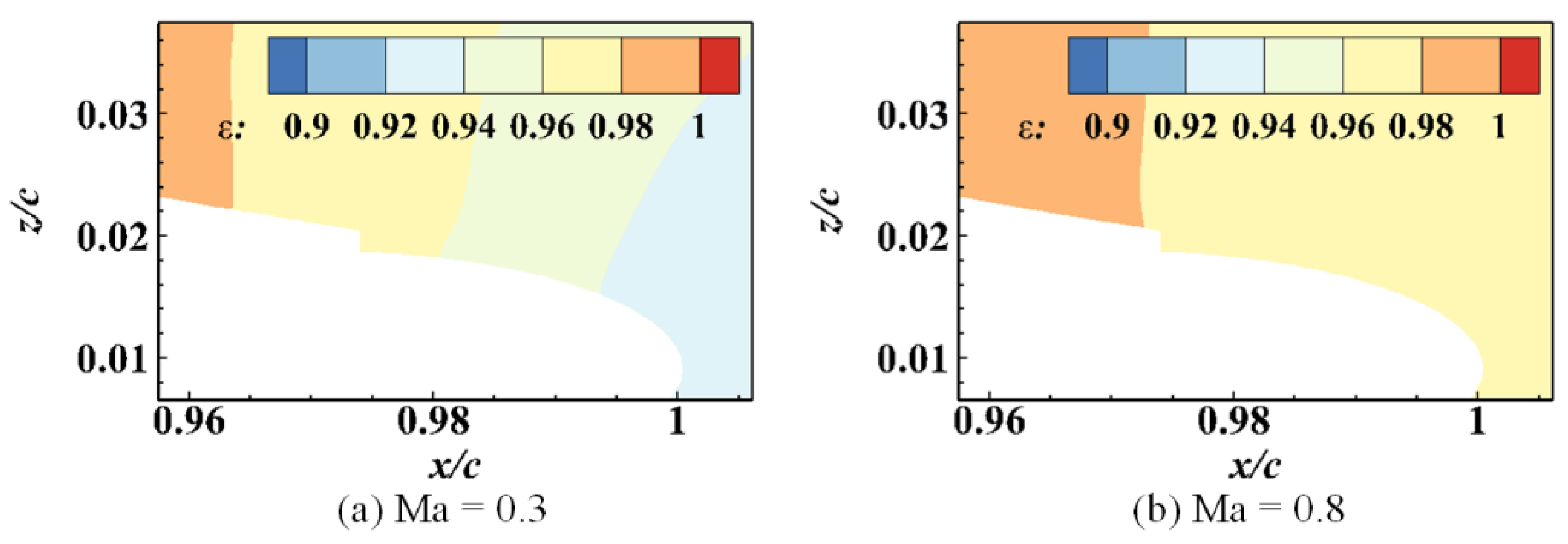
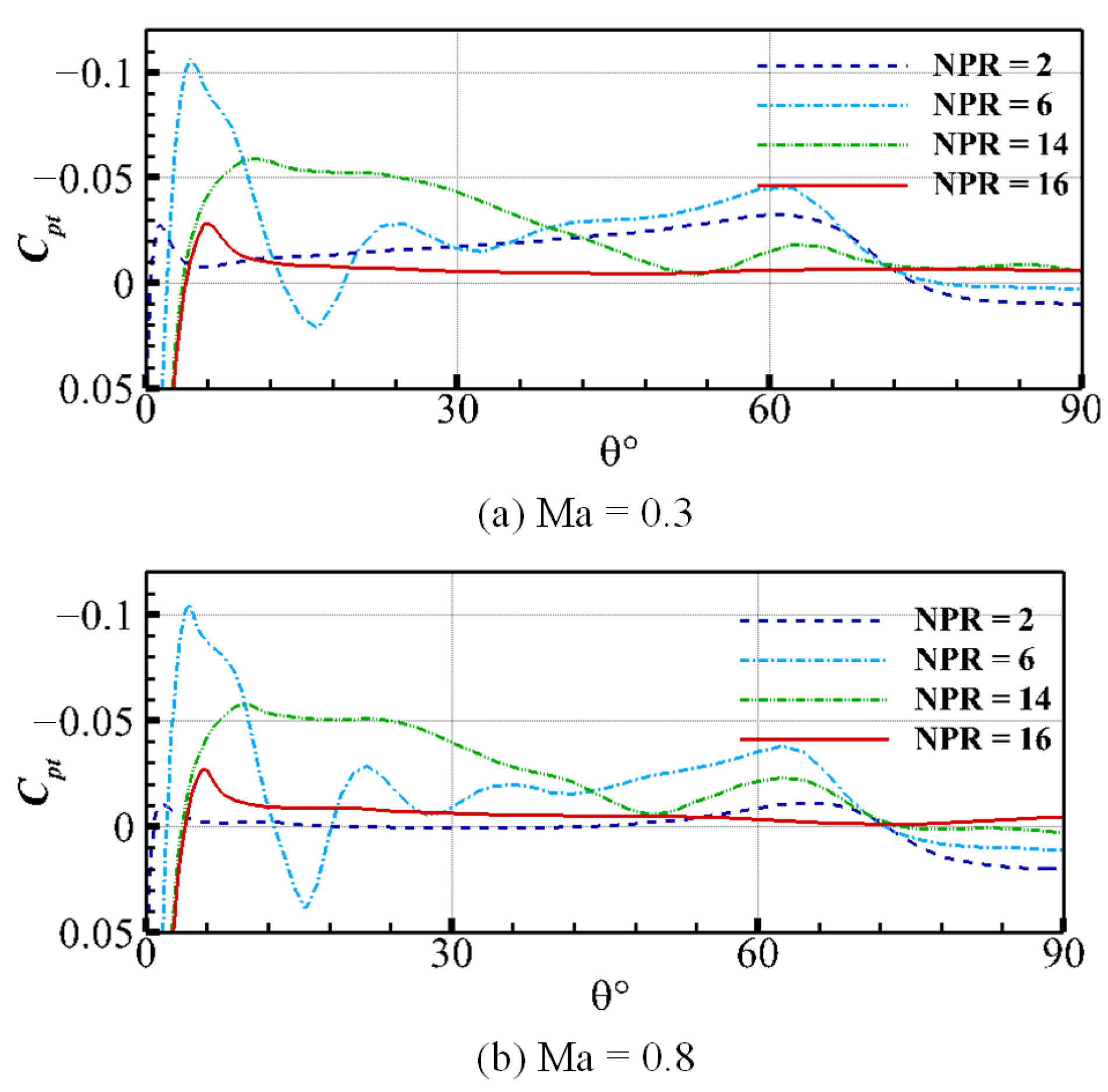
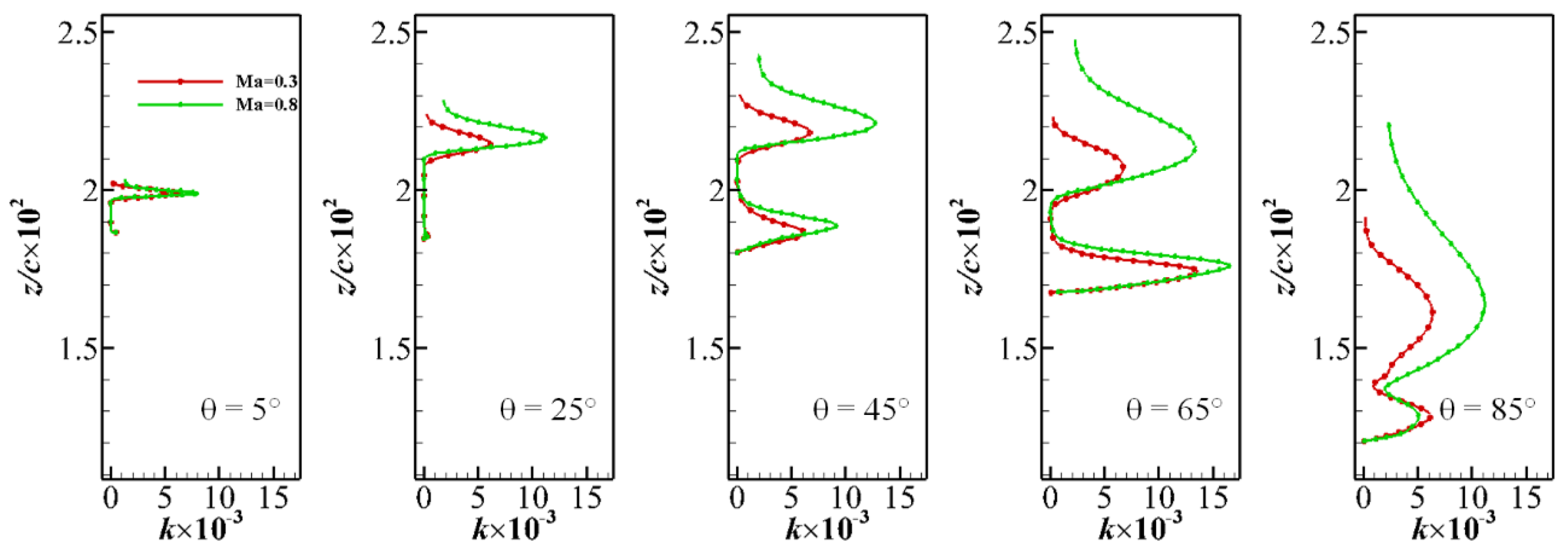
4.2. CC Jet Behaviors at and 0.8
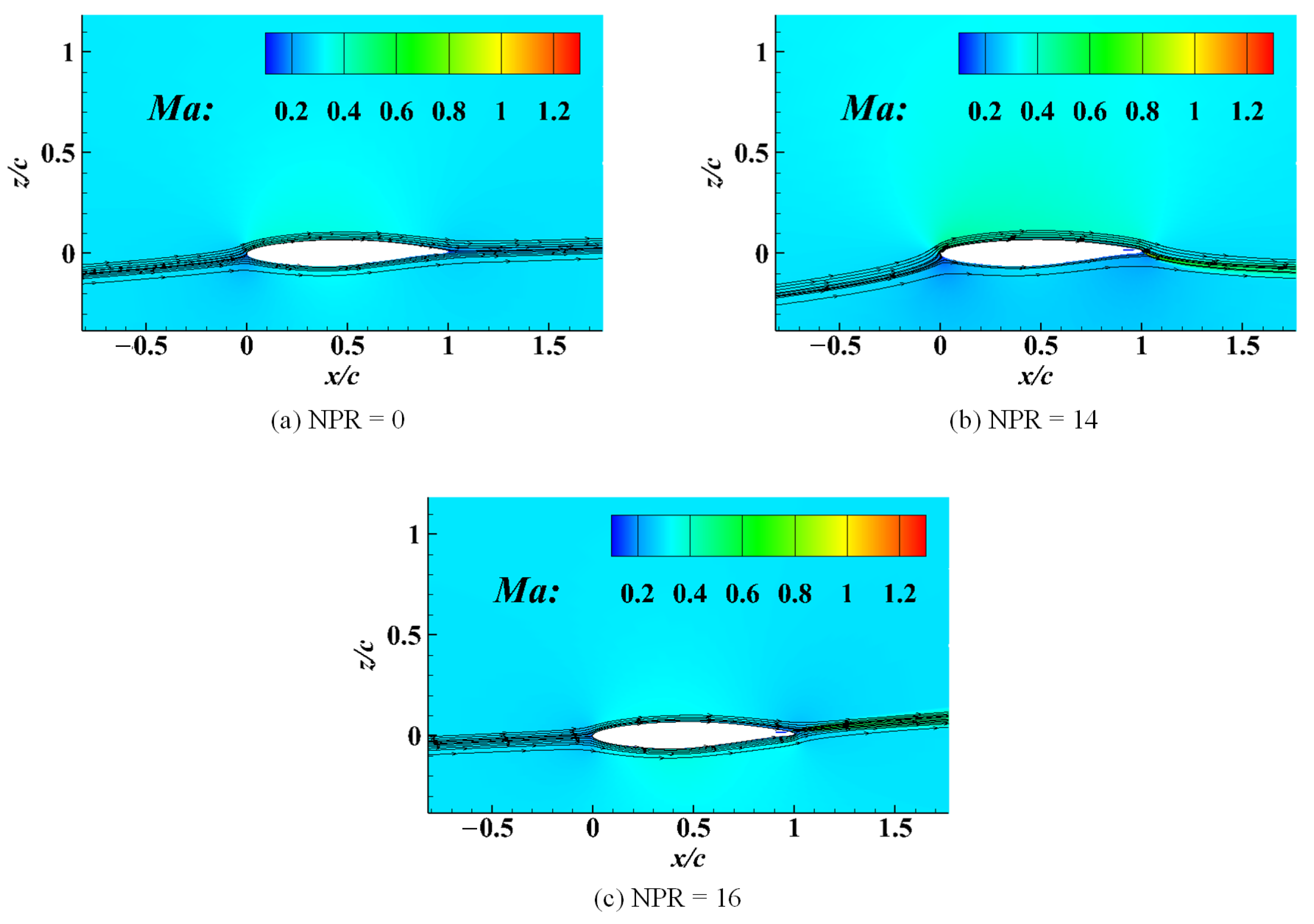
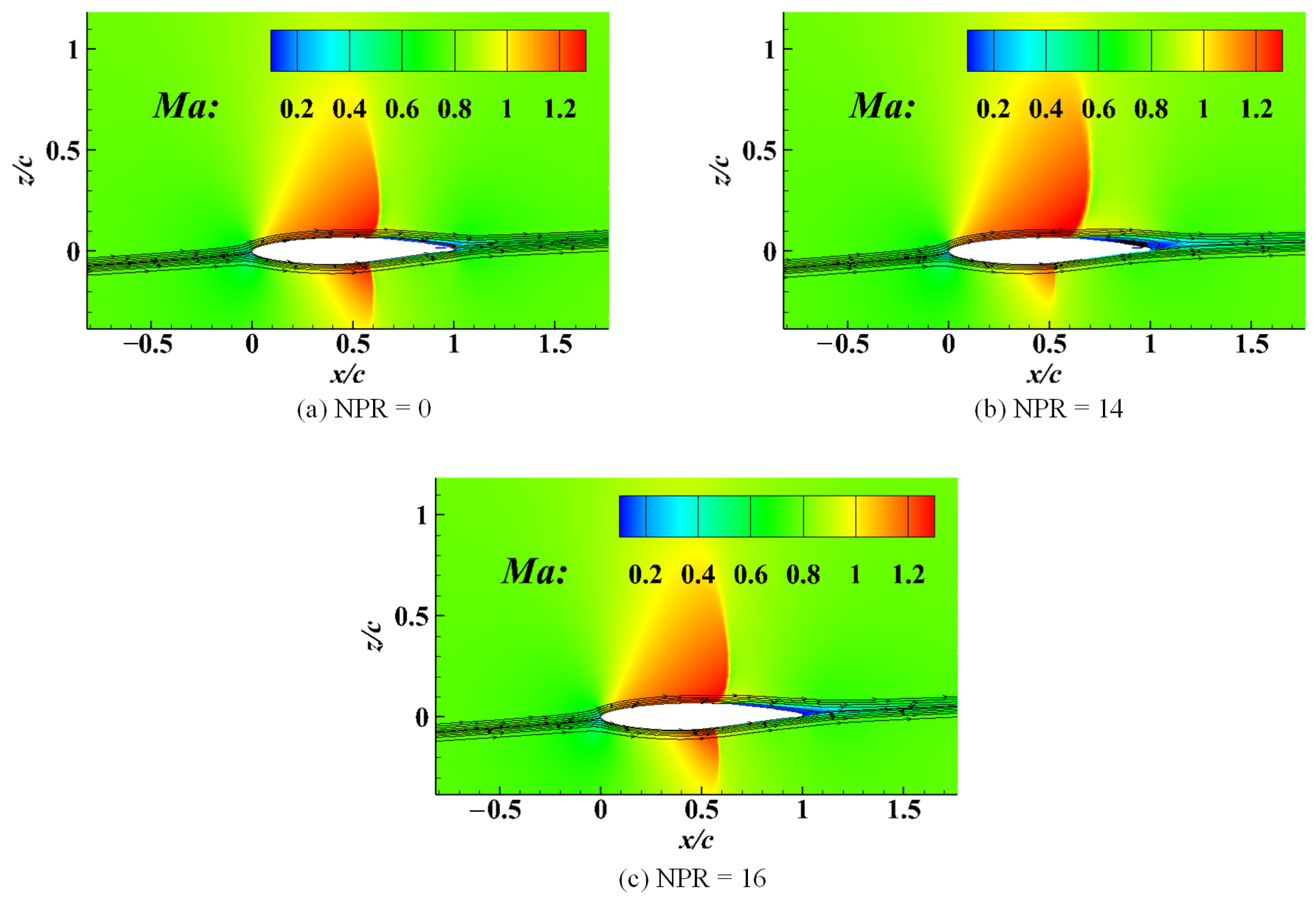
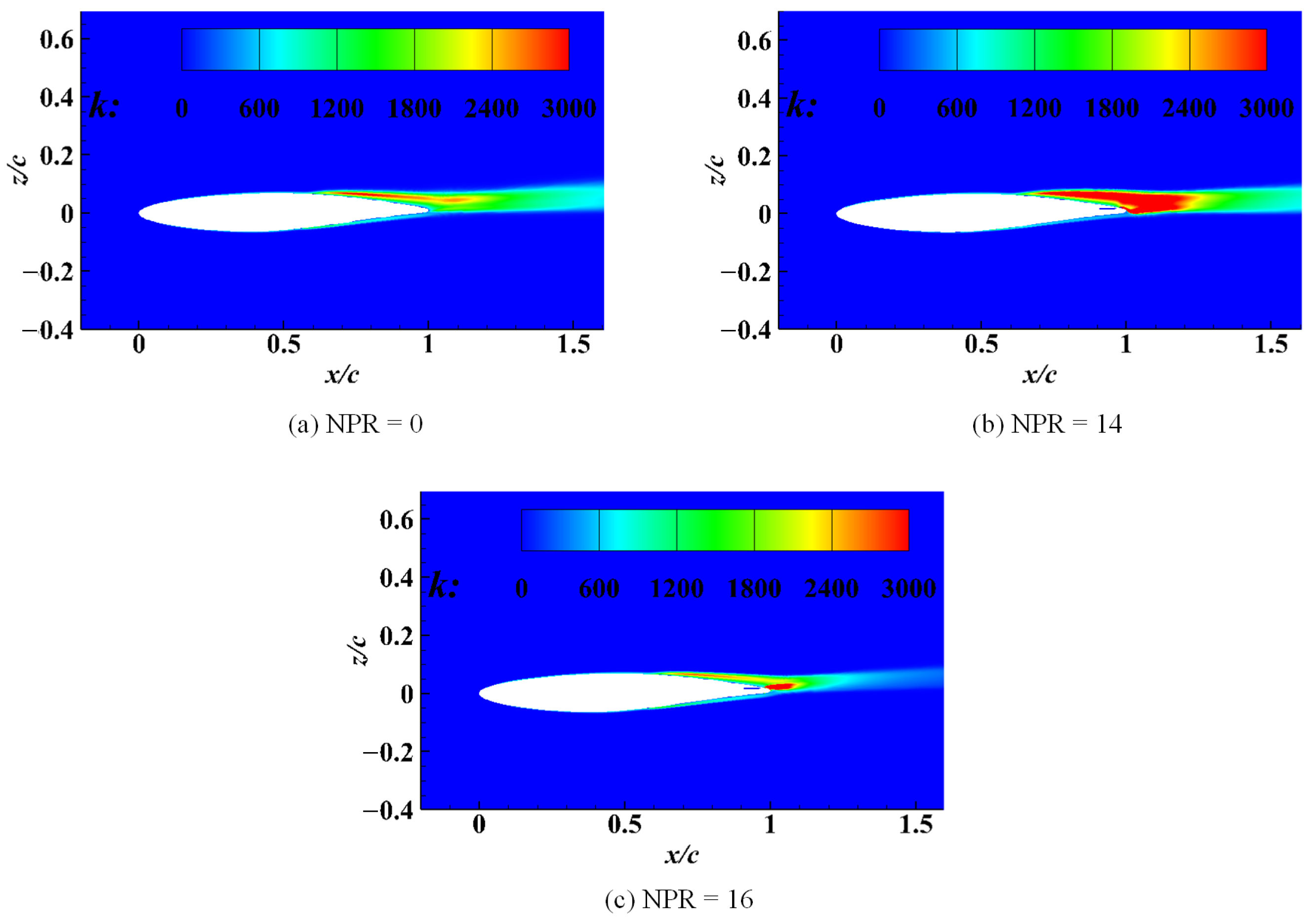
4.3. Flow Field Structure at NPRs of 14 and 16
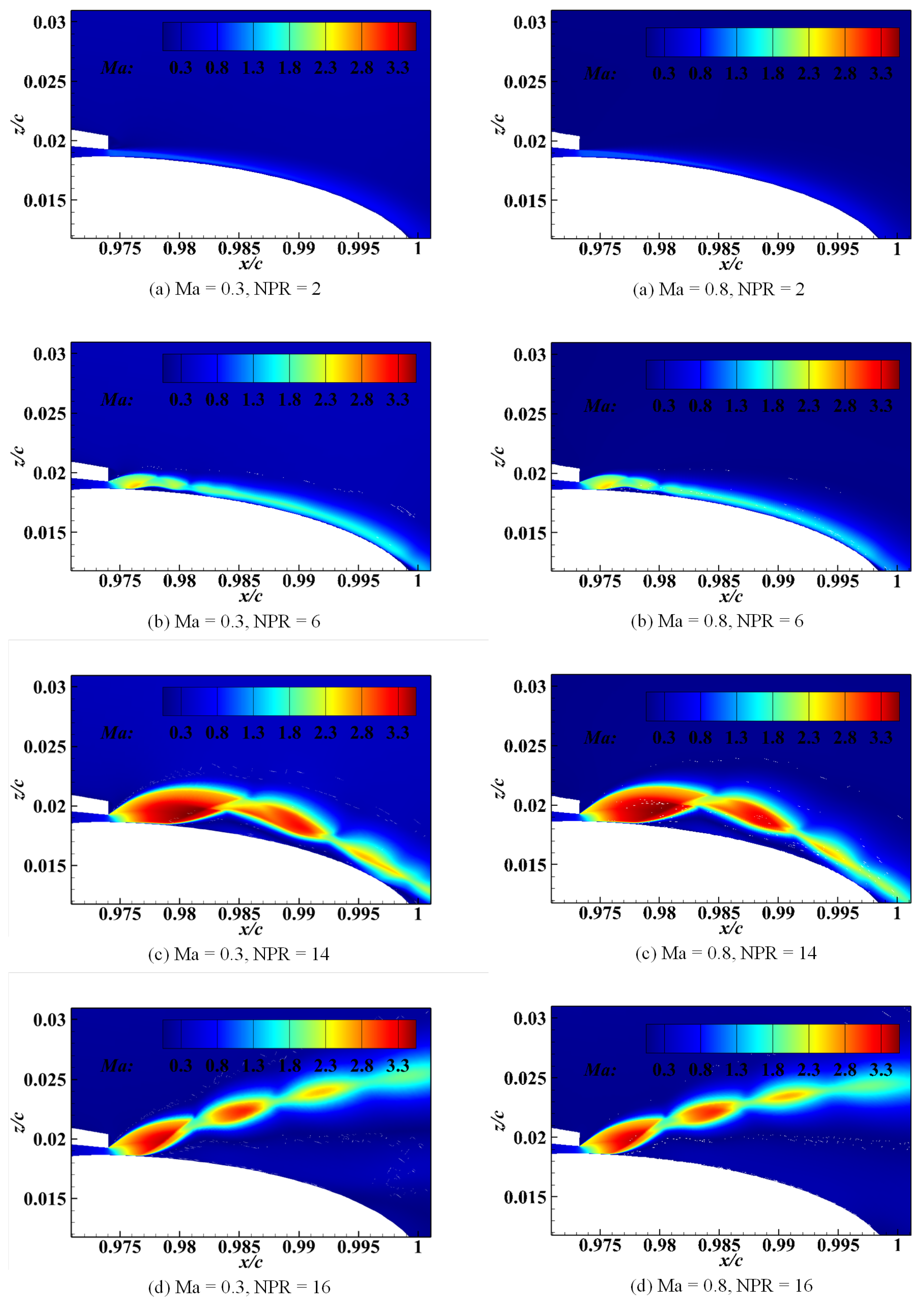
4.3.1. Shock Structures
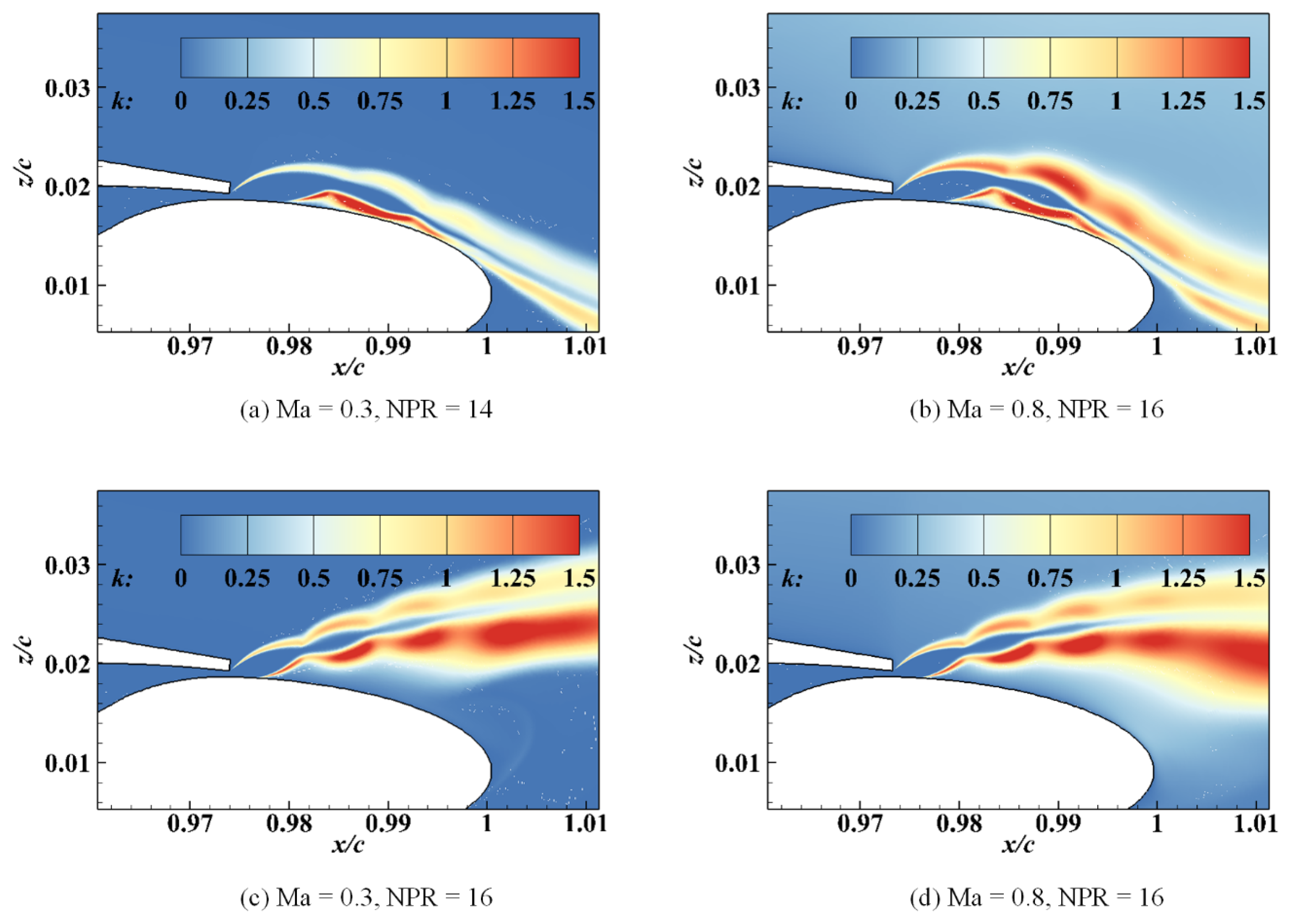
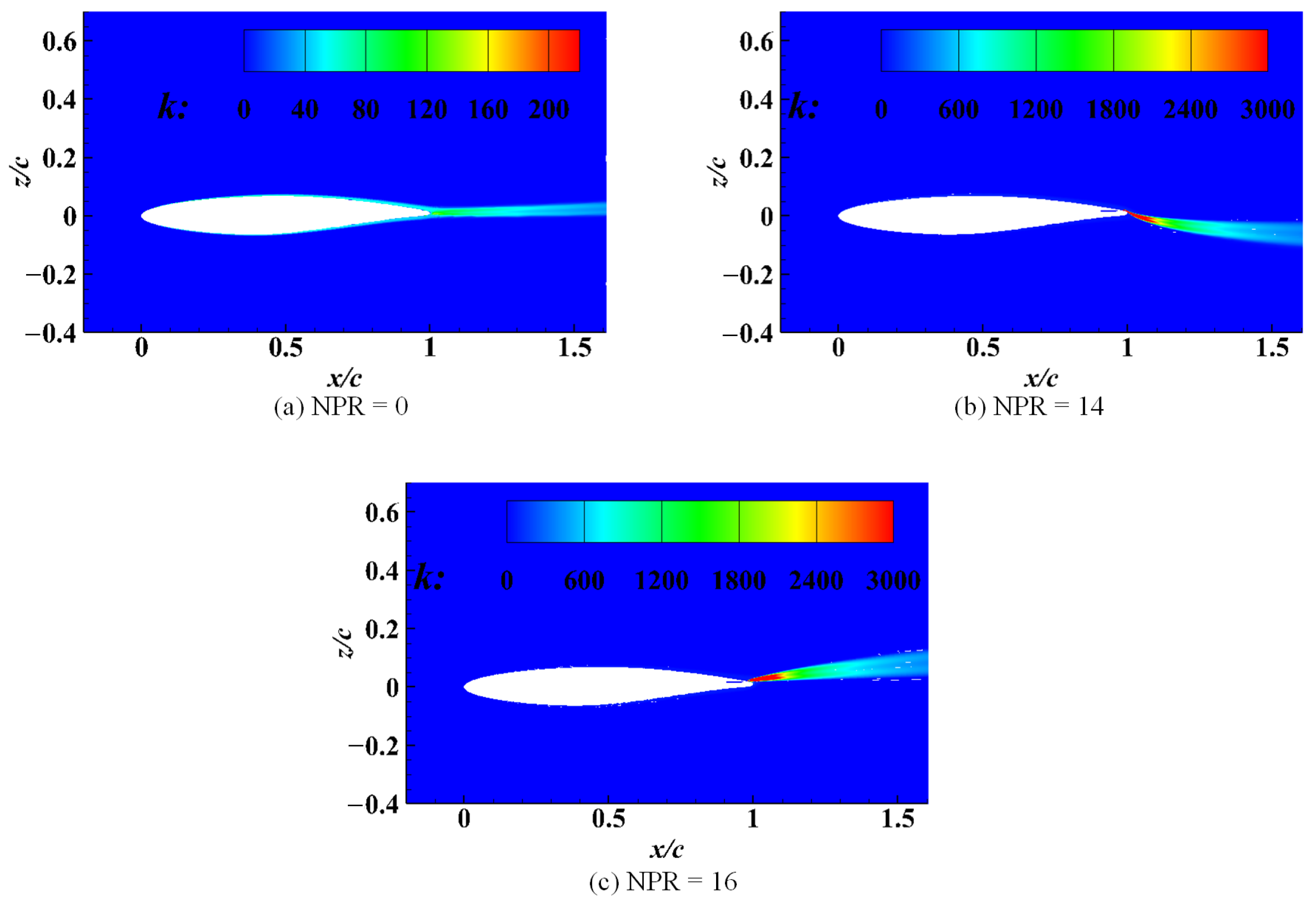
4.3.2. Shear Layer Development
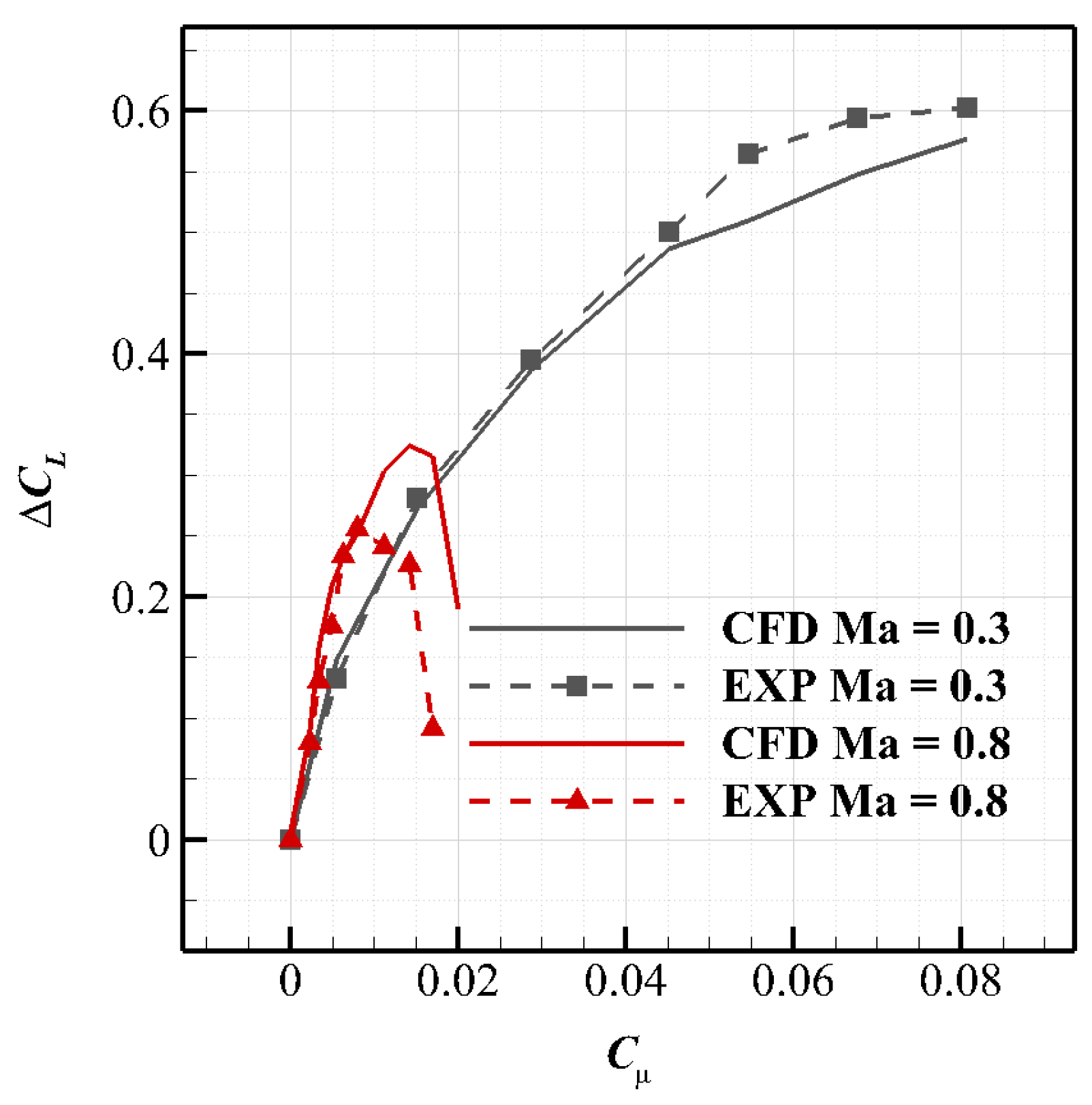
5. Mechanisms of Lift Augmentation in Transonic Flow
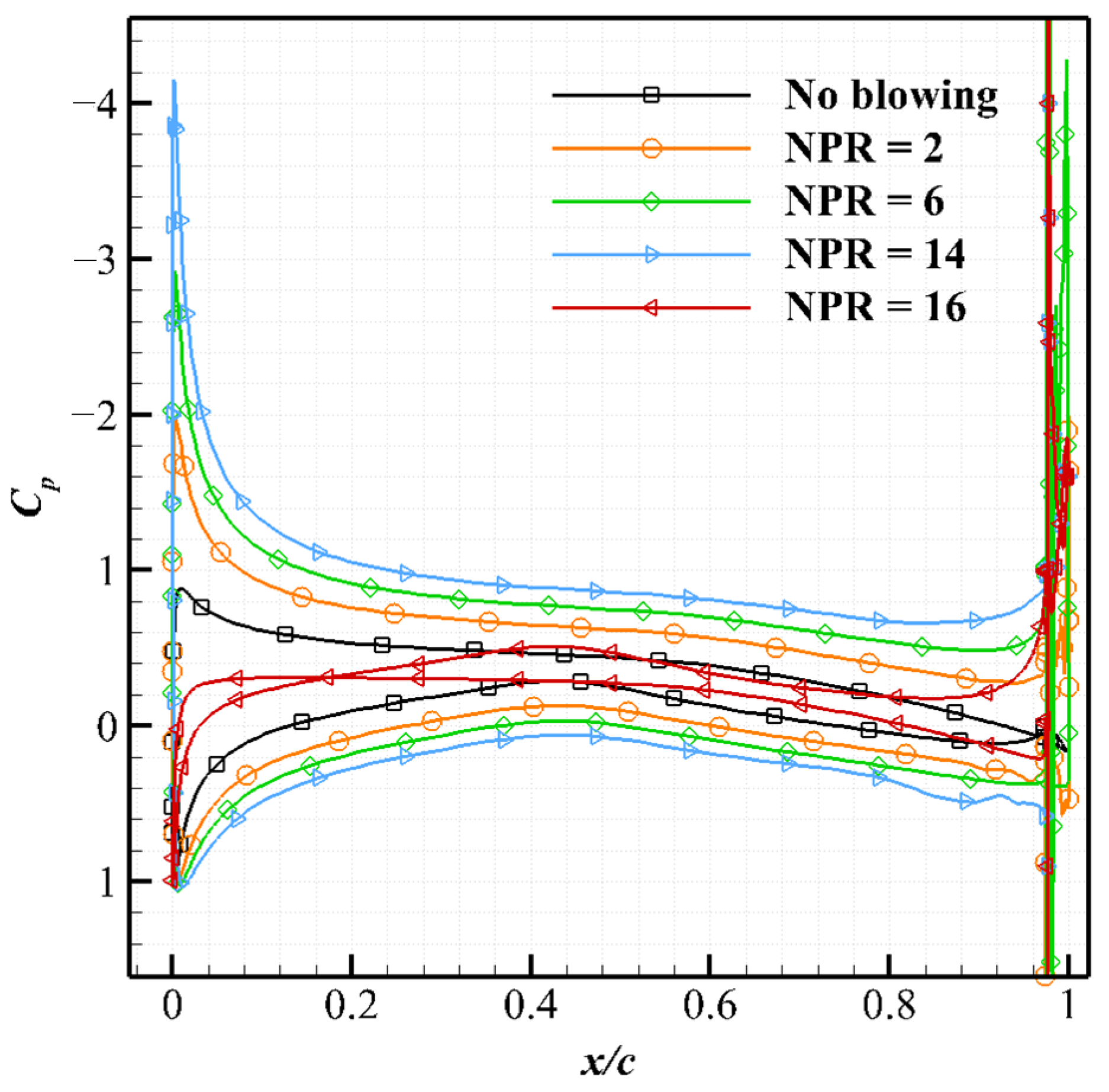
5.1. Mechanism of Lift Augmentation for Subsonic Freestream
5.2. Mechanism of Lift Augmentation for Transonic Freestream
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AVT | applied vehicle technology |
| NPR | nozzle pressure ratio |
| SBLI | shock boundary layer interactions |
References
- Li, Y.; Qin, N. Airfoil gust load alleviation by circulation control. Aerosp. Sci. Technol. 2020, 98, 105622. [Google Scholar] [CrossRef]
- Traub, L.W.; Biegner, M. Experimental evaluation of a self-contained circulation-control wing. J. Aircr. 2013, 50, 764–777. [Google Scholar] [CrossRef]
- Itsariyapinyo, P.; Sharma, R.N. Large eddy simulation of a NACA0015 circulation control airfoil using synthetic jets. Aerosp. Sci. Technol. 2018, 82–83, 545–556. [Google Scholar] [CrossRef] [Green Version]
- Davidson, I.M. Aerofoil Boundary Layer Control Systems. U.S. Patent. Office Patent Number US3062483 A, 6 November 1962. [Google Scholar]
- Wetzel, D.A.; Griffin, J.; Cattafesta, L.N. Experiments on an elliptic circulation control aerofoil. J. Fluid Mech. 2013, 730, 99–144. [Google Scholar] [CrossRef]
- Ganesh, N.; Arunvinthan, S.; Pillai, S.N. Effect of surface blowing on aerodynamic characteristics of tubercled straight wing. Chin. J. Aeronaut. 2019, 32, 1111–1120. [Google Scholar] [CrossRef]
- Pugliese, A.; Englar, R. Title of Presentation. In Proceedings of the Aircraft Systems and Technology Meeting, New York, NY, USA, 20–22 August 1979. [Google Scholar]
- Warsop, C.; Crowther, W.J. Fluidic flow control effectors for flight control. AIAA J. 2018, 56, 3808–3824. [Google Scholar] [CrossRef]
- Englar, R.J. Circulation control for high lift and drag generation on STOL aircraft. J. Aircr. 1975, 12, 457–463. [Google Scholar] [CrossRef]
- Englar, R.J.; Huson, G.G. Development of advanced circulation control wing high-lift airfoils. J. Aircr. 1984, 21, 476–483. [Google Scholar] [CrossRef]
- Crowther, W.J.; Wilde, P.I.A.; Gill, K.; Michie, S.M. Towards integrated design of fluidic flight controls for a flapless aircraft. Aeronaut. J. 2009, 113, 699–713. [Google Scholar] [CrossRef]
- Cook, M.V.; Buonanno, A.; Erbslöh, S.D. A circulation control actuator for flapless flight control. Aeronaut. J. 2008, 112, 483–489. [Google Scholar] [CrossRef]
- L<i>o</i>¨chert, P.; Huber, K.C.; Ghoreyshi, M.; Allen, J. Control device effectiveness studies of a 53∘ swept flying wing configuration. Experimental, computational, and modeling considerations. Aerosp. Sci. Technol. 2019, 93, 105319. [Google Scholar]
- Warsop, C.; Crowther, W.; Forster, M. NATO AVT-239 Task Group: Supercritical Coanda based circulation control and fluidic thrust vectoring. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Williams, D.R.; Seidel, J.; Osteroos, R.; McLaughlin, T.E. NATO AVT-239 Task Group: Flight control derivatives using active flow control effectors on the ICE/SACCON UAS Model. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Miller, D.N. NATO AVT-239 Task Group: Trade study approach toward assessing prospects of active flow control on a future UAS. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Novak, C.; Cornelius, K.; Roads, R. Experimental investigations of the circular wall jet on a circulation control airfoil. In Proceedings of the 25th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 24–26 March 1987. [Google Scholar]
- Ahmed, R.I.; Abu Talib, A.R.; Mohd Rafie, A.S.; Djojodihardjo, H. Aerodynamics and flight mechanics of MAV based on Coandă effect. Aerosp. Sci. Technol. 2017, 62, 136–147. [Google Scholar] [CrossRef]
- Min, B.-Y.; Lee, W.; Englar, R.; Sankar, L.N. Numerical investigation of circulation control airfoils. J. Aircr. 2009, 46, 1403–1410. [Google Scholar] [CrossRef]
- Keller, D.; Rudnik, R. Numerical investigation of engine effects on a transport aircraft with circulation control. J. Aircr. 2015, 52, 421–438. [Google Scholar] [CrossRef]
- Novak, N.; Nielsen, J. Circulation control airfoils—Past, present, future. In Proceedings of the 23rd Aerospace Sciences Meeting, Reno, NV, USA, 14–17 January 1985. [Google Scholar]
- Novak, C.; Cornelius, K. An LDV investigation of a circulation control airfoil flowfield. In Proceedings of the 24th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1986. [Google Scholar]
- Cornelius, K.C.; Lucius, G.A. Physics of Coanda jet detachment at high-pressure ratio. J. Aircr. 1994, 31, 591–596. [Google Scholar] [CrossRef]
- NTRS—NASA Technical Reports Server. Available online: https://ntrs.nasa.gov/api/citations/20050165090/downloads/20050165090.pdf (accessed on 7 September 2013).
- Wood, N.; Conlon, J. The performance of a circulation control airfoil at transonic speeds. In Proceedings of the 21st Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983. [Google Scholar]
- Forster, M.; Steijl, R. Numerical simulation of transonic circulation control. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Abramson, J.; Rogers, E.O. High-speed characteristics of circulation control airfoils. In Proceedings of the 21st Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983. [Google Scholar]
- Schlecht, R.; Anders, S. Parametric evaluation of thin, transonic circulation-control airfoils. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Forster, M.; Biava, M.; Steijl, R. Multipoint optimisation of Coanda surfaces for transonic circulation control using the adjoint method. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Milholen, W.E.; Jones, G.S.; Chan, D.T.; Goodliff, S.; Anders, S.; Pack Melton, L.G.; Carter, M.B.; Allan, B.G.; Capone, F. Enhancements to the FAST-MAC circulation control model and recent high-Reynolds number testing in the National Transonic Facility. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Rumsey, C.L.; Nishino, T. Numerical study comparing RANS and LES approaches on a circulation control airfoil. Int. J. Heat Fluid Flow 2011, 32, 847–864. [Google Scholar] [CrossRef] [Green Version]
- Cruz, J.; Anders, S. Assessment of an unstructured-grid method for predicting aerodynamic performance of jet flaps. In Proceedings of the 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Wu, M.; Martin, M.P. Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp. AIAA J. 2007, 45, 879–889. [Google Scholar] [CrossRef]
- Tong, F.; Li, X.; Yuan, X.; Yu, C. DIncident shock wave and supersonic turbulent boundarylayer interactions near an expansion corner. Comput. Fluids 2020, 198, 104385. [Google Scholar] [CrossRef]
- Zang, B.; Vevek, U.S.; Lim, H.; Wei, X.; New, T.H. An assessment of OpenFOAM solver on RANS simulations of round supersonic free jets. J. Comput. Sci. 2018, 28, 18–31. [Google Scholar] [CrossRef]
- Milholen, W.; Jones, G.; Chan, D. High-Reynolds number circulation control testing in the National Transonic Facility (invited). In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]



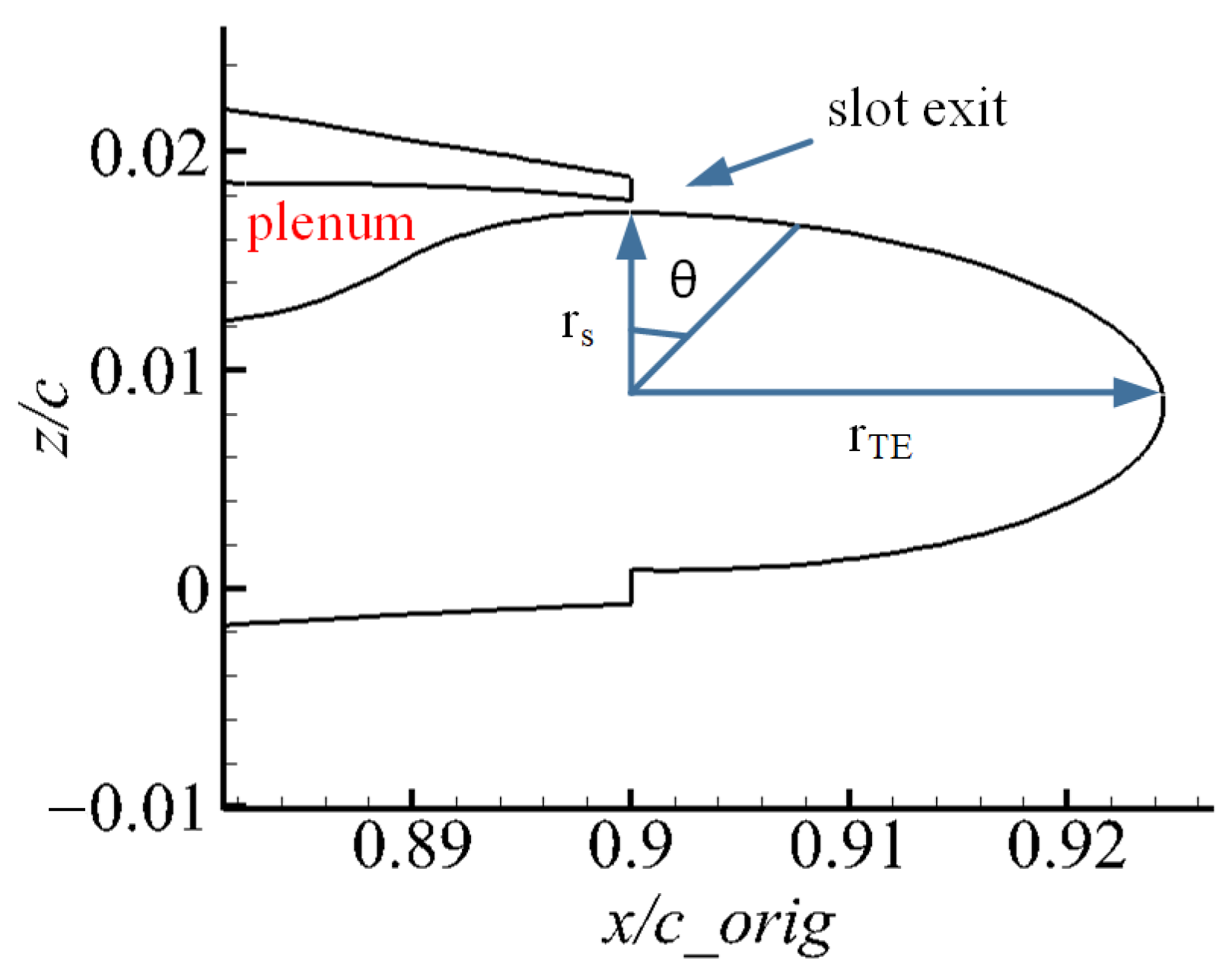
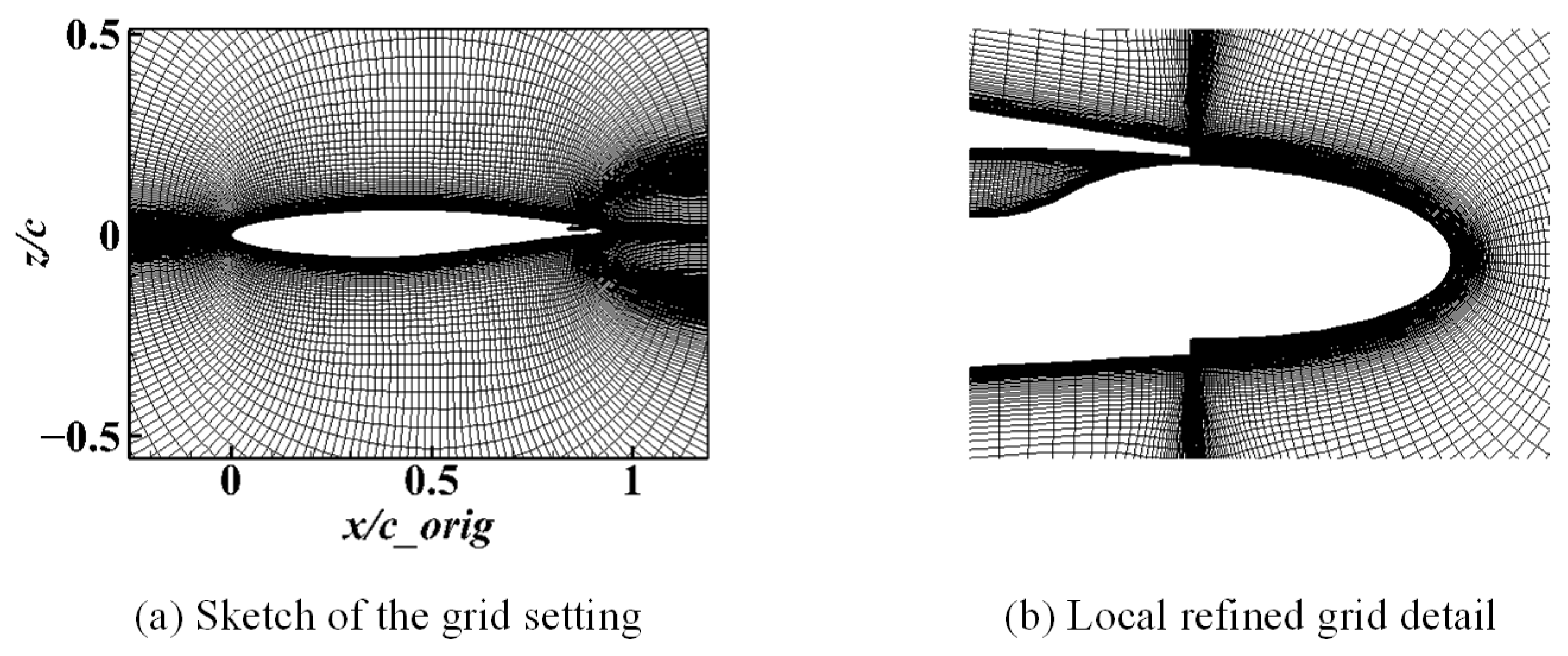
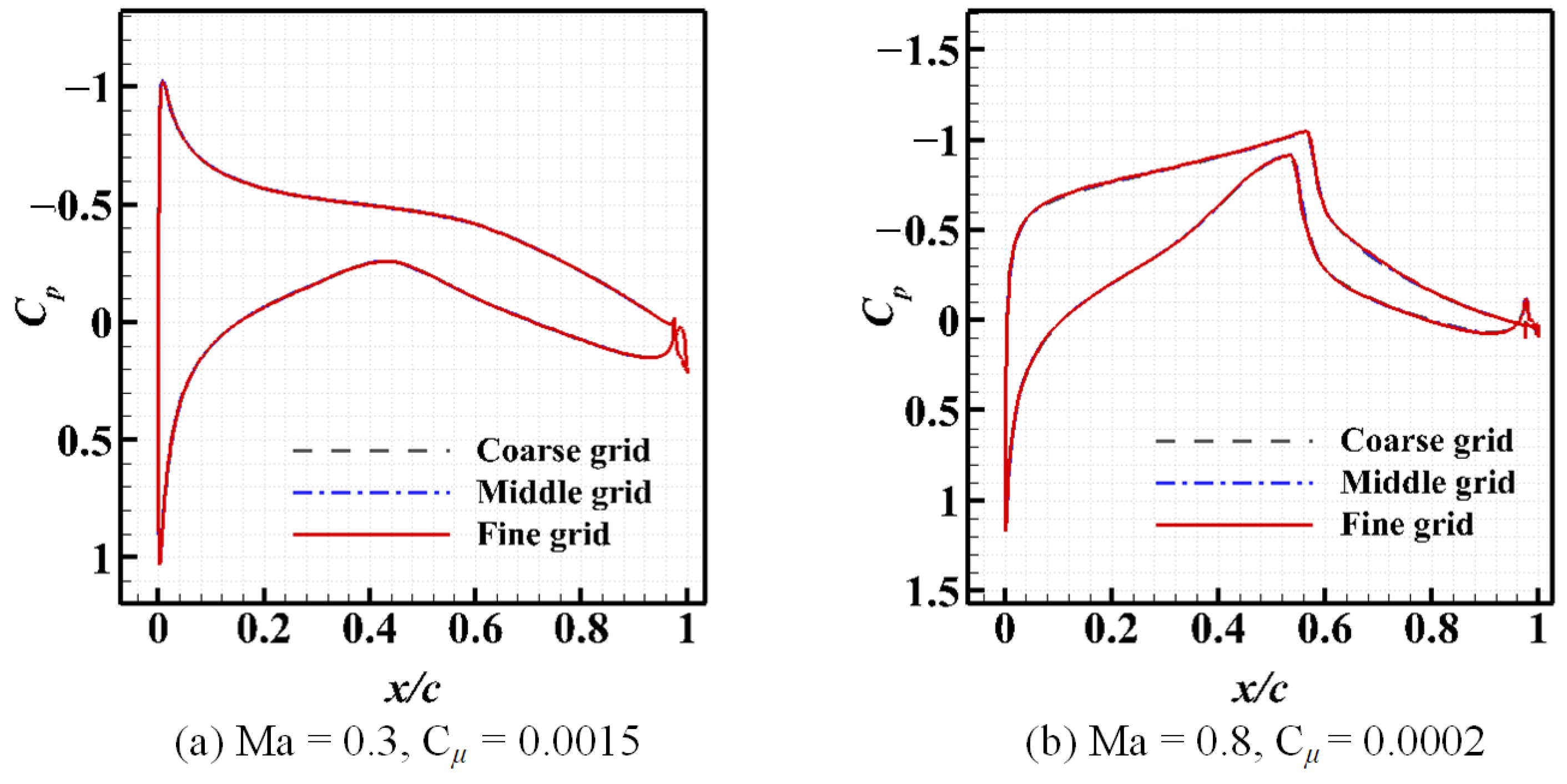
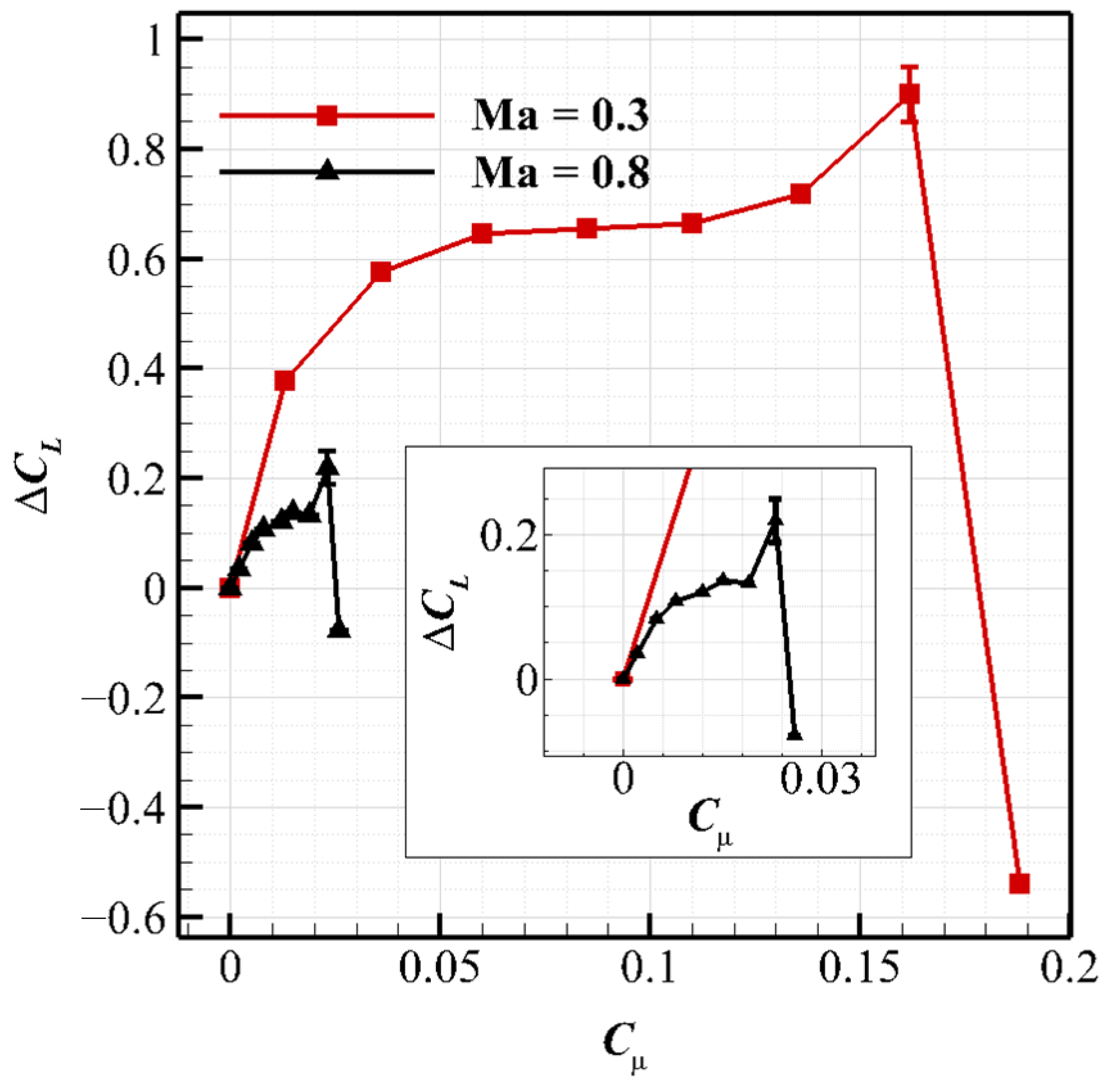


| NPR | ||
|---|---|---|
| 1.1 | 0.0015 | 0.0002 |
| 2 | 0.0130 | 0.0018 |
| 4 | 0.0359 | 0.0050 |
| 6 | 0.0598 | 0.0084 |
| 8 | 0.0846 | 0.0119 |
| 10 | 0.1100 | 0.0154 |
| 12 | 0.1357 | 0.0191 |
| 14 | 0.1619 | 0.0228 |
| 16 | 0.1882 | 0.0265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Hou, Z.; Deng, X.; Guo, Z.; Shao, S.; Xu, B. Numerical Study of the Lift Enhancement Mechanism of Circulation Control in Transonic Flow. Aerospace 2021, 8, 311. https://doi.org/10.3390/aerospace8110311
Chen Y, Hou Z, Deng X, Guo Z, Shao S, Xu B. Numerical Study of the Lift Enhancement Mechanism of Circulation Control in Transonic Flow. Aerospace. 2021; 8(11):311. https://doi.org/10.3390/aerospace8110311
Chicago/Turabian StyleChen, Ye, Zhongxi Hou, Xiaolong Deng, Zheng Guo, Shuai Shao, and Boting Xu. 2021. "Numerical Study of the Lift Enhancement Mechanism of Circulation Control in Transonic Flow" Aerospace 8, no. 11: 311. https://doi.org/10.3390/aerospace8110311
APA StyleChen, Y., Hou, Z., Deng, X., Guo, Z., Shao, S., & Xu, B. (2021). Numerical Study of the Lift Enhancement Mechanism of Circulation Control in Transonic Flow. Aerospace, 8(11), 311. https://doi.org/10.3390/aerospace8110311






