Movement Characteristics of a Dual-Spin Guided Projectile Subjected to a Lateral Impulse
Abstract
:1. Introduction
2. Nonlinear Dynamics Model
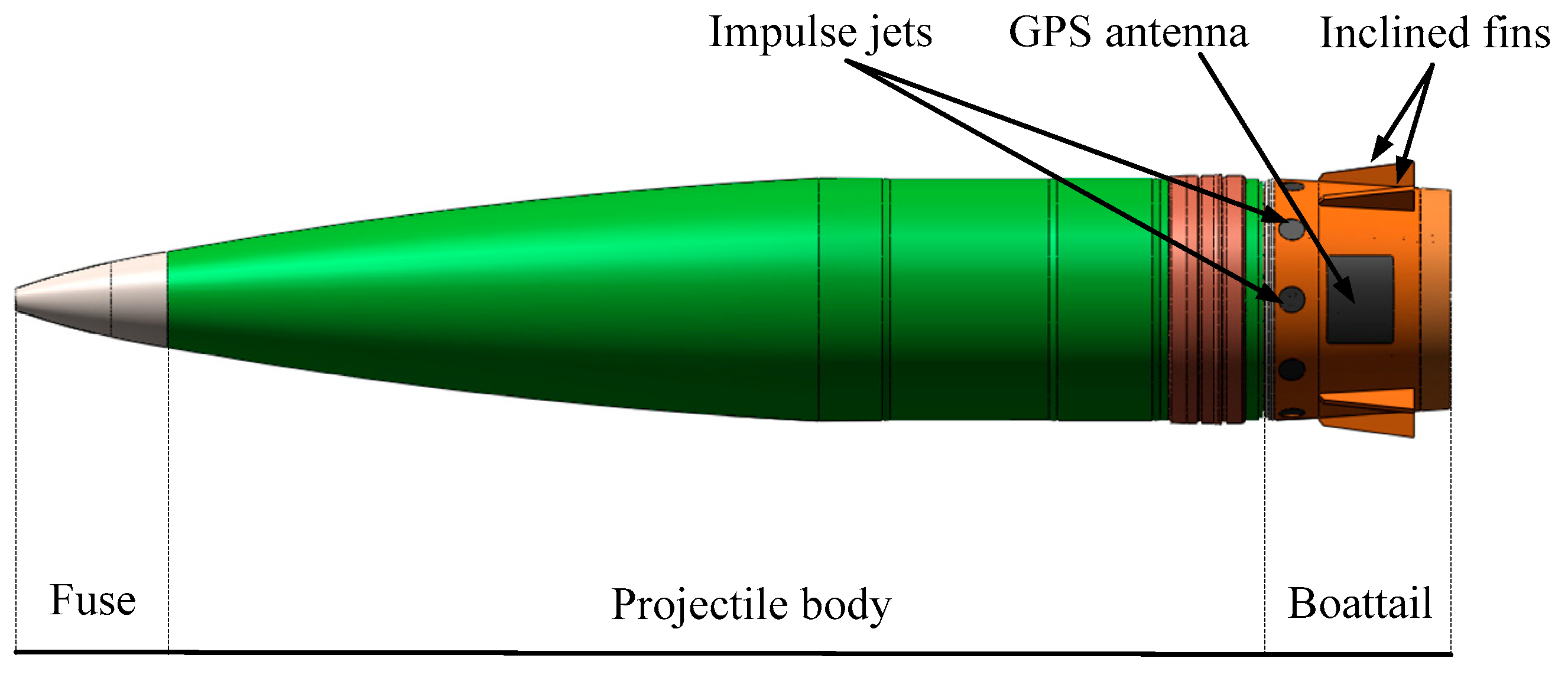
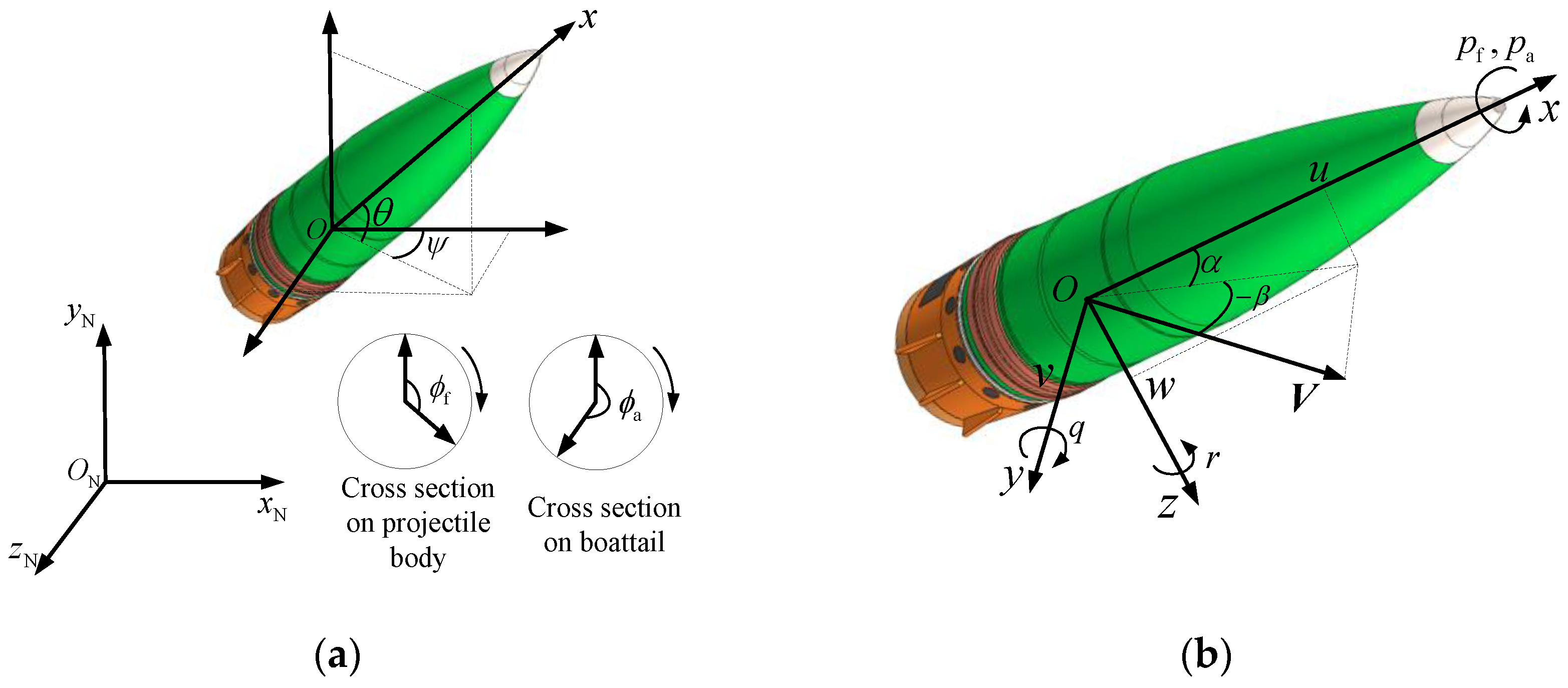
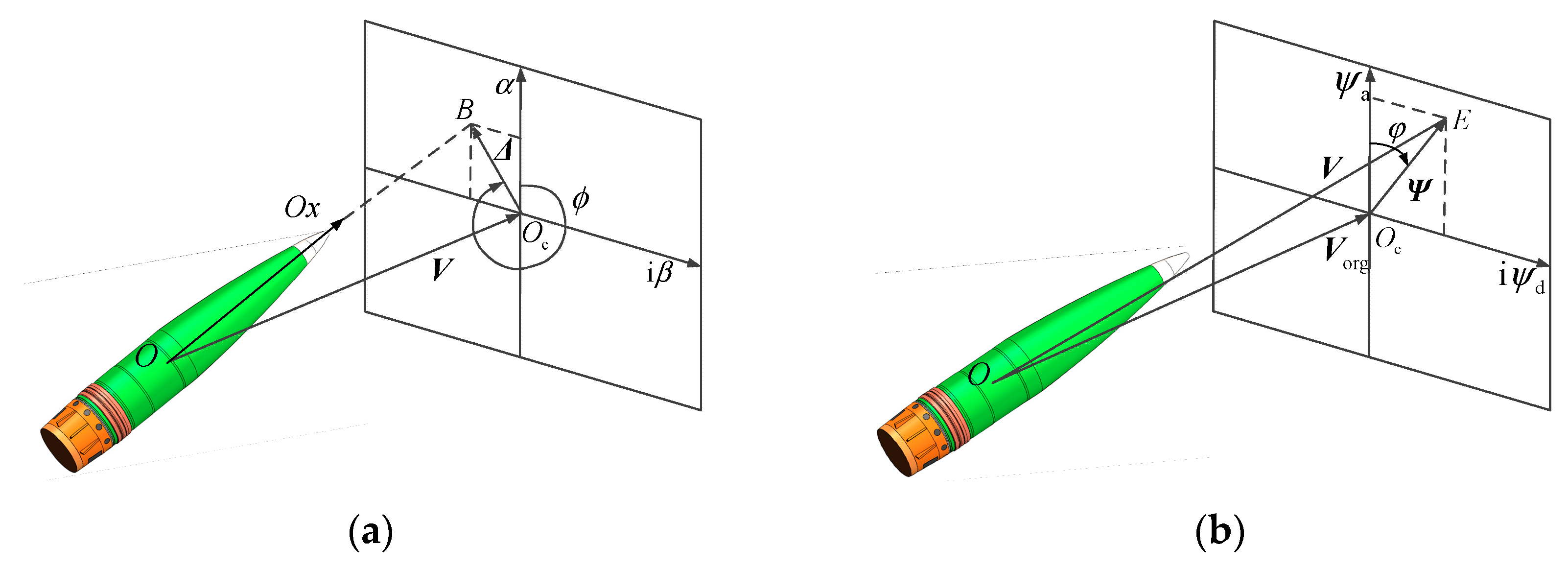
2.1. Concept Design and Reference Frames
2.2. Nonlinear Dynamics Model
2.3. Forces and Moments
2.3.1. Forces
2.3.2. Moments
2.3.3. Forces and Moments of Impulse Jets
2.3.4. Friction Moment of Bearing
3. Linearized Angular Motion Model
3.1. Assumptions for Linearization
- The projectile is mass balanced, such that the centers of gravity of both the projectile body and the boattail lie on the rotational axis of symmetry and ;
- The spin rates of the projectile body and the boattail are constant during the ignition;
- The change of projectile mass characteristics that are caused by the impulse jet ignition is ignored;
- The aerodynamic angles of attack are small so that , ;
- The quantities and are large compared to , , , and , such that products of the small quantities and their derivatives are negligible;
- The projectile is aerodynamically symmetrical;
- The thrust force of the impulse jet is constant and there is no ignition delay.
3.2. Projectile Motion Parameters Described in the Complex Field
3.3. Derivation of the Linear Angular Motion Equation
3.4. Analysis Solutions of the Linear Angular Motion Equation
4. Angular Motion of the Projectile Subjected to a Lateral Impulse
4.1. Angular Motion at the First Stage
4.2. Angular Motion at the Second Stage
4.3. Deflection Angle of the Velocity at the First Stage
4.4. Deflection Angle of the Velocity at the Second Stage
5. Results and Discussion
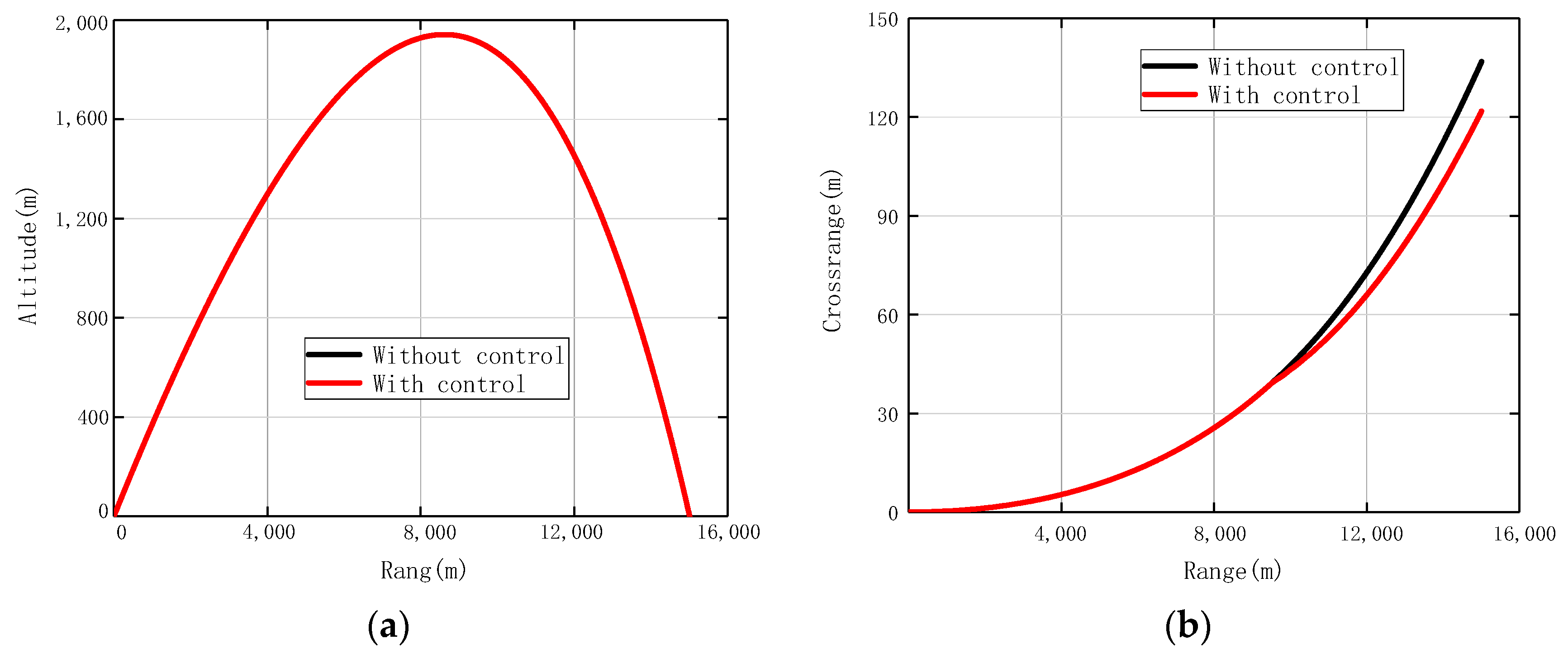
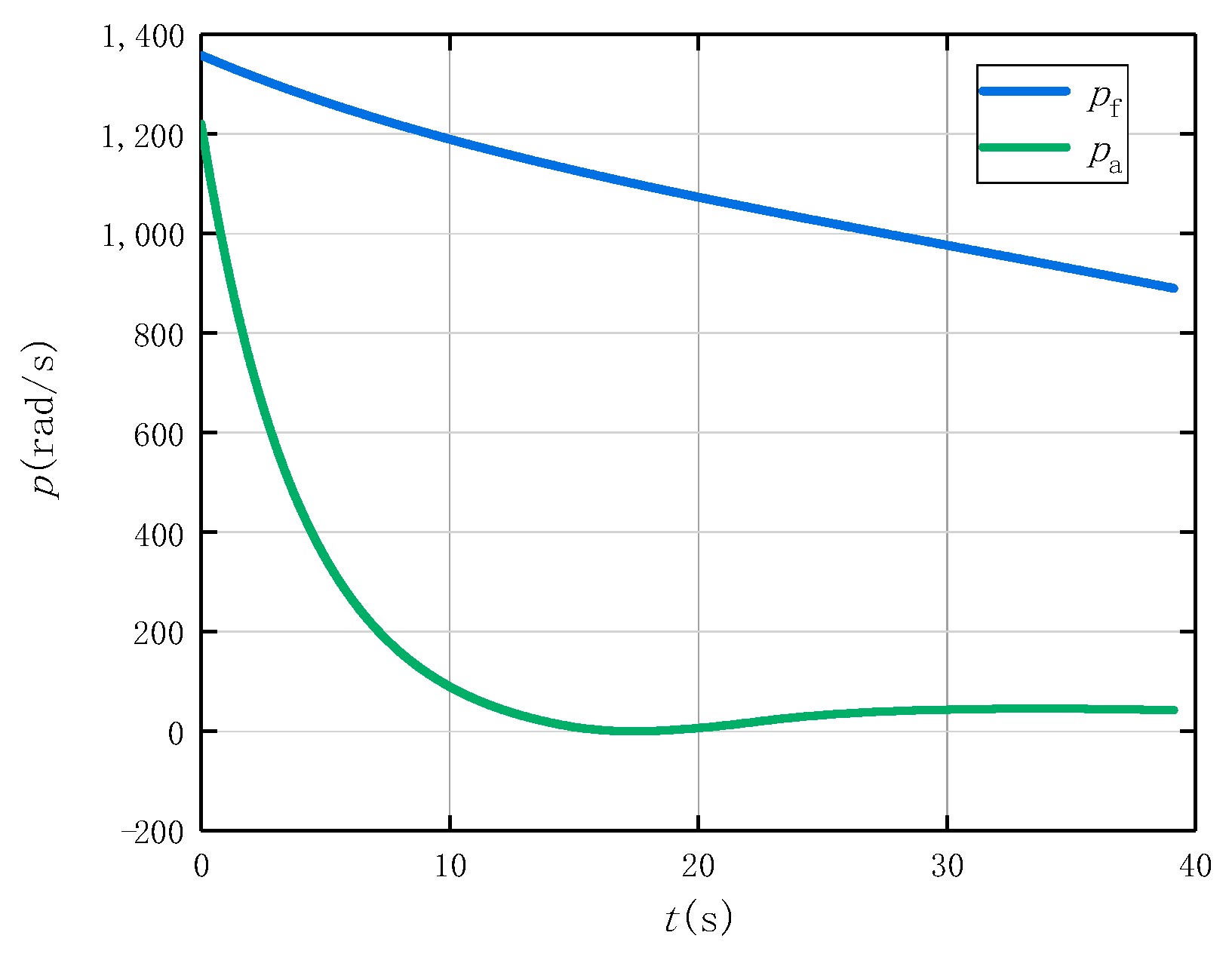
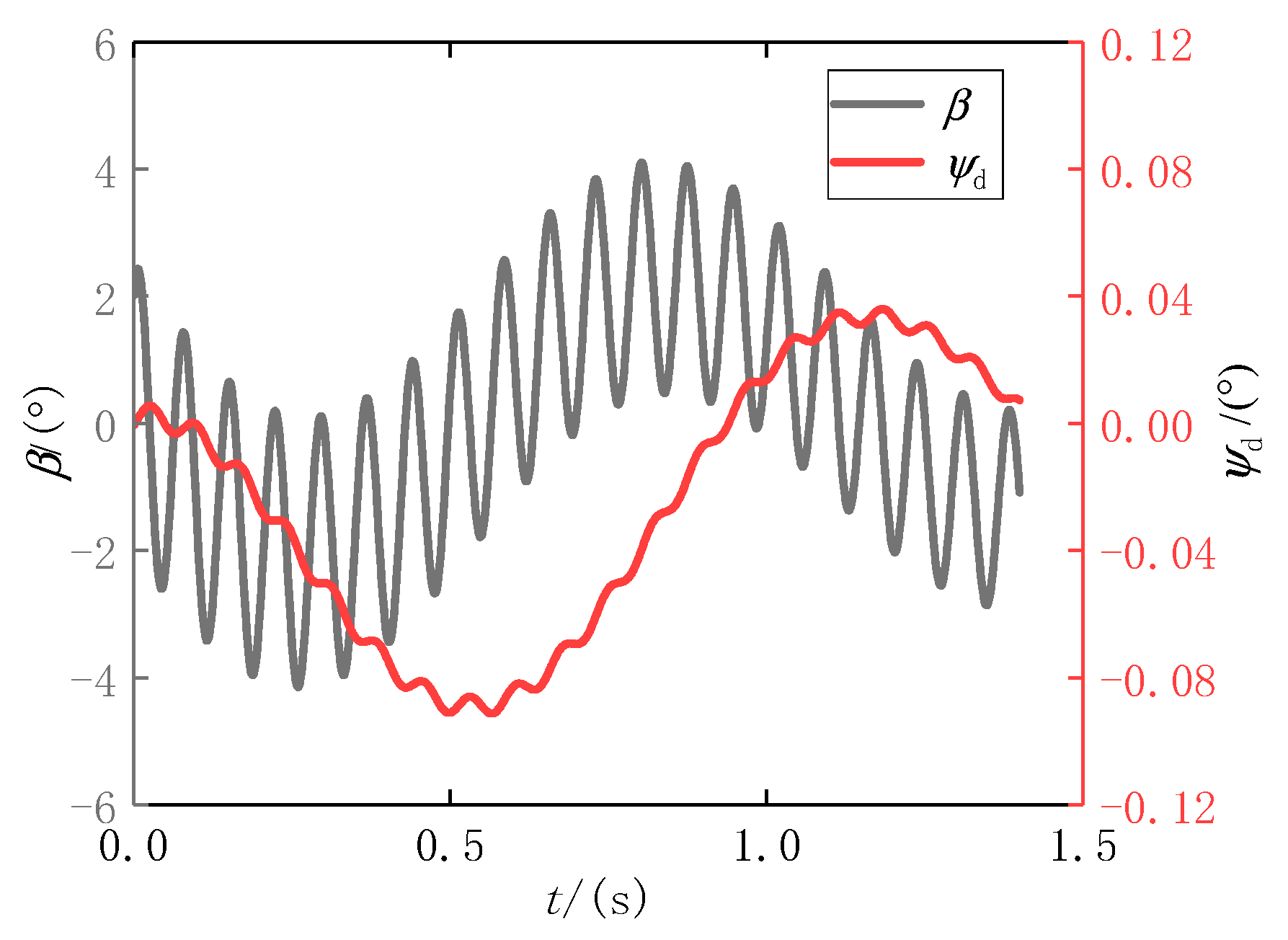
5.1. Numerical Simulation Results
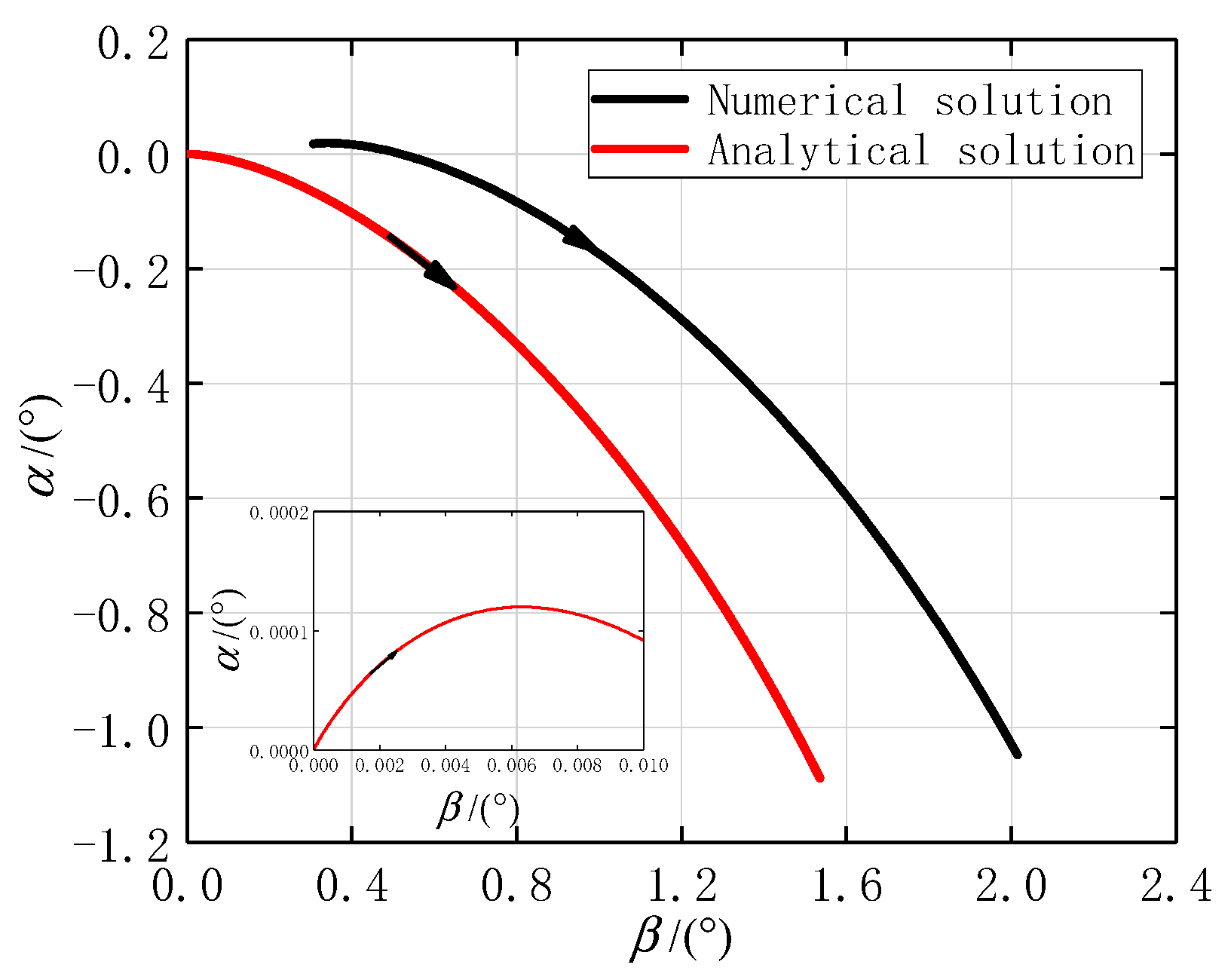
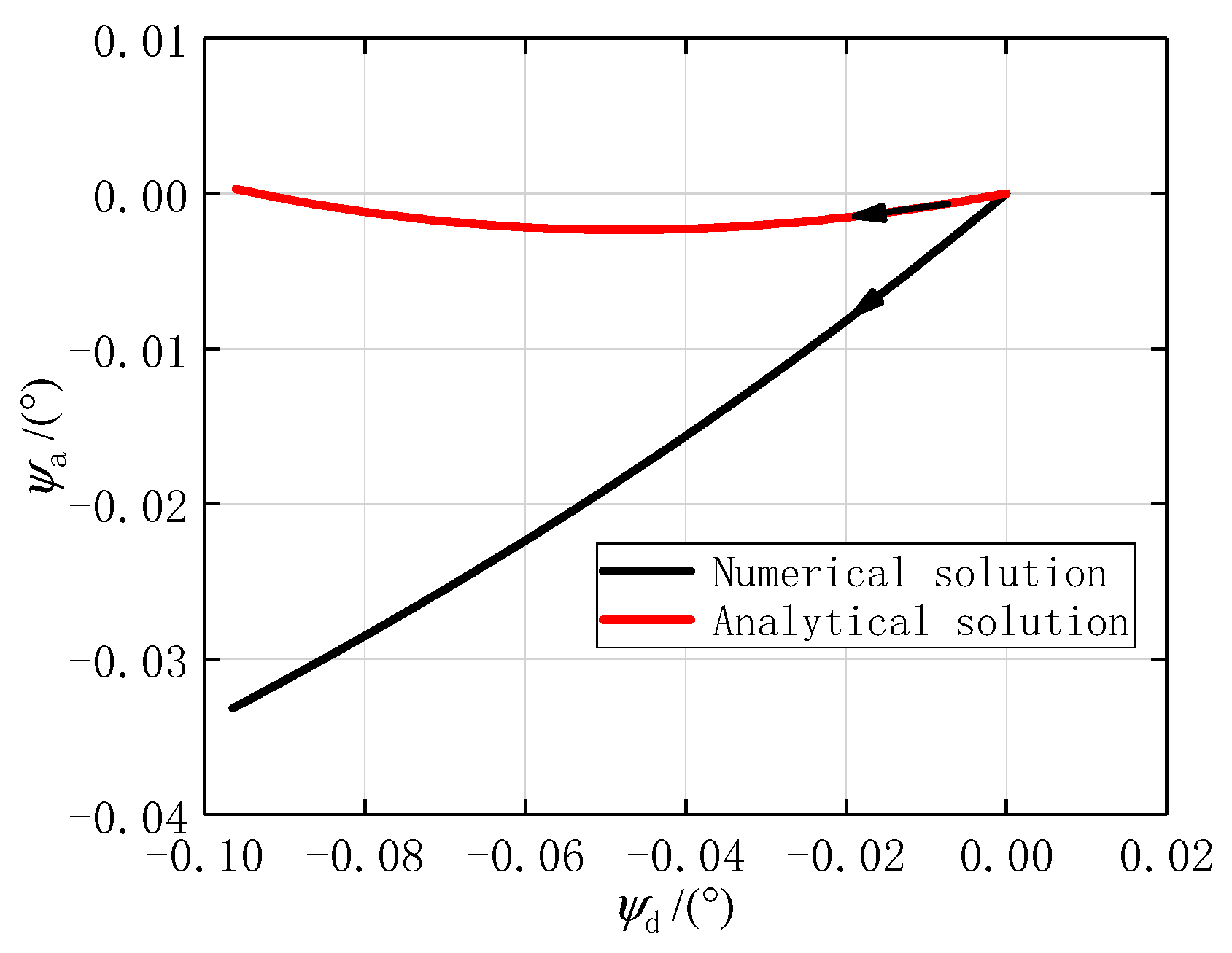
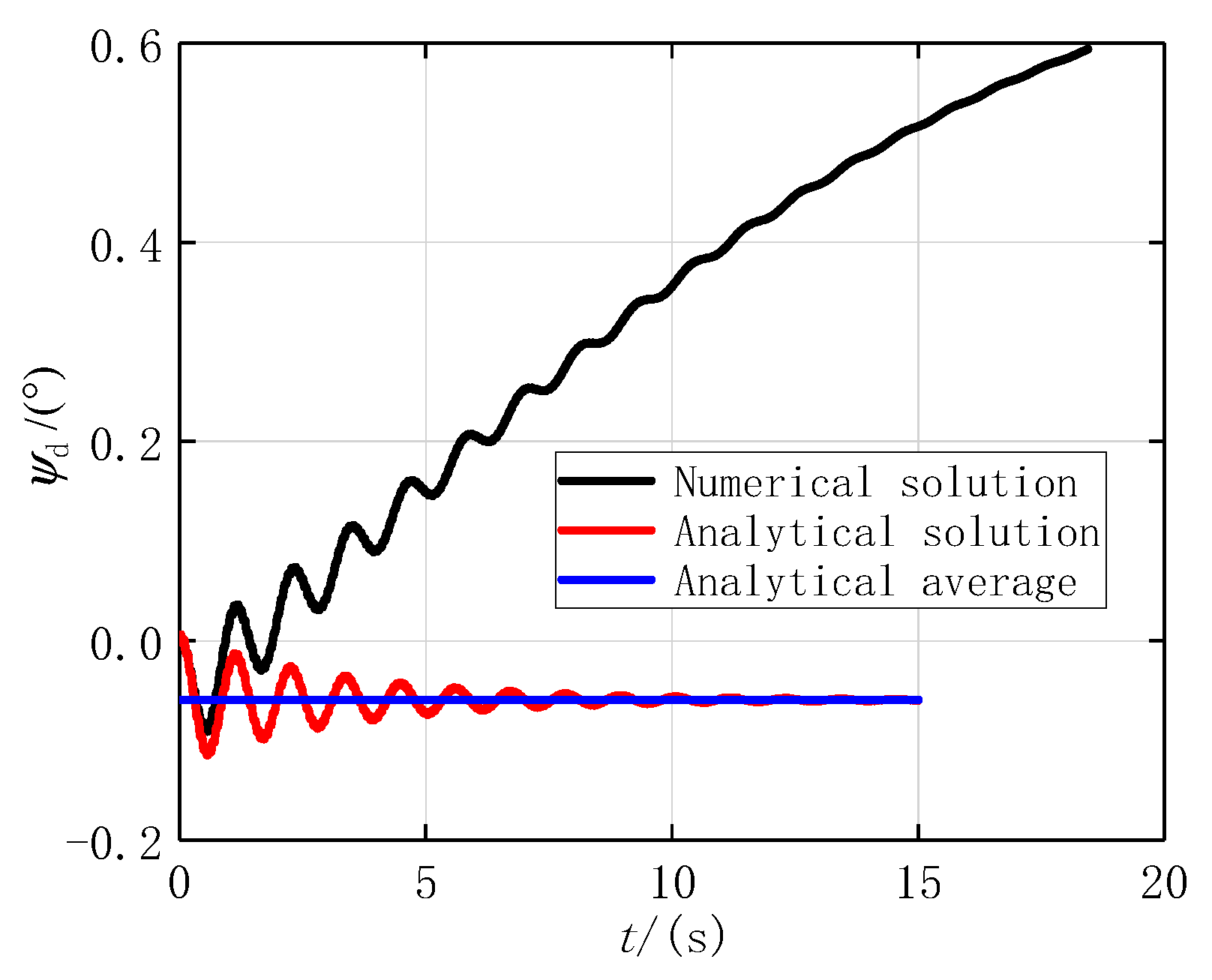
5.2. Numerical and Analytical Solutions at the First Stage
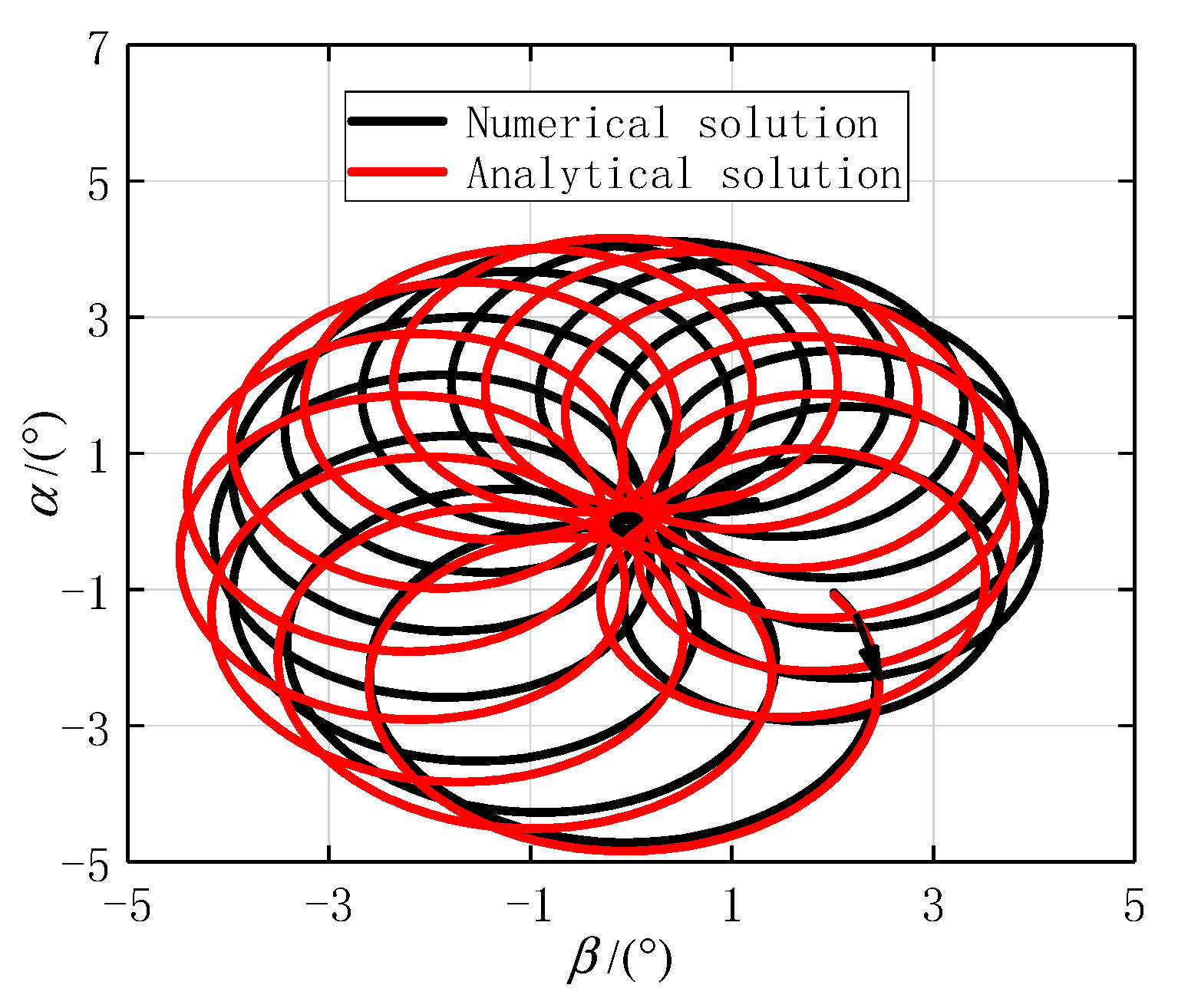
5.3. Numerical and Analytical Solutions at the Second Stage
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Z.W.; Wang, L.M.; Zhong, Y.W. Calculation method for the nonlinear angular motion attraction domain of spin-stabilized projectile. Acta Armamentarii 2021, 42, 1195–1203. [Google Scholar]
- Costello, M.; Peterson, A. Linear theory of a dual-spin projectile in atmospheric flight. J. Guid. Control Dyn. 2000, 23, 789–797. [Google Scholar] [CrossRef]
- Hainz, L.C.; Costello, M. Modified projectile linear theory for rapid trajectory prediction. J. Guid. Control Dyn. 2005, 28, 1006–1014. [Google Scholar] [CrossRef]
- Theodoulis, S.; Morel, Y.; Werbert, P. Trajectory-based accurate linearization of the 155 mm spin-stabilized projectile dynamics. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Chicago, IL, USA, 10–13 August 2009; pp. 1–21. [Google Scholar]
- Li, J.; He, G.; Guo, H. A study on the aerodynamic characteristics for a two-dimensional trajectory correction fuze. Appl. Mech. Mater. 2015, 703, 370–375. [Google Scholar] [CrossRef]
- Liang, K.; Huang, Z.; Zhang, J. Optimal design of the aerodynamic parameters for a supersonic two-dimensional guided artillery projectile. Def. Technol. 2017, 13, 206–211. [Google Scholar] [CrossRef]
- Liu, X.; Wu, X.; Yin, J. Aerodynamic characteristics of a dual-spin projectile with canards. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4541–4553. [Google Scholar] [CrossRef]
- Wernert, P.; Theodoulis, S. Modelling and stability analysis for a class of 155 mm spin-stabilized projectiles with course correction fuse (CCF). In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, OR, USA, 8–11 August 2011; pp. 1–14. [Google Scholar]
- Wang, Z.G.; Li, W. Analysis of free motion characteristics for dual-spin projectile. Appl. Mech. Mater. 2013, 427, 69–72. [Google Scholar] [CrossRef]
- Chang, S.J.; Wang, Z.Y.; Liu, T.Z. Analysis of spin-rate property for dual-spin-stabilized projectiles with canards. J. Spacecr. Rockets 2014, 51, 958–966. [Google Scholar] [CrossRef]
- Chang, S.J. Dynamic Response to canard control and gravity for a dual-spin projectile. J. Spacecr. Rockets 2016, 53, 558–566. [Google Scholar] [CrossRef]
- Gagnon, E.; Vachon, A. Efficiency analysis of canards-based course correction fuze for a 155-mm spin-stabilized projectile. J. Aerosp. Eng. 2016, 29, 04016055. [Google Scholar] [CrossRef]
- Spagni, J.; Theodoulis, S.; Wernert, P. Flight control for a class of 155 mm spin-stabilized projectile with reciprocating canards. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; pp. 1–8. [Google Scholar]
- Theodoulis, S.; Gassmann, V.; Wernert, P. Guidance and control design for a class of spin-stabilized fin-controlled projectiles. J. Guid. Control Dyn. 2013, 36, 517–531. [Google Scholar] [CrossRef]
- Theodoulis, S.; Seve, F.; Wernert, P. Robust gain-scheduled autopilot design for spin-stabilized projectiles with a course-correction fuze. Aerosp. Sci. Technol. 2015, 42, 477–489. [Google Scholar] [CrossRef]
- Thurman, S.W.; Flashner, H. Robust digital autopilot design for spacecraft equipped with pulse-operated thrusters. J. Guid. Control Dyn. 1996, 19, 1047–1055. [Google Scholar] [CrossRef]
- Zimpfer, D.J.; Shieh, L.S.; Sunkel, J.W. Digitally redesigned pulse-width modulation spacecraft control. J. Guid. Control Dyn. 1998, 21, 529–534. [Google Scholar] [CrossRef]
- Guidos, B.J.; Cooper, G.R. Linearized motion of a fin-stabilized projectile subjected to a lateral impulse. J. Spacecr. Rockets 2002, 39, 384–391. [Google Scholar] [CrossRef]
- Burchett, B.; Costello, M. Model predictive lateral pulse jet control of an atmospheric rocket. J. Guid. Control Dyn. 2002, 25, 860–867. [Google Scholar] [CrossRef]
- Corriveau, D.; Wey, P.; Berner, C. Thrusters pairing guidelines for trajectory corrections of projectiles. J. Guid. Control Dyn. 2011, 34, 1120–1128. [Google Scholar] [CrossRef]
- Bojan, P.; Milos, P.; Danilo, C. Frequency-modulated pulse-jet control of an artillery rocket. J. Spacecr. Rockets 2012, 49, 286–294. [Google Scholar]
- Glebocki, R.; Jacewicz, M. Parametric study of guidance of a 160-mm projectile steered with lateral thrusters. Aerospace 2020, 7, 61. [Google Scholar] [CrossRef]
- Lee, J.; Min, B.; Byun, Y. Computational investigation and design optimization of a lateral-jet-controlled missile. J. Aircr. 2006, 43, 1292–1300. [Google Scholar] [CrossRef]
- Liu, L.J.; Zhu, C.H.; Yu, Z. Guidance and ignition control of lateral-jet-controlled interceptor missiles. J. Guid. Control Dyn. 2015, 38, 2455–2460. [Google Scholar] [CrossRef]
- Glebocki, R.; Jacewicz, M. Sensitivity analysis and flight tests results for a vertical cold launch missile system. Aerospace 2020, 7, 168. [Google Scholar] [CrossRef]
- McCoy, R.L. Modern Exterior Ballistics, 2nd ed.; Schiffer Publishing Ltd.: Atglen, PA, USA, 1999; pp. 187–188. [Google Scholar]
- Han, Z.P. Exterior Ballistics of Projectiles and Rockets, 2nd ed.; Beijing Institute of Technology Press: Beijing, China, 2008; pp. 174–176. [Google Scholar]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Mass of projectile body | 39.24 kg | 1.61 kg·m2 | |
| Mass of boattail | 7.80 kg | Drag force coefficient | 0.3295 |
| Diameter of projectile | 0.155 m | Lift force coefficient | 1.9589 |
| Length of projectile body | 0.790 m | Pitching moment coefficient | 0.7752 |
| Length of boattail | 0.112 m | Magnus moment coefficient | −0.0491 |
| 0.14 kg·m2 | Pitching damping moment coefficient | 1.5251 | |
| 0.02 kg·m2 | Oblique angle of incline fins | −3 deg |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0 deg | 0.3295 | ||
| Thrust force | 1400 N | Working time | 20 ms |
| 0.2065 m | 9.6851 rad/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wang, L.; Chen, J. Movement Characteristics of a Dual-Spin Guided Projectile Subjected to a Lateral Impulse. Aerospace 2021, 8, 309. https://doi.org/10.3390/aerospace8100309
Yang Z, Wang L, Chen J. Movement Characteristics of a Dual-Spin Guided Projectile Subjected to a Lateral Impulse. Aerospace. 2021; 8(10):309. https://doi.org/10.3390/aerospace8100309
Chicago/Turabian StyleYang, Zhiwei, Liangming Wang, and Jianwei Chen. 2021. "Movement Characteristics of a Dual-Spin Guided Projectile Subjected to a Lateral Impulse" Aerospace 8, no. 10: 309. https://doi.org/10.3390/aerospace8100309
APA StyleYang, Z., Wang, L., & Chen, J. (2021). Movement Characteristics of a Dual-Spin Guided Projectile Subjected to a Lateral Impulse. Aerospace, 8(10), 309. https://doi.org/10.3390/aerospace8100309






