Numerical Simulations on Unsteady Nonlinear Transonic Airfoil Flow
Abstract
1. Introduction
2. Flow Solver: DLR TAU-Code
3. Numerical Mesh for the RAE2882 Airfoil
4. Test Cases and Numerical Settings
5. Results
5.1. Steady CFD Results
5.2. Unsteady Nonlinear Aerodynamic Responses
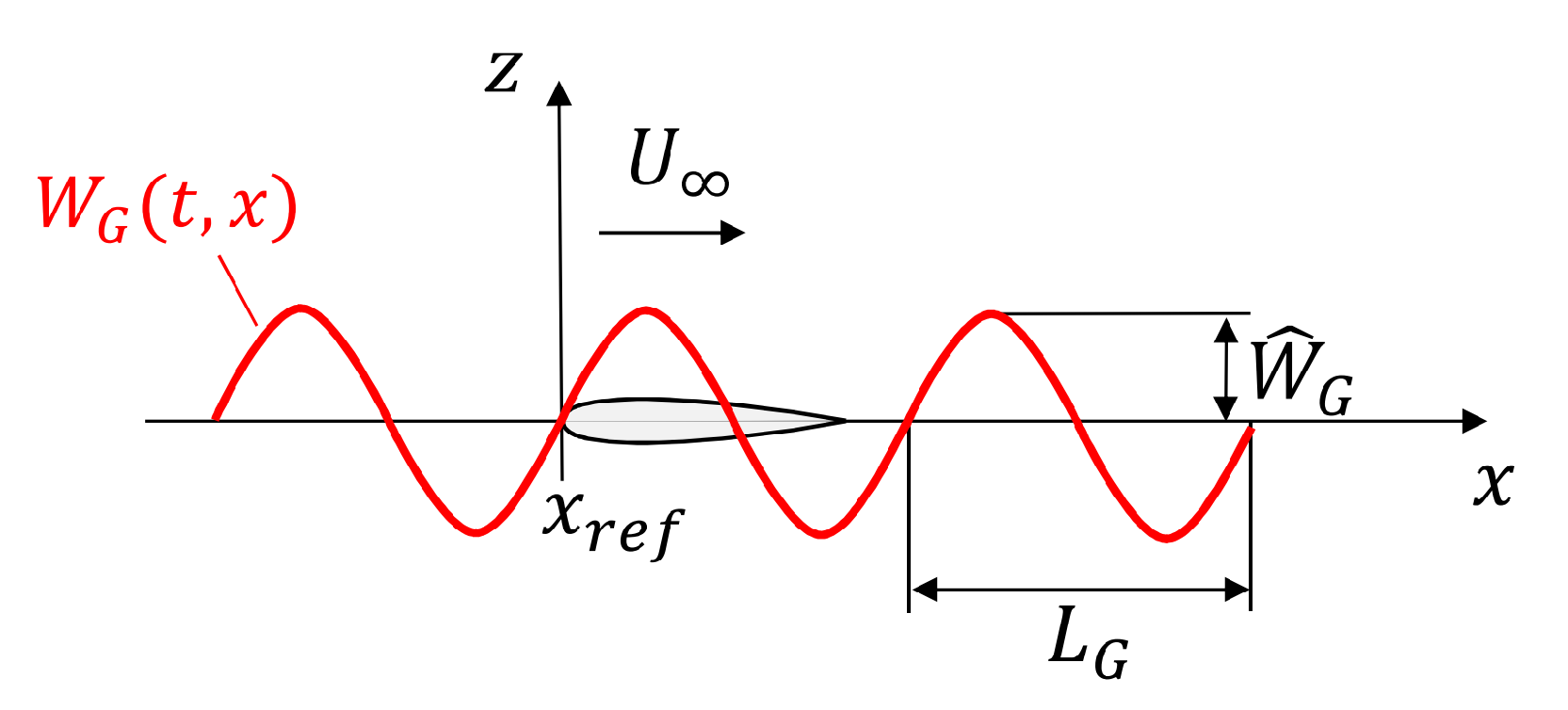
5.2.1. Definition of Variables
5.2.2. Time-Domain Representation
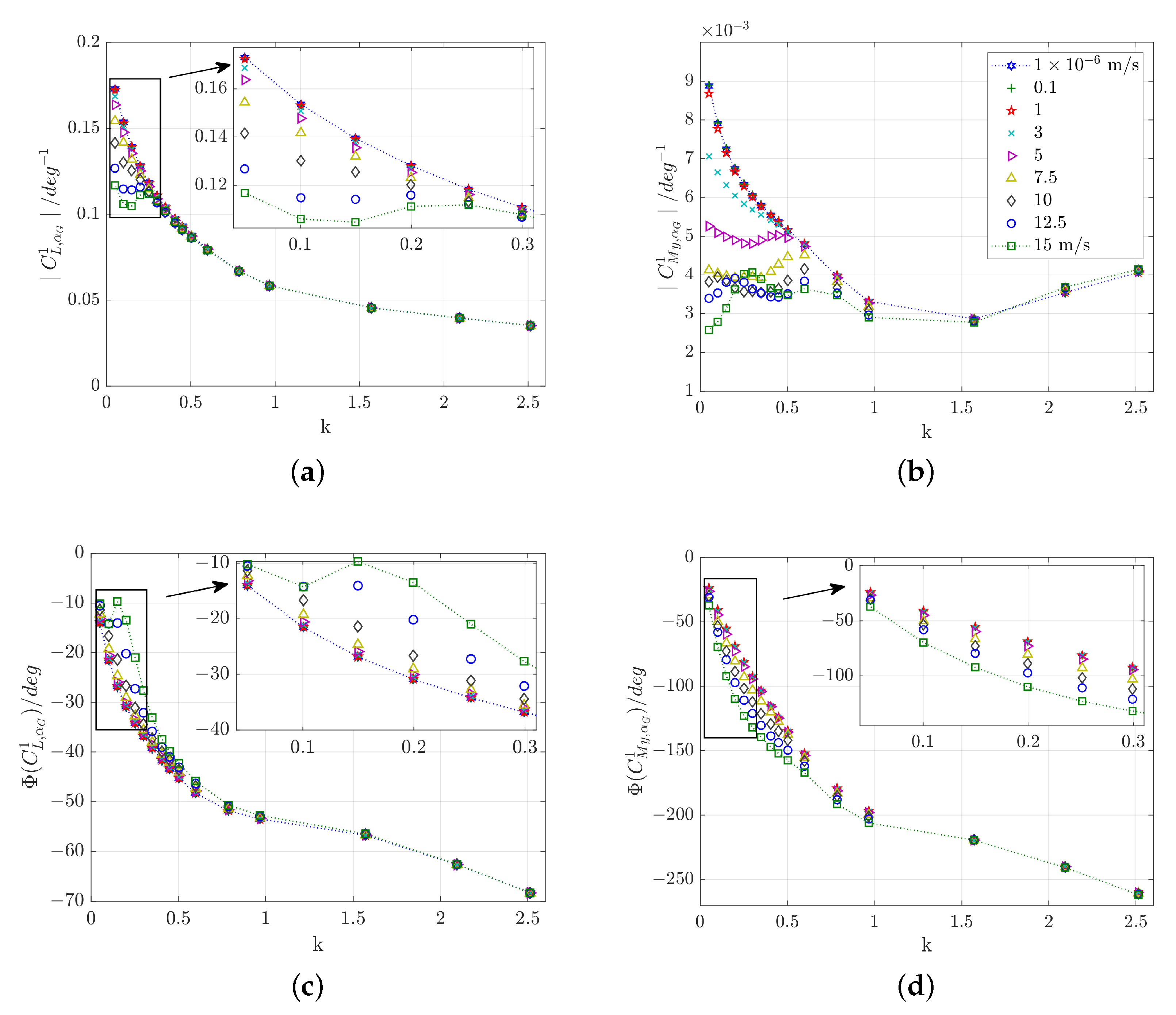
5.2.3. Frequency Content
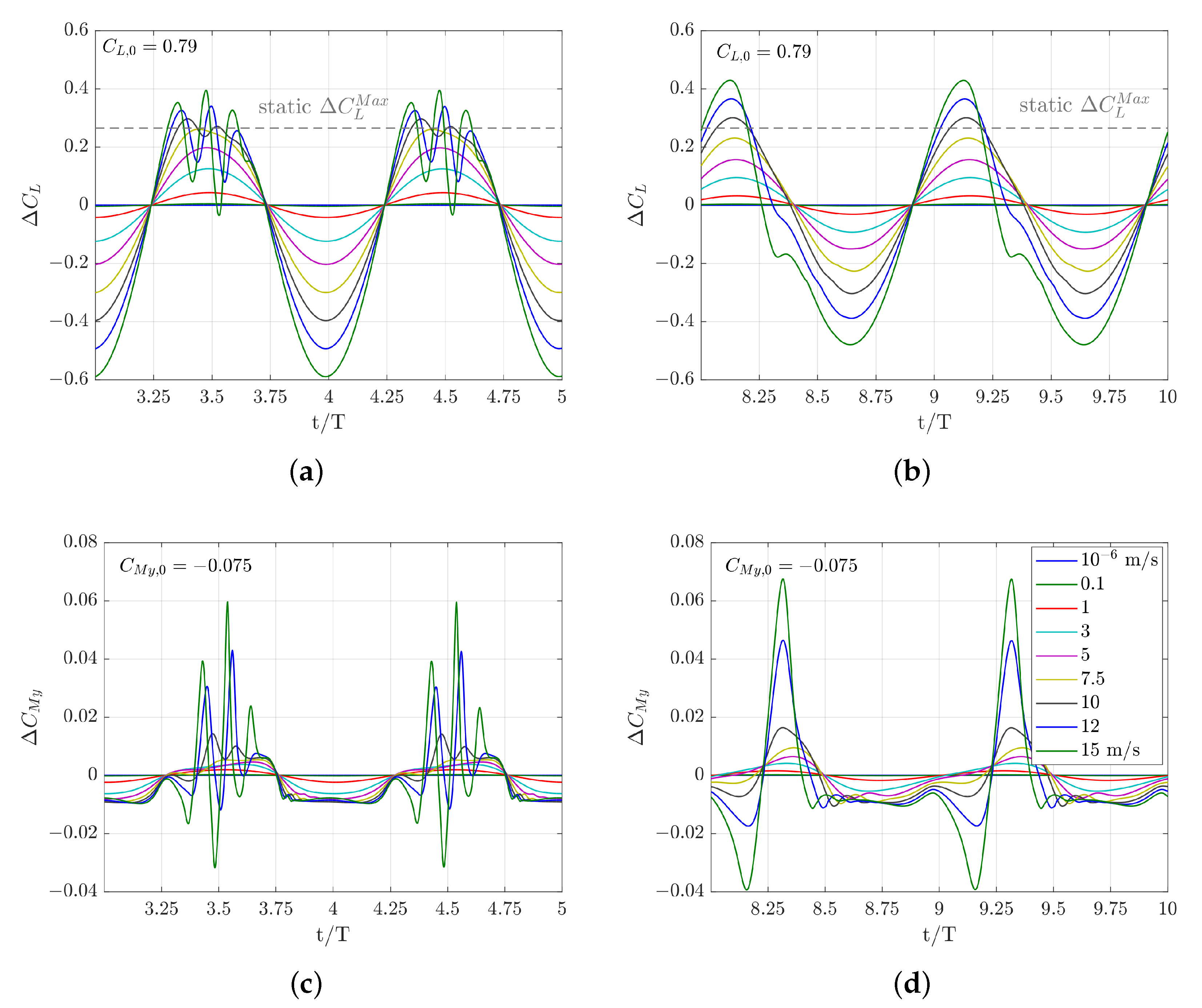
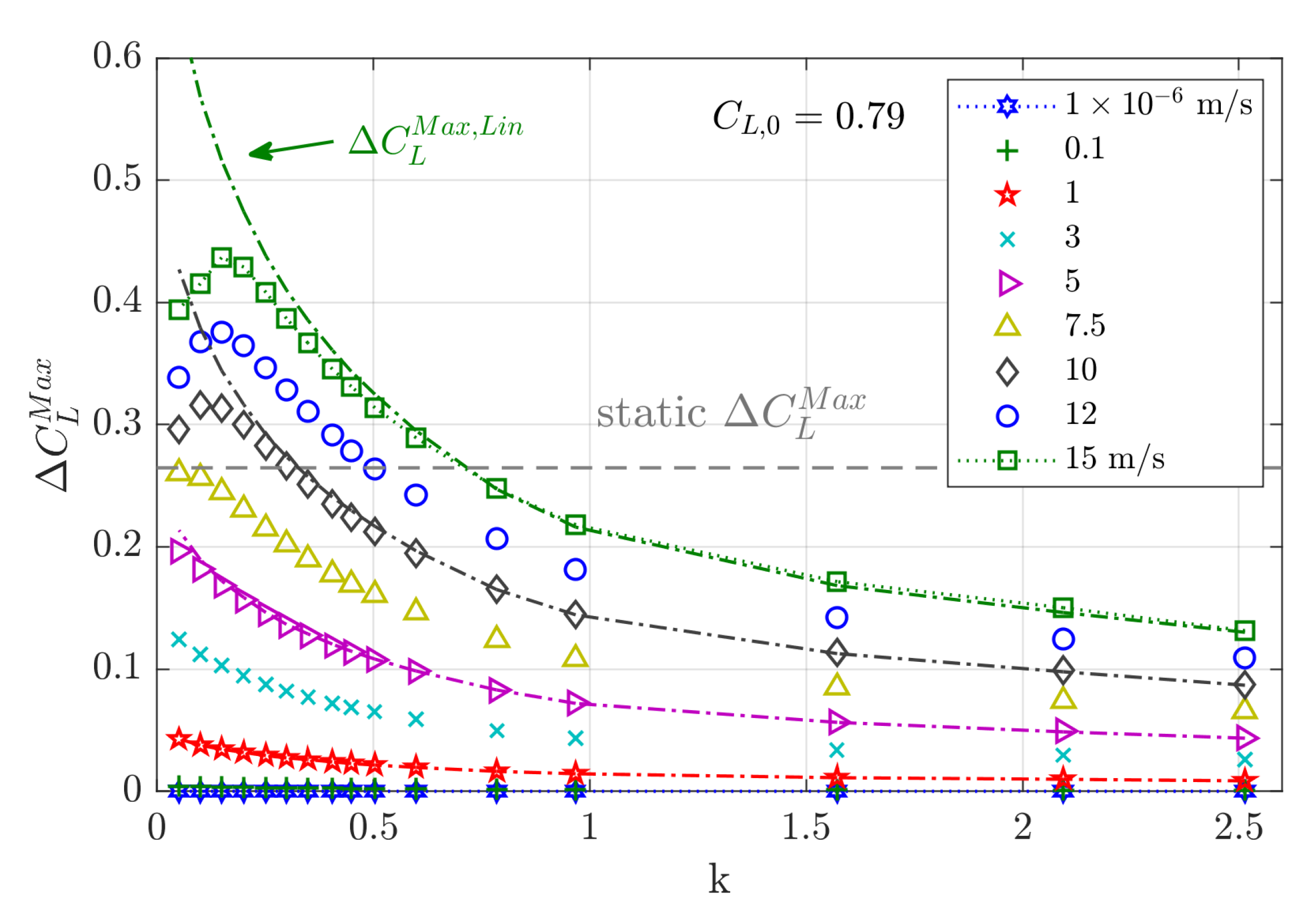
5.2.4. Maximum Lift Coefficient
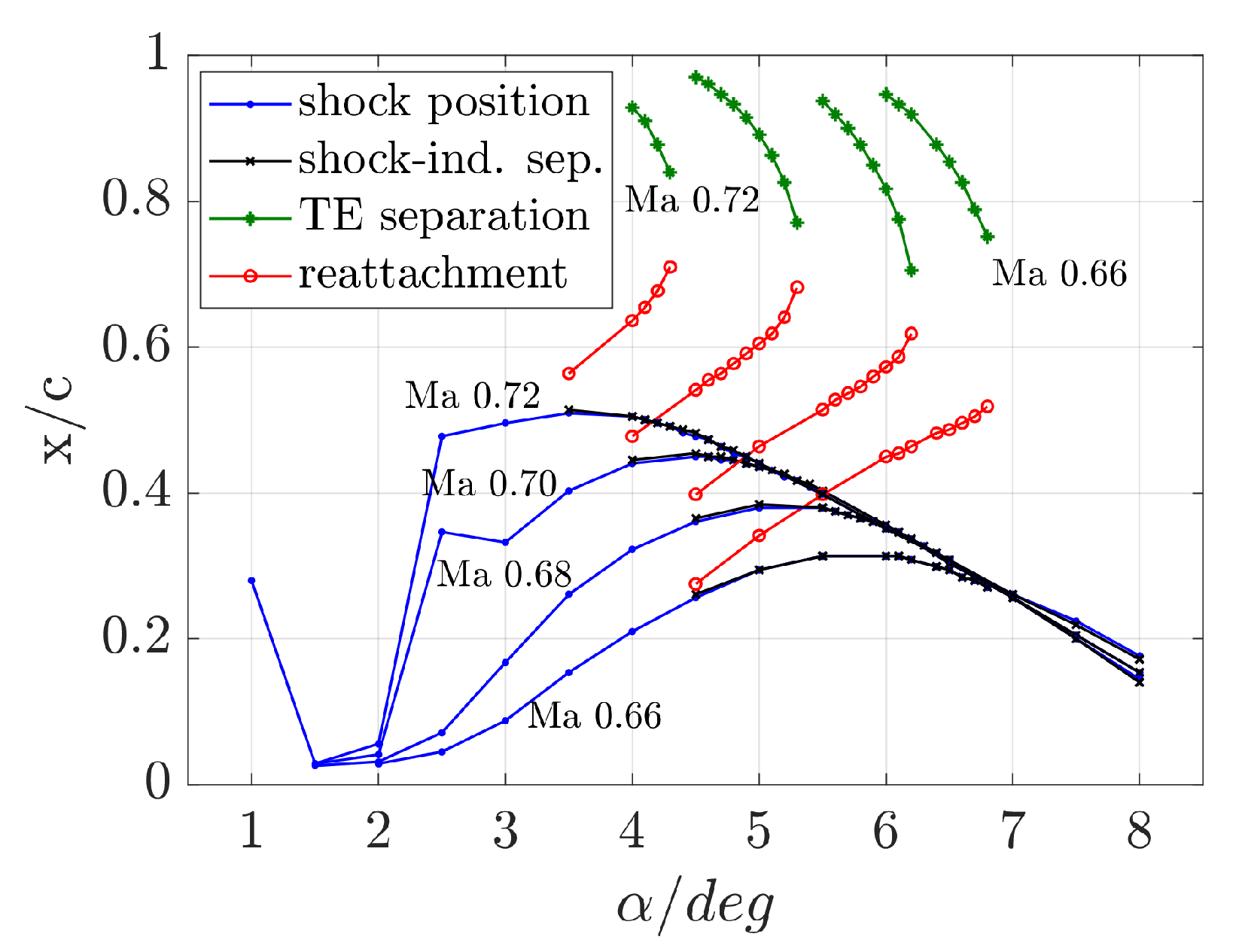
5.2.5. Unsteady Shock Motion
5.2.6. Examples of Instantaneous Flow Fields
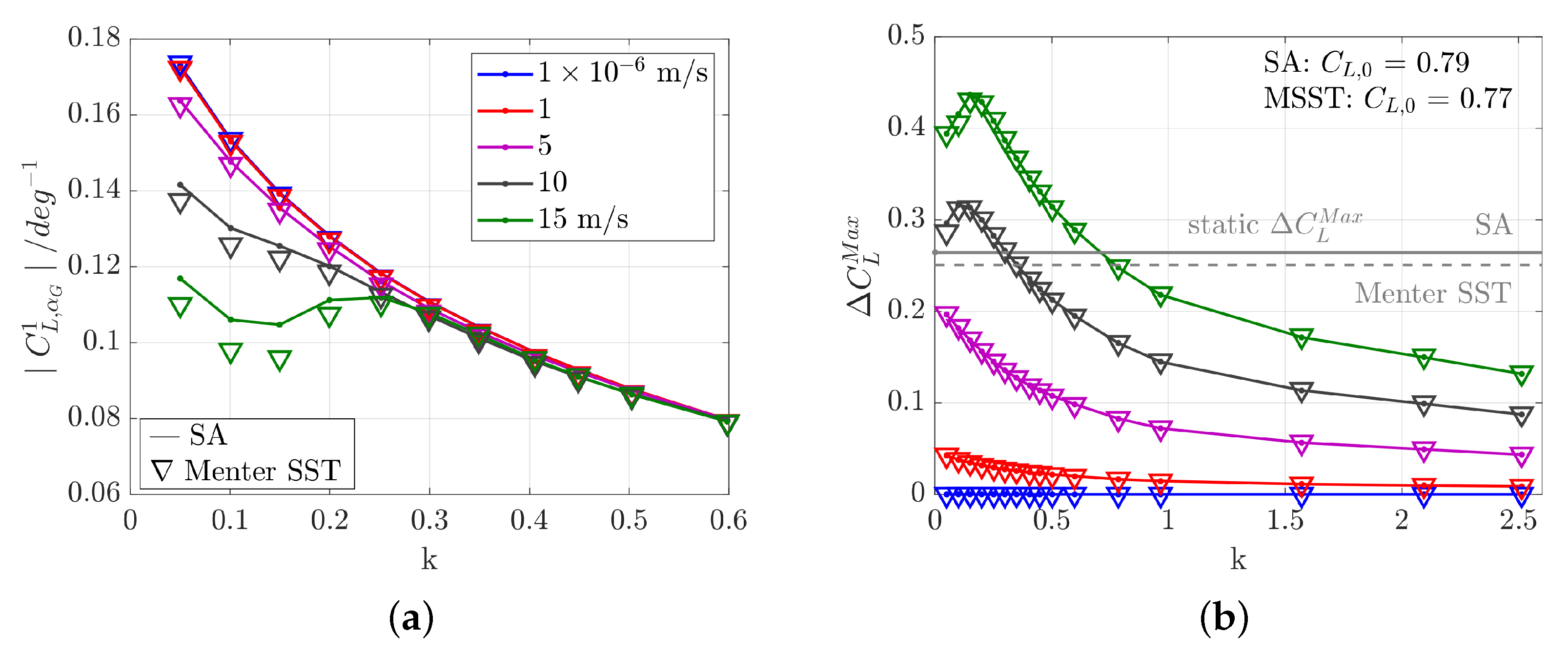
5.2.7. Influence of the Turbulence Model
5.3. Possible Indicators for the Assessment of Nonlinear Responses
5.3.1. Definition of Variables
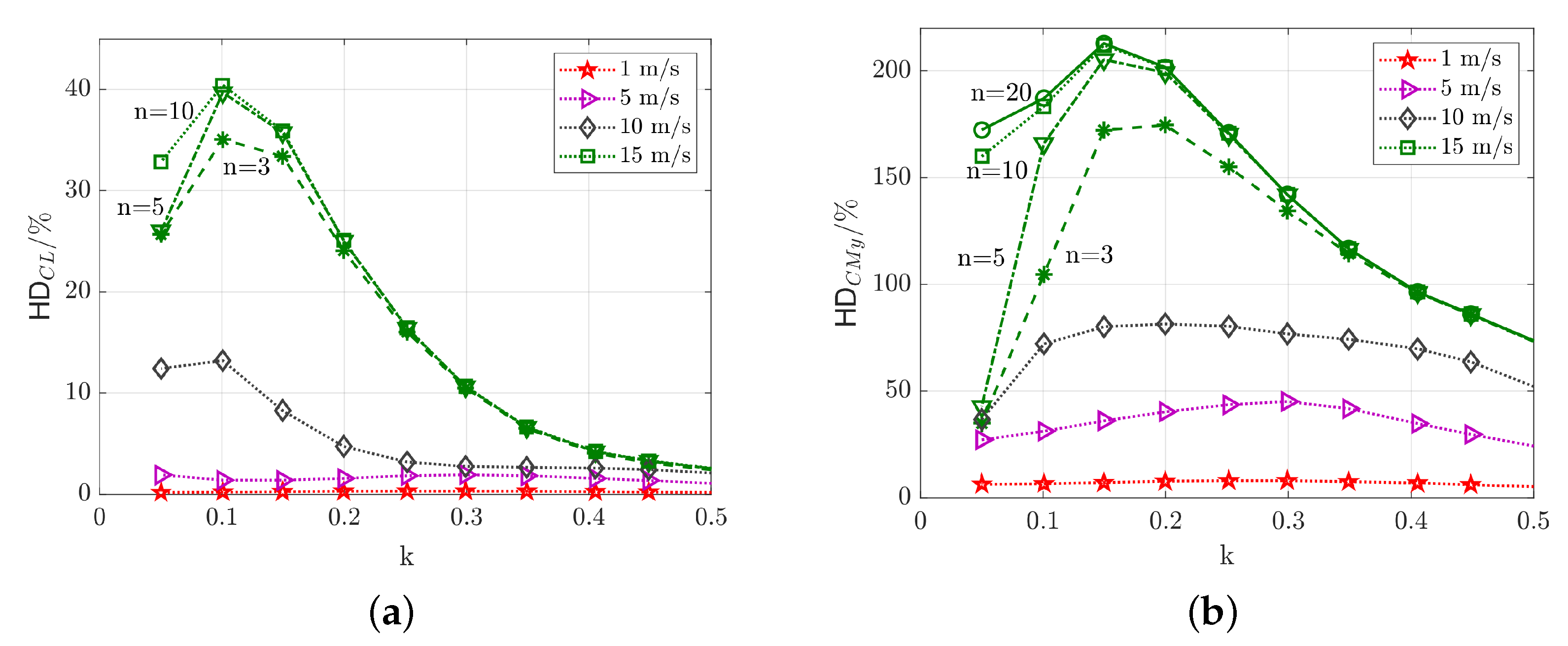
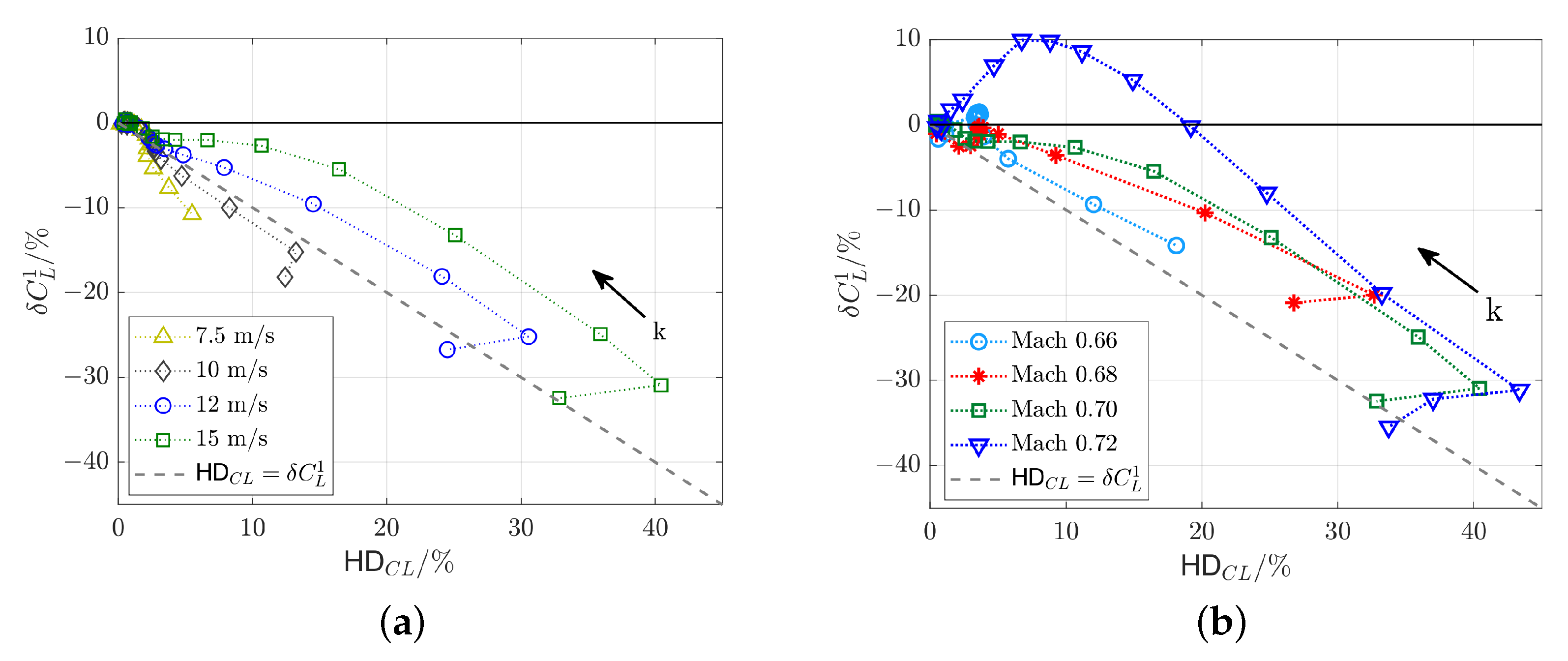
5.3.2. Harmonic Distortion
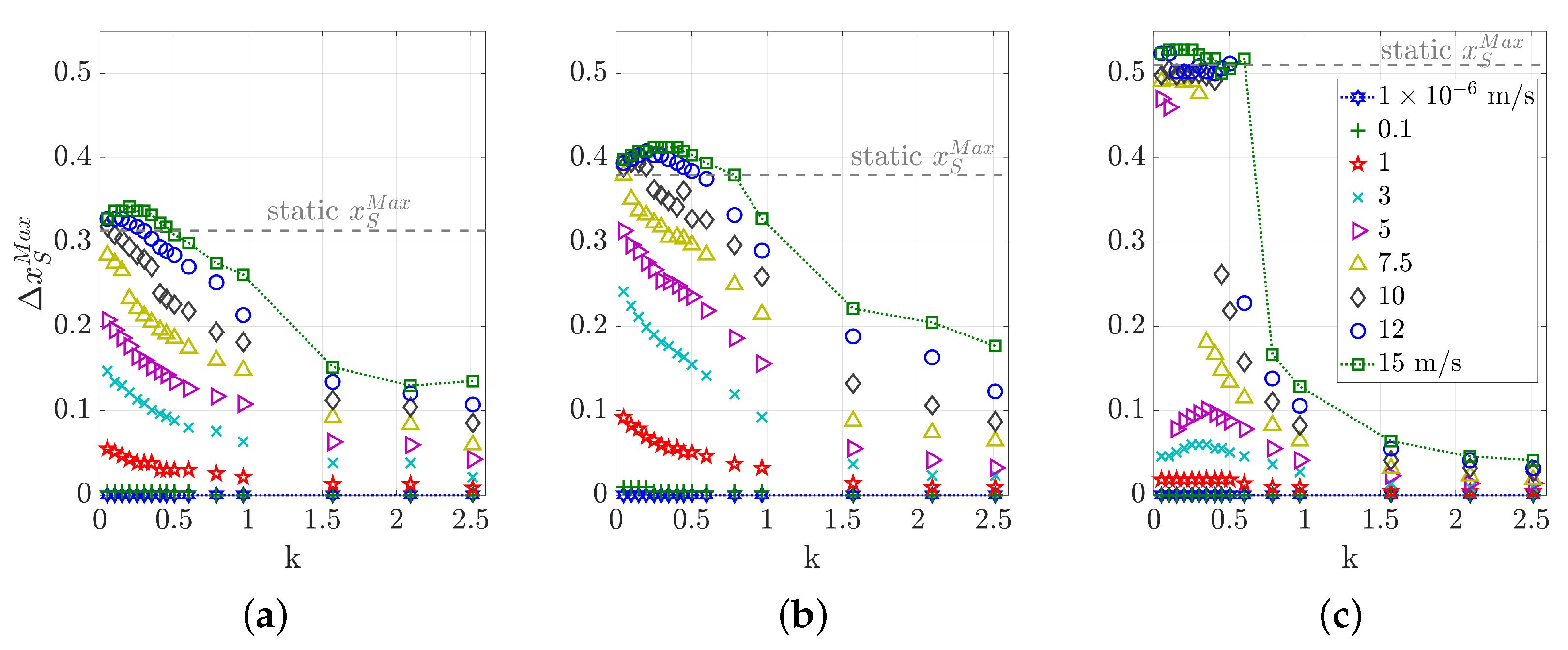
5.3.3. Maximum Shock Motion
6. Conclusions and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DFT | Discrete Fourier Transform |
| DLM | Doublet-Lattice Method |
| FRF | Frequency Response Function |
| LFD | Linear Frequency-Domain |
| RANS | Reynolds-Averaged Navier-Stokes |
| ROM | Reduced-Order Model |
| SA | Spalart-Allmaras |
| SST | Shear-Stress Transport |
| TE | Trailing Edge |
| URANS | Unsteady Reynolds-Averaged Navier-Stokes |
Appendix A. Numerical Sensitivities
Appendix A.1. Grid Sensitivity Study

Appendix A.2. Time Step Study

Appendix B. Verification of Linearity for Low-Amplitude Results

References
- Brink-Spalink, J.; Bruns, J.M. Correction of Unsteady Aerodynamic Influence Coefficients using Experimental or CFD Data; IFASD-2001-034. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Madrid, Spain, 5–7 June 2001. [Google Scholar]
- Karpel, M.; Moulin, B.; Chen, P.C. Dynamic Response of Aeroservoelastic Systems to Gust Excitation. J. Aircr. 2005, 42, 1264–1272. [Google Scholar] [CrossRef]
- Weigold, W.; Stickan, B.; Travieso-Alvarez, I.; Kaiser, C.; Teufel, P. Linearized Unsteady CFD for Gust Loads with TAU. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, IFASD-2017-187, Como, Italy, 25–28 June 2017. [Google Scholar]
- Albano, E.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Giesing, J.P.; Kalman, T.P.; Rodden, W.P. Correction Factor Techniques for Improving Aerodynamic Prediction Methods; NACA-CR-144967; Technical Report; McDonnell Douglas Corporation: St. Louis, MA, USA; NASA: Washington, DC, USA, 1976.
- Palacios, R.; Climent, H.; Karlsson, A.; Winzell, B. Assessment of Strategies for Correcting Linear Unsteady Aerodynamics Using CFD or Experimental Results. In Progress in Computational Flow-Structure Interaction; Haase, W., Selmin, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 209–224. [Google Scholar]
- Thormann, R.; Dimitrov, D. Correction of aerodynamic influence matrices for transonic flow. CEAS Aeronaut. J. 2014, 5, 435–446. [Google Scholar] [CrossRef]
- Banavara, N.K.; Dimitrov, D. Prediction of Transonic Flutter Behavior of a Supercritical Airfoil Using Reduced Order Methods. In New Results in Numerical and Experimental Fluid Mechanics IX; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; Volume 124, pp. 365–373. [Google Scholar] [CrossRef]
- Quero-Martin, D. An Aeroelastic Reduced Order Model for Dynamic Response Prediction to Gust Encounters. Ph.D. Thesis, Institute of Aeroelasticity, Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Katzenmeier, L.; Vidy, C.; Breitsamter, C. Correction Technique for Quality Improvement of Doublet Lattice Unsteady Loads by Introducing CFD Small Disturbance Aerodynamics. J. Aeroelasticity Struct. Dyn. 2017, 5, 17–40. [Google Scholar] [CrossRef]
- Bekemeyer, P.; Thormann, R.; Timme, S. Frequency-Domain Gust Response Simulation Using Computational Fluid Dynamics. AIAA J. 2017, 55, 2174–2185. [Google Scholar] [CrossRef]
- Bekemeyer, P.; Ripepi, M.; Heinrich, R.; Görtz, S. Nonlinear Unsteady Reduced-Order Modeling for Gust-Load Predictions. AIAA J. 2019, 57, 1839–1850. [Google Scholar] [CrossRef]
- Halder, R.; Damodaran, M.; Khoo, B.C. Deep Learning Based Reduced Order Model for Airfoil-Gust and Aeroelastic Interaction. AIAA J. 2020, 58, 4304–4321. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approaches for computational physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef]
- Hall, K.C.; Thomas, J.P.; Clark, W.S. Computation of Unsteady Nonlinear Flows in Cascades Using a Harmonic Balance Technique. AIAA J. 2002, 40, 879–886. [Google Scholar] [CrossRef]
- Leishman, J.G.; Beddoes, T.S. A Generalised Model for Airfoil Unsteady Aerodynamic Behaviour and Dynamic Stall Using the Indicial Method. In Proceedings of the American Helicopter Society (AHS) Annual Forum, New York, NY, USA, 2–5 June 1986. [Google Scholar]
- Reddy, T.S.R.; Kaza, K.R.V. Comparative Study of Some Dynamic Stall Models; Technical Report; NASA: Washington, DC, USA, 1987.
- Goman, M.; Khrabrov, A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack. J. Aircr. 1994, 31, 1109–1115. [Google Scholar] [CrossRef]
- Dowell, E.H.; Williams, M.H.; Bland, S.R. Linear/Nonlinear Behavior in Unsteady Transonic Aerodynamics. AIAA J. 1983, 21, 38–46. [Google Scholar] [CrossRef]
- Mallik, W.; Raveh, D.E. Kriging-Based Aeroelastic Gust Response Analysis at High Angles of Attack. AIAA J. 2020, 58, 3777–3787. [Google Scholar] [CrossRef]
- Kaiser, C.; Quero, D.; Nitzsche, J. Quantification of Nonlinear Effects in Gust Load Prediction. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Savannah, GA, USA, 10–13 June 2019. [Google Scholar]
- Mallik, W.; Raveh, D.E. Gust Response at High Angles of Attack. AIAA J. 2019, 57, 3250–3260. [Google Scholar] [CrossRef]
- Friedewald, D.; Thormann, R.; Kaiser, C.; Nitzsche, J. Quasi-steady doublet-lattice correction for aerodynamic gust response prediction in attached and separated transonic flow. CEAS Aeronaut. J. 2017, 9, 53–66. [Google Scholar] [CrossRef]
- European Aviation Safety Agency (EASA). Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes CS-25, Amendment 12; Technical Report; European Aviation Safety Agency (EASA): Cologne, Germany, 2012.
- Gerhold, T.; Galle, M.; Friedrich, O.; Evans, J. Calculation of complex three-dimensional configurations employing the DLR-TAU-code. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, San Diego, CA, USA, 5–9 January 1997. [Google Scholar] [CrossRef]
- Schwamborn, D.; Gerhold, T.; Heinrich, R. The DLR TAU-Code: Recent Applications in Research and Industry. In Proceedings of the European Conference on Computational Fluid Dynamics (ECCOMAS), Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical Solutions of the Euler Equations by the Finite Volume Methods Using Runge Kutta Time Stepping Schemes. In Proceedings of the 14th Fluid and Plasma Dynamics Conference, AIAA 81–1259, Palo Alto, CA, USA, 23–25 June 1981. [Google Scholar] [CrossRef]
- Jameson, A. Time Dependent Calculations using Multigrid, with Applications to Unsteady Flows past Airfoils and Wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, AlAA 91-1596, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar] [CrossRef]
- Heinrich, R. Simulation of Interaction of Aircraft and Gust Using the TAU-Code. In New Results in Numerical and Experimental Fluid Mechanics IX; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; Volume 124, pp. 503–511. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, AIAA-92-0439, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Deutsches Zentrum für Luft- und Raumfahrt (DLR). TAU-Code User Guide 2016.1.0; Technical Report; Deutsches Zentrum für Luft- und Raumfahrt (DLR): Braunschweig, Germany, 2016. [Google Scholar]
- Giannelis, N.F.; Vio, G.A.; Levinski, O. A review of recent developments in the understanding of transonic shock buffet. Prog. Aerosp. Sci. 2017, 92, 39–84. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 8, 1598–1605. [Google Scholar] [CrossRef]
- Cook, P.H.; McDonald, M.A.; Firmin, M.C.P. Aerofoil RAE 2822: Pressure Distributions, and Boundary Layer and Wake Measurements; Technical Report AGARD-AR-138, AGARD; North Atlantic Treaty Organization: Brussels, Belgium, 1979. [Google Scholar]
- Bardina, J.E.; Huang, P.G.; Coakley, T.J. Turbulence Modeling Validation, Testing and Development; NASA Technical Memorandum 110446; Ames Research Center: Moffett Field, CA, USA, 1997. [Google Scholar]
- Hellström, T.; Davidson, L.; Rizzi, A. Reynolds Stress Transport Modelling of Transonic Flow around the RAE2822 Airfoil. In 32nd Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics: Reno, NV, USA, 1994. [Google Scholar] [CrossRef]
- Knopp, T. Validation of the Turbulence Models in the DLR TAU Code for Transonic Flows—A Best Practice Guide; Forschungsbericht 2006-01; Institut für Aerodynamik und Strömungsmechanik: Göttingen, Germany, 2006. [Google Scholar]
- McCroskey, W.J.; McAlister, K.W.; Carr, L.W.; Pucci, S.L.; Lambert, O.; Indergrand, R.F. Dynamic Stall on Advanced Airfoil Sections. J. Am. Helicopter Soc. 1981, 26, 40–50. [Google Scholar] [CrossRef]
- Iovnovich, M.; Raveh, D. Transonic Unsteady Aerodynamics in the Vicinity of Shock-Buffet Instability. J. Fluids Struct. 2012, 29, 131–142. [Google Scholar] [CrossRef]
- Thormann, R.; Timme, S. Application of Harmonic Balance Method for Non-linear Gust Responses. In AIAA SciTech Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Ericsson, L.; Reding, J. Dynamic stall overshoot of static airfoil characteristics. In 12th Atmospheric Flight Mechanics Conference; American Institute of Aeronautics and Astronautics: Snowmass, CO, USA, 1985. [Google Scholar] [CrossRef]
- Harper, P.W.; Flanigan, R.E. The Effect of Rate of Change of Angle of Attack in the Maximum Lift of a Small Model; Technical Report NACA Technical Note 2061; NACA TN 2061; NACA: Alabama Birmingham, AL, USA, 1950. [Google Scholar]
- Dimitrov, D. Unsteady aerodynamics of wings with an oscillating flap in transonic flow. In Proceedings of the 8th PEGASUS-AIAA Student Conference, Poitiers, France, 11–13 April 2012. [Google Scholar]
- Shmilovitz, D. On the definition of total harmonic distortion and its effect on measurement interpretation. IEEE Trans. Power Deliv. 2005, 20, 526–528. [Google Scholar] [CrossRef]
- Davis, S.; Malcolm, G. Unsteady Aerodynamics of Conventional and Supercritical Airfoils. In Structures, Structural Dynamics, and Materials and Co-Located Conferences; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1980. [Google Scholar] [CrossRef]
- Thormann, R.; Widhalm, M. Linear-Frequency-Domain Predictions of Dynamic-Response Data for Viscous Transonic Flows. AIAA J. 2013, 51, 2540–2557. [Google Scholar] [CrossRef]
- Kaiser, C.; Thormann, R.; Dimitrov, D.; Nitzsche, J. Time-Linearized Analysis of Motion-Induced and Gust-Induced Airloads with the DLR TAU Code; Deutscher Luft-und Raumfahrtkongress: Rostock, Germany, 2015. [Google Scholar]














| Mach | [m/s] | dt [s] | Inner Iterations |
|---|---|---|---|
| 0.66 | 218.65 | 400 | |
| 0.68 | 225.28 | 400 | |
| 0.70 | 231.90 | 400 | |
| 0.72 | 238.52 | 400 |
| [ m] | k | SPP | nr. of Periods | ndt |
|---|---|---|---|---|
| 2.5 | 2.51 | 60 | 20 | 1200 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 18.0 | 0.35 | 432 | 20 | 8640 |
| 21.0 | 0.30 | 504 | 10 | 5040 |
| 25.0 | 0.25 | 600 | 10 | 6000 |
| 31.5 | 0.20 | 756 | 10 | 7560 |
| 42.0 | 0.15 | 1008 | 10 | 10,080 |
| 62.5 | 0.10 | 1500 | 5 | 7500 |
| 125.5 | 0.05 | 3012 | 5 | 15,060 |
| [ m/s] | [] |
|---|---|
| 0.1 | 0.025 |
| 1.0 | 0.25 |
| 3.0 | 0.74 |
| 5.0 | 1.24 |
| 7.5 | 1.85 |
| 10.0 | 2.47 |
| 12.5 | 3.09 |
| 15.0 | 3.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friedewald, D. Numerical Simulations on Unsteady Nonlinear Transonic Airfoil Flow. Aerospace 2021, 8, 7. https://doi.org/10.3390/aerospace8010007
Friedewald D. Numerical Simulations on Unsteady Nonlinear Transonic Airfoil Flow. Aerospace. 2021; 8(1):7. https://doi.org/10.3390/aerospace8010007
Chicago/Turabian StyleFriedewald, Diliana. 2021. "Numerical Simulations on Unsteady Nonlinear Transonic Airfoil Flow" Aerospace 8, no. 1: 7. https://doi.org/10.3390/aerospace8010007
APA StyleFriedewald, D. (2021). Numerical Simulations on Unsteady Nonlinear Transonic Airfoil Flow. Aerospace, 8(1), 7. https://doi.org/10.3390/aerospace8010007





