Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry
Abstract
1. Introduction
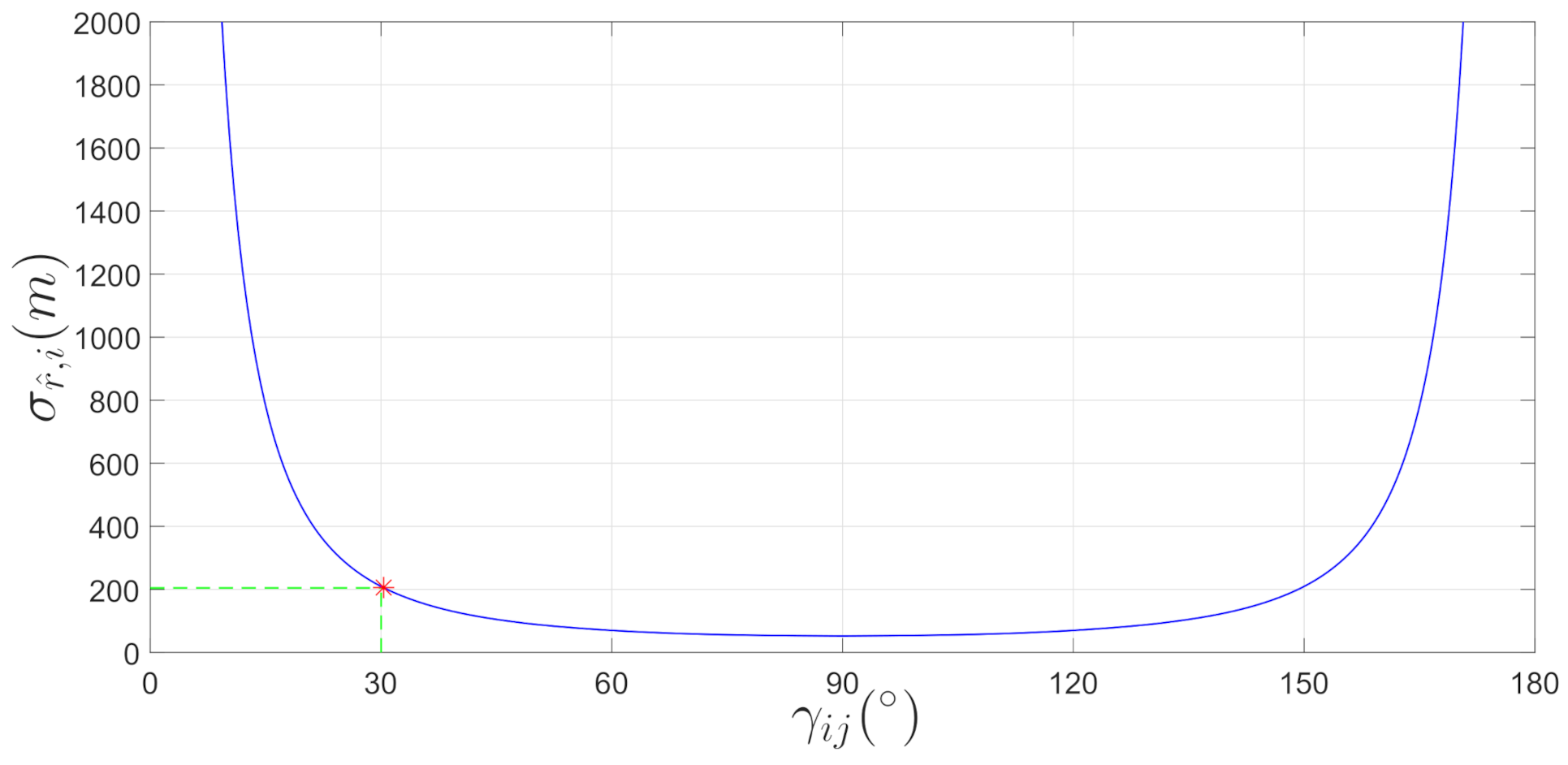
- The 3D maneuvering target tracking model is proposed without omitting the couplings between the elevation and the azimuth channels, the effect of the relative geometry on the observability of the missile-target range is analyzed in quantity.
- Based on convex optimization theory, a general coordination algorithm is proposed and the constraint of the relative geometry between the missiles and target is decomposed into the LOS angle constraints considering the input saturation.
- Based on fixed-time convergent control method and integral sliding mode control theory, a novel 3D fixed-time integral sliding mode guidance law (FxTISMGL) with LOS angle constraints is developed for the first time. The proposed 3D guidance law is more practical than the 2D ones and has a faster convergence rate.
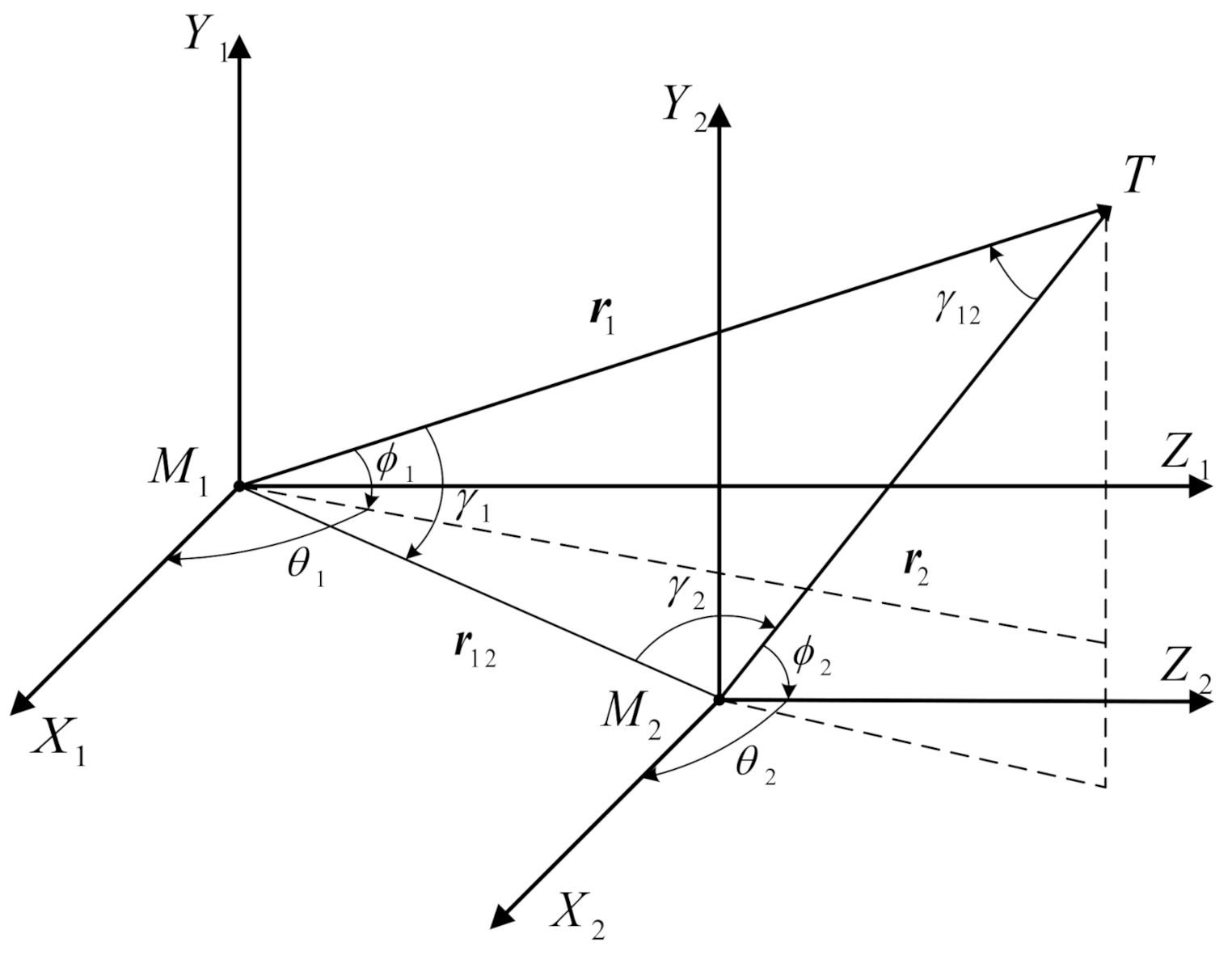
2. Formulation of Three-Dimensional Estimation Model
2.1. Kinematics and Dynamics
2.2. Measurement Model
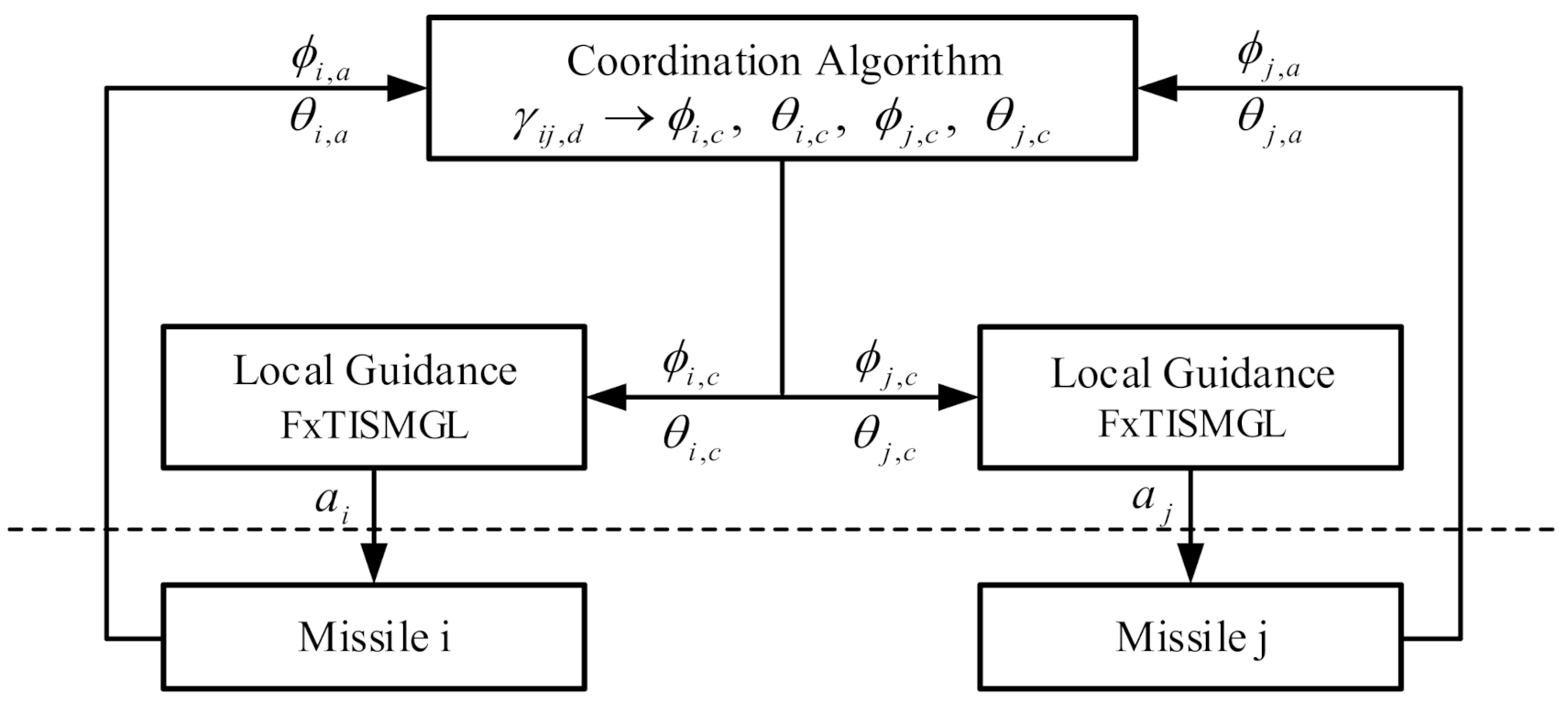
3. Two-Level Cooperative Interception Guidance Structure
3.1. Coordination Algorithm Based on Convex Theory
3.2. Fixed-Time Convergent Guidance Law Design
3.2.1. Definitions and Lemmas
3.2.2. The Design of Fixed-Time Convergent Guidance Law with LOS Angle Constraints
4. Experimental Results and Analysis
4.1. Simulation Environment and Scenario
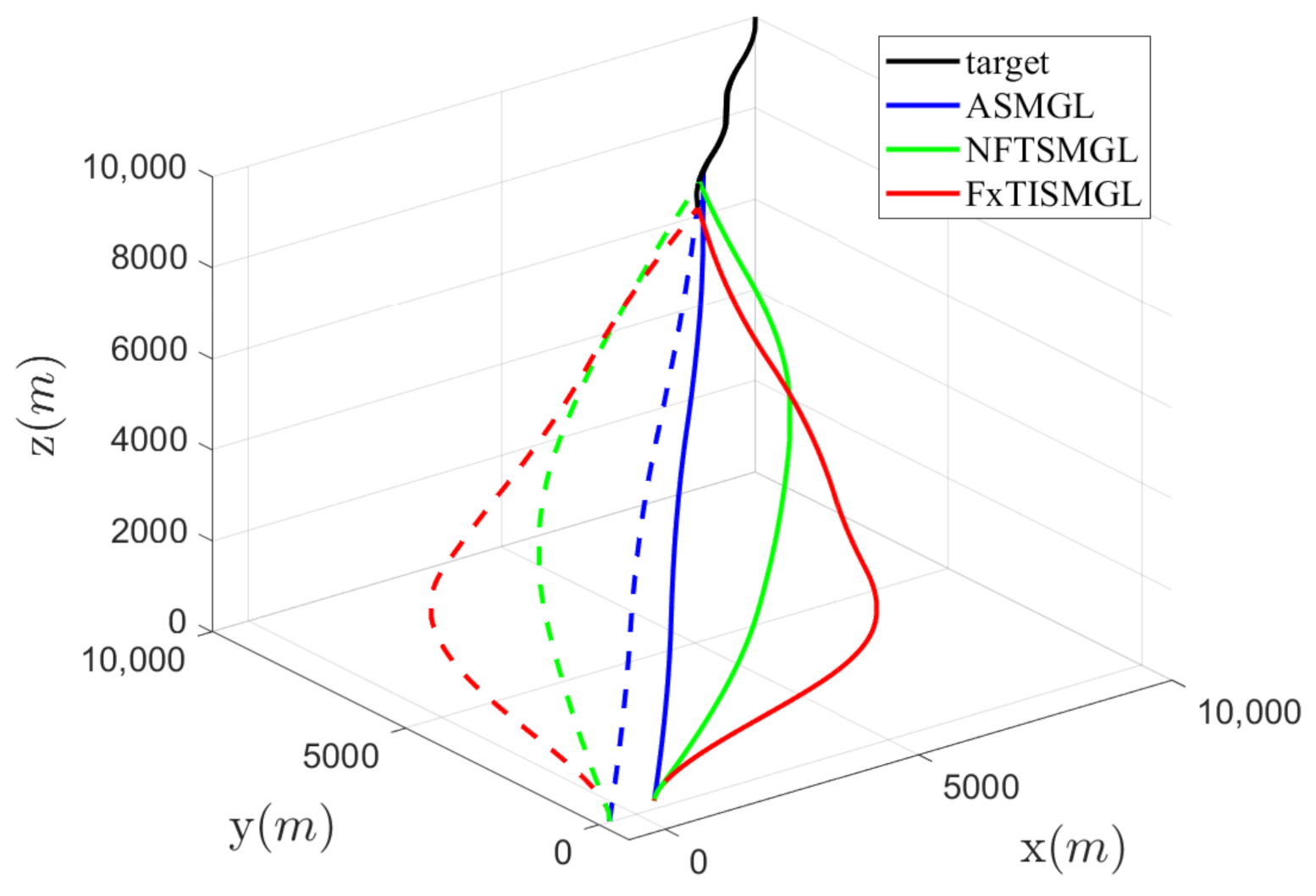
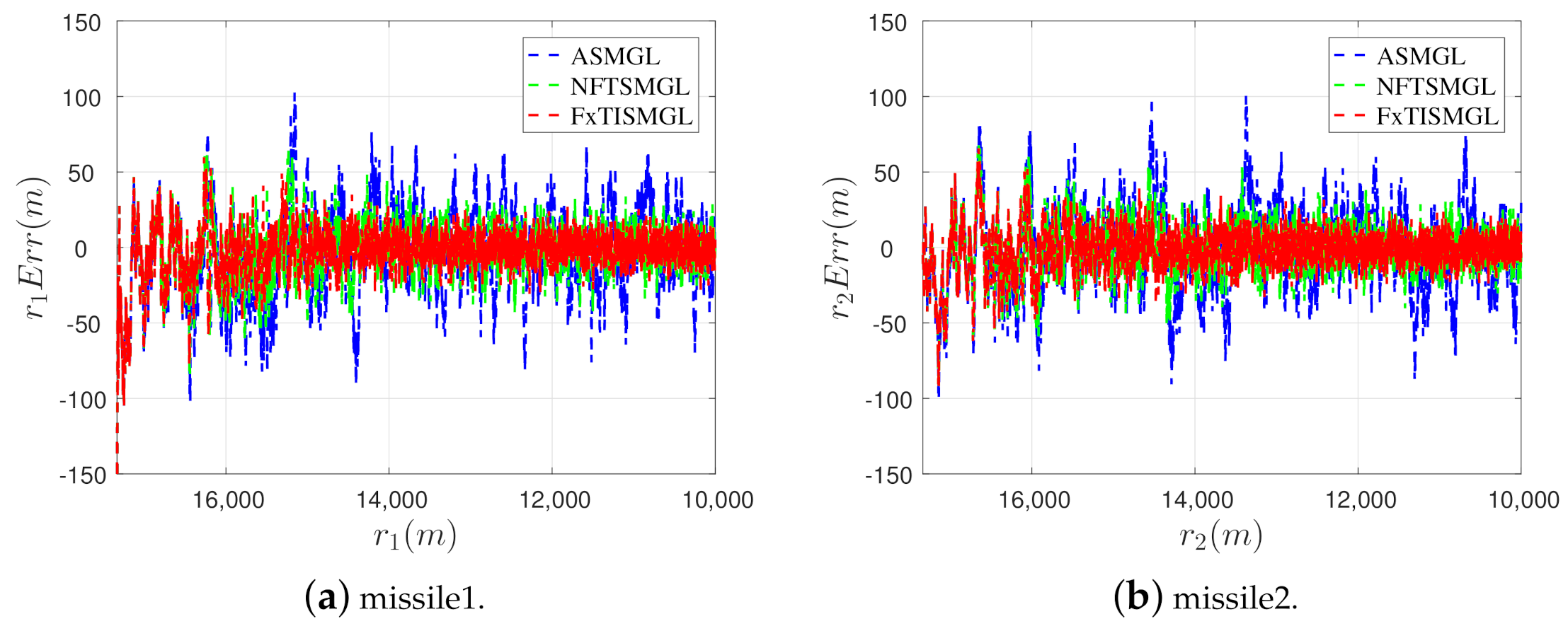
4.2. Simulation Results and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| LOS | Line of sight |
| WSN | Wireless sensor network |
| IR | Infra-red |
| OGL | Optimal guidance law |
| FxTISMGL | Fixed-time integral sliding mode guidance law |
| CKF | Cubature Kalman filter |
| ASMGL | Adaptive sliding mode guidance law |
| NFTSMGL | Nonlinear finite-time sliding mode guidance law |
| RMSE | Root mean square error |
Appendix A
References
- Fonod, R.; Shima, T. Estimation Enhancement by Cooperatively Imposing Relative Intercept Angles. J. Guid. Control Dyn. 2017, 40, 1711–1725. [Google Scholar] [CrossRef]
- Parayil, A.; Ratnoo, A. Maximizing Range Observability in Bearings-Only Rendezvous Guidance. In Proceedings of the 2017 AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Chen, T.; Xu, S. Double line-of-sight measuring relative navigation for spacecraft autonomous rendezvous. Acta Astronaut. 2010, 67, 122–134. [Google Scholar] [CrossRef]
- Chen, T.; Xu, S. Approach Guidance with Double-Line-of-Sight Measuring Navigation Constraint for Autonomous Rendezvous. J. Guid. Control Dyn. 2012, 34, 678–687. [Google Scholar] [CrossRef]
- Liu, Y.; Qi, N.; Shan, J. Cooperative Interception with Double-Line-of-Sight-Measuring. In Proceedings of the 2013 AIAA Guidance, Navigation, and Control Conference, Boston, MA, USA, 8–11 August 2011. [Google Scholar]
- Song, J.; Song, S.; Xu, S. Three-dimensional cooperative guidance law for multiple missiles with finite-time convergence. Aerosp. Sci. Technol. 2017, 67, 193–205. [Google Scholar] [CrossRef]
- Kim, B.S.; Lee, J.G. Biased PNG law for impact with angular constraint. IEEE Trans. Aerosp. Electron. Syst. AES 1998, 34, 277–288. [Google Scholar]
- Lee, J.; Jeon, I.; Tahk, M. Guidance law to control impact time and angle. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 301–310. [Google Scholar]
- Zhang, Y.; Ma, G.; Liu, A. Guidance law with impact time and impact angle constraints. Chin. J. Aeronaut. 2013, 26, 960–966. [Google Scholar] [CrossRef]
- Ratnoo, A.; Ghose, D. State-Dependent Riccati-Equation-Based Guidance Law for Impact-Angle-Constrained Trajectories. J. Guid. Control Dyn. 2009, 32, 320–326. [Google Scholar] [CrossRef]
- Lee, Y.I.; Kim, S.H.; Tahk, M.J. Optimality of Linear Time-Varying Guidance for Impact Angle Control. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2802–2817. [Google Scholar] [CrossRef]
- Zhang, W.; Xia, Q.; Li, W. Novel second-order sliding mode guidance law with an impact angle constraint that considers autopilot lag for intercepting manoeuvering targets. Aeronaut. J. 2020, 124, 1350–1370. [Google Scholar] [CrossRef]
- Lin, D.; Ji, Y.; Wang, W.; Wang, Y.; Wang, H.; Zhang, F. Three-dimensional impact angle-constrained adaptive guidance law considering autopilot lag and input saturation. Int. J. Robust Nonlinear Control 2020, 30, 3653–3671. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. A new class of finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Control 2014, 87, 363–370. [Google Scholar] [CrossRef]
- Huang, Y.; Jia, Y. Fixed-time consensus tracking control for second-order multi-agent systems with bounded input uncertainties via NFFTSM. IET Control Theory Appl. 2017, 11, 2900–2909. [Google Scholar] [CrossRef]
- Li, G.; Wu, Y.; Xu, P. Adaptive Fault-tolerant Cooperative Guidance Law for Simultaneous Arrival. Aerosp. Sci. Technol. 2018, 82–83, 243–251. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Optimal Guidance Laws for Imposing a Relative Intercept Angle. J. Guid. Control Dyn. 2015, 38, 1395–1408. [Google Scholar] [CrossRef]
- Shiyu, Z.; Rui, Z. Cooperative Guidance for Multimissile Salvo Attack. Chin. J. Aeronaut. 2008, 21, 533–539. [Google Scholar] [CrossRef]
- Yang, C.D.; Yang, C.C. Analytical solution of generalized three-dimensional proportional navigation. J. Guid. Control. Dyn. 1996, 19, 721–724. [Google Scholar] [CrossRef]
- Yang, C.D.; Yang, C.C. Analytical solution of 3D true proportional navigation. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1509–1522. [Google Scholar] [CrossRef]
- Zarchan, P. Tactical and Strategic Missile Guidance, 6th ed.; AIAA: Reston, VA, USA, 2012; pp. 187–211. [Google Scholar]
- Yuen, K.V.; Kuok, S.C. Online updating and uncertainty quantification using nonstationary output-only measurement. Mech. Syst. Signal Process. 2015, 66. [Google Scholar] [CrossRef]
- Kontoroupi, T.; Smyth, A. Online Noise Identification for Joint State and Parameter Estimation of Nonlinear Systems. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2015, 2, B4015006. [Google Scholar] [CrossRef]
- Hu, G.; Gao, B.; Zhong, Y.; Gu, C. Unscented Kalman Filter with Process Noise Covariance Estimation for Vehicular INS/GPS Integration System. Inf. Fusion 2020, 64. [Google Scholar] [CrossRef]
- Li, S.; Ma, M.; Tang, X.; Huang, Y.; Wang, F. Maximum Likelihood Criterion based Adaptive CKF Algorithm for Integrated Navigation. In Proceedings of the 11th China Satellite Navigation Conference, Chengdu, China, 23–25 November 2020. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Zhou, D.; Sun, S.; Teo, K. Guidance Laws with Finite Time Convergence. J. Guid. Control Dyn. 2009, 32. [Google Scholar] [CrossRef]
- Hong, Y. Finite-Time Stabilization and Stabilizability of a Class of Nonlinear Systems. Syst. Control Lett. 2002, 46, 231–236. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Parsegov, S.; Polyakov, A.; Shcherbakov, P. Fixed-time consensus algorithm for multi-agent systems with integrator dynamics. IFAC Proc. Vol. 2013, 46, 110–115. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Tian, B.; Lu, H.; Zuo, Z.; Wang, H. Fixed-time stabilization of high-order integrator systems with mismatched disturbances. Nonlinear Dyn. 2018, 94, 2889–2899. [Google Scholar] [CrossRef]
- Tian, B.; Lu, H.; Zuo, Z.; Yang, W. Fixed-Time Leader-Follower Output Feedback Consensus for Second-Order Multiagent Systems. IEEE Trans. Cybern. 2018, 49, 1545–1550. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Homing Guidance Law for Cooperative Attack of Multiple Missiles. J. Guid. Control Dyn. 2010, 33, 275–280. [Google Scholar] [CrossRef]
- Zhou, D.; Mu, C.; Xu, W. Adaptive Sliding-Mode Guidance of a Homing Missile. J. Guid. Control Dyn. 1999, 22, 589–594. [Google Scholar] [CrossRef]
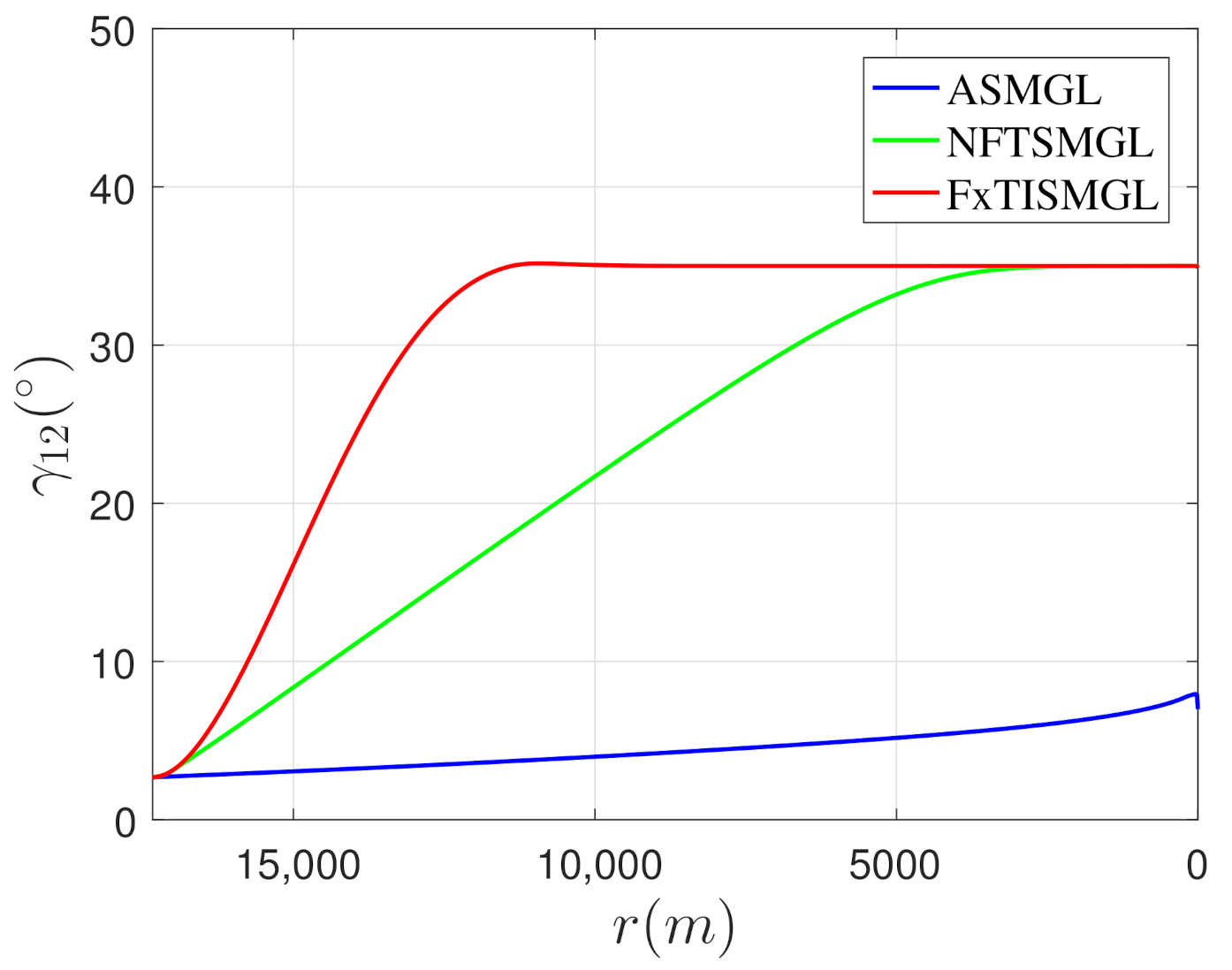
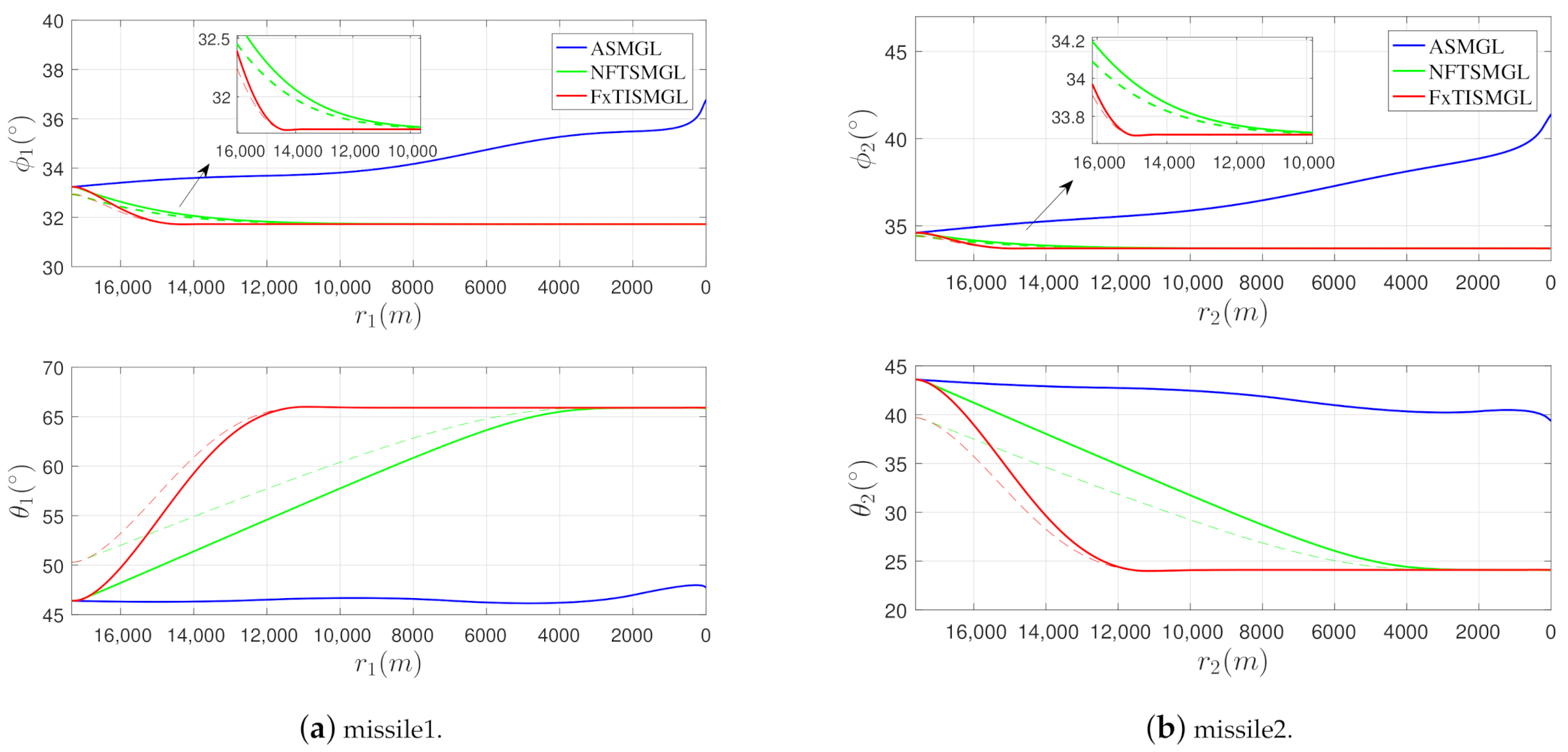
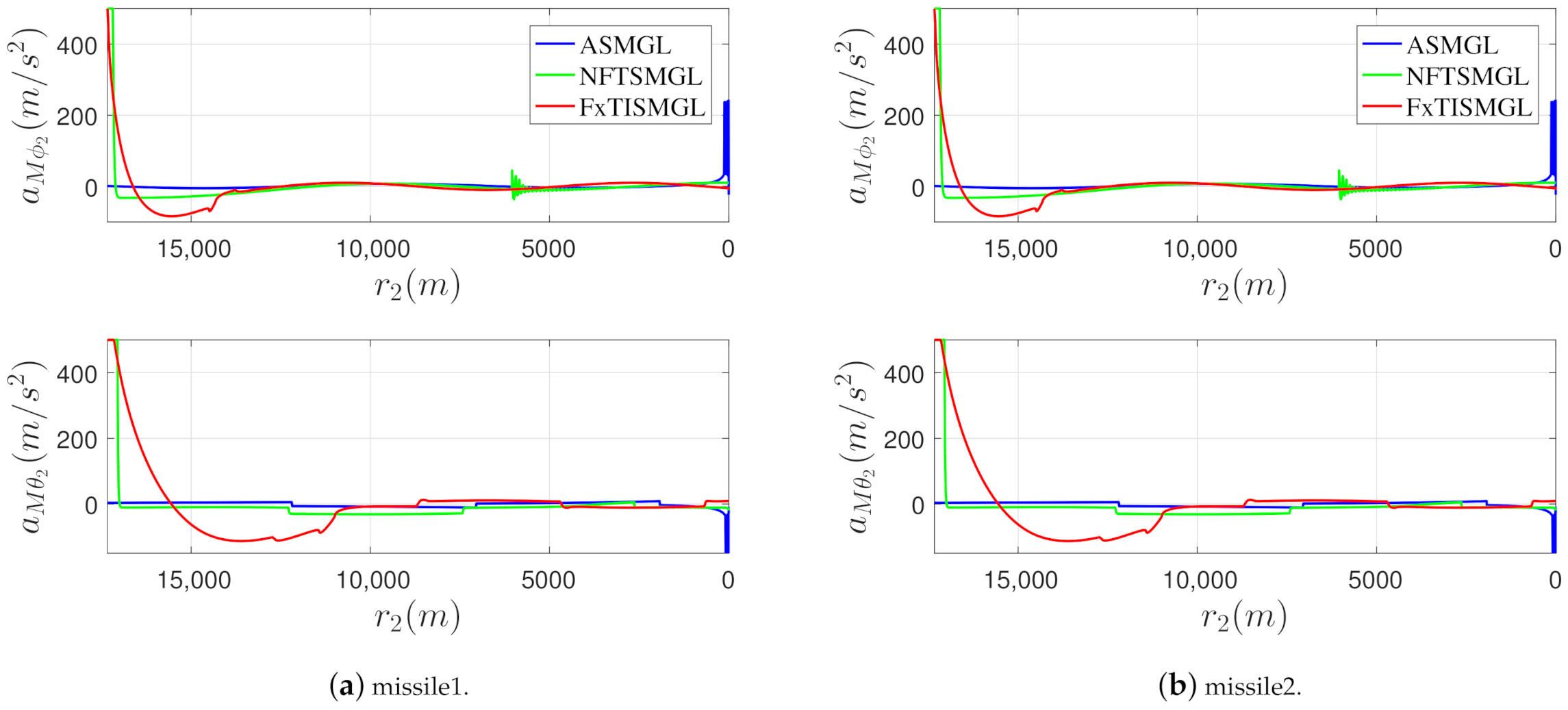
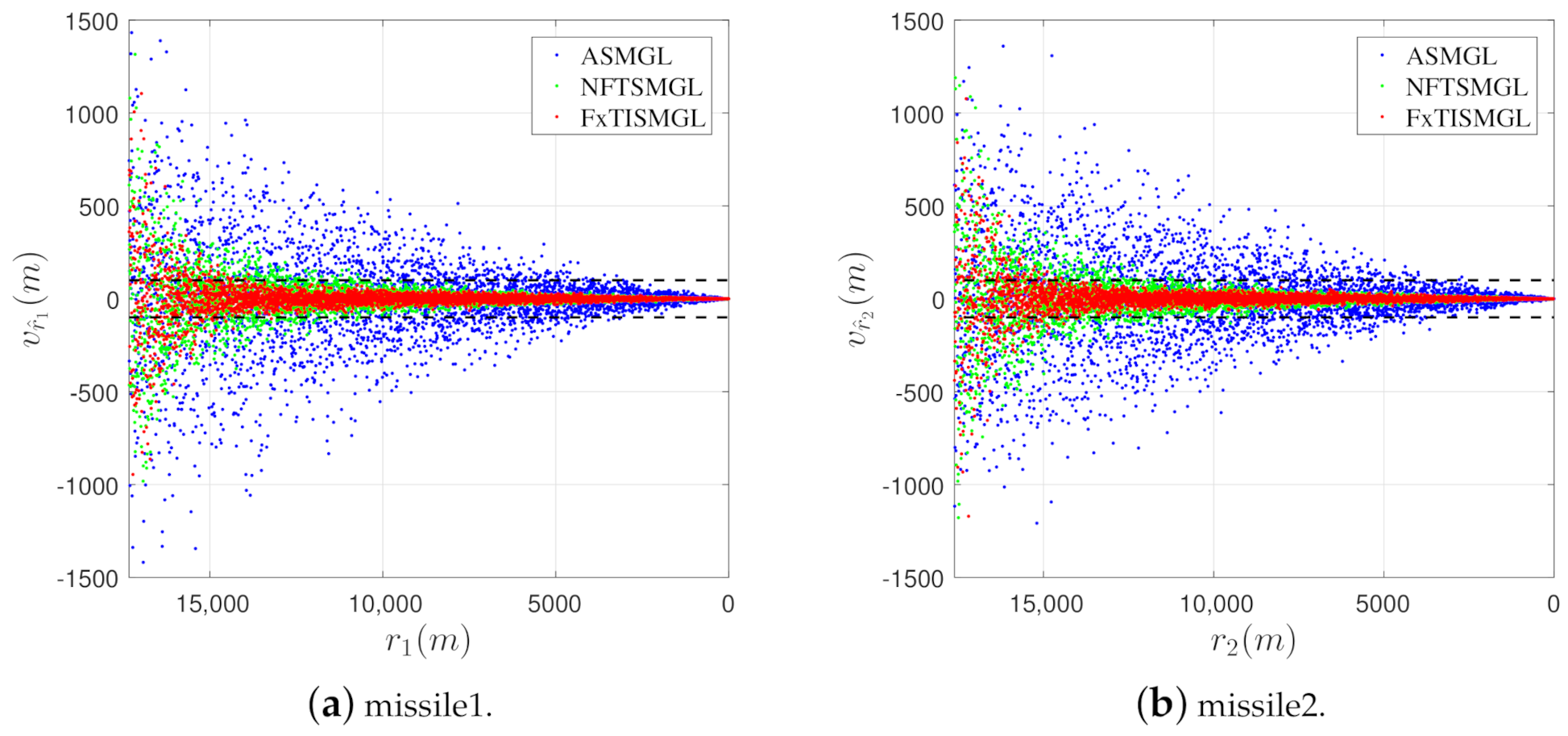
| Mode | Missile-1 | Missile-2 | Target | |
|---|---|---|---|---|
| position (m) | x | 0 | −500 | 10,000 |
| y | −500 | 0 | 10,000 | |
| z | 500 | 0 | 10,000 | |
| velocity (m/s) | x | 300 | 300 | 80 |
| y | 300 | 300 | −120 | |
| z | 300 | 300 | 40 | |
| Guidance Law | Miss Distance (m) | Convergent Time of (s) | Convergent Time of (s) | RMSE of r (m) | |
|---|---|---|---|---|---|
| ASMGL | Missile1 | 0.4312 | ∞ | ∞ | 30.2804 |
| Missile2 | 0.7153 | ∞ | ∞ | 29.3604 | |
| NFTSMGL | Missile1 | 0.2262 | 14.3610 | 25.9130 | 20.2227 |
| Missile2 | 0.3846 | 13.1960 | 24.4930 | 19.4695 | |
| FXISMGL | Missile1 | 0.1015 | 4.4800 | 10.5050 | 16.5124 |
| Missile2 | 0.1738 | 3.8830 | 10.3370 | 16.1186 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Han, Y.; Li, P.; Guo, H.; Wu, W. Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry. Aerospace 2021, 8, 6. https://doi.org/10.3390/aerospace8010006
Liu X, Han Y, Li P, Guo H, Wu W. Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry. Aerospace. 2021; 8(1):6. https://doi.org/10.3390/aerospace8010006
Chicago/Turabian StyleLiu, Xiaoma, Yang Han, Peng Li, Hongwu Guo, and Wenqi Wu. 2021. "Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry" Aerospace 8, no. 1: 6. https://doi.org/10.3390/aerospace8010006
APA StyleLiu, X., Han, Y., Li, P., Guo, H., & Wu, W. (2021). Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry. Aerospace, 8(1), 6. https://doi.org/10.3390/aerospace8010006





