Unsupervised Anomaly Detection in Flight Data Using Convolutional Variational Auto-Encoder
Abstract
1. Introduction
2. Related Work
3. Method
3.1. Variational Inference
3.2. Variational Auto-Encoder
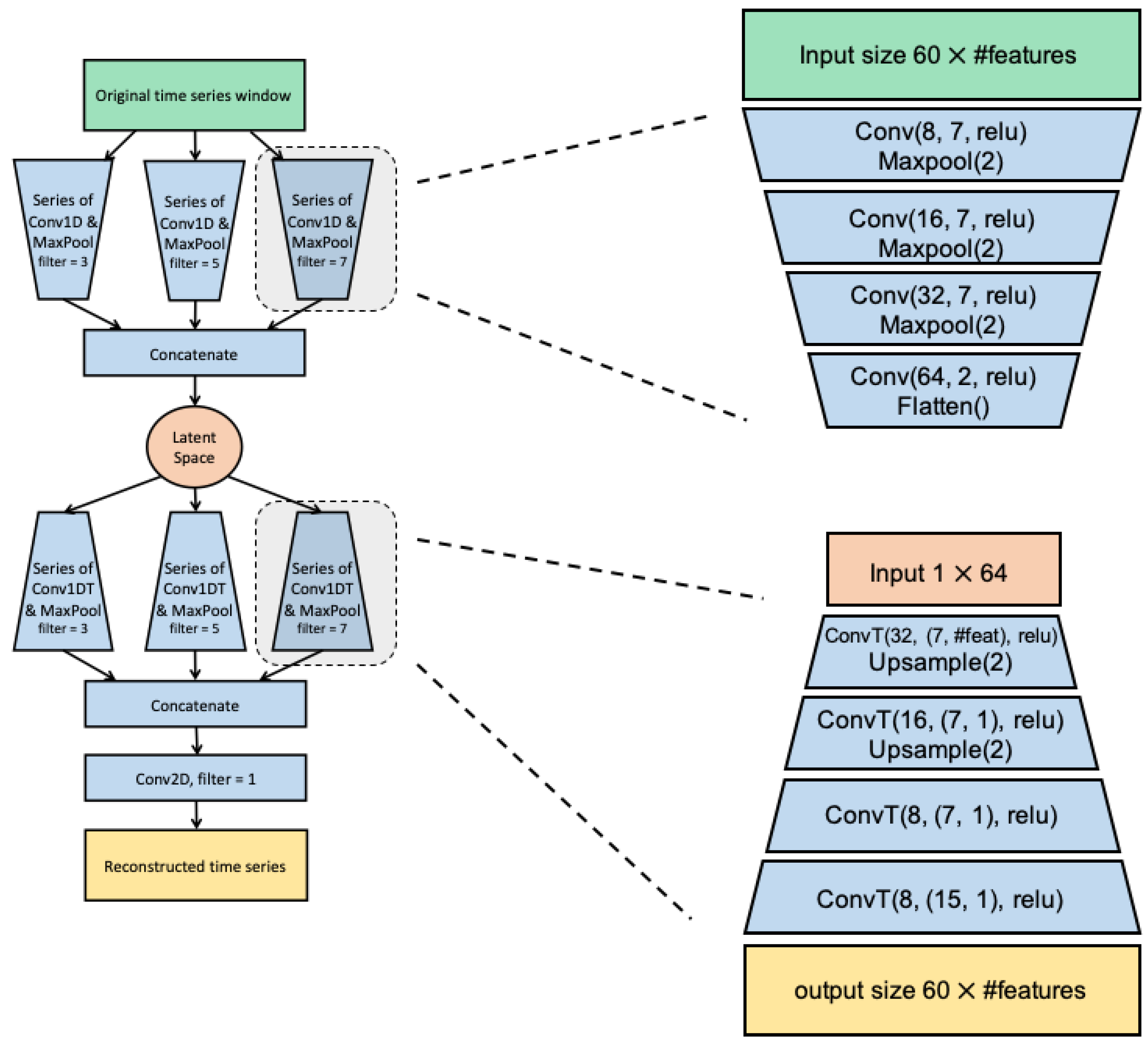
3.3. Convolutional Variational Auto-Encoder (CVAE)
3.4. Anomaly Detection Metric
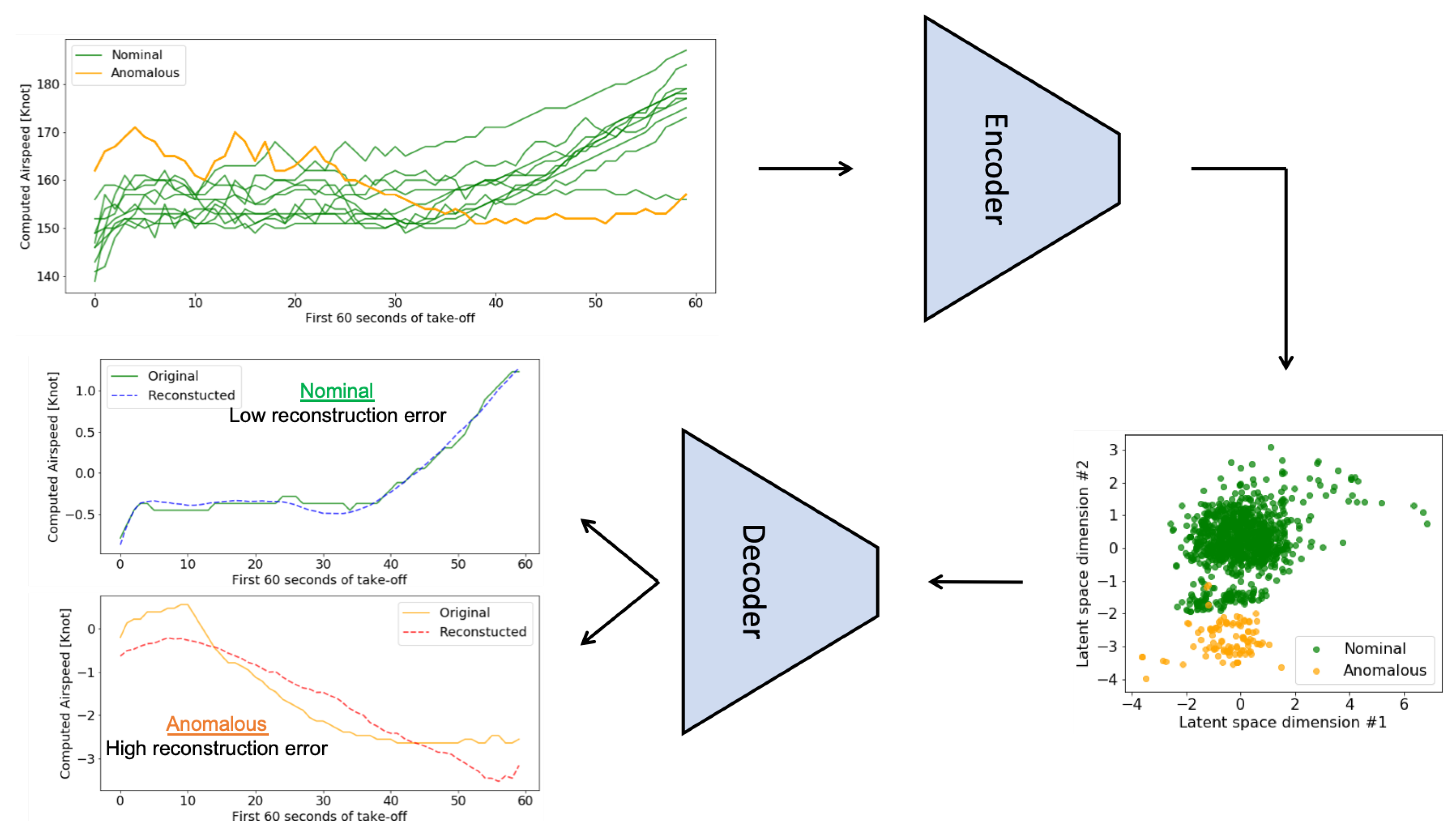
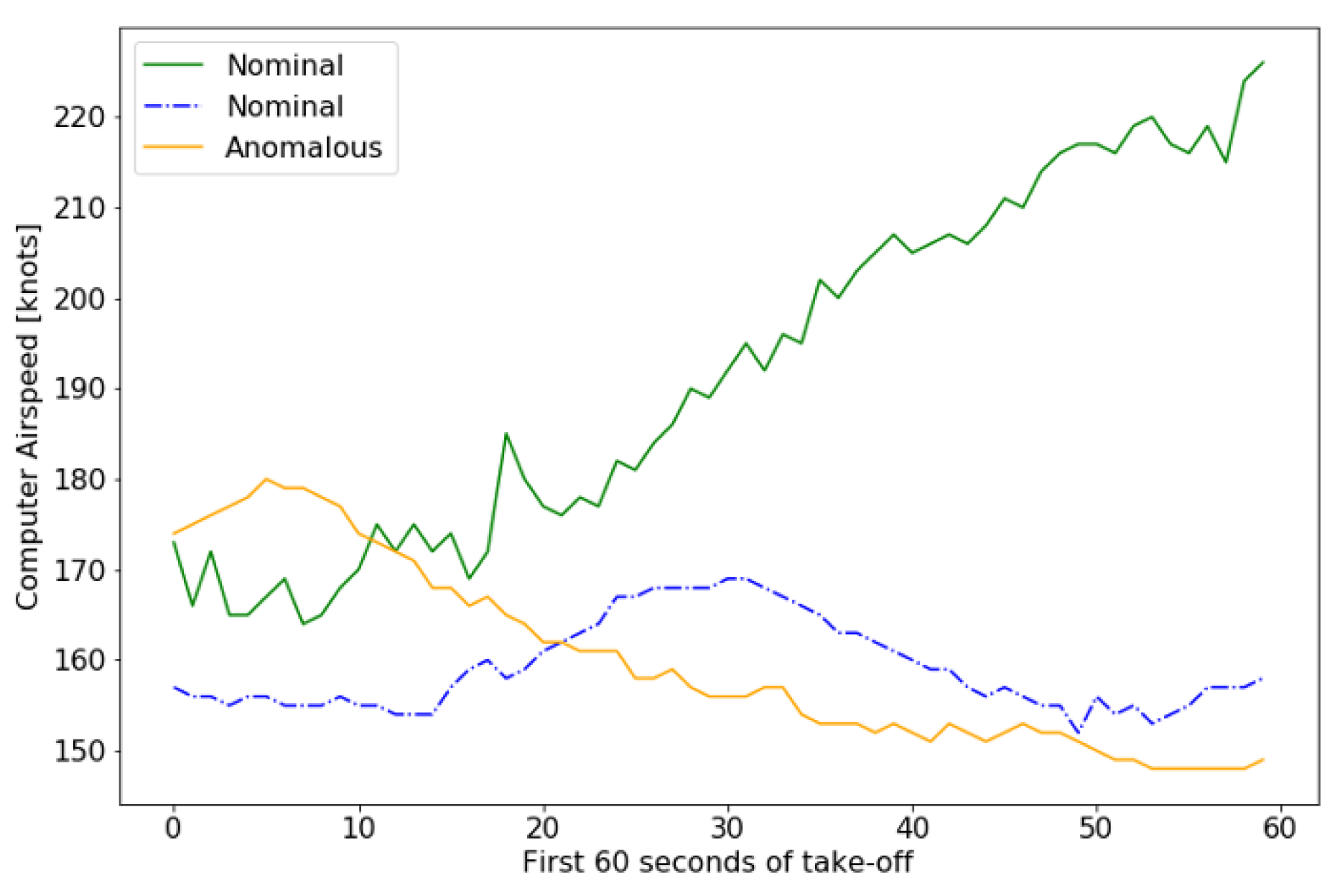
4. Results and Discussion
4.1. Validation on Yahoo!’s Data
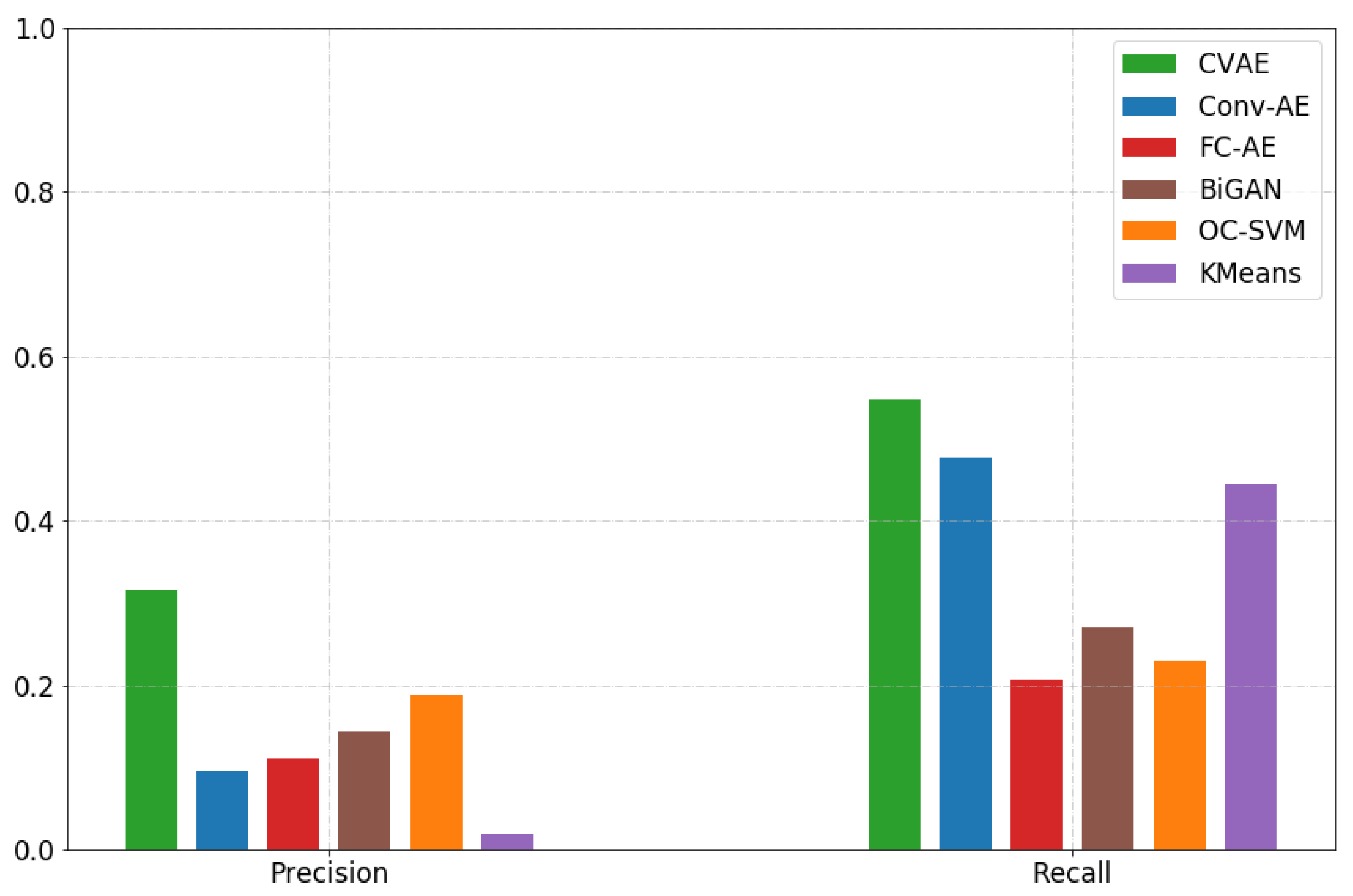
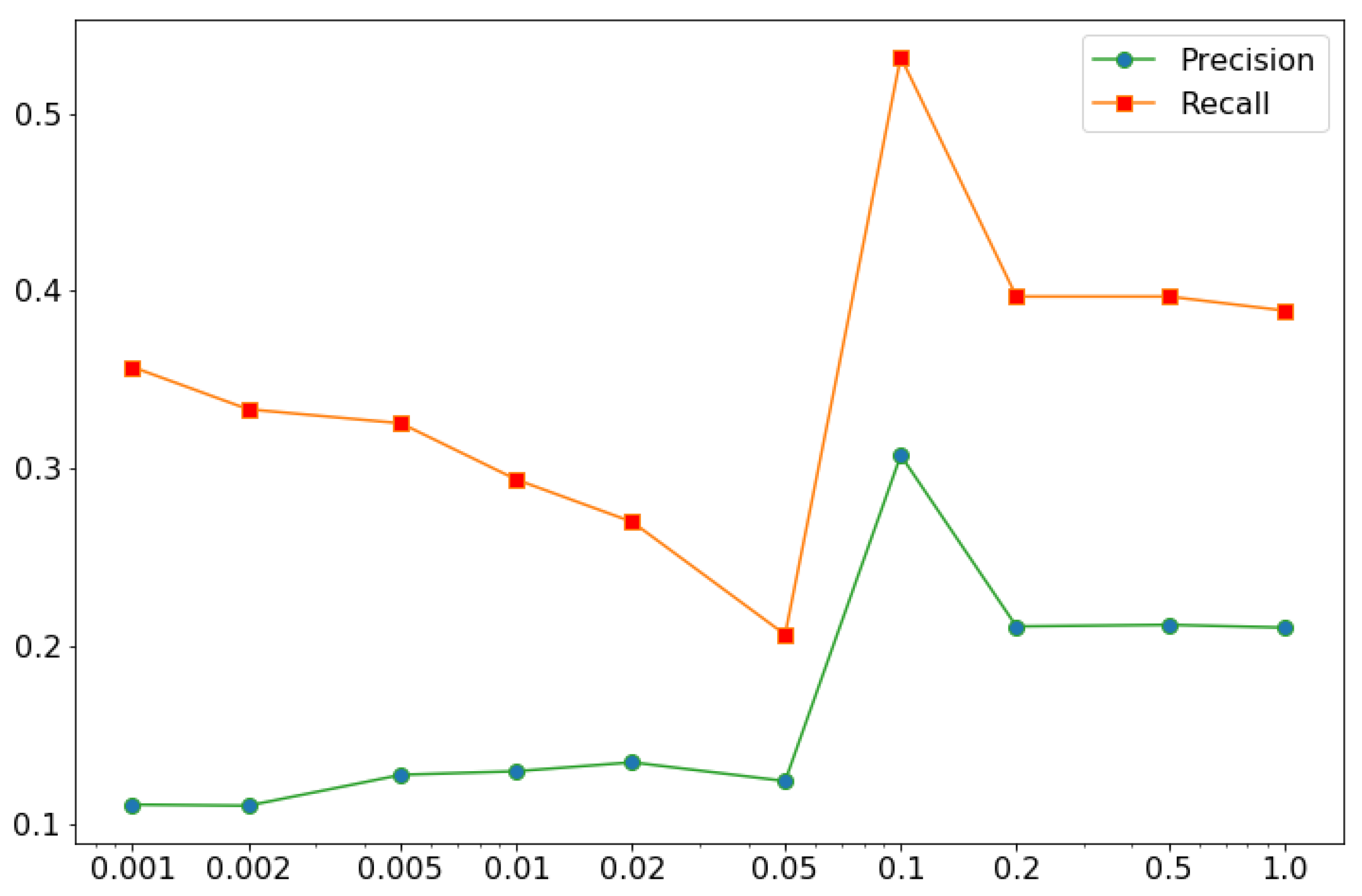
4.2. Anomaly Detection in FOQA Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NAS | National Airspace System |
| CVAE | Convolutional Variational Auto-Encoder |
| FOQA | Flight Operational Quality Assurance |
| NTSB | National Transportation Safety Board |
| FAA | Federal Aviation Administration |
| ASIAS | Aviation Safety Information and Sharing |
| IG | Inspector General |
| OC-SVM | Once-Class Support Vector Machine |
| BiGAN | Bidirectional Generative Adversarial Networks |
| VI | Variational Inference |
| MCMC | Markov Chain Monte Carlo |
| KL | Kullback–Leibler |
| FC-AE | Fully Connected Auto-Encoder |
| Conv-AE | Convolutional Auto-Encoder |
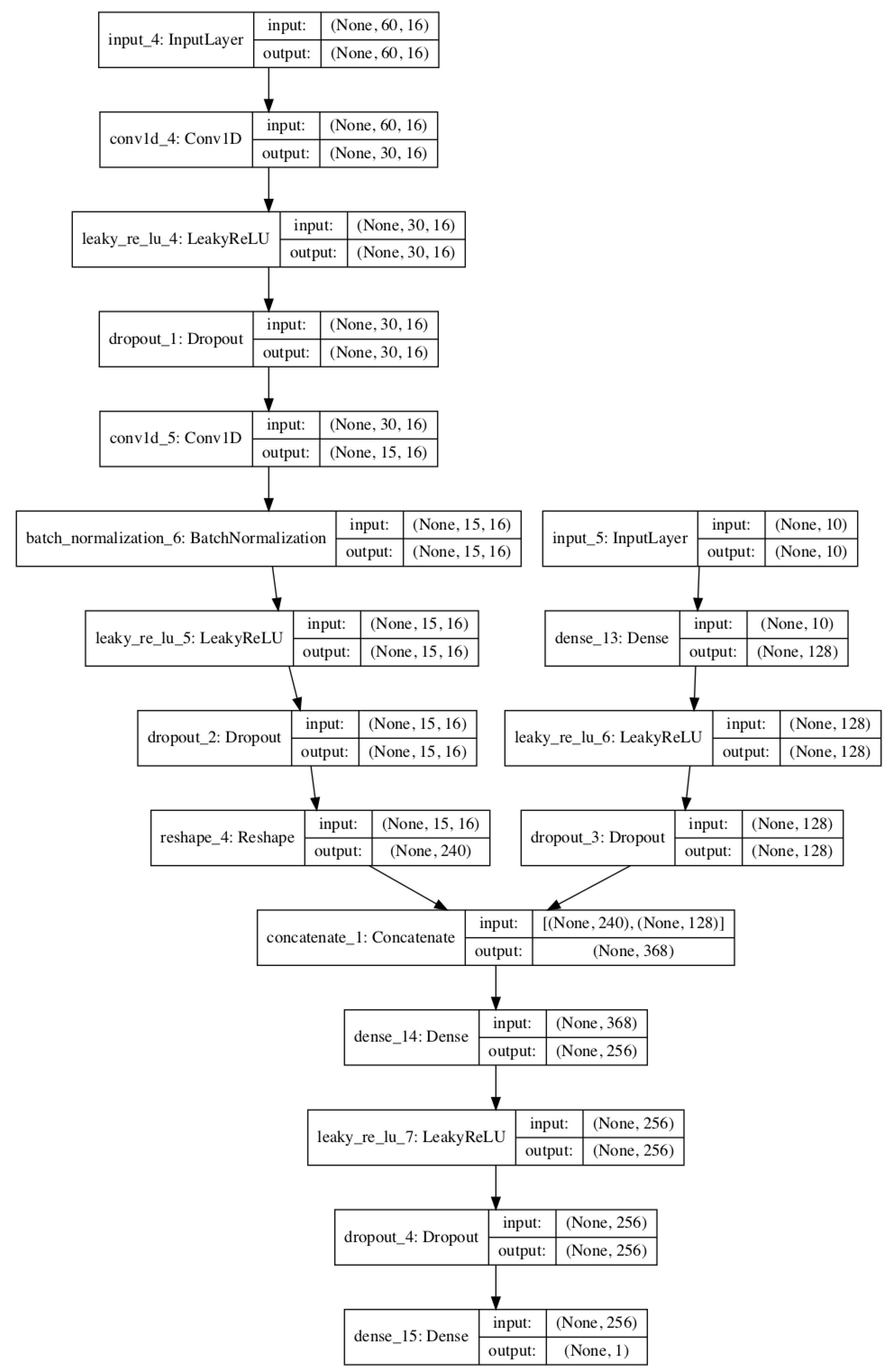
Appendix A
References
- National Transportation Safety Board (NSTB). Annual Summaries of US Civil Aviation Accidents. 2019. Available online: https://www.ntsb.gov/investigations/data/Pages/aviation_stats.aspx (accessed on 8 August 2020).
- National Transportation Safety Board (NSTB). US Transportation Fatality Statistics. 2017. Available online: https://www.bts.gov/content/transportation-fatalities-mode (accessed on 8 August 2020).
- Sprung, M.J.; Chambers, M.; Smith-Pickel, S. Transportation Statistics Annual Report; U.S. Department of Transportation: Washington, DC, USA, 2018.
- FAA Office of Air Traffic Organization. Safety Management System Manual. 2019. Available online: https://www.faa.gov/air_traffic/publications/media/ATO-SMS-Manual.pdf (accessed on 8 August 2020).
- National Transportation Safety Board (NSTB). National Transportation Safety Board Aviation Investigation Manual Major Team Investigations. 2002. Available online: https://www.ntsb.gov/investigations/process/Documents/MajorInvestigationsManual.pdf (accessed on 8 August 2020).
- Office of Inspector General Audit Report. FAA’s Safety Data Analysis and Sharing System Shows Progress, but More Advanced Capabilities and Inspector. 2014. Available online: https://www.oig.dot.gov/sites/default/files/FAA%20ASIAS%20System%20Report%5E12-18-13.pdf (accessed on 8 August 2020).
- Office of Inspector General Audit Report. INFORMATION: Audit Announcement | FAA’s Implementation of the Aviation Safety Information Analysis and Sharing (ASIAS) System. 2019. Available online: https://www.oig.dot.gov/sites/default/files/Audit%20Announcement%20-%20FAA%20ASIAS.pdf (accessed on 8 August 2020).
- National Transportation Safety Board (NSTB) Assumptions Used in the Safety Assessment Process and the Effects of Multiple Alerts and Indications on Pilot Performance. Dist. Columbia Natl. Transp. Saf. Board. 2019. Available online: https://trid.trb.org/view/1658639 (accessed on 8 August 2020).
- Federal Aviation Administration. Flight Operational Quality Assurance. Technical Report; 2004. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentID/23227 (accessed on 8 August 2020).
- Lee, H.; Madar, S.; Sairam, S.; Puranik, T.G.; Payan, A.P.; Kirby, M.; Pinon, O.J.; Mavris, D.N. Critical Parameter Identification for Safety Events in Commercial Aviation Using Machine Learning. Aerospace 2020, 7, 73. [Google Scholar] [CrossRef]
- Janakiraman, V.M. Explaining Aviation Safety Incidents Using Deep Temporal Multiple Instance Learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’18), London, UK, 19–23 August 2018; pp. 406–415. [Google Scholar]
- Bay, S.D.; Schwabacher, M. Mining distance-based outliers in near linear time with randomization and a simple pruning rule. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’03), Washington, DC, USA, 24–27 August 2003; ACM: New York, NY, USA, 2003; pp. 29–38. [Google Scholar] [CrossRef]
- Budalakoti, S.; Srivastava, A.N.; Otey, M.E. Anomaly Detection and Diagnosis Algorithms for Discrete Symbol Sequences with Applications to Airline Safety. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 101–113. [Google Scholar] [CrossRef]
- Iverson, D.L. Inductive System Health Monitoring. In Proceedings of the International Conference on Artificial Intelligence, Las Vegas, NV, USA, 21–24 June 2004. [Google Scholar]
- Matthews, B.; Srivastava, A.N.; Schade, J.; Schleicher, D.; Chan, K.; Gutterud, R.; Kiniry, M. Discovery of Abnormal Flight Patterns in Flight Track Data. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; p. 4386. [Google Scholar]
- Li, L.; Das, S.; Hansman, R.J.; Palacios, R.; Srivastava, A.N. Analysis of Flight Data Using Clustering Techniques for Detecting Abnormal Operations. J. Aerosp. Inf. Syst. 2015, 12, 587–598. [Google Scholar] [CrossRef]
- Das, S.; Matthews, B.; Srivastava, A.N.; Oza, N. Multiple Kernel Learning for Heterogeneous Anomaly Detection: Algorithm and Aviation Safety Case Study. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 47–56. [Google Scholar]
- Hinton, G.; SAlakhutdinov, R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Reddy, K.K.; Sarkar, S.; Venugopalan, V.; Giering, M. Anomaly Detection and Fault Disambiguation in Large Flight Data: A Multi-modal Deep Auto-encoder Approach. Annu. Conf. Progn. Health Monit. Soc. 2016, 7. Available online: http://www.phmsociety.org/node/2088/ (accessed on 8 August 2020).
- Guo, T.H.; Musgrave, J. Neural network based sensor validation for reusable rocket engines. In Proceedings of the 1995 American Control Conference-ACC’95, Seattle, WA, USA, 21–23 June 1995. [Google Scholar] [CrossRef]
- Zhou, C.; Paffenroth, R.C. Anomaly Detection with Robust Deep Autoencoders. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’17), Halifax, NS, Canada, 13–17 August 2017; pp. 665–674. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. International Conference on Learning Representations (ICLR). 2013. Available online: https://arxiv.org/abs/1312.6114 (accessed on 8 August 2020).
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the 31st International Conference on Machine Learning (ICML-14), Beijing, China, 21–26 June 2014; pp. 1278–1286. [Google Scholar]
- An, J.; Cho, S. Variational Autoencoder based Anomaly Detection using Reconstruction Probability. Spec. Lect. IE 2015, 2, 1–18. [Google Scholar]
- Xu, H.; Chen, W.; Zhao, N.; Li, Z.; Bu, J.; Li, Z.; Liu, Y.; Zhao, Y.; Peii, D.; Feng, Y.; et al. Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 187–196. [Google Scholar]
- Zenati, H.; Foo, C.S.; Lecouat, B.; Manek, G.; Chandrasekhar, V.R. Adversarial feature learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Dumoulin, V.; Belghazi, I.; Poole, B.; Mastropietro, O.; Lamb, A.; Arjovsky, M.; Courville, A. Adversarially Learned Inference. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Donahue, J.; Krahenbuhl, P.; Darrell, T. Adversarially Learned Anomaly Detection. In Proceedings of the 20th IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018. [Google Scholar]
- Chen, R.Q.; Shi, G.H.; Zhao, W.L.; Liang, C.H. Sequential VAE-LSTM for Anomaly Detection on Time Series. arXiv 2019, arXiv:1910.03818. [Google Scholar]
- Wang, X.; Du, Y.; Lin, S.; Cui, P.; Shen, Y.; Yang, Y. adVAE: A self-adversarial variational autoencoder with Gaussian anomaly prior knowledge for anomaly detection. Knowl. Based Syst. 2019, 190, 105187. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y. Time Series Anomaly Detection with Variational Autoencoders. arXiv 2019, arXiv:1907.01702. [Google Scholar]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumerzanu, C.; Cheng, W.; Ni, J.; Zhang, B.; Chen, H.; Chawla, N.V. A Deep Neural Network for Unsupervised Anomaly Detection and Diagnosis in Multivariate Time Series Data. In Proceedings of the AAAI-19, Honolulu, HI, USA, 27 January–1 February 2019; pp. 1409–1416. [Google Scholar]
- Park, D.; Hoshi, Y.; Kemp, C.C. A Multimodal Anomaly Detector for Robot-Assisted Feeding Using an LSTM-Based Variational Autoencoder. IEEE Robot. Autom. Lett. 2018, 3, 1544–1551. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’19), Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. β-VAE: Learning Basic Visual Concepts With A Constrained Variational Framework. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Chen, T.Q.; Li, X.; Grosse, R.B.; Duvenaud, D.K. Isolating Sources of Disentanglement in Variational Autoencoders. Adv. Neural Inf. Process. Syst. (NeurIPS) 2018, 31, 2610–2620. [Google Scholar]
- Kim, H.; Mnih, A. Disentangling by Factorising. In Proceedings of the International Conference on Machine Learning (ICML), Vancouver, BC, Canada, 30 April –3 May 2018. [Google Scholar]
- Yahoo!-Webscope. Dataset Ydata-Labeled-Time-Series-Anomalies-v10. 2019. Available online: https://webscope.sandbox.yahoo.com/catalog.php?datatype=s&did=70 (accessed on 8 October 2019).


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memarzadeh, M.; Matthews, B.; Avrekh, I. Unsupervised Anomaly Detection in Flight Data Using Convolutional Variational Auto-Encoder. Aerospace 2020, 7, 115. https://doi.org/10.3390/aerospace7080115
Memarzadeh M, Matthews B, Avrekh I. Unsupervised Anomaly Detection in Flight Data Using Convolutional Variational Auto-Encoder. Aerospace. 2020; 7(8):115. https://doi.org/10.3390/aerospace7080115
Chicago/Turabian StyleMemarzadeh, Milad, Bryan Matthews, and Ilya Avrekh. 2020. "Unsupervised Anomaly Detection in Flight Data Using Convolutional Variational Auto-Encoder" Aerospace 7, no. 8: 115. https://doi.org/10.3390/aerospace7080115
APA StyleMemarzadeh, M., Matthews, B., & Avrekh, I. (2020). Unsupervised Anomaly Detection in Flight Data Using Convolutional Variational Auto-Encoder. Aerospace, 7(8), 115. https://doi.org/10.3390/aerospace7080115





