Abstract
A micro air vehicle (MAV) is a class of miniature unmanned aerial vehicles that has a size restriction and may be autonomous. Fixed-wing MAVs are very attractive for outdoor surveillance missions since they generally offer better payload and endurance capabilities than rotorcraft or flapping-wing vehicles of equal size. This research paper describes the methodology applying indicial function theory and artificial neural networks for identification of aerodynamic derivatives for fixed-wing MAV. The formulation herein proposed extends well- known aerodynamic theories, which are limited to thin aerofoils in incompressible flow, to strake wing planforms. Using results from dynamic water tunnel tests and indicial functions approach allowed to identify MAV aerodynamic derivatives. The experiments were conducted in a water tunnel in the course of dynamic tests of periodic oscillatory motion. The tests program range was set at high angles of attack and a wide scope of reduced frequencies of angular movements. Due to a built-in propeller, the model’s structure test program was repeated for a turned-on propelled drive system. As a result of these studies, unsteady aerodynamics characteristics and aerodynamic derivatives of the micro-aircraft were identified as functions of state parameters. At the Warsaw University of Technology and the Air Force Institute of Technology, a “Bee” fixed wings micro aerial vehicle with an innovative strake-wing outline and a propeller placed in the wing gap was worked. This article is devoted to the problems of identification of aerodynamic derivatives of this micro-aircraft. The result of this research was the identification of the aerodynamic derivatives of the fixed wing MAV “Bee” as non-linear functions of the angle of attack, and reduced frequency. The identification was carried out using the indicial function approach.
1. Introduction
Fixed wings Micro air vehicles (MAVs), also known as micro-drones, may be defined as uninhabited micro aircrafts capable of completing surveillance or recognition missions in outdoor or indoor environments. Although a lot of attention has been paid so far to the embedded system, which includes sensors, autopilot and a payload, MAVs have now reached a level of maturity such that the problem of improving their aerodynamic performance is becoming a major concern. Because of severe Reynolds effect limitations, designing MAVs cannot just mean downsizing conventional aircraft. In open space, and in average weather conditions, temporary gusts of wind have a speed of 3–5 m/s (thus reaching 10% of the MAV’s maximum speed). In addition, the direction of such gusts changes quite often. This has a significant impact on MAV operation [1]. The speed of stronger wind gusts reaches a value comparable to the MAV cruising speed. Therefore, the key problem of MAV effective operation is to provide them with flight stabilization over a very wide range of operating conditions, in particular, at a high angles of incidence. The analysis of flight records clearly illustrates this problem. Changes in the angle of attack (AOA) are rapid and their amplitude ranges from to . The speed varies from 20 to 130 km/h and the altitude from 250 to 25 m [2]. Micro-drone flight in average atmospheric conditions can be compared to a passenger aircraft flight in hurricane conditions [3,4]. It can therefore be concluded that automatic class control systems, using linear proportional–integral–derivative (PID) controllers, do not always manage to stabilize flight in the event of atmospheric turbulence. Hence, it is very important to develop an exact MAV model, and in particular, to determine the aerodynamic forces and moments acting on the micro-drone.
Flows over an micro-aircraft at high angles of attack are complicated by the dynamics of flow separation and reattachment, the development and breakdown of vortex flow, and their interaction with dynamics of the aircraft. This causes significant non-linearities of unsteady aerodynamic characteristics, for example, non-uniqueness of stability derivatives and hysteresis of aerodynamic characteristics. Increasing computational capacity and the development of numerical techniques has recently led to significant progress in finding solutions for Navier–Stokes equations coupled with the dynamic equations governing aircraft motion and facilitating flight dynamics studies [5]. However, presently the issues of fluid mechanics and flight dynamics cannot be solved simultaneously in certain aerial mechanical applications—for example, in the case of realistic simulations of aircraft flight or control system design [6,7,8,9]. Solving such flight dynamics problems demands Reduced-Order Models (ROM) of unsteady aerodynamics describing non-linear phenomena observed within the extended range of flight parameters. Experimental data obtained from wind tunnel tests of Computational Fluid Dynamics (CFD) data are commonly used for the development of such models.
The presence of important outcomes of aerodynamic load non-stationarities requires special attention (the impact of acceleration to aerodynamic derivatives, in particular). Although these effects were first observed in the 1950s, in most cases they were of little importance in terms of analysing stability and manoeuvrability of a conventional aircraft (flying at relatively low angles of attack and low state parameter change amplitudes) [10,11]. However, in the case of micro aircraft, the flight of which is characterized by a sudden change in the angles of attack and slip resulting from atmospheric turbulence and wind gusts, a linear model of aerodynamic loads, based on stability derivatives, is a failure. MAVs are characterized by highly non-linear aerodynamic characteristics. Therefore, it is widely believed that one of the most important issues of contemporary flight dynamics is developing non-linear mathematical models for aerodynamic loads, as a state variable function. This is extremely paramount not only because of determining the level of aerodynamic loads present in the course of flight, but also due to the analysis of flight stability and manoeuvrability (preventing cases of in-flight manoeuvrability loss, in particular).
At the Warsaw University of Technology and the Air Force Institute of Technology, a “Bee” fixed wings micro aerial vehicle with an innovative strake-wing outline and a propeller placed in the wing gap was designed and built. This article is devoted to the problems of identification of aerodynamic derivatives of this micro-aircraft. Aerodynamic derivatives were identified by the indicial function method.
2. Modelling of Aerodynamic Coefficients—A Short Review of the Literature
A number of non-linear modelling techniques involving non-stationary aerodynamic characteristics of aircraft have been developed over the last decade. An example can be the research results of the following work groups: AVT-113 and AVT 201 of the Applied Vehicles Technology panel of the NATO Science and Technical Organization (NATO STO). The work of the AVT-113 task group “Cranked Arrow-Wing Aerodynamics Project International—CAWAPI” were devoted to studying the aerodynamics of the F-16 XL aircraft. In the 90s of the previous century, NASA conducted in-flight tests of the experimental F-16XL aircraft. This aircraft had a delta-wing with a specifically curved leading edge. The results of in-flight tests conducted at NASA were a reference for the works by the AVT-113 task group, which concentrated on evaluating the possible application of computational fluid mechanics to predict data obtained during the in-flight tests of the F-16XL aircraft. The results of this study were summarized in two special editions of the Journal of Aircraft (J. of Aircraft, vol. 56, No. 2 and 4 of 2017).
The work of the AVT-201 task group “Extended Assessment of Reliable Stability & Control Prediction Methods for NATO Air Vehicles” was devoted to extended assessment of methods for forecasting stability and control of NATO aircraft, including unmanned aerial vehicles. The efforts of AVT 201 were a continuation of the study by the AVT-161 work group, which were also dedicated to methods for predicting stability and control of NATO aircraft and vessels. The results of the work by AVT 201 were summarized in a special edition of Journal of Aircraft (J. of Aircraft, vol. 55 No. 2, March/April 2018). The objective of the work by the AVT-201 task group was to determine the general strategy for developing databases in terms of aircraft stability and manoeuvrability in the aspect of their application in simulation systems for these objects, and in the complete field of flight parameter envelope, including the issues of large and supercritical angles of attack. The studies discussed in a special edition of the J. of Aircraft quarterly included: evaluation of the possibilities of computational fluid mechanics methods for modelling the airflow around a manoeuvring airframe; application of experimental data for assessing the aircraft manoeuvrability; and precise flow field prediction, in order to validate computational methods, with particular regard to cases of flow asymmetry and its non-stationarity. The objective of the research was to expand the knowledge in the field of aerodynamic phenomena and to better understand aircraft flight dynamics. A series of dynamic tests in air and water aerodynamic tunnels were conducted, besides calculations using the numerical fluid mechanics methods.
The aforementioned research examples can be considered as valid and representative. Based on the analysis of the studies contained in the cited issues of the Journal of Aircraft quarterly, it can be concluded that they concentrate rather on assessing how closely the conducted calculations reflect the experimentally observed effects, than on their practical application in modelling and simulating aircraft flight.
The research work devoted to the practical application of non-stationary aerodynamics models in algorithms describing aircraft flight dynamics include: [5,11,12,13,14,15,16,17,18]. The authors of these cited articles analysed the effects of introducing aerodynamic derivatives calculated relative to accelerations, thus taking into account the outcomes of aircraft airflow non-stationarity. However, the results of cited papers are ambiguous. They can be summed up with a conclusion that the correctness of non-stationary aerodynamic models, as a function of the state parameter, “depends on the aircraft and manoeuvre”. There were also several papers published, in which the authors evaluated the effects of non-linear modelling of aircraft aerodynamic loads in terms of suitability within the engineering process of control laws [19,20,21,22,23,24,25]. The authors of these studies noticed that omitting the effects of aerodynamic load non-stationarity usually leads to decreased autopilot effectiveness. It can be seen that attempts at modifying and expanding the conventional model of stability derivatives within the process of modelling non-stationary aerodynamic loads are extremely interesting (from a practical point of view). Very often, in order to reflect transient aerodynamic effects, the classical model of “stability derivatives” is expanded by adding derivatives calculated relative to accelerations. Approximation of transforms using rational functions are often introduced in non-stationary issues. This leads to a model, where additional (aerodynamic) variables of the system state and additional differential equations are defined. In the case of high angles of attack, with occurring flows with separation, semi-empirical non-linear models are required to determine transient aerodynamic forces. They usually take the form of additional, non-linear ordinary differential equations. These equations include coefficients, which can be determined based on the results of experiments conducted in aerodynamic tunnels or in the course of in-flight tests. Examples include the ONERA model [26] developed to determine aerodynamic forces and moments acting on a helicopter blade aerofoil and other similar models by Leishman or Beddoes [27,28].
Estimating the aerodynamic characteristics of an aircraft based on its motional response to disturbances requires suggesting a mathematical model of its flight dynamics. The mathematical model includes both aircraft motion equations, as well as equations for aerodynamic forces and moments. The relationships describing the aerodynamic loads are also called aircraft aerodynamic model equations. In the field of the flight operating parameter envelope, which does not generally experience stream separations, the flow is stable and stationary, and the aerodynamic model equations are usually described as a linear approximation of the expansion of functions describing aerodynamic forces and moments in the Taylor series. It is a model of so-called aerodynamic derivatives, commonly applied since the beginning of the 20th century [17,23,29,30,31,32,33,34,35].
However, in conditions of overshooting, the nominal envelope of the flight parameters, a traditional aerodynamic derivative model, is no good. Therefore, it is necessary to generalize the mathematical model of aerodynamic loads in manner, which enables taking unusual flight conditions into account. Such a model shall reflect the presence of frequency relationships and non-linear responses to flight parameter disturbances. The results of numerous studies [28,36,37,38,39,40,41] indicated that aerodynamic parameters depended on frequency. This dependence is in contrast to the basic assumption of the aerodynamic derivative model, which assumes that stability derivatives can be treated as constant. When aerodynamic parameters exhibit dependence on frequency, the aerodynamic model equations can be effectively formulated using the indicial or step function, which enables capturing transient responses of the aircraft [10,15,16,22,42]. When the values of transient aerodynamic load coefficients depend on the aircraft movement amplitude and frequency, an approach allowing to determine aerodynamic loads using the Indicial function method, combined with the superposition principle, can be applied [10,22]:
where: is a vector of aerodynamic forces and moments coefficients, and: CX is a drag coefficient, CY is a side force coefficient, CZ is a lift coefficient, Cl is a rolling moment coefficient, Cm is a pitching moment coefficient, and Cn is a yawing moment coefficient.
is the matrix of a characteristic response function for step variance of flight parameters, such as angles of attack α, angles of slip β, bank angle γ, angular velocities of roll r, pitch q, yaw r, and displacements of control surfaces: elevator δe, and elevons δelv. These quantities can be expressed in the form of a vector .
Such an approach is efficient, however, combining the aforementioned functional representation of the aerodynamic loads with aircraft motion equations is not easy. It should be stressed that the aforementioned representation of aerodynamic characteristics can also be expanded onto non-linear cases, which take into account boundary layer separation. However, in the event of stream separation, the application of the above aerodynamic model becomes significantly more complicated because of difficulties connected with breakdown modeling of boundary-layer flow [22].
Models described with ordinary differential equations can be used to describe non-linear aerodynamic characteristics associated with the aircraft motion history. The base for such a description is the measurements of aerodynamic loads taken in aerodynamic tunnels or calculated with methods of numerical fluid mechanics. Measured or calculated aerodynamic characteristics can be described using the following dynamic input-output system [15,16,18,28,41]:
where: Di, Ni are certain smooth, non-linear functions, which can be identified with appropriate techniques [28,36,37,38,39,40,41].
This method is convenient for solving issues associated with flight dynamics, since transient aerodynamics models presented in the form above lead only to increasing the size of the problem and do not impact the possibility of studying motion stability using classical methods. One of the most important features regarding this method is the ability to describe aircraft aerodynamic loads as a function of state variables [15]. State variables are very critical parameters, which enable describing a dynamic system [43]. They provide information required to determine the current and future behaviour of a dynamic system, an aircraft in this case. State variables can be treated either formally or have well-defined physical significance. There is a close relationship between the aforementioned representation of aircraft aerodynamic characteristics within the state space and the characteristic function method. In a linear case, the characteristic function can be approximated using an indicial response function or through exponential functions. Such an approximation is equivalent to the application of a system of linear, ordinary differential equations, with exponential functions as the solution. The resulting exponential equations describe transient aerodynamics of an aerial vehicle and can be easily attached to the aircraft motion differential equations.
Approximation of aerodynamic characteristics in a state variable space, which describes the transient flow around the aerofoil for a linear case (flows without separations), was presented in the following research papers: [5,8,15,16]. The authors of these works applied this approach to describe the delay in the separation of the boundary layer, resulting from the impact of vortices flowing off the aerofoil.
With high angles of attack, the flow separation on the wing has several additional dynamic properties. They include delayed convection of the boundary layer (lift), effect of boundary layer sticking, effect of separation point displacement etc. Some of these phenomena impact the conditions of flow detachment appearing and disappearing. Others are associated with the expansion of detached flow and transitory processes. Instantaneous position of the separation point depends on all of these effects. In turn, the values of the total aerodynamic force and aerodynamic moment depend on the kinematic motion parameters and the flow separation point. Therefore, the position of the separation point in this case can be treated as an internal dynamic variable. Obtaining a mathematical model requires dynamic equations governing the behaviour of the separation point, depending on the kinematic motion properties of the aerofoil, as well as the dependence of the total aerodynamic force on the kinematic parameters and the separation point position. Similar aerodynamic processes govern the vortex-related separation of the flow around a low-elongation delta-wing. In this case, the position of vortex breakdown points can also be treated as internal dynamic variables. Although aerodynamic processes for the aerofoil and delta-wing differ significantly, the dynamic features of aerodynamic forces are similar.
Given the aforementioned features, one can suggest a mathematical model where the internal dynamic variables (vector x) approximately describe the state of separated and vortex-related flow around the micro-aircraft. These variables provide additional information required at a given time to calculate the aerodynamic forces and moments described by vector C. Vector C is also a function of system data (input) described by vector u. The result is the following system of differential and algebraic equations:
A complex air flow around a micro aircraft at high angles of attack, experiences both the phenomena of vortex separation, as well as breakdown. Dynamic properties of these phenomena can be described using equation [15]:
where τ1 and τ2 are time constants.
The generalized internal state variable x in this case has no defined physical significance. In a general case, the function g(x, u) in Equation (3) must be determined by the application of identification techniques, based on experimental data (on the basis of force and moment measurements in aerodynamic tunnels or based on data gathered during in-flight tests) [18,28,36,37,38,39,40,41,44].
Ultimately, the lift force and pitching moment coefficients take the form:
Equation (5) must be satisfied both for oscillatory motion of low amplitude, as well as for any movements, including the ones leading to dynamically achieving high angles of attack and high-amplitude oscillations.
Non-linear and coefficients can be expressed in the form:
where and , respectively, depend on the coefficients of CZ and Cm for x = 1 and x = 0. The functions are an envelope of the curves of the set of CZ and Cm coefficients obtained for various positive pitching speeds. Function g(x) acts as a normalized weight function , which enables expressing a simplified dependence on x. Function g(x) can be expressed in the form: , the value of constant is identified using the least squares method. In some cases, the functional Fourier analysis can also be used to develop models of transient aerodynamic characteristics. The aerodynamic characteristics were estimated based on measurements taken in a wind or water tunnel.
3. Water Tunnel Experiments
3.1. Water Tunnel Description
All tunnels tests were conducted using a water tunnel by Rolling Hills Research Corporation, Model 2436 [45]. It is a tunnel with closed working fluid circulation, where the measuring chamber space has a rectangular face section with the dimensions of 610 mm × 915 mm (Figure 1). This tunnel is a part of the Low Reynolds Number Laboratory of the Department of Mechanics and Power Engineering of the Wroclaw University of Technology.

Figure 1.
RHRC 2436 water tunnel; (a) water tunnel measuring space; (b) console for measured signal amplifiers and water flow speed display.
The RHRC 2436 tunnel was equipped with a bracket ensuring the movement of a studied model in three planes and a system, which supplies dyes to the model, enabling the execution of visualization tests involving flow around the tested object. The measuring element used for the tests is a five-component tensometric scale (Figure 2). There are five undercuts with stuck piezoelectric strain gauges, with specific resistance of 1000 Ω and a gain factor of 145, in the measuring section of the circular-section scale. Current voltage in the extensometers is the directly measured value. Voltage changes are transmitted onto full Wheatstone bridges [46]. Each signal is equipped with a separate amplifier with a Wheatstone bridge, which transmits the measured signal further onto a data acquisition board built into a PC (Figure 1b). The RHRC 2436 water tunnel is equipped with water flow velocity meter and a thermometer for the water in the measuring chamber [47]. The measurement of both values is used to calculate the Reynolds number for given conditions in the course of the experiment. The range of water flow velocities in the tunnel varies from 0 to 280 mm/s. Figure 1a shows an image of the tunnel’s measuring space, control system and the amplifier console.
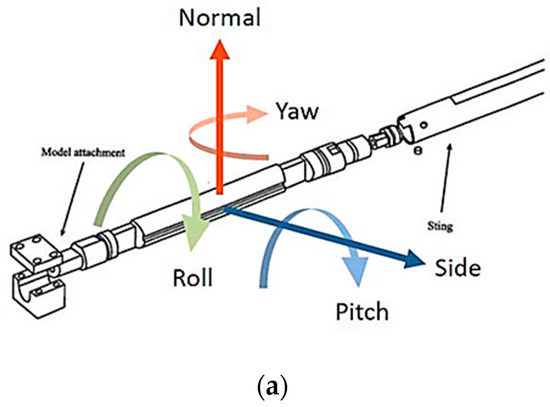

Figure 2.
(a) Diagram of a five-component aerodynamic balance, (it is shown “wind tunnel coordinate system” used in wind & water tunnel testing) [46], (b) tensometric scale with a calibration system.
The movements of the model within the measuring space are made possible by the bracket structure, which ensures freedom of motion within a range of angles of attack , angles of slip and angles of roll . A diagram of the model bracket for the RHRC2636 tunnel measuring space is shown in Figure 3.
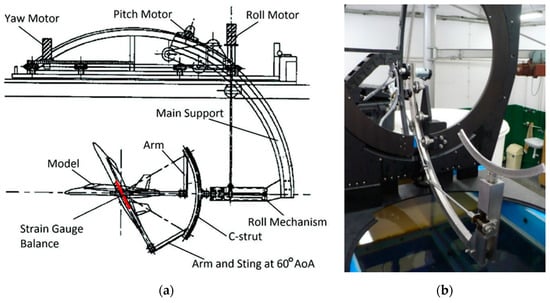
Figure 3.
(a) Model manipulator (up) and strain balance (down) scheme [46]; (b) support view.
Figure 3 shows a bracket fixed in the tunnel’s measuring space. The structure of the arm that fixes the tensometric scale with an attached model enables initial fastening of the model with a wedge angle in the range of , which given the option to mount the model in two positions (rolling angle of 0° and ), results in a possibility of conducting the tunnel test with an angle of attack . Changes in the spatial position angle of the model are achieved using stepper motors. This enables a smooth change of the model’s positions and ensures precise determination of the angular position, with an accuracy of . The water tunnel bracket enables conducting numerous dynamic tests. A diagram representation of such tests is shown in Figure 3. Initial experimental values and quantities measured by the aerodynamic scale are processed using the AAF-3PCI data acquisition board by Alligator Technologies [45,46,47].
The software for controlling the model within the measuring space was developed in the LabVIEW environment. Also, the data acquisition and storage procedures were developed in this programming environment. The software for tunnel control, as well as data acquisition and storage, enables executing the following actions:
- stationary and non-stationary tests,
- tensometric scale calibration,
- controlling the spatial positioning of the model,
- controlling the water flow velocity in the tunnel,
- graphic illustration of the test results,
- imaging voltages on the strain gauges in the five-component scale.
Furthermore, the software enables converting the measurements for other data (for example, after recalibrating the scale) and entering geometric data for the tested model.
3.2. The Model
Identification of non-stationary aerodynamic characteristics of a micro aerial vehicle was conducted based on the results of numerous tests. The research included both stationary, as well as non-stationary tests that were conducted. The micro-drone “Bee” model used for the study is shown in Figure 4a.

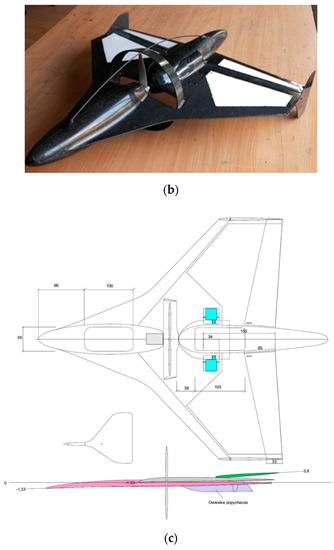
Figure 4.
(a) The “Bee” MAV model for testing in a water tunnel; (b) micro-drone “Bee”; (c) sketch of the “Bee” fixed wings MAV; the “Bee” data: wingspan = 500 mm, MTOW = 850 g, Vmax = 120 km/h, endurance = 30 min.
The stationary test cycle was conducted for a range of angles of attack and slip. The following characteristics were the outcome of the five-component aerodynamic balance measurements (Figure 2a): normal force coefficient CN = f(α), pitching moment coefficient Cm = f(α), side force (binormal force) coefficient CY = f(β), and rolling moment coefficient Cl = f(β). A cycle of dynamic tests was conducted for short-term oscillatory motions of the model for a range of angles of attack, slip and roll. The following non-stationary characteristics were obtained based on these tests: CN = f(α), CLM = f(α), CY = f(β), CLL = f(β), CLN = f(β), and CLL = f(γ). The time waveforms for the following characteristics were also obtained: CN = f(t), CLM = f(t), CY = f(t), CLL = f(t), and CLN = f(t). Measured aerodynamic moment coefficients were related to reference points on the aerodynamic balance. Coefficients CLL, CLM, and CLN are moment coefficients reduced to aerodynamic balance reference point [46].
A series of tests in the form of periodic, oscillatory changes to one of the angles defining the spatial position of the MAV model were conducted in order to acquire data for the identification of aerodynamic derivatives using artificial neural networks and the indicial function [10,18,28,36,37,38,39,40,41]. Selective, isolated motions within specific planes enabled obtaining data for the identification of derivatives, while maintaining certainty that a change of aerodynamic coefficients was impacted by displacement only within the assumed motion plane.
3.3. Similarity Criteria and Tests Setup
The basic similarity criteria in the course of aerodynamic tunnel tests are the Reynolds number, Re; and the Strouhal number, Sr, as well as the reduced frequency, f. These numbers are defined by the relationships:
where:
- Re
- Reynold’s number [-]
- V
- flight speed [m/s]
- cA
- mean aerodynamic chord [m]
- cA
- kinematic viscosity [m2/s]
- Sr
- Strouhal number [-]
- D
- propeller diameter [m]
- Ω
- propeller angular velocity [rpm]
- f
- reduced frequency of micro-aircraft angular displacements
- ω
- micro-aircraft manoeuvre angular velocity [1/s]
The starting point for selecting the values of similarity numbers in terms of planned water tunnel experiments was the MAV mission profile [48]. The flight speeds, with particular attention to the speeds similar to minimum speeds of tactical recon missions, were taken into account. In this phase, a micro aerial vehicle is most susceptible to disturbance caused by atmospheric turbulence. The Reynolds number for the assumed minimum operating flight speed is , whereby the aircraft, owing to large thrust surplus, is able to fly with a speed in the order of V = 7.5 m/s (Re ≅ 97,000) for short periods of time. In order to select the comparative criterion for propeller operation, the rotational speed of an electric model engine Ω = 10,800 rpm. was adopted. With the assumed propeller diameter of D = 0.15 [m], average aerodynamic chord cA = 0.306 m and reconnaissance flight speed V = 10 m/s, the Strouhal number is: Sr = 2.52. The angular velocity of micro aircraft manoeuvres was the next significant parameter in terms of planning non-stationary experiments. Based on flight parameter records, it was estimated that the average manoeuvre angular velocities were in the order of: p = q = r = 10.66 [1/s], which for the assumed reconnaissance flight speed results in a micro-aircraft angular displacement reduced frequency value of f = 0.02. The ranges for the probability numbers of planned experiments were specified based on the parameters determined for an actual micro-aircraft [48].
Due to the limitations resulting from the limit load capacity of the aerodynamic scale, the velocity of the water flow within the tunnel’s measuring space had to be reduced. Therefore, it was possible to conduct tests with a speed corresponding to Re = 50,000. For comparative reasons, the tests were also conducted for the second Reynolds number, Re = 28,000. The model intended for water tunnel testing was equipped with a motor-driven electric propeller. The tests were conducted for three scenarios:
- −
- “no-propulsion” configuration, i.e., with a stationary propeller hidden inside the wing gap;
- −
- for the propeller rotational speed corresponding to the Strouhal numbers of Sr=1.374 and Sr=2.522.
The outcome was a combination of six measurement cycles. The tests for both Re numbers were conducted with deactivated propulsion and propeller inscribed within the aerofoil contour, with an operation propulsion system.
Another similarity criterion for non-stationary tests was the reduced frequency of oscillatory movements performed by the MAV model within the measuring space of the water tunnel. The tests were conducted for both Re numbers and five angular velocities of the model induced by the bracket of the scale (Figure 3). This resulted in a series of five reduced frequencies, different for both Re (Table 1).

Table 1.
Reduced frequency values for both Re.
Range of angles of attack for the stationary tests fell between: α ∈. A series of tests was conducted for non-stationary measurements, where the model would perform oscillatory movements relative to a number of angles of attack: and a motion amplitude of which resulted in the total range of angles of attack for non-stationary tests in the range of Whereas stationary tests involving lateral characteristics were conducted for angles of slip in the range of . Non-stationary tests of asymmetric (lateral) characteristics were conducted for the following angles of slip: . The slip angle change amplitude amounted to . Measurements of the lateral force and the yawing moment were conducted for angles of attack in the range of: , with a step of , and angles of slip: . The slip angle change amplitude was .
Due to the structure of the tensometric scale, only the rolling moment was measured within the roll plane. A series of measurements with a set rolling angle and motion amplitude of was conducted. The determined angles of attack were identical to the ones for the tests in the yaw plane.
4. Results from Water Tunnel Tests
A tensometric balance, as a research tool, enables an accurate measurement of five force components and aerodynamic moments. The test results were obtained for three planes, namely, pitch, roll and yaw (Figure 2a). In the course of the measurements, the reference point of the aerodynamic balance was at ~85% of the mean aerodynamic chord cA. In order to determine the coefficient values of aerodynamic forces and moments, at 25% cA, the following relationships were used:
where: x—aerodynamic scale reference point distance from 25% mean aerodynamic chord cA (Figure 5).
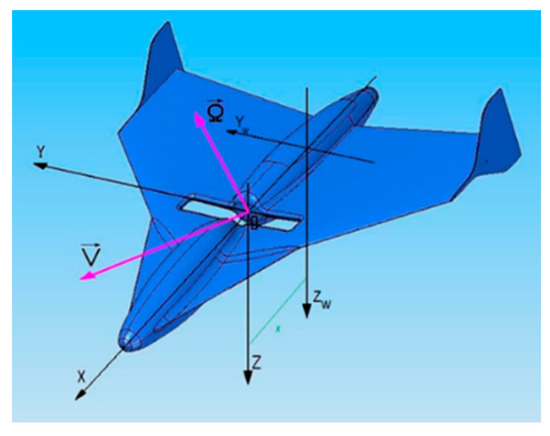
Figure 5.
The micro-aircraft coordinate systems bonded with the aerodynamic scale reference point and the point within the model symmetry plane, at 25% of the mean aerodynamic chord of the model cA.
A total of 750 measurements were designed and conducted, based on assumed values of similarity criteria and assumed angular ranges. The results of the experiments were grouped and elaborated on pursuant to the traditional division into motion planes. Stationary and non-stationary aerodynamic characteristics were determined in the plane of the lift force coefficient CZ; the pitching moment coefficient Cm; the lateral (binormal to aerodynamic balance axis) force coefficient CY; the yawing moment coefficient Cn; and the rolling moment coefficient Cl. Sample results of a test cycle involving an MAV model with a rotating propeller for Reynolds numbers Re = 28,000 and Re = 50,000, and the Strouhal numbers Sr = 1.374 and Sr = 2.522 are shown in Figure 6. The CZ(α) characteristic has a waveform typical for winged aircraft, with marked critical angle of attack αcr = 27° and a very gentle separation characteristic. It should be noted that the micro-aircraft is statically stable almost throughout the entire range of angles of attack . This proves the positive impact of a propeller located in the wing gap on the MAV stabilization in a longitudinal channel. The static characteristic of the pitching moment clearly shows the range of angles of attack , where the pitching moment coefficient derivative is positive relative to the angle of attack.
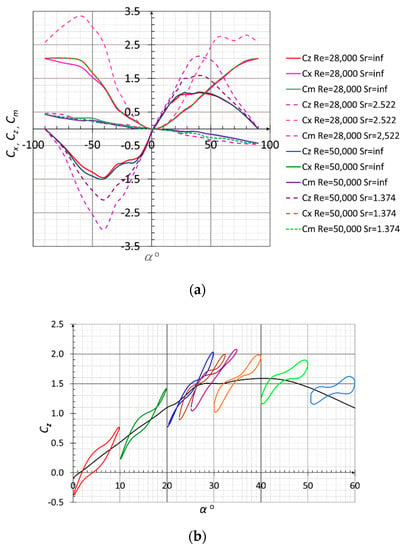
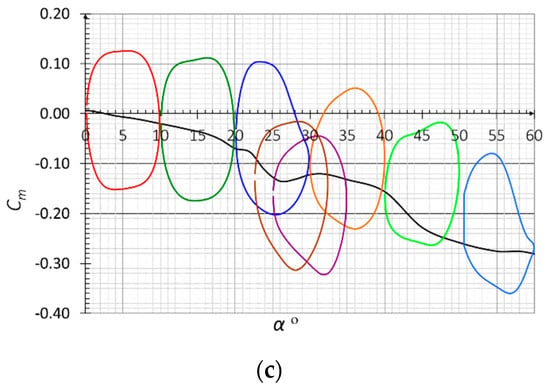
Figure 6.
(a) Collective lift force CZ coefficient and pitching moment coefficient Cm characteristics for stationary experiments; (b) lift force coefficient in the angle of attack function; f = 0.0161, Sr = 1.374, Re = 50,000; (c) pitching moment coefficient in the angle of attack function; f = 0.0161, Sr = 1.374, Re = 50,000.
Sample measurements of dynamic characteristics are shown in Figure 6b,c. The aerodynamic characteristics of the MAV, as a state variable function, was estimated based on the dynamic measurement results. The indicial function method was used to conduct this estimation.
5. Identification of Aerodynamic Derivatives using Indicial Function
5.1. Indicial Function Theory
The general form of an aerodynamic model, which enables a very broad scope of application for indicial functions, was described in the following papers: Tobak [10]; Tobak, Chapman, and Schiff [22]; Klein and Noderer [36,37]; Klein, Murphy, Curry, and J., Brandon [38]; Murphy, Klein, and Szyba [41]; and Murphy, Klein, and Frink [18]. The assumptions of the general model described in the cited papers have several limitations. In the case of the model applied herein, the basic assumption is the lack of micro-aircraft deformations (only the rigid body dynamics is taken into account) and the assumption that air density, air viscosity and dynamic pressure do not fluctuate significantly (which is acceptable in the case of an MAV flight characteristics). Assuming that the components of the aerodynamic coefficient vector are single-valued functions of the vector of state , where is the position vector and is the angular velocity vector, then, pursuant to the assumptions described by Tobak Chapman, and Schiff [22], the aerodynamic coefficient vector can be described using the following relationship [22,36]:
In the equation above, is the value of the aerodynamic coefficient for fixed initial conditions; l is the characteristic length (l = cA or l = b/2); and and are indicial function vectors. The components of vectors are responses of the aerodynamic coefficient C to single jumps of the ξ parameters.
Every indicial function can be described using equation:
where defines the change in the value of coefficient Ca along with parameter ξj, while the other parameters of the model remain unchanged; whereas is a deficiency function, which reaches zero for .
After substituting (10) to (9) we get the relationship:
Assuming that the aerodynamic coefficient Ca is linearly dependent on angular velocities ξ2 and expanding the Equation (13) into the Taylor series around point ξ = 0, we get an equation:
by simplifying the notation, Equation (13) can be expressed as follows:
where:
One of the possible forms of the deficiency function is described by the relationship:
where a and b are the polynomials of parameters α, β, γ.
Substituting relationships (14) to the deficiency function, we get:
Differentiating Equation (16) relative to time, we get:
After applying the Laplace transform to Equation (16), we get:
Hence, after the transformations we get:
Based on Equations (9) and (11) under the simultaneous assumption that the deviations of state coordinates from fixed conditions are minor, individual relationships of the aerodynamic coefficients will adopt the form:
Because experimental data used to identify experimental derivatives were obtained for an oscillatory motion with a single degree of freedom, it can be assumed that , which means , and . Substituting the above to Equation (19), we get:
The Laplace transform of Equation (20) has the form:
Substituting Laplace transform of the deficiency function (17) to Equation (20), we get:
After the transformations we get:
MAV aerodynamic Equations (13) and (23), after linearization around the equilibrium position for longitudinal characteristics Ca (a = X, Z, m), can be expressed in the following form:
whereas for asymmetric characteristics in the form Ca (a = Y, l, n):
In the equations above:
Equation (25) can be represented as a function of state parameters, by introducing the variable f through a given relationship:
Applying the Leibniz integration rule, the linearized relationship of the aerodynamic coefficient as a state parameter function takes the form:
In order to simplify the discussion, below can be found an analysis of a generalized aerodynamic coefficient Ca. Instead of the coefficients a1, a2, a3, b1, b2, and b3, the deficiency function equations will adopt the a parameter without subscript and the b1 parameter. Assuming that the data for parameter estimation were obtained as a result of a conducted water tunnel oscillation test with a single degree of freedom, it can be assumed that for the longitudinal characteristics, . Then the Laplace transform for Equation (28) takes the form:
Substituting relationship (29) to relationship (20), we get:
After algebraic transformations we get:
Four unknown values , a, and b1 present in Equation (31) can be estimated based on the time waveform measurements of parameters Ca(t), α(t), and q(t) obtained in the course of the aerodynamic (or water) tunnel measurements. Equation (32) can be expressed as:
or in a form similar to the transfer function of the aerodynamics model:
where:
5.2. Identification Method
A program developed in MATLAB, which utilizes the “System Identification Toolbox” and “Neural Network Toolbox” functions, was used to identify the non-stationary characteristics and aerodynamic derivatives. The measurement results were processed in a structured manner, ordering the data in accordance with similarity criteria and model motion planes within the measuring space of the tunnel and using the MS Office Excel package.
The parameters of the indicator function, described by transfer function (34), were determined using an ARX dynamic structure.
Equation (35) is a general linear description of a discrete and stationary system, where is the input signal, is the output signal, and is a disturbance in the form of white noise. Functions and are described by a sequence of parameters , .
The operator describes backward shift of the signal: . Parameters and are approximated using estimation algorithms. The vector of estimated parameters is marked with a symbol.
The aforementioned equation describes the class of models, the elements of which are defined by the parameter vector .
ARX model (40)—auto-regressive with an internal input is a general model describing the input-output stochastic processes. The ARX model parameter vector is in the form:
Next, we introduce differential polynomials (41) and (42) to Equation (39), which is described by Equation (33), for which the functions and adopt the form:
The term A(q)y(t) of Equations (39) and (40) is also called an auto-regressive term, whereas B(q)u(t) is responsible for the exogenous input of the system. In a general case, when na = 0, the system output is modelled as a filter with a finite indicial response (FIR).
The ARX model structure is described completely by three parameters:
- —number of pseudo-transmittance poles +1
- —number of pseudo-transmittance zeros
- —input signal delay
Pseudo transmittance described by the Equation (33) has three zeros = 3 and one pole = 1, except that the second element of the Apolynomial sequence . Due to the fact that the aerodynamic parameter values also depend on the current status of the output signal u(t), and = 0.
The ARX model structure is generated in MATLAB by executing the arx function. This function uses the least squares method for estimating the parameters. Target estimator function has the form:
In order to compare the indicator model identification quality, the software provides an identification algorithm based on a four-layer neural network. The project has implemented a feedfoward back-propagation network. The network training algorithm is Levenberg–Marquardt’s back propagation. Each of the network layers has a bias. The parameters of the three hidden network layers, i.e., number of neurons within a layer and the type of activation function are defined by the user. The last output network layer has a single output, which corresponds to the system output.
The neural network is created in MATLAB by executing the newff function. At the start of the procedure, the number of neurons for each network layer and their activation functions need to be specified. The model is identified through executing the nlarx (nonlinear ARX model) method, with a ’Nonlinearity = neuralnet(net)’ parameter. When executing the nlarx function, one should also enter the parameters of the ARX structure: , , .
5.3. Results of Identifying MAV Aerodynamic Characteristics
Longitudinal and asymmetric aerodynamic characteristics of a micro-aircraft were identified based on the tests conducted in the RHRC 2436 water tunnel. These tests were executed for two flow speeds, which correspond to the Reynolds numbers of Re = 28,000 and Re = 50,000, and a broad range of angles of attack and reduced frequencies of model oscillations within the water tunnel measuring space. The tests included configurations of a micro-aircraft model with an immobile, hidden in the wing gap propeller, (Strouhal number Sr = inf, “immobile propeller” in the figure description), and a rotating propeller (Strouhal number Sr = 2.522, “rotating propeller” in the figure description). Figure 7, Figure 8 and Figure 9 show sample results of identifying the derivatives of the lift force CZ and pitching moment Cm coefficients relative to the angle of attack α; the angular velocity of pitching; rate of changes in the angle of attack ; and the reduced frequency f; and . By tracking the maps and waveforms of longitudinal aerodynamic derivative, we can notice that a micro-aircraft is statically stable over a broad range of angles of attack and reduced pitching oscillation frequencies. Only in the range of near-critical angles of attack we can observe areas with minor positive values of the Cmα derivative, especially for higher reduced frequencies of the pitching oscillation. Based on maps CZα, it can be seen that the critical angle of attack decreases with increasing reduced frequency value. However, it is clearly visible that its value is higher, compared to the static characteristic. The pitching moment coefficient derivatives relative to the angles of attack are negative practically throughout the entire measurement range, at the same time indicating aircraft stability even for over-critical angles of attack. This feature of an MAV enables its sudden manoeuvres, and primarily indicates high resistance of this unmanned aerial vehicle to gusts of wind and atmospheric turbulence, which are the main in-flight threat. The maps shown in Figure 7, Figure 8 and Figure 9 depict both the derivatives for a smooth configuration, without a running propulsion system, as well as with a rotating propeller. With a running propulsion system, we can observe increased absolute value of longitudinal aerodynamic derivatives. Based on the aerodynamic derivatives and characteristics identified with the Indicial function method, it can be concluded that the “Bee” micro-aircraft is stable within the pitch plane, over a wide range of angles of attack and reduced pitching oscillation frequencies, including within over-critical flight parameter ranges. The propeller rotating within the wing gap positively impacts the lifting surfaces of the micro-aircraft, improving its flight properties. This clearly indicates that the aerodynamic system of a micro-aircraft with an aerofoil within a double-delta contour (leading-edge extension wing) and a wing inscribed in the aerofoil contour is a very good engineering solution in terms of unmanned aerial vehicles.
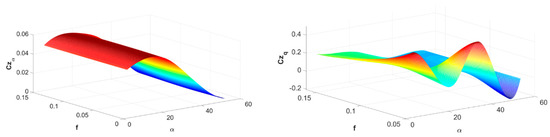
Figure 7.
Results of identifying derivatives: dCZ/dα [1/deg]; Re = 50,000, rotating propeller (Sr = 2.522) (left); dCz/dq; Re = 28,000, rotating propeller (Sr = 2.522) (right).
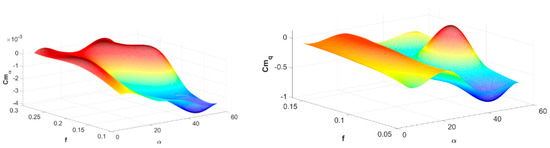
Figure 8.
Results of identifying derivatives: dCm/dα [1/deg]; Re = 50,000, immobile propeller (Sr = inf) (left); dCm/dq; Re = 28,000, immobile propeller (Sr = inf) (right).
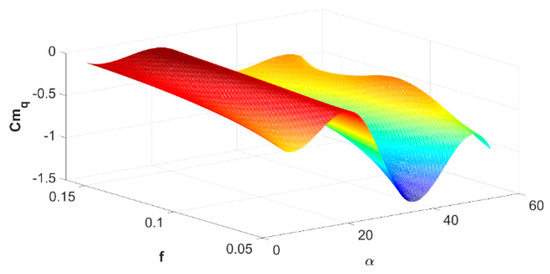
Figure 9.
Results of identifying derivative dCm/dq, Re = 28,000, rotating propeller (Sr = 2.522).
Selected results of asymmetric estimations of MAV aerodynamic characteristics in the function of the angle of attack and reduced frequency k are shown in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. The sign of the yawing moment coefficient derivative relative to the angle of slip is particularly important in terms of assessing the static directional stability of an aircraft. Derivative Cnβ is non-negative over a wide range of changes in the angle of attack and reduced yawing oscillation frequency. Similarly, derivative Clγ is positive over a wide range of angles of attack and reduced yawing oscillation frequency.
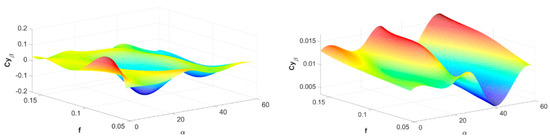
Figure 10.
Results of identifying aerodynamic derivatives dCy/dβ, Re = 50,000, immobile propeller (Sr = ∞) (left); dCy/dβ, Re = 50,000, rotating propeller (Sr = 2.52) (right).
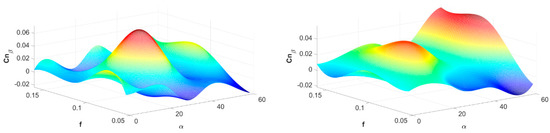
Figure 11.
Results of identifying aerodynamic derivatives: dCn/dβ, Re = 50,000, immobile propeller (Sr = ∞) (left); dCn/dβ, Re = 50,000, rotating propeller (Sr = 2.52) (right).
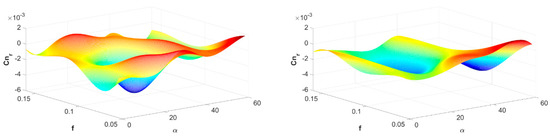
Figure 12.
Results of aerodynamic derivative identification: dCn/dr, Re = 50,000, immobile propeller (Sr = ∞) (left); dCn/dr, Re = 50,000, rotating propeller (Sr = 2.52) (right).
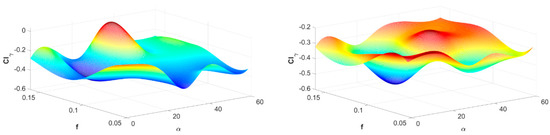
Figure 13.
Results of identifying aerodynamic derivatives dCl/dγ Re = 50,000, immobile propeller (Sr = ∞) (left); dCl/dγ Re = 50,000 rotating propeller (Sr = 2.52) (right).
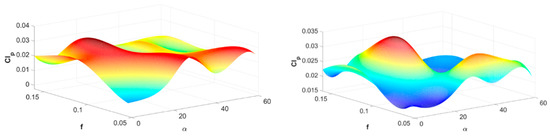
Figure 14.
Results of identifying aerodynamic derivatives dCl/dp Re = 50,000, immobile propeller (Sr = ∞) (left); dCl/dp Re = 50,000, ś rotating propeller (Sr = 2.52) (right).
In an attempt to evaluate the very course of the tests and derivative estimations, first of all, one must mention the significant influence of accurately designing the experiment itself. A properly optimized experiment enables obtaining data necessary to conduct the identification. Whereas, it is important to predict the appropriate duration of the entire measurement cycle. The accuracy of aerodynamic derivative identification utilizing the indicial function depends directly on the quantity of data obtained via the experiment. When evaluating the identification method itself, one can notice that the method developed for high-manoeuvrability combat aircraft can be directly applied in the case of fixed-wing micro-aircraft. Identification accuracy depends on a properly conducted experiment.
Similar to the case of mapping the waveforms of non-stationary measurements, the accuracy of mapping measured characteristics was determined also when identifying with the use of the Indicial function [49]. The graphs above show a summary of mapping accuracy for measurements Cz = f(α) for both Reynolds numbers (Figure 15).
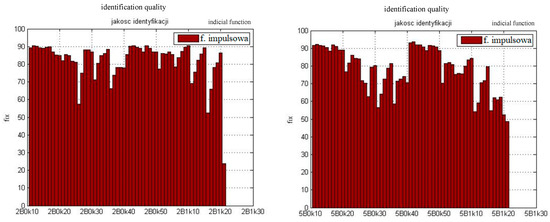
Figure 15.
Depicted accuracy of mapping waveforms of measured non-stationary characteristics for Re = 28,000 (left) and Re = 50,000 (right).
Figure 16, Figure 17, Figure 18 and Figure 19 show sample results of identifying time waveforms of aerodynamic coefficients and the hystereses of these coefficients. These waveforms confirm good identification quality.
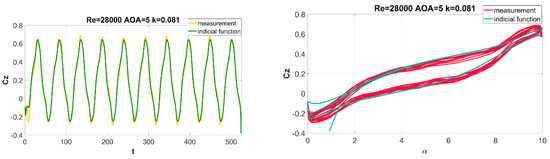
Figure 16.
Summary of identification results obtained with the indicial function for angles of attack in the range of α = (0°, 10°); time waveform of the lift force coefficient (left); and lift force coefficient hysteresis (right).
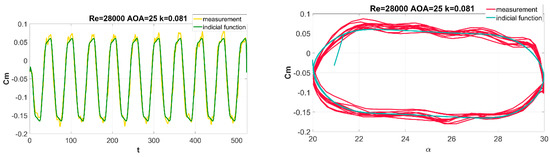
Figure 17.
Summary of identification results obtained with the indicial function for angles of attack in the range of α = (20°, 30°); time waveform of the pitching moment coefficient (left) and pitching moment coefficient hysteresis (right).
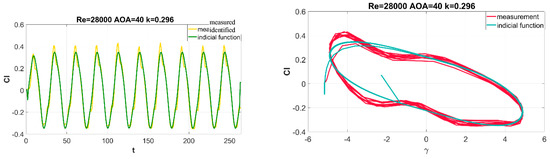
Figure 18.
Summary of identification results obtained with the Indicial function for angles of attack α = 40o and rolling angles in the range of γ = (−5°, 5°); time waveform of the rolling moment coefficient (left) and rolling moment coefficient hysteresis (right).
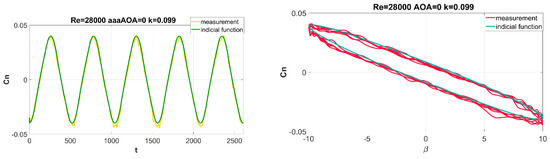
Figure 19.
Summary of identification results obtained with the Indicial function for angles of attack α = 0° and yawing angles in the range of β = (−5°, 5°); time waveform of the yawing moment coefficient (left) and yawing moment coefficient hysteresis (right).
6. Conclusions
The indicial function has been recognized as a tool for identifying the aerodynamic derivatives of aircraft for year [18,36,37,38,39,40,41,50]. The results of the tests discussed in this paper indicated that this method can also be successfully applied for the identification of micro-aircraft aerodynamic derivatives.
When comparing the results of derivative identification with the data from source literature, it can be concluded that the phenomena known from the field of aerodynamics of high angles of attack in fighter aircraft also occur in the case of aerodynamics under low Reynolds numbers. After exceeding a certain angle of attack, usually close to the critical value , the sign of the derivative Cnβ changes. It can be interpreted that for a certain range of angular positions, the yawing moment coefficient, instead of inducing a motion inverse to angular displacement, additionally increases them. Figure 10 shows a change in the yawing moment derivative in the function of the angle of attack and reduced yawing oscillation frequency of the aircraft. It can be observed that certain ranges of the change in the angle of attack and reduced pitching frequency exhibit a change in the waveforms of their derivatives. The conducted tests and identification allowed to prove good static and dynamic stability of the MAV in the pitch plane, which is confirmed by in-flight tests of an actual micro aerial vehicle. The results obtained in the course of micro-aircraft tests for other motion planes indicate that it exhibits stability loss for certain values of angular velocities and positions. The phenomenon of sudden oscillating rolling motions of an aircraft is known in publications as the “wing rock” [50,51]. These motions are often accompanied by oscillations within the yaw plane, which in the case of a micro-aircraft conducting a reconnaissance flight, involving filming of a certain area, can be an undesirable phenomenon. The nature of these vibrations and the susceptibility of a tensometric balance resulted in the need to limit the test cycle in this motion plane due to the fear of damaging the measuring device [47].
The formulation proposed in this article extends well-known aerodynamic theories, which are limited to thin airfoils in incompressible flow, to strake wing planforms. Using results from dynamic water tunnel tests and indicial functions approach allowed to identify fixed wings micro drone aerodynamic derivatives. The test’s program range was set at high angles of attack and a wide scope of reduced frequencies of angular movements. Due to a built-in propeller, the model’s structure test program was repeated for a turned-on propelled drive system. As a result of these studies, unsteady aerodynamics characteristics and aerodynamic derivatives of the micro-aircraft were identified as functions of state parameters. At the Warsaw University of Technology and the Air Force Institute of Technology, a “Bee” fixed wings micro aerial vehicle with an innovative strake-wing outline and a propeller placed in the wing gap was worked. This article is devoted to the problems of identification of aerodynamic derivatives of this micro-aircraft. The result of this research was the identification of the aerodynamic derivatives of the fixed wing MAV “Bee” as non-linear functions of the angle of attack, and reduced frequency. The identification was carried out using the indicial function approach.
Author Contributions
Conceptualization, K.S. and M.N.; methodology K.S. and D.R.; software, A.S.-M.; validation, A.Ż., D.R. and P.S.; formal analysis, K.S. and P.S.; investigation, W.W. and M.G.; resources, D.R. and W.W.; data curation, M.G.; writing—original draft preparation, K.S.; writing—review and editing, K.S. and A.S.-M.; visualization, A.S.-M. and M.G.; supervision, A.Ż. and K.S.; project administration, A.Ż.; funding acquisition, M.N. and A.Ż. All authors have read and agreed to the published version of the manuscript.
Funding
This research was internally funded by the Air Force Institute of Technology and National Centre of Research and Development, Republic of Poland.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdulrahim, M.; Watkins, S.; Segal, R.; Sheridan, J. Dynamic sensitivity to atmospheric turbulence of Fixed-Wing UAV with varying configuration. J. Aircr. 2010, 47, 1873–1883. [Google Scholar] [CrossRef]
- Wróblewski, W.; Sibilski, K.; Garbowski, M.; Żyluk, A. The gust resistant MAV—Aerodynamic measurements, performance analysis, and flight tests (AIAA2015—1684 CP). In Proceedings of the AIAA SciTech Forum and AIAA Atmospheric Flight Mechanics Conference, Kissimmee, Fl, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Galiński, C. Gust resistant fixed wing micro aerial vehicle. J. Aircr. 2006, 43, 1586–1588. [Google Scholar] [CrossRef]
- Panta, A.; Mohamed, A.; Marino, M.; Watkins, S.; Fisher, A. Unconventional control solutions for small fixed wing unmanned aircraft. Prog. Aerosp. Sci. 2018, 2, 122–135. [Google Scholar] [CrossRef]
- Abramov, N.B.; Goman, M.G.; Khrabrov, A.N.; Kolesnikov, E.N.; Fucke, L.; Soemarwoto, B.; Smaili, H. Pushing ahead—SUPRA Airplane Model for Upset Recovery (AIAA 2012-4631 CP). In Proceedings of the AIAA Modelling and Simulation Technologies Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar] [CrossRef]
- Da Ronch, A.; Vallespin, D.; Ghoreyshi, M.; Badcock, K.J. Evaluation of dynamic derivatives using computational fluid dynamics. Aiaa J. 2012, 50, 470–484. [Google Scholar] [CrossRef]
- Harrison, S.; Darragh, R.; Hamlington, P.; Ghoreyshi, M.; Lofthouse, A. Canard-wing interference effects on the flight characteristics of a Transonic Passenger Aircraft (AIAA 2016-4179 CP). In Proceedings of the 34th AIAA Applied Aerodynamics Conference and AIAA AVIATION Forum, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- Sereez, M.; Abramov, N.; Goman, M. Computational ground effect aerodynamics and airplane stability analysis during take-off and landing. In Proceedings of the 7th European Conference for Aeronautics and Aerospace Sciences (EUCASS), Milan, Italy, 3–6 July 2017; Available online: https://www.eucass.eu/doi/EUCASS2017-376.pdf (accessed on 12 July 2020).
- Ghoreyshi, M.; Jirásek, A.; Cummings, R. Computational approximation of nonlinear unsteady aerodynamics and aerodynamic model hierarchy. Aerosp. Sci. Technol. 2013, 28, 133–144. [Google Scholar] [CrossRef]
- Tobak, M. On the Use of the Indicial Function Concept in the Analysis of Unsteady Motions of Wings and Wing-Tail Combinations; NACA Report No. 1188; The National Advisory Committee for Aeronautics: Washington, DC, USA, 1954; Available online: http://naca.central.cranfield.ac.uk/reports/1954/naca-report-1188.pdf (accessed on 12 July 2020).
- Roads, D.; Shuler, J. A theoretical and experimental study of aeroplane dynamics in large disturbance manoeuvres. J. Aeronaut. Sci. 1957, 24, 507–526. [Google Scholar] [CrossRef]
- Mehra, R.K.; Kessel, W.C.; Carroll, J.V. Global Stability and Control Analysis of Aircraft at High Angles of Attack; Report ONR-CR215-248-1; Office of Naval Research: Cambridge, MA, USA, 1977; Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a084921.pdf (accessed on 12 July 2020).
- Orlik-Rückemann, K.J. Aerodynamic aspects of aircraft dynamics at high angles of attack. J. Aircraft. 1983, 20, 737–752. [Google Scholar] [CrossRef]
- Abed, E.H.; Lee, H.C. Nonlinear Stabilization of High Angle-of-Attack Flight Dynamics using Bifurcation Control. In Proceedings of the American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 2235–2238. [Google Scholar] [CrossRef]
- Goman, M.G.; Khrabrov, A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack. J. Aircr. 1994, 31, 1109–1115. [Google Scholar] [CrossRef]
- Goman, M.G.; Stolyarov, G.I.; Tyrtyshnikov, S.L.; Usolcev, S.P.; Khrabrov, A.N. Mathematical Description of Longitudinal Aerodynamic Characteristics at High Angles of Attack Accounting for Dynamic Effects of Separated Flow; TsAGI Preprint No. 9; Central Aerohydrodynamic Institute: Zhukovskiy, Moscow Oblast, Russia, 1990. (In Russian) [Google Scholar]
- Etkin, B.; Reid, L.D. Dynamics of Atmospheric flight, 3rd ed.; John Willey & Sons Inc.: New York, NY, USA, 1996; ISBN 0-471-03418-5. [Google Scholar]
- Murphy, P.C.; Klein, V.; Frink, N.T. Nonlinear Unsteady Aerodynamic Modeling Using Wind-Tunnel and Computational Data. J. Aircr. 2017, 54, 659–683. [Google Scholar] [CrossRef]
- Hancock, G.J. Problems of Aircraft Behaviour at High Angles of Attack; AGARDograph 136; Queen Mary Coll London: London, UK, 1969. [Google Scholar]
- Nguyen, L.T.; Ogburn, M.E.; Gilbert, W.P.; Kibler, K.S.; Brown, P.W.; Deal, P.L. Simulator Study of Stall/Post Stall Characteristics of a Fighter Aeroplane with Relaxed Longitudinal Static Stability; NASA TP-1538; National Aeronautics and Space Administration: Washington, DC, USA, 1979. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19800005879.pdf (accessed on 12 July 2020).
- Young, J.W.; Schy, A.A.; Johnson, K.G. Pseudo Steady—State Analysis of Non-Linear Aircraft Manoeuvres; NASA TP 1758; National Aeronautics and Space Administration: Moffet Field, CA, USA, 1980. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19810004554.pdf (accessed on 12 July 2020).
- Tobak, M.; Chapman, G.T.; Schiff, L. Mathematical Modeling of the Aerodynamic Characteristics in Flight Dynamics; NASA TM 85880; National Aeronautics and Space Administration: Moffet Field, CA, USA, 1984. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19850016895.pdf (accessed on 12 July 2020).
- Hafer, X.; Sachs, G. Flugmechanik Moderne Entwurfst—und Steuerungs Konzepte; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 978-3-642-86730-9. [Google Scholar]
- Brandon, J.M. Dynamic stall effects and applications to high performance aircraft. In Special Course on Aircraft Dynamics at High Angles of Attack: Experiments and Modeling, 2.1–2.15; AGARD Report No. 776; NATO Researc & Technology Organization, The NATO Research and Technology Organisation,: Neuilly sur Seine, France, 1991. [Google Scholar]
- Lin, G.F.; Lan, C.E. A generalized dynamic aerodynamic coefficient model for flight dynamics applications (AIAA 97-3643CP). In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar] [CrossRef]
- McAlister, K.W.; Lambert, O.; Petot, D. Application of the ONERA Model of Dynamic Stall; NASA TP2399/AVSCOM TP84-A-3; National Aeronautics and Space Administration, Moffett Field CA Ames Research Center: Mountain View, CA, USA, 1983; Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19850004554.pdf (accessed on 12 July 2020).
- Beddoes, T.S. Practical computation of the unsteady lift. Vertica 1984, 8, 55–71. [Google Scholar]
- Leishman, J.G. Validation of approximate indicial aerodynamic functions for two-dimensional subsonic flow. J. Aircr. 1988, 25, 914–922. [Google Scholar] [CrossRef]
- Bryan, G.H.; Williams, W.E. The longitudinal stability of gliders. Proc. Roy. Soc. Lond. 1904, 73, 100–116. [Google Scholar] [CrossRef]
- Bairstow, L. Applied Aerodynamics; Longmans, Green and Co.: London, UK, 1929. [Google Scholar]
- Glauert, H. The Force and Moment on an Oscillating Airfoil. In Vorträge aus dem Gebiete der Aerodynamik und verw andter Gebiete; Gilles, A., Hopf, L.V., Kármán, T., Eds.; Springer: Berlin, Heidelberg, 1930. [Google Scholar] [CrossRef]
- Von Karman, T.H.; Sears, W.R. Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 1938, 5, 379–390. [Google Scholar] [CrossRef]
- Zipfel, P.H. Modeling and Simulation of Aerospace Vehicle Dynamics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004; ISBN 978-1-56347-593-1. [Google Scholar]
- Abzug, N.J.; Larrabee, E.E. Airplane Stability and Control: A History of the Technologies that Made Aviation Possible, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005; ISBN 0-521-80992-4. [Google Scholar]
- Pamadi, B.N. Performance, Stability, Dynamics, and Control of Airplanes, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005; ISBN 0-521-80992-4. [Google Scholar]
- Klein, V.; Noderer, K.D. Modeling of Aircraft Unsteady Aerodynamic Characteristics. Part 1—Postulated Models; NASA TM 109120; National Aeronautics and Space Administration: Langley, VA, USA, 1994. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19940028445.pdf (accessed on 12 July 2020).
- Klein, V.; Noderer, K.D. Modeling of Aircraft Unsteady Aerodynamic Characteristics Part 2 – Parameters Estimated from Wind Tunnel Data; NASA TM 110161; National Aeronautics and Space Administration: Langley, VA, USA, 1996. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19950021418.pdf (accessed on 12 July 2020).
- Klein, V.; Murphy, P.C.; Curry, T.J.; Brandon, J.M. Analysis of Wind Tunnel Longitudinal Static and Oscillatory Data of the F-16XL Aircraft; NASA TM-97-206276; National Aeronautics and Space Administration: Washington, DC, USA, 1997. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19980007406.pdf (accessed on 12 July 2020).
- Klein, V.; Murphy, P.C.; Szyba, N.M. Analysis of Wind Tunnel Lateral Oscillatory Data of the F-16XL Aircraft; NASA TM-2004-213246; National Aeronautics and Space Administration: Washington, DC, USA, 2004. Available online: https://ntrs.nasa.gov/search.jsp?R=20040110955 (accessed on 12 July 2020).
- Murphy, P.C.; Klein, V. Estimation of aircraft unsteady aerodynamic parameters from dynamic wind tunnel testing (AIAA 2001-4016 CP). In Proceedings of the AIAA Atmospheric Flight Mechanics Conference & Exhibit, Montreal, Canada, 6–9 August 2001. [Google Scholar] [CrossRef][Green Version]
- Murphy, P.C.; Klein, V.; Szyba, N.M. Progressive aerodynamic model identification from dynamic water tunnel test of the F-16XL Aircraft (AIAA 2004-5277 CP). In Proceedings of the AIAA Atmospheric Flight Mechanics Conference & Exhibit, Providence, Rhode Island, 16–19 August 2004. [Google Scholar] [CrossRef][Green Version]
- Reisenthel, P.H. Development of a nonlinear indicial model for maneuvering fighter aircraft (AIAA 96-0896CP). In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996. [Google Scholar] [CrossRef]
- Ogata, K. State Space Analysis of Control Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1967. [Google Scholar]
- Lichota, P.; Szulczyk, J.; Noreña, D.A.; Vallejo Monsalve, F.A. Power spectrum optimization in the design of multisine manoeuvre for identification purposes. J. Appl. Mech. 2017, 55, 1193–1203. [Google Scholar] [CrossRef]
- Kerho, M.; Kramer, B.R. Research Water Tunnels—Specification; Rolling Hills Research Corporation (RHRC): El Segundo, CA, USA, 2003. [Google Scholar]
- Kerho, M.; Kramer, B.R. Five-Component Balance and Computer-Controlled Model Support System for Water Tunnel Applications; Rolling Hills Research Corporation (RHRC): El Segundo, CA, USA, 2009. [Google Scholar]
- Kerho, M.; Kramer, B.R. Ultrasonic Flowmeter and Temperature Probe; Rolling Hills Research Corporation (RHRC): El Segundo, CA, USA, 2010. [Google Scholar]
- Garbowski, M. Identification of Non-stationary Aerodynamic Characteristics of a Micro Aircraft in the Range Low Reynolds Numbers. Ph.D. Thesis, Department of Mechanics and Power Engineering, Wroclaw University of Technology, PRE, Wroclaw, Poland, 2014. [Google Scholar]
- Morelli, E.A.; Klein, V. Accuracy of aerodynamic model parameters estimated from flight test data. J. Guid. Control Dyn. 1997, 20, 74–80. [Google Scholar] [CrossRef]
- Ericsson, L.E. The fluid mechanics of slender wing rock. J. Aircr. 1984, 21, 322–328. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Lan, C.E. Theory of Wing Rock; NASA CR-176640; National Aeronautics and Space Administration: Hampton, VA, USA, 1984. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19860012049.pdf (accessed on 12 July 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).