3D Cruise Trajectory Optimization Inspired by a Shortest Path Algorithm
Abstract
1. Introduction
2. Aircraft, Search Space, Fuel Burn, and Weather Models
2.1. Aircraft Model
2.2. Weather Model
- Identify the four GDPS’s grid points surrounding the aircraft during the flight performance computation. In other words, not only at the waypoints;
- Determine the pressure altitude for the current aircraft’s flight level;
- Identify the immediate higher and lower pressures from the aircraft’s flight level from the GDPS forecast. For example, at 35,000 ft, the pressure is 230 hPa, and so the lower and higher available pressures would be 225 hPa and 250 hPa, respectively;
- Using the GDPS forecast, identify the immediate higher and lower time blocks from the current time. (For example, if the current time is 14 h 35 m, the lower and higher time blocks would be 12 h and 15 h, respectively, thus interpolations are executed for 14 h 35 m with these two limits.);
- Perform temporal linear Lagrange interpolations for the lower and higher pressure altitudes for the 4 points surrounding the aircraft, as shown in Figure 1a;
- Perform linear Lagrange interpolations in pressure levels (flight level) for the 4 points surrounding the aircraft, as indicated in Figure 1 and Figure 2 After executing these interpolations, the weather is known for the exact pressure altitude at the current time for the 4 points surrounding the aircraft; and
2.3. Search Space
2.4. Fuel Burn Model
2.4.1. Fuel Burn Model in the Cruise Phase
2.4.2. Fuel Burn Model for Climb and Descent during Cruise
- The Flight Time for a given horizontal distance is computed using the GS. This horizontal distance, although it changes depending on the distance between two waypoints, is generally around 25 NM.
- The ROCD is computed using Equation (16).
- The current altitude is computed with Equation (17).
- If the resulting Altitude (iteration) is equal to or higher than the targeted altitude, the algorithm computes the fuel burn as in the cruise phase (Section 2.4.1). Otherwise, the next distance is selected, and the procedure continues again at step 1.
2.5. Flight Cost Model
3. The Optimization Algorithm
3.1. The Floyd–Warshall Algorithm
3.2. The Floyd–Warshall (FW) Algorithm for the 3D Reference Trajectory
3.3. Special Considerations for the Trajectories on the Algorithm: The Path System
3.4. The 3D Optimization Algorithm Pseudo-Code
4. Results
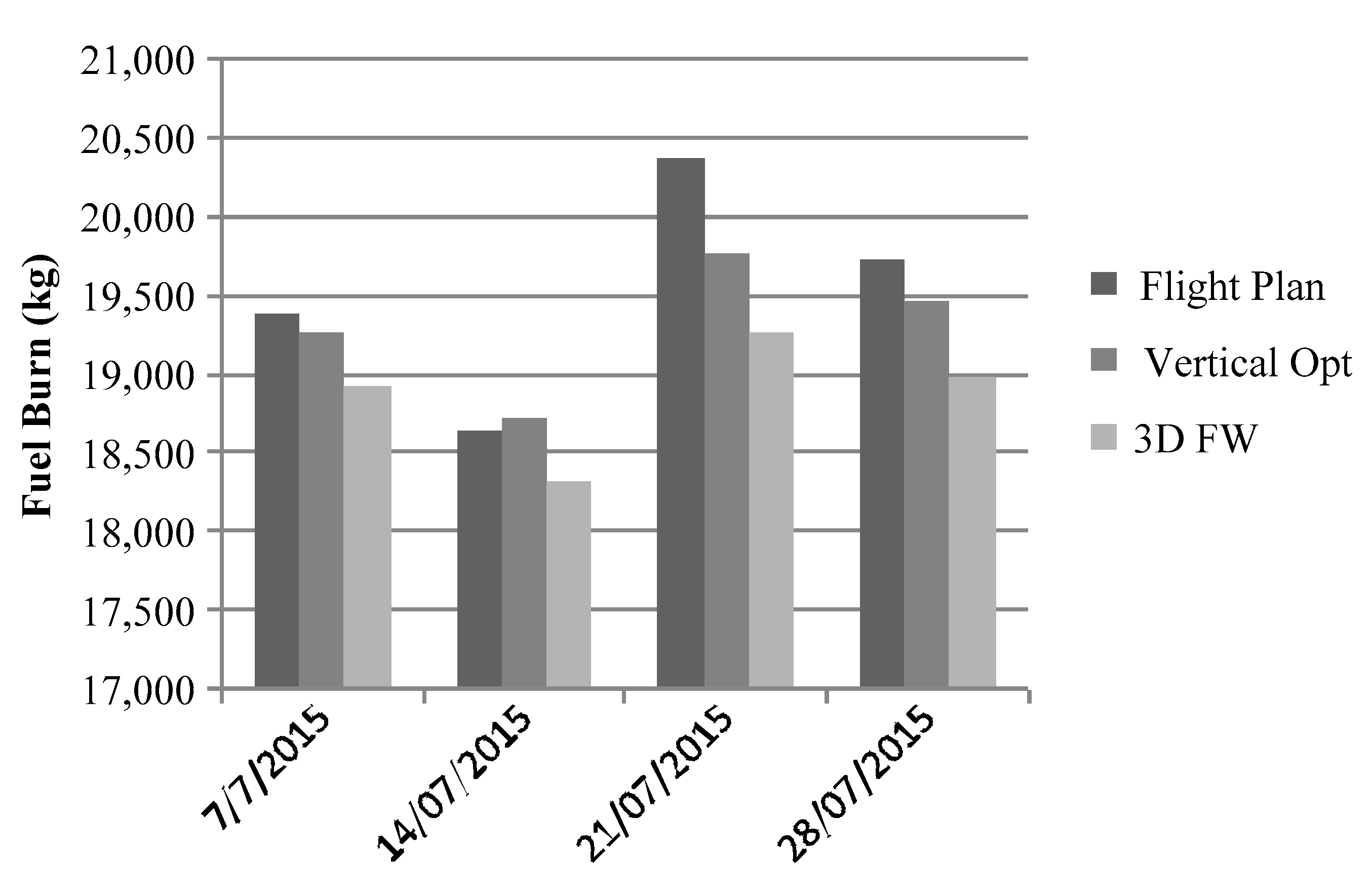
4.1. Flight Optimization from Airlines Computed Flight Plans
4.2. Flight Optimization from Airlines Computed Flight Plans
4.3. Flight Optimization for as-Flown Flights
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ATAG. Aviation Benefits Beyond Borders; Air Transport Action Group: Geneva, Switzerland, 2016; p. 80. [Google Scholar]
- Williams, P.D. Transatlantic flight times and climate change. Environ. Res. Lett. 2016, 11, 024008. [Google Scholar] [CrossRef]
- ICAO. Aviation’s Contribution to Climate Change; International Civil Aviation Organization: Montreal, QC, Canada, 2010; p. 260. [Google Scholar]
- McConnachie, D.; Wollersheim, C.; Hansman, R.J. The impact of fuel price on airline fuel efficiency and operations. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar]
- Clarke, J.P.; Brooks, J.; Nagle, G.; Scacchioli, A.; White, W.; Liu, S.R. Optimized profile descent arrivals at los angeles international airport. J. Aircr. 2013, 50, 360–369. [Google Scholar] [CrossRef]
- Kwok-On, T.; Anthony, W.; John, B. Continuous descent approach procedure development for noise abatement tests at louisville international airport, KY. In Proceedings of the AIAA’s 3rd Annual Aviation Technology, Integration, and Operations (ATIO) Forum, Denver, CO, USA, 17–19 November 2003. [Google Scholar]
- Johnson, C.M. Analysis of top of descent (tod) uncertainty. In Proceedings of the 2011 IEEE/AIAA 30th Digital Avionics Systems Conference (DASC), Seattle, WA, USA, 16–20 October 2011; pp. 2E3-1–2E3-10. [Google Scholar]
- Stell, L. Predictability of top of descent location for operational idle-thrust descents. In Proceedings of the 10th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Murrieta-Mendoza, A.; Botez, R.M.; Ford, S. New method to compute the missed approach fuel consumption and its emissions. Aeronaut. J. 2016, 120, 18. [Google Scholar]
- Dancila, R.; Botez, R.M.; Ford, S. Fuel burn and emissions evaluation for a missed approach procedure performed by a b737-400. Aeronaut. J. 2014, 118, 20. [Google Scholar] [CrossRef]
- Samà, M.; D’Ariano, A.; Corman, F.; Pacciarelli, D. Metaheuristics for efficient aircraft scheduling and re-routing at busy terminal control areas. Transp. Res. Part C Emerg. Technol. 2017, 80, 485–511. [Google Scholar] [CrossRef]
- Fisch, F.; Bittner, M.; Holzapfel, F. Optimal scheduling of fuel-minimal approach trajectories. J. Aerosp. Oper. 2013, 2, 145–160. [Google Scholar] [CrossRef]
- Samà, M.; D’Ariano, A.; Palagachev, K.; Gerdts, M. Integration methods for aircraft scheduling and trajectory optimization at a busy terminal manoeuvring area. OR Spectr. 2019, 41, 641–681. [Google Scholar] [CrossRef]
- Boeing. Improving Efficiency with Rnp and Gls; Boeing: Chigago, IL, USA, 2016. [Google Scholar]
- Marasa, J. RNP is revolutionizing the instrument approach. In Wings; Wings Magazine: Simcoe, ON, Canada, 2010. [Google Scholar]
- Lovegren, J.A. Estimation of Potential Aircraft Fuel Burn Reduction in Cruise Via Speed and Altitude Optimization Strategies; Massachusetts Institute of Technology: Cambridge, MA, USA, 2011. [Google Scholar]
- Jensen, L.; Tran, H.; Hansman, J.R. Cruise fuel reduction potential from altitude and speed optimization in global airline operations. In Eleventh USA/Europe Air Traffic Management Research and Development Seminar (ATM2015); ATM Seminar: Lisbon, Portugal, 2015. [Google Scholar]
- Jensen, L.; Hansman, J.R.; Venuti, J.; Reynolds, T. Commercial airline altitude optimization strategies for reduced cruise fuel consumption. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Jensen, L.; Hansman, J.R.; Venuti, J.C.; Reynolds, T. Commercial airline speed optimization strategies for reduced cruise fuel consumption. In Proceedings of the 2013 AIAA Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar]
- Turgut, E.T.; Cavcar, M.; Usanmaz, O.; Canarslanlar, A.O.; Dogeroglu, T.; Armutlu, K.; Yay, O.D. Fuel flow analysis for the cruise phase of commercial aircraft on domestic routes. Aerosp. Sci. Technol. 2014, 37, 1–9. [Google Scholar] [CrossRef]
- Franco, A.; Rivas, D. Minimum-cost cruise at constant altitude of commercial aircraft including wind effects. J. Guid. Control Dyn. 2011, 34, 1253–1260. [Google Scholar] [CrossRef]
- Sridhar, B.; Ng, H.; Chen, N. Aircraft trajectory optimization and contrails avoidance in the presence of winds. J. Guid. Control Dyn. 2011, 34, 1577–1584. [Google Scholar] [CrossRef]
- Rosenow, J.; Fricke, H. Individual condensation trails in aircraft trajectory optimization. Sustainability 2019, 11, 6082. [Google Scholar] [CrossRef]
- Campbell, S.E.; Bragg, M.B.; Neogi, N.A. Fuel-optimal trajectory generation for persistent contrail mitigation. J. Guid. Control Dyn. 2013, 36, 1741–1750. [Google Scholar] [CrossRef]
- Rosenow, J.; Lindner, M.; Fricke, H. Impact of climate costs on airline network and trajectory optimization: A parametric study. CEAS Aeronaut. J. 2017, 8, 14. [Google Scholar] [CrossRef]
- Dancila, B.; Botez, R.; Labour, D. Altitude optimization algorithm for cruise, constant speed and level flight segments. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Félix-Patrón, R.S.; Botez, R.M.; Labour, D. New altitude optimisation algorithm for the flight management system cma-9000 improvement on the a310 and l-1011 aircraft. Aeronaut. J. 2013, 117, 787–805. [Google Scholar] [CrossRef]
- Miyazawa, Y.; Wickramasinghe, N.K.; Harada, A.; Miyamoto, Y. Dynamic programming application to airliner four dimensional optimal flight trajectory. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Hagelauer, P.; Mora-Camino, F. A soft dynamic programming approach for on-line aircraft 4d-trajectory optimization. Eur. J. Oper. Res. 1998, 107, 87–95. [Google Scholar] [CrossRef]
- Bonami, P.; Olivares, A.; Soler, M.; Staffetti, E. Multiphase mixed-integer optimal control approach to aircraft trajectory optimization. J. Guid. Control Dyn. 2014, 36, 1267–1277. [Google Scholar] [CrossRef]
- Valenzuela, A.; Rivas, D. Optimization of aircraft cruise procedures using discrete trajectory patterns. J. Aircr. 2014, 51, 1632–1640. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Botez, R.M. Lateral navigation optimization considering winds and temperatures for fixed altitude cruise using the dijkstra’s algorithm. In Proceedings of the International Mechanical Engineering Congress & Exposition, Montreal, QC, Canada, 8–13 November 2014. [Google Scholar]
- Murrieta Mendoza, A.; Mugnier, P.; Botez, R.M. Vertical and horizontal flight reference trajectory optimization for a commercial aircraft. In Proceedings of the Sci-Tech 2017 AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Félix-Patrón, R.S.; Kessaci, A.; Botez, R. Horizontal flight trajectories optimisation for commercial aircraft through a flight management system. Aeronaut. J. 2014, 118, 20. [Google Scholar]
- Murrieta-Mendoza, A.; Botez, R.M. Methodology for vertical-navigation flight-trajectory cost calculation using a performance database. J. Aerosp. Inf. Syst. 2015, 12, 519–532. [Google Scholar] [CrossRef]
- Ng, H.K.; Sridhar, B.; Grabbe, S. Optimizing aircraft trajectories with multiple cruise altitudes in the presence of winds. J. Aerosp. Inf. Syst. 2014, 11, 35–47. [Google Scholar] [CrossRef]
- Félix-Patrón, R.S.; Botez, R.M. Flight trajectory optimization through genetic algorithms coupling vertical and lateral profiles. In Proceedings of the International Mechanical Engineering Congress & Exposition, Montreal, QC, Canada, 8–13 November 2014. [Google Scholar]
- Félix-Patrón, R.S.; Botez, R.M. Flight trajectory optimization through genetic algorithms for lateral and vertical integrated navigation. J. Aerosp. Inf. Syst. 2015, 12, 533–544. [Google Scholar]
- Franco, A.; Rivas, D. Optimization of multiphase aircraft trajectories using hybrid optimal control. J. Guid. Control Dyn. 2015, 38, 452–467. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Beuze, B.; Ternisien, L.; Botez, R.M. New reference trajectory optimization algorithm for a flight management system inspired in beam search. Chin. J. Aeronaut. 2017, 30, 1459–1472. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Botez, R.M. Aircraft vertical route optimization deterministic algorithm for a flight management system. In Proceedings of the SAE 2015 AeroTech Congress & Exhibition, Seattle, WA, USA, 22–24 September 2015; SAE Technical Paper 2015-01-2541. SAE International: Seattle, WA, USA, 2015; p. 13. [Google Scholar]
- Filippone, A. On the benefits of lower mach number aircraft cruise. Aeronaut. J. 2007, 111, 531–542. [Google Scholar] [CrossRef]
- Murrieta-Mendoza, A.; Hamy, A.; Botez, R.M. Mach number selection for cruise phase using the ant colony optimization algorithm with rta constrains. In Proceedings of the International Conference on Air Transport, Amsterdam, The Netherlands, 22–23 June 2015. [Google Scholar]
- Murrieta-Mendoza, A.; Bunel, A.; Botez, R.M. Aircraft vertical reference trajectory optimization with a rta constraint using the abc algorithm. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Murrieta-Mendoza, A.; Ruiz, H.; Kessaci, S.; Botez, R.M. 3D reference trajectory optimization using particle swarm optimization. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Villarroel, J.; Rodrigues, L. Optimal control framework for cruise economy mode of flight management systems. J. Guid. Control Dyn. 2016, 39, 1022–1033. [Google Scholar] [CrossRef]
- Rosenow, J.; Strunck, D.; Fricke, H. Trajectory optimization in daily operations. CEAS Aeronaut. J. 2019, 1–11. [Google Scholar] [CrossRef]
- EUROCONTROL. User Manual for the Base of Aircraft Data (Bada)—Family 4; Version 1.2.; EEC Technical Report No. 12/11/22-58; EUROCONTROL: Bruxelles, Belgium, 2014. [Google Scholar]
- Bronsvoort, J. Contributions to Trajectory Prediction Theory and Its Application to Arrival Management for Air Traffic Control. Ph.D. Thesis, Universidad Politecnica de Madrid, Madrid, Spain, 2014. [Google Scholar]
- Vincenty, T. Direct and inverse solutions of geodesics on the ellispoid with application of nested equations. Surv. Rev. 1975, 23, 88–93. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 5. [Google Scholar] [CrossRef]
- Warshall, S. A theorem on boolean matrices. J. ACM 1962, 9, 2. [Google Scholar] [CrossRef]












| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | S1,2 | S1,3 | S1,4 | S1,5 | S1,6 | S1,7 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| 2 | S2,8 | S2,9 | S2,11 | S2,12 | S2,14 | S2,15 | |||||||||
| 3 | S3,9 | S3,10 | S3,12 | S3,13 | S3,15 | ||||||||||
| 4 | S4,11 | S4,12 | S4,14 | S4,15 | |||||||||||
| 5 | S5,12 | S5,13 | S5,15 | ||||||||||||
| 6 | S6,14 | S6,15 | |||||||||||||
| 7 | S7,15 | ||||||||||||||
| … | |||||||||||||||
| 15 |
| Index | Value | Index | Value | Index | Value |
|---|---|---|---|---|---|
| 1 | S1,2 | 13 | S3,10 | 25 | S1,14(∞) |
| 2 | S1,3 | 14 | S1,11(∞) | 26 | S2,14 |
| 3 | S1,4 | 15 | S2,11 | 27 | S4,14 |
| 4 | S1,5 | 16 | S4,11 | 28 | S6,14 |
| 5 | S1,6 | 17 | S1,12(∞) | 29 | S1,15(∞) |
| 6 | S1,7 | 18 | S2,12 | 30 | S2,15 |
| 7 | S1,8 (∞) | 19 | S3,12 | 31 | S3,15 |
| 8 | S2,8 | 20 | S4,12 | 32 | S4,15 |
| 9 | S1,9(∞) | 21 | S5,12 | 33 | S5,15 |
| 10 | S2,9 | 22 | S1,13(∞) | 34 | S6,15 |
| 11 | S3,9 | 23 | S3,13 | 35 | S7,15 |
| 12 | S1,10(∞) | 24 | S5,13 |
| IATA Code | City |
|---|---|
| AMS | Amsterdam |
| BOD | Bordeaux |
| CDG | Paris |
| FCO | Rome |
| GLA | Glasgow |
| LHR | London |
| LIS | Lisbon |
| MAN | Manchester |
| MRS | Marseille |
| TLS | Toulouse |
| VCE | Venice |
| YUL | Montreal |
| YYZ | Toronto |
| # | Flight | Real Flight Fuel Burn (kg) | 3D Flight Fuel Burn (kg) | Fuel Burn Difference (kg) |
|---|---|---|---|---|
| 1 | YUL-BOD | 23,857 | 23,156 | 700 (2.94%) |
| 2 | YUL-FCO | 26,756 | 25,798 | 959 (3.58%) |
| 3 | TLS-YUL | 27,610 | 26,061 | 1550 (5.61%) |
| 4 | MRS-YUL | 29,568 | 27,691 | 1877 (6.35%) |
| 5 | LIS-YYZ | 27,923 | 25,906 | 2017 (7.22%) |
| 7 | CDG-YYZ | 28,695 | 26,913 | 1782 (6.20%) |
| 8 | YYZ-LIS | 23,471 | 23,002 | 468 (1.99%) |
| 9 | YYZ-MAN | 21,763 | 20,921 | 842 (3.86%) |
| 10 | YYZ-GLA | 22,261 | 21,550 | 712 (3.20%) |
| 11 | YYZ-AMS | 25,774 | 24,663 | 1110 (4.31%) |
| 12 | YUL-VCE | 25,961 | 25,043 | 918 (3.54%) |
| # | Flight | Real Flight Time (sec) | 3D Flight Time (sec) | Flight Time Difference (sec) |
|---|---|---|---|---|
| 1 | YUL-BOD | 20,793 | 20,679 | 114 (0.55%) |
| 2 | YUL-FCO | 23,240 | 23,181 | 59 (0.25%) |
| 3 | TLS-YUL | 24,066 | 23,522 | 544 (2.26%) |
| 4 | MRS-YUL | 25,760 | 25,172 | 588 (2.28%) |
| 5 | LIS-YYZ | 23,992 | 23,534 | 458 (1.91%) |
| 6 | CDG-YYZ | 24,778 | 24,104 | 674 (2.72%) |
| 7 | YYZ-LIS | 21,084 | 20,727 | 357 (1.69%) |
| 8 | YYZ-MAN | 18,622 | 18,321 | 301 (1.62%) |
| 9 | YYZ-GLA | 19,361 | 19,070 | 291 (1.50%) |
| 10 | YYZ-AMS | 22,476 | 22,162 | 314 (1.40%) |
| 11 | YUL-VCE | 22,814 | 22,637 | 177 (0.78%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murrieta-Mendoza, A.; Romain, C.; Botez, R.M. 3D Cruise Trajectory Optimization Inspired by a Shortest Path Algorithm. Aerospace 2020, 7, 99. https://doi.org/10.3390/aerospace7070099
Murrieta-Mendoza A, Romain C, Botez RM. 3D Cruise Trajectory Optimization Inspired by a Shortest Path Algorithm. Aerospace. 2020; 7(7):99. https://doi.org/10.3390/aerospace7070099
Chicago/Turabian StyleMurrieta-Mendoza, Alejandro, Charles Romain, and Ruxandra Mihaela Botez. 2020. "3D Cruise Trajectory Optimization Inspired by a Shortest Path Algorithm" Aerospace 7, no. 7: 99. https://doi.org/10.3390/aerospace7070099
APA StyleMurrieta-Mendoza, A., Romain, C., & Botez, R. M. (2020). 3D Cruise Trajectory Optimization Inspired by a Shortest Path Algorithm. Aerospace, 7(7), 99. https://doi.org/10.3390/aerospace7070099





