Computational Evaluation of Aerodynamic Loading on Retractable Landing-Gears
Abstract
1. Introduction
2. Computational Modeling
2.1. Methodology
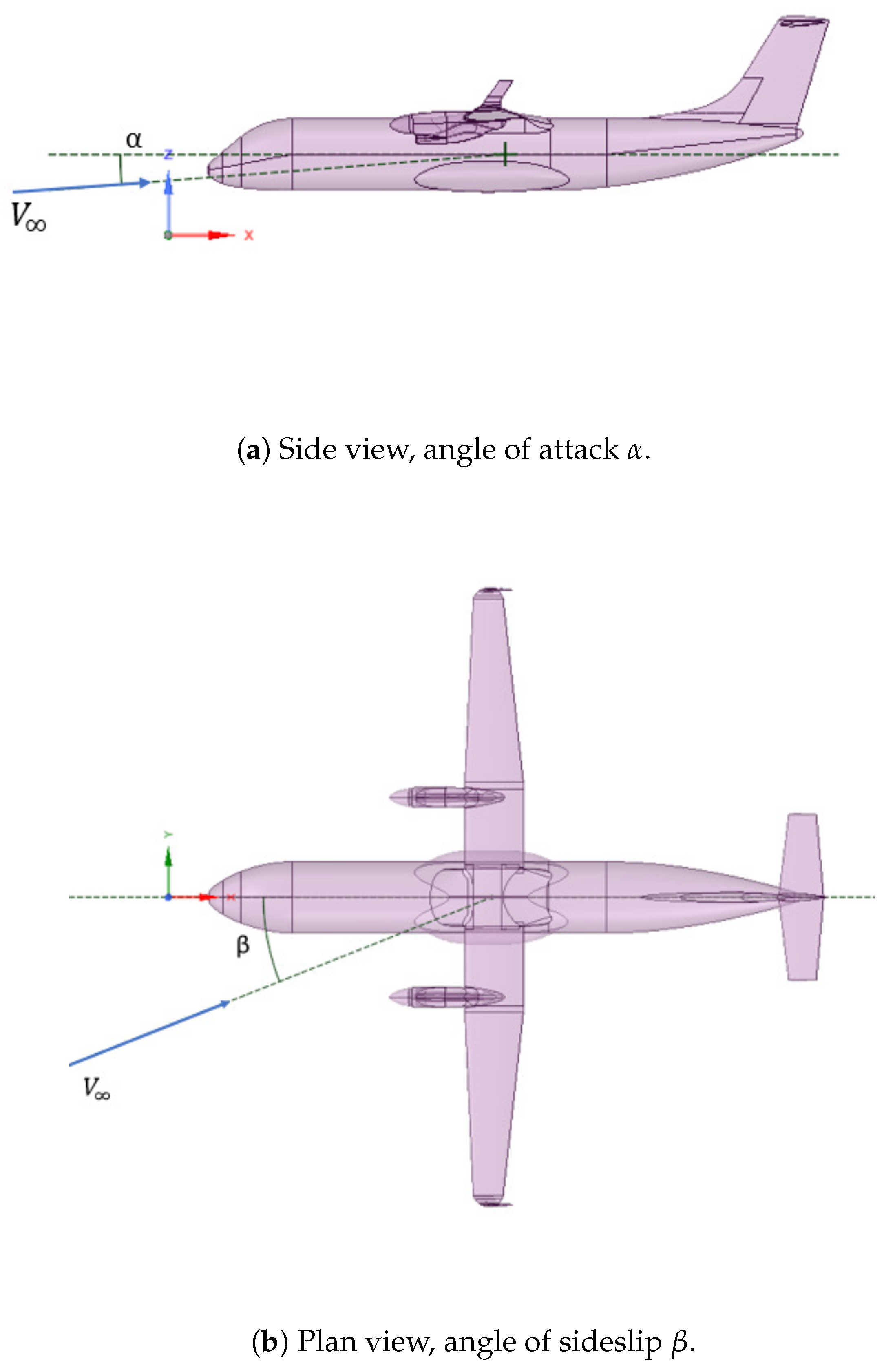
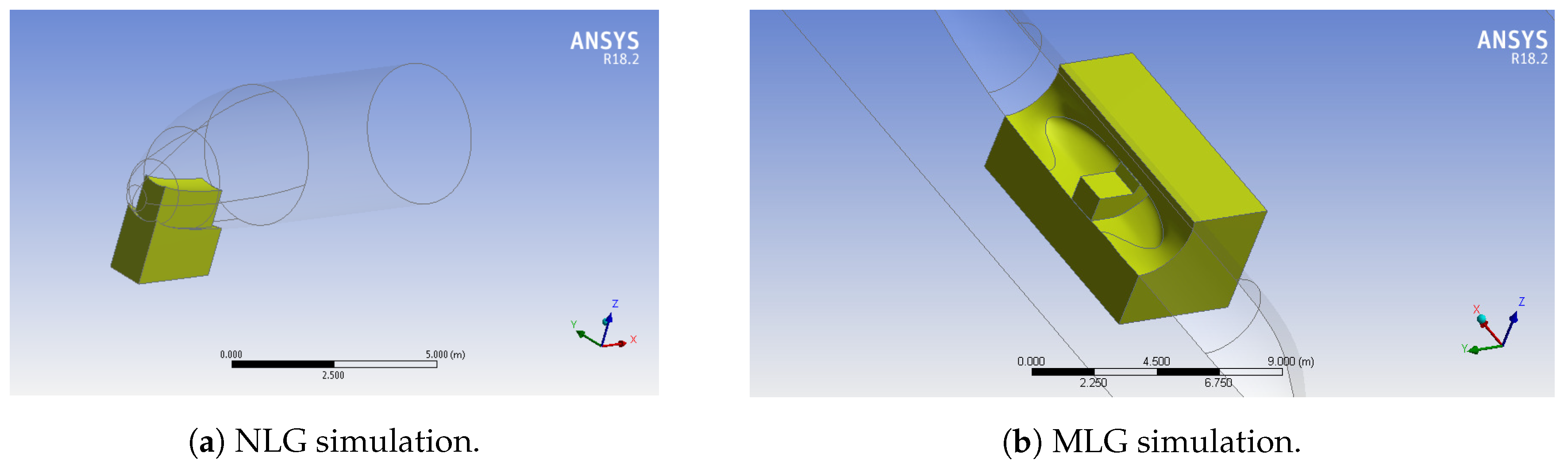
2.2. Geometric Models
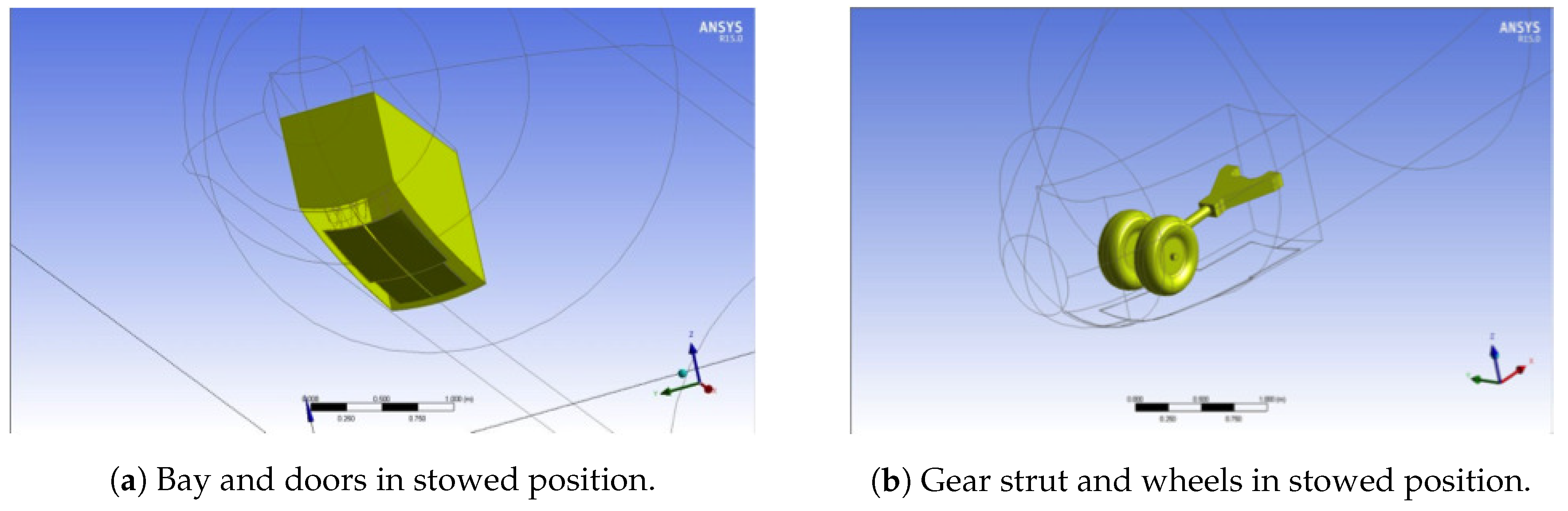
2.2.1. NLG Geometry
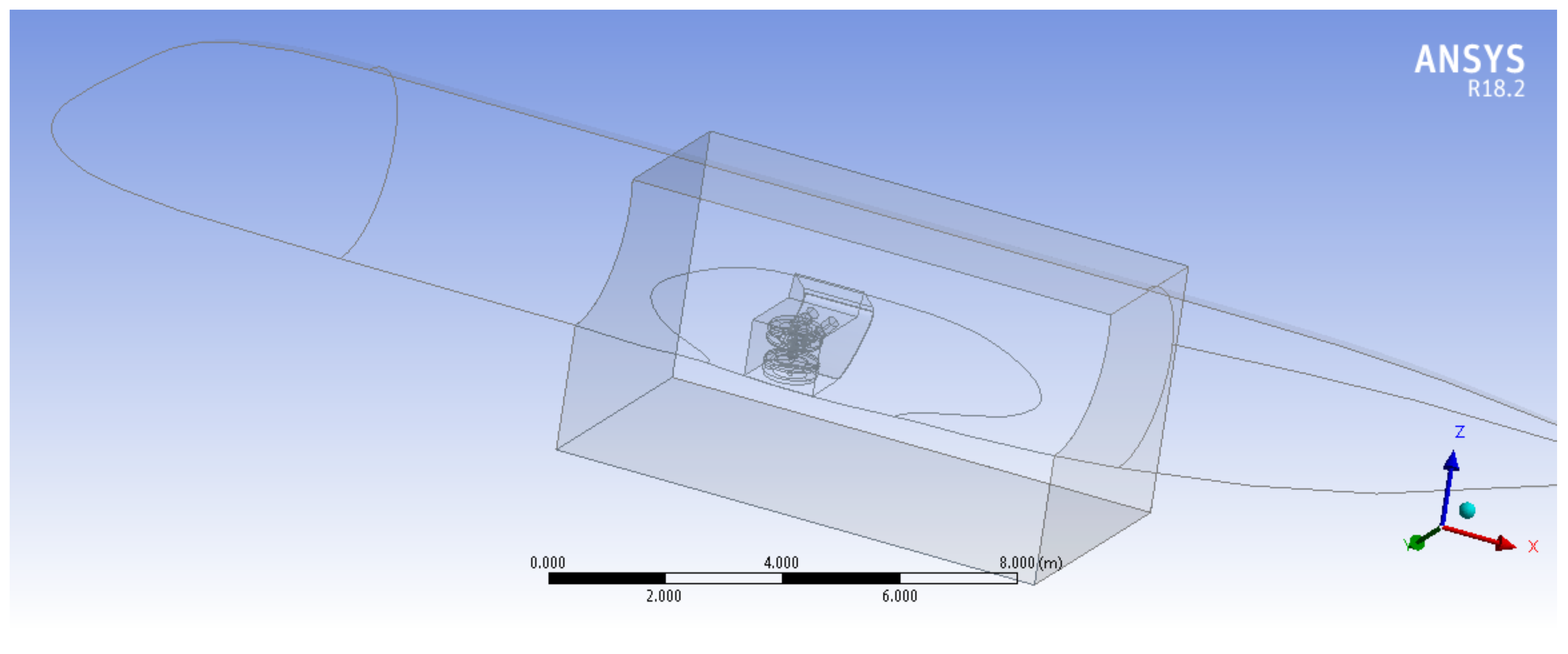
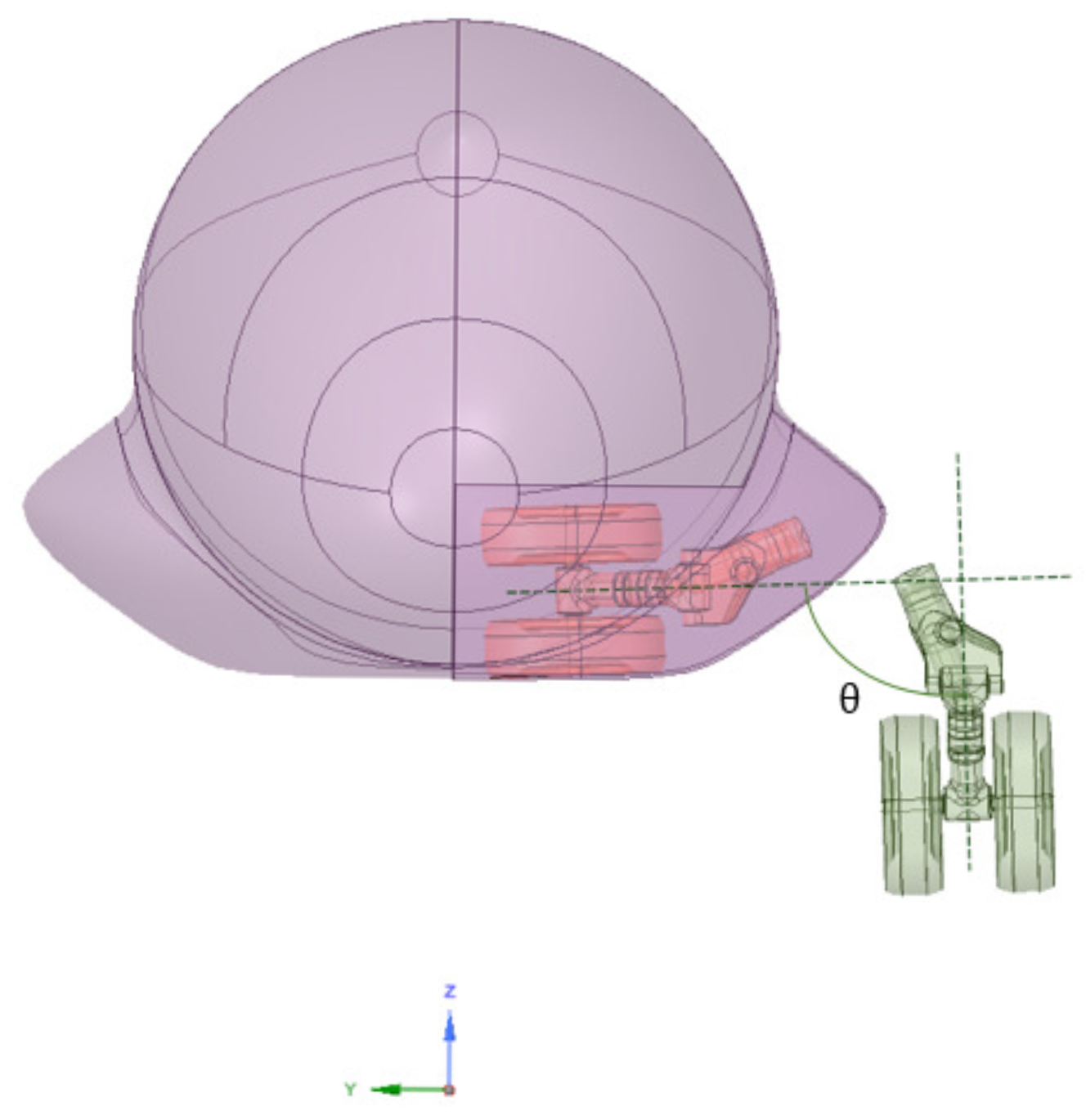
2.2.2. MLG Geometry
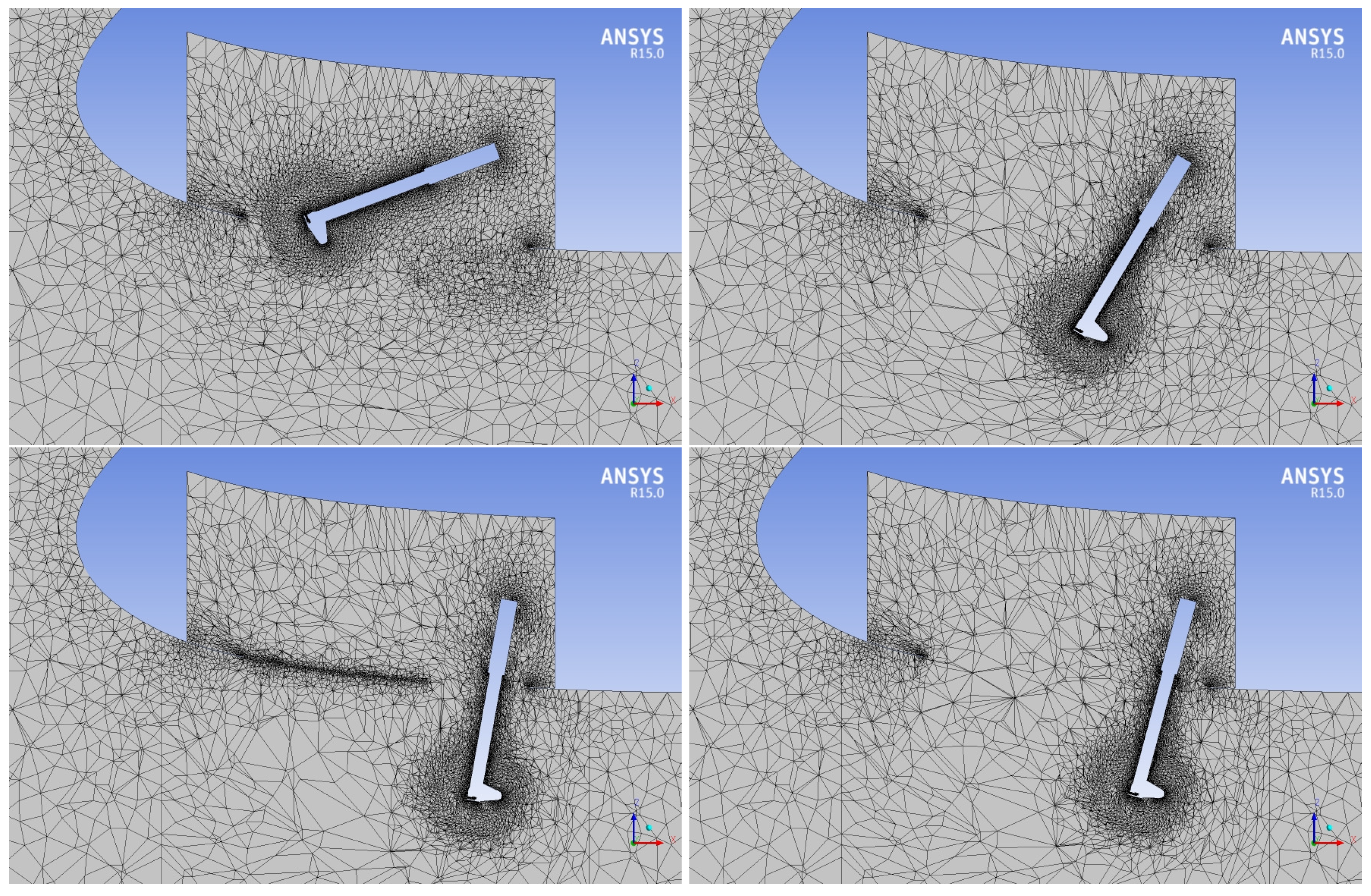
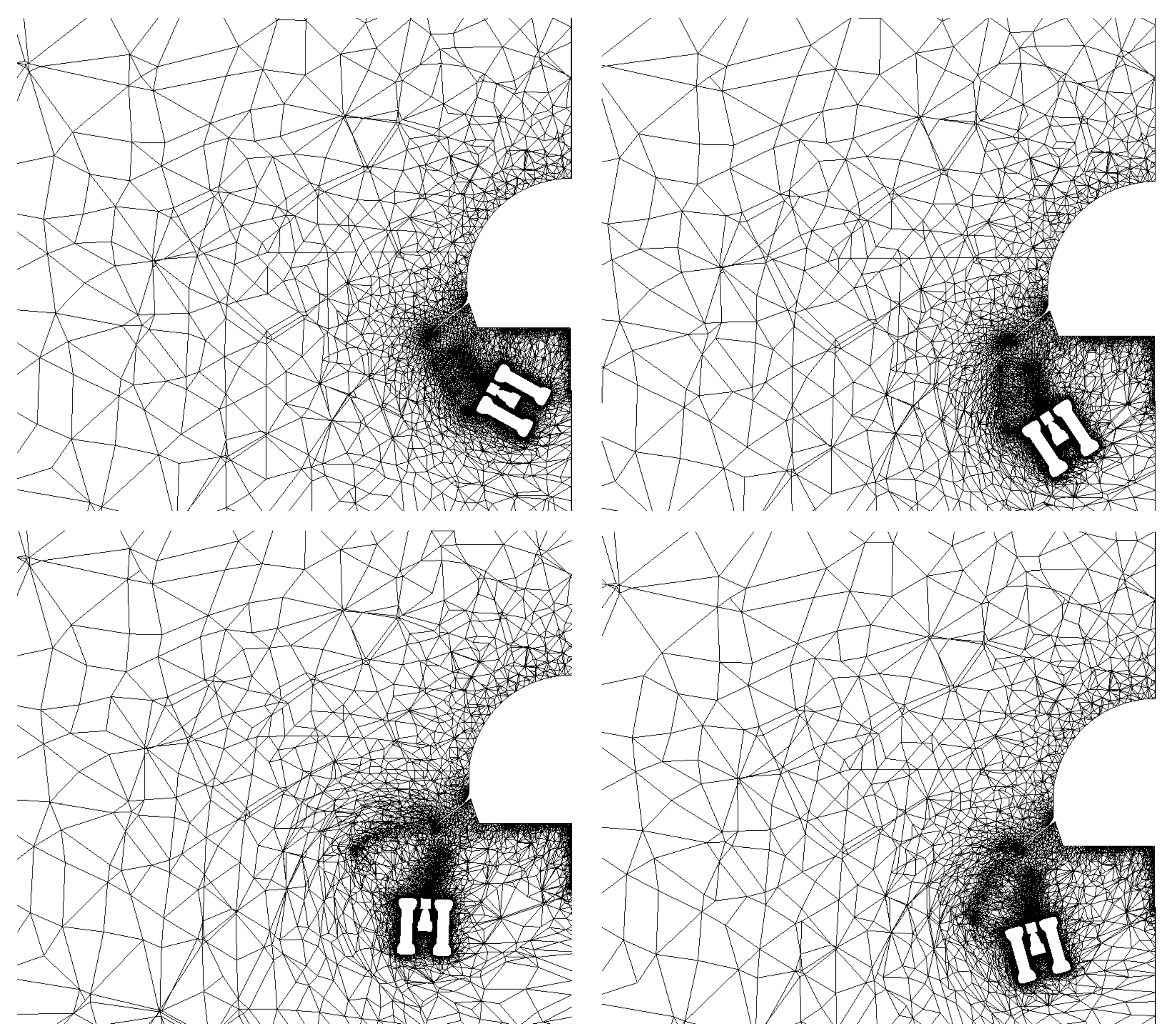
2.3. Dynamic Meshing
2.4. Turbulence Modeling
3. Results and Discussion
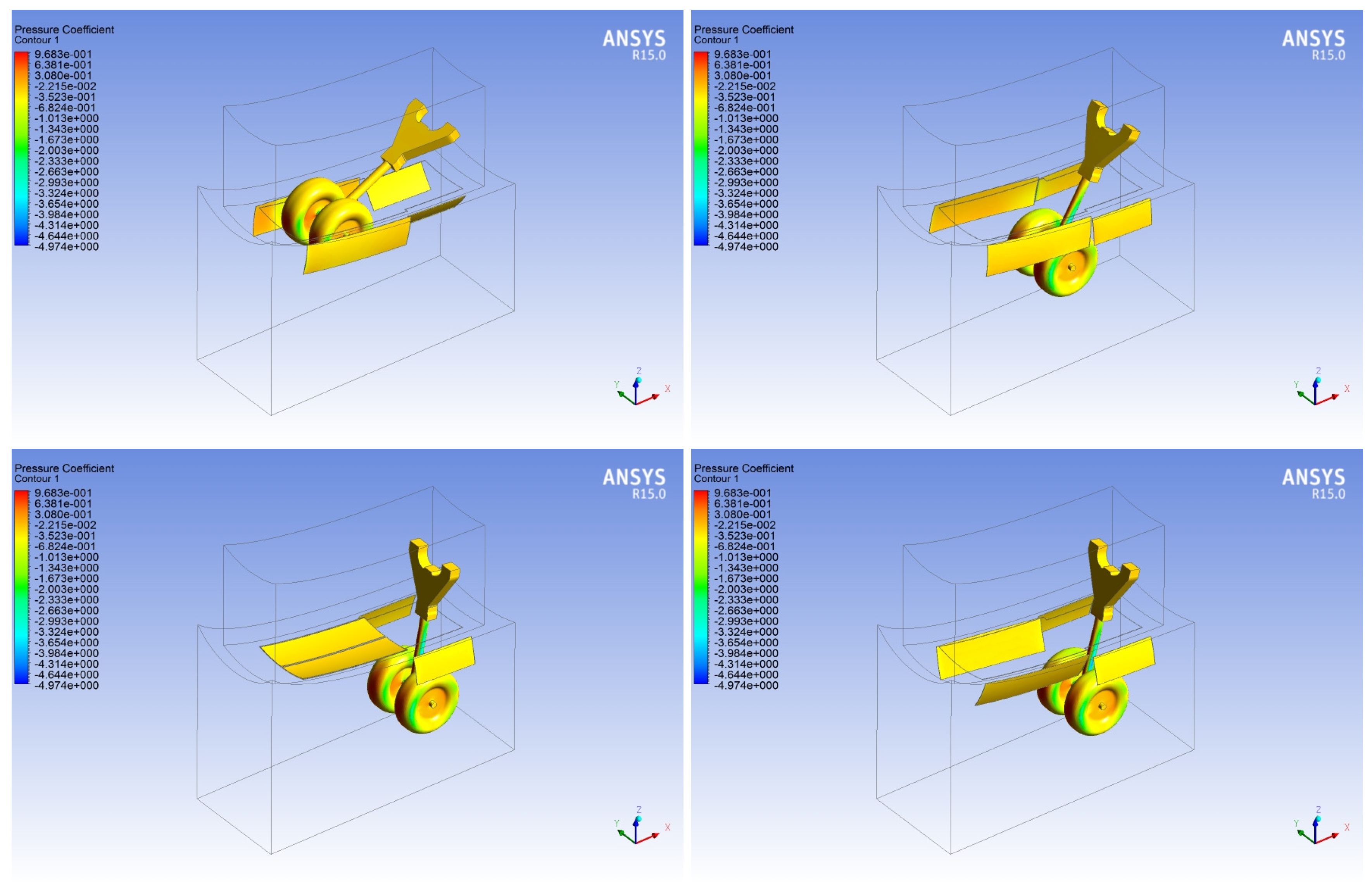
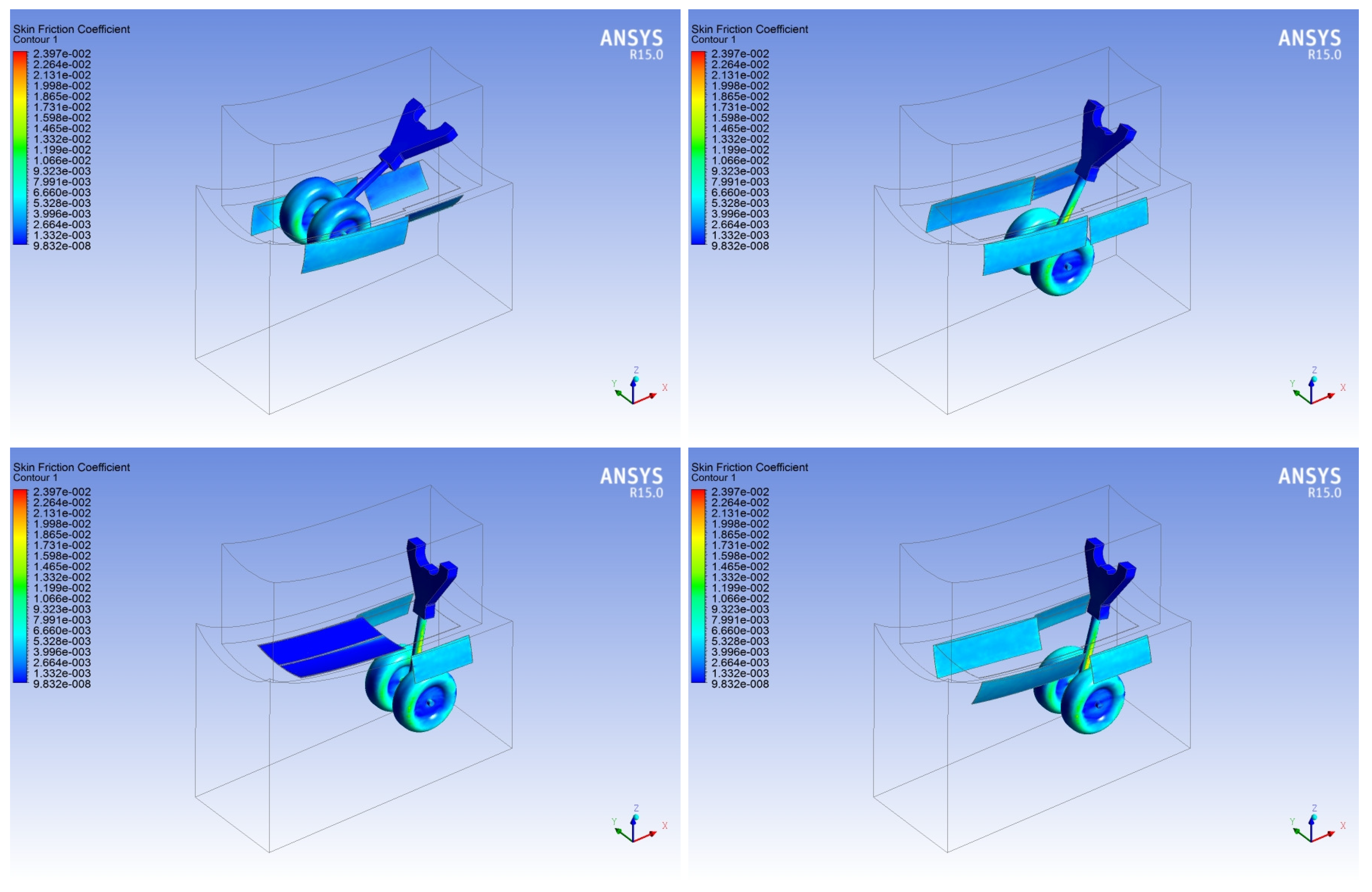
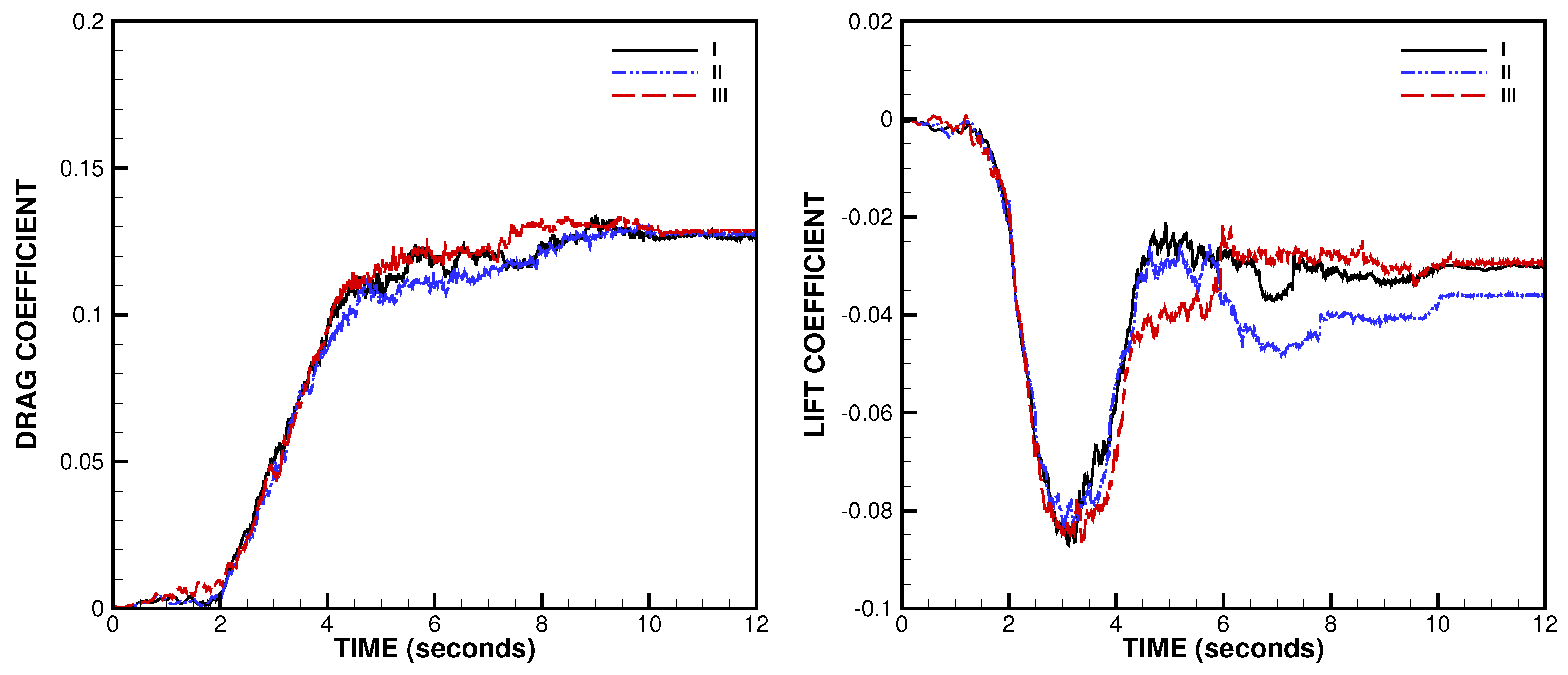
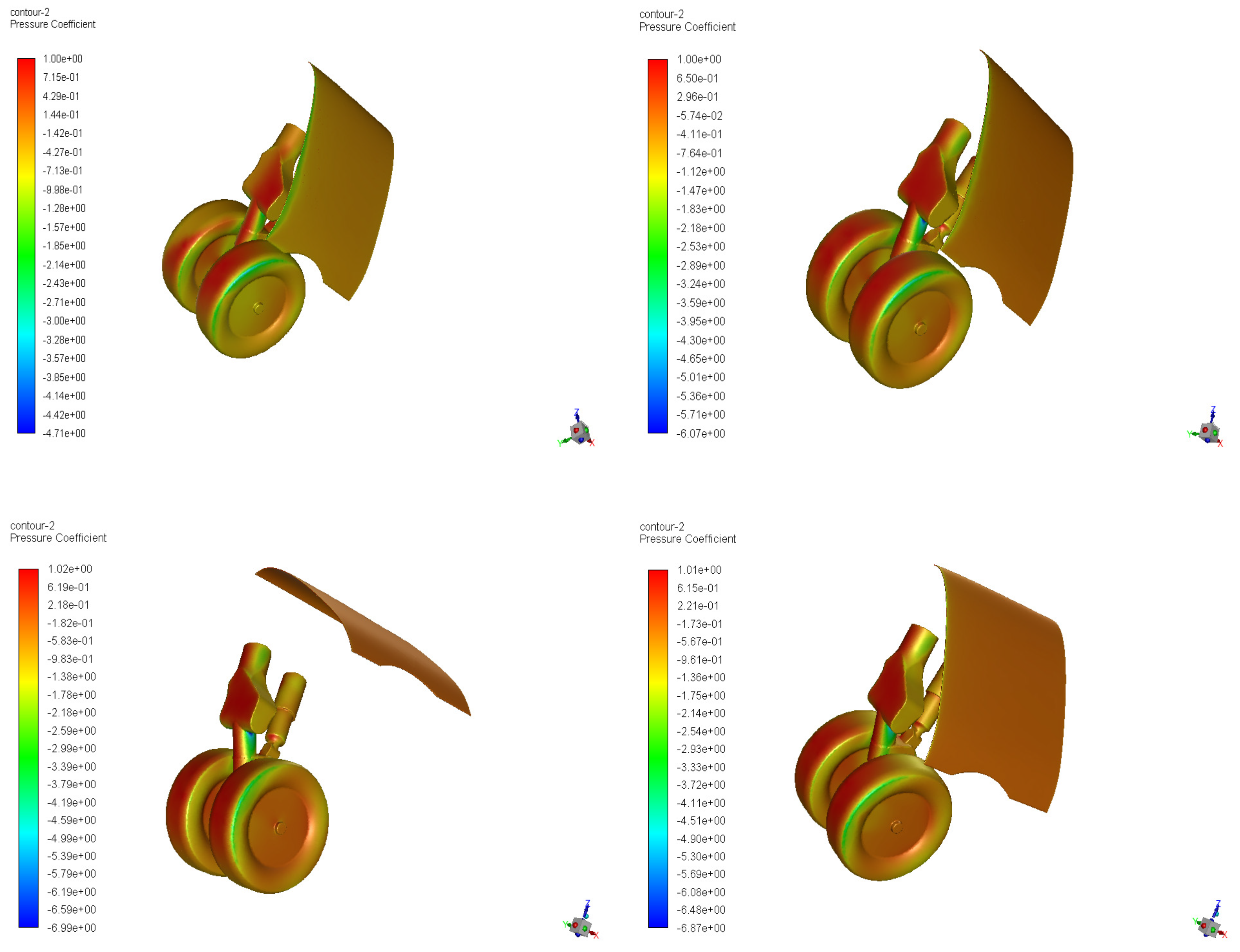
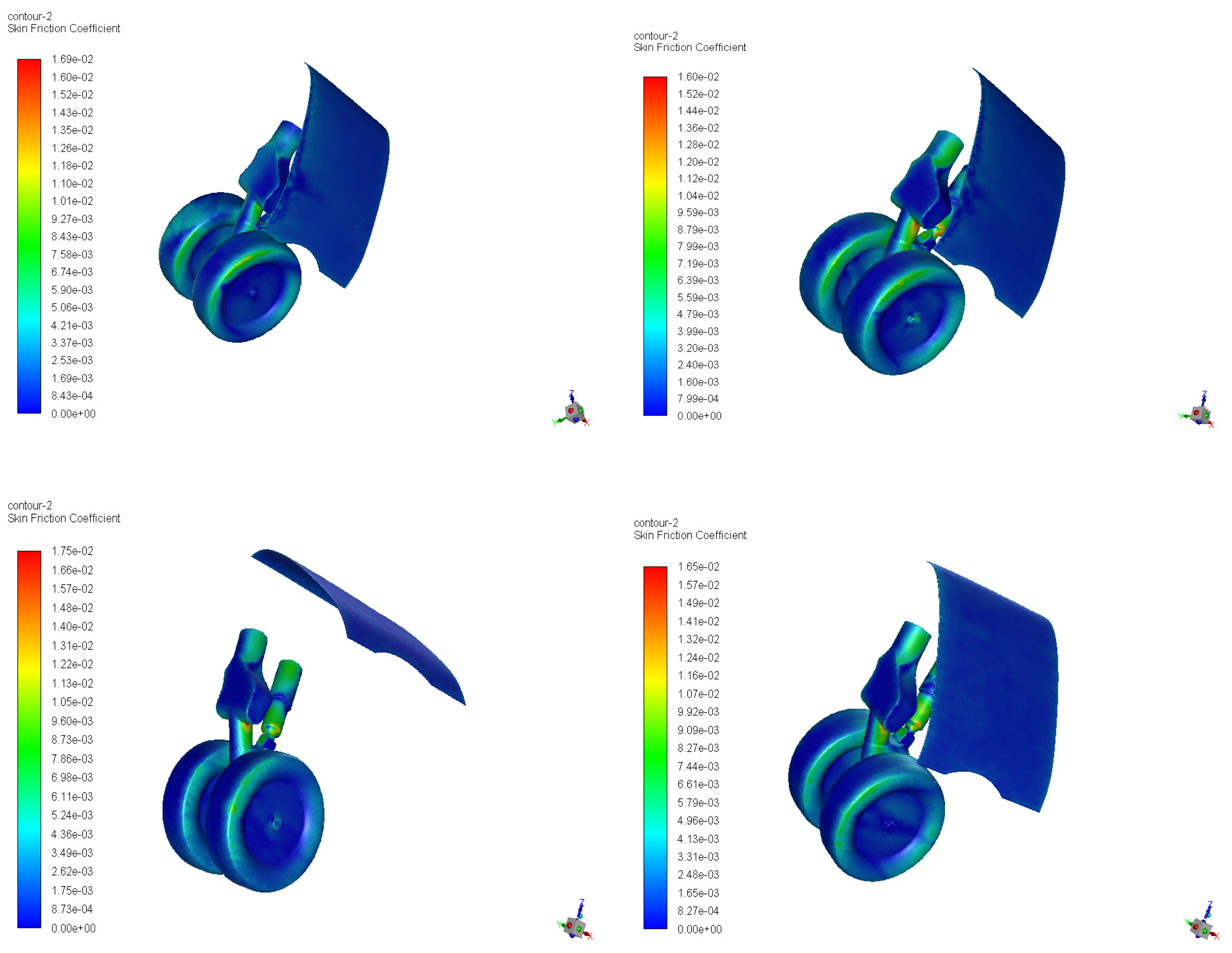
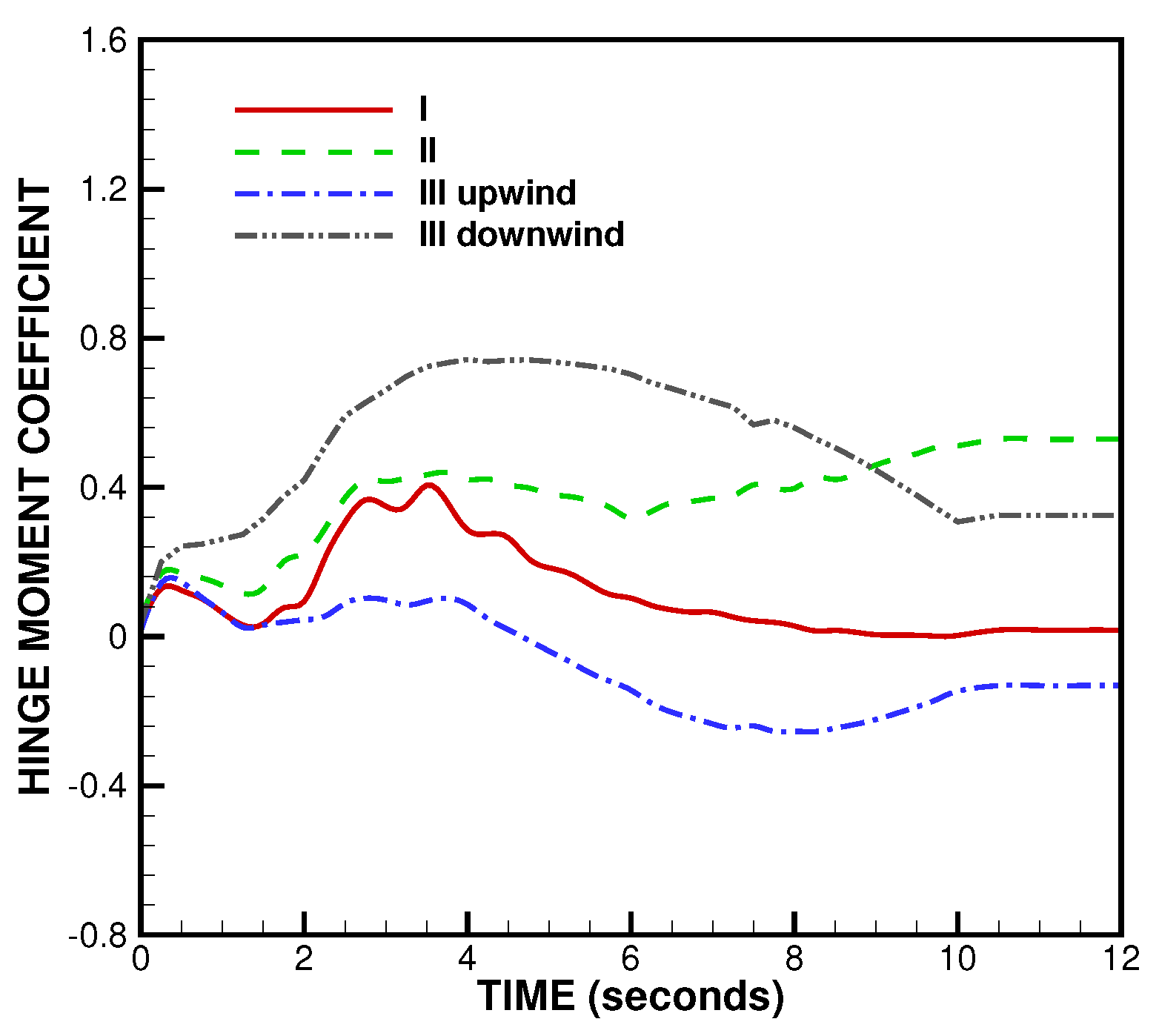
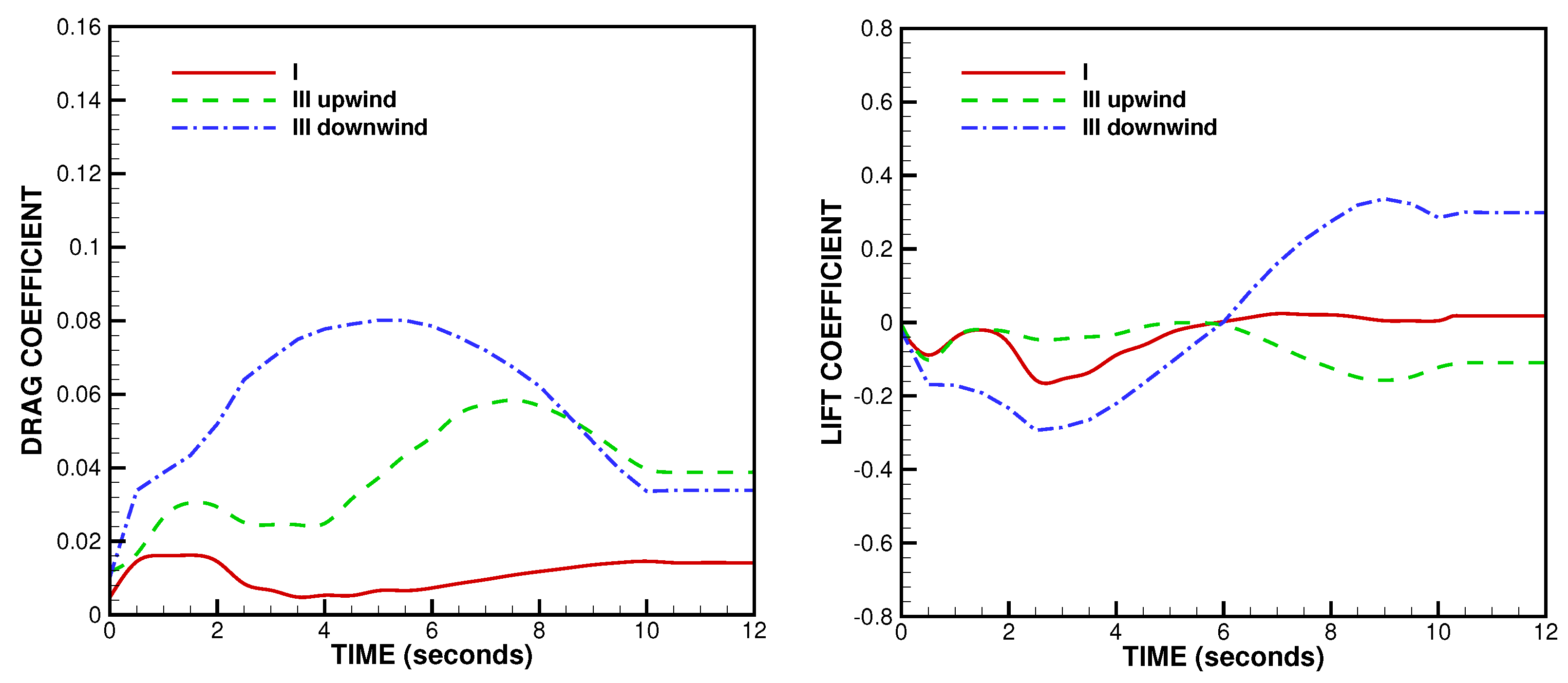
3.1. NLG Simulation
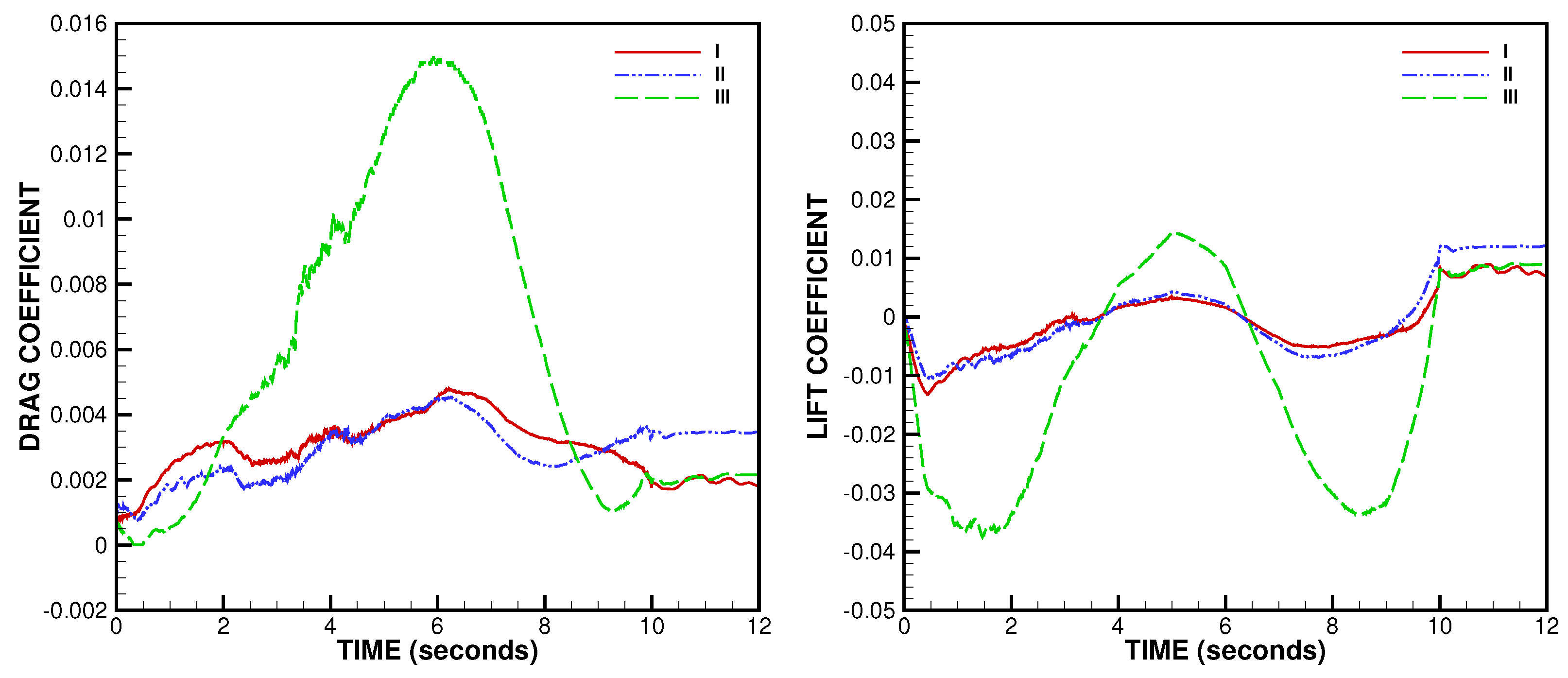
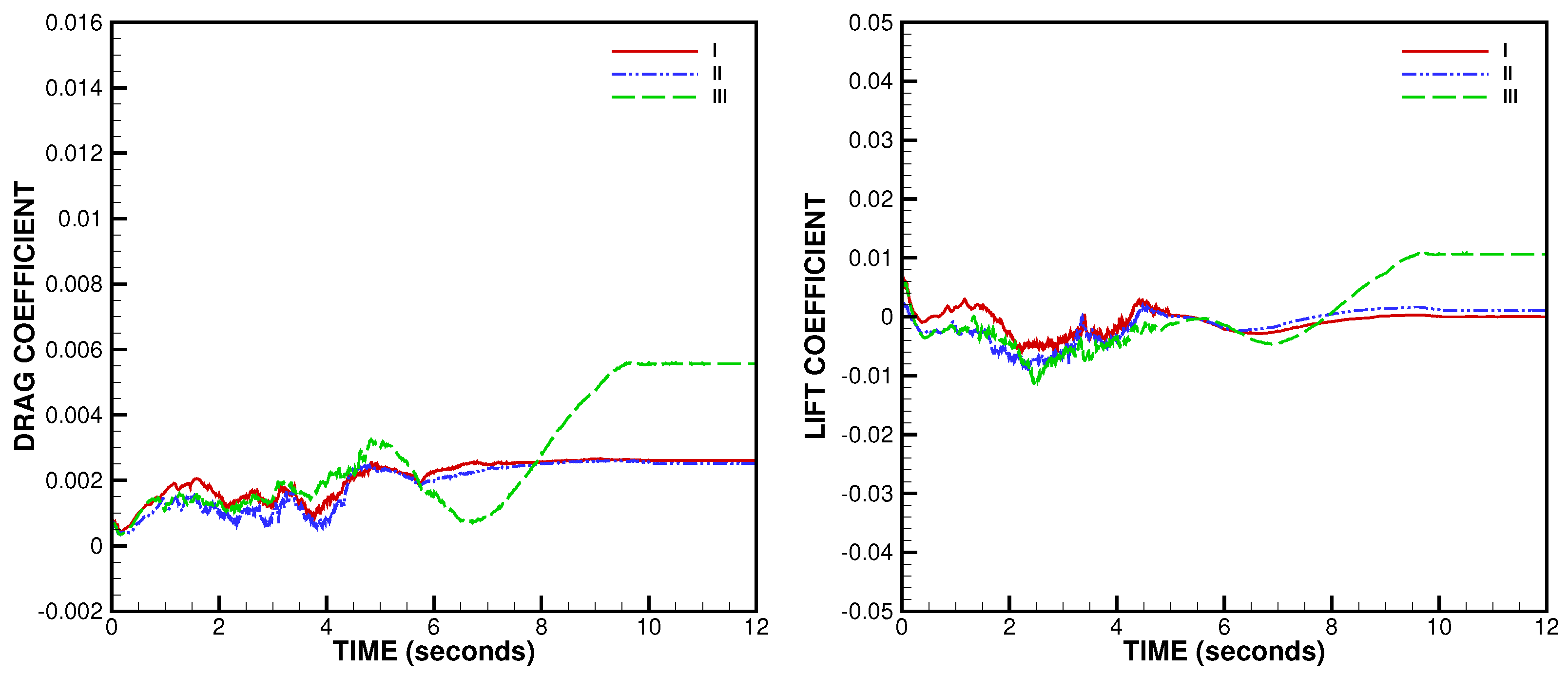
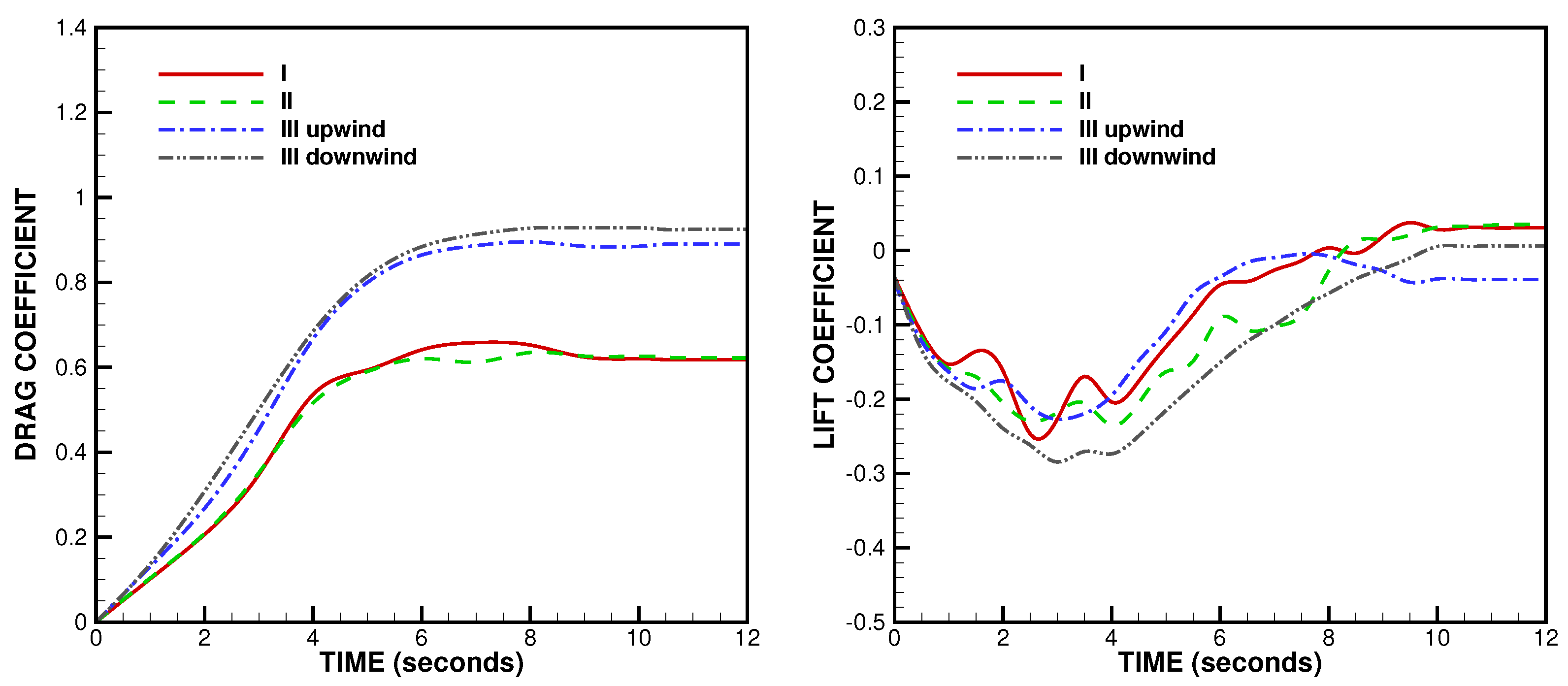
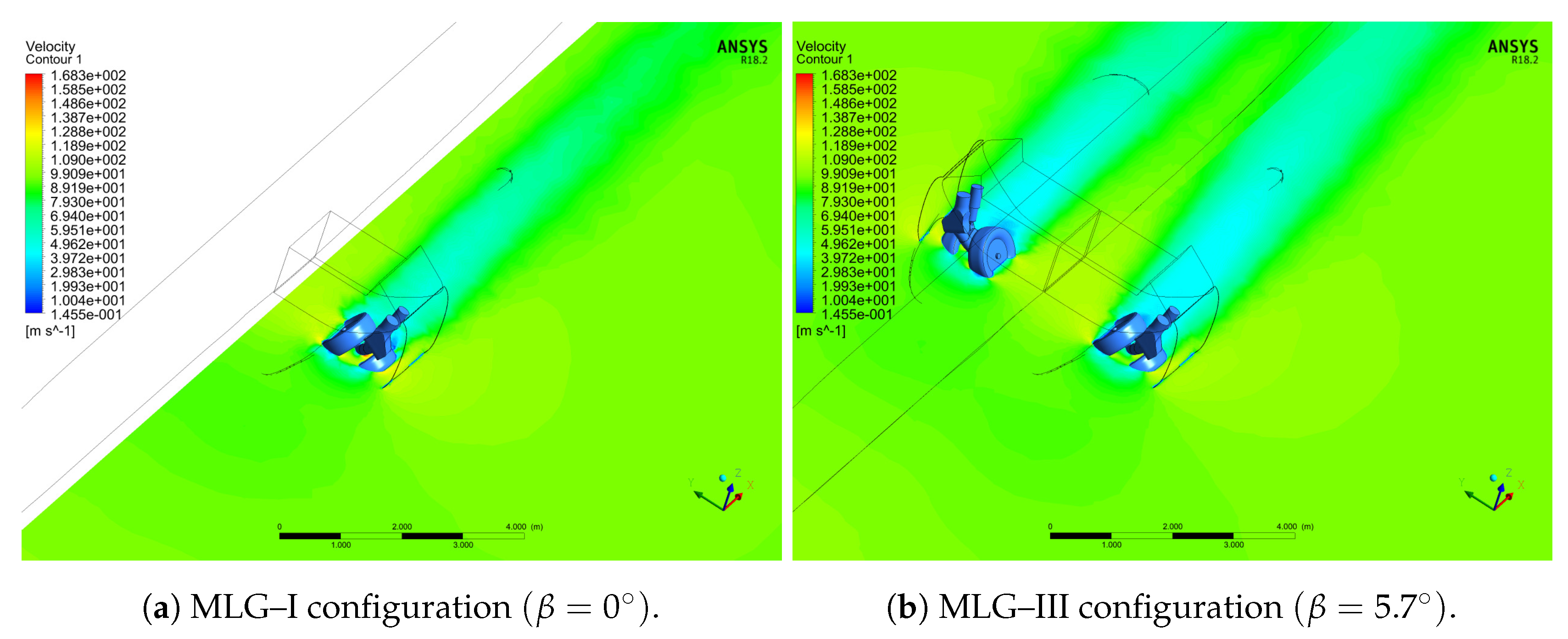
3.2. MLG Simulation
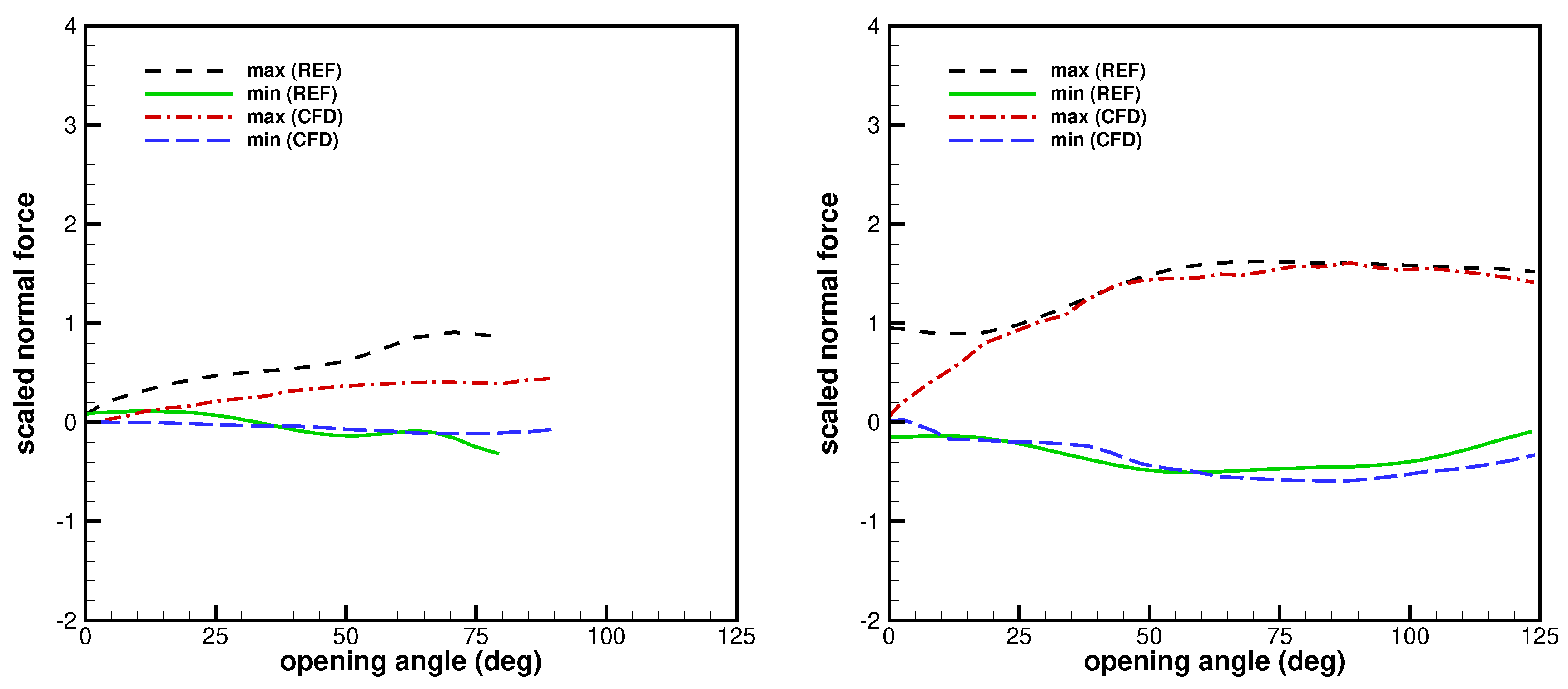
4. Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| FV | Finite Volume |
| RANS | Reynolds-Averaged Navier–Stokes |
| NLG | Nose Landing Gear |
| MLG | Main Landing Gear |
| CFL | Courant–Friedrichs–Lewy number |
References
- Johnson, F.T.; Tinoco, E.N.; Yu, N.J. Thirty years of development and application of CFD at Boeing Commercial Airplanes. Comput. Fluids 2005, 34, 1115–1151. [Google Scholar] [CrossRef]
- Spalart, P.R.; Venkatakrishnan, V. On the role and challenges of CFD in the aerospace industry. Aeronaut. J. 2016, 120, 209–232. [Google Scholar] [CrossRef]
- Imamura, T.; Hirai, T.; Amemiya, K.; Yokokawa, Y.; Enomoto, S.; Yamamoto, K. Aerodynamic and aeroacoustic simulations of a two-wheel landing-gear. Procedia Eng. 2010, 6, 293–302. [Google Scholar] [CrossRef]
- Spalart, P.R.; Mejia, K.M. Analysis of experimental and numerical studies of the rudimentary landing-gear. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- De Stefano, G.; Vasilyev, O.V. Wavelet-based adaptive simulations of three-dimensional flow past a square cylinder. J. Fluid Mech. 2014, 748, 433–456. [Google Scholar] [CrossRef]
- De Stefano, G.; Nejadmalayeri, A.; Vasilyev, O.V. Wall-resolved wavelet-based adaptive large-eddy simulation of bluff-body flows with variable thresholding. J. Fluid Mech. 2016, 788, 303–336. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-averaged Navier–Stokes simulations of wall-bounded compressible turbulent flows. AIAA J. 2020, 58, 1529–1549. [Google Scholar]
- Fröhlich, J.; von Terzi, D. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Langtry, R.B.; Spalart, P.R. Detached eddy simulation of a nose landing-gear cavity. Solid Mech. Appl. 2009, 14, 357–366. [Google Scholar]
- De Stefano, G.; Vasilyev, O.V.; Brown-Dymkoski, E. Wavelet-based adaptive unsteady Reynolds-averaged turbulence modeling of external flows. J. Fluid Mech. 2018, 837, 765–787. [Google Scholar] [CrossRef]
- Mo, J.-O.; Choudhry, A.; Arjomandi, M.; Kelso, R.; Lee, Y.-H. Effects of wind speed changes on wake instability of a wind turbine in a virtual wind tunnel using large eddy simulation. J. Wind Eng. Ind. Aerodyn. 2013, 117, 38–56. [Google Scholar] [CrossRef]
- Escobar, J.A.; Suarez, C.A.; Silva, C.; López, O.D.; Velandia, J.S.; Lara, C.A. Detached-eddy simulation of a wide-body commercial aircraft in high-lift configuration. J. Aircr. 2015, 52, 1112–1121. [Google Scholar] [CrossRef]
- Reina, G.P.; De Stefano, G. Computational evaluation of wind loads on sun-tracking ground-mounted photovoltaic panel arrays. J. Wind Eng. Ind. Aerodyn. 2017, 170, 283–293. [Google Scholar] [CrossRef]
- Rapagnani, D.; Buompane, R.; Di Leva, A.; Gialanella, L.; Busso, M.; De Cesare, M.; De Stefano, G.; Duarte, J.G.; Gasques, L.R.; Morales Gallegos, L.; et al. A supersonic jet target for the cross section measurement of the 12C(α, γ)16O reaction with the recoil mass separator ERNA. Nucl. Instrum. Meth. Phys. Res. B 2017, 407, 217–221. [Google Scholar] [CrossRef]
- Benaouali, A.; Kachel, S. Multidisciplinary design optimization of aircraft wing using commercial software integration. Aerosp. Sci. Technol. 2019, 92, 766–776. [Google Scholar] [CrossRef]
- Hedges, L.S.; Travin, A.K.; Spalart, P.R. Detached-eddy simulations over a simplified landing-gear. J. Fluids Eng. 2002, 124, 413–420. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, J.; Luo, K.; Huang, J.; Fu, S. Investigation of flows around a rudimentary landing-gear with advanced detached-eddy-simulation approaches. AIAA J. 2013, 51, 107–125. [Google Scholar] [CrossRef]
- Rhee, S.H.; Koutsavdis, E.K. Unsteady marine propulsor blade flow—A CFD validation with unstructured dynamic meshing. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Snyder, D.O.; Koutsavdis, E.K.; Anttonen, J.S.R. Transonic store separation using unstructured CFD with dynamic meshing. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries, Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Pavlenko, O.V.; Chuban, A.V. Numerical investigation of the hinge moments of the nose landing-gear doors in a passenger aircraft in the process of opening. TsAGI Sci. J. 2016, 47, 513–523. [Google Scholar] [CrossRef]
- Pavlenko, O.V.; Chuban, A.V. Determining hinge moments of the main landing-gear fuselage door by means of numerical flow simulation. TsAGI Sci. J. 2018, 49, 781–792. [Google Scholar] [CrossRef]




| Case | # Cells | ||
|---|---|---|---|
| NLG–I | 0° | 0° | 1 M |
| NLG–II | 4° | 0° | 1 M |
| NLG–III | 0° | 5.7° | 2 M |
| MLG–I | 0° | 0° | M |
| MLG–II | 4° | 0° | M |
| MLG–III | 0° | 5.7° | 5 M |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Stefano, G.; Natale, N.; Reina, G.P.; Piccolo, A. Computational Evaluation of Aerodynamic Loading on Retractable Landing-Gears. Aerospace 2020, 7, 68. https://doi.org/10.3390/aerospace7060068
De Stefano G, Natale N, Reina GP, Piccolo A. Computational Evaluation of Aerodynamic Loading on Retractable Landing-Gears. Aerospace. 2020; 7(6):68. https://doi.org/10.3390/aerospace7060068
Chicago/Turabian StyleDe Stefano, Giuliano, Nunzio Natale, Giovanni Paolo Reina, and Antonio Piccolo. 2020. "Computational Evaluation of Aerodynamic Loading on Retractable Landing-Gears" Aerospace 7, no. 6: 68. https://doi.org/10.3390/aerospace7060068
APA StyleDe Stefano, G., Natale, N., Reina, G. P., & Piccolo, A. (2020). Computational Evaluation of Aerodynamic Loading on Retractable Landing-Gears. Aerospace, 7(6), 68. https://doi.org/10.3390/aerospace7060068






