Cabin Layout Optimization for Vibration Hazard Reduction in Helicopter Emergency Medical Service
Abstract
1. Introduction
1.1. HEMS Subjects and Related Risks
1.1.1. Crew
1.1.2. Pilots
1.1.3. Patient
1.1.4. Medical Equipment
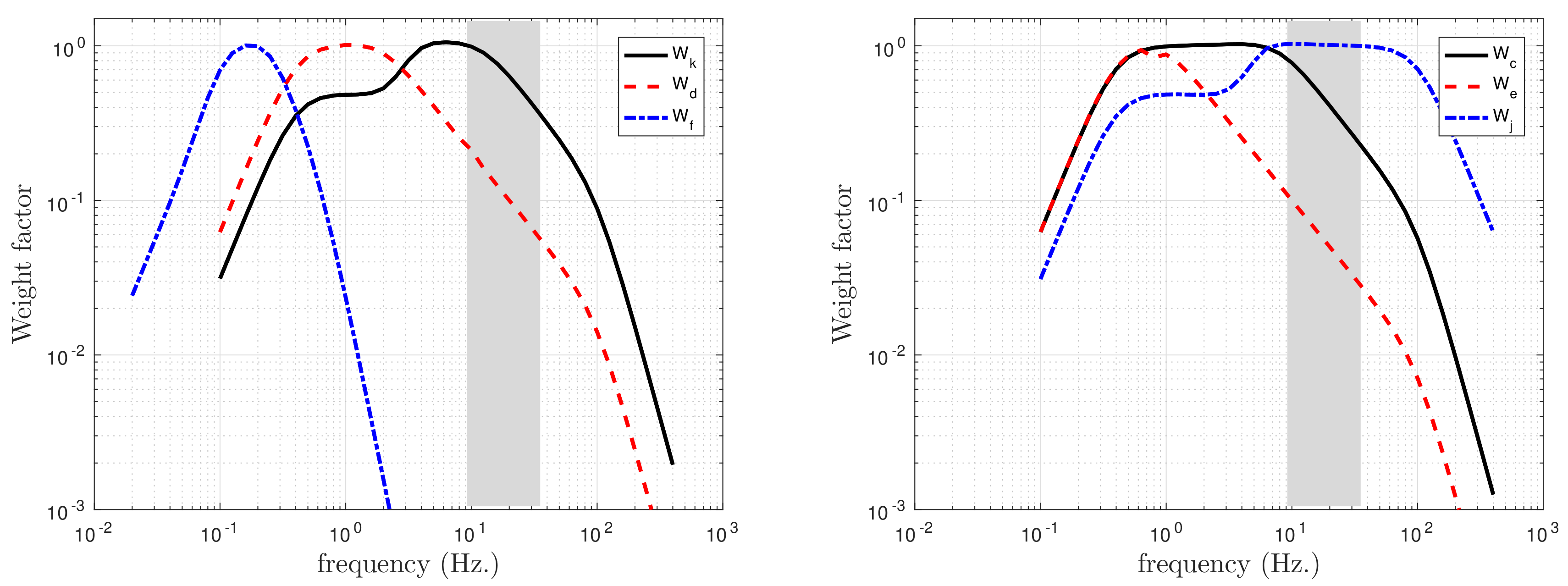
1.2. Vibration Rating
1.3. Scope
2. Method
- vehicle subcomponents (rotors, fuselage, etc.) formulated within their most natural modeling and analysis environment, which helps component engineers to focus on their task;
- high/uniform-fidelity overall modeling through sub-component assembly, thus a comprehensive analysis model is achieved within a shorter time;
- the capability of adding load paths between arbitrary structural points, which makes the definition of more accurate vibration performance formulations possible;
- exporting proper output models compatible for mounting medical equipment, human biodynamic models and corresponding interfaces, to support vehicle coupling with HEMS subjects;
- the capability of calculating the performance of the coupled design solutions, without the need to modify and reassemble the detailed baseline helicopter model, thus allowing engineers to find the optimum configuration among a variety of arrangements of medical equipment, recumbent patient, and seating occupants.
2.1. Aeroservoelastic Rotorcraft Model
2.2. Formulation of HEMS Subjects
2.3. Combining Helicopter and Subjects
- The input for the helicopter model is defined as the vibratory forces and moments applied at any airframe point and/or on the rotors. Typically, these loads originate from main and tail rotors and are transferred to the fuselage through the rotor hubs.
- The output of the helicopter model is chosen as the sensors of position, velocity, and acceleration of any airframe point, or rotor point in multiblade coordinates; thus, it is a linear function of the state and input of the model.
- The subjects create a feedback loop between the sensors corresponding to the motion and the forces exerted by the subjects () at their attachment points,such that the total force can be expressed as , where the negative feedback convention is used. The transfer matrix represents the synthesis of the subject’s state-space representation described in Section 2.2.
2.4. Processing Vibration Signals
2.5. Vibration Index
3. HEMS Model
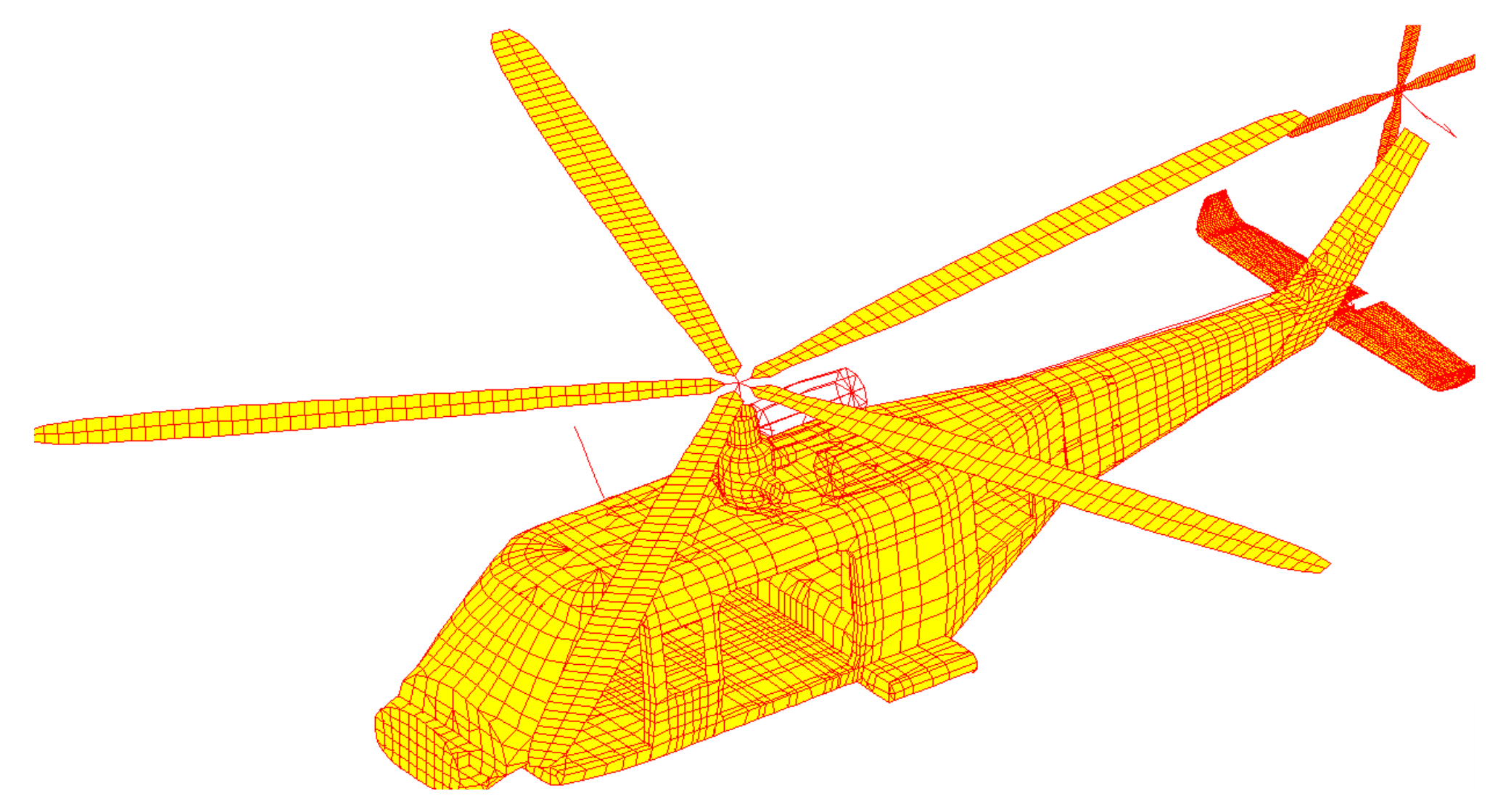
3.1. Baseline Helicopter
- six rigid body degrees of freedom;
- the airframe stability derivatives, calculated from the aerodynamic look-up tables of the fuselage, horizontal and vertical tail using CAMRAD/JA (a comprehensive rotorcraft analysis software [36]), which are required to capture the low-frequency flight mechanics behavior of the helicopter;
- the elastic bending and torsion modes of the airframe in a frequency range up to 50 Hz to include modes up to twice the rotor excitation frequency of 25 Hz. The modes are extracted from a NASTRAN (a popular Finite Element solver) detailed finite element model which. The model is characterized by more than 30,000 nodes and 17,000 elements. The elements include beams (for the main and tail rotor blades and main skeleton of the fuselage), shells (for the fuselage skin), and bricks (for non-structural parts);
- proportional structural damping, which is superimposed in MASST to the airframe portion of the model
- main and tail rotor aeroelastic models, computed using CAMRAD/JA and characterized by two bending modes (the first in lead-lag and the second in flap, typical of soft in-plane articulated rotors) plus one torsion mode (related to the control chain compliance), formulated in multiblade coordinates. The models represent the rotors at a specific maximum load flight condition. However, MASST allows for including multiple models (parametrized for example by flight speed, density, etc.), and find the corresponding model at a prescribed condition by means of interpolation.
- an axial dynamic inflow model, based on Pitt–Peters’ formulation (Ref. [37]) acting on the main rotor;
- the transfer functions of the main and tail rotor servoactuators, directly formulated in Matlab/Simulink, considering servo-valve and dynamic compliance [38]; a matrix of gear ratios is used to convert the linear actuator displacements into collective and cyclic commands;
- the nodes and coordinates for the sensors and the forces, which correspond to physical degrees of freedom, are directly defined in MASST.
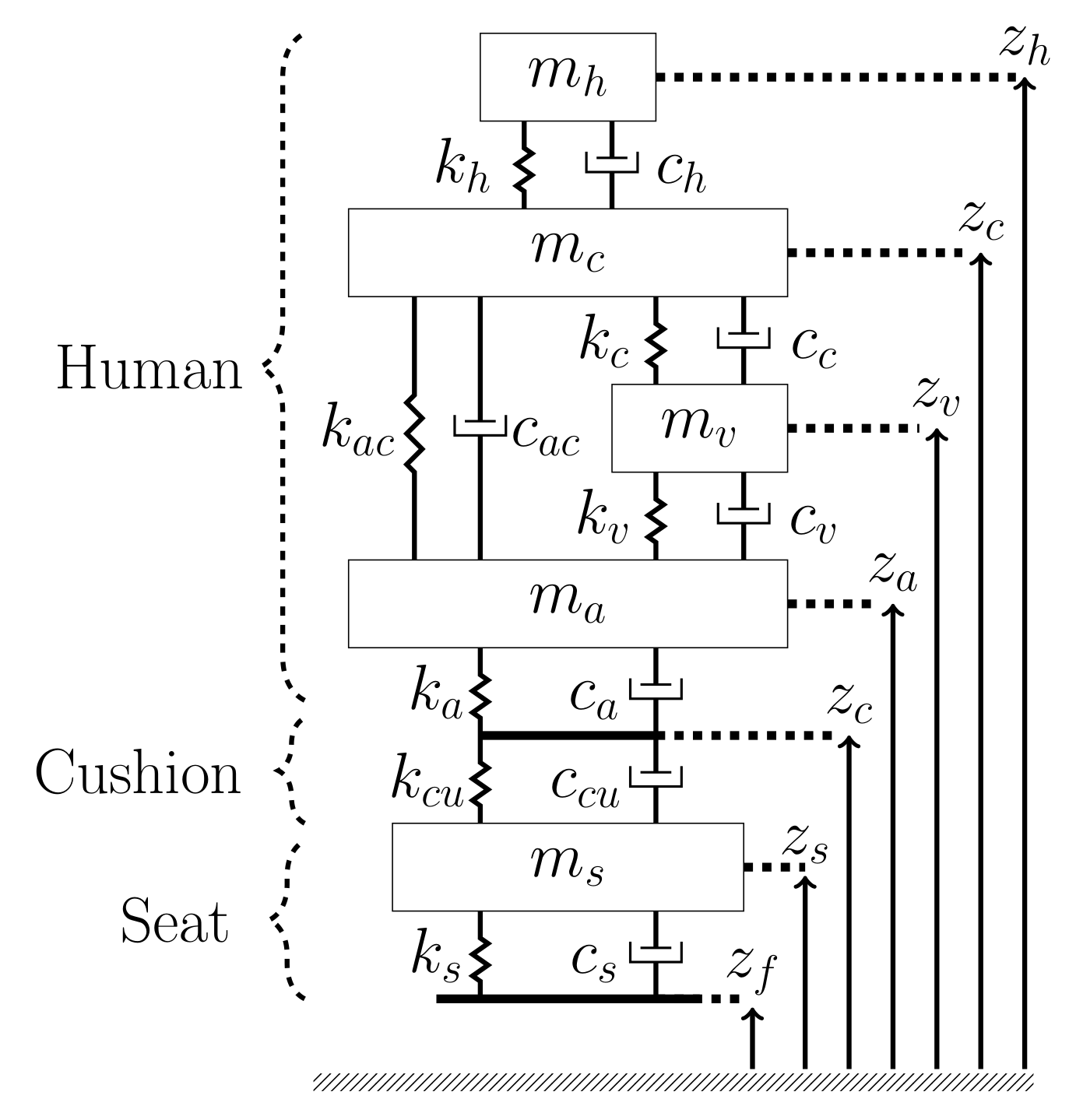
3.2. Occupant in Sitting Posture
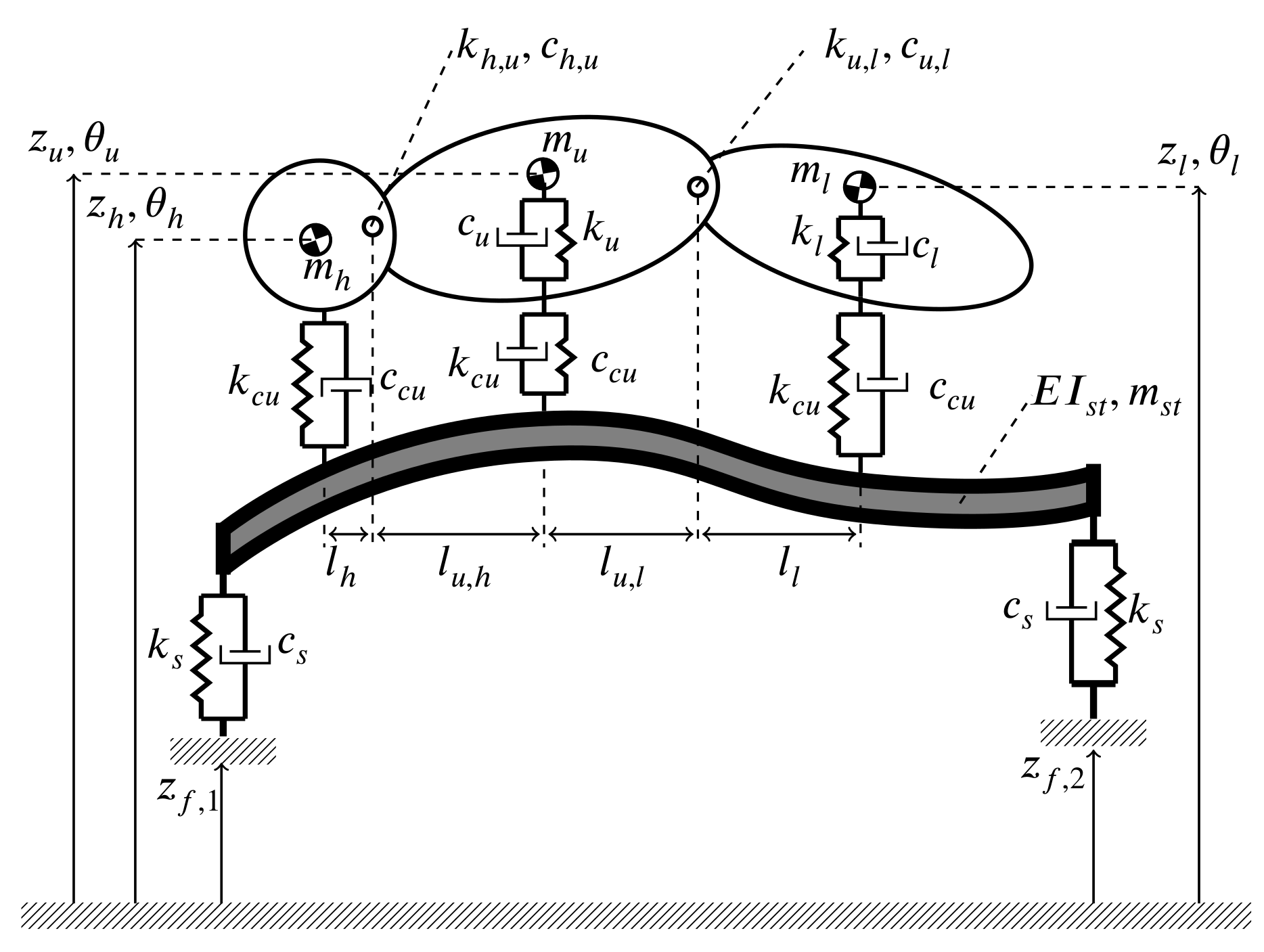
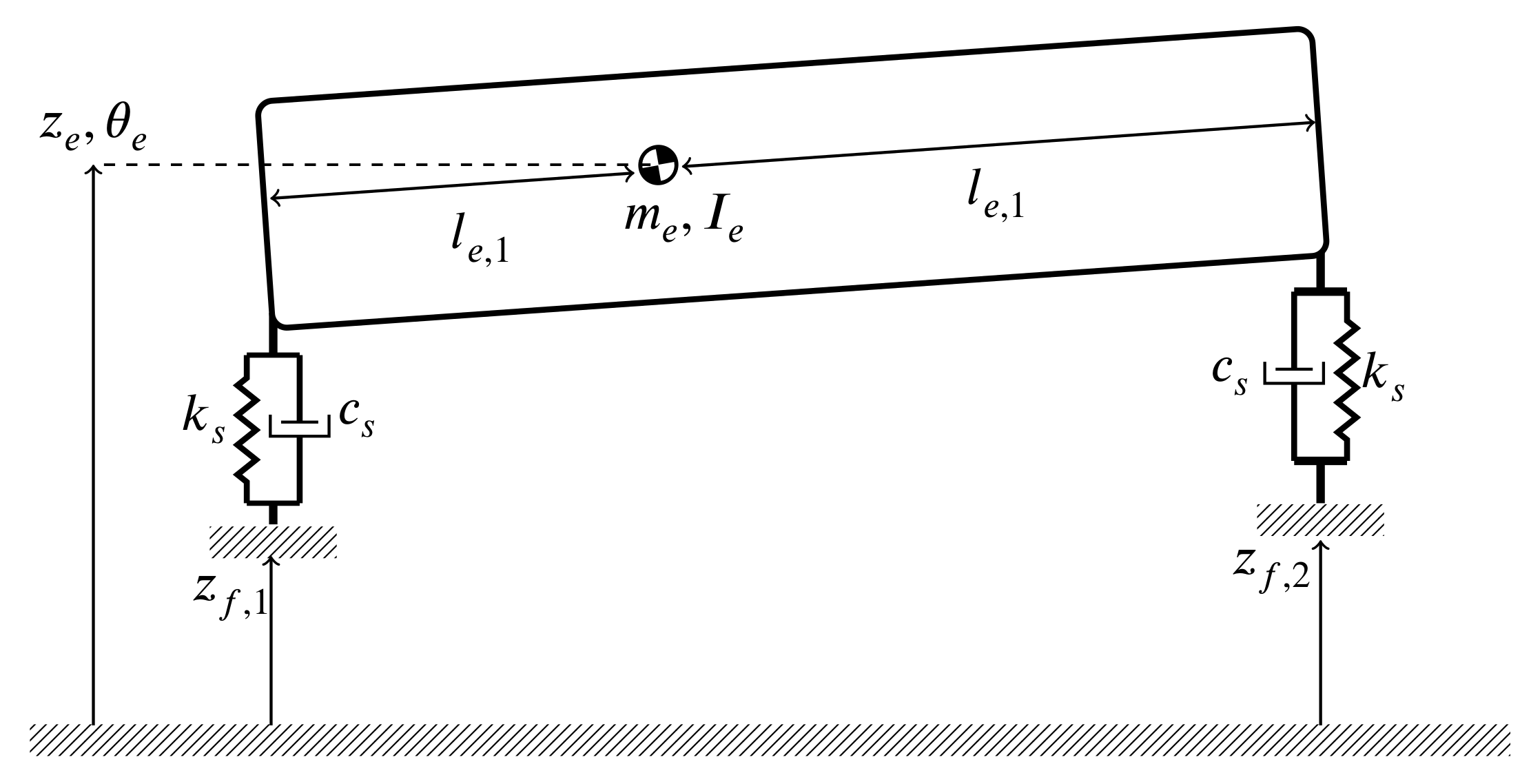
3.3. Patient
3.4. Medical Equipment
3.5. Vibration Source
3.6. Vibration Attenuation Devices
4. Analysis, Results, and Discussion
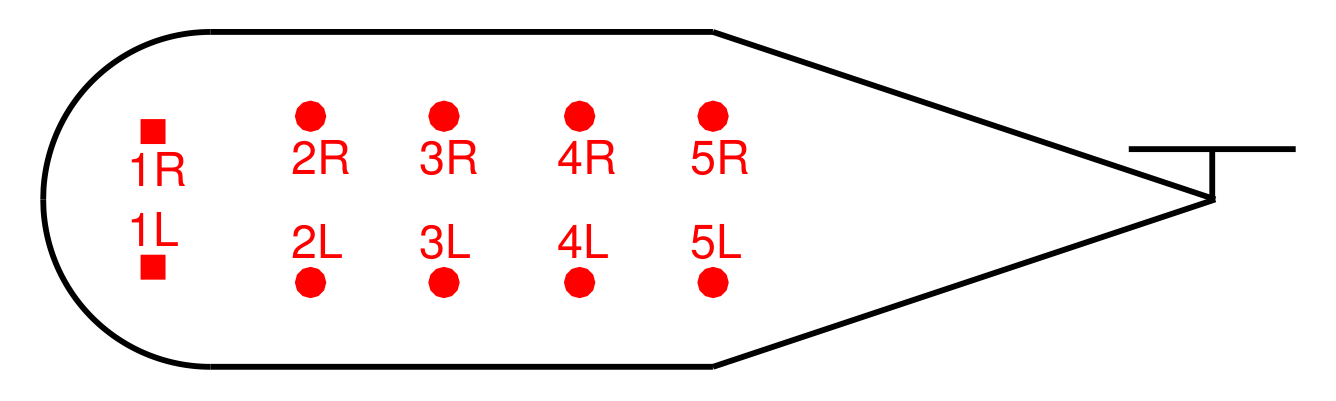
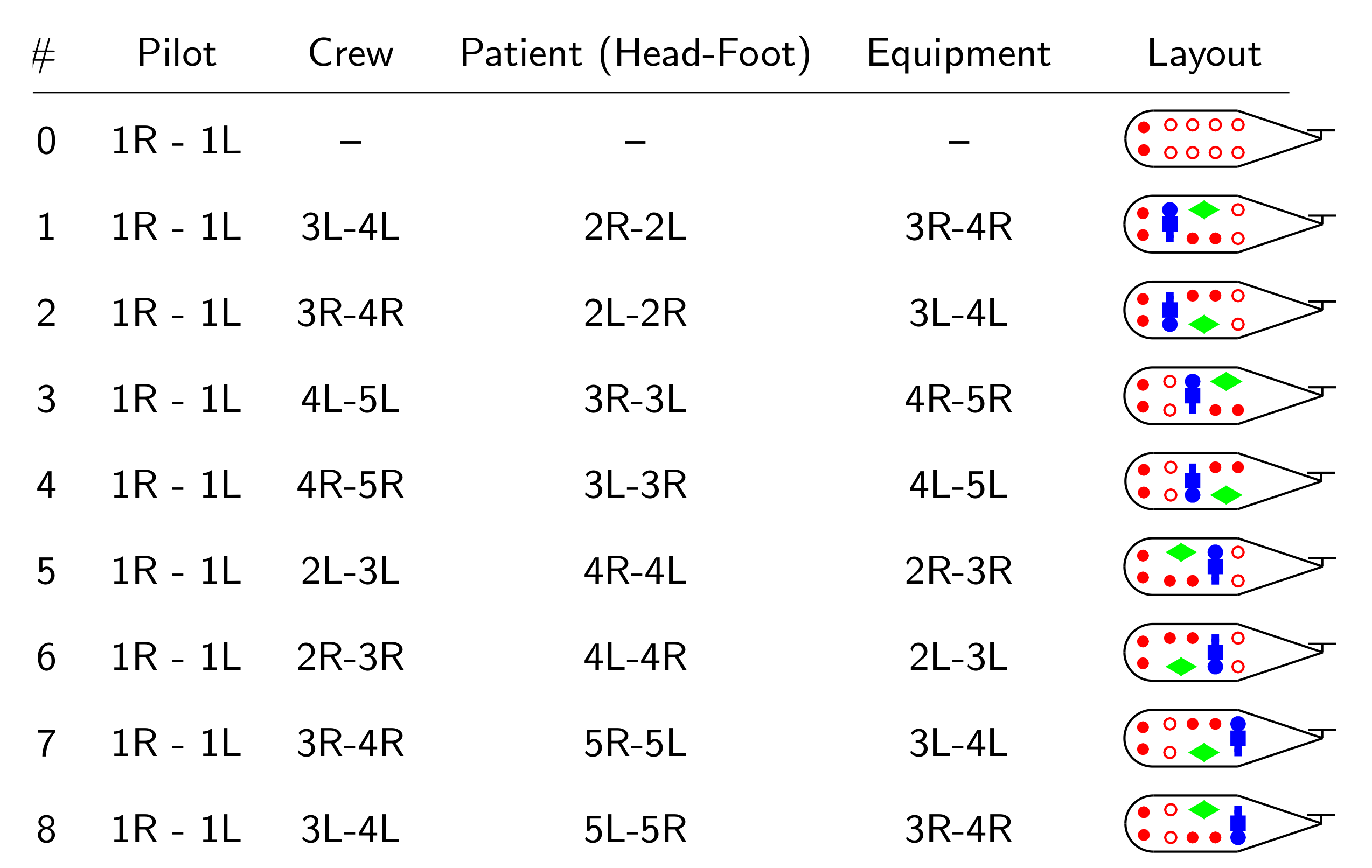
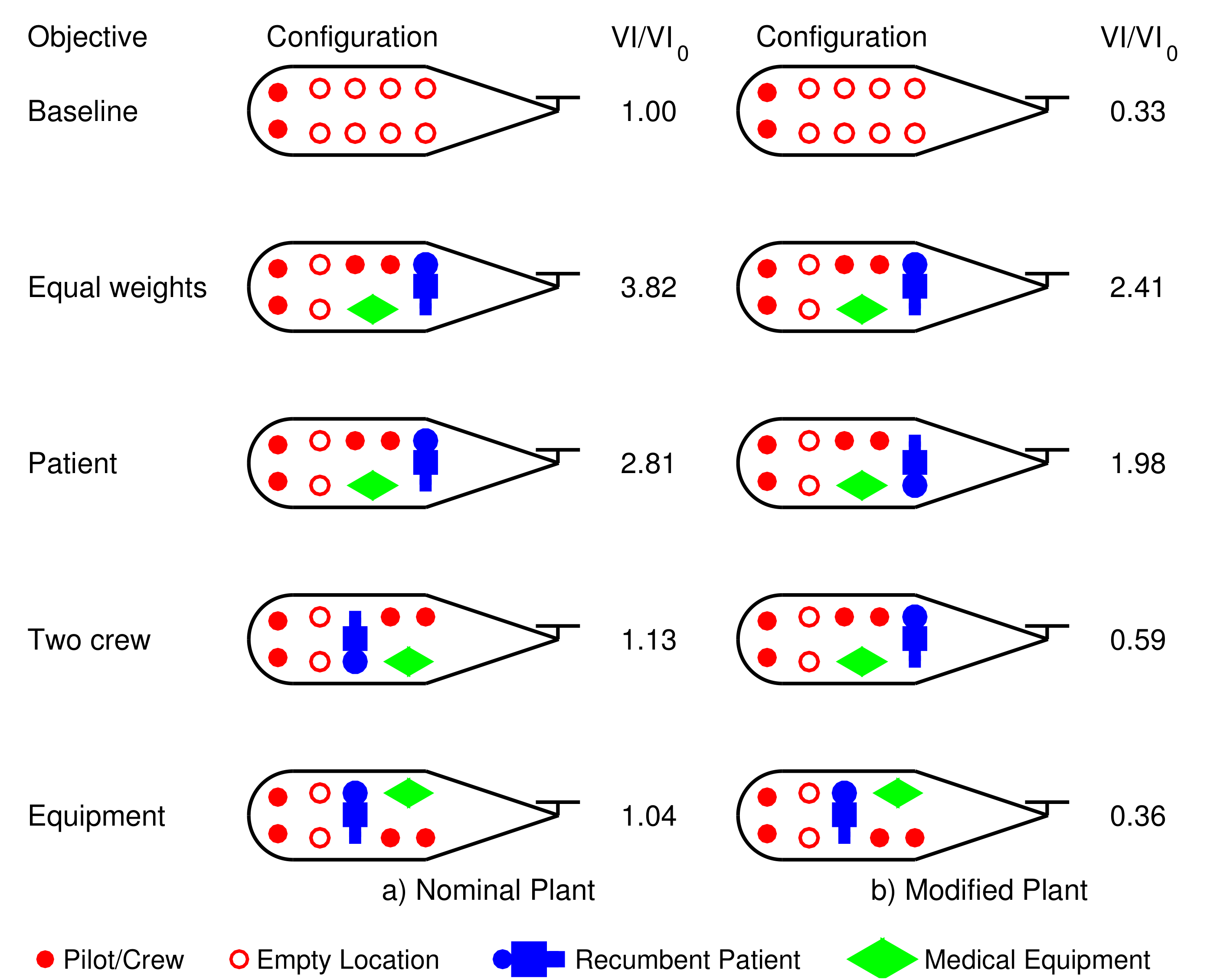
4.1. Configuration Optimization
- each seat shall be mounted on a single point, two for the pilot and co-pilot, and two for the crew;
- the seats of pilot and co-pilot are fixed at 1L and 1R; both are always considered occupied and included in the optimization;
- the stretcher is aligned laterally (which is safer in case of crash [52]), and shall be mounted on the floor at its two ends;
- the equipment shall be aligned longitudinally, and mounted on two points, one of which adjacent to the head of the patient;
- The crew shall sit adjacent to the equipment and to each other.
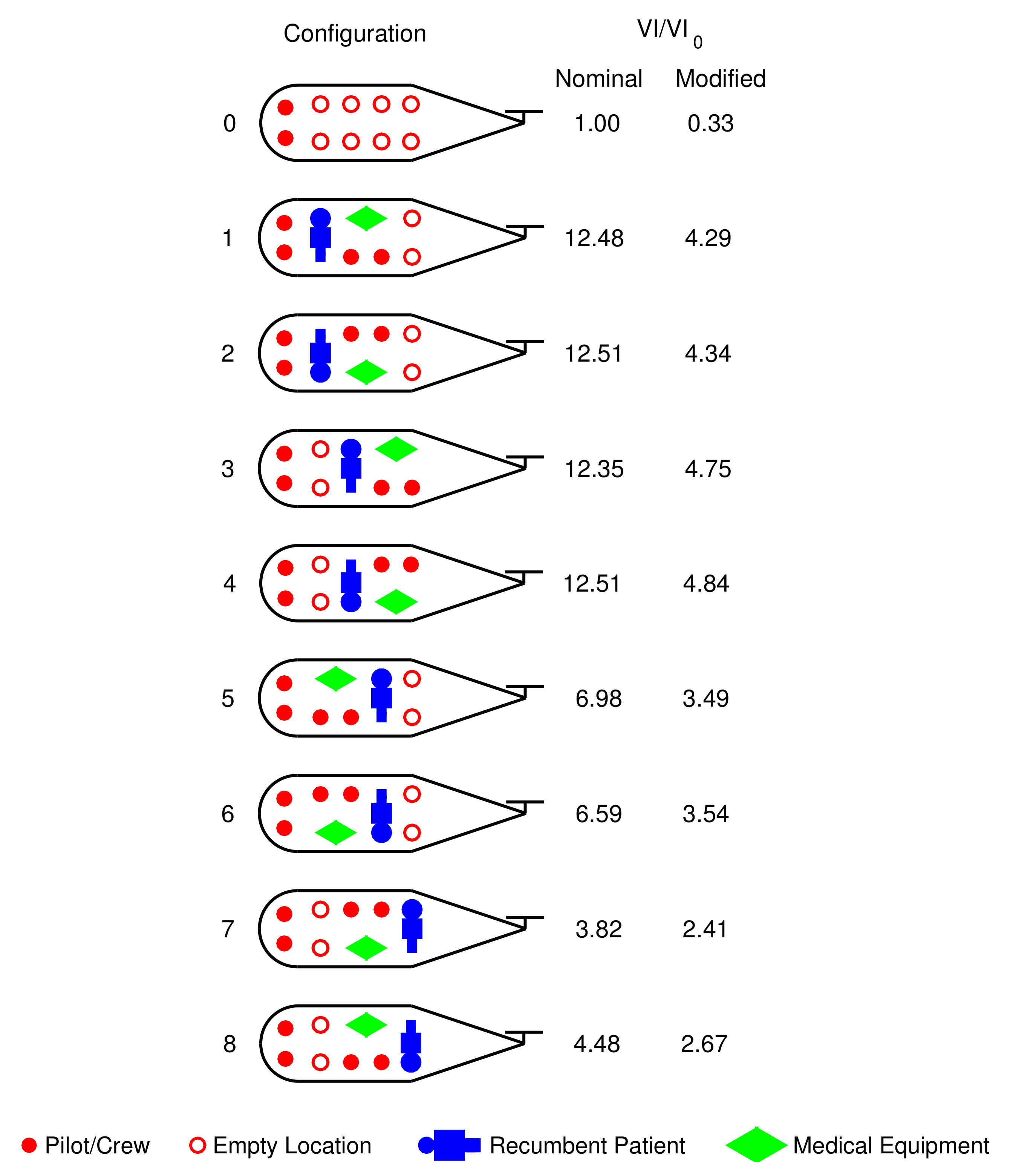
4.2. Results and Discussion
5. Conclusions
- it provides a high-fidelity analysis tool for rotorcraft, assembling subcomponents which are modeled in their most natural platform, which is instrumental for accurate estimation of vibrations;
- without spoiling and re-assembling the baseline helicopter model, the dynamical models of typical HEMS occupants and components can be included in the vibration analysis, their position can be modified, and vibration performance formulations can be fine-tuned. This reduces the set-up time and speeds up the optimization process of a HEMS configuration;
- a large number of possible HEMS configurations can be quickly evaluated; hence, optimum solution is found, and the effects of differently weighting each subject’s accelerations can be investigated effectively;
- different types of helicopters, unconventional HEMS configurations, and complex dynamical models of humans, equipment, seats, and stretchers can be easily handled;
- the larger the number of HEMS configurations allowed by the cabin structure increases, the more likely it is to achieve a low-vibration HEMS cabin layout;
- the relative weights of HEMS subjects can yield different cabin layouts; therefore, the relative importance of the subjects should be carefully defined;
- for HEMS, optimizing the cabin layout can be as effective as mounting vibration absorbers, but without the related weight penalty and maintenance cost;
- The application of vibration attenuation devices in HEMS is effective the most when accompanied by the cabin interior layout design, since they may have comparable impact.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Floccare, D.J.; Stuhlmiller, D.F.E.; Braithwaite, S.A.; Thomas, S.H.; Madden, J.F.; Hankins, D.G.; Dhindsa, H.; Millin, M.G. Appropriate and Safe Utilization of Helicopter Emergency Medical Services: A Joint Position Statement with Resource Document. Prehospital Emerg. Care 2013, 17, 521–525. [Google Scholar] [CrossRef]
- Sullivent, E.E.; Faul, M.; Wald, M.M. Reduced Mortality in Injured Adults Transported by Helicopter Emergency Medical Services. Prehospital Emerg. Care 2011, 15, 295–302. [Google Scholar] [CrossRef]
- Ausserer, J.; Moritz, E.; Stroehle, M.; Brugger, H.; Strapazzon, G.; Rauch, S.; Mair, P. Physician staffed helicopter emergency medical systems can provide advanced trauma life support in mountainous and remote areas. Injury 2017, 48, 20–25. [Google Scholar] [CrossRef]
- Watkinson, J. Art of the Helicopter; Elsevier, Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Ljungberg, J.K.; Neely, G. Stress, subjective experience and cognitive performance during exposure to noise and vibration. J. Environ. Psychol. 2007, 27, 44–54. [Google Scholar] [CrossRef]
- Mansfield, N. Human Response to Vibration; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Harrer, K.L.; Yniguez, D.; Maria, M.M.; Ellenbecker, D.; Estrada, N.; Geiger, M. Whole Body Vibration Exposure for MH-60S Pilots; Naval Medical Center San Diego (NMCSD): San Diego, CA, USA, 2005. [Google Scholar]
- Chafé, G.S.; Farrell, P.S.E. Royal Canadian Air Force CH-146 Griffon Aircrew 2014 Spinal Musculoskeletal Trouble Survey; Scientific Report DRDC-RDDC-2016-R179; DRDC–Toronto Research Centre: Toronto, ON, Canada, 2016. [Google Scholar]
- Griffin, M.J. Eye Motion during Whole-Body Vertical Vibration. Hum. Factors 1976, 18, 601–606. [Google Scholar] [CrossRef]
- Masarati, P.; Quaranta, G.; Gennaretti, M.; Serafini, J. An Investigation of Aeroelastic Rotorcraft-Pilot Interaction. In Proceedings of the 37th European Rotorcraft Forum, Paper No. 112. Vergiate/Gallarate, Italy, 13–15 September 2011. [Google Scholar]
- Quaranta, G.; Tamer, A.; Muscarello, V.; Masarati, P.; Gennaretti, M.; Serafini, J.; Colella, M.M. Rotorcraft Aeroelastic Stability Using Robust Analysis. CEAS Aeronaut. J. 2014, 5, 29–39. [Google Scholar] [CrossRef]
- Muscarello, V.; Masarati, P.; Quaranta, G.; Lu, L.; Jump, M.; Jones, M. Investigation of Adverse Aeroelastic Rotorcraft-Pilot Coupling Using Real-Time Simulation. In Proceedings of the American Helicopter Society 69th Annual Forum, Paper No. 193. Phoenix, AZ, USA, 21–23 May 2013. [Google Scholar]
- Special Investigation Report on Emergency Medical Services Operations; Aviation Special Investigation Report PB2006-917001; National Transportation Safety Board: Washington, DC, USA, 2006.
- Baker, S.P.; Grabowski, J.G.; Dodd, R.S.; Shanahan, D.F.; Lamb, M.W.; Li, G.H. EMS Helicopter Crashes: What Influences Fatal Outcome? Ann. Emerg. Med. 2006, 47, 351–356. [Google Scholar] [CrossRef]
- Hinkelbein, N.J.; Schwalbe, H.V.G. Helicopter emergency medical services accident rates in different international air rescue systems. Open Access Emerg. Med. 2010, 45–49. [Google Scholar] [CrossRef]
- Kubo, M.; Terauchi, F.; Aoki, H.; Matsuoka, Y. An investigation into a synthetic vibration model for humans:: An investigation into a mechanical vibration human model constructed according to the relations between the physical, psychological and physiological reactions of humans exposed to vibration. Int. J. Ind. Ergon. 2001, 27, 219–232. [Google Scholar] [CrossRef]
- Carchietti, E.; Cecchi, A.; Valent, F.; Rammer, R. Flight Vibrations and Bleeding in Helicoptered Patients with Pelvic Fracture. Air Med. J. 2013, 32, 80–83. [Google Scholar] [CrossRef]
- Björn-Markus, K.; Marie, L.; Markus, L.; Marcus, K.; Ronnie, L.; Stellan, H.; Urban, W.; van den Berg, J. Sound and vibration: Effects on infants’ heart rate and heart rate variability during neonatal transport. Acta Paediatr. 2011, 101, 148–154. [Google Scholar] [CrossRef]
- Veca, A. Vibration Effects on Helicopter Reliability and Maintainability; TM 73-11; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Wu, J.; Zhang, R.R.; Radons, S.; Long, X.; Stevens, K.K. Vibration analysis of medical devices with a calibrated FEA model. Comput. Struct. 2002, 80, 1081–1086. [Google Scholar] [CrossRef]
- Measurement and Evaluation of Human Exposure to Whole-Body Mechanical Vibration; Technical Report BS-6841; British Standard Institution: London, UK, 1987.
- ISO. ISO Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration; Technical Report ISO2631-1; ISO: Geneva, Switzerlands, 1997. [Google Scholar]
- Leatherwood, J.D.; Clevenson, S.A. A Design Tool for Estimating Passenger Ride Discomfort within Complex Ride Environments. J. Hum. Factors Ergon. Soc. 1980, 22, 291–312. [Google Scholar] [CrossRef]
- Anonymous. Requirements for Rotorcraft Vibration Specifications, Modeling and Testing; ADS-27A; US Army AMCOM: Redstone Arsenal, AL, USA, 2006. [Google Scholar]
- Smith, S.D.; Chervak, M.S.; Steinhauer, M.B. Special Investigation Report on Emergency Medical Services Operations; Technical Report AFRL-RH-WP-TR-2014-0053; Air Force Research Laboratory: Wright-Patterson AFB, OH, USA, 2014. [Google Scholar]
- Chen, Y.; Ghinet, S.; Price, A.; Wickramasinghe, V.; Grewal, A. Evaluation of Aircrew Whole-Body Vibration Exposure on a Canadian CH-147F Chinook Helicopter. J. Am. Helicopter Soc. 2017, 62, 1–11. [Google Scholar] [CrossRef]
- Rath, T.; Fichter, W. A Closer Look at the Impact of Helicopter Vibrations on Ride Quality. In Proceedings of the AHS 73rd Annual Forum, Fort Worth, TX, USA, 9–11 May 2017. [Google Scholar]
- Johnson, W. Rotorcraft Aeromechanics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Acosta, K.K.S. The Comparison of Two Supine Manikins and the Use of a Shock and Vibration Isolation System for Litter Patients in Air Medical Support. Master’s Thesis, The University of Nevada, Las Vegas, NV, USA, 2015. [Google Scholar]
- Khaksar, Z.; Anavatti, S.; Ceruti, A.; Shankar, K. The Simulation of Vibration at the Supine Patient’s Body in HEMS. In Proceedings of the 9th Australasian Congress on Applied Mechanics, Sydney, Australia, 27–29 November 2017. [Google Scholar]
- Johnson, W. A History of Rotorcraft Comprehensive Analyses; TP 2012-216012; NASA: Washington, DC, USA, 2012. [Google Scholar]
- Tamer, A.; Muscarello, V.; Masarati, P.; Quaranta, G. Evaluation of vibration reduction devices for helicopter ride quality improvement. Aerosp. Sci. Technol. 2019, 95, 105456. [Google Scholar] [CrossRef]
- Masarati, P.; Muscarello, V.; Quaranta, G. Linearized Aeroservoelastic Analysis of Rotary-Wing Aircraft. In Proceedings of the 36th European Rotorcraft Forum, Paris, France, 7–9 September 2010; p. 099. [Google Scholar]
- Masarati, P.; Muscarello, V.; Quaranta, G.; Locatelli, A.; Mangone, D.; Riviello, L.; Viganò, L. An Integrated Environment for Helicopter Aeroservoelastic Analysis: the Ground Resonance Case. In Proceedings of the 37th European Rotorcraft Forum, Vergiate/Gallarate, Italy, 13–15 September 2011; pp. 177.1–177.12. [Google Scholar]
- Craig, R.R., Jr.; Bampton, M.C.C. Coupling of Substructures for Dynamic Analysis. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- Johnson, W. CAMRAD/JA, A Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics; Johnson Aeronautics Version; Johnson Aeronautics: Palo Alto, CA, USA, 1988. [Google Scholar]
- Pitt, D.M.; Peters, D.A. Theoretical Prediction of Dynamic-Inflow Derivatives. Vertica 1981, 5, 21–34. [Google Scholar]
- Merritt, H.E. Hydraulic Control Systems; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Rakheja, S.; Dong, R.; Patra, S.; Boileau, P.E.; Marcotte, P.; Warren, C. Biodynamics of the human body under whole-body vibration: Synthesis of the reported data. Int. J. Ind. Ergon. 2010, 40, 710–732. [Google Scholar] [CrossRef]
- Mohajer, N.; Abdi, H.; Nahavandi, S.; Nelson, K. Directional and sectional ride comfort estimation using an integrated human biomechanical-seat foam model. J. Sound Vib. 2017, 403, 38–58. [Google Scholar] [CrossRef]
- Tamer, A.; Zanoni, A.; Muscarello, V.; Cocco, A.; Quaranta, G.; Masarati, P. Biodynamic Modeling Techniques for Rotorcraft Comfort Evaluation. Aerotec. Missili Spaz. 2019. [Google Scholar] [CrossRef]
- Bai, X.X.; Xu, S.X.; Cheng, W.; Qian, L.J. On 4-degree-of-freedom biodynamic models of seated occupants: Lumped-parameter modeling. J. Sound Vib. 2017, 402, 122–141. [Google Scholar] [CrossRef]
- Wan, Y.; Schimmels, J.M. Optimal seat suspension design based on minimum simulated subjective response. J. Biomech. Eng. 1997, 119, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Ciloglu, H.; Alziadeh, M.; Mohany, A.; Kishawy, H. Assessment of the whole body vibration exposure and the dynamic seat comfort in passenger aircraft. Int. J. Ind. Ergon. 2015, 45, 116–123. [Google Scholar] [CrossRef]
- Choi, Y.T.; Wereley, N. Biodynamic Response Mitigation to Shock Loads Using Magnetorheological Helicopter Crew Seat Suspensions. J. Aircr. 2005, 42, 1288–1295. [Google Scholar] [CrossRef]
- Rahmatalla, S.; DeShaw, J. Predictive discomfort of non-neutral head–neck postures in fore–aft whole-body vibration. Ergonomics 2011, 54, 263–272. [Google Scholar] [CrossRef]
- Law, A.H.; Beatty, H.E.W.; Keillor, J.; Wickramasinghe, V. Pilot Head and Neck Response to Helicopter Whole Body Vibration and Head-Supported Mass. In Proceedings of the AHS 73rd Annual Forum, Fort Worth, TX, USA, 9–11 May 2017. [Google Scholar]
- Rahmatalla, S.; DeShaw, J.; Barazanji, K. Biodynamics of supine humans and interaction with transport systems during vibration and shocks. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 808–816. [Google Scholar] [CrossRef]
- Cho, Y.; Yoon, Y.S. Biomechanical model of human on seat with backrest for evaluating ride quality. Int. J. Ind. Ergon. 2001, 27, 331–345. [Google Scholar] [CrossRef]
- DeShaw, J.; Rahmatalla, S. Predictive discomfort of supine humans in whole-body vibration and shock environments. Ergonomics 2016, 59, 568–581. [Google Scholar] [CrossRef]
- Lifesaving Systems Corp. Online Catalog. Available online: http://lifesavingsystems.com/store/lifesaving_catalog/mobile/index.html#p=5 (accessed on 9 February 2020).
- Weinberg, W.T. Aircraft Litter Retention Design Criteria; Technical Report AD632457; USAAVLABS: Fort Eustis, VA, USA, 1990. [Google Scholar]



| Posture | Location | |||
|---|---|---|---|---|
| Seat surface | 1.00 | 1.00 | 1.00 | |
| Seating | Back Rest | 0.80 | 0.50 | 0.40 |
| Feet | 0.25 | 0.25 | 0.40 | |
| Standing | Floor | 1.00 | 1.00 | 1.00 |
| Recumbent | Floor | 1.00 | 1.00 | 1.00 |
| Component | Identifier | () | () | () |
|---|---|---|---|---|
| Abdomen | a | 36.00 | 2475.00 | 49,341.60 |
| Viscera | v | 5.50 | 330.00 | 20,000.00 |
| Chest | c | 15.00 | 200.00 | 10,000.00 |
| Head | h | 4.17 | 250.00 | 134,400.00 |
| Spine | - | 909.09 | 192,000.00 | |
| Seat | s | 13.5 | 750.00 | 22,600.00 |
| Cushion | - | 159.00 | 37,700.00 |
| Parameter | Value | ||
|---|---|---|---|
| , | |||
| , | |||
| , | |||
| Human | , | 0.10 | 1.30 |
| , | 0.00 | 2576.5 | |
| , | 25.0 | 182.1 | |
| , | 17.2 | 380.6 | |
| Length | , | ||
| Cushion | , | 159.00 | 37.70 |
| Support | , | 750 | |
| Stretcher | , | 2200 |
| Parameter | Value | ||
|---|---|---|---|
| Equipment | , | 150 | |
| Dimensions | , | ||
| Support | , | 750 |
| Component | Amplitude (% TOW) | Phase (Deg.) |
|---|---|---|
| Longitudinal | 3.6 | 0 |
| Lateral | 1.4 | 0 |
| Vertical | 16.4 | 0 |
| ID | Definition | Cost Matrix (W) |
|---|---|---|
| 1 | Equal cost | |
| 2 | Focus on patient | |
| 3 | Focus on two crews | |
| 4 | Focus on equipment |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamer, A.; Muscarello, V.; Quaranta, G.; Masarati, P. Cabin Layout Optimization for Vibration Hazard Reduction in Helicopter Emergency Medical Service. Aerospace 2020, 7, 59. https://doi.org/10.3390/aerospace7050059
Tamer A, Muscarello V, Quaranta G, Masarati P. Cabin Layout Optimization for Vibration Hazard Reduction in Helicopter Emergency Medical Service. Aerospace. 2020; 7(5):59. https://doi.org/10.3390/aerospace7050059
Chicago/Turabian StyleTamer, Aykut, Vincenzo Muscarello, Giuseppe Quaranta, and Pierangelo Masarati. 2020. "Cabin Layout Optimization for Vibration Hazard Reduction in Helicopter Emergency Medical Service" Aerospace 7, no. 5: 59. https://doi.org/10.3390/aerospace7050059
APA StyleTamer, A., Muscarello, V., Quaranta, G., & Masarati, P. (2020). Cabin Layout Optimization for Vibration Hazard Reduction in Helicopter Emergency Medical Service. Aerospace, 7(5), 59. https://doi.org/10.3390/aerospace7050059







