1. Motivation
The aircraft cabin is steadily becoming more important for both aircraft manufacturers and airlines, as it is the most prominent aspect of an aircraft that passengers are in contact with during a commercial flight. In regards to this, the boarding performance of an aircraft plays a key part in the customer experience and enables cost saving potential by reducing the critical path and thus turnaround time at the airport [
1,
2].
An important aspect of today’s aircraft operational research is optimizing the boarding procedure and uncovering options for a reduction in boarding time while increasing passenger comfort throughout the process [
2,
3,
4]. In alignment with this focus, the boarding process is assessed during the course of the German research project “AdVanced Aircraft CONcepts” (AVACON). The project’s target is to develop a mid-range aircraft concept with a projected entry into service in the year 2028 [
5]. A secondary target is to strengthen the interdisciplinary connections within the German aerospace industry.
Throughout the course of the project, multiple design iterations of the aircraft concept are performed. For each of these concepts, the boarding process performance of the corresponding cabin layout has to be assessed. To do so, Bauhaus Luftfahrt is applying the PAXelerate boarding simulation tool to the different cabin concepts. As the project demands a greater level of detail for PAXelerate regarding the passenger movement, a novel methodology was both created and implemented into PAXelerate and is now introduced in the scope of this publication.
In order to assess different cabin layout modifications and changes to the passenger behavior throughout the project, it is required to model the passenger movement in more detail than previously. Especially the location of cabin monuments (e.g., lavatories, galleys, or cabin dividers) and their respective impact as well as other passengers within the cabin are of increased interest. The target is thus to develop a model capable of describing the passenger walking speed depending on the surrounding objects and their proximity. Other passengers walking ahead or already seated and their influence on moving passengers are also taken into consideration. The following
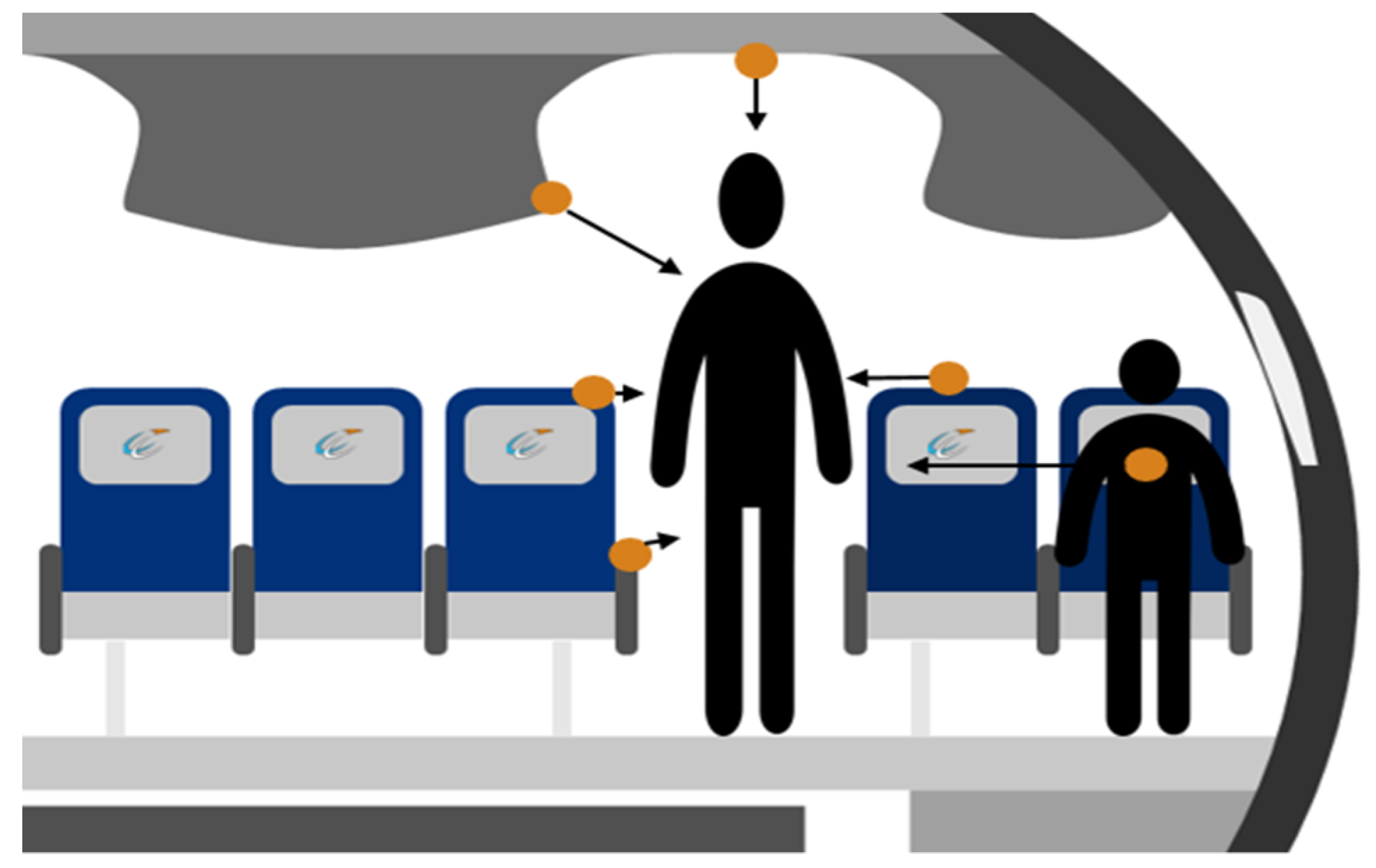
Figure 1 depicts the modelling approach for this problem. It is based on the fundamental assumption that every object in proximity of the passenger, its dimensions as well as its location in relation to a walking human affects the resulting walking speed. The challenges of this modelling approach are, as depicted in
Figure 1, the determination and modelling of the influence of all objects such as arm rests of seats, overhead bins, the ceiling as well as other passengers already seated or preceding the walking passenger. Specifically, the strength and range of these different influences as well as their interaction with each other has to be determined and properly dimensioned.
In recent developments, the global COVID-19 pandemic has also put the spotlight on the aircraft cabin and the health risks its passengers are exposed to. These risks are especially high during the boarding and de-boarding procedures where moving passengers walk within close proximity of each other. This is why airlines have introduced several measures that aim to reduce these risks by requiring masks at all times [
6], reducing on-board catering options, and restricting passenger movement during flight [
7]. During the boarding specifically, passengers are asked to keep a safe distance while queueing and to adhere to the given boarding sequence (e.g., boarding in zones) [
8]. Prior to cabin entry, a mandatory temperature screening or even a COVID-19 test can be required [
9]. All these measures can increase the turnaround time of a typical aircraft by up to 15 min [
10].
This situation has triggered research interest in different aspects of the boarding process and their implication on the infection risk of passengers. For example, different suggestions regarding the boarding strategy have emerged. These include back-to-front [
10] or window-to-aisle boarding [
11], a new reverse pyramid boarding [
12] as well as restrictions to hand luggage and a safe distance between passengers [
13].
The target for the new movement model of PAXelerate is to enable a more precise boarding process simulation, taking into account the aircraft cabin geometry and other passengers in proximity. Furthermore, it aims to provide a better control over the passenger walking behavior itself. These aspects will advance the new movement model compared to the previous implementation and can enable PAXelerate to contribute to the understanding of a future pandemic-proof boarding scenario.
2. Literature Review
Passenger flow simulations are the preferred tool for assessing and optimizing congested and crowded areas with regard to fast movement and safety. The following is an examination and assessment of various simulation frameworks regarding their implementation of passenger walking speed calculation depending on the environment and other people. Depending on the research purpose of the simulations, the concepts differ strongly. This is especially true concerning the modelling of human movement within the environment. Therefore, simulations focusing on the boarding of aircrafts are covered first.
An overview of existing passenger flow simulation frameworks focusing on an aircraft and terminal application is listed in
Table 1 below. Aspects of the simulation by Fuchte as well as MASim by Richter found application in the development of PAXelerate.
All of these simulation frameworks are either not published or only available for commercial use, thus preventing any examination of their passenger movement model. However, there are other simulation types that include a detailed human movement model such as for simulations of crowded places, e.g., events or public transport infrastructures. Depending on the particular situation, different approaches to simulate humans interacting with the environment find application. Passenger flows at events such as concerts, where many people move towards a common exit, are often modelled following gas kinetic analogies, whereas simulations for public transport facilities use approaches with a focus on the simulation of passengers as individuals [
22]. In addition, these simulations vary in their modelling of the environment and the shape of the human body [
23]. Finally, video recordings are applied to derive parameters or attributes of human individuals and surroundings from real-life tests [
24].
2.1. Categorization
In general, simulation models can be categorized depending on their characteristics. This includes distinguishing between macroscopic and microscopic as well as discrete and continuous models [
25]. Rather than modelling the behavior of each individual, macroscopic simulations model the passenger flow as a whole [
22]. In contrast, microscopic models calculate no overall states of passenger flows, but rather simulate every passenger as an individual. An overview of the different model types can be seen in the following
Table 2.
2.2. Obstacle Interaction
There are different existing concepts for passenger-obstacle interactions in passenger flow simulations [
28]. In social force models, the interaction between passengers and obstacles (e.g., seats, galleys or lavatories) is modelled using forces that act on the passenger. The driving forces for a desired walking speed and the attraction towards a goal are superimposed by braking forces of nearby obstacles.
Regarding cellular automata, a cell is only blocked by one passenger or obstacle at a time. Thus, a passenger cannot make a step on a cell occupied by an obstacle. Passengers can however access a cell next to an obstacle. To prevent this, an influence area around obstacles can be introduced by combining a cellular automaton and a social force model [
22]. Here, forces that would act on a passenger are converted into potential fields around obstacles that decline with increased distance. The passenger walking speed and direction can then be adapted according to this potential.
Other models use velocity-based approaches adapted from computer graphics and animations to anticipate collisions between passengers and obstacles by using speed vectors to recognize possible conflicts and adapt the vectors accordingly. Other approaches calculate three-dimensional distances, sometimes only in the field of vision of a passenger, to detect obstacles and avoid collisions. These methods require more computing power than the aforementioned methods [
28].
To achieve the most realistic results, the behavior of passengers close to obstacles can also be assessed using real-life experiments. This may include the reaction time from the perception of an obstacle in a certain distance to initiating an avoidance maneuver. To simplify test setups, these assessments could also be conducted with the aid of virtual reality [
29].
2.3. Passenger Interaction
Passenger interaction is based on the same concepts as obstacle interaction. However, forces, potentials, or three-dimensional distances are not only calculated for static objects but for moving passengers. This requires a recalculation after each location change as well as in the integration of novel aspects such as overtaking. Additionally, interactions between two passengers are not restricted to collision avoidance. Weidmann [
30] discusses the influence of passenger density on walking speed. The relation between walking speed and density can be explained by the two effects of maintaining personal space and speed as function of step length and frequency.
Passengers demand personal space free of other individuals (and objects) for comfort [
29]. To keep this personal space free, passengers tend to evenly spread over a given space and prefer to reduce their walking speed rather than compromising their personal space.
The walking speed is a function of individual step length and frequency of steps [
30]. With increasing density, the available space for each passenger decreases. The step length and/or frequency will be reduced and walking speed will decrease. Above a certain density, the remaining space for every passenger is just sufficient to stand, but it is no longer possible to walk.
3. PAXelerate
After the introduction of different crowd simulation types and modelling approaches, this chapter introduces the open-source passenger flow simulation PAXelerate [
31]. It is based on a 2D agent-based modelling approach with aspects of a cellular automaton (see
Section 3.2). It has been developed by Bauhaus Luftfahrt as a boarding assessment tool and provides fast and easy results for the boarding performance of both conventional and novel cabin layouts. The underlying algorithm for the simulation is called the cheapest path A Star and operates in a grid-based cabin representation [
14,
32].
3.1. General
For the AVACON project, support for the CPACS file format [
33] has been integrated into PAXelerate. This enables a fast import and integration of various aircraft concepts into the tool via an interface. CPACS, which can “hold data from a variety of disciplines considered in an aircraft design process” [
34] is a common language for aircraft design and can contain information on the shape and structure of the fuselage as well as the size and positioning of monuments and seats within the cabin.
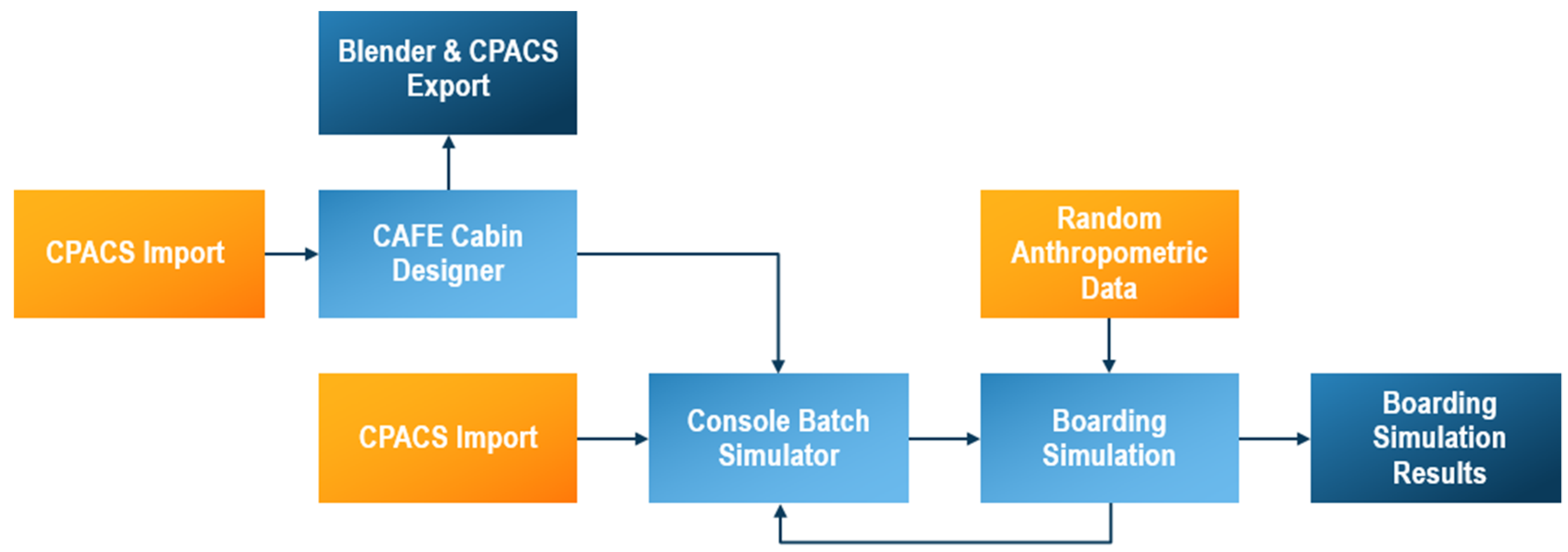
PAXelerate comprises the CAFE cabin designer and simulation module (
Figure 2), with the latter one being the focus of this publication. It enables the batch simulation of cabin scenarios generated with Monte Carlo based passenger and boarding properties and also contains movement and pathfinding models. The cabin input required for the simulation is delivered by the cabin configurator module, which allows for an import, modification and export of CPACS files. Additionally, common design rules and CS25 conformability can be assessed.
3.2. Current Movement Model
The currently implemented movement model of PAXelerate is based on a cellular automaton approach with a grid of nodes, where each node contains various properties. The cabin is discretized in the x-y-plane and the distance between neighboring nodes is currently set to 10 centimeters. Other distances are configurable as well. This delivers a node grid with a 10 by 10 nodes per square meter resolution of the cabin area along its width and length axis.
Each node contains properties defining its location comprising an x and y value as well as various other parameters such as whether the node represents an obstacle or a passenger is currently located on the node. An obstacle represents an object within the cabin that interacts with a passenger during the pathfinding and walking processes. This can be a galley, a lavatory, a seat or any other object located on the cabin floor. Additionally, each node contains a value providing information on the difficulty for a passenger to walk on the node. This is called the potential and makes the PAXelerate movement model a hybrid of a social force model and a cellular automaton. Each object in the cabin is surrounded by this potential with a linear gradient, creating a map. This motivates the passenger to keep a distance to objects, as the difficulty of using these nodes is higher compared to nodes with a larger distance to obstacles. The cheapest path, meaning the path with the lowest total sum of cost potential in all nodes being used for walking, is determined by an A star algorithm operating with the cheapest path condition.
The walking behavior of the passengers itself is modelled in a simplistic way, where the speed is derived by an age-speed-distribution. After a delay with a duration of the theoretical time needed to reach the next node position, the passenger object is moved one node ahead. No external factor has any influence on the walking speed, but the size and amount of luggage a passenger is carrying decreases the walking speed by a predetermined factor. A minimum distance to other passengers in combination with a check if the next scheduled node plus the minimum distance is already occupied delivers the decision to stop walking and wait for the preceding passenger to clear the path. Lastly, an acceleration and deceleration procedure consisting of a basic linear equation influences the walking speed when approaching the minimum distance mentioned above.
Summing up, the movement model in PAXelerate consists of an agent-based approach for the modelling of passengers and their characteristics, while the movement itself is based on a cellular automaton approach with a grid of nodes and discretized steps within the simulation bounds. The obstacle avoidance aspects are derived from a social force model, creating a hybrid model, as explained in
Section 2.2.
4. Novel Movement Modelling Approach
For the AVACON project, a new approach advances the movement model previously implemented in PAXelerate. The new design aims to calculate the walking speed of a passenger within the cabin as a function of its surroundings and other passengers, as seen in
Figure 1. Two challenges have been identified in this regard, with the first being the modelling of the impact of three-dimensional objects on the walking speed of passengers at every moment and every position within the cabin. The second challenge is the modelling of the influence of other, already seated and walking, passengers within the cabin environment on the walking speed. The following sections will give an overview of both aspects of the novel model.
4.1. Methodology
Ideally, the distance between each geometry surface of every element within the cabin and the passenger itself has to be calculated at every time step of the simulation in order to get an exact measurement of the surroundings of a passenger. The problem therein is the immense computational effort required to calculate 3D distances of every object surface to every passenger as well as all passengers amongst each other. As the procedure has to be repeated for every time step, there is a need for a more simplified approach, which can reduce the calculation effort by increased model abstraction, while yielding sufficient information for a reasonably accurate simulation. The solution to this problem lies in the structure of the PAXelerate boarding simulation, which consists of a discretized cabin area built out of a grid of nodes. As these nodes represent a specific location, each node can also contain the distance information to the closest cabin monument. It is thus possible to pre-calculate the distance of every node within the cabin to the closest monument in advance of a batch simulation, thereby reducing the required number of calculations to just one. This can be done given that no cabin monument changes position throughout the simulation loops.
Concerning the model abstraction, an additional measure has been taken. Looking at the human body, four distinctive elements of the human body were defined for modeling the influence on a human’s walking behavior in a constricted space. Those body parts are the knee, hip, shoulder and head, each positioned at a different height and each exposed to a different layout of the cabin at the respective height. As listed in
Table 3 below, the cabin model is thus in a first step divided into four layers, with each layer comprising of a different grid of nodes and each representing the cabin and the containing objects at a specific height above the cabin floor. The lower three layers contain information on the position and size of cabin monuments at the specific height, whereas the upper ceiling layer contains information about the cabin ceiling height as well as the size and position of the overhead bins.
The selection of the different heights is based on four neuralgic body parts of the human body during walking. This includes the knee in the ground layer, the waist in the mid layer as well as the shoulders and head in the top layer. The height of the layers is designed to surround the specific neuralgic point, based on average human body dimensions as seen in
Table 4 and in relation with the given cabin elements such as seat objects.
4.2. Modelling of Passengers
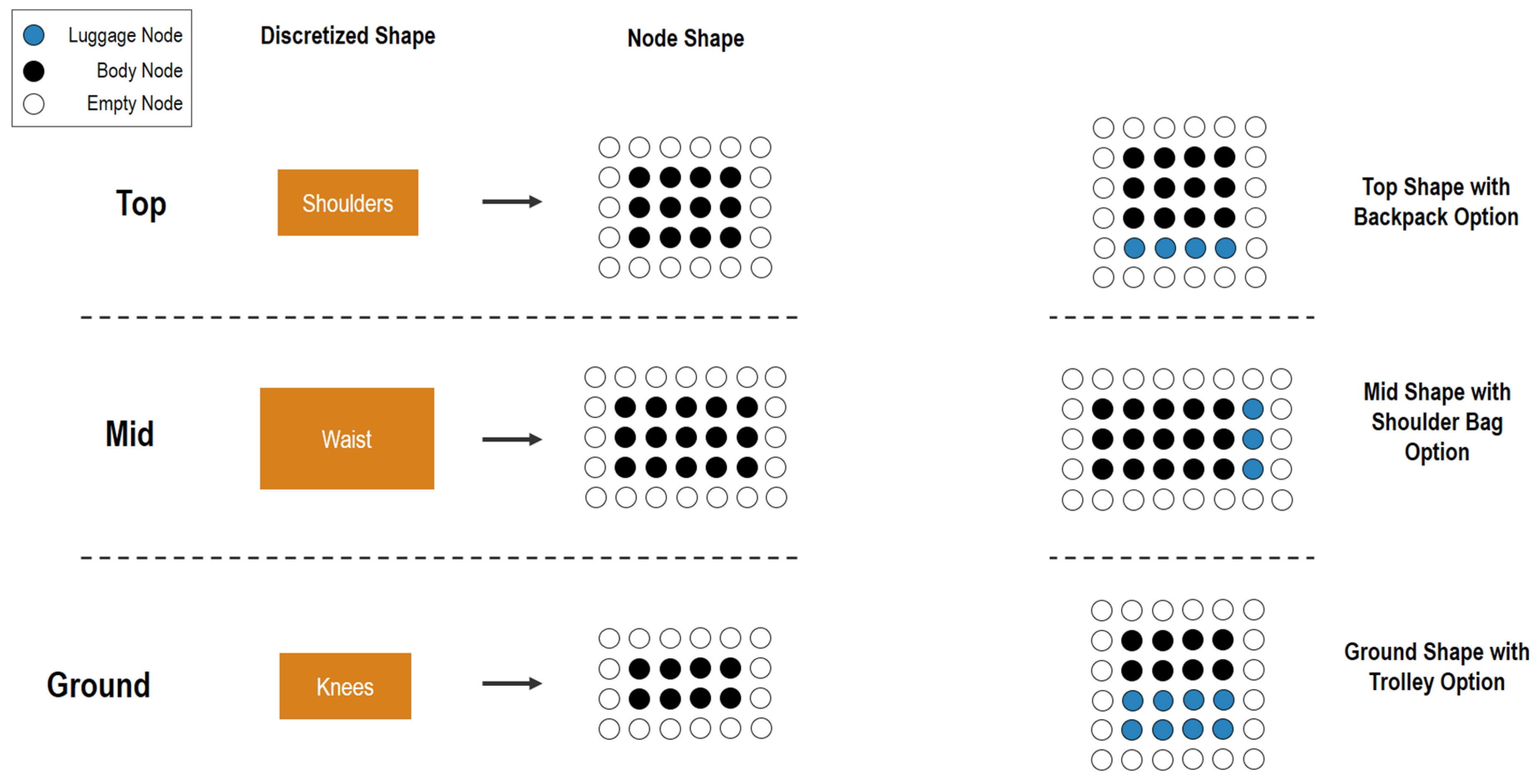
Inside the grid-based cabin layout of the PAXelerate boarding simulation, passengers are modelled as discretized rectangular shapes. At each of the different heights of the three modelling layers, the passenger is represented with a different size within the grid. As can be seen in
Figure 3 below, the top layer body shape consists of the shoulder dimensions, the mid layer consists of the waist width and depth and the ground layer contains the knee width and depth. All values are based on the data seen in
Table 5 below.
The values used in the simulation are, as PAXelerate uses a Monte Carlo approach for all anthropometric data, generated individually for each passenger from the mean and deviation values of a normal distribution.
A potential carry-on luggage is amended to the human body at respective height layer (see luggage nodes in
Figure 3 above). The luggage options currently implemented contain a backpack extending the shoulder and waist depth and a shoulder bag extending waist width. Additionally, the options contain a cabin trolley extending the knee depth backwards if pulled or in front if pushed. Lastly, a combination of multiple carry-on luggage items is also taken into account.
During the course of the boarding simulation, the carry-on luggage is considered an integral part of the human body up to the point of luggage stowing. Additionally, every luggage carried by the passenger decreases the walking speed by a certain factor.
4.3. Modelling of Cabin Monuments
The following
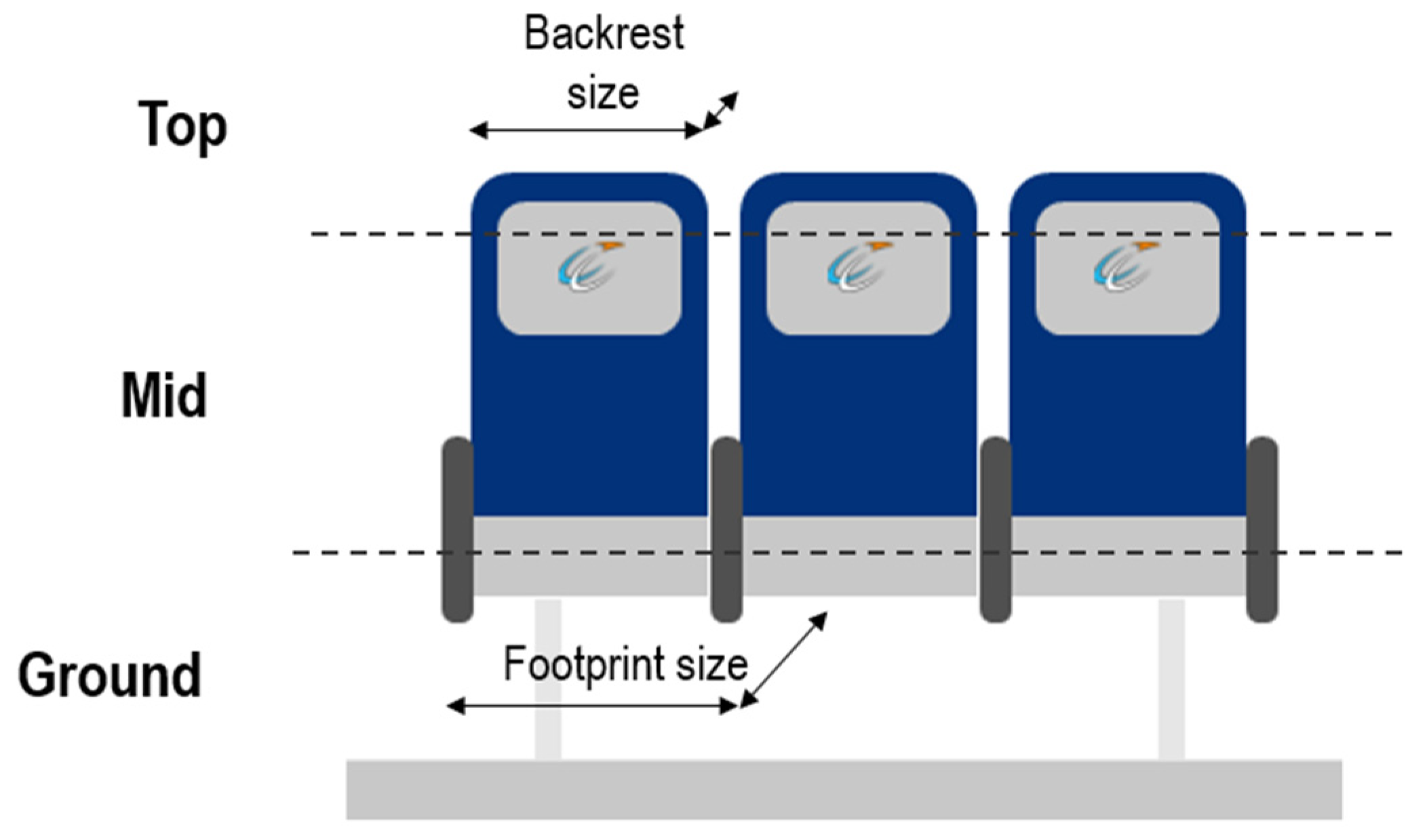
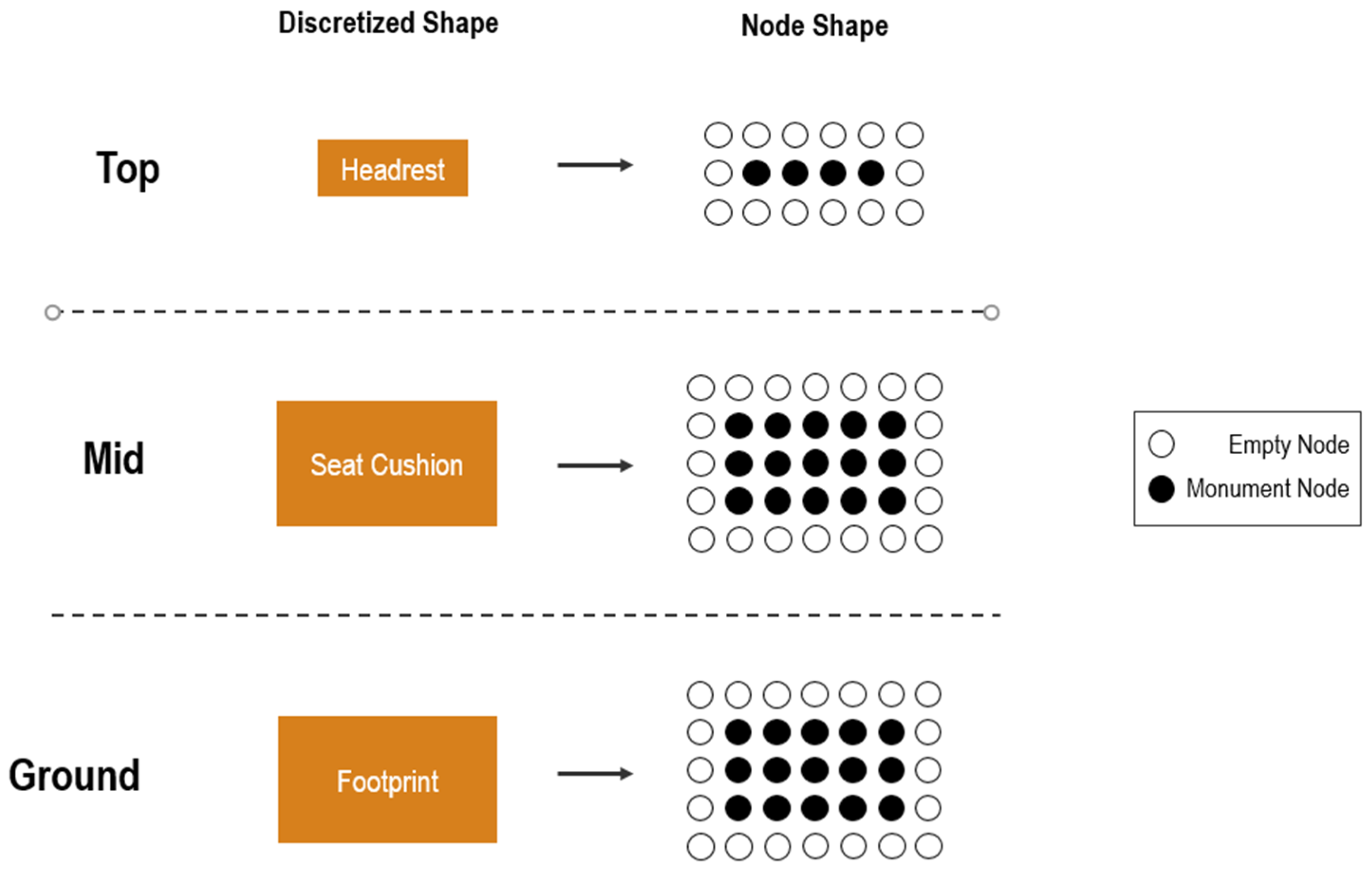
Figure 4 highlights the seat dimensions used for the discretized shape of cabin seats at the different height layers. As the width of a seat is almost identical at the armrest and floor level, the same dimension is used for the lower two layers. The top width is smaller due to the slimmer backrest dimensions. Considering the depth of the seats, each layer has a different dimension, beginning at the floor level with the base footprint size, continuing to the middle layer, where the armrest dimension is critical and ending at the top width of the seat, consisting of the backrest depth.
Figure 5 depicts the transition of the cabin seat into a discretized rectangle inside the PAXelerate node grid for each of the different layers. All other cabin monuments such as lavatories or galleys are modelled in the same way. However, monuments with a vertical wall are modelled with the same dimensions in each of the layers. The overhead bins are not considered cabin monuments and are thus not included in this modelling approach but rather dealt with in a separate fashion as described in a later section.
4.3.1. Influence Area of Cabin Monuments
In order to estimate the effect of the distance of objects to a passenger, each cabin monument inside the simulation grid is surrounded by a potential
, creating a so-called influence area (see Equation (1)). This is the core method of reducing the computation effort by pre-calculating the linear distance between objects for each simulation step. This is feasible, as each node knows its own position to the closest object in advance. A passenger walking through the nodes within this influence area will decrease their walking speed depending on the node’s properties and the pre-calculated distance value
stored within the node. The potential correlates to the linear interpolation between
and
in dependence of the inverse distance to the object.
The value of
and
were chosen in order to comply with boarding times published by Airbus [
36] or parameters extracted form video sequences by Steiner and Philipp [
37]. In fact, it requires real-life experiments to determine the detailed impact of different obstacle types on passenger walking speed.
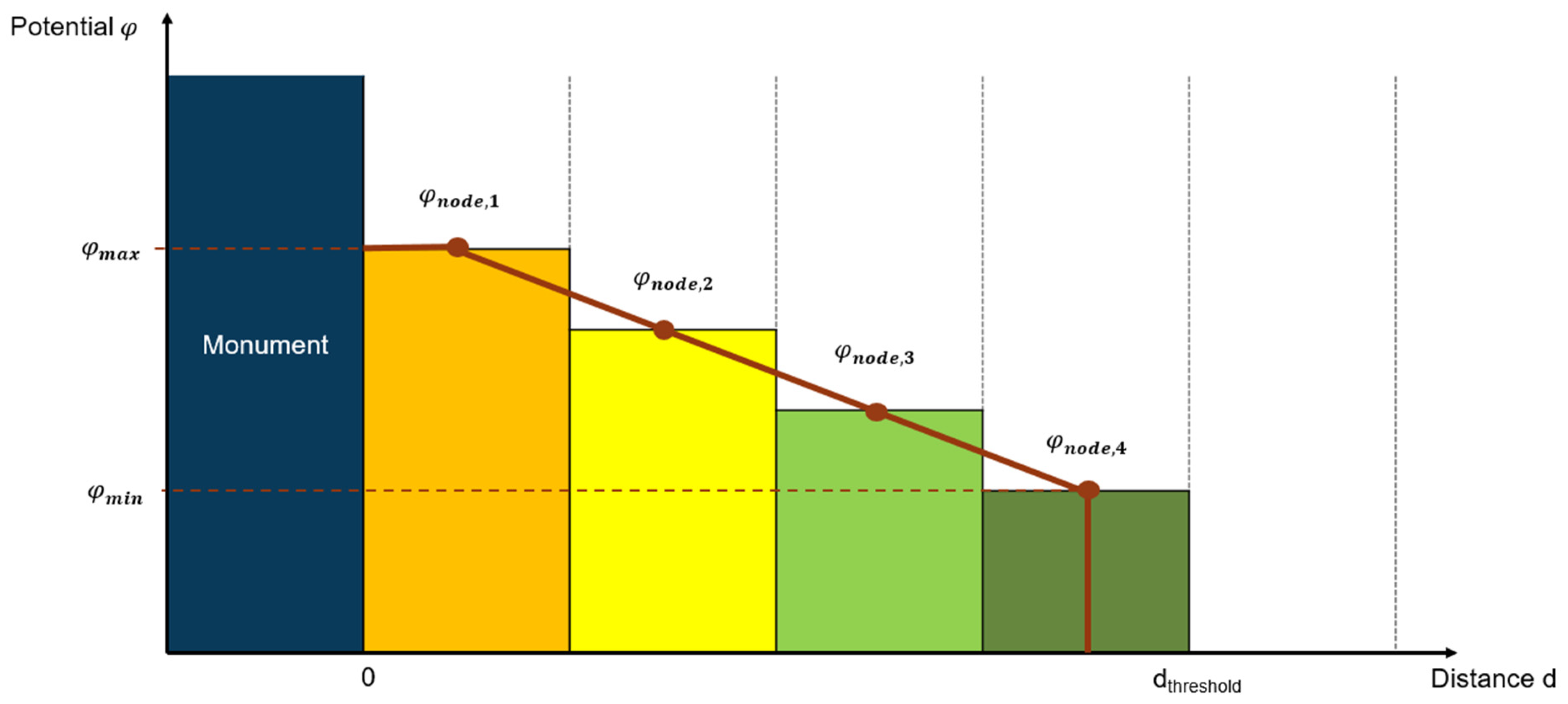
As can be seen in
Figure 6 below, the potential is cut off at a specific distance
of the object. This is based on the assumption that after surpassing a given distance, no effect on the walking speed can be detected and thus a computation and storing of these values is obsolete and would reduce the computation performance.
Figure 7 shows the potentials surrounding a group of seats at two different heights, one representing the lower parts of the seats and one representing only the backrests and their surrounding potential area.
The only time this node grid changes throughout a simulation is when a passenger is seated onto a seat. This increases the potential surrounding the respective seat by raising the value, thus integrating effects on the walking behavior of passengers by others already seated.
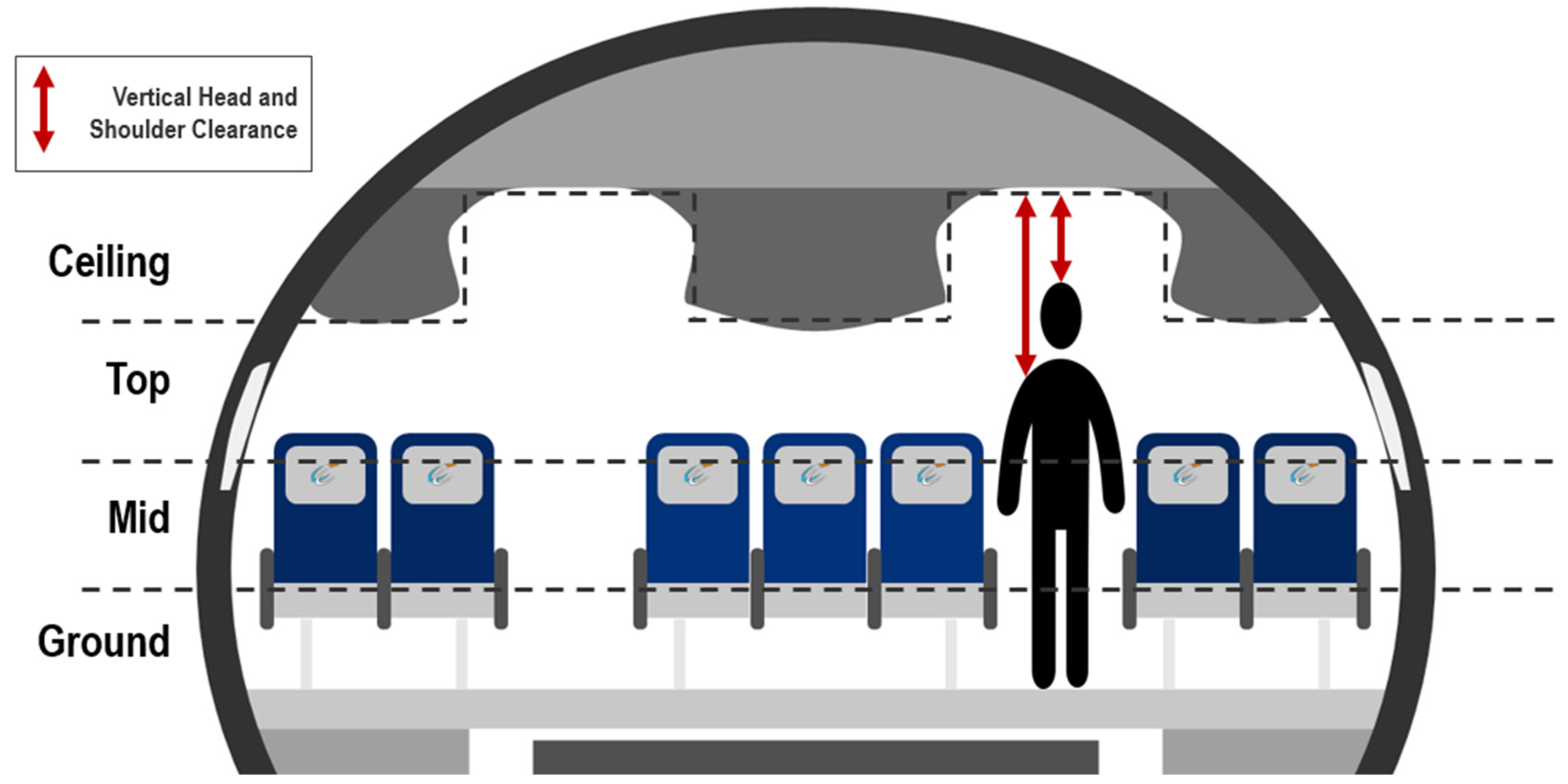
4.3.2. Modelling of the Overhead Bins and Ceiling
The ceiling layer is similar to other layers but further includes the ceiling height at a certain location as highlighted in
Figure 8. The head and shoulder clearances are thus additionally stored at each node covered by the ceiling-layer.
4.3.3. Calculating the Effect of Close Objects on the Walking Speed
At first, the sum of all potentials that act on a passenger while walking over a node is calculated for each step. All nodes occupied by the passenger, as seen in
Figure 3, represent the current position of the passenger. Each node can have a certain potential
in each layer from nearby objects (see
Figure 6). These potentials are first summed up over all occupied nodes of one layer and then over all layers from
, where
is the amount of layers in the model. Finally, the mean potential
is calculated by dividing this sum by the total number of nodes
occupied in all layers (see Equation (2)). This results in a potential
averaged over all nodes in all layers occupied by a passenger.
The same equation covers the low ceiling and overhead bin effects, but additionally the vertical distance between head, shoulders, and ceiling is considered within the function for
as well. The sum of
from Equation (2) and the potential of the ceiling
is divided by the maximum potential
defined in
Section 4.3.1 (see Equation (3)). This value is then subtracted from 1 and multiplied with the free walking speed
(see
Section 4.4.1). This results in the walking speed with obstacle interference
.
4.4. Impact of Passengers
4.4.1. Fundamental Relations
The modelling of the interaction between passengers and their impact on the walking speed is derived from the social force and cellular automaton hybrid approach explained in
Section 3. In general, the walking speed of a human in a crowded area—where free, unrestricted walking is not possible—depends on the crowd density. This approach is based on the so-called fundamental diagram by Weidmann [
30] as described in
Section 2.3. The diagram is based on the following Equation (4), where
= 1.34 m/s is the free walking speed and
= 5.4 m
−2 is the density of humans at which a standstill occurs.
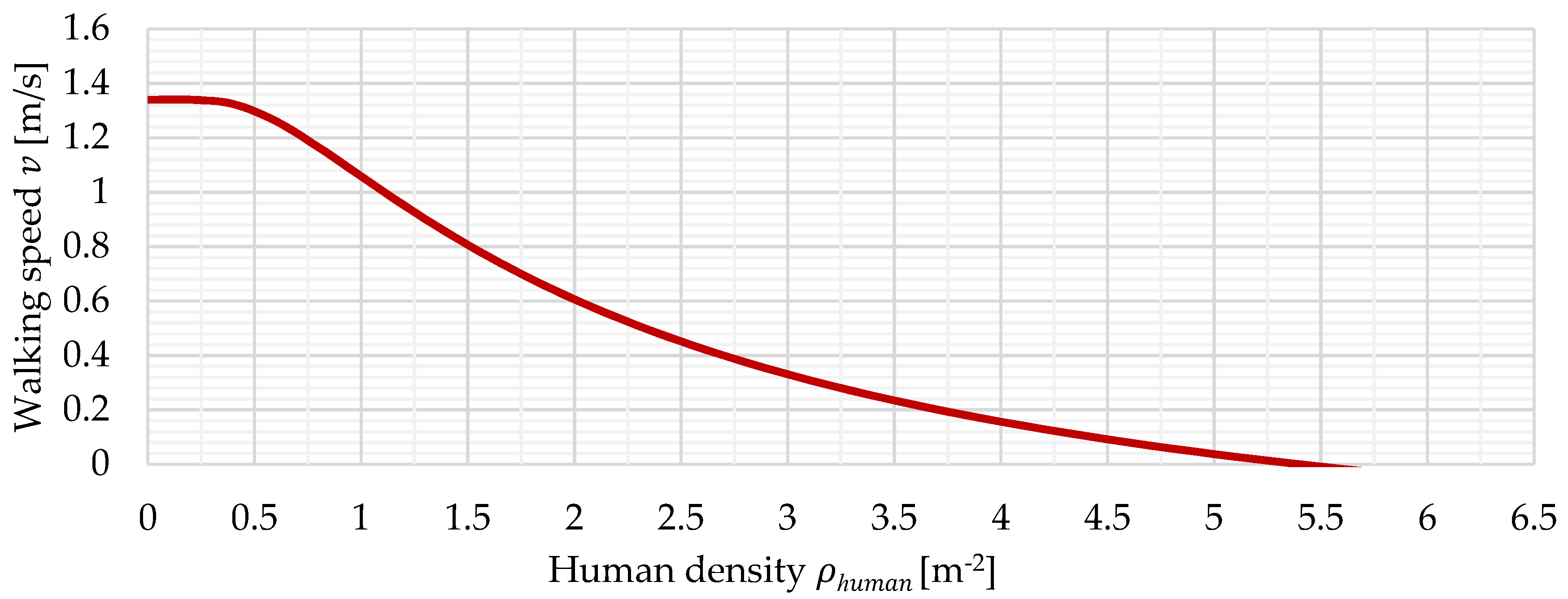
The resulting graph, depicting the walking speed in dependence of the density of people per square meter, can be seen in
Figure 9. As depicted, the walking speed reaches zero at a density of 5.4 people per square meter, resulting in a standstill. Free walking speed is maintained up to a density of roughly 0.4 people per square meter, after which a steeper decrease in walking speed can be observed.
Generally, there are other implementations of a walking speed and human density dependency such as for example the one used by Richter [
16] and seen in the following Equation (5). The model introduced in this paper however is based on the concepts introduced by Weidmann as his model has no case differentiation and consists of a single continuous equation.
4.4.2. Transition to Model for PAXelerate
As shown in Equation (4), the passenger density
inside the cabin is the only unknown variable that has to be determined. A widespread approach is to divide the simulated area into smaller parts and calculate the passenger density by dividing that area by the number of passengers inside [
16]. However, this force-based approach of applying a walking speed depending on an external variable contradicts the principle of independence of each passenger in PAXelerate’s agent-based approach.
Furthermore, today’s aircraft cabins usually offer narrow corridors for walking, which are often too tight to allow overtaking or counterflow. Future cabin layouts are, excluding modifiable seat designs which can temporarily alter the aisle width [
38], unlikely to increase aisle widths due to space and cost considerations. Additionally, passengers always prefer lane formation when walking in the same direction such as in aircraft cabins [
27].
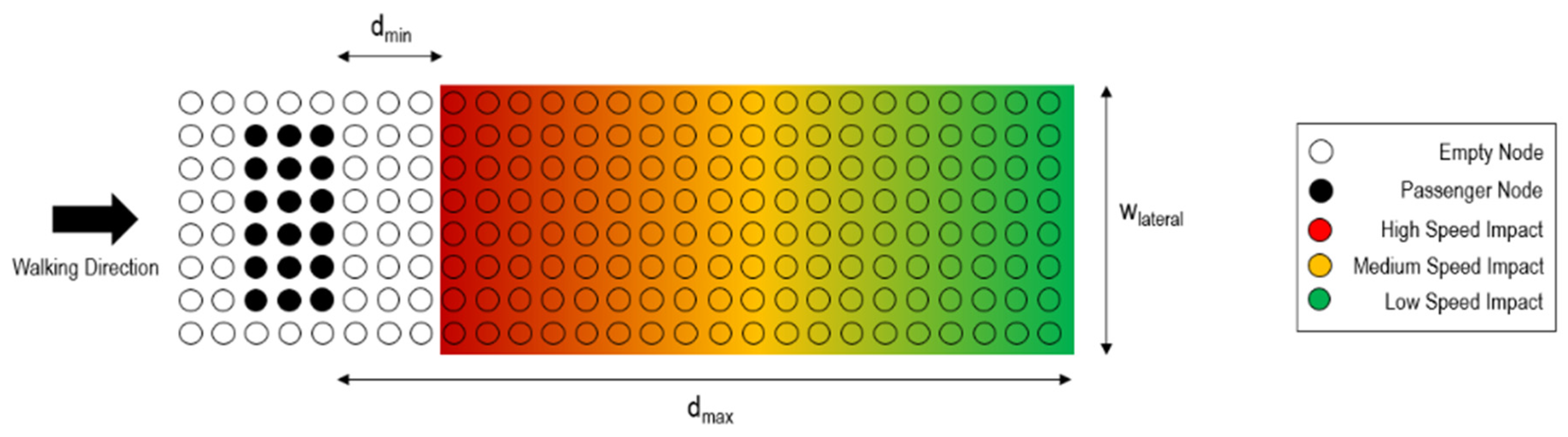
Due to this lane formation, a passenger is mainly influenced by the others walking directly ahead. Other passengers any further ahead or behind have no direct influence on the walking speed, as they are not directly perceived. Looking at a passenger individually, the critical area concerning crowd density effects and thus the area in which a passenger perceives others is solely the area directly in front. Consequently, the distance to the passenger in front determines the density experienced when walking in lane formation. The density can ultimately be seen as the free space in front of a passenger. If this space decreases, a passenger has to adapt the step size and slows down to avoid approaching the passenger ahead. The area of such as personal space is equal to the reciprocal of the density as seen in Equation (6).
Using the model of Weidmann and his assumptions regarding the needed lateral space while walking
= 0.71 m, a rectangular personal area can be defined together with the distance in walking direction d according to the following Equation (7).
Using Equations (6) and (7), the following Equation (8) can be derived. This equation delivers a dependency between the human density according to Weidmann and the personal space of a passenger.
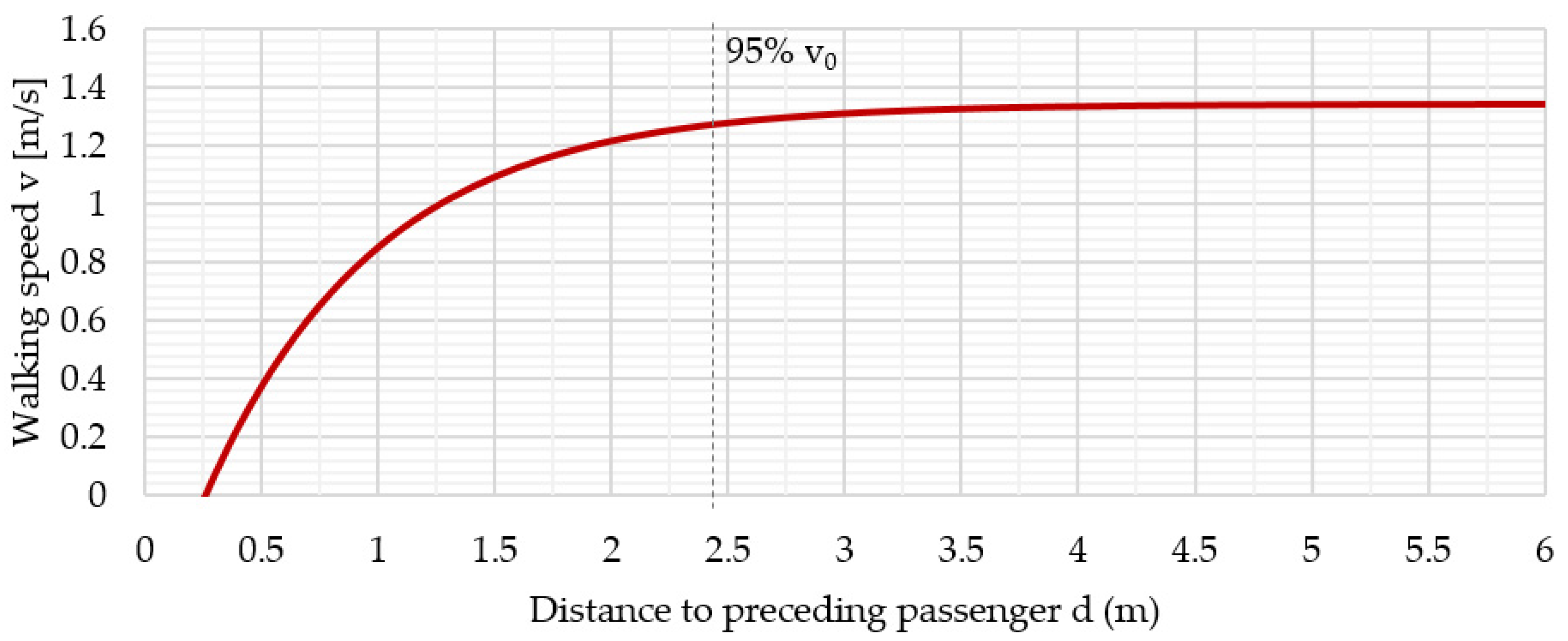
When integrating Equation (8) into Equation (4), the following Equation (9) results. The corresponding graph can be seen in
Figure 10. It depicts the dependency between the distance to a preceding passenger and the resulting walking speed.
The equation above also delivers the distance of
= 0.26 m, corresponding to a density
= 5.4 m
−2 and representing the minimum distance at which a standstill occurs. The curve is of asymptotic nature for
= 1.34 m/s, where 95% of
are reached at
= 2.47 m and 99% of
are reached at d = 3.65 m. For performance and simplification reasons, the maximum considered distance for a potential influence of preceding passengers is thus selected to be at the 95%
line. The two values of maximum and minimum influencing distance result in the rectangular of
Figure 11 below.
Combining the information from Equation (9) as well as
Figure 10 and
Figure 11, a passenger is in the free walking mode and is not influenced by any preceding passengers on the same path up to a distance of 2.47 m. This is explained by the fact that up to a distance d of greater than 2.47 m, the resulting
of Equation (9) is nearly constant. From 2.47 m down to a distance of 0.26 m, the walking speed will gradually slow down according to Equation (9). This can also be seen in the transition from a low to a high impact on the walking speed as seen in
Figure 11. At a distance of 0.26 m,
of Equation (9) equals 0 and the passenger comes to a standstill until the passenger in front increases the distance beyond the threshold.
4.4.3. Implementation of Model into PAXelerate
The shape, position, and personal influencing area of a passenger is saved in a discretized way, as seen in
Figure 11. The influence area is saved by applying a potential in the same way as for obstacles to each node within the rectangle. A node can save the potential of more than one passenger. If a passenger steps on a node that is part of such an influence area of other passengers, the speed factor is calculated according to Equation (9) if both passengers are walking. If the preceding passenger is already seated, the potential is rather used for the calculation of the factor and the other passenger is regarded as an obstacle. If different passengers have an influence on the current position, the most influencing passenger is determined by algorithms searching for the highest potential and considering the current orientation of the involved passengers. The speed factor is calculated only once by calculating an average footprint shape and not for each layer separately.
4.5. Model Summary
Information about nearby obstacles and influencing passengers are saved as a property for each node. At each step, the effects of nearby objects and other passengers on the walking speed are calculated separately. Finally, as seen in Equation (10), the lower speed, hence the higher and more influential speed factor is chosen to calculate the walking speed for the next step.
Generally, the approach chosen for the movement model was selected because it builds on the foundation of PAXelerate as a hybrid cellular automaton and agent-based simulation. The obstacle interaction is based on a social force approach and the interaction between passengers in the constricted aisle is based on an adapted walking speed and human density relation. Finally, the following
Table 6 provides an overview of changes to PAXelerate regarding the new movement model implementation.
5. Validation
This chapter presents the validation of the new movement model implemented for the AVACON project and is introduced in this paper. It comprises of a default boarding simulation loop with default passenger properties. As cabin layouts, the AVACON research baseline as well as an Airbus A320 type aircraft are selected.
5.1. AVACON Research Baseline
The AVACON research baseline (ARB) is a mid-range aircraft and the foundation of the AVACON project and is based on a Boeing 767 aircraft [
5]. The corresponding cabin layout can be seen in
Figure 12 below. In a related paper regarding PAXelerate and the AVACON project, the PAXelerate boarding simulation has been applied to this reference aircraft with a variety of different boarding doors and strategies [
39].
Due to the Monte Carlo approach used for all passenger properties within PAXelerate (see
Section 4.2), the simulation is non-deterministic and rather delivers a normal distribution of boarding time results. The following input parameters in
Table 7 are used for the assessment of both the old and new movement models using the ARB aircraft.
The following
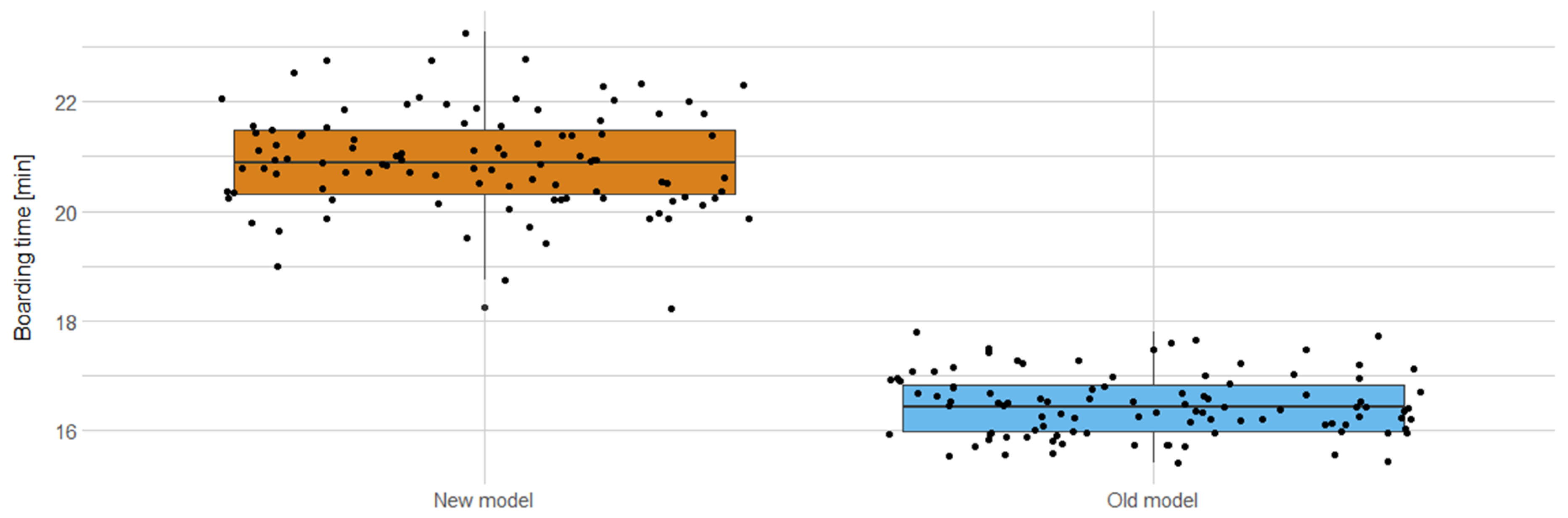
Figure 13 shows the boarding time distribution of the two models. Each dot represents a boarding time result for the respective model, whereas the bounds of the colored boxes represent the 25th and the 75th percentile, respectively. A horizontal line within the boxes represents the mean boarding time. For the old model, the execution of 100 simulation loops resulted in an average boarding time of 16:27 (mm:ss) for this twin aisle aircraft with 252 seats and the standard deviation accounted to 34 s. In comparison to this, the new version of PAXelerate incorporating the novel movement model and keeping all other settings resulted in a boarding time of 20:56 with a standard deviation of 54 s. This represents both longer boarding times compared to the previous implementation as well as an increased simulation uncertainty as represented by an increased box height in
Figure 13 and an increased standard deviation. For reference, official boarding process times for an Airbus A330 (which has a comparable cabin to the ARB) suggest ~25% higher values compared to the old PAXelerate simulation [
1]. The new results thus still lie within in an acceptable range. A further investigation into the cause of this increase will be performed in the future, but the fine-tuning of the model parameters for a single-aisle A320 style aircraft and the overall slowing of passenger movement are expected to have a strong influence.
As a statistical test for the results of the two boarding simulation models, the Welch two-sample t-test has been chosen as both result samples are normally distributed (Shapiro-Wilk normality test) but differ in their variance (f-test). The resulting p-value of <2.2 × 10−16 proves that the two models and their respective boarding time results are significantly different.
5.2. Airbus A320
As mentioned, the model parameters were first calibrated and fine-tuned for an A320 style aircraft, thus potentially explaining the deviations in the AVACON research baseline results. The parameters and settings for this validation remain unchanged compared to
Table 7, but the total number of passengers in the cabin layout depicted in
Figure 14 accounts to 180.
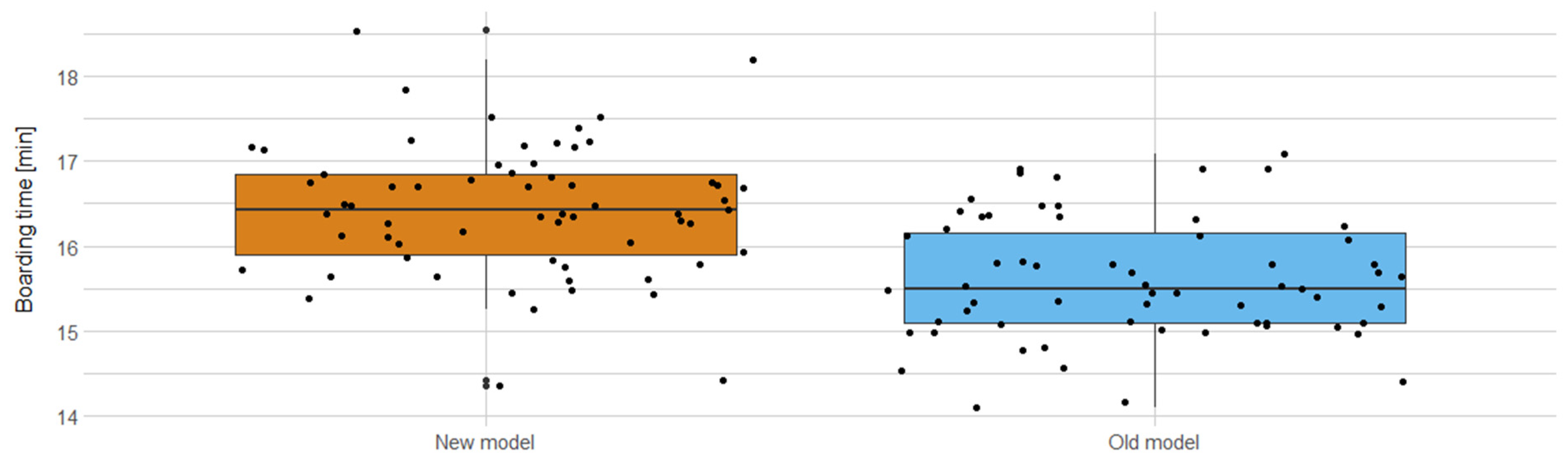
As highlighted by the boxes in
Figure 15 below, the simulation of the previous model results in an average boarding time of 15:36 with a standard deviation of 43 s using the old model. The new model results in a boarding time of 16:26 with a standard deviation of 47 s. Using the Welch two-sample t-test for a statistical test, the
p-value of 7.874 × 10
−9 proves that the two models and their boarding time results are significantly different. The results show that the new model increases the boarding times slightly. This behavior is again explainable by the overall reduction in passenger movement speed due to the new movement model.
5.3. Summary
The following
Table 8 highlights the results of the validation for both the AVACON research baseline aircraft and the Airbus A320 type aircraft.
The validation performed for this paper is able to show the applicability of the model to boarding simulations and the ability to generate better results compared to the previous implementation as the delta to official references decreases. In order to assess unconventional aircraft cabin concepts where no existing data is available, real world experiments and measurements need be performed for the determination of influence factors for the various cabin monuments. This can for example be done by recording a boarding procedure at an airport [
37] or even using virtual reality to get a more detailed insight into humans moving within a virtual 3D cabin space [
29].
6. Application and Implications
After the completed validation of the model for existing scenarios, PAXelerate can now be used to look at a customization of the cabin layout or passenger behavior changes. The actual scenarios assessed below include a modification of the aisle width and of the overhead bin location for an Airbus A320. Concerning the passenger behavior, a currently relevant topic is the impact of COVID-19. As a safe distance of 1.5 to 2.0 m to other people should be maintained at all times, this suggestion can also be applied to the boarding process [
40]. As the new model is capable of controlling this minimum distance to preceding passengers, an initial assessment of the impact of such a regulation will be performed below using an Airbus A320.
6.1. Changes to Cabin Geometry
The following assessment is based on a default Airbus A320 configuration. The modification to the cabin consists of an increase in aisle width of 25% or 50%, respectively. This results in a corresponding shift of the overhead bin location as well as an increase in fuselage width. All model parameters except the number of passengers remain the same compared to
Table 7. The resulting average boarding time of 50 iterations is 16:08 min with a standard deviation of 00:54 min for the 25% increase scenario and 15:55 min with a deviation of 00:55 for the 50% increase scenario. While the differences in the mean boarding times for the 50% wider aisle are significant (Welch two sample t-test
p-value = 0.002068), the deviation in boarding times for the 25% wider aisle scenario is insignificant (
p-value = 0.08598).
The slight decrease in average boarding times for the 50% change highlights the potential for an increased aisle width, as passengers might feel less constricted in a wider aisle, thereby reducing the mean boarding times by up to 3%. The effect of overtaking possibilities in combination with a wider aisle has not been considered. The true impact of this aisle widening depends on the parameters used in the potential of every node within the model. A deviation to the simulation result may thus occur after real life experiments have been executed and tweaked parameter values have been integrated. Nevertheless, the results indicate an effect of the altered cabin geometry on boarding times and lead the way for the model to evolve and improve with future versions of PAXelerate.
6.2. Changes to Passenger Behavior
In order to assess the passenger movements due to the COVID-19 restrictions, the model is adapted to include a minimum distance between passengers of
= 1.75 m, shifting the graph of Equation (9) along the positive x-axis. All other properties remain unchanged compared to the validation scenario of the A320. The decision for an Airbus A320 and against the ARB is because short distance travel seems to be the likelier option for a reemerging commercial flight schedule in the short term as intercontinental travel will be restricted for a longer period of time [
41,
42].
The average boarding time for 50 iterations is 27:30 min with a standard deviation of 1:19 min. The significance of this deviation is proven by a Welch two sample t-test with a
p-value of 2.2 ∗ 10
−16. This represents an increase in boarding times of 67.4% compared to the reference case presented in the validation chapter. The reason for this increase is partly explainable by the reduction of simultaneous actions being performed by passengers. Fewer passengers can stow luggage or enter the aircraft per time step, as the distance between passengers is 6.5 times higher, resulting in increasing overall boarding times. As the boarding process lies on the critical path of the turnaround process for most scenarios [
1], an increase in boarding times by this amount will lead to an extended airport turnaround duration and a negative economic impact. This result highlights the risks and effects of the application of this minimum distance regulation.
As the minimum distance requirement might also be enforced during flight, a suggested vacant middle seat in every seat group is another option to be considered [
40]. The following assessment thus combines the boarding process with a safe distance and an empty middle seat in each seat group, limiting the time two passengers come in very close contact to each other. For a study with 50 iterations, the average boarding time results in 16:23 min with a standard deviation of 37 s. The deviation of this result compared to the reference is insignificant (Welch two sample t-test
p-value = 0.8092). This shows that, with the reduced amount of passengers, the boarding sequence has on average the same duration as the reference scenario. However, as only 120 passengers can board the airplane, thus reducing the load factor to 66%, the economics of such a scenario render the application in a real world scenario questionable.
As mentioned in
Section 1, there are different other suggestions for boarding procedures with reduced interaction between passengers such as a window to aisle boarding, rear to front boarding [
40] and even more unconventional concepts [
10,
11,
12]. These scenarios distribute the passengers throughout a boarding process in a way that reduces the total amount of contact with already seated passengers. However, they can cause increased boarding times or aisle areas with high interference between passengers, as shown in a recent publication for the AVACON research baseline [
39].
6.3. Overview
The following
Table 9 highlights the results of the application for both the cabin modifications and the passenger behavior adaptions performed for this publication. All assessments are conducted using an Airbus A320 cabin.
7. Summary
The integration of the newly developed model empowers PAXelerate to simulate a more detailed boarding process and enables a better understanding of the influence of cabin layout changes to the aircraft’s boarding performance. This allows for the identification of critical aspects of a cabin layout such as a local narrowing of the aisle and therefore gives cabin designers the opportunity to tackle potential issues in an early design phase.
In general, the potential for a swifter boarding process by changing aspects of the cabin layout, such as altering the aisle width or relocating cabin monuments, may enable airlines to quicken the turnaround process without high effort. Passengers on the other hand may feel less crowded during the boarding procedure as potential bottlenecks can be removed in advance by rearranging monuments. Lastly, the model introduced in this paper also enables insight into potential paths for future improvements of the design of the AVACON project’s next aircraft iterations and their respective cabin layouts.
Concerning the COVID-19 assessment, it can be said that the suggested measures may effectively reduce close contact to other passengers. However, considering the vast economic impact of these measures by increasing boarding times or reducing the aircraft’s capacity, other mitigation methods such as an increased hygiene level or facial masks may be economically a less harmful measure to enable a safe and economic future travel scenario.
8. Future Work
The initial implementation of the new passenger movement model has proven to be a valuable addition to the PAXelerate boarding simulation. Specific aspects of the boarding simulation and the movement model in particular provide the potential for future model improvements. As mentioned previously, this includes the adjustment of the factors and parameters used in the novel movement model based on real world measurements and experiments during a boarding sequence, monitoring the impact of cabin monuments and their placement on the walking speed of real humans. This task will be dealt with during the next steps of the simulation framework enhancement.
Regarding the PAXelerate boarding simulation as a whole, the implementation of an advanced luggage handling and overhead bin storage model is of high priority. This includes a more realistic luggage model, incorporating the sizes and weights of luggage and their respective positioning inside the luggage bins by passengers. The size and position of the luggage bins play a crucial role, as there might not always be an empty luggage bin close to the passenger’s seat, thus delaying or complicating the luggage stowing procedure and the flow of passengers.
Lastly, a more detailed analysis of COVID-19 related parameters such as exposure time and distance between passengers will be introduced in the future, assessing potential paths for an infection risk reduction throughout the boarding process. This may also benefit novel methods for the luggage stowing procedure as well as the de-boarding of the aircraft.
Author Contributions
Conceptualization, methodology, validation, writing and visualization, M.E.; methodology, validation and visualization, T.K.; supervision, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding as part of AVACON, a research project supported by the German Federal Ministry for Economic Affairs and Energy in the national LuFo V program. Any opinions, findings, and conclusions expressed in this document are those of the authors and do not necessarily reflect the views of the other project partners.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| AVACON | AdVanced Aircraft CONcepts—LuFo research project |
| PAXelerate | Boarding simulation developed by Bauhaus Luftfahrt |
| CPACS | Common Parametric Aircraft Configuration Schema |
| CAFE | Cabin And Fuselage Environment, module of PAXelerate |
| Symbols | |
| Potential of a node |
| Density of humans |
| v | Walking speed of a passenger |
| d | Distance to preceding passengers on the aisle |
References
- Airbus, S.A.S. Airbus A330—Aircraft Characteristics—Airport and Maintenance Planning. Available online: https://www.airbus.com/content/dam/corporate-topics/publications/backgrounders/techdata/aircraft_characteristics/Airbus-Commercial-Aircraft-AC-A330.pdf (accessed on 13 September 2019).
- Schultz, M.; Kunze, T.; Fricke, H. Boarding on the critical path of the turnaround. Proceedings of the Tenth USA/Europe Air Traffic Management Research and Development Seminar (ATM2013), Chicago. 2013. Available online: http://www.atmseminar.org/seminarContent/seminar10/papers/316-Schultz_0127130604-Final-Paper-4-15-13.pdf (accessed on 19 December 2020).
- Yildiz, B.; Förster, P.; Feuerle, T.; Hecker, P.; Bugow, S.; Helber, S. A generic approach to analyze the impact of a future aircraft design on the boarding process. Energies 2018, 11, 303. [Google Scholar] [CrossRef]
- Milne, R.J.; Kelly, A.R. A new method for boarding passengers onto an airplane. J. Air Transp. Manag. 2014, 34, 93–100. [Google Scholar] [CrossRef]
- Wöhler, S.; Hartmann, J.; Prenzel, E.; Kwik, H. Preliminary aircraft design for a midrange reference aircraft taking advanced technologies into account as part of the AVACON Project for an entry into service in 2028. Dtsch. Luft Raumfahrtkongress 2018. [Google Scholar] [CrossRef]
- IATA. IATA Calls for Passenger Face Covering and Crew Masks. Available online: https://www.iata.org/en/pressroom/pr/2020-05-05-01/ (accessed on 2 December 2020).
- IATA. Precautions to Take When Flying. Available online: https://www.iata.org/en/youandiata/travelers/health/precautions-to-take-flying-by-air-in-covid-times/ (accessed on 2 December 2020).
- Flughafen München GmbH. Travelling in Times of the Coronavirus Pandemic. Available online: https://www.munich-airport.com/travelling-in-times-of-the-coronavirus-pandemic-8395611 (accessed on 2 December 2020).
- IATA. IATA Calls for Systematic COVID-19 Testing Before Departure. Available online: https://www.iata.org/en/pressroom/pr/2020-09-22-01/ (accessed on 2 December 2020).
- EUROCONTROL and Airport Research Center GmbH. Impact Assessment of COVID-19 Measures on Airport Performance. 2020. Available online: https://www.eurocontrol.int/sites/default/files/2020-09/eurocontrol-impact-assessment-covid-19-airport-performance-2020.pdf (accessed on 2 December 2020).
- Milne, R.; Delcea, C.; Cotfas, L.-A. Airplane boarding methods that reduce risk from COVID-19. Saf. Sci. 2020. [Google Scholar] [CrossRef]
- Milne, R.; Cotfas, L.-A.; Delcea, C.; Craciun, L.; Molanescu, A. Adapting the reverse pyramid airplane boarding method for social distancing in times of COVID-19. PLoS ONE 2020, 15. [Google Scholar] [CrossRef] [PubMed]
- Schultz, M.; Fuchte, J. Evaluation of aircraft boarding scenarios considering reduced transmissions risks. Sustainability 2020, 12, 5329. [Google Scholar] [CrossRef]
- Schmidt, M.; Engelmann, M. PAXelerate—An open source passenger flow simulation framework for advanced aircraft cabin layouts. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Airport Research Center GmbH. Cast Cabin. Available online: https://arc.de/ (accessed on 3 December 2020).
- Richter, T. Simulationsmethodik zur Effizienz und Komfortbewertung von Menschenflussprozessen in Verkehrsflugzeugen. In Disserataion, Technische Universität München, Institut für Luft und Raumfahrttechnik; Verlag Dr. Hut: München, Germany, 2007. [Google Scholar]
- Marelli, S.; Mattocks, G.; Merry, R. The role of computer simulation in reducing airplane turn time. AERO Mag. 1998, 1, 10. [Google Scholar]
- Schultz, M. Entwicklung eines individuenbasierten Modells zur Abbildung des Bewegungsverhaltens von Passagieren im Flughafenterminal. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2010. [Google Scholar]
- German Aerospace Center (DLR). Traffic Oriented Microscopic Simulator–TOMICS. Available online: https://www.dlr.de/fw/ (accessed on 3 December 2020).
- Fuchte, J. Enhancement of Aircraft Cabin Design Guidelines with Special Consideration of Aircraft Turnaround and Short Range Operations: Dissertation: Technische Universität Hamburg: Harburg, Germany, DLR e.V. 2014. Available online: https://elib.dlr.de/89599/1/Fuchte%20FB-2014-17%20Version%20Druck.pdf (accessed on 19 December 2020).
- Fire Safety Engineering Group, airExodus. Available online: http://fseg.gre.ac.uk/exodus/ (accessed on 3 December 2020).
- Kneidl, A. Methoden zur Abbildung Menschlichen Navigationsverhaltens bei der Modellierung von Fußgängerströmen. Dissertation, Technische Universität München, Lehrstuhl für Computergestützte Modellierung und Simulation, München, Germany. March 2013. Available online: https://mediatum.ub.tum.de/1131501 (accessed on 19 December 2020).
- Rindsfüser, G.; Klügl, F. Agent-based pedestrian simulation: A case study of the bern railway station. disP 2007, 170, 2007. [Google Scholar] [CrossRef]
- Bohari, Z.A.; Bachok, S.; Osman, M.M. Simulating the pedestrian movement in the public transport infrastructure. Procedia Soc. Behav. Sci. 2016, 222, 791–799. [Google Scholar] [CrossRef][Green Version]
- Schadschneider, A.; Klingsch, W.; Klüpfel, H.; Kretz, T.; Rogsch, C.; Seyfried, A. Evacuation dynamics: Empirical results, modeling and applications. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 3142–3176. [Google Scholar]
- Daamen, W. Modelling Passenger Flows in Public Transport Facilities. Ph.D. Thesis, Delft University, Delft, The Netherlands, September 2004. Available online: http://resolver.tudelft.nl/uuid:e65fb66c-1e55-4e63-8c49-5199d40f60e1 (accessed on 19 December 2020).
- Helbing, D.; Molnár, P. Social force model for pedestrian dynamics. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1995, 51, 4282–4286. [Google Scholar] [CrossRef] [PubMed]
- Kielar, P.M. Kognitive Modellierung und Computergestützte Simulation der Räumlich-Sequenziellen Zielauswahl von Fußgängern. Ph.D. Thesis, Technische Universität München, Lehrstuhl für Computergestützte Modellierung und Simulation, Munchen, Germany, May 2017. [Google Scholar]
- Sanz, F.A.; Olivier, A.-H.; Bruder, G.; Pettré, J.; Lécuyer, A. Virtual proxemics: Locomotion in the presence of obstacles in large immersive projection environments. In Proceedings of the IEEE Virtual Reality Conference, Arles, France, 23–27 March 2015; pp. 75–80. [Google Scholar]
- Weidmann, U. Transporttechnik der Fussgänger: Transporttechnische Eigenschaften des Fussgängerverkehrs, Literaturauswertung; ETH Zurich: Zürich, Switzerland, 1993. [Google Scholar]
- Bauhaus Luftfahrte, V. PAXelerate Boarding Simulation. Available online: www.paxelerate.com (accessed on 19 December 2020).
- Schmidt, M.; Engelmann, M. Boarding process assessment of novel aircraft cabin concepts. In Proceedings of the 30th International Congress of the Aeronautical Sciences (ICAS), Daejeon, Korea, 25–30 September 2016; p. 3568. [Google Scholar]
- Bachmann, A.; Kunde, M.; Litz, M.; Schreiber, A.; Bertsch, L. Automation of Aircraft Pre-design Using a Versatile Data Transfer and Storage Format in a Distributed Computing Environment. In Proceedings of the Third International Conference on Advanced Engineering Computing and Applications in Sciences, Sliema, Malta, 11–16 October 2009. [Google Scholar] [CrossRef]
- German Aerospace Center (DLR). CPACS—Common Language for Aircraft Design. Available online: https://cpacs.de/ (accessed on 3 July 2019).
- Gordon, C.G.; Churchill, T.; Clauser, C.E.; Bradtmiller, B.; McConville, J.T.; Tebbetts, I.; Walker, R.A. Anthropometric Survey of US Army Personnel; Summary Statistics, Interim Report for 1988; United States Army Natick Research, Development and Englneering Center: Natick, MA, USA, 1990.
- Airbus Customer Services. A320-200 Aircraft Charactersitics Airport and Maintenance Planning; Airbus S.A.S: Blagnac, France, 2019. [Google Scholar]
- Steiner, A.; Philipp, M. Speeding up the airplane boarding process by using pre-boarding areas. In Proceedings of the 9th Swiss Transport. Research Conference, Monte Verità, Ascona, 9–11 September 2009. [Google Scholar]
- Götz, M. Engineering Concept Study of an Innovative Sideward Retractable Aircraft Seat. Master‘s Thesis, Institute of Aircraft Design, Technische Universität München, Munich, Germany, May 2014. [Google Scholar]
- Engelmann, M.; Hornung, M. Boarding Process Assessment of the AVACON Research Baseline Aircraft; Deutscher Luft- und Raumfahrtkongress: Darmstadt, Germany, 2019. [Google Scholar] [CrossRef]
- IATA Medical Advisory Group. Restarting Aviation Following COVID-19: Medical Evidence for various Strategies being discussed as at 27 April 2020. 2020. Available online: https://www.iata.org/contentassets/f1163430bba94512a583eb6d6b24aa56/covid-medical-evidence-for-strategies-200508.pdf (accessed on 19 December 2020).
- Qantas Airways Limited, International Network Changes. Available online: https://www.qantas.com/au/en/travel-info/travel-updates/coronavirus/qantas-international-network-changes.html (accessed on 5 November 2020).
- New York Times. Coronavirus Travel Restrictions, Across the Globe. Available online: https://www.nytimes.com/article/coronavirus-travel-restrictions.html (accessed on 5 May 2020).
Figure 1.
Schematic highlighting the influence of all surrounding objects and passengers on a walking passenger as the basic concept behind the modelling approach.
Figure 1.
Schematic highlighting the influence of all surrounding objects and passengers on a walking passenger as the basic concept behind the modelling approach.
Figure 2.
PAXelerate module structure.
Figure 2.
PAXelerate module structure.
Figure 3.
Representation of the human body and luggage within the simulation grid.
Figure 3.
Representation of the human body and luggage within the simulation grid.
Figure 4.
Dimensions of a typical aircraft seat used for the different layers.
Figure 4.
Dimensions of a typical aircraft seat used for the different layers.
Figure 5.
Transition to discretized seat dimensions for each layer.
Figure 5.
Transition to discretized seat dimensions for each layer.
Figure 6.
View of the potential, representing the impact on passing objects.
Figure 6.
View of the potential, representing the impact on passing objects.
Figure 7.
Exemplary potential around a group of seats.
Figure 7.
Exemplary potential around a group of seats.
Figure 8.
Depiction of the ceiling and overhead bin layer. Shown here is the cross-section of the AVACON research baseline (ARB) [
5].
Figure 8.
Depiction of the ceiling and overhead bin layer. Shown here is the cross-section of the AVACON research baseline (ARB) [
5].
Figure 9.
Walking speed in dependence of crowd density according to [
30].
Figure 9.
Walking speed in dependence of crowd density according to [
30].
Figure 10.
Walking speed in dependence of the distance to the preceding passenger.
Figure 10.
Walking speed in dependence of the distance to the preceding passenger.
Figure 11.
Schematic of the influence area of a walking passenger. The walking speed depends on the distance d to a preceding passenger and if it is within the rectangle defined as the influence area.
Figure 11.
Schematic of the influence area of a walking passenger. The walking speed depends on the distance d to a preceding passenger and if it is within the rectangle defined as the influence area.
Figure 12.
Cabin layout depiction of the AVACON research baseline.
Figure 12.
Cabin layout depiction of the AVACON research baseline.
Figure 13.
Boarding times of the ARB when using the different movement model implementations.
Figure 13.
Boarding times of the ARB when using the different movement model implementations.
Figure 14.
Cabin layout depiction of an Airbus A320-200.
Figure 14.
Cabin layout depiction of an Airbus A320-200.
Figure 15.
Boarding time distribution of an Airbus A320 with the new movement model.
Figure 15.
Boarding time distribution of an Airbus A320 with the new movement model.
Table 1.
Overview of existing passenger flow simulation frameworks [
14].
Table 1.
Overview of existing passenger flow simulation frameworks [
14].
| Name | Author | Year | Purpose | Simulation Type |
|---|
| Cast Cabin | Airport Research Center [15] | - | Aircraft boarding | Agent-based |
| MASim | Richter [16] | 2007 | Aircraft boarding | Agent-based |
| PEDS | Marelli et. Al. [17] | 2008 | Aircraft boarding | Cellular automaton |
| - | Schultz [18] | 2010 | Airport terminal | Discrete event simulation |
| TOMICS | DLR [19] | 2011 | Aircraft boarding | Agent-based |
| - | Fuchte [20] | 2014 | Aircraft boarding | Agent-based |
| airExodus | Fire safety engineering group [21] | 2015 | Aircraft evacuation | Agent-based |
| PAXelerate | Bauhaus Luftfahrt [14] | 2016 | Aircraft boarding | Hybrid agent-based |
Table 2.
Overview of different passenger simulation types.
Table 2.
Overview of different passenger simulation types.
| | Macroscopic Simulation | Microscopic Simulation |
|---|
| Social Force Model | Cellular Automaton | Agent-Based |
|---|
| Foundation | Partial differential equations describe variables such as density, speed and flow [26]. | Individual modelling of passengers and characteristics. Models differ in modelling of interactions between individuals and the environment as well as the level of spatial discretization and modelling depth. [26] |
| Passenger behavior is modelled by motion equations [27]. The individual is acting based on external forces. The walking speed depends on the sum of all external forces [22]. | Discretization of space (rectangular or hexagonal cells) and time. Walking behavior is defined by rules and states for each cell [26]. Movement directions are limited. All passengers are modelled the same. | Autonomously acting agents with specific characteristics such as gender or age that interact with one another. Pathfinding and movement are derived by unique characteristics. Agents often have a cost minimization target. [22] |
| Human Model | Analogies from fluid dynamic particle flows with circular body shape. | Modelled in a continuous space in the shape of flat disks. | Modelled as single or multi cell sized. Shape can be rectangle or hexagon if multi cell shaped. [22] | Passenger models are not bound to specific concepts of spatial discretization or continuous spaces. |
Table 3.
Division of the cabin into multiple layers.
Table 3.
Division of the cabin into multiple layers.
| Layer Name | Start Height [m] | End Height [m] | Purpose |
|---|
| Ground layer | 0.0 | 0.65 | Passenger and object modelling |
| Mid layer | 0.65 | 1.10 |
| Top layer | 1.10 | Cabin height |
| Ceiling layer | - | - | Ceiling contour |
Table 4.
Neuralgic human body points [
35].
Table 4.
Neuralgic human body points [
35].
| Body Point | Mean Height Female [m] | Mean Height Male [m] | Layer |
|---|
| Knees | 0.46 | 0.50 | Ground |
| Waist | 0.84 | 0.89 | Mid |
| Shoulders | 1.33 | 1.44 | Top |
Table 5.
Neuralgic human body points [
35] (* estimated).
Table 5.
Neuralgic human body points [
35] (* estimated).
| Body Layer | Width [m] | Depth [m] |
|---|
| Female | Male | Female | Male |
|---|
| Knees * | Mean | 0.34 | 0.34 | 0.22 | 0.24 |
| deviation | 0.02 | 0.02 | 0.02 | 0.02 |
| Waist | Mean | 0.3427 | 0.3418 | 0.2271 | 0.2486 |
| deviation | 0.0224 | 0.0203 | 0.021 | 0.0207 |
| Shoulders | Mean | 0.4301 | 0.4912 | 0.2394 | 0.2432 |
| deviation | 0.023 | 0.026 | 0.0211 | 0.0215 |
Table 6.
Comparison of old and new passenger model in PAXelerate.
Table 6.
Comparison of old and new passenger model in PAXelerate.
| Aspect | Old Model | New Model | Section |
|---|
| Model dimensions | 2D cabin floor | 3D cabin using multiple stacked 2D layers | Section 4.1 |
| Passenger shape | 2D rectangle | Distinctive rectangle shape in each stacked cabin layer at neuralgic body points | Section 4.1 |
| Movement model | “Stop and go” using free walking speed when path is unobstructed and stopping when preceding passengers reach a threshold distance | Adapted speed and crowd density relation by Weidmann using the personal space around individuals | Section 3.2, Section 4.3 |
| Influence of other passengers | Collision avoidance only | Walking speed is decreased by all passengers in proximity, depending on their state (seated, standing, or walking) | Section 4.3 |
| Obstacle influence | Considered only for collision avoidance during initial path finding process | Obstacles decrease walking speed of passengers in their proximity depending on obstacle shape in each model layer | Section 4.2 |
Table 7.
Overview of the input parameters used in the boarding simulations.
Table 7.
Overview of the input parameters used in the boarding simulations.
| Parameter | Value | Unit |
|---|
| Passengers | 255 | - |
| Discretized cabin grid resolution | 10 × 10 | Nodes per m² |
| Boarding doors | Front left | - |
| Number of simulation loops | 100 | - |
| Load factor | 100 | % |
| Boarding sequence | Random | - |
| Boarding rate | 18 | Passengers per minute |
Table 8.
Overview of the validation results.
Table 8.
Overview of the validation results.
| Validation Case | Source | Mean Boarding Time (min) | Standard Deviation [min] |
|---|
| AVACON ARB | Old model | 16:27 | 00:34 |
| New model | 20:56 | 00:54 |
| Airbus A330 | Manufacturer data [1] | ~25% higher than old model | - |
| Airbus A320 | Old model | 15:36 | 00:43 |
| New model | 16:26 | 00:47 |
| Manufacturer data [36] | ~19 min | - |
Table 9.
Overview of the assessment results.
Table 9.
Overview of the assessment results.
| Airbus A320 Scenario | Average Boarding Time (min) | Standard Deviation (min) | Delta (%) |
|---|
| Reference | 16:26 | 00:48 | - |
| Aisle width + 25% | 16:08 | 00:54 | (−1.8) |
| Aisle width + 50% | 15:55 | 00:55 | −3.1 |
| Safe distance | 27:30 | 01:19 | +67.4 |
| Safe distance + vacant middle seats | 16:23 | 00:37 | (−0.2) |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).