An Agent-Based Empirical Game Theory Approach for Airport Security Patrols
Abstract
1. Introduction
2. Related Work
2.1. Airport Security
2.2. Security Games
2.3. Agent-Based Modeling
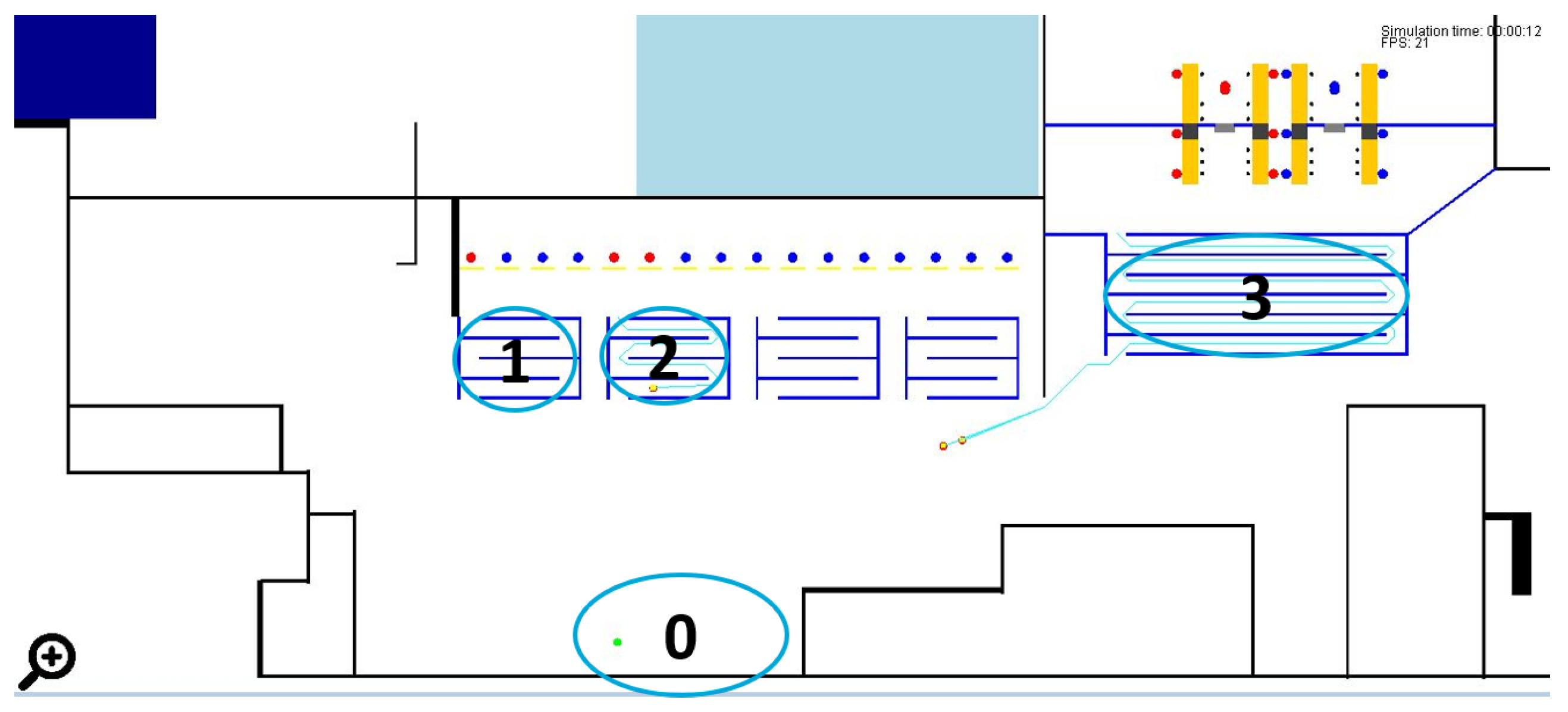
3. Case Study
4. Methodology
5. Models
5.1. Agent-Based Model
5.1.1. Operational Employee
5.1.2. Passenger
5.1.3. Attacker
5.1.4. Security Patrolling Agent
5.2. Game-Theoretic Model
5.2.1. Airport Graph
5.2.2. Patrolling Graph
5.2.3. Time Discretization
5.2.4. Players
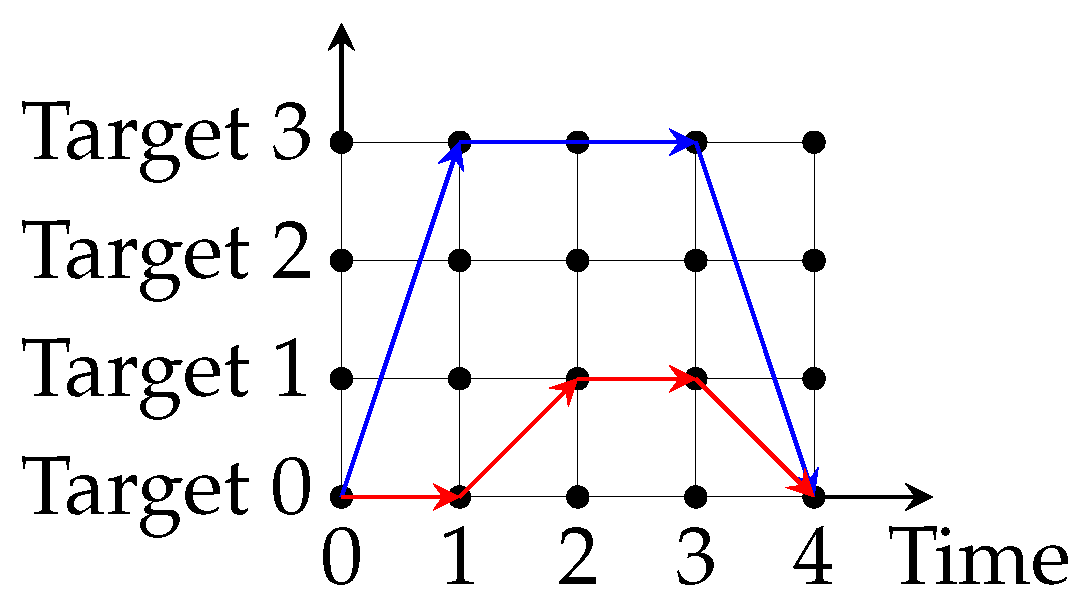
5.2.5. Strategies
Defender
Attacker
5.2.6. Payoff
5.2.7. Solution Concept
- Objective Function:
- Constraints:where , s, e, and refer to nodes of the patrolling graph , is a small positive number and is the strategy set of the attacker (defender). The nodes represents a target where the security officer starts her patrol shift. Constraint 7 illustrates a property of probabilities that for each intermediate node (node with both income and outcome edges) of the sum of all income probabilities must equal the sum of all outcome probabilities. Constraint 8 describes a second property of probabilities that the sum of probabilities going out from the root node equals 1. This means that the defender starts at the root node and must perform an action on what to do next. Constraint 9 assumes that the attacker strategy is the attacker optimal strategy. Moreover, ensures that this model does not rely on the “breaking-tie” assumption, but it is still optimal. The breaking-tie concept assumes that when the follower (attacker) is indifferent on payoffs by playing different pure strategies, he will play the strategy that is preferable for the leader (defender). Lastly, constraint 10 defines a zero-sum game. The Stackelberg equilibrium is found by getting the arguments () for which Equation (6) is maximum.
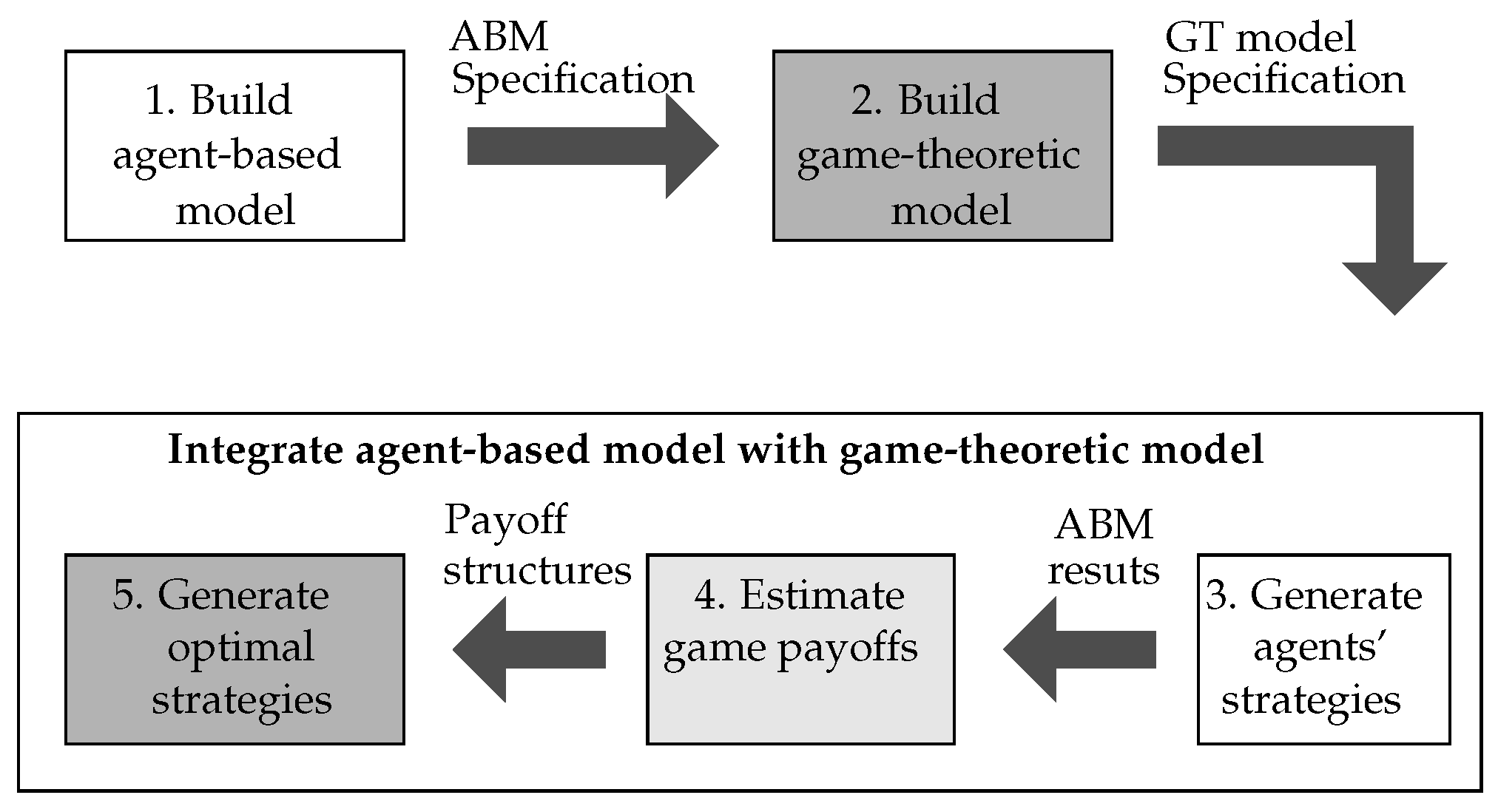
5.3. Integration of Agent-Based Results as Game-Theoretic Payoffs
5.3.1. Generate Agents’ Strategies
Defender Strategy
Attacker Strategy
5.3.2. Specify Payoffs Using Agent-Based Results
5.3.3. Verification of Optimal Strategies
6. Experiments and Results
6.1. Experimental Setup
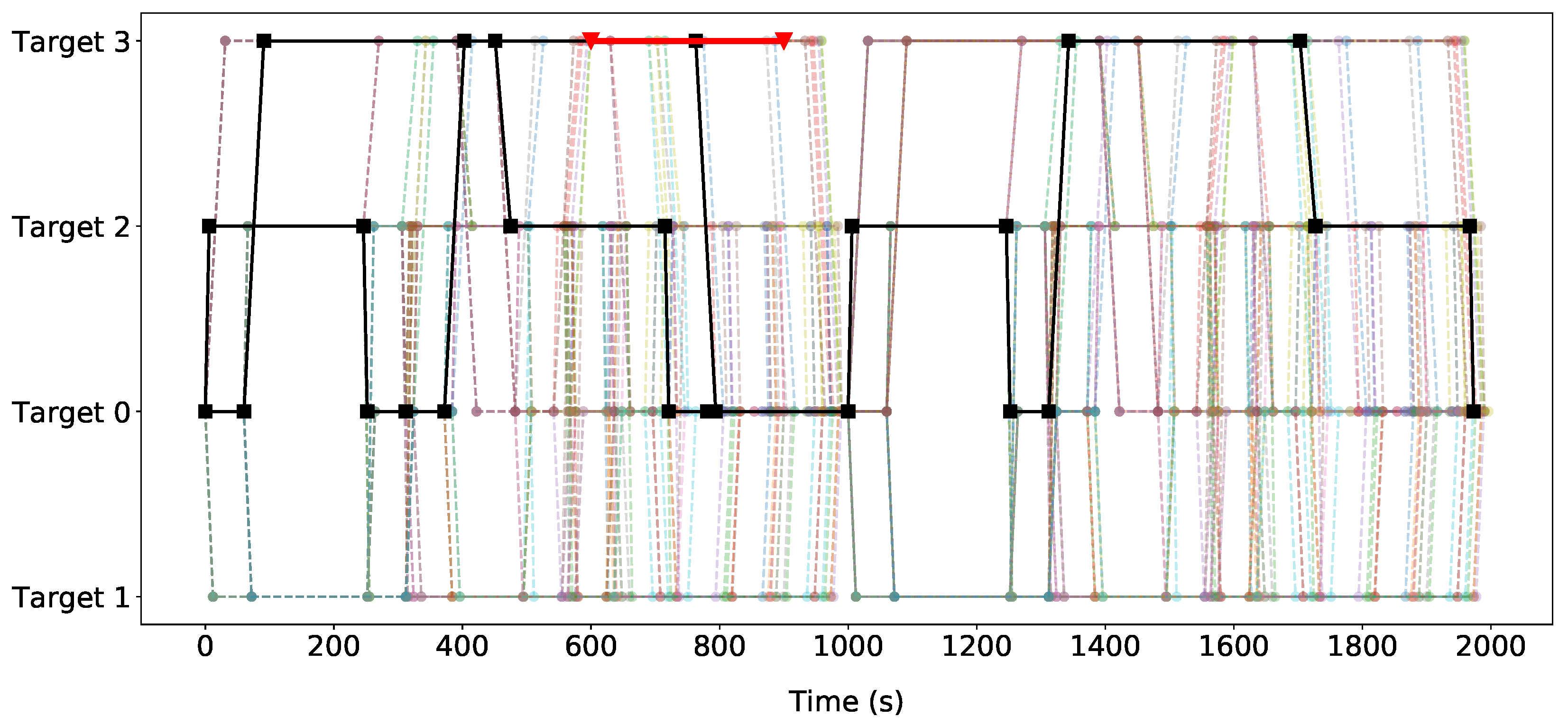
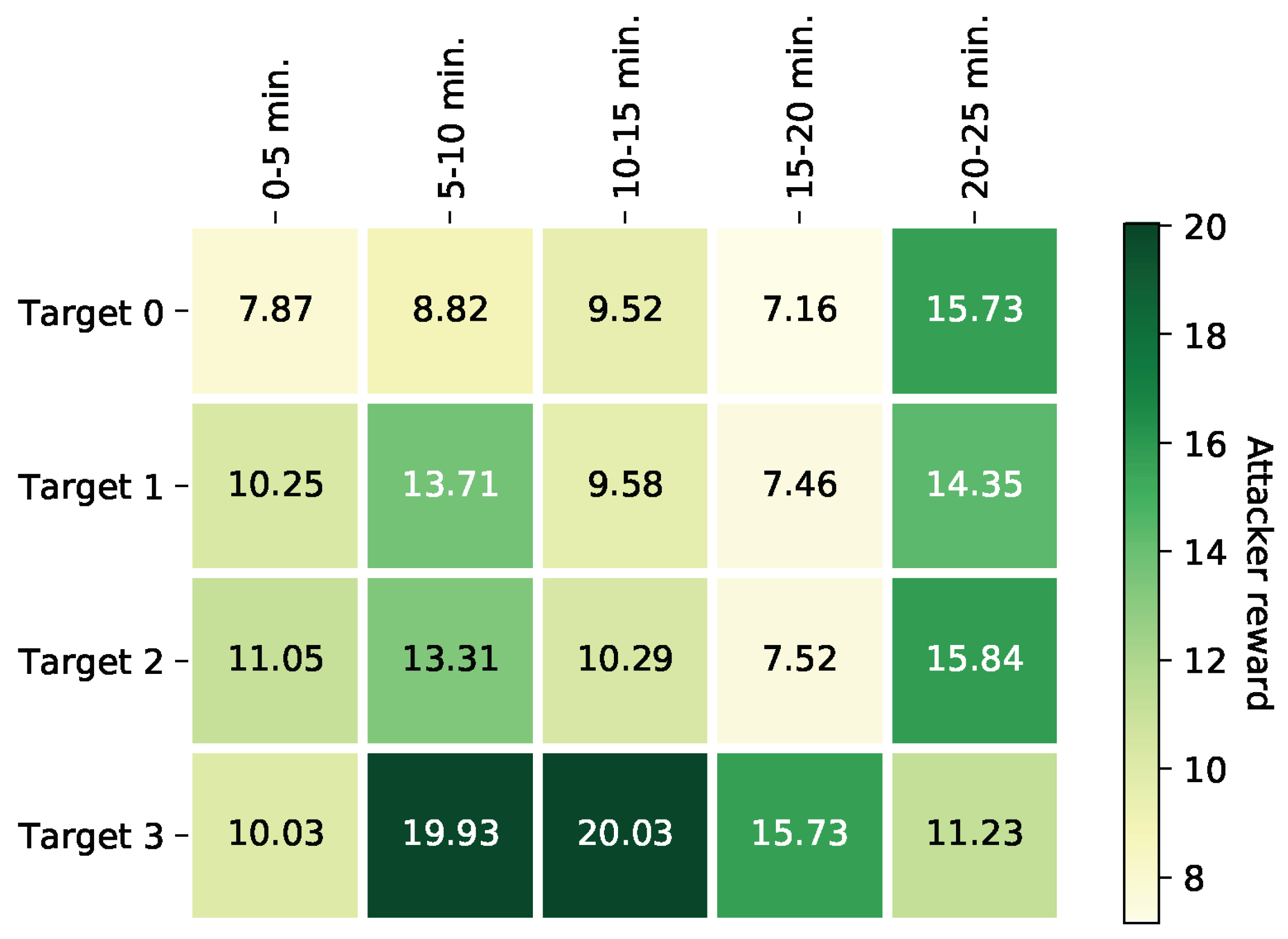
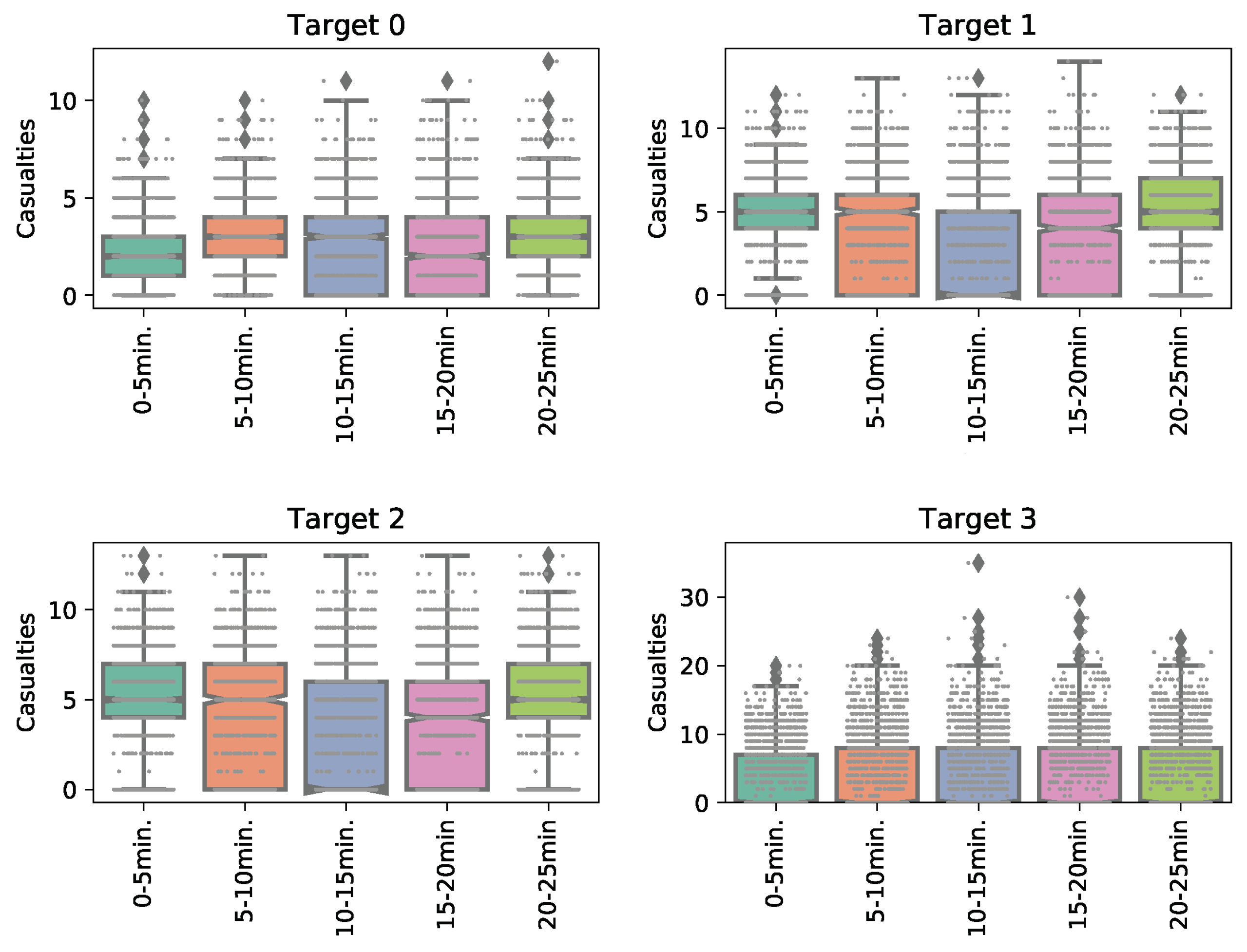
6.2. Agent-Based Model Results
6.3. Game-Theoretic Results
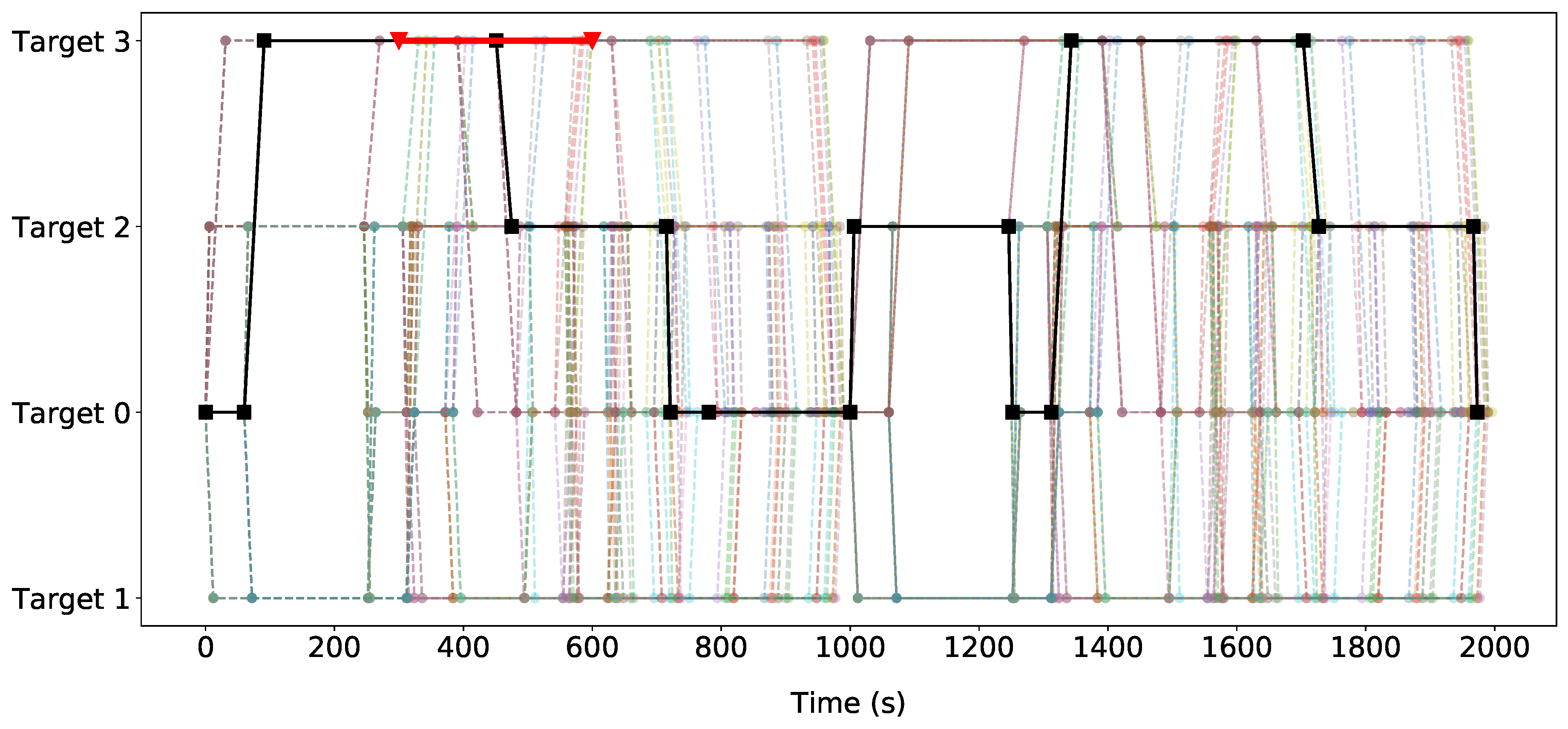
6.3.1. Stackelberg Game Solution
6.3.2. Deterministic Patrolling Strategy
6.4. Verification
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- National Consortium for the Study of Terrorism and Responses to Terrorism (START). The Global Terrorism Database (GTD) [Data File]. 2018. Available online: https://www.start.umd.edu/gtd (accessed on 14 January 2020).
- Tambe, M. Security and Game Theory: Algorithms, Deployed Systems, Lessons Learned; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Pita, J.; Jain, M.; Marecki, J.; Ordóñez, F.; Portway, C.; Tambe, M.; Western, C.; Paruchuri, P.; Kraus, S. Deployed ARMOR protection: The application of a game theoretic model for security at the Los Angeles International Airport. In Proceedings of the 7th International Joint Conference on Autonomous Agents and Multiagent Systems: Industrial Track. International Foundation for Autonomous Agents and Multiagent Systems, Estoril, Portugal, 12–16 May 2008; pp. 125–132. [Google Scholar]
- Pita, J.; Tambe, M.; Kiekintveld, C.; Cullen, S.; Steigerwald, E. GUARDS—Innovative application of game theory for national airport security. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 19–22 July 2011. [Google Scholar]
- Tsai, J.; Rathi, S.; Kiekintveld, C.; Ordonez, F.; Tambe, M. IRIS-a tool for strategic security allocation in transportation networks. AAMAS (Ind. Track) 2009, 37–44. [Google Scholar] [CrossRef][Green Version]
- Shieh, E.; An, B.; Yang, R.; Tambe, M.; Baldwin, C.; DiRenzo, J.; Maule, B.; Meyer, G. Protect: A deployed game theoretic system to protect the ports of the united states. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems-Volume 1. International Foundation for Autonomous Agents and Multiagent Systems, Valencia, Spain, 4–8 June 2012; pp. 13–20. [Google Scholar]
- Yin, Z.; Jiang, A.X.; Tambe, M.; Kiekintveld, C.; Leyton-Brown, K.; Sandholm, T.; Sullivan, J.P. TRUSTS: Scheduling randomized patrols for fare inspection in transit systems using game theory. AI Mag. 2012, 33, 59. [Google Scholar] [CrossRef]
- Heinrich, J.; Silver, D. Deep reinforcement learning from self-play in imperfect-information games. arXiv 2016, arXiv:1603.01121. [Google Scholar]
- Janssen, S.; Sharpanskykh, A. Agent-based modelling for security risk assessment. In Proceedings of the International Conference on Practical Applications of Agents and Multi-Agent Systems, Porto, Portugal, 21–23 June 2017; pp. 132–143. [Google Scholar]
- Weiss, W.E. Dynamic security: An agent-based model for airport defense. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 1320–1325. [Google Scholar]
- Janssen, S.; Sharpanskykh, A.; Curran, R. Agent-based modelling and analysis of security and efficiency in airport terminals. Transp. Res. Part C Emerg. Technol. 2019, 100, 142–160. [Google Scholar] [CrossRef]
- Jain, M.; Conitzer, V.; Tambe, M. Security scheduling for real-world networks. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems. International Foundation for Autonomous Agents and Multiagent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 215–222. [Google Scholar]
- Council of European Union. Council Regulation (EU) no 300/2008. 2008. Available online: http://data.europa.eu/eli/reg/2008/300/oj (accessed on 14 January 2020).
- Council of European Union. Council Regulation (EU) no 1998/2015. 2008. Available online: http://data.europa.eu/eli/reg_impl/2015/1998/oj (accessed on 14 January 2020).
- 107th Congress. Aviation and Transportation Security Act. 2001. Available online: https://www.gpo.gov/fdsys/pkg/PLAW-107publ71/pdf/PLAW-107publ71.pdf (accessed on 14 January 2020).
- ICAO. Aviation Security Manual (Doc 8973—Restricted); ICAO: Montreal, QC, Canada, 2017. [Google Scholar]
- Kirschenbaum, A.A. The social foundations of airport security. J. Air Transp. Manag. 2015, 48, 34–41. [Google Scholar] [CrossRef]
- Washington, A. All-Hazards Risk and Resilience: Prioritizing Critical Infrastructures Using the RAMCAP Plus [hoch] SM Approach; ASME: New York, NY, USA, 2009. [Google Scholar]
- Wagenaar, W.A. Generation of random sequences by human subjects: A critical survey of literature. Psychol. Bull. 1972, 77, 65. [Google Scholar] [CrossRef]
- Prakash, A.; Wellman, M.P. Empirical game-theoretic analysis for moving target defense. In Proceedings of the Second ACM Workshop on Moving Target Defense, Denver, CO, USA, 12 October 2015; pp. 57–65. [Google Scholar]
- Wellman, M.P. Methods for empirical game-theoretic analysis. In Proceedings of the AAAI, Boston, MA, USA, 16–20 July 2006; pp. 1552–1556. [Google Scholar]
- Tuyls, K.; Perolat, J.; Lanctot, M.; Leibo, J.Z.; Graepel, T. A generalised method for empirical game theoretic analysis. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems. International Foundation for Autonomous Agents and Multiagent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 77–85. [Google Scholar]
- Basilico, N.; Gatti, N.; Amigoni, F. Patrolling security games: Definition and algorithms for solving large instances with single patroller and single intruder. Artif. Intell. 2012, 184, 78–123. [Google Scholar] [CrossRef]
- Xu, H.; Ford, B.; Fang, F.; Dilkina, B.; Plumptre, A.; Tambe, M.; Driciru, M.; Wanyama, F.; Rwetsiba, A.; Nsubaga, M.; et al. Optimal patrol planning for green security games with black-box attackers. In International Conference on Decision and Game Theory for Security; Springer: Cham, Switzerland, 2017; pp. 458–477. [Google Scholar]
- Vorobeychik, Y.; An, B.; Tambe, M. Adversarial patrolling games. In Proceedings of the 2012 AAAI Spring Symposium Series, Palo Alto, CA, USA, 26–28 March 2012. [Google Scholar]
- Fang, F.; Jiang, A.X.; Tambe, M. Optimal patrol strategy for protecting moving targets with multiple mobile resources. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems. International Foundation for Autonomous Agents and Multiagent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 957–964. [Google Scholar]
- Xu, H.; Fang, F.; Jiang, A.X.; Conitzer, V.; Dughmi, S.; Tambe, M. Solving zero-sum security games in discretized spatio-temporal domains. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Zhang, L.; Reniers, G.; Chen, B.; Qiu, X. CCP game: A game theoretical model for improving the scheduling of chemical cluster patrolling. Reliab. Eng. Syst. Saf. 2018. [Google Scholar] [CrossRef]
- Kar, D.; Fang, F.; Delle Fave, F.; Sintov, N.; Tambe, M. A game of thrones: When human behavior models compete in repeated stackelberg security games. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems. International Foundation for Autonomous Agents and Multiagent Systems, Istanbul, Turkey, 4–8 May 2015; pp. 1381–1390. [Google Scholar]
- Nguyen, T.H.; Yang, R.; Azaria, A.; Kraus, S.; Tambe, M. Analyzing the effectiveness of adversary modeling in security games. In Proceedings of the Twenty-Seventh AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013. [Google Scholar]
- Kiekintveld, C.; Islam, T.; Kreinovich, V. Security games with interval uncertainty. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems. International Foundation for Autonomous Agents and Multiagent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 231–238. [Google Scholar]
- Nguyen, T.H.; Jiang, A.X.; Tambe, M. Stop the compartmentalization: Unified robust algorithms for handling uncertainties in security games. In Proceedings of the 2014 International Conference on Autonomous Agents and Multi-Agent Systems. International Foundation for Autonomous Agents and Multiagent Systems, Paris, France, 5–9 May 2014; pp. 317–324. [Google Scholar]
- Klima, R.; Tuyls, K.; Oliehoek, F.A. Model-Based Reinforcement Learning under Periodical Observability. In Proceedings of the 2018 AAAI Spring Symposium Series, Stanford, CA, USA, 26–28 March 2018. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Reddy, V.; Fookes, C.; Yarlagadda, P.K. Impact of passenger group dynamics on an airport evacuation process using an agent-based model. In Proceedings of the 2014 International Conference on Computational Science and Computational Intelligence, Las Vegas, NV, USA, 10–13 March 2014; Volume 2, pp. 161–167. [Google Scholar]
- US Government Accountability Office (GAO). Aviation Security: TSA Should Limit Future Funding for Behavior Detection Activities; US Government Accountability Office (GAO): Washington, DC, USA, 2013.
- Ford, B. Real-World Evaluation and Deployment of Wildlife Crime Prediction Models. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2017. [Google Scholar]
- Gholami, S.; Ford, B.; Fang, F.; Plumptre, A.; Tambe, M.; Driciru, M.; Wanyama, F.; Rwetsiba, A.; Nsubaga, M.; Mabonga, J. Taking it for a test drive: A hybrid spatio-temporal model for wildlife poaching prediction evaluated through a controlled field test. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Cham, Switzerland, 2017; pp. 292–304. [Google Scholar]
- Janssen, S.; Sharpanskykh, A.; Curran, R.; Langendoen, K. AATOM: An Agent-based Airport Terminal Operations Model Simulator. In Proceedings of the 51st Computer Simulation Conference, SummerSim 2019, Berlin, Germany, 22–24 July 2019. [Google Scholar]


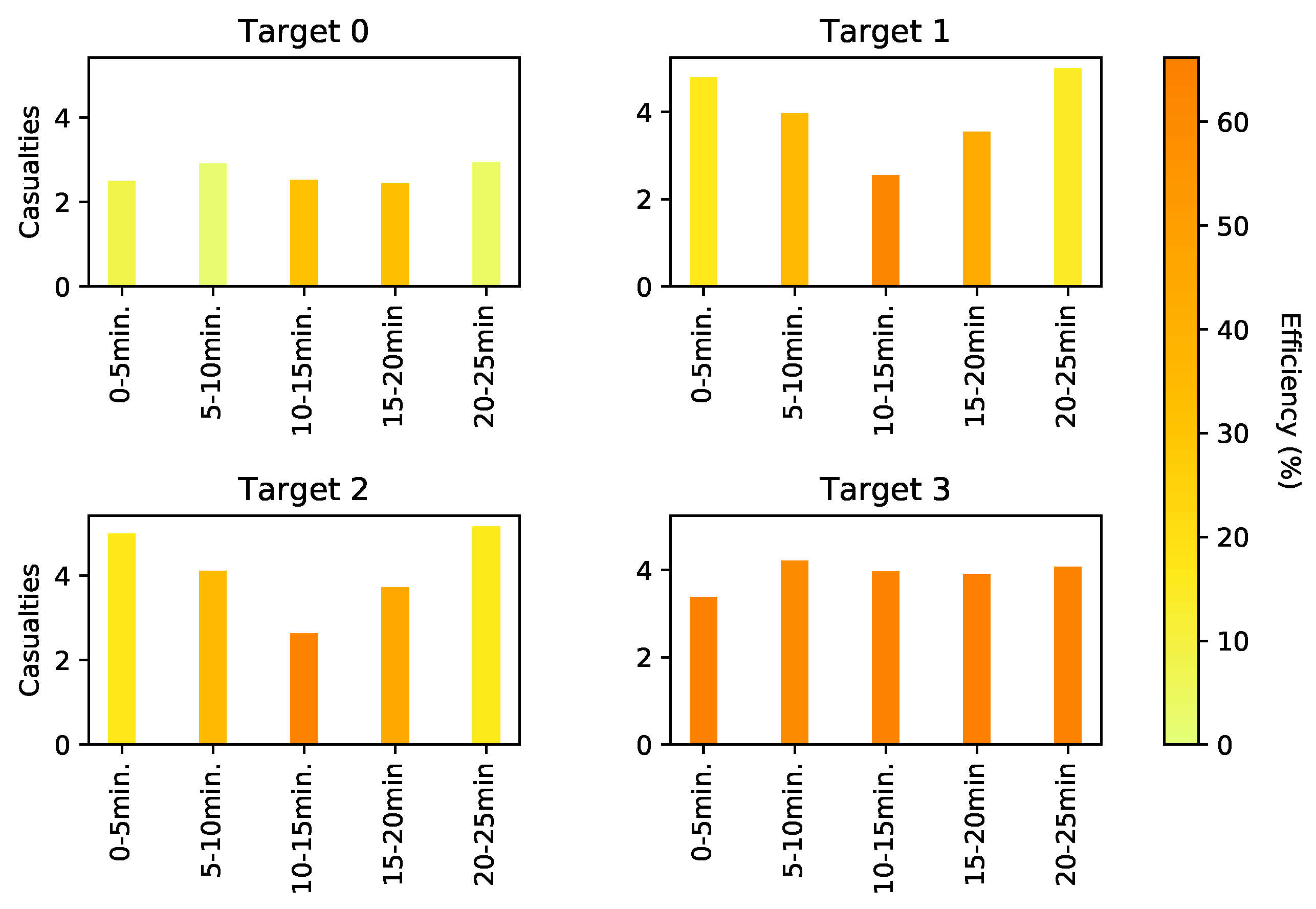
| Parameter | Value |
|---|---|
| Simulation parameters | |
| Simulation runs | 500 |
| Airport and flight parameters | |
| Flight departure time | 7200 s |
| Number of flights | 3 |
| Number of open checkpoint lanes | 2 |
| Number of open check-in desks | 3 |
| Agents parameters | |
| Proportion passengers check-in | 0.5 |
| Check-in time | Norm(60,6) s |
| Checkpoint time | Norm(45,4.5) s |
| Observation radius | 10 m |
| Security arrest probability | 0.8 |
| Start Node | End Node | Att. Strategy | Cas. | Eff. (%) |
|---|---|---|---|---|
| (Time (s), Target) | (Time (s), Target) | (Target, Time (min)) | ||
| (0, ) | (6, ) | – | 4.27 | 0 |
| (6, ) | (246, ) | – | 2.194 | 21.72 |
| (1933, ) | (1964, ) | – | - | - |
| (0, ) | (31, ) | – | 0 | 100 |
| (0, ) | (31, ) | – | - | - |
| (1582, ) | (1942, ) | – | 11.615 | 7.69 |
| Start Node | End Node | Prob. | Cas. | Eff. (%) |
|---|---|---|---|---|
| (Time (s), Target) | (Time (s), Target) | |||
| (403, ) | (763, ) | 0.129 | 2.286 | 72.67 |
| (763, ) | (794, ) | 0.129 | 1.540 | 78.94 |
| (794, ) | (1000, ) | 0.129 | 6.083 | 41.35 |
| (475, ) | (715, ) | 0.871 | 1.427 | 70.68 |
| (721, ) | (781, ) | 0.871 | 2.284 | 72.59 |
| (781, ) | (1000, ) | 0.871 | 5.430 | 47.70 |
| (1006, ) | (1246, ) | 1 | 10.789 | 0 |
| Start Node | End Node | Prob. | Cas. | Eff. (%) |
|---|---|---|---|---|
| (Time (s), Target) | (Time (s), Target) | |||
| (403, ) | (763, ) | 0.129 | 2.667 | 73.56 |
| (763, ) | (794, ) | 0.129 | 1.976 | 76.12 |
| (794, ) | (1000, ) | 0.129 | 5.602 | 43.08 |
| (475, ) | (715, ) | 0.871 | 1.413 | 71.26 |
| (721, ) | (781, ) | 0.871 | 2.096 | 82.61 |
| (781, ) | (1000, ) | 0.871 | 6.721 | 53.19 |
| (1006, ) | (1246, ) | 1 | 9 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janssen, S.; Matias, D.; Sharpanskykh, A. An Agent-Based Empirical Game Theory Approach for Airport Security Patrols. Aerospace 2020, 7, 8. https://doi.org/10.3390/aerospace7010008
Janssen S, Matias D, Sharpanskykh A. An Agent-Based Empirical Game Theory Approach for Airport Security Patrols. Aerospace. 2020; 7(1):8. https://doi.org/10.3390/aerospace7010008
Chicago/Turabian StyleJanssen, Stef, Diogo Matias, and Alexei Sharpanskykh. 2020. "An Agent-Based Empirical Game Theory Approach for Airport Security Patrols" Aerospace 7, no. 1: 8. https://doi.org/10.3390/aerospace7010008
APA StyleJanssen, S., Matias, D., & Sharpanskykh, A. (2020). An Agent-Based Empirical Game Theory Approach for Airport Security Patrols. Aerospace, 7(1), 8. https://doi.org/10.3390/aerospace7010008






