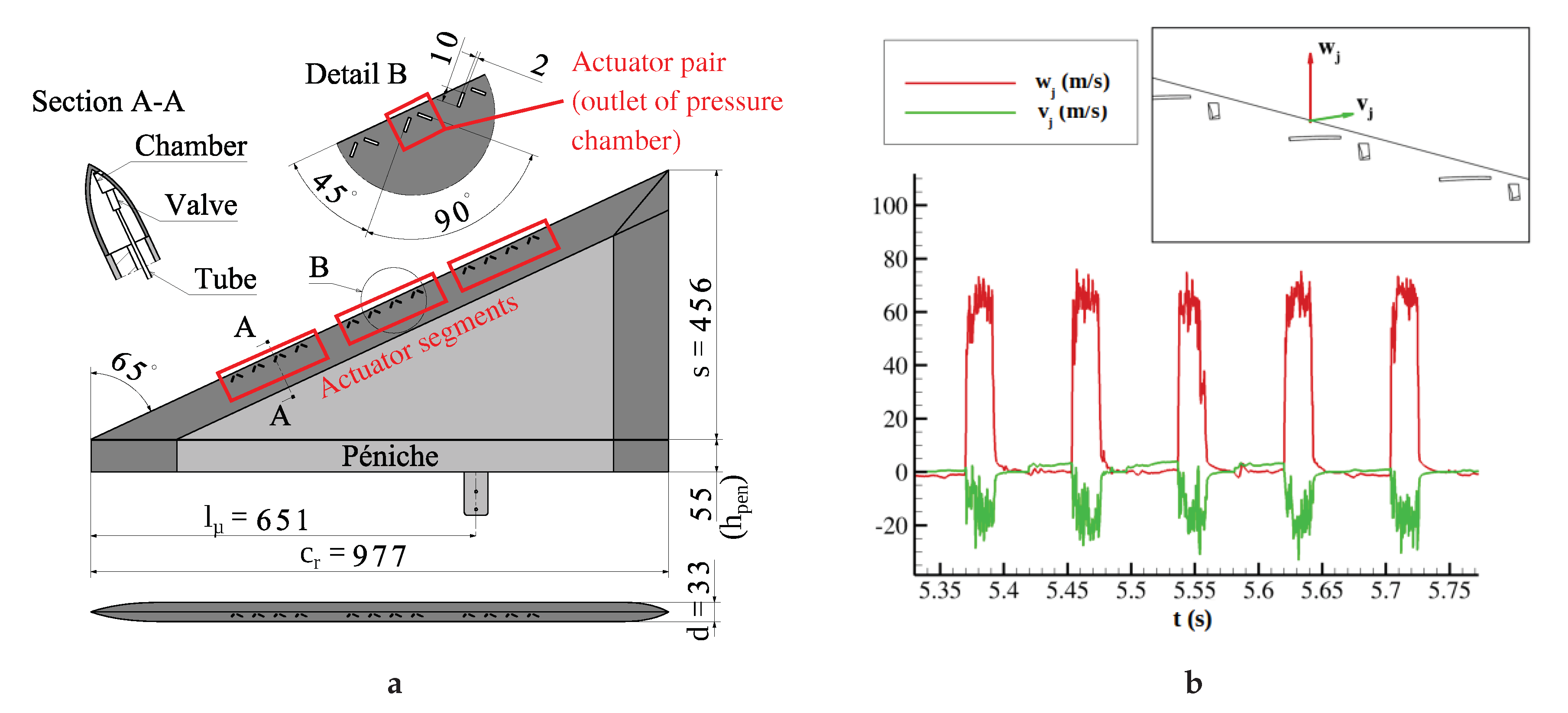
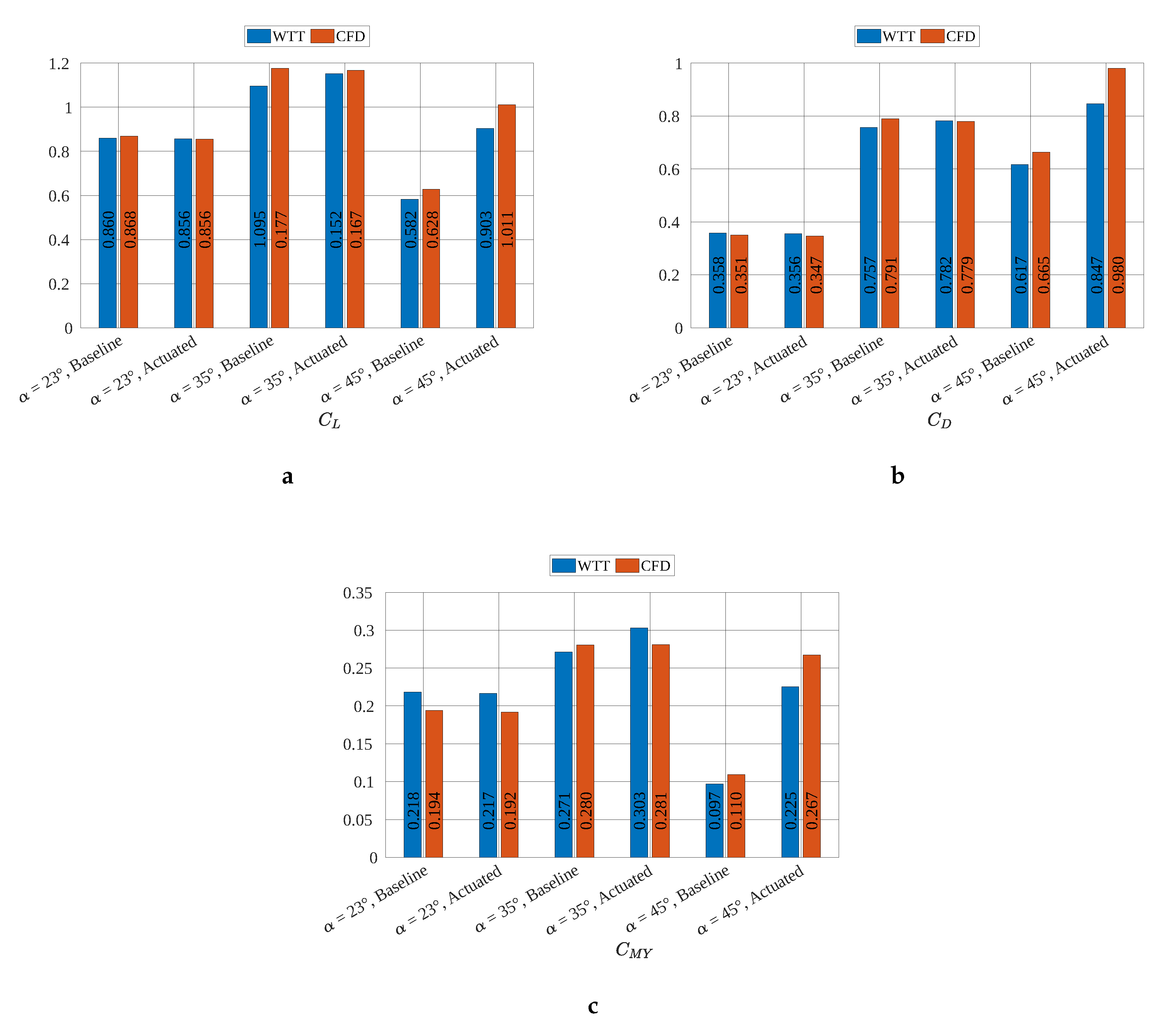
Based on the measured time and phase averaged velocity fields (PIV) and on the time accurate numerically solved velocity fields (DES), the current section discusses the effect of the applied periodic perturbation method on each flow field type. The mean aerodynamic coefficients, both from experimental measurements and from computed values, are assessed for each case investigated in
Figure 11. The measurement uncertainty read
for the lift and drag coefficient and
for the pitching moment coefficient [
20]. With increasing angle of attack, the computed force and moment coefficients diverged from the wind-tunnel test (WTT) results. Two sources might affect this spread: no application of open-jet wind-tunnel corrections and vortex approaching the symmetry boundary with increasing angle of attack.
3.4.1. Delay of Vortex Breakdown
When pulsed blowing was applied on the flow field dominated by vortex breakdown, the breakdown location was shifted downstream, depending on the angle of attack investigated. At
, PIV measurements along the core reported a mean delay of breakdown from
to
[
20]. The DES method estimated the breakdown location too far downstream compared to PIV, for both the undisturbed (
) and disturbed flow field (
). At
, the mean axial stagnation point offered a more suitable criterion for measuring the effect of blowing on the conical wake region. According to the PIV investigations, pulsed blowing reduced the low energy region, displacing it downstream by a chord distance of
. Due to the symmetry boundary condition constricting the apex flow field, the undisturbed flow at the stall angle of attack stagnated farther downstream (
) compared to the experimental findings (0.24). Hence, the computed mean flow responded to actuation by a
downstream displacement of the stagnation point.
Table 3 summarizes the computed and measured chordwise breakdown/stagnation positions based on the mean flow field. However, the average times between DES and PIV were largely unequal, in favor of the latter.
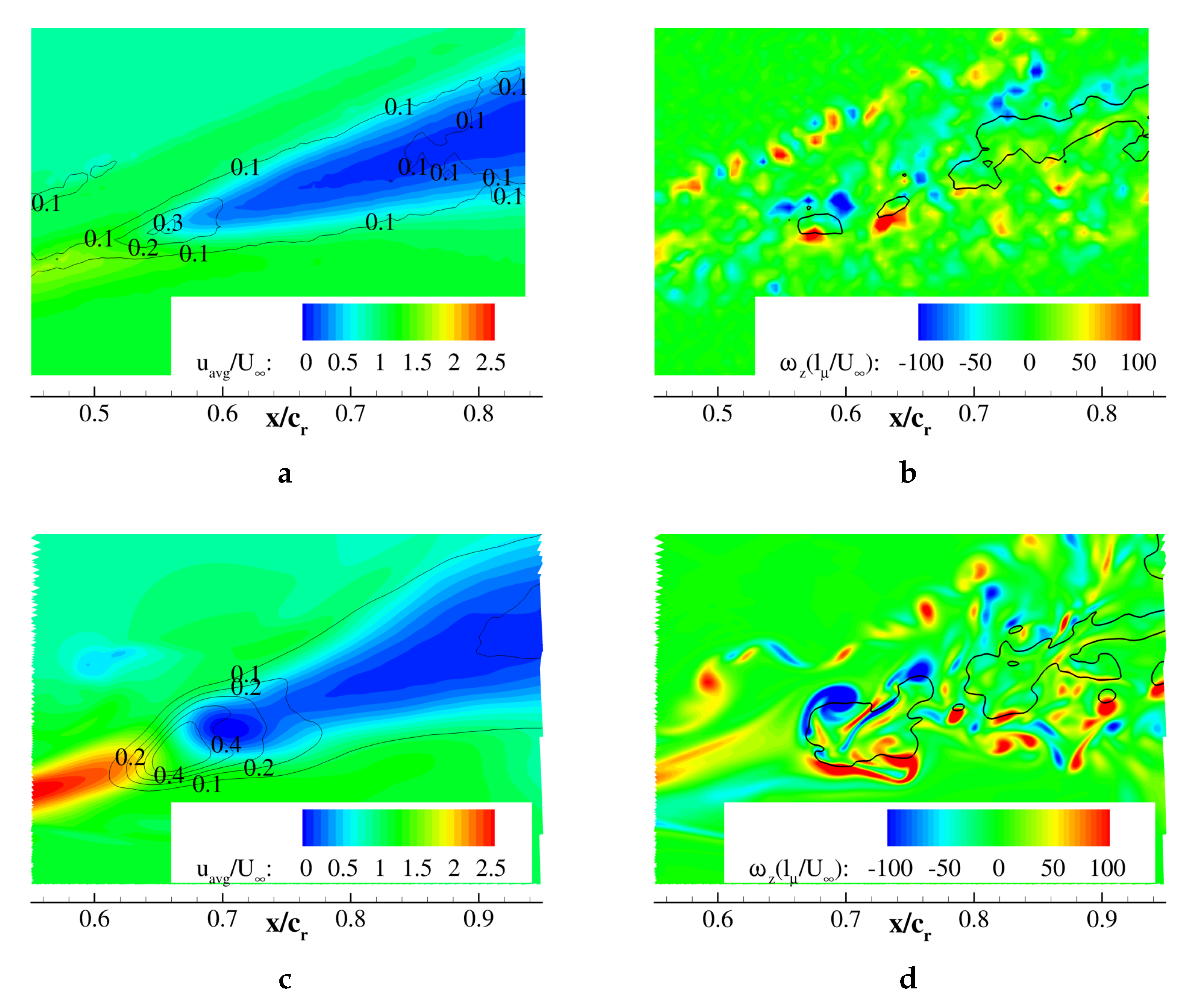
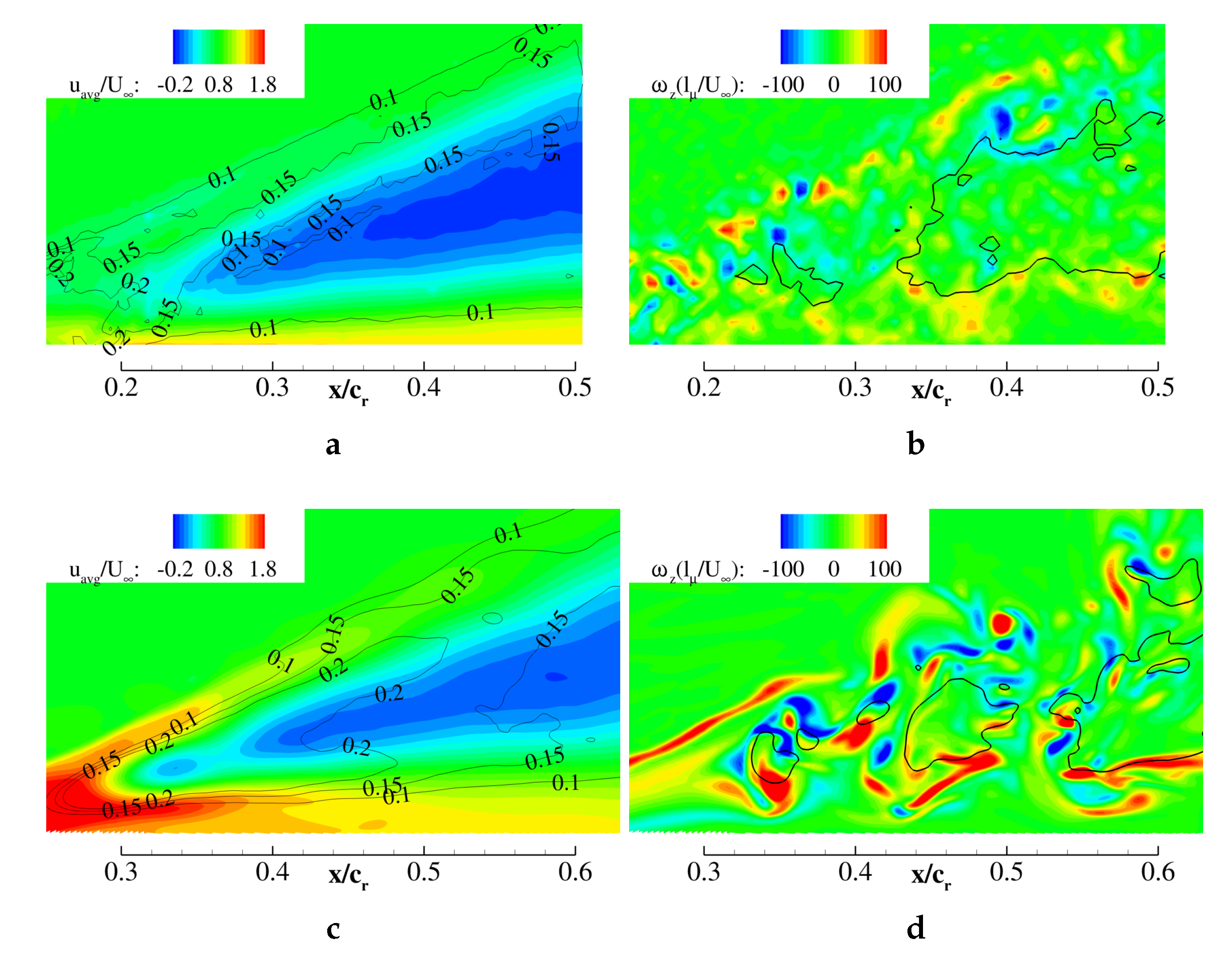
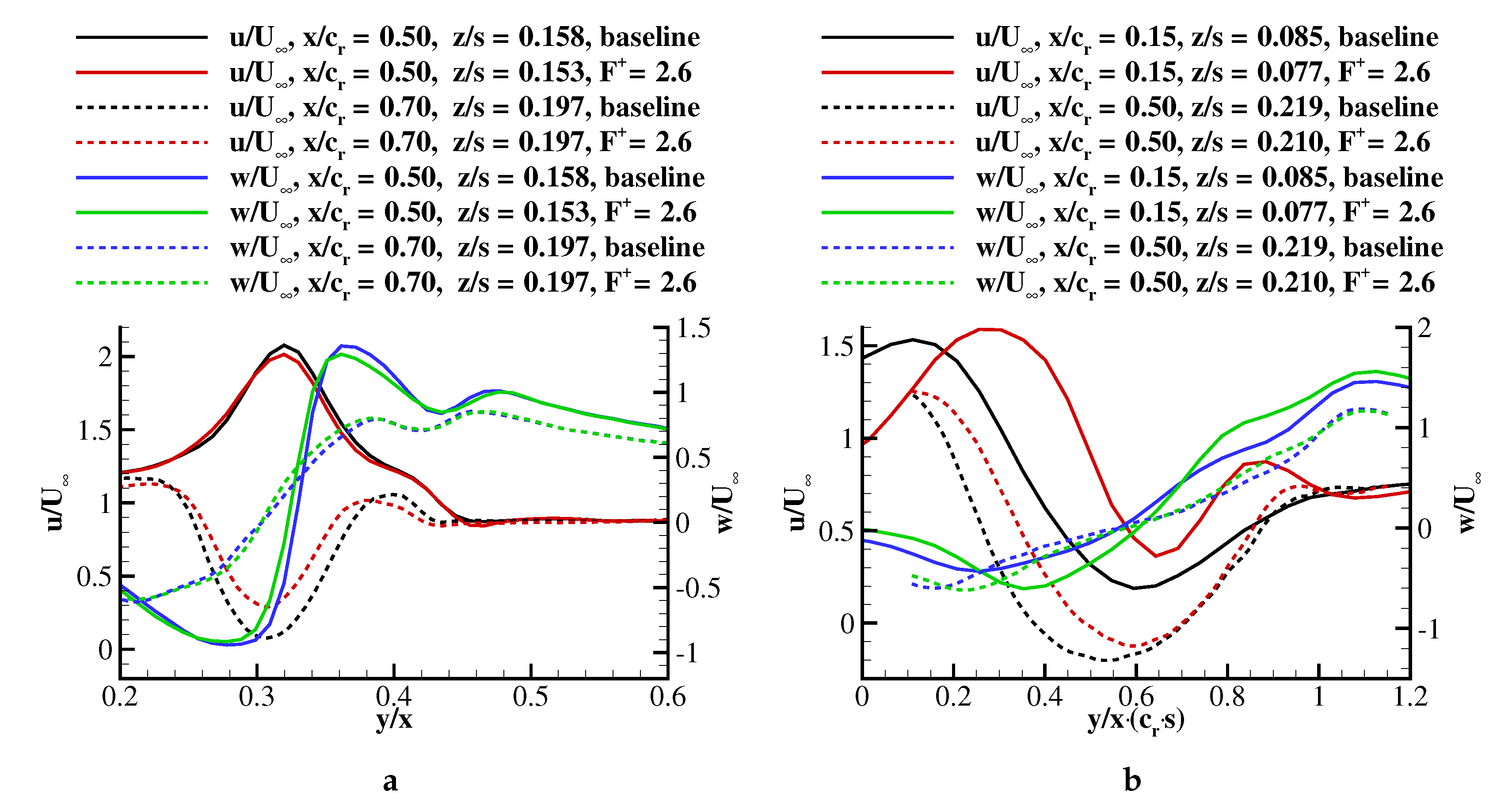
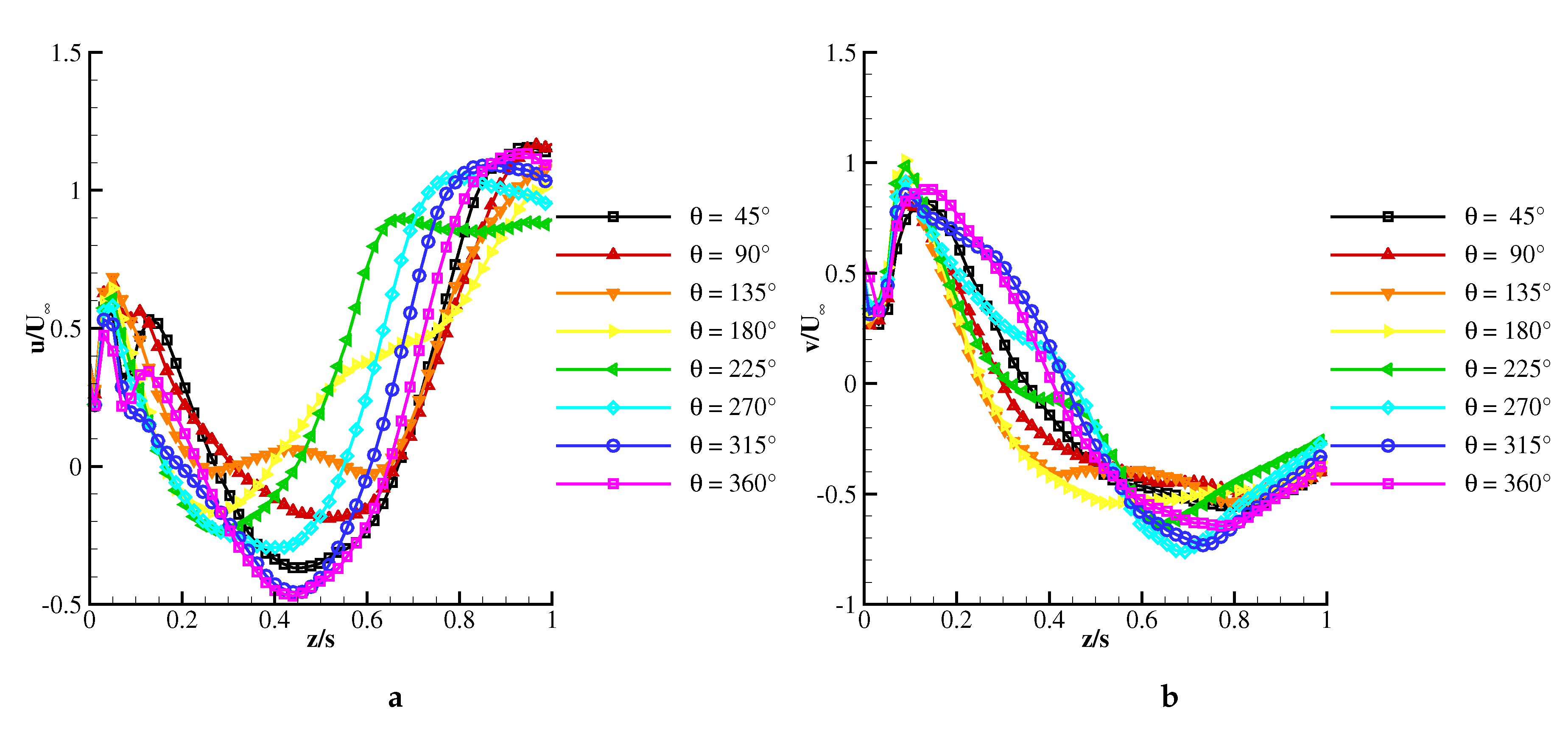
Figure 12 shows velocity profiles extracted from PIV crossflow planes across the vortex core for two angles of attack (a)
and (b)
. The effect of pulsed blowing was evidenced by assessing the baseline and the actuated velocity profiles. For the purpose of completeness, two chordwise locations were investigated. In
Figure 12a, the full and dashed lines represent the spanwise velocity distribution upstream (
) and downstream (0.70) of breakdown, respectively. Between these planes, the core flow transitioned from a jet-type (black line) to a wake-type flow (black dashes) with a decrease in swirl (blue graphs). Actuation had a minor effect in the pre-breakdown region, reducing both
u and
w (red and green) by a small amount. However, downstream of breakdown, pulsed blowing reduced the wake significantly and increased the gradient
in the core, suggesting an increase in swirl compared to the unactuated case.
At stall, wake flow was measured even at
(cf.
Figure 12b). The similarity of the cross-sectional velocity profiles downstream of breakdown for both angles of attack
(
) and
(
) revealed that pulsed blowing had a major influence on the flow region downstream of breakdown. The manipulation of the shear layer vortices by pulsed blowing increased the momentum transport in the radial direction with respect to the vortex axis. The actuation method was effective merely on the unstable vortex region, downstream of breakdown. For this reason, the flow field at
was more affected than at
(cf.
Table 3).
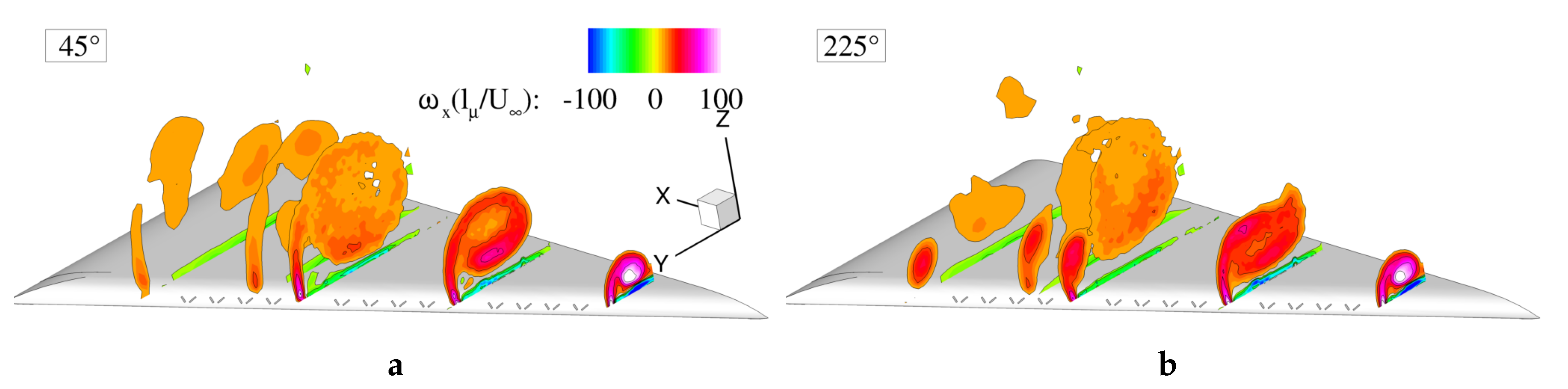
Crossflow phase averaged axial vorticity distribution extracted, during (
Figure 13a) and
after blowing (b), showed the mean periodic trajectory of vorticity peaks. During blowing, the vorticity distribution resembled the averaged flow field. At
, the vortex was stable with a jet-like topology. This region was rather unaffected by the disturbance injected downstream. Instead, the post-breakdown region showed a periodic movement initiated by the excitation. After half of a period, expressed also as a phase angle delay of
, strong shear layer vortices were generated along the leading-edge. These were responsible for the roll-up process and the enhanced momentum transport across the shear layer.
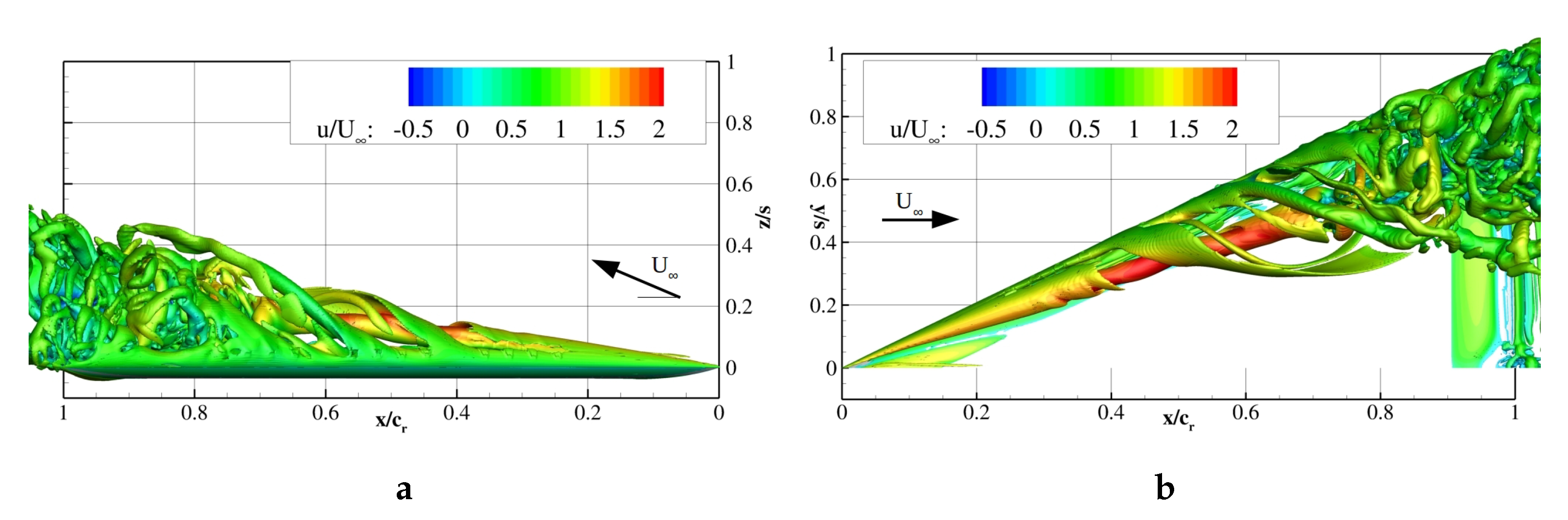
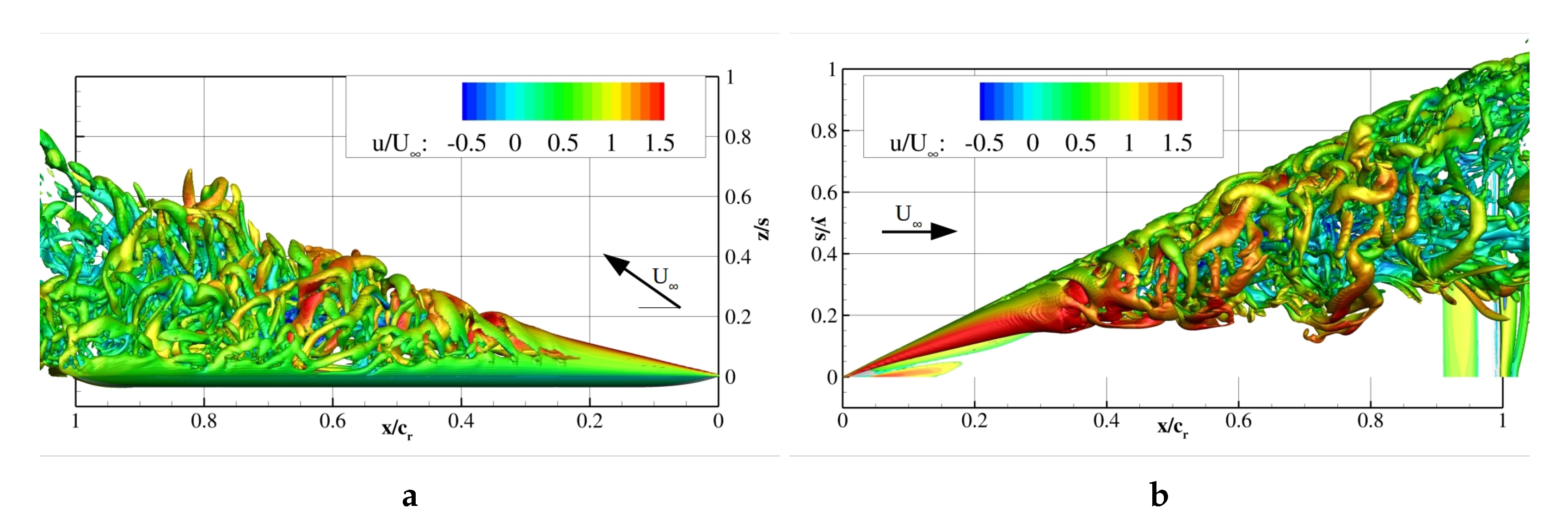
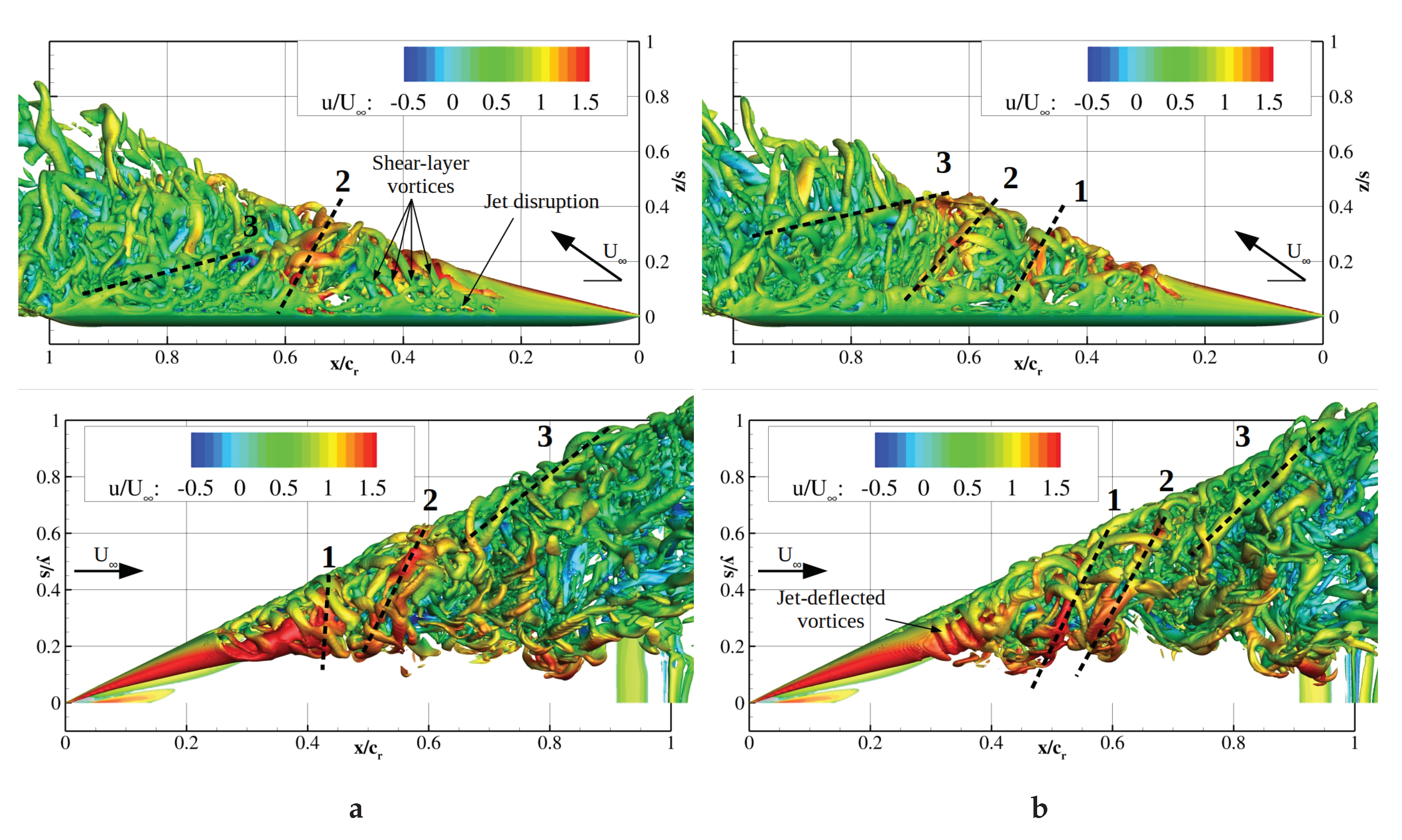
Computed Q-criterion isosurfaces (
s
) of the equivalent corresponding time steps, during and
after disturbance injection, are visualized in
Figure 14. Hence, the phase averaged vorticity peaks in
Figure 13 represented waves of local discrete vortices. Blowing excited merely the shear layer, but affected the whole vortex system with a time delay of
. In
Figure 14a, shear layer vortices spiral around the steady core. Downstream, the waves of vortices designated by dashed lines wound up in the opposite direction compared to the shear layer vortices upstream of breakdown. The disruptions of the shear layer in
Figure 14a were caused by the discrete jet being switched on/off. The flow field evolved
after the formation of discrete jet vortices at the apex and downstream injected front of multiple vortices according to
Figure 14b. At this particular time step, the numbered vortex clusters were located farther downstream with an increased tilting towards the freestream direction. In conclusion, synchronizing the jets at the leading-edge generated vortex clusters transporting high axial momentum
towards the core in a periodic manner.
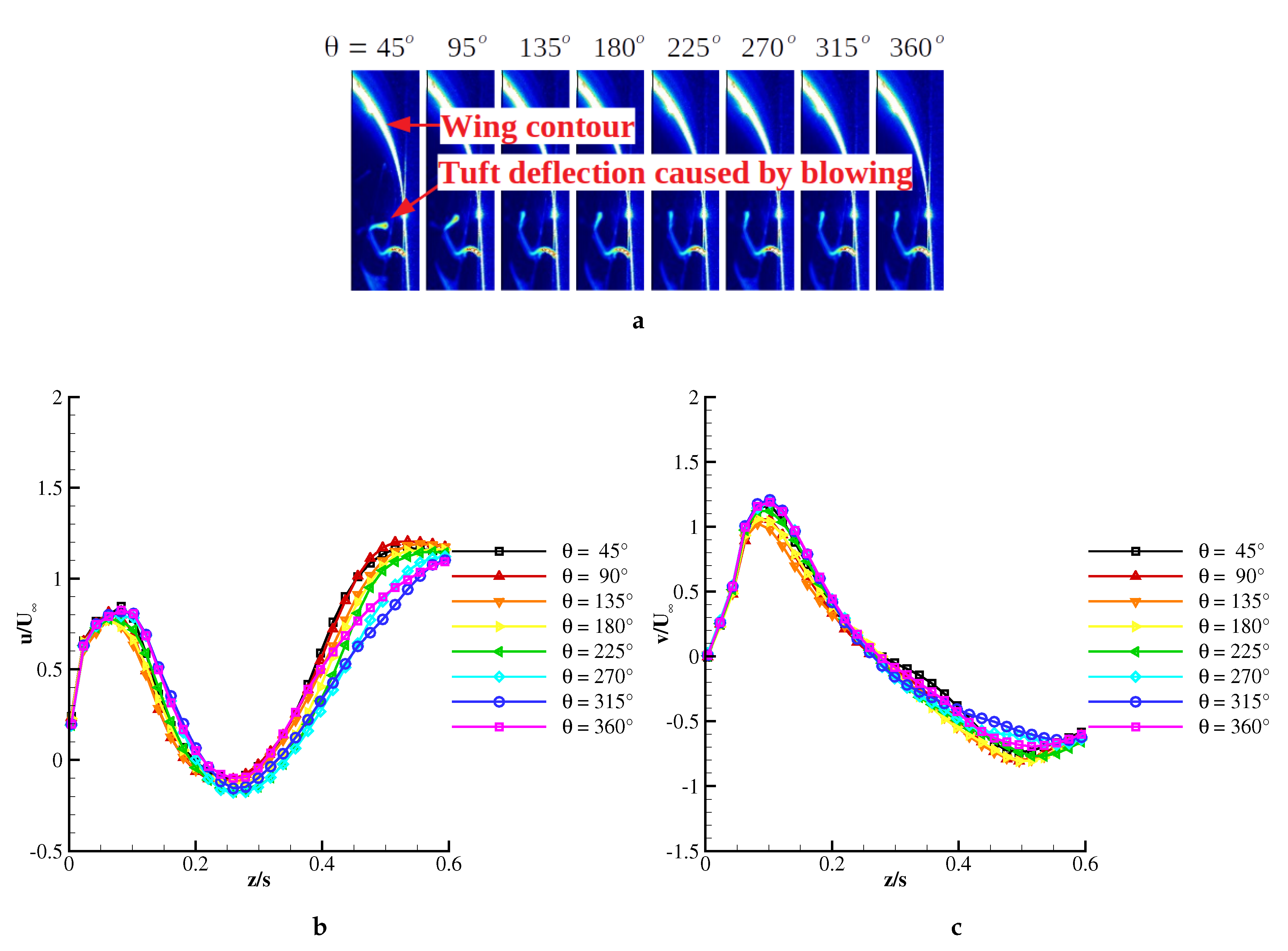
In order to investigate the transport of momentum, phase averaged vertical velocity profiles
and
were extracted from the crossflow plane at
(above the first slot pair of the second segment) and plotted in
Figure 15. The graphs represent eight equally distributed phases of one actuation period, in which the first 25% (
) of the period fluid was injected through the slots and the rest of the period, the jets were turned off. This is visualized by the deflection of a wool tuft placed above a slot in
Figure 15a. The spanwise position of the extracted velocity profiles coincided with the mean vortex position of the actuated case. At
, the mean vortex axis was located at lateral and vertical positions relative to the half span of
and
.
The near-wall region around
was dominated by velocity components close to the freestream value:
,
. In the wake region farther from the wall, the axial velocity decreased, reaching a minimum of
in the vortex rotation axis. Both near-wall and wake regions fluctuated during the blowing period. There was a delay in the flow response to the actuation observed in the presented graphs. The near-wall velocity decreased with advancing phase. The velocity peaks closest to the wall had a minimum at the phase
for both components (cf. the orange graphs in
Figure 15b,c). With progressing phase angle, the flow field recovered to the initial state with near-wall velocity components steadily increasing. Hence, the perturbation affected the flow field with a phase delay of approximately
(
).
Similarly, the wake region reacted to blowing by reducing axial velocity. The minimum value was reached at phases
–
, leading to a
delay relative to the blowing phase. After the blowing phase
, the wake cross-section increased steadily as suggested by the
distribution above
. Here, the lowest axial velocities corresponded to the blue line, representing
. Hence, the flow region above the wake responded to the actuation after a
period. The distribution of lateral velocity presented in
Figure 15c suggested a similar phase dependence as that of the axial velocity. The blue graph is situated above the other graphs both below and above the wake. The
distribution described a distinct inflection in the first phase. Advancing in phase decreased the inflection.
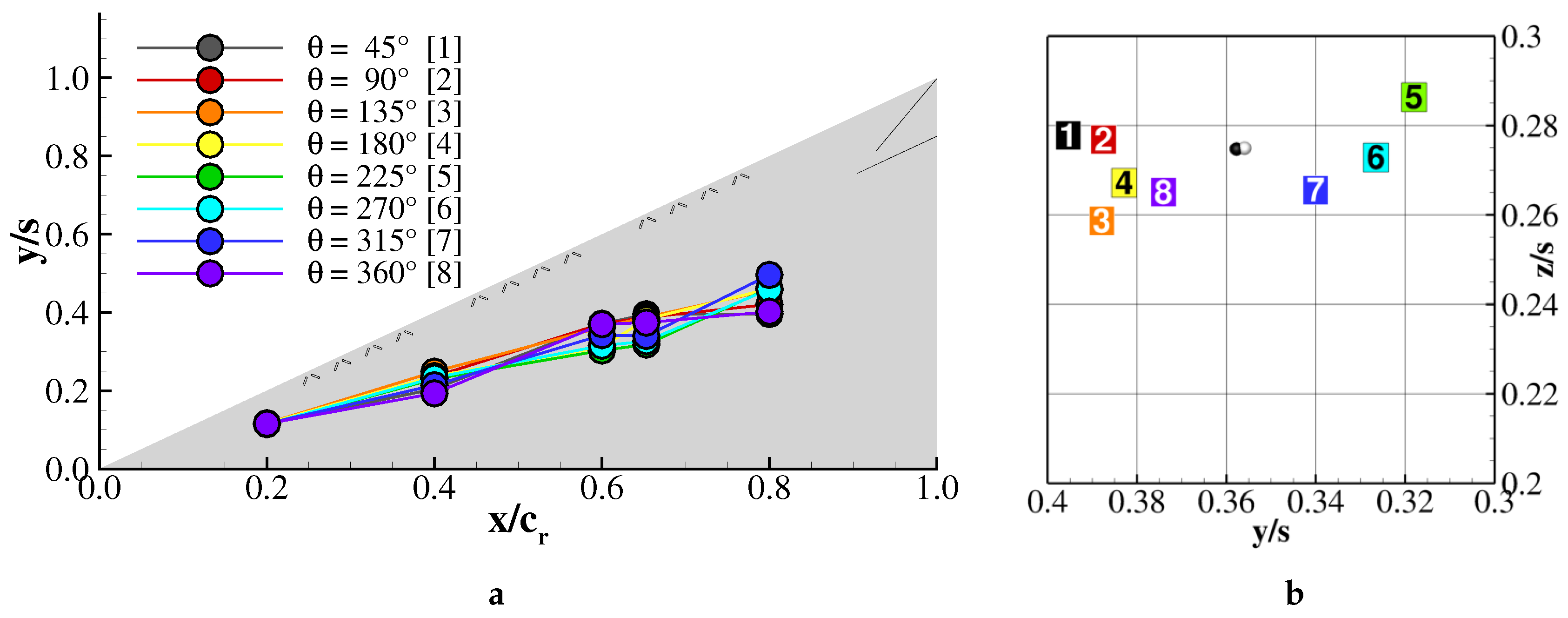
The above investigation into the flow field response based on phase averaged PIV measurements established a periodic displacement of the primary structure. The phase dependent location of the rotation axis is presented in
Figure 16 from two perspectives,
-plane (a) and cross-plane at
(b). The vortex rotation axis described a slight curling around the mean axis. During periodic blowing, the axis displaced in a nearly elliptical manner. In the crossflow plane presented, the lateral motion was more pronounced than the vertical one. The largest displacement occurred in the first and fifth phases investigated. Hence, concomitant with the blowing, the vortex had the most outboard position at
and remained in the vicinity up to the fourth phase (
), after which, it moved to
. In addition to the phase averaged locations,
Figure 16b displays in white the mean location of the baseline vortex axis and in black the one of the forced vortex axis. Although the vortex fluctuated and undulated under periodic forcing, its mean location was slightly outboards of the unforced vortex mean location. It should also be noted that the vortex pulsated at the forced frequency in the longitudinal direction.
3.4.2. Shear Layer Reattachment
In contrast to the stall case, in which pulsed blowing reduced the swirling wake, at
, the excitation targeted the shear layer reattachment that generated massive lift increase. The optimum reduced actuation frequency at this angle of attack was
, which was lower than the previous case. In [
25], the power spectral density of the shear layer velocity fluctuations described a reduction of the dominant frequency when the flow was actuated, which suggested that manipulation of the shear layer instability reordered the shear layer vortices. This interaction resulted in the previously mentioned reattachment of the mixing layer on the wing’s surface.
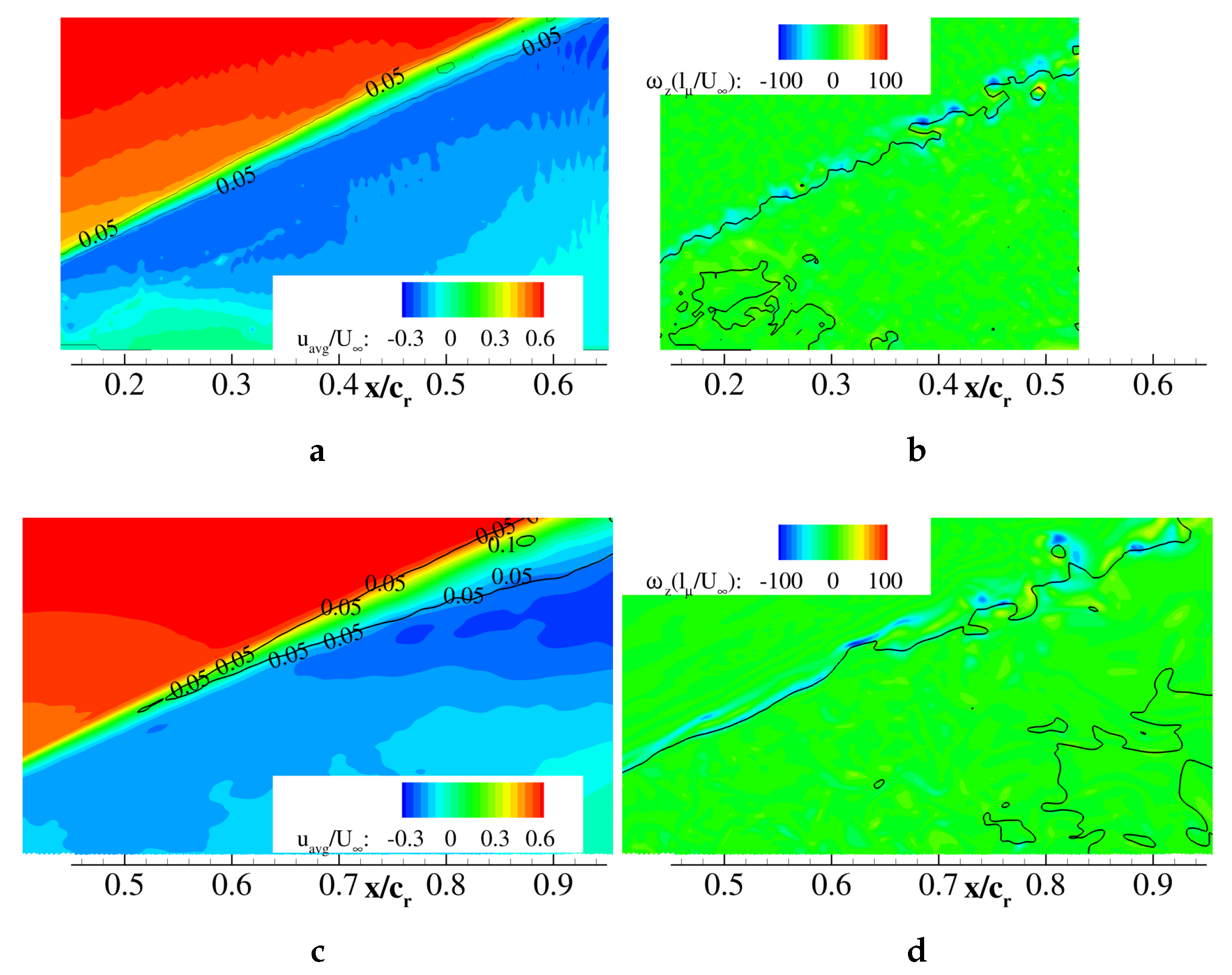
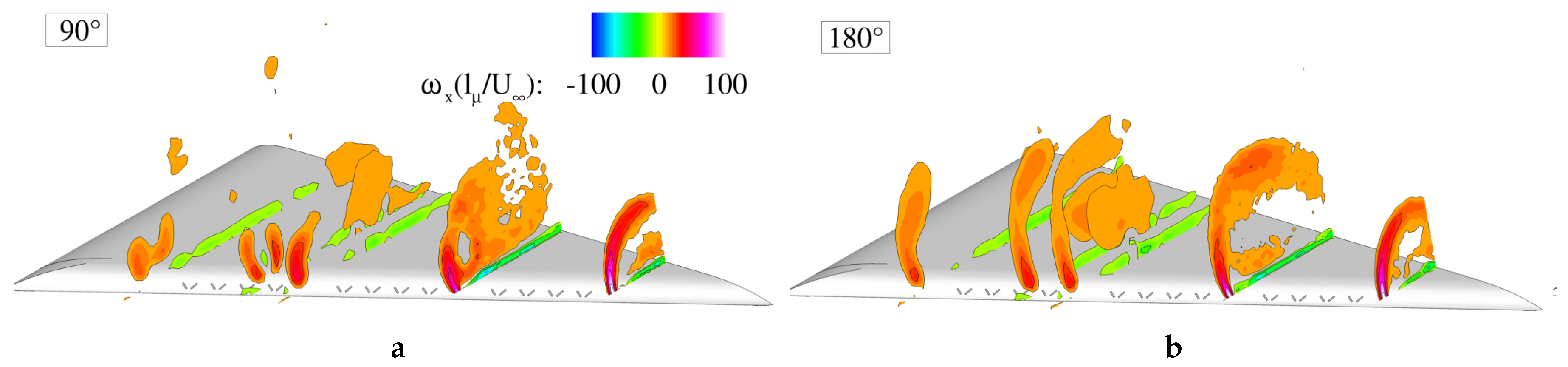
Figure 17 shows the phase averaged axial vorticity distribution at two phases of one blowing period. The phase on the left hand side corresponds to when the jets were switched off (
Figure 17a). Immediately after blowing, the generated jets disrupted the shear layer, generating high vorticity concentrations above the leading-edge. The subsequent phases described the clockwise rotation of vorticity peaks. At a time delay of
, the vorticity peaks were displaced along the shear layer (
Figure 17b).
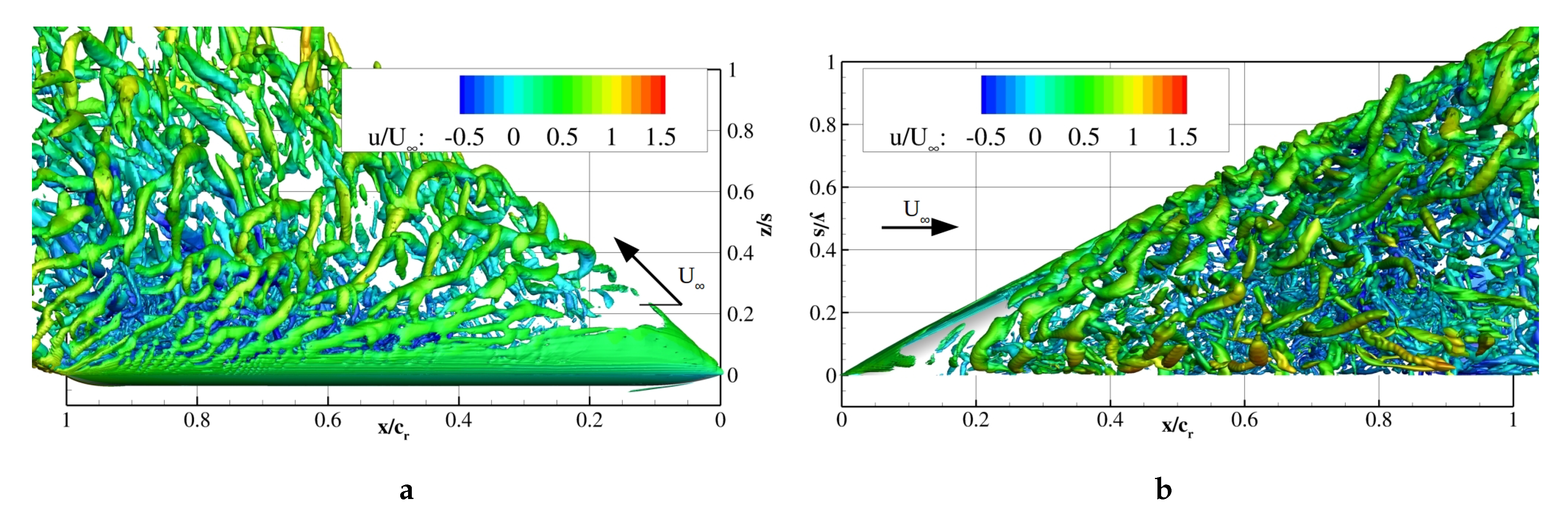
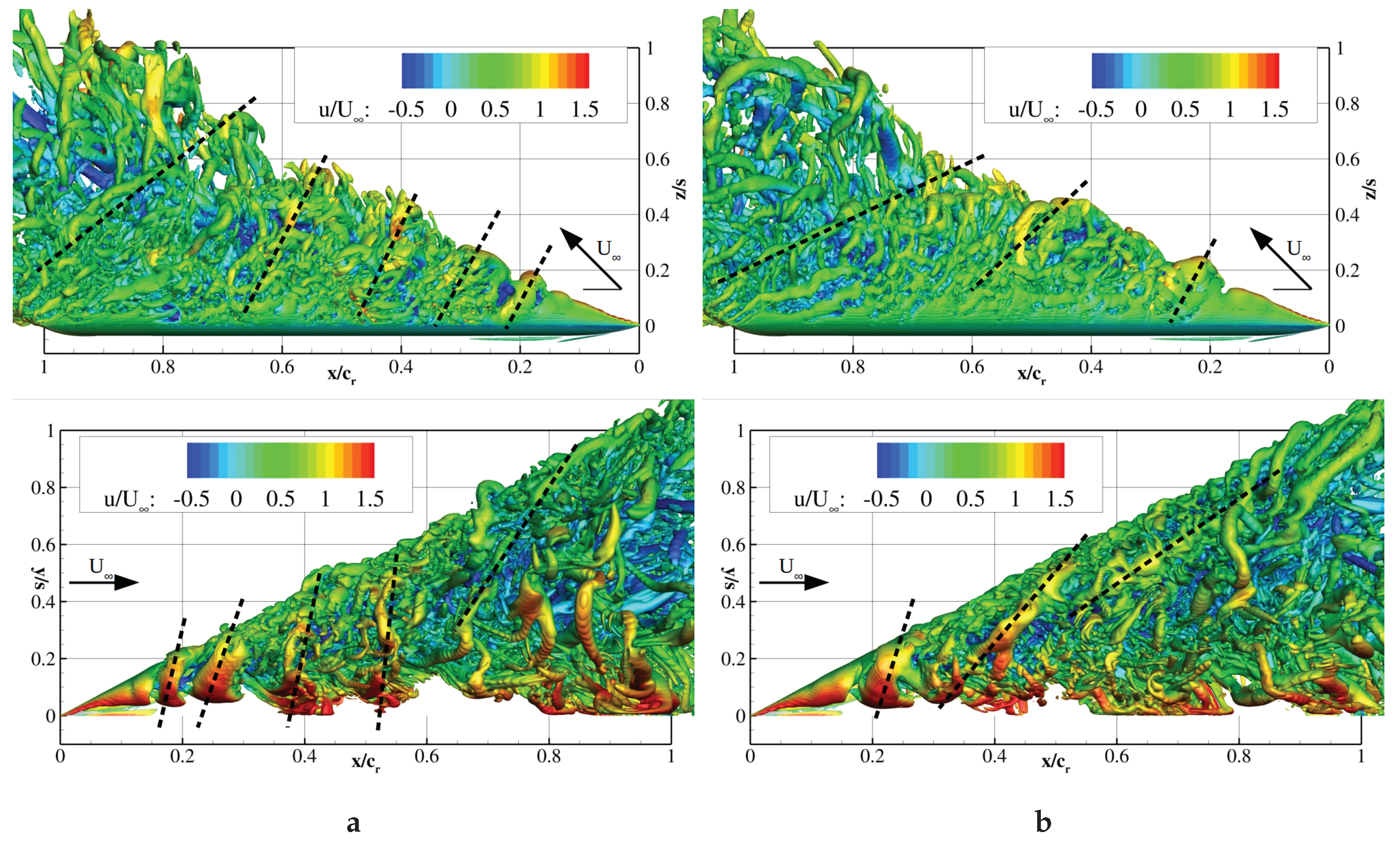
In
Figure 18, the Q-criterion
s
colored by the relative axial velocity in the range
showed both investigated phases. The reattachment of the shear layer generated a flow field resembling the stalled flow field. At post-stall, the forced primary structure extended from the symmetry plane to the leading-edge. The pulsed jets increased the circumferential momentum, on the one hand, and enforced a frequency dependent vortex shedding, on the other. As a result, the shear layer consisted of unsteady discrete vortices rotating around the reversed flow region. The leading-edge shedding occurred in a three-dimensional manner as in the baseline case (cf.
Figure 10). However, in the actuated case, the vortices were dominated by the jet interaction and increased in intensity downstream with specific curling around the wake. Dashed lines designate vortex fronts that demonstrated a certain periodicity. When the blowing ceases, the vortex fronts were ordered circumferentially and convected downstream; see
Figure 18a. These waves originated from the shear layer instability initiated at the apex. Inboard, the flow constriction led to high axial velocities.
, after blowing cessation, waves of shear layer vortices nearly parallel to the leading-edge were present in the flow field, disturbing the annular structures. Advancing within the blowing period, the discrete vortices were transported downstream in a spiraling path, recovering to the initial state. Throughout this process, mixing between the inner wake region and the outer region was sustained.
Figure 19 presents the vertical distribution of
and
across the mean vortex core at
and
. As in the previous case, jets were active during phases
and inactive during the rest of the blowing period. In the region adjacent to the wall, axial and spanwise momentum increased steadily up to
. As the phase progressed, both velocity components decreased, and the velocity deficit closer to the wing increased. Farther from the wall, the negative axial velocity peak fluctuated in a phase dependent manner. Axial velocity was at its lowest during the last quarter period,
. The blowing phase led to a rapid increase in axial velocity. The highest values corresponded to
. At this phase, the wake-type distribution showed two valleys. The spanwise velocity component demonstrated an inflection, as well at 135
, which remained up to
.
The fluctuation of the velocity field across the vortex described above suggested that the vortex underwent certain periodic motion within one blowing period. The location of the rotation axis corresponding to each phase investigated is plotted in
Figure 20. As in the previous case, the vortex rotation center wound downstream in a counter-clockwise direction, but described a clockwise rotating path as time passed. At
, the phase averaged axis of rotation described an ellipse. During blowing, the axis had the most inboard displacement. Up to
, the vortex axis shifted towards the wing, after which it described a lateral movement. Half a period after fluid injection, the vortex had the furthest outboard location. Comparing the phase averaged PIV investigations with the time accurate DES computations revealed that the primary structure consisted of many discrete structures that, on average, described an ordered motion.