Abstract
Shape-variable structures can change their geometry in a targeted way and thus adapt their outer shape to different operating conditions. The potential applications in aviation are manifold and far-reaching. The substitution of conventional flaps in high-lift systems or even the deformation of entire wing profiles is conceivable. All morphing approaches have to deal with the same challenge: A conflict between minimizing actuating forces on the one hand, and maximizing structural deflections and resistance to external forces on the other. A promising concept of shape variability to face this challenging conflict is found in biology. Pressure-actuated cellular structures (PACS) are based on the movement of nastic plants. Firstly, a brief review of the holistic design approach of PACS is presented. The aim of the following study is to investigate manufacturing possibilities for woven flexure hinges in closed cellular structures. Weaving trials are first performed on the material level and finally on a five-cell PACS cantilever. The overall feasibility of woven fiber reinforced plastics (FRP)-PACS is proven. However, the results show that the materials selection in the weaving process substantially influences the mechanical behavior of flexure hinges. Thus, the optimization of manufacturing parameters is a key factor for the realization of woven FRP-PACS.
1. Introduction
The aerodynamic performance of a conventional aircraft is optimized for one specific flight condition. Hence, a flight outside this design point leads to a decreased efficiency [1]. Shape-variable structures can change their geometry in a targeted way and thus adapt their outer shape to different boundary conditions. Classical kinematic concepts can be improved through a controlled change of shape and the thereby changing interaction between the structure and its environment, and completely new functionalities can be explored. Many studies are found in the literature that describe the advantages of morphing wings. A review presented by Thill et al. [2] summarizes the advantages of such morphing technologies as: reduction in drag and noise due to gap-free high lift systems, reduction in mass and cost by decreasing the overall system complexity, expanding range and flight envelope, stealth capability, and improved behavior regarding vibration and flutter. Many concepts for active as well as passive shape-variable structures exist, which show great potential, especially in aviation. However, the advantages of shape flexibility are often countered by additional peripheral or system-inherent costs. A detailed review of structural morphing concepts is presented by Barbarino et al. [3], which claims that a successful morphing approach has to overcome weight penalties resulting from the additional actuation mechanism. Different approaches to achieve shape variability were presented in literature, for example: The active Flexspar actuator that uses piezoelectric actuators [4], a vertebrate structure actuated by shape memory alloys [5], a flexible ripless trailing edge with mechanical actuators [6], or the horn concept driven by a linear hydraulic actuator [7]. All studies so far have to meet the same challenge: a conflict of objectives between the lowest possible actuating forces on the one hand, and high structural deflection and the demand for high resistance to external forces on the other. This often results in heavy structures that provide flexibility by overcoming great stiffnesses.
Hence, there is a need for structures to be stiff and flexible at the same time. A remedy is provided by plant-inspired adaptive structures that combine the advantages of fluidic actuators and compliant mechanisms [8]. Pneumatic and hydraulic actuators are characterized by high power density, large stroke, and high positioning accuracy compared to alternative actuator technologies [9]. Thus, morphing concepts with pneumatic actuators offer great potential for lightweight solutions [10]. Adaptive cellular honeycomb structures with pneumatic actuation were introduced by Dittrich and patented as the Cellular Actuator Device [11]. Based on this functional principle, Barrett and Vos developed [10,12] and patented [13] the concept of a pressure adaptive honeycomb using equilateral hexagonal cells. Furthermore, Vasista et al. presented the concept of a topology-optimized pressure-driven trailing edge with a focus on the potentials of topology optimization for the design of complex flexure hinges [14]. The concept of adaptive pressure-controlled cellular structures for large one-dimensional actuation strain was examined by Luo et al. [15,16]. Lv et al. introduced a design method for adaptive fluid-actuated cellular structures with polygonal motor cells using a multiscale topology optimization method [17]. Several more approaches with fluidic actuation for large deformation were recently published in the field of soft robotics [18,19]. None of the mentioned concepts has found an energy- and weight-efficient solution for the cell pressurization at high internal pressure loads so far.
This article deals with a bionic approach for shape variability based on pressure-actuated cellular structures (PACS). The biomimetic approach of PACS was first investigated by Pagitz et al. with regard to technical applications and translated into a two-dimensional concept [20]. Gramüller et al. further developed the theoretical concept to technical maturity and were able to demonstrate the outstanding flexibility of such structures to achieve arbitrary form functions [21,22]. The design methodology is based on an optimization algorithm developing a two-dimensional truss structure. Then, the truss structure is translated into a cross-sectional design considering flexure hinges and cell side geometries. The primary difference between PACS and the pressure adaptive honeycomb [10,12] is a direct optimization of the cell side lengths so that any single curved form-function can be achieved. The combination of actuator and functional surface reduces component complexity and offers lightweight potential. Another distinguishing feature is the extensive geometric degree of freedom and the possibility of realizing very large deformations. Thus, the potential applications of PACS in aviation are manifold and far-reaching. The substitution of conventional flaps in high-lift systems up to the deformation of entire wing profiles for adaptation to different flight conditions is conceivable.
First, Section 2 of this article outlines the basic design concept of PACS and the importance of extending the design approach to anisotropic structures with demand-oriented stiffness distributions. A joint project between the Institute of Adaptronics and Function Integration (iAF) at Technische Universität Braunschweig and the Institute of Textile Machinery and High Performance Material Technology (ITM) at Technische Universität Dresden is examining the aspects of woven PACS. The aim of the following study is the investigation of manufacturing possibilities for woven flexure hinges in closed cellular structures using fiber reinforced plastics (FRP). Section 3 of this article presents the flexure hinge design, material considerations, and the developed manufacturing process of woven FRP-PACS. Weaving trials are first performed on flat plate and flexure hinge specimens and finally on a five-cell PACS cantilever. The results for mechanical tests and microscopy examinations are presented in Section 4. The article concludes with a discussion of the obtained results and an outlook of transferring the concept of PACS into technical application on the example of a novel morphing flight control surface.
2. PACS—Concept and Approach
The concept of PACS faces the challenging conflict between flexibility and stiffness with the principle of actuation by internal pressure. This biomimetic approach is based on the movement of nastic plants. The Venus flytrap (Dionaea muscipula), for example, is able to fold its leaves quickly and powerfully to trap insects and spiders. The movement of the trap leaf is mainly based on the change of the cells’ turgor pressure in interaction with the geometric properties and flexibility of the plant’s cell walls. This allows the plant to move without the presence of muscles or discrete joints. A schematic motion sequence of the Venus flytrap is illustrated in Figure 1.
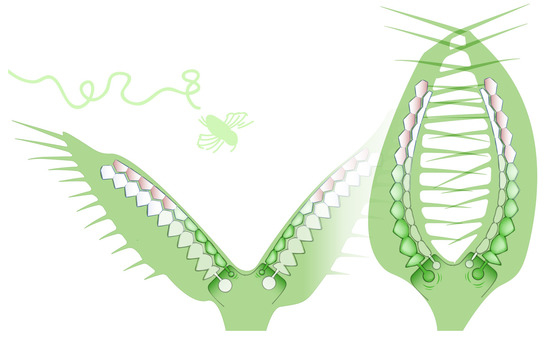
Figure 1.
Schematic cell structure of the Venus flytrap. Leaf movement actuated by a change in turgor pressure. Reprinted/adapted by permission from Springer Nature [23].
Transferring this mechanism of action to a technical concept can be explained on a single PACS cell. Initially, a pentagonal cell is considered that is composed of rigid cell walls and discrete joints without inherent stiffness. Increasing the pressure to causes the cell to expand until the maximum cross-sectional area is reached (cf. Figure 2). The state of maximum expansion leads to a minimum of internal energy. After reaching the maximum cross-sectional area, any further increase in pressure no longer leads to a change in geometry, but to a stiffening of the cell. Then, all hinges lie on a circle with diameter D. The maximum angular displacement is determined solely by the ratio of the cell side lengths.
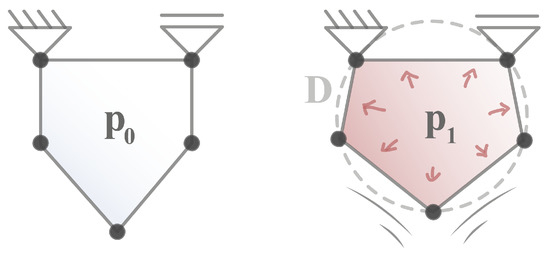
Figure 2.
Shape change of a pentagonal cell by pressure-induced volume increase. Reprinted/adapted by permission from Springer Nature [23].
A shape-variable structure is obtained by arranging several cells in a row. This determines the deformation behavior of the structure by combining the displacements of each cell. The state of maximum deformation is described by the sum of angular displacements of each individual cell, as illustrated on a single-row cantilever in Figure 3.
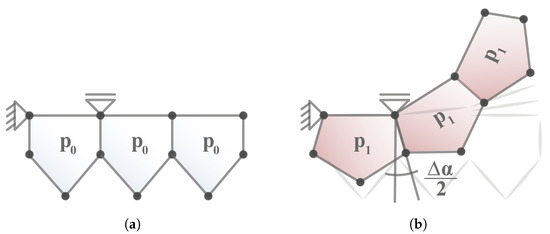
Figure 3.
Pressure-induced deformation of a single-row cantilever: (a) Initial state. (b) Target shape at maximum displacement. Reprinted/adapted by permission from Springer Nature [23].
Based on these fundamental analytical assumptions, a design methodology is developed that allows the formulation of a complete functionality envelope. For any polygonal cell structure, the approach of virtual work (AVW) can be used to calculate the pressure-dependent state of equilibrium. Equations (1) and (2) provide the basis for the iterative process of form-finding. The relationship between the initial state and target state is established via the sensitivity matrix and the virtual work . Knowing the equilibrium state of the cell structure, the element stresses are calculated using AVW.
The single row cantilever can only reach a single target shape determined for the angular displacement at maximum pressure. A remedy is the introduction of a second cell row, whereby different pressures are assigned to both cell rows. By simultaneously actuating both cell rows, a continuous switching between two target shapes is possible (cf. Figure 4). The iterative form-finding algorithm described above finally allows the design of arbitrary double-row PACS.
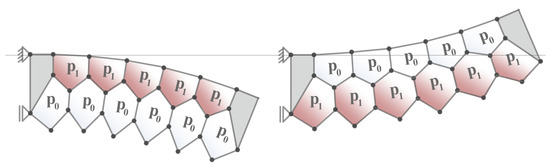
Figure 4.
Two independent target shapes of a double-row cantilever. Reprinted/adapted by permission from Springer Nature [23].
The basic principle of PACS results from the combination of rigid cell sides (high wall thickness) and flexible areas (reduced wall thickness). A key challenge is the design of the flexure hinges. On the one hand, they must allow for a significant degree of compliance. On the other, they are a structural weak point due to their small cross-sections. Thus, the dimensioning parameters for PACS are the stresses in the hinge areas that result from a combination of pressure-induced and bending loads. A cell with internal pressure p, diameter D, Young’s modulus E, and strength R is considered. Each flexural hinge i is designed with thickness t, length l, and hinge angle u (Figure 5). The angular deflection of the hinge results from the the deformation of the pressurized cell and is calculated by the change in hinge angle to .
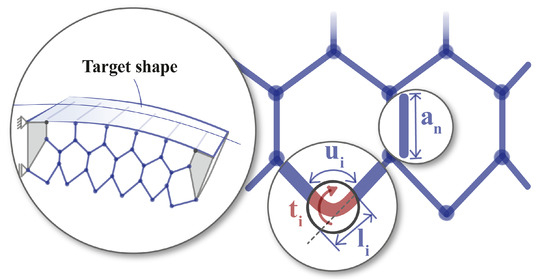
Figure 5.
Geometric design parameters used by the form-finding algorithm. Reprinted/adapted by permission from Springer Nature [23].
First, the internal pressure p leads to normal stresses that can be calculated with Barlow’s formula, which is valid for thin-walled pipes:
whereby D is the diameter of the inflated cell according to Figure 2. Second, bending stresses due to hinge deflection can be approximated by calculating the stiffness of a bending beam with the second moment of inertia . Hinge elements are substituted by rotational springs with the compensatory stiffness c.
Determining the bending moment with Equation (4), the maximum bending stresses at extreme fiber result in:
Thus, an estimation for the total stresses in the hinge elements is obtained. These must never exceed the material strength R.
Depending on the hinge thickness, the permissible pressure can be determined by rearranging Equation (6).
The optimum thickness that allows applying the maximum pressure to a PACS cell is obtained for :
Finally, the maximum pressure load for a given cell geometry with optimum thickness is determined by inserting Equation (8) into Equation (7).
The transfer of the previous results into technical application takes place on the example of a novel morphing flight control surface. Figure 6 shows the integration of a double-row PACS cantilever into the overall wing system. The aim is to outperform conventional flaps in the regard of weight and efficiency while maintaining the same operational performance.

Figure 6.
Design study of a morphing pressure-actuated cellular structure (PACS) flap.
In addition to the iterative form-finding algorithm described above, the technical implementation of PACS requires a holistic design approach. PACS are a complex system with mutual interactions between all subsystems. The modeling of individual subsystems cannot be considered separately from each other. Starting from a 2D geometry, the following steps are decisive:
- the transfer into a 3D construction model,
- the fluid flow concept,
- the shape-variable cell closure,
- the manufacturing process, and
- the experimental proof of concept.
For all of these subsystems, conceptual solutions are developed and presented in detail in previous publications [21,22,23,24,25]. The holistic design approach is illustrated in Figure 7. Using this approach, a double-row PACS cantilever is finally realized and manufactured in selective laser sintering (SLS) [25]. The experimental proof of the holistic design approach is provided. However, materials processed in SLS do not provide the necessary strength to withstand the internal cell pressure required for aerodynamic loads in typical aeronautical applications. Consequently, PACS can only unfold their true potential by considering a more sophisticated manufacturing process.
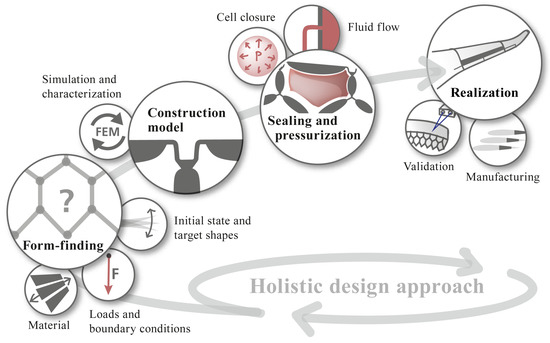
Figure 7.
Process chain for a holistic PACS design. Reprinted/adapted by permission from Springer Nature [23].
The aforementioned key conflict between low actuation forces and high structural deflection predestines PACS as an application of anisotropic materials. For high performance, a demand-oriented stiffness profile within the structure is essential. The requirements described above require flexible but high-strength materials. Equation (9) shows that the ratio of provides a crucial criterion for material selection. Accordingly, FRP prove to be particularly suitable for PACS. In initial trials, the functionality of PACS was demonstrated on a single-row cantilever made of pre-impregnated glass-fiber reinforced plastics (GFRP) [21]. However, the manufacturing process turns out to be complex, time-consuming, and difficult to reproduce. New manufacturing methods for integral and automated manufacturing of FRP-PACS have to be investigated. Therefore, to bring the PACS one step closer to aeronautical application, textile manufacturing possibilities are being researched. The following sections of this paper are dedicated to the technology development of woven FRP-PACS.
3. Materials and Methods
3.1. Flexure Hinge Design for PACS
The objective of the following investigation is the design and technical implementation of a PACS cantilever in integral textile manufacturing. Through energy-efficient pressurization and a focus on lightweight design, the aim is to outperform conventional plain flaps. The performance-driven boundary conditions for the shape-flexible PACS are a minimum bending radius and a maximum actuation pressure. Thus, a bending radius of less than 250 mm is required to compete with plain flaps in terms of typical dimensions and deflections. A maximum internal pressure of 0.75 MPa is defined to provide sufficient stiffness against external loads, such as aerodynamic gust and maneuver loads.
Considering the basic principle of PACS, a wall thickness ratio of 1:12 is to be reached between rigid cell sides and flexible hinge areas. The functionality of the PACS is finally achieved by arranging several unit cells with defined geometry. Using the form-finding algorithm described above, the preliminary design of the PACS is accomplished. In order to prove manufacturability of woven FRP-PACS, a single-row cantilever with five pentagonal cells will first be investigated. Manufacturing driven boundary conditions specify a maximum total length <200 mm as well as a maximum height <36 mm. In order to achieve the required bending radius, a maximum angular displacement per cell of is needed. This determines the size of a single PACS cell as 38 mm × 35.5 mm (Figure 8b). The length of the remaining cell sides can be calculated analytically, since in an idealized cell all hinges lie on a circle in the pressurized state. In this state, the inner surface reaches its maximum. The design parameters used are shown in Table 1 and Figure 8.
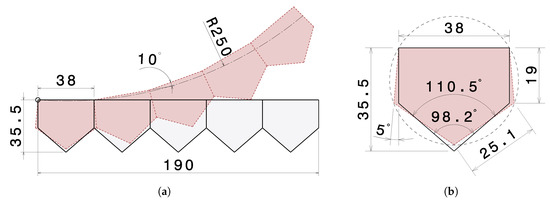
Figure 8.
PACS design parameters: (a) Five-cell PACS cantilever geometry. (b) PACS unit cell.

Table 1.
PACS design parameters.
For the analytical hinge design, the hinge is considered as a bending beam with the deflection . Thereby, has to be the maximum angular deflection of all hinges. In this case, the maximum hinge deflection is obtained at the lower hinge to . The maximum hinge thickness , at which the bending stresses at the extreme fiber do not exceeded the material strength, is calculated with Equation (8). With , and the material properties as determined in Section 4.1, the maximum permissible hinge thickness is . Thinner hinges reduce bending induced stresses and thus allow higher deformations. In order to increase the PACS performance and fathom the limits of the textile manufacturing processes, the hinge thickness is defined to mm. The transition zone between cell sides and hinge areas is designed with two radii of 2 mm each. The final hinge design is shown in Figure 9. Considering Equation (7), the maximum pressure results to mm) = 3.03 MPa, which is about four times higher than the design pressure of . Though, a further increase of actuation pressure is not intended, since the cell closure concept then becomes the limiting element [24].
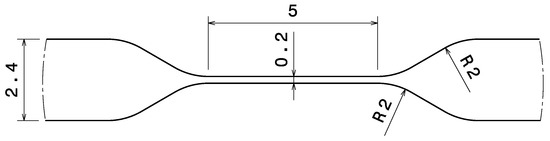
Figure 9.
Flexure hinge design parameters.
3.2. Material Selection for Weaving Process
The basis for the selection of materials is the possibility of automated manufacturing and good processing in the weaving process. E-glass is chosen as the fiber material. Due to their isotropic structure, glass-fibers (GF) are significantly less sensitive to compression than carbon or aramid fibers. They have a relatively high elongation at break, which is excellent for the application as flexure hinges with high deflection. Additionally, they can be processed very well around the weaving process. Due to their positive matrix properties, thermoplastic FRP are particularly suitable for the design of compliant PACS hinges. In contrast, thermoset FRP face the challenge of impregnating textile semi-finished products in closed cellular structures. In the case of a thermoplastic FRP, the matrix can be added directly in the weaving process as a thermoplastic fiber. Such semi-finished textile products based on hybrid yarns are also developed at the Institute of Textile Machinery and High Performance Material Technology at Technische Universität Dresden [26]. In contrast to thermoset matrices, only thermoplastic hybrid yarns achieve an even distribution of the matrix in the subsequent consolidation process for such complex structures as required for PACS. In the following work two different hybrid yarn materials are investigated with regard to the PACS design process as shown in Table 2. In both cases yarns consisting of GF with 46% fiber volume content (FVC) (67% content in weight) and a polyamide (PA) matrix are used. The first material is a hybrid twisted yarn developed at ITM. The idealized diameter of this yarn is with 0.7 mm already significantly larger than the desired hinge thickness of 0.2 mm. However, when the fabric is consolidated during hot compression molding (HCM), the yarn is fanned, so that the remaining diameter of the fabric in thickness direction will be substantially lower. As a second material, Enka® TecTape, a tape-like shaped pre-consolidated yarn, with a thickness of 0.2 mm is used that seems to be predestinated for producing very thin fabrics [26,27].

Table 2.
Yarn materials. Fiber volume content (FVC), glass-fiber (GF), polyamide (PA).
3.3. Manufacturing Process
The compliance of PACS results from large wall thickness differences between cell sides and hinge areas, whereby the compliance increases with increasing thickness ratios. The possibilities and limits for achieving these geometry specifications in the weaving process have been systematically investigated. As a result, plain weaves have been identified as a preferred solution for the realization of such thin-walled hinge areas. Single layer fabrics are made in plain weave using the materials described in Table 2. For pretests, weaving trials are performed with four different combinations of warp and weft threads, as shown in Figure 10: TecTape/TecTape, TecTape/Twisted yarn, Twisted yarn/TecTape, and Twisted yarn/Twisted yarn.
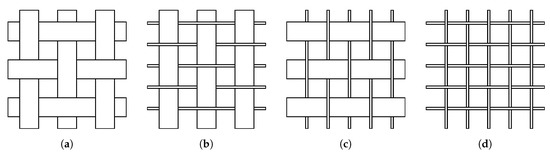
Figure 10.
Fabrics with different yarns in wrap (0°, upwards) and weft thread (90°, rightwards): (a) TecTape/TecTape. (b) TecTape/Twisted yarn. (c) Twisted yarn/TecTape. (d) Twisted yarn/Twisted yarn.
First, flat plates are manufactured in order to examine the quality of fiber alignment and direction-dependent material properties. For the mechanical tests, eight laminates are produced from these fabrics, two of each kind with a different number of layers according to the respective test requirements. For this purpose, single fabric layers are stacked on top of each other and then consolidated in HCM. For the tensile test, specimens with 10 layers 0°/90° laminate (2 mm thickness) are used and cut according to DIN EN ISO 527-4. The specimens of the shear tests consist of 14 layers ±45° laminate (2.8 mm thickness) and are manufactured in accordance with DIN EN 6031.
Further investigations focus on the manufacturing of compliant hinge areas with large ratios in the fabric thickness. A particular challenge is to achieve the required minimum composite thickness with available hybrid yarns while maintaining a closed surface without voids or dry spots. For a high load capacity it is crucial to have continuous fibers through the hinges. Hence, hinge areas are designed as unidirectional structures with only matrix material in the weft thread. A high thickness gradient in the transition from the hinge area requires completely new textile solutions. An important criterion for evaluating the manufacturing method is integral production, i. e. the omission of cutting processes. Consequently, the same number of warp threads must be used in the cell sides as in the hinge areas. Weaving trials show that a wall thickness ratio of maximum 1:4 can be achieved purely in terms of binding parameters. The required thickness ratio can therefore only be reached by integrating additional elements. Thus, the integration of pre-consolidated inserts of the same material has proven to be effective (Figure 11). The textile manufacturing process and the realization of woven cellular structures with inhomogeneous wall thicknesses is described in detail in [26,27]. With reference to the results of the flat plate tests, only the material combinations TecTape/Twisted yarn (Figure 10b) and Twisted yarn/Twisted yarn (Figure 10d) are further examined for hinge samples, since TecTape in the weft thread shows insufficient material behavior (cf. Section 4.1).
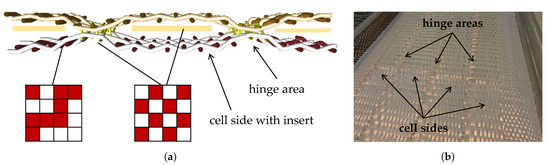
Figure 11.
Manufacturing of hinge areas and cell sides using pre-consolidated inlays [26]: (a) Structure and weave pattern design. (b) Weave trials.
Based on the results of manufacturing compliant hinge areas with large thickness ratios, the weaving process is extended to manufacture a PACS cantilever. The cantilever geometry that is described in Section 3.1 has to be formed by fabric layers for weaving realization. A combination of terry and spacer weaving enables the implementation of PACS in the weaving process. Using this approach, Sennewald et al. [26,27] have developed an algorithm that breaks down each unit cell into subareas and then reassembles the PACS (Figure 12). Thus, a complete solution matrix for the geometric formation of the PACS is determined by partial sections. Due to the necessary crossing of layers and the different layer lengths, gaps have to be filled with floats, which are retracted in the weaving process to form the structure.
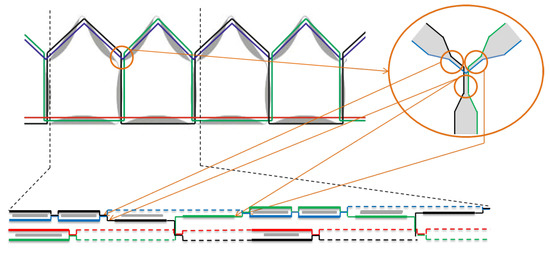
Figure 12.
Transfer of compliant sections into 2D weaving arrangement for textile manufacturing of a PACS cantilever (weave: —, float: - - -) [26].
3.4. Mechanical Testing
In preliminary investigations, the design and the corresponding mechanical properties of the flexure hinges have been found to be an essential influencing factor on the holistic behavior of PACS [21]. Both the transition areas between cell sides and hinges and the movement of the axis of rotation during pressurization and structural deformation lead to a complex behavior of these areas. Manufacturing tolerances, which are to be expected in such a highly complex manufacturing process, additionally increase potential deviations. Therefore, a comprehensive analysis of the material properties and structural elements is necessary.
First, tensile tests according to DIN EN ISO 527-4 and shear tests according to DIN EN 6031 are performed on flat plate specimens (cf. Section 3.3) using an Instron universal testing machine. In addition to an optical strain measurement, strain gauges are used to measure strains lengthwise and crosswise to the force application direction. GF/epoxy tabs are used as force application elements for all specimens and are bonded with an ethyl (2) cyanoacrylate adhesive (Sicomet® 50).
Furthermore, tensile tests on flexure hinge specimens are conducted in order to evaluate the material-dependent behavior in the hinge areas. There is no standardized test method for ultra-thin specimens with a high thickness gradient. The method described in DIN EN ISO 527-4 is adapted according to the limitations caused by the flexure hinge geometry. Compared to standard test specimens, the measuring length is clearly defined by the hinge length due to a large thickness ratio. Because of the short specimen length that is limited by the manufacturing process the use of strain gauges or extensometers is not possible. Therefore, the strain is calculated with crosshead displacement and corrected by the compliance of the testing machine that is determined experimentally to 60 μm/kN using a steel specimen with high tensile stiffness. Due to large failure strains and since no direct strain measurement is possible, the range for determining the Young’s modulus from the stress-strain curve is set to 0.5% to 2.5% contrary to the standard.
4. Results
4.1. Prestests on Woven Plates
The investigation on woven flat plate specimens is intended to identify the influence of warp and weft material on compound properties (Figure 10). Six specimens are tested for each yarn combination. All test data are presented with standard error at a confidence interval (CI) of 95%. Results from the tensile tests are shown in Figure 13 and Table 3. First, a variation of weft material reveals high influences on the mechanical behavior. For the samples using TecTape transversely to the load direction, the average tensile strength is 20–27% lower than the strength of the samples using twisted yarn. Furthermore, results for specimens with TecTape in weft thread show high scattering compared to twisted yarn specimens. Similar results are observed for Young’s modulus (13–15%) and elongation at break (11–20%). As stated in Section 2, an important factor for the material selection applying to PACS is the ratio of squared tensile strength to Young’s modulus . Due to significantly higher tensile strength, specimens using twisted yarns in the weft thread show substantially higher ratios of (27–38%). Secondly, a variation in warp material does not lead to significant differences in material properties (TecTape/Twisted yarn compared to Twisted yarn/Twisted yarn).
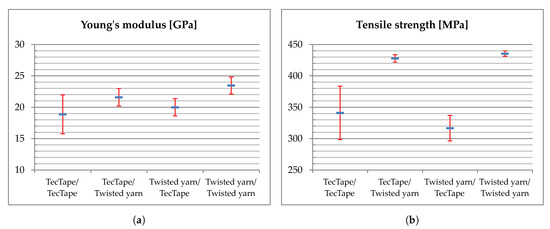
Figure 13.
Experimental results from tensile tests for flat plate specimens with CI of 95%: (a) Young’s modulus. (b) Tensile strength.

Table 3.
Experimental results from tensile tests for flat plate specimens with a confidence interval (CI) of 95%.
Figure 14 and Table 4 show the results from the shear tests. For samples with combined yarns in warp and weft thread, no major differences in shear properties are obtained (TecTape/Twisted yarn compared to Twisted yarn/TecTape). The observation is plausible since shear samples are made of fabric layers stacked in ±45° to their testing direction. In contrast, specimens using only TecTape reveal a 42% lower shear modulus and 39% lower shear strength compared to specimens using only twisted yarn in warp and weft thread.
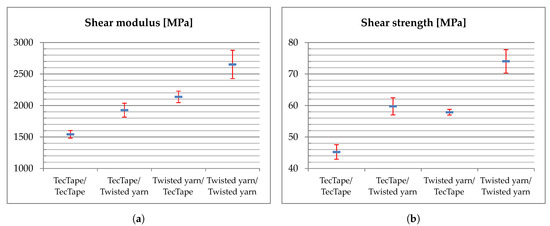
Figure 14.
Experimental results from shear tests for flat plate specimens with CI of 95%: (a) Shear modulus. (b) Shear strength.

Table 4.
Experimental results from shear tests for flat plate specimens with CI of 95%.
Summarizing the mechanical tests on flat plate specimens, a variation in yarn materials leads to high differences in mechanical properties. The investigation reveals that especially the weft thread material has a major influence on the tensile properties. Regarding the chosen manufacturing process, pre-consolidated TecTape shows unfavorable material properties. In particular, specimens with TecTape as the weft thread have insufficient tensile properties. Therefore, only fabrics with twisted yarns in the weft thread are further examined for tests on flexure hinges.
4.2. Woven FRP-Flexure Hinges
Further weave trials focus on the manufacturing of compliant hinge areas with large thickness ratios. The aim is to produce flexure hinge specimens with a geometry according to Figure 9. In particular, a hinge thickness of 0.2 mm, a hinge length of 5 mm, and a cell side thickness of 2.4 mm is to be reached. The manufacturing process is described briefly in Section 3.3 and in detail in [27]. For sample examination, microscopic images are taken with a Keyence digital microscope. Figure 15 illustrates that it is possible to achieve good shape accuracy in the transition zones due to consolidation with HCM, however, the geometry specifications can not be fulfilled. A hinge thickness of up to 1.5 mm and a cell side thickness of up to 3.6 mm is obtained. The samples show that a significant amount of weft threads are floating into the joint areas during HCM. High undulation in fibers are observed as well. Furthermore, in all TecTape specimens a significant amount of voids is found (cf. Figure 15a,b). Compared to that, twisted yarn specimens do not show voids at all.

Figure 15.
Microscope images of woven flexure hinges: Weave trials with 300 tex PA weft thread in hinge areas: (a) Twisted yarn/Twisted yarn. (b) TecTape/Twisted yarn.
The first weave trials show that the target thicknesses cannot yet be reached. An adjustment of the processing parameters is necessary to achieve larger wall thickness ratios. The target thickness of the cell sides could be met by adjusting the thickness of the pre-consolidated inserts (Figure 16). A reduction of weft thread fineness in the hinge areas from 300 tex to 15.5 tex allows a significant decrease of hinge thickness. In this way, a hinge thickness of about 0.5 mm is realized. The target parameter of has still not been reached. In addition, the maximum permissible thickness of according to Section 3.1 has not been reached as well. Therefore, a reduction in maximum angular deflection is required to ensure the functionality of PACS for the given boundary conditions. Reducing the maximum cell deflection from to results in a maximum hinge deflection of . This allows a maximum hinge thickness of and thus fits the current state of development. Figure 16a shows that continuous fibers were obtained in the hinges of twisted yarn specimens. In contrast, not all TecTape specimens show continuous fibers through the hinges. No voids are observed in any samples.
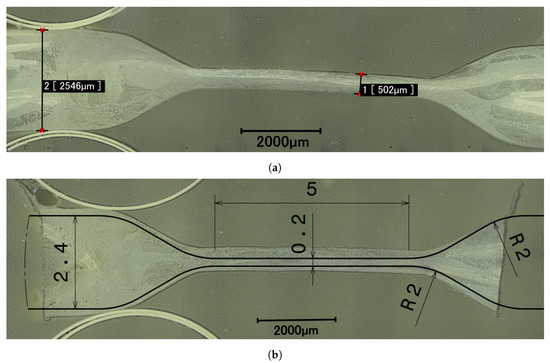
Figure 16.
Microscope images of woven flexure hinges: Improved weaving parameters and 15.5 tex weft thread in hinge areas: (a) Twisted yarn/Twisted yarn. (b) TecTape/Twisted yarn.
Generally, the manufacturability of thin-walled hinges in the weaving process is proven. However, the optical inspection already reveals high fiber undulation and irregularities in fiber orientation. Tensile tests are carried out on eight hinge specimens each that have been made with the same manufacturing parameters as specimens shown in Figure 16. The test procedure is described in Section 3.4. Figure 17 and Table 5 show the results of the tensile tests. A large scattering of the measured values indicates misaligned fibers and specimen inhomogeneities. Furthermore, TecTape specimens show a stiffness which is 38% lower compared to twisted yarn specimens. The strength values for both specimens are within the same range. Though, it should be mentioned that the strength values are not representative for the application on PACS since no abrupt failure occurred (Figure 18). A suitable failure criterion must be developed that better describes the strength degradation of PACS hinges. In particular, the type of failure must be determined that limits the functionality envelope of PACS.
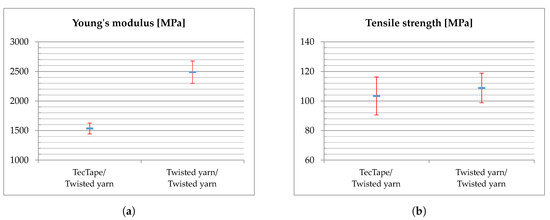
Figure 17.
Experimental results from tensile tests for flexure hinge specimens with CI of 95%: (a) Young’s modulus. (b) Tensile strength.

Table 5.
Experimental results from tensile tests for flexure hinge specimens with CI of 95%.

Figure 18.
Failure of flexure hinge specimen at tensile test.
Figure 13 and Figure 17 show that the Young’s modulus of flexure hinge specimens is one order of magnitude smaller than the Young’s modulus of flat plate specimens. Comparing these values with typical material parameters of PA reveals that the hinges are predominantly described by matrix properties. The fibers can barely develop their mechanical benefits at the hinge areas. An examination of the fracture pattern demonstrates this behavior (Figure 18). A clear break-off edge is not observed, which indicates a complex fiber orientation. A consideration of the ratio gives the impression that TecTape is better suited for PACS than twisted yarn. However, the evaluation of the failure type leads to the conclusion that the strength values in the hinge areas are not representative for PACS failure. Thus, the ratio is inconclusive at this point.
Based on the previous results, TecTape is omitted from further manufacturing trials. As a result of mechanical tests and microscope images, only the use of twisted yarns prove to be suitable for the realization of PACS.
4.3. Woven FRP-PACS Cantilever
A manufacturing process for a woven FRP-PACS cantilever is developed using the findings from the investigations described above. The combination of terry and spacer weaving has proven to be suitable. Figure 19 shows the first prototype of a PACS cantilever manufactured by applying this weaving process. The outer geometry of the structure is formed during the consolidation process, in such a way that the target geometry is achieved very precisely (cf. Figure 8a).

Figure 19.
Woven fiber reinforced plastics (FRP)-PACS Cantilever: (a) Crossover area. (b) Single hinge area.
Figure 20 shows microscope images for different hinge areas of the cantilever. The locations of the examined hinge areas are highlighted in Figure 20a. Exemplarily, a crossover area (Figure 20a) and a single hinge area (Figure 20b) are presented. The microscope images show continuous fibers through the hinges. Red circles in Figure 20a indicate notches that are created by the consolidation tool. Therefore, special attention should be paid to the consolidation process since these notches represent structural inhomogeneities and concentrate hinge bending in a confined area. Furthermore, non-uniform hinge thicknesses are observed. In summary, a proof of the manufacturing process was made, but manufacturing parameters must be further optimized to achieve homogeneous wall thicknesses.

Figure 20.
Microscope images of woven FRP-PACS cantilever. Red circles indicate notches created by the consolidation tool: (a) Crossover area. (b) Single hinge area.
5. Discussion
The concept of a pressure-actuated shape-variable structure is presented. The actuation principle based on internal pressure resolves the challenging conflict between high deformability and sufficient load capacity. The decisive factor for the realization of PACS is a holistic design approach that pays special attention to the manufacturability of such complex structures. The presented research aims to develop a novel production process for cellular structures with a high thickness ratio. The findings from the first weaving trials finally raise the possibility of realizing a woven FRP-PACS cantilever.
A working hypotheses of this research is that pre-consolidated tape-like shaped yarns are predestined for producing very thin fabrics. Two hybrid yarn materials are investigated in the context of manufacturing flexure hinges with high deflection. Pre-consolidated TecTape is compared to a twisted yarn. Overall, the material properties obtained on flat plate specimens are in a common order of magnitude of biaxial GFRP [28]. Though, mechanical tests show a significant difference in material behavior with varying yarns in the warp and weft thread. In particular, it is shown that it is primarily the weft material that influences mechanical properties. This is unexpected at first, as weft threads are oriented transversely to the load direction. Nevertheless, specimens with TecTape in the weft thread show higher fiber undulations and are more difficult to process during weaving. Additionally, microscope images show that twisted yarns lead to a better alignment of fibers along the hinges and have less voids. Contrary to the initial working hypothesis, pre-consolidated yarns prove to be unsuitable for the weaving process of cellular structures with large thickness ratios.
Secondly, the feasibility of manufacturing ultra-thin hinges in the weaving process was investigated. In particular, hinges with a thickness of 0.2 mm and a wall thickness ratio of 1:12 were chosen. The use of pre-consolidated inserts for cell walls is proven to be sufficient to obtain high thickness ratios. The current state of development enables minimum hinge thicknesses of about 0.5 mm. Herewith, the functionality of the PACS can be confirmed for a maximum angular deflection per cell of . Considering a five-cell PACS cantilever, this results in a total angular deflection of 41° and demonstrates the high potential of PACS for realizing large deformations. Additionally, performance improvements are expected from further reductions in hinge thickness. Mechanical tests on hinge areas showed that the hinge properties are mainly dominated by matrix behavior. The HCM process leads to fanned and dispersed fibers and a floating of weft fibers into the hinge areas. To further improve the performance of PACS, the consolidation process must be optimized.
Finally, the proof of concept of a woven FRP-PACS cantilever is made. A five-cell single-row cantilever is manufactured using the weaving process. The subject of current investigations is the integration of this woven FRP structure into the holistic PACS approach. The sealing and pressurization concept has to be adapted in regard to the FRP design. Afterward, the experimental investigation of the single-row cantilever is intended to prove the high deformation capability that has been theoretically investigated before. Within the scope of the current research project, the extension of the manufacturing process to a double-row cantilever is being investigated. Overall, it is expected to bring PACS one step closer to an integral and automated production. As an outlook on further research work, the application of PACS as a morphing flap is being evaluated. A detailed examination of the performance envelope of a PACS flight control surface is part of current work. Additionally, the implementation of a life-size demonstrator is planned.
Author Contributions
Conceptualization, P.M., J.B., C.S., C.H. and M.S.; methodology, P.M. and J.B.; software, P.M. and J.B.; validation, P.M., J.B. and C.H.; formal analysis, P.M. and J.B.; investigation, P.M. and J.B.; resources, C.S., M.V., C.H. and C.C.; data curation, P.M. and C.S.; writing–original draft preparation, P.M.; writing–review and editing, P.M., C.S., M.V. and M.S.; visualization, P.M. and J.B.; supervision, C.H., C.C. and M.S.; project administration, P.M., C.S. and C.H.; funding acquisition, C.H., C.C. and M.S.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Grant No. 280656304. The APC was funded by the German Research Foundation and the Open Access Publication Funds of the Technische Universität Braunschweig.
Acknowledgments
The authors are pleased to acknowledge the kind assistance of Institute of Joining and Welding Technology at Technische Universität Braunschweig and Institute of Composite Structures and Adaptive Systems at German Aerospace Center during sample preparation and mechanical testing.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AVW | Approach of virtual work |
| CI | Confidence interval |
| FRP | Fiber reinforced plastic |
| FVC | Fiber volume content |
| GF | Glass-fiber |
| GFRP | Glass-fiber reinforced plastic |
| HCM | Hot compression molding |
| PA | Polyamide |
| PACS | Pressure-actuated cellular structure |
| SLS | Selective laser sintering |
References
- Sanders, B.; Eastep, F.E.; Forster, E. Aerodynamic and Aeroelastic Characteristics of Wings with Conformal Control Surfaces for Morphing Aircraft. J. Aircr. 2003, 40, 94–99. [Google Scholar] [CrossRef]
- Thill, C.; Etches, J.; Bond, I.; Potter, K.; Weaver, P. Morphing skins. Aeronaut. J. 2008, 112, 117–139. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Barrett, R.M. Active aeroelastic tailoring of an adaptive Flexspar stabilator. Smart Mater. Struct. 1996, 5, 723–730. [Google Scholar] [CrossRef]
- Elzey, D.M.; Sofla, A.; Wadley, H. A bio-inspired, high-authority actuator for shape morphing structures. Smart Mater. Struct. 2003, 5053, 92–100. [Google Scholar]
- Bauer, C.; Martin, W.; Siegling, H.F.; Schürmann, H. A new structural approach to variable camber wing technology of transport aircraft. In Proceedings of the 39th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Long Beach, CA, USA, 20–23 April 1998; pp. 474–482. [Google Scholar] [CrossRef]
- Müller, D. Das Hornkonzept: Realisierung eines formvariablen Tragflügelprofils zur aerodynamischen Leistungsoptimierung zukünftiger Verkehrsflugzeuge. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2000. [Google Scholar]
- Li, S.; Wang, K.W. Plant-inspired adaptive structures and materials for morphing and actuation: A review. Bioinspir. Biomim. 2017, 12, 011001:1–011001:17. [Google Scholar] [CrossRef] [PubMed]
- Huber, J.E.; Fleck, N.A.; Ashby, M.F. The selection of mechanical actuators based on performance indices. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1997, 453, 2185–2205. [Google Scholar] [CrossRef]
- Barrett, R.M.; Barrett, C.M. Biomimetic FAA-certifiable, artificial muscle structures for commercial aircraft wings. Smart Mater. Struct. 2014, 23, 074011:1–074011:15. [Google Scholar] [CrossRef]
- Dittrich, K. Cellular Actuator Device and Methods of Making and Using Same. U.S. Patent US7055782B2, 6 June 2006. [Google Scholar]
- Vos, R.; Barrett, R.M. Pressure adaptive honeycomb: A novel concept for morphing aircraft structures. In Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences, Nice, France, 19–24 September 2010; pp. 1792–1801. [Google Scholar]
- Vos, R.; Barrett, R.M. Method and Apparatus for Pressure Adaptive Morphing Structure. U.S. Patent US8366057B2, 5 February 2013. [Google Scholar]
- Vasista, S.; Tong, L. Topology-Optimized Design and Testing of a Pressure-Driven Morphing-Aerofoil Trailing-Edge Structure. AIAA J. 2013, 51, 1898–1907. [Google Scholar] [CrossRef]
- Luo, Q.; Tong, L. Adaptive pressure-controlled cellular structures for shape morphing I: Design and analysis. Smart Mater. Struct. 2013, 22, 055014:1–055014:16. [Google Scholar] [CrossRef]
- Luo, Q.; Tong, L. Adaptive pressure-controlled cellular structures for shape morphing II: Numerical and experimental validation. Smart Mater. Struct. 2013, 22, 055015:1–055015:12. [Google Scholar] [CrossRef]
- Lv, J.; Tang, L.; Li, W.; Liu, L.; Zhang, H. Topology optimization of adaptive fluid-actuated cellular structures with arbitrary polygonal motor cells. Smart Mater. Struct. 2016, 25, 055021:1–055021:13. [Google Scholar] [CrossRef]
- van Meerbeek, I.M.; Mac Murray, B.C.; Kim, J.W.; Robinson, S.S.; Zou, P.X.; Silberstein, M.N.; Shepherd, R.F. Morphing Metal and Elastomer Bicontinuous Foams for Reversible Stiffness, Shape Memory, and Self-Healing Soft Machines. Adv. Mater. 2016, 28, 2801–2806. [Google Scholar] [CrossRef] [PubMed]
- Boyraz, P.; Runge, G.; Raatz, A. An Overview of Novel Actuators for Soft Robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef]
- Pagitz, M.; Lamacchia, E.; Hol, J. Pressure-actuated cellular structures. Bioinspir. Biomim. 2012, 7, 016007:1–016007:19. [Google Scholar] [CrossRef] [PubMed]
- Gramüller, B.; Boblenz, J.; Hühne, C. PACS—Realization of an adaptive concept using pressure actuated cellular structures. Smart Mater. Struct. 2014, 23, 115006:1–115006:17. [Google Scholar] [CrossRef]
- Gramüller, B.; Köke, H.; Hühne, C. Holistic design and implementation of pressure actuated cellular structures. Smart Mater. Struct. 2015, 24, 125027:1–125027:28. [Google Scholar] [CrossRef]
- Sinapius, M. Adaptronik: Prinzipe-Funktionswerkstoffe-Funktionselemente-Zielfelder mit Forschungsbeispielen; Springer: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Gramüller, B.; Tempel, A.; Hühne, C. Shape-variable seals for pressure actuated cellular structures. Smart Mater. Struct. 2015, 24, 095005:1–095005:20. [Google Scholar] [CrossRef]
- Gramüller, B. On Pressure-Actuated Cellular Structures. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2016. [Google Scholar]
- Sennewald, C.; Vorhof, M.; Schegner, P.; Hoffmann, G.; Cherif, C.; Boblenz, J.; Sinapius, M.; Hühne, C. Development of 3D woven cellular structures for adaptive composites based on thermoplastic hybrid yarns. IOP Conf. Ser. Mater. Sci. Eng. 2018, 369, 012041:1–012041:7. [Google Scholar] [CrossRef]
- Sennewald, C.; Vorhof, M.; Hoffmann, G.; Cherif, C. Overview of Necessary Development Steps for the Realization of Woven Cellular Structures for Adaptive Composites. J. Fash. Technol. Text. Eng. 2018, s5, 001:1–001:6. [Google Scholar] [CrossRef]
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials; Technomic Publishing Company: Lancaster, PA, USA, 1980. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).