Assessment of Aircraft Surface Heat Exchanger Potential
Abstract
1. Introduction
2. Aircraft Correlations
2.1. Aircraft Component Geometries
- Fuselage
- Wing
- Nacelles
- Horizontal tail
- Vertical tail
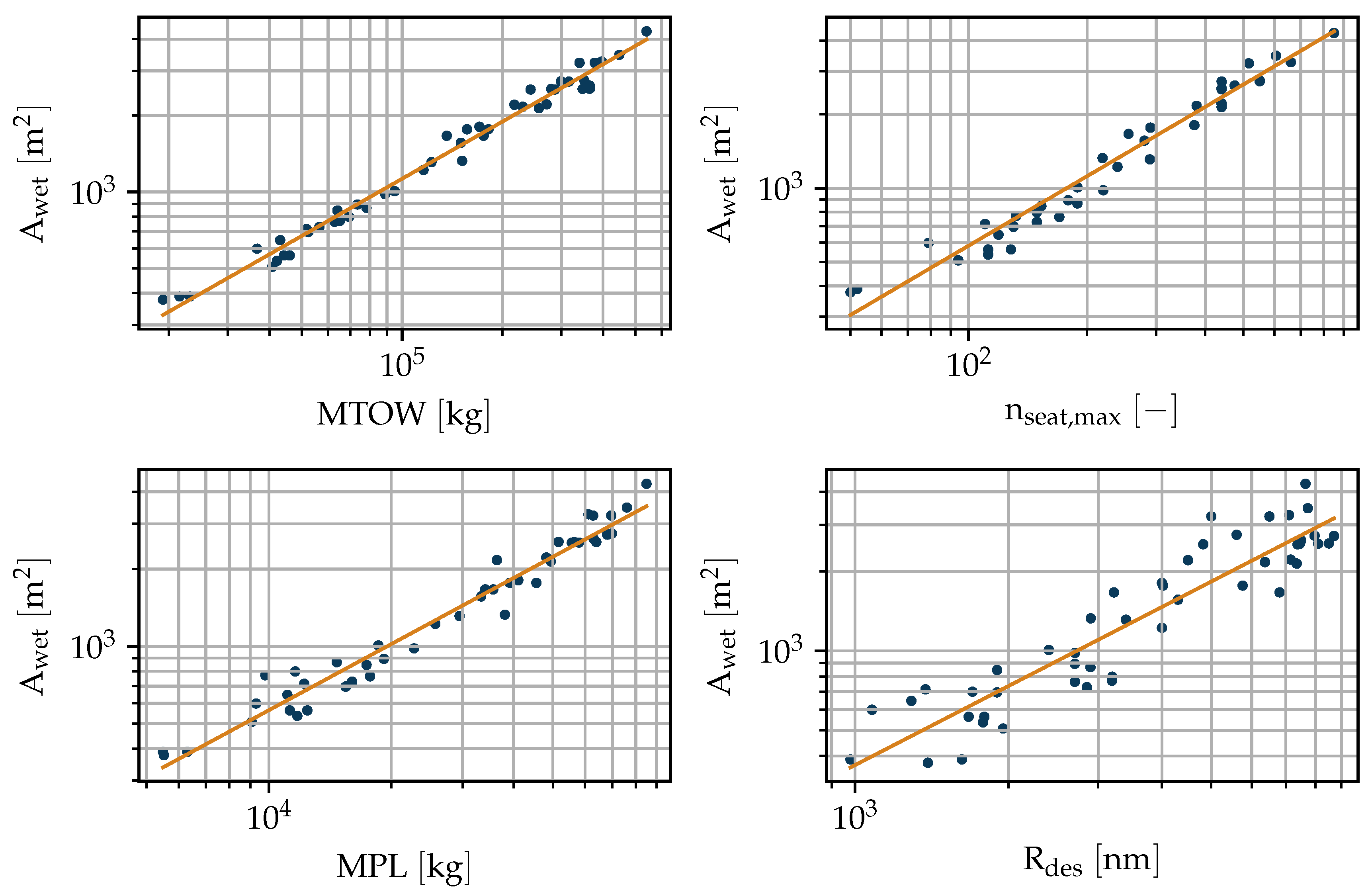
2.2. Surface Area Correlations
- Maximum Take-Off Weight ()
- Maximum number of seats ()
- Maximum payload ()
- Design range ()
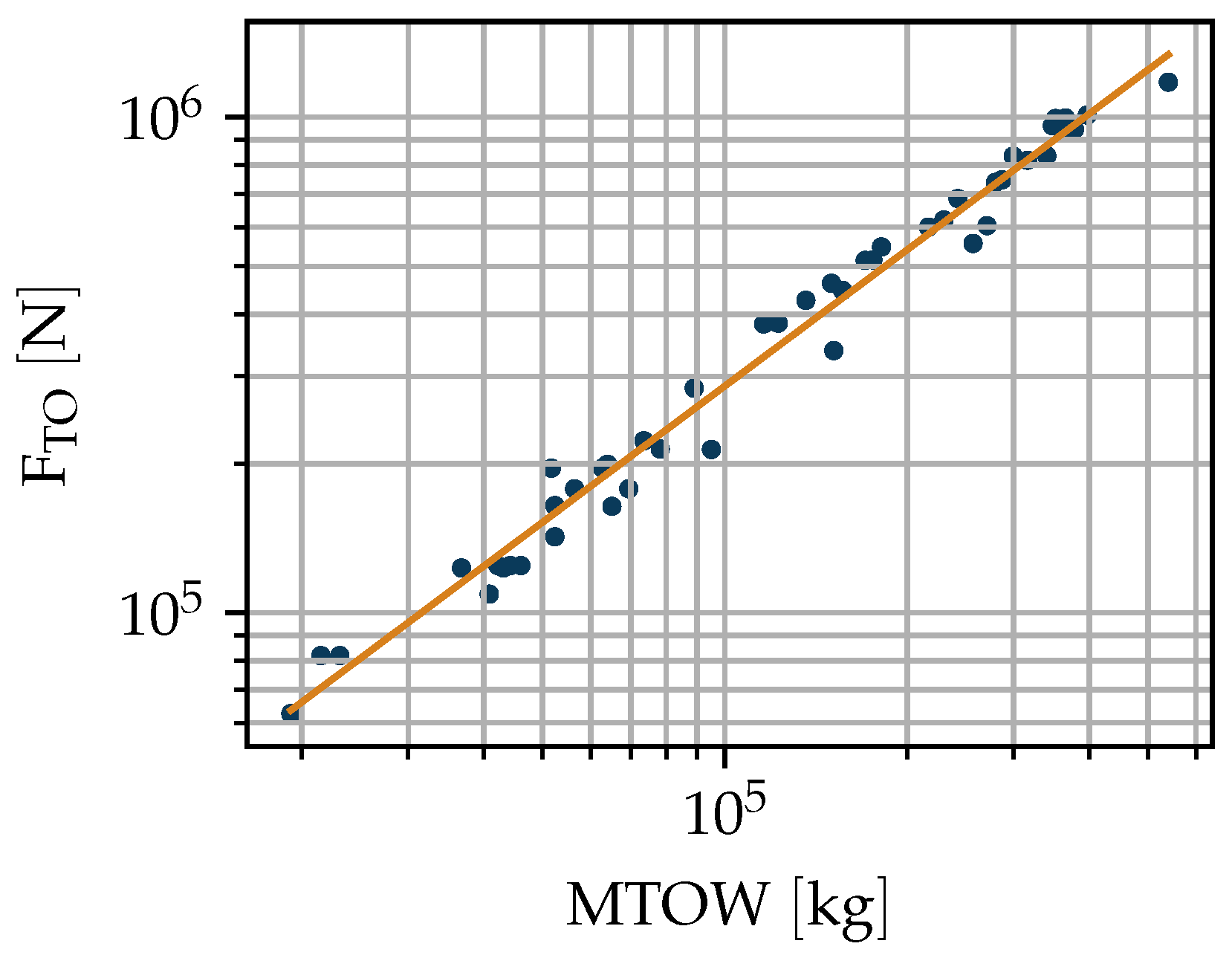
2.3. Propulsive Power
3. Surface Heat Transfer
3.1. Modeling
3.2. Sensitivities
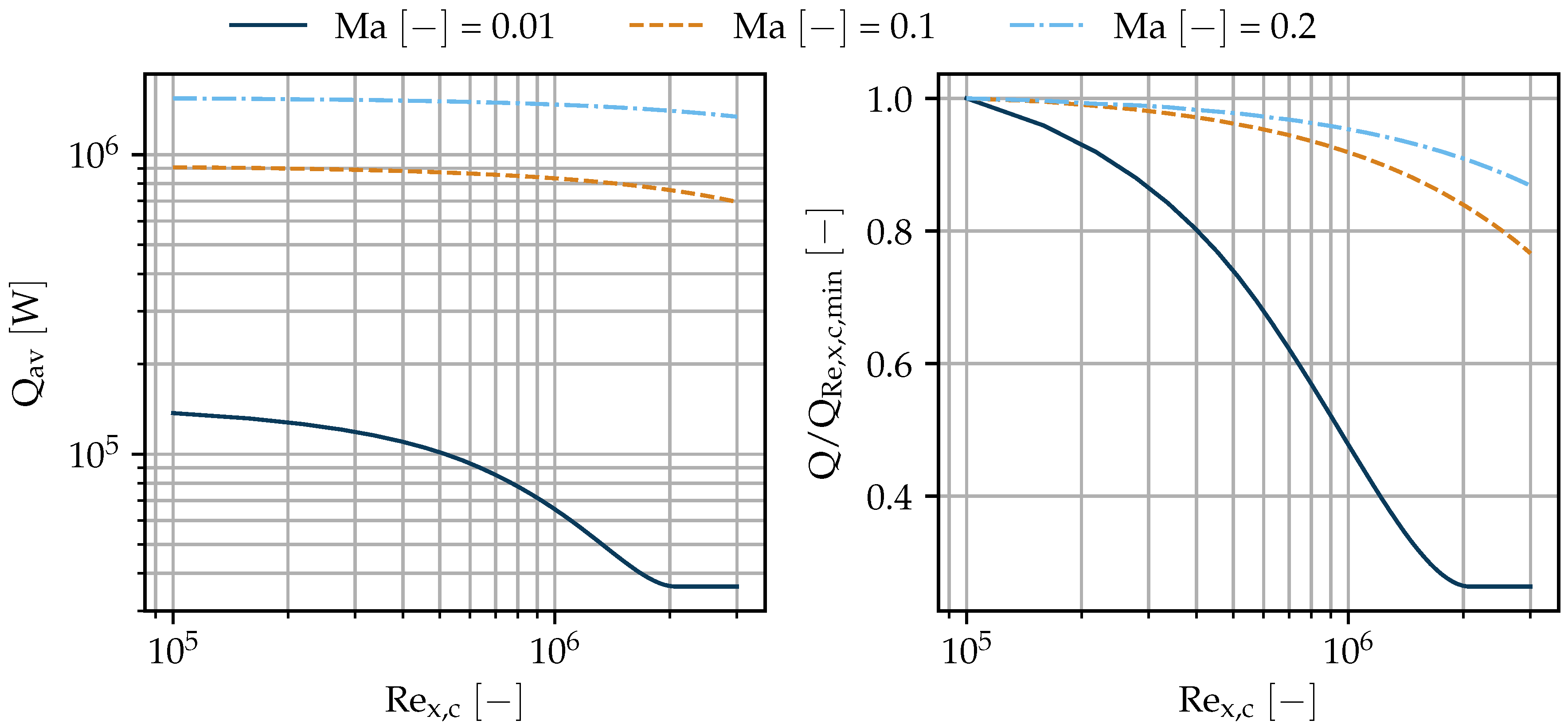
3.2.1. Transition Location
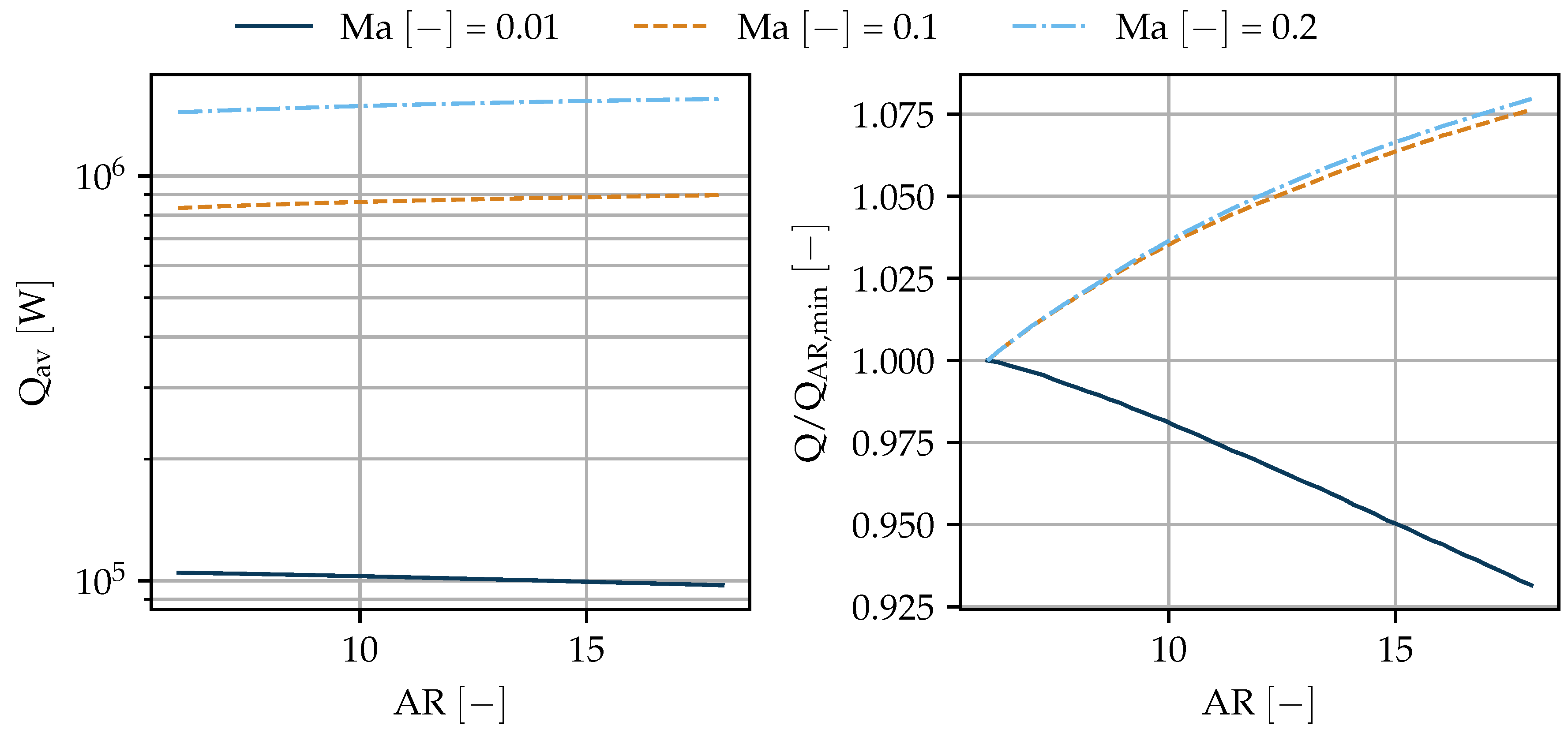
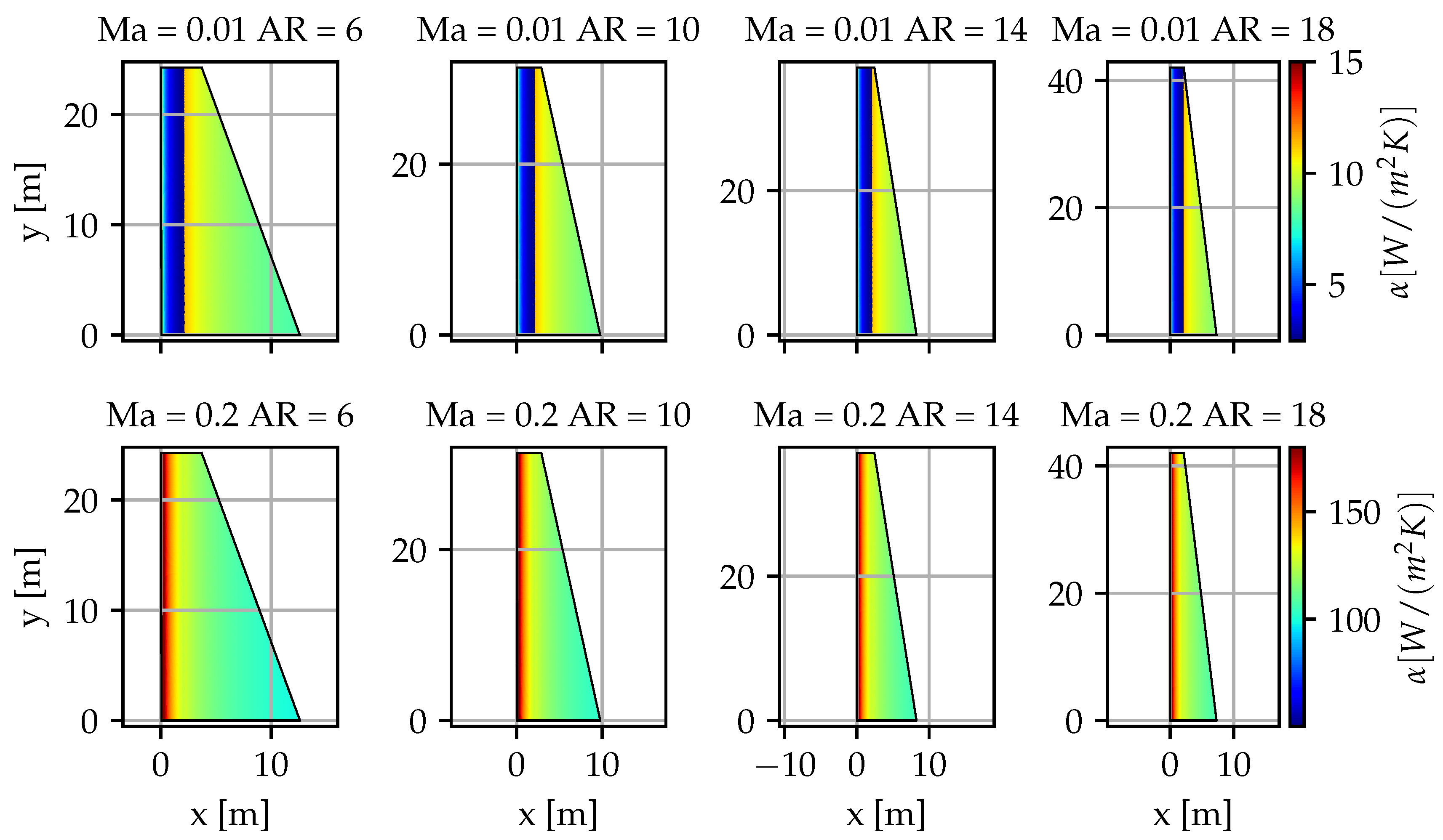
3.2.2. Wing Aspect Ratio
- In general, decreases along x because of the increasing thickness of the thermal boundary layer (). Therefore, higher favours heat transfer because for the same area, the average chord length is lower (cf. Figure 5 bottom graphs).
- The front section of the wing is laminar, which results in small . A higher increases the span and, thus, the laminar portion of the plate’s total area (cf. Figure 5 top two graphs). The depends on . For low the transition occurs further downstream, which means that this second effect contributes more.
3.2.3. Wing Taper Ratio
3.2.4. Fuselage Slenderness Ratio
3.3. Drag
- Transition delay of initially laminar flow
- Drag alteration of fully turbulent flow
- Heating/cooling of the whole wetted surface area
- Strategic heating/cooling of a part of the wetted surface area
4. Surface Cooling Potential
4.1. Area Reduction Assumptions
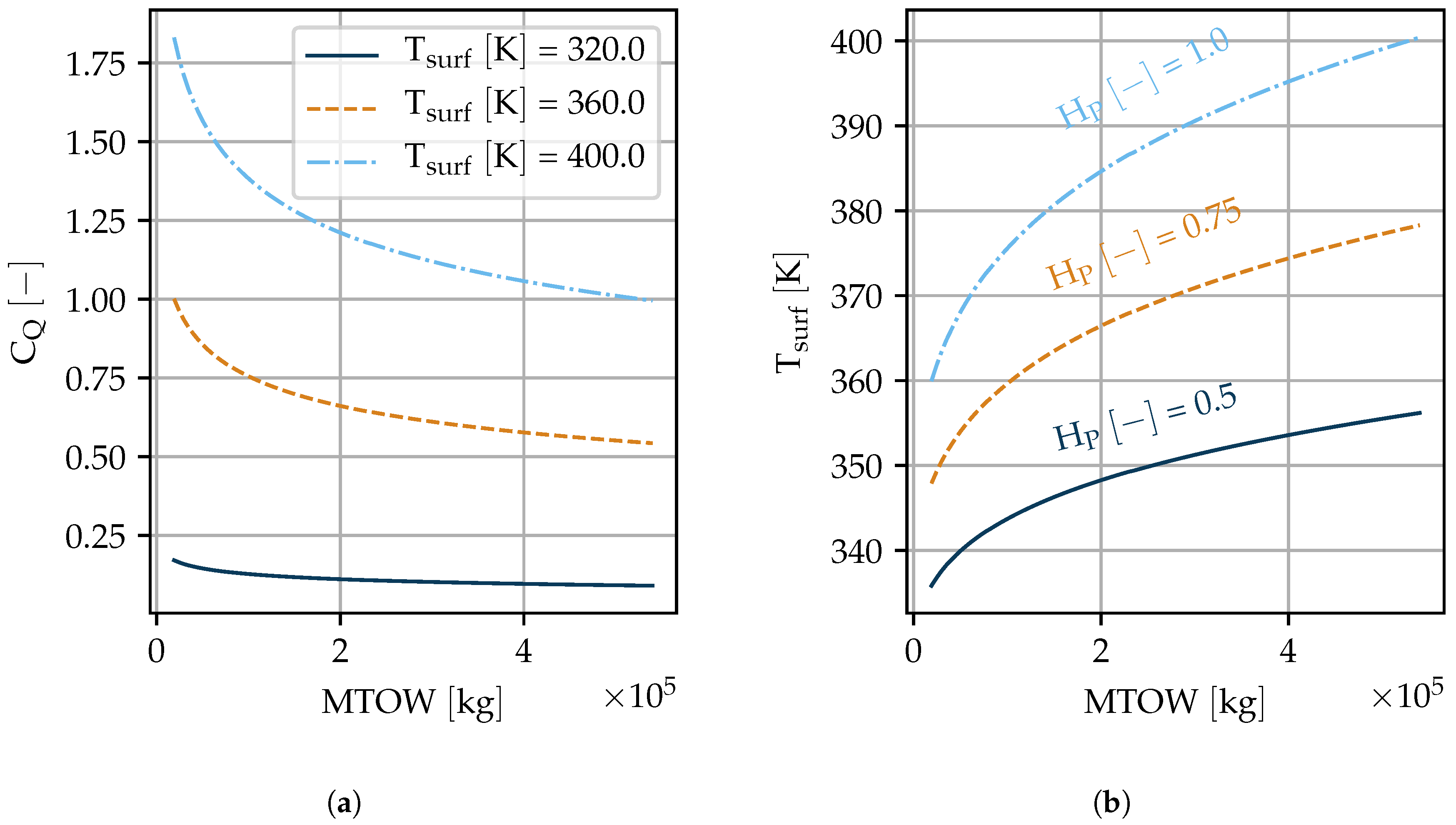
4.2. Cooling Potential for Typical Operating Points
4.3. Hot Day Take-Off Performance
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SRIA | Strategic Research and Innovation Agenda |
| TMS | Thermal Management System |
| ISA | International Standard Atmosphere |
| TO | Take-off |
| HTO | Hot Day Take-off |
| CL | Climb |
| CR | Cruise |
| ACOC | Air Cooled Oil Cooler |
| SACOC | Surface Air Cooled Oil Cooler |
| APU | Auxilliary Power Unit |
| MTOW | Maximum Take-off Weight |
| MPL | Maximum Payload |
| Roman Symbols | |
| A | Area |
| Temperature deviation | |
| T | Temperature |
| Altitude | |
| Mach number | |
| Q | Heat rate |
| n | Number |
| R | Range |
| Coefficient of determination | |
| H | Degree of Hybrdization |
| P | Power |
| F | Thrust |
| v | Velocity |
| Nusselt Number | |
| Reynolds Number | |
| Aspect Ratio | |
| l | Length |
| d | Diameter |
| x | Coordinate in flow direction |
| c | Coefficient |
| D | Drag Force |
| Temperature Ratio | |
| Ratio of Heat Rates | |
| Greek Symbols | |
| Standard deviation | |
| Boundary layer thickness | |
| Difference | |
| Efficiency | |
| Heat transfer coefficient | |
| Wing taper ratio | |
| Slenderness ratio | |
| Density | |
| Dynamic Viscosity | |
| Subscripts | |
| wetted | |
| required | |
| exposed | |
| simplified | |
| actual | |
| maximum | |
| design | |
| total | |
| available | |
| transmission | |
| electric | |
| radiation | |
| surface | |
| c | critical |
| minimum | |
| f | friction |
| h | heated |
| u | unheated |
| ambient |
References
- Advisory Council for Aviation Research and Innovation in Europe. Strategic Research and Innovation Agenda: Volume 1: 2017 Update; Advisory Council for Aviation Research and Innovation in Europe: Brussels, Belgium, 2017. [Google Scholar]
- Yakinthos, K.; Donnerhack, S.; Misirlis, D.; Flouros, M.; Vlahostergios, Z.; Goulas, A. Intercooled Recuperated Aero Engine: Early Development Stages and Optimization of Recuperation Based on Conventional Heat Exchangers. In Proceedings of the 2nd ECATS Conference, Athens, Greece, 7–9 November 2016. [Google Scholar]
- Kaiser, S.; Kellermann, H.; Nickl, M.; Seitz, A. A Composite Cycle Engine Concept for Year 2050. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Jacob, F.; Rolt, A.; Sebastiampillai, J.; Sethi, V.; Belmonte, M.; Cobas, P. Performance of a Supercritical CO2 Bottoming Cycle for Aero Applications. Appl. Sci. 2017, 7, 255. [Google Scholar] [CrossRef]
- Rosero, J.A.; Ortega, J.A.; Aldabas, E.; Romeral, L. Moving towards a more electric aircraft. IEEE Aerosp. Electron. Syst. Mag. 2007, 22, 3–9. [Google Scholar] [CrossRef]
- Pornet, C.; Isikveren, A.T. Conceptual design of hybrid-electric transport aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Schlabe, D.; Lienig, J. Model-Based Thermal Management Functions for Aircraft Systems; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Wang, T.; Britcher, C.; Martin, P. Surface heat exchangers for aircraft applications—A technical review and historical survey. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999; p. 245. [Google Scholar] [CrossRef]
- Wilkinson, S.P. Interactive wall turbulence control. In Viscous Drag Reduction in Boundary Layers; Bushnell, D.M., Hefner, J.N., Eds.; Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1990. [Google Scholar]
- Sousa, J.; Villafañe, L.; Paniagua, G. Thermal analysis and modeling of surface heat exchangers operating in the transonic regime. Energy 2014, 64, 961–969. [Google Scholar] [CrossRef]
- European Commission. Surface Heat Exchangers for Aero-Engines; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- European Commission. Surface Heat Exchangers For Aero Engines 2; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- European Commission. Aerodynamic upgrade of Surface Air Cooled Oil Cooler; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Sakuma, Y.; Saito, H.; Watanabe, T.; Himeno, T.; Inoue, C.; Tomida, S.; Takahashi, N. Conjugate Heat Tansfer Analysis on Plate Fin Surface Air Cooled Oil Cooler. In Proceedings of the Shanghai 2017 Global Power and Propulsion Forum, Shanghai, China, 30 October–1 November 2017. [Google Scholar]
- Liu, J.; Peck, J.; Yazawa, K.; Fisher, T.S.; Shih, T.I.P. Bypass, Loss, and Heat Transfer in Aircraft Surface Coolers. Front. Mech. Eng. 2019, 5, 219. [Google Scholar] [CrossRef]
- Kellermann, H.; Habermann, A.L.; Vratny, P.C.; Hornung, M. Assessment of Fuel as Alternative Heat Sink for Future Aircraft. Appl. Therm. Eng. 2019. under review. [Google Scholar]
- Jenkinson, L.; Simpkin, P.; Rhodes, D. Civil Jet Aircraft Design; American Institute of Aeronautics and Astronautics, Inc.: Washington, DC, USA, 1999. [Google Scholar] [CrossRef]
- Boeing Commercial Airplanes. 747-8 Airplane Characteristics for Airport Planning; Boeing Commercial Airplanes: Seattle, WA, USA, 2012. [Google Scholar]
- Airbus S.A.S. A350 Aircraft Characteristics Airport and Maintenance Planning; Airbus S.A.S.: Blagnac, France, 2016. [Google Scholar]
- Torenbeek, E. Synthesis of Subsonic Airplane Design: An introduction to the Preliminary Design of Subsonic General Aviation and Transport Aircraft, with Emphasis on Layout, Aerodynamic Design, Propulsion and Performance; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Pornet, C.; Gologan, C.; Vratny, P.C.; Seitz, A.; Schmitz, O.; Isikveren, A.T.; Hornung, M. Methodology for Sizing and Performance Assessment of Hybrid Energy Aircraft. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013; p. 35. [Google Scholar] [CrossRef]
- Lorenz, L.; Seitz, A.; Kuhn, H.; Sizmann, A. Hybrid Power Trains for Future Mobility. In Proceedings of the 62. Deutscher Luft- und Raumfahrtkongress, Stuttgart, Germany, 10–12 September 2013; Deutsche Gesellschaft für Luft- und Raumfahrt: Bonn, Germany, 2013. [Google Scholar]
- Haaland, S.E. Simple and Explicit Formulas for the Friction Factor in Turbulent Pipe Flow. J. Fluids Eng. 1983, 105, 89. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Principles of Heat and Mass Transfer, 7th ed.; International Student Version; Wiley: Singapore, 2013. [Google Scholar]
- Schultz-Grunow, F. New frictional resistance law for smooth plates. Luftfahrtforschung 1940, 1940, 239–246. [Google Scholar]
- Henninger, J.H. Solar Absorptance and Thermal Emittance of Some Common Spacecraft Thermal-Control Coatings; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1984. [Google Scholar]
- Arnal, D.; Reneaux, J.; Casalis, G. Numerical and Experimental Studies Related to Skin Friction Drag Reduction Problems. Proceedings of the Colloquium Transitional Boundary Layers in Aeronautics. 1996. Available online: https://www.dwc.knaw.nl/DL/publications/PU00011219.pdf (accessed on 19 November 2019).
- Reshotko, E. Drag Reduction by Cooling in Hydrogen-Fueled Aircraft. J. Aircr. 1979, 16, 584–590. [Google Scholar] [CrossRef]
- Masad, J.A.; Nayfeh, A.H. Laminar flow control of subsonic boundary layers by suction and heat–transfer strips. Phys. Fluids A Fluid Dyn. 1992, 4, 1259–1272. [Google Scholar] [CrossRef]
- Dovgal, A.V.; Levchenko, V.; Timopeev, V.A. Boundary Layer Control by a Local Heating of the Wall. In Laminar-Turbulent Transition; Springer: Berlin/Heidelberg, Germany, 1990; pp. 113–121. [Google Scholar]
- Kramer, B.; Smith, B.; Heid, J.; Noffz, G.; Richwine, D.; Ng, T. Drag reduction experiments using boundary layer heating. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. [Google Scholar] [CrossRef]
- Lin, J.C.; Ash, R. Wall temperature control of low-speed body drag. J. Aircr. 1986, 23, 93–94. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid-Dynamic Drag: Theoretical, Experimental and Statistical Information; Hoerner Fluid Dynamics: Bakersfield, CA, USA, 1965. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar] [CrossRef]
- Spalart, P.R.; Watmuff, J.H. Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 1993, 249, 337–371. [Google Scholar] [CrossRef]
- Ohta, S. Temperature Classes of Electrical Insulators. Three Bond Technical News, 1 December 1985. [Google Scholar]
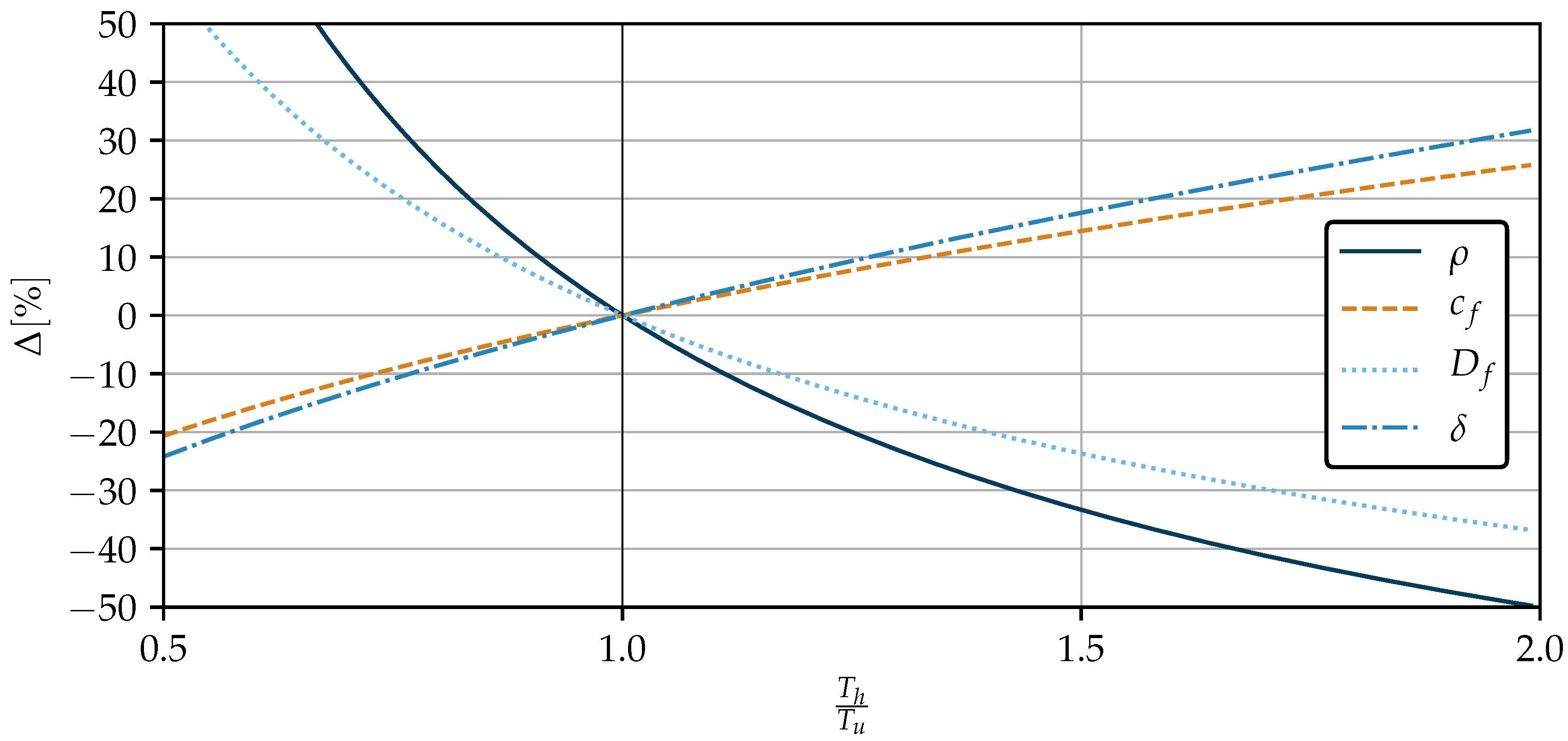
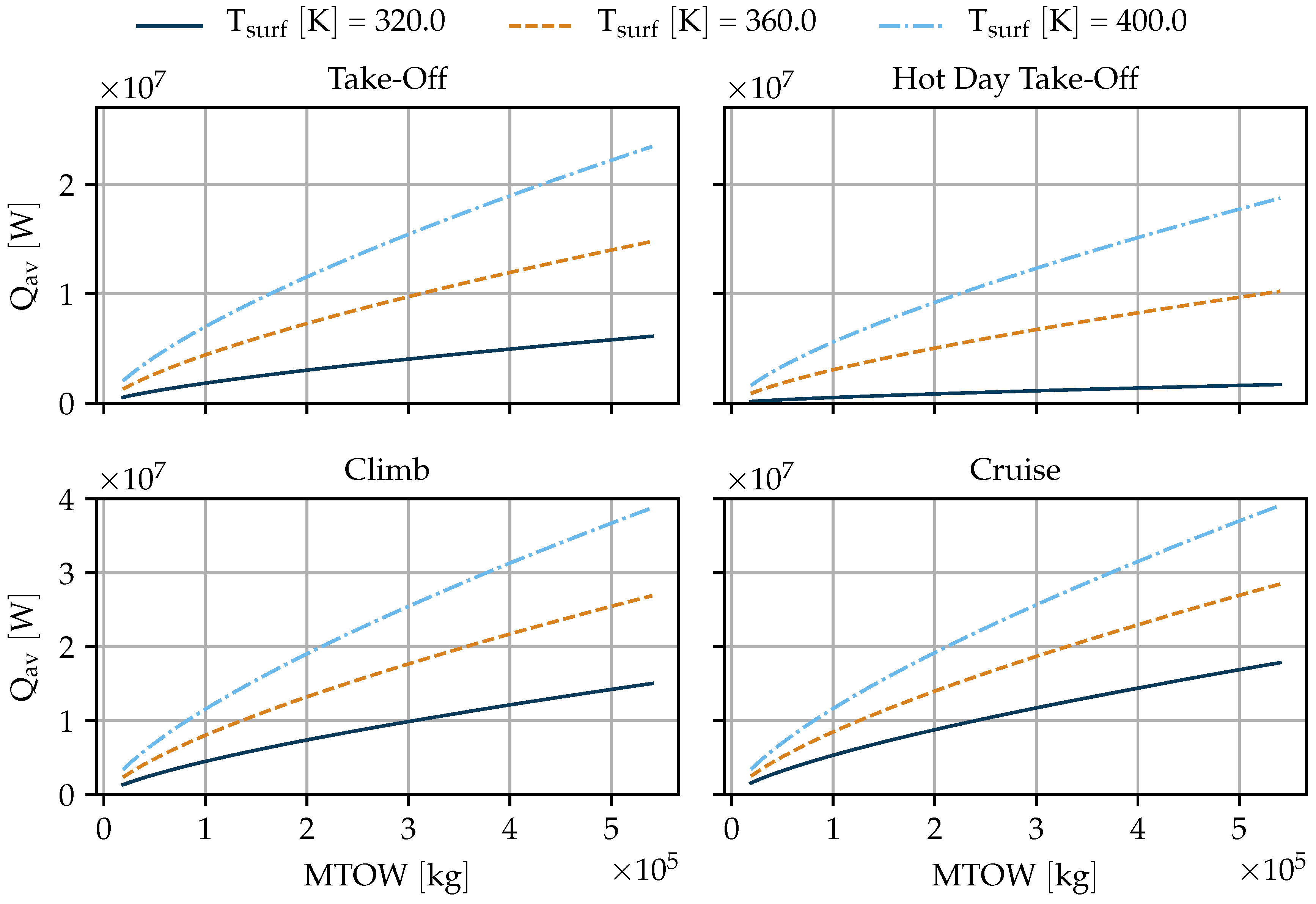
| Component | |||
|---|---|---|---|
| Fuselage | 478.0 | 412.9 | +15.8 |
| Wing | 202.4 | 208.7 | −3.0 |
| Nacelles | 55.8 | 52.4 | +6.4 |
| Horizontal tail | 48.4 | 49.6 | −2.4 |
| Vertical tail | 42.2 | 43.3 | −2.7 |
| Total | 826.8 | 766.9 | 7.8 |
| x | a | c | |
|---|---|---|---|
| 0.748 | −0.689 | 0.986 | |
| 0.940 | 0.887 | 0.963 | |
| 0.855 | −0.668 | 0.965 | |
| 0.995 | −0.417 | 0.859 |
| Component | ||
|---|---|---|
| Fuselage | 49 | 3.80 |
| Wing | 31 | 3.55 |
| Nacelles | 7 | 1.49 |
| Horizontal Tail | 8 | 1.21 |
| Vertical Tail | 5 | 0.83 |
| Parameter | Value |
|---|---|
| 200 m | |
| 12 | |
| 320 K |
| Opearting Point | (-) | (m) | (K) |
|---|---|---|---|
| TO | 0 | 0 | |
| HTO | 0 | ||
| CL | 5000 | 0 | |
| CR | 10,000 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kellermann, H.; Habermann, A.L.; Hornung, M. Assessment of Aircraft Surface Heat Exchanger Potential. Aerospace 2020, 7, 1. https://doi.org/10.3390/aerospace7010001
Kellermann H, Habermann AL, Hornung M. Assessment of Aircraft Surface Heat Exchanger Potential. Aerospace. 2020; 7(1):1. https://doi.org/10.3390/aerospace7010001
Chicago/Turabian StyleKellermann, Hagen, Anaïs Luisa Habermann, and Mirko Hornung. 2020. "Assessment of Aircraft Surface Heat Exchanger Potential" Aerospace 7, no. 1: 1. https://doi.org/10.3390/aerospace7010001
APA StyleKellermann, H., Habermann, A. L., & Hornung, M. (2020). Assessment of Aircraft Surface Heat Exchanger Potential. Aerospace, 7(1), 1. https://doi.org/10.3390/aerospace7010001