Abstract
Traditional hydraulic servomechanisms for aircraft control surfaces are being gradually replaced by newer technologies, such as Electro-Mechanical Actuators (EMAs). Since field data about reliability of EMAs are not available due to their recent adoption, their failure modes are not fully understood yet; therefore, an effective prognostic tool could help detect incipient failures of the flight control system, in order to properly schedule maintenance interventions and replacement of the actuators. A twofold benefit would be achieved: Safety would be improved by avoiding the aircraft to fly with damaged components, and replacement of still functional components would be prevented, reducing maintenance costs. However, EMA prognostic presents a challenge due to the complexity and to the multi-disciplinary nature of the monitored systems. We propose a model-based fault detection and isolation (FDI) method, employing a Genetic Algorithm (GA) to identify failure precursors before the performance of the system starts being compromised. Four different failure modes are considered: dry friction, backlash, partial coil short circuit, and controller gain drift. The method presented in this work is able to deal with the challenge leveraging the system design knowledge in a more effective way than data-driven strategies, and requires less experimental data. To test the proposed tool, a simulated test rig was developed. Two numerical models of the EMA were implemented with different level of detail: A high fidelity model provided the data of the faulty actuator to be analyzed, while a simpler one, computationally lighter but accurate enough to simulate the considered fault modes, was executed iteratively by the GA. The results showed good robustness and precision, allowing the early identification of a system malfunctioning with few false positives or missed failures.
1. Introduction
A servoactuator is a device intended to control the position or velocity of a mechanical element by converting power from different sources (usually hydraulic, electrical, or pneumatic) into a controlled motion. In aerospace applications, such devices are commonly used for operating the aircraft control surfaces and several utility systems like landing gear, cargo bay doors, or weapon systems. Most of these functions are safety critical, so redundancy is a necessary risk reduction method, alongside with the use of highly reliable components. With the traditional approach, regular scheduled maintenance should guarantee the continuous airworthiness of the system, but various failure modes occur on a random basis: therefore, maintenance interventions are often frequent and involve the preventive replacement of still functional components, with increased costs; moreover, nothing can exclude the occurrence of a failure before the scheduled substitution of the interested system. Monitoring the behavior of an actuator could enable to detect the early signs of different progressive faults, in order to timely correct them. If a tool would be available with a high grade of robustness to isolate those incipient faults, most failure modes of the flight control system could be identified before they start affecting the performance of the system in terms of dynamical response, stability, stall force, or positioning accuracy. The discipline aimed to this purpose is called Prognostics and Health Management (PHM) (as reported in [1]). The application of PHM strategies involves the analysis of functional parameters of the system in form of electrical signals: for this reason, the use of electrical actuators someway represents an advantage, because no conversion of the signals (and therefore no additional sensors) is needed. Due to the complexity and to the multi-disciplinary nature of the monitored systems, the FDI task on EMA systems is particularly challenging, since several failure modes interact and an acceptable accuracy is hardly achieved. Literature addresses these issues proposing a wide choice of FDI techniques, ranging from the direct comparison of the system response with that of a monitor model (as proposed by [2]), to the spectral analysis of well-defined system behaviors [3,4], to the use of Artificial Neural Networks (as shown in [5,6,7]), to the combination of these methods [8,9]. Usually, model-based approaches are more computationally expensive and require a detailed knowledge of the system, but lead to more accurate results than data driven methods. Data-driven techniques, despite being computationally light (not considering the offline training phase) treat the system with a black-box approach, to gain all knowledge its behavior from raw data, and require large experimental training datasets which are seldom available; for this purpose, NASA developed a Flyable Electro-Mechanical Actuator (FLEA) [10,11,12] test stand to collect EMA monitoring data. However, an exhaustive data collection, spanning different systems and different fault modes, remains a highly demanding task. Conversely, model-based metaheuristic approaches, such as that presented in this paper, take advantage of the knowledge acquired in the design phase in a more efficient way; as a result, less data is required for the training phase (i.e., for the calibration of the fault models). The main drawback is the increase of evaluation computational time, so hard real-time is not usually possible.
In applications related to aircraft flight control systems, the current tendency is to progressively replace the traditional hydromechanial and electrohydraulic actuators with EMAs, according to the “More Electric Aircraft” system architecture [13] or the “All Electric Aircraft” system architecture [14]. This technology is currently implemented on new generation aircraft (e.g., B-787) for secondary FCS and non-safety critical applications, as well as primary FCS of small UAVs. An EMA is basically composed of an electric motor transmitting rotational or linear motion to the user by means of a reduction gearbox; a position sensor and control electronics complete the servoactuator functional scheme, enabling the position control. These systems are relatively of recent adoption for aerospace applications, so their reliability level and their failure modes art not fully understood yet: for this reason, is important to develop robust and effective techniques for prognostic FDI, improving this way the overall safety of operations. Therefore, this work focuses on the study of electromechanical actuation systems for prognostic purpose.
2. Aim of This Work
The authors of this paper propose a new FDI tool based on Genetic Algorithms (GAs); this is optimized and then validated through the comparison between the identified values of fault parameters and the behavior of a numerical EMA virtual test bench, designed and modeled for the purpose. The strategy is intended to provide at least a comparable accuracy to existing ones, without requiring large datasets for training machine learning tools, at the expense of a longer computational time in evaluation; a computational time in the order of minutes is acceptable for detection of slowly progressing faults. The accuracy of the technique is then evaluated in different conditions to assess its field of applicability. According to the hypotheses proposed by [8], the FDI tool is tested under four different progressive failure modes: partial BLDC motor coil short circuit, backlash, dry friction and drift of the proportional gain of the PID (Proportional-Integrative-Derivative) position control logic. Those failure modes are chosen since they usually feature a progressive growth and are among the most common damages affecting electromechanical servoactuators, according to [10,11,12]. Moreover, differently from most work available in literature [4,15,16], we propose a single algorithm able to address multiple distinct fault modes, affecting different subsystems of the actuator at the same time.
3. Reference Model of the Electromechanical Actuator
Figure 1 is the functional block diagram of a typical EMA. Its main components are the following:
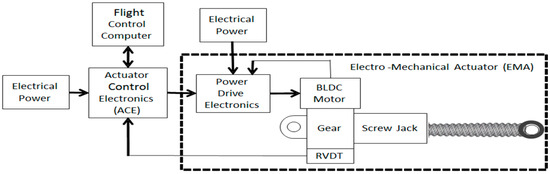
Figure 1.
Block diagram of a typical Electro-Mechanical Actuator (EMA) architecture.
- The Actuator Control Electronics (ACE) evaluates the corrective action for the motor bridge comparing the actual and commanded positions;
- The Power Drive Electronics (PDE) is the motor bridge itself, converting the DC power supply into the three-phase current necessary to drive the motor, modulated accordingly to rotor angular position and signal from the ACE module;
- An electric motor, usually BLDC type (BrushLess Direct Current), converts electrical power into mechanical power;
- A mechanical transmission, composed by a gear reducer and/or a rotary/linear conversion mechanism (e.g., a ball or roller screw) transfers the motion from the motor to the user, i.e., the aircraft control surface;
- A set of position, velocity and current transducers send their measured dimension to the ACE module, allowing the closure of the feedback loop.
The goal of this research is the proposal of a tool able to identify the early effects of the degrading of an EMA, while its performance is still compliant to the specifications and compatible with safe operations. In order to assess robustness and accuracy of this technique, a simulated test environment has been developed with the MATLAB/Simulink® platform. The reference model, formerly proposed by [8], enhanced according to [17,18], and reported in Figure 2, has a very high level of detail. It is able to simulate the dynamic response of a real system even in presence of the considered progressive faults and taking into account the effects of analogic to digital conversion of signals and electrical noise on signal lines. The model can be split into five different subsystems:
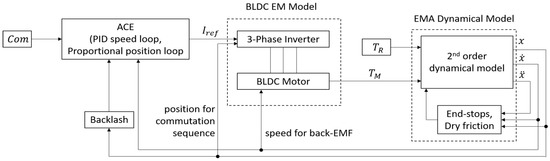
Figure 2.
High-level block diagram the Reference EMA Model employed in this work. BLDC: BrushLess Direct Current; ACE: Actuator Control Electronics.
- The ACE block simulates the behavior of the control electronics module by generating the output reference current Iref, as shown in [19];
- The BLDC EM Model subsystem represents the power drive electronic module and includes the electromagnetic model of the trapezoidal BLDC motor; it evaluates the torque delivered by the motor as a function of the voltages generated by the three-phase electrical power regulator (BLDC EM Model); this model, as employed in [17], has been developed according to the mathematical models and the assumptions propositioned by [20,21,22];
- The EMA Dynamical Model block simulates the mechanical effects within the motor and the transmission, by means of a single degree of freedom MCK model. Additionally, this model accounts for several non-linear effects that characterize the dynamic response of the mechanical system, such as dry friction [23,24], backlash [25], and mechanical end-stops [26].
- The Com input block simulates the pilot’s command and allows to generate different functions as steps, ramps, sine waves etc.;
- Another input block (TR), similar to the previous one, is used to consider the aerodynamic load on the control surface.
A validation of the model has been performed by comparing the dynamical response of the system under different operating conditions (control input, external load, boundary conditions and magnitude of different faults) with data available in literature [27,28]. In particular, it has been assessed that counter electromotive force, phase current waveforms and BLDC dynamical response show a good matching to experimental values, even when faults are considered.
4. EMA Degradations and Fault Modes
As already mentioned, EMAs are of relatively recent introduction in aerospace applications; for this reason, their cumulated flight hours are not enough to provide significant statistics about their most common failure modes. According to [29] it is possible to sort the failure modes into four different categories:
- Mechanical or structural failures;
- BLDC motor failures;
- electronics failures;
- sensor failures.
This study focuses on four particular faults, usually showing a progressive growth: backlash (BLK) and dry friction (FST) affecting the mechanical transmission because of worn components, partial coil-to-coil short circuit in one of the BLDC stator phases (Na) and a drift of the proportional gain of the PID controller (Gprop). These particular failure modes were chosen according to data available in literature, indicating them among those with the highest incidence and criticality [30,31,32]. It is commonly known that dry friction effects appear when two contact surfaces are in relative motion; in a mechanical transmission, the progressive wearing of components results in an increase of friction coefficients, requiring higher torque to be delivered by the motor. Borello and Dalla Vedova [33] showed how increased dry friction causes a reduction in the servomechanism accuracy along with the appearance of characteristic behaviors such as stick-slip and limit cycles. Another consequence of the mechanical wearing of moving components is the increase of the transmission backlash. When a relatively large mechanical play interacts with the actuator feedback logic, the stability and stiffness of the system are compromised, as highlighted by [25]. The main failure modes affecting BLDC motors are partial stator short circuit and rotor eccentricity due to the degradation of bearings. As shown by [34], it is commonly assessed that 35% to 40% of induction motor breakdowns can be ascribed to the stator winding short circuit; BLDC motors considered in this work share a very similar stator architecture to three phase induction machines, so similar failure modes are expected. The stator short circuit usually starts between two windings belonging to the same coil, and the resistance reduction causes a higher current to circulate. Therefore, the localized overheating damages the polymeric insulation of the adjacent windings, leading to the progressive growth of the fault. Eventually, when most of a phase is compromised or the short circuit propagates to another phase or to ground, the motor has a complete failure being no longer able to perform its function. Maggiore et al. [8] proposed a simplified model of this fault, avoiding the necessity of computationally expensive electromagnetic finite elements; since a stator short circuit affects the system behavior by modifying the electromagnetic stator-rotor coupling, it can be simulated by varying the counter-electromotive force constant according to the fault magnitude and the rotor angular position for each phase:
where i = a, b, c for the three electrical phases. The constants kea, keb, kec are then used to evaluate the torque generated by each phase (Cea, Ceb, Cec) and the counter-electromotive forces ea, eb, ec. Sensor and electronics faults usually feature a rather fast evolution in time; however, [35,36] highlighted that considering suitable time scales precursors of these failures can be found and used to take a corrective action.
kei = Kei Cei (1 + ζ cos (θr)),
Therefore, the authors took into account an electronic fault leading to an unexpected change in proportional gain, in order to evaluate the effectiveness of the proposed FDI algorithm in presence of this kind of fault, and in particular considering its interactions with the other fault modes.
5. Monitor Model of the Electromechanical Actuator
The high-fidelity model described in the previous sections emulates the dynamic response of the actual electromechanical servosystem in terms of both mechanical parameters (position, velocity, acceleration, torque) and electromagnetic parameters (i.e., phase current and voltages). The model computes the actuator response accounting for the actual command and load profiles (coming respectively from the pilot and the external aerodynamic forces on the control surface), the varying environmental conditions (temperature changes affecting the electromagnetic parameters of the motor, such as phase resistance) and multiple failure modes.
Then, even with the unavoidable limitations coming from its lumped parameters architecture, this model can be used as a simulated test bench to study the effects of incipient faults on the system response and to test diagnostic and prognostic monitoring techniques.
In all model-based approaches to system diagnostics and prognostics, the behavior of the system is monitored and compared to a simpler model. To this purpose, the authors developed a simplified Monitor Model (MM), with the same logical and functional architecture as the high-fidelity reference model. This simplified model is tailored to compute a response very close to the high fidelity one, although its applicability is restricted to a subset of the operating conditions accounted for by the RM.
The computational cost of the MM is reduced by more than an order of magnitude with respect to the RM, allowing it to be executed iteratively by the GA based FDI algorithm. The MM block diagram is shown in Figure 3; as clearly appears, the model exploits a single-phase DC representation which is globally equivalent to the three phase BLDC architecture of the RM. This, alongside with a simplified hysteresis current loop, allows to increase the integration time step and at the same time to reduce the computations required for each time step, resulting in a reduced computational effort.
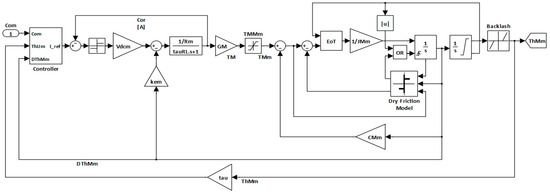
Figure 3.
Detailed block diagram the Monitor Model (MM) employed in this work.
6. Proposed Fault Detection and Identification Algorithm and Problem Setup
Model based FDI is a parameter estimation task [37] which can be solved with an optimization algorithm. An objective function is defined as a cumulative error between the actual system and the model. The optimization updates iteratively a set of parameters encoding the fault condition of the actuator; the optimization is stopped when an adequate match is found between the response of the actual system and that of the monitor model. For testing purposes, and to make up for the lack of actual field data, the high-fidelity reference model replaces the physical actuator in this work.
Several optimization techniques can be employed; they can be classified into two groups: deterministic methods generally rely on the local gradient (analytical or numerical) of the objective function to evaluate the next iteration, while probabilistic methods rely on a random search of the minimum of the objective function. As observed by [3], most optimization algorithms are more likely to converge to local minima, and often fail to find the global solution; in fact, a high dependency on the initial settings and the optimization starting point is usually observed. This behavior is detrimental to a robust and reliable fault detection, since it can possibly lead to the estimation of incorrect faults, with a high likelihood of false positives or missed detections. More robust global search methods, such as Genetic Algorithms and Simulated Annealing offer a higher success rate in detecting the global function minimum, at the expense of a longer computational time [38,39].
Genetic Algorithms (GAs) [40] have been employed in literature for a multitude of applications, solving problems ranging from optimal design of antennas and structural components, to control strategies for robotic applications, to aerodynamic optimization of turbomachinery [41,42,43,44]. Generally, GAs are best suited for problems featuring an expensive objective function depending on multiple variables. For this reason, in recent years many technical applications in the field of mechatronics and electrical machines have been employing Genetic Algorithms for model-based diagnostic and prognostic tasks [39]. In the specific application of electrical machinery fault detection, an example can be found in [38], where GA-based fault detection is leveraged to identify stator turn-to-turn coil short circuit faults with a parameter identification on a model accounting for the short circuit fault.
In light of the above, in this work we developed a model-based FDI strategy able to perform an identification and quantification of faults levels of an EMA. The algorithm analyzes the dynamic response of the system (RM) and compares it with that of a numerical model (MM), through a GA optimization. Specifically, the signals analyzed are the stator current and the motor speed. To compare the three-phase square-wave current of the RM with the single-phase equivalent current of the MM, the envelope of the three phases is considered. The objective function is defined as a quadratic cumulative error between the signals of the RM and the MM:
where i denotes the stator current, ω is the motor angular velocity, and a, b ≥ 0 are weighting coefficients. The weighting coefficients are needed to normalize the cumulative errors computed by integrating the current and velocity signals, obtaining non-dimensional quantities; the coefficients are adjusted to give the two contributions a range of variation of the same order of magnitude.
The RM response is computed with static fault parameters, while the fault parameters of the MM are the input of the objective function. In addition, the same command and external load time histories are fed to both models, since those signals have a strong influence on the system response. Obviously, the error is zero (or near zero) if the two models compute the same response: in this condition, we assume that the faults injected in the MM correspond to those affecting the RM or the actual system; otherwise, the error is always positive.
When the error function is minimized, the RM and MM responses match at their best. Since both models account for the same fault modes, and are validated to show a consistent behavior over a wide range of operating conditions, we can safely assume the fault parameters the MM as an approximation of those initially injected in the RM. A GA is then employed to search the global minimum of the objective function, by varying the fault parameters of the monitor model.
7. Genetic Algorithm Tuning
The core of the proposed FDI strategy is a standard Genetic Algorithm, as available in the Matlab optimization toolbox. Genetic Algorithms are a class of metaheuristic evolutionary optimization algorithms, inspired by the natural selection process.
Each iteration (or generation) of the algorithm evaluates the objective function (often referred to as the fitness function) of a population of points, called chromosomes or individuals. Each chromosome is a potential solution of the minimization; the individuals of each generation are then ranked according to their fitness, i.e., in ascending order of the corresponding objective function value. The best ranking individuals are chosen as parents for the next generation, which is composed by the best individuals of the previous iteration and new ones created using the operators called selection, crossover, and mutation. The process is repeated iteratively until a stopping criterion is satisfied, e.g., the best individuals are all within a tolerance (either in the objective function or in the space of chromosomes), a maximum number of iterations is reached, etc. A schematic representation of the process is given in the flow chart of Figure 4.
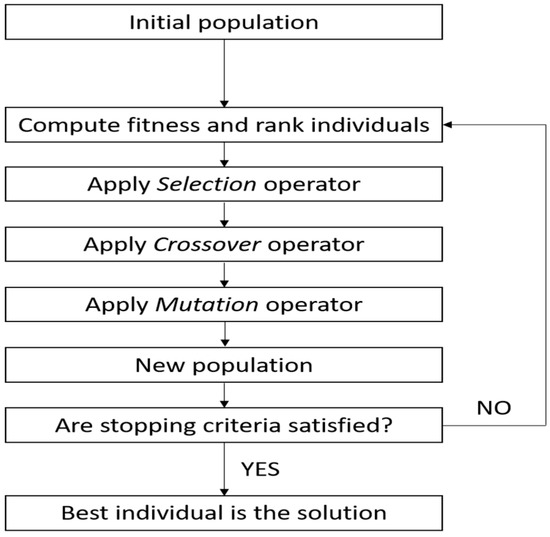
Figure 4.
Flow chart of a typical Genetic Algorithm (GA) optimization.
The setting of several parameters defining the behavior of the GA, such as the selection, crossover and mutation functions, as well as the stopping criteria, are strongly problem dependent and have a great influence on the convergence rate of the optimization. Then, these must be tuned for the optimization to perform correctly on a given application. The following sections explain in detail the settings employed for the considered problem.
7.1. Definition of Bounds and Constraints
The bounds and constraints of an optimization problem define the limits of the search space to be explored by the algorithm. It is important to determine the range of variability of each variable, in order to avoid the presence of an unwanted global minimum of the fitness function which lies outside the feasible space, that is for example, which is not in the space of applicability of the employed models. Additionally, a smaller search space often eases the convergence of the algorithm by excluding some of the local minima from the problem domain.
The fault parameters for the FDI problem studied here are bound between values determined by considerations related to the physical architecture and behavior of the system. As an example, the partial short circuit parameter Na cannot be higher than 1 (fully healthy system) or lower than 0.8 (full damage condition, the EMA is not working properly), or the dry friction coefficient cannot be higher than its nominal value. Table 1 summarizes the bounds set for all the considered parameters.

Table 1.
Summary of bounds considered for each.
7.2. Definition of Population Size
As a default setting, the GA solver available in the Matlab Optimization Toolbox computes 20 individuals for each iteration. Increasing the number of individuals allows a better exploration of the search space, since the higher diversity of the population avoids the optimization to get stuck into a local minimum. Additionally, the algorithm is likely to converge with less iterations. However, a large population results in a long computational time, since the objective function, which is usually the most computationally intensive part of the algorithm, is evaluated for each individual; this issue is somehow mitigated by the parallelization of computations.
For single fault isolation, we found that a population size of 20 individuals produces acceptable results; the increased complexity of the fitness function for multiple faults requires a larger population of 30 individuals.
7.3. Initialization of the First Generation
Some or all of the individuals included in the population of the first generation can be initialized to user-defined values. This way, if the solution is expected near a certain point in the search space, the convergence rate is improved. For the considered problem, we set an individual of the initial population to the value corresponding to an actuator in nominal condition. As a result, the optimization converges in a single iteration if the system is healthy, and few iterations are needed when the faults are small (i.e., in their early incipient condition), which is the case of most interest for prognostic analysis.
7.4. Definition of the Initial Range
The initial range parameter defines the dispersion of the individuals of the first generation. A small value for this parameter results in a small fraction of the search space being explored in the first iterations of the optimization. The convergence rate can be higher, but the algorithm risks to converge to a local minimum. Conversely, a larger initial range produces a slower convergence but a higher chance of finding the actual global minimum. For the given problem, the individuals of the first generation which are not initialized are spread cross the whole search space (i.e., the initial range is equal to the bounds of the problem). This way, being the problem constrained and being little known about the shape of the objective function, the algorithm has a good probability of converging in the wanted point.
7.5. Scaling of the Fitness Function
For the considered problem, we used a rank-based fitness function scaling. That is, the individuals of each iteration are ranked according their fitness and a progressive value is assigned to each one (i.e., the best individual gets a rank of 1, the second best gets 2, and so on). Then, individuals are chosen for reproduction with a probability depending on their rank, and not directly on their fitness. This way, diversity of the population is preserved even if one individual is much fitter than the others. In general, the distribution of the individual can result in some solutions having a fitness value orders of magnitude better than the others, and if the probability of selection was based directly on fitness the diversity would be greatly reduced, with the algorithm rapidly converging in a local minimum. Conversely, the use of a rank-based fitness scaling is intended to prevent such behavior.
7.6. Definition of the Selection Fuction
A stochastic uniform selection function was chosen to determine the individuals to be used for generating the new population. A geometric interpretation of the selection algorithm is given in the following. A line is drawn, and a segment is allocated for each individual, with a length proportional to the rank of the individual. Then, the algorithm performs a series of steps of constant random amplitude. A parent individual is chosen for each step, according to the segment the step lands on. This selection method gives a chance to be chosen also to the least fit individuals, preserving diversity of the population.
7.7. Setting of the Crossover Fraction and Crossover Function
Crossover is the process by which the algorithm creates a new individual combining data from two individuals belonging to the previous generation. Not all individuals are created by crossover, since a fraction results from a random process known as mutation. The crossover fraction parameter represents the amount of individuals created by crossover with respect to the population size. A crossover fraction too close to 1 (i.e., all individuals are generated by crossover) results in a fast convergence but a poor diversity; conversely, a small crossover function makes the algorithm similar to a random search, with a very slow convergence rate.
We use a heuristic crossover function, reported in [45] to be the best performing for the considered application. Once two parent individuals are selected for crossover, the children solutions are created on the line connecting the two parents on the search space, closer to the best fitting parent. This method has been shown to achieve a fast convergence on the considered problem, while the mutation function employed is the adaptive feasible algorithm which is standard for constrained fitness function applications.
8. Results
The FDI algorithm has been tested in presence of both single faults and multiple faults. Clearly, if only one fault mode is taken into account, the FDI problem becomes much simpler, and can be efficiently solved with deterministic, gradient based search strategies. However, in a real environment, the failure mode affecting the system cannot be known a priori, so the fault detection logic shall be able to recognize the actual damage among a set of possible known fault modes.
Additionally, unknown fault modes shall be detected as well, even if their identification is not possible without the necessary knowledge about their effect on the system behavior (i.e., without a model of the failure).
The detection of multiple faults requires to employ more robust algorithm than gradient based ones, hence in this work we propose the use of GAs. Moreover, the combined effect of two different faults affecting the system response at the same time can hide each other. As an example, while backlash and gain drift have very distinct influence on the behavior of the actuator, partial short circuit and dry friction affect the response in a similar way, i.e., modifying the motor speed for a given stator current. In particular, an increase in friction reduces speed for a given current, while a reduction of the healthy windings causes an increase in motor speed. Then, the fitness function plotted against friction coefficient and partial short (see Figure 5) has not a well-defined global minimum, since several combinations of FST and Na result approximately in the same minimum fitness value.
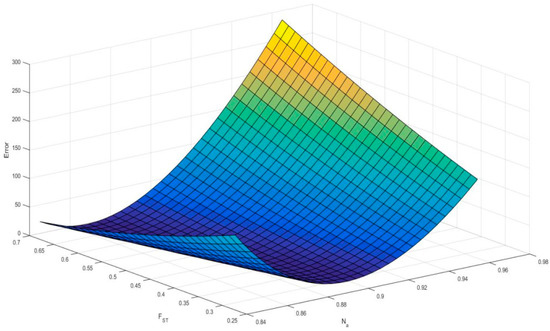
Figure 5.
3D plot of the fitness function against dry friction (FST) and partial short circuit of phase A (Na). The blue valley has a constant fitness value, meaning that those two fault modes hide each other in the considered case.
Two ways are possible to overcome this problem. One consists in employing more accurate monitor models, able to discriminate the effects of similar fault modes (citations needed). This strategy is not always viable since it usually leads to an increased computational time, while some combinations of faults are inherently difficult to identify being caused by similar physical phenomena. The alternative approach adopted for this work leverages a simplified and computationally light monitor model, but computes the system response in presence of different command and load time histories to detect differences among similar behaving faults. As an example, dry friction and short circuit have similar effects on motor speed for a given current value (as stated above). However, a given amount of friction causes a smaller effect on the response to a sine wave command and a larger one for a step command; conversely, a partial short circuit has a similar effect on both commands. This behavior enables the algorithm to identify these two faults correctly.
Results for Multiple Faults Identification
An extensive test campaign was carried out to validate the effectiveness of the proposed FDI strategy in different operating conditions and in presence of different fault combinations. The following paragraphs briefly describe the damage type and extent for each group of test cases considered:
- Nominal conditions: This test case corresponds to a non-damaged system. The FDI algorithm is able to quickly recognize this condition since the initial population setting contains an individual in nominal condition; then, the GA converges in a single iteration, and the execution is terminated as the stopping criteria are satisfied. Results of these tests are reported in Table 2.
 Table 2. Fault detection and isolation (FDI) results for nominal condition.
Table 2. Fault detection and isolation (FDI) results for nominal condition. - Incipient damage: This condition is of particular interest for the prognostic field since it represents the early stages of progressive faults; the extent of damages is small, so that they are detectable but do not compromise the system performance. Correctly identifying those damages is the goal of prognostic FDI and supplies the data necessary for estimation of the system Remaining Useful Life. Results of incipient damage tests are reported in Table 3.
 Table 3. FDI results for a low-level damage combination.
Table 3. FDI results for a low-level damage combination. - Full damage: A larger fault level results in a full damage, i.e., the system cannot meet its functional or performance requirements any more. This condition falls into the field of diagnostics since the system has already failed, and no estimation of Remaining Useful Life can be performed to plan a maintenance intervention. However, an FDI algorithm shall be robust enough to identify such conditions with acceptable accuracy, in order to trigger a corrective maintenance intervention. Results of these tests are reported in Table 4.
 Table 4. FDI results for a full damage combination.
Table 4. FDI results for a full damage combination. - Random damage combination: A last group of test cases includes fault combinations of heterogeneous extent, randomly sampled in the problem domain. This condition is expected to be the closest to the real operating condition of the proposed FDI strategy, since in a field operation multiple fault modes are likely to occur at the same time, but with widely different damage levels. Results of tests for random multiple faults are reported in Table 5.
 Table 5. FDI results for a random damage combination.
Table 5. FDI results for a random damage combination.
Figure 6 shows the residual estimation error of the proposed FDI algorithm. All the faults are detected with high accuracy, with an error at most in the order of 2%. The error can be addressed to the small discrepancy between the Reference and Monitor models of the actuator.
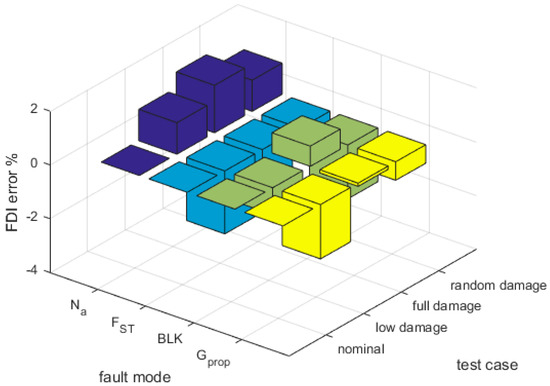
Figure 6.
Bar plot of the fault identification error.
In a real application scenario, FDI error would be caused mainly by approximations of the monitor model and by uncertainty in signal measurements, hence the need for accurately calibrated models of the system and high-quality sensors. Given the absence of a unified standard for testing fault detection algorithms [15], it is difficult to properly compare the accuracy of the proposed methodology with alternative approaches available in literature. However, it is important to remark the ability of the proposed strategy to estimate accurately the health condition of the system in presence of multiple failure modes affecting the same signals at the same time.
9. Discussion and Conclusions
A Fault Detection and Identification method based on a Genetic Algorithm solver has been proposed and validated. The results confirm the reliability and robustness of GA optimization when dealing with multi-variable, multimodal problems. The proposed algorithm has been tested on multiple fault conditions to assess its effectiveness and performance in situations as close as possible to field operations.
The algorithm demonstrated a high accuracy and an acceptable computational time in the order of minutes. The computations were performed on a common laptop, and better evaluation times can be achieved using higher performance hardware. Computational time is compatible with FDI performed during scheduled maintenance interventions, but not for real-time fault estimation (for which the actual load time history experienced by the flight control actuator should be known and measured by dedicated sensors). Additionally, convergence time varies quite widely depending on the test case. In particular, small damage levels result in a lower number of iterations, with the extreme case of nominal condition tests converging in a single iteration taking a few seconds. This behavior is ascribable to the initial population setting, so that nominal condition is explored by the first generation of solutions, speeding up convergence for nominal and incipient fault conditions.
A good repeatability of results was achieved in the performed tests. Actually, being GAs non-deterministic optimization algorithms, two executions starting from the same conditions produce different results. However, the proposed algorithm proved to be repeatable and robust, since similar results were found on several runs for a given test case, both with and without the presence of noise on the measured signals.
Further developments on this work will include the study of a larger set of failure modes, the extension to other system architecture (such as electrohydraulic actuation systems), the optimization of models and algorithms to reduce the computational requirements of the FDI strategy, and the experimental validation of the models.
Author Contributions
These authors have contributed equally to this work. In detail, M.D.L.D.V. developed the test case, the methodology and the numerical models defined, A.G. carried out the numerical investigation and collected the results, while P.C.B. and P.M. have developed the postprocessing analysis and revised the results.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Byington, C.S.; Watson, W.; Edwards, D.; Stoelting, P. A Model-Based Approach to Prognostics and Health Management for Flight Control Actuators. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 6–13 March 2004. [Google Scholar]
- Borello, L.; Dalla Vedova, M.D.L.; Jacazio, G.; Sorli, M. A Prognostic Model for Electrohydraulic Servovalves. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009. [Google Scholar]
- Dalla Vedova, M.D.L.; Maggiore, P.; Pace, L. Proposal of Prognostic Parametric Method Applied to an Electrohydraulic Servomechanism Affected by Multiple Failures. WSEAS Trans. Environ. Dev. 2014, 10, 478–490. [Google Scholar]
- Bindu, S.; Thomas, V.V. A Modified Direct-Quadrature Axis Model for Characterization of Air-Gap Mixed Eccentricity Faults in Three-Phase Induction Motor. Int. Rev. Model. Simul. 2018, 11, 6. [Google Scholar] [CrossRef]
- Battipede, M.; Dalla Vedova, M.D.L.; Maggiore, P.; Romeo, S. Model based analysis of precursors of electromechanical servomechanisms failures using an artificial neural network. In Proceedings of the AIAA SciTech Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Elasha, F.; Shanbr, S.; Li, X.; Mba, D. Prognosis of a Wind Turbine Gearbox Bearing Using Supervised Machine Learning. Sensors 2019, 19, 3092. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Hu, W.; Cao, D.; Zhang, B.; Huang, Q.; Chen, Z.; Blaabjerg, F. An Imbalance Fault Detection Algorithm for Variable-Speed Wind Turbines: A Deep Learning Approach. Energies 2019, 12, 2764. [Google Scholar] [CrossRef]
- Maggiore, P.; Dalla Vedova, M.D.L.; Pace, L.; Desando, A. Evaluation of the correlation coefficient as a prognostic indicator for electromechanical servomechanism failures. Int. J. Progn. Health Manag. 2015, 6, 1–13. [Google Scholar]
- Liu, H.; Qin, C.; Liu, M. A Rail Fault Diagnosis Method Based on Quartic C2 Hermite Improved Empirical Mode Decomposition Algorithm. Sensors 2019, 19, 3300. [Google Scholar] [CrossRef]
- Quigley, R.E.J. More electric aircraft. In Proceedings of the Eighth Annual IEEE Applied Power Electronics Conference—APEC 93, San Diego, CA, USA, 7–11 March 1993. [Google Scholar]
- Howse, M. All-electric aircraft. Power Eng. 2003, 17, 35–37. [Google Scholar] [CrossRef]
- Balaban, E.; Bansal, P.; Stoelting, P.; Saxena, A.; Goebel, K.F.; Curran, S. A diagnostic approach for electro-mechanical actuators in aerospace systems. In Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009. [Google Scholar]
- Balaban, E.; Saxena, A.; Goebel, K.; Byington, C.S.; Bharadwaj, S.P.; Smith, M. Experimental Data Collection and Modeling for Nominal and Fault Conditions on Electro-Mechanical Actuators. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009. [Google Scholar]
- Balaban, E.; Saxena, A.; Narasimhan, S.; Roychoudhury, I.; Goebel, K.; Koopmans, M. Airborne Electro-Mechanical Actuator Test Stand for Development of Prognostic Health Management Systems. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Portland, OR, USA, 10–16 October 2010. [Google Scholar]
- Fico, V.M.; Rodríguez Vázquez, A.L.; Martín Prats, M.Á.; Bernelli-Zazzera, F. Failure Detection by Signal Similarity Measurement of Brushless DC Motors. Energies 2019, 12, 1364. [Google Scholar] [CrossRef]
- De Martin, A.; Jacazio, G.; Vachtsevanos, G. Windings fault detection and prognosis in electro-mechanical flight control actuators operating in active-active configuration. Int. J. Progn. Health Manag. 2017, 8, 2. [Google Scholar]
- Dalla Vedova, M.D.L.; Berri, P.C.; Re, S. Novel metaheuristic bio-inspired algorithms for prognostics of onboard electromechanical actuators. Int. J. Mech. Control 2018, 19, 95–101. [Google Scholar]
- Dalla Vedova, M.D.L.; Germanà, A.; Maggiore, P. Proposal of a new simulated annealing model-based fault identification technique applied to flight control EM actuators. In Risk, Reliability and Safety: Innovating Theory and Practice, Proceedings of the 26th European Safety and Reliability Conference (ESREL 2016), Glasgow, Scotland, 25–29 September 2016; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Todić, I.; Miloš, M.; Pavišić, M. Position and speed control of electromechanical actuator for aerospace applications. Teh. Vjesn. 2013, 20, 853–860. [Google Scholar]
- Çunkas, M.; Aydoğdu, O. Realization of Fuzzy Logic Controlled Brushless DC Motor Drives using Matlab/Simulink. Math. Comput. Appl. 2010, 15, 218–229. [Google Scholar] [CrossRef]
- Halvaei Niasar, A.; Moghbelli, H.; Vahedi, A. Modelling, Simulation and Implementation of Four-Switch Brushless DC Motor Drive Based on Switching Functions. In Proceedings of the IEEE EUROCON 2009, St. Petersburg, Russia, 18–23 May 2009. [Google Scholar]
- Hua, J.; Zhiyong, H. Simulation of Sensorless Permanent Magnetic Brushless DC Motor Control System. In Proceedings of the IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008. [Google Scholar]
- Dalla Vedova, M.D.L.; Maggiore, P.; Pace, L. A new prognostic method based on simulated annealing algorithm to deal with the effects of dry friction on electromechanical actuators. Int. J. Mech. 2015, 9, 236–245. [Google Scholar]
- Borello, L.; Villero, G.; Dalla Vedova, M.D.L. New asymmetry monitoring techniques: Effects on attitude control. Aerospace Science and Technology 2009, 13, 475–487. [Google Scholar] [CrossRef]
- Borello, L.; Villero, G.; Dalla Vedova, M.D.L. Flap failure and aircraft controllability: Developments in asymmetry monitoring techniques. J. Mech. Sci. Technol. 2014, 28, 4593–4603. [Google Scholar] [CrossRef]
- Dalla Vedova, M.D.L.; De Fano, D.; Maggiore, P. Neural network design for incipient failure detection on aircraft EM actuator. Int. J. Mech. Control 2016, 17, 77–83. [Google Scholar]
- Lee, B.K.; Ehsani, M. Advanced Simulation Model for Brushless DC Motor Drives. Electr. Power Compon. Syst. 2003, 31, 841–868. [Google Scholar] [CrossRef]
- Kaliappan, E.; Chellamuthu, C. Simplified Modeling, Analysis and Simulation of Permanent Magnet Brushless Direct Current Motors for Sensorless Operation. Am. J. Appl. Sci. 2012, 9, 1046–1054. [Google Scholar]
- Gökdere, L.U.; Chiu, S.L.; Keller, K.J.; Vian, J. Lifetime control of electromechanical actuators. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 5–12 March 2005. [Google Scholar]
- Kenjo, T.; Nagamori, S. Brushless Motors: Advanced Theory and Modern Applications; Sogo Electronics Press: Tokyo, Japan, 2003. [Google Scholar]
- Chesley, J.C. Handbook of Reliability Prediction Procedures for Mechanical Equipment; NSWC Carderock Division: Bethesda, MD, USA, 2011. [Google Scholar]
- Weiss, J. Control Actuation Reliability and Redundancy for Long Duration, Underwater Vehicle Missions with High Value Payloads. In Proceedings of the 2014 Underwater Intervention Conference, New Orleans, LA, USA, 11–13 February 2014. [Google Scholar]
- Borello, L.; Dalla Vedova, M.D.L. A Dry Friction Model and Robust Computational Algorithm for Reversible or Irreversible Motion Transmission. Int. J. Mech. Control 2012, 13, 37–48. [Google Scholar]
- Shashidhara, S.M.; Raju, P.S. Stator Winding Fault Diagnosis of Three-Phase Induction Motor by Parks Vector Approach. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 2901–2906. [Google Scholar]
- Ginart, A.; Brown, D.; Kalgren, P.; Roemer, M. On-line Ringing Characterization as a PHM Technique for Power Drives and Electrical Machinery. In Proceedings of the IEEE Autotestcon 2007, Baltimore, MD, USA, 17–20 September 2007. [Google Scholar]
- Ginart, A.; Brown, D.; Kalgren, P.; Roemer, M. Inverter Power Drive Transistor Diagnostic and Extended Operation under One-Transistor Trigger Suppression. In Proceedings of the Applied Power Electronics Conference and Exposition 2008 (APEC 2008), Austin, TX, USA, 24–28 February 2008. [Google Scholar]
- Berri, P.C.; Dalla Vedova, M.D.L.; Mainini, L. Diagnostics of Actuation System Faults from Dynamic Data. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6), European Community on Computational Methods in Applied Sciences (ECCOMAS), Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Raie, A.; Rashtchi, V. Using a genetic algorithm for detection and magnitude determination of turn faults in an induction motor. Electr. Eng. 2002, 84, 275–279. [Google Scholar] [CrossRef]
- Alamyal, M.; Gadoue, S.M.; Zahawi, B. Detection of induction machine winding faults using genetic algorithm. In Proceedings of the 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 157–161. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, UK, 1996. [Google Scholar]
- Mishra, R.G.; Mishra, R.; Kuchhal, P.; Kumari, P. Optimization and Analysis of High Gain Wideband Microstrip Patch Antenna using Genetic Algorithm. Int. J. Eng. Technol. 2018, 7, 176–179. [Google Scholar] [CrossRef][Green Version]
- Kahraman, M.; Erbatur, F. A GA Approach for Simultaneous Structural Optimization. In Proceedings of the International Conference on Structural Engineering, Mechanics and Computation, Cape Town, South Africa, 2–4 April 2001. [Google Scholar]
- Vijay, M.; Jena, D. GA Based Adaptive Controller for 2DOF Robot Manipulator. IFAC Proc. Vol. 2016, 47, 670–675. [Google Scholar] [CrossRef]
- Shimoyama, K.; Yoshimizu, S.; Jeong, S.; Obayashi, S.; Yokono, Y. Multi-Objective Design Optimization for a Steam Turbine Stator Blade Using LES and GA. J. Comput. Sci. Technol. 2011, 5, 134–147. [Google Scholar] [CrossRef]
- Germanà, A. Genetic Algorithms for the prognostic of electro-mechanic servomechanisms for aeronautical applications. Master’s Thesis, Politecnico di Torino, Turin, Italy, 2015. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).