1. Introduction
Automatic controls refer to the application of control theory to regulate systems or processes without human intervention, and the notion is often usefully applied to space applications. A key part of controlling flexible space robotics is the control-structures interaction of a light, flexible structure whose first resonant modes lie within the bandwidth of the controller. Very flexible materials are ubiquitous in space robotics because stiffness cannot be achieved by high-mass objects due to the cost of spaceflight. In this instance, the designed control excites the problematic resonances of the highly flexible structure. In order to optimize the control of such challenging systems, a brief review of mechanics and ubiquitous control techniques is warranted.
Mechanical motion of mass in six degrees of freedom is completely described by separate treatment of three degrees of freedom of translation plus three additional degrees of freedom of rotation as articulated in the year 1830 [
1] and expanded and modernized over the following two centuries [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. Translational degrees of freedom are governed by Newton’s law, while rotational degrees of freedom behave in accordance with Euler’s law. While translation is straightforward (a second-order ordinary differential equation), rotation is complex since the governing equations are nonlinear and coupled and remain unsolved in general form without simplifying assumptions. Thus, rotational motion remains an area of considerable recent developments [
14,
15,
16,
17,
18,
19], where [
14,
15,
16] are recent works in the control of rotational mechanics, while [
17,
18,
19] represent very recent developments in system identification, in particular, identification of material properties and system parameters (e.g., modal properties like natural frequencies and moment of inertia) that permit control design of highly flexible multi-body systems. New research in kinematic representations of the motion is presented in [
20]. With the complete analytic description of translational and rotational motion, multi-body dynamics is used to apply these two governing relations to masses that move relative to each other (vibrate, flex, etc.).
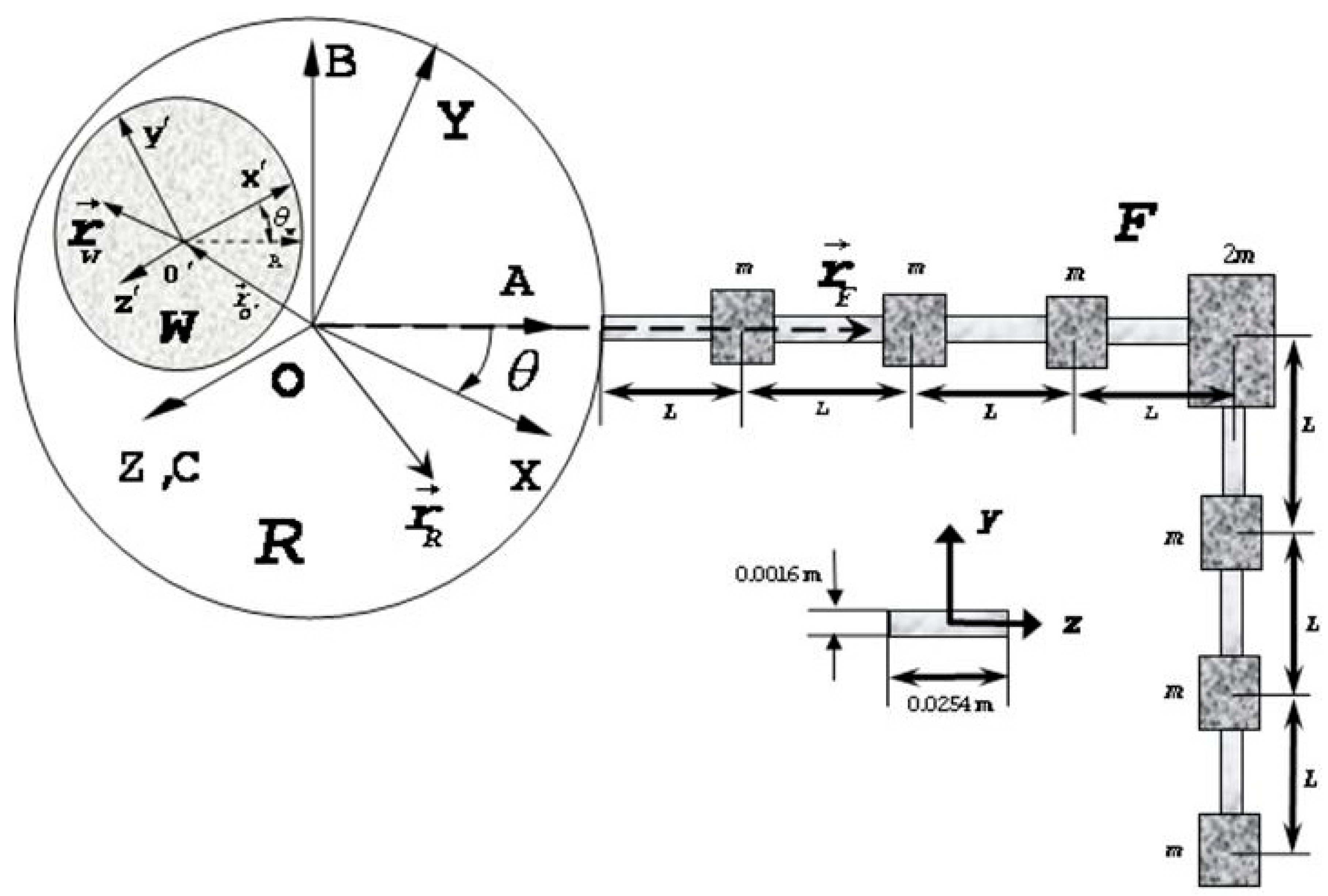
The hybrid coordinate system [
21] was used to separate the model into two subsystems: the rigid body and the flexible appendage, which is assumed to be linearly elastic. The A, B, C axes are inertially fixed with the X, Y, Z axes being allowed to rotate to easily express rotational degrees of freedom. The x’, y’, z’ axes are permitted to rotate with the control actuator (reaction wheel). The rigid body motion due to flexible motion was written in flexible-body modal coordinates, then transformed to central body coordinates for translations and rotations. The elastic deformation in terms of cantilever modal coordinates was combined with the flexible body deformations via a rigid–elastic coupling term. An elastic stress/deformation relationship is assumed under the small deformation assumption. The flexible spacecraft simulator (FSS) depicted in
Figure 1 was broken into nodes for finite element analysis of the flexible system as displayed in
Figure 2 and
Table 1. Finite element analysis was performed to yield a mathematical model of the system with the flexible appendage.
Hamilton’s principle was used to derive the equations of motion via Newton’s law and Lagrange’s method and compared to previous analyses [
22,
23,
24,
25,
26] of somewhat similar systems. Extensive efforts are expended modeling the free–free vibration equations of the flexible system, and this extensive modeling yields a distinct improvement over the just-cited literature. Ward [
22] completed the initial basic design of a different version of the flexible spacecraft simulator (FSS). Watkins [
23] and Harrington [
24] each implemented proportional-derivative (PD) control and linear–quadratic–Gaussian (LQG) compensators on various configurations of the FSS. Hailey [
25] performed experimental verification of the analytical results for PD and linear–quadratic regulator (LQR), and additionally tested a classic bang–bang controller, furthermore implementing control input shaping to eliminate an undesirable spike in the response of the PD controller. Harrington later performed [
26] multivariate control (using LQG) with piezoelectric sensors [
16] and actuators along the length of the flexible appendage. Burke performed experimental verification of Harrington’s technique. Each referenced author derived the equations of motion and used finite element analysis to analyze their respective flexible appendage in various computer languages (FORTRAN, MATLAB, and SIMULINK).
A key part of flexible system control is the control-structures interaction of a light, flexible structure whose first resonant modes lie within the bandwidth of the controller. This introduction to designing compensators will prove capable of minimum-time performance of an in-plane maneuver with zero residual vibration (ZV) and zero residual vibration-derivative (ZVD) at the end of the maneuver. This optimal time will provide a figure of merit for synthesis of control techniques. For a flexible spacecraft simulator (FSS) free-floating planar robotic arm, this paper will first model the flexible system in detail and then use general purposed pseudospectral optimization software to seek an optimal control, proceeding afterwards to validate optimality via six theoretical optimization necessary conditions: (1) Hamiltonian minimization condition; (2) adjoint equations; (3) terminal transversality condition; (4) Hamiltonian final value condition; (5) Hamiltonian evolution equation; and (6) Bellman’s principle. The investigation opens an interesting question of what to declare when the six necessary conditions are not necessarily in agreement (we choose not to declare finding the optimal control, instead calling it suboptimal). Control derived by the pseudospectral method will be numerically revealed using MATLAB via a general optimization program [
27]. By comparison, recall classical compensators and those designed to control flexible systems [
28,
29,
30,
31,
32,
33,
34] ubiquitously command maneuvers in the direction of the desired end state. To validate this claim, reviews of classical compensators [
35] and frequency domain shaping filters [
36] were performed by Wie and Agrawal, respectively. Xu et al. [
37] studied optimized compensator designs, but the dynamics were cantilever vibration modes, neglecting the so-called “free–free” dynamics illustrated by anti-resonance/resonance pairs in the frequency domain. “Free–free” refers to the fact that both ends of the vibrating structure are free to vibrate (e.g., in space, suspended in the atmosphere, etc.). Sands, et al. developed deterministic artificial intelligence methods stemming from a combination of system identification [
17,
18,
19], physics-based methods [
38] and adaptive control [
39,
40], yet all of these embody the former design paradigm of first designing compensation, then seeking optimization. In parallel, a new paradigm is emerging that begins the process with solution of an optimization problem that is subsequently used in compensation design [
41]. That new paradigm is adopted here.
Constituting an improvement over the recently published literature, Newtonian derivation of the equations of motion elaborating the free–free vibration modes is shown to be equivalent to the derivation by Hamilton’s principle, Lagrange’s method, and Euler–Lagrange’s method. Since optimization via Pontryagin’s minimization principle is articulated using the Lagrangian and Hamiltonian, the equivalence permits the original derivation of the dynamics to be used in the optimized calculation of the control compensator.
2. Materials and Methods
Here, the equations of motion are derived from Hamilton’s principle, then converted into the format required by general purpose optimization software. A commonplace MATLAB software package called DIDO [
27] was used here to solve for the optimal control. The chosen optimization software is not particularly important, but significant and detailed explanation and formatting is given in this manuscript to augment repeatability by other researchers. The reader is urged to initially focus on the critical analysis of the discovered results, and only in the event they seek to repeat the results, then emphasize the syntax and formatting required by DIDO. The key novel contribution is the whiplash nature of the control, which will be validated in
Section 3 using six disparate theoretical optimization criteria.
2.1. Equations of Motion from Hamilton’s Principle
Hamilton’s principle implies that the Lagrange method must:
Differentiating leads to a minimization equation expression that may be combined with the adjoint equation to produce the Euler–Lagrange equation, which by algebraic manipulation becomes Newton’s law.
Hamilton’s principle of minimizing the Lagrangian results in two methods to derive equations of motion: Newton’s law and the Euler–Lagrange equation. Newton’s method sums the forces and moments about each point in the inertial frame, while the Lagrange approach uses the system’s energy to derive the equations of motion. Each technique is valid for the flexible spacecraft simulator and yields identical results, and both methods are used next to validate the derived equations of motion to be subsequently optimized.
2.2. Equations of Motion from Euler–Lagrange’s Method
Lagrange’s method is appropriate regardless of various coordinate systems, since it utilizes the system’s kinetic (
T) and potential energy (
V) to derive the equations of motion.
where
is the velocity of a particle on the rigid body;
is the velocity of a particle on the flexible body;
is the velocity of a particle on the reaction wheel;
r vectors are position vectors to the respective particles;
is elastic deformation vectors of particles on the flexible body;
are unit vectors in the x’, y’, z’ axes of the reaction wheel.
Expanding all the terms in the equation for kinetic energy,
T:
Utilizing generalized coordinates
θ,
θw,
δ, assuming the reaction wheel rotates about its center of mass, and invoking the small displacement assumption simplifies the kinetic energy equation to:
where
.
Now convert the elastic deformation
δ into cantilever modal coordinates [
27] using
and
. This relationship describes the displacement at time
t of a point at position
x along the FSS is related to the mode shape
ϕ (
x and
y components) and the generalized coordinate or modal coordinate,
is a sinusoidal function. The mode shape is a time-independent characteristic of the flexible structure. Using this relationship, kinetic energy
in terms of the generalized coordinates is:
where rigid elastic coupling term
.
Potential energy comes from stiffness and can be expressed in generalized coordinates as:
where
is the natural frequency of the
ith mode. The virtual work is given [
35] as:
where
is disturbance torques and
is total torques (not to be confused with
T = kinetic energy). Revisiting the Euler–Lagrange equation, substituting potential and kinetic energy yields the equations of motion in terms of the generalized coordinates.
Next, verify that Euler–Lagrange’s method generates the same equations of motion as Newton’s law. These equations of motion have been derived from Hamilton’s principle via Lagrange’s method. The equations need to be converted into DIDO Dynamics format. But first note below that Newton’s law results in the identical equations of motion.
Newton’s law: ∑
F = ma applies at each node of the system, where coordinates are defined in the hybrid-coordinate system [
21].
[M] is the system’s global mass matrix (to be derived by finite element analysis);
[K] is the system’s global stiffness matrix (to be derived by finite element analysis);
{F} is the force vector.
Including structural damping results in:
. The two degrees of freedom are
x/
y displacements and
rotations.
x/
y rotations are mutually exclusive, since we are not allowing plane stress and plane strain. That means the members are not allowed to lengthen/shorten (bending displacements only). So, for the horizontal members, the
in the equation of Newton’s law corresponds to the
y-direction bending displacements. Similarly, for vertical members, the
corresponds to
x-direction bending displacements. The nodal degrees of freedom are constrained to zero at the attachment point of the flexible and rigid bodies (forcing the appendage to stay attached). Also note that the corner node of the flexible body does not permit
x or
y displacement degrees of freedom leaving only
θ rotations. This reduces our anticipated (14 × 14) system to (12 × 12), eliminating the displacement degrees of freedom at the attachment point and corner. Translating Newton’s law into rotational form and adding the rigid–elastic coupling method results in:
where
= body principle moment of inertia with respect to the Z-axis;
= angular acceleration of the system rotation angle, ;
D = rigid–elastic coupling term;
= acceleration in generalized displacement coordinates;
= reaction wheel principle moment of inertia with respect to C, Z-axis;
= angular acceleration of the reaction wheel rotation angle, θw;
= disturbance torques.
Torques may be combined to more closely resemble the basic expression of Newton’s law:
where
T = sum of disturbance torques, and control torques of the reaction wheel.
Isolating the first term:
and also note:
3. Results
3.1. Conversion of Equations for Input to DIDO General Purposed Optimization Software
Either
or
must be eliminated to put this into standard state space form. Subsequently, the equations can quickly be formulated as the dynamics equations to enter in DIDO. Using generalized coordinates from Equation (13),
to express the displacements
x and
y:
Substitute into Equation (20):
Recall the expressions for the rigid–elastic coupling using modal coordinates:
where
’s are mode shapes from finite element analysis using the eigenvalues of K/M (stiffness/mass). The system stiffness matrix is included in
Table 2 and mass matrix in
Table 3 result in the natural frequencies and mode shapes for the flexible system in
Table 4 and
Table 5 as depicted in
Figure 3.
3.2. Analysis
This flexible plant’s state space matrices in
Table 6 and Equations (31) and (32) display anti-resonances/resonance pairs that occur at discrete natural frequencies. These illustrate an improvement to Figure 11b in [
37], which lacks the anti-resonances generated by inclusion of the free–free vibration mode in the dynamics (thus the extensive development of the dynamic equations here). These nonlinear features are a challenging aspect of flexible spacecraft. The anti-resonance/resonance pairs are indicative of correct modeling of the “free–free” vibrating multi-body system.
3.3. Convert Standard State Space Form to DIDO Dynamics Form
DIDO uses the format of fundamental optimization problems where the derivative terms are on the left side of the equal sign in an equation as in the standard state space expression above). To enter the dynamics equations in DIDO, we simply multiply out the matrix expression
resulting in
Nx = 12 equations for the DIDO Dynamics file.
Note the expansion of [B]{u} has been simplified for single control input (rotation of the spacecraft only). Thus, the u2, u3 … u12 terms are zero in the simplified expression above. These are the DIDO Dynamics equations. The odd states (x1, x3, x5, x7, x9, and x11) correspond to x/y displacements, while the even states (x2, x4, x6, x8, x10, and x12) are rotations. Referencing the system graphic on the first page: x1, x3, x5 are y-direction displacements, while x7, x9, and x11 are x-direction displacements.
3.4. Fundamental Optimization Problem
Formulation of the scaled problem
Minimize
Subject to
Note that only the final state and derivative (
statedot) of the end node (
x11) are constrained:
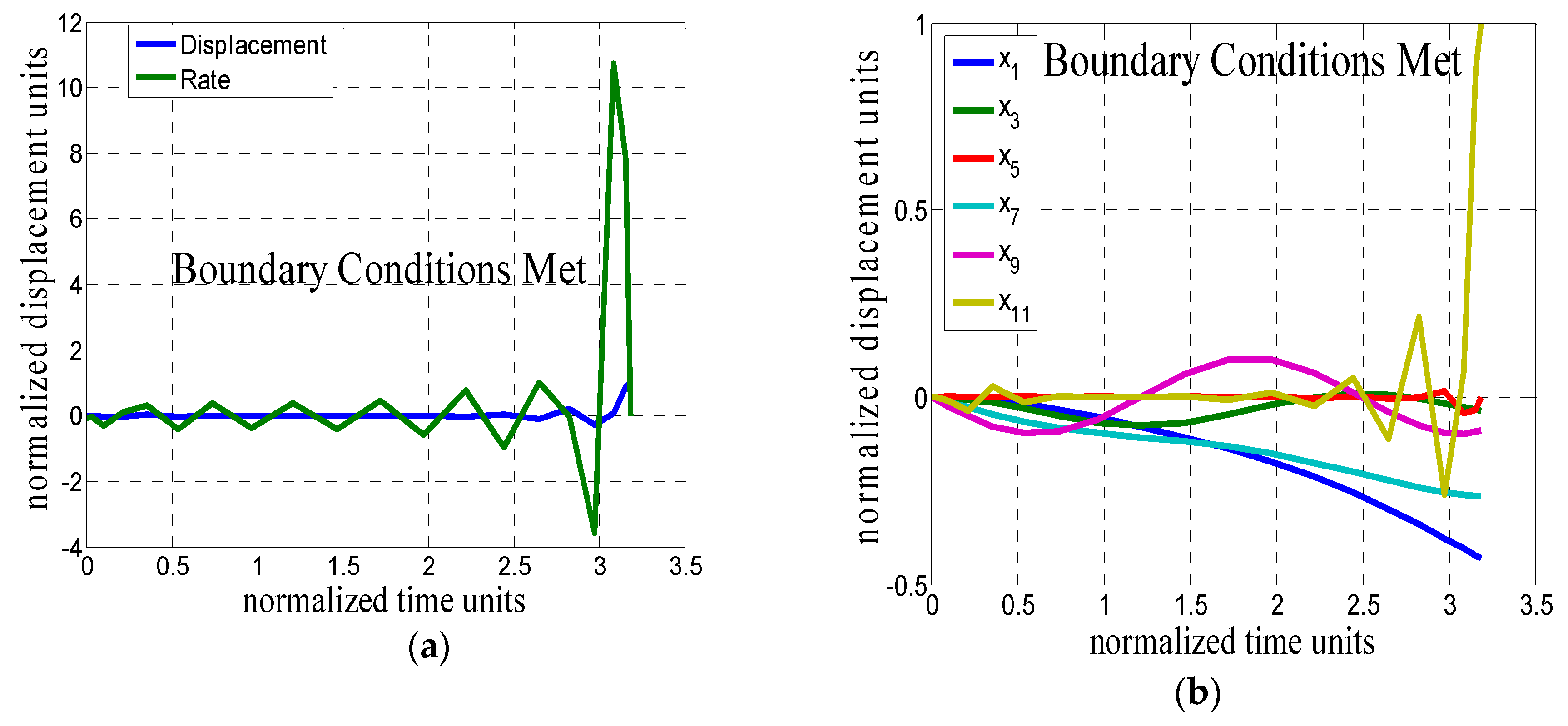
, as depicted in
Figure 4. This keeps the problem in its simplest form. The other nodes are permitted to have any final values, but
x11 must be fixed at
tf to a value of 1 and have no rate. It is entirely possible that the mathematical solution will result in those other nodes’ final states being such that the member retains its original shape. But, that is not forced in this problem formulation.
3.5. Necessary Conditions of Optimality
Per Pontryagin’s minimization principle, write the control Hamiltonian in general terms, specifically as Consider the nonlinear programming case where we wish to implement a control limit. is assumed differentiable where the control set in Equation (35) is given by . The Lagrangian of the Hamiltonian adjoins the control constraint in general terms with a reformatted fundamental optimization problem. Minimize with respect to , subject to . The Lagrangian of the Hamiltonian: specifically, it may be expressed as the following
3.5.1. Minimization Condition
, and the constraint–multiplier pair at each instant of time satisfies the complimentary condition (switching structure of the optimal control):
For this first problem iteration, no control constraint was imposed. After successfully completing this initial problem formulation, a control constraint was added. The minimization of the Lagrangian of the Hamiltonian was used in the necessary conditions of optimality in the subsequent problem analysis. For this analysis, simply apply the minimization condition directly to the control Hamiltonian: such that
3.5.2. Adjoint Equations
If we find an optimal solution, it should satisfy the following conditions: All costates are roughly constant over small changing values of
.
3.5.3. Terminal Transversality Condition
The costate at the final time is transverse with the gradient of the endpoint Lagrangian at the final time.
.
3.5.4. Hamiltonian Final Value Condition
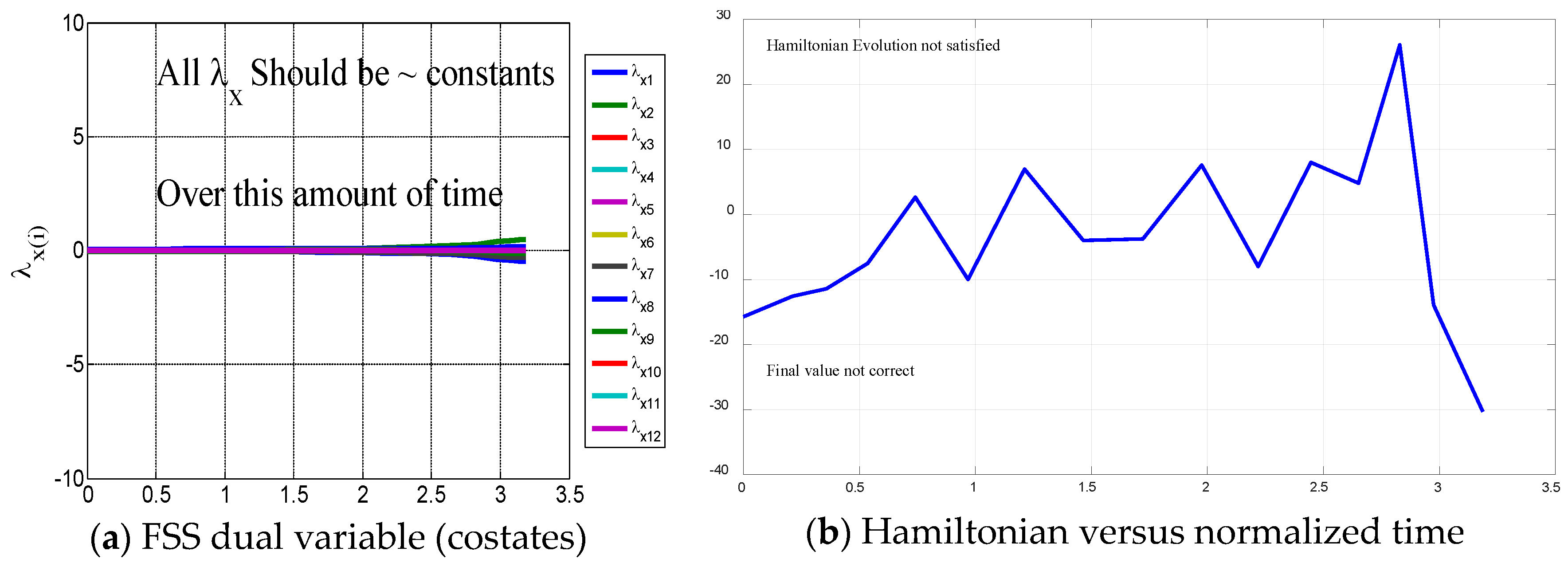
as depicted in
Figure 5.
3.5.5. Hamiltonian Evolution Equation
. So, if we find an optimal solution, it should satisfy the following condition: Hamiltonian should be constant, −1 for all
t as depicted in
Figure 5.
The discovered solution meets most (but not all) of the theoretical optimization criteria. This result could be called astounding. If analysis had stopped at Pontryagin’s principle of minimizing the control Hamiltonian (or the adjoint equation or one of the other successful criteria), we would have rightfully declared an optimal control that is consistent with theory. However, if we had instead chosen the Hamiltonian evolution condition, we would have rightly chosen to declare that we had not found an optimal control consistent with theory. Certainly, both cannot be true.
Therefore this “optimal control” will therefore be referred to as a suboptimal control solution. All the conditions of optimality are met so far except the Hamiltonian value condition. Next, review Bellman’s principle to confirm that this suboptimal solution satisfies that additional criteria. Notice we henceforth refer to the “optimal control” synonymous with “suboptimal control”, since the Hamiltonian evolution equation is not satisfied, despite four other necessary conditions of optimality being met (so far).
3.6. Demonstration of Computational Optimality via Bellman’s Principle
Lemma: The optimal path (x(∙), y(∙), v(∙),u(∙),t(∙)) should lie on the previous suboptimal trajectory if this were the optimal trajectory.
Choosing node 10 from the previous analysis as the new starting point: If DIDO found a suboptimal solution, perhaps there may be some difference in the two trajectories (just as we saw in the necessary conditions for optimality).
>> primal.nodes(10) = 1.4651 … new t(0).
>> primal.states(1,10) = −0.1064 … new x1(0).
>> primal.states(2,10) = 0.1475 … new x2(0).
>> primal.states(3,10) = −0.0683 … new x3(0)
>> primal.states(4,10) = −1.7291 × 10−4 … new x4(0)
>> primal.states(5,10) = 0.0016 … new x5(0)
>> primal.states(6,10) =−1.0705 × 10−5 … new x6(0)
>> primal.states(7,10) = −0.1175 … new x7(0)
>> primal.states(8,10) = 0.1389 … new x8(0)
>> primal.states(9,10) = 0.0600 … new x9(0)
>> primal.states(10,10) = −3.7851 × 10−4 … new x10(0)
>> primal.states(11,10) = 0.0041 … new x11(0)
>> primal.states(12,10) = −1.1934 × 10−5 … new x12(0)
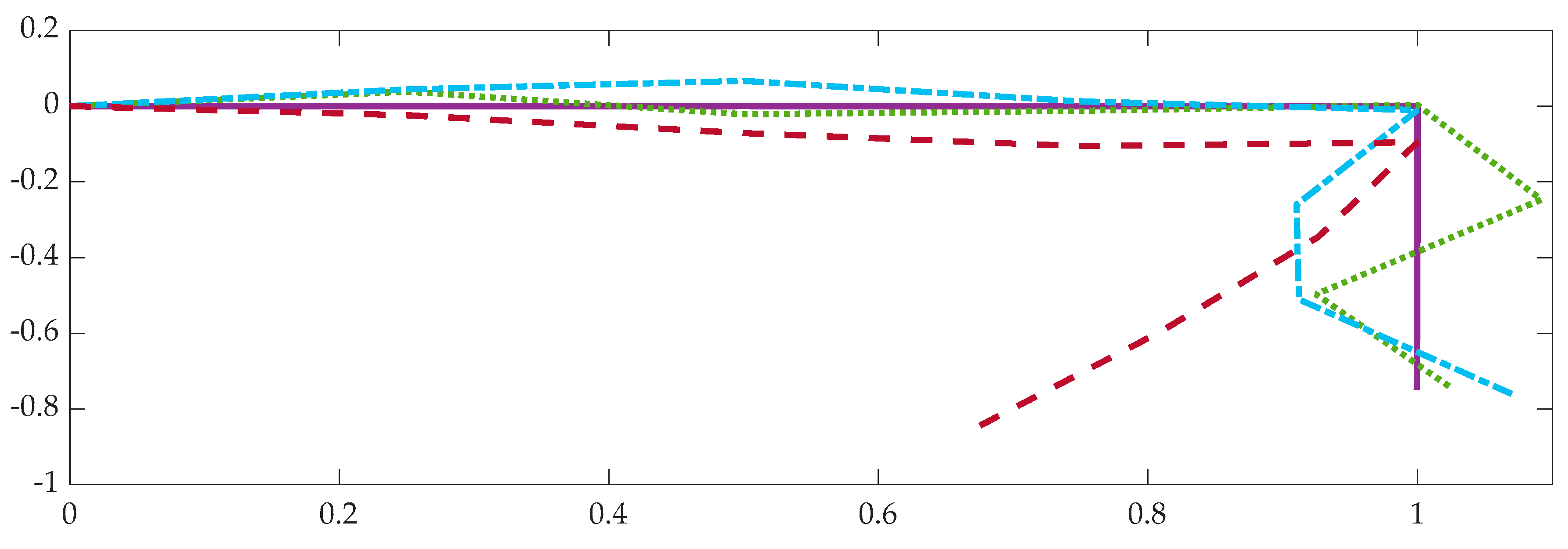
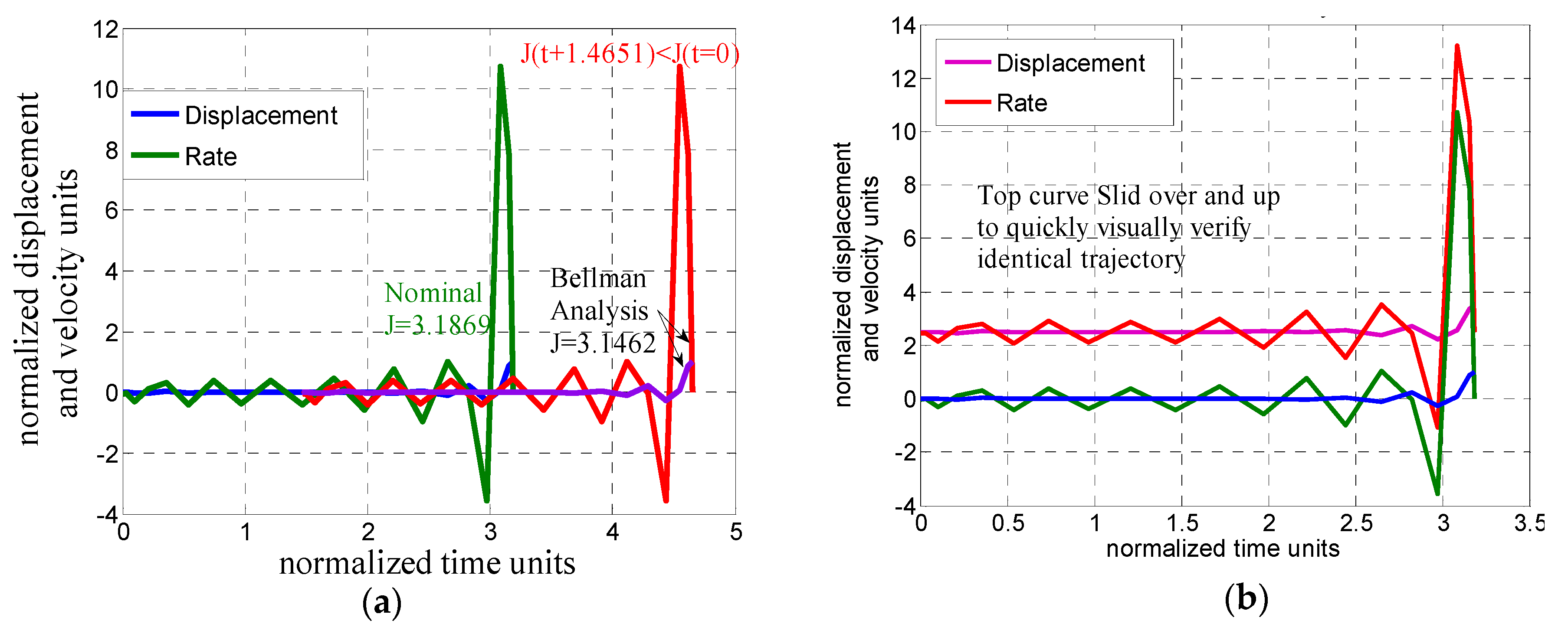
Bellman’s principle holds true for this extremal control. The trajectory is the same and the cost function is less than the previous cost function. Plots containing the trajectories for the nominal zero start point and the Bellman’s analysis are simultaneously displayed in
Figure 6a,b. This helps to quickly see the identical trajectory (slide to the right for the different start point). The results plotted in
Figure 6a,b are identical but plotted differently for heuristic comparison.
Despite not being able to declare the control in
Figure 7 an optimal control in accordance with all theories, even the sub-optimal time of just over 3 s is impressive, especially considering that the extremal control met the zero vibration and derivative requirements.