Effect of Local Grid Refinement on Performance of Scale-Resolving Models for Simulation of Complex External Flows
Abstract
1. Introduction
2. Turbulence Models
2.1. Algebraic WMLES Turbulence Model
2.2. SST-Improved Delayed Detached Eddy Turbulence Model
2.3. The One-Equation SAS Turbulence Model
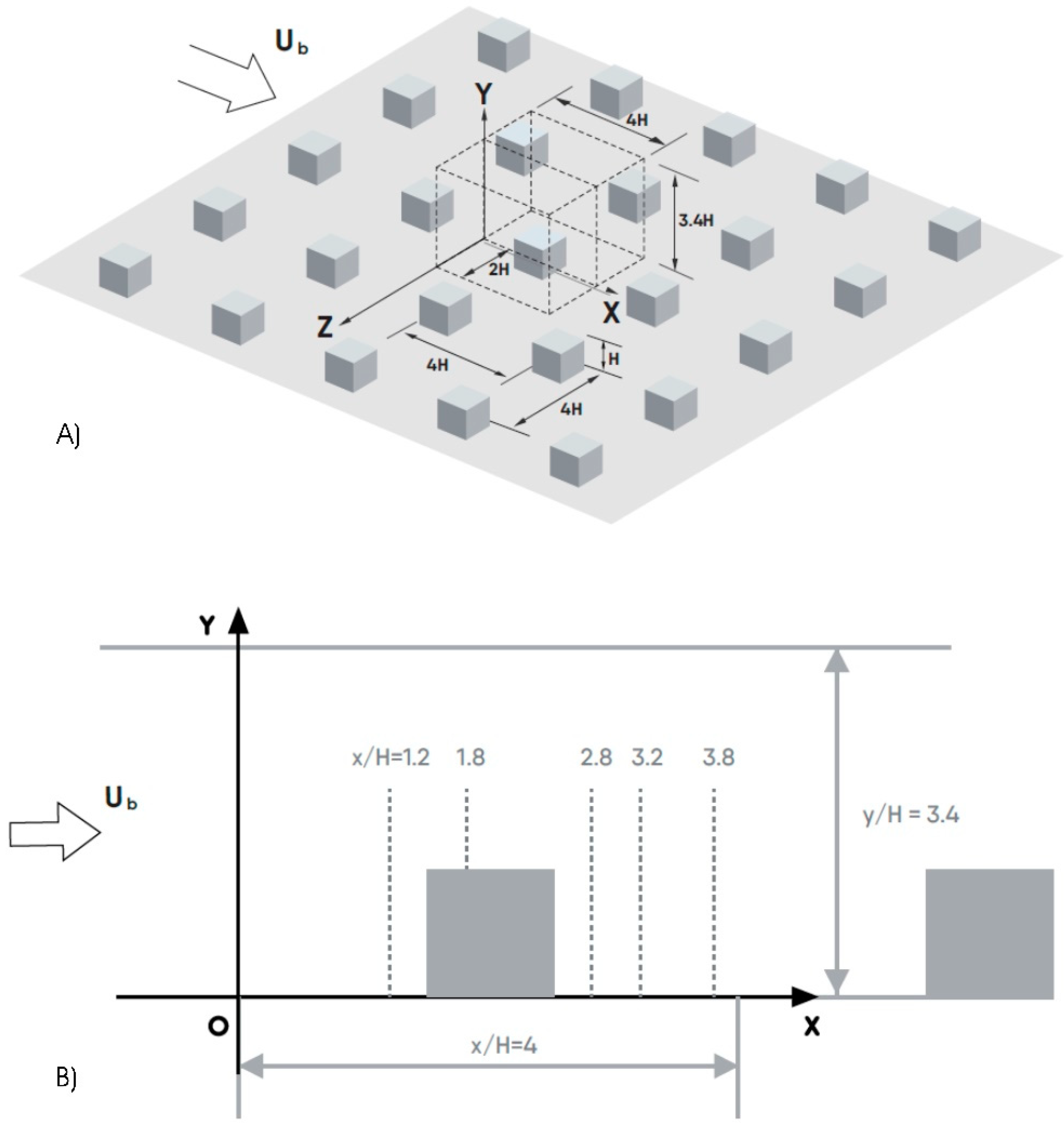
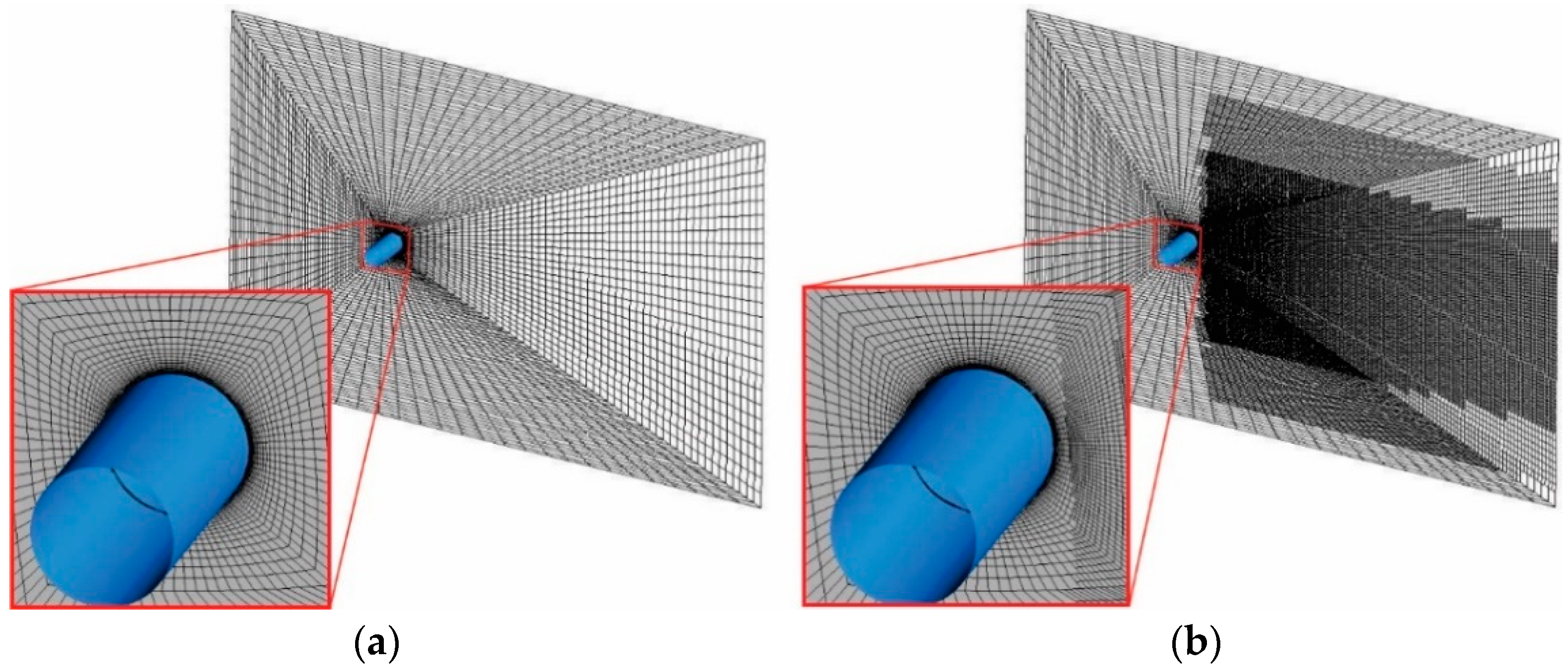
3. Numerical Approach
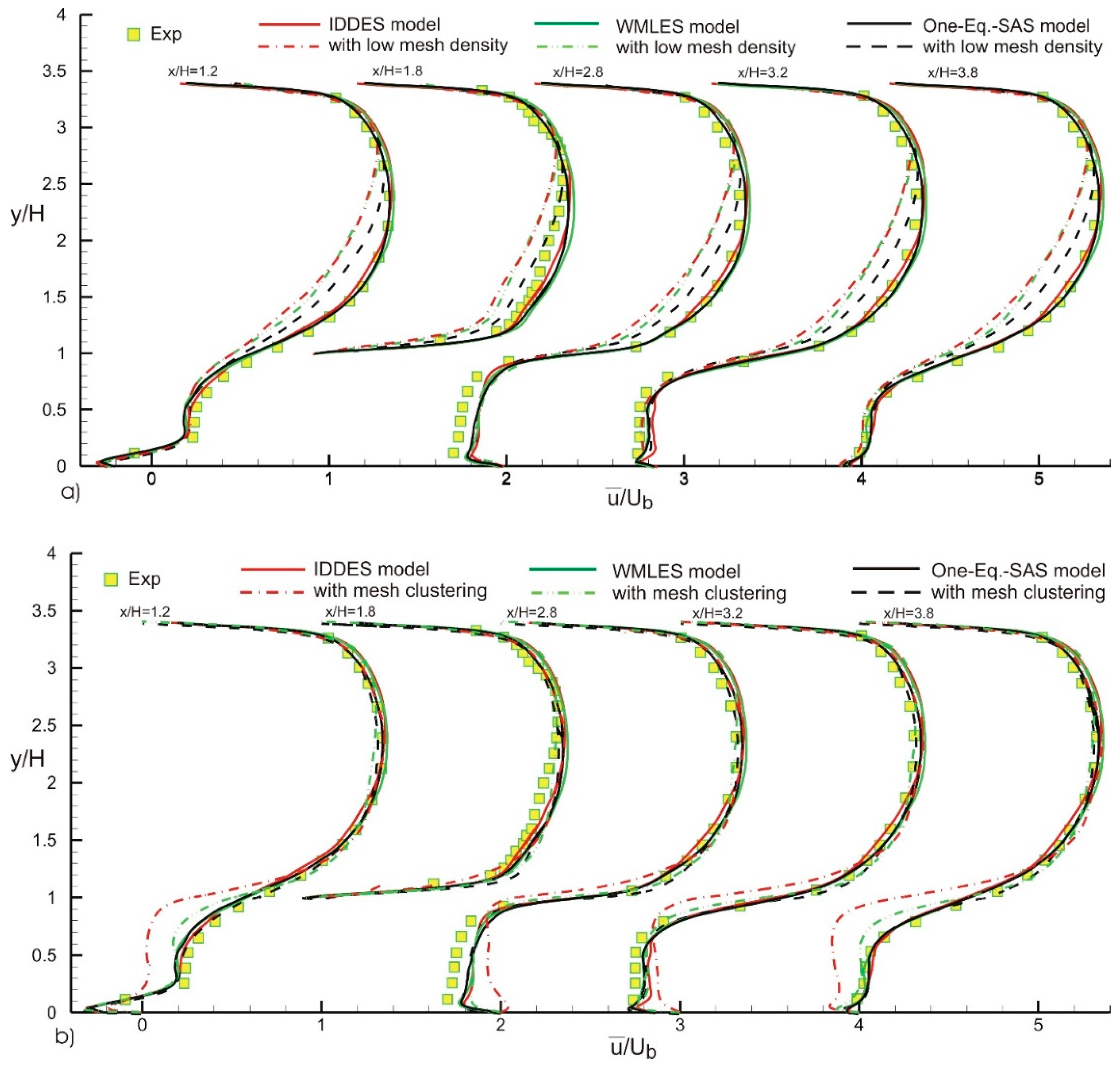
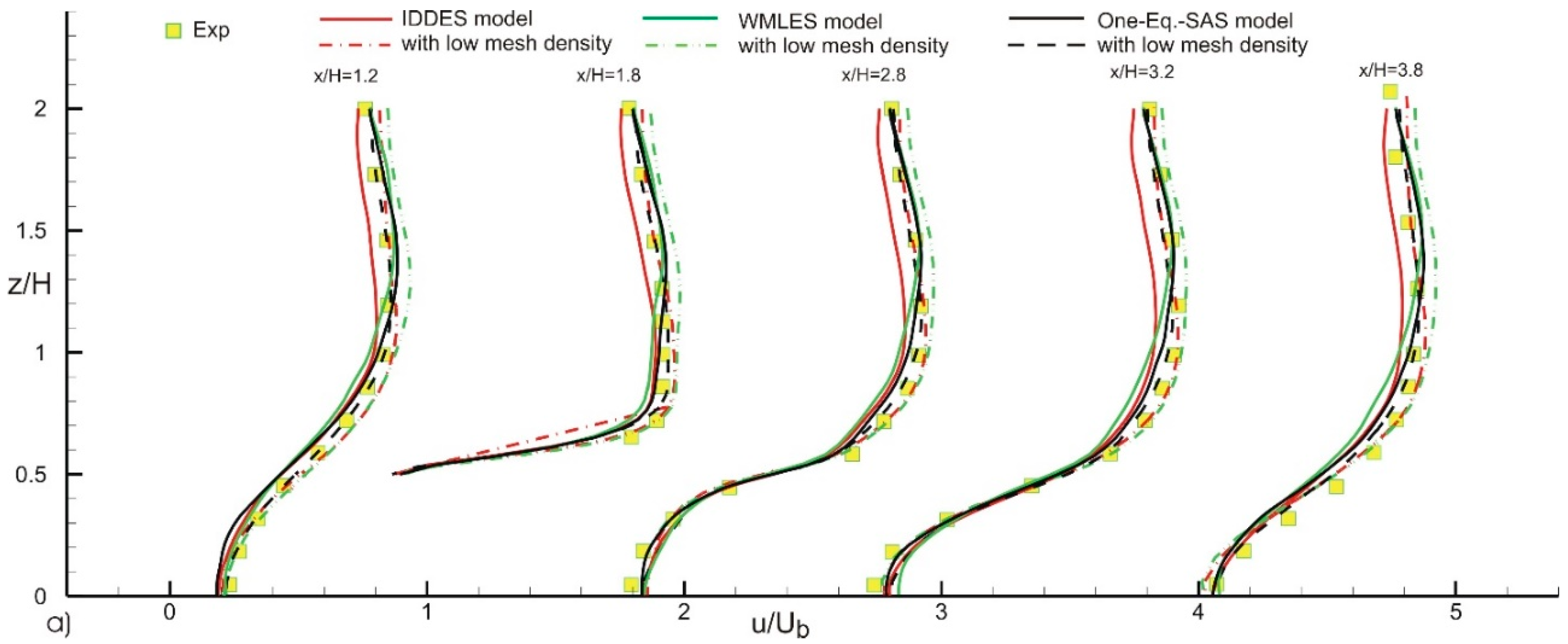
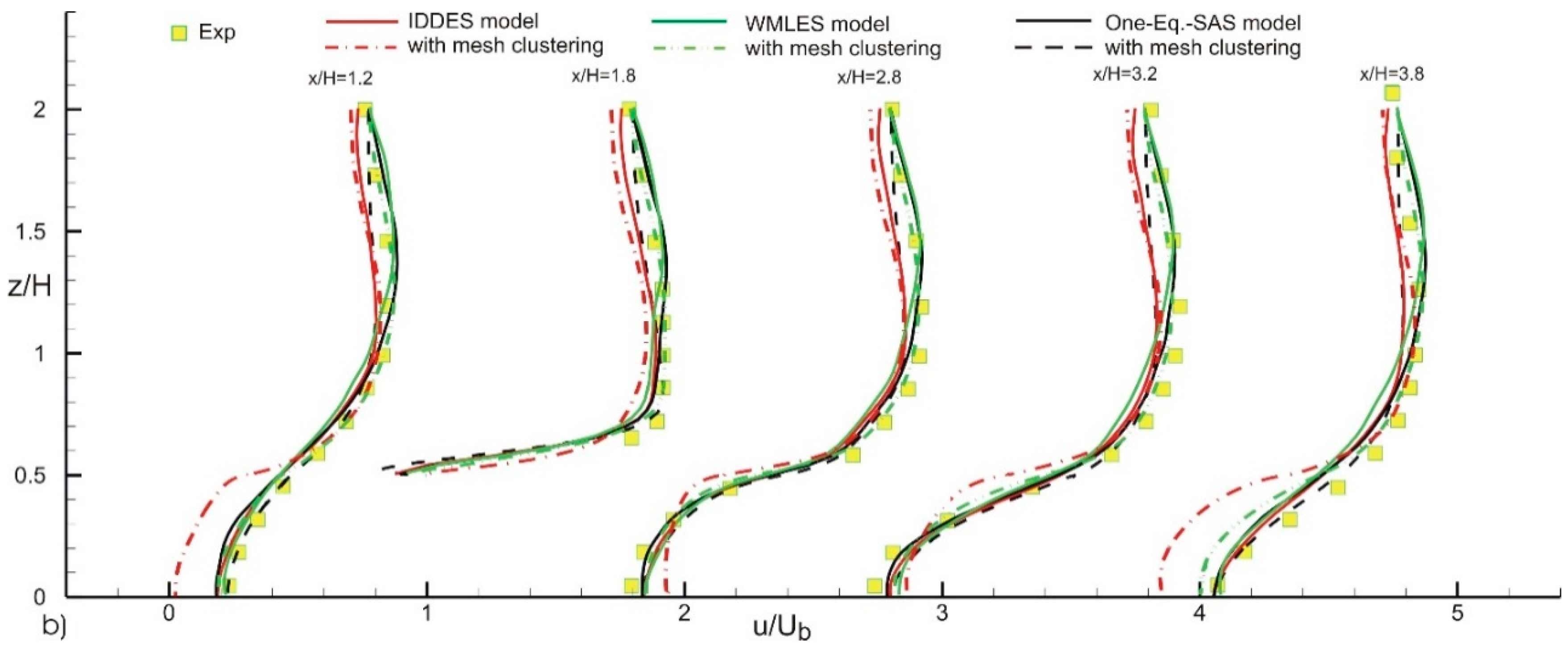
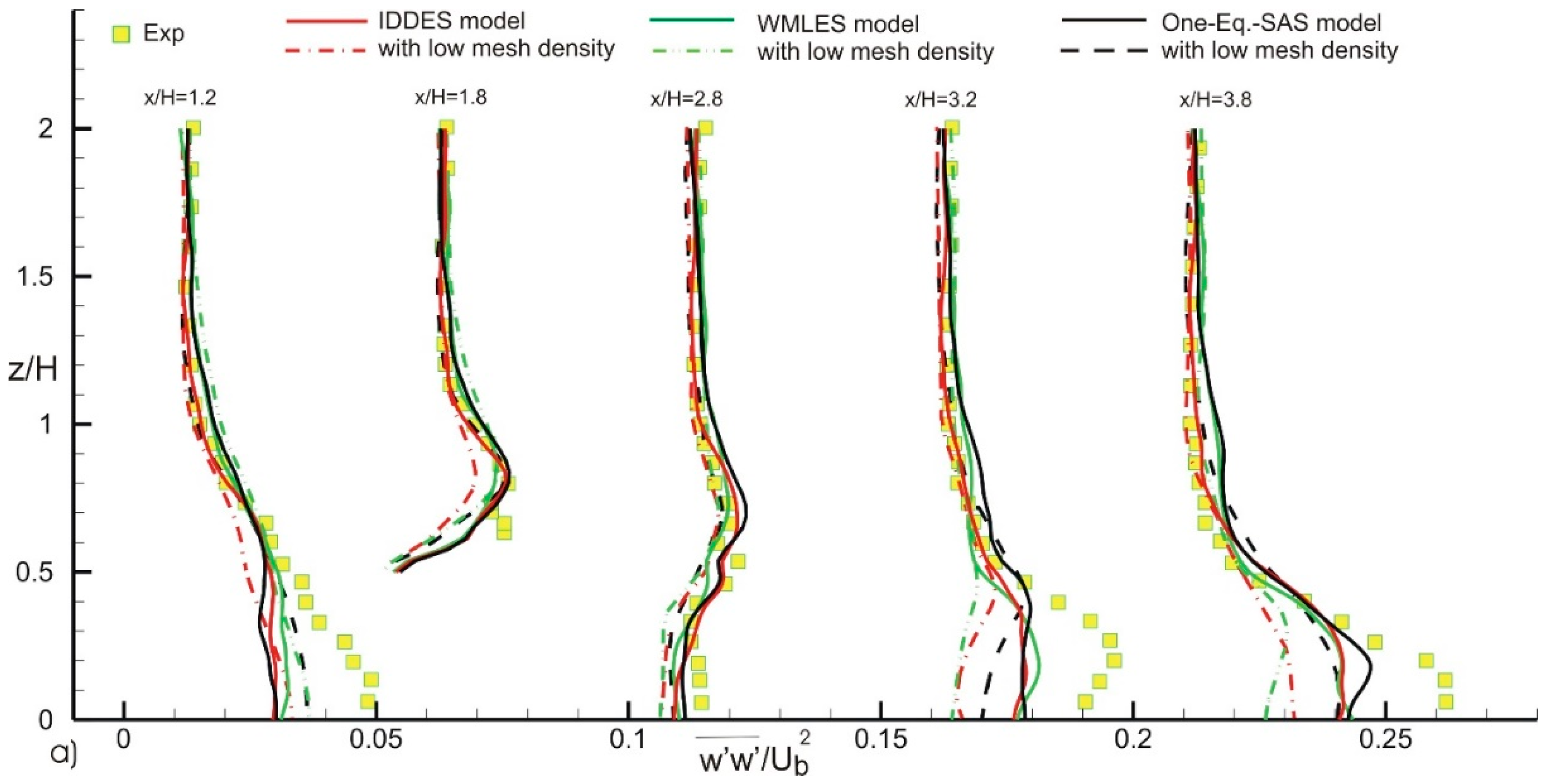
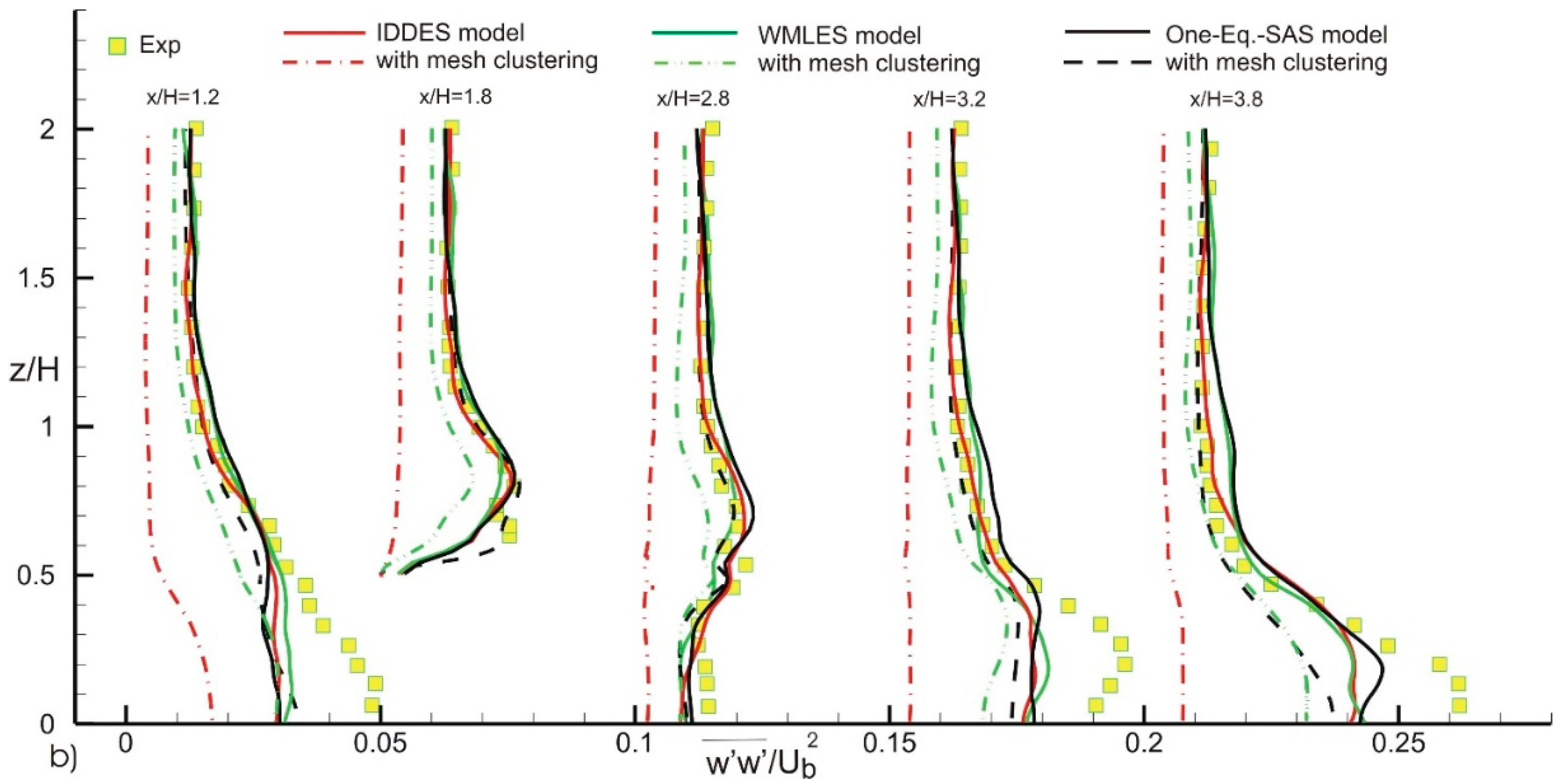
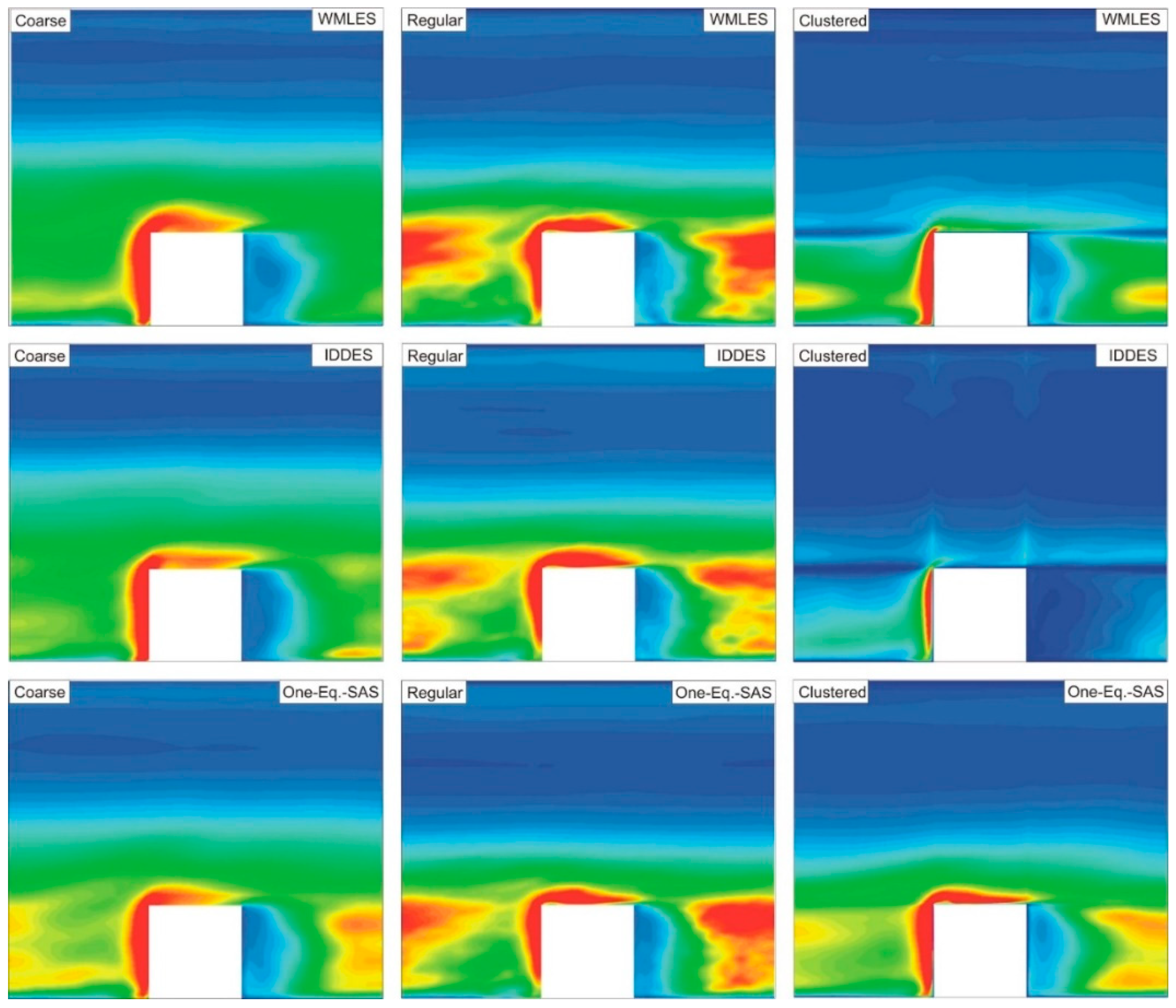
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tominaga, Y.; Stathopoulos, T. CFD Modeling of Pollution Dispersion in Building Array: Evaluation of turbulent scalar flux modeling in RANS model using LES results. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 484–491. [Google Scholar] [CrossRef]
- Wright, N.G.; Easom, G.J. Non-linear k-ε turbulence model results for flow over a building at full-scale. Appl. Math. Model. 2003, 27, 1013–1033. [Google Scholar] [CrossRef]
- Kubilay, A.; Neophytou, M.K.A.; Matsentides, S.; Loizou, M.; Carmeliet, J. The pollutant removal capacity of urban street canyons as quantified by the pollutant exchange velocity. Urban Clim. 2017, 21, 136–153. [Google Scholar] [CrossRef]
- Nazarian, N.; Kleissl, J. CFD simulation of an idealized urban environment: Thermal effects of geometrical characteristics and surface materials. Urban Clim. 2015, 12, 141–159. [Google Scholar] [CrossRef]
- Hu, Z.X.; Cui, G.X.; Zhang, Z.S. Numerical study of mixed convective heat transfer coefficients for building cluster. J. Wind Eng. Ind. Aerodyn. 2018, 172, 170–180. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.G.; Castro, I.P.; Belcher, S.E. Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Bound.-Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Xie, Z.; Castro, I.P. LES and RANS for turbulent flow over arrays of wall-mounted obstacles. Flow Turbul. Combust. 2006, 76, 291–312. [Google Scholar] [CrossRef]
- Basara, B. Fluid flow and conjugate heat transfer in a matrix of surface-mounted cubes: A PANS study. Int. J. Heat Fluid Flow 2015, 51, 166–174. [Google Scholar] [CrossRef]
- Cheng, Y.; Lien, F.S.; Yee, E.; Sinclair, R. A comparison of large Eddy simulations with a standard k-ε Reynolds-averaged Navier-Stokes model for the prediction of a fully developed turbulent flow over a matrix of cubes. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1301–1328. [Google Scholar] [CrossRef]
- Goodfriend, E.; Chow, F.K.; Vanella, M.; Balaras, E. Large-Eddy Simulation of Flow Through an Array of Cubes with Local Grid Refinement. Bound.-Layer Meteorol. 2016, 159, 285–303. [Google Scholar] [CrossRef]
- Razak, A.A.; Hagishima, A.; Ikegaya, N.; Tanimoto, J. Analysis of airflow over building arrays for assessment of urban wind environment. Build. Environ. 2013, 59, 56–65. [Google Scholar] [CrossRef]
- Moonen, P.; Dorer, V.; Carmeliet, J. Effect of flow unsteadiness on the mean wind flow pattern in an idealized urban environment. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 389–396. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Stathopoulos, T.; van Heijst, G.J.F. CFD simulation of near-field pollutant dispersion on a high-resolution grid: A case study by LES and RANS for a building group in downtown Montreal. Atmos. Environ. 2011, 45, 428–438. [Google Scholar] [CrossRef]
- Calhoun, R.; Gouveia, F.; Shinn, J.; Chan, S.; Stevens, D.; Lee, R.; Leone, J. Flow around a Complex Building: Experimental and Large-Eddy Simulation Comparisons. J. Appl. Meteorol. 2005, 44, 571–590. [Google Scholar] [CrossRef]
- Ricciardelli, F.; Polimeno, S. Some characteristics of the wind flow in the lower Urban Boundary Layer. J. Wind Eng. Ind. Aerodyn. 2006, 94, 815–832. [Google Scholar] [CrossRef]
- Lateb, M.; Meroney, R.N.; Yataghene, M.; Fellouah, H.; Saleh, F.; Boufadel, M.C. On the use of numerical modelling for near-field pollutant dispersion in urban environments—A review. Environ. Pollut. 2016, 208, 271–283. [Google Scholar] [CrossRef]
- Stathopoulos, T. Computational wind engineering: Past achievements and future challenges. J. Wind Eng. Ind. Aerodyn. 1997, 67–68, 509–532. [Google Scholar] [CrossRef]
- Santiago, A.D.J.L.; Martin, A.M.F.; Pinelli, A. Comparison Between Large-Eddy Simulation and Reynolds-Averaged Navier—Stokes Computations for the MUST Field Experiment. Part II: Effects of Incident Wind Angle Deviation on the Mean Flow and Plume Dispersion. Bound.-Layer Meteorol. 2010, 135, 133–150. [Google Scholar] [CrossRef]
- Mohamed, S.; Buccolieri, R.; Chan, A.; Di, S. Numerical simulation of atmospheric pollutant dispersion in an urban street canyon: Comparison between RANS and LES. J. Wind Eng. Ind. Aerodyn. 2011, 99, 103–113. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD modeling of pollution dispersion in a street canyon: Comparison between LES and RANS. J. Wind Eng. Ind. Aerodyn. 2011, 99, 340–348. [Google Scholar] [CrossRef]
- Xie, Z.; Castro, I.P. Large-eddy simulation for flow and dispersion in urban streets. Atmos. Environ. 2009, 43, 2174–2185. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Comparison of various types of k–ε models. Atmos. Environ. 2009, 43, 3200–3210. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD simulation of near-field pollutant dispersion in the urban environment: A review of current modeling techniques. Atmos. Environ. 2013, 79, 716–730. [Google Scholar] [CrossRef]
- Longo, R.; Ferrarotti, M.; Sánchez, C.G.; Derudi, M.; Parente, A. Advanced turbulence models and boundary conditions for flows around different configurations of ground-mounted buildings. J. Wind Eng. Ind. Aerodyn. 2017, 167, 160–182. [Google Scholar] [CrossRef]
- Piomelli, B.U.; Kang, S.; Ham, F.; Iaccarino, G. Effect of Discontinuous Filter Width in Large-Eddy Simulations of Plane Channel Flow. In Center for Turbulence Research Proceedings of the Summer Program 2006, Stanford University, CA, USA, 9 July–4 August 2006. [Google Scholar]
- Vanella, M.; Piomelli, U.; Balaras, E. Effect of grid discontinuities on large-eddy simulation statistics and flow fields. J. Turbul. 2008, 9, 5248. [Google Scholar] [CrossRef]
- Elkhoury, M.; Elcheik, A. Scale-resolving simulation of flow through a periodic array of cubes. WIT Trans. Eng. Sci. 2018, 120, 161–172. [Google Scholar] [CrossRef]
- Menter, F.; Kuntz, M.; Bender, R. A Scale-Adaptive Simulation Model for Turbulent Flow Predictions. In Proceedings of the 41st Aerospace Sciences Meeting Exhibit, Reno, NV, USA, 6–9 January 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Menter, F.R. Eddy Viscosity Transport Equations and Their Relation to the k-ε Model. J. Fluids Eng. 1997, 119, 876–884. [Google Scholar] [CrossRef]
- Elkhoury, M. Assessment and Modification of One-Equation Models of Turbulence for Wall-Bounded Flows. J. Fluids Eng. 2007, 129, 921–928. [Google Scholar] [CrossRef]
- Elkhoury, M. Modified Menter Model in Comparison with Recently Developed Single-Equation Turbulence Closures. AIAA J. 2011, 49, 1399–1408. [Google Scholar] [CrossRef]
- Elkhoury, M. A low-Reynolds-number one-equation model of turbulence. Aeronaut. J. 2008, 112, 101–108. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Menter, F.; Egorov, Y. A Scale Adaptive Simulation Model using Two-Equation Models. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting Exhibit, Reno, NV, USA, 10–13 January 2005; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. [Google Scholar] [CrossRef]
- Elkhoury, M. Partially Lagging One-Equation Turbulence Model. AIAA J. 2015, 53, 3661–3673. [Google Scholar] [CrossRef]
- Albring, W. J. C. Rotta, Turbulente Strömungen. (Leitfäden der angewandten Mathematik und Mechanik, Band 15). 267 S. m. 104 Fig. Stuttgart 1972. B. G. Teubner. Preis geb. 68,—DM. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 1974, 54, 129–130. [Google Scholar] [CrossRef]
- ANSYS® Academic Research Mechanical. Release 18.1. Canonsburg, PA 15317, USA.
- Chorin, A.J. Numerical Solution of the Navier-Stokes Equations. Math. Comput. 1968, 22, 745. [Google Scholar] [CrossRef]
- Dejoan, A.; Leschziner, M.A. Large eddy simulation of a plane turbulent wall jet. Phys. Fluids 2005, 17, 025102. [Google Scholar] [CrossRef]
- Akselvoll, K.; Moin, P. Large-eddy simulation of turbulent confined coannular jets. J. Fluid Mech. 1996, 315, 387–411. [Google Scholar] [CrossRef]
- Eggels, J.G.M.; Unger, F.; Weiss, M.H.; Westerweel, J.; Adrian, R.; Friedrich, R.; Nieuwstadt, F.T.M. Fully Developed Turbulent Pipe Flow: A Comparison Between Direct Numerical Simulation and Experiment. J. Fluid Mech. 1994, 268, 175–210. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P.; Kim, J. Turbulent Drag Reduction: Studies of Feedback Control and Flow over Riblets; Tech. Rep. Report TF-55; Stanford, CA, USA, 1992. [Google Scholar]
- Boersma, B.J.A.; Brethouwer, G.A.; Nieuwstadt, F.T.M.A. A numerical investigation on the effect of the inflow conditions on the self-similar region of a round jet. Phys. Fluids 1998, 10, 899–909. [Google Scholar] [CrossRef]
- Pierce, C.D.; Moin, P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H. Large eddy simulation of a circular jet: Effect of inflow conditions on the near field. J. Fluid Mech. 2009, 620, 383–411. [Google Scholar] [CrossRef]
- Elkhoury, M. Assessment of turbulence models for the simulation of turbulent flows past bluff bodies. J. Wind Eng. Ind. Aerodyn. 2016, 154, 10–20. [Google Scholar] [CrossRef]
- Meinders, E.R. Experimental Study of Heat Transfer in Turbulent Flows over Wall-Mounted Cubes; Delft University of Technology: Delft, The Netherlands, 1998. [Google Scholar]
- Meinders, E.R.; Hanjalić, K. Vortex structure and heat transfer in turbulent flow over a wall-mounted matrix of cubes. Int. J. Heat Fluid Flow 1999, 20, 255–267. [Google Scholar] [CrossRef]
- Spalart, R. Young-Person’s Guide Simulation Grids Detached-Eddy; NASA: Hampton, VA, USA, 2001.
- Hsieh, K.-J.; Lien, F.-S.; Yee, E. Towards a Unified Turbulence Simulation Approach for Wall-Bounded Flows. Flow Turbul. Combust. 2010, 84, 193. [Google Scholar] [CrossRef]
- Yang, X.I.A.; Sadique, J.; Mittal, R.; Meneveau, C. Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 2015, 27, 25112. [Google Scholar] [CrossRef]
- Zheng, W.; Yan, C.; Liu, H.; Luo, D. Comparative assessment of SAS and DES turbulence modeling for massively separated flows. Acta Mech. Sin. 2016, 32, 12–21. [Google Scholar] [CrossRef]
- Cantwell, B.; Coles, D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 1983, 136, 321. [Google Scholar] [CrossRef]
- Catalano, P. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. Int. J. Heat Fluid Flow 2003, 24, 463–469. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P. Detached-eddy simulations past a circular cylinder. Flow Turbul. Combust. 2000, 63, 293–313. [Google Scholar] [CrossRef]

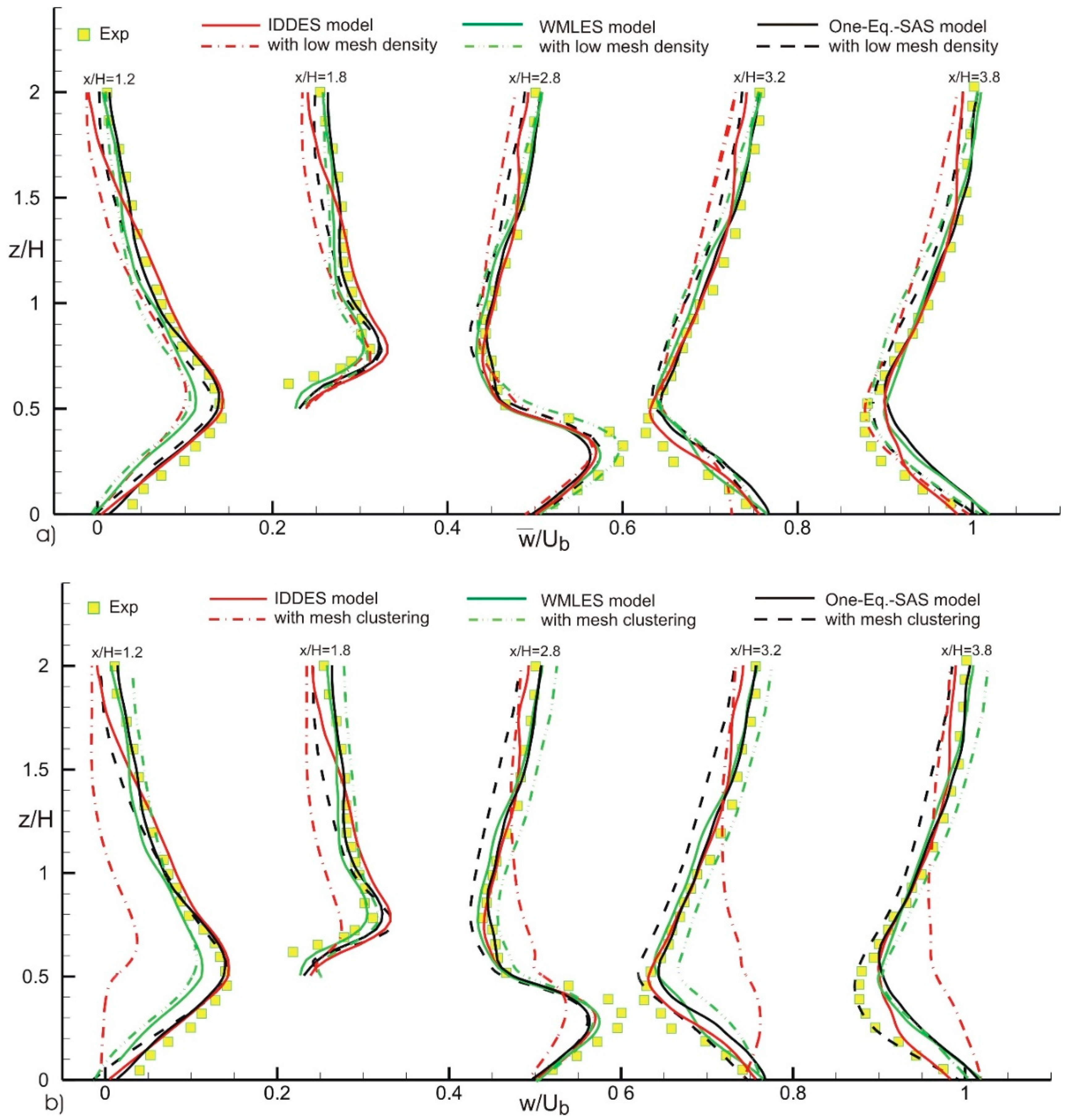
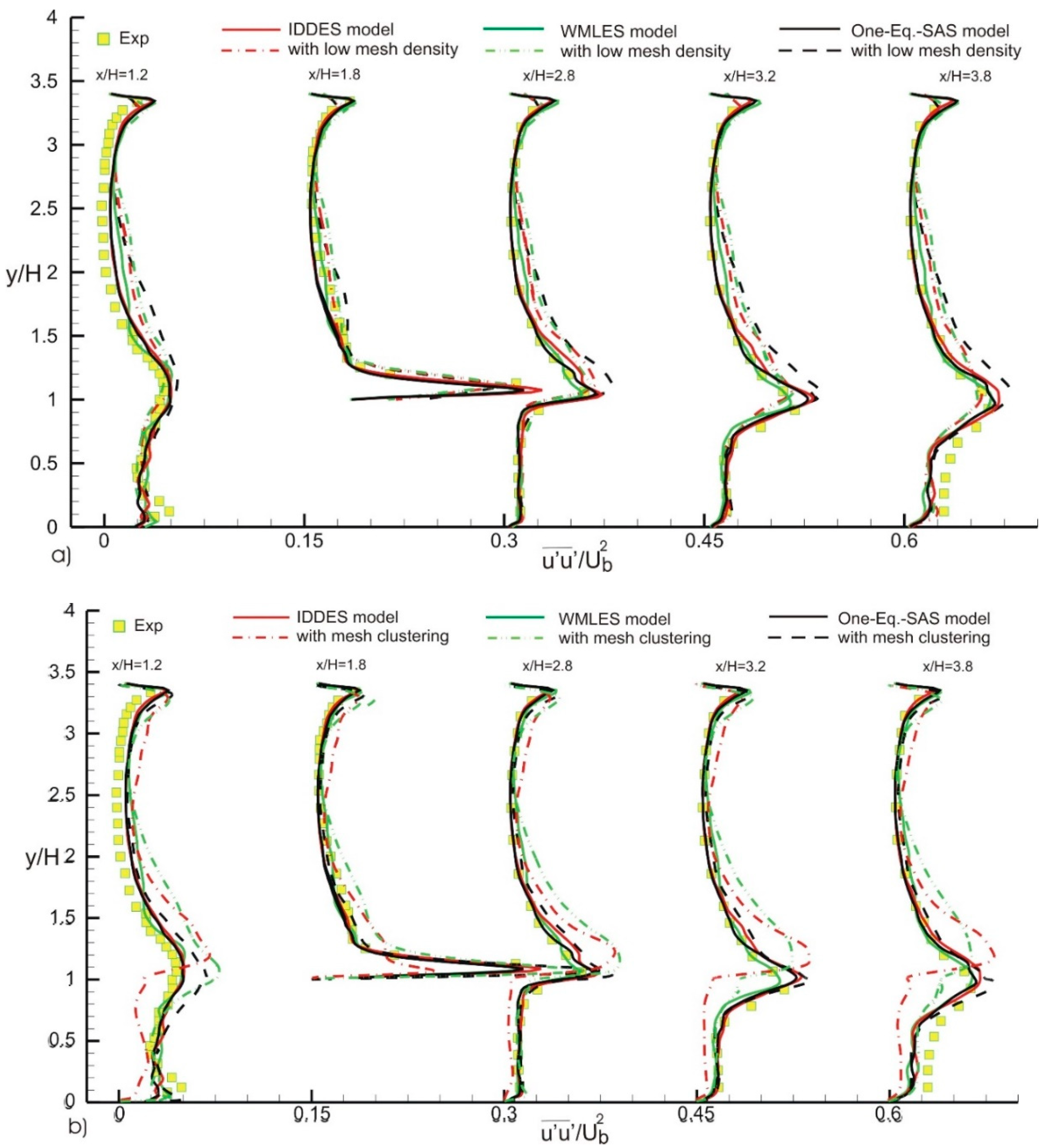
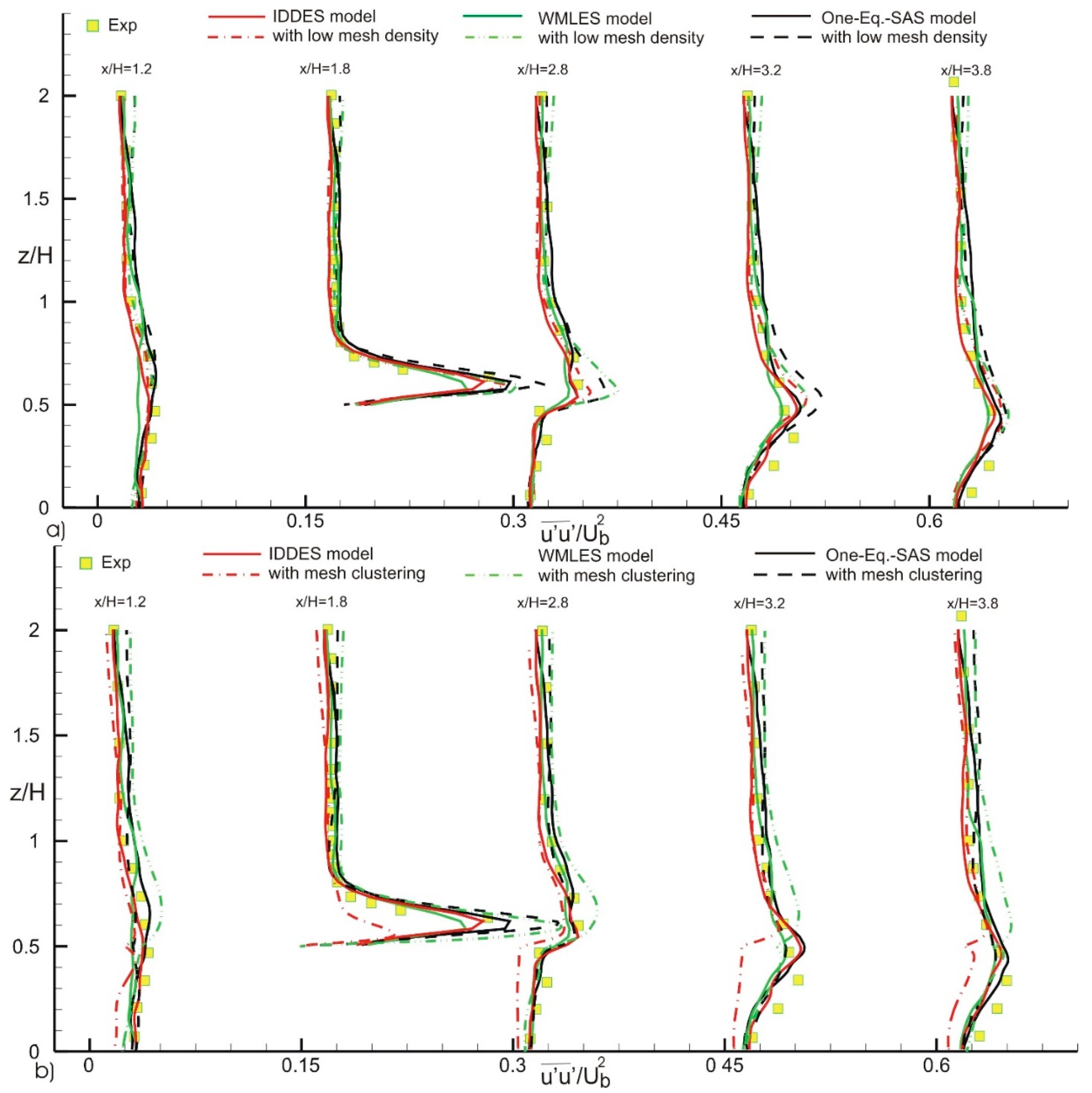
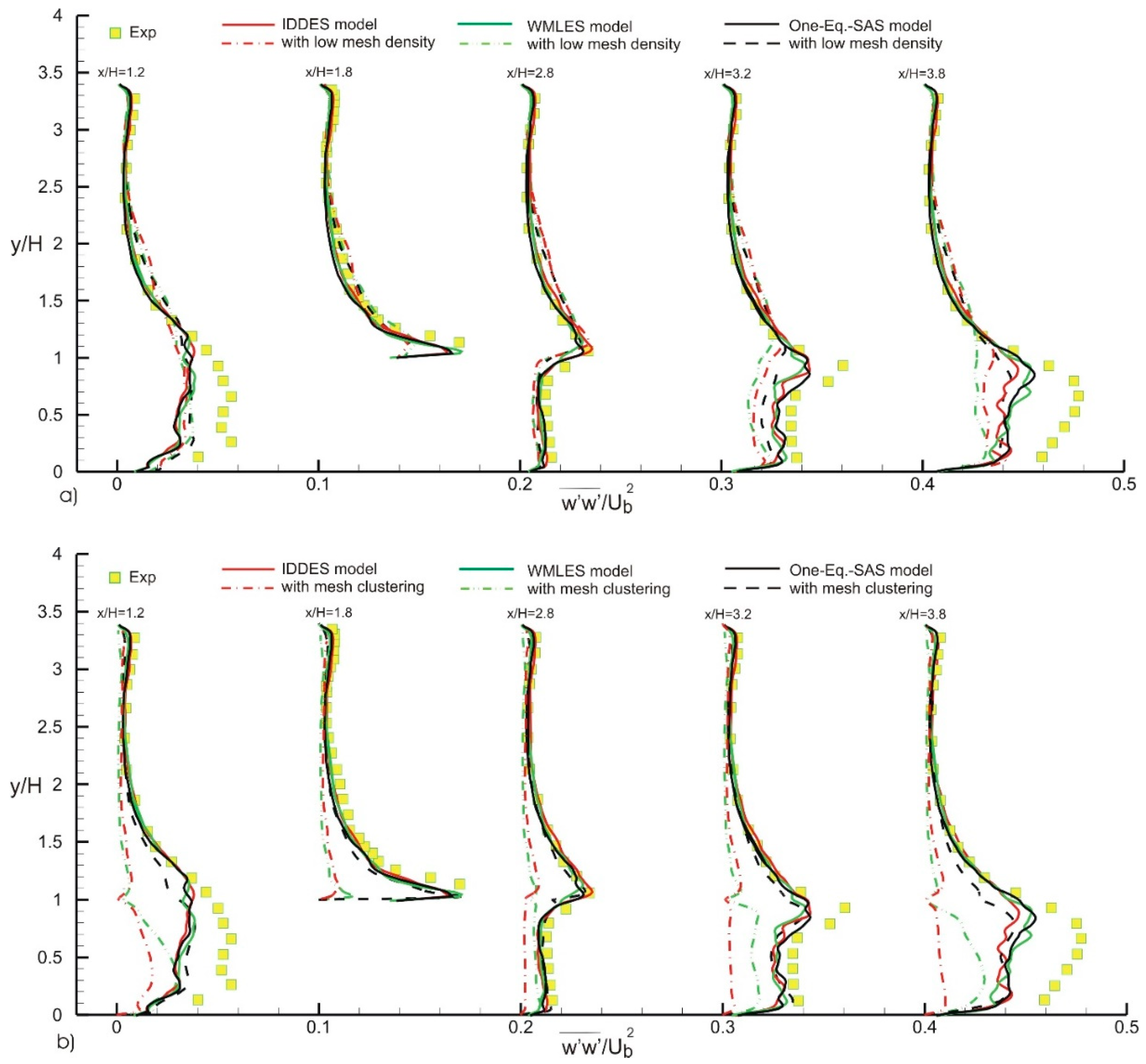
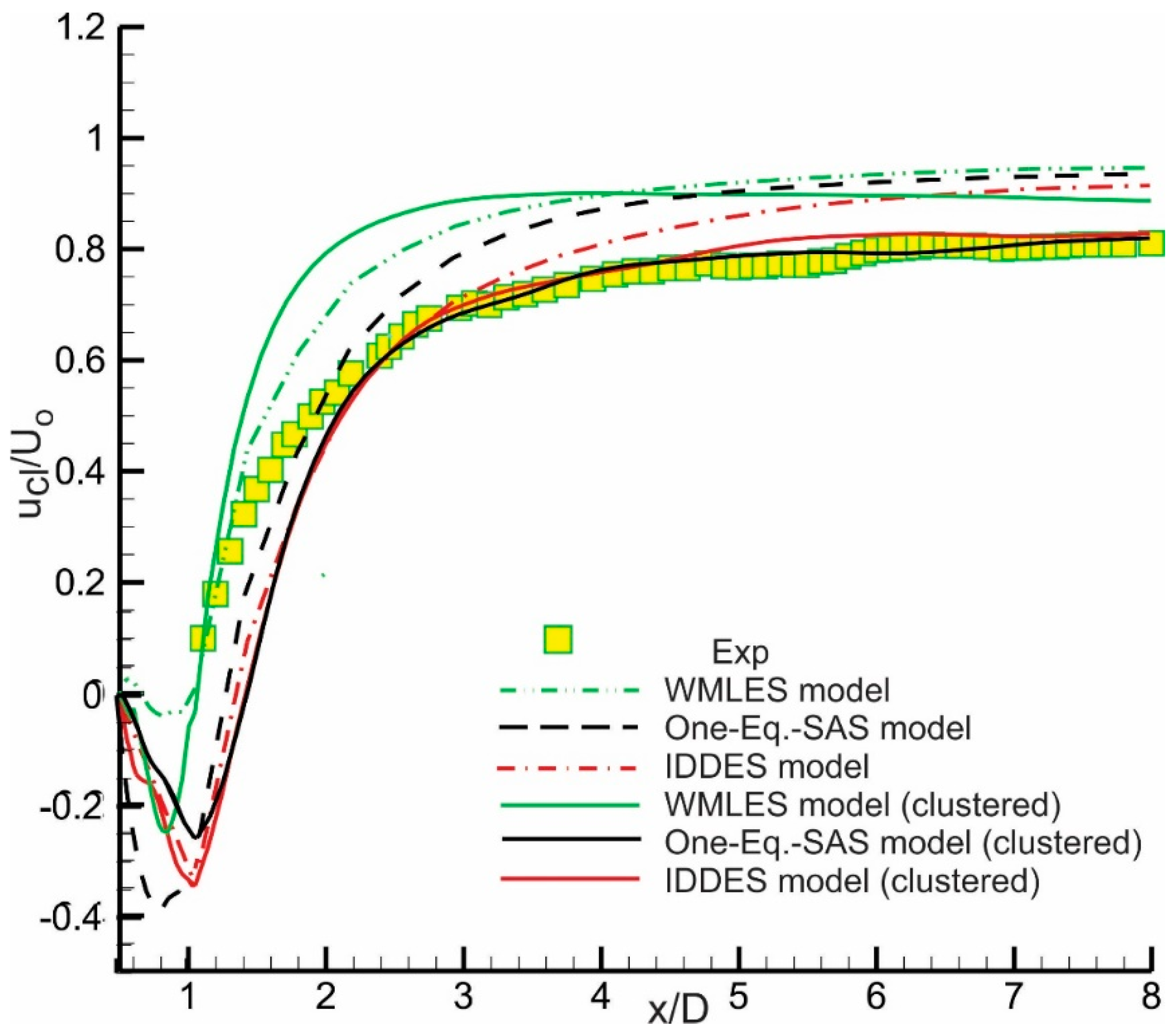
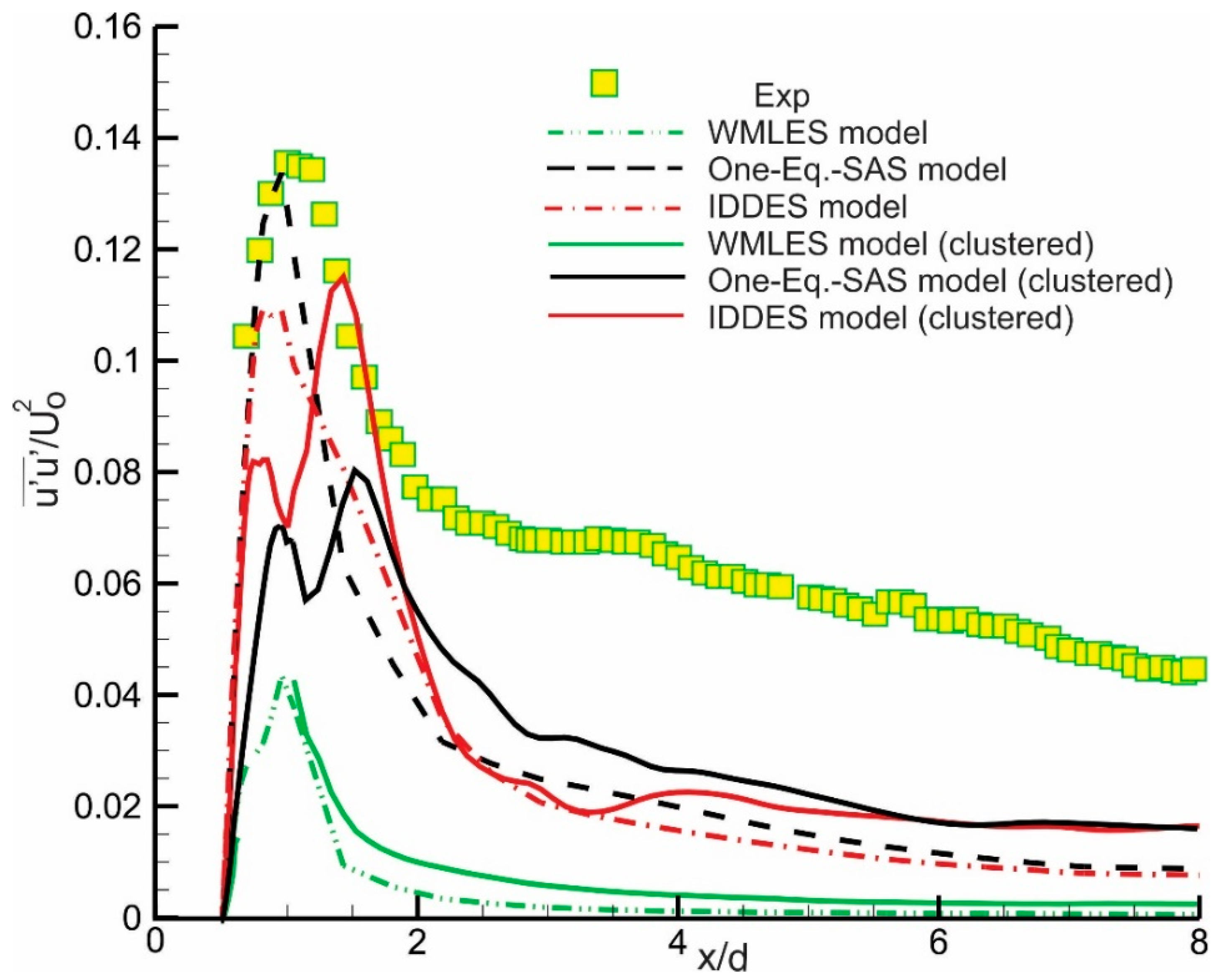
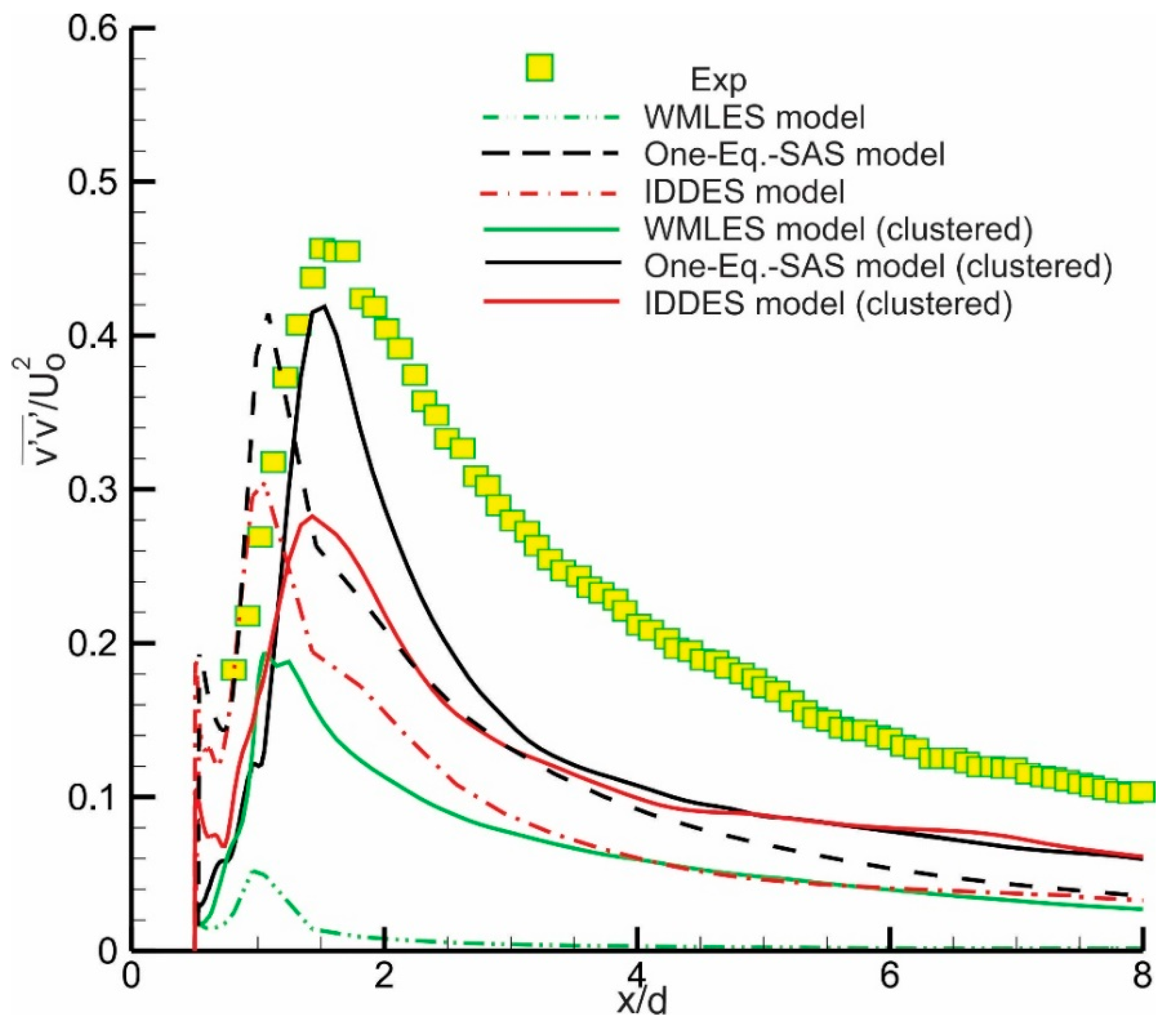
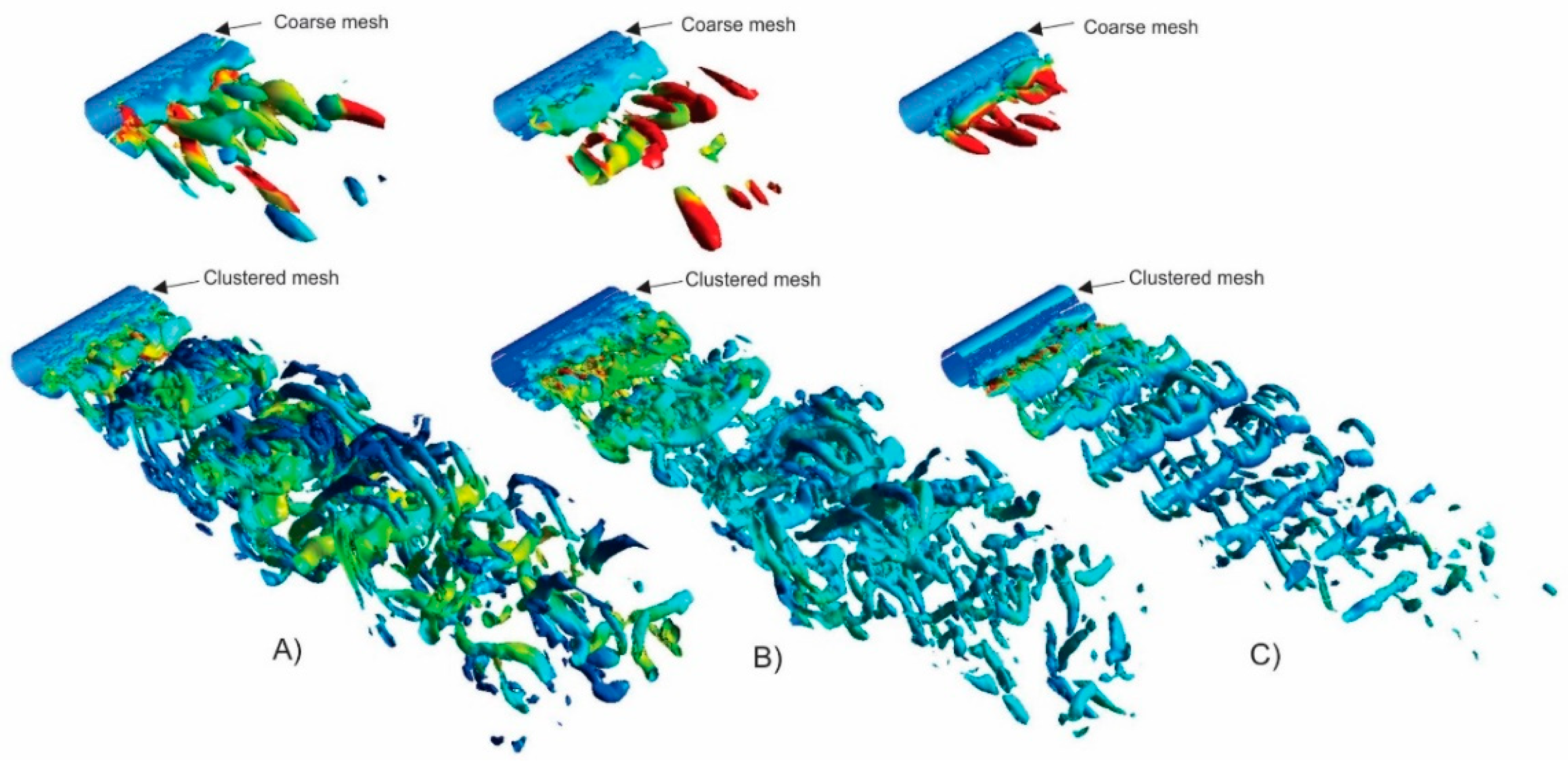
| Contributor | Model | Grid, Nx, Ny, Nz | Number of Points on Cube Side |
|---|---|---|---|
| Hsieh et al. (2010) [50] | LES-Standard Smogarinsky, PANS, k-ε RANS | 49 × 49 × 49 | -- |
| Yang et al. (2015) [51] | Integral wall-modeled LES | 32 × 32 × 32 | 8 |
| Goodfriend et al. (2016) | LES-Standard and mixed model | 84 × 96 × 84 | 28 |
| Present | Wmles | 55 × 45 × 55 | 15 |
| SST-IDDES | 150 × 180 × 150 | 70 | |
| One-Equation SAS | 150 × 180 × 150 Clustered | 70 |
| Model | Uniform Coarse-Mesh | Uniform Fine Mesh | Non-Uniform Clustered Mesh | |
|---|---|---|---|---|
| WMLES | y+ | 8.66 | 5.27 | 0.699 |
| SST-IDDES | 8.14 | 5.5 | 0.648 | |
| One-Equation SAS | 8.5 | 5.05 | 0.568 | |
| Growth Rate | 1.088 | 1 | 1.1727 | |
| ∆+(∆/H) | 0.012 | 0.0085(vertical direction) 0.01(horizontal direction) | 0.0002 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
ElCheikh, A.; ElKhoury, M. Effect of Local Grid Refinement on Performance of Scale-Resolving Models for Simulation of Complex External Flows. Aerospace 2019, 6, 86. https://doi.org/10.3390/aerospace6080086
ElCheikh A, ElKhoury M. Effect of Local Grid Refinement on Performance of Scale-Resolving Models for Simulation of Complex External Flows. Aerospace. 2019; 6(8):86. https://doi.org/10.3390/aerospace6080086
Chicago/Turabian StyleElCheikh, Amne, and Michel ElKhoury. 2019. "Effect of Local Grid Refinement on Performance of Scale-Resolving Models for Simulation of Complex External Flows" Aerospace 6, no. 8: 86. https://doi.org/10.3390/aerospace6080086
APA StyleElCheikh, A., & ElKhoury, M. (2019). Effect of Local Grid Refinement on Performance of Scale-Resolving Models for Simulation of Complex External Flows. Aerospace, 6(8), 86. https://doi.org/10.3390/aerospace6080086





