Numerical Simulations of Combustion Instabilities in a Combustor with an Augmentor-Like Geometry
Abstract
1. Introduction
2. Approach
2.1. Governing Equations
2.2. Numerical Method
2.3. Configuration
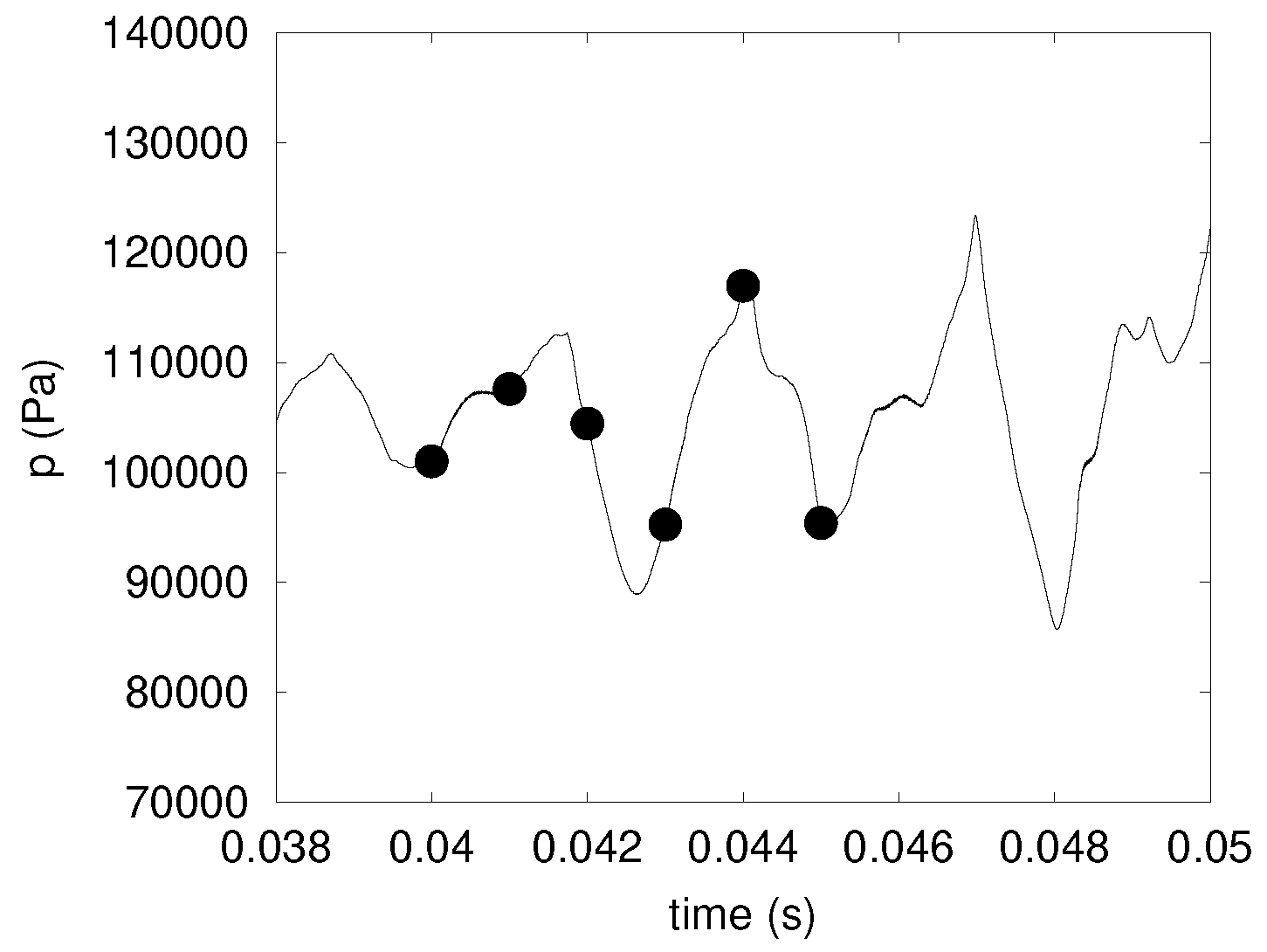
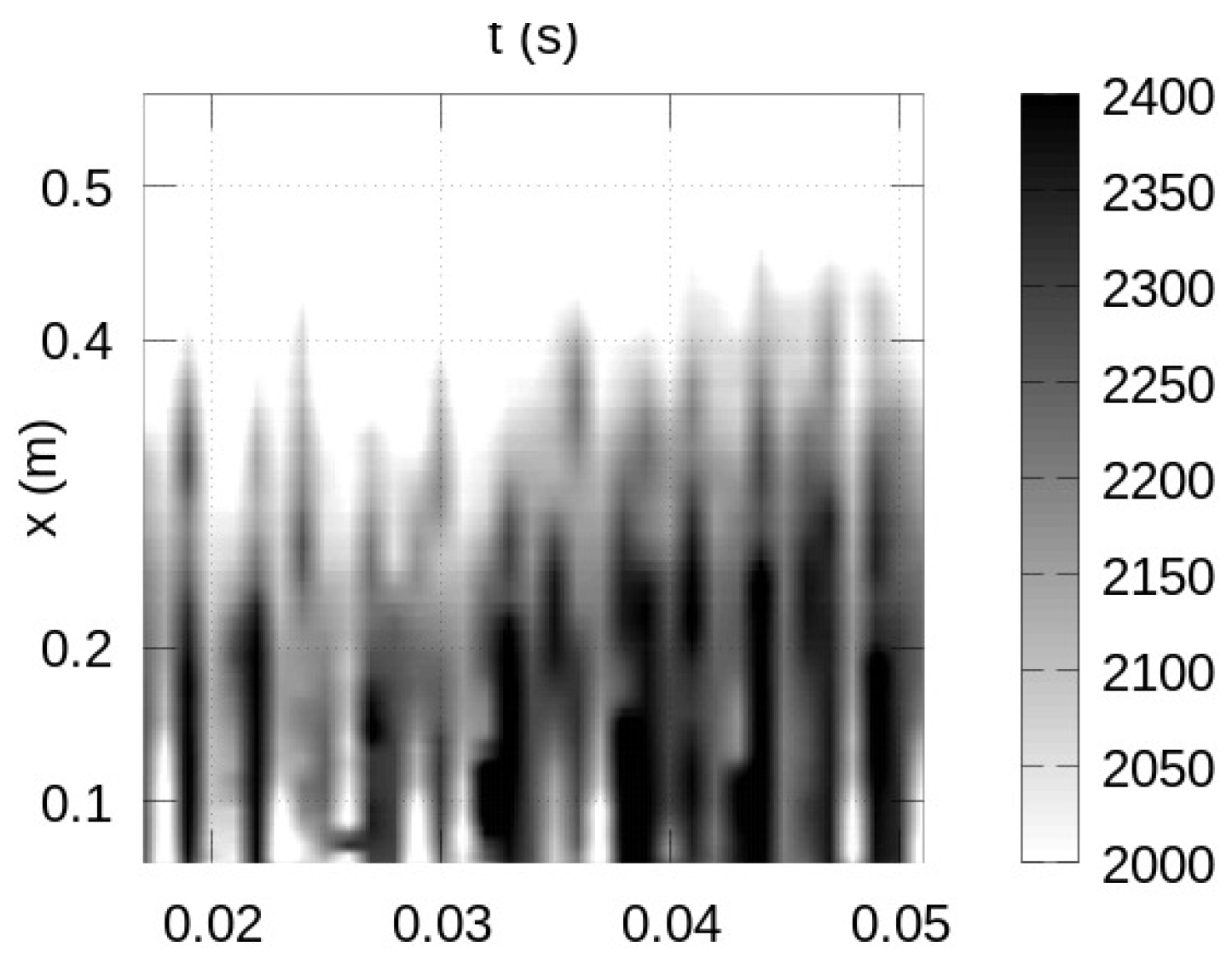
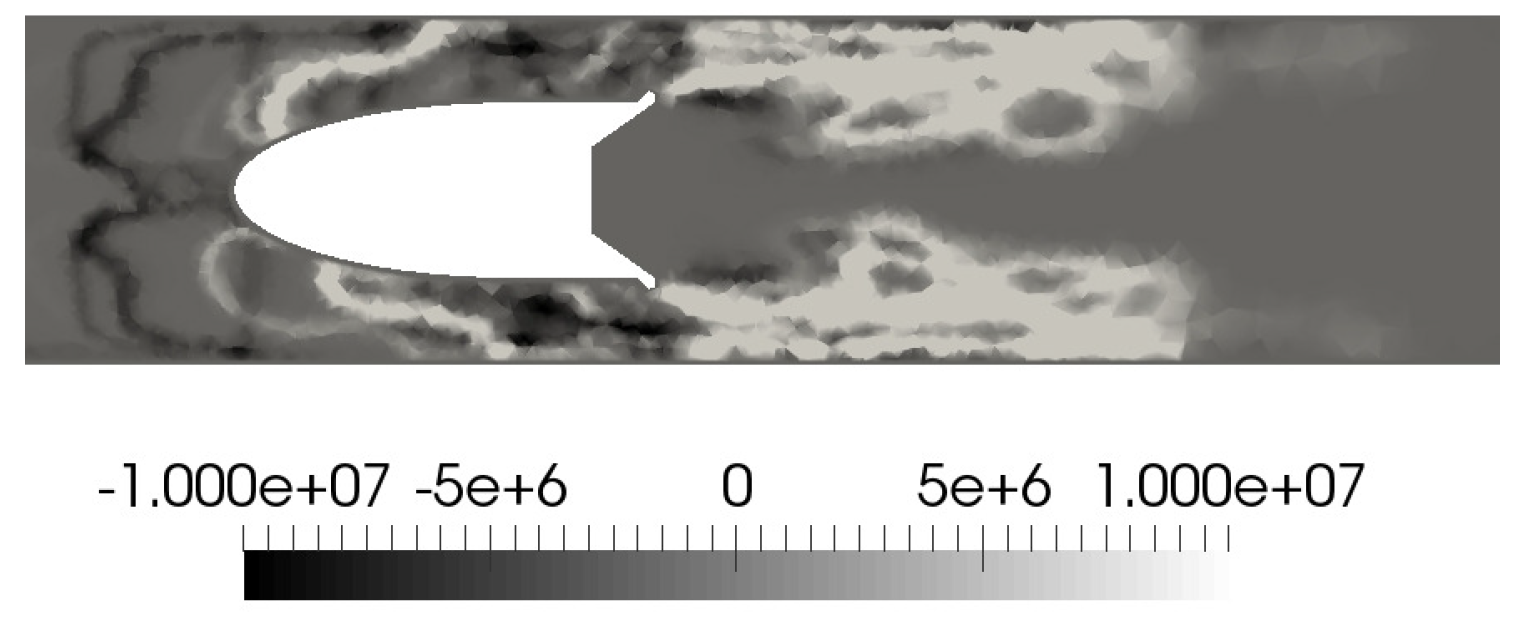
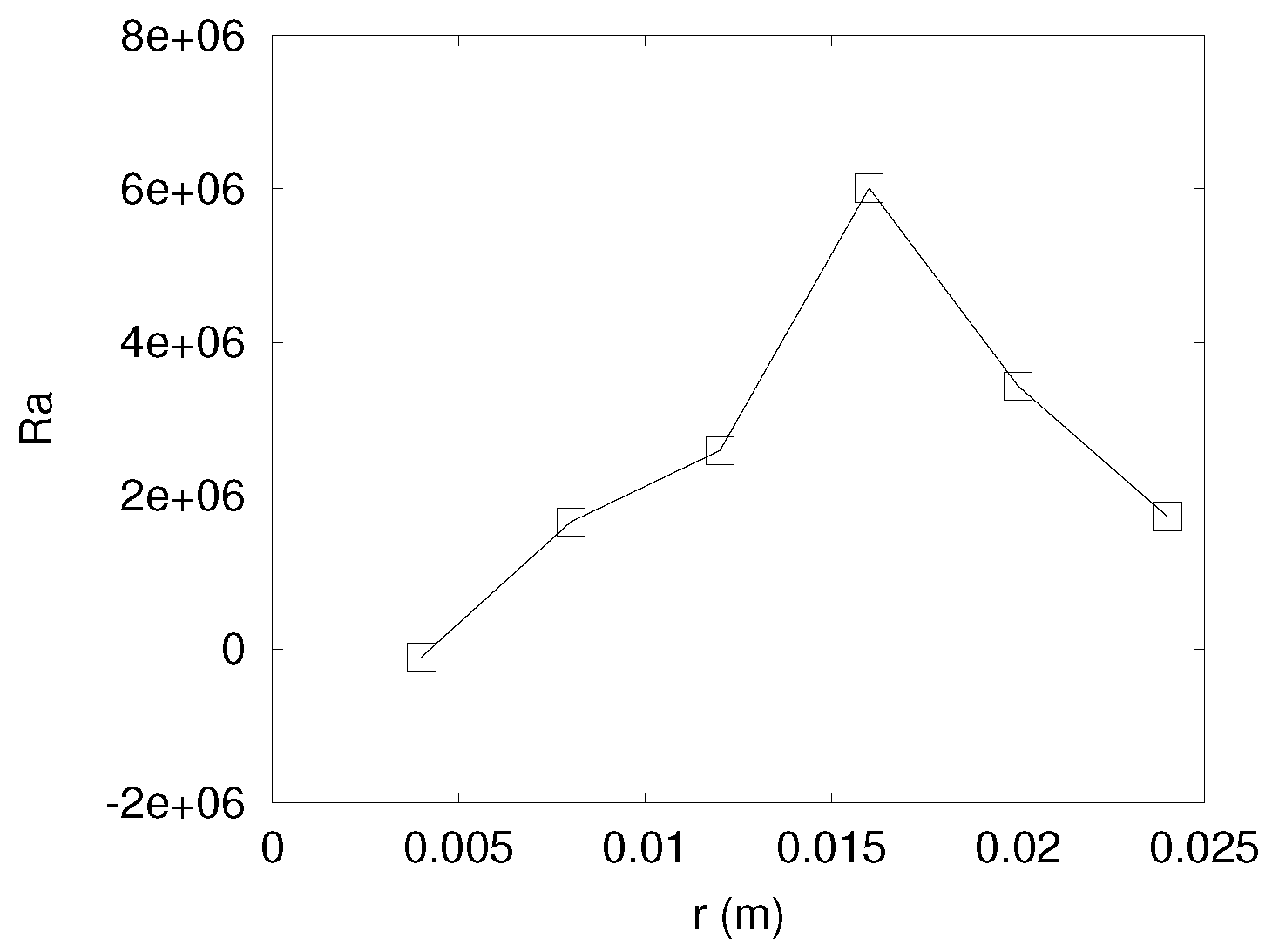
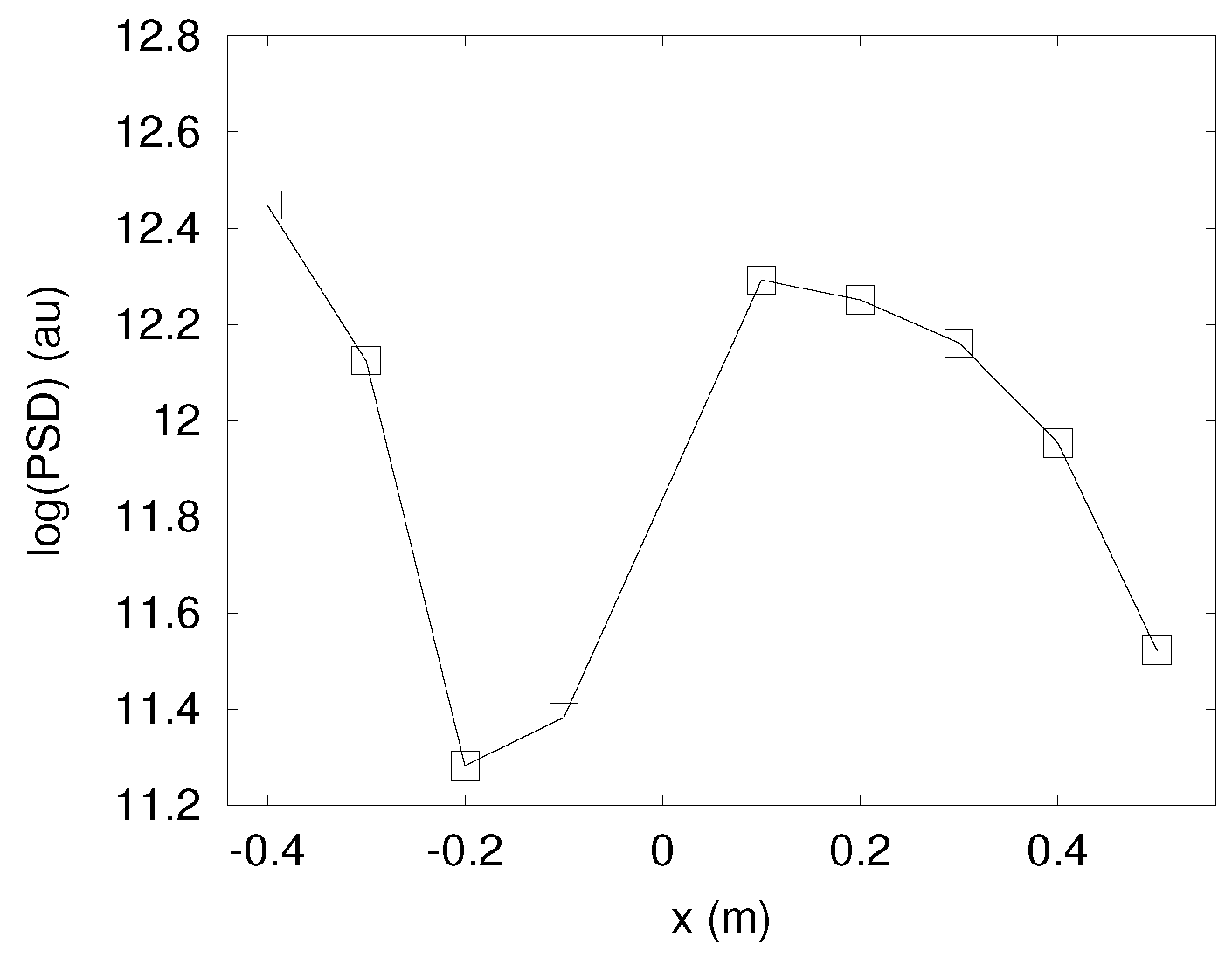
3. Results
4. Analysis
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Culick, F.E. Unsteady Motions in Combustion Chambers for Propulsion Systems; Research and Technology Organisation/North Atlantic Treaty Organisation: Neuilly, France, 2006. [Google Scholar]
- Lieuwen, T.C.; Yang, V.; Lu, F.K. Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms and Modeling; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 2005. [Google Scholar]
- Yang, V. Liquid Rocket Engine Combustion Instability; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1995; Volume 169. [Google Scholar]
- Poinsot, T. Prediction and Control of Combustion Instabilities in Real Engines. Proc. Combust. Inst. 2017, 36, 1–28. [Google Scholar] [CrossRef]
- Menon, S. Active Control of Combustion Instability in a Ramjet Using Large Eddy Simulations; AIAA Paper 1991-0411; AIAA: Reston, VA, USA, 1991. [Google Scholar]
- Möller, S.; Lundgren, E.; Fureby, C. Large Eddy Simulation of Unsteady Combustion. Symp. (Int.) Combust. 1996, 26, 241–248. [Google Scholar] [CrossRef]
- Huang, Y.; Sung, H.; Hsieh, S.; Yang, V. Large-Eddy Simulation of Combustion Dynamics of Lean-Premixed Swirl-Stabilized Combustor. J. Propuls. Power 2003, 19, 782–794. [Google Scholar] [CrossRef]
- Martin, C.E.; Benoit, L.J.; Sommerer, Y.; Nicoud, F.; Poinsot, T. Large-Eddy Simulation and Acoustic Analysis of a Swirled Staged Turbulent Combustor. AIAA J. 2006, 44, 741–750. [Google Scholar] [CrossRef]
- Wolf, P.; Staffelbach, G.; Roux, A.; Gicquel, L.; Poinsot, T.; Moureau, V. Massively Parallel LES of Azimuthal Thermo-Acoustic Instabilities in Annular Gas Turbines. C. R. Mec. 2009, 337, 385–394. [Google Scholar] [CrossRef]
- Staffelbach, G.; Gicquel, L.; Boudier, G.; Poinsot, T. Large Eddy Simulation of Self Excited Azimuthal Modes in Annular Combustors. Proc. Combust. Inst. 2009, 32, 2909–2916. [Google Scholar] [CrossRef]
- Gicquel, L.Y.M.; Roux, A. LES to Ease Understanding of Complex Unsteady Combustion Features of Ramjet Burners. Flow Turbul. Combust. 2011, 87, 449–472. [Google Scholar] [CrossRef]
- Wolf, P.; Balakrishnan, R.; Staffelbach, G.; Gicquel, L.; Poinsot, T. Using LES to Study Reacting Flows and Instabilities in Annular Combustion Chambers. Flow Turbul. Combust. 2012, 88, 191–206. [Google Scholar] [CrossRef]
- Hernández, I.; Staffelbach, G.; Poinsot, T.; Román Casado, J.C.; Kok, J. LES and Acoustic Analysis of Thermo-Acoustic Instabilities in a Partially Premixed Model Combustor. C. R. Mec. 2013, 341, 121–130. [Google Scholar] [CrossRef]
- Harvazinski, M.E.; Talley, D.G.; Sankaran, V. Comparison of Laminar and Linear Eddy Model Closures for Combustion Instability Simulations; AIAA Paper 2015-3842; AIAA: Reston, VA, USA, 2015. [Google Scholar]
- Harvazinski, M.E.; Huang, C.; Sankaran, V.; Feldman, T.W.; Anderson, W.E.; Merkle, C.L.; Talley, D.G. Coupling between Hydrodynamics, Acoustics, and Heat Release in a Self-Excited Unstable Combustor. Phys. Fluids 2015, 27, 045102. [Google Scholar] [CrossRef]
- Bauerheim, M.; Staffelbach, G.; Worth, N.A.; Dawson, J.R.; Gicquel, L.Y.M.; Poinsot, T. Sensitivity of LES-based harmonic flame response model for turbulent swirled flames and impact on the stability of azimuthal modes. Proc. Combust. Inst. 2015, 35, 3355–3363. [Google Scholar] [CrossRef]
- Ghani, A.; Poinsot, T.; Gicquel, L.; Staffelbach, G. LES of Longitudinal and Transverse Self-excited Combustion Instabilities in a Bluff-body Stabilized Turbulent Premixed Flame. Combust. Flame 2015, 162, 4075–4083. [Google Scholar] [CrossRef]
- Ghani, A.; Miguel-Brebion, M.; Selle, L.; Duchaine, F.; Poinsot, T. Effect of Wall Heat Transfer on Screech in a Turbulent Premixed Combustor. In Proceedings of the Summer Program of the Center for Turbulence Research; Center for Turbulence Research: Stanford, CA, USA, 2016; p. 133. [Google Scholar]
- Gonzalez-Juez, E.D. Numerical Simulations of Screech; AIAA Paper 2015-3965; AIAA: Reston, VA, USA, 2015. [Google Scholar]
- Rogers, D.E.; Marble, F.E. A Mechanism for High-Frequency Oscillation in Ramjet Combustors and Afterburners. J. Jet Propuls. 1956, 26, 456–462. [Google Scholar] [CrossRef]
- Elias, I. Acoustical Resonances Produced by Combustion of a Fuel-Air Mixture in a Rectangular Duct. J. Acoust. Soc. Am. 1959, 31, 296–304. [Google Scholar] [CrossRef]
- Langhorne, P.J. Reheat Buzz: An Acoustically Coupled Combustion Instability. Part 1. Experiment. J. Fluid Mech. 1988, 193, 417–443. [Google Scholar] [CrossRef]
- Sjunnesson, A.; Nelson, C.; Max, E. LDA Measurements of Velocities and Turbulence in a Bluff Body Stabilized Flame. In Proceedings of the 4th International Conference on Laser Anemometry, Cleveland, OH, USA, 5–9 August 1991. [Google Scholar]
- Chakravarthy, S.R.; Sivakumar, R.; Shreenivasan, O.J. Vortex-Acoustic Lock-on in Bluff-Body and Backward-Facing Step Combustors. Sadhana 2007, 32, 145–154. [Google Scholar] [CrossRef]
- Cuppoletti, D.R.; Kastner, J.; Reed, J., Jr.; Gutmark, E.J. High Frequency Combustion Instabilities with Radial V-Gutter Flameholders; AIAA Paper 2009-1176; AIAA: Reston, VA, USA, 2009. [Google Scholar]
- Hield, P.A.; Brear, M.J. A Laboratory Combustor for Studies of Premixed Combustion Instability. In Proceedings of the 16th Australasian Fluid Mechanics Conference (AFMC), School of Engineering, The University of Queensland, Brisbane, Australia, 3–7 December 2007; pp. 99–103. [Google Scholar]
- Hield, P.A.; Brear, M.J. Comparison of Open and Choked Premixed Combustor Exits During Thermoacoustic Limit Cycle. AIAA J. 2008, 46, 517–526. [Google Scholar] [CrossRef]
- Hield, P.A.; Brear, M.J.; Jin, S. Thermoacoustic Limit Cycles in a Premixed Laboratory Combustor with Open and Choked Exits. Combust. Flame 2009, 156, 1683–1697. [Google Scholar] [CrossRef]
- Song, J.; Jung, C.; Hwang, J.; Yoon, Y. An Experimental Study on the Flame Dynamics with V-Gutter Type Flameholder in the Model Combustor; AIAA Paper 2011-6126; AIAA: Reston, VA, USA, 2011. [Google Scholar]
- Roman Casado, J.C. Nonlinear Behavior of the Thermo Acoustic Instabilities in the Limousine Combustor. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
- O’Connor, J.; Acharya, V.; Lieuwen, T. Transverse Combustion Instabilities: Acoustic, Fluid Mechanic, and Flame Processes. Prog. Energy Combust. Sci. 2015, 49, 1–39. [Google Scholar] [CrossRef]
- Hield, P.A. An Experimental and Theoretical Investigation of Thermoacoustic Instability in a Turbulent Premixed Laboratory Combustor. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 2007. [Google Scholar]
- Shahi, M.; Kok, J.; Pozarlik, A.K.; Casado, J.C.R.; Sponfeldner, T. Sensitivity of the Numerical Prediction of Turbulent Combustion Dynamics in the LIMOUSINE Combustor. J. Eng. Gas Turbines Power 2014, 136, 021504. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Horiuti, K. A Statistically-Derived Subgrid-Scale Kinetic Energy Model for the Large Eddy Simulation of Turbulent Flows. Phys. Soc. Jpn. J. 1985, 54, 2834–2839. [Google Scholar] [CrossRef]
- Ghiji, M.; Goldsworthy, L.; Brandner, P.; Garaniya, V.; Hield, P. Analysis of Diesel Spray Dynamics Using a Compressible Eulerian/VOF/LES Model and Microscopic Shadowgraphy. Fuel 2017, 188, 352–366. [Google Scholar] [CrossRef]
- Nordin, P.A. Complex Chemistry Modeling of Diesel Spray Combustion. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2001. [Google Scholar]
- Turns, S.R. An Introduction to Combustion; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- OpenFOAM. Available online: www.openfoam.org (accessed on 19 July 2019).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to Computational Continuum Mechanics Using Object-Oriented Techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College, London, UK, 1996. [Google Scholar]
- Persson, S. Development of a Test Suite for Verification and Validation of OpenFOAM. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2017. [Google Scholar]
- Li, X.; Gao, H.; Soteriou, M.C. Investigation of the impact of high liquid viscosity on jet atomization in crossflow via high-fidelity simulations. Phys. Fluids 2017, 29, 082103. [Google Scholar] [CrossRef]
- Ashton, N.; Skaperdas, V. Verification and Validation of OpenFOAM for High-Lift Aircraft Flows. J. Aircr. 2019. [Google Scholar] [CrossRef]
- Fureby, C. Large Eddy Simulation Modelling of Combustion for Propulsion Applications. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2009, 367, 2957–2969. [Google Scholar] [CrossRef]
- Chapuis, M.; Fureby, C.; Fedina, E.; Alin, N.; Tegnér, J. LES Modeling of Combustion Applications Using OpenFOAM. In Proceedings of the V European Conference on Computational Dynamics ECCOMAS CFD, Lisbon, Portugal, 14–17 June 2010; pp. 1–20. [Google Scholar]
- Wang, Y.; Chatterjee, P.; de Ris, J.L. Large Eddy Simulation of Fire Plumes. Proc. Combust. Inst. 2011, 33, 2473–2480. [Google Scholar] [CrossRef]
- Gong, C.; Jangi, M.; Bai, X. Large Eddy Simulation of n-Dodecane Spray Combustion in a High Pressure Combustion Vessel. Appl. Energy 2014, 136, 373–381. [Google Scholar] [CrossRef]
- Fiorina, B.; Mercier, R.; Kuenne, G.; Ketelheun, A.; Avdić, A.; Janicka, J.; Geyer, D.; Dreizler, A.; Alenius, E.; Duwig, C. Challenging Modeling Strategies for LES of Non-Adiabatic Turbulent Stratified Combustion. Combust. Flame 2015, 162, 4264–4282. [Google Scholar] [CrossRef]
- Huang, Z.; He, G.; Qin, F.; Wei, X. Large Eddy Simulation of Flame Structure and Combustion Mode in a Hydrogen Fueled Supersonic Combustor. Int. J. Hydrog. Energy 2015, 40, 9815–9824. [Google Scholar] [CrossRef]
- Gonzalez-Juez, E.D. Numerical Simulations of Thermoacoustic Combustion Instabilities in the Volvo Combustor; AIAA Paper 2017-4686; AIAA: Reston, VA, USA, 2017. [Google Scholar]
- Angelberger, C.; Veynante, D.; Egolfopoulos, F.; Poinsot, T. Large Eddy Simulations of Combustion Instabilities in Premixed Flames. In Proceedings of the Summer Program of the Center for Turbulence Research; Center for Turbulence Research: Stanford, CA, USA, 1998; pp. 61–82. [Google Scholar]
- Mani, A. On the Reflectivity of Sponge Zones in Compressible Flow Simulations. In Annual Research Briefs of the Center for Turbulence Research; Center for Turbulence Research: Stanford, CA, USA, 2010; pp. 117–133. [Google Scholar]
- Selle, L.; Nicoud, F.; Poinsot, T. Actual Impedance of Nonreflecting Boundary Conditions: Implications for Computation of Resonators. AIAA J. 2004, 42, 958–964. [Google Scholar] [CrossRef]
- Poinsot, T.; Lele, S.K. Boundary Conditions for Direct Simulations of Compressible Viscous Flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Jaensch, S.; Sovardi, C.; Polifke, W. On the Robust, Flexible and Consistent Implementation of Time Domain Impedance Boundary Conditions for Compressible Flow Simulations. J. Comput. Phys. 2016, 314, 145–159. [Google Scholar] [CrossRef]
- Dowling, A.P. Nonlinear Self-excited Oscillations of a Ducted Flame. J. Fluid Mech. 1997, 346, 271–290. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S. The Theory of Sound; Dover Publications: New York, NY, USA, 1896. [Google Scholar]
- Nicoud, F.; Poinsot, T. Thermoacoustic Instabilities: Should the Rayleigh Criterion be Extended to Include Entropy Changes? Combust. Flame 2005, 142, 153–159. [Google Scholar] [CrossRef]
- Luong, T.; Howe, M.; McGowan, R. On the Rayleigh Conductivity of a Bias-flow Aperture. J. Fluids Struct. 2005, 21, 769–778. [Google Scholar] [CrossRef]
- Zhao, D.; Gutmark, E.; Reinecke, A. Mitigating Self-excited Flame Pulsating and Thermoacoustic Oscillations Using Perforated Liners. Sci. Bull. 2019, 64, 941–952. [Google Scholar] [CrossRef]
- Harvazinski, M.E.; Talley, D.G.; Sankaran, V. Application of Detailed Chemical Kinetics to Combustion Instability Modeling; AIAA Paper 2016-1931; AIAA: Reston, VA, USA, 2016. [Google Scholar]
- Hernandez, I. Soot Modeling in Flames and Large-Eddy Simulations of Thermo-Acoustic Instabilities. Ph.D. Thesis, University of Toulouse, Toulouse, France, 2011. [Google Scholar]
- Gonzalez-Juez, E.; Lee, J.G.; Santavicca, D.A. A Study of Combustion Instabilities Driven by Flame-Vortex Interactions; AIAA Paper 2005-4330; AIAA: Reston, VA, USA, 2005. [Google Scholar]
- Lieuwen, T.C. Unsteady Combustor Physics; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Schadow, K.C.; Gutmark, E. Combustion Instability Related to Vortex Shedding in Dump Combustors and their Passive Control. Prog. Energy Combust. Sci. 1992, 18, 117–132. [Google Scholar] [CrossRef]
- Emerson, B.; Murphy, K.; Lieuwen, T. Flame Density Ratio Effects on Vortex Dynamics of Harmonically Excited Bluff Body Stabilized Flames; ASME Paper GT2013-94284; ASME Press: New York, NY, USA, 2013. [Google Scholar]
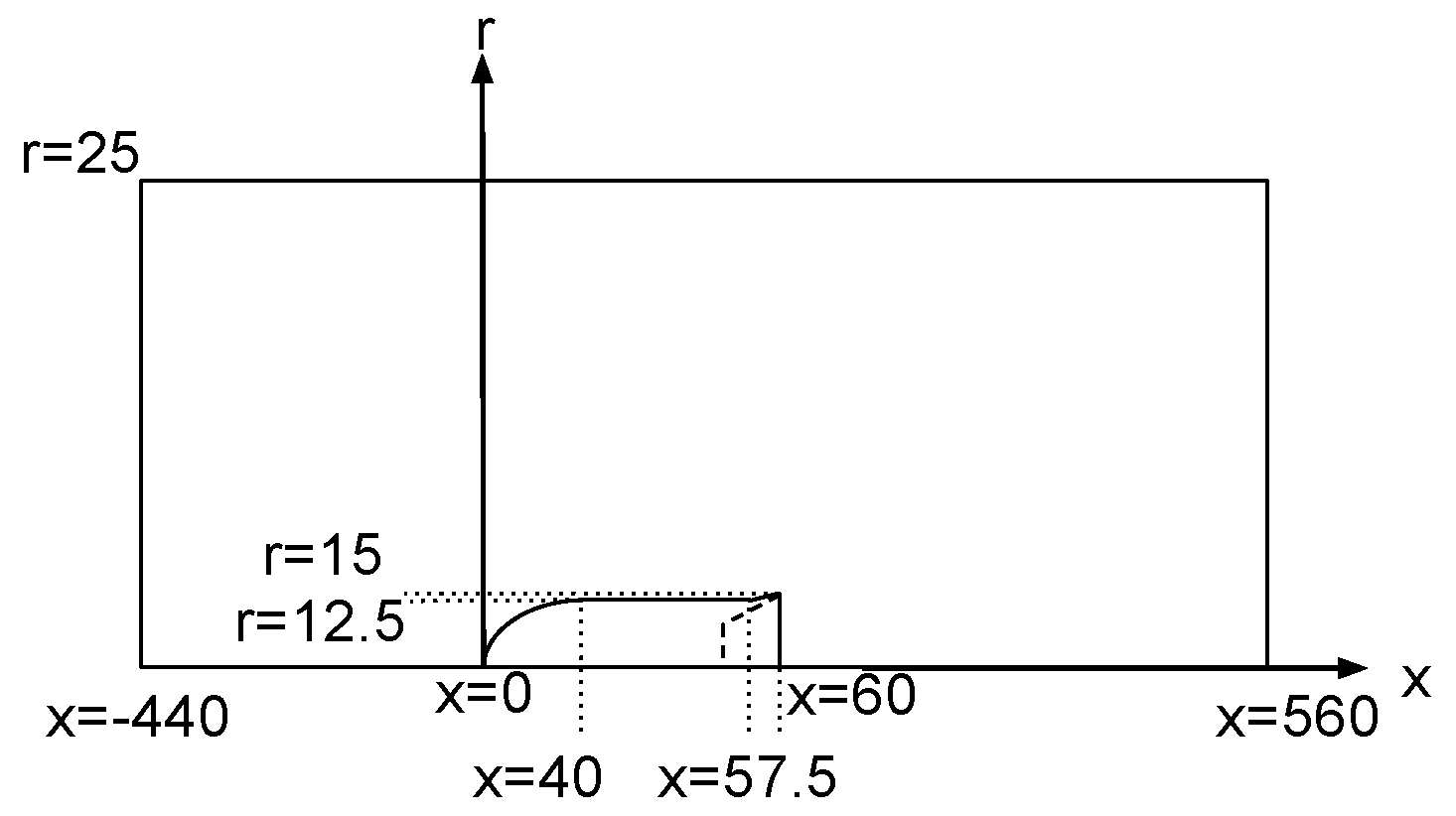

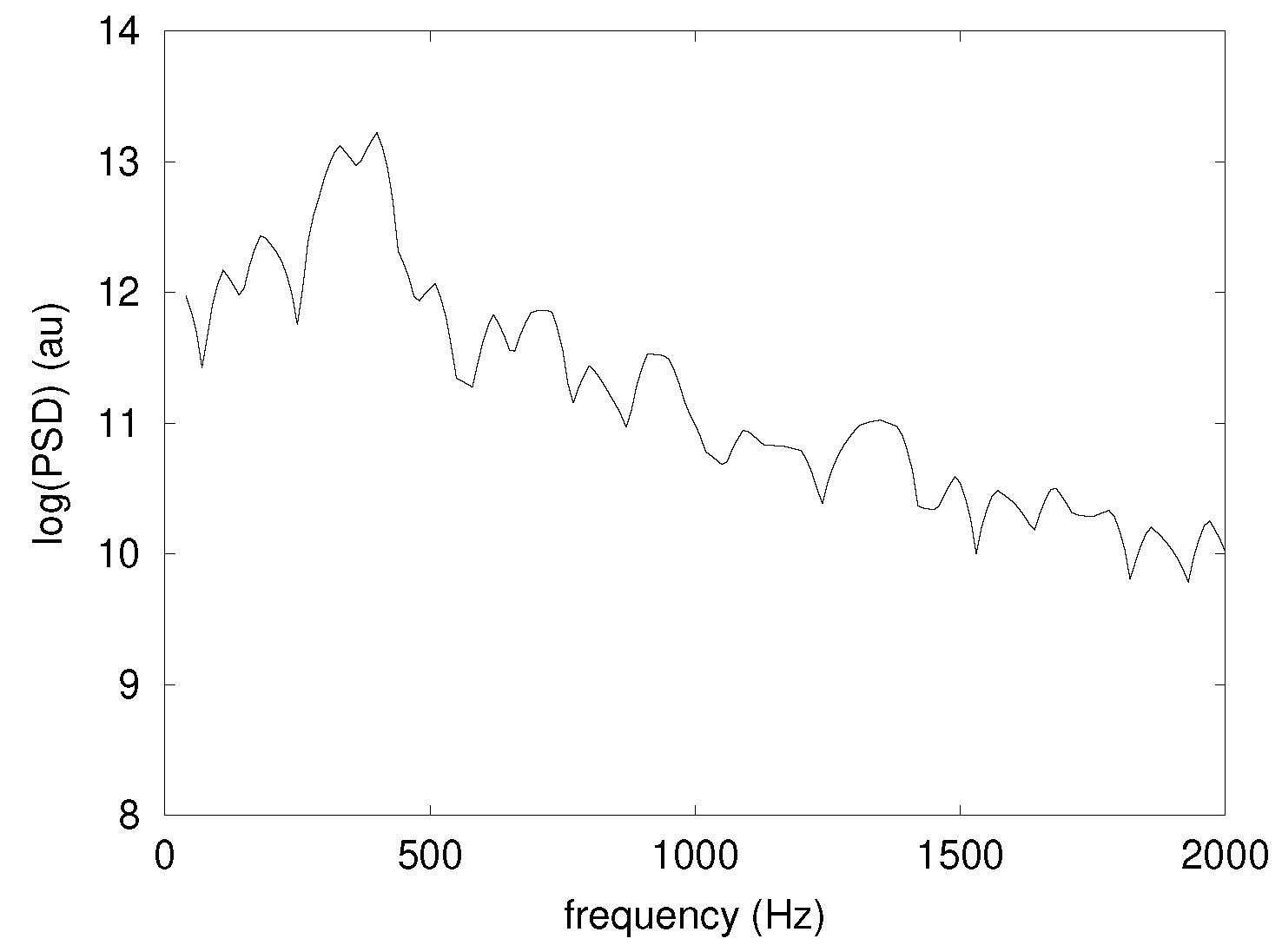
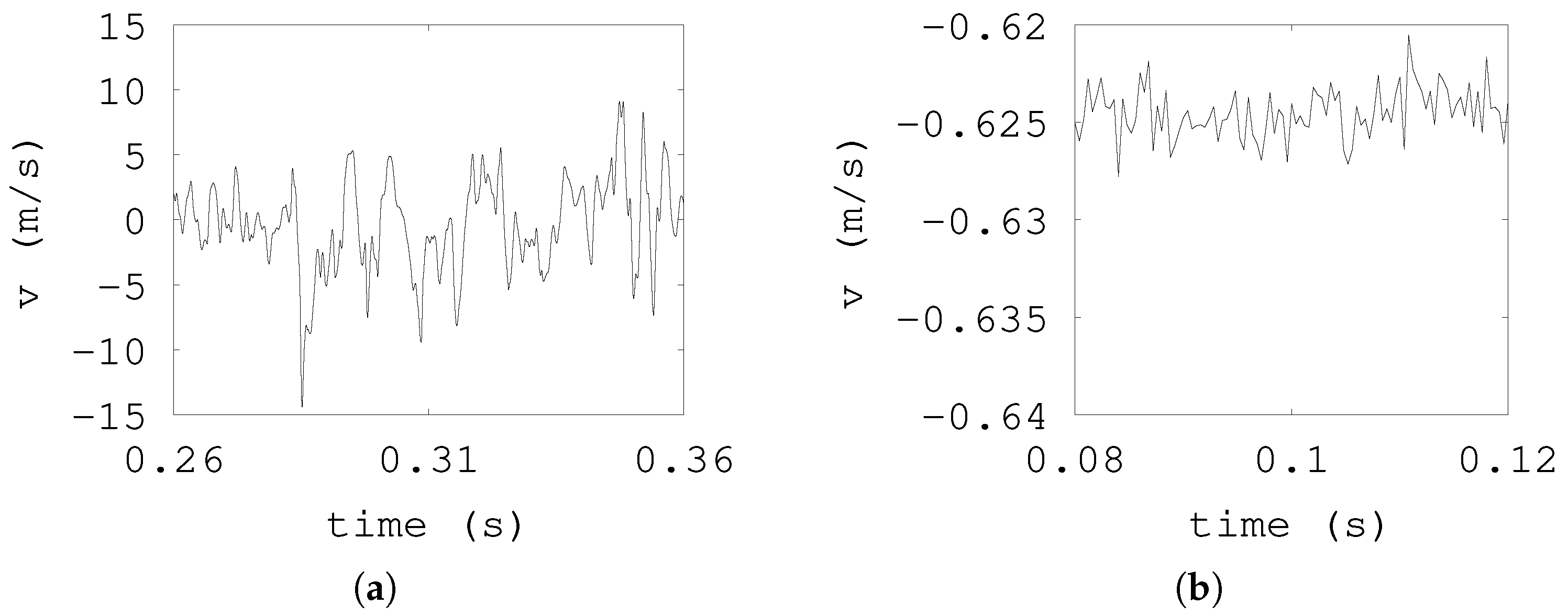
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Juez, E. Numerical Simulations of Combustion Instabilities in a Combustor with an Augmentor-Like Geometry. Aerospace 2019, 6, 82. https://doi.org/10.3390/aerospace6070082
Gonzalez-Juez E. Numerical Simulations of Combustion Instabilities in a Combustor with an Augmentor-Like Geometry. Aerospace. 2019; 6(7):82. https://doi.org/10.3390/aerospace6070082
Chicago/Turabian StyleGonzalez-Juez, Esteban. 2019. "Numerical Simulations of Combustion Instabilities in a Combustor with an Augmentor-Like Geometry" Aerospace 6, no. 7: 82. https://doi.org/10.3390/aerospace6070082
APA StyleGonzalez-Juez, E. (2019). Numerical Simulations of Combustion Instabilities in a Combustor with an Augmentor-Like Geometry. Aerospace, 6(7), 82. https://doi.org/10.3390/aerospace6070082



