1. Introduction
In the last two decades, increasing interest regarding the More Electric Aircraft (MEA) concept has been generated [
1] with the aim of reducing fuel consumption, reducing emissions released into the atmosphere, increasing the redundancy and the reliability of onboard power systems, and reducing aircraft noise.
Recently, several research projects have led to the substantial electrification of onboard pneumatic components in order to increase the efficiency of flight systems—which has also introduced redundancies across the subsystems [
2]—and the necessity to propose new power system architectures for the reduction of weight, increase of the reliability and to assure the correct performance of electrical drives [
3]. Moreover, in order to increase the reliability and decrease the weight, DC-microgrids [
4] seem to be the most suitable solution for future aircraft.
The current trend also envisages the use of electrical technology in aircraft propulsion [
5,
6,
7,
8] and both fully electric and hybrid propulsion aircraft prototypes have been presented. In the all-electric propulsion concept, the fuel and the thermal engine are completely substituted with energy storage systems (above all, fuel cells and battery) that are able to provide the entirety of the electric power required by the aircraft. The use of these new energy systems on board aircraft has been analyzed widely in the literature. In [
9], an aircraft design that relies on fuel cells for propulsion and that is characterized by an unusual motor placement in order to maximize efficiency is presented, while in reference [
10], the behavior of batteries that are used for the propulsion of small unmanned aircraft vehicles (UAV) at different temperatures is discussed. Additionally, Tariq [
11] presents an overview of the battery systems for the MEA with an analysis of battery management systems for Li-ion batteries. Hybrid propulsion [
12,
13,
14,
15] is quite similar to the hybrid traction used in automotive applications; the propulsion can be achieved with the use of electric motors or with both electric motors and internal combustion engines (ICEs). The electric power is provided by ICEs coupled with an electric generator and usually from a battery pack; the possible series and parallel configurations are similar to the scheme used in the automotive industry [
16,
17]. In this paper, the approach used was applied to an existing aircraft and the “electrification” of propulsion was made without any change to the aircraft structures, the maximum take-off weight, or the aerodynamic performance. The possibility of changing the complete structure of the aircraft surely permits an increase in the performance and convenience of hybrid propulsion [
18].
The sizing of electrical energy storage systems is a critical issue for their integration in aircraft and its optimization is mandatory. Different sizing tools for supercapacitor or battery systems are suggested in [
19,
20]. In these tools, only one storage system is sized at a time and with one pre-chosen cell.
Novel approaches based on optimization algorithms—so-called integrated design by optimization—are becoming increasingly mature and will become particularly powerful if subsequent efforts are made in terms of modeling for design.
The integrated optimal design approach consists of coupling sizing models with an optimization algorithm that automatically tunes the parameters to optimize system criteria (mass, losses, etc.) while satisfying the technological and operational constraints.
Many types of optimization procedures can be utilized in engineering applications: single or multi-objective, continuous or discrete optimization, linear or non-linear optimization, non-gradient optimization techniques, etc. The choice of the type of optimization is related to specific mathematical problems and to the technical boundary conditions (e.g., the necessity of using integer variables). Regarding the considered problems, as mentioned above, the necessity of reducing pollution requires the determination of an optimal trade-off problem between the size of the onboard energy storage system and the mass of the fuel. The objective functions can be different, as proposed in the literature (e.g., [
21]). The problem is solved by the optimization of three different objective functions related to the energy cost, which is the primary energy required in order to guarantee flight completion and the reduction of CO
2 emissions. In [
22], the size of the hybrid storage system which is constituted by supercapacitors and batteries is optimized and the objective function is inherent to the reduction of the total mass of the primary energy. In [
13], a simple conceptual design approach is proposed to determine the optimal size of the battery system in order to maximize the range or duration of the flight for the available fuel in the aircraft’s tank. In [
22,
23], a sizing tool for reducing the global storage system’s weight by taking several constraints (environmental and electrical ones) into account and by adjusting some parameters—such as the discharge ratio of the storage components and the ambient temperature—within a proper energy management strategy was proposed. The sizing method was improved upon with an optimization algorithm solved by a simulated annealing method. In [
24], a sizing methodology for the battery of an UAV is proposed. The methodology is based on the use of an integral formulation for the constant discharge of battery power, thereby obtaining the optimal size of the batteries.
In this paper, an integer optimization procedure is proposed, which permits the integer character of some variables and the simultaneous solution to both the mechanical flight problem and electrical problem related to the energy storage systems to be taken into account. Regarding the mechanical flight problem, a mathematical approach that is able to solve the mechanical flights equation during the climb phase, based on the energy minimization is proposed. The solution of the optimization procedure is mainly based on the use of an integer differential evolution approach (IDEA) [
25]. The differential evolution is a simple and efficient algorithm which permits the solution of the optimization problem with a rapid convergence to the solution. The need to use an integer optimization is due to the nature of the battery packs, where the number of cells or modules are integer numbers. In the literature [
20,
24,
26], it is typically found that the battery storage systems are of optimal size in terms of both energy and power; therefore, the determination of the number of cells is postponed; in this way, it is guaranteed that the optimal value of the energy and power is achieved, but it is not guaranteed that the number of cells is optimal.
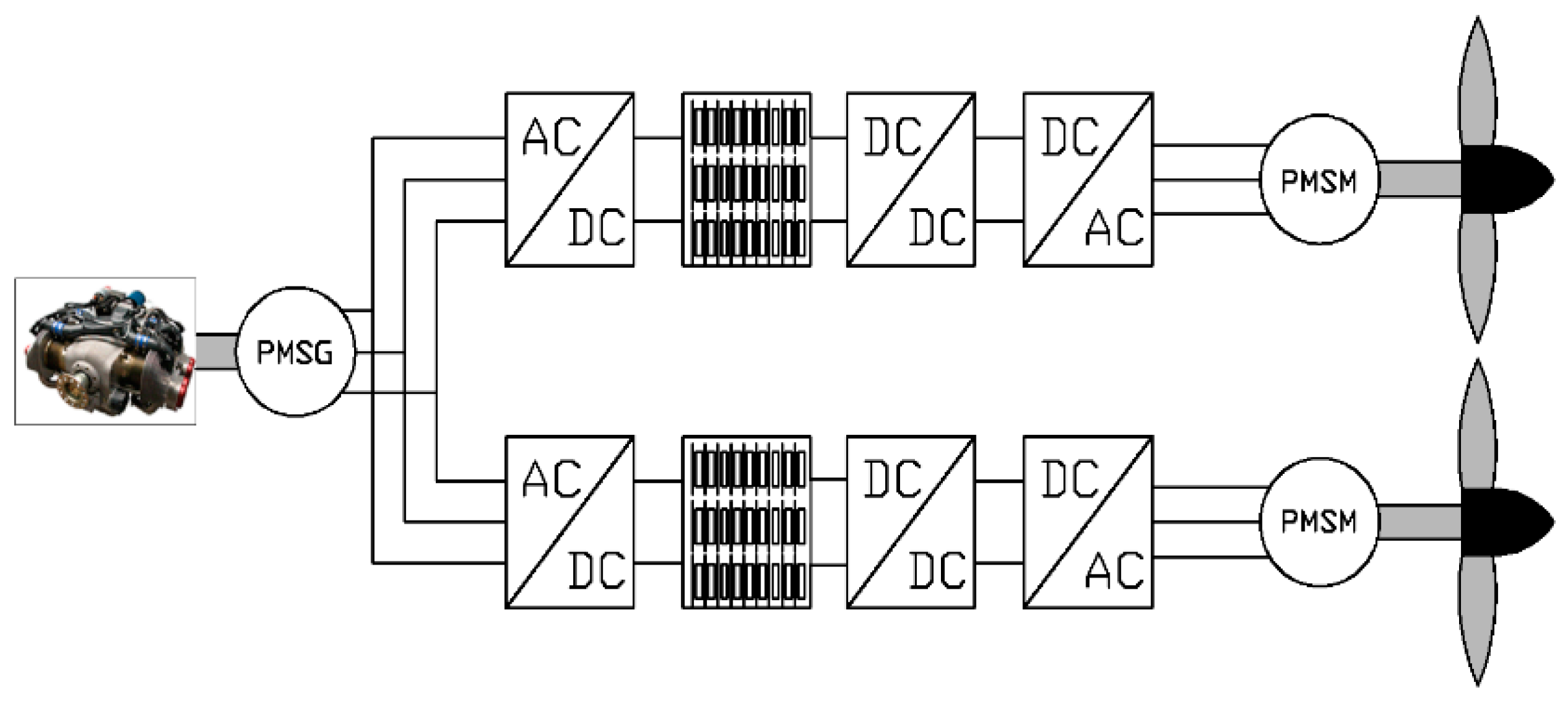
Starting from an assigned flight profile (cruise altitude, cruise speed, cruise range), the aim of this paper is to develop an optimization procedure which can be used during the pre-flight settings and is able to evaluate the optimal integration of the battery storage system and ICE to guarantee the correct operation during the execution of the flight profile.
The main novelty of the proposed optimization procedure regards the possibility to use it as a pre-mission energy management process. In fact, with the possibility to develop a modular battery pack and considering the mission profile, it is possible to calculate the optimal size of the battery pack. Through a new disposition of the module of the pack (each module can be constituted by a certain number of parallel and series cells), it is possible to minimize and reduce the useless weight of the aircraft.
The optimized design approach of the sizing of the energy storage system of a series-hybrid aircraft is detailed and validated in this paper. In the next section, the hybrid propulsion system of the aircraft is defined. In the third section, the dynamic equations of the aircraft profile are detailed and in
Section 4 the battery system model is explained. The optimization sizing procedure is proposed in
Section 5 and validated by simulation in
Section 6 where the results are reported and discussed.
5. Optimization Procedure
The optimization procedure is mainly based on the use of an integer differential evolution approach (IDEA) [
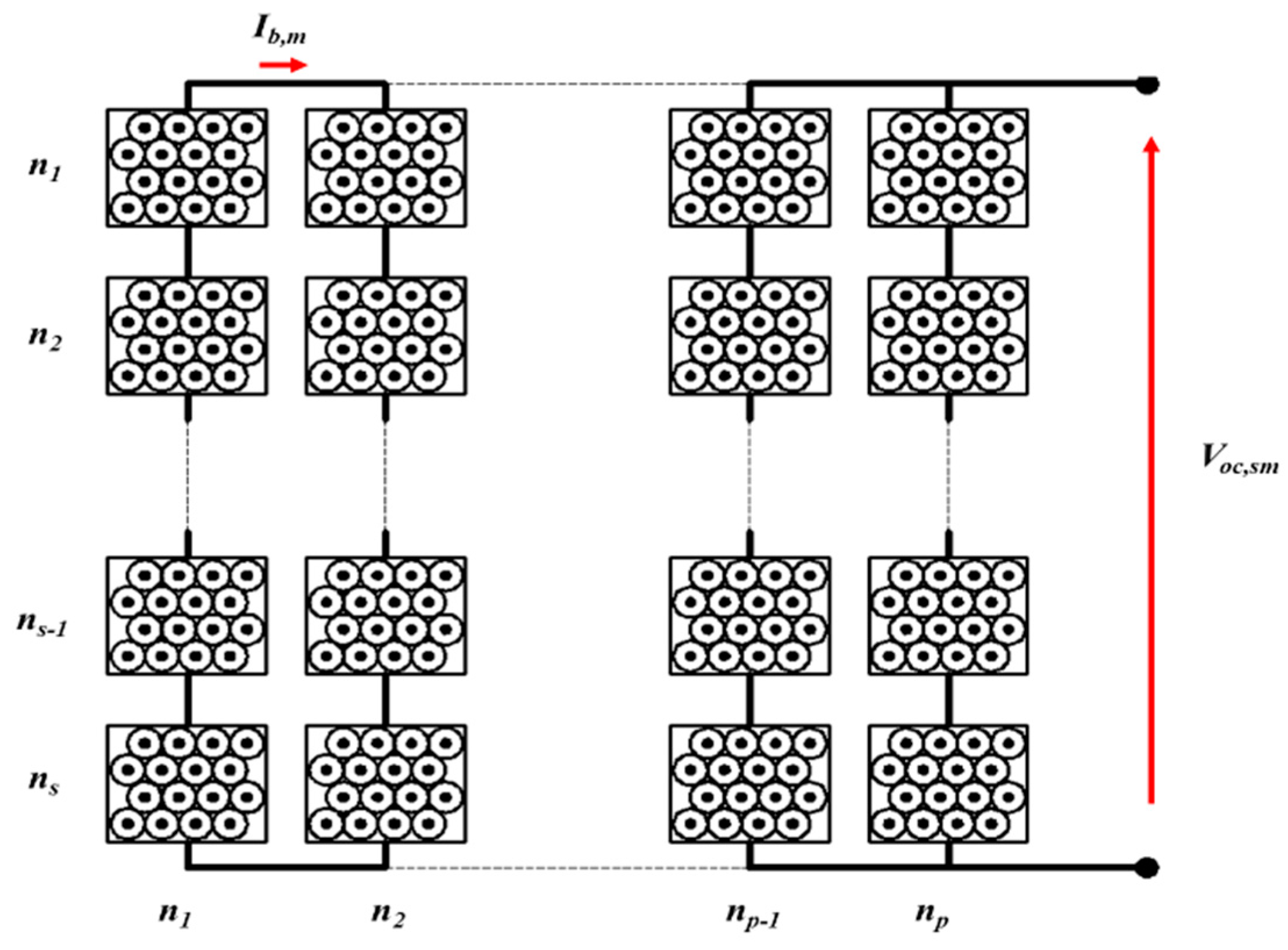
21] with the aim to minimize (or maximize) certain parameters of the aircraft or the physical parameters of the aircraft trajectories. The optimization procedure is realized on more levels; the external level is inherent to the IDEA technique and acts on three variables: the number of parallel cells
np and series cells
ns, and the weight of fuel. At each iteration of the optimization, the procedure solves another three problems linked to the optimization of the trajectories.
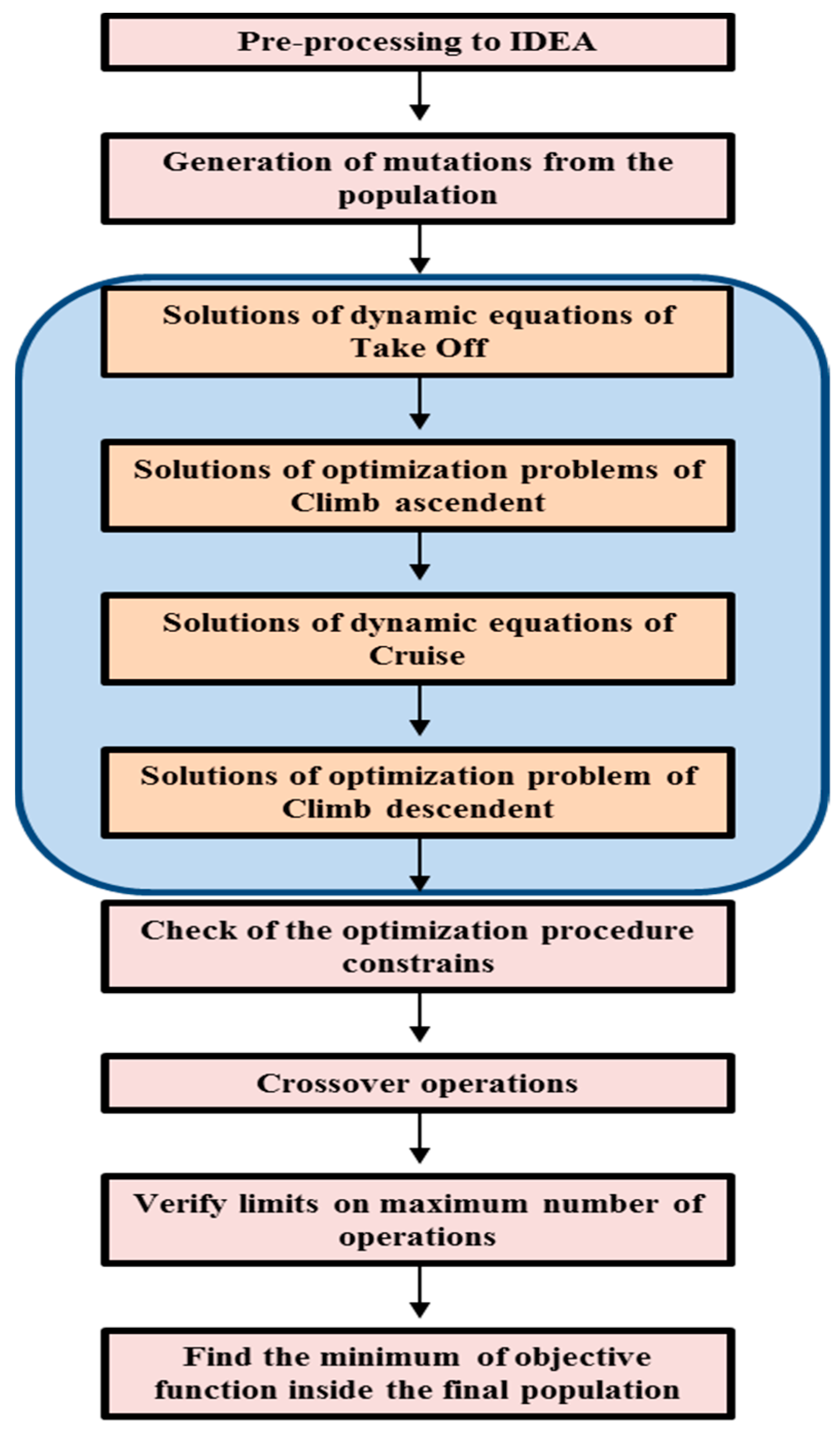
Figure 4 shows a flowchart of the procedure.
5.1. Pre-Processing to IDEA
Before initializing the procedure, a population of
npop possible solutions is generated:
5.2. Generation of Mutations
The mutations (that is the new candidate solution) are generated according to the procedure represented schematically in
Figure 4.
The parameters ρ1, ρ2, and ρ3 are random integer numbers comprised in the range (1,npop), α is a random positive real number below 1, and the function “int” rounds the number obtained in the square brackets to the nearest integer. If the obtained solution is positive, a candidate solution is found and processed inside the modeling of aircraft dynamics.
The solution of Equations (A1) and (1) permits the calculation of the take-off time and the total energy,
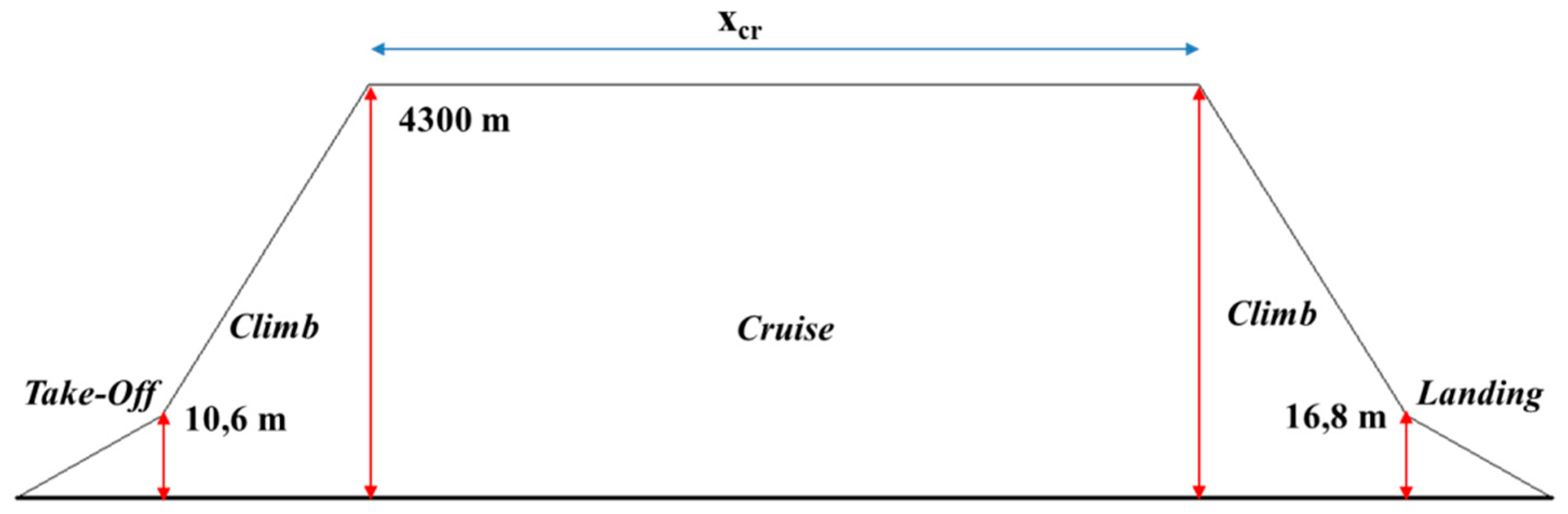
Eto, required during this phase. It is imposed that the take-off starts at a level of 0 m and is completed at
zto,f (about 10.6 m) [
26]. The final condition of the battery pack is evaluated by calculating the required electrical power. These values are used as initial values for the next step in the optimization problem.
5.3. Solutions of Optimization Problems of Climb Ascendant/Descendent
The optimization of the climb phase is more complex with respect to that of take-off. In fact, in this case, an objective optimization is carried out inside the IDEA. The goal of this optimization is the minimization of the total energy required for the climb phase. The simulated climb phase is assumed to possess a uniform acceleration. Considering the fact that the climb phase commences at
zto,f and the final altitude is the cruise altitude,
zcr, it is also considered that the final speed must be equal to the cruise speed (in this case, any acceleration during the cruise phase is avoided). In the hypothesis of uniform acceleration, the altitude climb is divided in a certain number of divisions, in order to obtain that:
where Δ
vk is the variation of the velocity in each division. The used objective function is the total energy required in the climb:
where the unknown variables are:
Then, the objective function becomes:
In Equation (14), the sum of the energy calculated in each sub-interval considered for the climb phase is given. In particular, the numerator is presented as the product between the propeller trust, the velocity, and the time duration and this product is divided by the global efficiency of the electric propulsion chain.
The variation in the altitude and aircraft speed must satisfy the following equations:
The first two equations are related to the fact that the final altitude and the final aircraft speed must be equal to the desired cruise altitude and cruise speed; therefore, the optimal value obtained for the altitude and speed variation in each sub-interval must be related to these values. The third equation relates the climb angle to all the dynamic variables.
The first two inequalities are used in order to limit the variation of the aircraft speed and altitude; the last two ensure that the maximum time for the climb phase and the climb angle are respected.
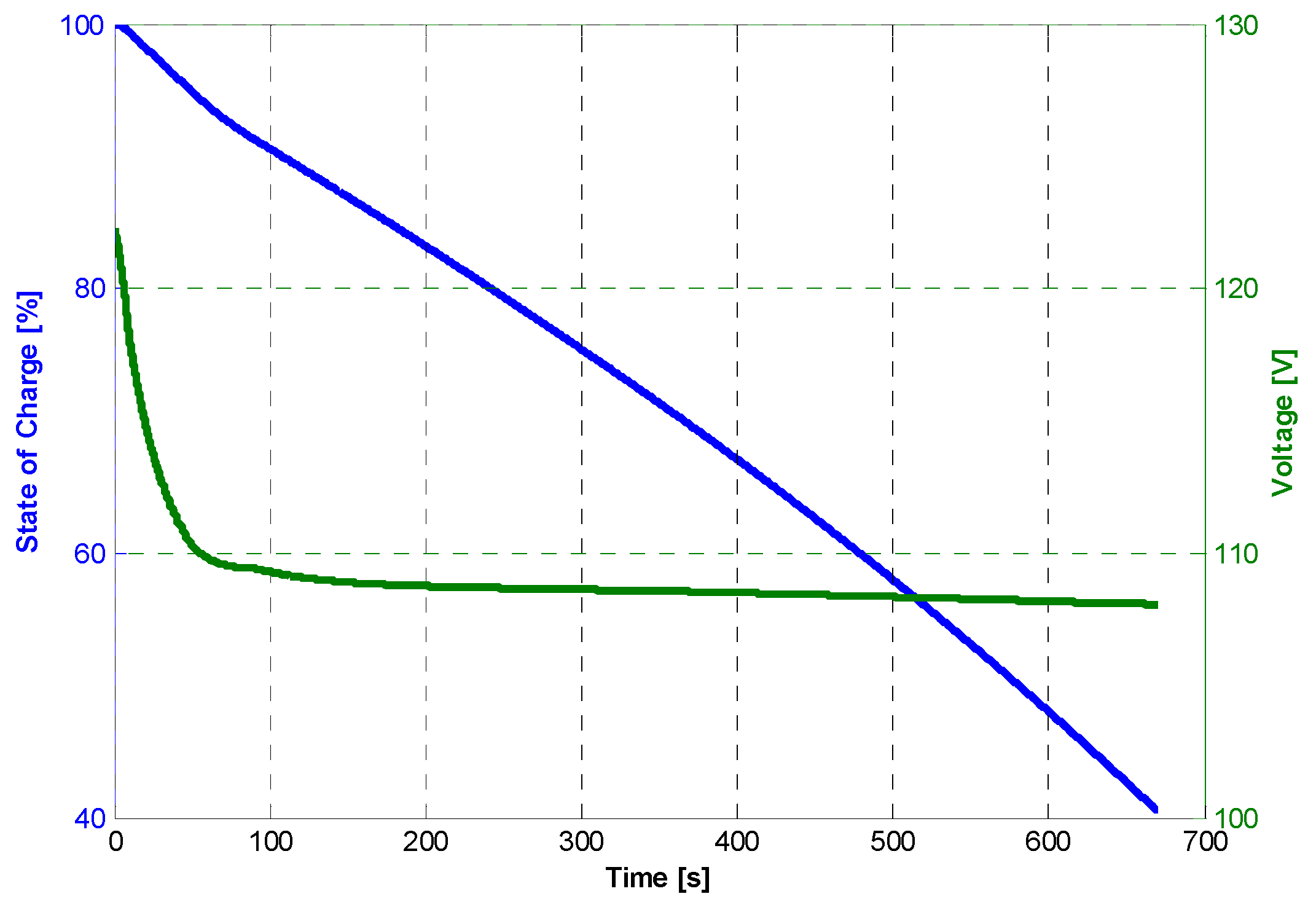
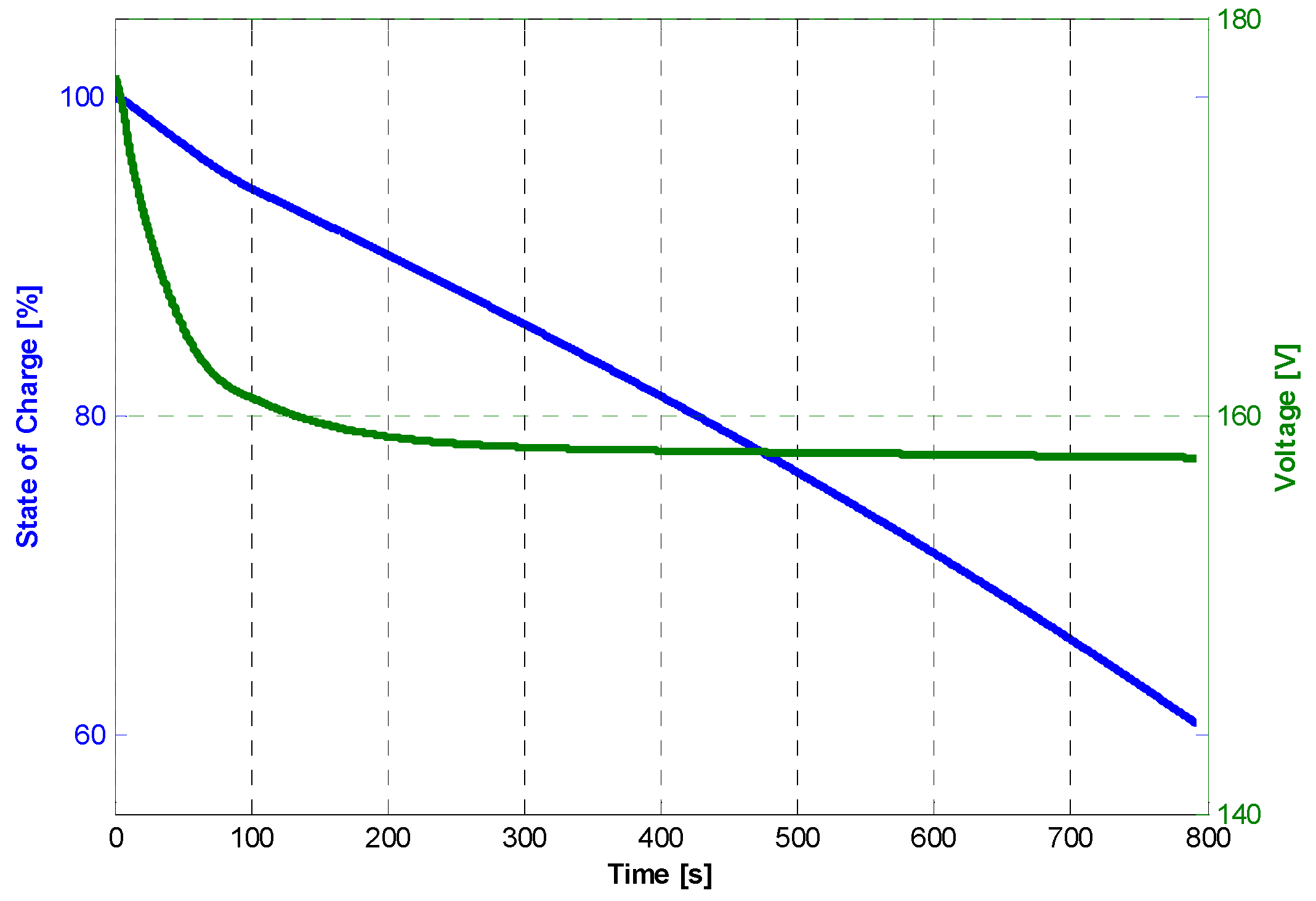
Starting from the final condition of the battery packs after take-off, the final state of charge and the final value of the open-circuit voltage Voc,sm are calculated. The same approach is used in the descendent phase of the climb.
5.4. Solutions of Dynamic Equations of the Cruise
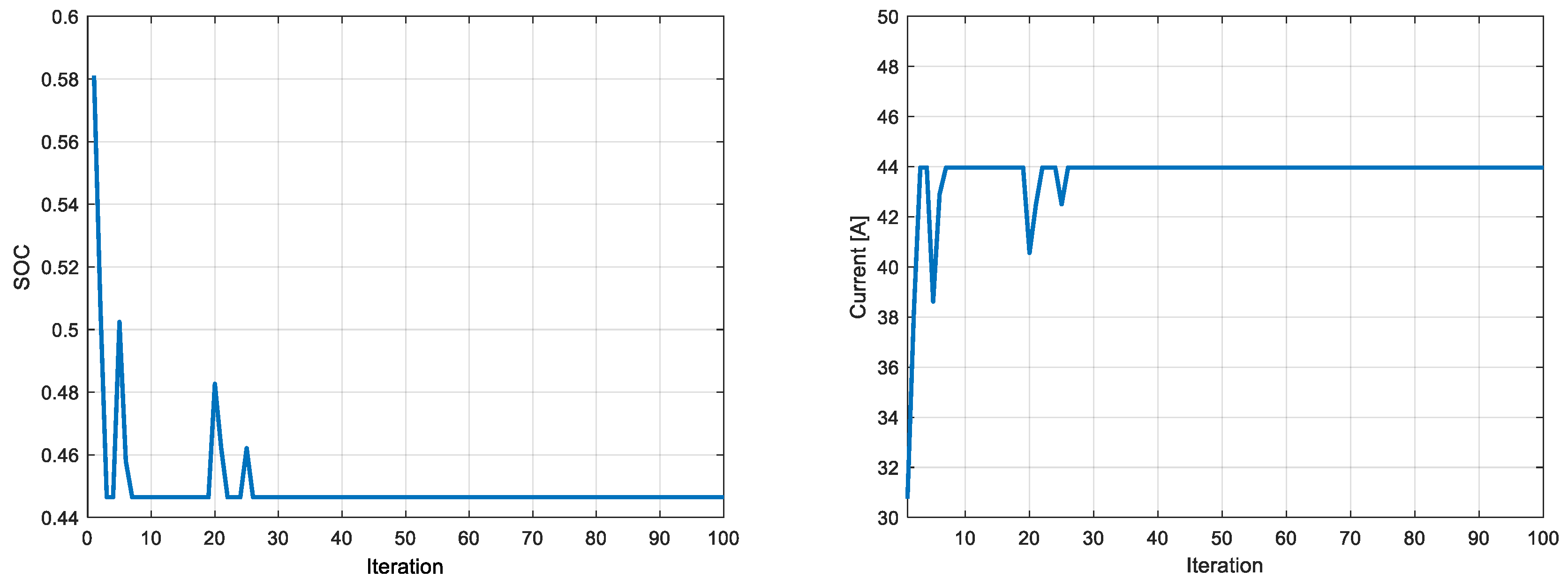
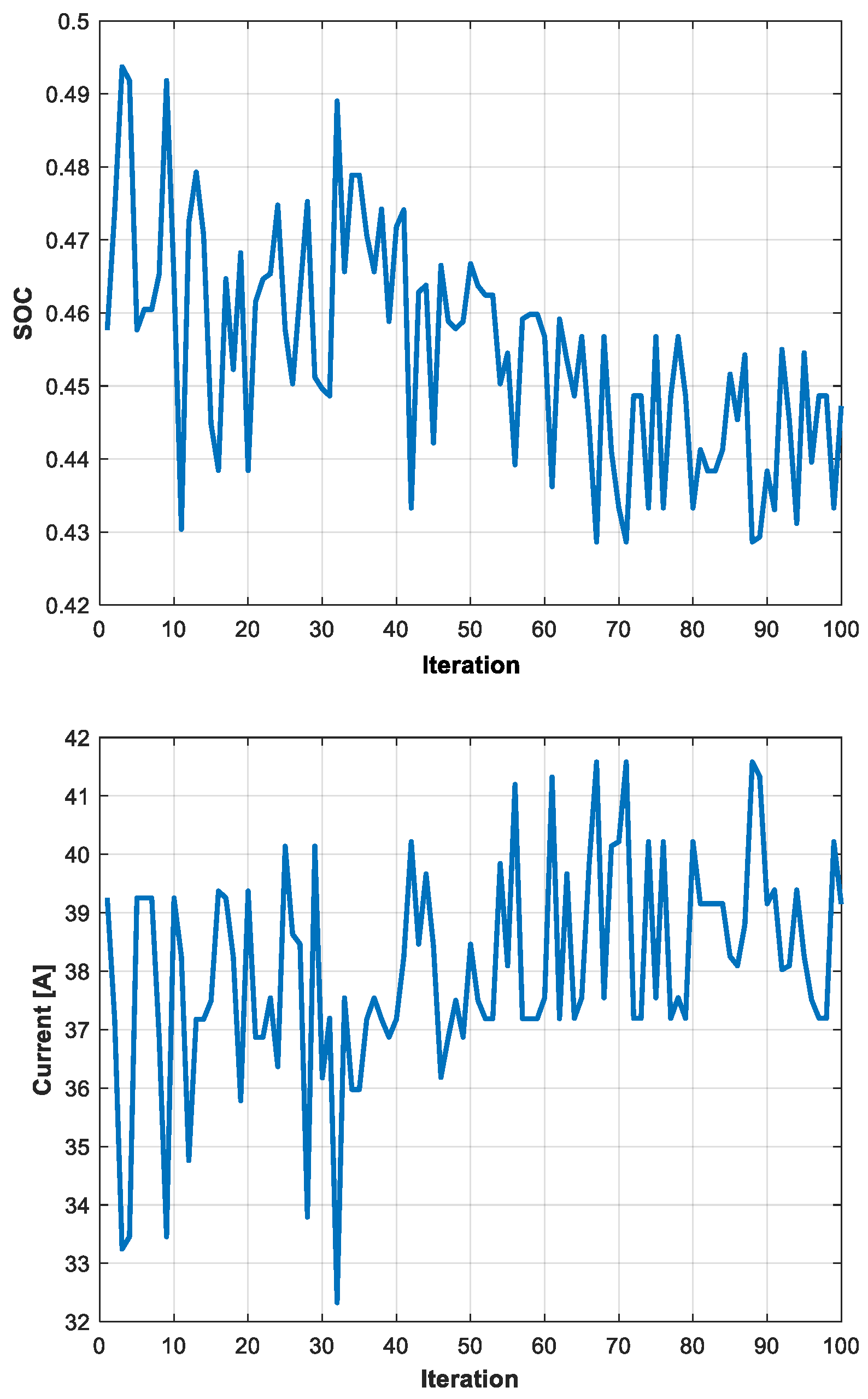
The solution of Equation (A5) gives the operation characteristics of the cruise. In particular, the cruise range, xcr, is used as the objective function in the optimization procedure. According to the control strategy, during the cruise, all the power is obtained by the thermal engine coupled with the electric generator; therefore, it is possible to assume that the state of charge (SoC) of the battery is essentially constant and equal to the final values obtained in the ascendant climb phase, and will be modified only in the descendent climb phase. At each iteration, whether the power chosen for the ICE is sufficient to guarantee the required trust at the cruise speed is determined.
As previously mentioned, the landing phase is not considered in the simulations because a large part of the energy needed to decelerate the aircraft can be provided by the mechanical braking of the propeller.
5.5. Check of the Optimization Procedure Constraints and Choice of Objective Function
The output obtained by the solutions of mechanical flights and the electric state of the battery storage system are used to verify some constrains applied to the differential evolution optimization.
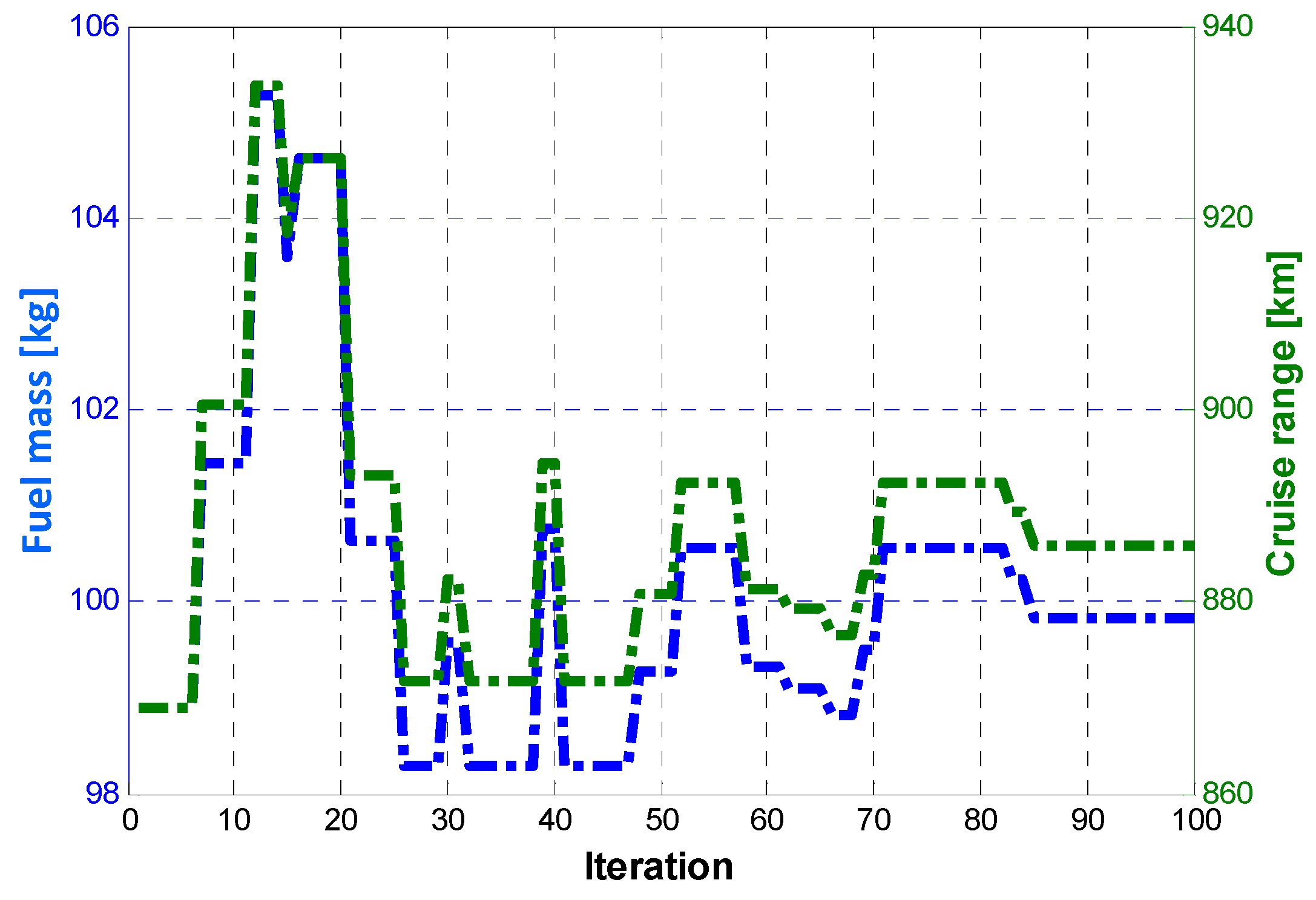
Specifically, two different problems are analyzed. In the first problem there is the minimization of difference between the cruise range and a target cruise value; the approach allows for a trade-off between the battery mass and fuel mass, which guarantees a certain cruise range. The adopted problem could be applied to a training course and in the application no fuel reserve is considered. The constrains are inherent to:
- -
the respect of the maximum take-off aircraft mass;
- -
the final SoC of the battery;
- -
the maximum duty-ratio between the output voltage battery pack and the required DC-link voltage;
- -
the energy stored in the battery pack must be at least equal to the energy required in the take-off and in the climb phase;
- -
the maximum value of the discharge current of the battery pack in the take-off and climb phases must be below the maximum discharge current of the battery cells used.
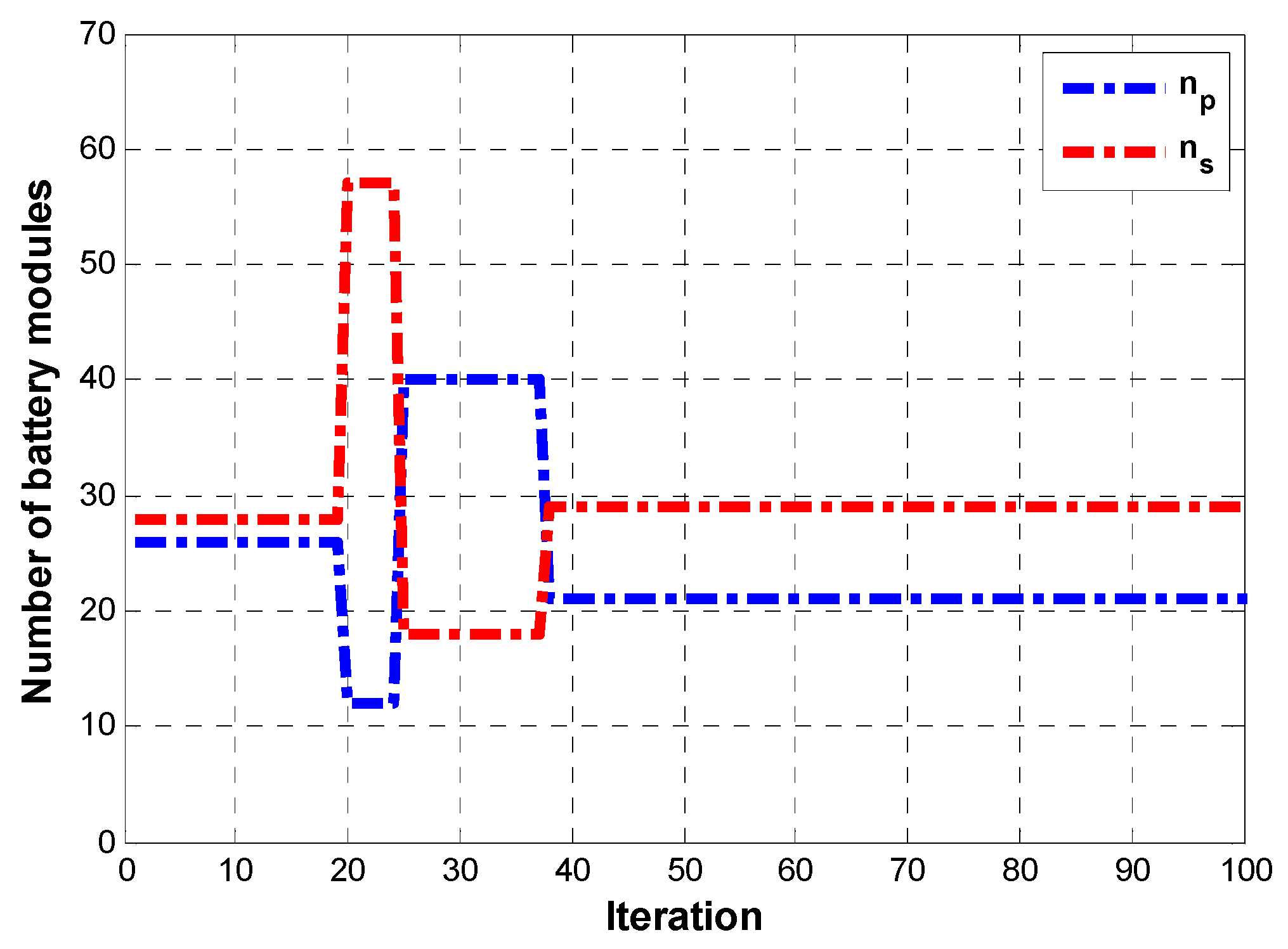
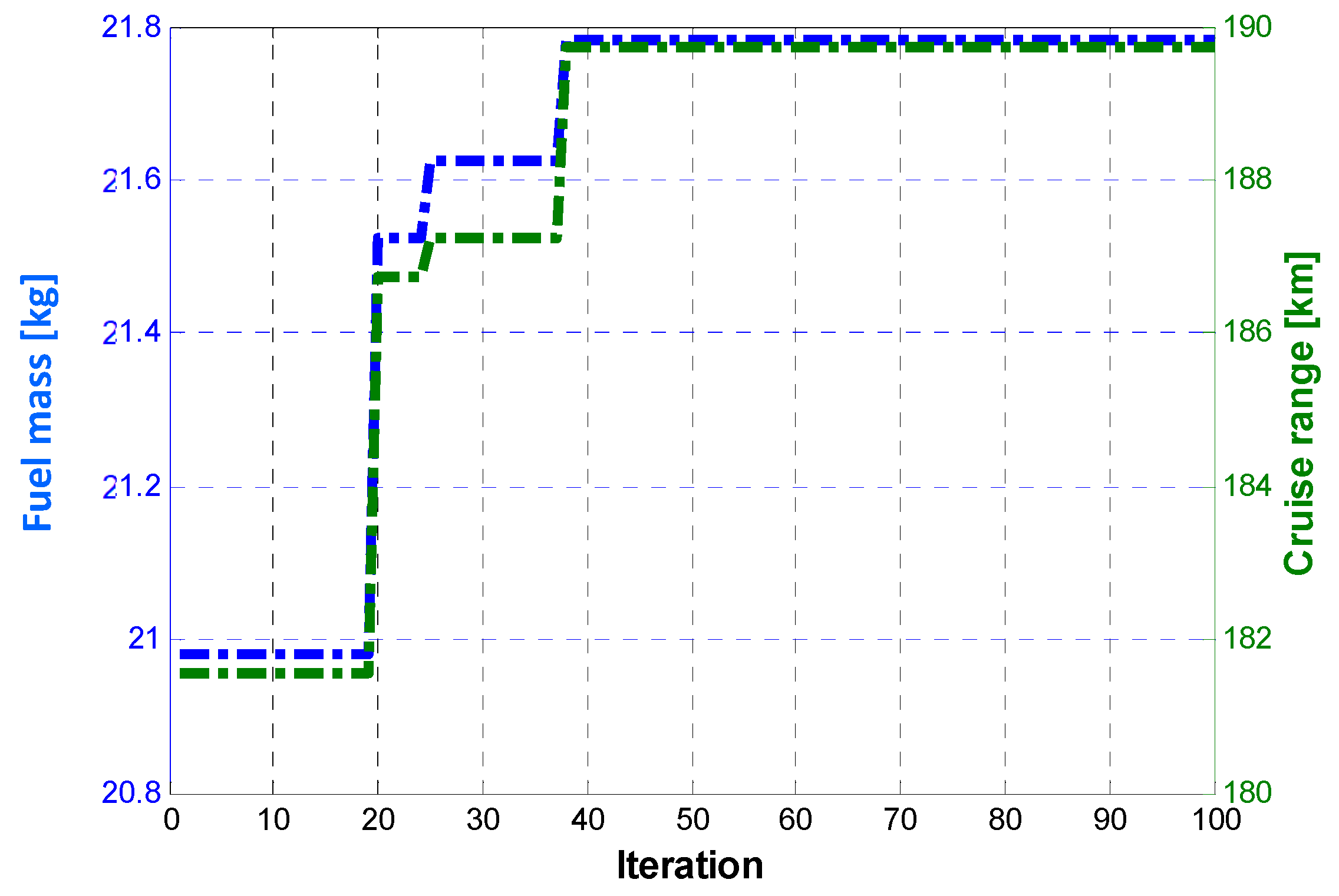
5.5.1. Problem 1
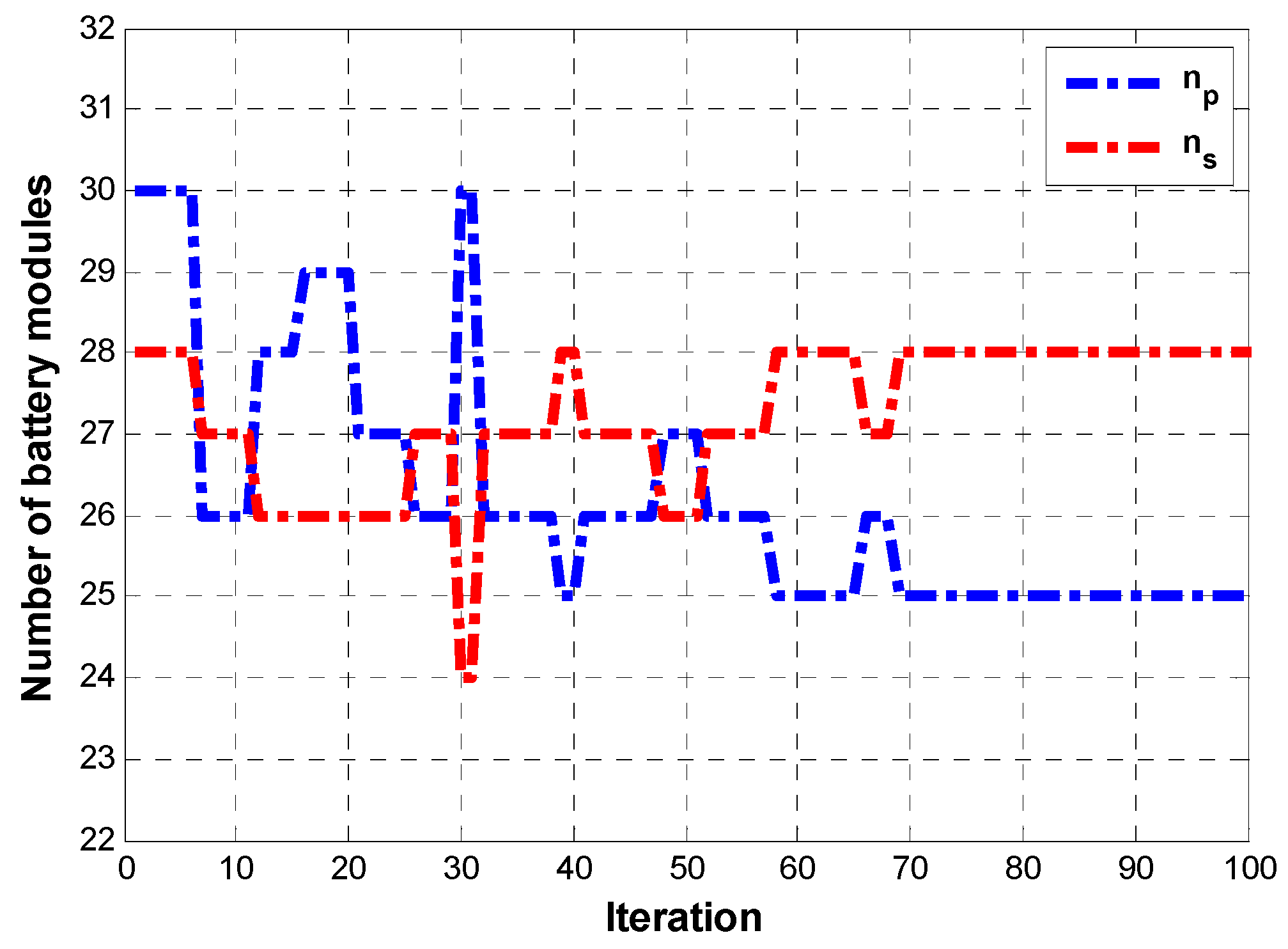
The second problem is related to the reduction in the battery costs: the minimization of the energy surplus contained in the battery (this surplus comes from the fact that the modules are defined as integer numbers) reduces the weight of the aircraft (or increases the amount of fuel with an increase in the cruise range) as well as the cost of battery installations.
5.5.2. Problem 2
The goal of Problem 1 is linked to the optimization of the fuel weight; it has to provide a trade-off between the battery mass and fuel mass which maximizes the cruise. Problem 2 is related to the reduction in the battery costs: the minimization of the energy surplus contained in the battery (this surplus comes from the fact that the modules are defined as integer numbers) reduces the weight of the aircraft (or increases the amount of fuel with an increase in the cruise range) as well as the cost of battery installations.
5.6. Crossover Operations and Check of Maximum Iterations Limit
As presented in [
25], the crossover conserves the original characteristics of the population and also, introduces a new diversity, with an effect similar to genetic algorithms and other heuristics methods. The crossover works are as follows: if the generated solution satisfies all the constraints of the optimization problem and, therefore, becomes a possible new solution, the crossover introduces a new probabilistic constraint. That is, the replacement of the determined solution only occurs if a generated number is greater than a certain threshold value. If that happens, and the number of iterations of the system is below the maximum number of iterations, the procedure is finished. If the value of the obtained objective functions is greater than the value of an element of the starting populations, the new populations replace the old elements of the populations. Otherwise, the procedure is tried again. When the maximum number of iterations is reached, the minimum (or maximum, depending on the objective function) of the final populations is the optimal value.