Optimization of the Energy Storage of Series-Hybrid Propelled Aircraft by Means of Integer Differential Evolution

Abstract

The possibility of realizing full electric or hybrid electric propulsion for aircraft has been considered due to the constant growth in the use of electric technologies in aircraft and the availability of high-power-density electrical machines and converters. In this paper, an optimized design approach is proposed with reference to the optimal trade-off between energy storage system sizing and the fuel mass of a series of hybrid aircraft. The problem is approached using an integer optimization algorithm based on differential evolution and by mixing both the flight mechanics and the electrical issues inherent to hybrid flights. This method has been validated by means of implementing numerical simulations and the results are reported and discussed in the paper.

1. Introduction

In the last two decades, increasing interest regarding the More Electric Aircraft (MEA) concept has been generated [1] with the aim of reducing fuel consumption, reducing emissions released into the atmosphere, increasing the redundancy and the reliability of onboard power systems, and reducing aircraft noise.

Recently, several research projects have led to the substantial electrification of onboard pneumatic components in order to increase the efficiency of flight systems—which has also introduced redundancies across the subsystems [2]—and the necessity to propose new power system architectures for the reduction of weight, increase of the reliability and to assure the correct performance of electrical drives [3]. Moreover, in order to increase the reliability and decrease the weight, DC-microgrids [4] seem to be the most suitable solution for future aircraft.

The current trend also envisages the use of electrical technology in aircraft propulsion [5,6,7,8] and both fully electric and hybrid propulsion aircraft prototypes have been presented. In the all-electric propulsion concept, the fuel and the thermal engine are completely substituted with energy storage systems (above all, fuel cells and battery) that are able to provide the entirety of the electric power required by the aircraft. The use of these new energy systems on board aircraft has been analyzed widely in the literature. In [9], an aircraft design that relies on fuel cells for propulsion and that is characterized by an unusual motor placement in order to maximize efficiency is presented, while in reference [10], the behavior of batteries that are used for the propulsion of small unmanned aircraft vehicles (UAV) at different temperatures is discussed. Additionally, Tariq [11] presents an overview of the battery systems for the MEA with an analysis of battery management systems for Li-ion batteries. Hybrid propulsion [12,13,14,15] is quite similar to the hybrid traction used in automotive applications; the propulsion can be achieved with the use of electric motors or with both electric motors and internal combustion engines (ICEs). The electric power is provided by ICEs coupled with an electric generator and usually from a battery pack; the possible series and parallel configurations are similar to the scheme used in the automotive industry [16,17]. In this paper, the approach used was applied to an existing aircraft and the “electrification” of propulsion was made without any change to the aircraft structures, the maximum take-off weight, or the aerodynamic performance. The possibility of changing the complete structure of the aircraft surely permits an increase in the performance and convenience of hybrid propulsion [18].

The sizing of electrical energy storage systems is a critical issue for their integration in aircraft and its optimization is mandatory. Different sizing tools for supercapacitor or battery systems are suggested in [19,20]. In these tools, only one storage system is sized at a time and with one pre-chosen cell.

Novel approaches based on optimization algorithms—so-called integrated design by optimization—are becoming increasingly mature and will become particularly powerful if subsequent efforts are made in terms of modeling for design.

The integrated optimal design approach consists of coupling sizing models with an optimization algorithm that automatically tunes the parameters to optimize system criteria (mass, losses, etc.) while satisfying the technological and operational constraints.

Many types of optimization procedures can be utilized in engineering applications: single or multi-objective, continuous or discrete optimization, linear or non-linear optimization, non-gradient optimization techniques, etc. The choice of the type of optimization is related to specific mathematical problems and to the technical boundary conditions (e.g., the necessity of using integer variables). Regarding the considered problems, as mentioned above, the necessity of reducing pollution requires the determination of an optimal trade-off problem between the size of the onboard energy storage system and the mass of the fuel. The objective functions can be different, as proposed in the literature (e.g., [21]). The problem is solved by the optimization of three different objective functions related to the energy cost, which is the primary energy required in order to guarantee flight completion and the reduction of CO₂ emissions. In [22], the size of the hybrid storage system which is constituted by supercapacitors and batteries is optimized and the objective function is inherent to the reduction of the total mass of the primary energy. In [13], a simple conceptual design approach is proposed to determine the optimal size of the battery system in order to maximize the range or duration of the flight for the available fuel in the aircraft’s tank. In [22,23], a sizing tool for reducing the global storage system’s weight by taking several constraints (environmental and electrical ones) into account and by adjusting some parameters—such as the discharge ratio of the storage components and the ambient temperature—within a proper energy management strategy was proposed. The sizing method was improved upon with an optimization algorithm solved by a simulated annealing method. In [24], a sizing methodology for the battery of an UAV is proposed. The methodology is based on the use of an integral formulation for the constant discharge of battery power, thereby obtaining the optimal size of the batteries.

In this paper, an integer optimization procedure is proposed, which permits the integer character of some variables and the simultaneous solution to both the mechanical flight problem and electrical problem related to the energy storage systems to be taken into account. Regarding the mechanical flight problem, a mathematical approach that is able to solve the mechanical flights equation during the climb phase, based on the energy minimization is proposed. The solution of the optimization procedure is mainly based on the use of an integer differential evolution approach (IDEA) [25]. The differential evolution is a simple and efficient algorithm which permits the solution of the optimization problem with a rapid convergence to the solution. The need to use an integer optimization is due to the nature of the battery packs, where the number of cells or modules are integer numbers. In the literature [20,24,26], it is typically found that the battery storage systems are of optimal size in terms of both energy and power; therefore, the determination of the number of cells is postponed; in this way, it is guaranteed that the optimal value of the energy and power is achieved, but it is not guaranteed that the number of cells is optimal.

Starting from an assigned flight profile (cruise altitude, cruise speed, cruise range), the aim of this paper is to develop an optimization procedure which can be used during the pre-flight settings and is able to evaluate the optimal integration of the battery storage system and ICE to guarantee the correct operation during the execution of the flight profile.

The main novelty of the proposed optimization procedure regards the possibility to use it as a pre-mission energy management process. In fact, with the possibility to develop a modular battery pack and considering the mission profile, it is possible to calculate the optimal size of the battery pack. Through a new disposition of the module of the pack (each module can be constituted by a certain number of parallel and series cells), it is possible to minimize and reduce the useless weight of the aircraft.

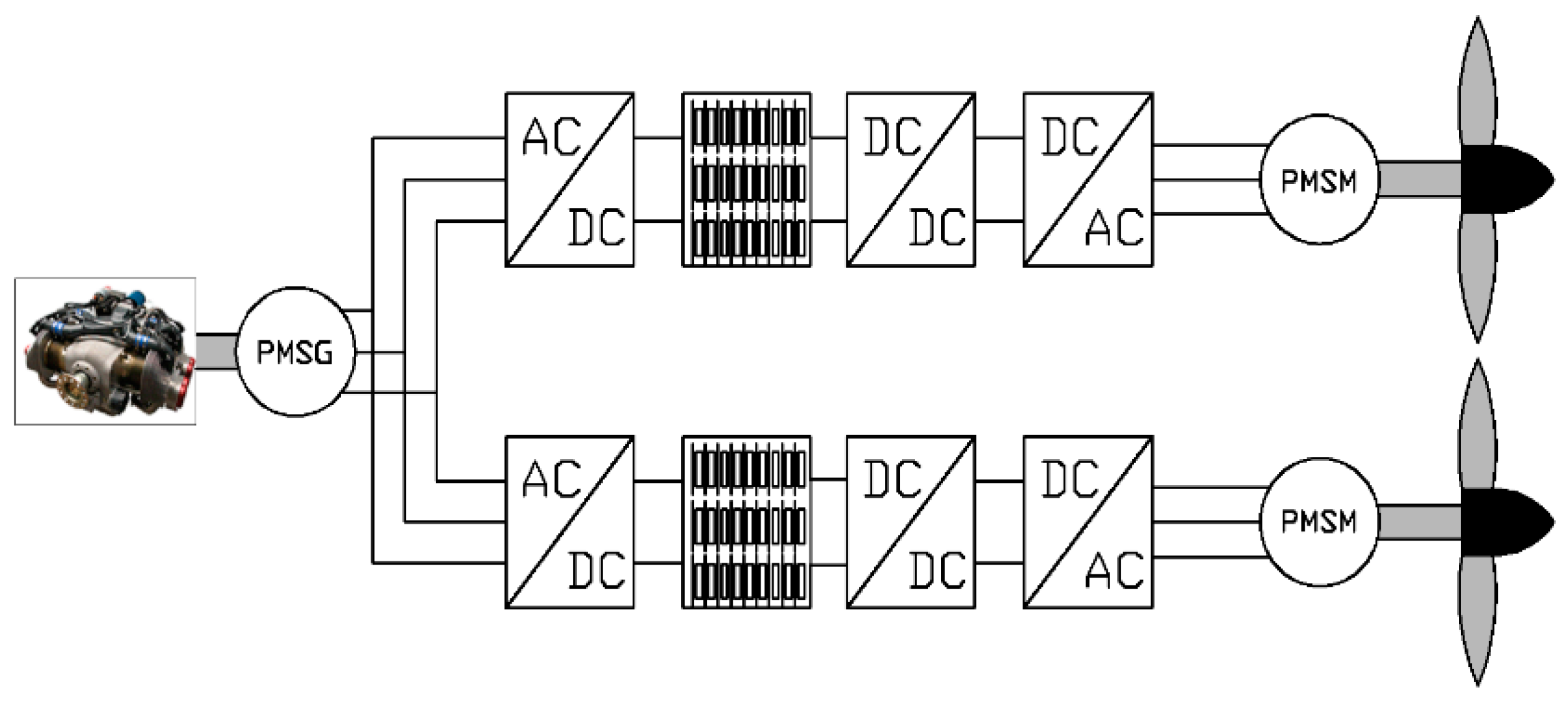
The optimized design approach of the sizing of the energy storage system of a series-hybrid aircraft is detailed and validated in this paper. In the next section, the hybrid propulsion system of the aircraft is defined. In the third section, the dynamic equations of the aircraft profile are detailed and in Section 4 the battery system model is explained. The optimization sizing procedure is proposed in Section 5 and validated by simulation in Section 6 where the results are reported and discussed.

2. Hybrid Propulsion Scheme

A series-hybrid propulsion scheme is considered in the present work. The advantages of a series-hybrid propulsion are different, for example, the thermal engine can be controlled to let it operate at a fixed point during the recharging of the batteries, with the possibility to keep constant and maximize the efficiency. Furthermore, the series propulsion provides the possibility of having only electric propulsion of the propellers, avoiding the mechanical gear between the engine and the propeller, and increasing the efficiency (in particular when the propellers have a fixed pitch, and in this case, the variation of the speed within a certain range is necessary). Figure 1 shows a scheme of the series-hybrid architecture considered in the paper.

The architecture is based on a twin-propeller civil aircraft. Each propeller is controlled by a permanent magnet synchronous motor (to increase the reliability, it is also possible to use a motor with more than three phases), a cascade of a DC-DC converter, and a VSI links the battery modules to the motor. A single energy storage system and a single controlled rectifier for both the propellers are considered in the scheme. The reliability of the system can be increased by dividing the battery pack into two parts and using two different rectifiers (Figure 2). In this way, the propulsion system is not completely compromised when a fault occurs in either the storage system or in one of the converters.

3. Dynamics Equations of Aircraft Load Profile

To determine the dimension of the batteries and AVGAS, which must be used for the aircraft flight, it is necessary to model the aircraft trajectories, which can be divided into take-off, climb, cruise, and landing. The energy management strategy considered in this paper is based on the use of an all-electric propulsion during the take-off and climb phases and a mixed electric and series-hybrid propulsion during the cruise. The use of full electric propulsion during the take-off and the climb reduces the noise and pollution emissions of the aircraft, in particular when the aircraft is near the airport and the city; therefore, it is considered a so-called “green” integration of the airport in the city. The sizing of the battery and the determination of the fuel weight depend on the trajectories of the aircraft and their values’ influence the performance of the aircraft. The modeling of the aircraft profile can be done using the equation of dynamics.

3.1. Take-Off Dynamics Equation

During the take-off, two different types of forces act upon the aircraft: the friction forces due to the weight of the aircraft and the contact between the tires and the ground and the aerodynamic drag. Considering Equations (A1)–(A3) in Appendix A, it is possible to determine the length of the take-off using the following equation:

$$x_{to}=-\frac{W}{\rho gS\left(C_d-\mu C_l\right)}\log \left[\frac{\left(T-\mu W-1,44\frac{\left(C_d-\mu C_l\right)}{C_{l,\max }}\right)}{\left(T-\mu W\right)}\right]$$

(1)

During the take-off, it is assumed that the propulsion happens with a constant power equal to the maximum power of the propulsion system.

3.2. Climb Phase Dynamics Equation

Considering that the trust vector is parallel to the climb trajectory, the variation of the climb angle during the flight is negligible, and taking into account the dynamic Equation (A4), the duration of the climb [22] can be calculated by integrating the following equations:

$$\frac{dt}{dh}=\frac{1}{P_s}\left(\frac{v}{g}\frac{dv}{dh}+1\right)$$

(2)

where P_S is equal to:

$$P_s=\frac{v\left(T-D\right)}{W}$$

(3)

and defines the specific excess power. The equations of Equation (A4) are referred to an ascendant climb phase and can also be considered for the descendent climb, with a variation of the signs in the equilibrium of the dynamic quantities.

3.3. Cruise Phase

The cruise phase is modeled supposing that the speed cruise and the altitude are kept constant; taking into account that during the cruise, the propulsion is electric but the energy is provided both by the batteries and the fuel. Starting from Equation (A5) and using some manipulations of the formula, it is possible to determine the Breguet range [27] equation, which depends on the initial and final value of the weight of the aircraft and also, on the fuel consumption:

$$x_c={\eta }_p\frac{H}{g}\frac{C_l}{C_d}\log \left(\frac{W}{W_f}\right)$$

(4)

with η_p equal to the product of thermal engine efficiency, propeller efficiency, electric generator and motor efficiency, battery conversion efficiency, and converter efficiency.

4. Modeling of the Electrical Storage System

The sizing of the energy storage system and the determination of the fuel mass necessary for the optimal thermal engine performance can be done by means of models of the electric components of the propulsion system. The electric motor and power converter can be modeled considering only the power density (kW/kg) and the efficiency, which depend on the load. The power densities of the electrical machines and converters are calculated considering the data of commercially available three-phase permanent magnet machines and converters with a high power density (all of the considered components are liquid cooled), the efficiency is modeled using a polynomial which depends on the required load power and is obtained from the datasheet of the commercial components.

Battery Modeling

The battery storage system is modeled according to [26]:

$$\{\begin{array}{l}{V}_{oc,sm}=c_0 SoC\left(t\right)+c_1\\ I_{b,m}\left(t\right)n_p\left[n_s{V}_{oc,sm}-R_b{I}_{b,m}\left(t\right)\right]=P_{ele}\\ SoC\left(t\right)=SoC\left(t_0\right)-\frac{1}{Q_b}{\displaystyle \underset{t_0}{\overset{t_f}{\int }}{I}_{b,m}\left(t\right)dt}\end{array}$$

(5)

where the meaning of the utilized symbols can be found in Figure 3. n_s indicates the number of series cells, while n_p is the number of parallel branches. The current of a single cell is I_b,m; the sum of the currents of each branch gives the total current of the battery pack. Without any current, the output voltage is V_oc,sm (due to the internal voltage drop, this value decreases when the battery is not zero).

It is assumed that the battery temperature is kept constant (the variation of temperature could be due to the variation in the ambient temperature at different altitudes or to the losses generated during the operations). With this assumption, it is possible to avoid the dependence of battery parameters on the variable temperature, with a reduction of the complexity of the problem.

5. Optimization Procedure

The optimization procedure is mainly based on the use of an integer differential evolution approach (IDEA) [21] with the aim to minimize (or maximize) certain parameters of the aircraft or the physical parameters of the aircraft trajectories. The optimization procedure is realized on more levels; the external level is inherent to the IDEA technique and acts on three variables: the number of parallel cells n_p and series cells n_s, and the weight of fuel. At each iteration of the optimization, the procedure solves another three problems linked to the optimization of the trajectories. 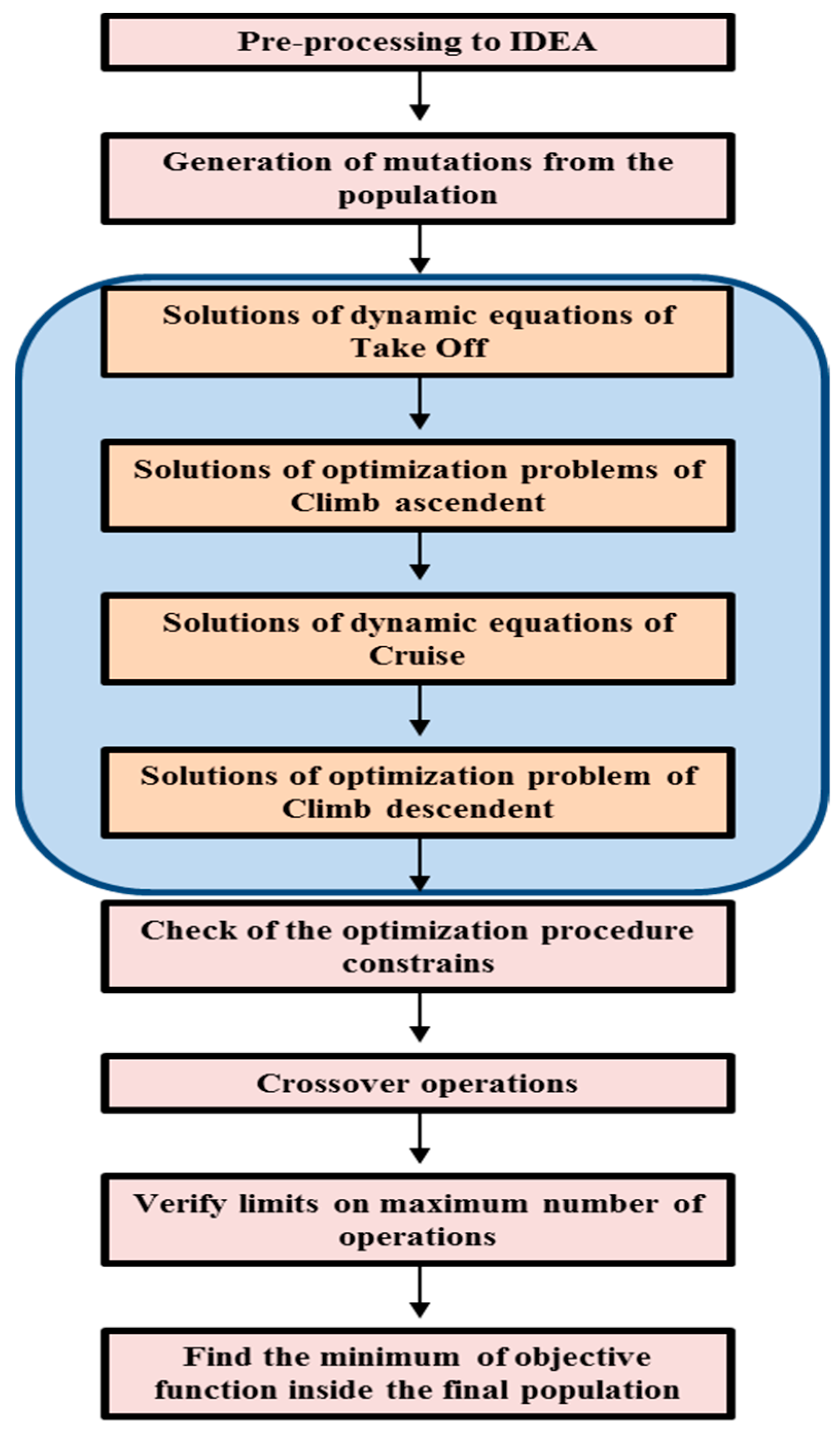Figure 4 shows a flowchart of the procedure.

5.1. Pre-Processing to IDEA

Before initializing the procedure, a population of n_pop possible solutions is generated:

$${\mathbf{x}}_{\mathbf{pop}}=\left[\begin{array}{ccc}{n}_{p,1}& n_{s,1}& m_{fuel,1}\\ n_{p,2}& n_{s,2}& m_{fuel,2}\\ ⋮& ⋮& ⋮\\ n_{p,npop}& n_{s,npop}& m_{fuel,npop}\end{array}\right]$$

(6)

5.2. Generation of Mutations

The mutations (that is the new candidate solution) are generated according to the procedure represented schematically in Figure 4.

$$n_{p,new}=n_{p,{\rho }_1}+\mathrm{int}\left[\alpha \left(n_{p,{\rho }_2}-n_{p,{\rho }_3}\right)\right]$$

(7)

$$n_{s,new}=n_{s,{\rho }_1}+\mathrm{int}\left[\alpha \left(n_{s,{\rho }_2}-n_{s,{\rho }_3}\right)\right]$$

(8)

$$m_{fuel,new}=m_{fuel,{\rho }_1}+\alpha \left(m_{fuel,{\rho }_2}-m_{fuel,{\rho }_3}\right)$$

(9)

The parameters ρ₁, ρ₂, and ρ₃ are random integer numbers comprised in the range (1,n_pop), α is a random positive real number below 1, and the function “int” rounds the number obtained in the square brackets to the nearest integer. If the obtained solution is positive, a candidate solution is found and processed inside the modeling of aircraft dynamics.

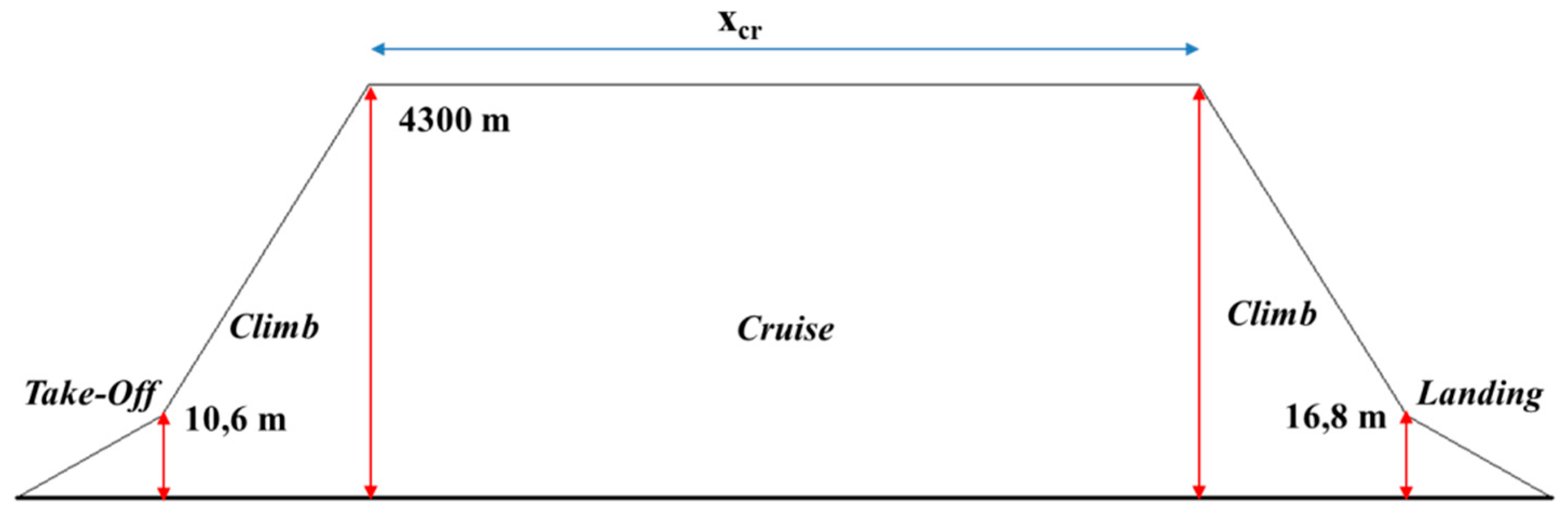
The solution of Equations (A1) and (1) permits the calculation of the take-off time and the total energy, E_to, required during this phase. It is imposed that the take-off starts at a level of 0 m and is completed at z_to,f (about 10.6 m) [26]. The final condition of the battery pack is evaluated by calculating the required electrical power. These values are used as initial values for the next step in the optimization problem.

5.3. Solutions of Optimization Problems of Climb Ascendant/Descendent

The optimization of the climb phase is more complex with respect to that of take-off. In fact, in this case, an objective optimization is carried out inside the IDEA. The goal of this optimization is the minimization of the total energy required for the climb phase. The simulated climb phase is assumed to possess a uniform acceleration. Considering the fact that the climb phase commences at z_to,f and the final altitude is the cruise altitude, z_cr, it is also considered that the final speed must be equal to the cruise speed (in this case, any acceleration during the cruise phase is avoided). In the hypothesis of uniform acceleration, the altitude climb is divided in a certain number of divisions, in order to obtain that:

$$z_{cr}-z_{to,f}={\displaystyle \sum _{k=1}^{n_{div}}\Delta z_k}$$

(10)

$$v_{cr}=v_f+{\displaystyle \sum _{k=1}^{n_{div}}\Delta v_k}$$

(11)

where Δv_k is the variation of the velocity in each division. The used objective function is the total energy required in the climb:

$$\begin{array}{l}\min E_{cl}\left({\mathbf{x}}_{\mathbf{cl}}\right)\\ \{\begin{array}{l}{g}_1\left({\mathbf{x}}_{\mathbf{cl}}\right)=0\\ g_2\left({\mathbf{x}}_{\mathbf{cl}}\right)=0\\ ⋮\\ g_{eq}\left({\mathbf{x}}_{\mathbf{cl}}\right)=0\\ s_1\left({\mathbf{x}}_{\mathbf{cl}}\right)\le 0\\ s_2\left({\mathbf{x}}_{\mathbf{cl}}\right)\le 0\\ ⋮\\ s_{ineq}\left({\mathbf{x}}_{\mathbf{cl}}\right)\le 0\end{array}\end{array}$$

(12)

where the unknown variables are:

$${\mathbf{x}}_{\mathbf{cl}}=\left[\Delta v_1,\dots ,\Delta v_{n_{div}},\Delta z_1,\dots ,\Delta z_{n_{div}},T_1,\dots ,T_{n_{div}},\gamma \right]$$

(13)

Then, the objective function becomes:

$$\min E_{cl}\left({\mathbf{x}}_{\mathbf{cl}}\right)=\min \left[{\displaystyle \sum _{k=1}^{n_{div}}\frac{T_k\left(v_f+{\displaystyle \sum _{h=1}^k\Delta v_h}\right)\Delta t_k}{{\eta }_{batt}{\eta }_{VSI}{\eta }_{dc}{\eta }_{mot}}}\right]$$

(14)

In Equation (14), the sum of the energy calculated in each sub-interval considered for the climb phase is given. In particular, the numerator is presented as the product between the propeller trust, the velocity, and the time duration and this product is divided by the global efficiency of the electric propulsion chain.

The variation in the altitude and aircraft speed must satisfy the following equations:

$$\begin{array}{l}\{\begin{array}{l}{g}_1\left({\mathbf{x}}_{\mathbf{cl}}\right)=z_{cr}-z_{to,f}-{\displaystyle \sum _{k=1}^{n_{div}}\Delta z_k}\\ g_2\left({\mathbf{x}}_{\mathbf{cl}}\right)=v_{cr}-v_f-{\displaystyle \sum _{k=1}^{n_{div}}\Delta v_k}\\ g_{2+k}\left({\mathbf{x}}_{\mathbf{cl}}\right)=\left(v_f+{\displaystyle \sum _{h=1}^k\Delta v_h}\right)\frac{\Delta v_k}{\Delta z_k}\sin \left(\gamma \right)-\frac{g}{W}\left[T_k-D_k-W\sin \left(\gamma \right)\right]\end{array}\end{array}$$

(15)

The first two equations are related to the fact that the final altitude and the final aircraft speed must be equal to the desired cruise altitude and cruise speed; therefore, the optimal value obtained for the altitude and speed variation in each sub-interval must be related to these values. The third equation relates the climb angle to all the dynamic variables.

The inequalities are:

$$\begin{array}{l}\{\begin{array}{l}0,9\left(\frac{v_{cr}-v_f}{n_{div}}\right)\le \Delta v_k\le 1,1\left(\frac{v_{cr}-v_f}{n_{div}}\right)\\ 0,9\left(\frac{z_{cr}-z_{to,f}}{n_{div}}\right)\le \Delta z_k\le 1,1\left(\frac{z_{cr}-z_{to,f}}{n_{div}}\right)\\ 0\le T_k\le T_{\max }\\ 0\le \gamma \le {\gamma }_{\max }\end{array}\end{array}$$

(16)

The first two inequalities are used in order to limit the variation of the aircraft speed and altitude; the last two ensure that the maximum time for the climb phase and the climb angle are respected.

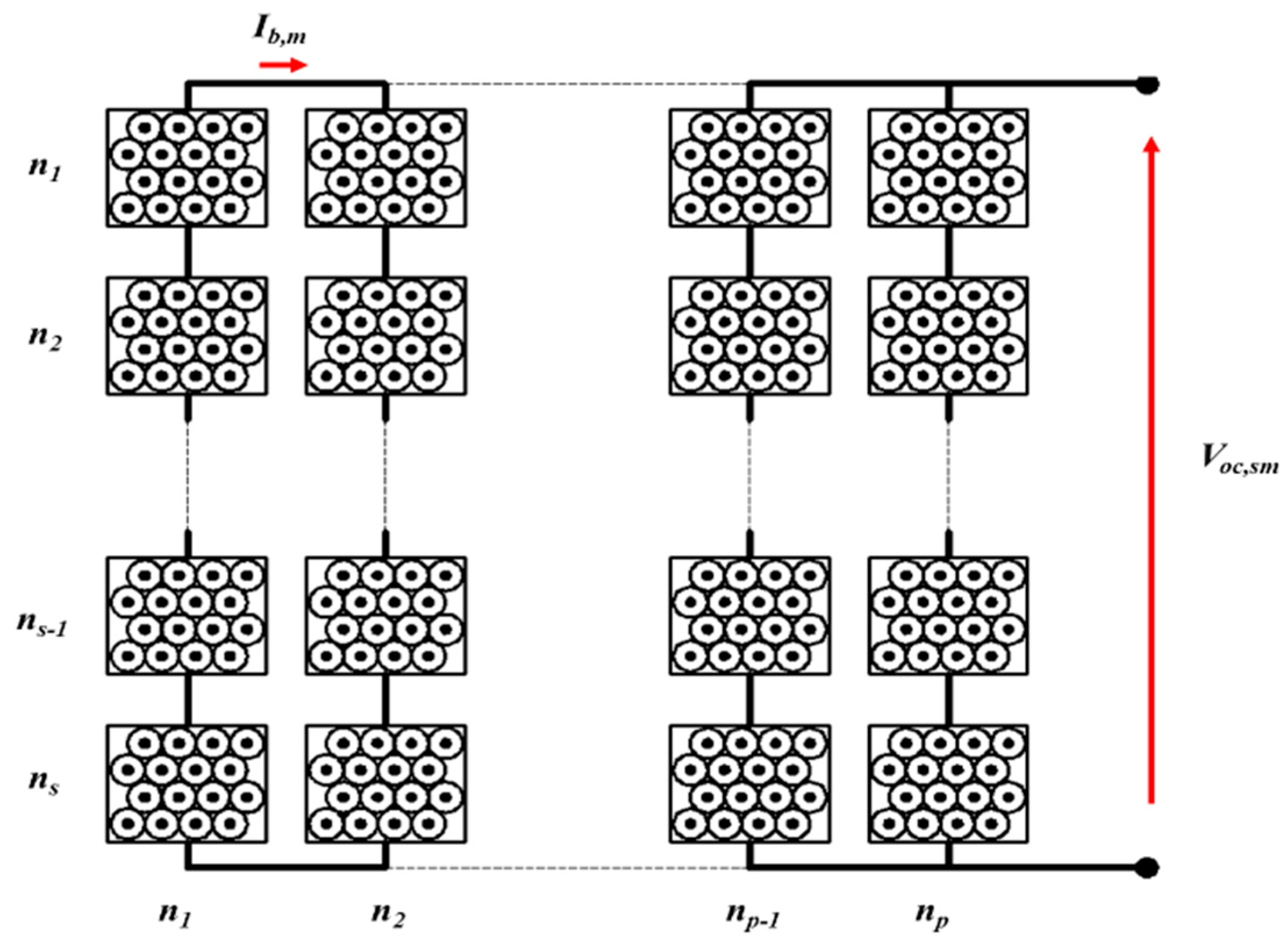
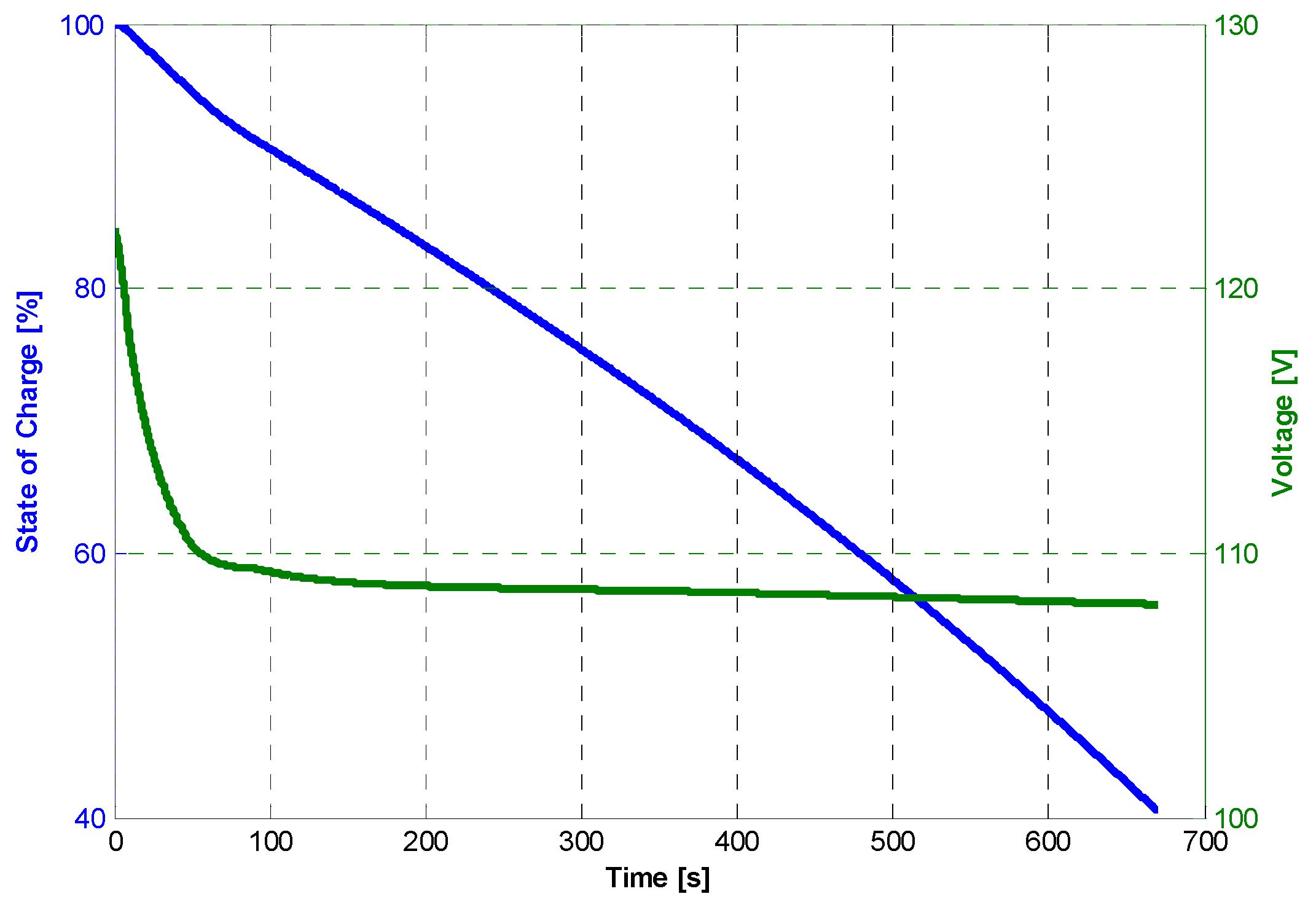
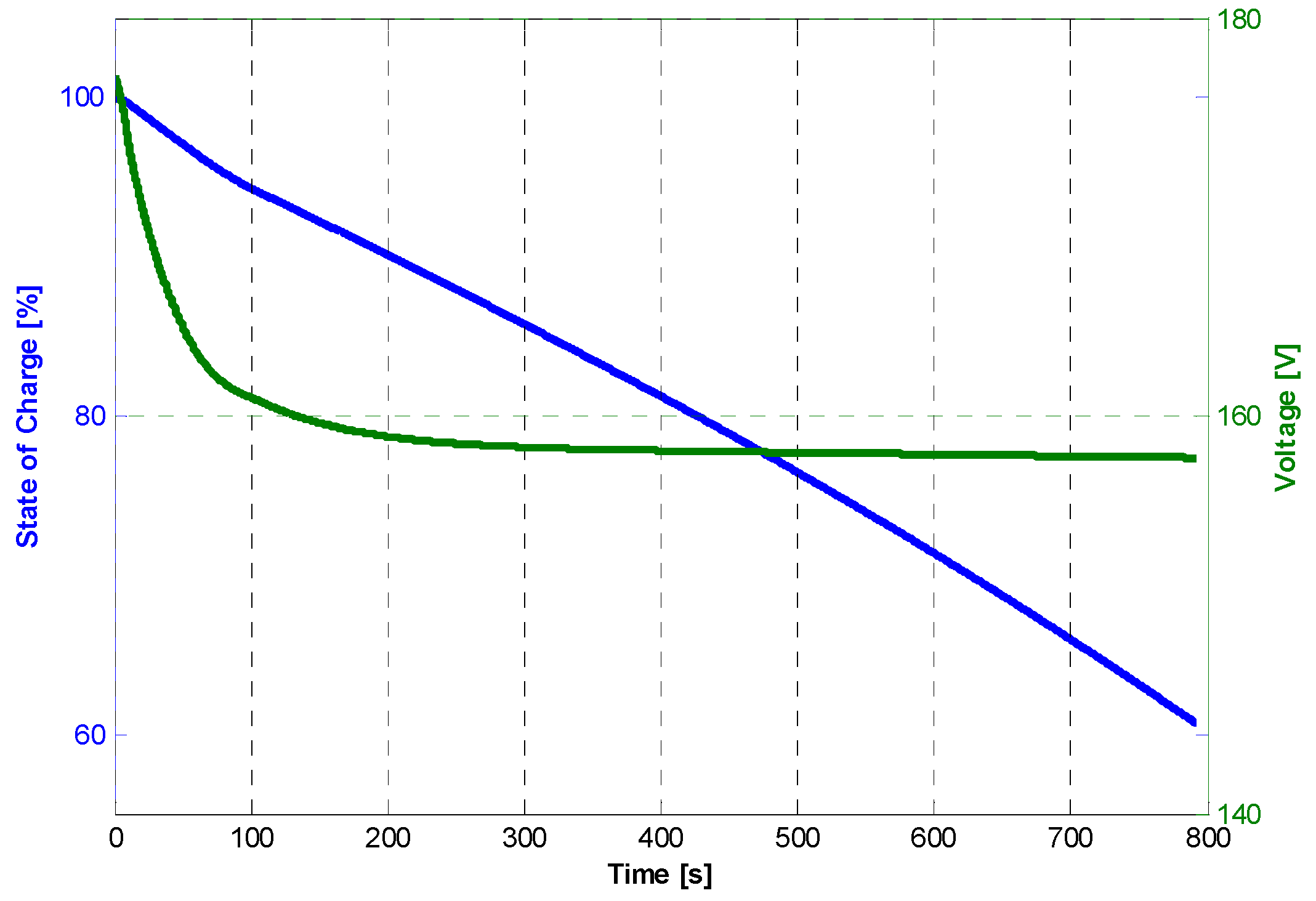
Starting from the final condition of the battery packs after take-off, the final state of charge and the final value of the open-circuit voltage V_oc,sm are calculated. The same approach is used in the descendent phase of the climb.

5.4. Solutions of Dynamic Equations of the Cruise

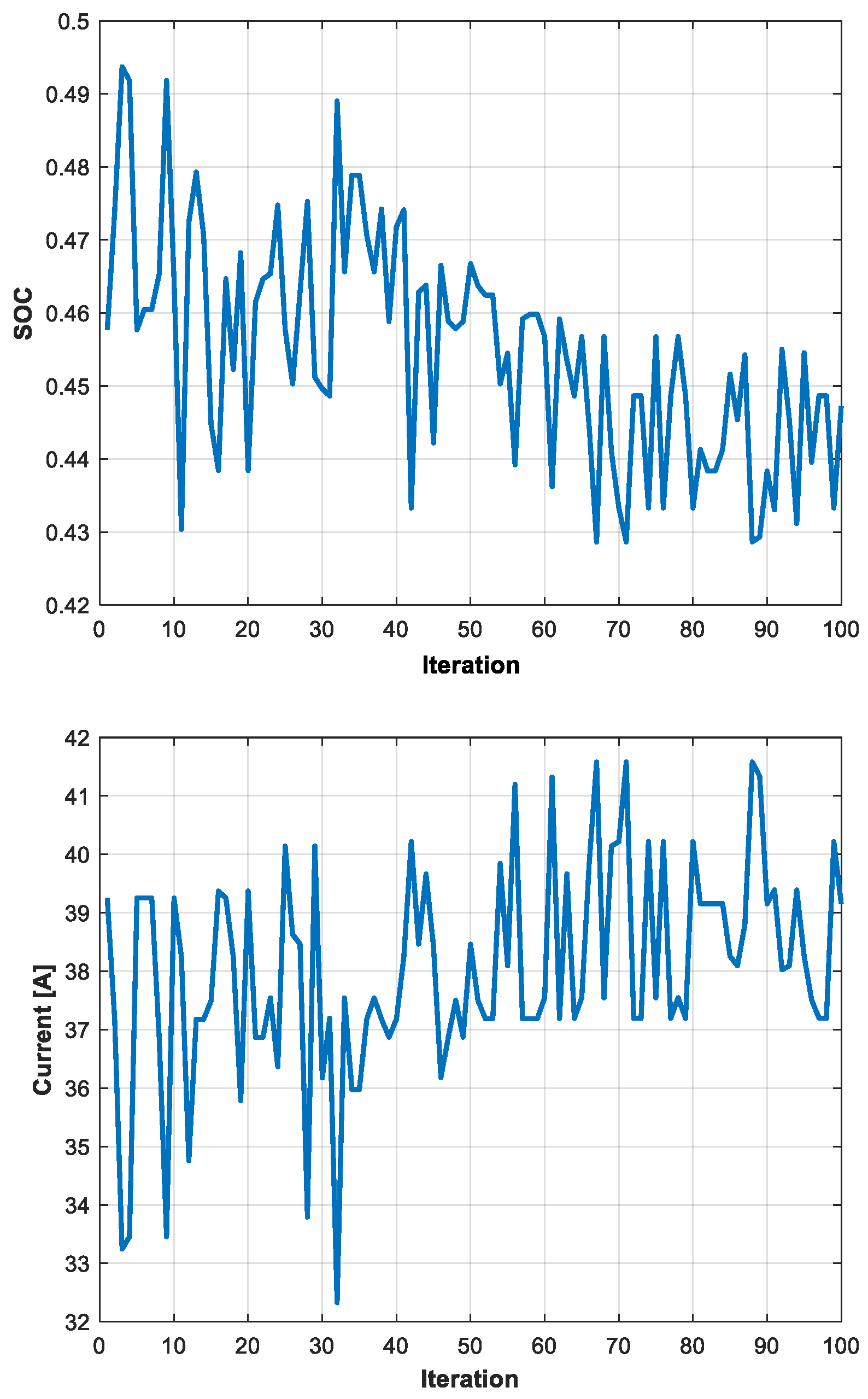
The solution of Equation (A5) gives the operation characteristics of the cruise. In particular, the cruise range, x_cr, is used as the objective function in the optimization procedure. According to the control strategy, during the cruise, all the power is obtained by the thermal engine coupled with the electric generator; therefore, it is possible to assume that the state of charge (SoC) of the battery is essentially constant and equal to the final values obtained in the ascendant climb phase, and will be modified only in the descendent climb phase. At each iteration, whether the power chosen for the ICE is sufficient to guarantee the required trust at the cruise speed is determined.

As previously mentioned, the landing phase is not considered in the simulations because a large part of the energy needed to decelerate the aircraft can be provided by the mechanical braking of the propeller.

5.5. Check of the Optimization Procedure Constraints and Choice of Objective Function

The output obtained by the solutions of mechanical flights and the electric state of the battery storage system are used to verify some constrains applied to the differential evolution optimization.

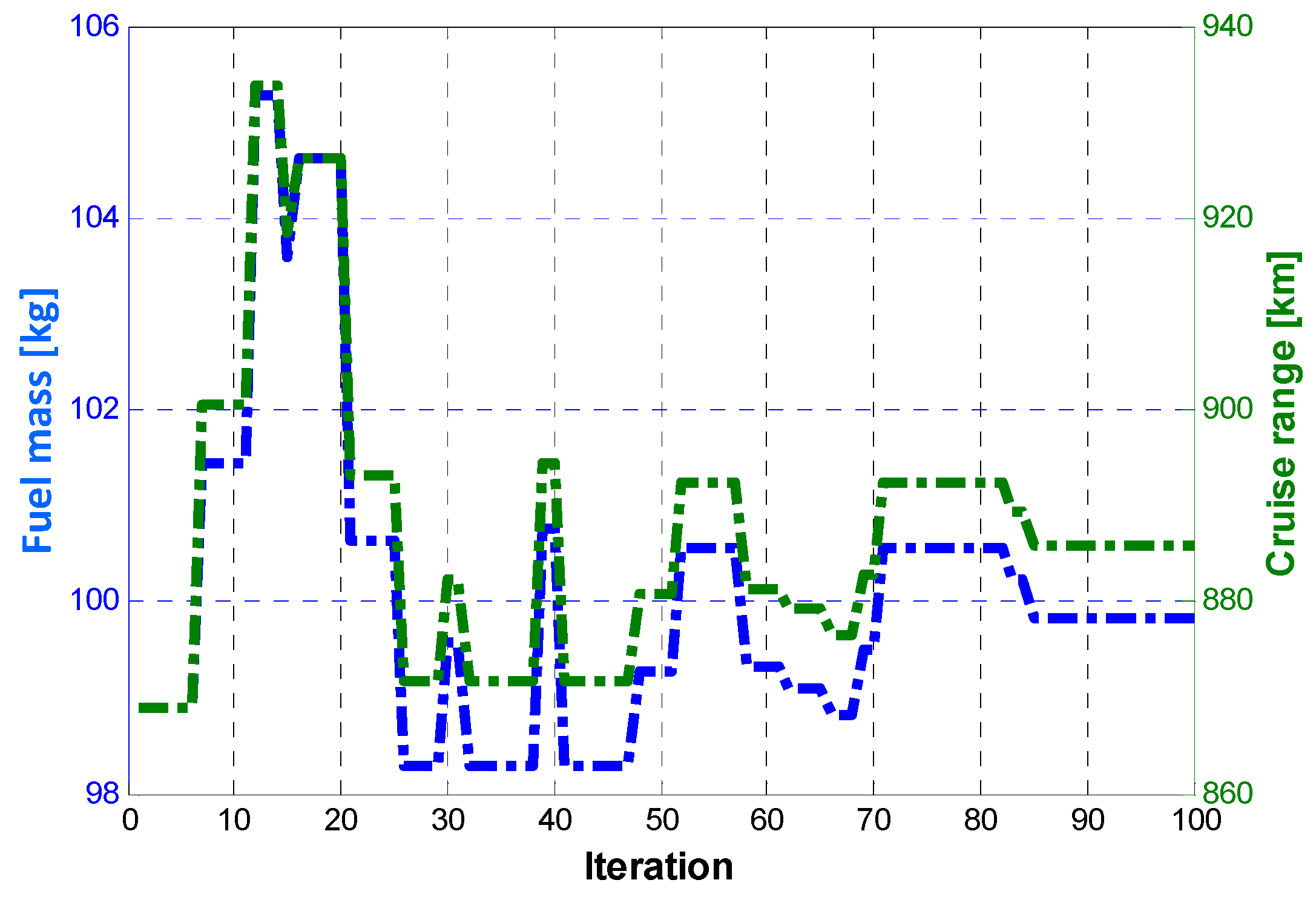
Specifically, two different problems are analyzed. In the first problem there is the minimization of difference between the cruise range and a target cruise value; the approach allows for a trade-off between the battery mass and fuel mass, which guarantees a certain cruise range. The adopted problem could be applied to a training course and in the application no fuel reserve is considered. The constrains are inherent to:

-

the respect of the maximum take-off aircraft mass;

-

the final SoC of the battery;

-

the maximum duty-ratio between the output voltage battery pack and the required DC-link voltage;

-

the energy stored in the battery pack must be at least equal to the energy required in the take-off and in the climb phase;

-

the maximum value of the discharge current of the battery pack in the take-off and climb phases must be below the maximum discharge current of the battery cells used.

5.5.1. Problem 1

$$\begin{array}{l}\min \left(x_{cr}-x_{cr,tar}\right)\\ \{\begin{array}{l}{n}_p{n}_s{m}_{s,c}+m_{fuel}+m_{m,o}+m_{pay}<=m_{m,to}\\ So{C}_{fin}>20\%\\ \frac{V_{dc}}{V_{oc,sm,fin}}<d_{\max }\\ n_p{n}_s{m}_{s,c}{\delta }_{batt}\ge \left(E_{to}+E_{cl}\right)\\ \max \left[I_{b,m,dec},I_{b,m,cl}\right]<{\mathrm{I}}_{\max ,b,p}\end{array}\end{array}$$

(17)

The second problem is related to the reduction in the battery costs: the minimization of the energy surplus contained in the battery (this surplus comes from the fact that the modules are defined as integer numbers) reduces the weight of the aircraft (or increases the amount of fuel with an increase in the cruise range) as well as the cost of battery installations.

5.5.2. Problem 2

$$\begin{array}{l}\min \left[n_p{n}_s{m}_{s,c}{\delta }_{batt}-\left(E_{to}+E_{cl}\right)\right]\\ \max \left(x_{cr}\right)\\ \{\begin{array}{l}{n}_p{n}_s{m}_{s,c}+m_{fuel}<=m_{m,to}\\ So{C}_{fin}>20\%\\ \frac{V_{dc}}{V_{oc,sm,fin}}<d_{\max }\\ \max \left[I_{b,m,dec},I_{b,m,cl}\right]<{\mathrm{I}}_{\max ,b,p}\end{array}\end{array}$$

(18)

The goal of Problem 1 is linked to the optimization of the fuel weight; it has to provide a trade-off between the battery mass and fuel mass which maximizes the cruise. Problem 2 is related to the reduction in the battery costs: the minimization of the energy surplus contained in the battery (this surplus comes from the fact that the modules are defined as integer numbers) reduces the weight of the aircraft (or increases the amount of fuel with an increase in the cruise range) as well as the cost of battery installations.

5.6. Crossover Operations and Check of Maximum Iterations Limit

As presented in [25], the crossover conserves the original characteristics of the population and also, introduces a new diversity, with an effect similar to genetic algorithms and other heuristics methods. The crossover works are as follows: if the generated solution satisfies all the constraints of the optimization problem and, therefore, becomes a possible new solution, the crossover introduces a new probabilistic constraint. That is, the replacement of the determined solution only occurs if a generated number is greater than a certain threshold value. If that happens, and the number of iterations of the system is below the maximum number of iterations, the procedure is finished. If the value of the obtained objective functions is greater than the value of an element of the starting populations, the new populations replace the old elements of the populations. Otherwise, the procedure is tried again. When the maximum number of iterations is reached, the minimum (or maximum, depending on the objective function) of the final populations is the optimal value.

6. Simulation Results

The performance of the proposed optimization procedure is verified by means of numerical simulations implemented in Matlab ©. The aircraft parameters are reported in

Table 1. Main parameters of the aircraft selected as a case study.

Parameter	Value
Number of electric motors	2
Number of thermal engines	1
Rated power electric motor	75 kW
Maximum power of thermal engine	100 kW
DC-link voltage	270 V
Number of passengers	1
Maximum cruise speed	260 km/h
Wing area	14.8 m2
Empty aircraft mass	760 kg
Maximum take-off mass	1230 kg
Zero-lift drag coefficient Cd0	0.025

; the parameters are the same as those of Tecnam P2006T [28], where it is supposed that the ICEs are substituted with an electric motor with the same power, and the empty aircraft mass is unchanged. The ICE considered for the hybrid flight has a maximum power less than the total power of the electric motor because it operates only in the cruise phase, when the required trust is usually below the maximum power of the propeller motors. The evaluation of the optimum value of rated power for the electric motor and of the maximum power of the ICE is not considered in this paper.

The simulation refers to the flight profile reported in Figure 5. In

Table 2. Main parameters of the considered lithium battery pack.

Parameter	Value
Rated voltage	3.7 V
Battery capacity	11 Ah
c0	3 V
c1	1.2 V
Imax,b,p	88 A

, the main parameters of the considered battery pack are reported. The first simulation reported demonstrates the convergence of the optimization problems. For each problem, other simulations using different cells [29] and two different voltages for the DC-link are carried out.

6.1. Simulation of Problem 1

The problem described by Equation (17) is simulated, imposing a maximum value of d_max = 6.5. An initial population of n_pop = 8 is generated, and the values α, ρ₁, ρ₂, ρ₃ and the threshold for the crossover operations are obtained using the random generators of Matlab. The number of mutation substitutions is set as 100. The cruise range is fixed as 180 km. The final optimized values obtained for 11 Ah batteries with a continuous discharge rate of 8 C and a DC-link voltage of 270 V, are reported in

Table 3. Final values of Problem 1.

Parameter	Value
np	21
ns	29
mfuel,tot	22 kg
xcr	190 km
SoCfin	44%

.

Figure 6 and Figure 7 show the trends of mutation substitutions of the battery module numbers (both in series and parallel) of the fuel mass and the cruise range. It is possible to note that the convergence of the method occurs at approximately 40 iterations. In Figure 8, the trends in SoC and the maximum current in the climb phase are reported.

In

Table 4. Problem 1 for different cells and the DC-link voltage.

Q [Ah]	Continuous Discharge Rate	Vdc [V]	np	ns	mfuel,tot [kg]	SoCfin [%]	xcr [km]
7.5	5	270	19	45	22	47.2	192
11	8	270	21	29	22	44.6	190
16	5	270	10	40	20.5	47.6	180
7.5	5	540	24	46	21	55.6	180
11	8	540	25	42	21	63.4	180
16	5	540	25	23	21	50.2	182

, the results obtained for different cells (with equal nominal voltage and parameters d₀ and d₁) and for an inverter DC-link of 270 V and 540 V are shown.

It is evident that the cruise range is closer to the fixed value, but the final SoC is higher than that in the case of the DC-Link at 270 V. This happens because the number of cells is increased to respect the maximum duty cycle imposed for the DC–DC converter. It can be concluded that the excess stored energy can also be used for the reduction of pollutant emissions and to increase the cruise range.

6.2. Simulation of Problem 2

The problem described by Equation (18) is simulated, imposing a maximum value of d_max = 6.5 and the number of iterations is 100. The parameters for the IDEA are calculated in the same manner as in Problem 1. The optimal solution obtained for 11 Ah batteries with a continuous discharge rate of 8 C and a DC-link voltage of 270 V is indicated in

Table 5. Final values of Problem 2.

Parameter	Value
np	25
ns	28
mfuel,tot	105 kg
xcr	729 km
SoCfin	44.4%
Energy stored in excess	12.65 kWh

.

Figure 9 and Figure 10 show the trends of the mutation substitution of battery module numbers in series and in parallel, and the variation of the energy stored in excess and in the cruise range.

The results of simulations demonstrate that, in Problem 2, the type of optimization used enables the cruise range to be increased while reducing the energy stored in excess in the battery pack. This is due to the relationship between the fuel mass and the energy stored in the battery: if the fuel mass increases, more energy is needed for the take-off and climb phases, resulting in greater utilization of the battery and an increase in the cruise range as shown in Figure 11.

In

Table 6. Problem 2 for different cells and DC-link voltages.

Q [Ah]	Continuous Discharge Rate	Vdc [V]	np	ns	mfuel,tot [kg]	mfuel,reserve [kg]	SoCfin [%]	xcr [km]
7.5	5	270	29	34	105	20.9	47	774
11	8	270	25	28	101	21.1	44.4	729
16	5	270	26	18	100	20.9	47.3	728
7.5	5	540	12	92	112	21.1	49	834
11	8	540	13	58	113	21.2	46.8	837
16	5	540	31	23	111	21.3	44.3	811

, the results obtained for Problem 2 are reported and related to different types of cells and two voltage levels of the DC-link. With respect to the results of Problem 1, in this case it is possible to note that the use of a higher value for the DC-link improves the performance of the aircraft, especially for the maximization of the cruise range. Furthermore, the minimization of the residual energy stored in the batteries is also evident for the DC-link of 540 V.

As mentioned in Table 1, in the mission profile, the presence of at least one passenger must be guaranteed. From the calculation of the total mass required by the mission profile it is possible to obtain that for both; the best payloads are obtained with a DC-link of 270 V and with a battery of 16 Ah. Specifically, the maximum payload for Problem 1 is about 313 kg and is about 211 kg for Problem 2. This confirms the respect of all the constraints (electrical and mechanical) and highlights the possibility to effectively optimize the pre-flight settings of the aircraft.

Regarding the convenience of the hybrid technologies, it is possible to highlight the following results:

-

with the series topologies adopted, the emissions during the take-off and climb phases are eliminated; these are the parts of the flight that occur close to built-up areas, such as cities;

-

to date, an economically beneficial way to replace a traditional piston engine aircraft with a hybrid propelled aircraft does not exist. In fact, excluding the cost of the electric powertrain and considering only the battery costs of $176/kWh [29], a cost of $30,000 regarding implementing a hybrid propelled aircraft for the first problem and a cost of $34,500 for the second one is obtained. Evidently, the introduction of a new battery type or the rapid increase of the battery energy density, will dramatically increase the viability of hybrid/all-electric technologies.

6.3. Verification of the Results Through the Real-Time Simulations of the Battery Pack

Real-time simulations of the performance of the battery pack during the take-off and climb phases are carried out with Simulink©. The battery cells are modeled according to [27] and using the parameters of the Kokam cells [30]. The simulations performed are related to the results obtained in Problem 1 and for the cases of an 11 Ah cell (Table 4). The results for a DC-link voltage of 270 V are depicted in Figure 12, while the case of 540 V is shown in Figure 13.

As it is possible to note in both the cases, the final values of SoC are very close to the value obtained from the optimization. In this way, real-time simulations demonstrate the effectiveness of the proposed optimization procedure.

7. Conclusions

All electric aircraft and the hybrid electric aircraft are currently feasible technologies which can be applied to UAVs and passenger aircraft. A crucial problem is the correct integration and sizing of the storage systems utilized on board. This factor influences the performance of the aircraft in terms of battery and fuel costs, flight distance range and flight time, and safety. An optimization procedure for a series-hybrid aircraft has been proposed in this paper based on an integer differential evolution approach, which taking into account the electrical and flight mechanical behavior of the aircraft, gives the optimal trade-off between the battery size and the mass of fuel. The series-hybrid architecture provides a take-off and climb phase (both ascendant and descendent) in the electric mode, with the goal of reducing the noise emission and pollution in the phase when the aircraft is nearest to the airport. The sizing optimization procedure has been applied to a real case and validated by implementing numerical simulations in Matlab, and the results have been verified by real-time scenario simulations. The results demonstrate the fast convergence of the method and the importance of the main electrical parameters (such as the DC-link voltage) in the application. The proposed procedure respected all the electrical and mechanical constraints and also determines the minimum payload which must be guaranteed in the aircraft. Future work will include the optimization of the power-train performance with the integration of the energy store optimization and the optimization of the drives control and the propulsion motor sizing procedure.