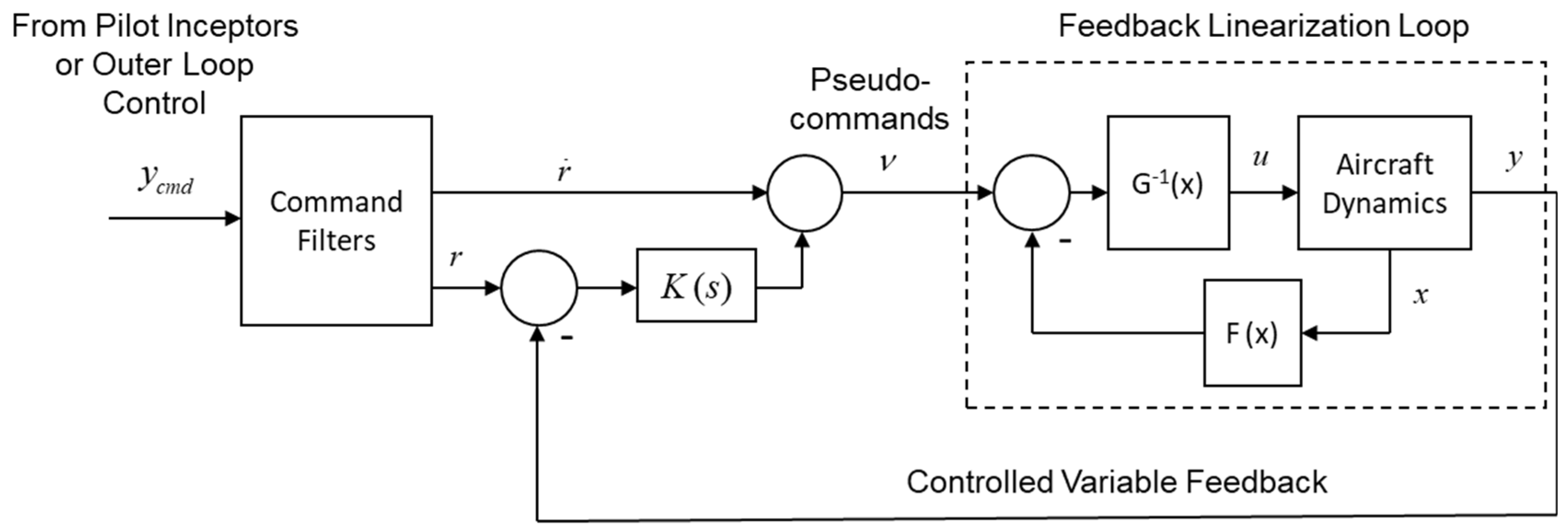
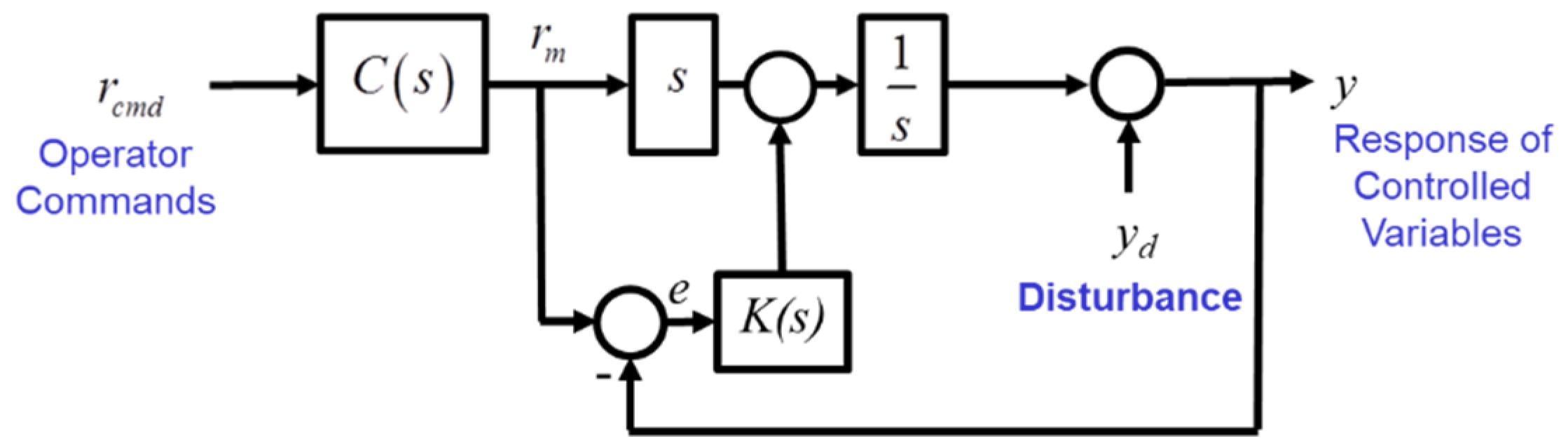
The stability and performance of the DI controller were investigated using the validated simulation of the utility helicopter. A linear systems analysis was used to study the closed-loop stability of the system and the impact of NMP zeros. Stability margins versus disturbance rejection bandwidth properties were studied to understand tradeoffs between stability robustness and disturbance rejection performance. In addition, non-linear simulations are conducted to view command tracking performance and to verify the linear model analyses.
4.1. Linear Analysis
An analysis of the linearized dynamics (both open-loop and closed-loop) was conducted to demonstrate the stability and performance of the DI control design. Analysis is focused on the 80 kts flight condition as presented in the validation
Section 3.3. The open loop system dynamics (as modelled by the full and reduced order models) are illustrated in
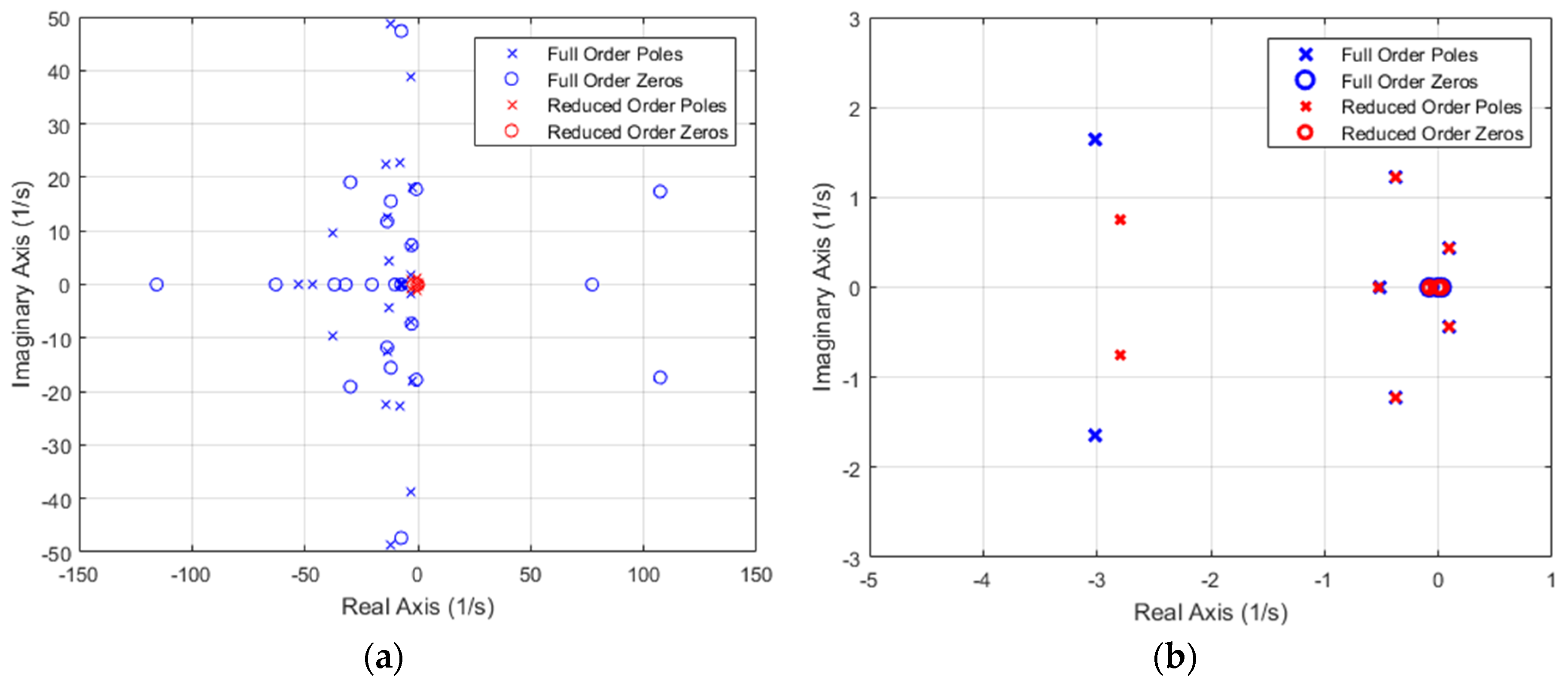
Figure 7, which shows the eigenvalues and transmission zeros of the MIMO system (from inputs to controlled variable outputs). The figure on the right shows a close up of the low-frequency poles and zeros associated with the rigid body dynamics. The poles (eigenvalues) are summarized in
Table 2, which identifies the modes based on analysis of the eigenvectors, and the transmission zeros are shown in
Table 3.
The analysis shows that the reduced order model is indeed a good approximation of the low frequency dynamics of the aircraft. Furthermore, the high order model has a number of high-frequency zeros, which would be problematic if one applied feedback linearization on the full order system. Those zeros would result in quickly divergent unstable modes of the closed loop system. The reduced order model has one very low frequency zero, which would result in a low-frequency instability.
Now the feedback linearization loop is applied to the full- and reduced-order systems with no controlled variable feedback (K(s) = 0). For the reduced order model, we have perfect inversion, and indeed there are four zero eigenvalues, and four eigenvalues identical to the zeros of the reduced order model. For the full-order system with approximate feedback linearization, there are still four zero eigenvalues, as well as four eigenvalues slightly different from the zeros for the reduced order model. In addition, there are several stable high frequency modes.
Note that the unstable eigenvalue increases with application of feedback linearization to the full-order mode, but there are no large magnitude, unstable eigenvalues corresponding to the large NMP zeros of the full-order system. The eigenvalue at 0.123 is in fact manageable; its value is reduced with CV feedback and then can be stabilized with outer loop control or pilot compensation. Application of this model results in a slow airspeed instability. A physical explanation is that if one constrains the pitch attitude of the rotorcraft, it will have no tendency to return to the trim airspeed. For the purpose of this study, the mode will be handled through output redefinition. A small component of forward speed is added to the pitch axis CV
The change in CV results in stable closed loop dynamics. In practice, the forward speed measurement is sent through a high-pass filter to avoid issue of defining perturbation from trim airspeed.
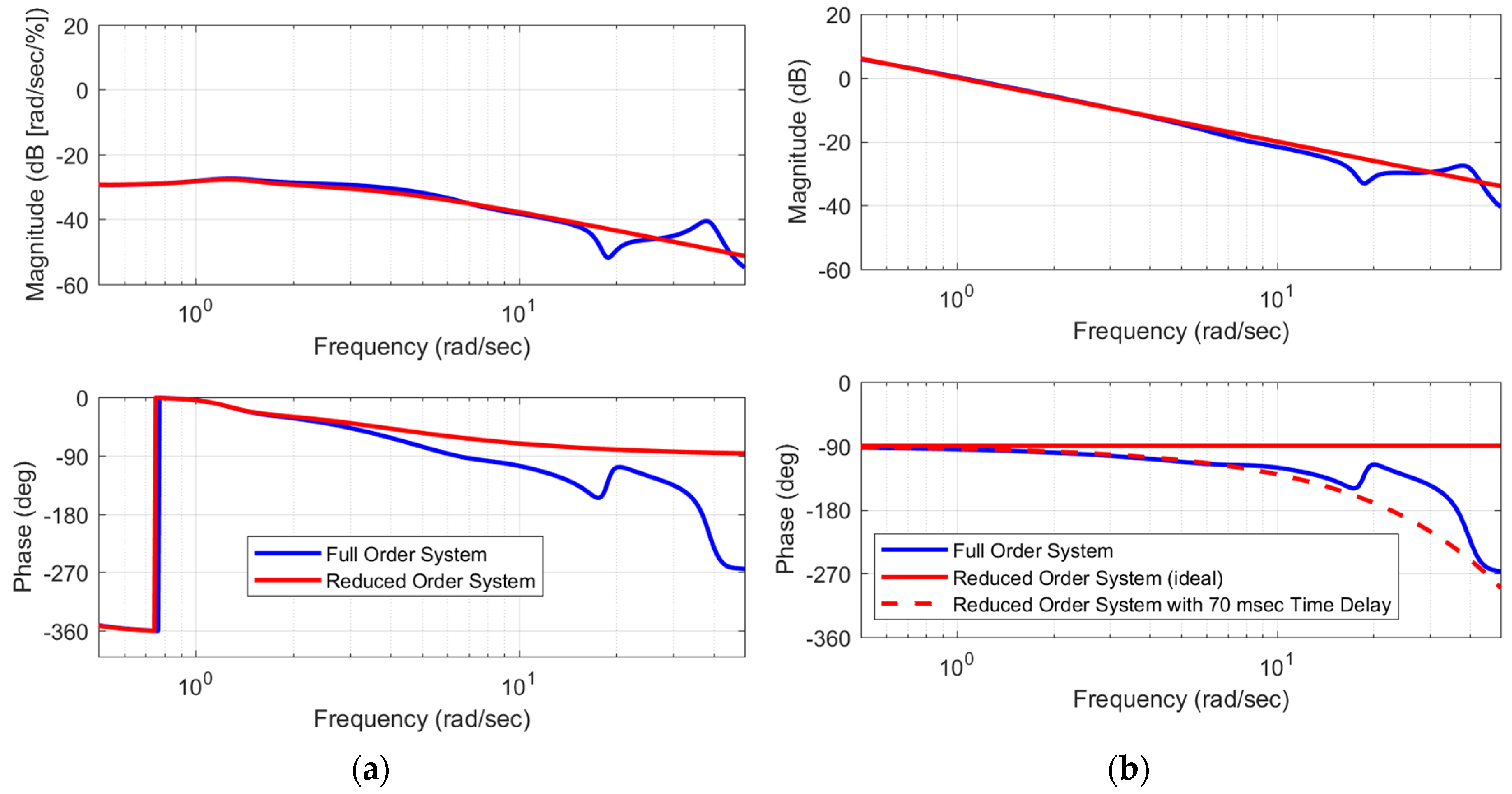
Figure 8 shows sample roll-axis frequency responses of the open loop systems and the full- and reduced-order systems with feedback linearization. As expected, the reduced order model shows perfect conversion to integrator dynamics. The full-order system approximates an integrator with and added time delay (estimated as 70 ms). Thus, when we apply controlled variable feedback to the full-order system we expect some added phase lag and reduced stability margin relative to the case of ideal feedback linearization.
CV feedback is applied in the form of proportional + integral + double integral (PII) feedback for roll and pitch rates, and PI feedback for vertical speed and yaw using the nominal gains described in
Table 1.
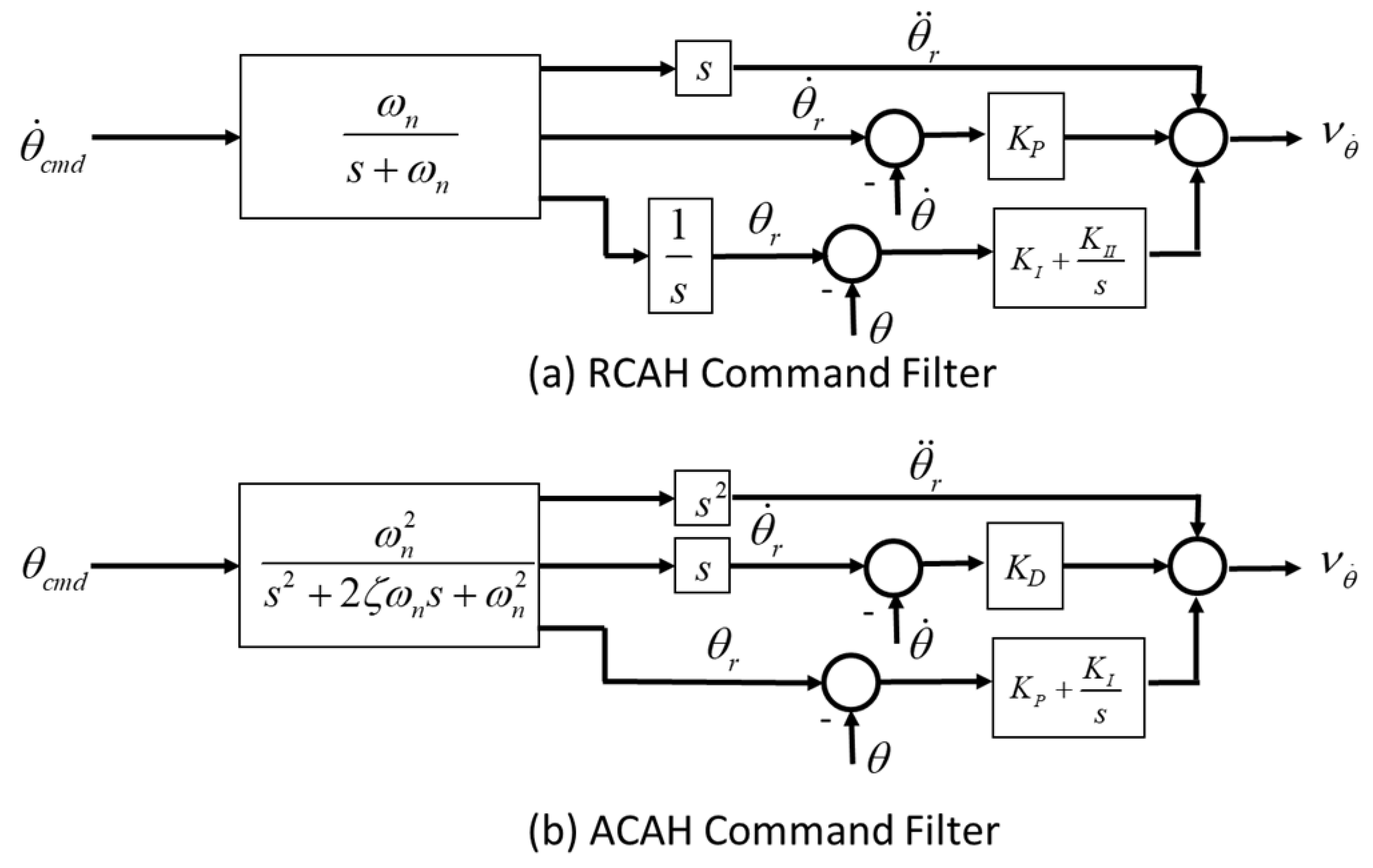
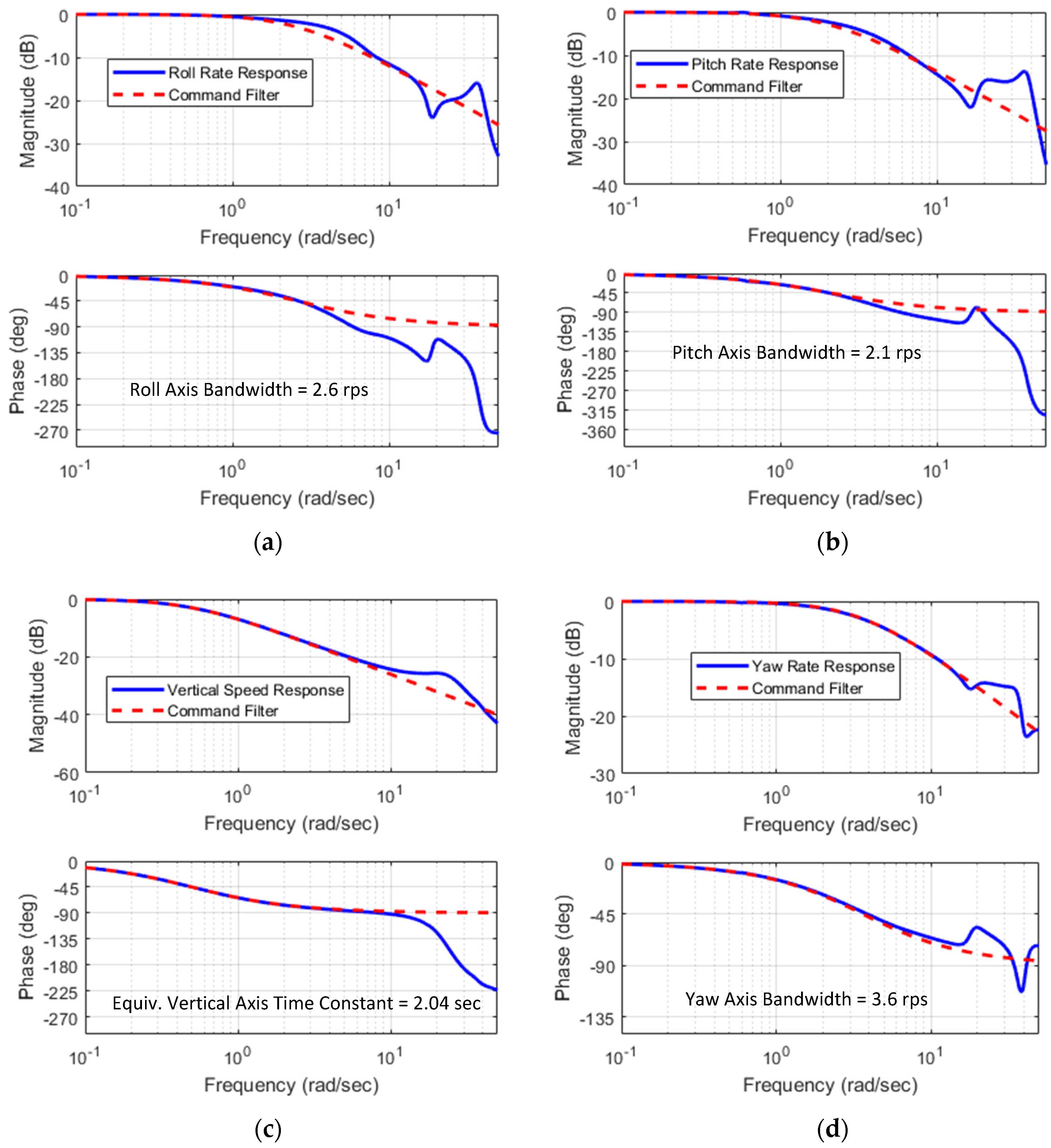
Figure 9 shows sample closed-loop bode plots from each commanded CV to the response of the corresponding CV. The ideal command filter is also shown for reference (when using the reduced order plant model, the analysis shows this response is followed perfectly).
Note that ADS-33F defines the phase margin bandwidth as the frequency where phase of the attitude response to pilot input passes through −135°. Since these plots are for the attitude rates, the bandwidth is seen as the crossing of −45° (since attitudes are a pure integration of the rates). Attitude frequency responses were also evaluated to ensure that the gain margin bandwidth was not less than the phase margin bandwidth and to evaluate the equivalent phase delays. The resulting bandwidth values from roll, pitch, and yaw matched the command filter design natural frequency in
Table 1 within two significant figures. The vertical axis frequency response is first order up to 10 rad/s with a break frequency 0.49 rad/s. This also matched the design natural frequency and resulted in equivalent time constant of 2.04 s (which corresponds to Level I vertical response for ADS-33E-PRF).
The feedback design is based on a tradeoff of stability margins and disturbance rejection of the controller [
10,
22,
23]. Stability margins were evaluated by extracting linear models of the open loop plant due to a disturbance at each actuator, as is standard practice for flight control design on piloted military aircraft [
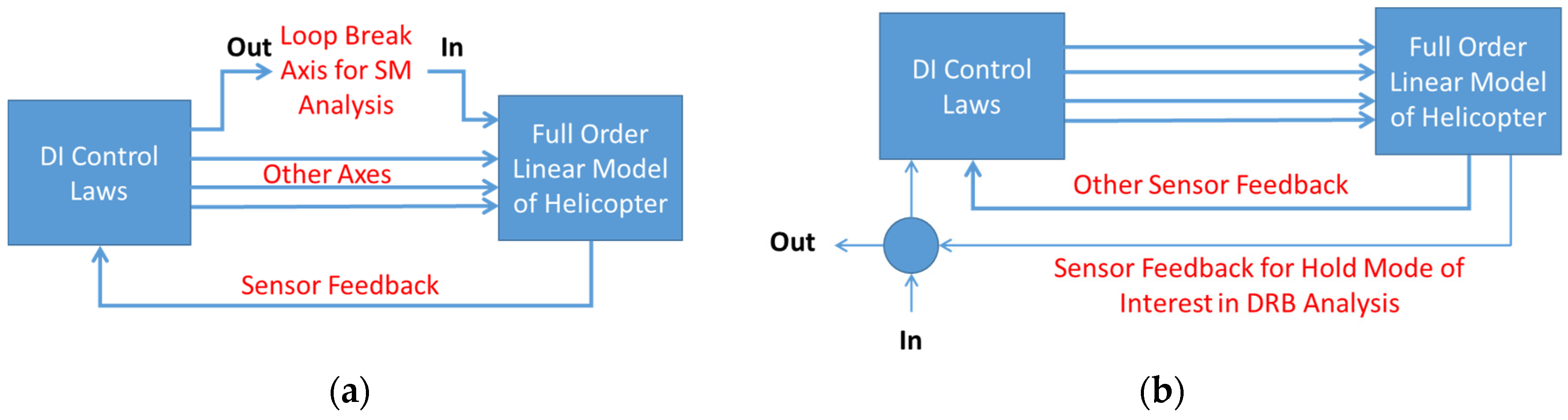
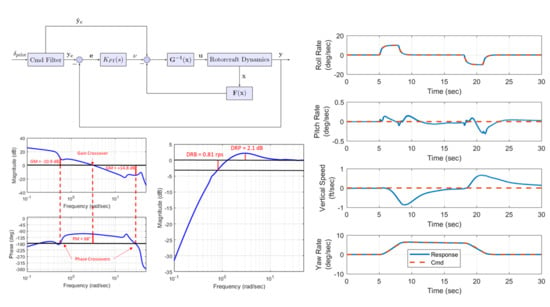
24]. The analysis considers single-axis loop breaks, and extracts the linear model from the actuator to the loop break, as shown in
Figure 10a. The disturbance rejection bandwidth (DRB) was evaluated by analyzing the closed-loop linear model from a disturbance at the plant output to the corresponding output as shown in
Figure 10b. The outputs of interest for each axis are those of the hold feature of the controller: roll attitude, pitch attitude, altitude, and heading. The resulting system is a zero DC gain transfer function, as was shown in Equation (9) for the perfect inversion. The full order dynamics produce a much higher order zero DC gain system, and the frequency at which the magnitude crosses −3 dB is defined as the DRB. As described in [
22], this provides a measure of the disturbance rejection performance of the hold modes of the controller by defining the frequency below which external disturbances are effectively rejected. In addition, the disturbance rejection peak (DRP) is defined as the peak amplitude of the frequency response. This provides measure of the system damping or tendency to overshoot responding to disturbances.
Note that the DRB analysis provides a single input/single output (SISO) variant of the sensitivity function commonly used in robust control theory for MIMO systems. The stability margin analysis is a SISO analysis of robustness, similar to small gain theory used in MIMO robust control theory but with the added measure of robustness to phase delay. The SISO analysis is appropriate due to the decoupling achieved by the DI inner loop, as will be illustrated in the gain optimization.
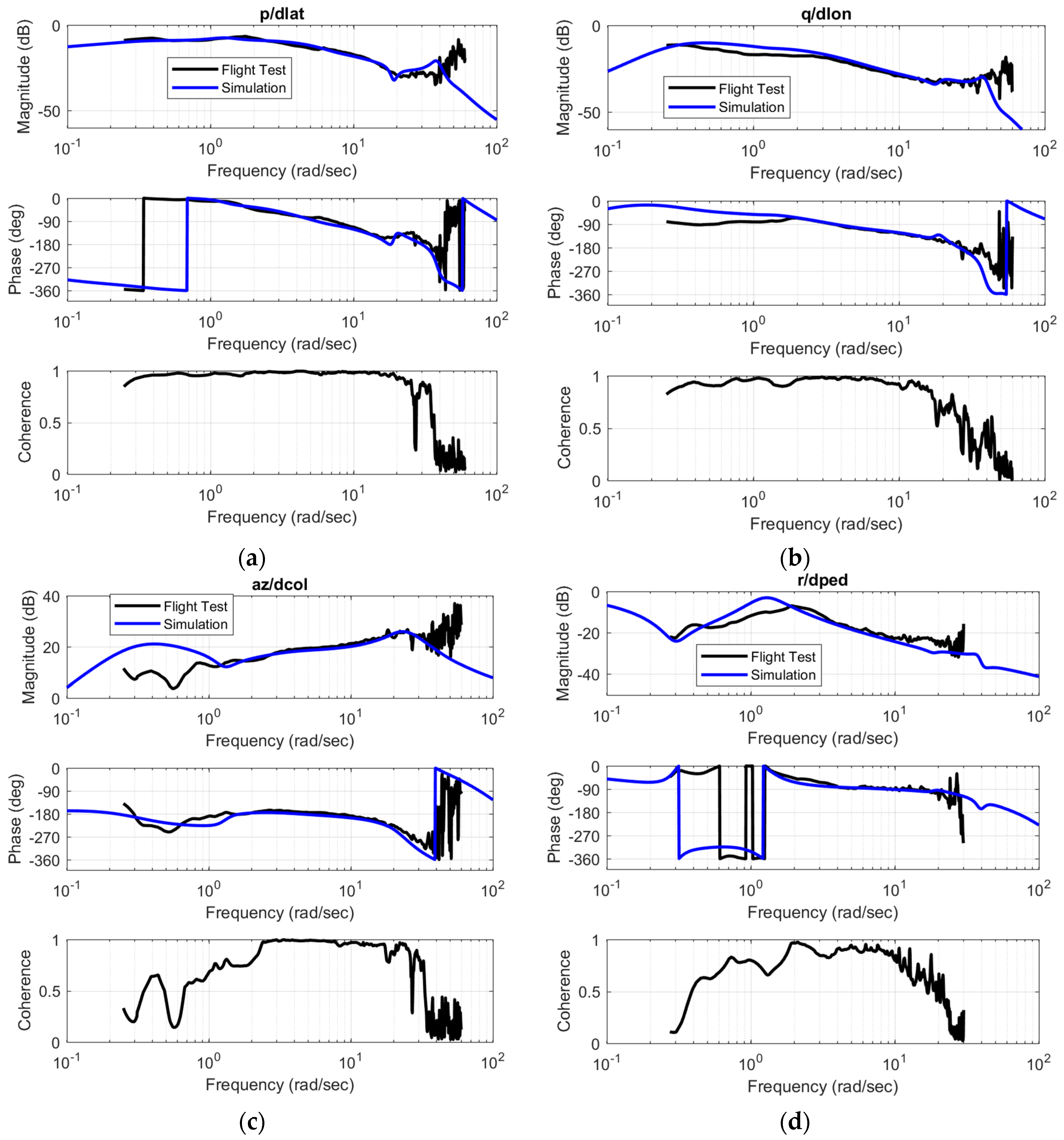
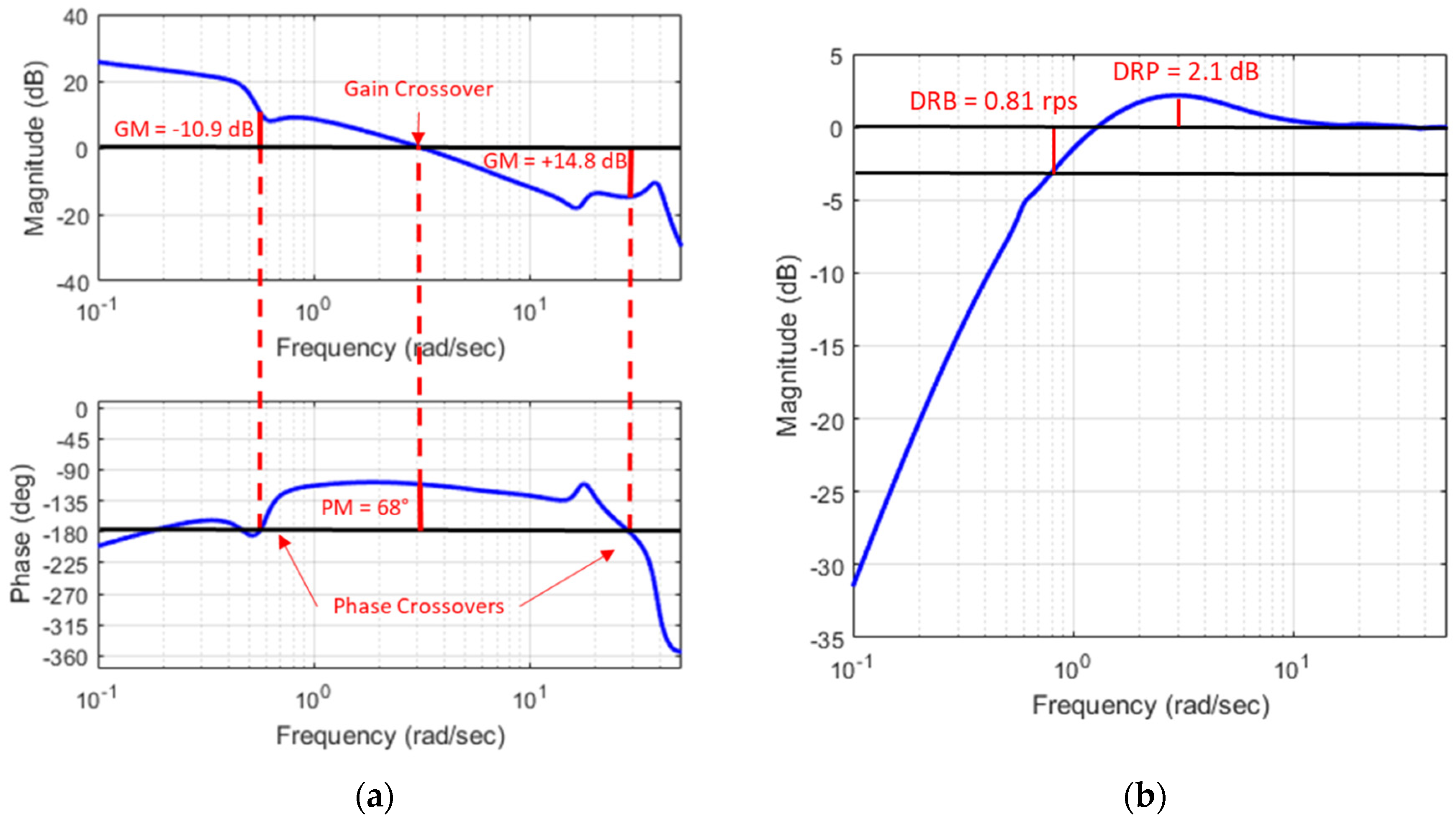
Figure 11 shows sample frequency responses used in stability margin (SM) and DRB/DRP analyses for the pitch axis with the nominal controller gains.
Figure 11 shows sufficiently high gain and phase margins in the pitch axis. Standard design practice requires 6 dB gain margin (GM) and 45° of phase margin (PM) [
24], and thus the stability analysis implies there is significant design space to increase gains and optimize the disturbance rejection performance of the pitch axis controller. This is in fact true of all four control axes.
Now a gain optimization study is performed to maximize disturbance rejection performance of the aircraft while maintaining constraints on stability margins and the disturbance rejection peak. As discussed above, control design guidelines require 6 dB gain margin and 45° phase margin. In addition, the time delay margin (DM) can also be evaluated as phase margin divided by the gain crossover frequency. A design can have good phase margin, but with high gain crossover the time delay margin can be unacceptably low. For this design, we set a DM constraint of 100 ms. For disturbance rejection, recent studies have proposed minimum DRB values for each axis, and a maximum DRP of 5 dB [
25]. The recommended Level 1 DRB values are 0.8 rad/s for roll attitude hold, 0.5 rad/s in pitch attitude hold, 0.7 rad/s in yaw attitude hold, and 0.17 rad/s for altitude hold. The nominal design meets all of these requirements. However, disturbance rejection can be considered a performance objective that can be optimized in order to minimize tracking errors due to both modeling error and disturbances.
For brevity, only the pitch axis gain optimization will be presented.
Table 4 shows the variation in stability margins, DRB, and DRP with increases in the natural frequency of the pitch axis error dynamics. As discussed in Equation (9), this parameter is used for feedback gain selection. The real pole is set at one fifth of the natural frequency, and the damping ratio fixed at 1.0. The table shows the expected trend of decreasing stability margins and increasing disturbance rejection bandwidth as the gains are increased. Above natural frequency 4.0, the gain margin is below design requirements, and the delay margin drops below 100 ms. At
ωn = 7.0 rad/s, the gain margin is very small, and in fact the controller becomes unstable around
ωn = 7.3 rad/s.
Table 5 shows the behavior of the roll axis with variation in the pitch axis gains. The roll axis gains, as well as the other two axes, are fixed at the nominal values set by
Table 1. The table, therefore, shows the behavior of different axes to gain variation in pitch. With the exception of the gain margin, stability and performance of the roll axis virtually unaffected by the pitch axis gain variation. The same is true for the yaw and vertical axes. Gain margin decreases, but is generally well above the design requirement, until the closed-loop system becomes nearly unstable, at which all gain margins approach 0. The results show the effective de-coupling of the DI control scheme.
The gain optimization was performed independently for each axis, varying single axis gains while holding the gains for the other axes at their nominal value. The final gain parameters were then applied to all axes, and the performance was evaluated. Some additional tuning was required as the gain margins degraded slightly with increased gain in multiple axes (compared to the single axis gain optimization). On the other hand, individual axis tuning was a good predictor of the final phase margins and DRB. The final parameters and the performance are summarized in
Table 6. The underlined margin indicates the critical stability margin for that axis, with the exception of the yaw axis where the gain crossover was constrained to less than 10 rad/s. Higher crossovers would likely cause problems with actuators or structural modes. If structural modes were included in the model, the yaw axis crossover would probably need to be reduced even further.
4.2. Time Response of Non-Linear Simulation
The controller was tested in the complete non-linear simulation, PSUHeloSim, with the non-linear controller.
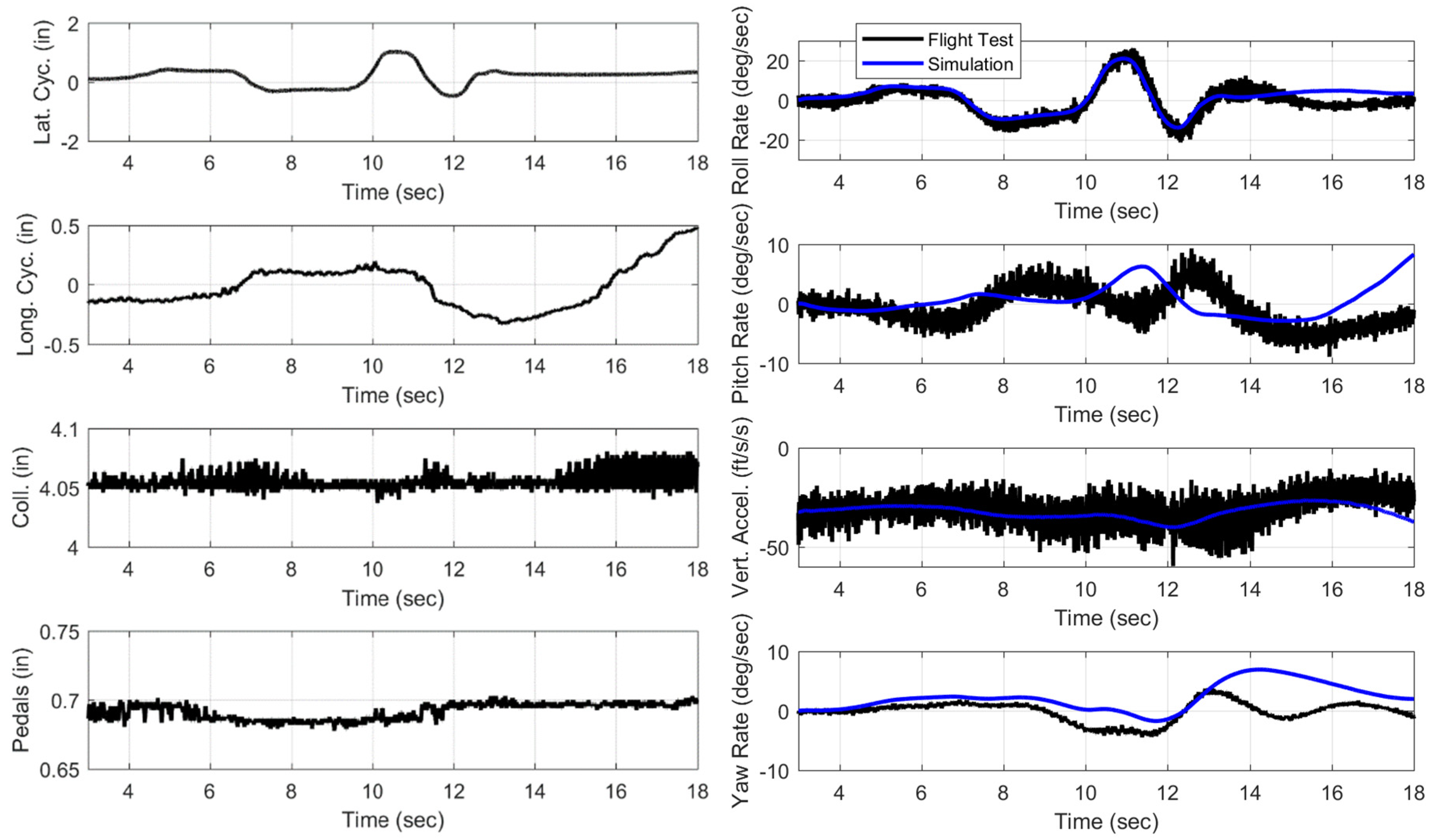
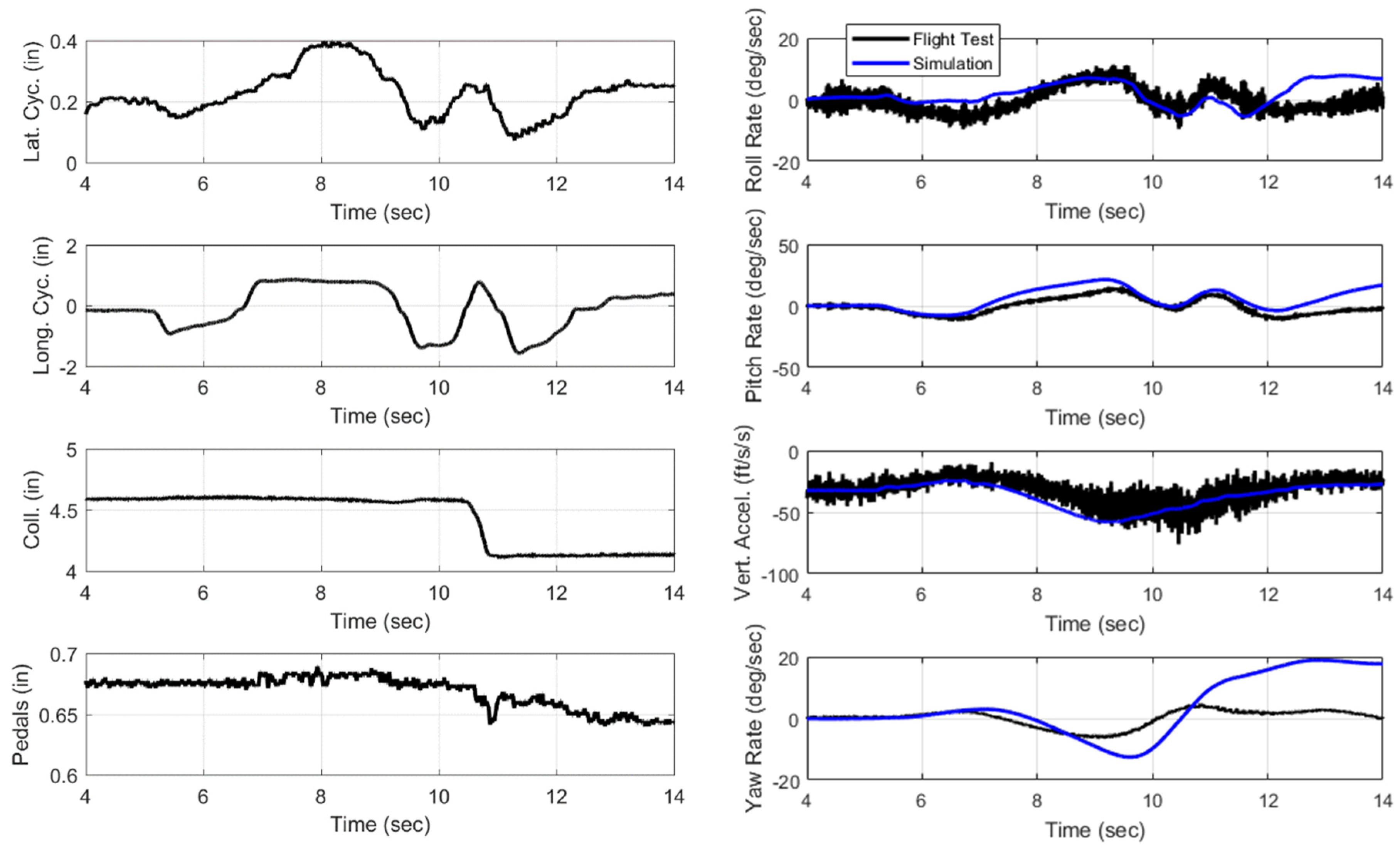
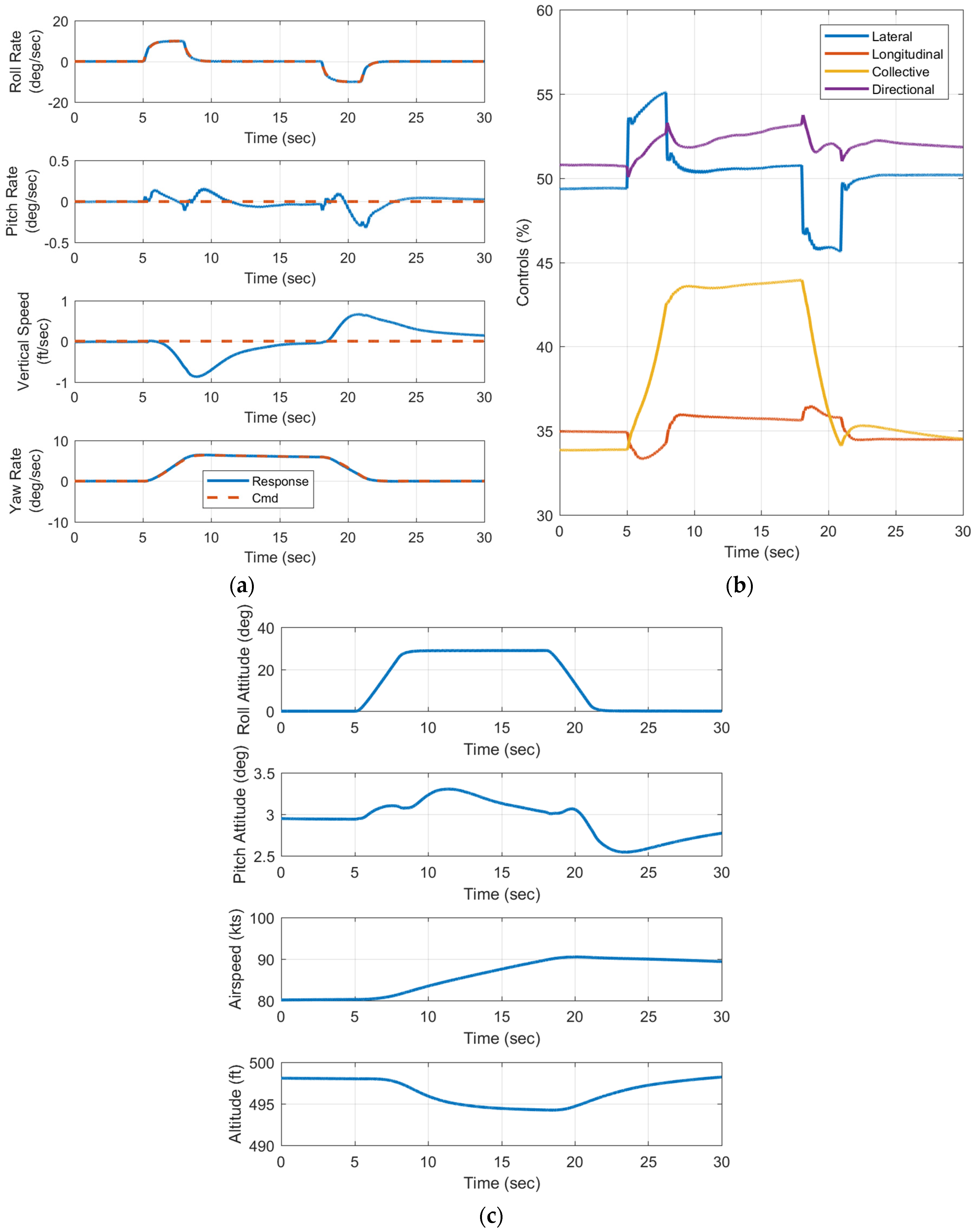
Figure 12 shows time history response of a 30° banked turn maneuver at 80 kts. The maneuver is achieved by a 10 deg/s roll rate pulse command to the right followed 10 s later by an equal magnitude pulse to left. The turn coordination logic in the yaw axis (Equation (32)) produces the yaw rate command for a coordinated turn. The figure shows the controller tracks the reference model commands very well, with root-mean-squared (RMS) tracking error of 0.120 deg/s, 0.0676 deg/s, and 0.0561 deg/s in roll, pitch, and yaw respectively. The tracking error in vertical speed is 0.344 ft/s. The actuator activity is also shown along with the attitude, airspeed, and altitude time histories.
To illustrate the performance of the controller across a range of operating conditions, the same maneuver was repeated at airspeeds of 60 kts, 100 kts, 120 kts, and 140 kts. The RMS tracking errors were evaluated for each case and are summarized in
Table 7. The results show very consistent performance for every airspeed (with some mild degradation at 140 kts), even though the feedback gains are exactly the same for each case. The results show the reduced reliance on gain scheduling when using NDI. A rigorous design would still perform stability margin analysis at every condition and possibly schedule gains to meet desired margins, but the method simplifies design since it effectively separates the command tracking performance and stability analysis.
As noted in the derivation, two potential pitfalls in DI design are NMP zeros, and excessive CV feedback gain causing instability due to the high order dynamics. In the control development an output redefinition scheme was applied to address NMP zeros.
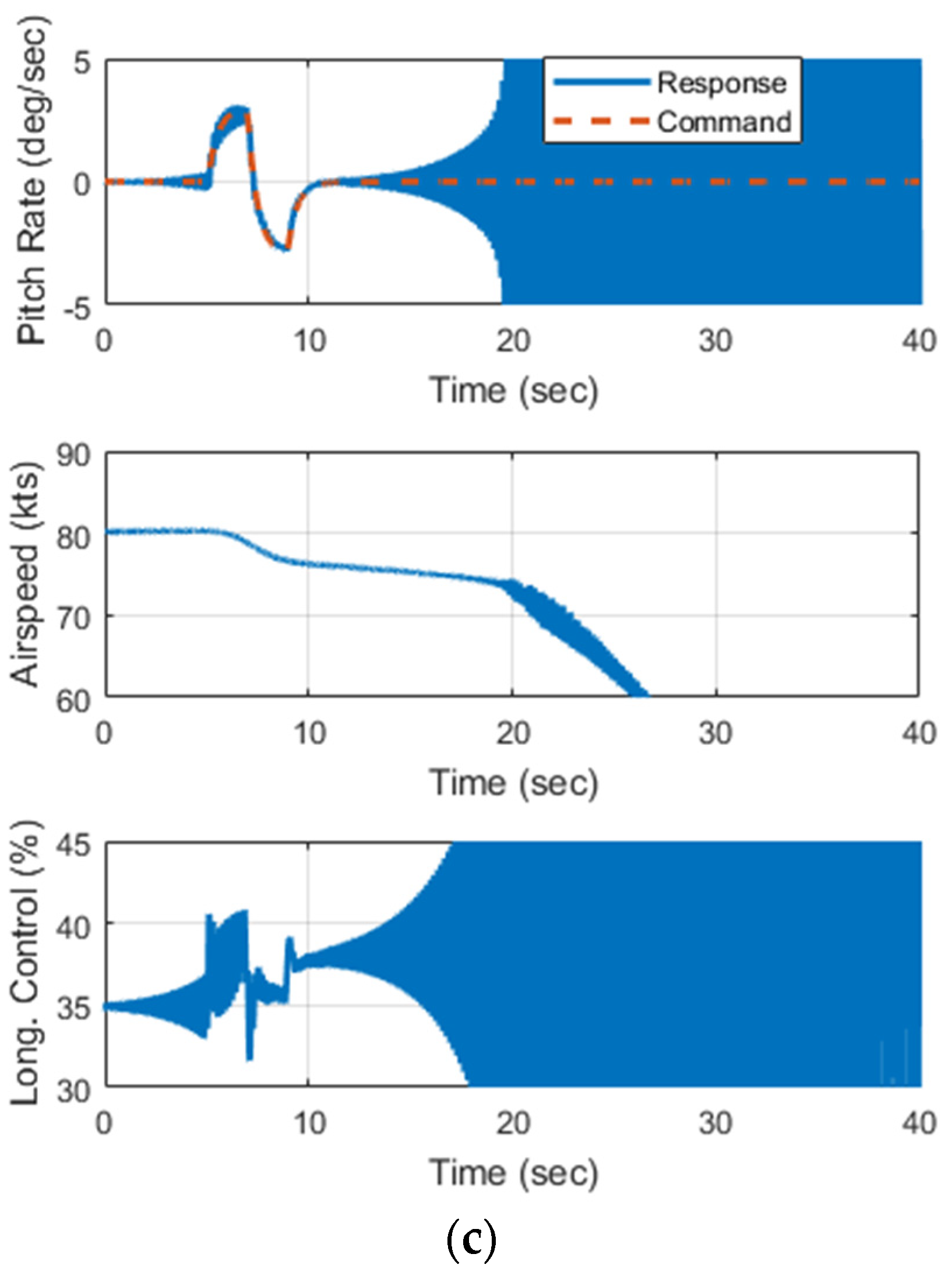
Figure 13a shows response due to a pitch rate doublet with the final controller design. The tracking is reasonably good, but a slow divergence of the airspeed is observed. In
Figure 13b, the output redefinition is removed such that the pitch axis CV is simply pitch attitude rate, and the same maneuver was simulated. The results show that the rate of airspeed divergence is slightly increased, but the attitude rate tracking is actually improved. The results tend to indicate that the output redefinition method was not successful, and that the best method to handle the NMP zero and unstable airspeed mode is with an outer loop controller. Finally,
Figure 13c shows the result of excessive feedback gain in the pitch axis. The natural frequency parameter for the pitch axis was increased in 0.2 rad/s increments and the corresponding gains recalculated. The pitch doublet maneuver was repeated until instability was observed. This occurred when
ωn = 6.8 rad/sec, slightly lower than the value predicted by linear analysis (
ωn = 7.3 rad/s). The result indicates the need for some conservativeness when choosing gains and final stability margins, but generally the analysis was effective.