Verification of Boundary Conditions Applied to Active Flow Circulation Control
Abstract
1. Introduction
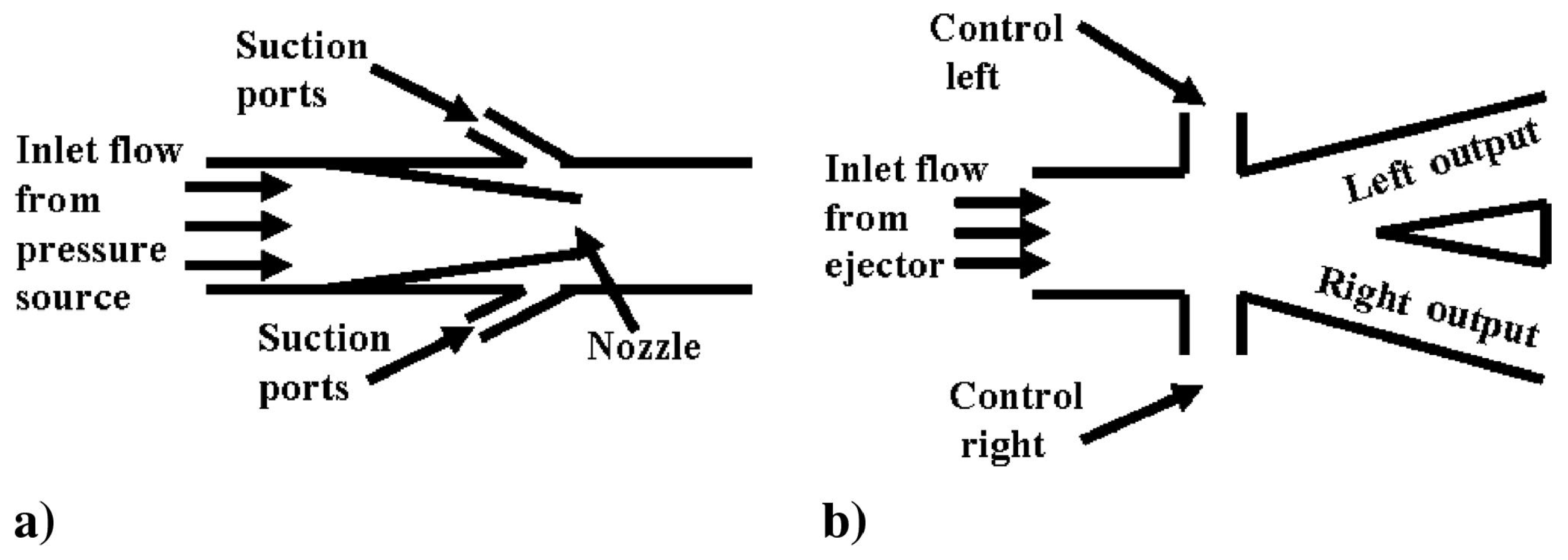
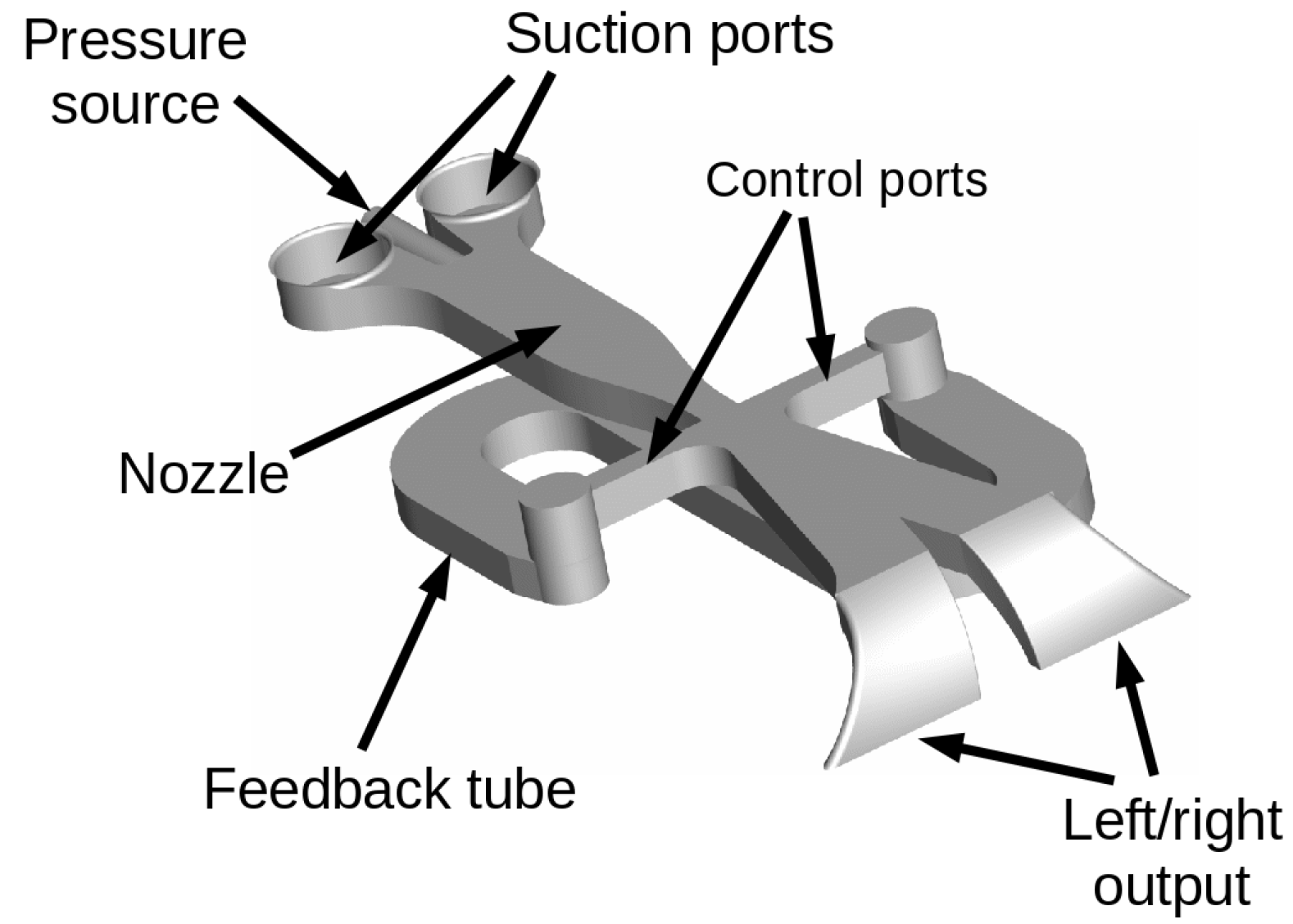
2. Characterization of the SaOB Actuator
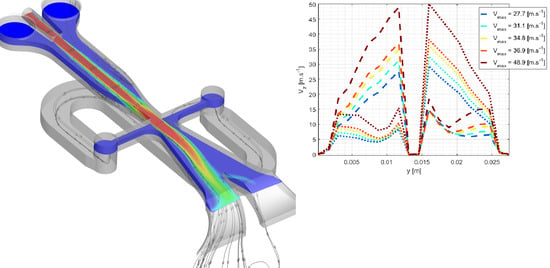
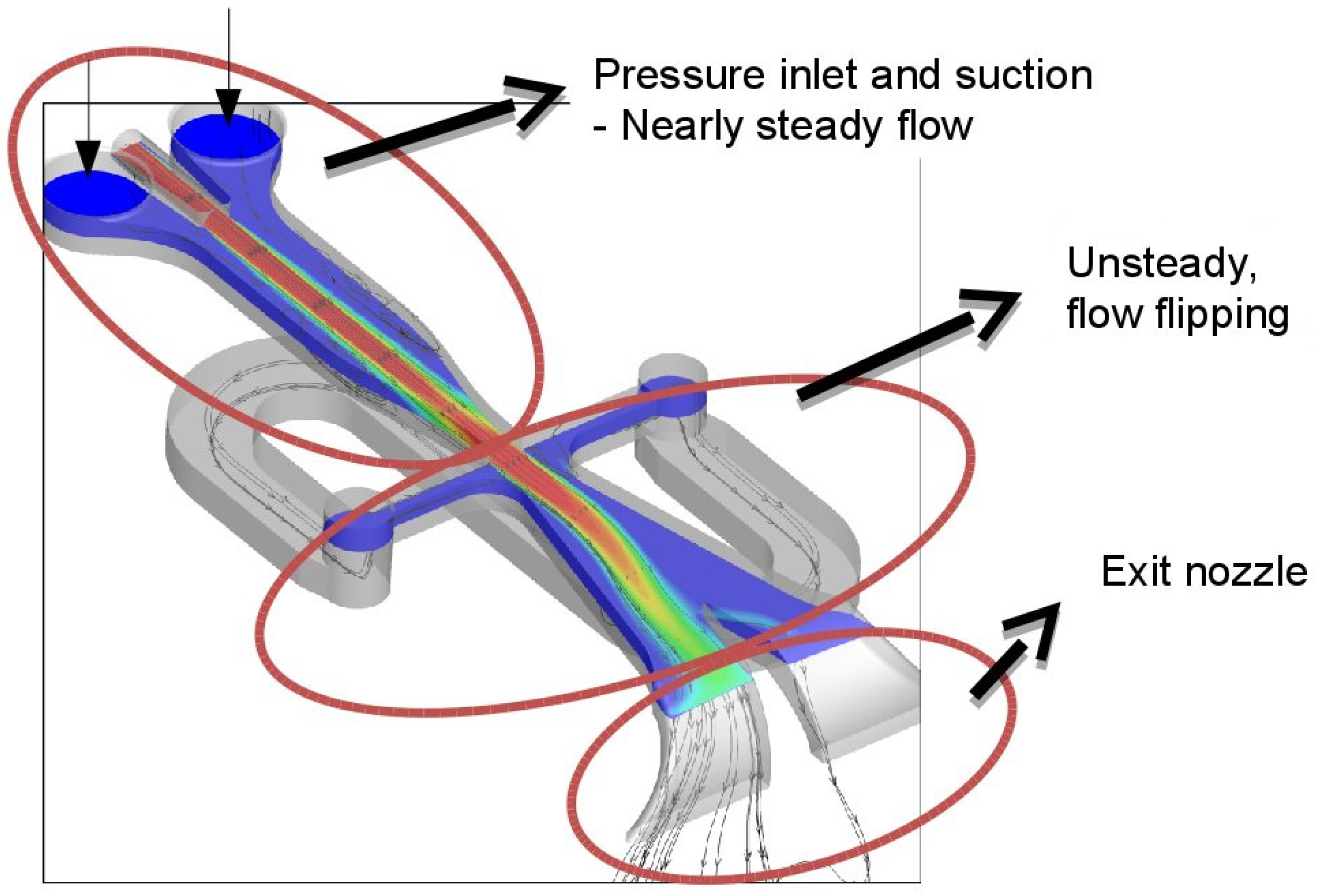
2.1. CFD Simulation of the Isolated SaOB Actuator
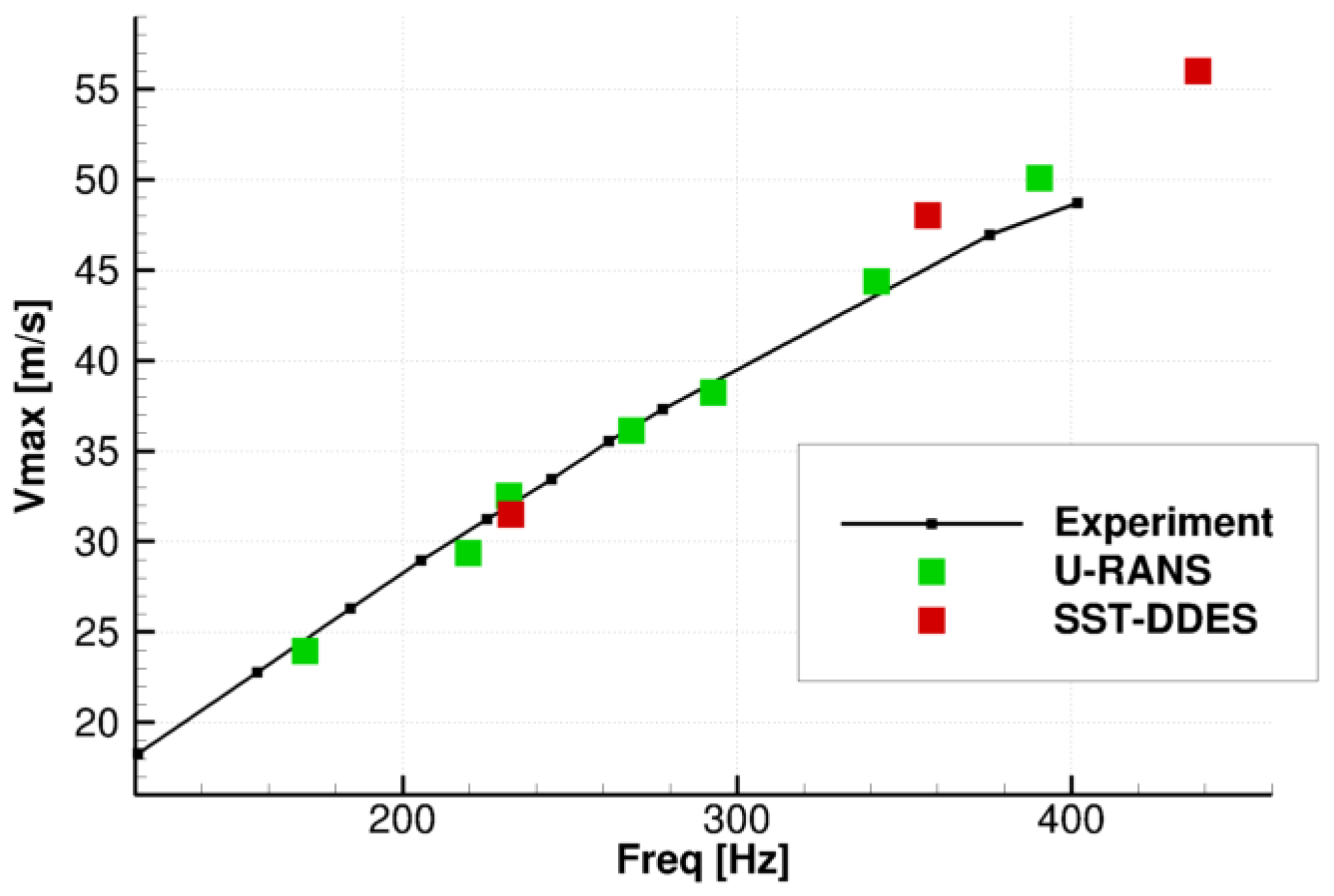
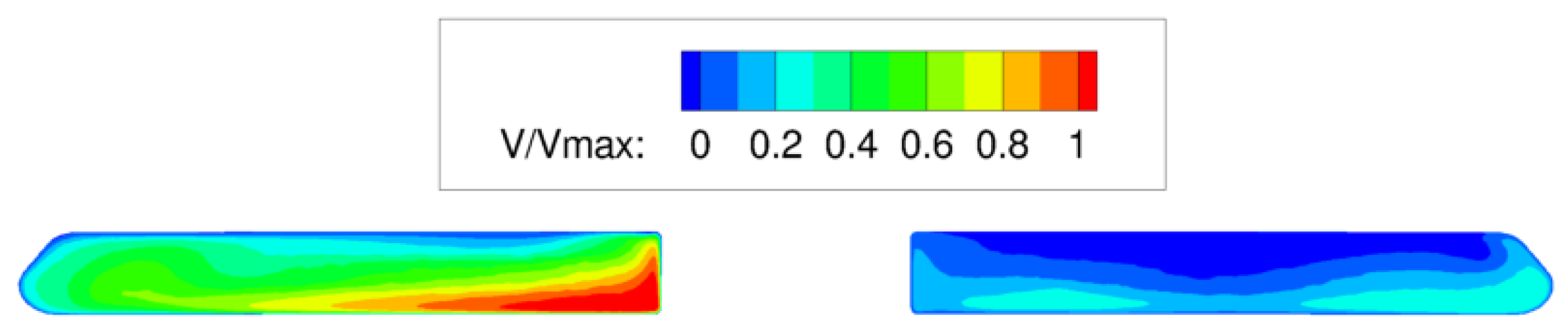
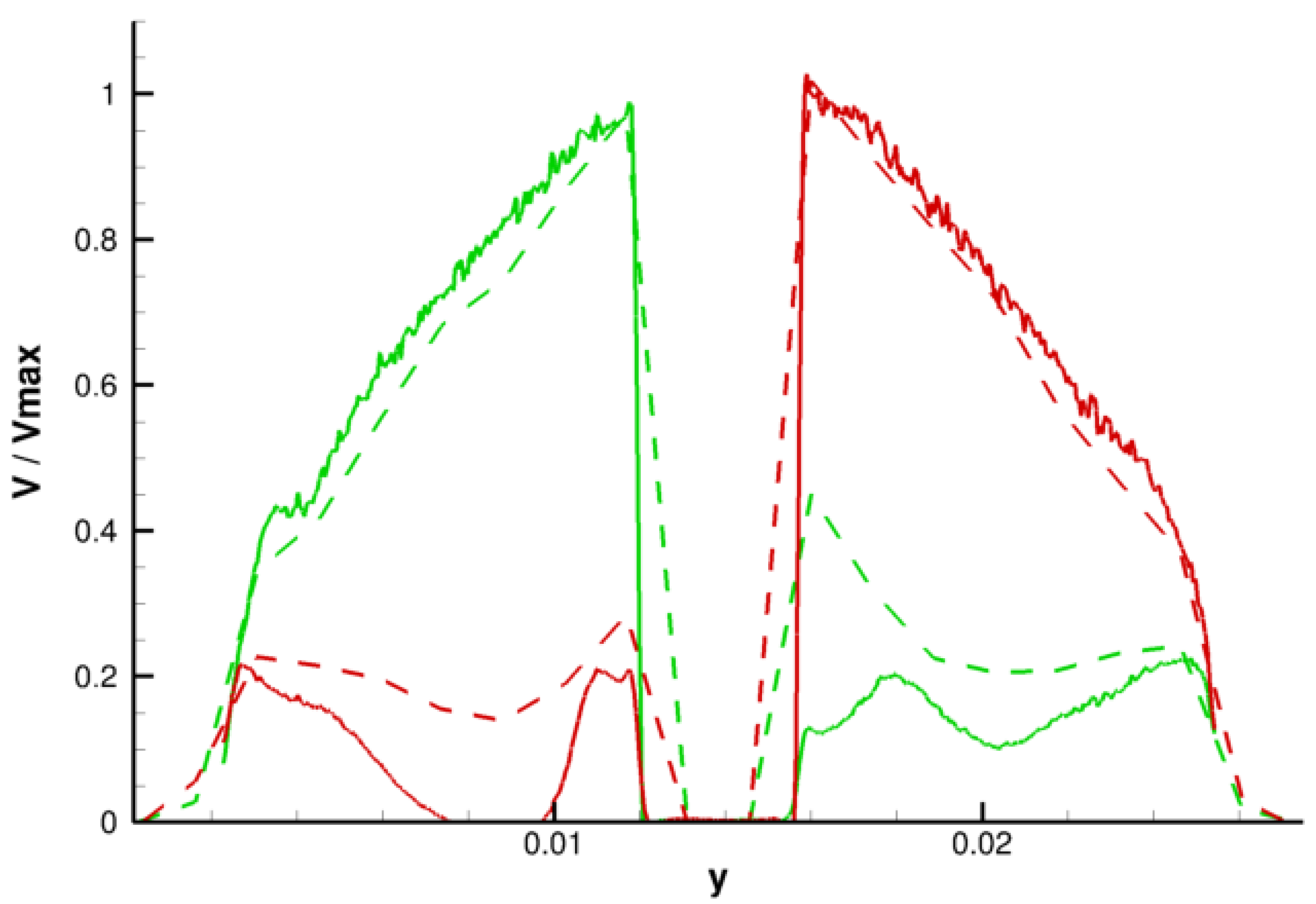
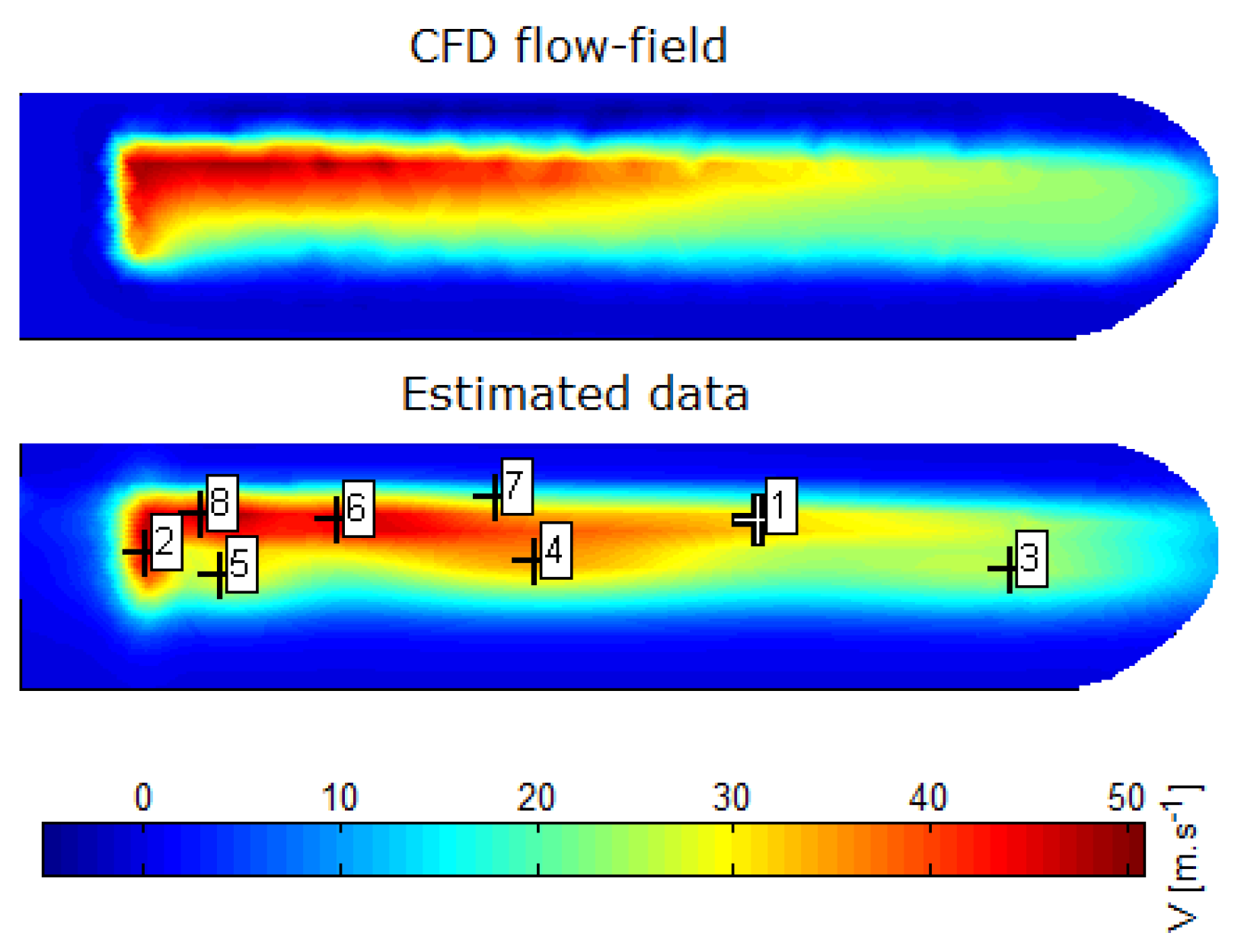
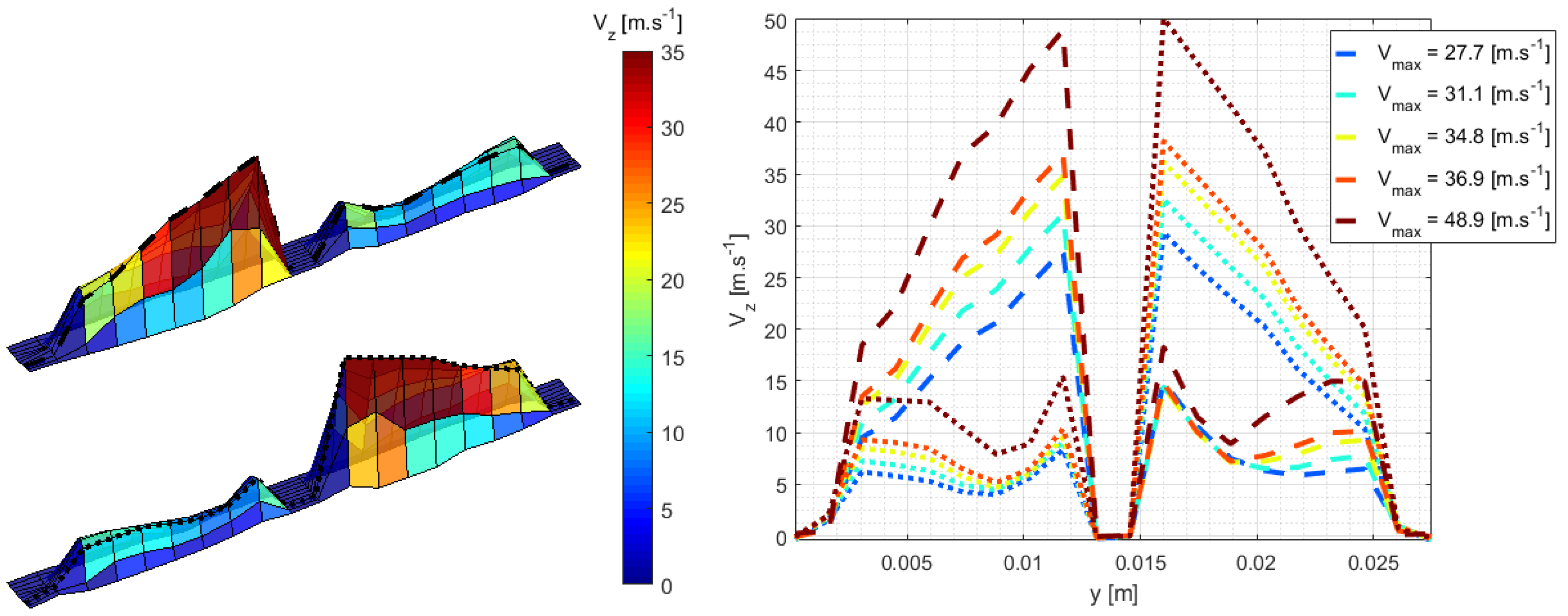
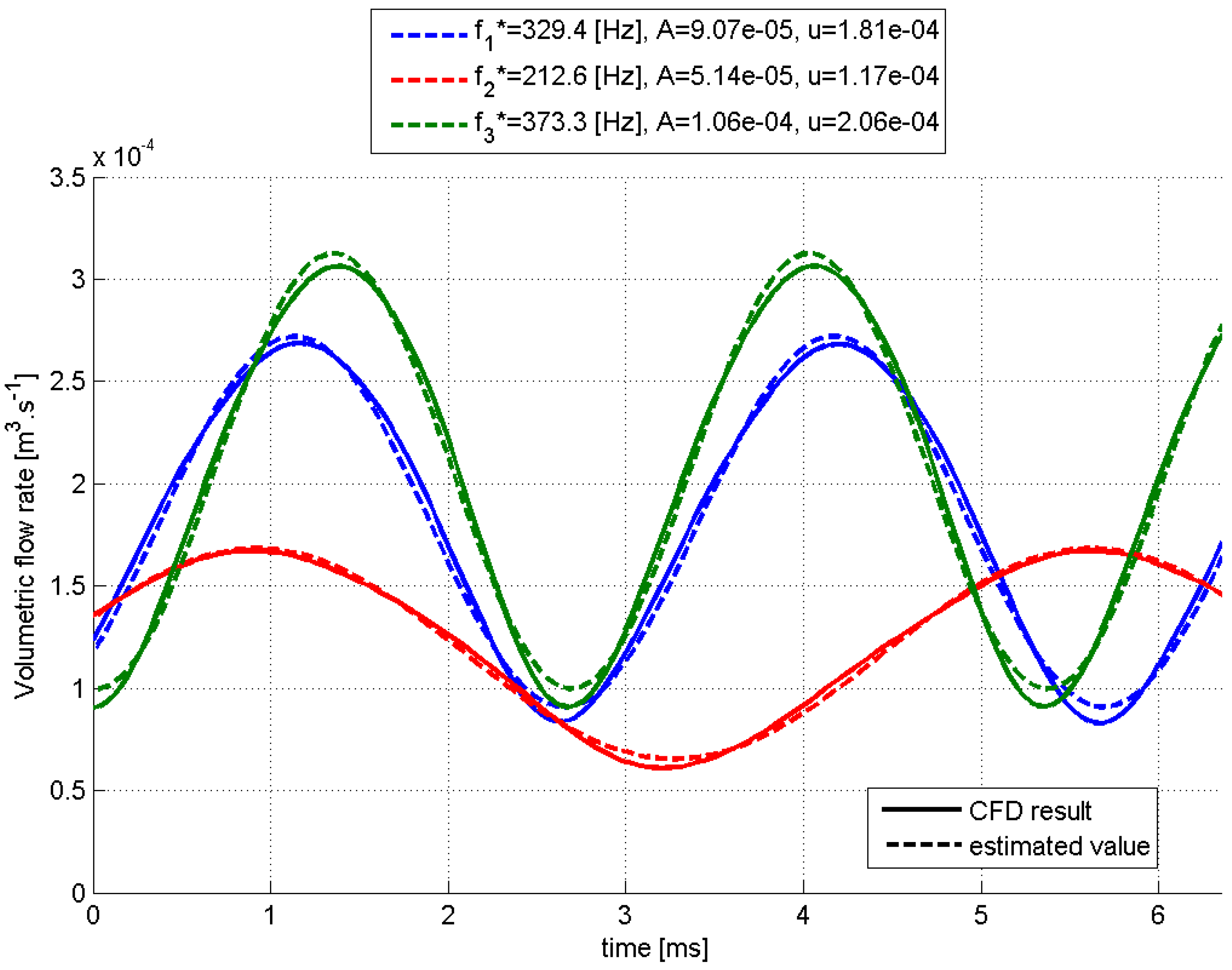
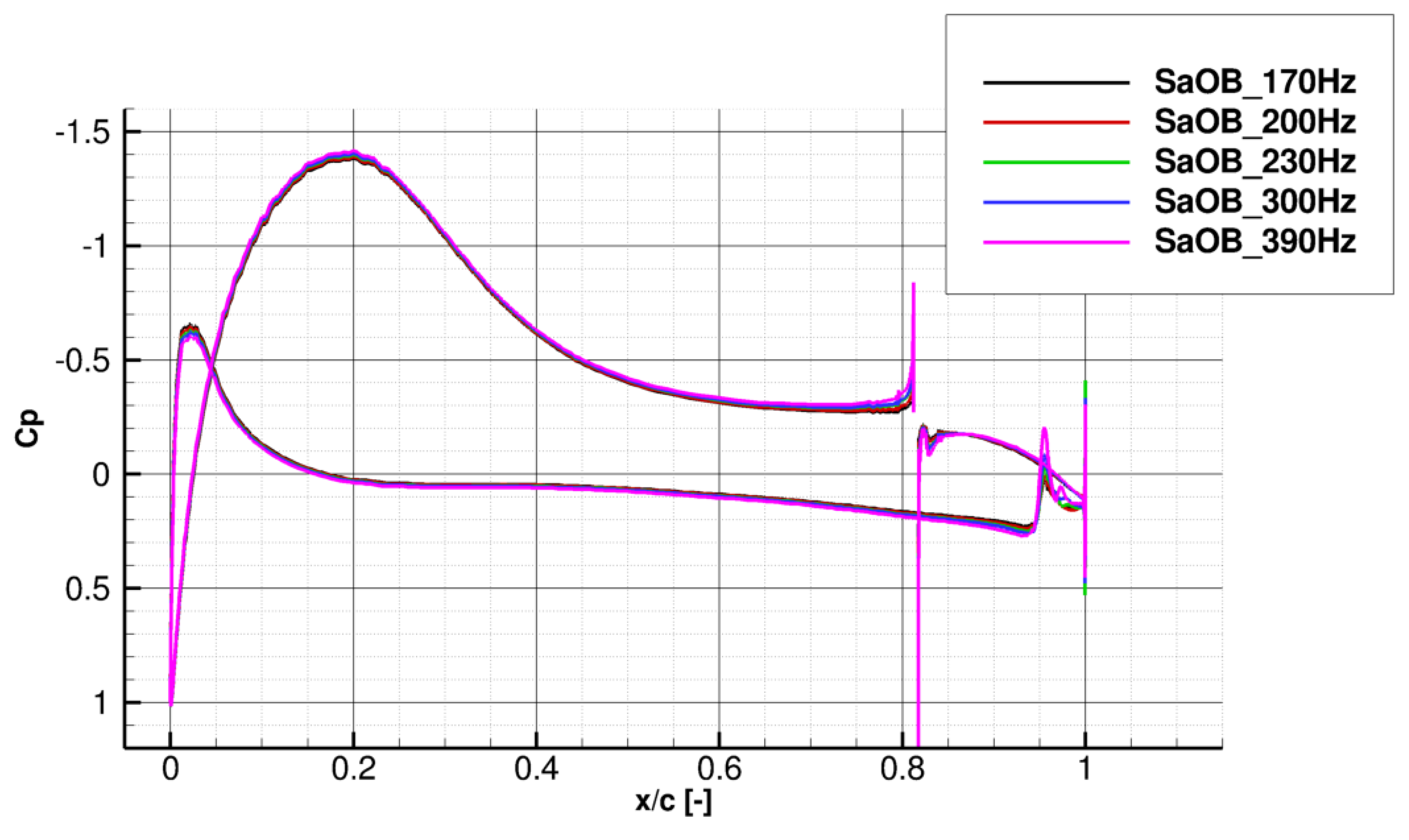
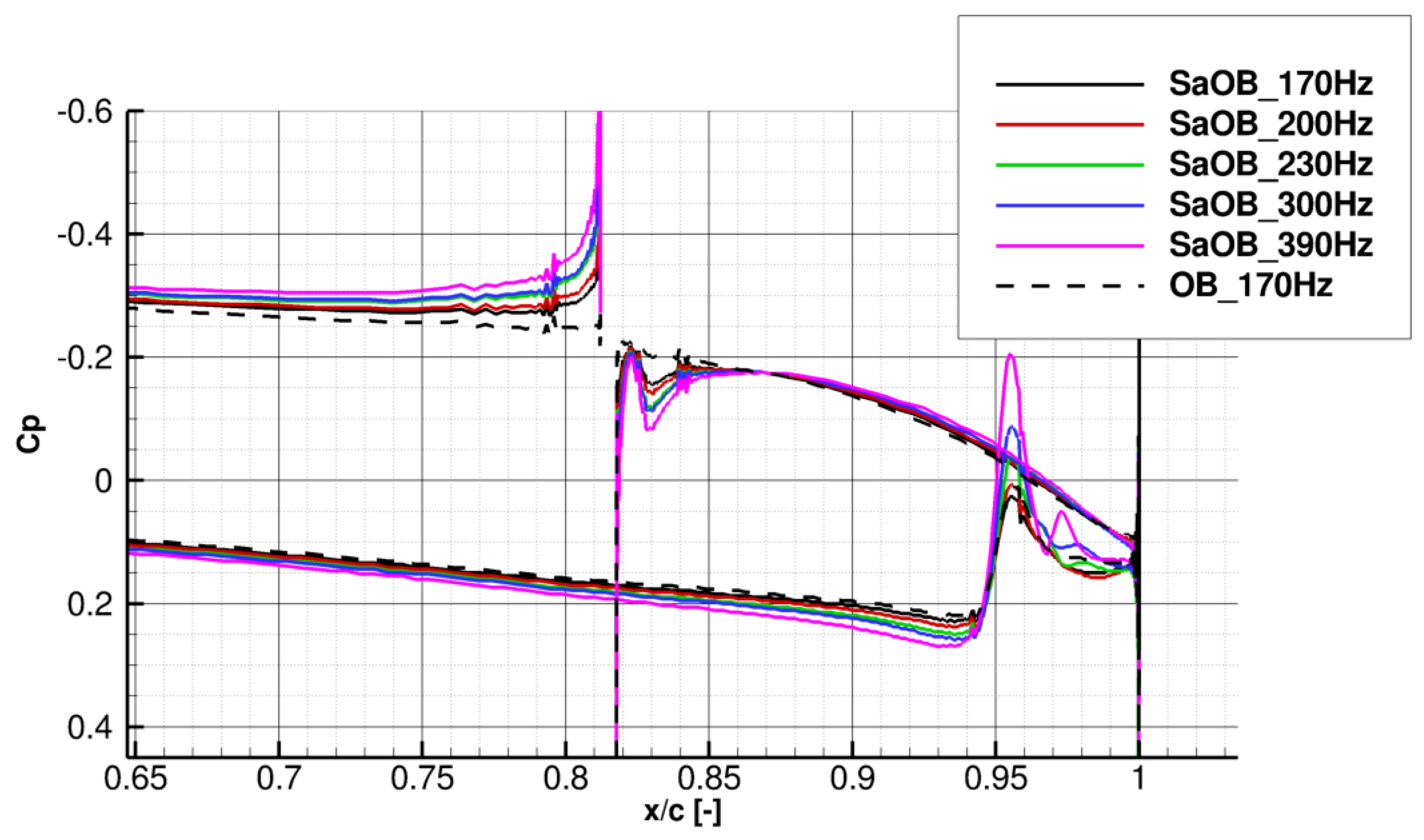
2.2. CFD Results and Interpretation
3. Definition of the Boundary Condition
4. Application to Circulation Control
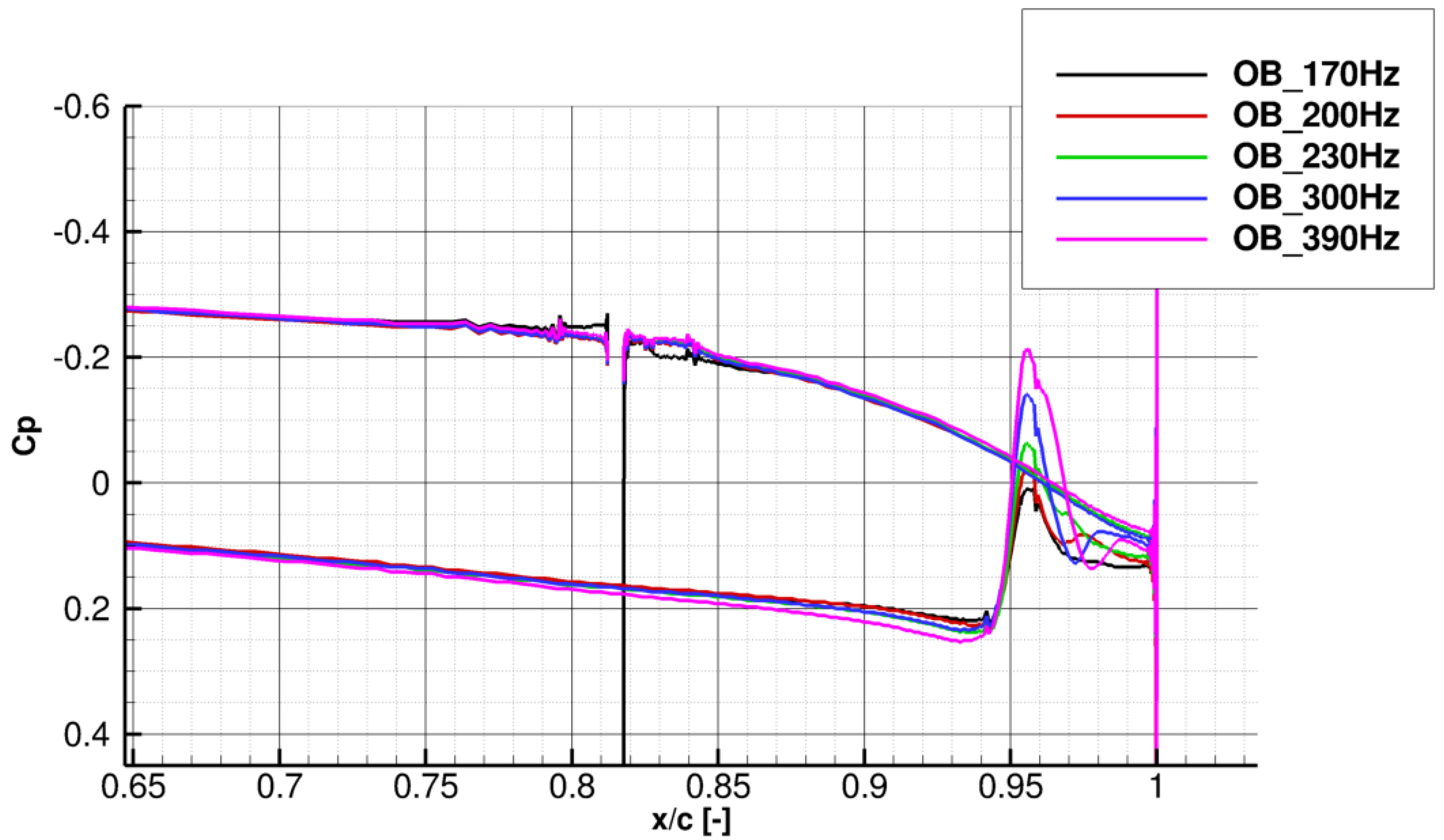
4.1. CFD Simulations with the SaOB Boundary Condition
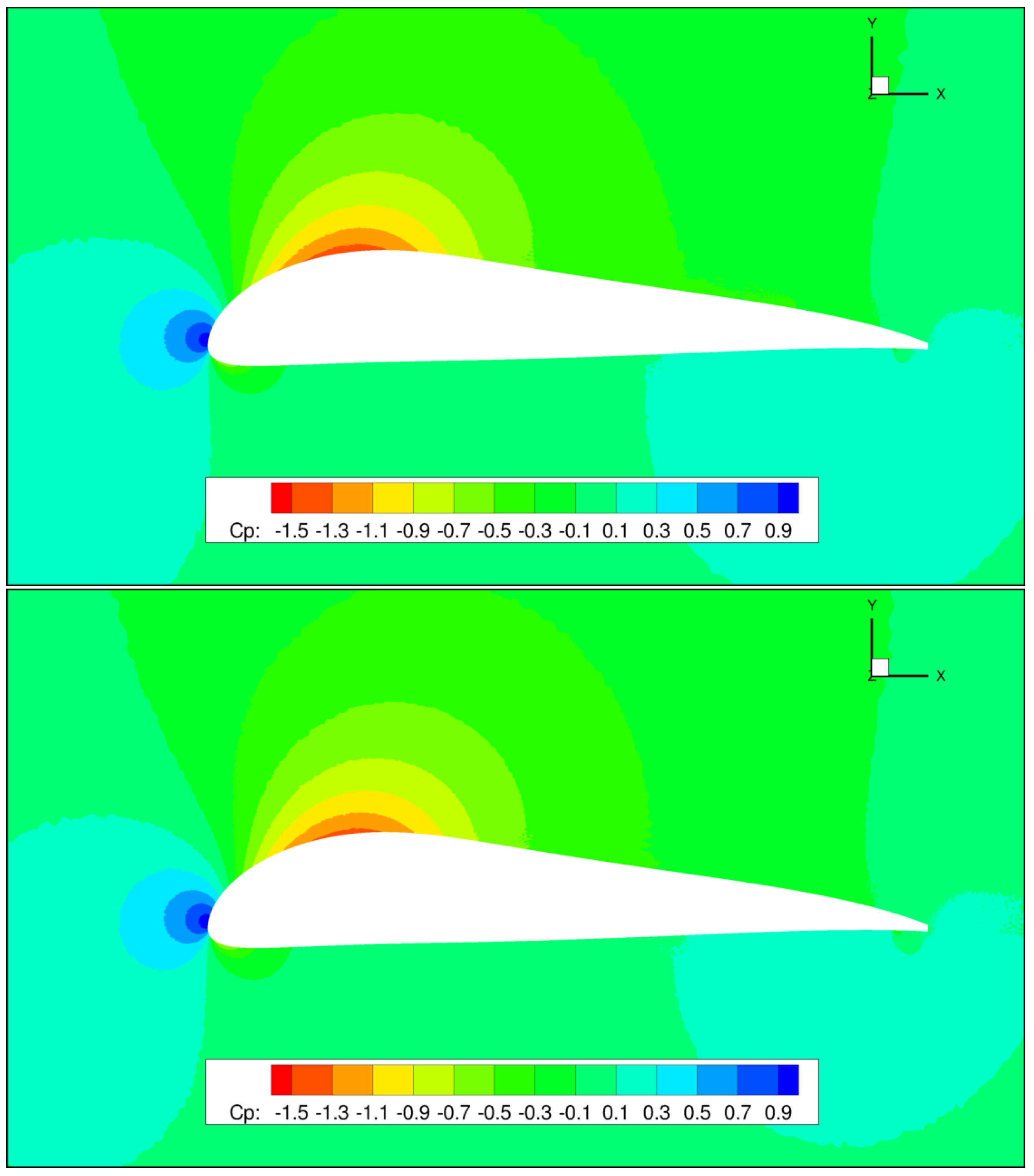
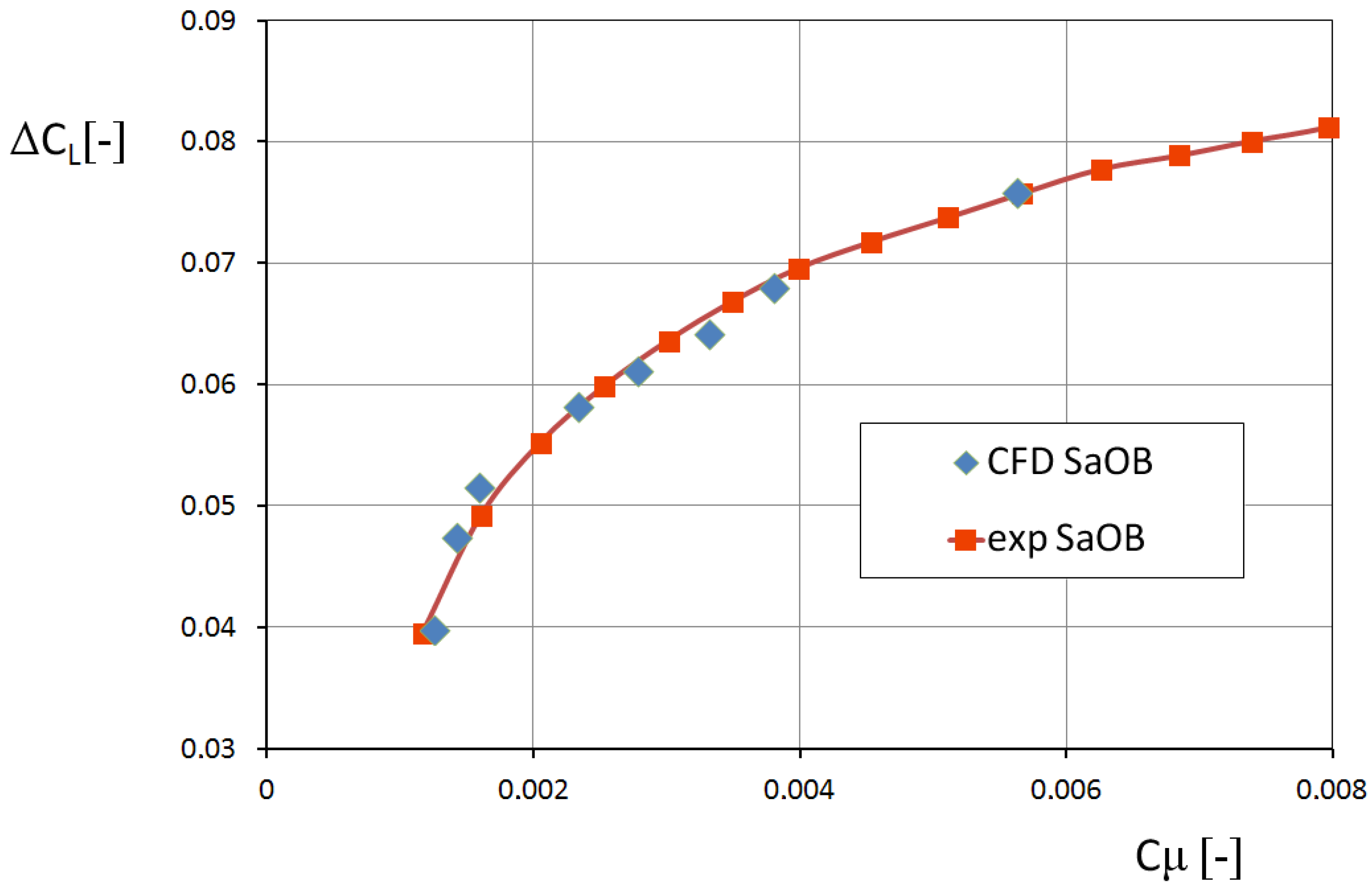
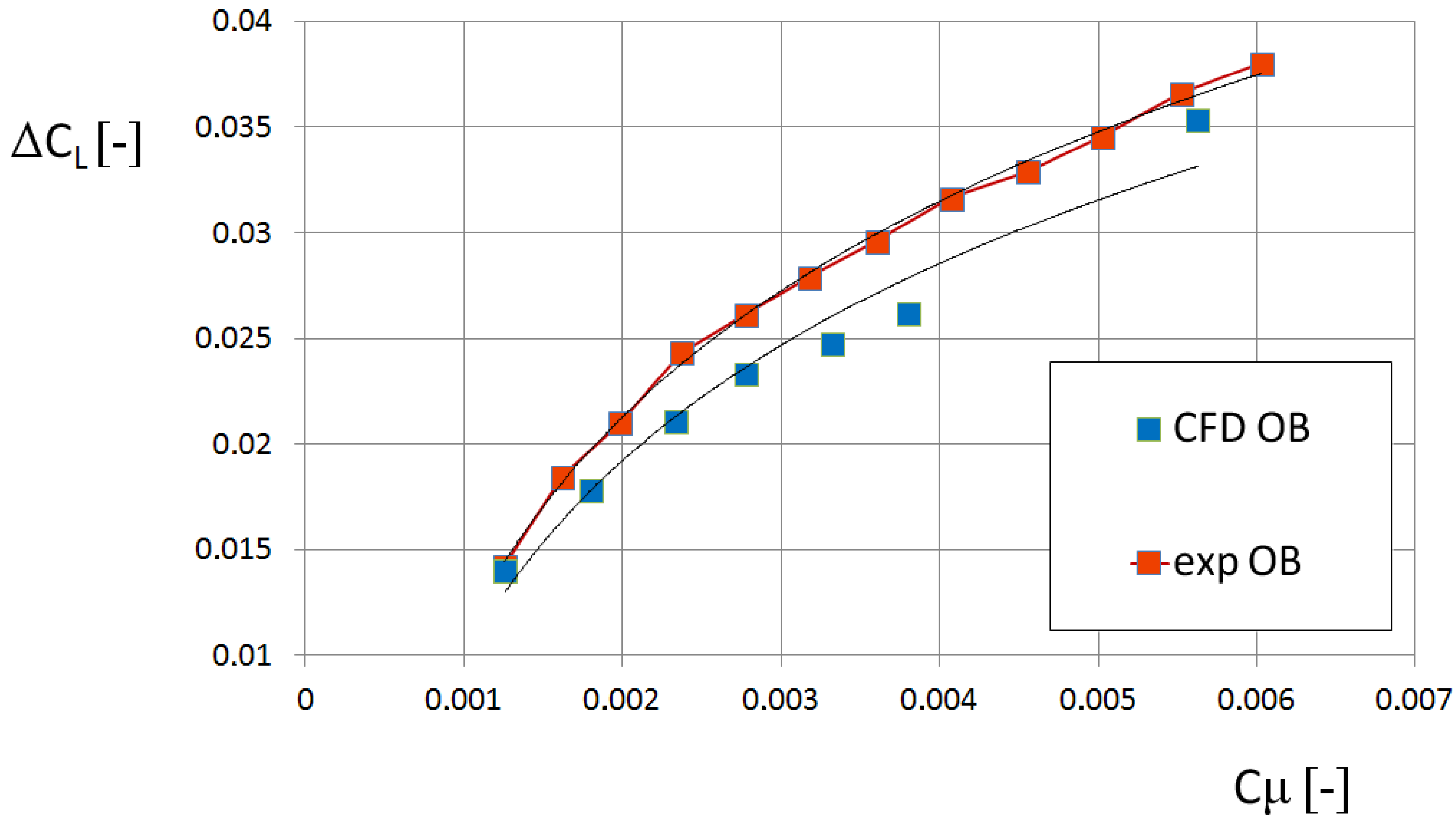
4.2. CFD Results and Experimental Data Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AFC | Active Flow Control |
| AoA | Angle of Attack |
| CFD | Computational Fluid Dynamics |
| CPU | Central Processing Unit |
| Jet momentum coefficient, | |
| DDES | Delayed Detached Eddy Simulation |
| f | frequency (Hz) |
| LES | Large Eddy Simulation |
| PIV | Particle Image Velocimetry |
| RANS | Reynolds Average Navier–Stokes |
| SST | Menter’s Shear Stress Transport (turbulence model) |
| Reference area | |
| Outlet slot area | |
| t | Time (s) |
| Maximum jet velocity (m/s) | |
| Free stream velocity (m/s) | |
| URANS | Unsteady Reynolds Average Navier–Stokes |
| Maximum velocity from the SaoB actuator nozzle (m/s) |
References
- Blaylock, M.; Chow, R.; Cooperman, A.; van Dam, C.P. Comparison of pneumatic jets and tabs for Active Aerodynamic Load Control. Wind Energy 2014, 17, 1368–1384. [Google Scholar] [CrossRef]
- Rumsey, C. Successes and Challenges for Flow Control Simulations (Invited). In Proceedings of the 4th Flow Control Conference, Fluid Dynamics and Co-located Conferences, AIAA 2008-4311, Seattle, WA, USA, 23–26 June 2008. [Google Scholar] [CrossRef]
- Lengers, M. Industrial assessment of overall aircraft driven local active flow control. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Seifert, A.; Shtendel, T.; Dolgopyat, D. From lab to full scale Active Flow Control drag reduction: How to bridge the gap? J. Wind Eng. Ind. Aerodyn. 2015, 147, 262–272. [Google Scholar] [CrossRef]
- Morgulis, N.; Seifert, A. Fluidic flow control applied for improved performance of Darrieus wind turbines. Wind Energy 2016, 19, 1585–1602. [Google Scholar] [CrossRef]
- Vrchota, P.; Hospodář, P. Response Surface Method Application to High-Lift Configuration with Active Flow Control. J. Aircr. 2012, 49, 1796–1802. [Google Scholar] [CrossRef]
- Galbraith, M. Numerical Simulations of a High-Lift Airfoil Employing Active Flow Control. In Proceedings of the 44th AIAA Aerospace Sciences Meeting, Reno, Nevada, 9–12 January 2006. [Google Scholar] [CrossRef]
- Yousefi, K.; Saleh, R. Three-dimensional suction flow control and suction jet length optimization of NACA 0012 wing. Meccanica 2015, 50, 1481–1494. [Google Scholar] [CrossRef]
- Huang, L.; Huang, P.G.; LeBeau, R.P.; Hauser, T. Numerical Study of Blowing and Suction Control Mechanism on NACA0012 Airfoil. J. Aircr. 2004, 41, 1005–1013. [Google Scholar] [CrossRef]
- Yousefi, K.; Saleh, R. The Effects of Trailing Edge Blowing on Aerodynamic Characteristics of the NACA 0012 Airfoil and Optimization of the Blowing Slot Geometry. J. Theor. Appl. Mech. 2014, 52, 165–179. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Nishino, T. Numerical study comparing RANS and LES approaches on a circulation control airfoil. Int. J. Heat Fluid Flow 2011, 32, 847–864. [Google Scholar] [CrossRef]
- Schatzman, D.M.; Wilson, J.; Maron, L.; Palei, V.; Seifert, A.; Arad, E. Suction and oscillatory blowing interaction with boundary layers. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Lakebrink, M.T.; Mani, M.; Winkler, C. Numerical Investigation of Fluidic Oscillator Flow Control in an S-Duct Diffuser. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Vrchota, P. Active Flow Separation Control Applied at Wing-Pylon Junction of a Wing Section in Landing Configuration. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0491. [Google Scholar]
- Vatsa, V.; Koklu, M.; Wygnanski, I. Numerical Simulation of Fluidic Actuators for Flow Control Applications. In Proceedings of the 6th Flow Control Conference, Fluid Dynamics and Co-located Conferences, New Orleans, LA, USA, 25–28 June 2012. AIAA 2012-3239. [Google Scholar] [CrossRef]
- Kara, K. Numerical Study of Internal Flow Structures in a Sweeping Jet Actuator. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2015. AIAA 2015-2424. [Google Scholar]
- Troshin, V.; Palei, V.; Shtendel, T.; Seifert, A. Characterization of the Suction and Oscillatory Blowing Actuator in Still Air. In Proceedings of the 54th Israel Annual Conference on Aerospace Sciences, Tel Aviv, Israel, 19–20 February 2014. [Google Scholar]
- Arwatz, G.; Fono, I.; Seifert, A. Suction and oscillatory blowing actuator modeling and validation. AIAA J. 2008, 46, 1107–1117. [Google Scholar] [CrossRef]
- Wallin, S.; Johansson, A.V. An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. J. Fluid Mech. 2000, 403, 89–132. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES Formulations for the k–ω Shear Stress Transport Model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Dolgopyat, D.; Seifert, A. Active Flow Control Virtual Maneuvering System Applied to Conventional Airfoil. AIAA J. 2019, 57, 72–89. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Seifert, A. Large-Eddy Simulation-Based Characterization of Suction and Oscillatory Blowing Fluidic Actuator. AIAA J. 2017, 55, 2566–2579. [Google Scholar] [CrossRef]
- Vrchota, P.; Prachař, A.; Hospodář, P.; Dolgopyat, D.; Seifert, A. Development and Verification of Simplified Boundary Condition of SaOB Actuator. In Proceedings of the 58th Israel Annual Conference on Aerospace Sciences, Tel Aviv, Israel, 14–15 March 2018. [Google Scholar]
- Dolgopyat, D.; Seifert, A. Conventional Airfoil Active Flow Control Virtual Maneuvering System. In Proceedings of the 55th Israel Annual Conference on Aerospace Sciences, Tel Aviv, Israel, 25–26 February 2015. [Google Scholar]
- Vrchota, P.; Prachař, A.; Hospodář, P.; Dolgopyat, D.; Seifert, A. Development of Simplified Boundary Condition of SaOB Actuator Based on High-Fidelity CFD Simulations. In Proceedings of the 52nd 3AF International Conference on Applied Aerodynamics—Progress in Flow Control, Lyon, France, 27–29 March 2017. [Google Scholar]
- Prachař, A.; Vrchota, P. Characterization of the Suction-and-Oscillatory-Blowing actuator by the hybrid RANS-LES CFD. In Proceedings of the 2018 Flow Control Conference, AIAA AVIATION Forum, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Eliasson, P. EDGE, a Navier-Stokes Solver for Unstructured Grid; ISTE Ltd.: London, UK, 2002; pp. 527–534. [Google Scholar]
- Swanson, R.C.; Radespiel, R.; Turkel, E. On Some Numerical Dissipation Schemes. J. Comput. Phys. 1998, 147, 518–544. [Google Scholar] [CrossRef]
- Zhang, X.S. Neural Networks in Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 46. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Jirasek, A. Mass flow boundary conditions for subsonic inflow and outflow boundary. AIAA J. 2006, 44, 939–947. [Google Scholar] [CrossRef]


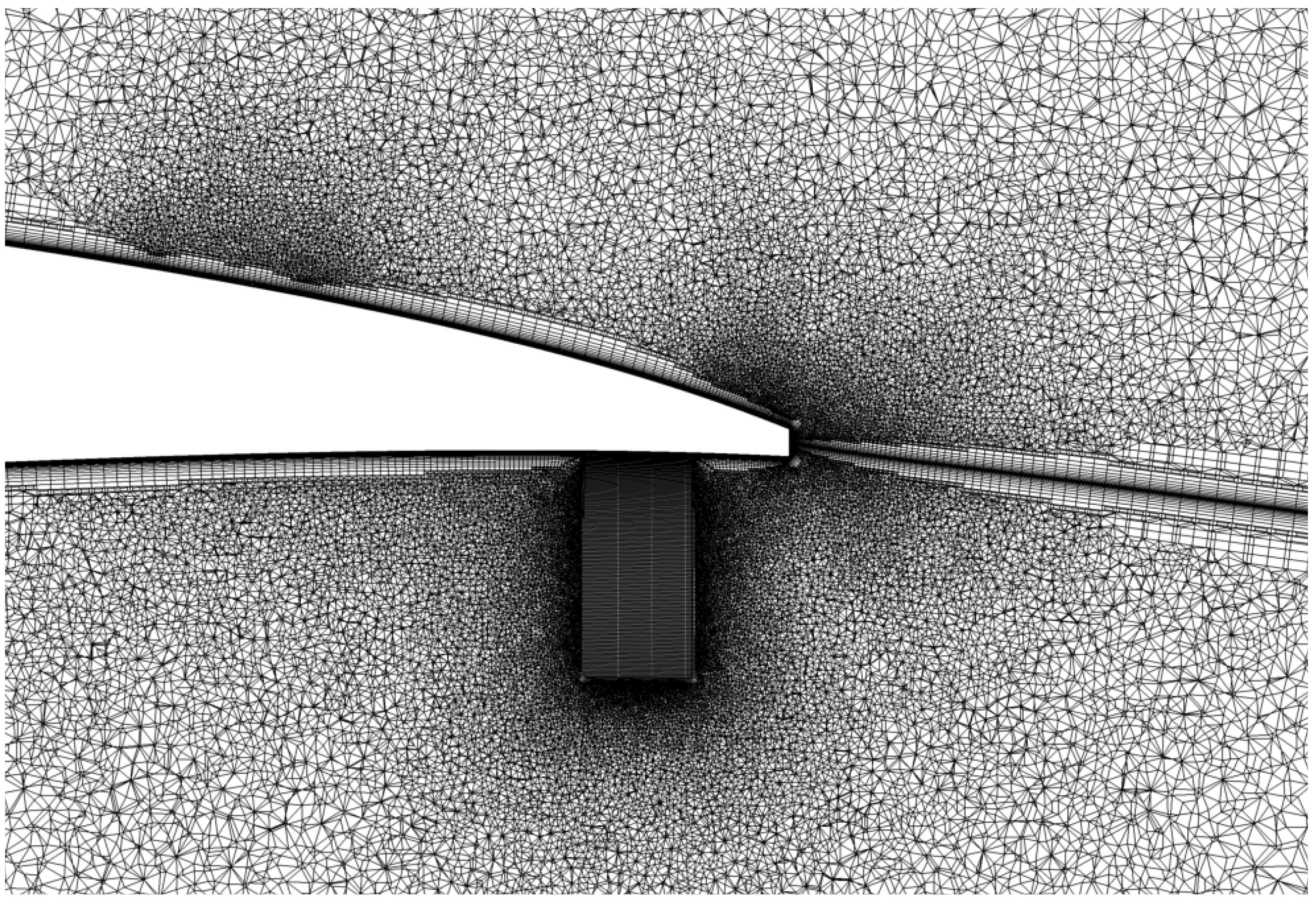
| Grid Part | URANS Grid | SST-DDES Grid | ||
|---|---|---|---|---|
| # Points | First Cell (mm) | # Points | First Cell (mm) | |
| Total | 5,418,072 | – | 20,770,098 | – |
| Feedback tube | 398,033 | 0.01 | 3,882,487 | 0.003 |
| Nozzle and outputs | 2,668,014 | 0.01–0.001 | 7,819,016 | 0.008–0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrchota, P.; Prachař, A.; Hospodář, P. Verification of Boundary Conditions Applied to Active Flow Circulation Control. Aerospace 2019, 6, 34. https://doi.org/10.3390/aerospace6030034
Vrchota P, Prachař A, Hospodář P. Verification of Boundary Conditions Applied to Active Flow Circulation Control. Aerospace. 2019; 6(3):34. https://doi.org/10.3390/aerospace6030034
Chicago/Turabian StyleVrchota, Petr, Aleš Prachař, and Pavel Hospodář. 2019. "Verification of Boundary Conditions Applied to Active Flow Circulation Control" Aerospace 6, no. 3: 34. https://doi.org/10.3390/aerospace6030034
APA StyleVrchota, P., Prachař, A., & Hospodář, P. (2019). Verification of Boundary Conditions Applied to Active Flow Circulation Control. Aerospace, 6(3), 34. https://doi.org/10.3390/aerospace6030034