To Burn-In, or Not to Burn-In: That’s the Question
Abstract
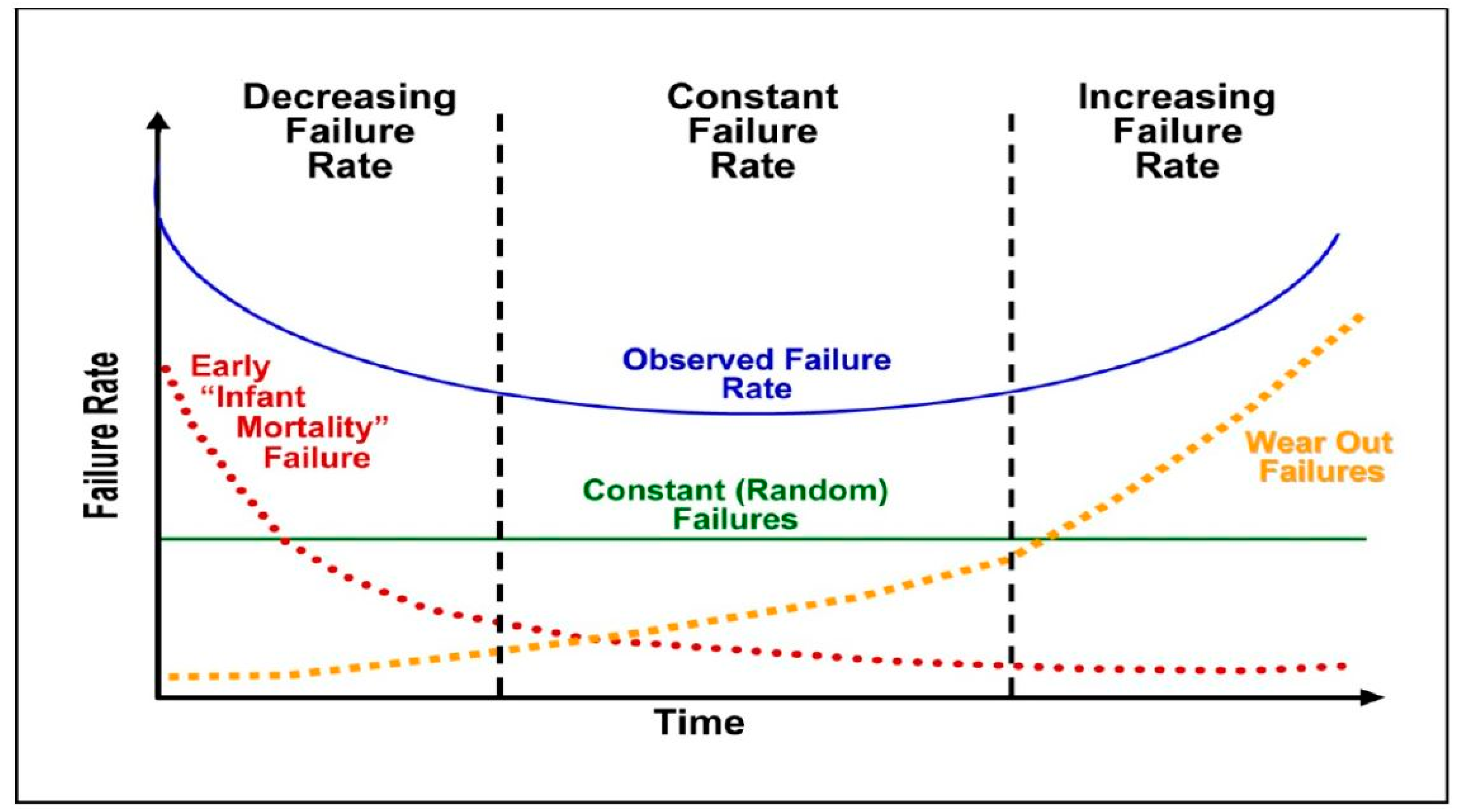
:1. Introduction
2. Analysis
2.1. Prediction Based on the Analytical Approximation of the Bathtub-Curve (BTC)
2.2. Prediction Based on the Analysis of the SFR Process
3. Conclusions
- Two mutually complementing modeling studies have been carried out: (1) the analysis of the configuration of the IMP of the BTC, the reliability “passport” of an established semiconductor technology; and (2) the analysis of the role of the random SFR of the mass-produced components that the product of interest is comprised of.
- The first analysis has shown that the BTC-based time-derivative of the failure rate at the initial moment of time can be considered as a suitable criterion of whether BIT should or does not have to be conducted. If this derivative is small, no BIT might be needed, because the initial part of the IMP is more-or-less parallel to the time axis, and this is an indication that there are no highly unreliable items (“freaks”) in the lot and that the initial moment of time is, in effect, the start of the steady-state BTC condition. In the opposite extreme case, when this derivative is significant, BIT is needed, but could be made very short, because the “freaks” are so unreliable that even a very short and weak BIT could successfully remove them.
- The second analysis has indicated that the above criterion is, in effect, the variance of the random SFR of the mass-produced components that the product manufacturer received from numerous vendors, whose commitments to reliability were unknown, and their random SFR might vary therefore in a very wide range, from zero to infinity.
- A solution for the case of the normally distributed random SFR was obtained. Using this solution, probabilities of non-failure as functions of time and the ratio of the mean value of the random SFR of the mass-produced components to its standard deviation (in analysis of structures this ratio is known as safety factor) were calculated. This adds useful information to the next-step investigations and a more effective answer to our fundamental “question in question”.
- Although this paper does not offer a straightforward and an ultimate answer to this question, the suggested physics-of-failure and statistics-of-failure based criterion, and the calculated probabilities of non-failure for the given loading conditions and time of testing, provide a useful step forward in advancing today’s BIT practice, which is based on the HALT, a “black box” that has many merits, but does not quantify reliability, even on a deterministic basis.
- Future work should include experimental verification of the suggested “to burn-in or not to burn in” criterion, as well as its acceptable values, which would enable to answer the “to burn-in or not to burn-in” question. It should include also investigation of the effects of other possible distributions of the random SFR, such as, for example, Rayleigh distribution.
Conflicts of Interest
Acronyms
| BAZ | Boltzmann-Arrhenius-Zhurkov’s (equation) |
| BIT | Burn-in Testing |
| BTC | Bathtub Curve |
| DfR | Design for Reliability |
| FOAT | Failure Oriented Accelerated Testing |
| HALT | Highly Accelerated Life Testing |
| IMP | Infant Mortality Portion (of the BTC) |
| PDfR | Probabilistic Design for Reliability |
| SFR | Statistical Failure Rate |
Appendix A
SFR of a Product Comprised of Mass-Produced Components
Appendix B
Prediction Based on the Application of the BAZ Equation
References
- Matisoff, B. Handbook of Electronics Manufacturing Engineering, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Kececioglu, D.; Sun, F.-B. Burn-in-Testin: Its Quantification and Optimization; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Ebeling, C. An Introduction to Reliability and Maintainability Engineering; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Vollertsen, R.-P. Burn-In. In Proceedings of the 1999 IEEE International Integrated Reliability Workshop Final Report, Lake Tahoe, CA, USA, 18–21 October 1999; pp. 167–173. [Google Scholar]
- Quality and Reliability; ASIC Products Application Note; Revision 3. SA 14-2280-03; IBM Microelectronics Division: Essex Junction, VT, USA, 1999; p. 15.
- Whipple, P.J.; Lanoux, J.A.; Richard, J.W.; Vu, V.V.; Motorola, Inc. Massive Parallel Semiconductor Manufacturing Test Process. U.S. Patent 6,433,568, 13 August 2002. [Google Scholar]
- Burn-In. MIL-STD-883F: Test Method Standard, Microchips. Method 1015.9; US DoD: Washington, DC, USA, 2004.
- Noel, M.; Dobbin, A.; van Overloop, D. Reducing the Cost of Test in Burn-in—An Integrated Approach. In Proceedings of the Burn-in and Test, Socket Workshop, Mesa, AZ, USA, 3–6 March 2004; pp. 34–59. [Google Scholar]
- Ooi, M.P.-L.; Abu Kassim, Z.; Demidenko, S. Shortening Burn-In Test: Application of HVST Weibull Statistical Analysis. IEEE Trans. Instrum. Meas. 2007, 56, 990–999. [Google Scholar] [CrossRef]
- Ng, Y.-H.; Low, Y.-H.; Demidenko, S.N. Improving Efficiency of IC Burn-In Testing. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Victoria, BC, Canada, 12–15 May 2008. [Google Scholar]
- Duane, J.T.; Collins, D.H.; Jason, K.; Freels, J.K.; Huzurbazar, A.V.; Warr, R.L.; Brian, P.; Weaver, B.P. Accelerated Test Methods for Reliability Prediction. IEEE Trans. Aerosp. 1964, 2, 563. [Google Scholar] [CrossRef]
- Nelson, W.B. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Crowe, D.; Feinberg, A. Design for Reliability (Electronics Handbook Series), 1st ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Suhir, E.; Ghaffarian, R. Electron Device Subjected to Temperature Cycling: Predicted Time-to-Failure. J. Electron. Mater. 2019, 48, 778–779. [Google Scholar] [CrossRef]
- Suhir, E. HALT, FOAT and Their Role in Making a Viable Device into a Reliable Product. In Proceedings of the IEEE-AIAA Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014. [Google Scholar]
- Suhir, E. Failure-Oriented-Accelerated-Testing (FOAT) and Its Role in Making a Viable IC Package into a Reliable Product. Circuits Assembly, July 2013. [Google Scholar]
- Suhir, E. Probabilistic Design for Reliability. Chip Scale Rev. 2010, 14, 6. [Google Scholar]
- Suhir, E. Remaining Useful Lifetime (RUL): Probabilistic Predictive Model. Int. J. Progn. Health Monit. (PHM) 2011, 2, 140. [Google Scholar]
- Zhurkov, S.N. Kinetic Concept of the Strength of Solids. Int. J. Fract. Mech. 1965, 1, 311–323. [Google Scholar] [CrossRef]
- Suhir, E.; Kang, S. Boltzmann-Arrhenius-Zhurkov (BAZ) Model in Physics-of-Materials Problems. Mod. Phys. Lett. B (MPLB) 2013, 27, 1330009. [Google Scholar] [CrossRef]
- Suhir, E.; Bensoussan, A. Application of Multi-Parametric BAZ Model in Aerospace Optoelectronics. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014. [Google Scholar]
- Arrhenius, S.A. Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte. Z. Phys. Chem. 1889, 4, 96–116. (In German) [Google Scholar] [CrossRef]
- Katz, A.; Pecht, M.; Suhir, E. Accelerated Testing in Microelectronics: Review, Pitfalls and New Developments. In Proceedings of the International Symposium on Microelectronics and Packaging, IMAPS, Tel-Aviv, Israel, 15 June 2000. [Google Scholar]
- Suhir, E. Statistics- and Reliability-Physics-Related Failure Processes. Mod. Phys. Lett. B (MPLB) 2014, 28, 1450105. [Google Scholar] [CrossRef]
- Suhir, E.; Bensoussan, A. Degradation Related Failure Rate Determined from the Experimental Bathtub Curve. In Proceedings of the SAE Conference, Seattle, WA, USA, 22–24 September 2015. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products; Academic Press: San Diego, CA, USA, 1980. [Google Scholar]
| −3.0 | −2.5 | −2.0 | −1.5 | −1.0 | −0.5 | −0.25 | 0 | 0.25 | |
| 3.0000 | 2.5005 | 2.0052 | 1.5302 | 1.1126 | 0.7890 | 0.6652 | 0.5642 | 0.4824 | |
| −0.9990 | −0.9906 | −0.9500 | −0.8352 | −0.6472 | −0.4952 | −0.4040 | −0.3272 | −0.2644 | |
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | |
| 0.4163 | 0.3194 | 0.2541 | 0.2080 | 0.1618 | 0.1456 | 0.1300 | 0.1166 | 0.1053 | |
| −0.1938 | −0.1306 | −0.0922 | −0.0924 | −0.0324 | −0.0312 | −0.0268 | −0.0226 | −0.0190 | |
| 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | 11.0 | 12.0 | 13.0 | |
| 0.0958 | 0.0809 | 0.0699 | 0.0615 | 0.0549 | 0.0495 | 0.0451 | 0.0414 | 0.0391 | |
| −0.0149 | −0.0110 | −0.0084 | −0.0066 | −0.0054 | −0.0044 | −0.0037 | −0.0023 | −0.0030 | |
| 15.0 | 20.0 | 30.0 | 50.0 | 100.0 | 200.0 | 500.0 | 1000.0 | 1500.0 | |
| 0.0332 | 0.0249 | 0.0166 | 0.0100 | 0.0050 | 0.0025 | 0.0010 | 0 | 0 | |
| −0.0017 | −0.0008 | −0.0003 | −0.0001 | −2.5 × 10−5 | −5.0 × 10−6 | −2.0 × 10−6 | 0 | 0 |
| s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| 0.5642 | 0.6021 | 0.6433 | 0.6881 | 0.7366 | 0.7890 | 0.8451 | 0.9033 | 0.9708 | |
| s | 0.9 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | |
| 1.0397 | 1.1126 | 1.5302 | 2.0052 | 2.5005 | 3.0000 | 3.5000 | 4.0000 |
| −3.0 | −2.5 | −2.0 | −1.5 | −1.0 | −0.5 | −0.25 | 0 | 0.25 | |
| 3.0000 | 2.5005 | 2.0052 | 1.5302 | 1.1126 | 0.7890 | 0.6652 | 0.5642 | 0.4824 | |
| x | x | x | x | x | x | x | x | x | |
| 0 | x | x | x | x | x | x | x | 1.0000 | 0.7857 |
| 1 | x | x | x | x | 1.0000 | 0.4543 | 0.3687 | 0.3236 | 0.2393 |
| 2 | x | x | 1.0000 | 0.2165 | 0.1081 | 0.0938 | 0.0975 | 0.1047 | 0.1141 |
| 3 | 1.0000 | 0.0820 | 0.0181 | 0.0101 | 0.0117 | 0.0194 | 0.0258 | 0.0339 | 0.0435 |
| 4 | 2.4788 × 10−3 | 5.5226 × 10−4 | 3.2856 × 10−4 | 4.7557 × 10−4 | 1.2613 × 10−3 | 3.9938 × 10−3 | 6.8125 × 10−3 | 1.0959 × 10−2 | 0.0166 |
| 5 | 6.1442 × 10−6 | 3.7173 × 10−6 | 5.9555 × 10−6 | 2.2289 × 10−5 | 1.3638 × 10−4 | 8.2428 × 10−4 | 1.8010 × 10−3 | 3.5458 × 10−3 | 0.6313 × 10−2 |
| 6 | 1.5230 × 10−8 | 2.5022 × 10−8 | 1.0795 × 10−11 | 1.0447 × 10−6 | 1.4724 × 10−5 | 1.7012 × 10−4 | 4.7614 × 10−4 | 1.1472 × 10−3 | 2.4055 × 10−3 |
| 7 | 3.7751 × 10−11 | 1.6843 × 10−10 | 1.9567 × 10−9 | 4.8963 × 10−8 | 1.5909 × 10−6 | 3.5111 × 10−5 | 1.2588 × 10−4 | 3.7119 × 10−4 | 9.1664 × 10−4 |
| 8 | 9.3576 × 10−14 | 1.1337 × 10−12 | 3.5468 × 10−2 | 2.2948 × 10−9 | 1.7189 × 10−7 | 7.2464 × 10−6 | 3.3278 × 10−5 | 1.2010 × 10−4 | 5.6584 × 10−4 |
| 9 | 2.3195 × 10−16 | 7.6314 × 10−15 | 6.4289 × 10−13 | 1.0756 × 10−10 | 1.8572 × 10−8 | 1.4956 × 10−6 | 8.7979 × 10−6 | 3.8858 × 10−5 | 1.3310 × 10−4 |
| 10 | 5.7495 × 10−19 | 5.1369 × 10−17 | 1.165 × 10−14 | 5.041 × 10−12 | 2.0066 × 10−9 | 3.0867 × 10−7 | 1.2572 × 10−6 | 5.7495 × 10−5 | 5.3226 × 10−5 |
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | |
| 0.4163 | 0.3194 | 0.2541 | 0.2080 | 0.1618 | 0.1456 | 0.1300 | 0.1166 | 0.1053 | |
| x | x | x | x | x | x | x | x | x | |
| 0 | 0.6595 | 0.5279 | 0.4666 | 0.4352 | 0.4453 | 0.4174 | 0.4025 | 0.3935 | 0.3876 |
| 1 | 0.2868 | 0.2787 | 0.2807 | 0.2871 | 0.3222 | 0.3120 | 0.3104 | 0.3116 | 0.3140 |
| 2 | 0.1247 | 0.1471 | 0.1689 | 0.1894 | 0.2331 | 0.2332 | 0.2393 | 0.2468 | 0.2544 |
| 3 | 5.4253 × 10−2 | 7.7677 × 10−2 | 0.1016 | 0.1249 | 0.1687 | 0.1743 | 0.1845 | 0.1955 | 0.2061 |
| 4 | 2.3595 × 10−2 | 4.1008 × 10−2 | 6.1109 × 10−2 | 8.2414 × 10−2 | 0.1220 | 0.1302 | 0.1423 | 0.1548 | 0.1669 |
| 5 | 1.0262 × 10−2 | 2.1649 × 10−2 | 3.6762 × 10−2 | 5.4367 × 10−2 | 8.8301 × 10−2 | 9.7335 × 10−2 | 0.1097 | 0.1226 | 0.1352 |
| 6 | 4.4632 × 10−3 | 1.1429 × 10−2 | 2.2115 × 10−2 | 3.5865 × 10−2 | 6.3890 × 10−2 | 7.2745 × 10−2 | 8.4585 × 10−2 | 9.7101 × 10−2 | 0.1096 |
| 7 | 1.9411 × 10−3 | 6.0337 × 10−3 | 1.3304 × 10−2 | 2.3659 × 10−2 | 4.6227 × 10−2 | 5.4367 × 10−2 | 6.5219 × 10−2 | 7.6904 × 10−2 | 8.8753 × 10−2 |
| 8 | 8.4422 × 10−4 | 3.1853 × 10−3 | 8.0033 × 10−3 | 1.5608 × 10−2 | 3.3447 × 10−2 | 4.0632 × 10−2 | 5.0287 × 10−2 | 6.0907 × 10−2 | 7.1898 × 10−2 |
| 9 | 3.6716 × 10−4 | 1.6816 × 10−3 | 4.8146 × 10−3 | 1.0296 × 10−2 | 2.4200 × 10−3 | 3.0367 × 10−2 | 3.8774 × 10−2 | 4.8238 × 10−2 | 5.8245 × 10−2 |
| 10 | 1.5969 × 10−4 | 8.8777 × 10−4 | 2.8964 × 10−3 | 6.7921 × 10−3 | 1.7510 × 10−2 | 2.2695 × 10−2 | 2.9897 × 10−2 | 3.8205 × 10−2 | 4.7184 × 10−2 |
| 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | 11.0 | 12.0 | 13.0 | |
| 0.0958 | 0.0809 | 0.0699 | 0.0615 | 0.0549 | 0.0495 | 0.0451 | 0.0414 | 0.0391 | |
| x | x | x | x | x | x | x | x | x | |
| 0 | 0.3837 | 0.3788 | 0.3758 | 0.3738 | 0.3722 | 0.3716 | 0.3708 | 0.3702 | 0.3618 |
| 1 | 0.3168 | 0.3222 | 0.3268 | 0.3305 | 0.3335 | 0.3366 | 0.3388 | 0.3408 | 0.3346 |
| 2 | 0.2615 | 0.2741 | 0.2842 | 0.2923 | 0.2989 | 0.3048 | 0.3096 | 0.3137 | 0.3094 |
| 3 | 0.2159 | 0.2331 | 0.2471 | 0.2585 | 0.2678 | 0.2761 | 0.2829 | 0.2888 | 0.2862 |
| 4 | 0.1783 | 0.1983 | 0.2149 | 0.2286 | 0.2399 | 0.2501 | 0.2585 | 0.2659 | 0.2646 |
| 5 | 0.1472 | 0.1687 | 0.1868 | 0.2021 | 0.2150 | 0.2265 | 0.2362 | 0.2447 | 0.2447 |
| 6 | 0.1215 | 0.1435 | 0.1624 | 0.1787 | 0.1926 | 0.2052 | 0.2158 | 0.2253 | 0.2263 |
| 7 | 0.1003 | 0.1220 | 0.1413 | 0.1580 | 0.1726 | 0.1858 | 0.1972 | 0.2074 | 0.2093 |
| 8 | 8.2844 × 10−2 | 0.1038 | 0.1228 | 0.1397 | 0.1546 | 0.1683 | 0.1802 | 0.1909 | 0.1936 |
| 9 | 6.8399 × 10−2 | 8.8301 × 10−2 | 0.1424 | 0.1236 | 0.1386 | 0.1524 | 0.1646 | 0.1757 | 0.1790 |
| 10 | 5.6473 × 10−2 | 7.5110 × 10−2 | 9.2866 × 10−2 | 0.1093 | 0.1242 | 0.1646 | 0.1504 | 0.1618 | 0.1655 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suhir, E. To Burn-In, or Not to Burn-In: That’s the Question. Aerospace 2019, 6, 29. https://doi.org/10.3390/aerospace6030029
Suhir E. To Burn-In, or Not to Burn-In: That’s the Question. Aerospace. 2019; 6(3):29. https://doi.org/10.3390/aerospace6030029
Chicago/Turabian StyleSuhir, Ephraim. 2019. "To Burn-In, or Not to Burn-In: That’s the Question" Aerospace 6, no. 3: 29. https://doi.org/10.3390/aerospace6030029
APA StyleSuhir, E. (2019). To Burn-In, or Not to Burn-In: That’s the Question. Aerospace, 6(3), 29. https://doi.org/10.3390/aerospace6030029





