Computational Analysis of Compressed Stiffened Composite Panels with Impact Damage
Abstract
1. Introduction
2. Statement of Work and Governing Equations
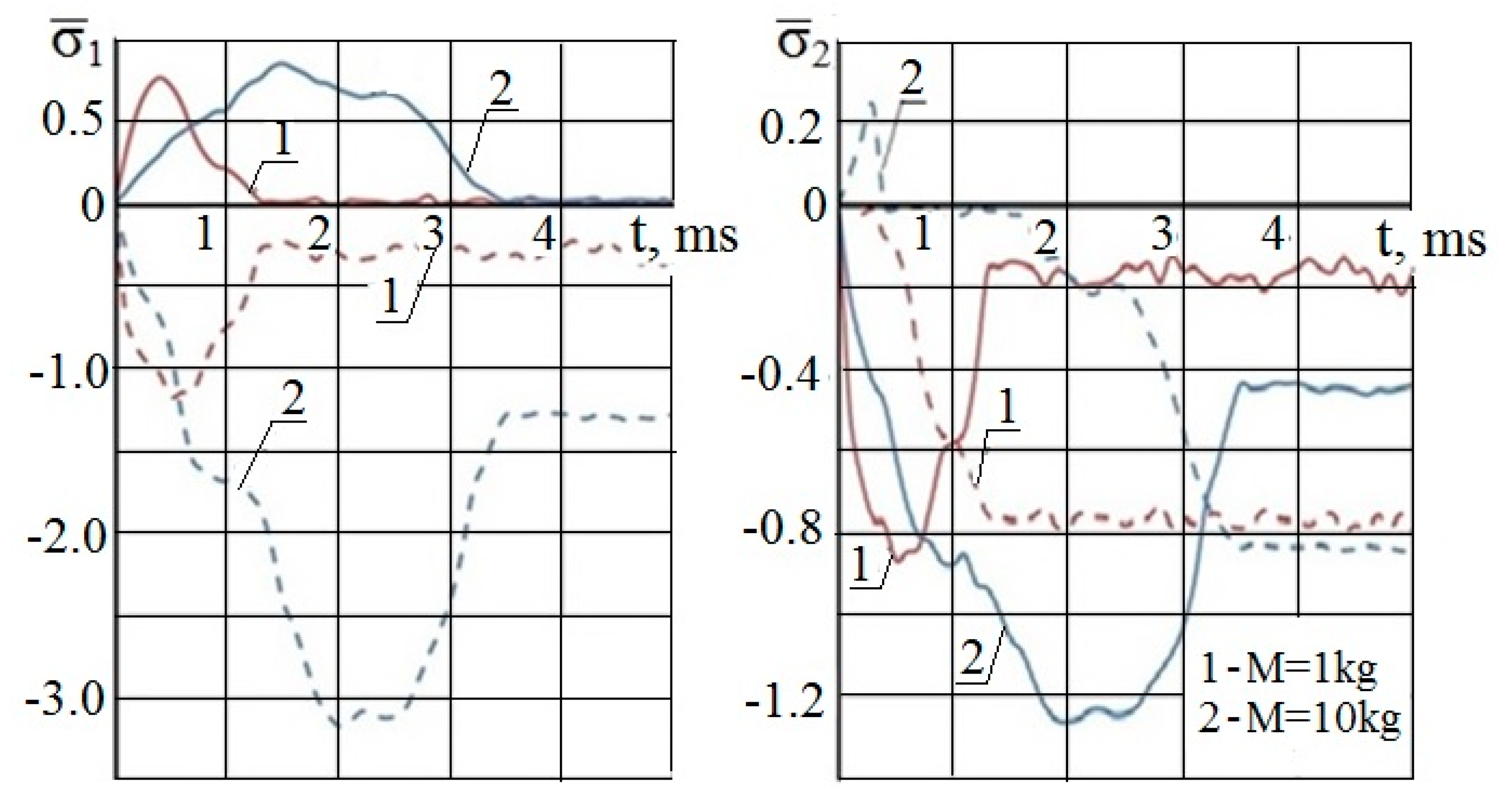
3. Local Dynamic Deformation of the Panel
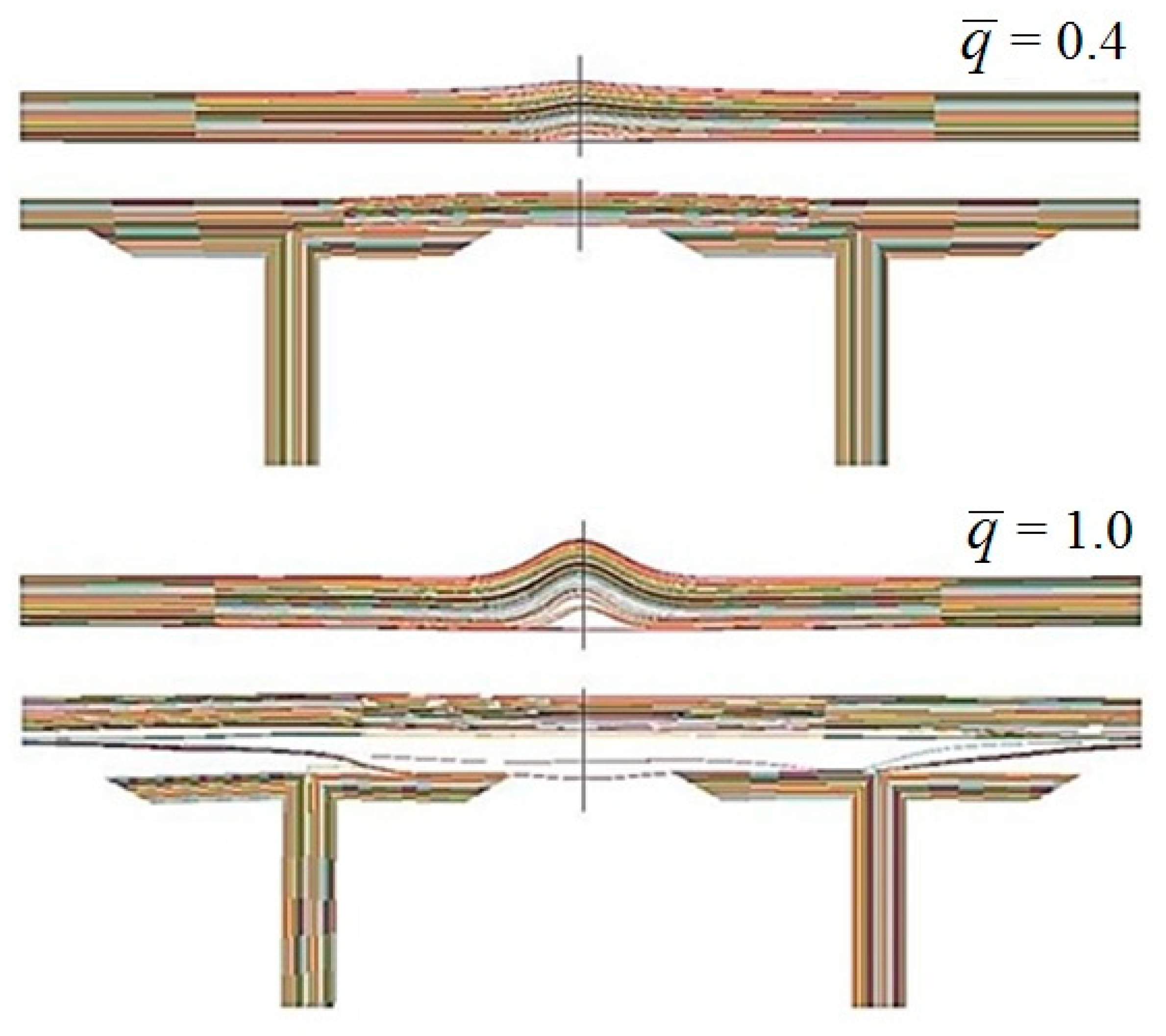
4. Quasi-Static Compression of the Panel
5. Conclusions
- A complex modeling technique has been developed on the basis of the LS-Dyna code for the prediction of local impact damage and its influence on the carrying capacity of a compressed flat stiffened composite panel. The numerical analysis shows that local buckling of delaminated fibers in impact damage zone is one of the main reasons for a significant reduction of the carrying capacity of the compressed FRP stiffened panel.
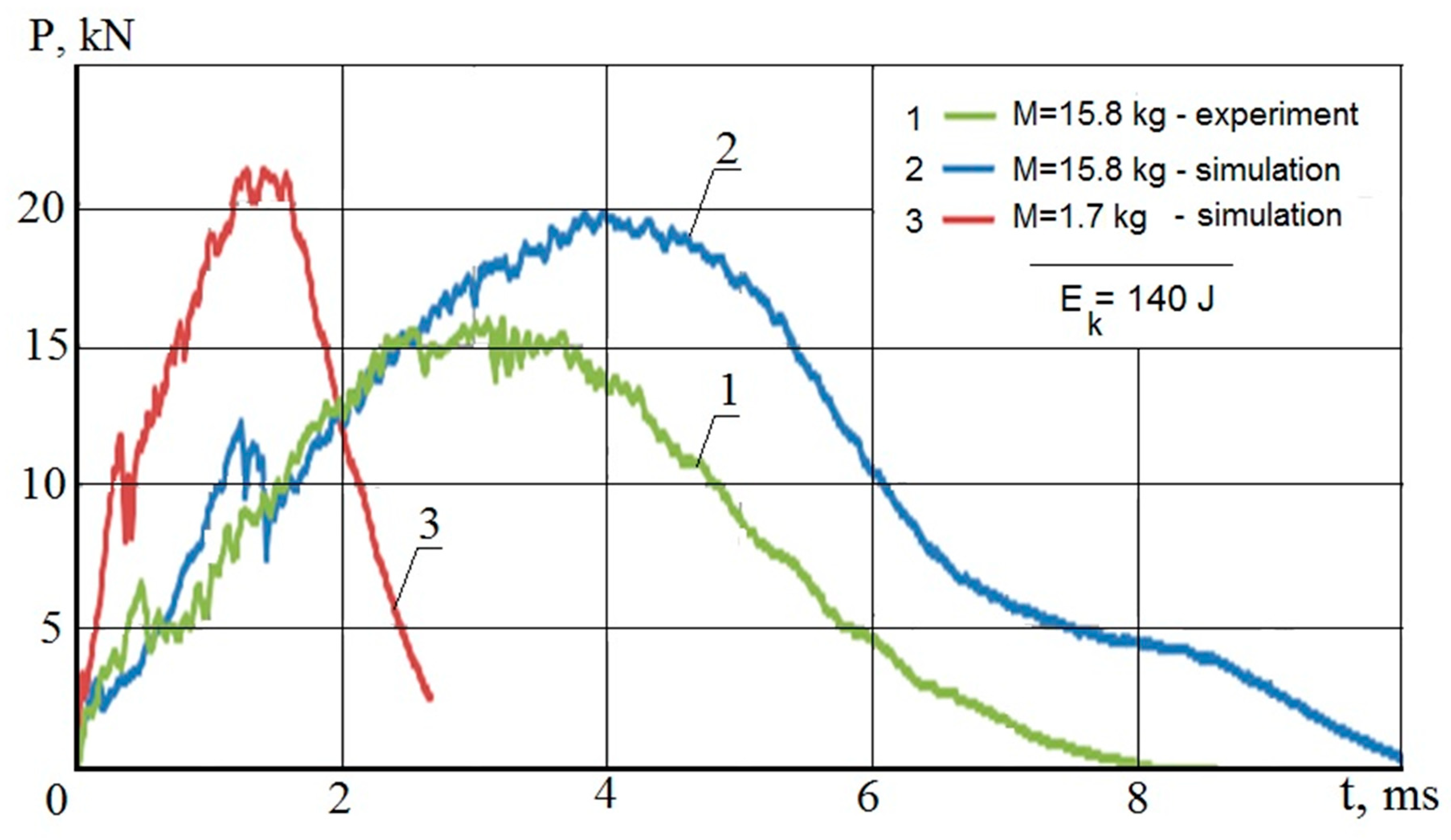
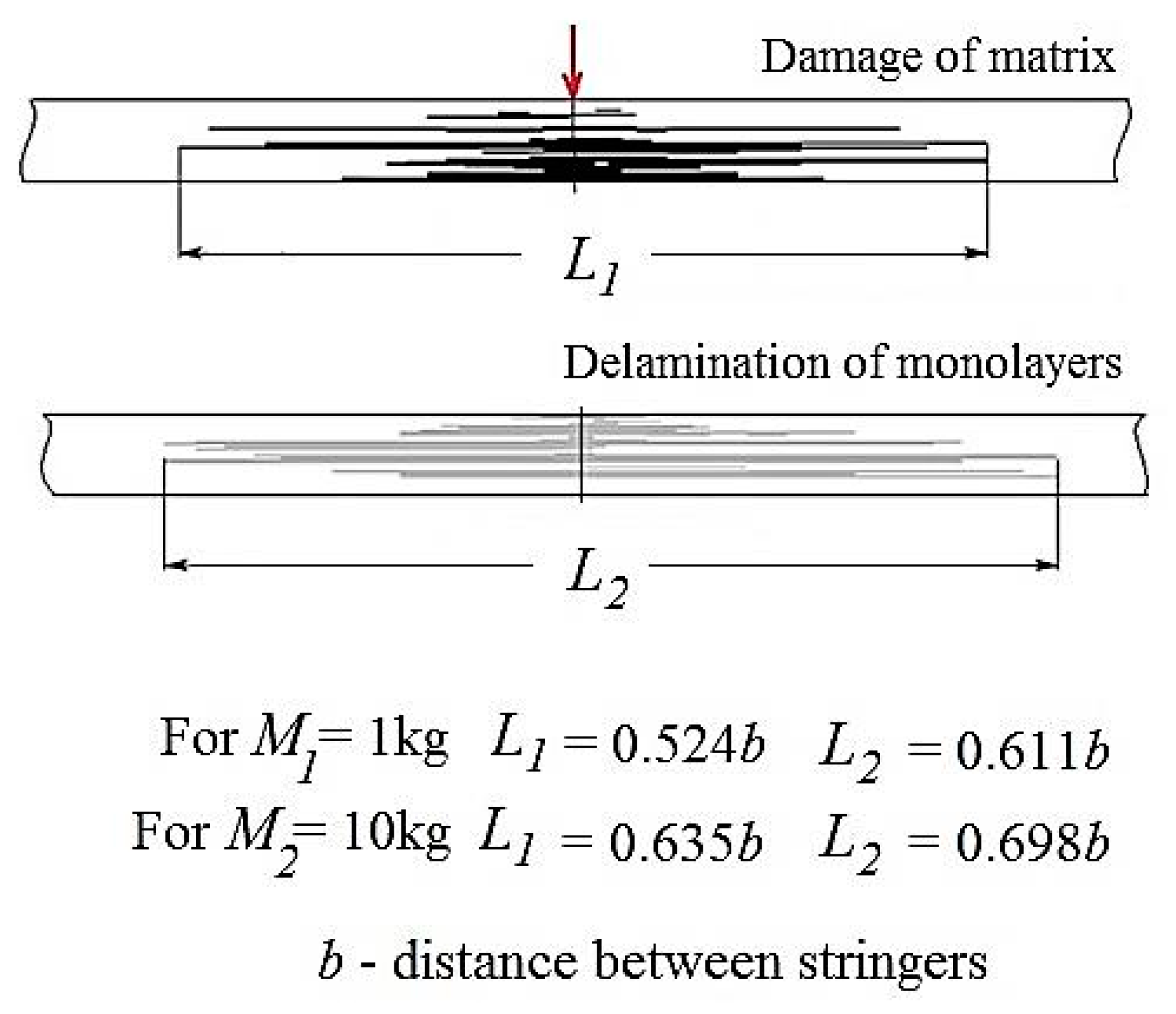
- The validity of the modeling technique was confirmed by the agreement between the numerical and experimental results. The maximal dynamic force and impulse duration in the simulation of local impact exceed experimental data by no more than ~20%. The numerical and experimental sizes of the impact damage zone are ~0.7b and close to each other. These predictions could be quite acceptable for preliminary engineering analysis.
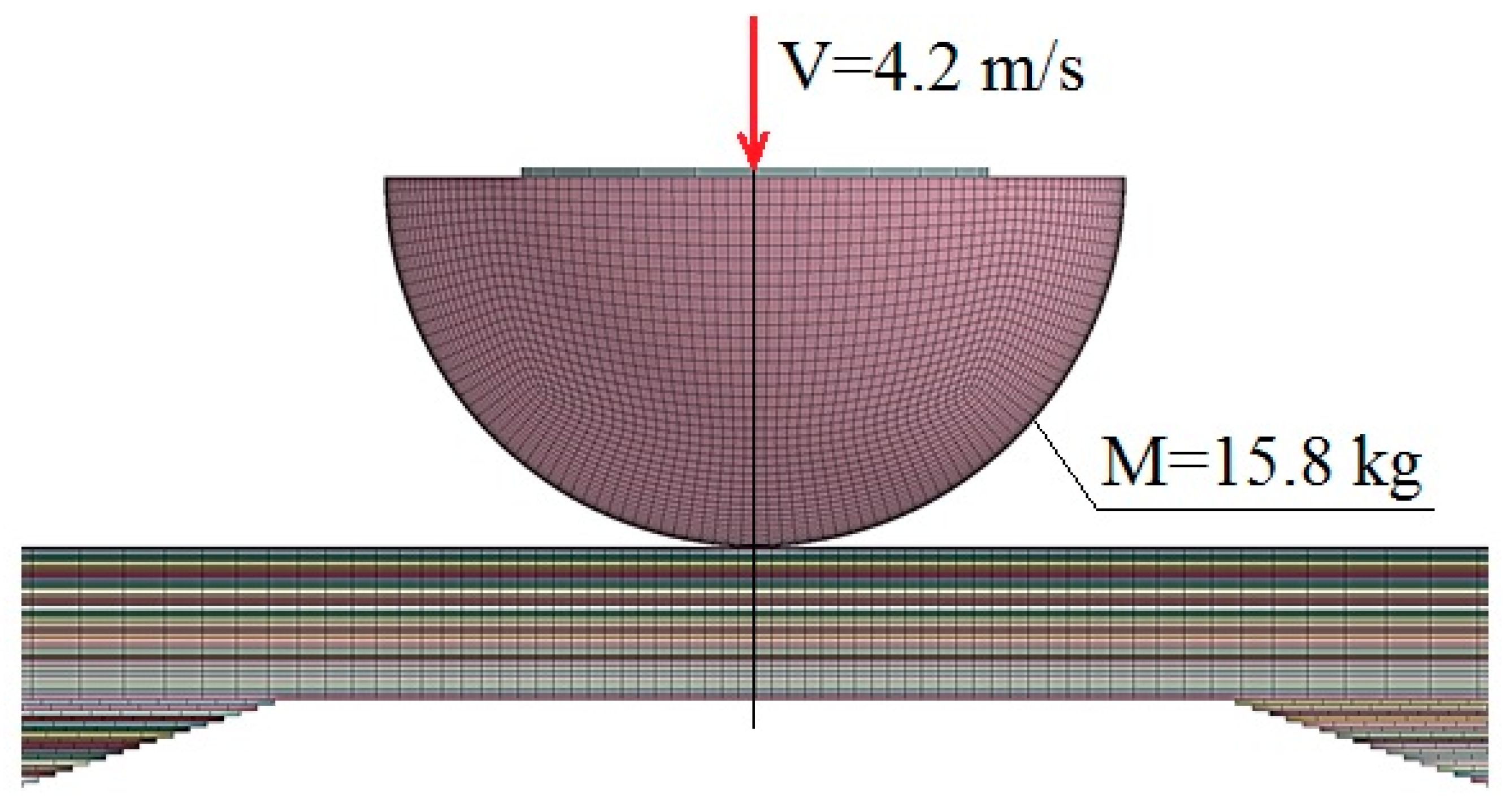
- The fixed level of the kinetic energy of Ek = const. is not a fully correct measure of local damage for FRP stiffened panel, since the decrease of the impactor weight and keeping Ek = const. cause decreasing sizes of damage zone.
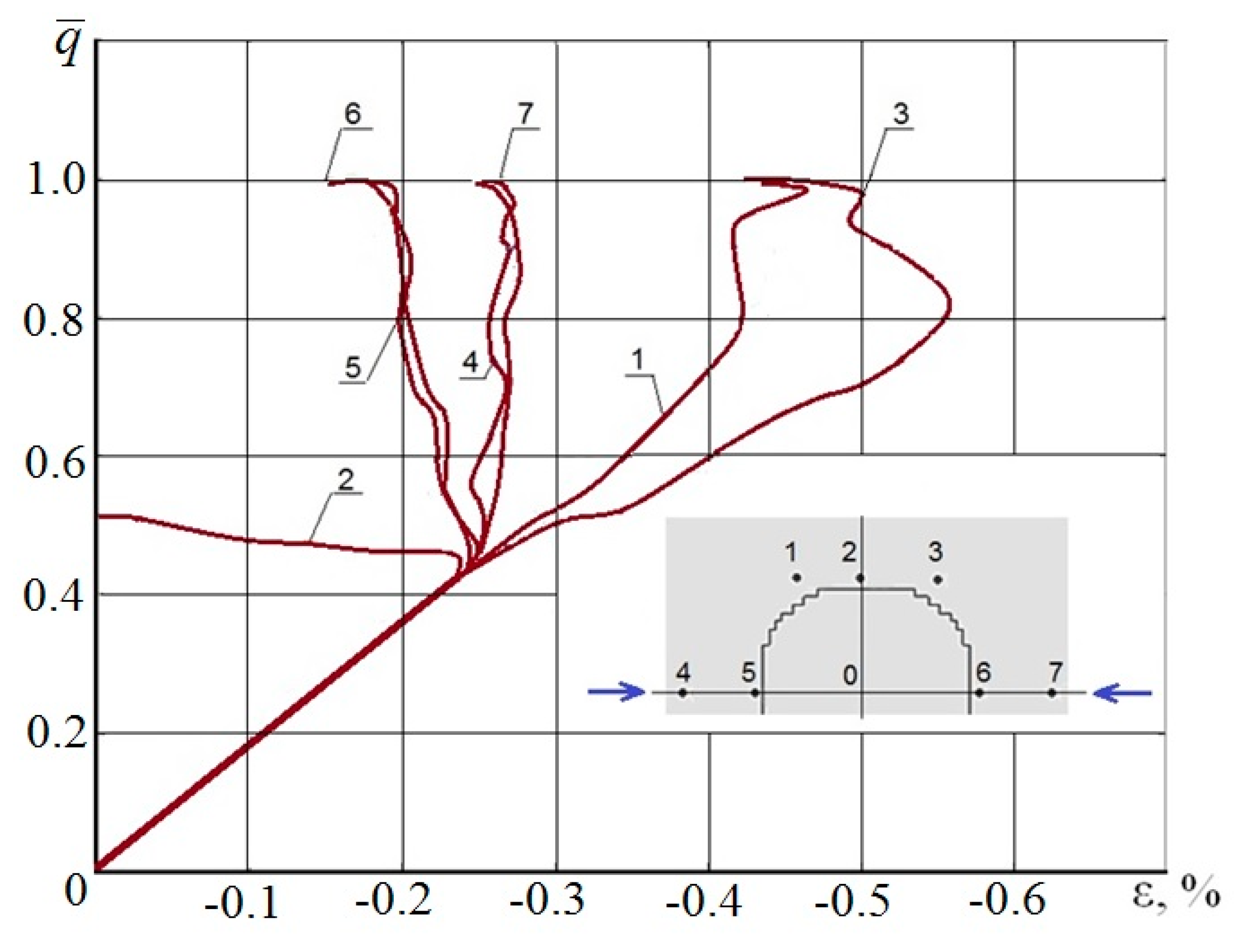
- Quasi-static simulation of the damaged panel at the stage of longitudinal compression allows the prediction of the ultimate longitudinal strains near the impact damage zone: εnum = −0.25 to −0.48%, which are close to the experimental levels: εexp = −0.27% to −0.45%, corresponding to the carrying load of the FRP panel.
- The obtained numerical results show that the local impact damage zone can reduce the carrying capacity of the compressed composite panel by more than 50% compared to the undamaged composite panel.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bolotin, B.V.; Novichkov, Y.N. Mechanics of Multilayers Structures; Mashinostroenie: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Mechanics and Analysis of Composite Materials; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Abrosimov, N.A.; Bazhenov, V.G. Nonlinear Problems of Dynamics of the Composite Structures; NNSU: Nizhny Novgorod, Russia, 2002; 400p. (In Russian) [Google Scholar]
- Ladeveze, P.; Le Dantec, E. Damage modeling of the elementary ply for laminated composites. Compos. Sci. Technol. 1992, 43, 257–267. [Google Scholar] [CrossRef]
- Kenane, M.; Benzeggagh, M.L. Mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites under fatigue loading. Compos. Sci. Technol. 1997, 57, 597–605. [Google Scholar] [CrossRef]
- Zinoviev, P.A.; Grigoriev, S.V.; Lebedeva, O.V.; Tairova, L.P. The strength of multilayered composites under a plane-stress state. Compos. Sci. Technol. 1998, 57, 1209–1223. [Google Scholar] [CrossRef]
- Camanho, P.P.; Da’vila, C.G.; Pinho, S.T.; Iannucci, L.; Robinson, P. Prediction of in situ strengths and matrix cracking in composites under transverse tension and in-plane shear. Compos. Part A Appl. Sci. Manuf. 2006, 37, 165–176. [Google Scholar] [CrossRef]
- Da´vila, C.; Camanho, P.P.; Turon, A. Effective simulation of delamination in aeronautical structures using shells and cohesive elements. J. Aircr. 2008, 45, 663–672. [Google Scholar] [CrossRef]
- Krueger, R.; Ratcliffe, J.G.; Minguet, P.J. Panel stiffener debonding analysis using a shell/3D modeling technique. Compos. Sci. Technol. 2009, 69, 2352–2362. [Google Scholar] [CrossRef]
- Gutkin, R.; Pinho, S.T.; Robinson, P.; Curtis, P.T. On the transition from shear-driven fiber compressive failure to fiber kinking in notched CFRP laminates under longitudinal compression. Compos. Sci. Technol. 2010, 70, 1223–1231. [Google Scholar] [CrossRef]
- Backer, A.; Dutton, S.; Kelly, D. Composite Materials for Aircraft Structures, 2nd ed.; American Institute of Aeronautic and Astronautic, Inc.: Reston, VA, USA, 2004. [Google Scholar]
- Ostergaard, M.G.; Ibbotson, A.R.; Le Roux, O.; Prior, A.M. Virtual Testing of Aircraft Structures. CEAS Aeronaut. J. 2011, 1, 83–103. [Google Scholar] [CrossRef]
- Clark, G.; Saunders, D.S. Morphology of Impact Damage Growth by Fatigue in Carbon Fiber Composite Laminates. Mater. Forum 1991, 15, 333–342. [Google Scholar]
- Naganarayana, B.P.; Atluri, S.N. Computational Model for Analysis Interactive Buckling and Delamination Growth in Composite Structures. Sadhana Acad. Proc. Eng. Sci. 1996, 21, 547–575. [Google Scholar]
- Reeder, J.R.; Kyongchan, S.; Chunchu, P.B.; Ambur, D.R. Postbuckling and Growth of Delaminations in Composite Plates Subjected to Axial Compression. In Proceedings of the AIAA 2002-1746, 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Material Co-Located Conferences, Denver, CO, USA, 22–25 April 2002. [Google Scholar]
- Patel, B.P.; Gupta, A.K. An investigation on nonlocal continuum damage models for composite laminated panels. Compos. B Eng. 2014, 60, 485–494. [Google Scholar] [CrossRef]
- Wan, Y.; Sun, B.; Gu, B. Multi-scale structure modeling of damage behaviors of 3D orthogonal woven composite materials subject to quasi-static and high strain rate compression. Mech. Mater. 2016, 94, 1–25. [Google Scholar] [CrossRef]
- Cantwell, W.; Morton, J. An assessment of residual strength of an impact damaged carbon-fiber reinforced epoxy. Compos. Struct. 1990, 14, 303–317. [Google Scholar] [CrossRef]
- Hull, D.; Shi, B.Y. Damage mechanism characterization in composite damage tolerance investigations. Compos. Struct. 1993, 23, 99–120. [Google Scholar] [CrossRef]
- Davies, G.A.; Zhang, X. Impact Damage Predictions in Carbon Composite Structures. J. Impact Eng. 1995, 16, 149–170. [Google Scholar] [CrossRef]
- Greenhalgh, E.; Bishop, S.M.; Braz, D.; Hughes, D.; Lahiff, S.; Millson, B. Characterization of impact damage in skin-stringer composite structures. Compos. Struct. 1996, 36, 187–207. [Google Scholar] [CrossRef]
- Zhang, X. Impact Damage in Composite Aircraft Structures—Experimental Testing and Numerical Simulation. J. Aerosp. Eng. 1998, 212, 245–259. [Google Scholar] [CrossRef]
- Rajbhandari, S.P.; Scott, M.L.; Thomson, R.S. An Approach to Modelling and predicting Impact Damage in Composite Structures. In Proceedings of the ICAS 2002 Congress, Toronto, ON, Canada, 8–13 September 2002. [Google Scholar]
- Imielinska, K.; Wojtyra, R.; Kozlowski, M. On Delamination Threshold Loads in Low Velocity Impact on Glass-Carbon/Epoxy Composites. Kompozyty (Compos.) 2005, 5, 69–74. [Google Scholar]
- Olsson, R. Modelling of impact damage zone in composite laminates for strength after impact. Aeronaut. J. 2012, 116, 1349–1365. [Google Scholar] [CrossRef]
- Al-Hadrayi Ziadoon, M.R.; Zhou, C. Effect the Stacking Sequences of Composite Laminates under Low Velocity Impact on Failure Modes by Using Carbon Fiber Reinforced Polymer. Int. J. Eng. Sci. (IJES) 2016, 5, 53–62. [Google Scholar]
- Bazhenov, V.G.; Demareva, A.V.; Zhestkov, M.N.; Kibets, A.I. Special features of numerical simulation for elastic-plastic buckling of hemispherical shells under loading with the rigid indenter. PNRPU Mech. Bull. 2016, 2, 22–33. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B. Nonlinear Finite Elements for Continua and Structures; John Wiley & Sons: New York, NY, USA, 2000; 600p. [Google Scholar]
- Washizu, K. Variational Methods in Elasticity and Plasticity; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress concentrations. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]
- Hallquist John, O. LS-DYNA Theory Manual LSTC; Livermore Software Technology Corporation: Livermore, CA, USA, 2017. [Google Scholar]
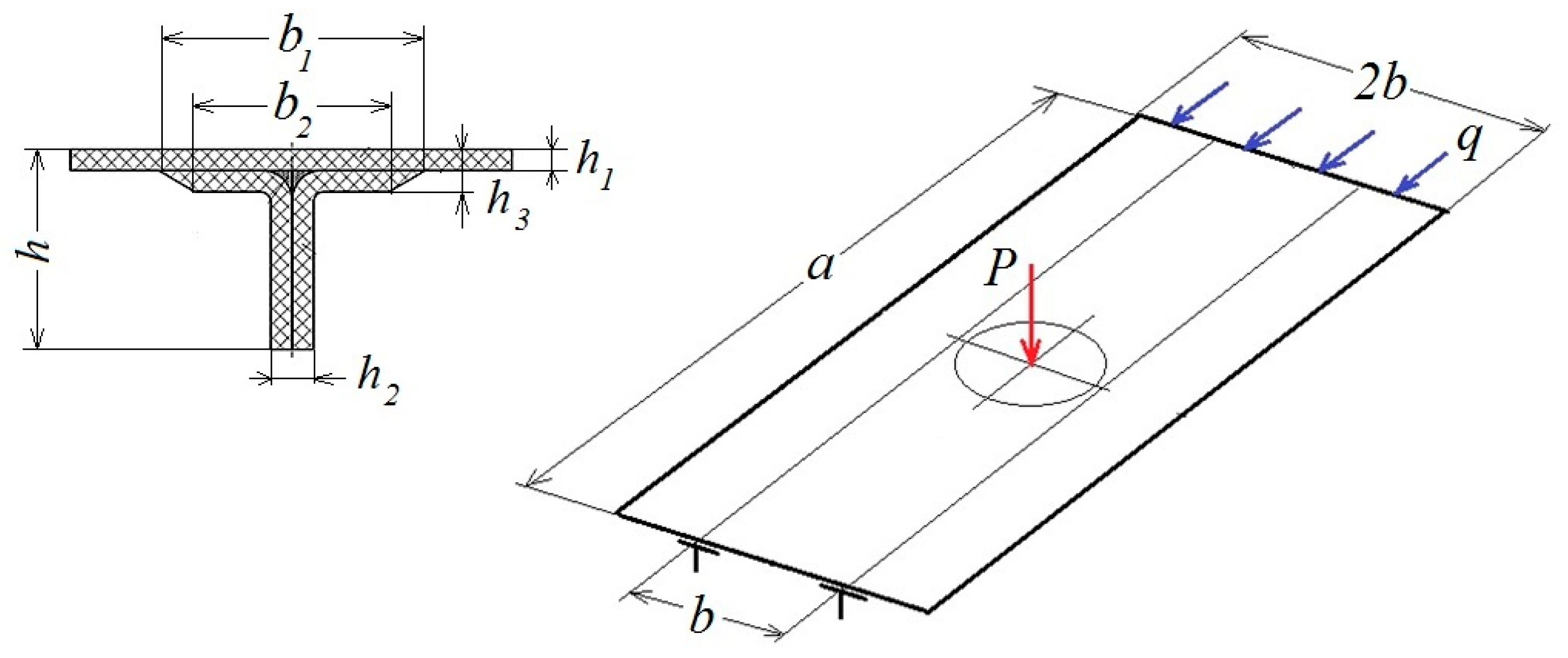

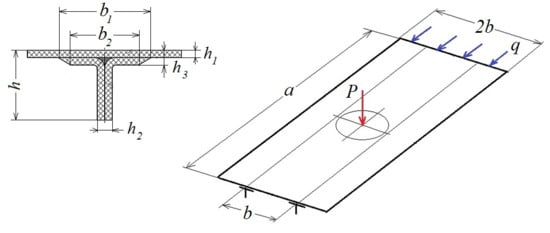
| h | h2 | h3 | a | b | b1 | b2 |
|---|---|---|---|---|---|---|
| 7.5 | 2.0 | 2.0 | 66 | 23.3 | 17.0 | 11.4 |
| Results | Experiment | Simulation * |
|---|---|---|
| Size in X direction | 0.64–0.75b | 0.65b |
| Size in Y direction | 0.63–0.70b | 0.88b |
| Load | Points | Experimental ε, % | Numerical ε, % |
|---|---|---|---|
| 1.0 | 1 | −0.45 | −0.44 |
| 3 | −0.48 | −0.45 | |
| 4 | −0.26 | −0.25 | |
| 7 | −0.30 | −0.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryabov, A.A.; Maslov, E.E.; Strelets, D.Y.; Slobodchikov, V.G. Computational Analysis of Compressed Stiffened Composite Panels with Impact Damage. Aerospace 2019, 6, 25. https://doi.org/10.3390/aerospace6030025
Ryabov AA, Maslov EE, Strelets DY, Slobodchikov VG. Computational Analysis of Compressed Stiffened Composite Panels with Impact Damage. Aerospace. 2019; 6(3):25. https://doi.org/10.3390/aerospace6030025
Chicago/Turabian StyleRyabov, Alexander A., Evgeny E. Maslov, Dmitry Y. Strelets, and Vladimir G. Slobodchikov. 2019. "Computational Analysis of Compressed Stiffened Composite Panels with Impact Damage" Aerospace 6, no. 3: 25. https://doi.org/10.3390/aerospace6030025
APA StyleRyabov, A. A., Maslov, E. E., Strelets, D. Y., & Slobodchikov, V. G. (2019). Computational Analysis of Compressed Stiffened Composite Panels with Impact Damage. Aerospace, 6(3), 25. https://doi.org/10.3390/aerospace6030025