High-Bandwidth Morphing Actuator for Aeroelastic Model Control
Abstract
:1. Introduction
2. High-Bandwidth Morphing Actuator (HMBA) Design
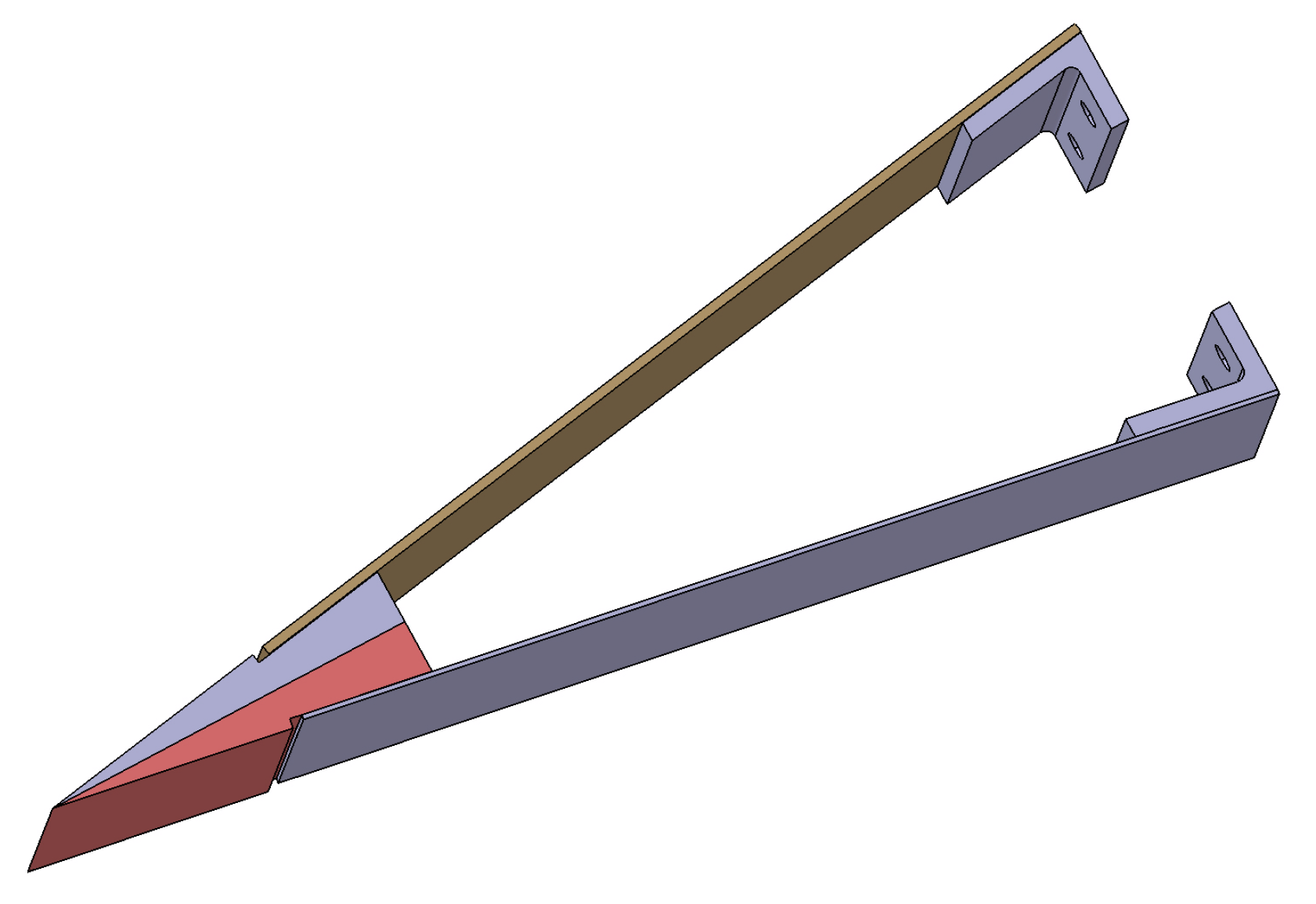
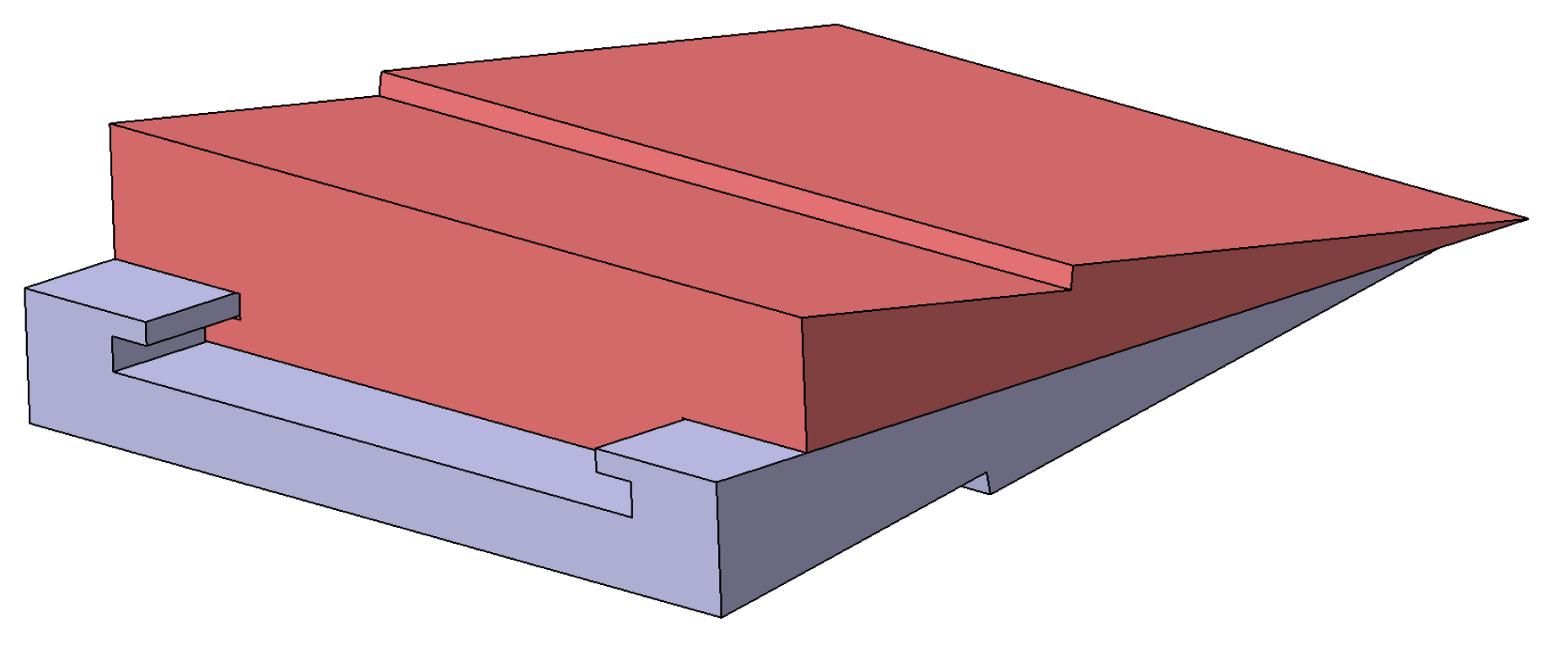
2.1. Actuator Configuration
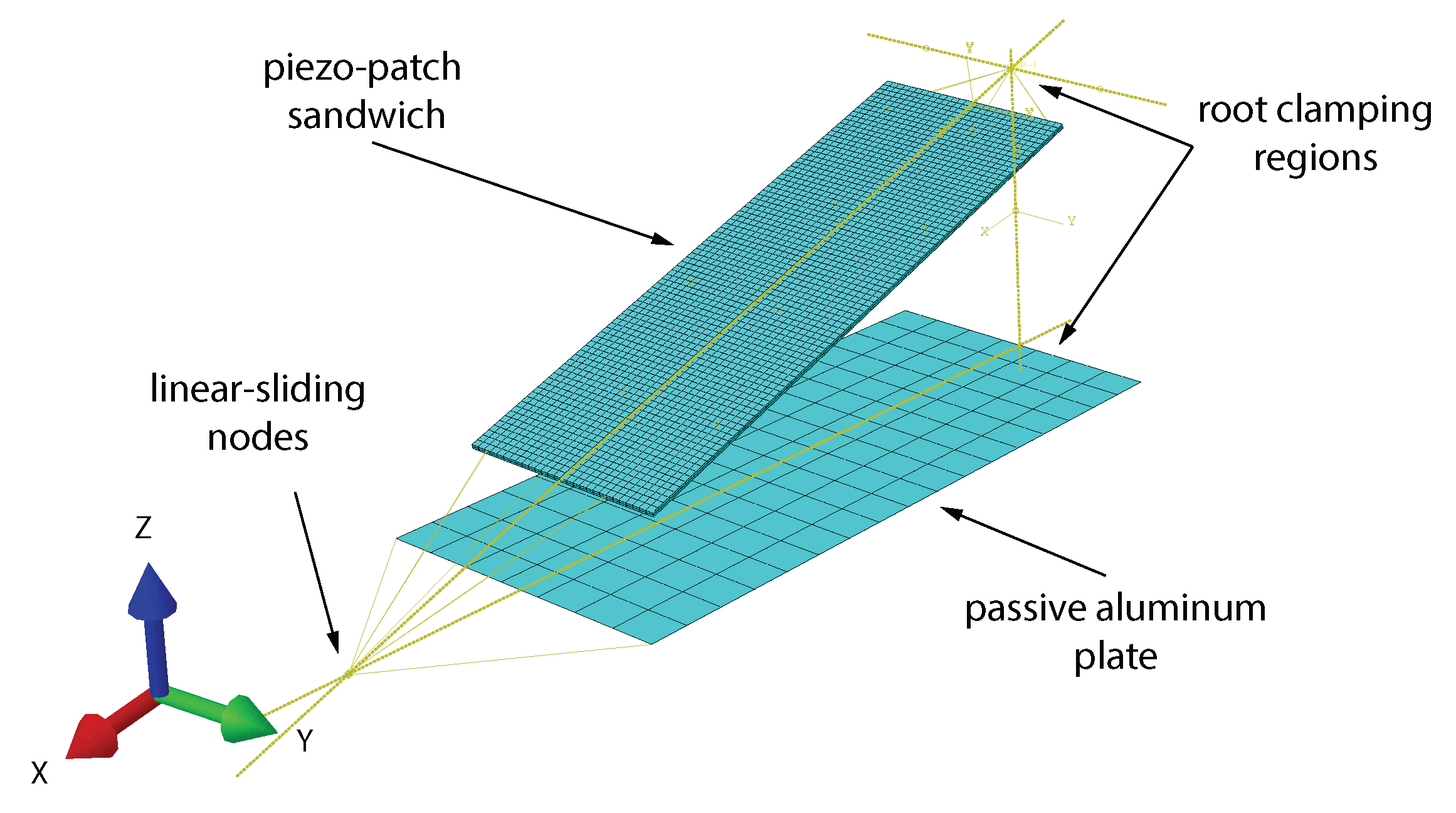
2.2. Actuation Design Comparison
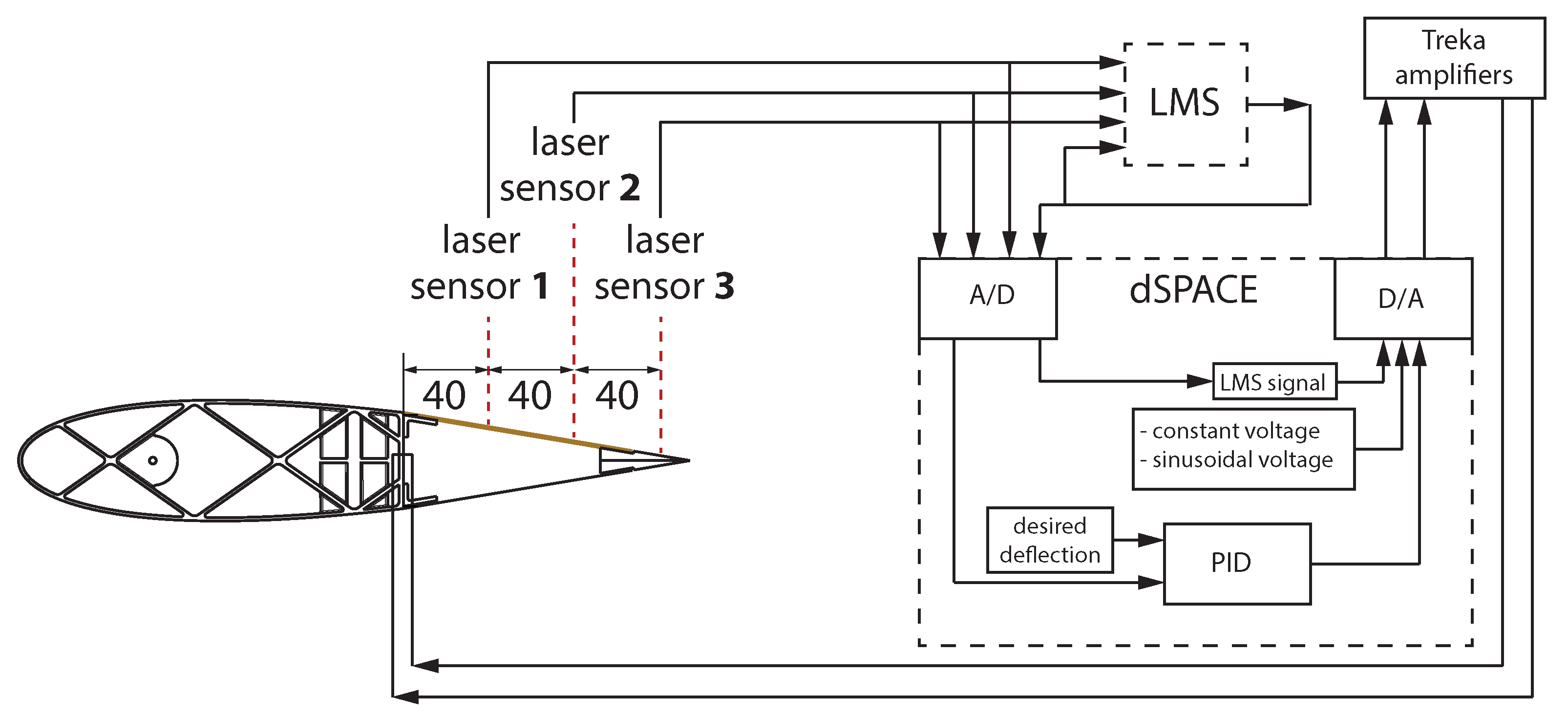
3. Experimental Tests
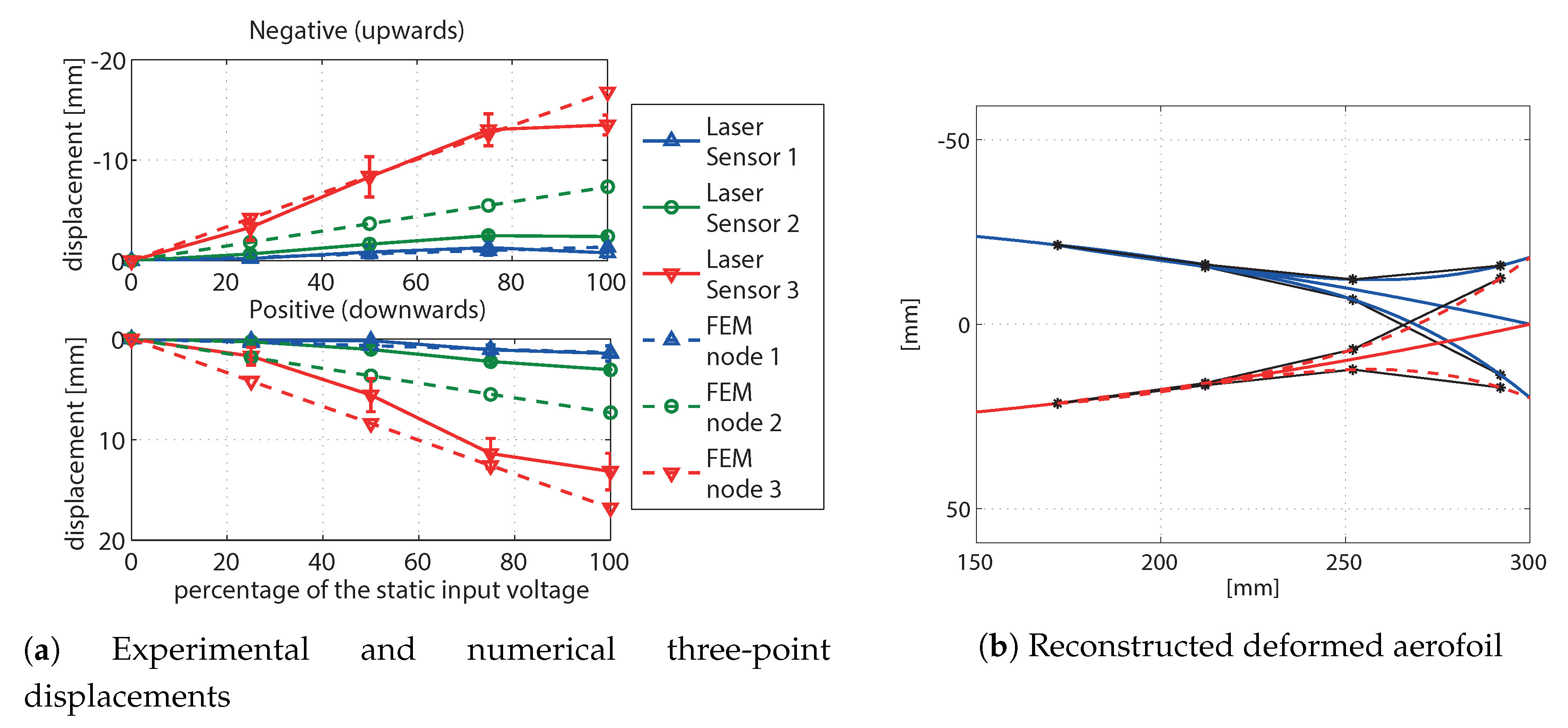
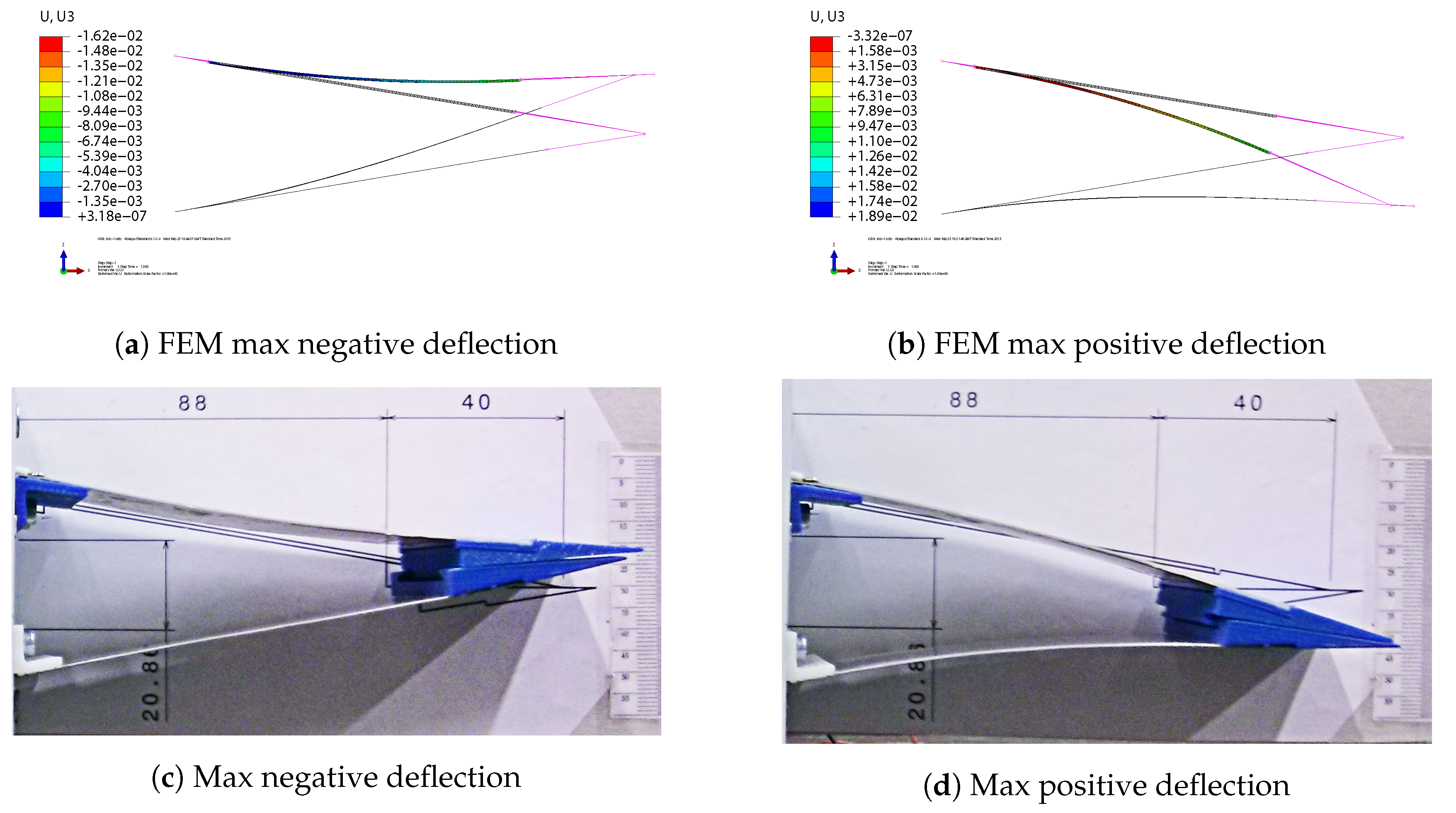
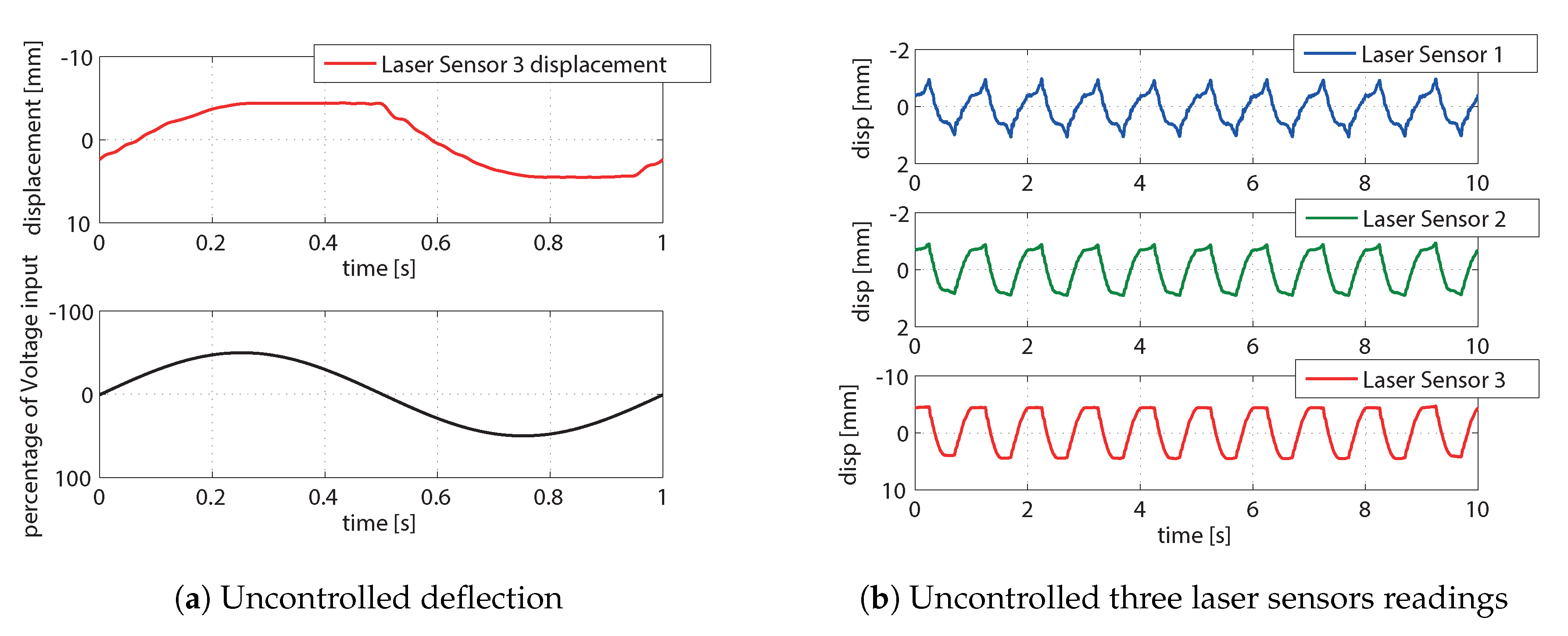
3.1. Static Deflection Test
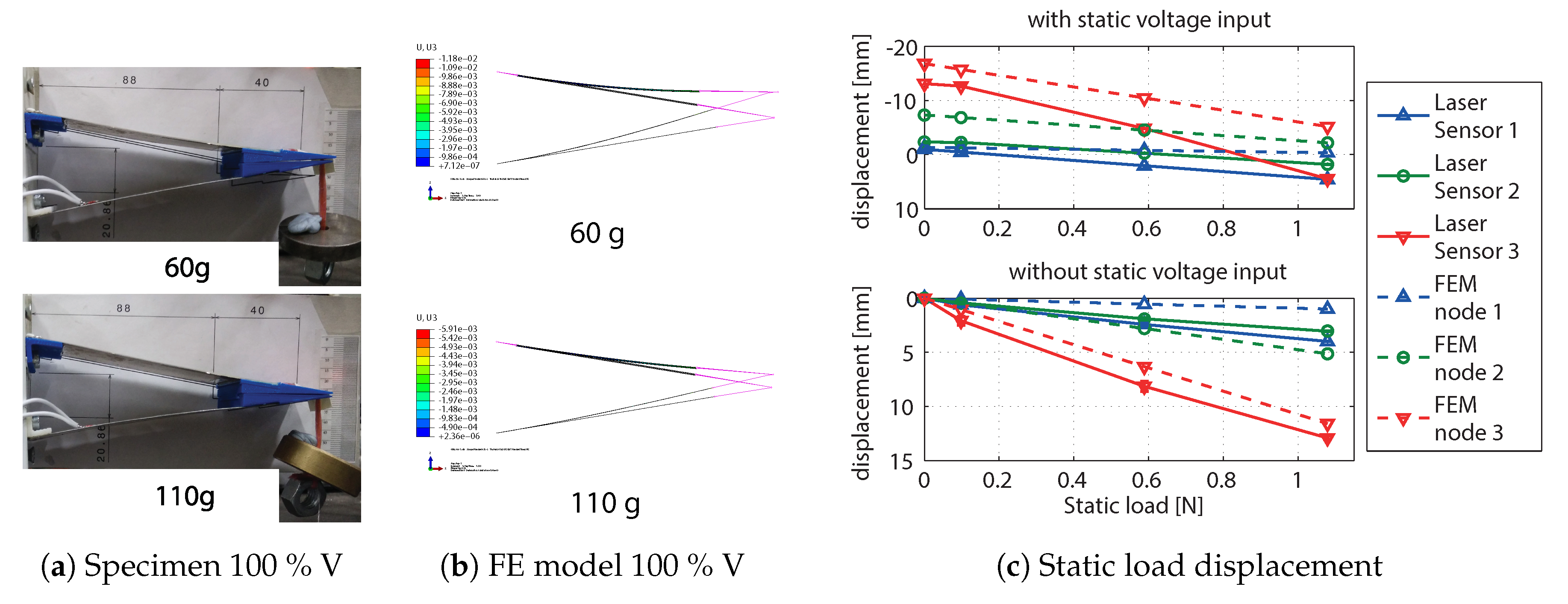
3.2. Static Load Test
3.3. Dynamic Test
3.4. Ability of the Actuator to Follow a Prescribed Motion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FE | Finite Element |
| HBMA | High Bandwidth Morphing Actuator |
| MFC | Macro-Fibre Composites |
| MODFLEX | MODular aeroelastic FLEXible wing |
| NACA | National Advisory Committee for Aeronautics |
| PID | Proportional Integral Derivative |
References
- Ricci, S.; Scotti, A.; De Gaspari, A.; Riccobene, L. Active Aeroelastic Control over a Multisurface Wing: Modelling and Wind-Tunnel Testing. AIAA J. 2009, 47, 1995–2010. [Google Scholar] [CrossRef]
- Arena, M.; Amoroso, F.; Pecora, R.; Amendola, G.; Dimino, I.; Concilio, A. Numerical and experimental validation of a full scale servo-actuated morphing aileron model. Smart Mater. Struct. 2018, 27, 105034. [Google Scholar] [CrossRef]
- Ardelean, E.V. High Performance “V-stack” Piezoelectric Actuator. J. Intell. Mater. Syst. Struct. 2004, 15, 879–889. [Google Scholar] [CrossRef]
- Papatheou, E.; Wei, X.; Jiffri, S.; Prandina, M.; Tehrani, M.G.; Bode, S.; Singh, K.V.; Mottershead, J.E.; Cooper, J. Flutter control using vibration test data: Theory, rig design and preliminary results. In Proceedings of the International Seminar on Modal Analysis (ISMA2012), Leuven, Belgium, 17–19 September 2012. [Google Scholar]
- Heinze, S.; Karpel, M. Analysis and Wind Tunnel Testing of a Piezoelectric Tab for Aeroelastic Control Applications. J. Aircr. 2006, 43, 1799–1804. [Google Scholar] [CrossRef]
- Lazarus, K.B.; Crawley, E.F.; Bohlmann, J.D.; Worth, F. Static aeroelastic control using strain actuated adaptive structures. J. Intell. Mater. Syst. Struct. 1991, 2, 386–440. [Google Scholar] [CrossRef]
- Barrett, R.M. All-moving active aerodynamic surface research. Act. Mater. Smart Struct. 1995, 2427, 2–15. [Google Scholar] [CrossRef]
- Barrett, R.M.; Gross, R.S.; Brozoski, T.F. Design and Testing of a Subsonic All-Moving Adaptive Flight Control Surface. AIAA J. 1997, 35, 1217–1219. [Google Scholar] [CrossRef]
- Barrett, R.M.; Gross, R.S.; Brozoski, T.F. Missile flight control using active flexspar actuators. Smart Mater. Struct. 1999, 5, 121–128. [Google Scholar] [CrossRef]
- Pinkerton, J.L.; Moses, R.W. A Feasibility Study to Control Airfoil Shape Using THUNDER; Technical Report 4767; NASA: Washington, DC, USA, 1997. [Google Scholar]
- Wilkie, W.K.; Bryant, R.G.; High, J.W.; Fox, R.L.; Hellbaum, R.F.; Jalink, A.; Little, B.D.; Mirick, P.H. Low-cost piezocomposite actuator for structural control applications. Proc. SPIE 2000, 3991, 323–334. [Google Scholar] [CrossRef]
- Wilkie, W.K.; Bryant, R.G.; Fox, R.L.; Hellbaum, R.F.; High, J.W.; Jalink, A., Jr.; Little, B.D.; Mirick, P.H. Method of fabricating a piezoelectric composite apparatus. U.S. Patent 6,629,341 B2, 7 October 2003. [Google Scholar]
- Browning, J.; Cobb, R.; Canfield, R.; Miller, S. F-16 Ventral Fin Buffet Alleviation Using Piezoelectric Actuators. In 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar] [CrossRef]
- Bilgen, O.; Kochersberger, K.B.; Inman, D.J.; Ohanian, O.J. Novel, Bidirectional, Variable-Camber Airfoil via Macro-Fiber Composite Actuators. J. Aircr. 2010, 47, 303–314. [Google Scholar] [CrossRef]
- Pankonien, A.; Faria, C.T.; Inman, D. Synergistic Smart Morphing Aileron. In 54th AIAA/ASME/ ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Molinari, G.; Quack, M.; Arrieta, A.F.; Morari, M.; Ermanni, P. Design, realization and structural testing of a compliant adaptable wing. Smart Mater. Struct. 2015, 24, 105027. [Google Scholar] [CrossRef]
- Debiasi, M.T.; Chan, W.L.; Jadhav, S. Measurements of a Symmetric Wing Morphed by Macro Fiber Composite Actuators. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1565. [Google Scholar]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Experimental and Theoretical Study on Aeroelastic Response of High-Aspect-Ratio Wings. AIAA J. 2001, 39, 1430–1441. [Google Scholar] [CrossRef]
- Fichera, S.; Jiffri, S.; Mottershead, J.E. Design and wind tunnel test of a MODular aeroelastic FLEXible wing (MODFLEX). In Proceedings of the International Conference on Noise and Vibration Engineering ISMA 2016, Leuven, Belgium, 19–21 September 2016. [Google Scholar]
- Latalski, J. Modelling of macro fiber composite piezoelectric active elements in ABAQUS system. Eksploat. Niezawodn. Maint. Reliab. 2011, 1, 72–78. [Google Scholar]
- Debiasi, M.T.; Bouremel, Y.; Lu, Z.; Ravichandran, V.; Khoo, H.H.; Luo, S. Deformation of the Upper and Lower Surfaces of an Airfoil by Macro Fiber Composite Actuators. In 31st AIAA Applied Aerodynamics Conference; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Peeters, B.; Auweraer, H.V.D.; Guillaume, P.; Leuridan, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Aström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]


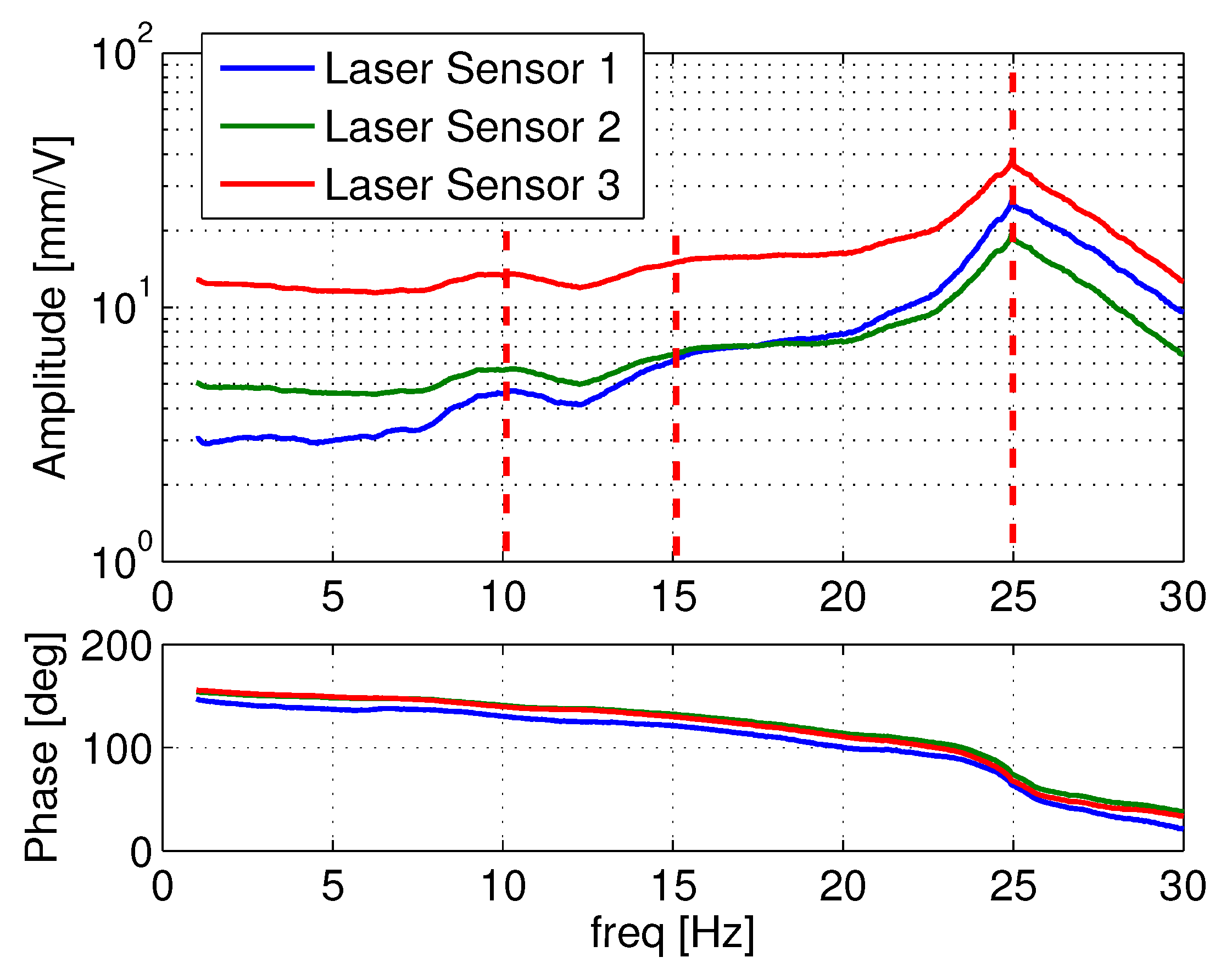

| Mode Shape | Freq (Hz) | (%) |
|---|---|---|
| Actuator support mode | 10.97 | 18.9 |
| Actuator support mode | 15.3 | 8.8 |
| HBMA first bending mode | 24.95 | 4.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fichera, S.; Isnardi, I.; Mottershead, J.E. High-Bandwidth Morphing Actuator for Aeroelastic Model Control. Aerospace 2019, 6, 13. https://doi.org/10.3390/aerospace6020013
Fichera S, Isnardi I, Mottershead JE. High-Bandwidth Morphing Actuator for Aeroelastic Model Control. Aerospace. 2019; 6(2):13. https://doi.org/10.3390/aerospace6020013
Chicago/Turabian StyleFichera, Sebastiano, Irma Isnardi, and John E. Mottershead. 2019. "High-Bandwidth Morphing Actuator for Aeroelastic Model Control" Aerospace 6, no. 2: 13. https://doi.org/10.3390/aerospace6020013
APA StyleFichera, S., Isnardi, I., & Mottershead, J. E. (2019). High-Bandwidth Morphing Actuator for Aeroelastic Model Control. Aerospace, 6(2), 13. https://doi.org/10.3390/aerospace6020013





