Abstract
The turbine tip geometry can significantly alter the performance of the turbine stage; its design represents a challenge for a variety of reasons. Multiple disciplines are involved in its design and their requirements limit the creativity of the designer. Multi-Disciplinary Design Optimisation (MDO) offers the capability to improve the performance whilst satisfying all the design constraints. This paper presents a novel design of a turbine tip achieved via MDO techniques. A fully parametrised Computer-Aided Design (CAD) model of the turbine rotor is used to create the squealer geometry and to control the location of the cooling and dust holes. A Conjugate Heat Transfer Computational Fluid Dynamics (CFD) analysis is performed for evaluating the aerothermal performance of the component and the temperature the turbine operates at. A Finite Element (FE) analysis is then performed to find the stress level that the turbine has to withstand. A bi-objective optimisation reduces simultaneously the aerodynamic loss and the stress level. The Multipoint Approximation Method (MAM) recently enhanced for multi-objective problems is chosen to solve this optimisation problem. The paper presents its logic in detail. The novel geometry offers a significant improvement in the aerodynamic performance whilst reducing the maximum stress. The flow associated with the new geometry is analysed in detail to understand the source of the improvement.
1. Introduction
In a high pressure turbine, a third of the loss can be associated with the leakage flow at the tip. A classic design with a shroud above the tip can help in reducing this loss acting effectively as a seal [1,2]; however, this configuration has become less feasible in recent large civil aircraft engines. In fact, the common trend in more efficient engines is to increase the total temperature at the inlet of the turbine. This implies that more coolant is required for protecting the shroud and, as the rotor speed increases, it becomes harder to withstand the centrifugal forces. Therefore, all major gas turbine engine producers are moving towards a shroudless configuration. Provided that a small clearance is achieved, the shroudless configuration can match or even outperform a shrouded rotor [3]. It remains equally important to control the temperature of the tip also for the shroudless configuration [4].
Different Computational Fluid Dynamics (CFD) studies and experiments on tip configurations have shown that the geometry of the rotor close to the endwalls may have a positive effect on the performance of the turbine. Some researchers suggest using a recessed cavity within the tip (also referred to as squealer) [5], others prefer an enlarged tip section (also referred to as winglet) [6]. The first configuration acts as a seal forcing the flow to get contracted twice over the Pressure Side (PS) and Suction Side (SS) rim. The second one reduces the pressure difference between PS and SS (the driving force of the leak) and, due to a longer flow path, the leakage gets more aligned to the main flow. Studies also show that a combination of the two designs is possible and the positive effects of both are preserved [7,8]. Moreover, opening the squealer may alter the performance as suggested by CFD in [9] where a Heavy Duty turbine benefits from an opening at the Trailing Edge (TE) of the rotor. Previous works [10,11] showed that the temperature performance is also affected by the opening. In particular, the opening on the SS side of the aerofoil was providing the highest benefit.
As stated above, a wide range of choices are available to the designer; therefore, a formal procedure to choose the design with the highest performance is fundamental. Multi-Disciplinary Design Optimisation (MDO) is such a procedure [12]; it formally compares different designs and improves the performance accordingly taking into account, simultaneously, multiple disciplines as it is required by the tip design. Previous studies [8,11] have shown the potential of optimisation applied to the tip design. In [8], the turbine blade was studied from an aerodynamic point of view through CFD simulations and the mechanical point of view through Finite Element Method (FEM) analysis; a reduction of of the leakage (satisfying the stress constrains) was achieved by a large winglet tip. In [11], the trade-off between the efficiency and cooling requirements was studied; an opened squealer configuration was found to be the best for cooling and higher efficiency was achievable by varying the width of the winglet.
This work starts from the results of [10], but here the fidelity of the CFD modelling is significantly improved. Conjugate Heat Transfer(CHT) analysis is key to capturing both the thermal and aerodynamic performance of the tip design. The optimisation problem and an effective and efficient way to solve it are presented. A multi-objective optimisation problem and the suggested way to solve it will be presented and the method will be applied to the design of the tip, concluding with the analysis of the optimum.
2. Optimisation Strategy
The optimisation relies on the Multipoint Approximation Method (MAM) [13,14], also referred to as the Mid-range Approximation Method. The method has been expanded and generalised to accommodate multi-objective optimisation problems.
2.1. Multipoint Approximation Method
The framework of the MAM can be described as follows. It is an iterative process that attempts to solve a sequence of constrained optimization sub-problems by using approximations of the objective function and constraints in a series of trust regions. The trust region strategy depends on the quality of approximations in each trust region and seeks to zoom onto the region where the constrained minimum is achieved. It aims at finding a trust region that is sufficiently small for the approximations to be reasonably good and that contains the point of the constrained minimum as its interior point.
The problem of a constrained optimization is formulated as follows:
where is the vector of design variables, Q is the box , and are the lower and upper bounds for the design parameters, respectively, is the objective function, is the j-th constraint and is the upper bound for the j-th constraint. The numbers of design variables and constraints are N and m, respectively.
The MAM algorithm is organized as follows:
- Initialization: choose a starting point and initial trust region such that .In practice, the initial subregion is a box centred at .
- At the k-th iteration, the current approximation to the constrained minimum is , and the current trust region is .
- (a)
- Choose a set of points that will be used to build approximations. This procedure is often referred to as the Design of Experiments (DoE).
- (b)
- Build approximations using any suitable method. Two approximation techniques are currently implemented in the MAM: the Metamodel Assembly [15] and the Moving Least Squares Method [16].Denote the approximate objective function and constraints by and , , respectively.
- (c)
- Replace the original optimization problem (Equation (1) by the following one:Find the next approximation to the optimal point, solving the approximate problem (Equation (2)).
- (d)
- Define the next trust region using the trust region strategy (for details, the reader is referred, for example, to [15,17]), set , and go either to 2 or to 3 depending on the fulfillment of the termination condition (which is a part of the trust region strategy).
- Terminate optimization. The obtained approximation to the solution of problem (Equation (1)) is .
Figure 1 shows graphically how the trust regions are progressively shrunk and moved towards the optimum in a 2D optimisation problem.
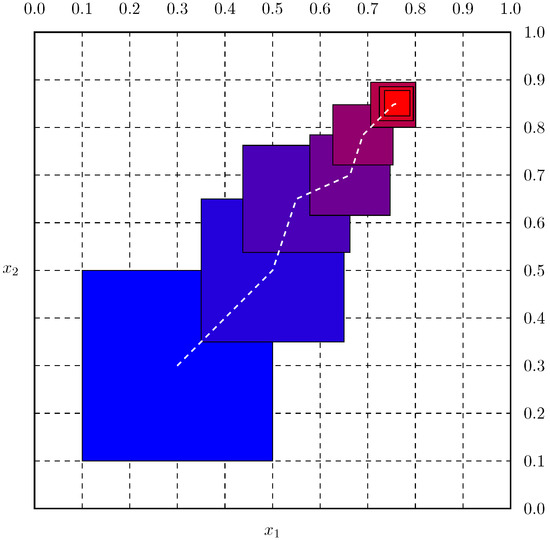
Figure 1.
The Multipoint Approximation Method (MAM) sequences of trust regions.
2.2. Multi-Objective Problem Formulation
Multi-objective optimisation problems arise in cases when the designer has several criteria that describe the quality of a design. Formally, a constrained multi-objective optimisation problems can be written as:
where n is the number of objectives, m is the number of constrains, Q is the design space, is the i-th objective function, is the j-th constraint, and is the upper bounds on the j-th constraint. Let the number of design variables be N.
Mathematically, multi-objective optimisation problems are quite different from single-objective ones. Unlike single-objective problems, there is no unique solution to a multi-objective problem (except for some very special cases); instead, the so-called Pareto fronts are obtained, which consist of all non-dominated designs. A design is called non-dominated if there is no other feasible design that is not worse in any objective and better in at least one. Pareto fronts can be approximated by solving a number of single-objective problems derived from the original multi-objective one.
2.3. Bound Formulation of Minmax Problems
One possible approach to the solution of multi-objective problems is a sequence of minmax problems. As the name suggests, in a minmax problem, one looks for a solution that minimises the maximum of all the objectives . The different objectives may have a different order of magnitude. It is therefore necessary to normalise them through the used of a scaling factor (also called target). These targets usually have a clear engineering meaning and allow the designer to define desired trade-offs in application-related terms and derive an aggregate objective function. Assuming all objectives in Equation (3) to be strictly positive and choosing targets , we derive the formulation of the minmax problem as follows:
The problem becomes a single-objective problem and one can attempt to solve it by an appropriate single-objective optimisation method. However, this formulation has an important drawback: the objective function in Equation (4) is non-smooth even if all original objectives are. This creates problems for all gradient-based methods as the function is non-differentiable where the limiting objective changes. In addition, metamodelling-based techniques are posed a challenge due to the increased complexity of the functions to be approximated and the areas where it is non-differentiable. However, the bound formulation [18] offers an efficient way of solving the problem. Let us introduce an artificial variable and rewrite Equation (4) as a problem with variables and constraints:
One can easily verify the equivalence of problems described by Equations (4) and (5). Even thou the optimiser has to handle an increased number of constraints, the optimisation is well posed. In fact, if all original objectives are smooth, the additional constraints also are. This formulation can also be used in single-objective problems (i.e., ). In this case, the scaling factor does not play any role other then helping to ensure numerical stability. One can also see that the bound formulation preserves convexity (problem in Equation (5) is a convex optimisation problem in the new variable if all functions involved are convex functions of ).
The bound formulation of the minmax problem has been integrated into the MAM. The positiveness requirement for the objectives and the targets are always satisfied, since all responses (objectives and constraints) as well as targets are internally scaled using the user-supplied a priori lower bounds and . The resulting problem actually solved by the MAM optimiser is as follows:
2.4. Analitycal Verification
The capability of the MAM optimiser in handling optimisation problems with multiple objectives was evaluated. A comparison with the ARMOGA (Adaptive Range Optimiser Genetic Algorithm) was used to benchmark the performance of the new optimiser. The optimisation problem involves the minimisation of two objectives and whilst satisfying one single constraint (). There are 12 design variables, or rather 6 couples of parameters. Each design parameter is within the range. Equations (7) is the mathematical formulation of the objectives and the constraint of the problem. In the MAM optimisation, the targets are progressively varied to establish the approximation of the whole Pareto front:
Analytically, the solution of the problem can be achieved by studying a single couple at the time. In fact, the problem could be solved looking at all the six identical 2D sub-problems. Figure 2 shows the values of the objectives for a given couple . In this case, can be seen as the squared distance from the point , whilst represents the squared distance from the point . The unconstrained solution is the straight segment connecting the two points. However, the constraint () limits the feasible design space. Only a smaller segment can be taken as the solution; this is represented by a segmented line in the figure.
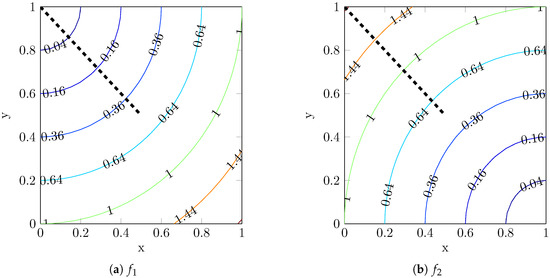
Figure 2.
Contours of the objectives ( and ) and analytical solution of the problem (segmented line).
Figure 3 shows the results achieved by both ARMOGA and MAM. For each evaluated design, the objectives are shown with a dot. If the design is feasible, the dot is green; on the contrary, if the design is unfeasible, a red dot is used. The analytical Pareto front is represented by a segmented line. It can be clearly seen that the number of analyses performed by the MAM and the ARMOGA have a different magnitude. Whilst the MAM focuses the majority of the points close to the Pareto front, the ARMOGA evaluates a significant number of designs far from it. Moreover, the MAM does not waste a significant number of simulations in the unfeasible design space a part from solving the right leg of the Pareto front. The Pareto front at the far left extreme is properly captured only by the MAM. In MAM, the Pareto front is resolved through a series of optimisations where the targets are progressively moved. If necessary, it is possible to vary by a smaller amount these targets and have a finer resolution of the Pareto front.
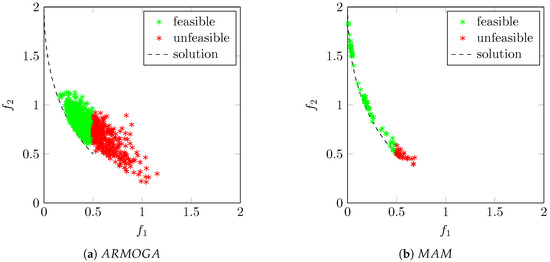
Figure 3.
Optimisation history and analytical Pareto front.
Figure 4 shows the history of all the candidates considered by both optimisers (ARMOGA and MAM). A red dashed line shows the analytical solution; however, bear in mind that a non-dominated solution is achieved only when all 6 couples of parameters are exactly on the same point. The values for the genetic algorithm are more scattered and cover almost all the design space. In the MAM, the sequence of trust regions can be seen. It starts with a wide area located at the centre of the design space ( for ). It zooms towards one corner of the Pareto front (where the constraint is activated). Then, the MAM walks along the Pareto front to capture all the other not-dominated solutions.
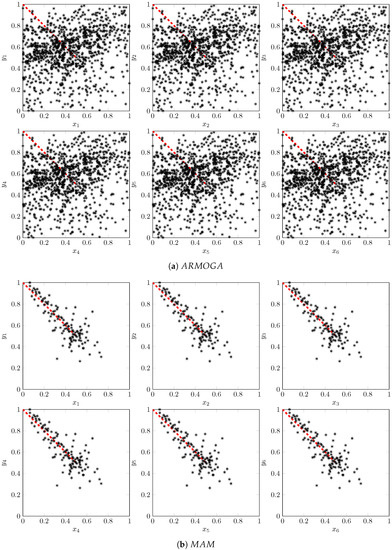
Figure 4.
Scatterplot of candidates in the design space. The analytical solution is in red.
The comparison between the optimisers shows that not only the number of simulations required by the MAM is significantly smaller, but also that it is possible to solve correctly both legs of the Pareto front by an appropriate strategy for varying the targets.
3. Application
Having been satisfied by the analytical evaluation of the MAM optimiser, it was possible to apply with confidence the approach to the design of a high pressure turbine. The target is to improve the aerodynamic performance and simultaneously reduce the stress experienced by the tip. The simulation workflow and the objectives are now explained in the following section.
3.1. Simulation Workflow and Objectives
Figure 5 shows the flowchart of all the steps involved to analyse a given design of the rotor tip. In the figure, it can be also seen how the information is passed between the used models. All of the steps are fully scripted, which is a requirement for an automatic optimisation.
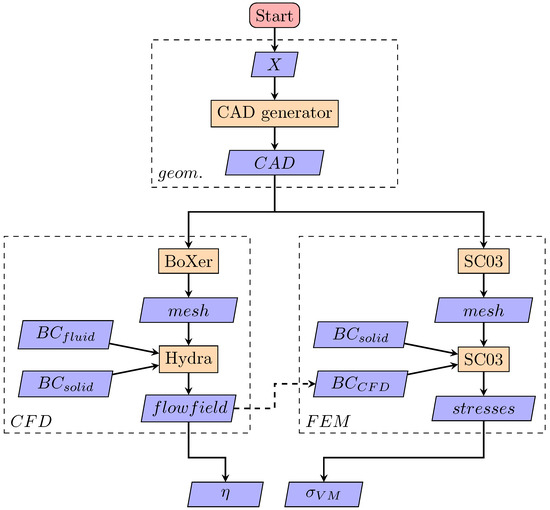
Figure 5.
Flowchart of each simulation for the Multi-Disciplinary Design Optimisation (MDO).
The simulation consists of three main steps:
- The Geometry Creation (),
- The Thermal-fluid analysis (),
- The Structural analysis ().
A brief description of each step below.
3.1.1. Geometry
The geometry of the rotor of the Low Emissions Core-Engine Technologies (LEMCOTEC) research turbine is optimised. The starting point of the optimisation is the result of the previous studies [10,11,19] and offers already a high performance (both aerodynamicly an thermally). This design will be referred to as a reference design and used for comparison with the optimum found by the MDO. It features a small winglet on the SS, the squealer is opened close to the TE with the opening facing the SS of the aerofoil. The thickness of the squealer rim is constant and corresponds to of the radial span. The depth of the gutter corresponds to of the radial span. Cooling holes are present on the PS of the blade close to the tip. In addition, three dust holes are positioned on the camber line. Each of these is located above one passage of the internal cooling serpentine.
A parametrised CAD model is used to generate and alter the geometry. Each surface of the CAD model is tagged to ease the steps of meshing and simulation setup. In the optimisation, twelve parameters are used to modify the shape of the rotor tip. The first eight are used for the tip external geometry whilst the rest are for the cooling.
Tip Design
Figure 6 shows the tip of the LEMCOTEC turbine as parametrised in the CAD.The winglet shape is perturbed by modifying the location of two control points A and B. The thickness of the PS and SS rim can be altered independently ( and ). Moreover, the thickness at the Leading Edge (LE) can be increased or decreased by varying the radius of the fillet between PS and SS rim. The opening is positioned on the SS of the aerofoil and its width is controlled by a parameter (). Finally, the gutter depth can be modified. Two parameters control the depth at the LE and at the TE ( and ); this allows the creation of a slope inside the gutter.
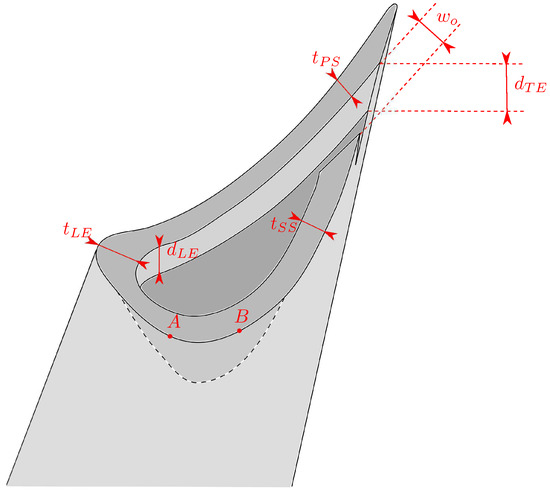
Figure 6.
Parametrisation of the tip geometry.
Internal Cooling System
For the cooling system, the generation of the internal passages is fully automated. In fact, the U-bends are recomputed taking into account the variable depth of the gutter. The optimiser is allowed to vary the location of the dust holes and the film cooling holes on the pressure side. Figure 7 shows the design space for the cooling system. The location of the dust holes is referred to the camber line. The location of the first and the second dust hole ( and ) can be altered by moving along or normal to the camber line. The location of the third dust hole is fixed; this is because the gutter is narrow in this area and also because the third internal cooling passage (underneath the dust hole) does not offer enough room for movement. Moreover, the angles and defining the two rows of film cooling holes on the PS can be modified (Figure 7); is the angle in a Blade-to-Blade section whilst in a meridional section. The cooling holes are parametrised in such a way that the first seven cooling holes belong to the first U-bend whilst the last three holes are connected to the last passage. The actual height of the row depends on the gutter depth.
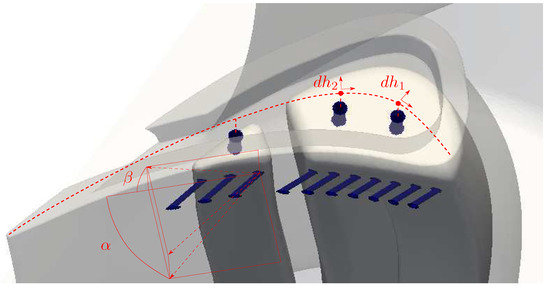
Figure 7.
Parametrisation of the cooling system at the tip of the blade.
3.1.2. Thermal-Fluid Analysis (CFD)
In the CFD simulation, the domain studied consists of the turbine rotor. Boundary conditions at the inlet and exit are computed from a full stage analysis; this is necessary to properly capture the state of the boundary layer at the inlet of the rotor [20]. A lean burn was simulated in the full stage analysis; therefore, a significant variation in the radial distribution of temperature persists at the inlet of the rotor (for more details, refer to [21]). Figure 8 shows the boundary conditions that represent the lean burn used for the full stage analysis (before the optimisation). For properly capturing the swirl, it is necessary to impose a 2D-field at the inlet of the stage for the inlet total pressure, the total temperature as well as whirl and pitch angle.
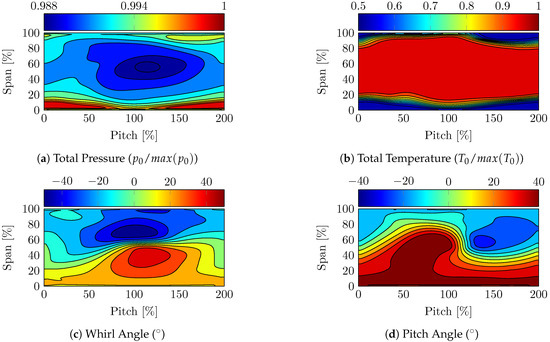
Figure 8.
Boundary condition representing the lean-burn.
From the full stage simulation, the boundary conditions at the inlet of the rotor are extracted. Figure 9 shows the extracted values; these are used for the optimisation. At the inlet, total values for pressure and temperature are imposed and the whirl and pitch angles are constrained. For the exit of the rotor, a radial distribution of static pressure is applied.
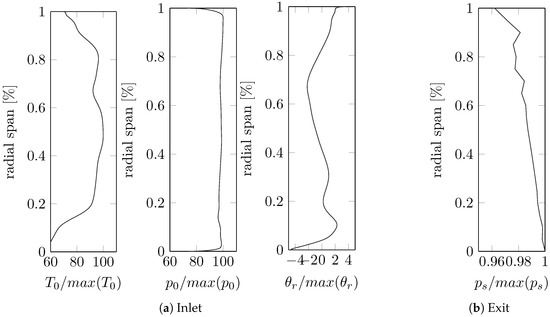
Figure 9.
Rotor boundary conditions.
The simulation requires the generation of the mesh for both the solid and the fluid domains. This is achieved by the meshing software BoXeR (by Cambridge Flow Solutions ltd, Cambridge, UK) [22], which is an octree mesher based on a implicit level-set approach to define the geometry (further details provided in [23]). An unstructured hexa-dominant mesh is created and it is fully conformal at the interface between solid and fluid that eliminates any numerical error due to interpolation when exchanging fluxes at the domain interfaces. Figure 10 shows a typical mesh in the proximity of a dust hole with both solid and fluid domain shown. Local refinements are applied in the BoXer mesh to capture the steepest change in the flow. In particular, the refinements cover the wake, the vortices in the tip area and the cooling holes. Prismatic layers are grown in the fluid domain over the wall surfaces to resolve the development of the boundary layer. A around 1 is obtained by 15 layers. A good mesh near the surface is important to capture the heat flux. A mesh independent solution was obtained with mesh point in the rotor (solid plus fluid) with a small variation in the actual size depending on the tip geometry (that keeps changing during the optimisation).
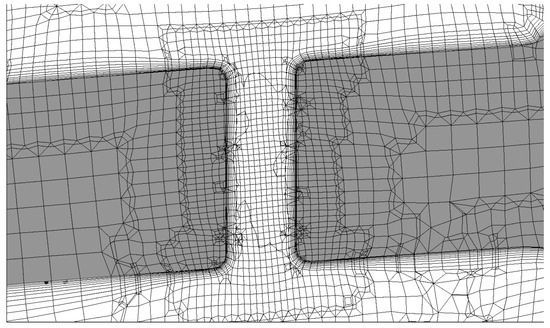
Figure 10.
Conformal mesh of a dust hole created by BoXer.
The in-house developed CFD solver HYDRA (by Rolls-Royce plc, Derby, UK) [24] has been tailored and tuned for turbomachinery applications. It is an edge-based unstructured solver for the RANS equations with second-order accuracy. Turbulent effects are approximated by the two equations turbulence model SST. Before the optimisation, the solver was validated for turbine tip analyses and CHT computation (for more details, refer to [10]). The flow field in the fluid domain is initialised by iterating for 100 iterations with a fixed temperature in the solid domain. After the initialisation, the coupling starts and iterates, updating the temperature at the interface between solid and fluid domain until the convergence is achieved. From this simulation, both the flow field in the fluid and the temperature field in the solid are obtained. By post-processing the flow field, it is possible to gain the aerodynamic efficiency of this given design (). As the analysis is all but adiabatic, the efficiency is corrected as suggested by [25] to consider the effect of heat fluxes in the rotor; an equivalent adiabatic efficiency is computed in this way. This is the first of the two objectives considered.
3.1.3. Structural Analysis (FEA)
The CAD is re-used in an in-house FE software SC03 (by Rolls-Royce plc, Derby, UK) to generate the mesh and setup the simulation. Second-order tetrahedral elements are used for representing the geometry. Only a structural analysis is necessary, the thermal analysis has been accomplished already by the CHT simulation. Most of the boundary conditions need to be extracted from the CHT simulation and interpolated to the mesh for the structural analysis. In particular, this operation is required for the pressure field on all wet surfaces as well as the temperature distribution in the solid domain. The chosen interpolation method is the weighted sum average [26]. In this method, the value used for the FE () is an average based on the values obtained by the CFD simulation () considering only the nodes within a given radius of threshold ().
The inverse of distance of each node is used as the weight:
This way, a close point has more importance than a point that is far. For stability reasons, another threshold is used. In fact, the weight tends to infinity for a point very close or that is coincident. If a point is closer than , that value is automatically assigned. The choice of the thresholds is important, and big values of tends to an inaccurate approximation. On the other hand, big values of tend to a smoothing of the field of the temperature/heat flux.
Figure 11 shows two meshes and the concept of interpolation just described. The CFD mesh is structured and is shown in blue. The FE mesh is unstructured and is shown in red. The threshold circle is shown in green.
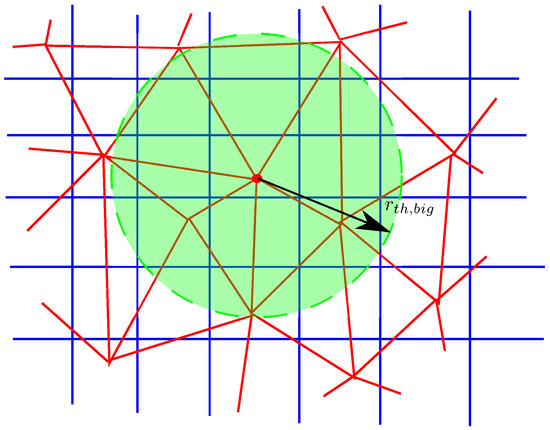
Figure 11.
Interpolation between meshes: CFD in blue and FE in red.
The additional boundary condition is to fix the root of the turbine blade to the disk. The final condition is to specify that the frame is rotating on the main axis; this is to consider the centrifugal load experienced by the rotor. From this analysis, the stress experienced by the blade can be computed. This is the second objective of the optimisation. In this case, the maximum value of the von Mises stress in the tip area is taken [27].
3.2. Objectives
In this particular optimisation case, both the objectives have been normalised based on the value achieved in the reference design (). The minmax formulation relies on a minimisation of positive objectives. Therefore, the efficiency objective has been slightly modified, i.e., the optimiser is trying to reduce the deficit towards a value of efficiency:
In Equation (9), both objectives are already scaled to the same order of magnitude—exactly 1 for the reference design. In this case, the target values of the minmax formulation are used only to guide the optimiser towards one or the other objective. In this optimisation, a target value of 0.75 for both objectives have been chosen. It is quite optimistic to achieve this improvement; however, with these values, the optimiser gives the same importance to efficiency and stress.
3.3. Optimisation History
Figure 12 shows the optimisation history. The x-axis corresponds to the aerodynamic efficiency whilst the y-axis shows the maximum stress experienced at the tip. The optimiser tries to increase the former whilst reducing the latter; hence, the optimum resides in the fourth quadrant (bottom right). The initial DoE is shown in green whilst the following simulations in blue. The optimum configuration is represented by a red circle. After the initial DoE, MAM moved the trust region seven times before terminating the optimisation. The optimiser managed to improve the efficiency by and obtained a reduction of stress by . The improvement in the aerodynamic efficiency is significant considering the fact that the starting point already features a small winglet on the SS and an opening on the TE. We demonstrated in previous studies [10,11] their importance and both of them have been optimised to achieve an even higher performance.
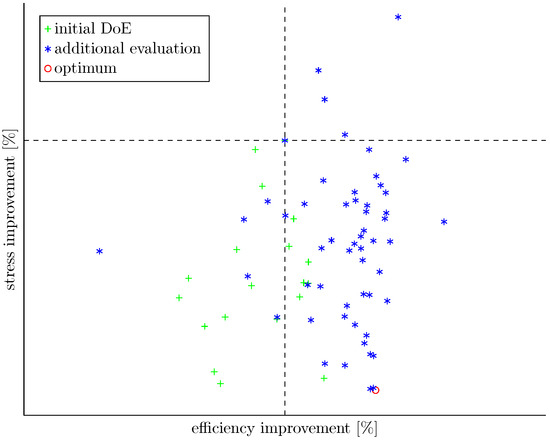
Figure 12.
Optimisation history.
4. Study of the Optimum
Once the optimisation is accomplished, the most important step is to understand the origin of the improvement. This guarantees that, in a following optimisation or design study, the designer can focus on the most relevant features of the geometry. Moreover, it allows the designer to understand the limit of the current design space and enlarge it if necessary.
4.1. Geometry
Figure 13 shows the geometry of the optimum in comparison with the reference design. The winglet is slightly more pronounced in the optimum configuration. The rim is thicker in both the LE and the SS rim. The optimiser has found beneficial to create a slope inside the gutter. Whilst the depth close to the LE has remained similar to the original (98% of the original), towards the TE, it has been increased significantly (150% of the original). This is a novel feature that has not been found in other studies available in the literature.

Figure 13.
Geometry comparison between reference and optimum design.
The opening at the TE is increased in width (140% of the original) that, if combined with the increase in height (the depth of the gutter at the TE), guarantees an even larger area of the gutter connected with the main passage (186% of original value).
For the cooling, the dust holes have migrated towards the PS rim. This resembles the study [28] where an improvement in the thermal performance was achieved by moving the dust holes closer to the PS than the camber line. Interestingly, in this optimisation, the thermal distribution is not directly optimised by the MAM but indirectly through the stress-related objective. The first two dust holes are also farther apart; as it will be shown, this helps to achieve an even more uniform temperature distribution in the gutter.
4.2. Aerodynamic Consideration
Regarding the aerodynamic efficiency, the evolution of the overtip leakage vortex helps in understanding the optimum design. Figure 14 shows how the optimum design compares to the reference design. The relative total pressure identifies the areas of high loss and mixing. A low level of pressure (shown in blue) corresponds to a region with high loss (and correlates with the location of vortices).
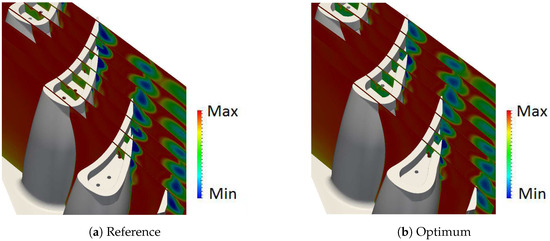
Figure 14.
Relative total pressure contour at seven axial sections.
The evolution of the OTL and passage vortex remains separated for the front part of the blade thanks to the presence of the winglet in both designs. The growth of the OTL is reduced at the optimum. In fact, the area affected by the OTL just before mixing with the flow exiting the gutter is significantly smaller. This is also seen in the mixing downstream of the opening.
Figure 15 shows the pressure loading experienced by the aerofoil close to the tip area, in particular at and of the radial span. Between and of the axial chord, the data is missing as it is where the rim is opened. In the reference design, at around of the axial chord there is an increment of pressure followed by a rapid decrement, this can be seen at both heights and corresponds to the presence of the leakage over the tip. In the optimum design, this is further delayed (around ), and very close to the tip the effect is significantly reduced.
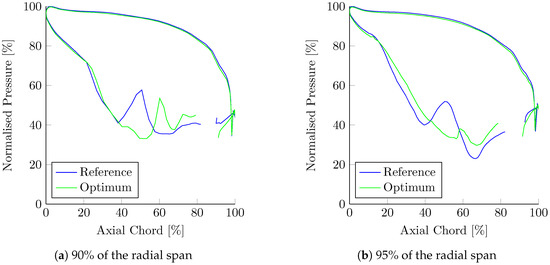
Figure 15.
Pressure distribution close to the tip.
Figure 16 shows the development of the gutter vortex. In particular, the streamlines originate from the PS rim. The optimum design has proven to have a higher sealing factor in the first part of the SS. In fact, the vast majority of the flow leaking over the PS rim remains trapped within the gutter until the opening at the TE.

Figure 16.
Streamlines over the PS rim and massflow leakage.
A more quantitative analysis was performed by studying the massflow leaking over the tip.
Table 1 shows the amount of the leakage and the repartition between SS rim and TE opening. All of the values have been rescaled by the total leakage experienced in the reference design. The optimum design shows a small increment in the whole integral value of the leakage. A significant reduction of the leakage flow over the SS rim has been obtained. On the contrary, the leakage through the opening has increased. Therefore, the optimum design has been able to redistribute the leak towards the TE delaying the creation and growth of the OTL vortex.

Table 1.
Leakage in the tip.
This is also confirmed by looking at the leakage distribution along the SS. Figure 17 shows both the massflow and the mismatch angle of the leakage with the main flow. Referring to Denton’s loss model [29] associated with the overtip leakage, the loss is proportional to both the massflow and the mismatch angle. Looking only at the integral values can be misleading (i.e., the massflow is increased by ; however, the efficiency is increased). In Figure 17, a positive value for the massflow corresponds to a leak over the SS rim towards the main passage. On the other hand, a negative value corresponds to a flow of air entering the gutter of the squealer. At the optimum, a reduction of the leak from to of the axial chord is clearly visible. In the optimum configuration, the gutter spans between to of the axial chord. In this range, the leakage flow has a higher mass compared to the reference (the opening in the reference is between to ). Towards the TE, the two designs behave in a similar manner. Similarly, the benefits of the optimum are confirmed by considering the distribution of the mismatch angle. The optimum offers a better alignment between the leakage and the main flow in the whole area before the opening ( to ). In the opening and at the TE, both designs show a similar behaviour. It is important to note that the flow exiting through the opening is more aligned with the main flow compared to the leakage over the rim (50 degrees against 80 degrees).
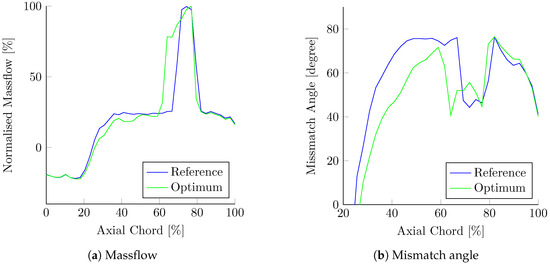
Figure 17.
Distribution of leakage flow over the SS rim.
Therefore, even though the amount of the total leak is increased by around , the aerodynamic performance has improved. This is because the optimum design favours the leak in the area where it is less detrimental. Exiting at the TE, the interaction with the passage vortex is reduced; moreover, the flow has more permanence time in the gutter to get aligned with the main flow.
4.3. Thermal and Stress Consideration
Figure 18 shows the temperature distribution at the tip of the blade. Areas of low temperature are denoted by a blue colour whilst areas with high temperature are marked in red.
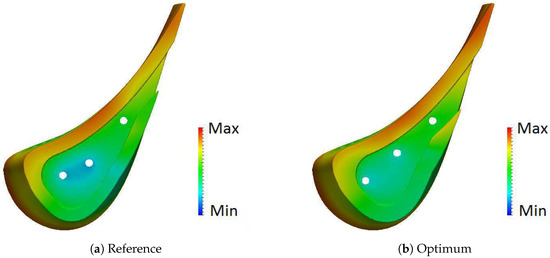
Figure 18.
Temperature distribution top view.
In the optimum configuration, the first and the second dust holes have been pushed closer to the rim of the squealer. The first dust hole is moved forward towards the LE whilst the second dust hole has moved backwards. This guarantees that all the dust holes are spread more evenly in the gutter hub. A more uniform temperature distribution is therefore obtained. In the reference design, the first and the second dust hole are quite close to each other and between them a very low temperature is experienced. In the optimum design, this is no longer the case. Moving the dust holes closer to the rim also reduces the temperature of the rim at the LE and at mid-chord. On the contrary, the squealer rim remains at a warmer temperature towards the TE. This is due to the deeper gutter, hence an increased height of the rim at the TE.
The location of the maximum stress of the tip is in the U-bend underneath the squealer rim. The location is the same for both the reference and the optimum. Figure 19 shows the stress distribution in an axial cut in correspondence to the maximum stress location. The new distribution of the dust holes offers a more uniform temperature in this area reducing the temperature gradient. The reduction of the stress is around in the maximum value. The FE simulation was rerun with and without the temperature gradient. If the thermal stress is not considered, only half of the performance benefit is obtained.
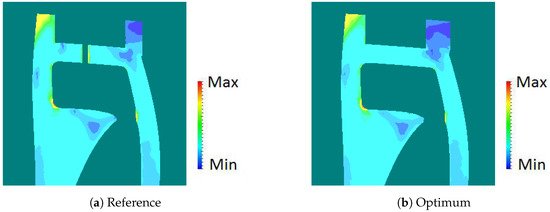
Figure 19.
Distribution of von Mises stress (axial cut).
5. Conclusions
This work shows the benefit of using automatic optimisation for a practical design of a high pressure turbine rotor tip that is driven by multiple disciplines. The logic of the MAM optimiser is described in detail both for single-objective optimisation problems as well as multi-objective problems. The capability of the optimiser has been evaluated on an analytical problem and is compared to a genetic algorithm-based optimiser. The newly developed MAM is able to more accurately and efficiently find the optimal designs compared to the more expensive genetic algorithm. The optimiser has been applied for improving the rotor tip of the high pressure turbine. The optimisation relies on a high fidelity model of the turbine making use of conjugate heat transfer analyses of the tip as well as thermal-stress investigations. The models were previously validated. The resultant optimum outperforms the reference both aerodynamically ( efficiency improvement) and mechanically ( reduction in maximum stress). The main contribution for the aerodynamic improvement is related to an enlarged opening at the TE of the squealer and a more pronounced winglet. These modifications favour the leakage to exit towards the rear of the rotor instead at mid-chord, hence reducing the associated mixing loss. Regarding the thermal performance, the dust holes are migrated towards the PS rim and spread more uniformly. This ensures a better coverage of the coolant in the tip area resulting in a more uniform temperature distribution that reduces the stress experienced at the tip.
Author Contributions
Conceptualization and Methodology, S.C., S.S. and V.V.T., Validation and Formal Analysis, S.C.; Writing—Original Draft Preparation, S.C.; Writing—Review and Editing, S.C., S.S. and V.V.T.; Supervision, S.S. and V.V.T.
Funding
The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Program FP7 2012 under REA Grant No. 316394.
Acknowledgments
The authors would like to thank Rolls-Royce (Derby, UK) for giving permission to publish this work. The authors would also like to thank Yury Korolev (Queen Mary University of London, London, UK) for the implementation of multi-objective techniques in the MAM that were fundamental for this research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Cooling hole horizontal angle | |
| Cooling hole vertical angle | |
| Equivalent adiabatic efficiency | |
| Stress component | |
| Bound value | |
| Whirl angle | |
| c | Constraint value |
| d | Depth |
| Dust dole | |
| Objective function | |
| Constraint function | |
| Design vector | |
| n | Number of objectives |
| N | Number of design variables |
| m | Number of constraints |
| p | Pressure |
| t | Thickness |
| T | Temperature |
| Q | Design space |
| w | Width |
| ARMOGA | Adaptive Range Multi-Objective Genetic Algorithm |
| CAD | Computer aided design |
| CFD | Computational fluid dynamic |
| CHT | Conjugate heat transfer |
| DoE | Design of experiment |
| FE | Finite element |
| HD | Heavy duty |
| LE | Leading edge |
| MAM | Multipoint approximation method |
| MDO | Multi-disciplinary design optimisation |
| OTL | Over tip leakage |
| PS | Pressure side |
| RANS | Reynolds-averaged Navier-Stokes equations |
| SS | Suction side |
| SST | Shear stress transport |
| TE | Trailing edge |
References
- Harvey, N.W. Aerothermal Implications of Shroudless and Shrouded Blades; VKI Lecture Series 2004; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2004. [Google Scholar]
- Harvey, N.W.; Ramsden, K. A computational study of a novel turbine rotor partial shroud. J. Turbomach. 2001, 123, 534–543. [Google Scholar] [CrossRef]
- Yoon, S.; Curtis, E.; Denton, J.D.; Longley, J.P. The effect of clearance on shrouded and unshrouded turbines at two levels of reaction. J. Turbomach. 2014, 136, 021013. [Google Scholar] [CrossRef]
- Bunker, R.S. Blade Tip Heat Transfer and Cooling Techniques; VKI lecture series 2004; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2004. [Google Scholar]
- Ameri, A.A.; Steinthorsson, E.; Rigby, D.L. Effect of squealer tip on rotor heat transfer and efficiency. J. Turbomach. 1998, 120, 753–759. [Google Scholar] [CrossRef]
- Coull, J.D.; Atkins, N.R.; Hodson, H.P. Winglets for improved aerothermal performance of high pressure turbines. J. Turbomach. 2014, 136, 091007. [Google Scholar] [CrossRef]
- Coull, J.D.; Atkins, N.R.; Hodson, H.P. High efficiency cavity winglets for high pressure turbines. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Schabowski, Z.; Hodson, H.P.; Giacche, D.; Power, B.; Stokes, M.R. Aeromechanical optimisation of a winglet-squealer tip for an axial turbine. J. Turbomach. 2014, 136, 071004. [Google Scholar] [CrossRef]
- Lomakin, N.; Granovskiy, A.; Shchaulov, V.; Szwedowicz, J. Effect of Various Tip Clearance Squealer Design on Turbine Stage Efficiency. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QU, Canada, 15–19 June 2015. [Google Scholar]
- Caloni, S.; Shahpar, S. Multi-Disciplinary Analyses for the Design of a High Pressure Turbine Blade Tip. In Proceedings of the ASME Turbo Expo 2016: Turbine Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Caloni, S.; Shahpar, S.; Coull, J.D. Numerical Investigations of Different Tip Designs for Shroudless Turbine Blades. In Proceedings of the 11th European Turbomachinery Conference, At Madrid, Spain, 23–27 March 2015; pp. 1–13. [Google Scholar]
- Martins, J.R.R.A.; Lambe, A.B. Multidisciplinary design optimization: a survey of architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef]
- Toropov, V.V. Simulation approach to structural optimization. Struct. Optim. 1989, 1, 37–46. [Google Scholar] [CrossRef]
- Toropov, V.V.; Filatov, A.A.; Polynkin, A. Multiparameter structural optimization using FEM and multipoint explicit approximations. Struct. Optim. 1993, 6, 7–14. [Google Scholar] [CrossRef]
- Polynkin, A.; Toropov, V.V. Mid-range metamodel assembly building based on linear regression for large scale optimization problems. Struct. Multidiscip. Optim. 2012, 45, 515–527. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Van Keulen, F.; Toropov, V.V. New developments in structural optimization using adaptive mesh refinement and multipoint approximations. Eng. Optim. 1997, 29, 217–234. [Google Scholar] [CrossRef]
- Olhoff, N. Multicriterion structural optimization via bound formulation and mathematical programming. Struct. Optim. 1989, 1, 11–17. [Google Scholar] [CrossRef]
- Caloni, S.; Shahpar, S. Investigation Into Coupling Techniques for a High Pressure Turbine Blade Tip. In Proceedings of the 11th European Turbomachinery Conference, At Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Coull, J.D.; Atkins, N.R. The influence of boundary conditions on tip leakage flow. J. Turbomach. 2015, 137, 061005. [Google Scholar] [CrossRef]
- Khanal, L.; He, L.; Northall, J.; Adami, P. Analysis of Radial Migration of Hot-Streak in Swirling Flow Through HP Turbine Stage. J. Turbomach. 2013, 135, 041005. [Google Scholar] [CrossRef]
- Demargue, A.A.; Evans, R.O.; Tiller, P.J.; Dawes, W.N. Practical and reliable mesh generations for complex real-world geometries. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Dawes, W.N.; Kellar, W.P.; Harvey, S.A. Using level sets as the basis for a scalable, parallel geometry engine and mesh generation system. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Moinier, P.; Giles, M.B. Preconditioned Euler and Navier-Stokes Calculations on Unstructured Grids. In Proceedings of the 6th ICFD Conference on Numerical Methods for Fluid Dynamics, Oxford, UK, 31 March–3 April 1998. [Google Scholar]
- Atkins, N.R.; Ainsworth, R.W. Turbine aerodynamic performance measurements under nonadiabatic conditions. J. Turbomach. 2012, 134, 061001. [Google Scholar] [CrossRef]
- Verstraete, T. Multidisciplinary Turbomachinery Component Optimisation Considering Performance, Stress and Internal Heat Transfer. Ph.D. Thesis, Universiteit Gent, Gent, Belgium, June 2008. [Google Scholar]
- Kazimi, S.M.A. Solid Mechanics; McGraw-Hill Education: NewYork, NY, USA, 1982. [Google Scholar]
- Dawes, W.N.; Kellar, W.P.; Richardson, G.A. Application of topology-free optimization to manage cooled turbine tip heat load. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009. [Google Scholar]
- Denton, J.D. Loss mechanisms in turbomachines. J. Turbomach. 1993, 115, V002T14A001. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).