On the Wake Properties of Segmented Trailing Edge Extensions
Abstract
1. Introduction
1.1. Vortex Mitigation Techniques
2. Experimental Setup
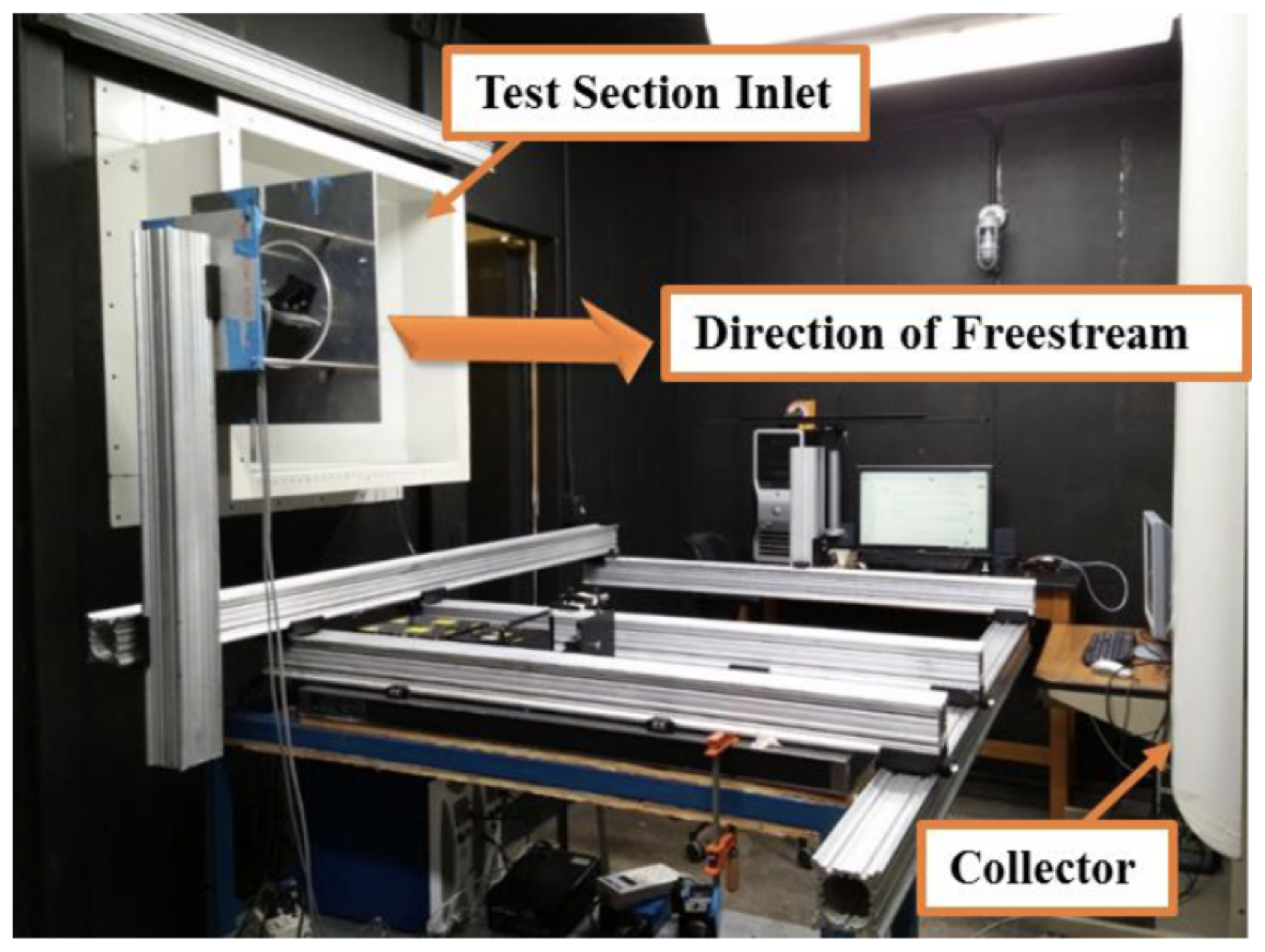
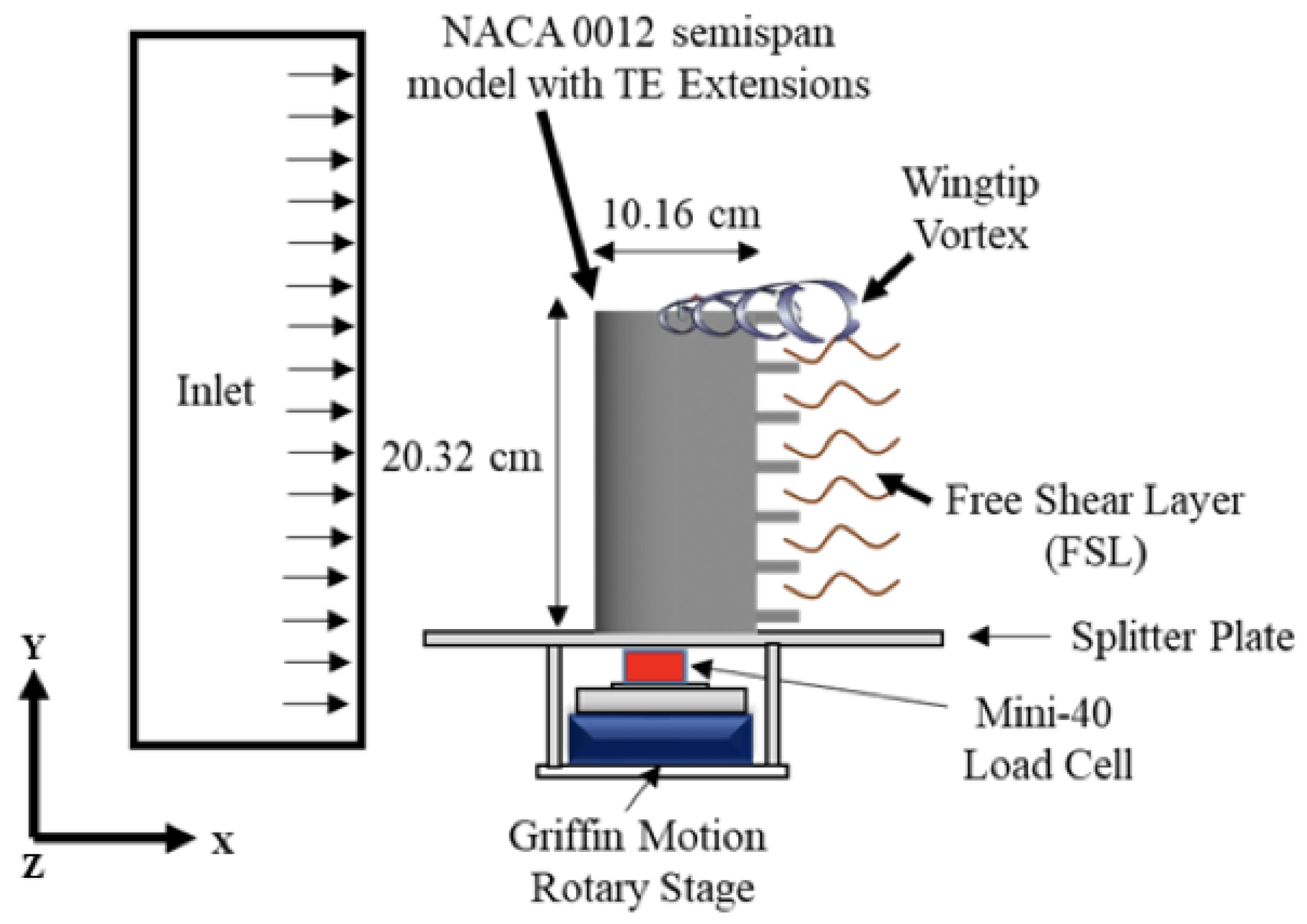
2.1. Wind Tunnel
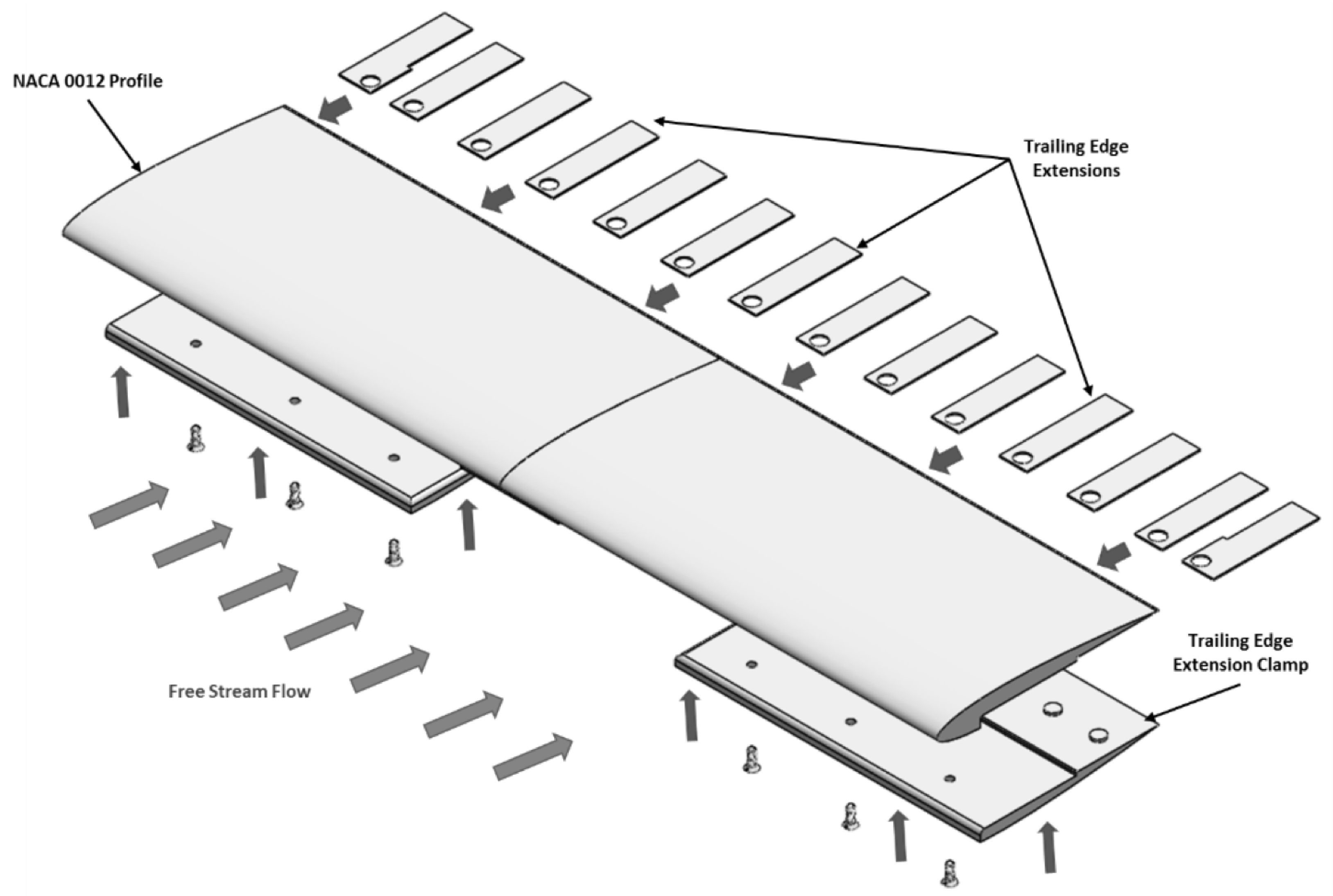
2.2. Test Model
2.3. Force Based Experiment
2.4. Force Transducer
2.5. Particle Image Velocimetry (PIV) Setup
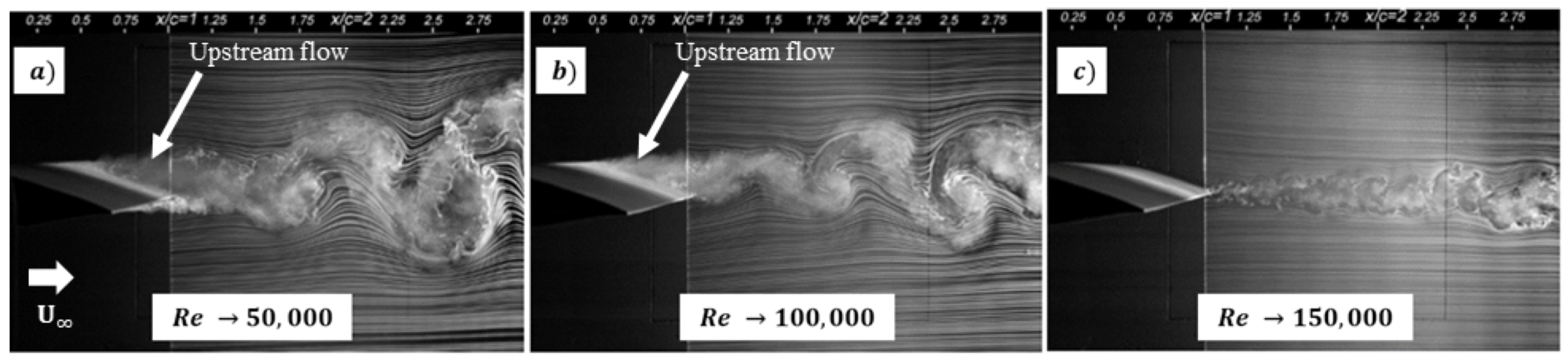
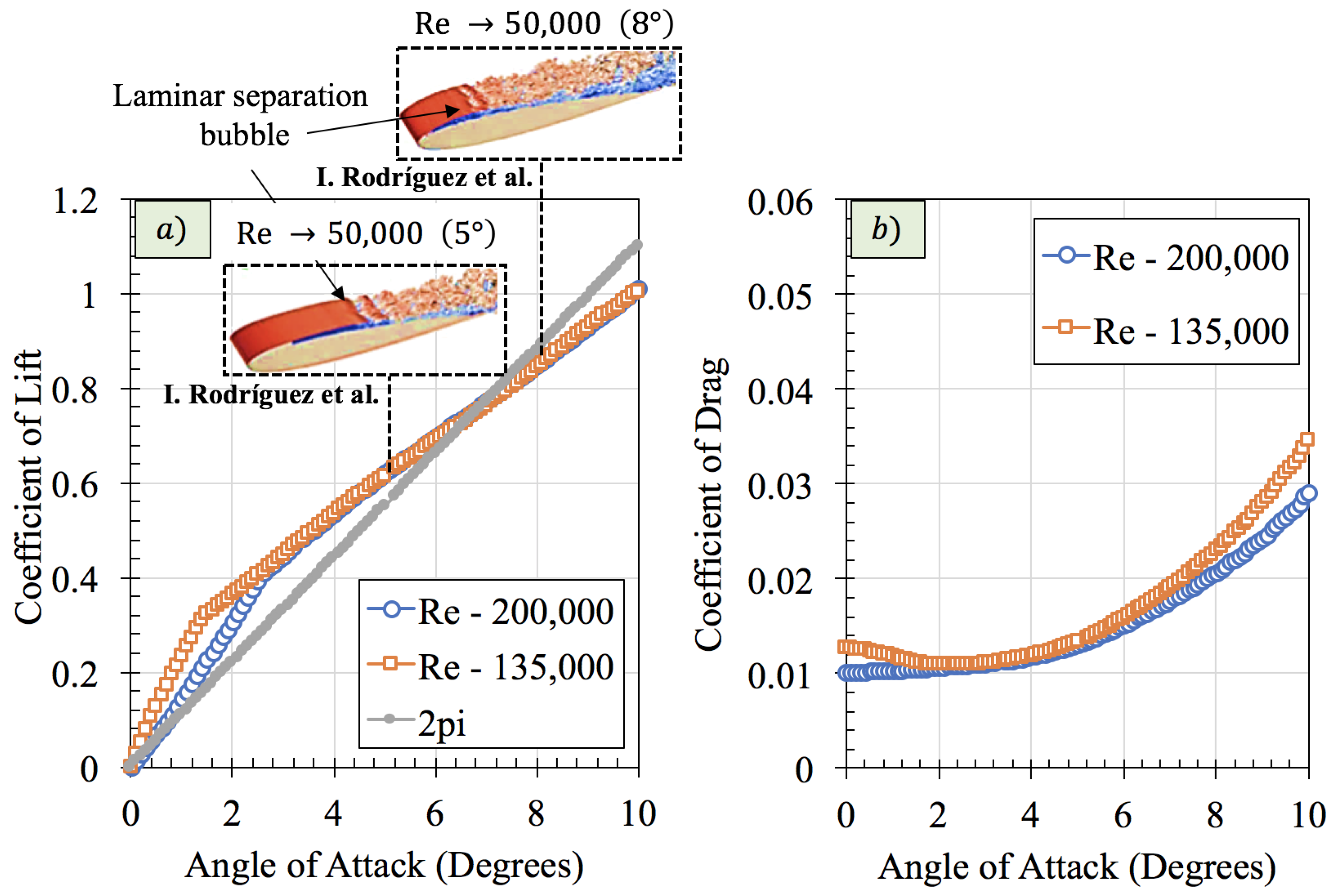
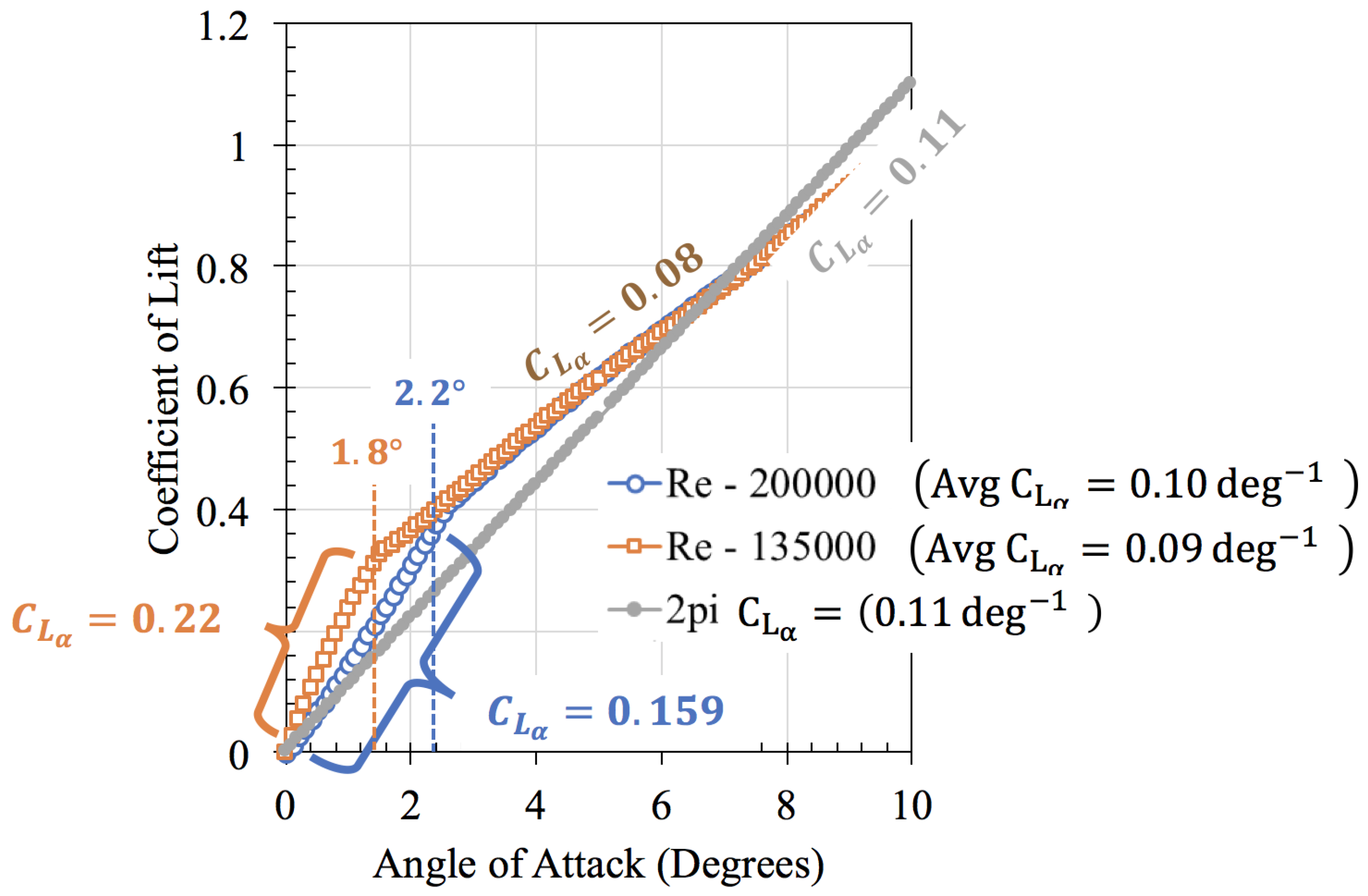
3. Influence of Reynolds Number
4. Results
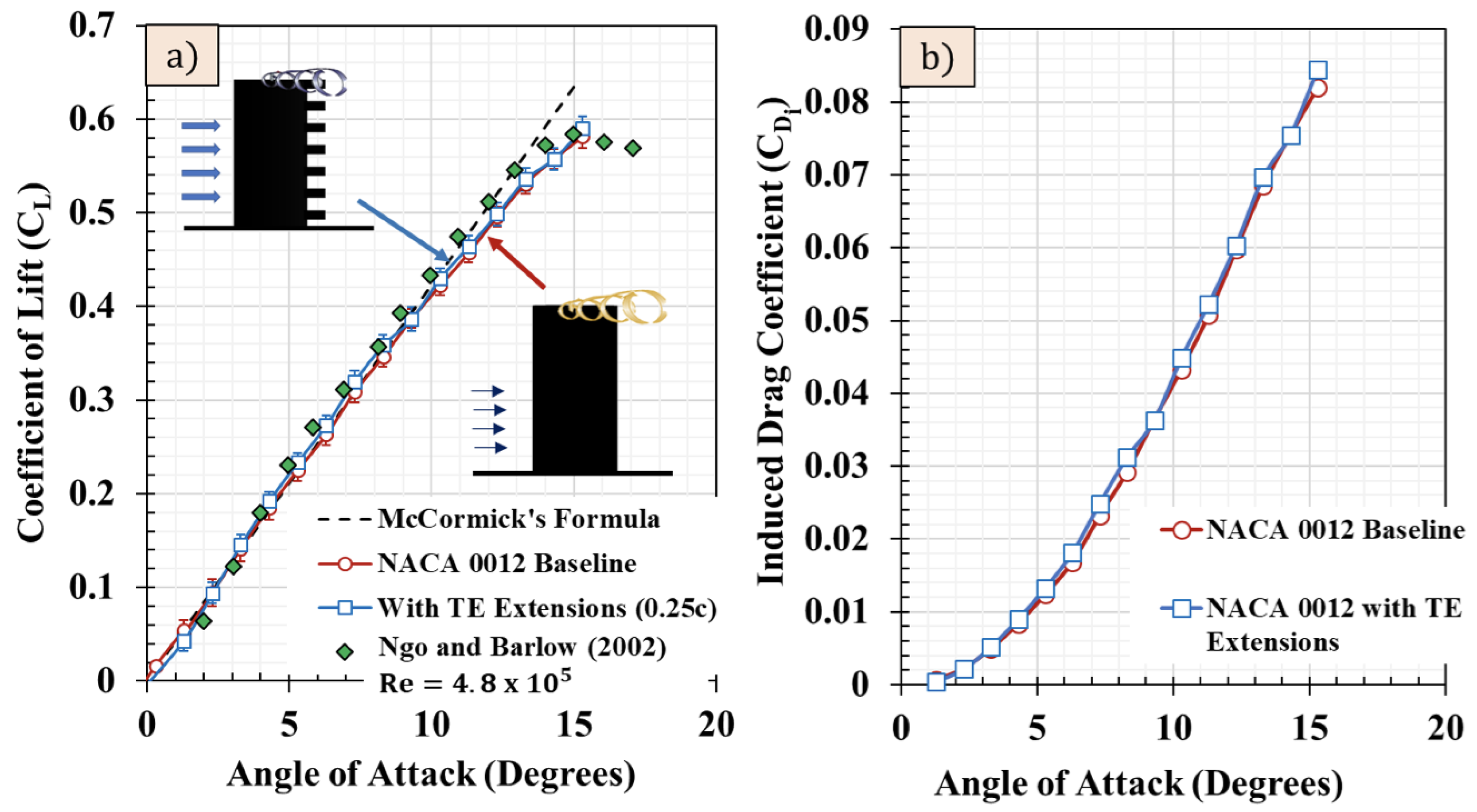
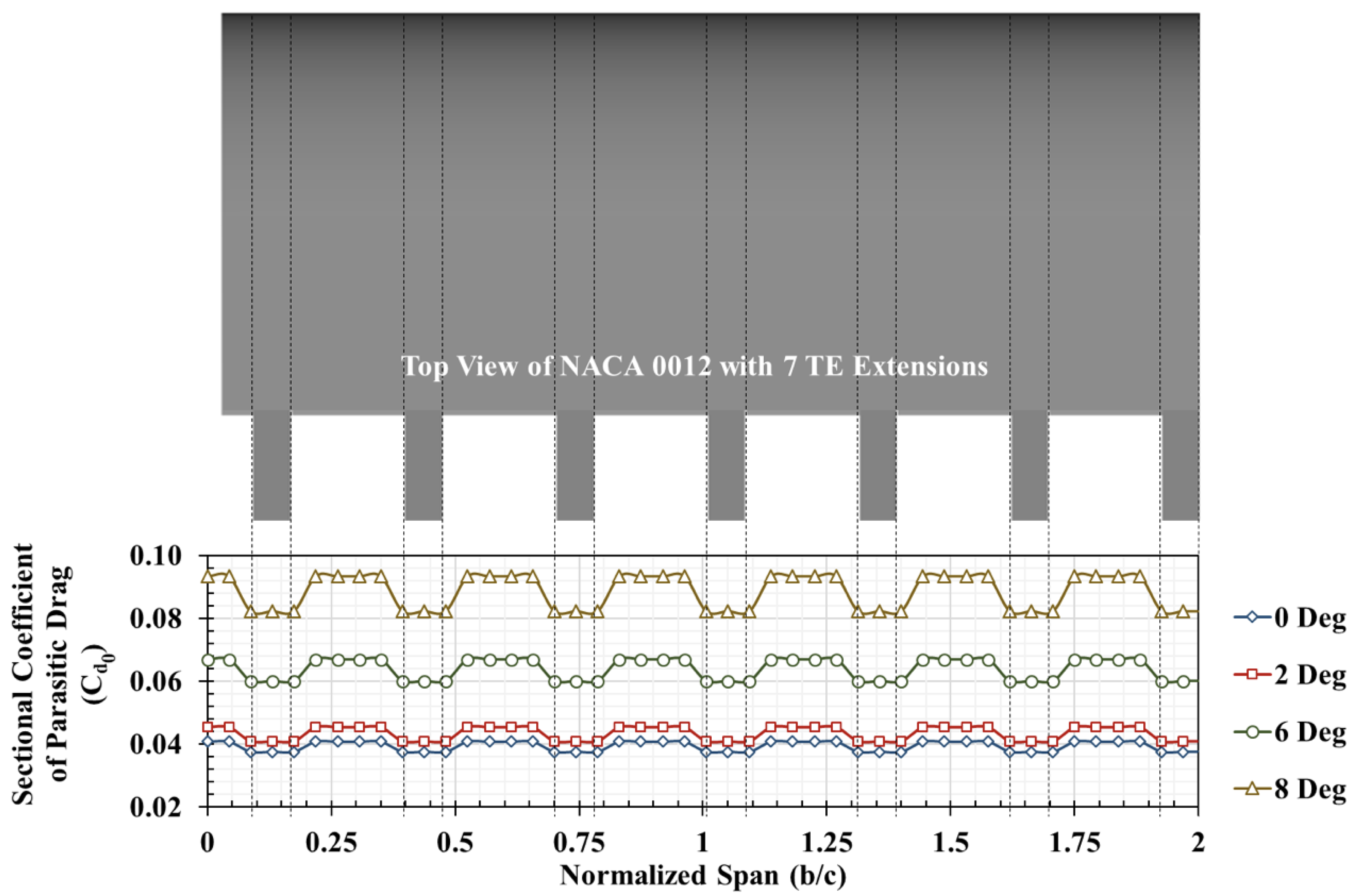
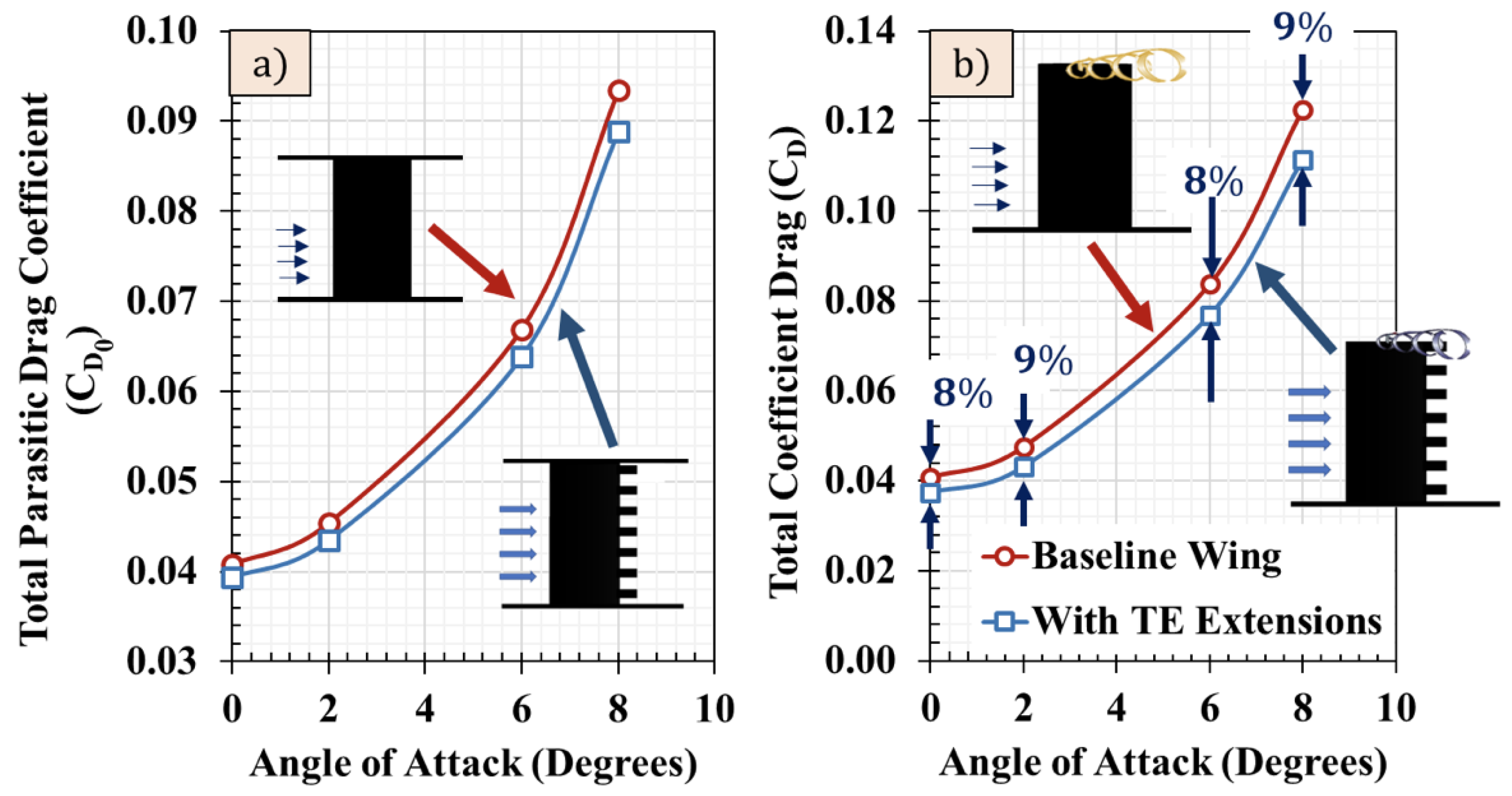
4.1. Force-Based Experimental Results
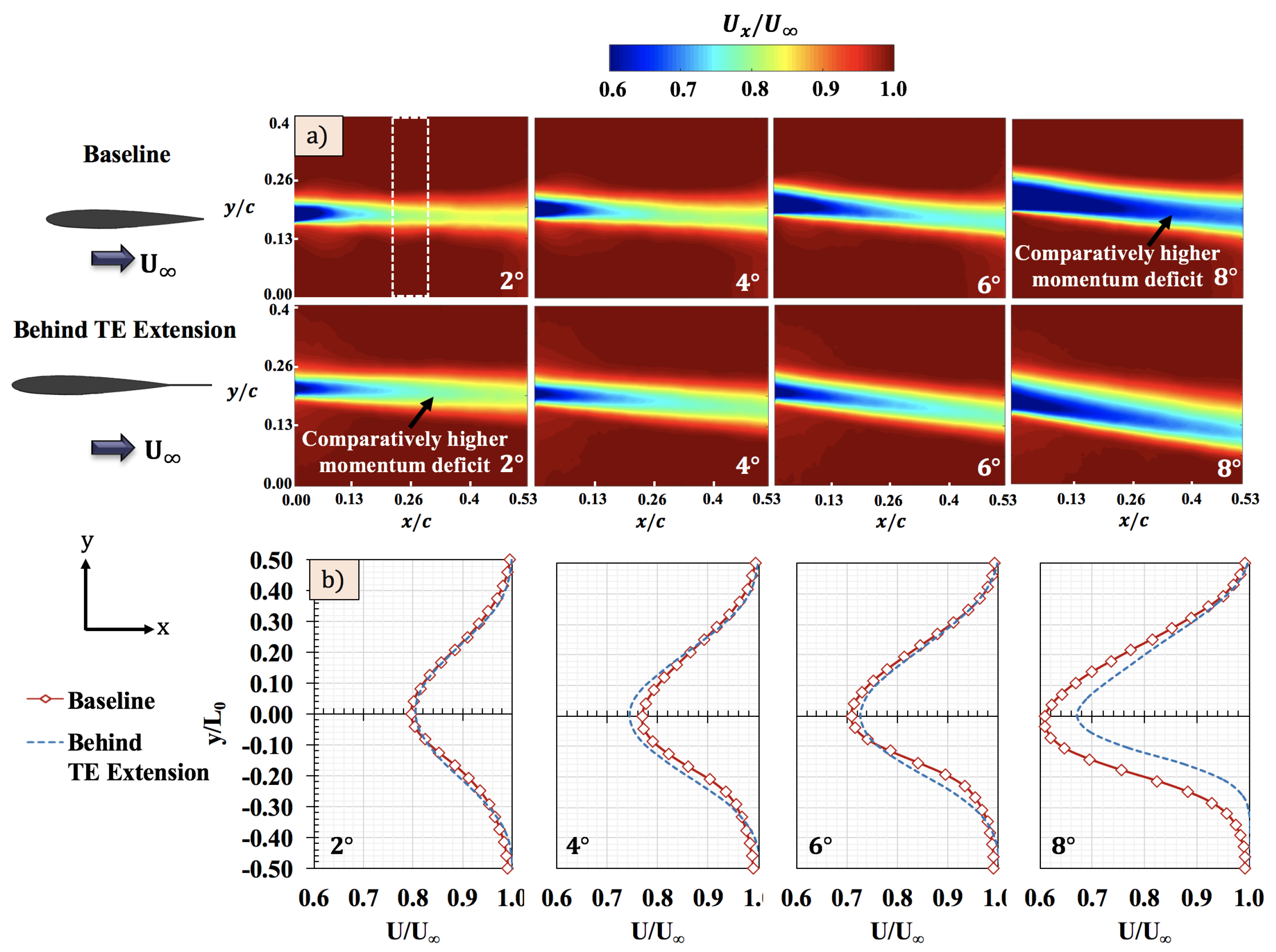
4.2. Momentum Deficit
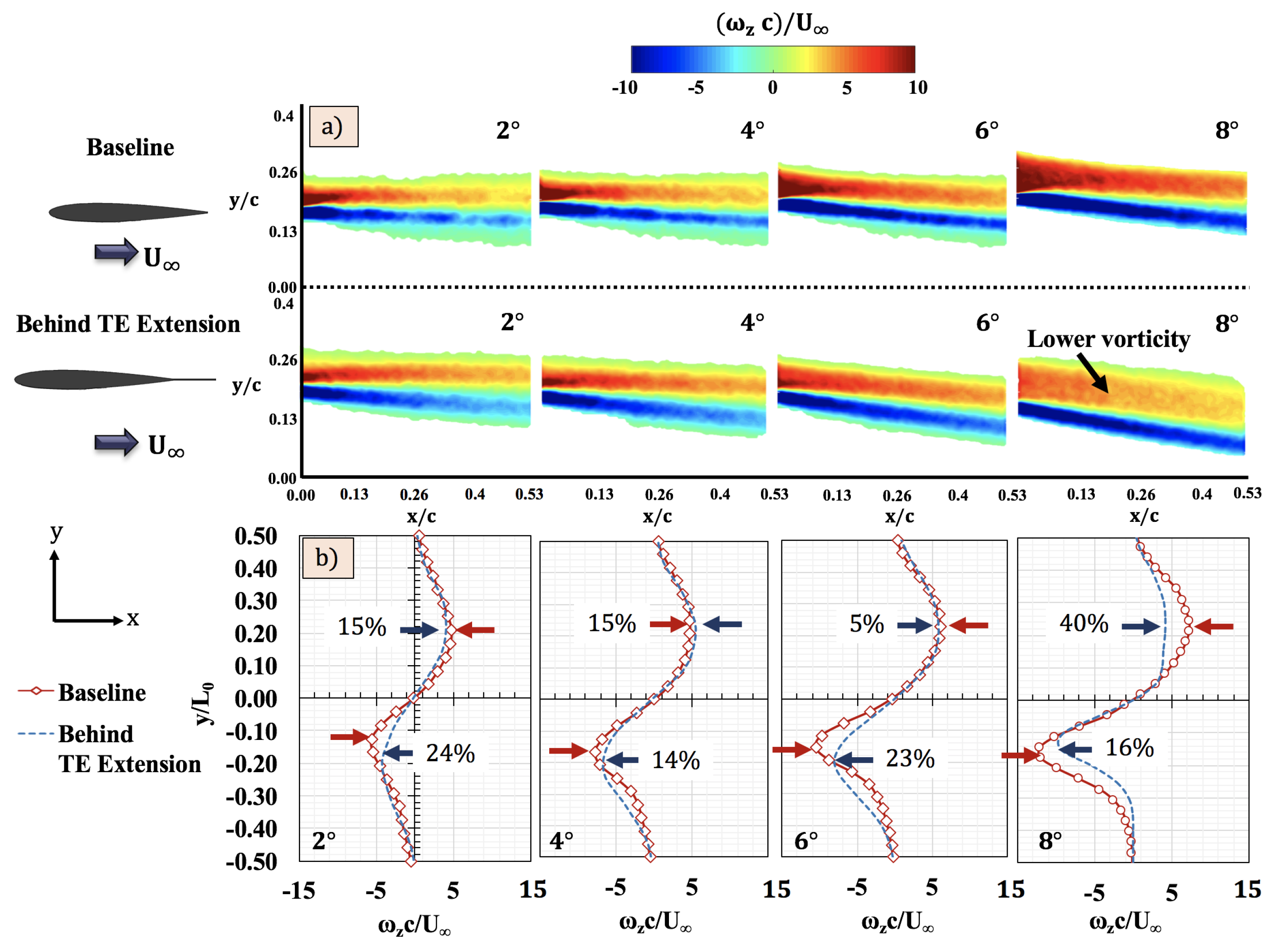
4.3. Z-Vorticity
4.4. Coherent Structures
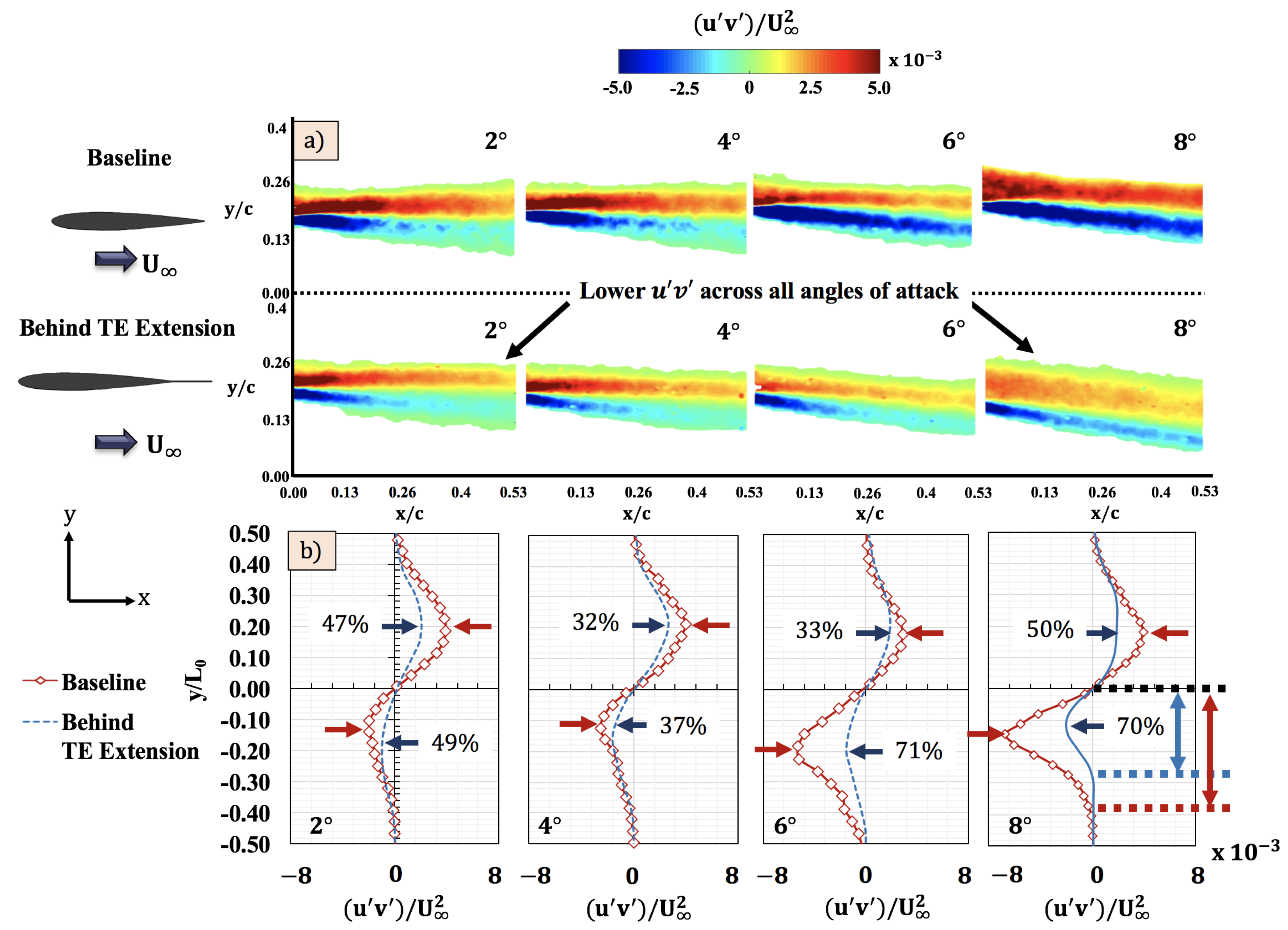
4.5. Reynolds Stress
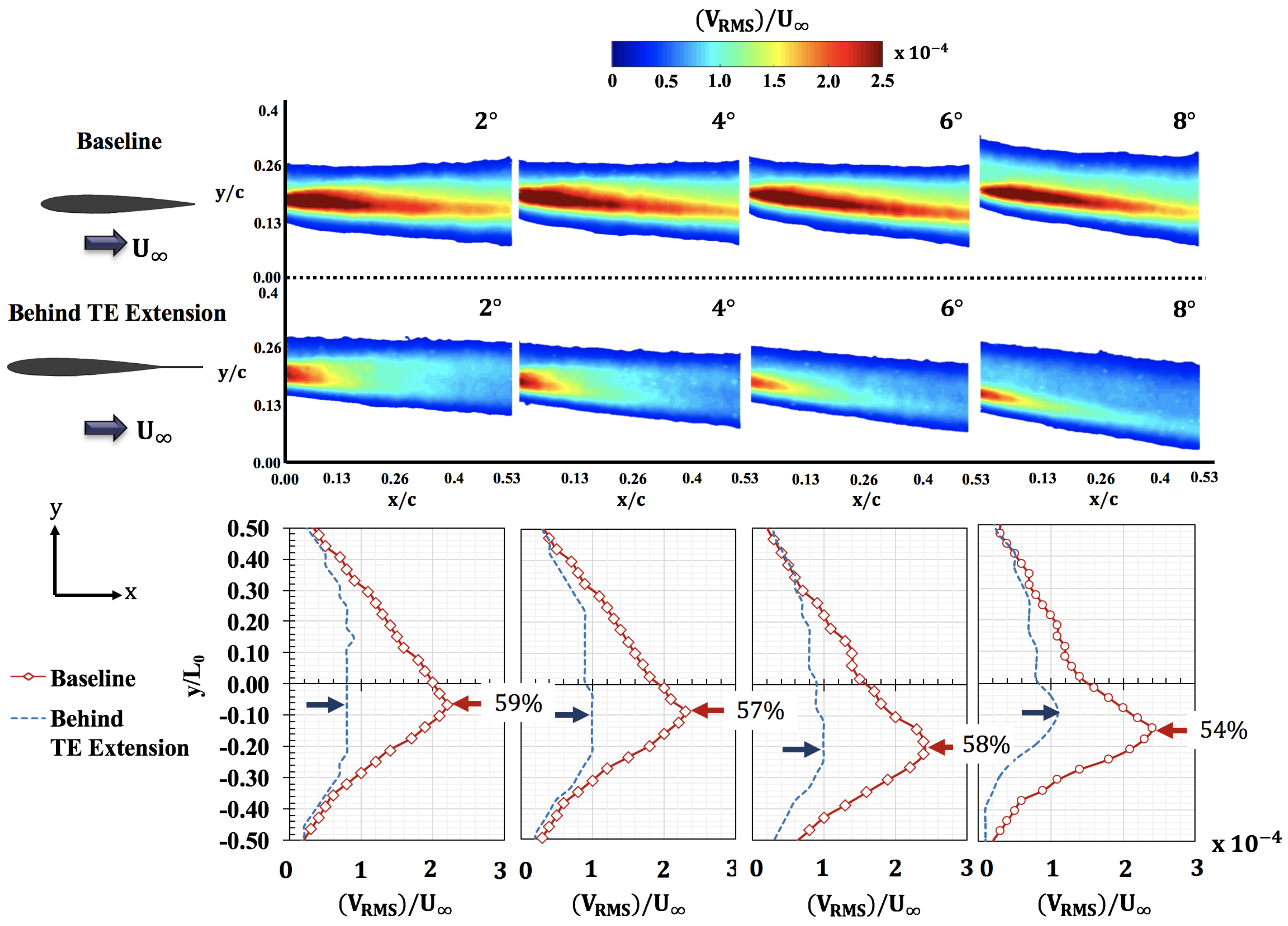
4.6. Root-Mean Square (RMS) Velocities
5. Conclusions
- The TE extensions had a minor effect on the coefficient of lift but had measurable impact on the coefficient of drag at high angles of attack. With the segmented TE extensions, the total drag coefficient reduced by 8% at an 8° angle of attack.
- Evidence for the cause of reduction in parasitic drag with TE extensions was supported by mean flow quantities, such as mean velocity and normalized vorticity. Both parameters showed measurable and significant reductions when compared to the baseline, especially in the vorticity case. The average reduction in vorticity is in the order of 40% at an 8° angle of attack.
- The reduction in vorticity behind TE extensions was further supported by determining the coherent structures in the wake. A comparatively lower correlation of the wake and the upper surface shear layer indicates lower velocity and pressure fluctuations behind the TE extensions when compared to the baseline.
- The lower pressure fluctuations can be supported by the changes observed in the Reynolds stress. On average, the magnitude of the Reynolds stress was reduced by 40% on the upper surface and by 55% on the lower surface.
- The reduction in fluctuations are further validated by determining and , which showed an average decrease in magnitude of 15% and 57%, respectively.
Author Contributions
Funding
Conflicts of Interest
References
- Theodorsen, T.; Stickle, G.W. Effect of a Trailing-Edge Extension on the Characteristics of a Propeller Section; National Advisory Committee for Aeronautics: Washington, DC, USA, 1944.
- Ito, A. The effect of trailing edge extensions on the performance of the Göttingen 797 and the Wortmann FX 63–137 aerofoil sections at Reynolds numbers between 3 × 105 and 1 × 106. Aeronaut. J. 1989, 93, 283–289. [Google Scholar]
- Yarusevych, S.; Sullivan, P.E.; Kawall, J.G. On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 2009, 632, 245–271. [Google Scholar] [CrossRef]
- Huang, R.F.; Lin, C.L. Vortex shedding and shear-layer instability of wing at low-Reynolds numbers. AIAA J. 1995, 33, 1398–1403. [Google Scholar] [CrossRef]
- Huang, R.F.; Lee, H.W. Turbulence effect on frequency characteristics of unsteady motions in wake of wing. AIAA J. 2000, 38, 87–94. [Google Scholar] [CrossRef]
- Guan, Y.; Pröbsting, S.; Stephens, D.; Gupta, A.; Morris, S.C. On the wake flow of asymmetrically beveled trailing edges. Exp. Fluids 2016, 57, 78. [Google Scholar] [CrossRef]
- Butler, S. Aircraft Drag Prediction for Project Appraisal and Performance Estimation. 1973. Available online: http://discovery.nationalarchives.gov.uk/details/r/C10818307 (accessed on 2 August 2018).
- Stanewsky, E. Adaptive wing and flow control technology. Prog. Aerosp. Sci. 2001, 37, 583–667. [Google Scholar] [CrossRef]
- Neuhart, D.H.; Pendergraft, O.C., Jr. A Water Tunnel Study of Gurney Flaps; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1988.
- Jang, C.S.; Ross, J.C.; Cummings, R.M. Numerical investigation of an airfoil with a Gurney flap. Aircr. Des. 1998, 1, 75. [Google Scholar] [CrossRef]
- Storms, B.L.; Jang, C.S. Lift enhancement of an airfoil using a Gurney flap and vortex generators. J. Aircr. 1994, 31, 542–547. [Google Scholar] [CrossRef]
- Traub, L.W. Examination of Gurney Flap Pressure and Shedding Characteristics. J. Aircr. 2017, 54, 1990–1995. [Google Scholar] [CrossRef]
- Liu, T.; Montefort, J.; Liou, W.; Pantula, S.; Shams, Q. Lift enhancement by static extended trailing edge. J. Aircr. 2007, 44, 1939–1947. [Google Scholar] [CrossRef]
- Lee, H.T.; Kroo, I.; Bieniawski, S. Flutter suppression for high aspect ratio flexible wings using microflaps. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002; p. 1717. [Google Scholar]
- Spedding, G.; McArthur, J. Span efficiencies of wings at low Reynolds numbers. J. Aircr. 2010, 47, 120–128. [Google Scholar] [CrossRef]
- Rodríguez, I.; Lehmkuhl, O.; Borrell, R.; Oliva, A. Flow past a NACA0012 airfoil: from laminar separation bubbles to fully stalled regime. In Direct and Large-Eddy Simulation IX; Springer: Berlin, Germany, 2015; pp. 225–231. [Google Scholar]
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics; Wiley: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Ngo, H.T.; Barlow, L.E. Lifting Surface with Active Variable Tip Member and Method for Influencing Lifting Surface Behavior Therewith. U.S. Patent 6,394,397, 28 May 2002. [Google Scholar]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Random Data Analysis and Measurement Procedures; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Mohsen, A.M. Experimental Investigation of the Wall Pressure Fluctuations in Subsonic Separated Flows; Technical Report; Boeing Commercial Airplane Co.: Renton, WA, USA, 1967. [Google Scholar]


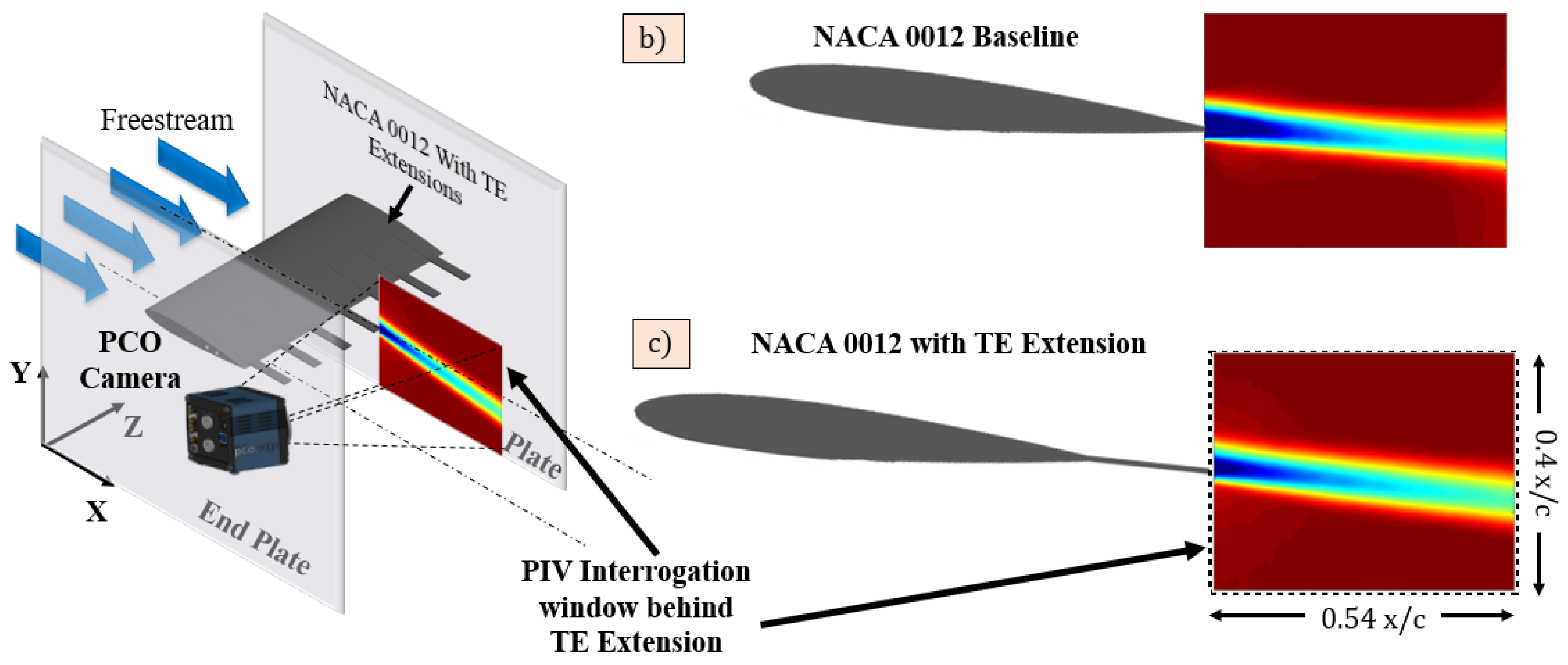




| Test Model | Reynolds Number | Angle of Attack (Degrees) |
|---|---|---|
| AR 4 NACA 0012 without TE Extensions | 200,000 | −15 to 15 |
| AR 4 NACA 0012 with TE Extensions | 200,000 | −15 to 15 |
| (N) | (N) | (N) | (Nm) | (Nm) | (Nm) | |
|---|---|---|---|---|---|---|
| Range | 40 | 40 | 120 | 2 | 2 | 2 |
| Resolution | 1/100 | 1/100 | 1/50 | 1/4000 | 1/4000 | 1/4000 |
| Test Model | Angle of Attack (Degrees) | Interrogation Location |
|---|---|---|
| AR 4 NACA 0012 without TE Extensions | 0, 2, 4, 6, 8 | Behind TE |
| AR 4 NACA 0012 with TE Extensions | 0, 2, 4, 6, 8 | Behind TE Extension |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunasekaran, S.; Curry, D. On the Wake Properties of Segmented Trailing Edge Extensions. Aerospace 2018, 5, 89. https://doi.org/10.3390/aerospace5030089
Gunasekaran S, Curry D. On the Wake Properties of Segmented Trailing Edge Extensions. Aerospace. 2018; 5(3):89. https://doi.org/10.3390/aerospace5030089
Chicago/Turabian StyleGunasekaran, Sidaard, and Daniel Curry. 2018. "On the Wake Properties of Segmented Trailing Edge Extensions" Aerospace 5, no. 3: 89. https://doi.org/10.3390/aerospace5030089
APA StyleGunasekaran, S., & Curry, D. (2018). On the Wake Properties of Segmented Trailing Edge Extensions. Aerospace, 5(3), 89. https://doi.org/10.3390/aerospace5030089





