Transient Temperature Effects on the Aerothermoelastic Response of a Simple Wing
Abstract
1. Introduction
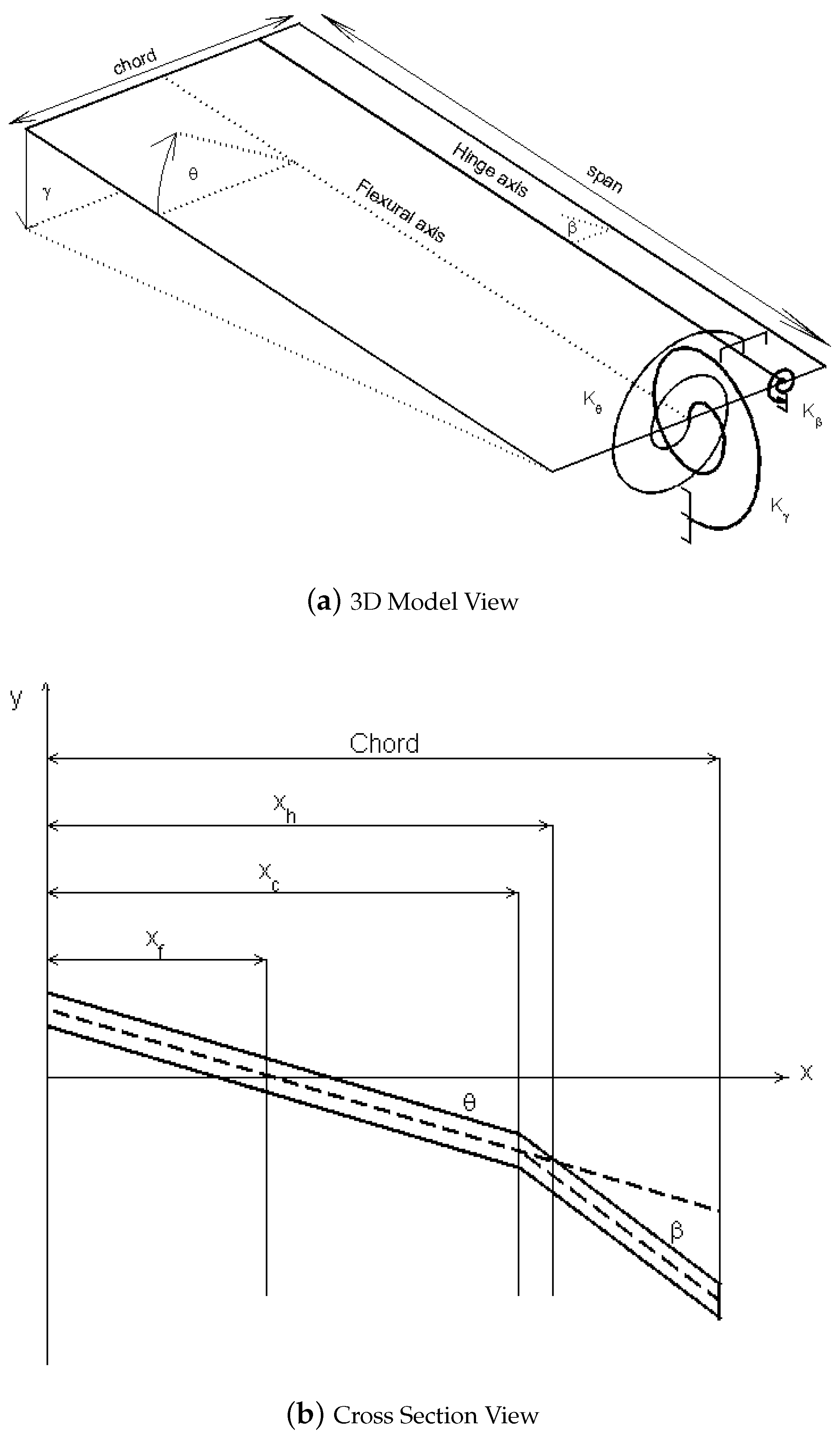
2. Theoretical Analysis
2.1. Aerodynamic Model
Aerodynamic Coefficients
2.2. Temperature Model
2.2.1. Modelling the Structural Thermal Expansion
2.2.2. Modelling of Heat Effects on Stiffness
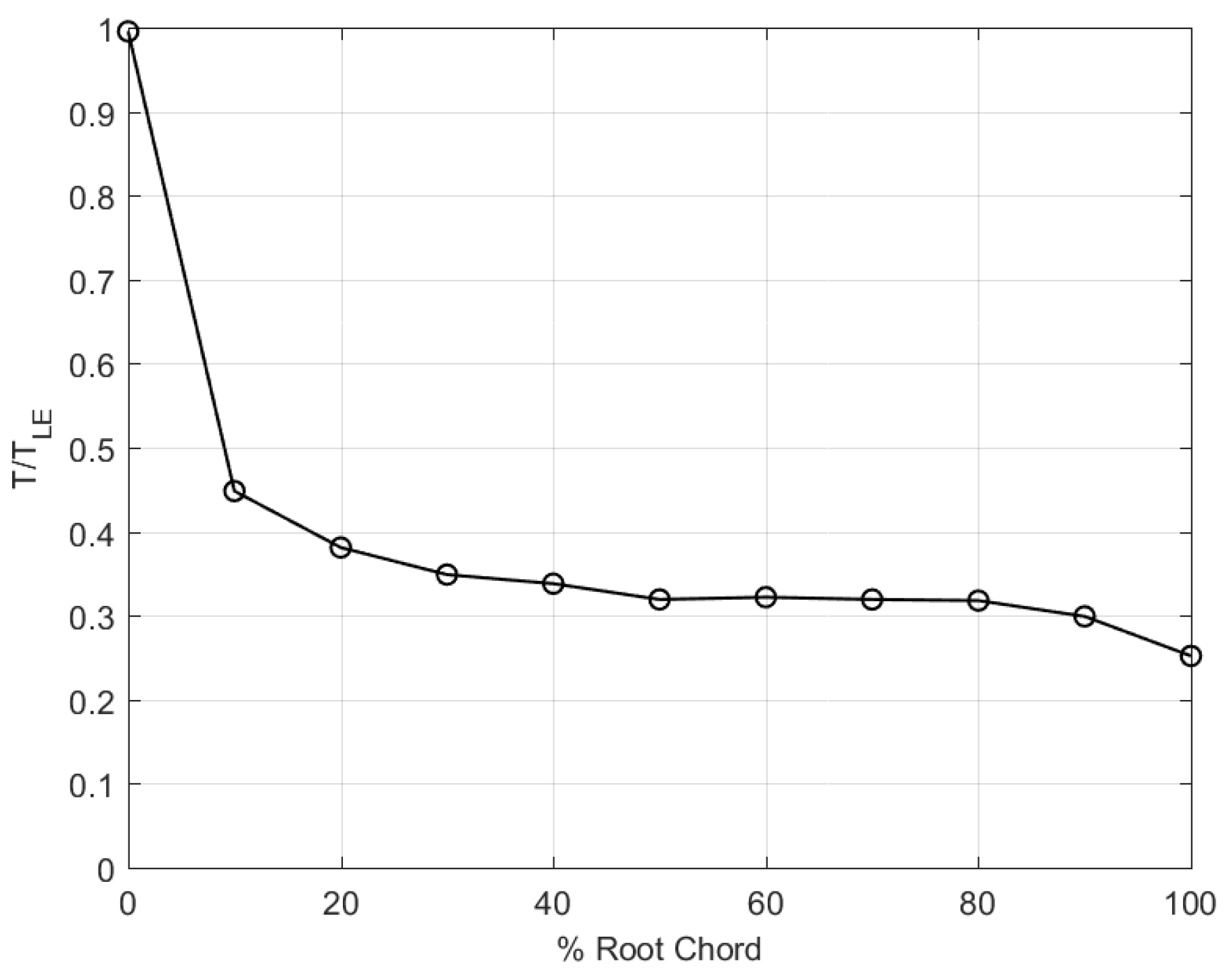
2.2.3. Temperature Distribution
2.3. Model Coupling
3. Results and Discussion
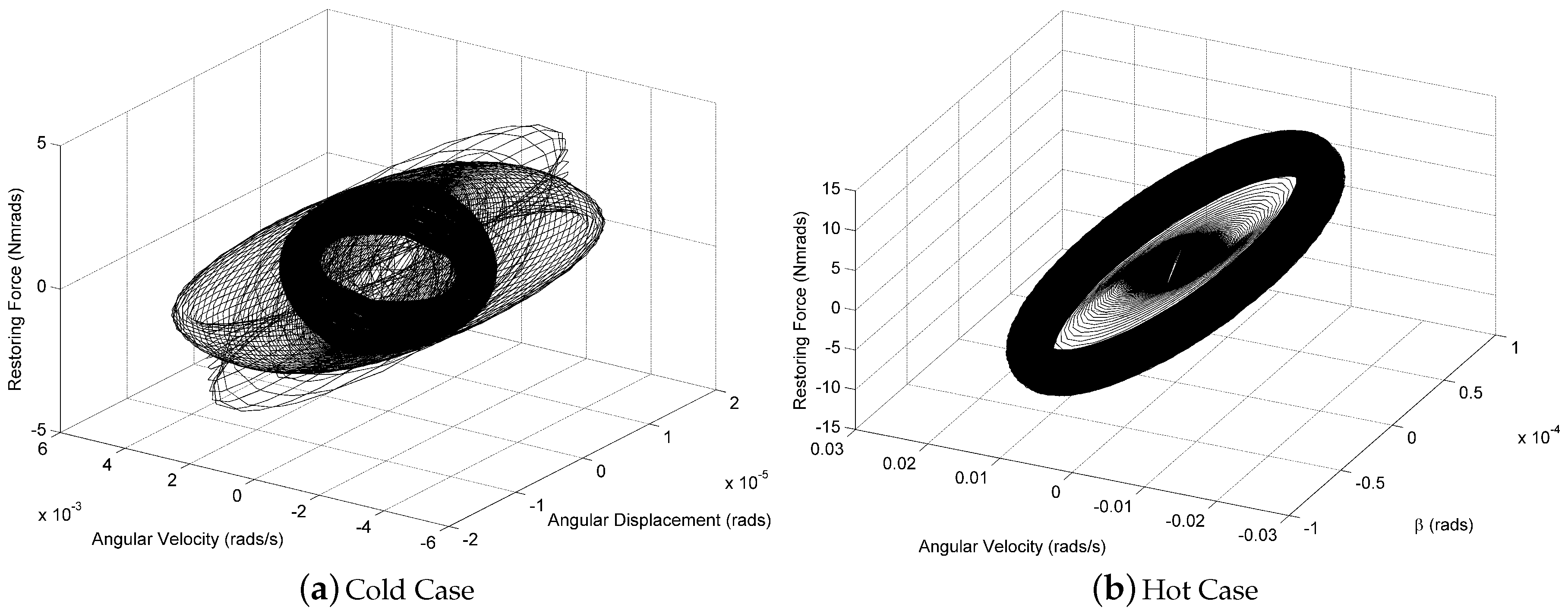
3.1. Wing at Room Temperature
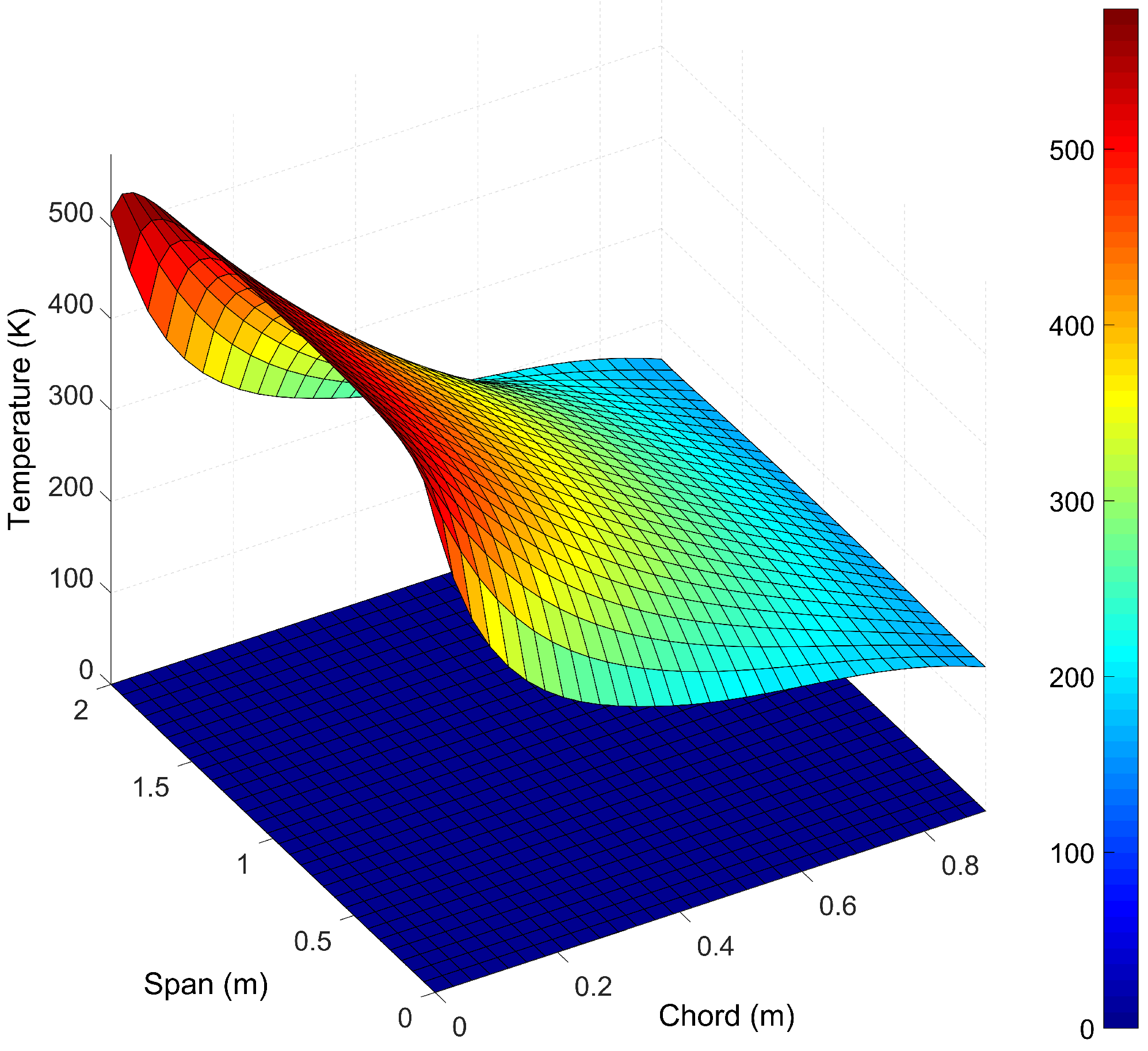
3.2. Steady-State Heat Distribution
3.3. Transient Heat Distribution
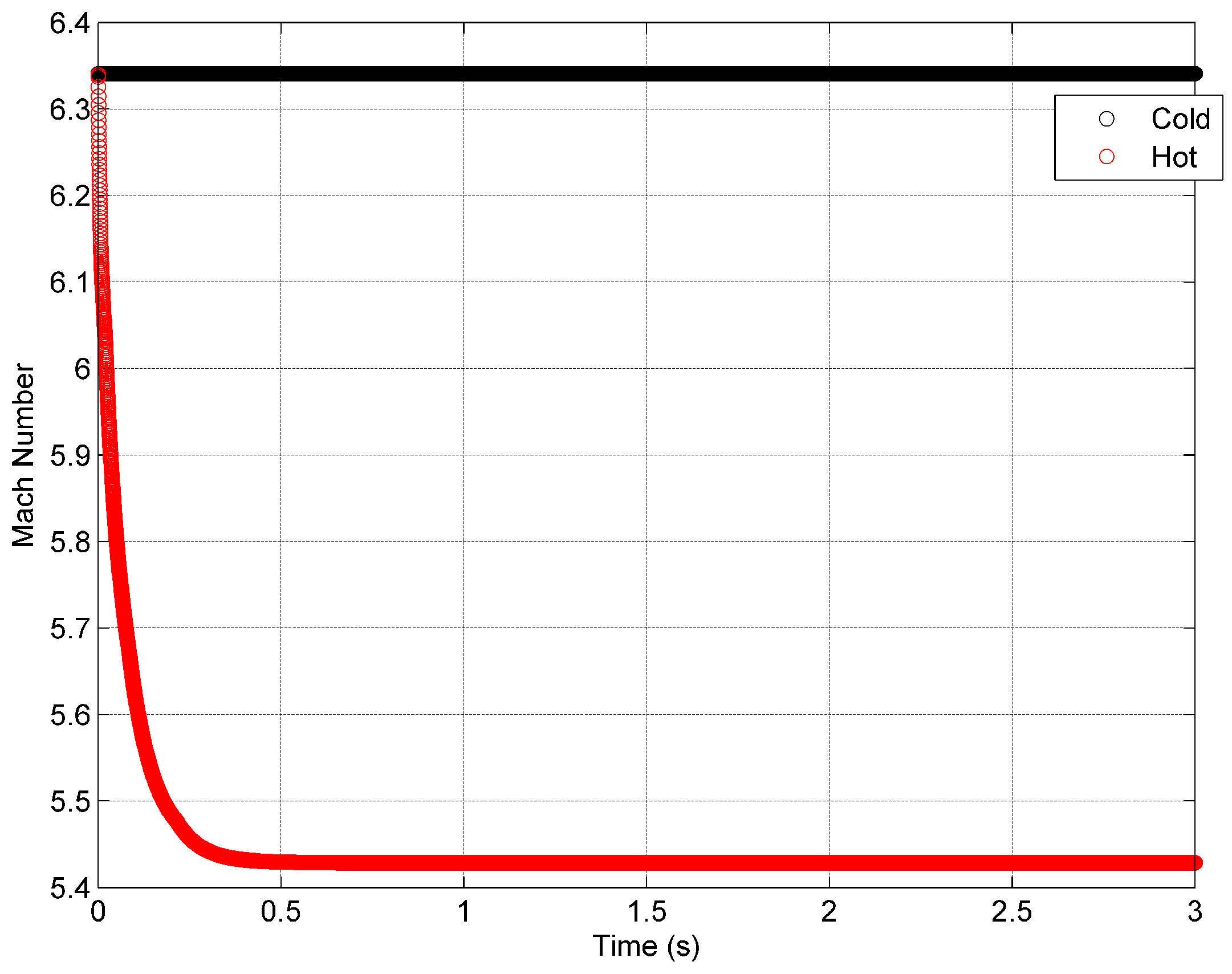
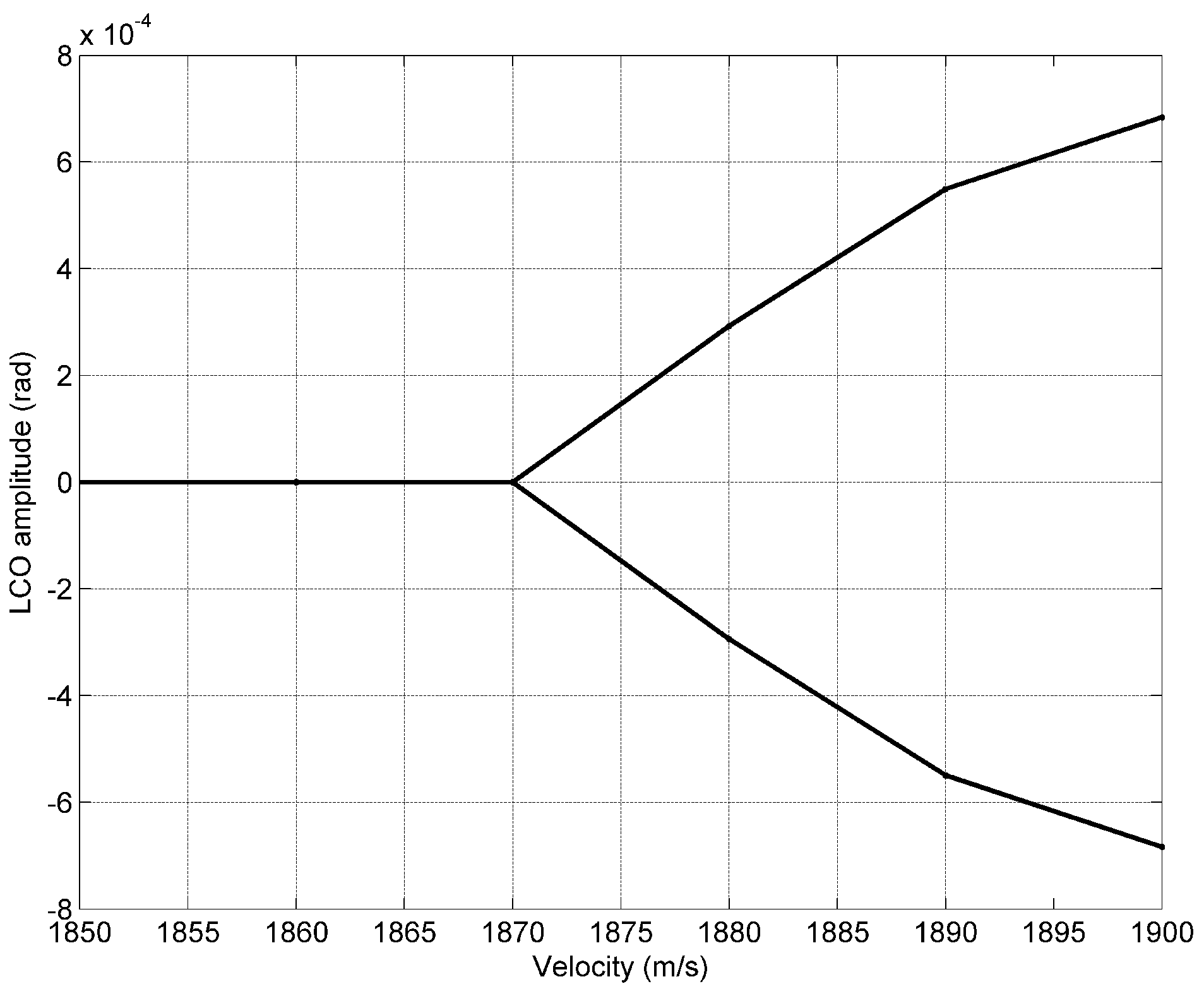
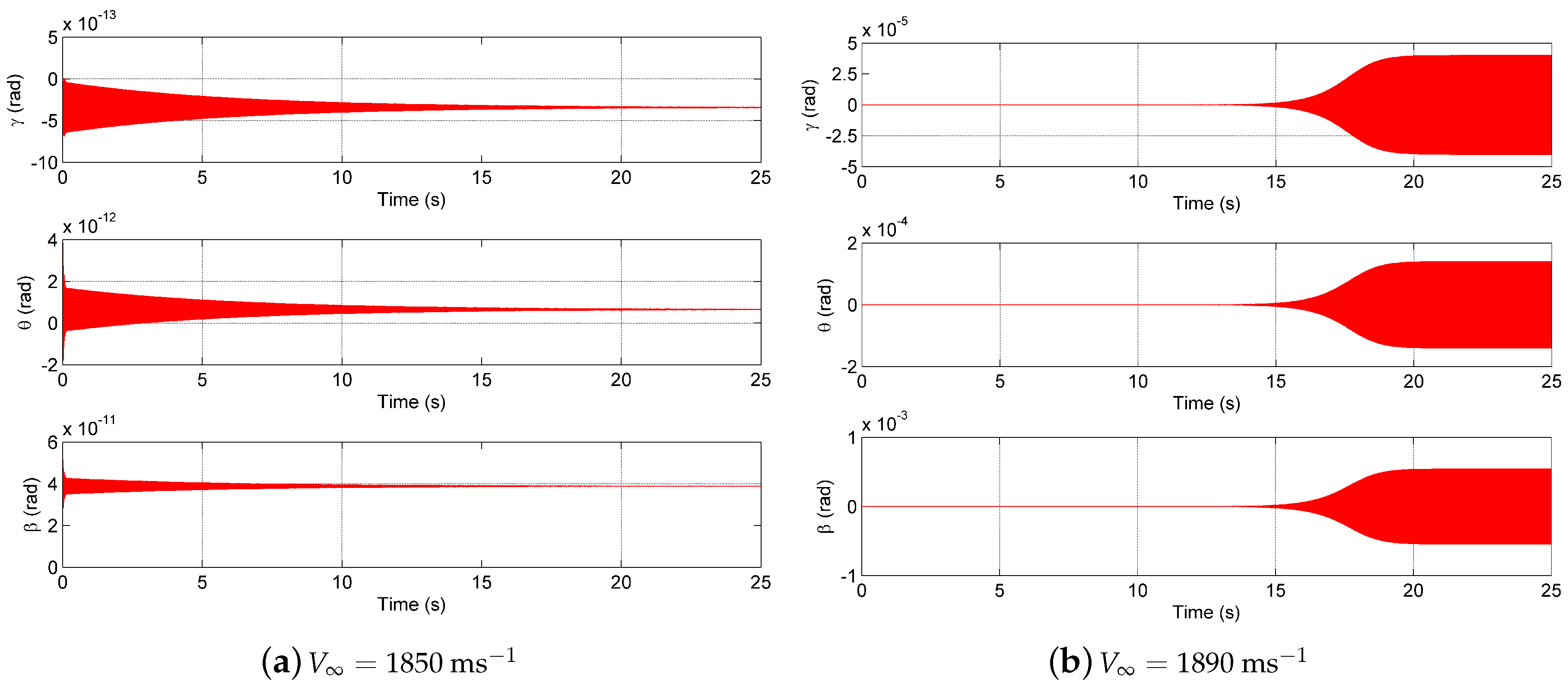
3.4. Comparison between Heat Loads
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Biot, M.A. Influences of Thermal Stresses on the Aeroelastic Stability of Supersonic Wings. J. Aeronaut. Sci. 1957, 24, 418–420. [Google Scholar] [CrossRef]
- McNamara, J.J.; Friedmann, P.P. Aeroelastic and Aerothermoelastic Analysis of Hypersonic Flow: Past, Present and Future. AIAA J. 2011, 49, 1089–1122. [Google Scholar] [CrossRef]
- Livne, E.; Weisshaar, T.A. Aeroelasticity of Nonconventional Airplane Configurations: Past and Future. J. Aircr. 2003, 40, 1047–1065. [Google Scholar] [CrossRef]
- Heeg, J.; Zeiler, T.A.; Pototzky, A.S.; Spain, C.V.; Engelund, W.C. Aerothermoelastic Analysis of a NASP Demonstrator Model. In Proceedings of the 34th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, La Jolla, CA, USA, 19–22 April 1993. No. 1993-1366. [Google Scholar]
- Heeg, J.; Gilbert, M.G.; Pototzky, A.S. Active Control of Aerothermoelastic Effects for a Conceptual Hypersonic Aircraft. J. Aircr. 1993, 30, 453–458. [Google Scholar] [CrossRef]
- Mansour, N.; Pittman, J.; Olson, L. Fundamental Aeronautics Hypersonics Projects: Overview. In Proceedings of the 39th AIAA Thermophysics Conference, Fluid Dynamics and Co-located Conferences, Miami, FL, USA, 25–28 June 2007. No. 2007-4263. [Google Scholar]
- Dolvin, D.J. Hypersonic International Flight Research and Experimentation (HIFiRE) Fundamental Sciences and Technology Development Strategy. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. No. 2008-2581. [Google Scholar]
- Bolender, M.A.; Doman, D.B. Nonlinear Longitudinal Dynamic Model of an Airbreathing Hypersonic Vehicle. J. Spacecr. Rocket. 2007, 44, 374–387. [Google Scholar] [CrossRef]
- Falkiewicz, N.J.; Cesnik, C.E.S.; Crowell, A.R.; McNamara, J.J. Reduced-Order Aerothermoelastic Framework for Hypersonic Vehicle Control Simulation. AIAA J. 2011, 49, 1625–1646. [Google Scholar] [CrossRef]
- Crowell, A.R.; McNamara, J.J. Model Reduction of Computational Aerothermodynamics for Hypersonic Aerothermoelasticity. AIAA J. 2012, 50, 74–84. [Google Scholar] [CrossRef]
- Stanford, B.; Beran, P. Aerothermoelastic Topology Optimization with Flutter and Buckling Metrics. Struct. Multidiscip. Optim. 2013, 48, 149–171. [Google Scholar] [CrossRef]
- Lamorte, N.; Friedmann, P.P.; Glaz, B.; Culler, A.J.; Crowell, A.R.; McNamara, J.J. Uncertainty Propagation in Hypersonic Aerothermoelastic Analysis. J. Aircr. 2014, 51, 192–203. [Google Scholar] [CrossRef]
- Lamorte, N.; Friedmann, P.P. Hypersonic Aeroelastic and Aerothermoelastic Studies Using Computational Fluid Dynamics. AIAA J. 2014, 52, 2062–2078. [Google Scholar] [CrossRef]
- McNamara, J.J.; Friedmann, P.P.; Powell, K.G.; Thuruthimattam, B.J. Aeroelastic and Aerothermoelastic Behavior in Hypersonic Flow. AIAA J. 2008, 46, 2591–2610. [Google Scholar] [CrossRef]
- Librescu, L.; Marzocca, P.; Silva, W.A. Linear/nonlinear Supersonic Panel Flutter in a High-Temperature Field. J. Aircr. 2004, 41, 918–924. [Google Scholar] [CrossRef]
- McNamara, J.J.; Friedmann, P.P.; Powell, K.G. Three-Dimensional Aeroelastic and Aerothermoelastic Behavior in Hypersonic Flow. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005. No. 2005-2175. [Google Scholar]
- Bisplinghoff, R.L.; Dugundji, J. Influence of Aerodynamic Heating on Aeroelastic Phenomena. Pergamon 1958, 28, 288–312. [Google Scholar]
- Runyan, H.L.; Jones, N.H. Effect of Aerodynamic Heating on the Flutter of a Rectangular Wing at a Mach Number of 2; Technical Report RM L58C31; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1958.
- Ericsson, L.; Almroth, B.; Bailie, J. Hypersonic Aerothermoelastic Characteristics of a Finned Missile. In Proceedings of the 16th Aerospace Sciences Meeting, Aerospace Sciences Meetings, Huntsville, AL, USA, 16–18 January 1978. No. 1978-0231. [Google Scholar]
- Spain, C.V.; Soistmann, D.L.; Linville, T.W. Integration of Thermal Effects into Finite Element Aerothermoelastic Analysis with Illustrative Results; Technical Report CR 1059; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1989.
- Gupta, K.K.; Ibrahim, A. Development of an Aerothermoelastic-Acoustics Simulation Capability of Flight Vehicles. In Proceedings of the 48th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2010. No. 2010-0050. [Google Scholar]
- Gupta, K.K.; Voelker, L.S.; Bach, C.; Doyle, T.; Hahn, E. CFD-Based Aeroelastic Analysis of the X-43 Hypersonic Flight Vehicle. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, NV, USA, 8–11 January 2001. No. 2001-0712. [Google Scholar]
- Thuruthimattam, B.J.; Friedmann, P.P.; McNamara, J.J.; Powell, K.G. Modeling Approaches to Hypersonic Aerothermoelasticity with Application to Reusable Launch Vehicles. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. No. 2003-1967. [Google Scholar]
- Crowell, A.R.; McNamara, J.J.; Miller, B.A. Hypersonic Aerothermoelastic Response Prediction of Skin Panels Using Computational Fluid Dynamic Surrogates. J. Aeroelast. Struct. Dyn. 2011, 2, 3–30. [Google Scholar]
- McNamara, J.J.; Crowell, A.R.; Friedmann, P.P.; Glaz, B.; Gogulapati, A. Approximate Modeling of Unsteady Aerodynamics for Hypersonic Aeroelasticity. J. Aircr. 2010, 47, 1932–1945. [Google Scholar] [CrossRef]
- Thuruthimattam, B.J.; Friedmann, P.P.; Powell, K.G.; Bartels, R.E. Computational Aeroelastic Studies of a Generic Hypersonic Vehicle. Aeronaut. J. 2009, 113, 763–774. [Google Scholar] [CrossRef]
- Crowell, A.R.; Miller, B.A.; McNamara, J.J. Robust and Efficient Treatment of Temperature Feedback in Fluid-Thermal-Structural Analysis. AIAA J. 2014, 52, 2395–2413. [Google Scholar] [CrossRef]
- Verstraete, D.; Vio, G.A. Temperature Effects on Flutter of a Mach 5 Transport Aircraft Wing. In International Mechanical Engineering Congress and Exposition; ASME: New York, NY, USA, 2012; Volume 1, pp. 227–234. [Google Scholar]
- McNamara, J.J.; Thuruthimattam, B.J.; Friedmann, P.P.; Powell, K.G.; Bartels, R.E. Hypersonic Aerothermoelastic Studies for Reusable Launch Vehicles. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. No. 2004-1590. [Google Scholar]
- Cazier, F.W.; Ricketts, R.H. Structural Dynamic and Aeroelastic Considerations for Hypersonic Vehicles. In Proceedings of the 32nd Structures, Structural Dynamics, and Materials Conference, Baltimore, MD, USA, 8–10 April 1991. No. 1991-1255. [Google Scholar] [CrossRef]
- Culler, A.J.; McNamara, J.J. Studies on the Fluid-Thermal-Structural Coupling for Aerothermoelasticity in Hypersonic Flow. AIAA J. 2010, 48, 1721–1738. [Google Scholar] [CrossRef]
- Cebeci, T.; Shao, J.P.; Kafyeke, F.; Laurendeau, E. Computational Fluid Dynamics for Engineers, 1st ed.; Horizons Publishing: Hammond, IN, USA, 2005. [Google Scholar]
- Dimitriadis, G.; Cooper, J. Limit cycle oscillation control and suppression. Aeronaut. J. 1999, 103, 257–263. [Google Scholar] [CrossRef]
- Lighthill, M.J. Oscillating Airfoils at High Mach Numbers. J. Aeronaut. Sci. 1953, 20, 402–406. [Google Scholar] [CrossRef]
- Jones, R.A.; Gallagher, J.J. Heat Transfer and Pressure Distribution of a 60° Swept Delta Wing with Dihedral at a Mach Number of 6 and Angles of Attack for 0° to 52°; Technical Report; Langley Research Centre Langley Field: Hampton, VA, USA, 1961. [Google Scholar]
- Varvill, R.; Bond, A. LAPCAT II A2 Vehicle Structure Design Specification; Technical Report, Long Term Advanced Propulsion Concepts and Technologies II; European Commission: Brussels, Belgium, 2008. [Google Scholar]
- Munk, D.J.; Vio, G.A.; Verstraete, D. Response of a Three-Degree-of-Freedom Wing with Stiffness and Aerodynamic Nonlinearities at Hypersonic Speeds. Nonlinear Dyn. 2015, 81, 1665–1688. [Google Scholar] [CrossRef]
- Bertin, J.J. Hypersonic Aerothermodynamics; AIAA Education Series; AIAA: Reston, VA, USA, 1994. [Google Scholar]
- Vosteen, L.F. Effect of Temperature on Dynamic Modulus of Elasticity of Some Structural Alloys; Technical Report; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1958.
- McNamara, J.J.; Friedmann, P.P. Aeroelastic and Aerothermoelastic Analysis of Hypersonic Vehicles: Current Status and Future Trends. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Structures, Structural Dynamics, and Materials and Co-Located Conferences, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Houghton, E.L.; Carpenter, P.W. Aerodynamics for Engineering Students, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Munk, D.; Vio, G.; Verstraete, D. Transient Temperature Effect on the Aerothermoelastic Response of a Wing. J. Fluids Struct. 2017, 75, 45–76. [Google Scholar] [CrossRef]
- Stanciu, V.; Stroe, G.; Andrei, I.C. Linear Models and Calculation of Aeroelastic Flutter. UPB Sci. Bull. 2012, 74, 29–38. [Google Scholar]


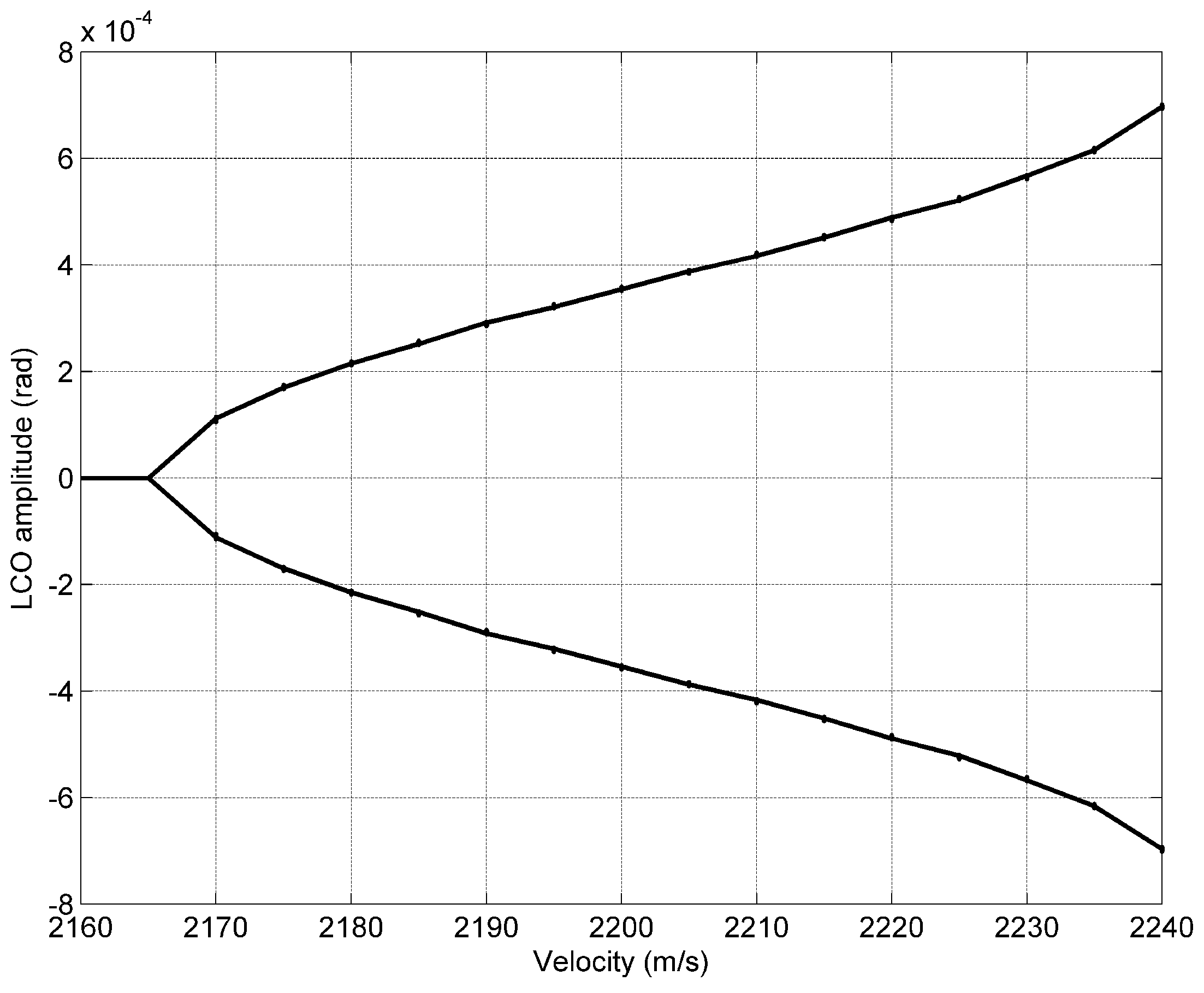
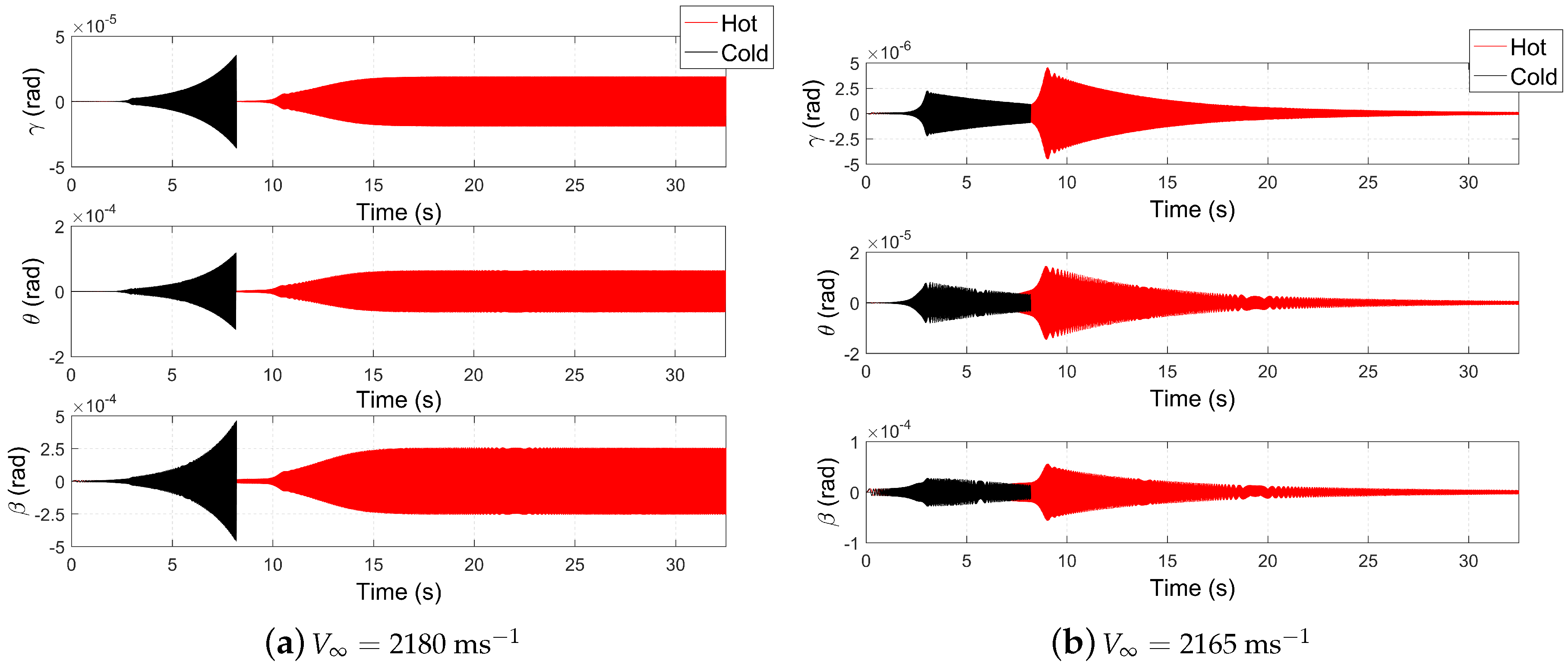
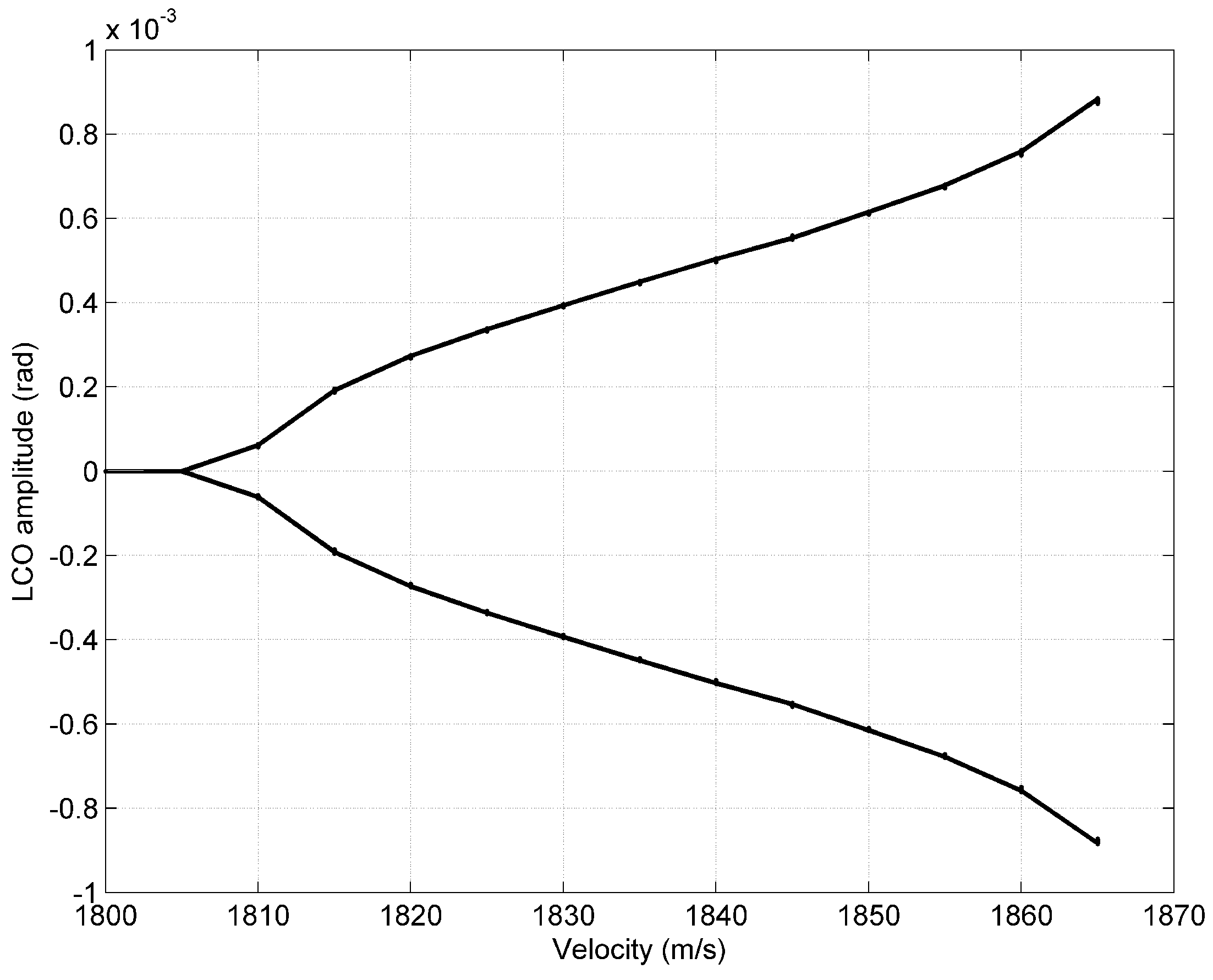
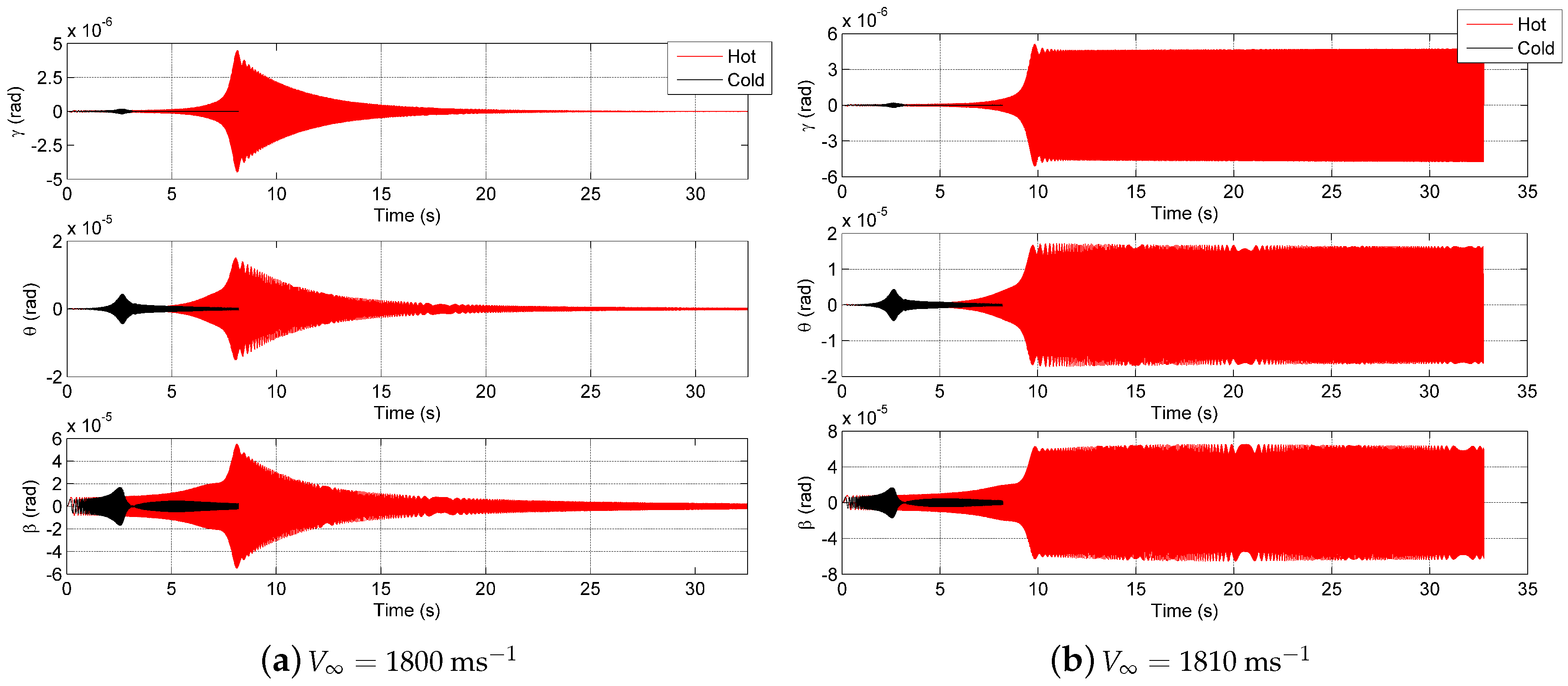
| Case | (ms) | (ms) |
|---|---|---|
| Cold Wing | 2165 | 2240 |
| Steady-State Heat Load | 1805 | 1865 |
| Transient Heat Load | 1870 | 1900 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vio, G.A.; Munk, D.J.; Verstraete, D. Transient Temperature Effects on the Aerothermoelastic Response of a Simple Wing. Aerospace 2018, 5, 71. https://doi.org/10.3390/aerospace5030071
Vio GA, Munk DJ, Verstraete D. Transient Temperature Effects on the Aerothermoelastic Response of a Simple Wing. Aerospace. 2018; 5(3):71. https://doi.org/10.3390/aerospace5030071
Chicago/Turabian StyleVio, Gareth A., David J. Munk, and Dries Verstraete. 2018. "Transient Temperature Effects on the Aerothermoelastic Response of a Simple Wing" Aerospace 5, no. 3: 71. https://doi.org/10.3390/aerospace5030071
APA StyleVio, G. A., Munk, D. J., & Verstraete, D. (2018). Transient Temperature Effects on the Aerothermoelastic Response of a Simple Wing. Aerospace, 5(3), 71. https://doi.org/10.3390/aerospace5030071






