Use of Cost-Adjusted Importance Measures for Aircraft System Maintenance Optimization
Abstract
:1. Introduction
- Research, development, test and evaluation (RDT&E) cost.
- Investment cost, which is related to production, procurement, manufacture, and infrastructure maintenance activities among others.
- Operating and support (O&S) cost, which also includes the maintenance cost.
- Disposal cost.
- Modular design architecture, which facilitates the removal and installation process for the subsystems and components of the system, which can then be forwarded to the respective repair shops, thus eliminating the need for ‘on-board’ repair work.
- Interoperability of subsystems and components with the use of standard interface protocols, which facilitates the prompt repair or upgrade of the system simply by installing a new and/or upgraded subsystem or component.
- Prognostics, which enables the monitoring, tracking and recording of the operational data, a feature which helps the user to identify operational limit exceedances and potential failures, while suggesting preventive actions.
- ‘Fail-safe’ design, which isolates the subsystems and components in case of a system failure, protecting them from further failures and malfunctions.
- Accessibility, especially for subsystems and components that need to be inspected in frequent intervals.
- Commonality with other systems.
- Standardization of subsystems, components and support tools and equipment.
- Opportunistic maintenance and maintenance-free operating periods.
- Commercial off-the-shelf (COTS) support.
- Low probability of diminishing manufacturing sources (DMS), material shortage, intellectual property rights and monopolies.
- Use of technical orders and digital training of the maintenance personnel.
- Centralized and automated analysis and reporting of the operational and support data, using appropriate key performance indicators (KPIs).
- Network-centric management of the supply chain.
- Appropriate packaging, handling, storage and transportation.
- Spares optimization as well as personnel allocation optimization.
- Follow-on support programs.
1.1. Basic Terminology
- Run-to-Failure or Breakdown Maintenance. It is implemented on a nonscheduled basis, following the failure of a system/subsystem/component. Its objective is the identification, isolation and rectification of a failure to return the system/subsystem/component within its established operating limits [12].
- Preventive Maintenance. Its objective is to reduce the probability of a nonscheduled maintenance, which typically incurs high costs and considerably lengthy times to return the system to service. Preventive maintenance is implemented through a variety of tools, such as non-destructive inspections (NDI) and planned component replacement (PCR) [12].
- Opportunistic Maintenance. It is a combination of breakdown and preventive maintenance philosophies. Its objective is to reduce the maintenance cost, by taking advantage of any failure and its subsequent downtime, so as to intervene and implement preventive maintenance of subsystems/components which have not failed yet, aiming to reduce the probability of future failure [13].
- Upgrade or Modification. It aims to upgrade the system to enhance its performance and maintainability. It might be required as a solution to a design or manufacturing problem.
- Predictive or Condition Based Maintenance (CBM). It is based on continuous condition and operational data monitoring of a system with an objective to predict its future failure [14].
- Reliability Centered Maintenance (RCM). It is a structured process that aims to optimize the management of the failures of a system [12]. Its objective is to sustain the operation of the system within the desired performance levels, to manage the consequences of the failures and to define the optimum and applicable maintenance policy, by taking into account existing constraints with regard to resources, environmental, health and safety legislation [15].
- Risk Based Maintenance (RBM). It focuses on the management of the risk of active and potential damage mechanisms and its effects to the health, safety and the environment. Severity and probability are assessed for each identified risk, with an objective to define the maintenance schedule which minimizes the overall risk [16].
- Design-Out Maintenance. Its aim is to detect possible defects during the design phase of a system, thus avoiding future system failures. It focuses on possible critical failures which should incur costs which are higher than certain affordable levels.
1.2. Reliability
1.3. An Overview of the ‘Component Importance Measures’
1.3.1. Importance Measures Based Solely on System Structure
1.3.2. Importance Measures Based on System Structure and Component’s Reliability
2. Materials and Methods
2.1. Basic Assumptions
2.2. System Structure Function
2.3. Minimal Cut Sets
2.4. Components Reliability Functions
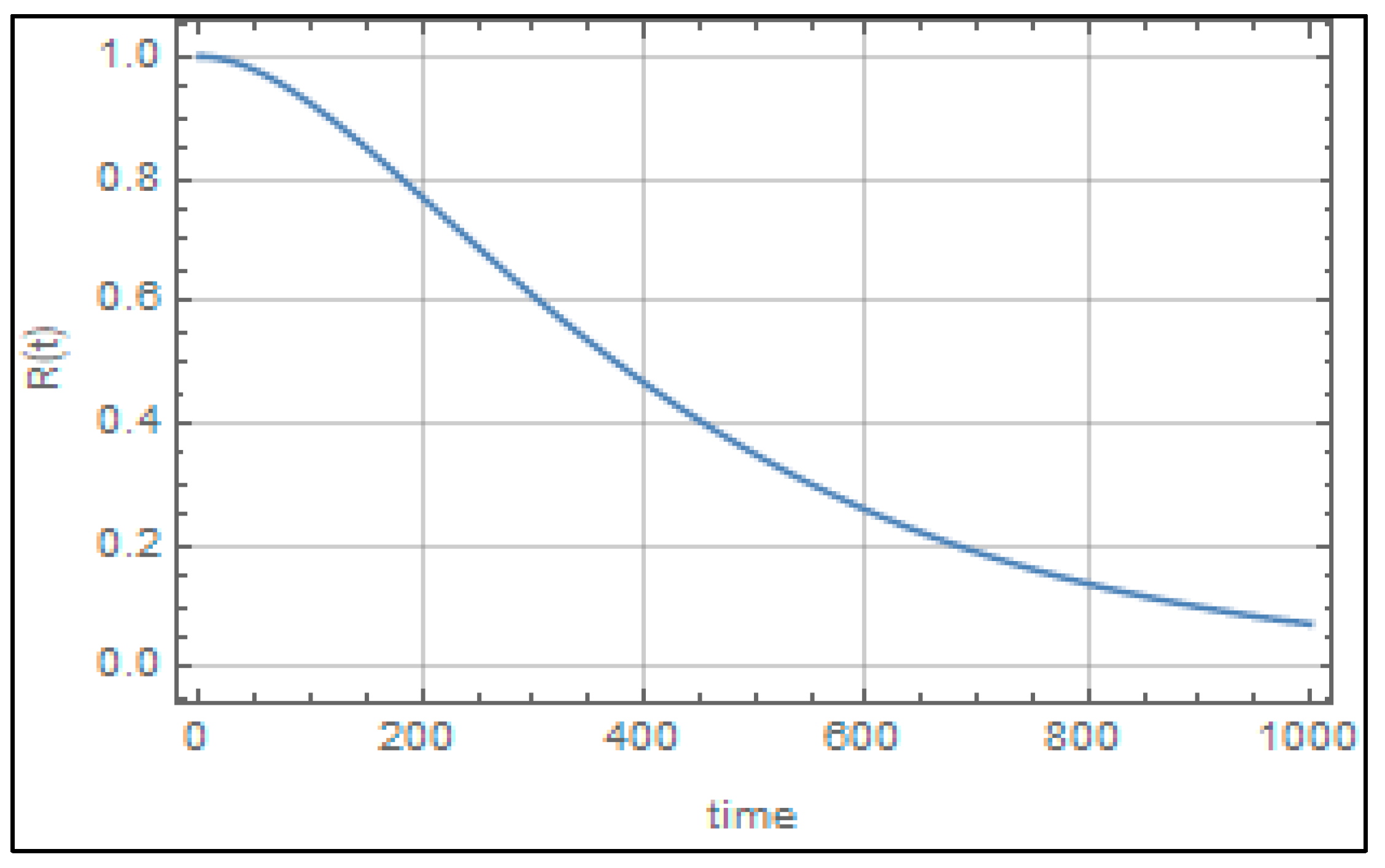
2.5. System Reliability Function
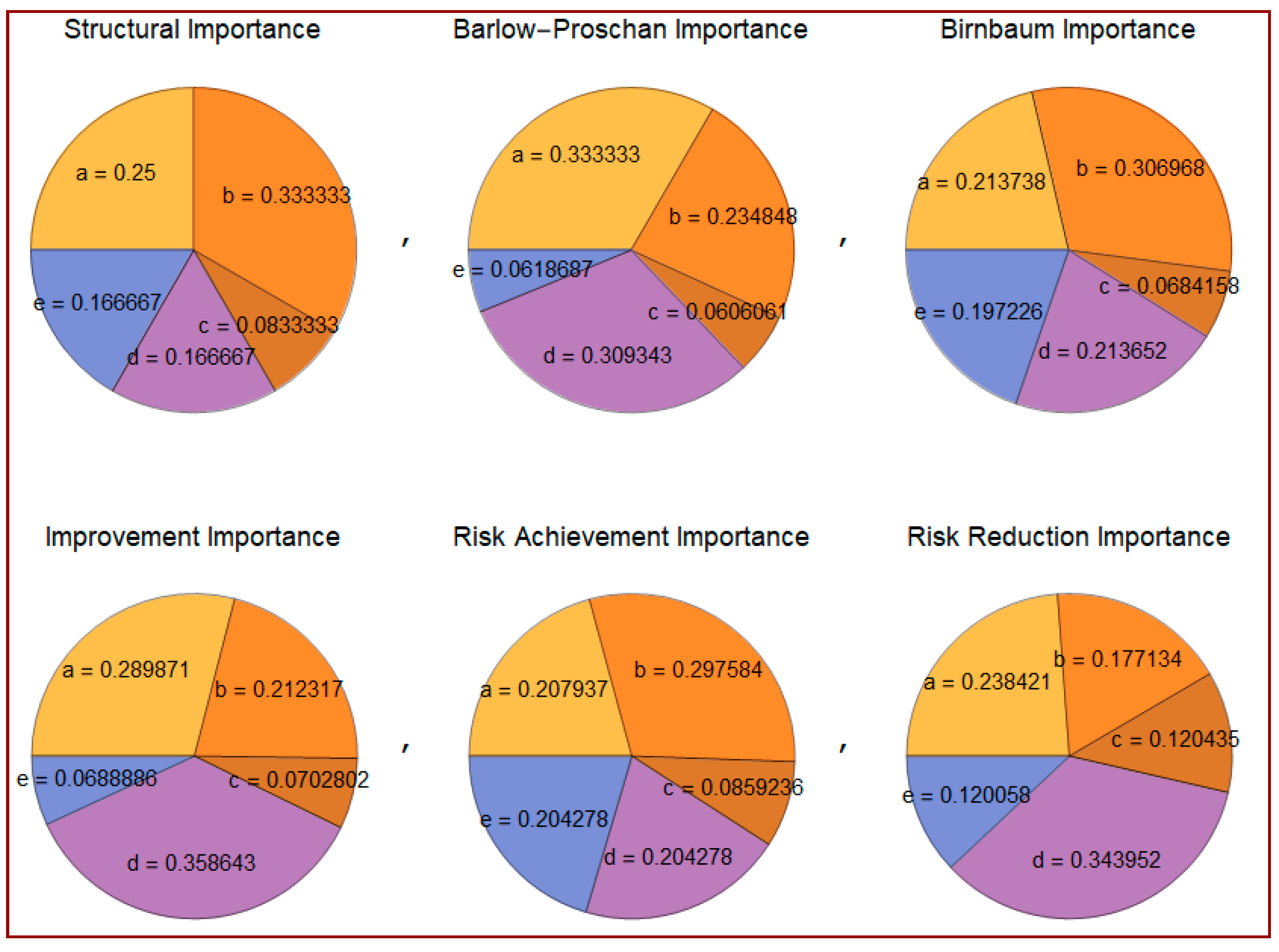
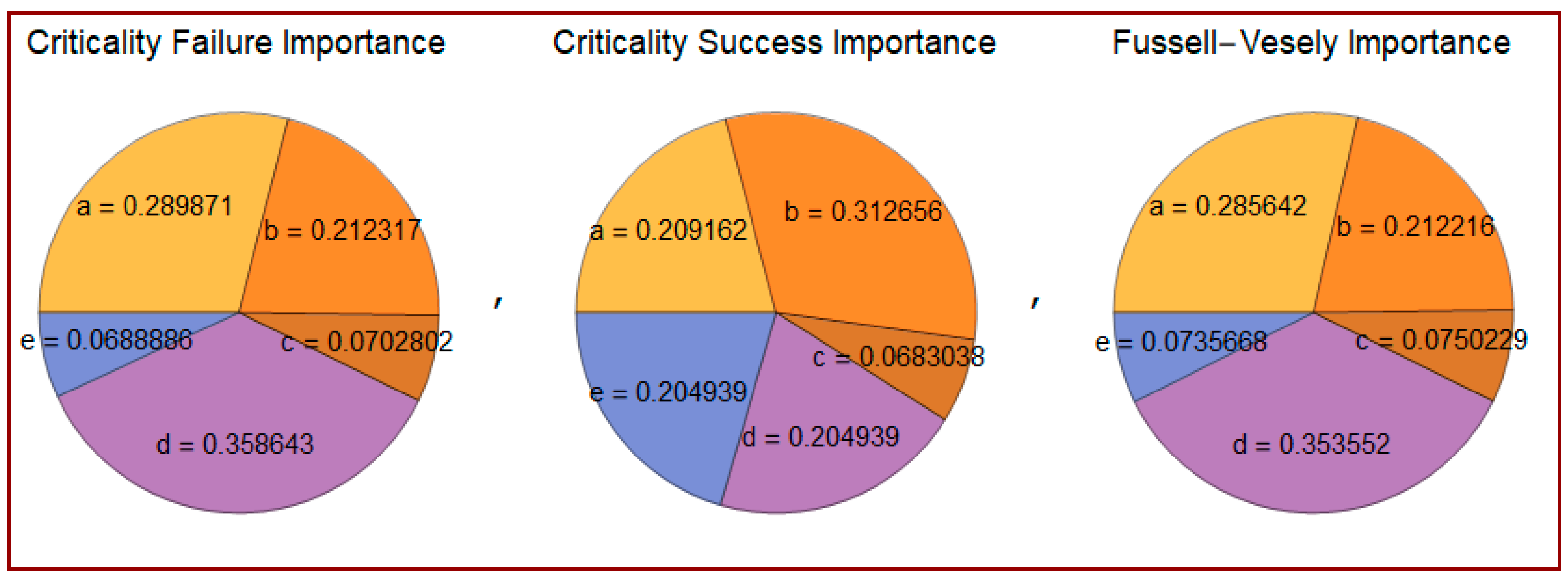
2.6. Calculation of the Components’ Importance Measures
2.7. Estimation of the Optimum Maintenance Plan
2.7.1. Inputs
- The structure of the system.
- The life cycle of the system, more specifically the timeframe of the maintenance plan of the system.
- The reliability distribution of each component.
- The importance measure which is going to be used as an objective criterion to determine the component which will be replaced on a preventive basis during the implementation of the scheduled maintenance of the system. The specified importance measure will be cost-adjusted according to the cost inputs that follow.
- The cost of the scheduled preventive replacement of each component with a brand new one. In other words, the cost of scheduled preventive maintenance for each component after which the cumulative time of operation of the component is zero.
- The cost of the nonscheduled replacement of each component with a brand new one. In other words, the cost of nonscheduled maintenance for each component after which the cumulative time of operation of the component is zero.
- The cost of scheduled preventive replacement of all the components, at once, with brand new ones. In other words, the cost of scheduled preventive maintenance for all components simultaneously, after which the cumulative time of operation of the components is zero.
- The confidence level for the fulfilment of the nonscheduled maintenance requirements, in case of system failures.
2.7.2. Processing
| Estimate system structure function For N = 0 to 98:
|
2.7.3. Outputs
- The diagram of the procedure for which the lowest value of the criterion ‘cost/benefit’ is achieved.
- The reliability function diagram of the system for the optimum scheduled maintenance scenario.
- The average reliability of the system.
- The lowest value of the reliability of the system, at which the system has to be grounded for scheduled maintenance.
- The MTTF of the system.
- The replacement schedule for the system’s components.
- The required number of spare parts for each component, for both scheduled and nonscheduled maintenance (at the determined confidence level).
- The cost analysis for both scheduled and nonscheduled replacement of the components.
3. Exemplified Example/Results
3.1. Task
3.2. Components Replacement Cost
- Scheduled replacement of a unique component (preventive maintenance)
- Nonscheduled replacement of a unique component (corrective maintenance)
- Scheduled replacement of all the components simultaneously (preventive maintenance)
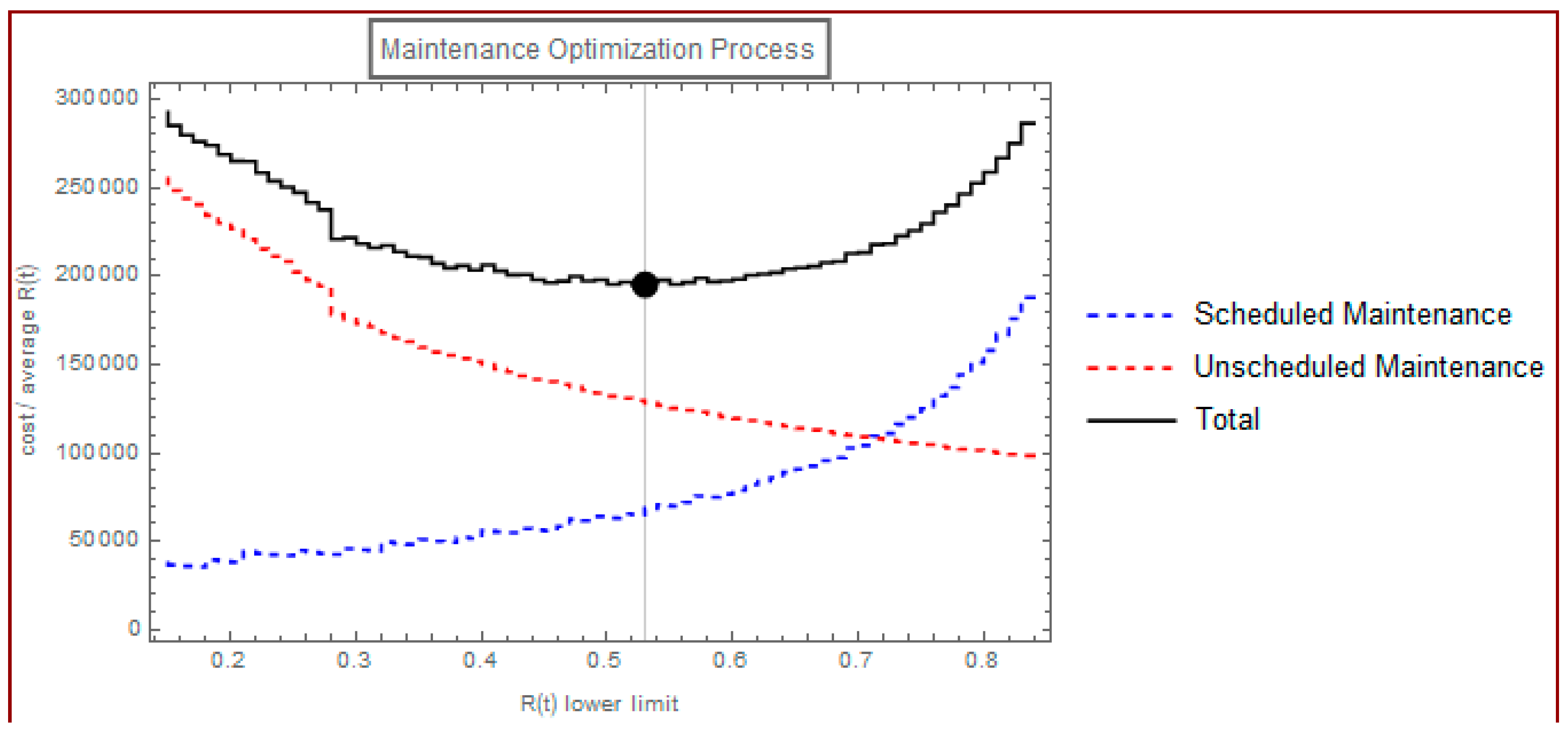
3.3. Optimization Criterion
3.4. Optimum Number of Spare Components for Scheduled Maintenance
3.5. Optimum Number of Spare Components for Non-Scheduled Maintenance
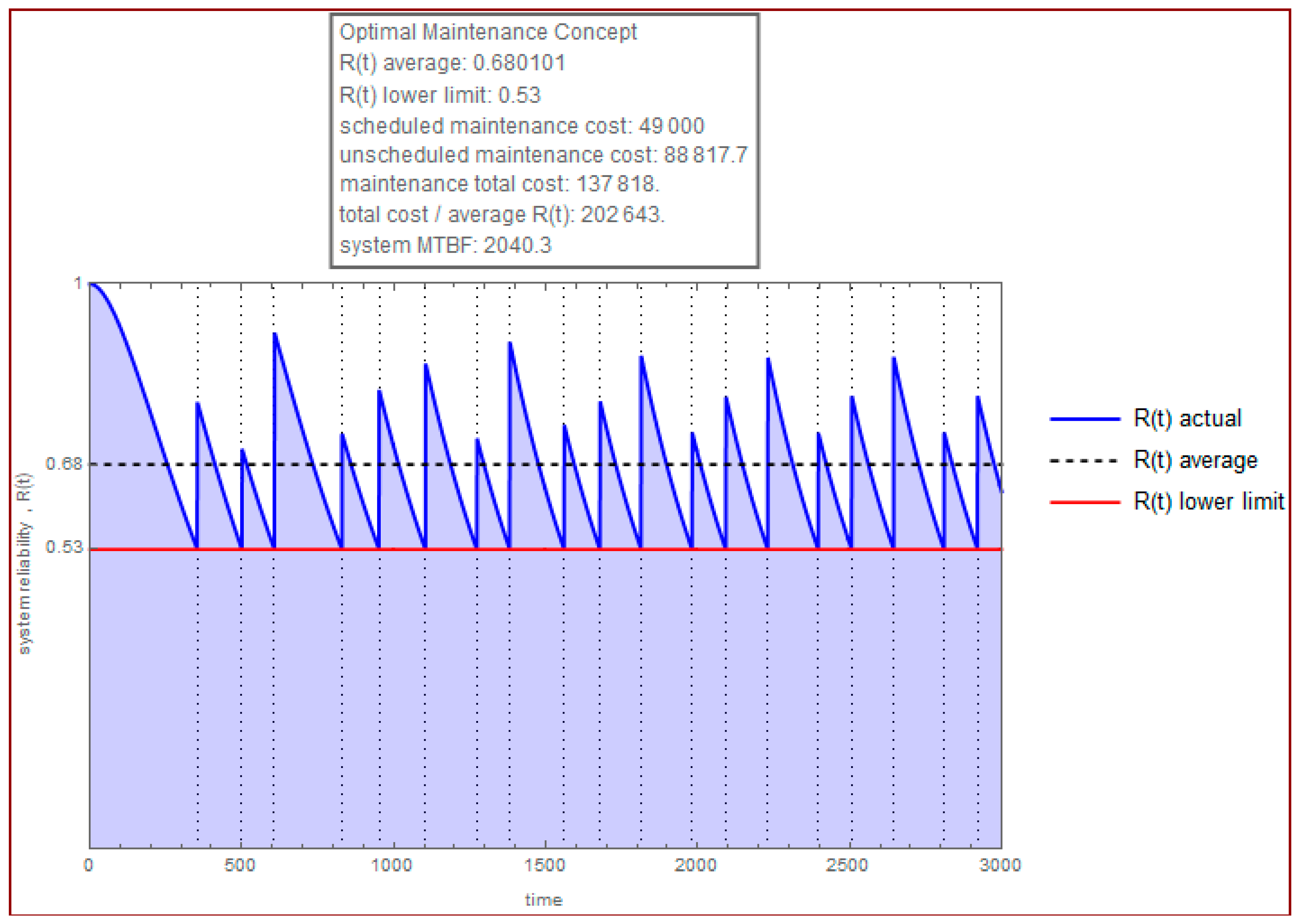
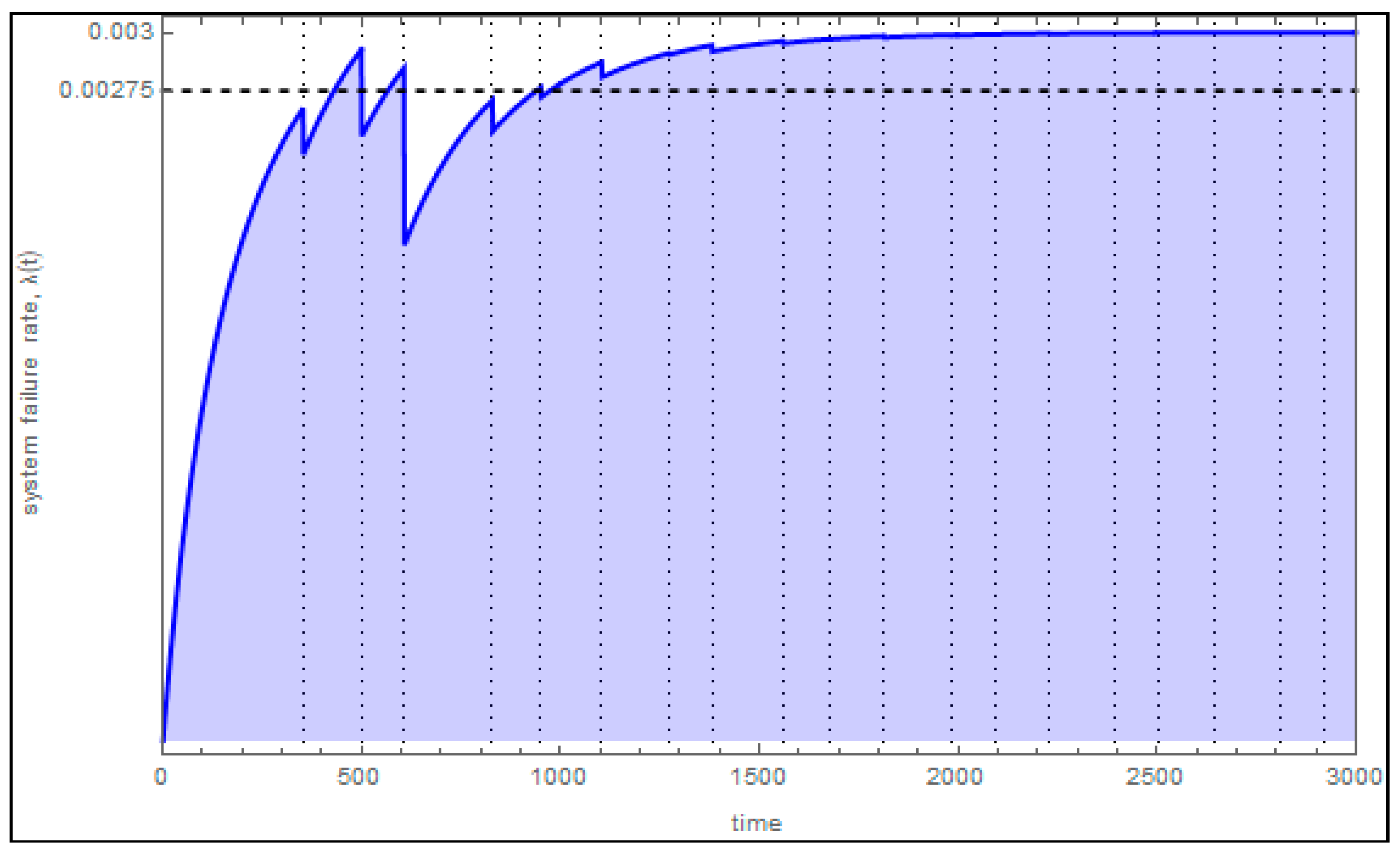
3.6. Results
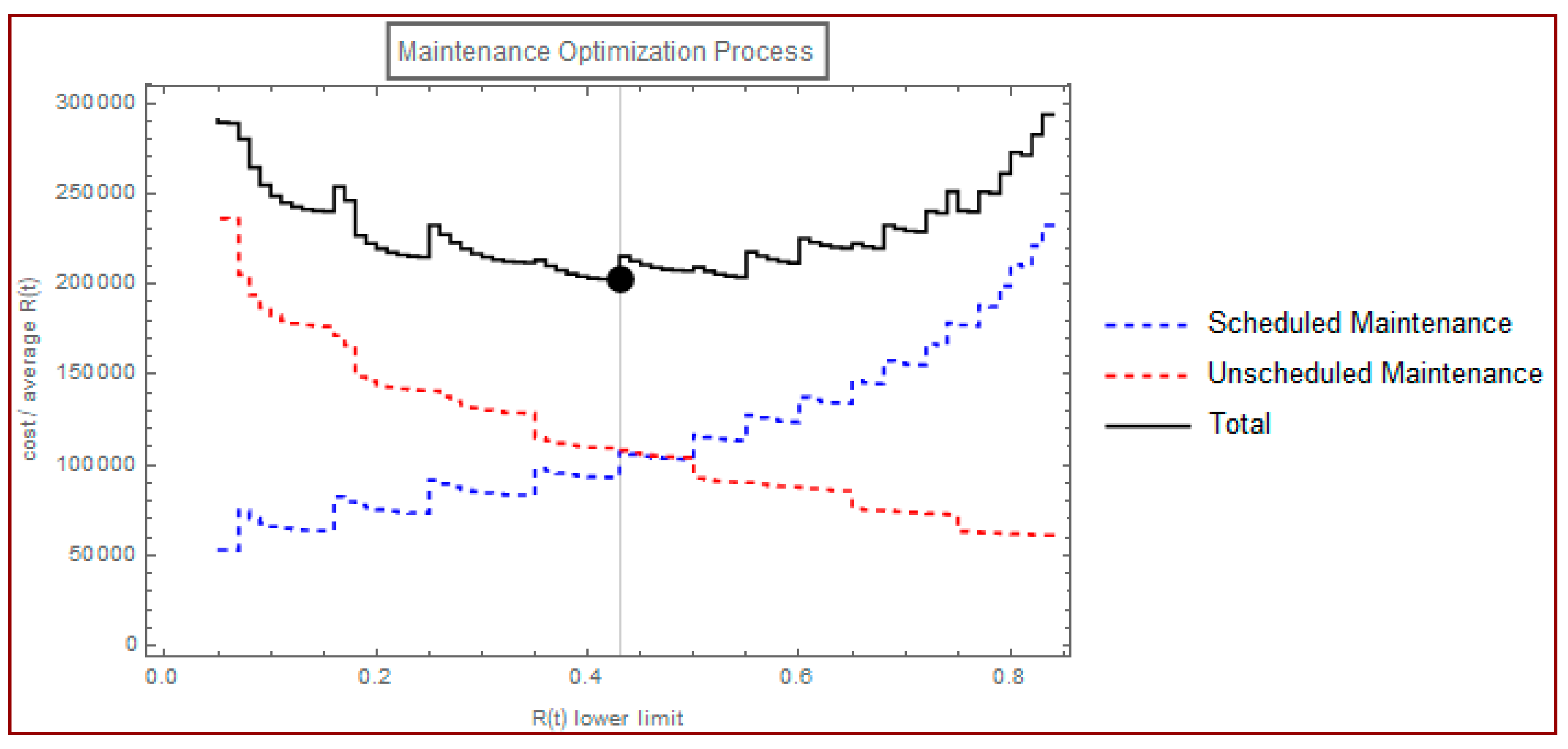
3.7. An Alternative Scenario: All Components Are Replaced Simultaneously
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Samaranayake, P.; Kiridena, S. Aircraft maintenance planning and scheduling: An integrated framework. J. Qual. Maint. Eng. 2012, 18, 432–453. [Google Scholar] [CrossRef]
- Rosenzweig, V.V.; Domitrovic, A.; Bubic, M. Planning of training aircraft flight hours. Croat. Oper. Res. Rev. (CRORR) 2010, 1, 170–179. [Google Scholar]
- Kozanidis, G.; Gavranis, A.; Kostarelou, E. Mixed integer least squares optimization for flight and maintenance planning of mission aircraft. Naval Res. Logist. 2012, 59, 212–229. [Google Scholar] [CrossRef]
- Gavranis, A.; Kozanidis, G. An exact solution for maximizing the fleet availability of a unit of aircraft subject to flight and maintenance requirements. Eur. J. Oper. Res. 2015, 242, 631–643. [Google Scholar] [CrossRef]
- Antonakis, A.S.; Giannakoglou, K.C. Optimization of military aircraft engine maintenance subject to engine part shortages using asynchronous metamodel-assisted particle swarm optimization and Monte-Carlo simulations. Int. J. Syst. Sci. Oper. Logist. 2017. [Google Scholar] [CrossRef]
- Papakostas, N.; Papachatzakis, P.; Xanthakis, V.; Mourtzis, D.; Chryssolouris, G. An approach to operational aircraft maintenance planning. Decis. Support Syst. 2010, 48, 604–612. [Google Scholar] [CrossRef]
- Cheung, A.; Ip, W.H.; Lu, D. Expert system for aircraft maintenance services industry. J. Qual. Maint. Eng. 2005, 11, 348–358. [Google Scholar] [CrossRef]
- Joo, S.J. Scheduling preventive maintenance for modular designed components: A dynamic approach. Eur. J. Oper. Res. 2009, 192, 512–520. [Google Scholar] [CrossRef]
- Gustavsson, M.P.; Patriksson, M.; Stomberg, A.B.; Wojciechowski, A.; Onnheim, M. Preventive maintenance scheduling of multi-component systems with interval costs. Comput. Ind. Eng. 2014, 76, 390–400. [Google Scholar] [CrossRef]
- Vianna, W.O.L.; Yoneyama, T. Predictive maintenance optimization for aircraft redundant systems subjected to multiple wear profiles. IEEE Syst. J. 2018, 12, 1170–1181. [Google Scholar] [CrossRef]
- Office of the Secretary of Defense. Cost Assessment and Program Evaluation; Office of the Secretary of Defense: Washington, DC, USA, 2014.
- Department of Defense. MIL-STD-3034 ‘Reliability-Centered Maintenance (RCM) Process’; Department of Defense: Washington, DC, USA, 2011.
- Wojciechowski, A. On the Optimization of Opportunistic Maintenance. Thesis for the Degree of Licentiate of Engineering, Chalmers University of Gothenburg, Gothenburg, Sweden, 2010. [Google Scholar]
- Deputy under Secretary for Logistics and Materiel Readiness. Memorandum ‘Condition Based Maintenance Plus; Deputy under Secretary for Logistics and Materiel Readiness: Washington, DC, USA, 2002.
- SAE JA1011 ‘Evaluation criteria for Reliability-Centered Maintenance Processes; SAE International: Warrendale, PA, USA, 2009.
- API Recommended Practice 580 ‘Risk Based Inspection; American Petroleum Institute: Washington, DC, USA, 2016.
- Chairman of the Joint Chiefs of Staff Manual. CJCSM 3170.01C ‘Operation of the Joint Capabilities Integration and Development System’; Chairman of the Joint Chiefs of Staff Manual: Washington, DC, USA, 2017. [Google Scholar]
- Cheok, M.C.; Parry, G.W.; Sherry, R.R. Use of importance measures in risk-informed regulatory applications. Reliab. Eng. Syst. Saf. 1998, 60, 213–226. [Google Scholar] [CrossRef]
- Vasseur, D.; Llory, M. International survey on PSA figures of merit. Reliab. Eng. Syst. Saf. 1999, 66, 261–274. [Google Scholar] [CrossRef]
- Van Der Borst, M.; Schoonakker, H. An overview of PSA importance measures. Reliab. Eng. Syst. Saf. 2001, 72, 241–245. [Google Scholar] [CrossRef]
- Vaurio, J.K. Ideas and developments in importance measures and fault-tree techniques for reliability and risk analysis. Reliab. Eng. Syst. Saf. 2010, 95, 99–107. [Google Scholar] [CrossRef]
- Vaurio, J.K. Importance measures in risk-informed decision making: Ranking, optimization and configuration control. Reliab. Eng. Syst. Saf. 2011, 96, 1426–1436. [Google Scholar] [CrossRef]
- Rocco, C.M.; Ramirez-Marquez, J.E. Innovative approaches for addressing old challenges in component importance measures. Reliab. Eng. Syst. Saf. 2012, 108, 123–130. [Google Scholar] [CrossRef]
- Wolfram Language and System Documentation Center. Available online: http://reference.wolfram.com/language/ (accessed on 25 May 2018).
- Leemis, L.M. Reliability: Probabilistic Models and Statistical Methods; Prentice Hall, Inc.: Englewood Clifs, NJ, USA, 1995; ISBN 9780137205172. [Google Scholar]
- Nicolai, R.P.; Dekker, R. Optimal Maintenance of Multi-Component Systems: A Review; Erasmus University Rotterdam, Erasmus School of Economics: Rotterdam, The Netherlands, 2006. [Google Scholar]
- Wang, H. A survey of maintenance policies of deteriorating systems. Eur. J. Oper. Res. 2002, 139, 469–489. [Google Scholar] [CrossRef]
- Wang, H.; Pham, H. Availability and optimal maintenance of series systems subject to imperfect repair and correlated failure and repair. Eur. J. Oper. Res. 2006, 17, 1706–1722. [Google Scholar] [CrossRef]
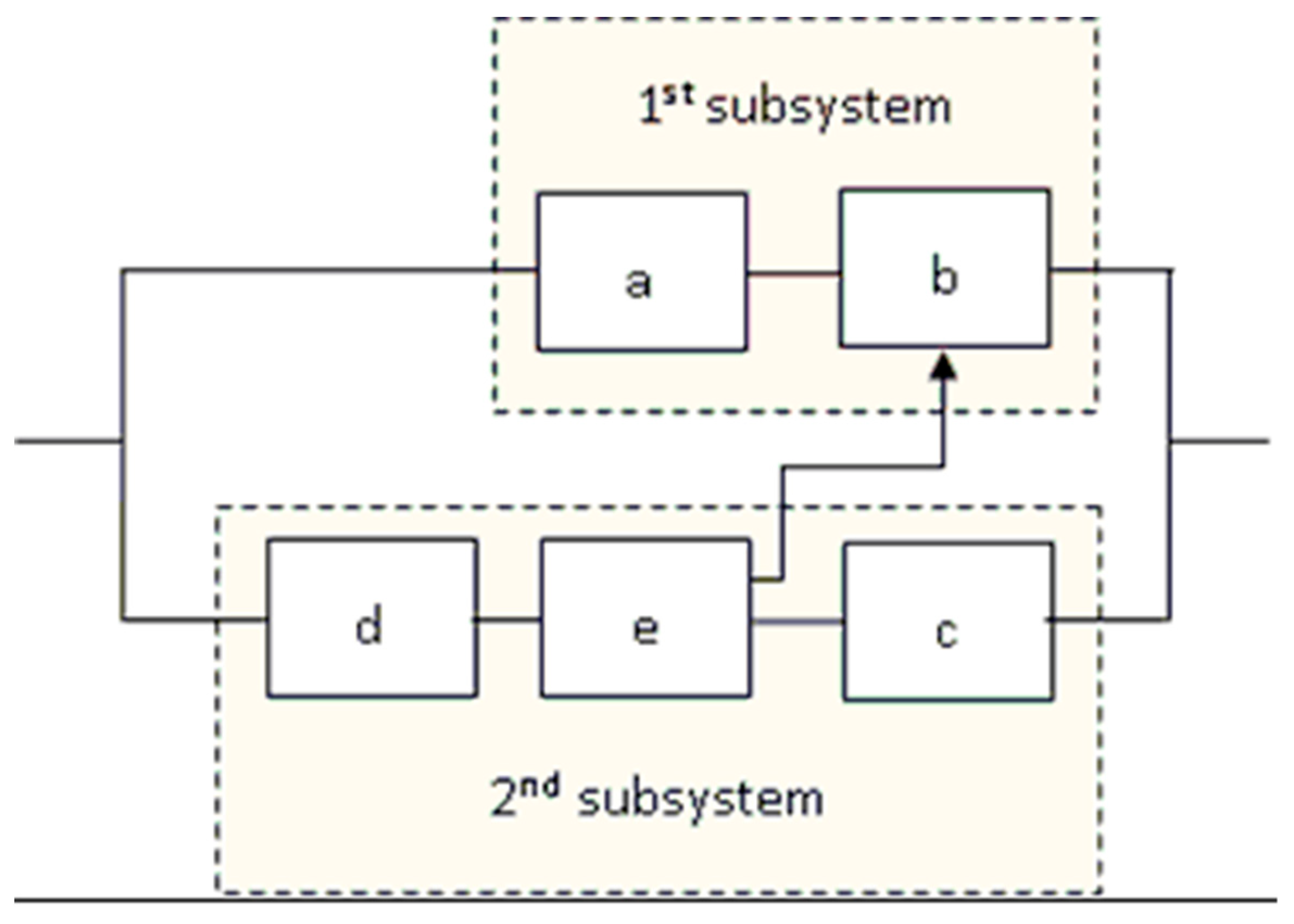
| Notation | Description |
|---|---|
| System reliability function | |
| System unreliability function | |
| Component reliability function | |
| Component unreliability function | |
| System reliability function, whereas (perfect component ) | |
| System reliability function, whereas (failed component ) | |
| System unreliability function, whereas (perfect component ) | |
| System unreliability function, whereas (failed component ) |
| Component MTTF (Hours) | Component Failure Rate (Constant) | Component Reliability Function | Cost of Scheduled Replacement of a Single Component (Euros) | Cost of Unscheduled Replacement of a Single Component (Euros) |
|---|---|---|---|---|
| Part Type | Items | Cost |
|---|---|---|
| A | 5.02131 | 20,085.20 |
| B | 4.36118 | 26,167.10 |
| C | 0.462472 | 3699.78 |
| D | 2.6525 | 31,830.00 |
| E | 0.502543 | 7035.60 |
| Fails | ||
| (95.7391%) | 13 | 88,817.70 |
| Part Type | Replace at |
|---|---|
| d | 353.653 |
| b | 500.406 |
| a | 607.353 |
| a | 829.207 |
| b | 951.600 |
| a | 1104.010 |
| b | 1273.250 |
| a | 1381.720 |
| a | 1560.730 |
| b | 1678.180 |
| a | 1813.860 |
| a | 1981.150 |
| b | 2092.210 |
| a | 2230.450 |
| a | 2396.240 |
| b | 2506.640 |
| a | 2644.860 |
| a | 2810.480 |
| b | 2920.860 |
| Part Type | Items | Cost |
|---|---|---|
| a | 11 | 22,000 |
| b | 7 | 21,000 |
| c | 0 | 0 |
| d | 1 | 6000 |
| e | 0 | 0 |
| Total sched. | 19 | 49,000 |
| Part Types | Replace at |
|---|---|
| a, b, c, d, e | 429.21 |
| a, b, c, d, e | 858.42 |
| a, b, c, d, e | 1287.64 |
| a, b, c, d, e | 1716.85 |
| a, b, c, d, e | 2146.06 |
| a, b, c, d, e | 2575.27 |
| Part Type | Items | Cost |
|---|---|---|
| a | 6 | |
| b | 6 | |
| c | 6 | |
| d | 6 | |
| e | 6 | |
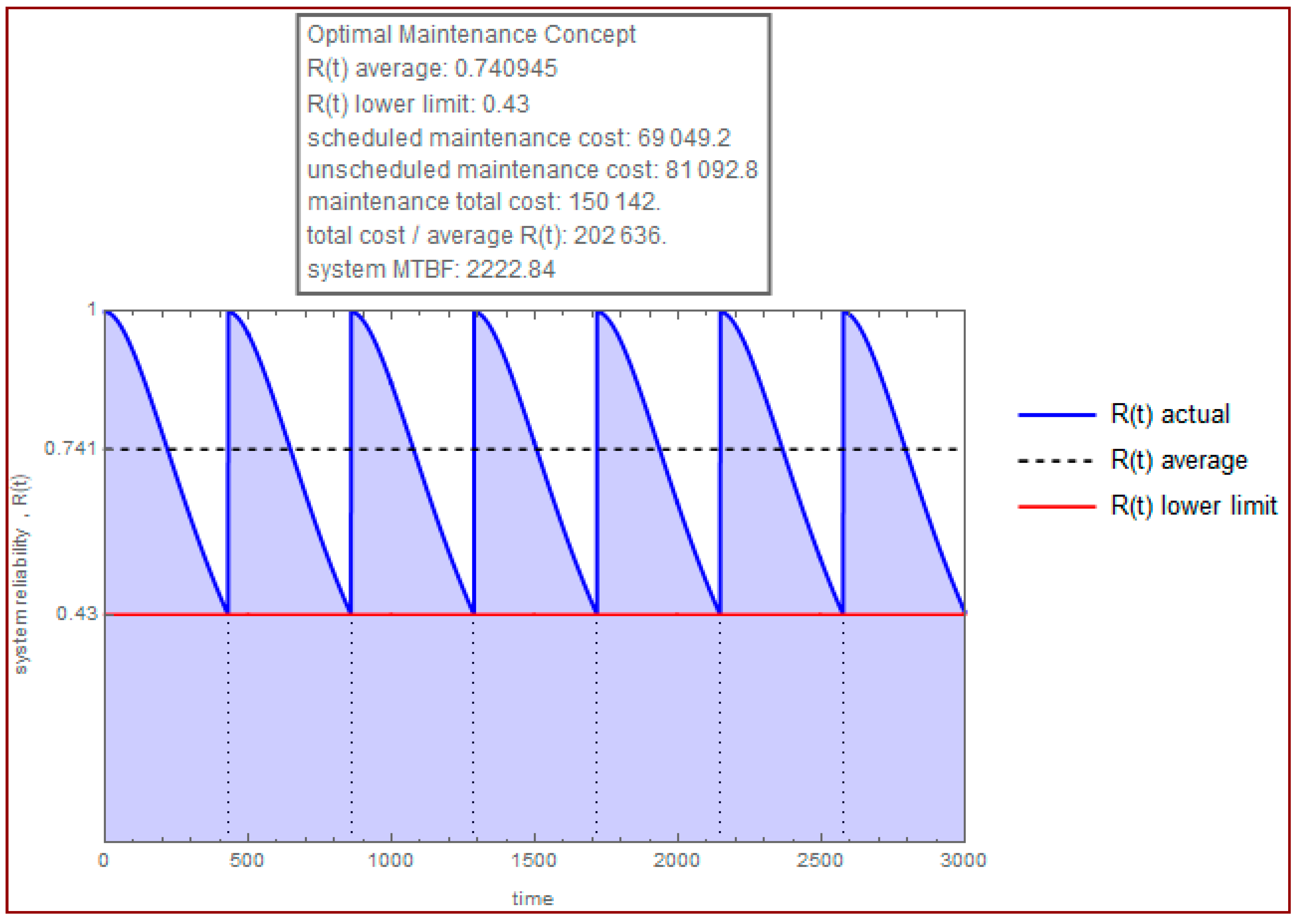
| Total sched. | 30 | 69,049.20 |
| Part Type | Items | Cost |
|---|---|---|
| a | 3.200540 | 12,802.10 |
| b | 1.983480 | 11,900.90 |
| c | 0.618516 | 4948.13 |
| d | 3.661420 | 43,937.10 |
| e | 0.536043 | 7504.60 |
| Fails. | 10 | 81,092.80 |
| Initial Scenario | Alternative Scenario | |||||
| Average reliability | 0.68 | 0.74 | ||||
| Reliability lower limit | 0.53 | 0.43 | ||||
| Cost of scheduled maintenance | 49,000 | 69,049 | ||||
| Cost of unscheduled maintenance | 88,817 | 81,093 | ||||
| Total maintenance cost | 137,818 | 150,142 | ||||
| Total maintenance cost/average reliability | 202,643 | 202,636 | ||||
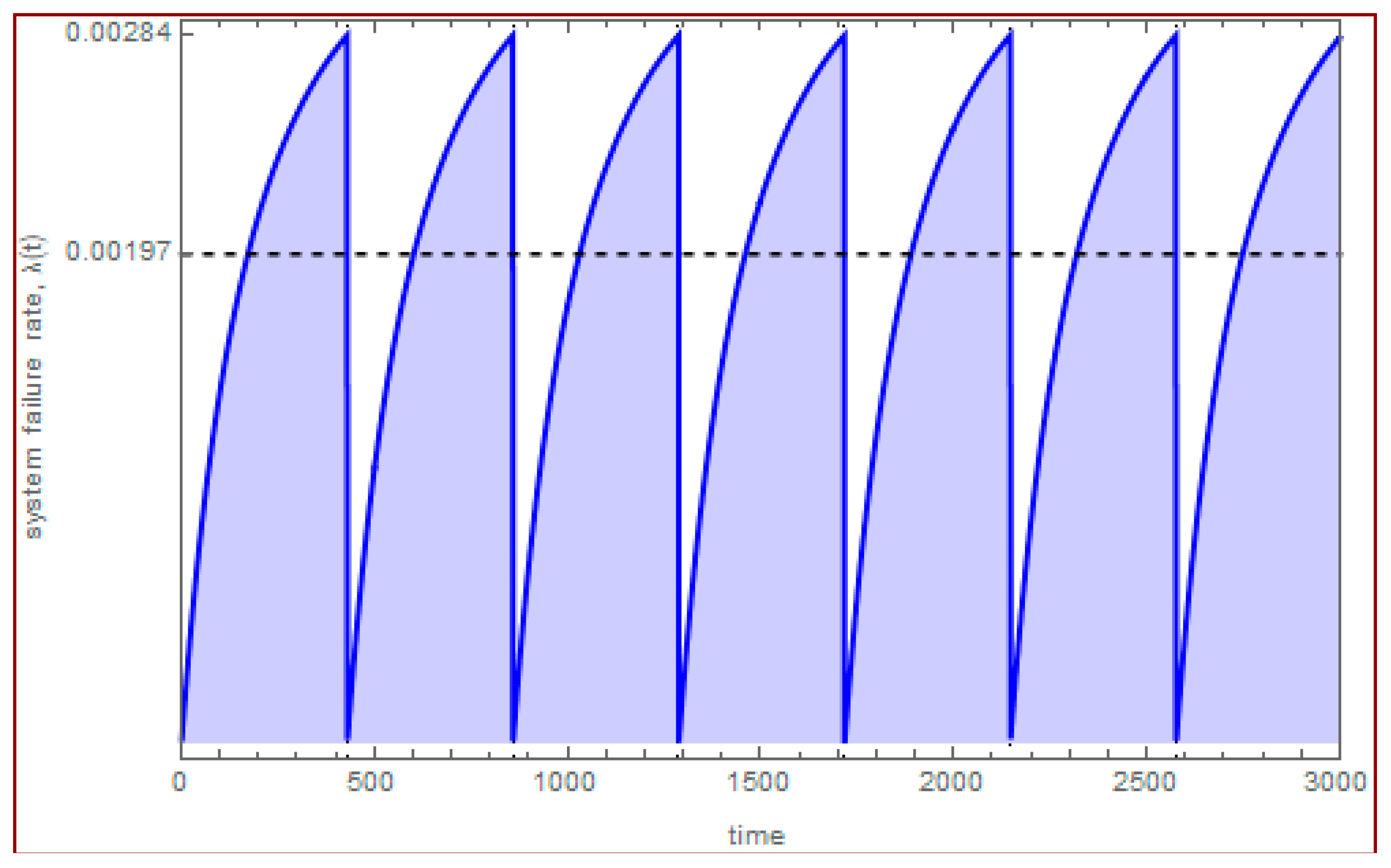
| Average failure rate per 1000 h of operation | 2.75 | 1.97 | ||||
| MTTF | 2040 | 2223 | ||||
| Component Types | Sched. | Unsched. | Total | Sched. | Unsched. | Total |
| A | 11 | 5.0 | 16.0 | 6 | 3.2 | 9.2 |
| B | 7 | 4.4 | 11.4 | 6 | 2.0 | 8.0 |
| c | 0.5 | 0.5 | 6 | 0.6 | 6.6 | |
| d | 1 | 2.7 | 3.7 | 6 | 3.7 | 9.7 |
| e | 0.5 | 0.5 | 6 | 0.5 | 6.5 | |
| Total | 19 | 13 | 32 | 30 | 10 | 40 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bozoudis, M.; Lappas, I.; Kottas, A. Use of Cost-Adjusted Importance Measures for Aircraft System Maintenance Optimization. Aerospace 2018, 5, 68. https://doi.org/10.3390/aerospace5030068
Bozoudis M, Lappas I, Kottas A. Use of Cost-Adjusted Importance Measures for Aircraft System Maintenance Optimization. Aerospace. 2018; 5(3):68. https://doi.org/10.3390/aerospace5030068
Chicago/Turabian StyleBozoudis, Michail, Ilias Lappas, and Angelos Kottas. 2018. "Use of Cost-Adjusted Importance Measures for Aircraft System Maintenance Optimization" Aerospace 5, no. 3: 68. https://doi.org/10.3390/aerospace5030068
APA StyleBozoudis, M., Lappas, I., & Kottas, A. (2018). Use of Cost-Adjusted Importance Measures for Aircraft System Maintenance Optimization. Aerospace, 5(3), 68. https://doi.org/10.3390/aerospace5030068





