Uncertainty Management at the Airport Transit View
Abstract
1. Introduction and Motivation
2. Background and Contribution
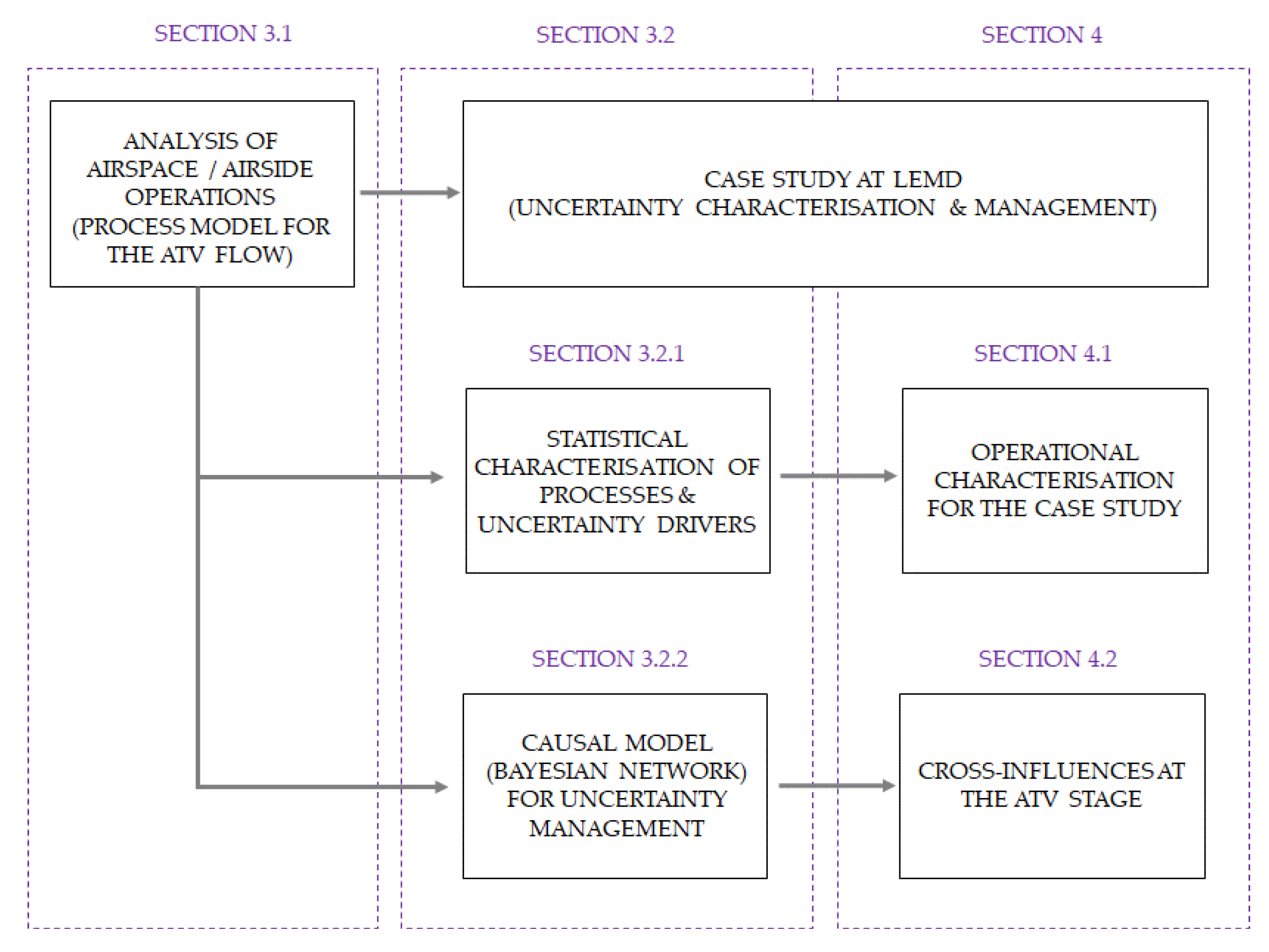
3. Materials and Methods
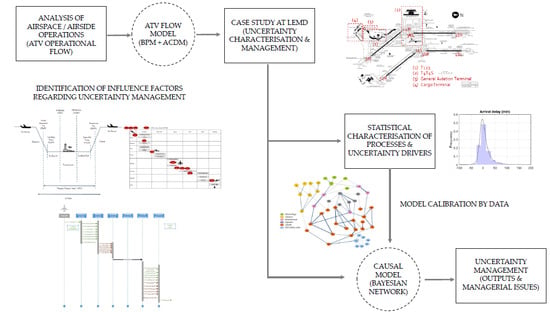
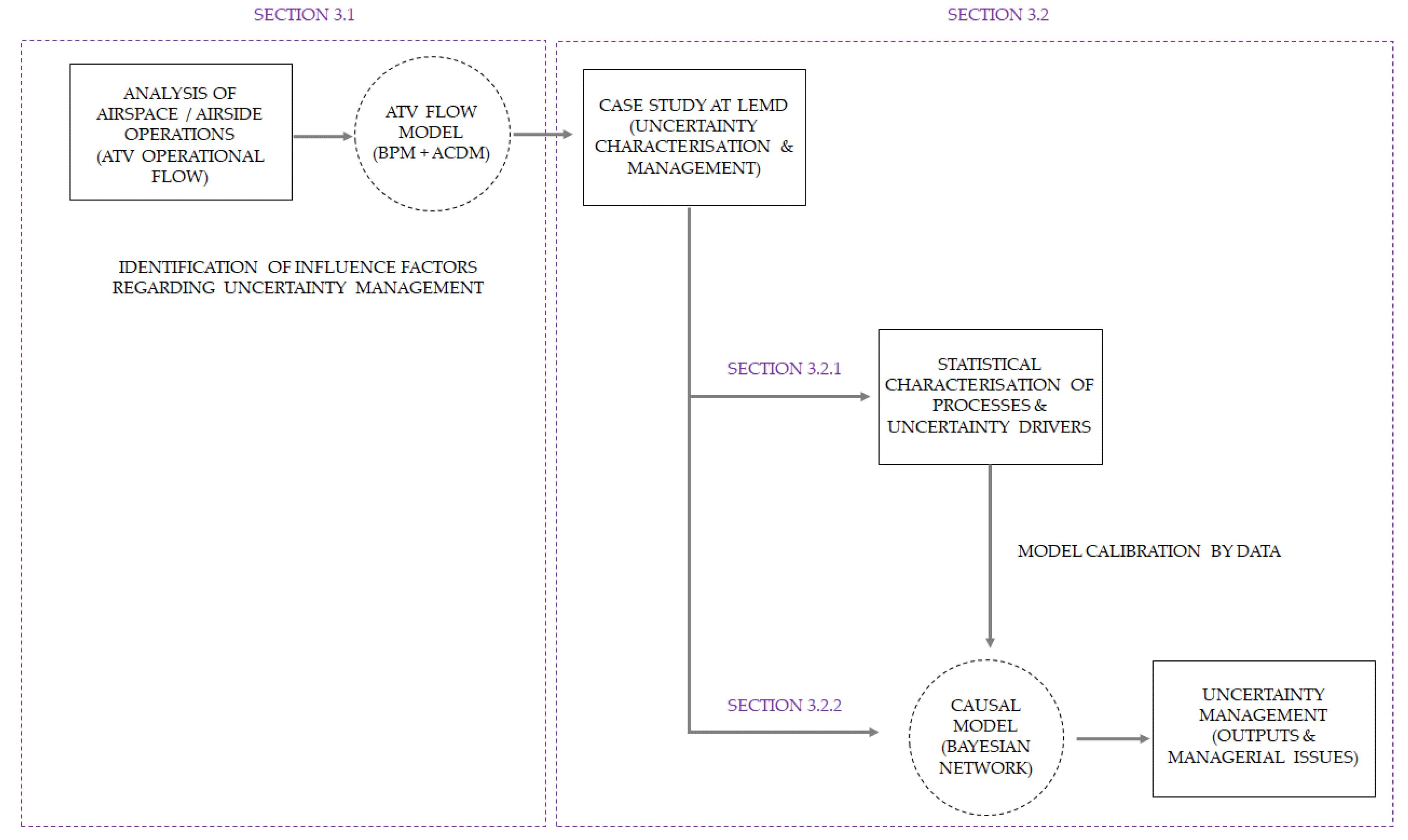
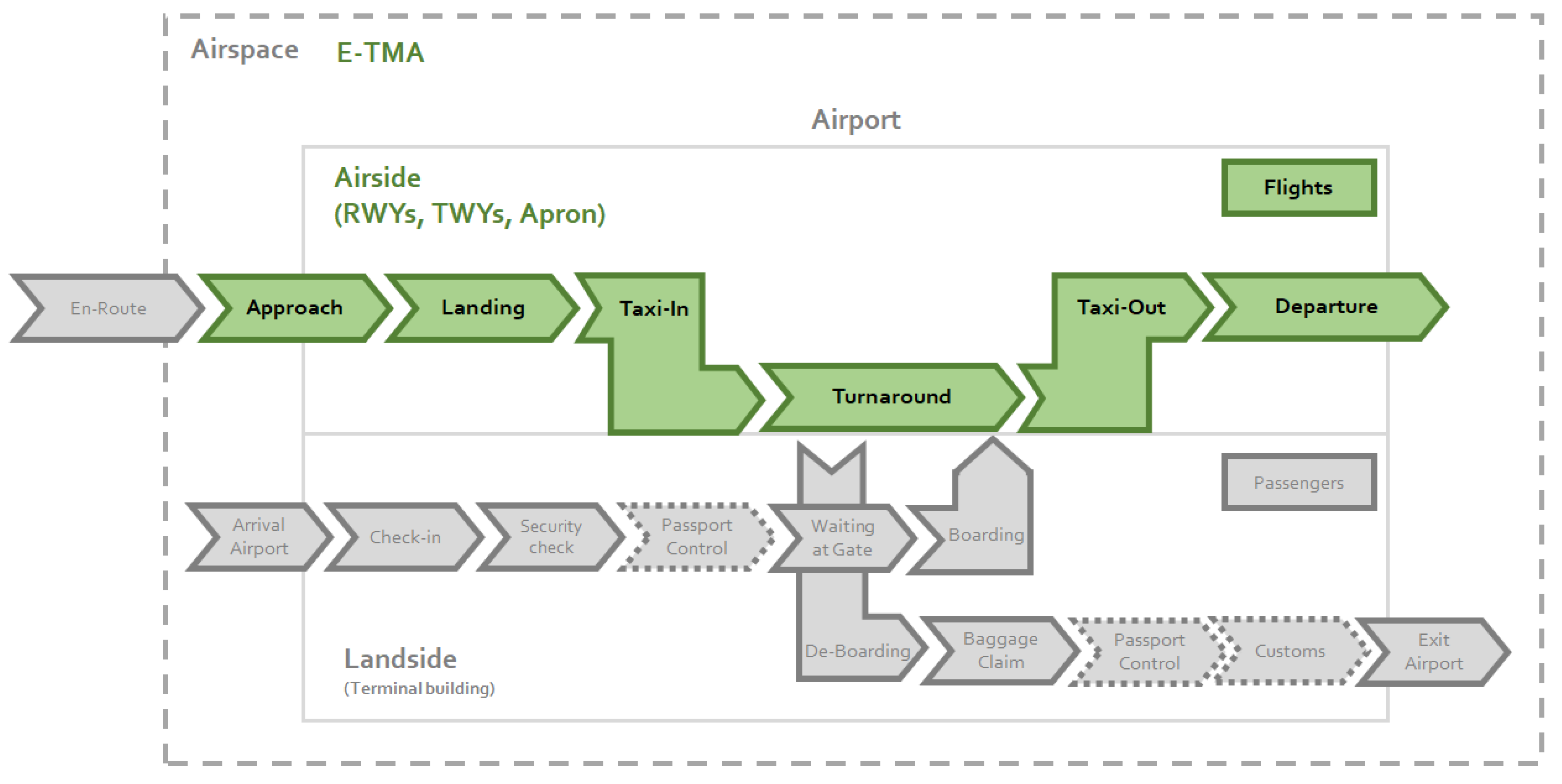
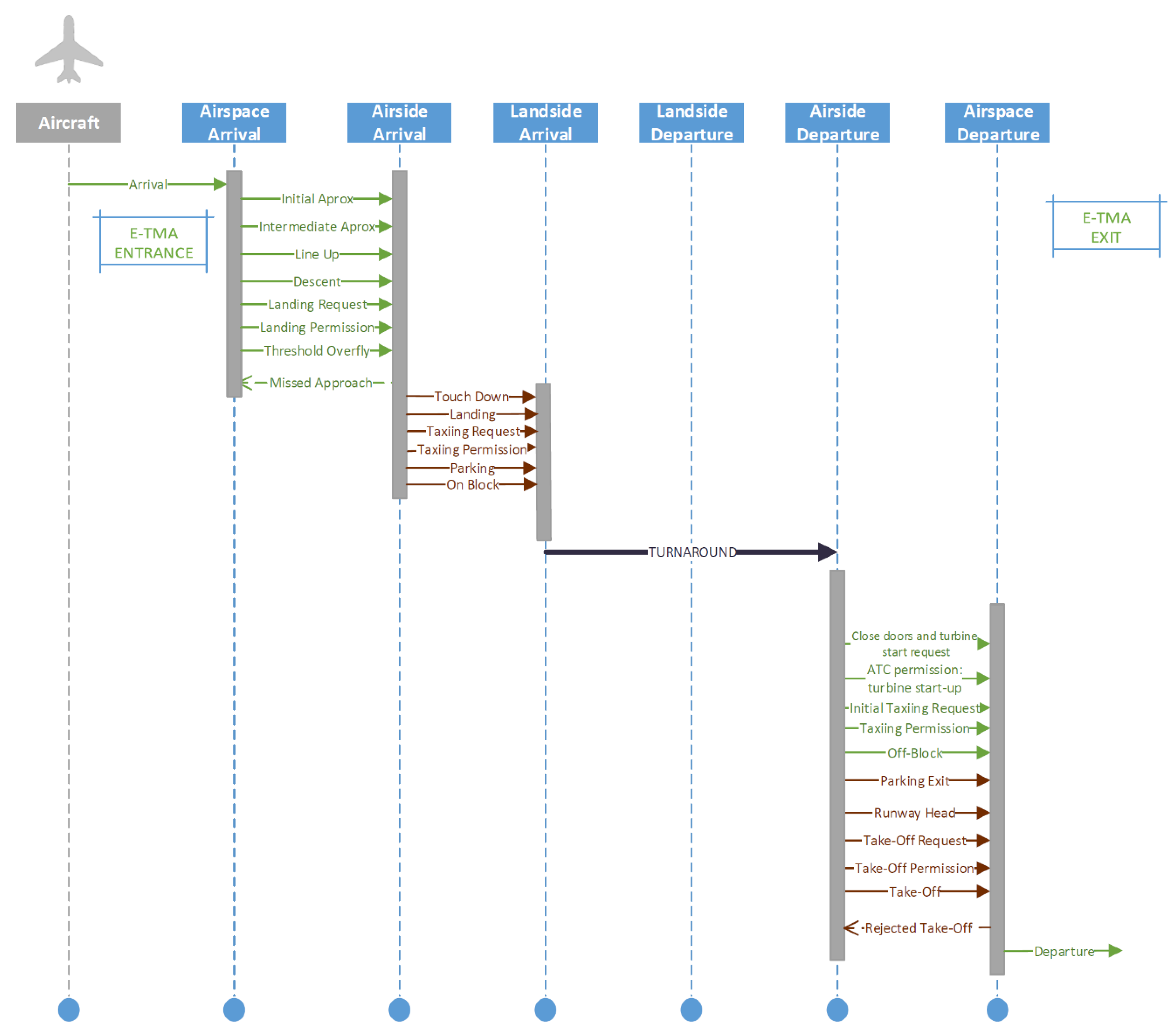
3.1. Model for Airspace/Airside Integrated Operations
- The final approach and inbound ground section of the inbound flight.
- The turnaround process section in which the inbound and the outbound flights are linked.
- The outbound ground section and the initial climb segment of the outbound flight.
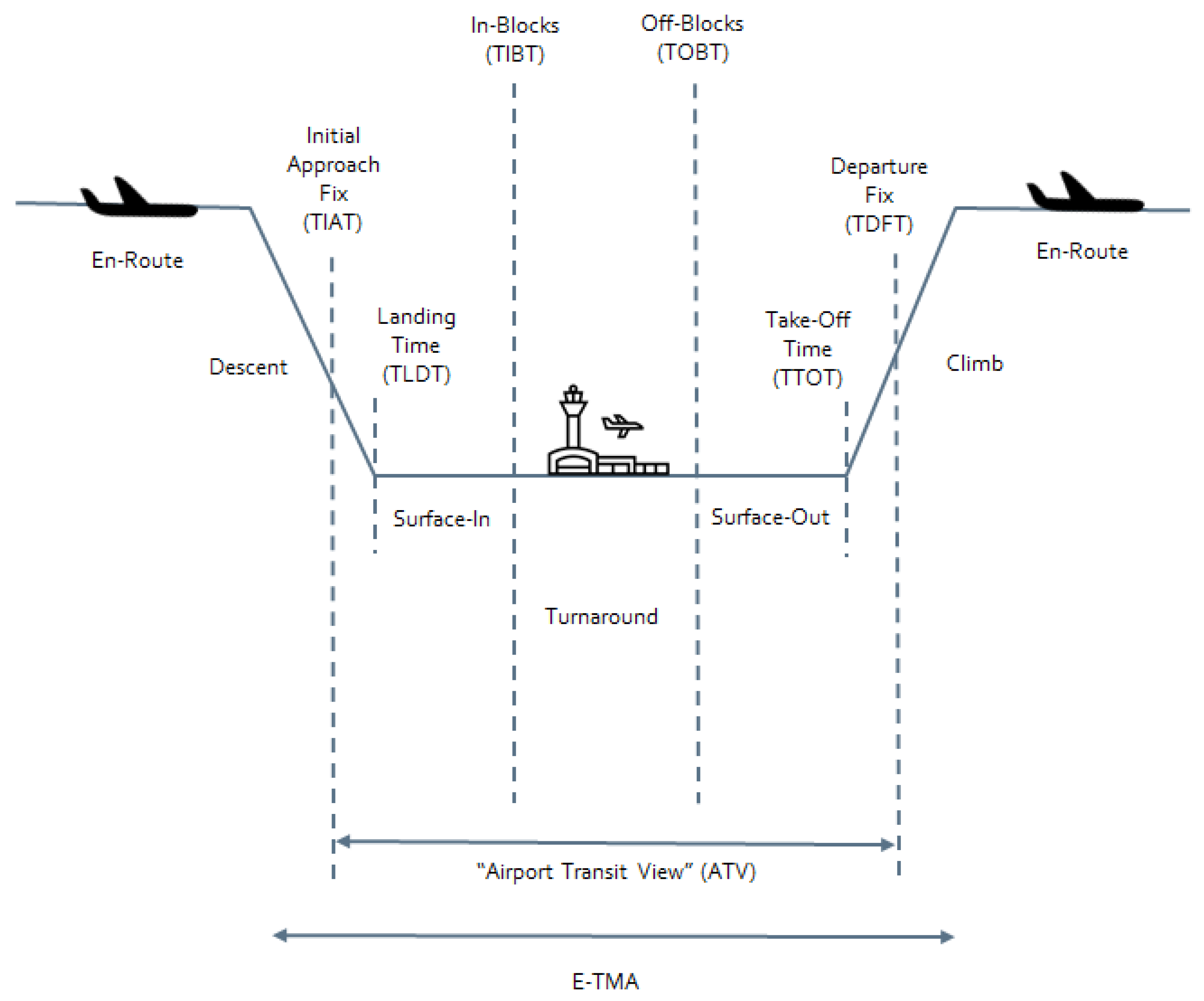
- Arrival delay: ALDT-SLDT.
- Taxi-in delay: Actual taxi-in duration (AIBT-ALDT) versus scheduled taxi-in duration (SIBT-SLDT)
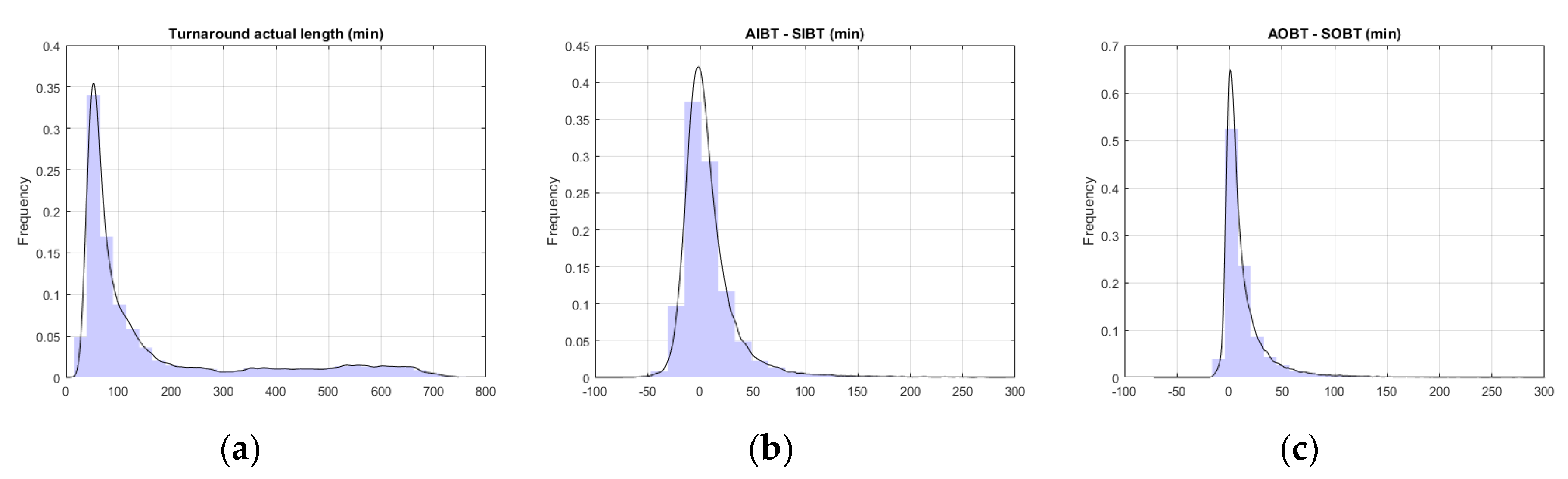
- Turnaround delay: Actual turnaround time (AIBT-AOBT) versus scheduled turnaround time (SIBT-SOBT)
- Taxi-out delay: Actual taxi-out duration (AOBT-ATOT) versus scheduled taxi-out duration (SOBT-STOT)
- Departure delay: The sum of arrival upstream delay (reactionary) and the aggregated delay at the on-ground stage: system delay (primary delay), which is composed of taxi-in, turnaround and taxi-out delays. Hence, four mutually exclusive and complementary stages were evaluated to characterise the system’s schedule adherence: arrival, taxi-in, turnaround and taxi-out.
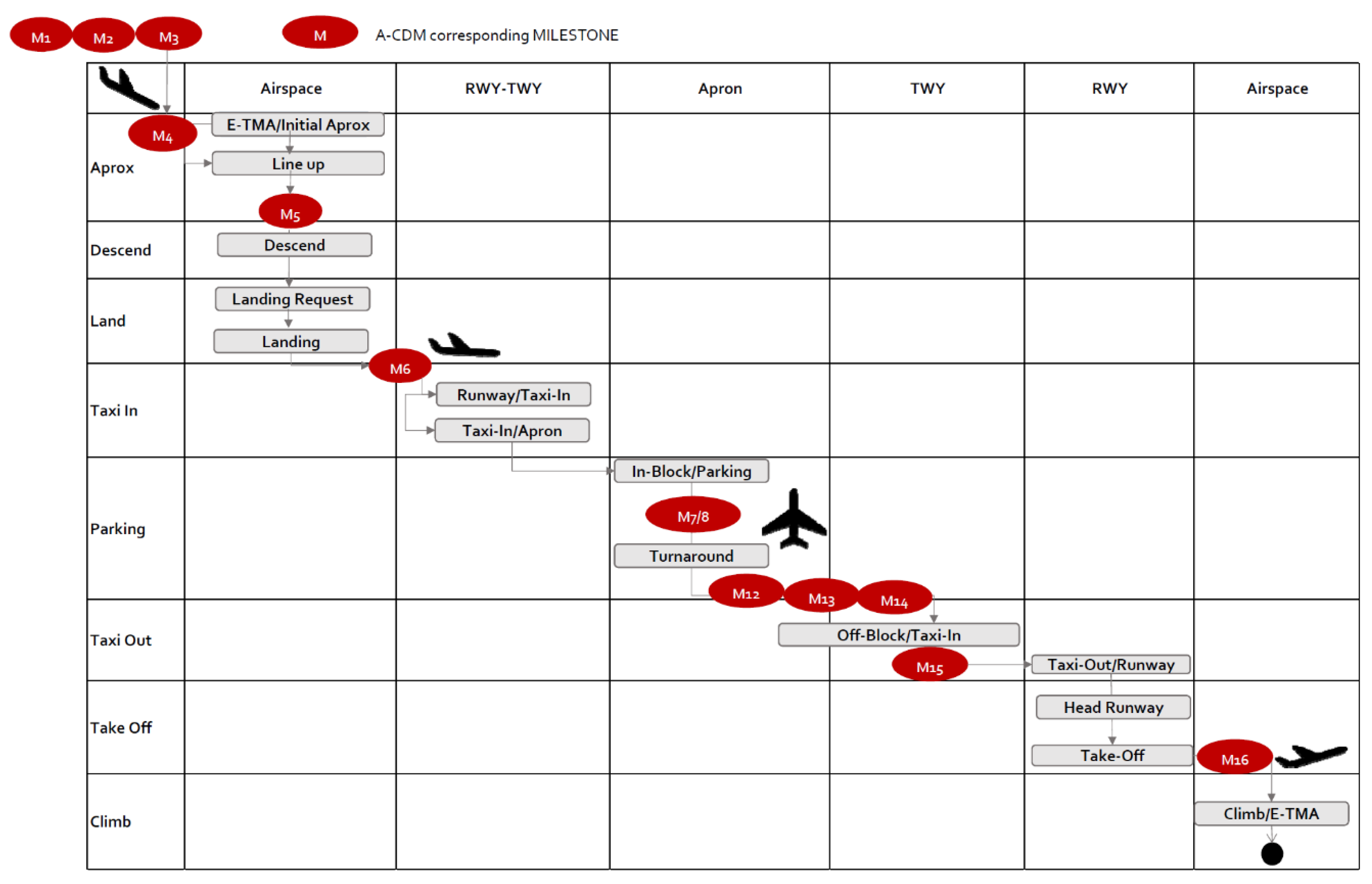
- Determine significant events to track the progress of a flight (arrival, landing, taxi-in, turnaround, taxi-out and departure) and the distribution of these key events as milestones.
- Ensure linkage between arriving and departing flights.
- Assess time efficiency performance, which is measured for each milestone or between two milestones.
- Enable early decision-making when there are disruptions to an event.
- Appraise the operational relationships and interdependences between processes that will shape the structure of the causal model for uncertainty management (identify variables).
3.2. Case Study for Uncertainty Characterisation and Management at the ATV
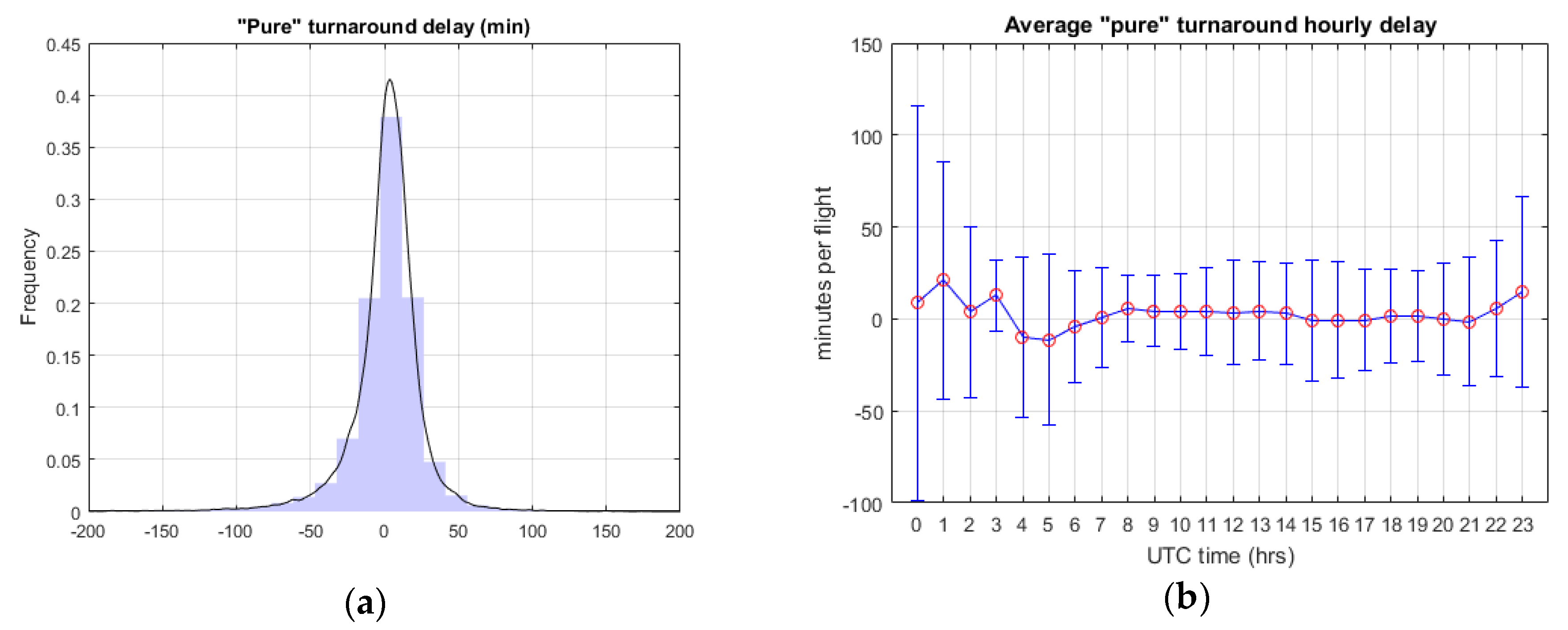
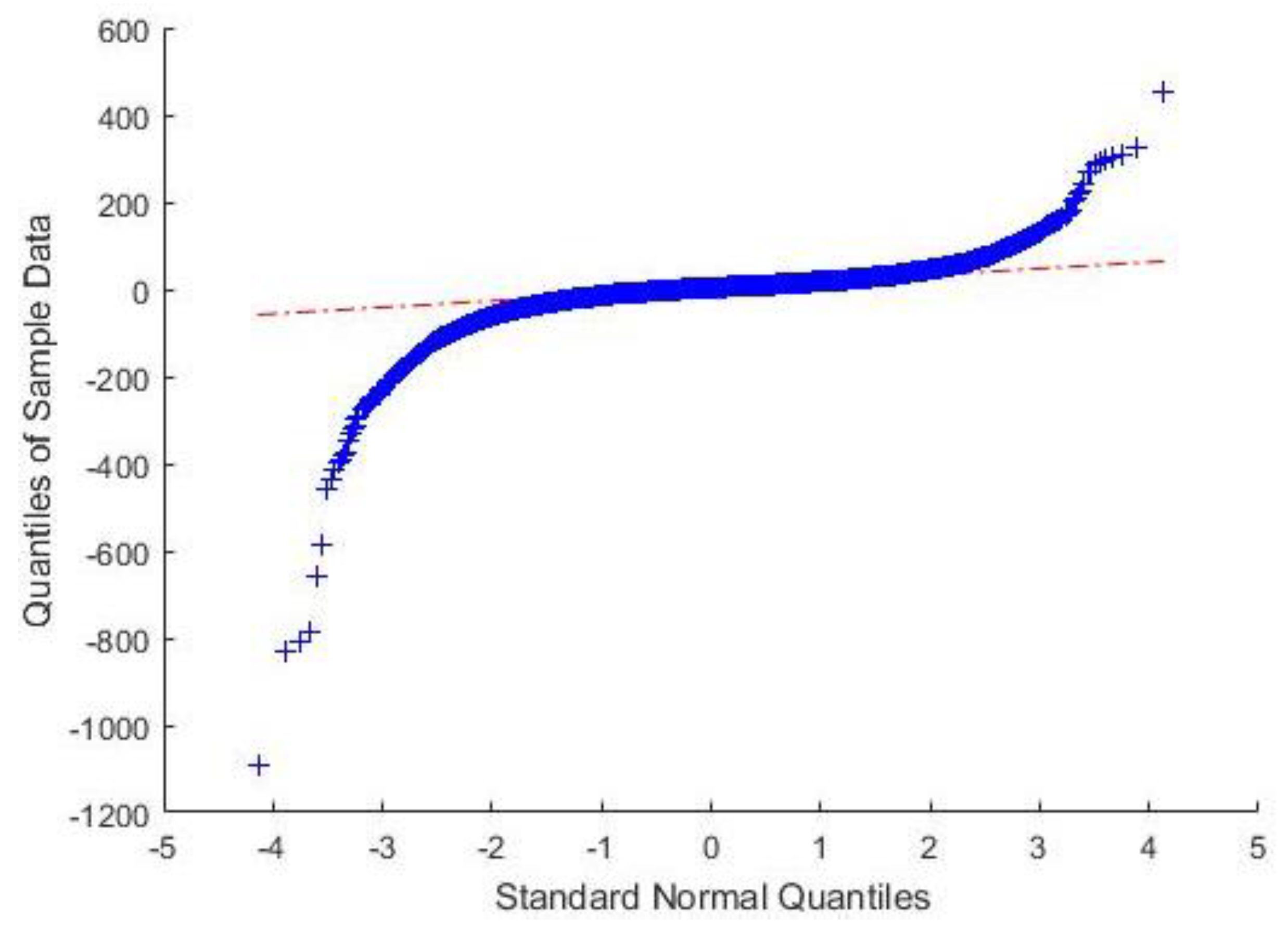
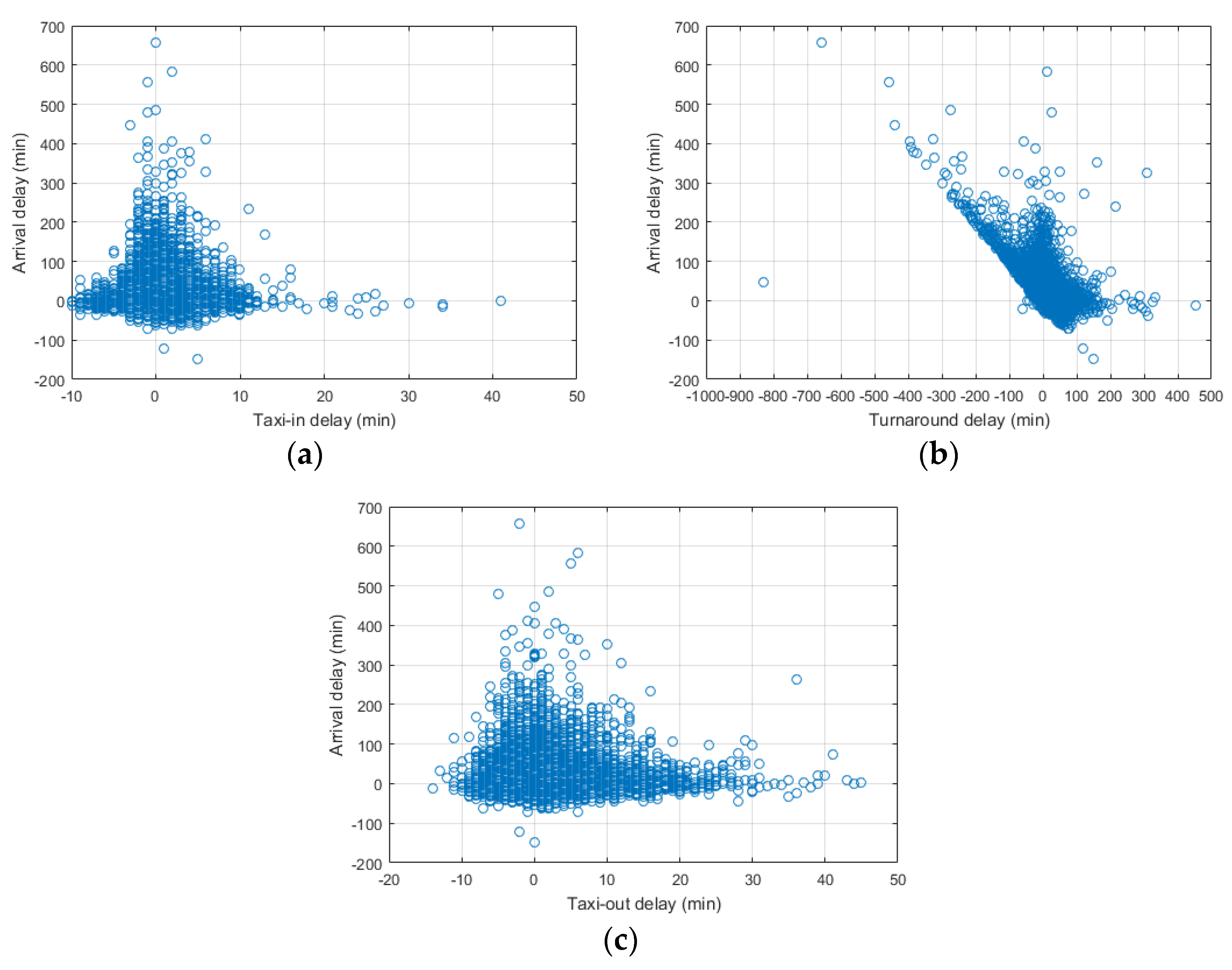
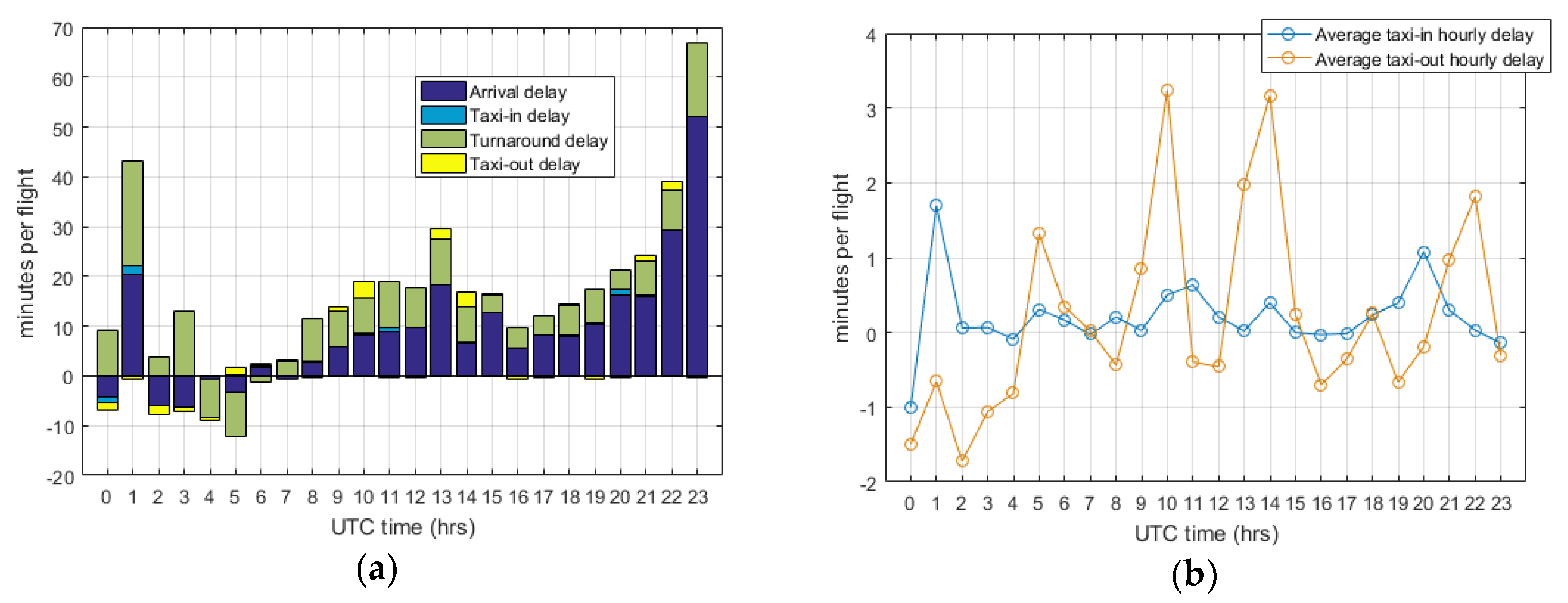
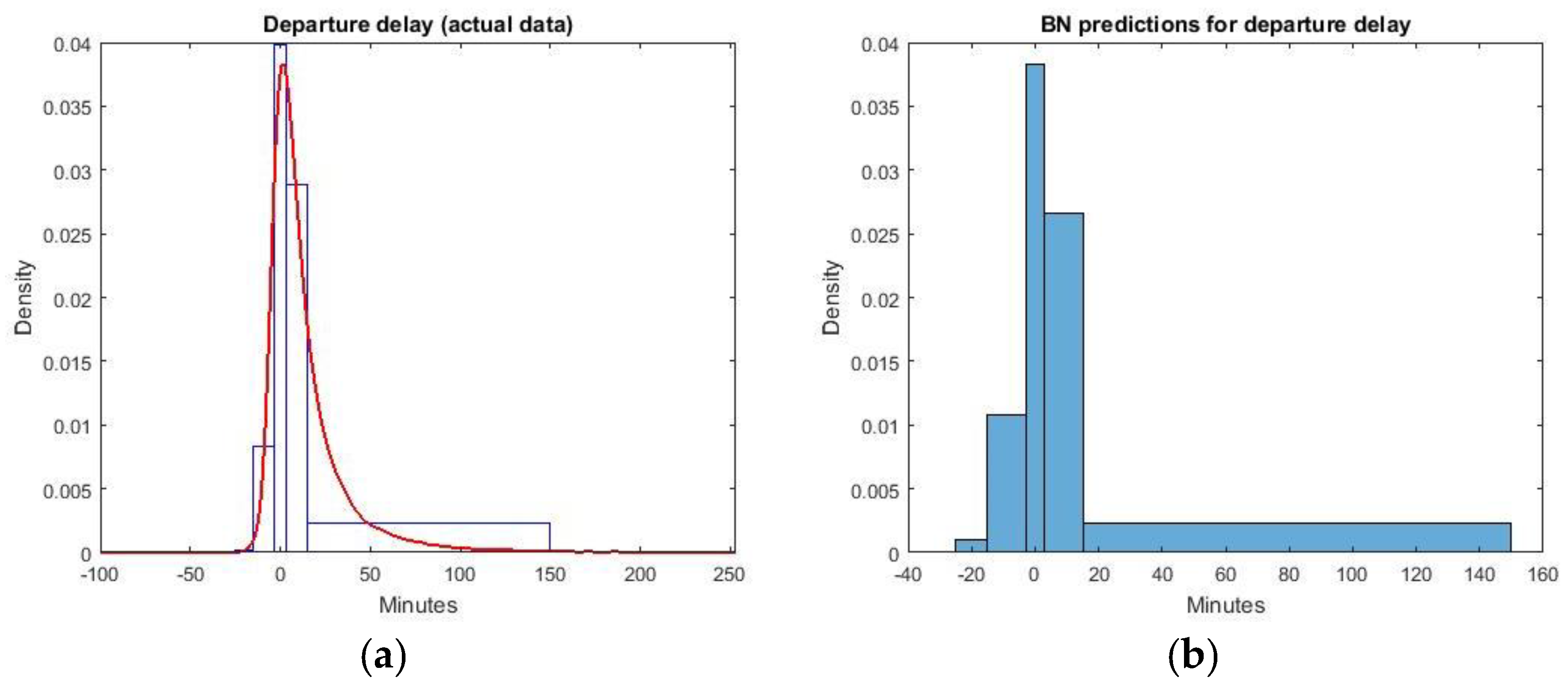
3.2.1. Statistical Characterisation of Processes and Uncertainty Drivers at the ATV
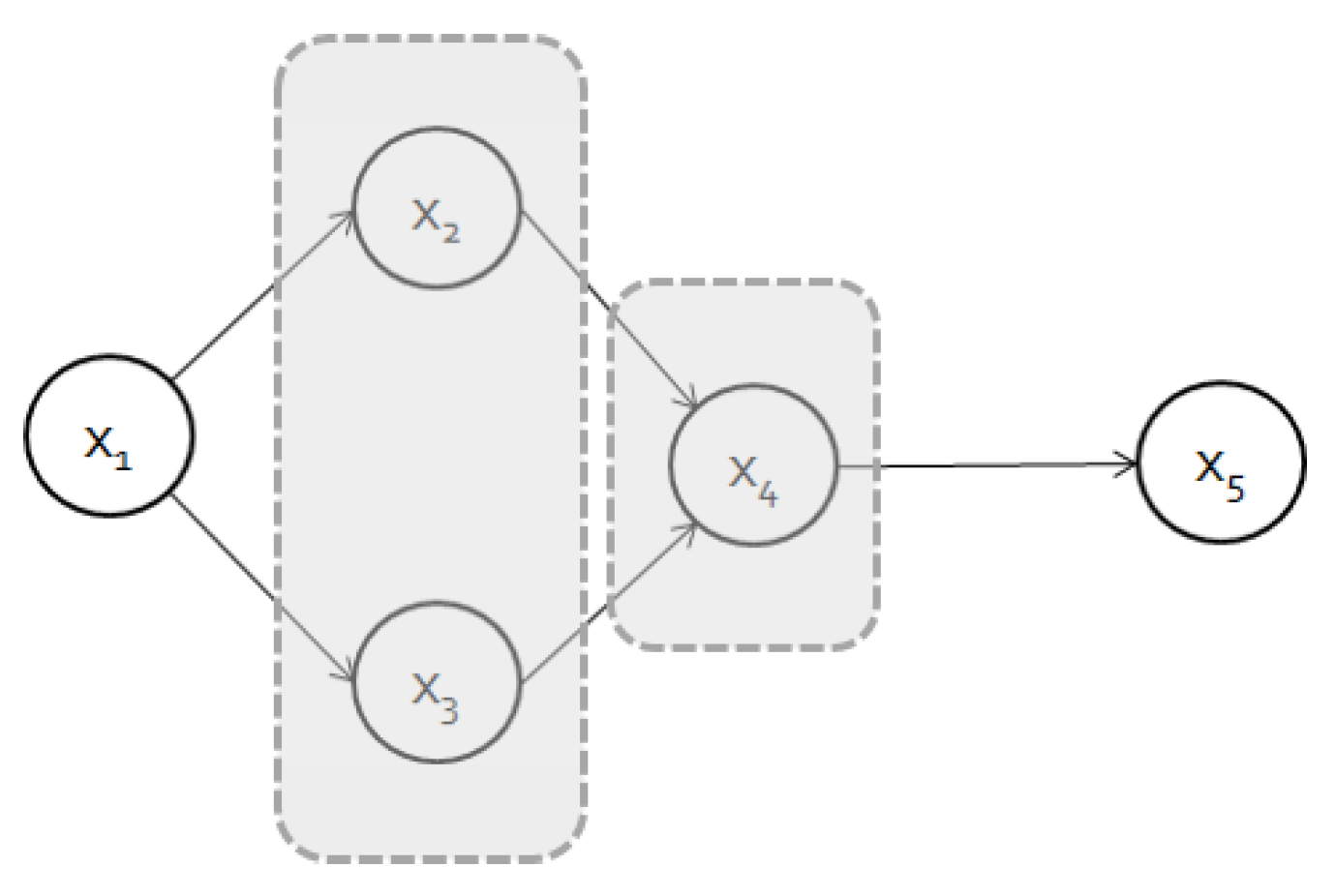
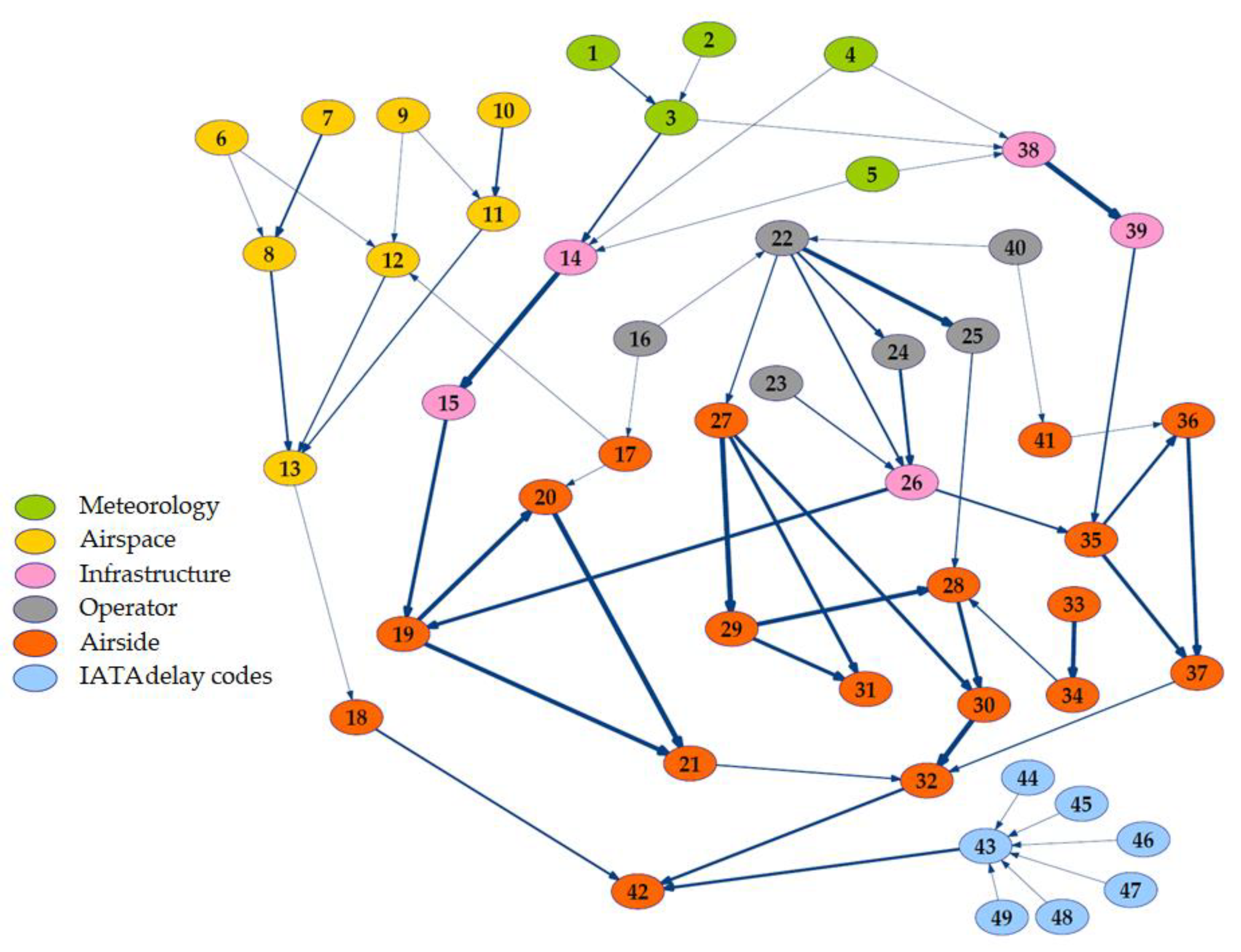
3.2.2. Causal Model for Uncertainty Management at the ATV
- Nodes 1–5 represent meteorological conditions.
- Nodes 6–13 include data regarding the arrival airspace: timestamps and congestion metrics (throughput, queues and holdings).
- Nodes 14–15, 26 and 38–39 illustrate infrastructure information.
- Nodes 16, 22–25 and 40 refer to operator, aircraft, route and flight data.
- Nodes 17–21, 27–37 and 41–42 include data regarding airside operational times and regulations.
- Nodes 43–49 represent delay causes according to the IATA coding system [74].
- Scenario 1 (forward/inter-causal scenario). The model predicts departure delay (output-child node) by setting the probability of having a certain configuration, i.e., by setting one or more parent-input nodes.
- Scenario 2 (backward inference). The model delivers a particular configuration in the parent nodes by setting the delay node to a target value. It provides understanding about the main contributors to delay (if delay is settled to a high positive value) or what configuration optimises operations (if delay is settled to a negative value).
4. Results and Discussion
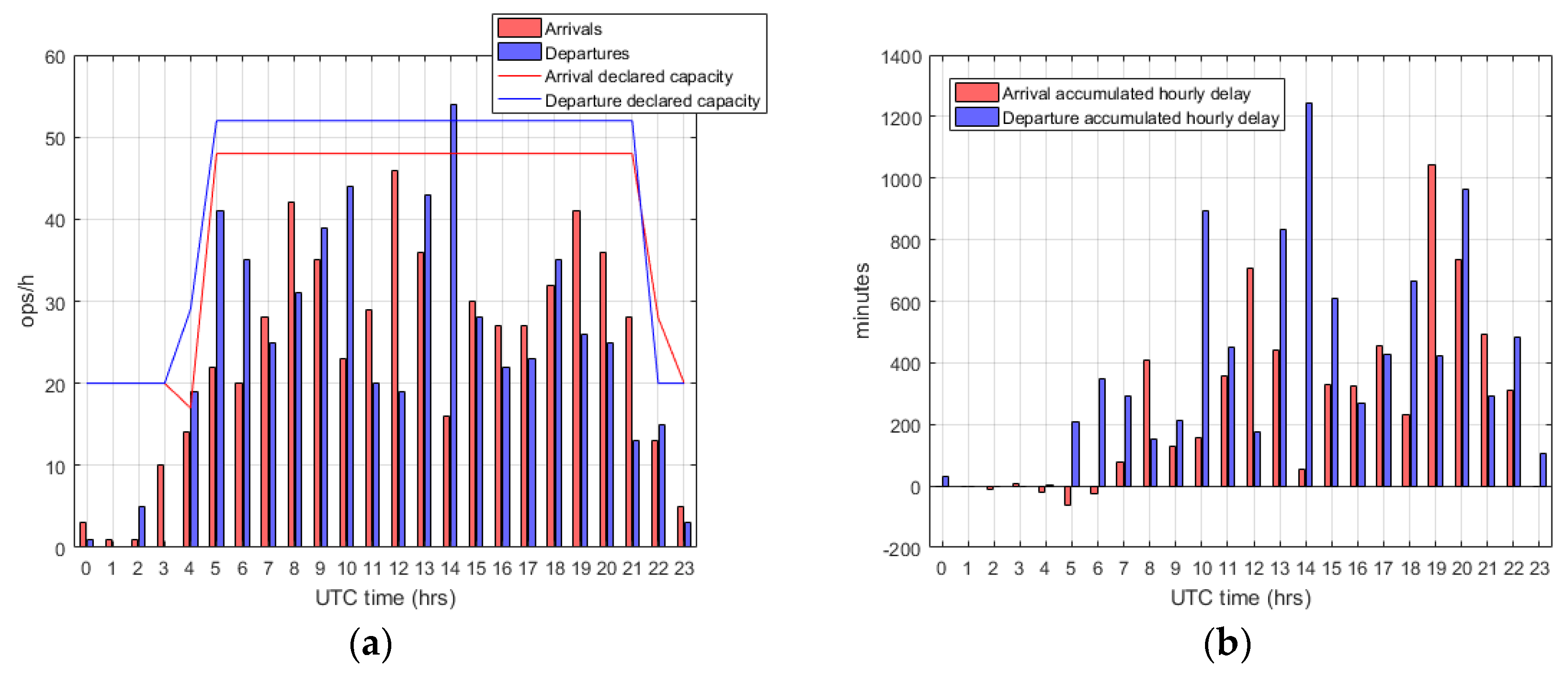
4.1. Operational Characterisation for the Case Study
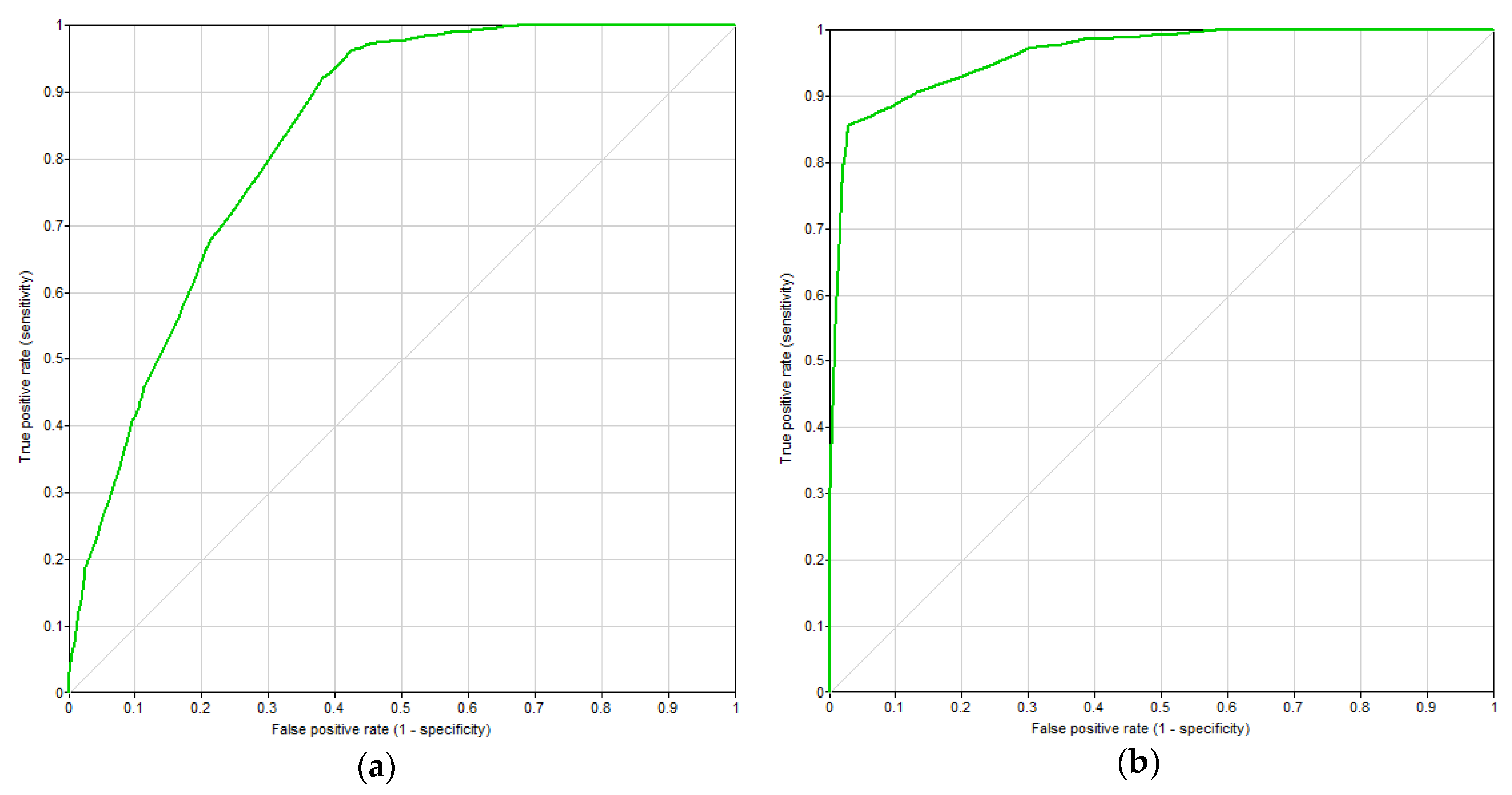
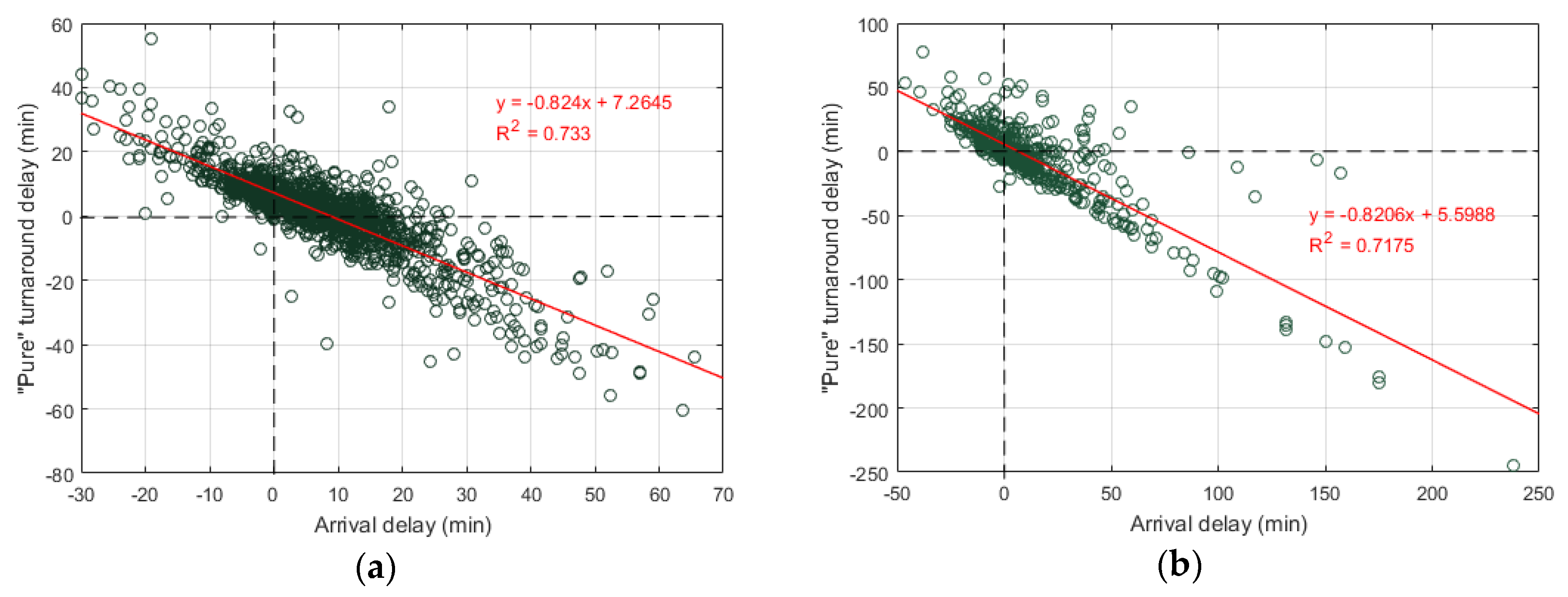
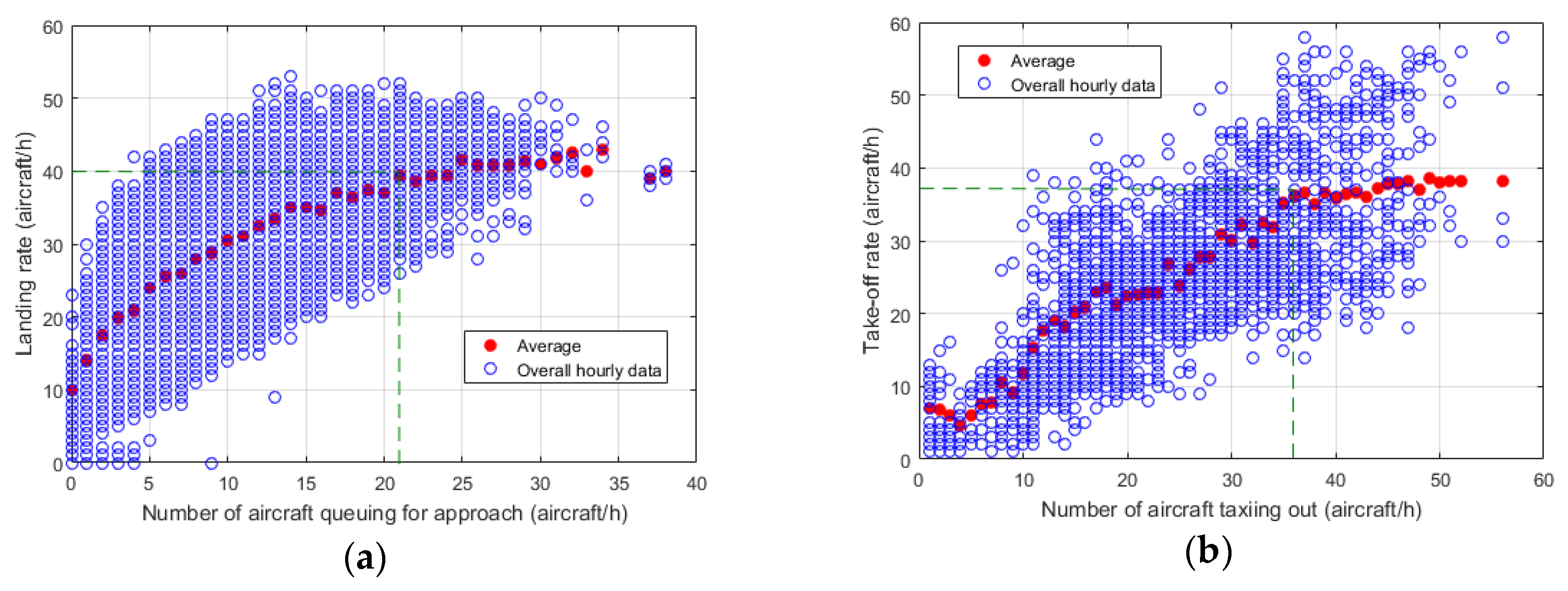
4.2. Cross-Influences at the ATV Stage
- Main delay triggers and their quantitative influences, e.g., a high amount of arrivals at early hours of the day, congestion at ASMA and E-TMA, bad weather conditions, tight scheduled duration of processes, LCCs operating domestic flights, changes in runway configuration, departure rates approaching runway capacity, and the existence of external delay causes (traffic flow restrictions, aircraft technical problems, crew schedule adherence requisites).
- Ability of processes to compress themselves and achieve punctuality (potential for recovery), e.g., the overall turnaround delay decreases at a higher rate when the airport throughput is below the threshold of 20 operations/h, taxiing processes reduce their delay at certain runway configurations, longer scheduled turnarounds at midday and late evening act as time-efficiency “protectors” for the system, the unconstrained duration of airspace processes reaches a limit when the airport is operating near its declared capacity, and certain airlines are especially active in recovering arrival delay on the ground (reducing duration of processes).
5. Summary and Conclusions
- Achieve a comprehensive understanding of operations at the ATV stage (airspace/airside integration).
- Appraise the influence of changes in tactical decisions and policies on delay management (“what-if” scenarios).
- Ensure some target levels of efficiency are met, improve predictability and manage uncertainty regarding operations through the causal model.
- Estimate the final departure delay (settlement of buffer time and optimal rotation times) using “forward” analysis.
- Identify the main contributors (causes) to a final delay (locate inefficiencies) using “backward” analysis.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Goedeking, P. Networks in Aviation: Strategies and Structures; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Belobaba, P.; Odoni, A.; Barnhart, C. The Global Airline Industry, 2nd ed.; John Wiley & Sons, Ltd.: New York, NY, USA, 2015. [Google Scholar]
- Ashford, N.J.; Stanton, H.P.M.; Moore, C.A.; Coutu, P.; Beasley, J.R. Airport Operations, 3rd ed.; McGraw-Hill: New York, NY, USA, 2013. [Google Scholar]
- Janić, M. The flow management problem in air traffic control: A model of assigning priorities for landings at a congested airport. Transp. Plan. Technol. 1997, 20, 131–162. [Google Scholar] [CrossRef]
- Beatty, R.; Hsu, R.; Berry, L.; Rome, J. Preliminary Evaluation of Flight Delay Propagation through an Airline Schedule. Air Traffic Control Q. 1999, 7, 259–270. [Google Scholar] [CrossRef]
- Wu, C.L. Airline Operations and Delay Management: Insights from Airline Economics, Networks and Strategic Schedule Planning, 1st ed.; Ashgate Publishing: Surrey, UK, 2012. [Google Scholar]
- Wu, C.L. Inherent delays and operational reliability of airline schedules. J. Air Transp. Manag. 2005, 11, 273–282. [Google Scholar] [CrossRef]
- Pyrgiotis, N.; Malone, K.M.; Odoni, A. Modelling delay propagation within an airport network. Transp. Res. Part C Emerg. Technol. 2013, 27, 60–75. [Google Scholar] [CrossRef]
- SESAR. SESAR Concept of Operations Step 2 Edition 2014 (Ed. 01.01.00); SESAR Joint Undertaking: Brussels, Belgium, 2014. [Google Scholar]
- Kazda, A.; Caves, R.E. Airport Design and Operations, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Zellweger, A.G.; Donohue, G.L. Air Transportation Systems Engineering, 1st ed.; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2001. [Google Scholar]
- ICAO. Doc 9854: Global Air Traffic Management Operational Concept; International Aviation Civil Organization: Montreal, QC, Canada, 2005. [Google Scholar]
- SESAR. European ATM Master Plan—Edition 2015; Publications Office of the European Union: Luxembourg, 2015. [Google Scholar]
- FAA. The Future of the NAS, Washington D.C: U.S. Department of Transportation, Federal Aviation Administration, Office of NextGen. 2016. Available online: https://www.faa.gov/nextgen/media/futureofthenas.pdf (accessed on 16 January 2018).
- Wu, C.L.; Caves, R.E. Modelling and simulation of aircraft turnaround operations at airports. Transp. Plan. Technol. 2004, 27, 25–46. [Google Scholar] [CrossRef]
- Cook, A. European Air Traffic Management: Principles, Practice and Research, 1st ed.; Ashgate: Aldershot, UK, 2007. [Google Scholar]
- Simaiakis, I.; Balakrishnan, H. A Queuing Model of the Airport Departure Process. Transp. Sci. 2015, 50, 94–109. [Google Scholar] [CrossRef]
- Neyshabouri, S.; Sherry, L. Analysis of Airport Surface Operations: A Case-Study of Atlanta Hartfield Airport. In Proceedings of the Transportation Research Board 93rd Annual Meeting, Washington, DC, USA, 12–16 January 2014. [Google Scholar]
- Zografos, K.G.; Andreatta, G.; Odoni, A.R. Modelling and Managing Airport Performance; Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Dobruszkes, F.; Givoni, M.; Vowles, T. Hello major airports, goodbye regional airports? Recent changes in European and US low-cost airline airport choice. J. Air Transp. Manag. 2017, 59, 50–62. [Google Scholar] [CrossRef]
- Fageda, X.; Flores-Fillol, R. How do airlines react to airport congestion? The role of networks. Reg. Sci. Urban Econ. 2016, 56, 73–81. [Google Scholar] [CrossRef]
- Redondi, R.; Gudmundsson, S.V. Congestion spill effects of Heathrow and Frankfurt airports on connection traffic in European and Gulf hub airports. Transp. Res. Part A Policy Pract. 2016, 92, 287–297. [Google Scholar] [CrossRef]
- Suau-Sanchez, P.; Voltes-Dorta, A.; Rodríguez-Déniz, H. Measuring the potential for self-connectivity in global air transport markets: Implications for airports and airlines. J. Transp. Geogr. 2016, 57, 70–82. [Google Scholar] [CrossRef]
- Wu, C.L. Monitoring Aircraft Turnaround Operations—Framework Development, Application and Implications for Airline Operations. Transp. Plan. Technol. 2008, 31, 215–228. [Google Scholar] [CrossRef]
- Filar, J.A.; Manyem, P.; White, K. How Airlines and Airports Recover from Schedule Perturbations: A Survey. Ann. Oper. Res. 2001, 108, 315–333. [Google Scholar] [CrossRef]
- Mukherjee, A.; Hansen, M.; Grabbe, S. Ground delay program planning under uncertainty in airport capacity. Transp. Plan. Technol. 2012, 35, 611–628. [Google Scholar] [CrossRef]
- Ciruelos, C.; Arranz, A.; Etxebarria, I.; Peces, S. Modelling Delay Propagation Trees for Scheduled Flights. In Proceedings of the 11th USA/EUROPE Air Traffic Management R&D Seminar, Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- Cook, A.; Tanner, G.; Cristobal, S.; Zanini, M. Delay propagation: New metrics, new insights. In Proceedings of the 11th USA/EUROPE Air Traffic Management R&D Seminar, Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- Campanelli, B.; Fleurquin, P.; Eguíluz, V.M.; Ramasco, J.J.; Arranz, A.; Etxebarría, I.; Ciruelos, C. Modeling Reactionary Delays in the European Air Transport. In Proceedings of the 4th SESAR Innovation Days, Madrid, Spain, 26 November 2014. [Google Scholar]
- Rebollo, J.J.; Balakrishnan, H. Characterization and prediction of air traffic delays. Transp. Res. Part C Emerg. Technol. 2014, 44, 231–241. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Balakrishnan, H.; Jordan, R. Deconstructing Delay Dynamics: An Air Traffic Delay Example. In Proceedings of the International Conference on Research in Air Transportation, Philadelphia, PA, USA, 20–24 June 2016. [Google Scholar]
- Fricke, H.; Schultz, M. Delay impacts onto turnaround performance. In Proceedings of the 8th USA/Europe Air Traffic Management Research and Development Semina, Napa, CA, USA, 29 June–2 July 2009. [Google Scholar]
- Katsaros, A.; Sánchez, A.C.S.; Zerkowitz, S.; Kerulo, B.; Stark, N.; Rekiel, J.; Pascual, S.P. Limiting the impact of aircraft turnaround inefficiencies on airport and network operations: The TITAN project. J. Airpt. Manag. 2013, 7, 289–317. [Google Scholar]
- Oreschko, B.; Kunze, T.; Gerbothe, T.; Fricke, H. Turnaround prediction and controling with micrsocopic process modelling GMAN proof of concept & possiblities to use microscopic process szenarios as control options. In Proceedings of the 6th International Conference on Research in Air Transportation, Istanbul, Turkey, 26–30 May 2014. [Google Scholar]
- Eurocontrol. A-CDM Impact Assessment; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2016. [Google Scholar]
- Schmitt, D.; Gollnick, V. Air Transport System, 1st ed.; Springer: Wien, Austria, 2016. [Google Scholar]
- Daley, B. Air Transport and the Environment, 1st ed.; Routledge: Abington-on-Thames, UK, 2010. [Google Scholar]
- Cook, A.; Tanner, G. European Airline Delay Cost Reference; University of Westminster Comissioned by Eurocontrol Performance Review Unit: Brussels, Belgium, 2014. [Google Scholar]
- Bazargan, M. Airline Operations and Scheduling, 2nd ed.; Ashgate: Aldershot, UK, 2010. [Google Scholar]
- Marintseva, K.; Yun, G.; Kachur, S. Resource allocation improvement in the tasks of airport ground handling operations. Aviation 2015, 19, 7–13. [Google Scholar] [CrossRef]
- Norin, A.; Granberg, T.A.; Yuan, D.; Värbrand, P. Airport logistics—A case study of the turn-around process. J. Air Transp. Manag. 2012, 20, 31–34. [Google Scholar] [CrossRef]
- Wang, P.T.R.; Schaefer, L.; Wojcik, L.A. Flight connections and their impacts on delay propagation. In Proceedings of the 22nd Digital Avionics Systems Conference, Indianapolis, IN, USA, 12–16 October 2003. [Google Scholar]
- Tu, Y.; Ball, M.O.; Jank, W.S. Estimating Flight Departure Delay Distributions—A Statistical Approach with Long-Term Trend and Short-Term Pattern. J. Am. Stat. Assoc. 2008, 103, 112–125. [Google Scholar] [CrossRef]
- AhmadBeygi, S.; Cohn, A.; Guan, Y.; Belobaba, P. Analysis of the potential for delay propagation in passenger airline networks. J. Air Transp. Manag. 2008, 14, 221–236. [Google Scholar] [CrossRef]
- Fleurquin, P.; Campanelli, B.; Eguíluz, V.M.; Ramasco, J.J. Trees of Reactionary Delay: Addressing the Dynamical Robustness of the US Air Transportation Network. In Proceedings of the 4th SESAR Innovation Days, Madrid, Spain, 25–27 November 2014. [Google Scholar]
- Abdel-Aty, M.; Lee, C.; Bai, Y.; Li, X.; Michalak, M. Detecting periodic patterns of arrival delay. J. Air Transp. Manag. 2007, 13, 355–361. [Google Scholar] [CrossRef]
- Wong, J.T.; Tsai, S.C. A survival model for flight delay propagation. J. Air Transp. Manag. 2012, 23, 5–11. [Google Scholar] [CrossRef]
- Churchill, A.; Lovell, D.; Ball, M. Examining the temporal evolution of propagated delays at individual airports: Case studies. In Proceedings of the 7th USA/Europe Air Traffic Management Research Devlopment Seminar, Barcelona, Spain, 2–5 July 2007. [Google Scholar]
- Deutschmann, A. Prediction of airport delays based on non-linear considerations of airport systems. In Proceedings of the 28th Congress of the International Council of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- Belkoura, S.; Zanin, M. Phase changes in delay propagation networks. In Proceedings of the 7th the International Conference for Research in Air Transportation, Philadelphia, PA, USA, 20–24 June 2016. [Google Scholar]
- Pearl, J. Fusion, propagation, and structuring in belief networks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Pearl, J. Belief networks revisited. Artif. Intell. 1993, 59, 49–56. [Google Scholar] [CrossRef]
- Fenton, N.; Neil, M. Risk Assessment and Decision Analysis with Bayesian Networks; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques, 1st ed.; The MIT Press: Cambridge, UK, 2011. [Google Scholar]
- Bujor, A.; Ranieri, A. Assessing Air Traffic Management Performance Interdependencies through Bayesian Networks: Preliminary Applications and Results. J. Traffic Transp. Eng. 2016, 4, 34–48. [Google Scholar] [CrossRef]
- Farr, A.C.; Kleinschmidt, T.; Johnson, S.; Yarlagadda, P.K.D.V.; Mengersen, K.L. Investigating effective wayfinding in airports: A Bayesian network approach. Transport 2013, 90–99. [Google Scholar] [CrossRef]
- Laskey, K.B.; Xu, N.; Chen, C.H. Propagation of delays in the national airspace system. In Proceedings of the 22nd Conference in Uncertainty in Artificial Intelligence, Cambridge, MA, USA, 13–16 July 2006. [Google Scholar]
- Xu, N.; Donohue, G.; Laskey, K.B.; Chen, C. Estimation of delay propagation in the national aviation system using bayesian networks. In Proceedings of the 6th USA/Europe Air Traffic Management Research and Development Semina, Baltimore, MD, USA, 27–30 June 2005. [Google Scholar]
- Liu, Y.; Wu, H. A Remixed Bayesian Network Based Algorithm for Flight Delay Estimating. Int. J. Pure Appl. Math. 2013, 85, 465–475. [Google Scholar] [CrossRef]
- Morales-Napoles, O.; Hanea, A.; Kurowicka, D.; Cooke, R.M.; Roelen, A. Causal modelling in the Aviation Industry: An application for controlled flight into terrain. In Safety Reliability Management Risk; Guedes, C., Soares, E.Z., Eds.; Taylor & Francis: London, UK, 2006; pp. 1831–1838. [Google Scholar]
- Londner, E.H.; Moss, R.J. A Bayesian Network Model of Pilot Response to TCAS Resolution Advisories. In Proceedings of the 12th USA/Europe Air Traffic Management R&D Seminar, Seattle, WA, USA, 27–30 June 2017. [Google Scholar]
- Yorukoglu, M.; Kayakutlu, G. Bayesian Network Scenarios to improve the Aviation Supply Chain. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011; Volume 2. [Google Scholar]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-J.; Ma, S. Flight Delay and Delay Propagation Analysis Based on Bayesian Network. In Proceedings of the 2008 Knowledge Acquisition and Modeling, Wuhan, China, 21–22 December 2008; pp. 318–322. [Google Scholar]
- Zio, E.; Sansavini, G. Modeling interdependent network systems for identifying cascade-safe operating margins. IEEE Trans. Reliab. 2011, 60, 94–101. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Cao, W.-D.; Ma, S. Estimation of Arrival Flight Delay and Delay Propagation in a Busy Hub-Airport. In Proceedings of the 4th International Conference on Natural Computation, Jinan, China, 18–20 October 2008. [Google Scholar]
- Schaefer, L.; Noam, T. Aircraft Turnaround Times for Air Traffic Simulation Analyses. In Proceedings of the Transportation Research Board 82nd Annual Meeting Compendium of Papers CD-ROM, Washington DC, USA, 12–16 January 2003. [Google Scholar]
- Eurocontrol, ACI, IATA. Airport CDM Implementation: The Manual; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2012. [Google Scholar]
- Bagieu, S. SESAR Solution Development, Unpacking SESAR Solutions, Extended AMAN; SESAR Joint Undertaking Solutions Workshop: Paris, France, 2015. [Google Scholar]
- Wilke, S.; Majumdar, A.; Ochieng, W.Y. Airport surface operations: A holistic framework for operations modeling and risk management. Saf. Sci. 2014, 63, 18–33. [Google Scholar] [CrossRef]
- Kirwan, B.; Ainsworth, L.K. A Guide To Task Analysis: The Task Analysis Working Group, 1st ed.; Taylor & Francis: London, UK, 1992. [Google Scholar]
- IBERIA. Flight Operations Manuals; IBERIA: Madrid, Spain, 2015. [Google Scholar]
- IBERIA. Ground Handling Operations Manuals; IBERIA: Madrid, Spain, 2014. [Google Scholar]
- IATA. Airport Handling Manual, 35th ed.; International Air Transport Association: Montreal, QC, Canada, 2015. [Google Scholar]
- ICAO. Annex 14 to the Convention on International Civil Aviation, Volume 1: Aerodrome Design and Operations, 7th ed.; International Aviationl Civil Organization: Montreal, QC, Canada, 2016. [Google Scholar]
- ICAO. Document 9157: Aerodrome Design Manual, 3rd ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2006. [Google Scholar]
- ICAO. Document 8168: Procedures for Air Navigation Services—Aircraft Operations, 5th ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2006. [Google Scholar]
- ICAO. Safety Oversight Manual—Part A, 2nd ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2006. [Google Scholar]
- Engels, G.; Förster, A.; Heckel, R.; Thöne, S. Process modeling using UML. In Process-Aware Information Systems: Bridging People and Software Through Process Technology, 1st ed.; Dumas, M., van der Aalst, W.M.P., Hofstede, A.H.M.T., Eds.; Wiley & Sons: Chichester, UK, 2005; pp. 85–118. [Google Scholar]
- Carlier, S.; de L´epinay, I.; Hustache, J.; Jelinke, F. Environmental impact of air traffic flow management delays. In Proceedings of the 7th USA/Europe Air Traffic Management Research and Development, Barcelona, Spain, 2–5 July 2007. [Google Scholar]
- ENAIRE, Aeronautical Information Publication (AIP). Aeronautical Information Service (AIS). 2018. Available online: https://ais.enaire.es/aip/aipcd_en.aspx (accessed on 16 January 2018).
- Rakas, J. Defining and Measuring Aircraft Delay and Airport Capacity Thresholds; Airport Cooperative Research Program (ACRP) Report 104; Transportation Research Board (TRB): Washington, DC, USA, 2014. [Google Scholar]
- Garson, G.D. Curve Fitting and Nonlinear Regression; Statistical Associates Publishers: Asheboro, NC, USA, 2012. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization, 2nd ed.; Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Kjærulff, U.B.; Madsen, A.L. Bayesian Networks and Influence Diagrams—A Guide to Construction and Analysis, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Darwiche, A. Bayesian networks. Commun. ACM 2010, 53, 80–90. [Google Scholar] [CrossRef]
- Neapolitan, R.E. Learning Bayesian Networks, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Nielsen, T.D.; Jensen, F.V. Bayesian Network and Decision Graph; Springer: New York, NY, USA, 2007. [Google Scholar]
- Pearl, J. Causality, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Cook, A.; Tanner, G.; Zannin, M. Towards superior air transport performance metrics—Imperatives and methods. J. Aerosp. Oper. 2013, 2, 3–19. [Google Scholar] [CrossRef]
- GeNIe Modeler, version 2.2; BayesFusion, LLC: Pittsburgh, PA, USA, 2017.
- Cooper, G.F.; Herskovits, E. A bayesian method for the induction of probabilistic networks from data. Mach. Learn. 1992, 9, 309–347. [Google Scholar] [CrossRef]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian Networks: The Combination of Knowledge and Statistical Data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- Suzuki, J. A Theoretical Analysis of the BDeu Scores in Bayesian Network Structure Learning. Behaviormetrika 2017, 44, 97–116. [Google Scholar] [CrossRef]
- Koiter, J.R. Visualizing Inference in Bayesian Networks, PhD Thesis in the Faculty of Electrical Engineering, Mathematics, and Computer Science; Department of Man-Machine Interaction, Delft University of Technology: Delft, The Netherlands, 2006. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- IATA. Airport Development Reference Manual, 10th ed.; International Air Transport Association: Montreal, QC, Canada, 2016. [Google Scholar]
- ICAO. Document 8643: Aircraft Type Designators; International Civil Aviation Organization: Montreal, QC, Canada, 2016. [Google Scholar]
- EUROCONTROL, CODA (Central Office for Delay Analysis) Digest: All-Causes Delay and Cancellations to Air Transport in Europe—2016; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2017.
- Tukey, J.W. Exploratory Data Analysis, 1st ed.; Pearson: London, UK, 1977. [Google Scholar]
- Pujet, N.; Delcaire, B.; Feron, E. Input-Output Modeling and Control of the Departure Process of Busy Airports. Air Traffic Control Q. 2000, 8, 1–32. [Google Scholar] [CrossRef]
- Cook, A.; Tanner, G.; Cristóbal, S.; Zanin, M. Passenger-Oriented Enhanced Metrics. In Proceedings of the 2nd SESAR Innovation Days, Braunschweig, Germany, 28 November 2012. [Google Scholar]
- Jetzki, M. The Propagation of Air Transport Delays in Europe. Ph.D. Thesis, Department of Airport and Air Transportation Research, RWTH Aachen University, Aachen, Germany, 2009. [Google Scholar]
- Sherry, L.; Wang, D.; Xu, N.; Larson, M.; Sherry, L.; Xu, N.; Larson, M. Statistical Comparison of Passenger Trip Delay and Flight Delay Metrics. J. Chem. Inf. Model. 2013, 53, 1689–1699. [Google Scholar] [CrossRef]




| Organisation | Stakeholder |
|---|---|
| AENA—Spanish Airport Authority and Airport Manager | Airport operator |
| IBERIA—Member of the International Airlines Group (IAG) | Airline |
| ENAIRE—Spanish Air Navigation Service Provider | Air Navigation Service Provider (ANSP) |
| IBERIA Airport Services | Ground Handling Agent |
| DGAC—Spanish General Directorate of Civil Aviation (a public body answerable to the Ministry of Public Works) | Policy maker—Regulator |
| Milestone Number | Milestone Meaning |
|---|---|
| M1 | EOBT (estimated off-block time)—3 h |
| M2 | EOBT (estimated off-block time)—2 h |
| M3 | Take-off from outstation |
| M4 | Local radar update |
| M5 | Final approach |
| M6 | ALDT (actual landing time) |
| M7 | AIBT (actual in-block time) |
| M8 | Actual ground handling starts |
| M9 | TOBT (target off-block time) |
| M10 | TSAT (target start-up approval time) |
| M11 | Boarding start |
| M12 | ARDT (aircraft ready time) |
| M13 | ASRT (actual start-up request time) |
| M14 | ASAT (actual start-up approval time) |
| M15 | AOBT (actual off-block time) |
| M16 | ATOT (actual take-off time) |
| Type of Data | Information |
|---|---|
| Airport infrastructure | Runway and stand use (terminal area). Runway declared capacity (arrivals, departures and total). |
| Airline | Operator, type (low cost carrier/network/cargo/general aviation) and associated handling agent. |
| Aircraft | Model, wake turbulence category (super heavy/heavy/medium/light), size (narrow/wide body) and registration number. |
| Flight | Flight number, type (commercial or private) and Air Traffic Control (ATC) call sign. |
| route | Origin and destination, category (Domestic/European/Long Haul). |
| Operational times & regulations | Date, aircraft milestones (from the E-TMA entrance to its exit: approach, on-ground turnaround and climb), timestamps (schedule adherence), duration of processes, holding patterns, aircraft separation, number of aircraft queuing for the inbound traffic flow and ATFCM regulations. |
| Arrival congestion | Arrival Sequencing and Metering Area (ASMA) additional time (average arrival runway queuing time on the inbound traffic flow, during congestion periods). |
| Throughput (airspace and airside) | E-TMA throughput (movements per hour), runway throughput (movements per hour). |
| Meteorology | Wind (direction and intensity), visibility, RVR (runway visual range), clouds (type and amount), temperature, atmospheric pressure and presence of fog. |
| Delay causes | Delay causes according to the codes developed by IATA [74] |
| Node Number | Meaning | Node Number | Meaning |
|---|---|---|---|
| 1 | Amount of clouds | 26 | Terminal area (T1/T2/T3/T4/T4S/cargo area/general aviation area)—associated to stand location (ramp) |
| 2 | Type of clouds | 27 | Scheduled turnaround time (SOBT–SIBT) |
| 3 | Visibility | 28 | Actual turnaround time (AOBT–AIBT) |
| 4 | Wind direction | 29 | Actual “pure” turnaround time (without considering ATFCM delay) |
| 5 | Wind intensity | 30 | Turnaround delay for the operation |
| 6 | Aircraft queuing at ASMA 60 NM | 31 | “Pure” turnaround delay for the operation |
| 7 | Throughput (aircraft landed) in the previous hour, when aircraft reaches ASMA 60 NM | 32 | System delay for the operation |
| 8 | Additional ASMA time (60 NM) | 33 | Existence of ATFCM regulation for this flight |
| 9 | Aircraft queuing at ASMA 40 NM | 34 | ATFCM delay for the operation |
| 10 | Throughput (aircraft landed) in the previous hour, when aircraft reaches ASMA 40 NM | 35 | Scheduled taxi-out time |
| 11 | Additional ASMA time (40 NM) | 36 | Actual taxi-out time (ATOT–AOBT) |
| 12 | Amount of holding patterns | 37 | Taxi-out delay for the operation |
| 13 | E-TMA arrival transit time | 38 | Departure configuration (north/south) |
| 14 | Arrival configuration (north/south) | 39 | Departure runway |
| 15 | Arrival runway | 40 | Route destination (domestic/European/long-haul) |
| 16 | Route origin (domestic/European/long-haul) | 41 | Departure time–associated with ATOT (morning/afternoon/evening/night) |
| 17 | Arrival time–associated with ALDT (morning/afternoon/evening/night) | 42 | Departure delay for the operation |
| 18 | Arrival delay for the operation | 43 | Existence of delay according to the IATA coding system [74] |
| 19 | Scheduled taxi-in time | 44 | Air Traffic Management related codes [74] |
| 20 | Actual taxi-in time (AIBT–ALDT) | 45 | Aircraft related delay codes [74] |
| 21 | Taxi-in delay for the operation | 46 | Airline related delay codes [74] |
| 22 | Type of airline operator (low cost/network/cargo/general aviation) | 47 | Airport related delay codes [74] |
| 23 | Aircraft size (narrow body/wide body) | 48 | Meteorology related delay codes [74] |
| 24 | Wake-turbulence category (H/M/L) | 49 | Other delay codes [74] |
| 25 | Handling agent |
| Arrival Configuration | Arrival Runway | Terminal Area | Most Used Parking Stands | Fleet Mix (Wake Turbulence Category) [99] | Traffic Share | Origin | Departure Configuration | Departure Runway | Destination |
|---|---|---|---|---|---|---|---|---|---|
| North (76%) | 32L (34%) 32R (66%) | T4-T4S (55%) T123 (45%) | Ramps 10–11–12 (41%) | Super heavy (0.2%) Heavy (15.9%) Medium (83.5%) Light (0.4%) | NCs (69%) LCCs (29%) Cargo (1%) General aviation (1%) | Domestic (34%) European (48%) Long haul (18%) | North (90%) South (10%) | 36L (44%) 36R (46%) 14L (5%) 14R (5%) | Domestic (33%) European (48%) Long haul (19%) |
| South (24%) | 18L (64%) 18R (36%) | T4-T4S (54%) T123 (46%) | Ramps 10-11–12 (44%) | Super heavy (0.1%) Heavy (9.7%) Medium (90.1%) Light (0.1%) | NCs (67%) LCCs (31%) Cargo (1%) General aviation (1%) | Domestic (34%) European (55%) Long haul (11%) | North (28%) South (72%) | 36L (14%) 36R (14%) 14L (40%) 14R (32%) | Domestic (35%) European (53%) Long haul (12%) |
| Metric | Mean Value (μ) and Standard Deviation (σ) |
|---|---|
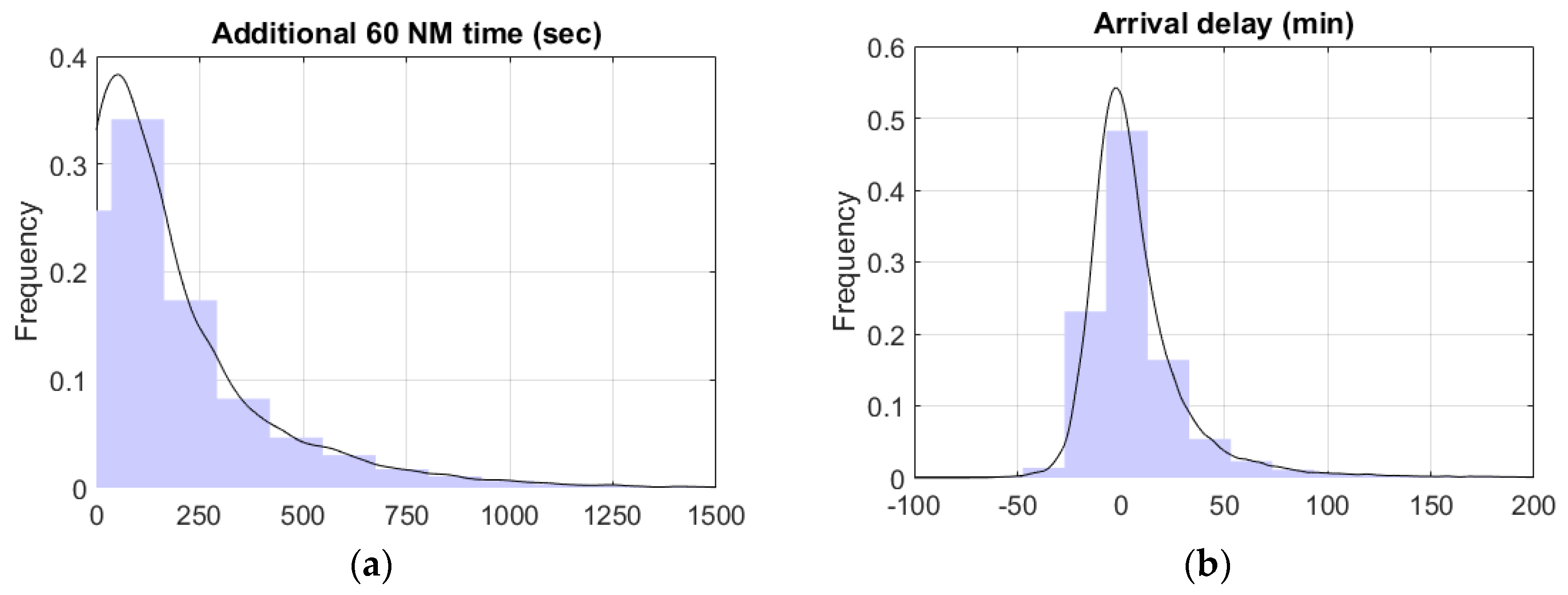
| E-TMA transit time | μ = 29.6 min, σ = 10.0 min |
| Additional ASMA 40 NM. Excess in approach queuing time | μ = 1.3 min, σ = 2.2 min |
| ASMA 40 NM transit time | μ = 13.6 min, σ = 3.7 min |
| Arrival delay. | μ = 8.3 min, σ = 30.5 min |
| Taxi-in delay | μ = 0.3 min, σ = 2.2 min |
| Actual taxi-in time | μ = 8.9 min, σ = 3.6 min |
| In-block adherence (AIBT-SIBT) | μ = 8.6 min, σ = 30.6 min |
| Turnaround delay | μ = 4.8 min, σ = 28.2 min |
| Actual turnaround time | μ = 165.6 min, σ = 179.7 min |
| Push delay | μ = 3.2 min, σ = 8.9 min |
| Start-up delay | μ = −1.2 min, σ = 16.5 min |
| Off-block adherence (AOBT–SOBT) | μ = 13.4 min, σ = 25.7 min |
| Taxi-out delay | μ = 0.9 min, σ = 4.4 min |
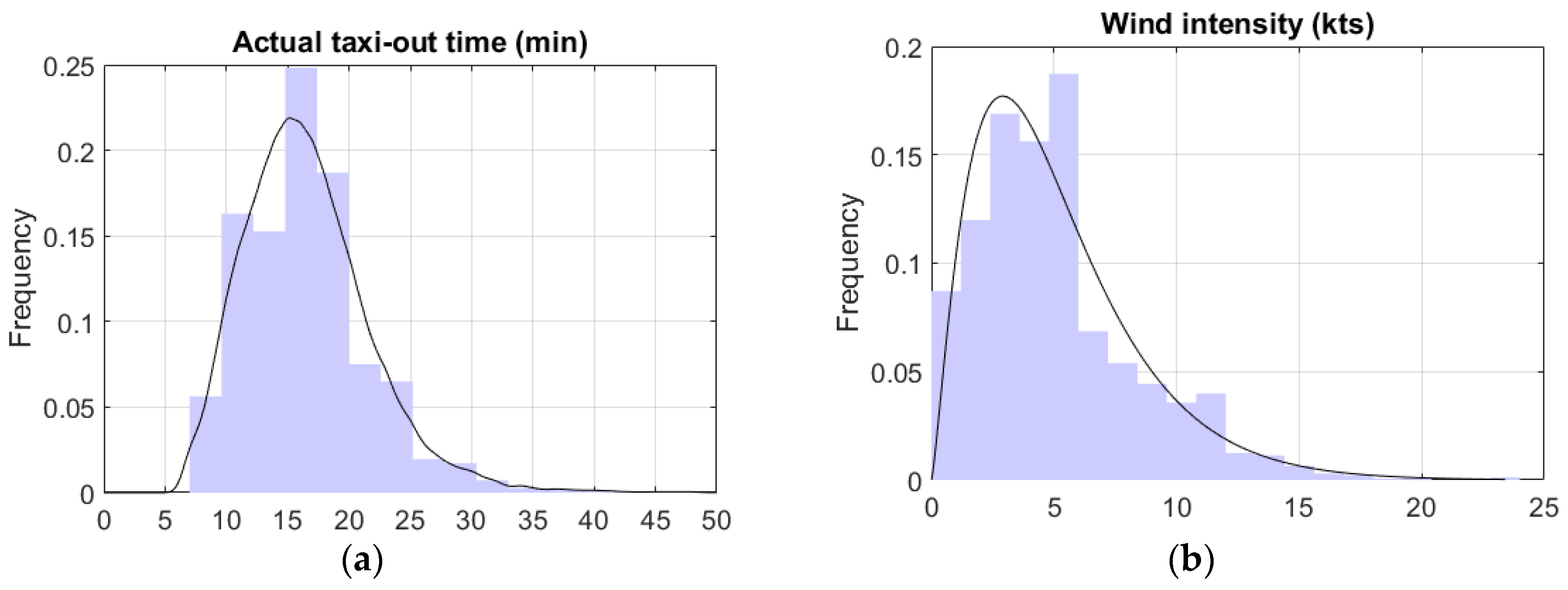
| Actual taxi-out time | μ = 16.6 min, σ = 5.3 min |
| System delay (primary delay) | μ = 5.8 min, σ = 28.6 min |
| Departure delay (total delay) | μ = 14.1 min, σ = 26.5 min |
| BN Layer | Most Influential Factor | Threshold for Reaching a Probability of Having Departure Delay >15 min above 60% |
|---|---|---|
| Meteorology | East wind (coming from the east and blowing toward the west) | An intensity over 15 kts |
| Airspace | ASMA 60 NM Additional time and holding patterns | Above 10 min for ASMA 60 NM additional time and more than 2 holding patterns |
| Infrastructure | South runway configuration | Combination of south runway configuration, terminal area T123 and 14L departing runway |
| Operator, aircraft type and route | LCCs operating a domestic or intra-European flight, with NB aircraft | |
| Airside | Tight scheduled duration of processes | Turnaround and taxi allocated times below the average for each operation type |
| IATA delay codes | Reactionary | Probability of an inherited reactionary delay above 50% |
| Departure Delay (min) | Departure Configuration & Departure Runway | Terminal Area | Aircraft Type (NB-WB) | Departure Time Frame (ALDT) | Route Destination & Operator Type |
|---|---|---|---|---|---|
| d < −15 | North (75%), 36R (38%) | T4 (40%) | NB (84%) | Evening (13–20 UTC) (42%) | European (70%), NCs (70%) |
| −15 ≤ d < −3 | North (75%), 36R (38%) | T4 (41%) | NB (83%) | Evening (13–20 UTC) (39%) | European (70%), NCs (68%) |
| −3 ≤ d < 3 | North (70%), 36R (35%) | T4 (41%) | NB (80%) | Evening (13–20 UTC) (41%) | Domestic (39%), NCs (69%) |
| 3 ≤ d < 15 | North (69%), 36R (37%) | T123 (43%) | NB (85%) | Morning (6–11 UTC) (39%) | European (49%), NCs (69%) |
| 15 ≤ d | North (65%), 36R (39%) | T123 (42%) | NB (80%) | Morning (6–11 UTC) (38%) | European (51%), NCs (70%) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Sanz, Á.; Gómez Comendador, F.; Arnaldo Valdés, R.; Cordero García, J.M.; Bagamanova, M. Uncertainty Management at the Airport Transit View. Aerospace 2018, 5, 59. https://doi.org/10.3390/aerospace5020059
Rodríguez-Sanz Á, Gómez Comendador F, Arnaldo Valdés R, Cordero García JM, Bagamanova M. Uncertainty Management at the Airport Transit View. Aerospace. 2018; 5(2):59. https://doi.org/10.3390/aerospace5020059
Chicago/Turabian StyleRodríguez-Sanz, Álvaro, Fernando Gómez Comendador, Rosa Arnaldo Valdés, Jose Manuel Cordero García, and Margarita Bagamanova. 2018. "Uncertainty Management at the Airport Transit View" Aerospace 5, no. 2: 59. https://doi.org/10.3390/aerospace5020059
APA StyleRodríguez-Sanz, Á., Gómez Comendador, F., Arnaldo Valdés, R., Cordero García, J. M., & Bagamanova, M. (2018). Uncertainty Management at the Airport Transit View. Aerospace, 5(2), 59. https://doi.org/10.3390/aerospace5020059