Buoyancy-Induced Heat Transfer inside Compressor Rotors: Overview of Theoretical Models

Abstract

Increasing pressures in gas-turbine compressors, particularly in aeroengines where the pressure ratios can be above 50:1, require smaller compressor blades and an increasing focus on blade-clearance control. The blade clearance depends on the radial growth of the compressor discs, which in turn depends on the temperature and stress in the discs. As the flow inside the disc cavities is buoyancy-driven, calculation of the disc temperature is a conjugate problem: the heat transfer from the disc is coupled with the air temperature inside the cavity. The flow inside the cavity is three-dimensional, unsteady and unstable, so computational fluid dynamics is not only expensive and time-consuming, it is also unable to achieve accurate solutions at the high Grashof numbers found in modern compressors. Many designers rely on empirical equations based on inappropriate physical models, and recently the authors have produced a series of papers on physically-based theoretical modelling of buoyancy-induced heat transfer in the rotating cavities found inside compressor rotors. Predictions from these models, all of which are for laminar flow, have been validated using measurements made in open and closed compressor rigs for a range of flow parameters representative of those found inside compressor rotors. (The fact that laminar buoyancy models can be used for large Grashof numbers (up to ${10}^{12}$), where most engineers expect the flow to be turbulent, is attributed to the large Coriolis accelerations in the fluid core and to the fact that there is only a small difference between the rotational speed of the core and that of the discs.) As many as 223 separate tests were analysed in the validation of the models, and good agreement between the predictions and measurements was achieved for most of these cases. This overview paper has collected together the equations from these papers, which should be helpful to designers and research workers. The paper also points out the limitations of the models, all of which are for steady flow, and shows where further experimental evidence is needed.

1. Introduction

Increasing pressures in gas-turbine compressors, particularly in aeroengines where the pressure ratios can be above 50:1, require smaller compressor blades and an increasing focus on blade-clearance control. To calculate the transient and steady clearances between the blades and casing of a high-pressure compressor in an aeroengine (see Figure 1), it is necessary to calculate the radial growth of the compressor discs. This in turn requires the calculation of the temperatures of the discs, which involves the calculation of the flow and heat transfer inside the cavity between the corotating discs.

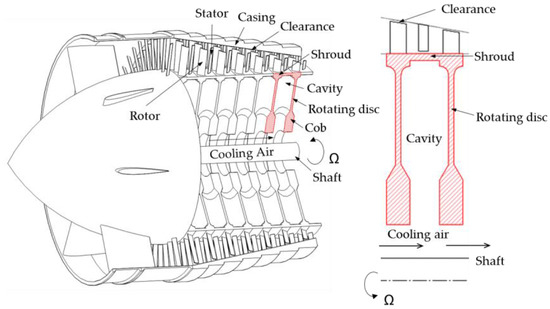
Figure 1. High-pressure aeroengine compressor and schematic diagram of open rotating cavity.

The buoyancy-induced flow that occurs inside these cavities is three-dimensional, unsteady and unstable, and the prediction of these flows using computational fluid dynamics (CFD) is very expensive and usually inaccurate, particularly at the high Grashof numbers found in compressors. Many designers rely on empirical equations based on inappropriate physical models, and recently the authors have produced a series of papers on physically-based theoretical modelling of buoyancy-induced heat transfer in the rotating cavities found inside compressor rotors. These papers form the basis for the overview presented below.

A review of research into buoyancy-induced rotating flow in closed and open cavities was given in [1]. However since that review there have been some significant developments in the theoretical modelling of these flows [2,3,4,5,6], and it is the object of this paper to bring all these models together in a form that can be readily used by the designers of aeroengines and industrial compressors.

A background to buoyancy-induced rotating flow is given in Section 2. Section 3 and Section 4 summarise the models and the equations for heat transfer from the shroud and discs. Section 5 combines these equations for the rotating cavity in a compressor with axial throughflow, including the calculation of the temperature rise of the throughflow, and the main conclusions are given in Section 6. The Appendix includes the linear equations for inviscid rotating fluids and the equations for adiabatic flow in a rotating core of inviscid fluid.

The definition of symbols not defined in the text below can be found in the Nomenclature.

2. Buoyancy-Induced Rotating Flow

To understand rotating flows, it is necessary to understand some of the effects of the Coriolis forces on these flows. The so-called linear equations (where the linear Coriolis accelerations are much greater than the nonlinear inertial terms) are given in the Appendix.

In the steady-state, the outer shroud is relatively hot compared with the inner one (for closed cavities) or with the axial throughflow (for open cavities). This radial temperature gradient creates buoyancy-induced flow; for a radial flow to occur then either it must be confined to the viscous boundary layers (referred to here as Ekman layers, where the Coriolis forces are produced by shear stresses) or the inviscid flow must be non-axisymmetric (in which regions of cyclonic and anti-cyclonic flow produce circumferential pressure gradients that create the Coriolis forces). An example of these non-axisymmetric flows is shown in Figure 2, first reported by Farthing et al. [7]. These flows are three-dimensional (3D), unsteady and unstable, making them extremely difficult and expensive to compute using computational fluid dynamics (CFD).

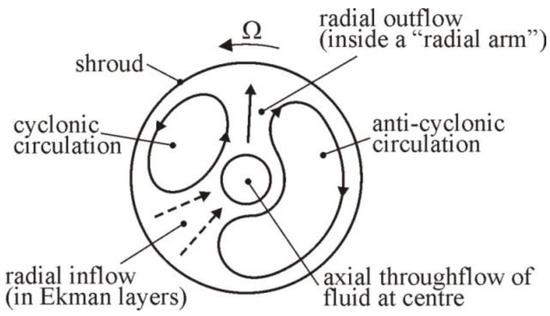
Figure 2. Schematic of flow structure in heated rotating cavity with axial throughflow of cooling air [7].

Under transient conditions in aeroengines, the throughflow can be hotter than the outer shroud, in which case stratified flow occurs and heat transfer takes place by conduction and radiation. The heat transfer for buoyancy-induced flow is much higher than for stratified flow, and the transition from one state to the other can give rise to flow instabilities.

Coriolis forces tend to attenuate velocity fluctuations, and so it is probable that the critical Rayleigh numbers, Ra, for transition from laminar to turbulent flow will be much higher in a rotating cavity than in a stationary one. In fact, it is shown below that the flow in the Ekman layers could remain laminar even at engine operating conditions, where $\mathrm{Ra}>{10}^{12}$.

Buoyancy-induced flow in rotating cavities is similar to that in the earth’s atmosphere: both are affected by temperature gradients and by rotation. In both cases, the temperature gradients (radial for cavities where the centripetal acceleration dominates or vertical for the atmosphere where gravity is controlling) can be calculated assuming adiabatic flow. This gives rise to the adiabatic lapse rate in the atmosphere and to a radial temperature gradient in a rotating cavity. It is shown in the Appendix that the radial temperature gradient in the rotating core increases as ${\mathsf{\Omega }}_{\mathrm{c}}$, the angular speed of the core, increases. However, as $\mathrm{Nu}$, the Nusselt number for buoyancy-induced rotating flow, increases as $\mathrm{Ra}$ (and hence as $\mathsf{\Omega }$) increases, it follows that there must be a critical value of $\mathrm{Ra}$ at which $\mathrm{Nu}$ is a maximum: below this critical value, $\mathrm{Nu}$ increases as $\mathrm{Ra}$ increases; above it, $\mathrm{Nu}$ decreases as $\mathrm{Ra}$ increases. It is shown below that this can and does occur in practice.

3. Heat Transfer from Shrouds

The equations below are based on those derived in [2] for a closed rotating cavity with adiabatic discs. Results from these equations are compared with experimental measurements in Section 3.3.

3.1. Calculation of Nusselt Numbers

As shown in Figure 3, it is assumed that there are thin boundary layers on the inner and outer cylindrical surfaces at $r=a$ and $r=b$ between which is a core of inviscid fluid rotating at the same angular speed, $\mathsf{\Omega }$, as that of the discs. The temperatures of the inner and outer surfaces are $T_a$ and $T_b$, where $T_a<T_b$, and the corresponding temperatures of the core at the edge of the boundary layers are $T_{c,a}$ and $T_{c,b}$.

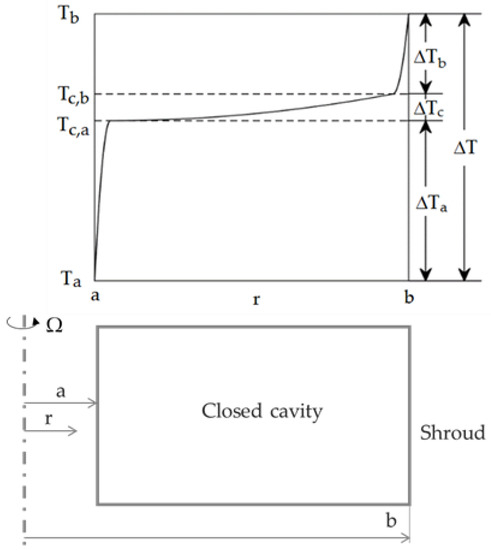
Figure 3. Simplified diagram of temperature distribution inside closed cavity [2].

It can be seen from Figure 3 that

$$\mathsf{\Delta }{T}_a=T_{c,a}-T_a$$

(1)

$$\mathsf{\Delta }{T}_b=T_b-T_{c,b}$$

(2)

$$\mathsf{\Delta }{T}_c=T_{c,b}-T_{c,a}$$

(3)

and

$$\mathsf{\Delta }T=T_b-T_a$$

(4)

Assuming that the thickness of the boundary layers on the inner and outer surfaces are negligible compared with the radial height of the cavity, it can be shown from the Appendix that

$$\mathsf{\Delta }{T}_c=\frac{{\mathsf{\Omega }}^2}{2C_p}\left(b^2-a^2\right)$$

(5)

In the absence of heat transfer from the discs, the total heat flow rate through the inner surface is assumed to equal that through the outer one, so that the heat rates are related by

$$\dot{Q}={\dot{Q}}_a={\dot{Q}}_b$$

(6)

Hence

$$q_a{S}_a=q_b{S}_b$$

(7)

The following definitions are used:

$$\mathrm{Nu}\stackrel{\mathrm{def}}{=}\frac{\dot{Q}}{{\dot{Q}}_{cond}}$$

(8)

where ${\dot{Q}}_{cond}$ is the heat flow rate due to conduction, which is given by

$${\dot{Q}}_{cond}=2\pi ks\frac{\mathsf{\Delta }T}{\ln \left(b/a\right)}$$

(9)

The Nusselt numbers and Grashof numbers on the inner and outer cylindrical surfaces are defined as

$${\mathrm{Nu}}_{\mathrm{a}}\stackrel{\mathrm{def}}{=}\frac{q_a{L}_a}{k\mathsf{\Delta }{T}_a}$$

(10)

$${\mathrm{Nu}}_{\mathrm{b}}\stackrel{\mathrm{def}}{=}\frac{q_b{L}_b}{k\mathsf{\Delta }{T}_b}$$

(11)

$${\mathrm{Gr}}_{\mathrm{a}}\stackrel{\mathrm{def}}{=}\frac{{\rho }^2{\mathsf{\Omega }}^{2}a{L}_a^3\beta \mathsf{\Delta }{T}_a}{{\mu }^2}$$

(12)

$${\mathrm{Gr}}_{\mathrm{b}}\stackrel{\mathrm{def}}{=}\frac{{\rho }^2{\mathsf{\Omega }}^{2}b{L}_b^3\beta \mathsf{\Delta }{T}_b}{{\mu }^2}$$

(13)

where $L_a$ and $L_b$ are appropriate length scales.

By analogy with free convection from a horizontal plate [8], it is assumed that heat transfer from the rotating cylindrical surfaces is by laminar free convection but with the gravitational acceleration replaced by the centripetal acceleration. The Nusselt numbers are then given by

$${\mathrm{Nu}}_{\mathrm{a}}=c{\left({\mathrm{Gr}}_{\mathrm{a}}\mathrm{Pr}\right)}^{1/4}$$

(14)

$${\mathrm{Nu}}_{\mathrm{a}}=c{\left({\mathrm{Gr}}_{\mathrm{a}}\mathrm{Pr}\right)}^{1/4}$$

(15)

For a hot horizontal plate with cold air above, or a cold plate with hot air below, the constant c = 0.54. For the rotating cavity, where centripetal acceleration occurs, these cases respectively apply to the outer and inner cylindrical surfaces. For horizontal surfaces, the length scale is taken to be the area/perimeter ratio of the plate; for cylindrical surfaces, this corresponds to $L_a=L_b=s/2$.

Using the above equations, and noting that $\mathrm{Ra}=\mathrm{Pr}\mathrm{Gr}$, it can be shown (see [2]) that

$$\mathrm{Nu}=c\xi {\mathrm{Ra}}^{1/4} {\left(1-\chi {\mathrm{Re}}^2\right)}^{5/4}$$

(16)

$$\mathrm{Nu}=c\xi {\mathrm{Ra}}^{1/4} {\left(1-\psi \mathrm{Ra}\right)}^{5/4}$$

(17)

where $\xi$ is a geometric parameter given by

$$\xi =\frac{a}{b}\ln \left(\frac{\mathrm{b}}{\mathrm{a}}\right){\left(\frac{a}{l_a}\right)}^{\frac{1}{4}}{\left(\frac{2}{\left(1+a/b\right){\left(1-a/b\right)}^3}\right)}^{\frac{1}{4}}{\left(1+{\left(\frac{a}{b}\right)}^{1/5}{\left(\frac{l_b}{l_a}\right)}^{1/5}{\left(\frac{S_a}{S_b}\right)}^{4/5}\right)}^{-5/4}$$

(18)

and $\chi$ and $\psi$ are compressibility parameters given by

$$\chi \stackrel{\mathrm{def}}{=}\frac{2{\mu }^2}{{\rho }^2{C}_p\mathsf{\Delta }T\left(b^2-a^2\right)}$$

(19)

$$\psi \stackrel{\mathrm{def}}{=}\frac{{\mu }^2}{{\rho }^2{C}_p\mathsf{\Delta }T{\left(b-a\right)}^2\beta \mathsf{\Delta }T \mathrm{Pr}}$$

(20)

3.2. Maximum Nusselt Number

It follows from Equation (16) that,

$$\mathrm{Nu}\propto {\mathrm{Re}}^{1/2}{\left(1-\chi {\mathrm{Re}}^2\right)}^{5/4}$$

(21)

There will therefore be a maximum value of $\mathrm{Nu}$ at a critical value of $\mathrm{Re}$ where

$${\mathrm{Re}}_{\mathrm{crit}}={\left(6\chi \right)}^{-1/2}$$

(22)

or, from Equation (17), at a critical value of $\mathrm{Ra}$ where

$${\mathrm{Ra}}_{\mathrm{crit}}={\left(6\psi \right)}^{-1}$$

(23)

It can be seen from Equations (19), (20), (22) and (23) that ${\mathrm{Re}}_{\mathrm{crit}}$ and ${\mathrm{Ra}}_{\mathrm{crit}}$ increase as $\rho$ increases or as $\mathsf{\Delta }T$ increases. (The increase in $\rho$ was achieved in the experiments of Bohn et al. [9] by pressurising the cavity. In their experiments, $\mathsf{\Delta }T$ decreased as $\mathrm{Re}$ increased, which would reduce the critical value given by Equation (22)). It should also be noted that, as $\chi \propto {\rho }^{-2}$ and $\mathrm{Re}\propto \rho$, it follows that ${\mathsf{\Omega }}_{\mathrm{crit}}$, the critical value of $\mathsf{\Omega }$, is invariant with the density and is therefore unaffected by the pressure in the cavity.

3.3. Comparison with Experimental Measurements

The theoretical model was validated using the experimental measurements of Bohn et al. [9]. The measurements were made in 194 separate experiments, over a wide range of Rayleigh numbers, in three closed cavities, A, B and C, each of which had different geometries. There was good agreement between Equation (17)—using a value of $c=0.32$—and the experimental data obtained from all three cavities. The results shown in Figure 4 were for Cavity A, where $a=125 \mathrm{mm}$, $b=355 \mathrm{mm}$ and $s=120 \mathrm{mm}$ and the experiments were conducted with an absolute cavity pressure of 4 bar. It should be noted that the shroud temperature decreased as $\mathrm{Ra}$ increased, and the empirical correlation of Bohn et al. for cavity A was

$${\mathrm{Nu}}_{\mathrm{A}}=0.246 {\mathrm{Ra}}^{0.228}$$

(24)

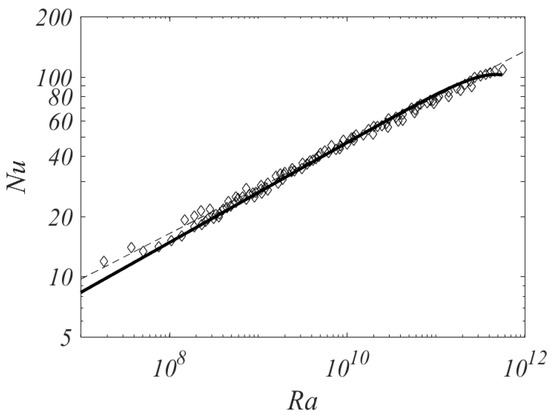
Figure 4. Variation of $\mathrm{Nu}$ with $\mathrm{Ra}$ for Cavity A of Bohn et al. [2] (Symbols denote experimental data [9]; solid curve denotes theoretical solutions; broken curve denotes empirical correlations).

The theoretical curve shows a good fit to the experimental data, particularly at the highest values of $\mathrm{Ra}$ where the data points begin to deviate from the empirical correlation: these data points are consistent with, but are not proof of, a maximum value of $\mathrm{Nu}$.

It is significant that a laminar theoretical model fits the experimental data for values of $\mathrm{Ra}$ approaching ${10}^{12}$, where most engineers would expect the flow to be turbulent. As stated in Section 2, Coriolis forces tend to attenuate the effects of turbulence, and the fact that the fluid in the cavity is expected to rotate close to the angular speed of the shrouds means that any speed difference across the boundary layers would be very small.

4. Heat Transfer from Discs

The equations below are based on those derived in [3] for the discs in an open cavity with an axial throughflow of cooling air. This is a conjugate problem: the heat transfer from the discs and the temperature in the core are coupled. Results from these equations are compared with experimental measurements in Section 4.5.

4.1. Assumptions for Buoyancy Model

The Ekman-layer equations for buoyancy-induced flow were based on those used for isothermal laminar source-sink flow in [10]. As shown in Figure 5, for heated discs and a cold core the flow will be radially inward inside the Ekman layers. In practice, the flow in the core will be 3D and unsteady, with the radial outflow of cold fluid and the inflow of hot fluid facilitated by pairs of cyclonic and anti-cyclonic vortices. The 1D model assumes axisymmetric flow inside the Ekman layers: in effect, this uses the spatial and temporal averages of the velocities and temperature.

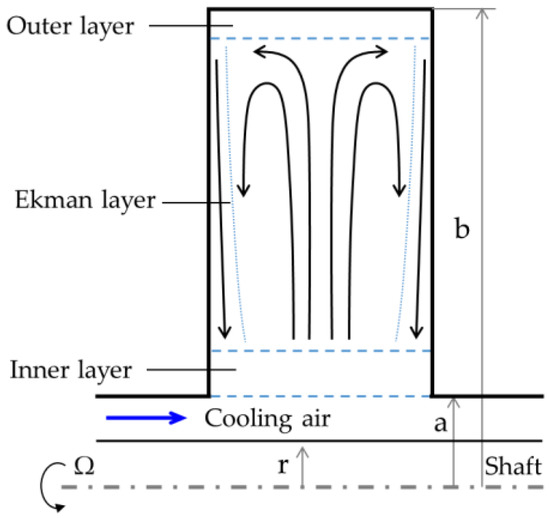
Figure 5. Assumed flow structure.

In the solutions presented below, although it is assumed that heat is transferred from the Ekman layers to the core, it is also assumed that there is no significant heat transfer between the radial plumes of air and the vortices in the core. Consequently the circumferential-average temperature of the core can be considered to increase adiabatically with radius, as assumed in the Appendix.

It was shown by Owen and Pincombe [11] that the axial throughflow can create a toroidal vortex inside the cavity, with the possibility of vortex breakdown in the swirling axial flow. The strength and size of the toroidal vortex decreases as the Rossby number decreases, and at the small values of $\mathrm{Ro}$ found in compressors (where $\mathrm{Ro}$ is of the order of ${10}^{-1}$) it is probable that the vortex will have decayed to leave a shear layer between the throughflow and the buoyancy-induced flow inside the cavity, shown as the inner layer in Figure 5; the outer layer corresponds to the boundary layer on the shroud. Although heat will be transferred across the inner layer, with a temperature difference proportional to the heat flux, the amount of mass transfer is likely to be very small.

4.2. Modelled Nusselt Numbers

The term modelled Nusselt numbers is used here to refer to the values that are determined using the equations given below, which are based on the Ekman-layer model in [3]. The modelled Nusselt number is defined as

$${\mathrm{Nu}}_{\mathrm{c}}\stackrel{\mathrm{def}}{=}\frac{h_{c}r}{k}$$

(25)

where the local heat transfer coefficient $h_c$, is given

$$h_c\stackrel{\mathrm{def}}{=}\frac{q_o}{T_o-T_c}$$

(26)

$T_o$ and $T_c$ are the temperatures of the disc and core respectively, and $q_o$ is the heat flux from the disc surface to the core. It is shown in [3] that the Nusselt number for the discs is given by

$${\mathrm{Nu}}_{\mathrm{c}}=\frac{1}{2}\frac{x_a^{1/2}}{I^{1/4}}{\mathrm{Gr}}_{\mathrm{c}}^{1/4}{\left[\left(\theta -\mathrm{Co}\right){\left(\frac{{\rho }_c}{{\rho }_{c,b}}\right)}^2{x}^5\right]}^{1/3}$$

(27)

The nondimensional temperature $\theta$ is defined by

$$\theta \stackrel{\mathrm{def}}{=}\frac{T_o-T_c}{T_{o,b}-T_{c,b}}$$

(28)

It is $\theta$ that couples the heat transfer from the disc to the temperature of the core. The Grashof number, ${\mathrm{Gr}}_{\mathrm{c}}$, is defined by

$${\mathrm{Gr}}_{\mathrm{c}}\stackrel{\mathrm{def}}{=}\frac{{\rho }_{c,b}^2{\mathsf{\Omega }}_c^2{b}^4}{{\mu }^2}\beta \left(T_{o,b}-T_{c,b}\right)$$

(29)

The so-called Coriolis parameter, $\mathrm{Co}$, which can be thought of as the ratio of Coriolis forces to buoyancy forces, is defined by

$$\mathrm{Co}\stackrel{\mathrm{def}}{=}2(1-\frac{{\mathsf{\Omega }}_{\mathrm{c}}}{\mathsf{\Omega }})\frac{1}{\beta \left(T_{o,b}-T_{c,b}\right)}$$

(30)

$\mathrm{Co}$ is treated as an empirical parameter, and for the experiments discussed below a value of $\mathrm{Co}=0.07$ was found to provide the best fit between the predicted and measured temperatures. (In almost all experimental cases analysed in this paper, it was found that $N{u}_c\to 0$ as $r\to a$, so that Equation (27) implies that $\theta \approx \mathrm{Co}$ at $r=a$. From the definition of $\theta$ in Equation (28), the choice of $\mathrm{Co}$ determines the value of $T_{c,a}$ used in the solution of the equations.)

$I$, which is an integral that accounts for the momentum exchange between the flow in the core and that in the Ekman layers on the discs, is defined by

$$I={{\displaystyle \int }}_{x_a}^1{x}^{11/3}{\left[\left(\theta -\mathrm{Co}\right){\left(\frac{{\rho }_c}{{\rho }_{c,b}}\right)}^2\right]}^{1/3}dx$$

(31)

$T_{c,b}$ is calculated from Equation (A14) in the Appendix, and it follows from Equation (A15) that

$$\frac{{\rho }_c}{{\rho }_{c,b}}={\left[\frac{1+\frac{\gamma -1}{2}M{a}_c^2\left(x^2-x_a^2\right)}{1+\frac{\gamma -1}{2}M{a}_c^2\left(1-x_a^2\right)}\right]}^{1/\left(\gamma -1\right)}$$

(32)

The other symbols are defined in the Nomenclature.

4.3. Modelled Disc Temperatures

In [4], Equation (27) was solved in conjunction with the numerical solution of the general fin equation for the disc, which is given by

$$\frac{d^2{T}_o}{d{r}^2}+\left(\frac{1}{r}-\frac{2}{t}\frac{cos\alpha }{sin\alpha }+\frac{1}{k_s}\frac{d{k}_s}{d{T}_o}\frac{d{T}_o}{dr}\right)\frac{d{T}_o}{dr}-\frac{2h_f}{k_{s}tsin\alpha }\left(T_o-T_f\right)=0$$

(33)

(In principle, the 2D version of Laplace’s equation could be used for the conduction calculations, but the 1D fin equation has the advantage of simplicity, and it is much easier to use in conjunction with a Bayesian statistical model [5].) The geometry of the disc, which is shown in Figure 6, is based on the experimental Sussex rig described in [12]. The thermal conductivity, $k_s$, of the titanium disc and the finite-difference equations used for the numerical solution of Equation (33) are given in [4]. The measured temperatures at $r=b$ and $r=a^{\prime }$ (see Figure 6) were used as the boundary conditions.

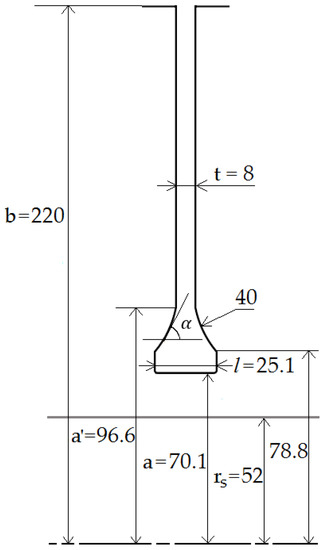
Figure 6. Simplified diagram of instrumented disc of Sussex rig (Dimensions in mm) [4].

The coupled Equations (27) and (33) were solved iteratively to calculate the modelled Nusselt numbers and disc temperatures.

4.4. Experimentally Derived Nusselt Numbers and Disc Temperatures

The general fin equation, Equation (33), was solved numerically—in conjunction with the measured disc temperatures, using the Bayesian statistical model described in [5]—to calculate what are referred to here as the experimentally derived Nusselt numbers and disc temperatures. The Nusselt numbers and the 95% confidence interval were determined from the inverse solution of Equation (33) (where the temperature distribution was specified); the disc temperatures were determined from the direct solution (where the Nusselt numbers were specified).

The temperatures of both surfaces of the instrumented disc were measured in the experiments; for the inverse solution of Equation (33), both the two sets of measured temperatures were used to calculate the averaged Nusselt numbers. (Apart from those on the cob surfaces, the differences between the two sets of temperature were smaller than the uncertainty in the measured values.)

4.5. Comparison with Experimental Measurements

Table 1 shows the main parameters and average Nusselt numbers for the 19 test cases of Atkins and Kanjirakkad [12]. For each of the four approximate Rossby numbers, the cases are presented in order of ascending Grashof number. It should be noted that all the cases shown in Table 1 were analysed in [4], but only selected cases are discussed below.

Table 1. Flow parameters and average Nusselt numbers for experiments of Atkins and Kanjirakkad [4].

Cases	Ro ≈ 5						Ro ≈ 1							Ro ≈ 0.6		Ro ≈ 0.3
	1a	1b	1c	1d	1e	1f	2a	2b	2c	2d	2e	2f	2g	3a	3b	4a	4b	4c	4d
$\mathrm{Ro}$	4.7	4.7	4.9	4.9	4.5	4.5	0.8	0.8	0.9	0.9	1.0	1.0	1.0	0.6	0.6	0.3	0.3	0.3	0.3
${\mathrm{Gr}}_{\mathrm{f}}/{10}^{11}$	0.0017	0.0030	0.0085	0.015	0.062	0.14	0.065	0.10	0.44	0.84	1.7	2.5	3.9	5.7	9.1	0.4	1.0	3.7	7.8
${\mathrm{Re}}_{\mathsf{\varphi }}/{10}^6$	0.078	0.077	0.19	0.19	0.46	0.45	0.46	0.45	1.1	1.1	2.1	2.1	2.1	3.5	3.1	1.4	1.4	3.1	3.0
$\mathsf{\beta }\mathsf{\Delta }\mathrm{T}$	0.08	0.17	0.05	0.11	0.09	0.24	0.09	0.16	0.11	0.23	0.13	0.19	0.32	0.15	0.32	0.06	0.16	0.12	0.29
${\mathrm{Re}}_{\mathrm{z}}/{10}^5$	0.19	0.19	0.50	0.50	1.1	1.1	0.19	0.18	0.51	0.50	1.1	1.1	1.1	1.1	1.1	0.20	0.20	0.48	0.48
${\mathrm{Nu}}_{\mathrm{av},\exp }$	28.7	30.7	51.6	58.2	92.3	109	47.4	53.4	96.7	126	131	170	233	126	225	45.3	82.5	72.1	146
${\mathrm{Nu}}_{\mathrm{av},\mathrm{th}}$	32.5	37.2	56.2	66.5	103	128	59.4	64.7	109	135	149	175	216	133	214	50.5	83.5	78.0	142

Figure 7 and Figure 8 show the comparison between the experimentally derived and modelled values of $\Theta$ and ${\mathrm{Nu}}_{\mathrm{f}}$ for two of the 19 cases analysed in [4]. These cases are typical of all the cases for ${\mathrm{Gr}}_{\mathrm{f}}>6\times {10}^9$, and it is believed that buoyancy-induced flow is unlikely to dominate at lower Grashof numbers. The solid curves in the figures show the theoretical distributions of $\Theta$ and ${\mathrm{Nu}}_{\mathrm{f}}$ obtained using the buoyancy model in conjunction with the general fin equation between $a^{\prime }$ and b, and the broken curves show the experimentally derived distributions. In general, an overestimate of the Nusselt numbers will result in an underestimate of the temperatures.

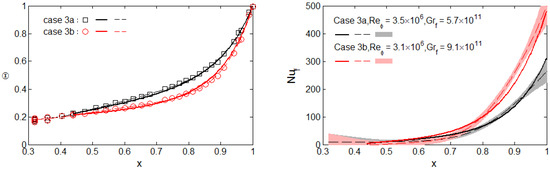
Figure 7. Distributions of temperature and Nusselt numbers for Ro ≈ 0.6. (Symbols denote measured temperatures; broken and solid lines represent experimental and theoretical results respectively; shading shows 95% confidence intervals on experimental Nusselt numbers) [4].

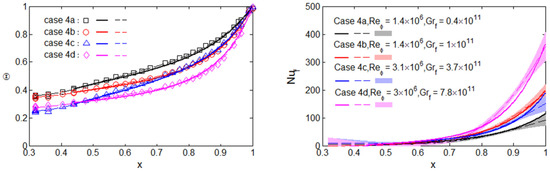
Figure 8. Distributions of temperature and Nusselt numbers for Ro ≈ 0.3. (Symbols denote measured temperatures; broken and solid lines represent experimental and theoretical results respectively; shading shows 95% confidence intervals on experimental Nusselt numbers) [4].

In Figure 7, for $\mathrm{Ro}\approx 0.6$, the Nusselt numbers increase as the Grashof number increases, but they all converge to a low value at the smaller radii. This suggests that, as the disc temperature tends to that in the core, the effects of buoyancy are weak in the inner part of the cavity.

Figure 8, for $\mathrm{Ro}\approx 0.3$, again shows mainly good agreement between the theoretical and experimental distributions of $\Theta$ and ${\mathrm{Nu}}_{\mathrm{f}}$. However, it should be noted that the maximum value of ${\mathrm{Nu}}_{\mathrm{f},\exp }$ for ${\mathrm{Gr}}_{\mathrm{f}}=3.7\times {10}^{11}$ is smaller than that for ${\mathrm{Gr}}_{\mathrm{f}}={10}^{11}$. This is an example of the compressibility effect discussed for the shrouds in Section 3: increasing the rotational speed increases the core temperature, which reduces the heat transfer from the disc to the core. As for the shrouds, there will be a maximum disc Nusselt number and a critical rotational speed above which the Nusselt number will decrease as the speed is further increased. The theoretical values of ${\mathrm{Nu}}_{\mathrm{f}}$ also show this effect, but it is not as marked as the experimental one.

5. Buoyancy-Induced Heat Transfer inside Compressor Rotors

Heat transfer from the shrouds and discs is discussed in Section 3 and Section 4, and in this section (which is based on [6]) the results are applied to the case of an open rotating cavity with an axial throughflow of cooling air. This includes calculating the temperature rise of the throughflow, which in turn involves estimating the heat transfer from the cob bore to the air.

5.1. Model of Heat Transfer from Shroud to Core

The equations derived in Section 3 are adapted for use here. To compare the theoretical predictions with the experimental measurements, the temperature of the shroud, $T_{sh}$, was assumed to equal $T_{o,b}$, the measured disc temperature at $r=b$, and the air temperature in the core close to the shroud, $T_{c,b}$, was calculated from Equation (A14) for $x=1$. Consequently

$${\mathrm{Nu}}_{\mathrm{sh}}=C{\left({\mathrm{Gr}}_{\mathrm{sh}}\mathrm{Pr}\right)}^{0.25}$$

(34)

where $C$ is an empirical constant, and the definitions of ${\mathrm{Nu}}_{\mathrm{sh}}$ and ${\mathrm{Gr}}_{\mathrm{sh}}$ are

$${\mathrm{Nu}}_{\mathrm{sh}}\stackrel{\mathrm{def}}{=}\frac{h_{sh}\left(s/2\right)}{k_{c,b}}=\frac{q_{sh}\left(s/2\right)}{k_{c,b}\left(T_{sh}-T_{c,b}\right)}$$

(35)

and

$${\mathrm{Gr}}_{\mathrm{sh}}\stackrel{\mathrm{def}}{=}\frac{{\rho }_{c,b}^2{\mathsf{\Omega }}_{\mathrm{c}}^{2}b}{{\mu }_{c,b}^2}\frac{T_{sh}-T_{c,b}}{T_{c,b}} {\left(\frac{s}{2}\right)}^3$$

(36)

The theoretical heat flux from the shroud can then be computed by

$$q_{sh}=2{\mathrm{Nu}}_{\mathrm{sh}}{k}_{c,b}\left(T_{sh}-T_{c,b}\right)/s$$

(37)

and

$${\dot{Q}}_{sh}=2\pi bs{q}_{sh}=4\pi b{k}_{c,b}{\mathrm{Nu}}_{\mathrm{sh}}\left(T_{o,b}-T_{c,b}\right)$$

(38)

5.2. Model of Heat Transfer from Cob to Axial Throughflow

The heat transfer from the cob bore to the throughflow is assumed to be by forced convection. In [6], it was assumed for simplicity (and to fit the available data) that

$${\mathrm{Nu}}_{\mathrm{cob}}=0.69{\mathrm{Re}}_{\mathrm{T}}{}^{0.37}$$

(39)

where

$${\mathrm{Nu}}_{\mathrm{cob}}\stackrel{\mathrm{def}}{=}\frac{q_{cob}l}{k_f\left(T_{cob}-T_f\right)}$$

(40)

and

$${\mathrm{Re}}_{\mathrm{T}}\stackrel{\mathrm{def}}{=}\frac{{\rho }_{f}Ul}{{\mu }_f}$$

(41)

The heat flow from the cob to the throughflow can then be calculated from

$${\dot{Q}}_{cob}=2\pi al{q}_{cob}$$

(42)

5.3. Model of Temperature Rise of Axial Throughflow

The heat transferred from the discs and shroud to the core, together with the heat transferred from the cob, all contribute to the temperature rise of the throughflow. Referring to the control volume shown in Figure 9, for disc i, it is assumed that ${\dot{Q}}_{u,i}\approx {\dot{Q}}_{d,i}$. It is also assumed that, as the rotational speed of the core is very close to that of the discs, the work term is significantly smaller than the heat transfer terms. If ${\dot{m}}_f$ is the mass flow rate of the throughflow, then an energy balance for the control volume shows that

$$\mathsf{\Delta }{T}_f=\frac{2{\dot{Q}}_{u,i}+{\dot{Q}}_{sh,i}+{\dot{Q}}_{cob,i}}{C_p{\dot{m}}_f}$$

(43)

where $\mathsf{\Delta }{T}_f=T_{f,i+1/2}-T_{f,i-1/2}$.

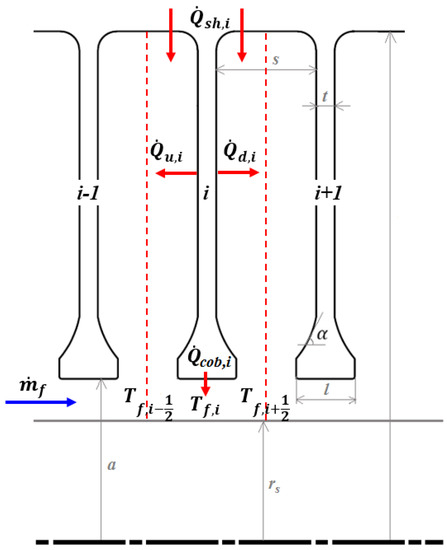
Figure 9. Control volume for temperature rise of axial throughflow [6].

5.4. Comparison between Theoretical and Experimental Values

5.4.1. Disc Nusselt Numbers and Temperatures

The experimentally derived Nusselt numbers were calculated from the temperature measurements using the Bayesian method described in Section 4. The modelled temperatures and Nusselt numbers for the discs were predicted using the buoyancy model in conjunction with the direct solution of the general fin equation. (It should be noted that the Nusselt numbers are the average for the upstream and downstream surfaces of the instrumented disc.) The ranges of the experimental parameters shown in Table 2 were: $4.1\times {10}^{11}<{\mathrm{Gr}}_{\mathrm{f}}<{10}^{12}, 0.15<\beta \mathsf{\Delta }T<0.35, 1.6\times {10}^6<{\mathrm{Re}}_{\mathsf{\varphi }}<3.0\times {10}^6, 1.1\times {10}^5<{\mathrm{Re}}_{\mathrm{z}}<5.1\times {10}^5$ and $0.1<\mathrm{Ro}<0.6$. It should be noted that all the cases shown in Table 2 were analysed in [6], but only selected cases are discussed below.

Table 2. Flow parameters and experimental and theoretical average disc temperatures [6].

Case	Ro ≈ 0.6	Ro ≈ 0.3		Ro ≈ 0.2						Ro ≈ 0.1
	a	b1	b2	c1	c2	c3	c4	c5	c6	d
Ro	0.61	0.31	0.31	0.16	0.16	0.18	0.17	0.17	0.17	0.10
Grf/1011	2.5	10	10	4.2	4.5	6.8	7.2	7.2	7.8	4.1
$\beta \left(T_b-T_f\right)$	0.32	0.35	0.35	0.15	0.16	0.33	0.32	0.32	0.34	0.29
Reϕ/106	1.6	3.0	3.0	3.0	3.0	2.5	2.7	2.7	2.7	2.1
Rez/104	5.1	5.0	5.0	2.5	2.5	2.4	2.4	2.4	2.5	1.1
$N_{shaft}/N_{disc}$	1.0	0.34	1.0	0.34	−0.34	1.0	0.34	−0.34	0	0
${\Theta }_{av,exp}$	0.347	0.349	0.330	0.499	0.494	0.357	0.377	0.385	0.368	0.413
${\Theta }_{av,th}$	0.334	0.332	0.334	0.540	0.518	0.364	0.370	0.367	0.357	0.427

The Coriolis parameter defined by Equation (30) was chosen to minimise the difference between the theoretical and experimental average disc temperatures, ${\Theta }_{av,th}$ and ${\Theta }_{av,exp}$ respectively, where

$${\Theta }_{av}=\frac{2{\int }_{x_a}^1\Theta xdx}{1-x_a^2}$$

(44)

A value of $\mathrm{Co}=0.030$ provided a good fit with a standard deviation of 0.019, and the individual values of ${\Theta }_{av,th}$ and ${\Theta }_{av,exp}$ are included in Table 2. (It was shown in [4] that the theoretical Nusselt numbers were relatively insensitive to the value of $\mathrm{Co}$. In that paper, the Rossby numbers tended to be higher and their range ($0.3<\mathrm{Ro}<5$) larger than for the experiments described here, which are more representative of the Rossby numbers found in aeroengine compressors; a value of $\mathrm{Co}=0.07$ was found to give the best fit to the data. It is possible that $\mathrm{Co}$ may increase as $\mathrm{Ro}$ increases, but more evidence is required to support that conjecture.)

As in [4], and consistent with the experimental evidence, the modelled Nusselt numbers were assumed to be zero at the inner radius of the disc and, as stated above, a value of $\mathrm{Co}=0.030$ was used for the Coriolis parameter in all 10 cases. It should be noted that—unlike in [4]—the results shown here include the modelled Nusselt numbers and temperatures for the cob. An over-prediction of ${\mathrm{Nu}}_{\mathrm{f}}$ tends to result in an under-prediction of the disc temperature, and vice versa, but in the main there was good agreement between the modelled and experimental results. It should also be noted that the relative speed of the inner shaft (see Table 2) appears to have had no significant effect on the results. (This was also observed in [13] for heat transfer measurements on the shroud in a multi-cavity compressor rig.)

Comparison between Figure 10 and Figure 11 shows the effect of compressibility on the Nusselt numbers. The Grashof number is lower but the maximum value of ${\mathrm{Nu}}_{\mathrm{f}}$ is higher in Figure 10 than the corresponding values in Figure 11. The reduction in ${\mathrm{Nu}}_{\mathrm{f}}$ despite the increase in ${\mathrm{Gr}}_{\mathrm{f}}$ is caused by the fact that ${\mathrm{Re}}_{\mathsf{\varphi }}$ in Figure 11 is higher (and therefore the rise in core temperature is also higher) than that in Figure 10. (It should also be noted that the modelled temperatures tended to be less accurate in [6] compared with those in [4]. The reason for this is that a convective boundary condition was used at $r=a$ in [6] whereas the measured temperatures at $r=a^{\prime }$ were used in [4].)

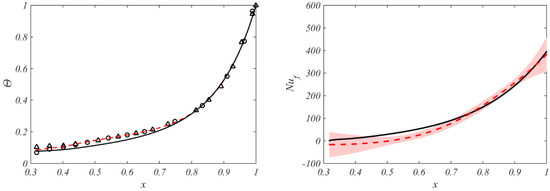
Figure 10. Distributions of nondimensional temperature and Nusselt numbers for Case a ($\mathrm{Ro}\approx 0.6,{\mathrm{Gr}}_{\mathrm{f}}=2.5\times {10}^{11},{\mathrm{Re}}_{\mathsf{\varphi }}=1.6\times {10}^6,{\mathrm{Re}}_{\mathrm{z}}=5.1\times {10}^4$) Solid lines are theoretical curves; broken lines are results from Bayesian model, and shading shows uncertainty in ${\mathrm{Nu}}_{\mathrm{f}}$; symbols denote temperature [6].

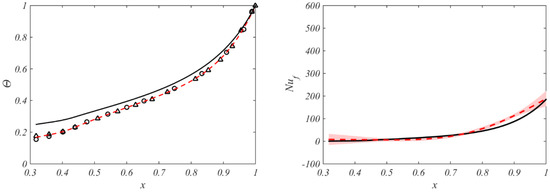
Figure 11. Distributions of nondimensional temperature and Nusselt numbers for Case c1 ($\mathrm{Ro}\approx 0.2,{\mathrm{Gr}}_{\mathrm{f}}=4.2\times {10}^{11},{\mathrm{Re}}_{\mathsf{\varphi }}=3.0\times {10}^6,{\mathrm{Re}}_{\mathrm{z}}=2.5\times {10}^4$). Solid lines are theoretical curves; broken lines are results from Bayesian model, and shading shows uncertainty in Nu; symbols denote temperature measurements [6].

5.4.2. Temperature Rise of Throughflow

The method used to predict $\mathsf{\Delta }{T}_f$, the bulk-mean total-temperature rise of the axial throughflow, was described in Section 5.3. For convenience, Equation (43) is repeated below removing the subscript i and adding th to denote the theoretical or modelled value of $\mathsf{\Delta }{T}_f$.

$$\mathsf{\Delta }{T}_{f,th}=\frac{2{\dot{Q}}_u+{\dot{Q}}_{sh}+{\dot{Q}}_{cob}}{C_p{\dot{m}}_f}$$

(45)

Knowing the radial distribution of the disc temperatures and the Nusselt numbers, ${\dot{Q}}_u$, the heat transfer from the upstream surface of the disc, can be calculated by integrating the heat flux from $r=a$ to $r=b$. Knowing the value of $T_{c,b}$, the modelled core temperature at $r=b$, ${\dot{Q}}_{sh}$, the heat transfer from the shroud, can be calculated using Equations (34) to (38). Knowing the value of $T_{o,a}$, ${\dot{Q}}_{cob}$, the heat transfer from the cob, can be calculated using Equations (39) to (42).

Figure 12 shows the comparison between the modelled and experimental values of ${\mathsf{\Delta }\Theta }_f$ where

$${\mathsf{\Delta }\Theta }_f=\frac{\mathsf{\Delta }{T}_f}{T_{o,b}-T_f}$$

(46)

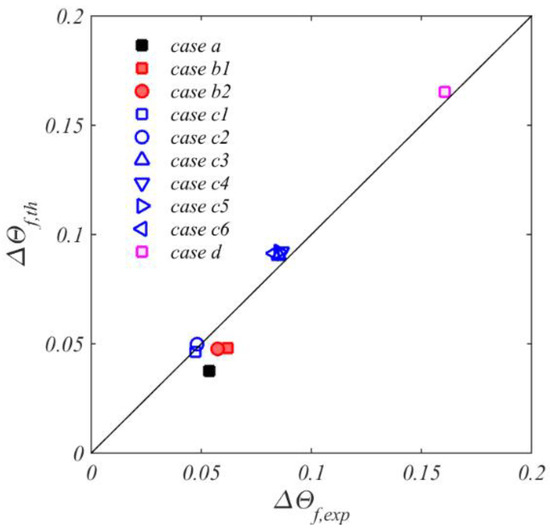
Figure 12. Comparison between modelled and experimental nondimensional temperature rise of axial throughflow [6].

The modelled values were calculated using a value of $C=0.44$ in Equation (34) for the shroud heat transfer. This value, which was chosen to minimise the least-squares error between the modelled and experimental values, is intermediate between 0.54 for laminar free convection from a horizontal plate [8] and 0.32 for the shrouds in closed rotating cavities [2]. (The correlation of Long and Childs [13] produced significant overestimates of the temperature rise.) The predicted relative contributions of heat transfer from the shroud, both disc surfaces and the cob bores to the rise in throughflow temperature were approximately 62%, 37% and 1% respectively for the range of conditions tested.

It is important to emphasise that the empirical correlation for the cob Nusselt number given by Equation (39) may not be valid outside the range of experiments reported in this paper. The values of ${\mathrm{Nu}}_{\mathrm{cob}}$ used here were between 42 and 52, and an average value of 48 gave predictions similar to the ones discussed. As the relative effect of the heat transfer from the cob bore has only a very small effect on the temperature rise of the throughflow, and as the results are only weakly affected by the precise value of ${\mathrm{Nu}}_{\mathrm{cob}}$, it is unlikely that other correlations would make a significant difference to the predictions.

6. Conclusions

This overview paper has collected together the equations from five separate papers on theoretical modelling of buoyancy-induced flow and heat transfer inside rotating cavities. Predictions from the models, all of which are for laminar flow, have been compared with measurements made in open and closed compressor rigs for a range of Rossby, Reynolds and Grashof numbers representative of those found inside the compressor rotors of aeroengines. A total of 223 separate tests was analysed in the validation of the models, and good agreement between the predictions and measurements was achieved for most of these cases.

For rotating flows, the gravitational term in the Grashof number is replaced by the local centripetal acceleration in the cavity. It should also be noted that buoyancy-induced flows are strongly conjugate: the buoyancy equations are coupled with the conduction equations for the discs. For the discs, the temperatures were solved using the 1D conduction equation for a circular fin, which proved to be acceptably accurate for the cases studied. In addition, a Bayesian statistical model was used, in conjunction with the fin equation, to compute the Nusselt numbers from experimental temperature measurements. (A 2D or 3D version of Laplace’s equation could be used instead of the fin equation but this would take more time to solve.)

The buoyancy model for the disc is based on laminar Ekman-layer flow, and it includes a Coriolis parameter, Co, which is in effect the ratio of Coriolis to buoyancy forces inside the cavity. For the range of experimental cases analysed, Co was treated as an empirical constant with a value between 0.03 and 0.07. It typically took only seconds for a laptop to solve the coupled buoyancy and conduction equations for each case: by contrast, CFD would take days or even weeks to solve a single case.

The model for the shrouds is based on a standard correlation for laminar free convection from a horizontal plate but with the gravitational acceleration replaced by the centripetal one. This correlation requires an empirical constant, C, the value of which was taken to be between 0.32 and 0.44 (compared with 0.54 for a horizontal plate) for the range of experimental cases analysed.

The inviscid compressible core in the cavity, which rotates at an angular speed close to that of the discs, is assumed to be adiabatic. Consequently the core temperature increases with increasing rotational speed, and this increase attenuates the heat transfer from the discs and shrouds. There are therefore maximum Nusselt numbers for the discs and shrouds: above a critical Grashof number, the Nusselt numbers decrease as the Grashof number increases.

The heat transfer between the bore of the cobs and the axial throughflow in an open cavity was assumed to be by forced convection. An empirical correlation was assumed for the cob Nusselt number, and two empirical constants were chosen to provide the best fit between the measured and predicted disc temperatures. The relative heat flow from the cob to the throughflow was very small (about 1% of the total heat flow), and so the predicted temperature rise of the throughflow was relatively insensitive to the magnitude of the cob Nusselt numbers.

The modelled values of the heat flow from the shroud, discs and cob were used to predict the temperature rise of the throughflow, and good agreement was achieved between the predicted and measured values. The average contributions from the shroud, both disc surfaces and the cob bores to the temperature rise were predicted to be approximately 62%, 37% and 1% respectively for the range of conditions tested.

From experiments at large Rossby numbers and small Grashof numbers, it appeared that buoyancy-induced flow was not the dominant convective mode below Grashof numbers of the order of ${10}^9$. The fact that laminar buoyancy models can be used for large Grashof numbers (up to ${10}^{12}$), where most engineers would expect the flow to be turbulent, is attributed to the large Coriolis accelerations in the fluid core and to the fact that there is only a small difference between the rotational speed of the core and that of the discs. It should also be noted that the available experimental evidence suggests that neither the rotational speed of the inner shaft nor the relative direction of its rotation had any significant effect on the heat transfer inside the cavity.

Caution should be exercised when applying these models to engine conditions. The values of the empirical constants (particularly C and Co) used here are likely to be dependent on the cavity geometry and on the Rossby number, but more experimental evidence is needed to confirm this. In particular, there is reason to believe that the empirical constants will change as the axial gap between the cobs decreases and the open cavity starts to behave like a closed one, with a corresponding decrease in the Nusselt numbers. Although the results from 223 tests provide strong evidence that laminar flow occurs for Grashof numbers up to ${10}^{12}$, there is no evidence to confirm—as the authors believe—that the flow will remain laminar at the larger Grashof numbers found in some aeroengine compressors.

The buoyancy models have so far been validated only for steady-state conditions, and transient comparisons cannot be made until suitable experimental data becomes available. The conditions for transition between buoyancy-induced and stratified flow have yet to be accurately quantified, and last—but by no means least—the effects of different temperatures between the two discs in a cavity have yet to be investigated. The authors are currently building a compressor rig to address many of the above points, and in the coming years more experimental data will become available.

References [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54] provide some additional background reading on buoyancy-induced rotating flows.