Abstract
Formal methods offer well-defined means for mathematical verification of the functional specifications of software systems. For model-based engineering, model checking is a verification technique that explores all possible system states. The Aviation Scenario Definition Language is a domain-specific language designed based on a scenario development process from a model-driven engineering perspective. It aims at providing a well-structured definition language to specify departure, en route, re-route, and landing scenarios. This paper uses statecharts and a model checker for the verification of each scenario generated and uses examples to demonstrate conformance to the rules established in the statecharts to verify the logic of all future scenarios.
1. Introduction
Verification and validation (V&V) are software processes that enable checking to ensure that the software conforms to requirements and that requirements are correctly formulated, respectively. Basically, verification demonstrates that a program is consistent with its specifications. Model-based verification techniques are based on models describing the possible system behavior in a mathematically precise and unambiguous manner. Verification is essential because it is likely that it leads to the discovery of incompleteness, ambiguities, and inconsistencies in informal system specifications [1].
Formal methods are a set of well-defined mathematical languages and techniques for the specification, modeling, and verification of systems [2]. In both software and hardware design of complex systems, verification takes up more time and effort than construction. Formal methods offer a large potential to obtain an early integration of verification in the design process, to provide more effective verification techniques, and to reduce the verification time [1].
The Aviation Scenario Definition Language (ASDL) has been proposed as a domain-specific language providing a well-structured definition language to specify departure, en route, re-route, and landing scenarios [3]. Using the Eclipse Modeling Framework (EMF), ASDL offers a holistic conceptual metamodel, which can be used to define all entities, attributes, and relationships needed to specify a complete flight scenario [4].
At the current conceptual level, while all the specifications have been captured and simple scenarios generated using the tool, there has been no formal approach for the verification of the abilities of neither the tool nor the scenarios. In this paper, statecharts will be utilized for the verification of each scenario generated using ASDL. The underlying assumption is that once a set of rules has been established and verified for the type of scenario required, all other scenarios of that type only need to conform to these rules. That is, there is no need for separate verification of each generated scenario as long as its adheres to these ASDL guidelines.
2. Background
2.1. ASDL
Domain-Specific Languages (DSLs) are computer programming languages with considerable expressiveness, which is focused on a specific domain [5]. They are developed based on the concepts, terms, and the relations among them within the context of that domain. Such languages support higher levels of abstractions than general-purpose modeling languages and are closer to the problem domain than they are to the implementation domain. Consequently, a DSL follows the domain abstractions and semantics, allowing modelers to perceive themselves as working directly with domain concepts. Furthermore, the rules of the domain can be included into the language as constraints, disallowing the specification of illegal or incorrect models [6].
ASDL was designed as an aviation-specific DSL using a scenario development process from a Model-Driven Engineering (MDE) perspective [7]. The aim of the design process was to create a conceptual model, and then to provide transformation of the model from the source [4]. A model in this context consists of objects and relationships between them. The meta-model of the modeling language specifies the types of all the objects and their possible interrelationships in a specific domain [8]. Essentially, a metamodel is a model that defines the structure of a modeling language [9]. The Base Object Model (BOM) metamodel was used as the underlying metametamodel for ASDL [10]. ASDL was modeled using an ontological approach similar to the one outlined by Pereira et al. [11]. The ontology was first defined in Web Ontology Language (OWL) format using protégé; however, the mapping from ontology to DSL metamodel was performed manually. Further discussion about the ontological development of ASDL has been presented by the authors in [12].
ASDL uses basic BOM elements such as the concepts of the sequence of events and interplay between various simulation elements, but has extended the base metamodel to constitute a set of entities that are specific to the aviation domain. This metamodel, which comprises of both BOM and the aviation-specific metamodel, can be used to model conceptual flight scenarios which can later be transformed into executable scenarios and deployed in simulators. The metamodel was defined using EMF to describe the entities involved and the relationships between them [13].
The ASDL Scenario object currently allows users to define three different kinds of scenarios: departure, rerouting and landing. It also includes pilots, airports, runways, control towers, flight properties, weather patterns and aircraft. This metamodel was integrated with the BOM entities of interplays, state machines and events to describe a flight scenario [4].
The current scenario generation process for flight simulators requires a domain expert to explain scenarios to a modeling and simulation expert, who then creates the scenarios and delivers them for the target simulator. ASDL aims to simplify this process by providing an interface to create scenarios directly, which are validated before deployment. Thus, users of flight simulators can create scenarios to practice as and when needed without needing an expert at hand. The full ASDL metamodel has been described by the authors in [4].
2.2. Formal Methods
Formal verification is the application of formal or mathematical methods to perform the verification of a system. This can be done in a multitude of ways by using, 1) exhaustive exploration (model checking); (2) experiments with a restrictive set of scenarios in the model (simulation); or (3) experiments with a restrictive set of scenarios in the real world (testing) [1].
Model checking is an automatic technique for verifying finite state concurrent systems [14]. It explores all possible system states to determine all paths that could be taken. In this case, a model of a program or process is constructed. A model of a program consists of states and transitions. A specification or property is a logical formula that must hold true for the system to pass a verification check. A model checker, which is the software tool that performs the model checking, examines all possible system scenarios in a systematic manner. This model checker exhaustively analyses all possible executions of the model to establish that some property holds. These properties need to be derived from system requirements. Therefore, it is possible to use a model checker to formally verify that in every execution of a given program, the program will always do something desirable. In other words, it can be formally verified that a given system model truly satisfies a certain property [1].
Model checkers work with formal models of the systems to be analyzed, which in many cases are either automatically extracted from the system or created based on the domain logic of the model [15]. Among various methods, one of the common approaches to contrast formal models is utilizing finite state transition systems or finite state machines [16]. Finite state machines and their corresponding state-transition diagrams (or statecharts) are formal mechanism for describing the dynamic behavior of complex systems [17]. Statecharts are basically directed graphs, with nodes denoting states and arrows denoting transitions. These arrows are labelled with the triggering events and guarding conditions in order to capture the circumstances around transitions.
A state describes some information about the behavior of a system at a certain moment. Transitions specify how the system can evolve from one state to another [1]. A transition system is described in the form of a finite ordered list of elements (tuple). The definition of a transition system TS is that it is a tuple (S, Act, →, I) where
- S is a set of states,
- Act is a set of actions,
- →⊆ S × Act × S is a transition relation, and
- I ⊆ S is a set of initial states.
TS is called a finite transition system if S and Act are finite. An essential measure used in the verification of properties of a transition system is the idea of reachable states. For a transition system TS = (S, Act, →, I), a state s ∈ S is called reachable in TS if there exists an initial, finite execution fragment such that [1]
Reach (TS) denotes the set of all reachable states in TS. In order to prove that a model works, it is essential that all transitions to reachable states meet the properties defined in the transition system. This verification will be attempted by the model checker described here.
A finite automaton (FA) is a graph with a finite number of vertices, which depict the states. Edges of an FA are used to define transitions and are annotated with symbols showing the events that lead to transitions [18]. In addition, one of the states must be the (unique) initial state, and any number of states, from 0 to the total number of states n, are chosen as final states (visually depicted with a circle inside a circle). FA graphs have been used to present the transition system used to define ASDL scenarios in this paper.
2.3. Model Checking Tools
Domain-specific modeling (DSM) is a manner of developing systems that uses domain-specific languages (DSLs) to represent the various facets of a system, in terms of models [19]. DSLs follow the domain abstractions and semantics, allowing modelers to work directly with domain concepts and knowledge.
One of the principles used for model-checking uses time as a formalism for specification of the properties of a system. This is called Temporal Logic (TL) and is used for reactive systems, where changes happen based on events or messages that are triggered. One type of TL is Linear Temporal Logic (LTL), which consists of a sequence of states where each point in time has a unique successor based on a linear-time perspective [1].
In order to explicitly define and check the behavior of such systems, there are a few tools that are currently in use. SPIN is a generic verification system that supports the design and verification of asynchronous process systems [20]. SPIN accepts correctness properties expressed in LTL. The algorithm terminates when an acceptance cycle is found, or, when no counterexample exists, when the complete intersection product has been computed [20]. This means that every possible state transition has been computed, and no example of the language violating the LTL property has been found. The LTL model checker included in SPIN accepts programs that are written in the PROcess MEta Language (PROMELA) [21]. PROMELA differs from ordinary programming languages in that it has certain non-deterministic specification oriented constructs [22]. The SPIN model checker can automatically determine whether a program satisfies a property, and in case it does not, can generate an error trace that shows where the rules are being violated. SPIN is available for use for free under the General Public License (GPL), which is an open-source license.
Another symbolic model checker, called NuSMV, is designed to be an open and flexible platform for model checking [23]. The underlying principle of NuSMV is exactly the same as that of SPIN: the verified system is modeled as a finite state transition system, and the specifications are expressed in LTL. Then, state space of the transition system is exhaustively explored to check if the specifications are satisfied. When a specification is found not to hold, a counterexample is produced. The termination of model checking is guaranteed by the finiteness of the model [23]. NuSMV is available with an open-source license and has a separate syntax for its input language, which is explained in the user manual [24].
Two open-source tools have been discussed briefly that allow for the definition of models and perform automated checking to ensure all defined properties are met. Both these tools are available readily for use and can be utilized to implement a model checker for ASDL. However, two problems arise in using such a tool: (1) the input language is different, so code needs to be written separately for model checking, and (2) the tools are not a part of EMF which is the platform ASDL is built on, so an integration code would be required to invoke the model checker from the scenario builder in order to check that it meets the requirements. For these two reasons, the authors decided that a model checker that provides these core functionalities of checking whether properties are satisfied and providing a trace of states covered would be written in Java within EMF for ASDL scenario verification.
3. Formal Model for ASDL Landing Scenario
The elements of the Aircraft class in ASDL are callSign, origin, destination, landingRunway, weatherProperties, FlightProperties, pilot, atc and state. The purpose of the state attribute included here is to describe the behavior of the aircraft at any specific time. In this case, state change occurs when Air Traffic Control (ATC) issues or denies the specific clearance requested by the pilot. The clearance status is changed by ATC and in response to this clearance, the state of the aircraft is changed by the pilot to reflect the next action required [4].
Statecharts constitute a visual formalism for describing states and transitions in a modular fashion [17]. A simple state diagram for a normal landing scenario of an aircraft can be seen in Figure 1.
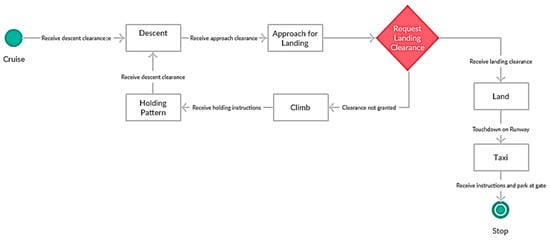
Figure 1.
Statechart for normal landing scenario.
In this case, it can be seen that the state space for an aircraft while landing is
where
The actions undertaken to get from one state to another are
where
Given these states and actions along with the statechart defining the transitions, the transition relations (→⊆ S × Act × S) can be said to be the following ordered pairs:
- Cruise → Receive Descent Clearance → Descent: (c, rdc, d)
- Descent → Receive Approach Clearance → Approach: (d, rac, a)
- Approach → Receive Landing Clearance → Land: (a, rlc, l)
- Approach → Clearance Not Granted → Climb: (a, cng, cl)
- Climb → Receive Holding Instructions → Holding Pattern: (c, rhi, h)
- Holding Pattern → Receive Descent Clearance → Descent: (h, rdc, d)
- Land → Touchdown on Runway → Taxi: (l, trw, t)
- Taxi → Park at Gate → Stop: (t, pag, s)
The statechart can be translated into a transition system as shown in Figure 2. For all simulations or “runs” of this transition system, the initial state is always cruise and the terminal state is always stop. Any other scenario is not considered valid and would be rejected during the verification process by the model checker.
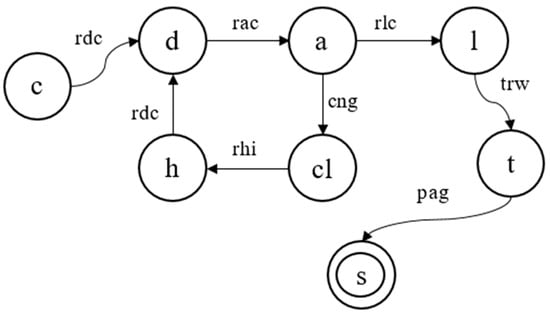
Figure 2.
Finite automaton (FA) of states and allowed transitions based on statechart.
However, such a simple transition system has limitations. While a normal landing can easily be defined using these parameters, it takes away the ability to model unusual scenarios. In the event that an emergency landing is required and no tower can be contacted, there will be no authority issuing clearances, yet the aircraft will need to descend in order to make a safe return to the ground. In the same manner, if an unexpected landing is made on a landing strip unattached to an airport, the aircraft will still be able to come to a complete stop without parking at a gate. These extraordinary events need to be considered in order to make a formal model comprehensive, otherwise these tests will not be passed. After considering such events, a revised transition system was obtained with additional actions that help the aircraft transition between states. In our case, manual modes were added so that the pilot can change the state of the aircraft without receiving instructions from ATC. These are switching to manual descent mode (mdm), manual approach mode (mam) and manual landing mode (mlm). Furthermore, touchdown on runway (trw) was changed to say touchdown on ground (tdg) and park at gate (pag) was changed into brake to a halt (bth). The new set of possible Actions is
Given the newer sets of actions along with the statechart defining the transitions, the transition relations (→⊆ S × Act × S) can be said to be the following ordered pairs:
- Cruise → Receive Descent Clearance → Descent: (c, rdc, d)
- Cruise → Manual Descent Mode → Descent: (c, mdm, d)
- Descent → Receive Approach Clearance → Approach: (d, rac, a)
- Descent → Manual Approach Mode → Approach: (d, mam, a)
- Approach → Receive Landing Clearance → Land: (a, rlc, l)
- Approach → Manual Landing Mode → Land: (a, mlm, l)
- Approach → Clearance Not Granted → Climb: (a, cng, cl)
- Climb → Receive Holding Instructions → Holding Pattern: (c, rhi, h)
- Climb → Manual Descent Mode → Holding Pattern: (c, mdm, d)
- Holding Pattern → Receive Descent Clearance → Descent: (h, rdc, d)
- Holding Pattern → Manual Descent Mode → Descent: (h, mdm, d)
- Land → Touchdown on Ground → Taxi: (l, tdg, t)
- Taxi → Brake to Halt → Stop: (t, bth, s)
The newer transition system is shown in Figure 3. The ‘˅’ operator refers to logical or, such that either of the actions could result in the state transition. It can be observed that no changes are made in the holding loop of the transition system, as this state would only be entered in the event that landing clearance is not granted, and hence, there is no need to have a manual mode for it. However, under emergency conditions, it is possible that the pilot may want to descend or land on his own without clearance, so he is able to engage that mode both from the climb and the hold states.
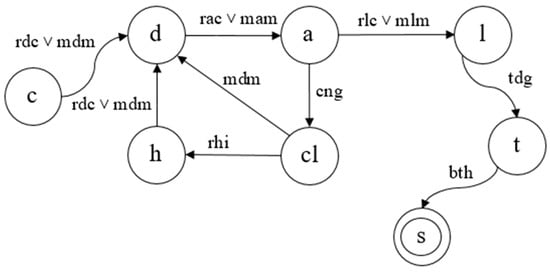
Figure 3.
Modified transition system based on new rules.
In this modified transition system, while actions have been expanded to suit our needs, the states and transitions have not changed. For all simulations or “runs” of this transition system, the initial state is still cruise and the terminal state is still stop. Any other scenario is not considered valid and would be rejected during the verification process by the model checker.
4. Verification Using Formal Model
The transition system shown in Figure 3 is considered the formal model of the system which defines the behavior of the system. This can be used to verify the completeness and correctness of a generated scenario. Completeness occurs when the scenario begins in the initial state and ends at the terminal state. Correctness means that the actions and transitions that occur between states conform to the formal statechart used to describe the model.
Model verification takes in the transitions of a system and then verifies that all runs or simulations of that system satisfy given properties. In the case of landing scenarios in ASDL, the properties are
- P1: The initial state must be cruise.
- P2: The terminal state must be stop.
- P3: A minimum of five transitions must occur between cruise and stop.
- P4: Each sequence must begin with cruise → descent → approach.
- P5: Each sequence must end with land → taxi → stop.
In order to verify this, an ASDL landing model checker was implemented by the authors in Java within Eclipse Modeling Framework. Given all the states and transitions as defined earlier, the model checker accepts two inputs: (1) the initial state; and (2) the set of actions. In this case, each unique action only leads to one state, so the paths can be defined easily without needing to run the model multiple times for the same input sequence. Once these values are provided, the model checker runs through the transitions based on the actions and determines whether the input scenario meets the conditions for a valid model or not.
The code in the model checker provides a list of all the properties that must be true as well as all the transitions possible from any given state, and the actions which trigger these transitions. Once an initial state has been provided, the first action is checked against that state. If the action triggers a transition, it is recorded, and the next action is checked with respect to all the transitions possible from the newer state. If, on the other hand, the action does not trigger a transition, no changes are made and the code proceeds to the next action to check the same. Once all actions have been processed, the code looks at the states that were reached and verifies that the sequence satisfies all the properties of the model.
In the case of ASDL, there are few properties that need to be satisfied, and all of these can be checked simply by looking at the sequence of states. However, additional data is provided by the model checker in the form of the number of states present within the transition system, the number of states that were reached during the scenario, and the number of actions that were performed. A list of transitions that occurred during the run is also provided by the model checking code. In the case that any property is not met, the entire model run is considered invalid.
5. Scenario Case Studies
A normal landing is defined in ASDL for a flight cruising on its way to the destination airport. In natural language, the sequence of events that occurs is described as follows:
An aircraft begins in cruise mode and the pilot receives descent and approach clearance as requested. Landing clearance is granted next and the pilot is able to touchdown, taxi, and park at the gate in order to complete a normal landing.
When this scenario is described in ASDL, the state machine code is generated in XML Metadata Interchange (XMI) format and a snippet is shown in Figure 4.

Figure 4.
XMI code for landing scenario.
This can be seen as part of the EMF user interface snapshot in Figure 5. Each state is associated with another state as a part of its exit condition (or the next state) and has an action associated with the transition. In the case of ASDL, each action must have a sending and a receiving entity as well as the event that triggers the transition.
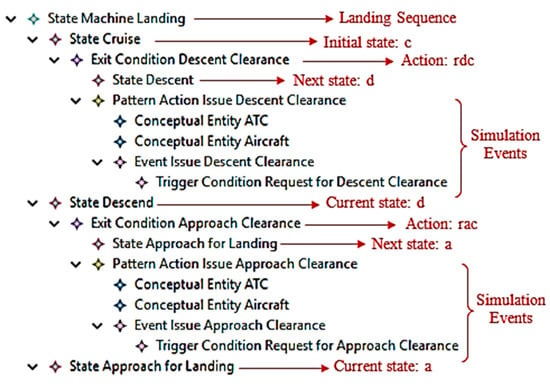
Figure 5.
State machine of normal landing scenario.
For this sample scenario, the states are in the order: c, d, a, l, t, s. Consulting the state transition diagram (Figure 3), the following items need to be checked:
Initial state is cruise: This is correct in the given scenario. P1 is met.
Final state is stop: This is correct in the given scenario. P2 is met.
The transitions are correct: c → d → a → l → t → s is an acceptable path in the formal model. This is correct in the given scenario. There are five transitions between c → s, the starting sequence is c → d → a, and the ending sequence is l → t → s. P3, P4 and P5 are met.
The actions are correct if
- c → d occurs when the action is rdc: meets the requirement
- d → a occurs when the action is rac: meets the requirement
- a → l occurs when the action is rlc: meets the requirement
- l → t occurs when the action is tdg: meets the requirement
- t → s occurs when the action is bth: meets the requirement
Now that it has been performed manually, it can be compared to the model checker. Running the initial state {c} and the set and order of actions {rdc, rac, rlc, tdg, bth} through the automated model checker gives the output shown in Figure 6.

Figure 6.
Model checker output for sample scenario.
It can thus be shown that this given scenario meets all the rules set forth by ASDL for a correct landing scenario. This scenario can now be generated and used for simulation purposes. In this case, six out of eight total states were reached and the order of transitions can be seen in the output frame.
One other scenario which required the pilot to enter into a holding pattern twice was verified with the model checker. The natural language description of the scenario is as follows:
An aircraft begins in cruise mode, and the pilot receives descent and approach clearance as requested. Landing clearance is not granted when requested, and the pilot is given holding instructions. After some time, the same process is repeated, where descent and approach clearances are granted, but the runway is again not available for immediate landing. Further holding instructions are sent to the pilot. Finally, all the clearances are received in order, and a normal landing is completed by the pilot.
In this case, the sequence of actions would be {rdc, rac, cng, rhi, rdc, rac, cng, rhi, rdc, rac, rlc, tdg, bth}. By looking over the state transition diagram, the expected output is that all eight states are reached and thirteen actions are performed.
For this sample scenario, the states are in the order: c, d, a, cl, h, d, a, cl, h, d, a, l, t, s. Consulting the state transition diagram (Figure 3), the following items need to be checked:
Initial state is cruise: This is correct in the given scenario. P1 is met.
Final state is stop: This is correct in the given scenario. P2 is met.
The transitions are correct: c → d → a → cl → h → d → a → cl → h → d → a → l → t → s is an acceptable path in the formal model. This is correct in the given scenario. There are 13 transitions between c → s, the starting sequence is c → d → a, and the ending sequence is l → t → s. P3, P4 and P5 are met.
The actions are correct if
- c → d occurs when the action is rdc: meets the requirement
- d → a occurs when the action is rac: meets the requirement
- a → cl occurs when the action is cng: meets the requirement
- cl → h occurs when the action is rhi: meets the requirement
- h → d occurs when the action is rdc: meets the requirement
- a → l occurs when the action is rlc: meets the requirement
- l → t occurs when the action is tdg: meets the requirement
- t → s occurs when the action is bth: meets the requirement
Now that it has been performed manually, it can be compared to the model checker. When this data was input into the model checker, the output shown in Figure 7 was obtained.
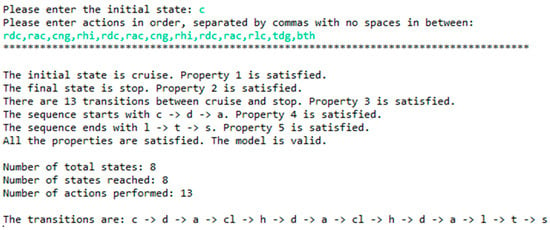
Figure 7.
Model checker output for sample scenario with holding pattern.
It can be seen that the output obtained matches the expected output exactly. The transitions listed by the model checker can be traced in the transition system diagram. Now that the model checker has been shown to verify the properties and rules of the ASDL state transition system, other scenarios for different types of landing can be considered, and the same method can be used to verify their completeness and correctness.
6. Conclusions
This paper looked at the creation of scenarios in ASDL and created a formal model to define landing scenarios using statecharts and transition systems. This was then verified using a model checker implemented using EMF to fully define the rules of the language and an example scenario was checked against this formal model. The landing scenario model has been verified as being valid as long as all the properties defined in the formal model are satisfied. The model checker implemented has been shown to model two landing scenarios: a normal landing, and a landing with a holding pattern. This process can be extended for the four other general landing scenarios: crosswind landing, short-field landing, soft-field landing and unprepared field landing, and also provides the ability to define a scenario in manual mode for emergency landings. This extension has not been described, but can be observed within the statecharts as the steps have all been described. More complex scenarios would loop around the same states in order to land an aircraft. This model checker has been implemented using Java in the EMF environment in the same manner as the main ASDL metamodel. A major advantage of this approach is that it is integrated within the framework that ASDL is built upon, so no external plugins need to be invoked to verify scenarios generated using the language. However, this model checker is specific to the states experienced by an aircraft in flight and cannot be readily modified to work for any other DSL without extensive changes to the code. In the same manner, if the metamodel and statecharts experience any changes, the model checker needs to be modified to reflect those changes. The checker is extensible in case other states or actions are added, but there is no automated procedure to allow for changes without manual addition of code. In the case of ASDL, this is not a major challenge as the states that can be experienced by an aircraft are finite and transitions can be determined in advance.
The next part of this model-checking implementation involves invoking it directly when a scenario is generated using the ASDL interface. Any scenario that does not follow the established rules will not be accepted by the tool, thus allowing for an automated verification of the scenario before it is used for simulation purposes. Such use of a model checker prior to execution of a scenario would help cut down on the time and resources used to perform a simulation where no result would be achieved due to incorrect specification of the scenario, making the use of ASDL and the flight simulator more efficient. This is a description of the use of the tool for runtime verification; however, it can be extended to state space exploration. For future work once other stages of flight can be verified using this tool, the checker could output all possible valid paths instead of just checking the one being simulated. That would enable the automatic generation of scenarios where all valid options are computed and a random scenario is selected for the pilot to practice. As this language is in its infancy, it will be necessary to revisit the formal model once newer scenarios are generated in case extraordinary circumstances were overlooked in its definition. In addition, such a formal model now needs to be defined and verified for three other sets of flight scenarios: departure, en route and reroute scenarios in order to fully formalize the rules and scenario definitions in ASDL.
Author Contributions
Bharvi Chhaya implemented the statecharts algorithm and test cases. Shafagh Jafer verified the correctness of the algorithm and test results. Umut Durak provided technical feedback and recommendations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baier, C.; Katoen, J.P. Principles of Model Checking; The MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Wing, J.M. A specifier’s introduction to formal methods. Computer 1990, 23, 8–22. [Google Scholar] [CrossRef]
- Jafer, S.; Chhaya, B.; Durak, U. Graphical Specification of Flight Scenarios with Aviation Scenario Defintion Language (ASDL). In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Dallas, TX, USA, 9–13 January 2017; p. 1311. [Google Scholar]
- Jafer, S.; Chhaya, B.; Durak, U.; Gerlach, T. Formal Scenario Definition Language for Aviation: Aircraft Landing Case Study. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Washington, DC, USA, 13–17 June 2016; p. 3521. [Google Scholar]
- Mernik, M.; Heering, J.; Sloane, A.M. When and How to Develop Domain-Specific Languages. ACM Comput. Surv. 2005, 37, 316–344. [Google Scholar] [CrossRef]
- Romero, R.; Rivera, J.E.; Duran, F.; Vallecillo, A. Formal and Tool Support for Model Driven Engineering with Maude. J. Object Technol. 2007, 6, 187–207. [Google Scholar] [CrossRef]
- Durak, U.; Topcu, O.; Siegfried, R.; Oguztuzun, H. Scenario Development: A Model-Driven Engineering Perspective. In Proceedings of the 2014 IEEE International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH), Vienna, Austria, 28–30 August 2014; pp. 117–124. [Google Scholar]
- Sen, S.; Baudry, B.; Vangheluwe, H. Towards Domain-specific Model Editors with Automatic Model Completion. Simulation 2010, 86, 109–126. [Google Scholar] [CrossRef]
- Da Silva, A.R. Model-driven engineering: A survey supported by the unified conceptual model. Comput. Lang. Syst. Struct. 2015, 43, 139–155. [Google Scholar]
- SISO Base Object Model Product Development Group. Base Object Model (BOM) Template; SISO Base Object Model Product Development Group: Orlando, FL, USA, 2006. [Google Scholar]
- Pereira, M.J.V.; Fonseca, J.; Henriques, P.R. Ontological approach for DSL development. Comput. Lang. Syst. Struct. 2016, 45, 35–52. [Google Scholar] [CrossRef]
- Jafer, S.; Chhaya, B.; Durak, U. OWL ontology to Ecore metamodel transformation for designing a domain specific language to develop aviation scenarios. In Proceedings of the Symposium on Model-driven Approaches for Simulation Engineering, Virginia Beach, VA, USA, 23–26 April 2017; p. 3. [Google Scholar]
- Budinsky, F. Eclipse Modeling Framework: A Developer’s Guide; Addison-Wesley Professional: Boston, MA, USA, 2004. [Google Scholar]
- Clarke, E.M.; Grumberg, O.; Peled, D. Model Checking; The MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Salmerón, A.; Merino, P. Integrating model checking and simulation for protocol optimization. Simulation 2015, 9, 3–25. [Google Scholar] [CrossRef]
- Bolton, M.L.; Bass, E.J.; Siminiceanu, R.I. Using Formal Verification to Evaluate Human-Automation Interaction: A Review. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 488–503. [Google Scholar] [CrossRef]
- Harel, D. Statecharts: A Visual Formalism for Complex Systems. Sci. Comput. Programm. 1987, 8, 231–274. [Google Scholar] [CrossRef]
- Drusinsky, D. Modeling and Verification Using UML Statecharts, 1st ed.; Elsevier Inc.: Oxford, UK, 2006. [Google Scholar]
- Rivera, J.E.; Durán, F.; Vallecillo, A. Formal Specification and Analysis of Domain Specific Models Using Maude. Simulation 2009, 85, 778–792. [Google Scholar] [CrossRef]
- Holzmann, G.J. The Model Checker SPIN. IEEE Trans. Softw. Eng. 1997, 23, 279–295. [Google Scholar] [CrossRef]
- Mikk, E.; Lakhnech, Y.; Siegel, M.; Holzmann, G.J. Implementing Statecharts in PROMELA/SPIN. In Proceedings of the 2nd IEEE Workshop on Industrial Strength Formal Specification Techniques, Boca Raton, FL, USA, 20–23 October 1998; pp. 90–101. [Google Scholar]
- Havelund, K.; Pressburger, T. Java Pathfinder, a Translator from Java to Promela. In Proceedings of the 6th International SPIN Workshops on Practical Aspects of Model Checking, Toulouse, France, 21–24 September 1999. [Google Scholar]
- Cimatti, A.; Clarke, E.; Giunchiglia, E.; Giunchiglia, F.; Pistore, M.; Roveri, M.; Sebastiani, R.; Tacchella, A. NuSMV 2: An opensource tool for symbolic model checking. In Proceedings of the International Conference on Computer Aided Verification, Copenhagen, Denmark, 27–31 July 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 359–364. [Google Scholar]
- Cavada, R.; Cimatti, A.; Jochim, C.A.; Keighren, G.; Olivetti, E.; Pistore, M.; Roveri, M.; Tchaltsev, A. NuSMV 2.4 User Manual. Available online: http://nusmv.fbk.eu/NuSMV/userman/v24/nusmv.pdf (accessed on 16 January 2005).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).