On a Non-Symmetric Eigenvalue Problem Governing Interior Structural–Acoustic Vibrations
Abstract
:1. Introduction
2. Structural–Acoustic Vibrations
- (i)
- The eigenvalue problem and its adjoint problem have a zero eigenvalue with corresponding one-dimensional eigenspaces and where , and is the unique solution of the variational problem for every .
- (ii)
- The function is an eigensolution of the right eigenvalue problem corresponding to an eigenvalue if and only if is an eigensolution of the adjoint eigenvalue problem corresponding to the same eigenvalue.
- (iii)
- Eigenfunctions and of Problem (2) corresponding to distinct eigenvalues are orthogonal with respect to the inner product:
- (iv)
- Assume that is an eigensolution of Problem (2) and an eigensolution of the adjoint Problem (4) corresponding to the eigenvalues and , respectively.If , then it holds that:If and , then it holds that:
- (v)
- The eigenvalue Problem (2) has only real nonnegative eigenvalues, the only accumulation point of which is ∞.
3. Variational Characterizations of Eigenvalues
- (i)
- (Rayleigh’s principle)
- (ii)
- (minmax characterization)
- (iii)
- (maxmin characterization)where:
4. Discretization by Finite Elements
5. Structure Preserving Numerical Methods
| Algorithm 1 Rayleigh functional iteration for fluid–solid eigenvalue problems. |
Require: initial vector
|
5.1. Structure-Preserving Iterative Projection Methods
- (i)
- Since the dimension of the projected eigenproblem is quite small, it is solved by a dense solver, and therefore, approximations to further eigenpairs are at hand without additional cost.
- (ii)
- In the inner while clause, we check whether approximations to further eigenpairs already satisfy the specified error tolerance. Moreover, at the end of the while-loop,an approximation to the next eigenpair to compute and the residual r are provided.
- (iii)
- If the dimension of the search space has become too large, we reduce the matrices and , such that the columns of the new (and ) form a (and )orthonormal basis of the space spanned by the structure and the fluid part of the eigenvectors found so far. Notice that the search space is reduced only after an eigenpair has converged because the reduction spoils too much information, and the convergence can be retarded.
- (iv)
- The preconditioner is chosen, such that a linear system can be solved easily, for instance as a (incomplete) Cholesky or (incomplete) LU factorization. It is updated if the convergence measured by the reduction of the residual norm has become too slow.
- (v)
- It may happen that a correction t is mainly concentrated on the structure and the fluid, respectively, and the part of the complementary structure is very small. In this case, we do not expand in Step 22 and in Step 19, respectively.
- (vi)
| Algorithm 2 Structure-preserving nonlinear Arnoldi method for fluid–solid eigenvalue problems. |
|
Find approximate solution of the correction Equation (23) (for instance, by a preconditioned Krylov solver).
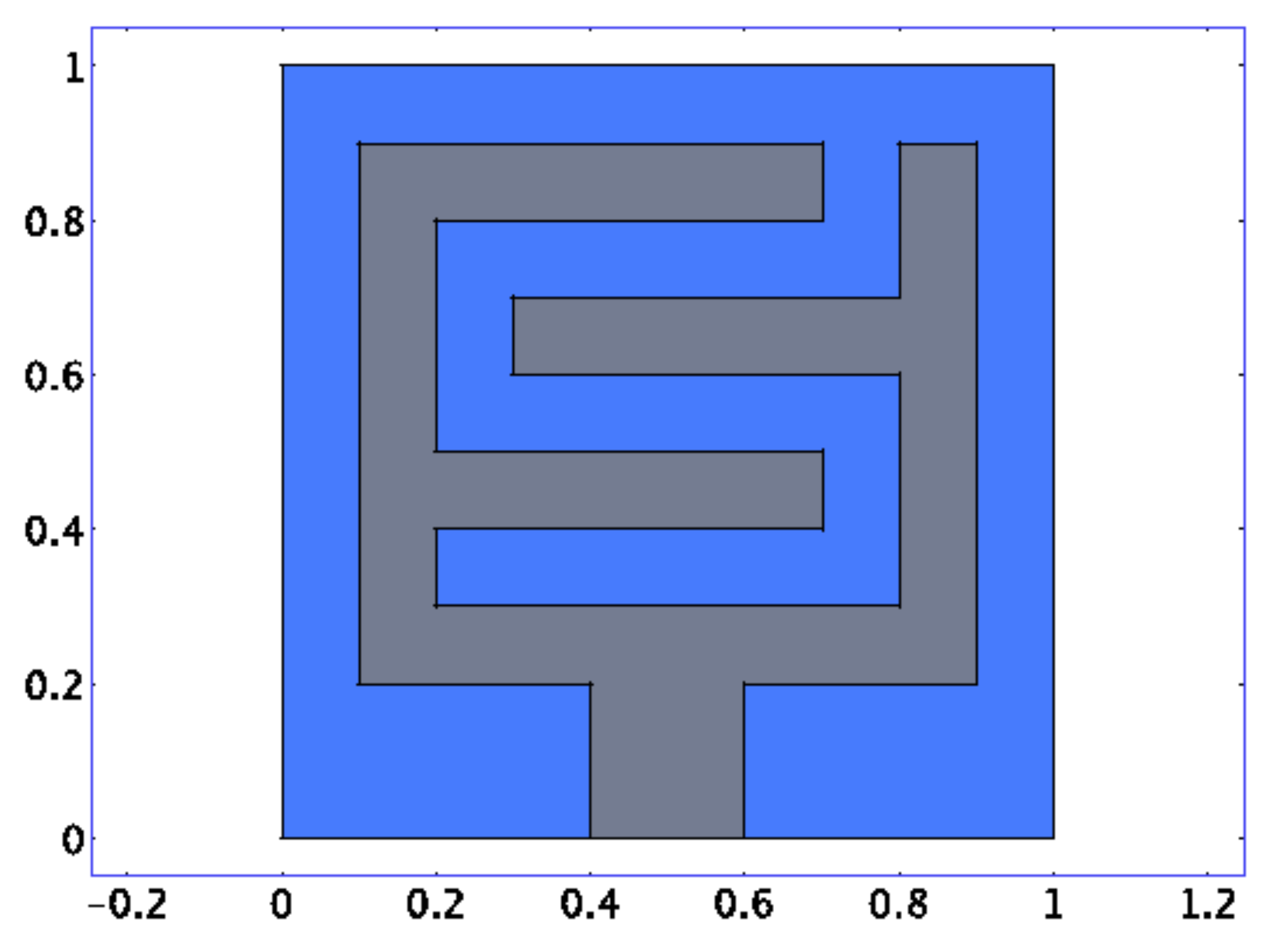
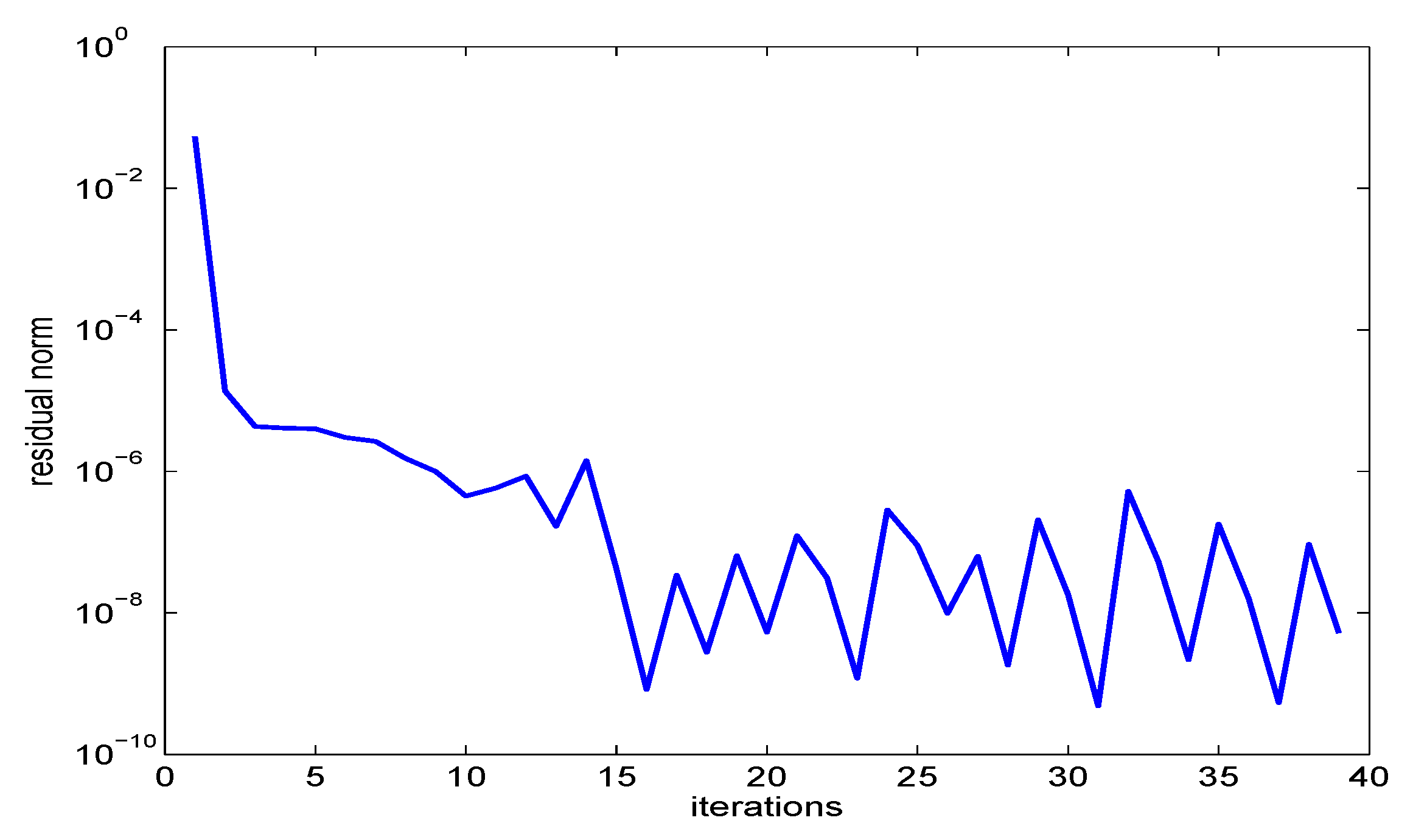
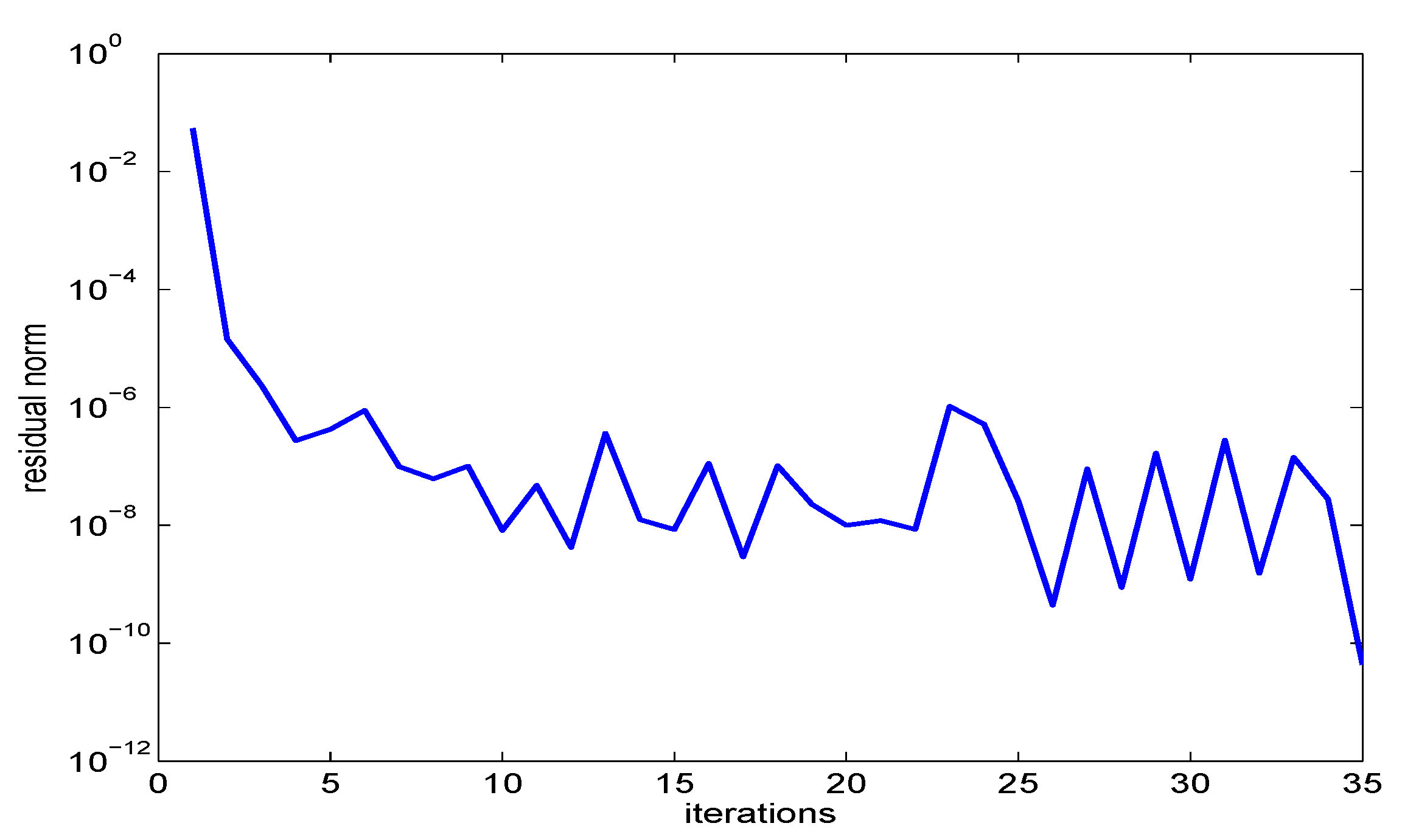
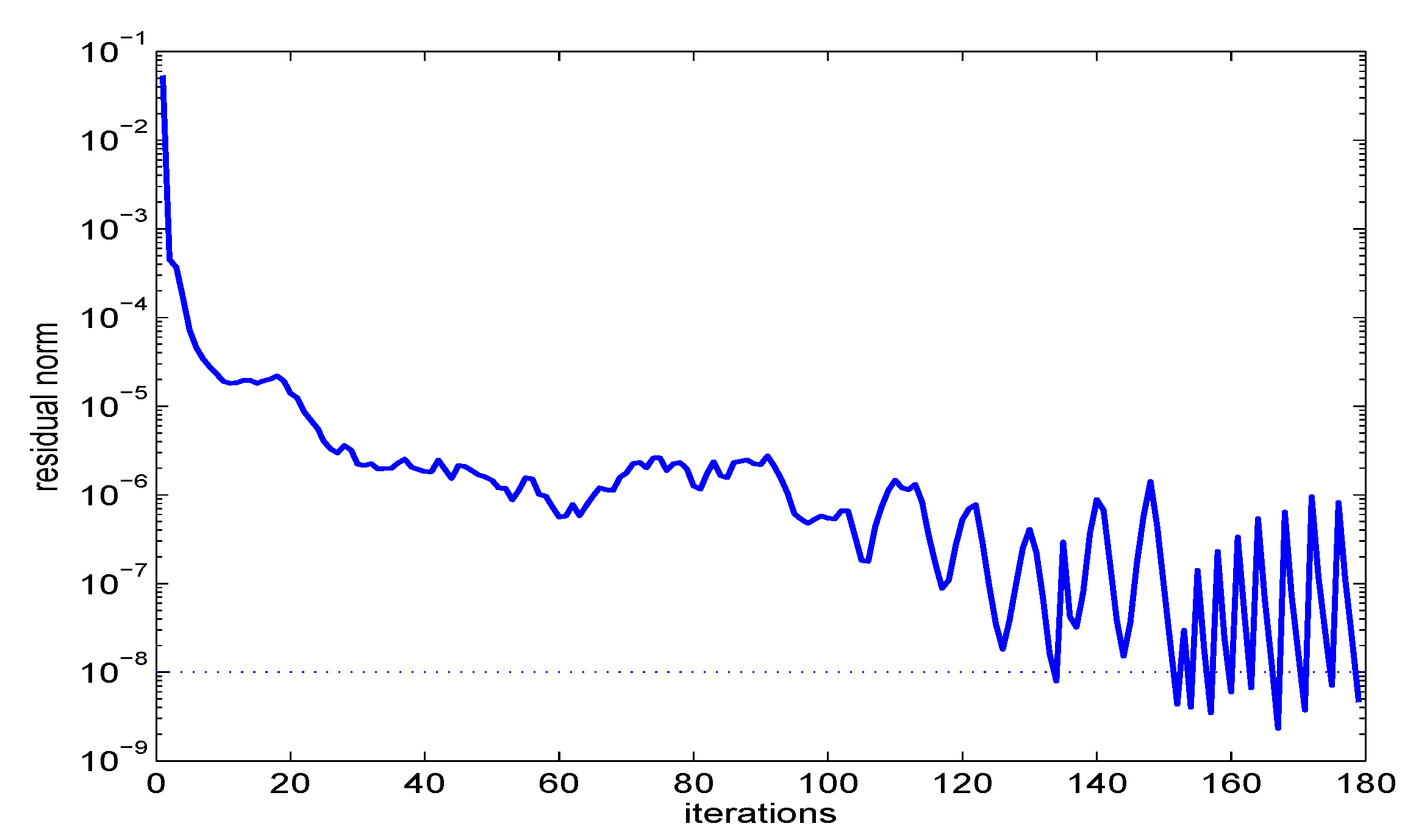
5.2. Numerical Example
6. Automated Multi-Level Sub-Structuring
6.1. Automated Multi-Level Sub-Structuring for Hermitian Problems
6.2. AMLS Reduction for Fluid–Solid Interaction Problems
6.3. Numerical Results
7. Conclusions
Conflicts of Interest
References
- Belytschko, T. Fluid–structure interaction. Comput. Struct. 1980, 12, 459–469. [Google Scholar] [CrossRef]
- Craggs, A. The transient response of a coupled plate-acoustic system using plate and acoustic finite elements. J. Sound Vib. 1971, 15, 509–528. [Google Scholar] [CrossRef]
- Deü, J.-F.; Larbi, W.; Ohayon, R. Variational formulation of interior structural-acoustic vibration problem. In Computational Aspects of Structural Acoustics and Vibrations; Sandberg, G., Ohayon, R., Eds.; Springer: Wien, Austria, 2008; pp. 1–21. [Google Scholar]
- Ohayon, R. Reduced models for fluid–structure interaction problems. Int. J. Numer. Meth. Eng. 2004, 60, 139–152. [Google Scholar] [CrossRef]
- Petyt, M.; Lea, J.; Koopmann, G. A finite element method for determining the acoustic modes of irregular shaped cavities. J. Sound Vib. 1976, 45, 495–502. [Google Scholar] [CrossRef]
- Sandberg, G.; Wernberg, P.-A.; Davidson, P. Fundamentals of fluid–structure interaction. In Computational Aspects of Structural Acoustics and Vibrations; Sandberg, G., Ohayon, R., Eds.; Springer: Wien, Austria, 2008; pp. 23–101. [Google Scholar]
- Zienkiewicz, O.; Taylor, R. The Finite Element Method; McGraw-Hill: London, UK, 1991; Volume 2. [Google Scholar]
- Everstine, G. A symmetric potential formulation for fluid–structure interaction. J. Sound Vib. 1981, 79, 157–160. [Google Scholar] [CrossRef]
- Olson, L.; Bathe, K.-J. Analysis of fluid–structure interaction. A direct symmetric coupled formulation based on the fluid velocity potential. Comput. Struct. 1985, 21, 21–32. [Google Scholar] [CrossRef]
- Bathe, K.J.; Nitikipaiboon, C.; Wang, X. A mixed displacement-based finite element formulation for acoustic fluid–structure interaction. Comput. Struct. 1995, 56, 225–237. [Google Scholar] [CrossRef]
- Morand, H.; Ohayon, R. Substructure variational analysis of the vibrations of coupled fluid–structure systems. Finite element results. Int. J. Numer. Meth. Eng. 1979, 14, 741–755. [Google Scholar] [CrossRef]
- Sandberg, G.; Göranson, P. A symmetric finite element formulation for acoustic fluid–structure interaction analysis. J. Sound Vib. 1988, 123, 507–515. [Google Scholar] [CrossRef]
- Babuska, I.; Osborn, J. Eigenvalue problems. In Handbook of Numerical Analysis; Ciarlet, P., Lions, J., Eds.; North Holland: Amsterdam, The Netherlands, 1991; Volume II, pp. 641–923. [Google Scholar]
- Alonso, A.; Russo, A.-D.; Padra, C.; Rodriguez, R. A posteriori error estimates and a local refinement strategy for a finite element method to solve structural-acoustic vibration problems. Adv. Comput. Math. 2001, 15, 25–59. [Google Scholar] [CrossRef]
- Bermudez, A.; Gamallo, P.; Noguieras, N.; Rodriguez, R. Approximation of a structural acoustic vibration problem by hexahedral finite elements. IMA J. Numer. Anal. 2006, 26, 391–421. [Google Scholar] [CrossRef]
- Bermudez, A.; Rodriguez, R. Finite element computation of the vibration modes of a fluid–solid system. Comput. Meth. Appl. Mech. Eng. 1994, 119, 355–370. [Google Scholar] [CrossRef]
- Bermudez, A.; Rodriguez, R. Analysis of a finite element method for pressure/potential formulation of elastoacoustic spectral problems. Math. Comput. 2002, 71, 537–552. [Google Scholar] [CrossRef]
- Rodriguez, R.; Solomin, J. The order of convergence of eigenfrequencies in finite element approximations of fluid–structure interaction problems. Math. Comput. 1996, 65, 1463–1475. [Google Scholar] [CrossRef]
- Stammberger, M.; Voss, H. Variational characterization of eigenvalues of a non-symmetric eigenvalue problem governing elastoacoustic vibrations. Appl. Math. 2014, 59, 1–13. [Google Scholar] [CrossRef]
- Strutt, J.W. Some general theorems relating to vibrations. Proc. Lond. Math. Soc. 1873, 4, 357–368. [Google Scholar]
- Poincaré, H. Sur les equations aux dérivées partielles de la physique mathématique. Am. J. Math. 1890, 12, 211–294. [Google Scholar] [CrossRef]
- Courant, R. Über die Eigenwerte bei den Differentialgleichungen der mathematischen Physik. Math. Z. 1920, 7, 1–57. [Google Scholar] [CrossRef]
- Fischer, E. Über quadratische Formen mit reellen Koeffizienten. Monatshefte Math. 1905, 16, 234–249. [Google Scholar] [CrossRef]
- Weyl, H. Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen (mit einer Anwendung auf die Theorie der Hohlraumstrahlung). Math. Ann. 1912, 71, 441–479. [Google Scholar] [CrossRef]
- Stammberger, M.; Voss, H. On an unsymmetric eigenvalue problem governing free vibrations of fluid–solid structures. Electr. Trans. Numer. Anal. 2010, 36, 113–125. [Google Scholar]
- Voss, H. A maxmin principle for nonlinear eigenvalue problems with application to a rational spectral problem in fluid–solid vibration. Appl. Math. 2003, 48, 607–622. [Google Scholar] [CrossRef]
- Voss, H. A minmax principle for nonlinear eigenproblems depending continuously on the eigenparameter. Numer. Linear Algebra Appl. 2009, 16, 899–913. [Google Scholar] [CrossRef]
- Hadeler, K.-P. Variationsprinzipien bei nichtlinearen Eigenwertaufgaben. Arch. Ration. Mech. Anal. 1968, 30, 297–307. [Google Scholar] [CrossRef]
- Voss, H. Variational principles for eigenvalues of nonlinear eigenproblems. In Numerical Mathematics and Advanced Applications—ENUMATH 2013; Abdulle, A., Deparis, S., Kressner, D., Nobile, F., Picasso, M., Eds.; Springer: Berlin, Germany, 2015; pp. 305–313. [Google Scholar]
- Voss, H. A Rational Spectral Problem in Fluid–Solid Vibration. Electr. Trans. Numer. Anal. 2003, 16, 94–106. [Google Scholar]
- Stammberger, M. On an Unsymmetric Eigenvalue Problem Governing Free Vibrations of Fluid–Solid Structures. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2010. [Google Scholar]
- ANSYS. Theory Reference for ANSYS and ANSYS Workbench; Release 11.0.; ANSYS, Inc.: Canonsburg, PA, USA, 2007. [Google Scholar]
- Ihlenburg, F. Sound in vibrating cabins: Physical effects, mathematical formulation, computational simulation with fem. In Computational Aspects of Structural Acoustics and Vibrations; Sandberg, G., Ohayon, R., Eds.; Springer: Wien, Austria, 2008; pp. 103–170. [Google Scholar]
- Kropp, A.; Heiserer, D. Efficient broadband vibro–acoustic analysis of passenger car bodies using an FE–based component mode synthesis approach. J. Comput. Acoust. 2003, 11, 139–157. [Google Scholar] [CrossRef]
- Bennighof, J.; Kaplan, M. Frequency window implementation of adaptive multi-level substructuring. J. Vib. Acoust. 1998, 120, 409–418. [Google Scholar] [CrossRef]
- Bennighof, J.; Lehoucq, R. An automated multilevel substructuring method for the eigenspace computation in linear elastodynamics. SIAM J. Sci. Comput. 2004, 25, 2084–2106. [Google Scholar] [CrossRef]
- Bai, Z.; Demmel, J.; Dongarra, J.; Ruhe, A.; van der Vorst, H. Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Voss, H. An Arnoldi method for nonlinear eigenvalue problems. BIT Numer. Math. 2004, 44, 387–401. [Google Scholar] [CrossRef]
- Voss, H.; Stammberger, M. Structural-acoustic vibration problems in the presence of strong coupling. J. Press. Vessel Technol. 2013, 135, 011303. [Google Scholar] [CrossRef]
- Voss, H. A new justification of the Jacobi–Davidson method for large eigenproblems. Linear Algebra Appl. 2007, 424, 448–455. [Google Scholar] [CrossRef]
- Fokkema, D.; Sleijpen, G.; van der Vorst, H. Jacobi–Davidson style QR and QZ algorithms for the partial reduction of matrix pencils. SIAM J. Sci. Comput. 1998, 20, 94–125. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Sleijpen, G.; van der Vorst, H. A Jacobi–Davidson iteration method for linear eigenvalue problems. SIAM J. Matrix Anal. Appl. 1996, 17, 401–425. [Google Scholar] [CrossRef]
- Bennighof, J. Adaptive multi-level substructuring method for acoustic radiation and scattering from complex structures. In Computational Methods for Fluid/Structure Interaction; Kalinowski, A., Ed.; American Society of Mechanical Engineers: New York, NY, USA, 1993; Volume 178, pp. 25–38. [Google Scholar]
- Kaplan, M. Implementation of Automated Multilevel Substructuring for Frequency Response Analysis of Structures. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2001. [Google Scholar]
- Elssel, K. Automated Multilevel Substructuring for Nonlinear Eigenvalue Problems. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2006. [Google Scholar]
- Gao, W.; Li, X.; Yang, C.; Bai, Z. An implementation and evaluation of the AMLS method for sparse eigenvalue problems. ACM Trans. Math. Softw. 2008, 34, 20. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A Software Package for Partitioning Unstructured Graphs, Partitioning Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices, Version 4.0; Technical Report; University of Minnesota: Minneapolis, MN, USA, 1998. [Google Scholar]
- Hendrickson, B.; Leland, R. The Chaco User’s Guide: Version 2.0; Technical Report SAND94-2692; Sandia National Laboratories: Albuquerque, NM, USA, 1994. [Google Scholar]
- Hurty, W. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Craig, R., Jr.; Bampton, M. Coupling of sub-structures for dynamic analysis. AIAA J. 1968, 6, 1313–1319. [Google Scholar]
- Elssel, K.; Voss, H. An a priori bound for automated multilevel substructuring. SIAM J. Matrix Anal. Appl. 2006, 28, 386–397. [Google Scholar] [CrossRef]
- Stammberger, M.; Voss, H. Automated multi-level sub-structuring for fluid–solid interaction problems. Numer. Linear Algebra Appl. 2011, 18, 411–427. [Google Scholar] [CrossRef]
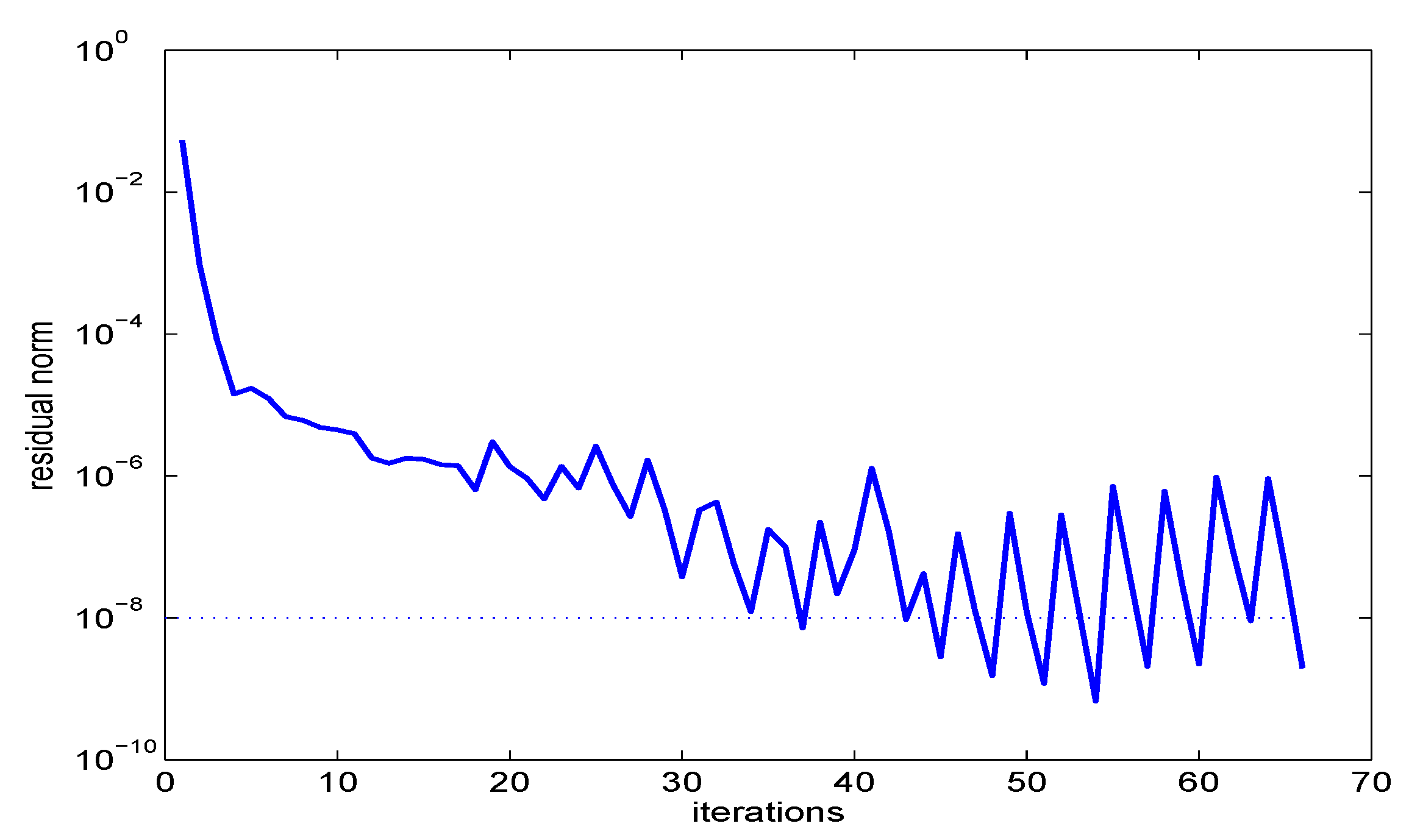
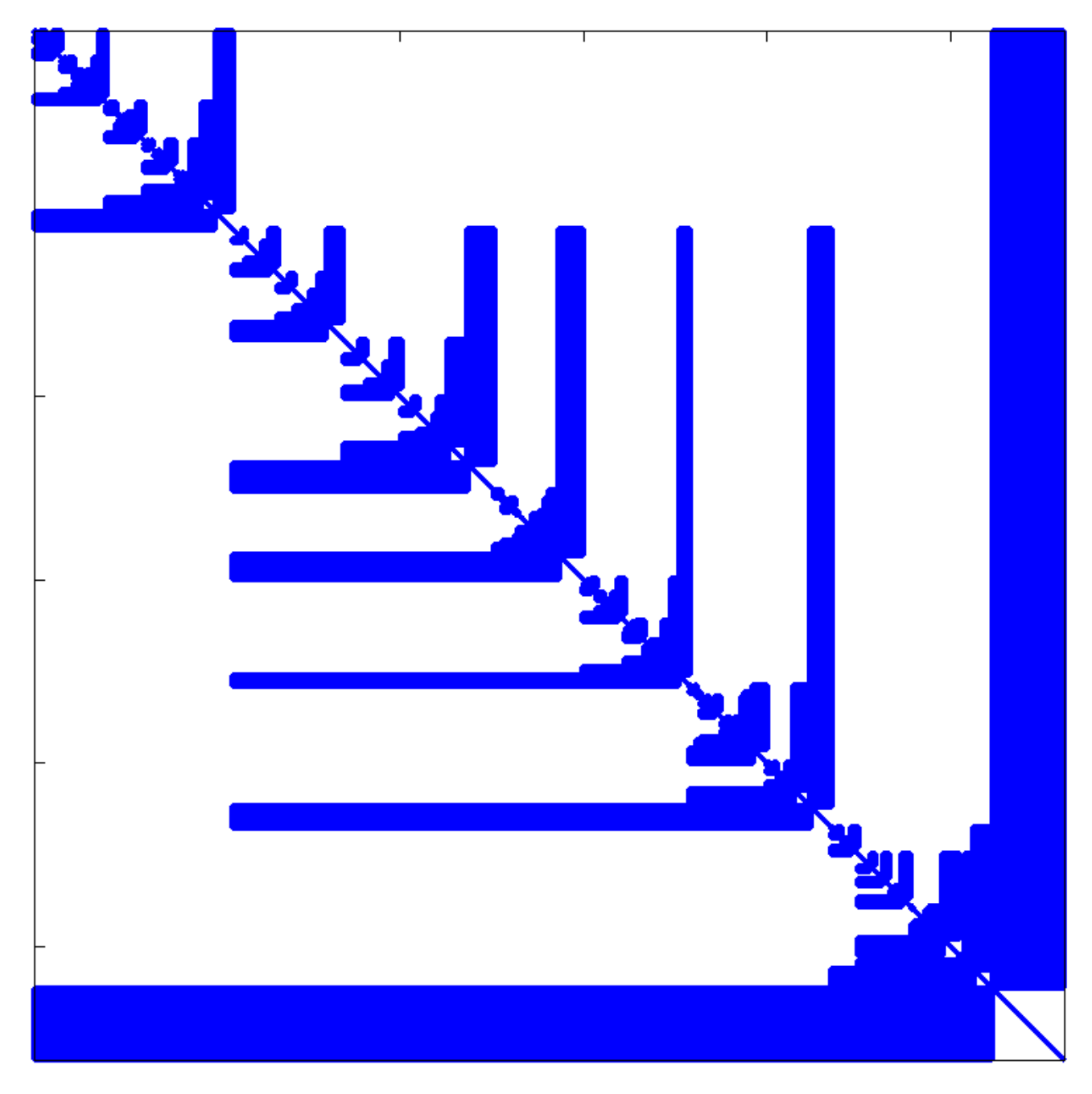
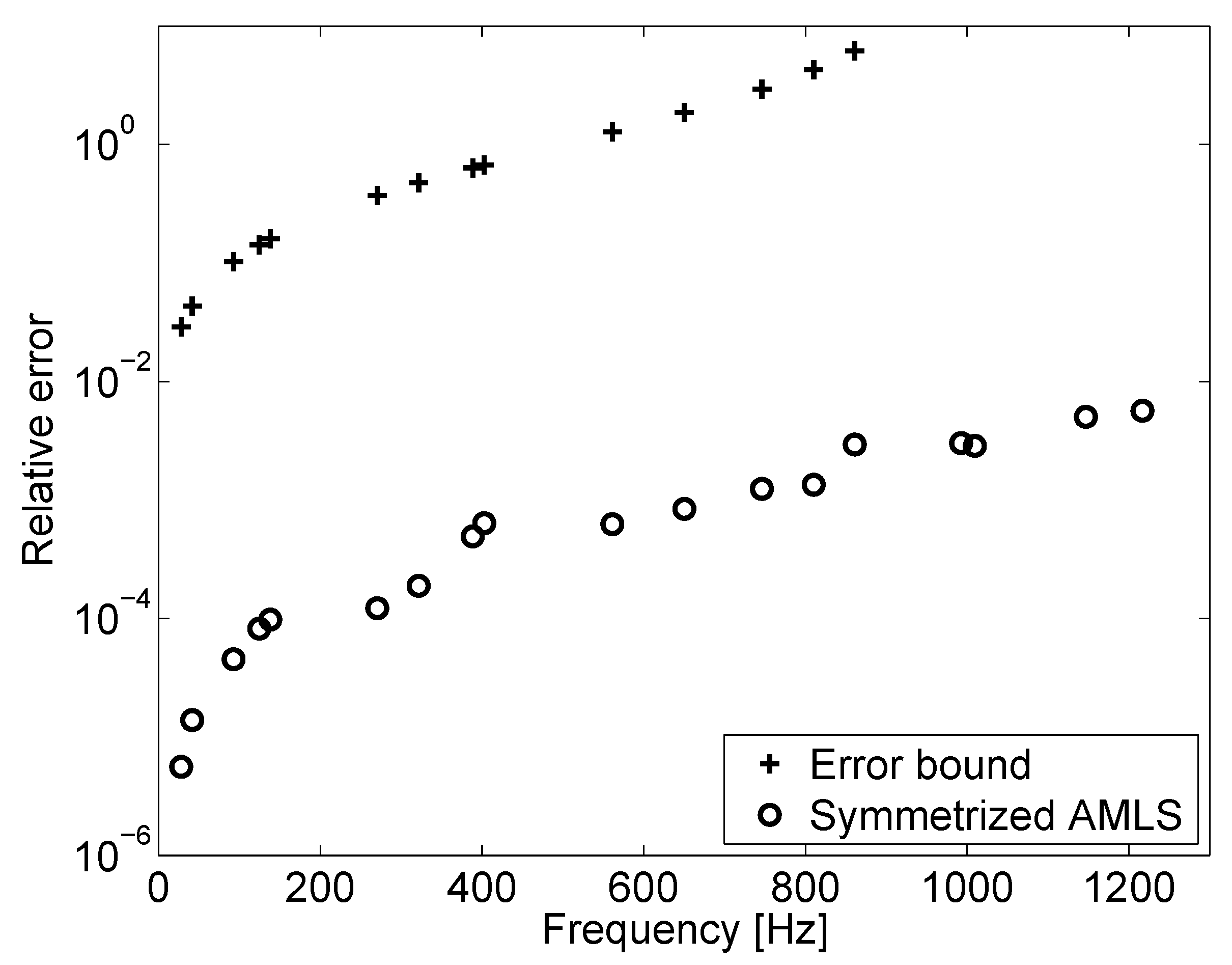
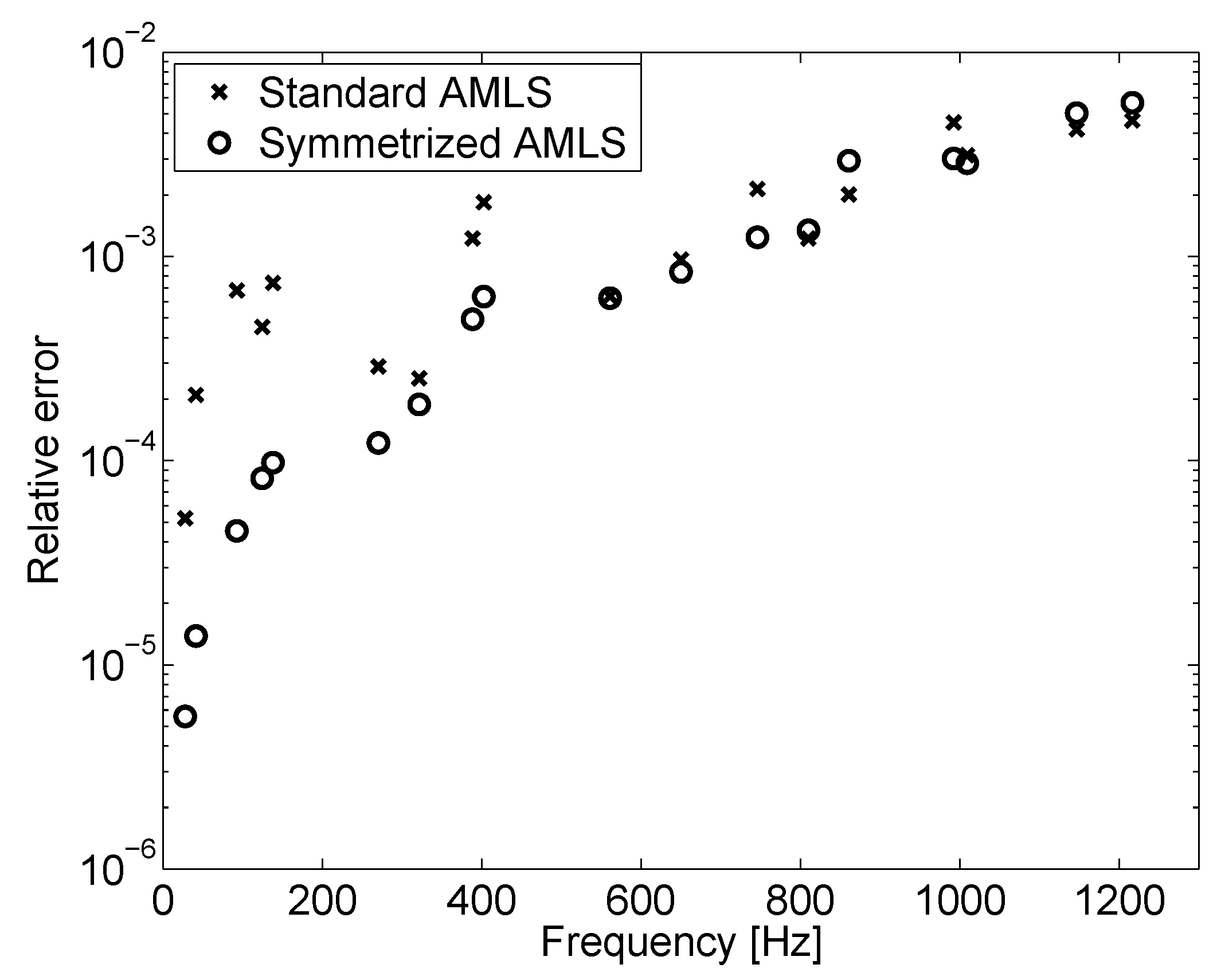
| Coupled | Steel | Air | Rel. Dev. | Rel. Err. Proj. |
|---|---|---|---|---|
| 0.00 | 0.00 | |||
| 41.25 | 41.32 | 0.16 | 2.5 × 10 | |
| 48.67 | 48.71 | 0.08 | 2.7 ×10 | |
| 56.96 | 56.90 | 0.11 | 2.2 ×10 | |
| 75.55 | 75.51 | 0.06 | 3.3 ×10 | |
| 93.18 | 93.19 | 0.01 | 1.0 ×10 | |
| 129.99 | 130.04 | 0.05 | 6.1 ×10 | |
| 150.94 | 151.03 | 0.06 | 3.5 ×10 | |
| 158.16 | 158.18 | 0.01 | 1.8 ×10 | |
| 186.64 | 186.66 | 0.12 | 4.2 ×10 |
| Coupled | Steel | Water | Proj. | Rel. Err. |
|---|---|---|---|---|
| 0.00 | 56.90 | 0.00 | 0.00 | |
| 28.01 | 75.51 | 178.63 | 28.33 | 1.2 |
| 41.54 | 151.03 | 210.64 | 43.01 | 3.5 |
| 92.73 | 186.66 | 402.93 | 101.98 | 10.0 |
| 124.70 | 225.54 | 133.60 | 7.1 | |
| 138.26 | 451.76 | 141.87 | 2.6 | |
| 270.40 | 472.45 | 285.18 | 5.5 | |
| 321.79 | 343.80 | 6.8 | ||
| 388.73 | 416.87 | 7.2 | ||
| 402.77 | 439.83 | 9.2 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voss, H. On a Non-Symmetric Eigenvalue Problem Governing Interior Structural–Acoustic Vibrations. Aerospace 2016, 3, 17. https://doi.org/10.3390/aerospace3020017
Voss H. On a Non-Symmetric Eigenvalue Problem Governing Interior Structural–Acoustic Vibrations. Aerospace. 2016; 3(2):17. https://doi.org/10.3390/aerospace3020017
Chicago/Turabian StyleVoss, Heinrich. 2016. "On a Non-Symmetric Eigenvalue Problem Governing Interior Structural–Acoustic Vibrations" Aerospace 3, no. 2: 17. https://doi.org/10.3390/aerospace3020017
APA StyleVoss, H. (2016). On a Non-Symmetric Eigenvalue Problem Governing Interior Structural–Acoustic Vibrations. Aerospace, 3(2), 17. https://doi.org/10.3390/aerospace3020017





