CFD Study of an Annular-Ducted Fan Lift System for VTOL Aircraft

Abstract

The present study aimed at assessing a novel annular-ducted fan lift system for VTOL aircraft through computational fluid dynamics (CFD) simulations. The power and lift efficiency of the lift fan system in hover mode, the lift and drag in transition mode, the drag and flight speed of the aircraft in cruise mode and the pneumatic coupling of the tip turbine and jet exhaust were studied. The results show that the annular-ducted fan lift system can have higher lift efficiency compared to the rotor of the Apache helicopter; the smooth transition from vertical takeoff to cruise flight needs some extra forward thrust to overcome a low peak of drag; the aircraft with the lift fan system enclosed during cruise flight theoretically may fly faster than helicopters and tiltrotors based on aerodynamic drag prediction, due to the elimination of rotor drag and compressibility effects on the rotor blade tips; and pneumatic coupling of the tip turbine and jet exhaust of a 300 m/s velocity can provide enough moment to spin the lift fan. The CFD results provide insight for future experimental study of the annular-ducted lift fan VTOL aircraft.

1. Introduction

The primary drawback to conventional fixed-wing aircraft is that they must have a runway to create sufficient airflow over the wings such that they may take off and land. Much effort has been directed towards the development of aircraft capable of vertical takeoff or landing (VTOL), which are not restricted to airport runways, but can land and takeoff from any relatively small open area. There are four types of successful and practical VTOL aircraft so far, which are helicopters, vectored jet aircraft, tiltrotors and ducted lift fan aircraft. These aircraft provide solutions to this problem, but also have some disadvantages. Helicopters have complex and costly rotor control system and usually have a limited forward speed of less than 200 knots due to compressibility effects on the rotor blade tips. Vectored jet aircraft, such as the AV-8A Harrier, utilize a turbofan engine for both hover and cruise propulsion. The nozzles are designed for efficient high speed forward thrust, but are very inefficient in vertical lift mode, and the high speed and force of exhausting air requires takeoff and landing pads, which must be specially prepared so as not to be damaged. The tilt rotor concept, found in the V-22 Osprey aircraft, uses large diameter propellers powered by two cross-shafted turboshaft engines. Its disc loading is higher than a helicopter, but lower than a turbofan, thus being efficient in the vertical flight modes. However, the large propellers limit the top speed to about 300 knots. Another problem with tiltrotors involves stability control difficulties. Turbulent rotational flow on the propeller blades may occur in descent and cause a vortex-ring state, which causes unsteady shifting of the flow along the blade span and may lead to roughness and loss of aircraft control.

The last approach to VTOL aircraft is the use of a ducted lift fan or fans mounted in the airframe for developing vertical thrust aligned with the aircraft center of mass. The duct is usually closed off during level flight, while forward thrust is provided by horizontal jet engines. Compared to the conventional VTOL aircrafts, lift fan aircraft fly faster and require minimum ground preparation, without high discharge velocity and high surface temperatures to cause ground erosion and reingestion of hot gases to cause the lift engines to stall and lose lift [1,2]. Ducted fans have no exposed rotor, thus being safer than helicopters and tiltrotors. Its compact structure, low pneumatic noise and high safety make it a highly efficient, safe and quiet vertical propulsion method [3,4,5]. The latest development of ducted lift fan aircraft is the Lockheed Martin F-35B joint strike fighter [1].

However, the ducted fans so far are all a circular duct or its variants with a central inlet. The fans are submerged in the fuselage or wings. This design not only limits the size of the fans due to the constraints of the fuselage and wing size, but also increases drag because the wings containing the fans have to be made relatively thick to maintain the depth of the fan ducts. The thick wings create unacceptable drag during forward flight. If the thickness of the wings is made much smaller than the diameter of the fan ducts, the benefits of the duct will be reduced, and the vertical thrust produced by the fan system will be limited. Because of the relatively small size, the circular ducted lift fans thus far all have high disc loading in order to provide sufficient vertical thrust to raise the aircraft off the ground.

According to the momentum theory of ducted fans, high disc loading means higher power required to lift the aircraft, thus leading to lower lift efficiency (see below). To increase lift efficiency while maintaining the lift, the fan area has to be increased. However, the space in the conventional aircraft for circular ducted fans is limited. Like the Ryan XV-5A, the wing size is not big enough to contain larger low disc loading circular fans. Other designs, such as a huge circular lift fan in the center of the aircraft or a plurality of small circular ducted fans around the aircraft, suffer from other problems, such as difficult layout for the fuselage, thick wings and increased complexity, which have made them impractical so far.

It is therefore desirable to provide a design that increases the lift fan area and lift efficiency while keeping all of the benefits of a ducted fan and also avoiding the drawbacks of the conventional VTOL aircraft, such as slow cruise speed, dangerous exposed rotor blades, hot downward high speed and pressure exhausting air, poor stability, etc. We present here an annular-ducted fan lift system for VTOL aircraft with a central fuselage to solve this problem. The annular-ducted fan lift system is mounted between the central fuselage and the peripheral wing (see Section 3.1). With the fuselage in the center, the annular duct can be made much larger around the fuselage; thus, the fan area can be greatly increased to realize low disc loading and high lift efficiency that is comparable to a helicopter rotor. Meanwhile, the larger diameter of the annular duct does not require a very thick wing. A relatively thin wing containing the annular duct can provide enough duct effect. In cruise mode, the annular duct is closed off by upper shutters or aperture and lower louvers to reduce drag and provide aerodynamic lift; thus, the forward speed will not be limited by compressibility effects on the fan blade tips, as in the case of helicopters and tiltrotors.

In the last two decades, as a result of continuing efforts spent in computational fluid dynamics (CFD) calculations and more diffuse access to adequate computational resources, many aerodynamic researches have moved into the branch of CFD, which is more affordable, practical, systematic and reliable [6]. A numerical investigation of the novel annular-ducted fan system before expensive experiments is necessary to provide insights for future studies. The present work describes a CFD study of the annular-ducted fan lift system. Several CFD analyses were performed. First, the power and lift efficiency of the annular-ducted fan system in hover mode were studied and compared to the rotor of a helicopter. Next, the lift and drag of the aircraft with the annular duct system opened during transition from VTOL to horizontal flight were studied. Then, the drag and lift of the aircraft with the annular duct enclosed in cruise mode were predicted to estimate the theoretical maximum flight speed of the aircraft. Finally, pneumatic coupling of the tip turbine and jet exhaust gases for a gas-driven lift fan during VTOL was simulated.

2. Momentum Theory of the Ducted Lift Fan in Hover Mode

As shown in Figure 1, with zero velocity (V₀ = 0) of incoming flow to the ducted lift fan, the thrust and power can be calculated:

Total thrust of the lift fan system:

$$T=T_{rotor}+T_{duct}=\text{ρ}A{V}_1{V}_2=\text{ρσ}A{V}_2^2$$

(1)

$$V_1=\text{σ}{V}_2$$

(2)

where ρ is the density of air; ρ = 1.225 kg/m³; A is area of lift fan; σ is the duct diffusion ratio, σ = 0.5–1 and for an unducted rotor σ = 0.5; V₁ is the velocity under the rotor; and V₂ is the far wake velocity.

Figure 1. The momentum model of the ducted lift fan system.

Figure 1. The momentum model of the ducted lift fan system.

Lift fan thrust:

$$T_{rotor}=A(\mathrm{\Delta }p)=\frac{1}{2}\text{ρ}A{V}_2^2$$

(3)

$$\frac{T_{rotor}}{T}=\frac{1}{2\text{σ}}$$

(4)

Power of the lift fan:

$$P\text{η}=T_{rotor}{V}_1=\text{σ}{T}_{rotor}{V}_2=\frac{T^{3/2}}{\sqrt{4\text{σρ}A}}$$

(5)

where η is the rotor efficiency.

Lift efficiency (power loading):

$$\frac{T}{P}=2\frac{\text{η}}{V_2}=2\text{η}\sqrt{\frac{\text{σρ}A}{T}}$$

(6)

The power required to provide the same thrust for the ducted fan and an unducted rotor:

$$\frac{P_{ducted}}{P_{unducted}}=\frac{\frac{T^{3/2}}{\sqrt{4\text{σρ}{A}_{ducted}}}}{\frac{T^{3/2}}{\sqrt{2\text{ρ}{A}_{unducted}}}}=\sqrt{\frac{A_{unducted}}{2\text{σ}{A}_{ducted}}}$$

(7)

Equations (1)–(7) describe the momentum model of the ducted lift fan in the VTOL design [5]. It can be seen from Equations (5) and (6) that high disc loading T/A results in higher power, thus lower lift efficiency.

3. Geometry and Computational Mesh

3.1. Geometry Definition

The annular-ducted lift fan system and the aircraft with the system considered in the paper are shown in Figure 2a. The central fuselage is connected to the peripheral wing through bridges (not shown). The annular-ducted lift fan system is mounted in the annular duct located between the central fuselage and the peripheral wing. The lift fan system has two counter-rotating fans mechanically or pneumatically coupled with two forward turbofan jet engines incorporated in the peripheral wing during VTOL. For this study, the diameter of the aircraft is set to 20 m (R = 10 m). The height of the central fuselage is 2 m with a diameter of 8 or 10 m. The annular duct system is in an area of a radius from 4 or 5 to 7 m, containing two fans of 36 blades (Figure 2b). The width of the annular duct and the length of the fan blades (angle of incidence 27°, chord length 0.53 m, thin blade) are 2 m (7–5 m) or 3 m (7–4 m). The depth of the annular duct is 1 m. The annular duct system is closed off in cruise mode by shutters, a diaphragm or aperture at the upper surface and louvers at the lower surface of the aircraft (Figure 2c). The weight of the aircraft is 10.433 tons.

Figure 2. (a) The annular-ducted lift fan system and the aircraft with the annular duct opened; (b) the lift fans; (c) the top front view of the aircraft with the annular duct system enclosed by upper aperture and lower louvers; (d) the lift fan and its tip turbine in a gas chamber. The upper wall of the chamber has been removed to expose the tip turbine inside.

Figure 2. (a) The annular-ducted lift fan system and the aircraft with the annular duct opened; (b) the lift fans; (c) the top front view of the aircraft with the annular duct system enclosed by upper aperture and lower louvers; (d) the lift fan and its tip turbine in a gas chamber. The upper wall of the chamber has been removed to expose the tip turbine inside.

The size of the annular-ducted fan lift system and the weight of the aircraft were so determined in order to compare to the Boeing AH-64E Apache helicopter, because the length of the rotor blades of the Apache is 7.32 m. The rotor of the Apache (four rigid blades, length 7.32 m, chord length 0.53 m, angle of incidence 10°) with a simplified fuselage was also numerically simulated to validate the CFD simulation and to compare to the annular-ducted lift fan system.

One structural problem with the lift fan aircraft may be the weak bridges connecting the central fuselage and the peripheral wing. The bridges cannot be too coarse and too great that they may block the inlet and outlet of the annular duct. This is a challenge, but may be solved by balanced consideration of the aerodynamics of the duct and the mechanical strength of the aircraft.

The control of the aircraft can be performed not only by aerodynamic control surfaces but also by thrust vector control of the two turbofan engines respectively. Especially in transition mode, attitude control such as roll, pitch, yaw, can be manipulated by thrust vectoring together with the annular-ducted fan lift system.

The lift fans in the annular duct can be shaft driven or gas driven by forward turbofan engines in VTOL mode. For gas-driven mode, the lift fan can be pneumatically coupled with jet exhaust gases by the tip turbine in a gas chamber. Figure 2d shows the lift fan with its tip turbine in a gas chamber. The tip turbine is fixed to the fan blades. The exhaust gases from the jet engine flow along the chamber and exit to the annular duct from the outlets located between the turbine blades on the inner wall of the chamber. The circulating gases push the turbine and fan to rotate.

3.2. Computational Mesh

The unstructured mesh technique has been successfully applied to solve CFD problems [6,7,8,9]. CFD methods based on unstructured grids have an advantage of easily handling complex geometries and can improve the solution accuracy by refining cells locally as required [7]. In this study, unstructured volume meshes were created using ANSYS 14.5 Meshing.

The tetrahedral volume mesh of the annular-ducted lift fan system and the aircraft in a 20R × 10R × 10R flow field in hover and transition mode is shown in Figure 3a. A dimension sensitivity study was carried out to make sure that the dimension was big enough, so that the simulation results would not change with the computational fluid domain dimension (data not shown). The flow field was divided into four volumes in which the two small blocks were dedicated to the fans. The mesh contained 3.0 M cells with three prismatic boundary layers. The first layer height of the boundary layer was fixed to 1–3 mm to make sure that the y⁺ value was within the range of 30–300 on most of the surface area.

In cruise mode for aerodynamic surface drag simulation, the annular duct was enclosed. The whole aircraft was like a blended wing body. Due to the symmetry of the aircraft, only half of the aircraft in a 20R × 5R × 10R flow field was simulated (Figure 3b). The mesh contained 650 K cells with 12 prismatic boundary layers. Very small prismatic cells were used in the boundary layer region, with the first layer height only 2 μm. This high resolution was needed to fully resolve the thin boundary layer down to the viscous sublayer. Because the thickness of the viscous sublayer decreases with increasing flow Re number and the Re numbers for airflow around the aircraft are very large (10⁸), the viscous sublayer at the surface is very thin. As a result, a very high grid resolution is required close to the walls. This is important because boundary layer separation from the surface determines to a large extent the aerodynamic drag [10]. A value of y⁺ < 1 was achieved for the attached flow on the surface of the aircraft.

The volume mesh with 1.7 M cells inside and outside the tip turbine chamber is shown in Figure 3c. The computational domain included the gas chamber and part of the annular duct. Hexahedral grids were created inside the chamber to reduce the number of cells and to save computing time.

Figure 3. (a) Volume mesh of the annular-ducted lift fan system in the central plane for the hover and transition mode study. Different colors show different blocks; (b) surface mesh on the surface of the aircraft and the symmetry plane for the aerodynamic drag study; (c) volume mesh in the central plane of the gas chamber for the tip turbine study.

Figure 3. (a) Volume mesh of the annular-ducted lift fan system in the central plane for the hover and transition mode study. Different colors show different blocks; (b) surface mesh on the surface of the aircraft and the symmetry plane for the aerodynamic drag study; (c) volume mesh in the central plane of the gas chamber for the tip turbine study.

Mesh sensitivity studies were carried out in all simulations (Table 1, Table 2 and Table 3). Three cases were considered: coarse grid, medium grid and fine grid. The results show that the differences between medium and fine grid are small. Therefore, all simulations in the study were performed in the range of a medium–fine grid. The grid independency study was also performed in the validation studies to compare the simulation results with known experimental data. According to Table 4 and Table 5, the comparison of the results shows that the medium and fine grid are close and in agreement with the experimental data.

Table 1. Grid sensitivity analysis in the power prediction study.

Parameters	Coarse Grid	Medium Grid	Fine Grid
Element number	1.5M	2.3M	3.0M
Power (kW)	2117	2097	2085

Table 1. Grid sensitivity analysis in the power prediction study.

Parameters	Coarse Grid	Medium Grid	Fine Grid
Element number	1.5M	2.3M	3.0M
Power (kW)	2117	2097	2085

Table 2. Grid sensitivity analysis in the drag prediction study.

Parameters	Coarse Grid	Medium Grid	Fine Grid
Element number	323K	650K	1.26M
CD	0.00842	0.00680	0.00676

Table 2. Grid sensitivity analysis in the drag prediction study.

Parameters	Coarse Grid	Medium Grid	Fine Grid
Element number	323K	650K	1.26M
CD	0.00842	0.00680	0.00676

Table 3. Grid sensitivity analysis in the tip turbine study.

Parameters	Coarse Grid	Medium Grid	Fine Grid
Element number	323K	670K	1.7M
Time-averaged moment (kN m)	162	158	156

Table 3. Grid sensitivity analysis in the tip turbine study.

Parameters	Coarse Grid	Medium Grid	Fine Grid
Element number	323K	670K	1.7M
Time-averaged moment (kN m)	162	158	156

Table 4. Grid independency study of the helicopter power.

Parameters	Coarse Grid	Medium Grid	Fine Grid	Actual
Element number	1.12M	2.43M	4.68M
Power (kW)	2845	2688	2685	2676

Table 4. Grid independency study of the helicopter power.

Parameters	Coarse Grid	Medium Grid	Fine Grid	Actual
Element number	1.12M	2.43M	4.68M
Power (kW)	2845	2688	2685	2676

Table 5. Airfoil grid resolution study.

Parameters	Coarse Grid	Medium Grid	Fine Grid	Experimental
Cell number	355K	638K	1.55M
CL	0.266	0.260	0.258	0.241
CD	0.0110	0.0088	0.0075	0.0079

Table 5. Airfoil grid resolution study.

Parameters	Coarse Grid	Medium Grid	Fine Grid	Experimental
Cell number	355K	638K	1.55M
CL	0.266	0.260	0.258	0.241
CD	0.0110	0.0088	0.0075	0.0079

4. Boundary Condition and Simulation Setup

Fluid dynamic simulations were performed using ANSYS Fluent 14.5, which has been used in various studies [6,9,10,11,12]. The 3D Reynolds-averaged Navier–Stokes (RANS) equations for the mean flow quantities were solved with different turbulence models. The RANS method uses the Boussinesq hypothesis to relate the Reynolds stresses to the mean velocity gradients to facilitate closure of the governing equations.

For the lift fan system in hover and transition mode, a pressure-based solver type with absolute velocity formulation, the Green–Gauss node-based gradient option and steady approach were used in the analyses. The shear stress transport (SST) k–ω turbulence model developed by Menter [13,14] was selected for the turbulence model. This model incorporates a blending function designed to activate the standard k–ω turbulence model in the near-wall region and to activate the k–ε turbulence model away from the surface. The SST k–ω turbulence model also incorporates a damped cross-diffusion derivative term in the ω equation, along with a modified definition of turbulent viscosity to account for the transport of the turbulent shear stress [15]. These features make the SST k–ω model more accurate and reliable for adverse pressure gradient flows, airfoils and transonic shock waves. The Semi Implicit Method for Pressure Linked Equations (SIMPLE) scheme was used to resolve the pressure–velocity coupling with the second order discretization for the pressure equation, the third order Monotonic Upstream-Centered Scheme for Conservation Laws (MUSCL) for the momentum, the turbulent kinetic energy and turbulent dissipation rate [6]. Multiple reference frames were used for the rotor fluid zone and the stationary fluid zone. Velocity-inlet, pressure-inlet and pressure-outlet boundary conditions were applied over the inlet and outlet sections. In transition mode, unsteady calculations were performed. The areas surrounding the fans were designated as a sliding mesh. Sliding interfaces separated the rotating domain from the stationary domain. The initial data for the unsteady run were obtained from steady calculations.

For aerodynamic surface drag prediction, a density-based solver type with the SST k–ω turbulence model was used. The second order upwind discretization was used for the flow, turbulent kinetic energy and specific dissipation rate. The air was treated as an ideal gas having constant specific heat, whereas viscosity was bound to the three coefficients the Sutherland law, which automatically enabled the energy equation resolution, because it is dependent on the actual temperature [6]. Velocity-inlet and pressure-outlet conditions were imposed over the inlet and outlet sections.

For the tip turbine study, the k-epsilon realizable model was selected for turbulence model [16]. This model is more precise for flows involving rotation, separation and recirculation. PREssure STaggering Option (PRESTO!) was used for discretization of the pressure equation and the third order MUSCL for the momentum, the turbulent kinetic energy and turbulent dissipation rate. The boundary condition used to simulate the jet exhaust at the inlet of the gas chamber was velocity-inlet. Unsteady calculations were performed using a sliding mesh to simulate the tip turbine blades rotating in the gas chamber. The initial data for the unsteady run were obtained from steady calculations.

All simulations were performed with double precision.

5. Numerical Model Validation

Because this is a concept study of a novel annular-ducted fan lift system, no experimental data are available now for the exact geometry. The validations were performed on similar models using the same settings and meshes to compare the predicted results with the known experimental data. The power of the AH-64E Apache helicopter, the lift and drag coefficients of a generic fan-in-wing configuration [1] and the lift and drag coefficients of a rectangular wing of the NACA 0012 airfoil were simulated and compared.

5.1. Validation of Power Prediction

A helicopter rotor of the VR-12 airfoil with a simplified fuselage in hover mode was created. The settings for the power prediction of the annular-ducted fan lift system were applied to study the power of the AH-64E Apache. A tetrahedral mesh of 2.43 M elements was created. The computational domain was a 20R × 10R × 10R flow field, which was divided into two volumes in which the small block was dedicated to the rotor. y⁺ = 30–300.

The results show that the rotor generates a long wake in the flow field. Three-dimensional streamline analysis demonstrates that the wake is swirling around the central axis (Figure 4a). There is energy wasted on swirling and also on vortex at the rotor tips (Figure 4b).

When the rotor rotates at 344 rpm, the net lift of the helicopter is obtained as 102,243 N (10.433 tons, the maximal weight of the Apache).

According to Equation (5), the induced power of the rotor:

$$P_{induced}=\frac{T^{3/2}}{\sqrt{4\text{σρ}A}}=1615\text{kW}$$

(8)

where σ = 0.5 for the unducted rotor, and rotor area A = 167.33 m².

The mechanical shaft power of the rotor can be calculated based on the moment of the rotor and the rotational speed:

$$P_{shaft}=\text{ω}rF=2\text{π}\frac{n}{60}rF=2685\text{kW}$$

(9)

where moment rF = 74,548 N m, and rotational speed n = 344 rpm.

Figure 4. (a) Three-dimensional swirling streamlines in front of the central plane of the helicopter in hover mode; (b) the rotor tip vortex in the central plane of the helicopter.

Figure 4. (a) Three-dimensional swirling streamlines in front of the central plane of the helicopter in hover mode; (b) the rotor tip vortex in the central plane of the helicopter.

Therefore, the rotor efficiency of the model is:

$$\text{η}=\frac{T^{3/2}}{P_{shaft}\sqrt{4\text{σρ}A}}=0.601$$

(10)

Lift efficiency T/P_shaft = 10,433/2685 = 3.88 kg/kW.

The simulated power 2685 kW is very close to the actual value of the Apache power 2 × 1487 × 0.9 = 2676 kW, supposing that the mechanical transmission efficiency is 0.9. The actual rotor efficiency η = P_induced/P = 0.603, and lift efficiency T/P = 3.89 kg/kW. Therefore, the prediction of the power is quite accurate.

5.2. Validation of Transition Mode

The simulation of a three-dimensional configuration with a fan rotating in the plane of a wing [3] was repeated with an unstructured tetrahedral grid to validate the transition study. The model airfoil is of the NACA 16-020 type. One single circular fan is submerged at the rear part of the wing as in the case of the annular-ducted lift fan (Figure 5). In [3], a structured mesh was used, and three different freestream velocities and three different fan rotation speeds were investigated; however, here, only freestream velocity U = 30 m/s, corresponding to a Reynolds number Re = 1.5 × 10⁶, and rotation speed N = 21,000 rpm at different angles of attack were repeated to compare to the experimental data in [3]. The settings for the transition study were used. Ten chords were used in each direction from the wing to create the computational domain. The mesh contained 1.2 M tetrahedral cells. y⁺ = 30–300 was achieved on the surface of the wing. However, for an angle of attack of 20°, flow separation happened, which caused significantly drop of lift, and the iterations could not converge; therefore, y⁺ = ~1 on the surface of the wing was used.

The CFD results show a good agreement with the experimental data [3] (Figure 6), although the drag coefficients may be a little under-predicted. As shown in Figure 5, the main features encountered in a jet in crossflow are predicted by the simulation as in [3]. Even at the high angle of attack of 20°, the flow remains attached.

Figure 5. Streamlines in the central plane of the generic fan-in-wing configuration at an angle of attack of 20°. Freestream velocity U = 30 m/s, and fan speed N = 21,000 rpm.

Figure 5. Streamlines in the central plane of the generic fan-in-wing configuration at an angle of attack of 20°. Freestream velocity U = 30 m/s, and fan speed N = 21,000 rpm.

Figure 6. Lift and drag coefficients as a function of the angle of attack for U = 30 m/s and N = 21,000 rpm. The experimental data come from Thouault [3].

Figure 6. Lift and drag coefficients as a function of the angle of attack for U = 30 m/s and N = 21,000 rpm. The experimental data come from Thouault [3].

5.3. Validation of Aerodynamic Drag Prediction

The aerodynamic drag prediction was validated with a three-dimensional rectangular wing of the NACA 0012 airfoil (c = 0.635 m, b = 2.438 m) in an eight-foot wind tunnel at M = 0.7 and Re = 9 × 10⁶ with the transition point fixed at 5% chord on both the upper and lower surfaces of the airfoil [17]. The unstructured grid and the settings for drag prediction were validated. Ten chord were used from the wing to create the computational domain with 1.55 M tetrahedral cells. y⁺ = ~1 was achieved on the surface of the airfoil.

Figure 7. Comparison of computed and experimental data for the NACA-0012 airfoil at M = 0.7 and Re = 9 × 10⁶. (a) Lift vs. angle of attack; (b) lift vs. drag polar; (c) pressure coefficient distribution at z = 1 and α = 1.55°. The experimental data come from Harris [17].

Figure 7. Comparison of computed and experimental data for the NACA-0012 airfoil at M = 0.7 and Re = 9 × 10⁶. (a) Lift vs. angle of attack; (b) lift vs. drag polar; (c) pressure coefficient distribution at z = 1 and α = 1.55°. The experimental data come from Harris [17].

As shown in Figure 7, good agreement at the given angle of attack α is obtained by correction of α and C_L for wall interference according to Harris’s estimates [17,18,19]. The results indicate that the simulation may slightly under-predict lift and drag.

6. Numerical Simulation Results

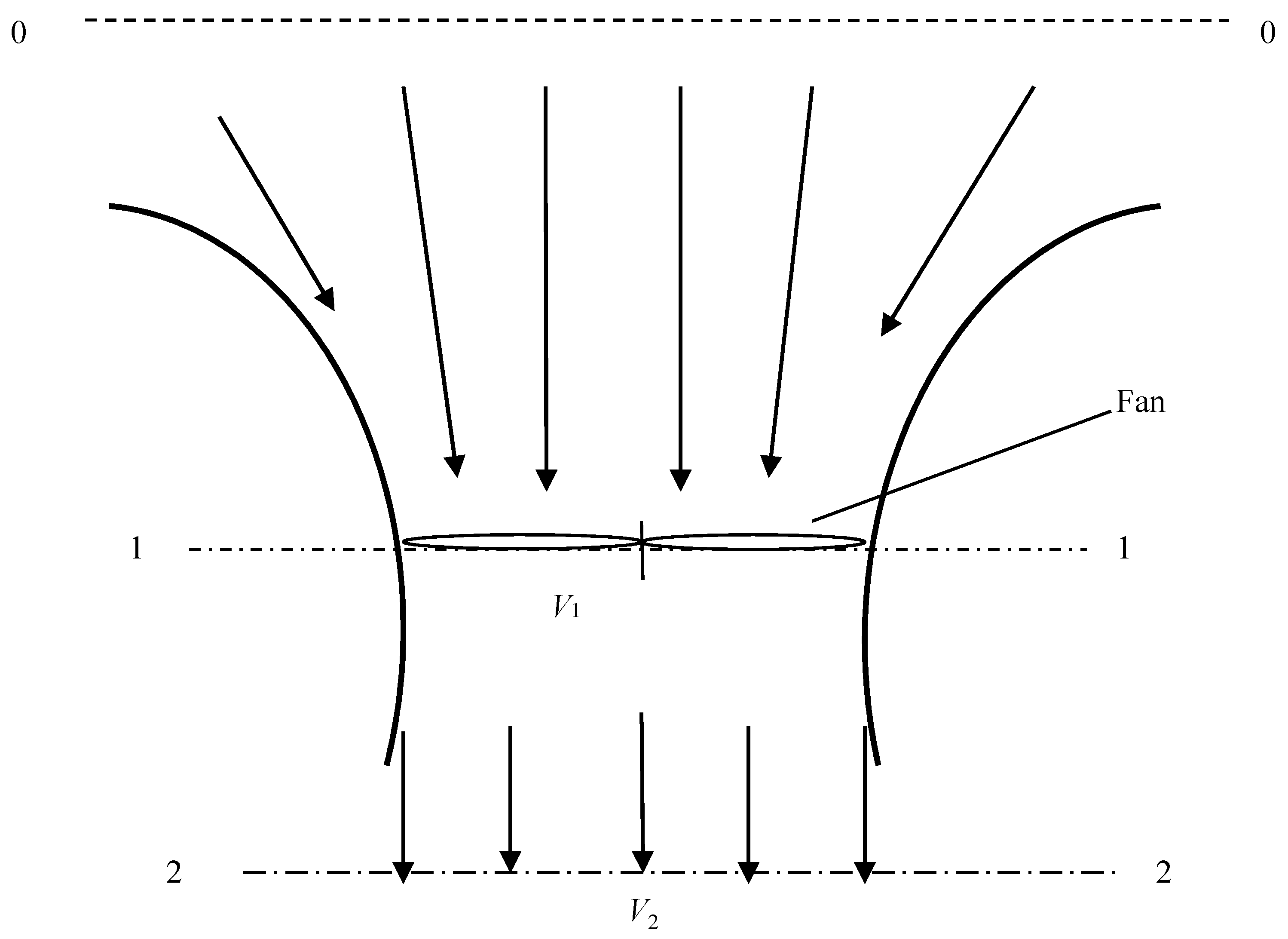
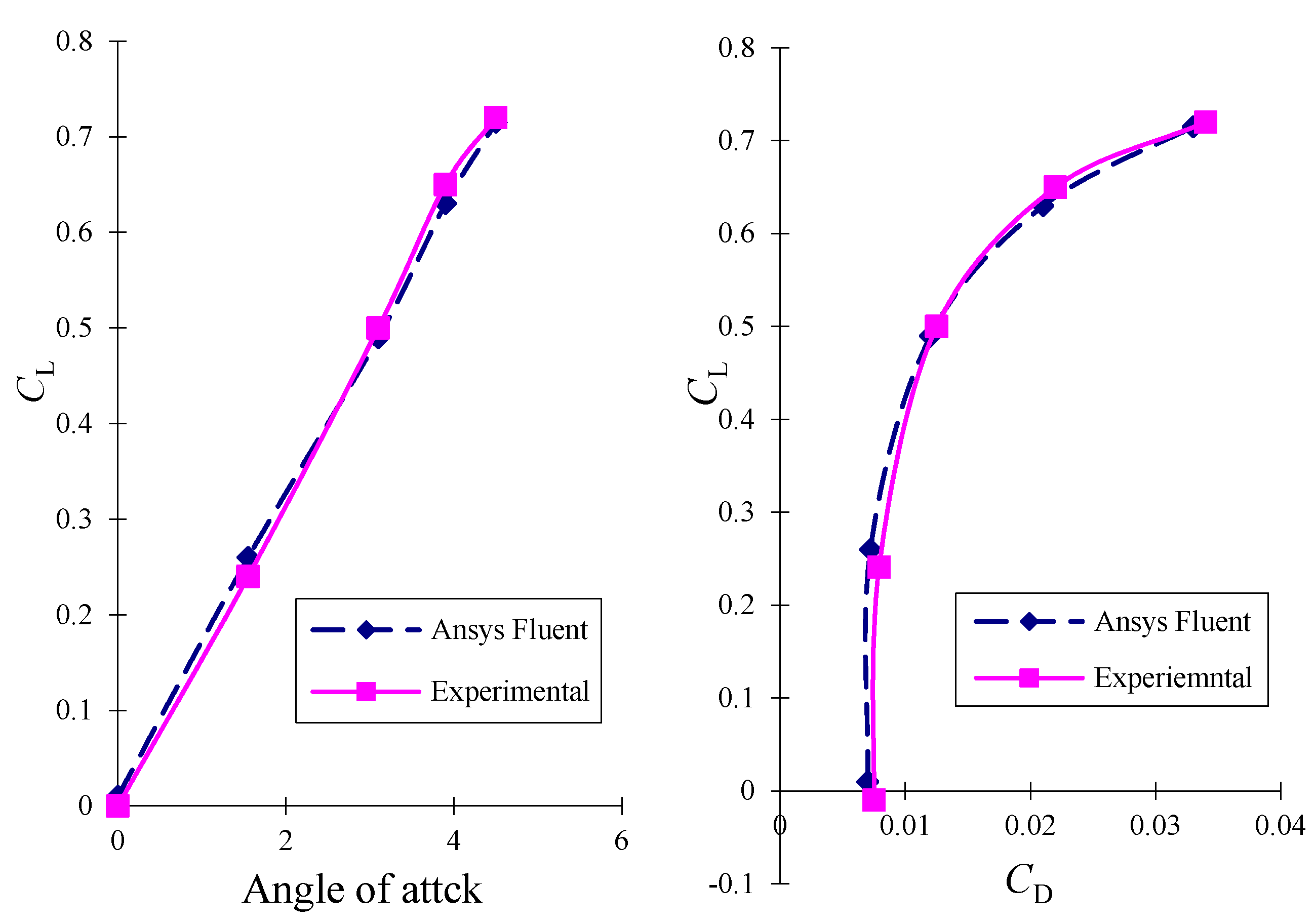
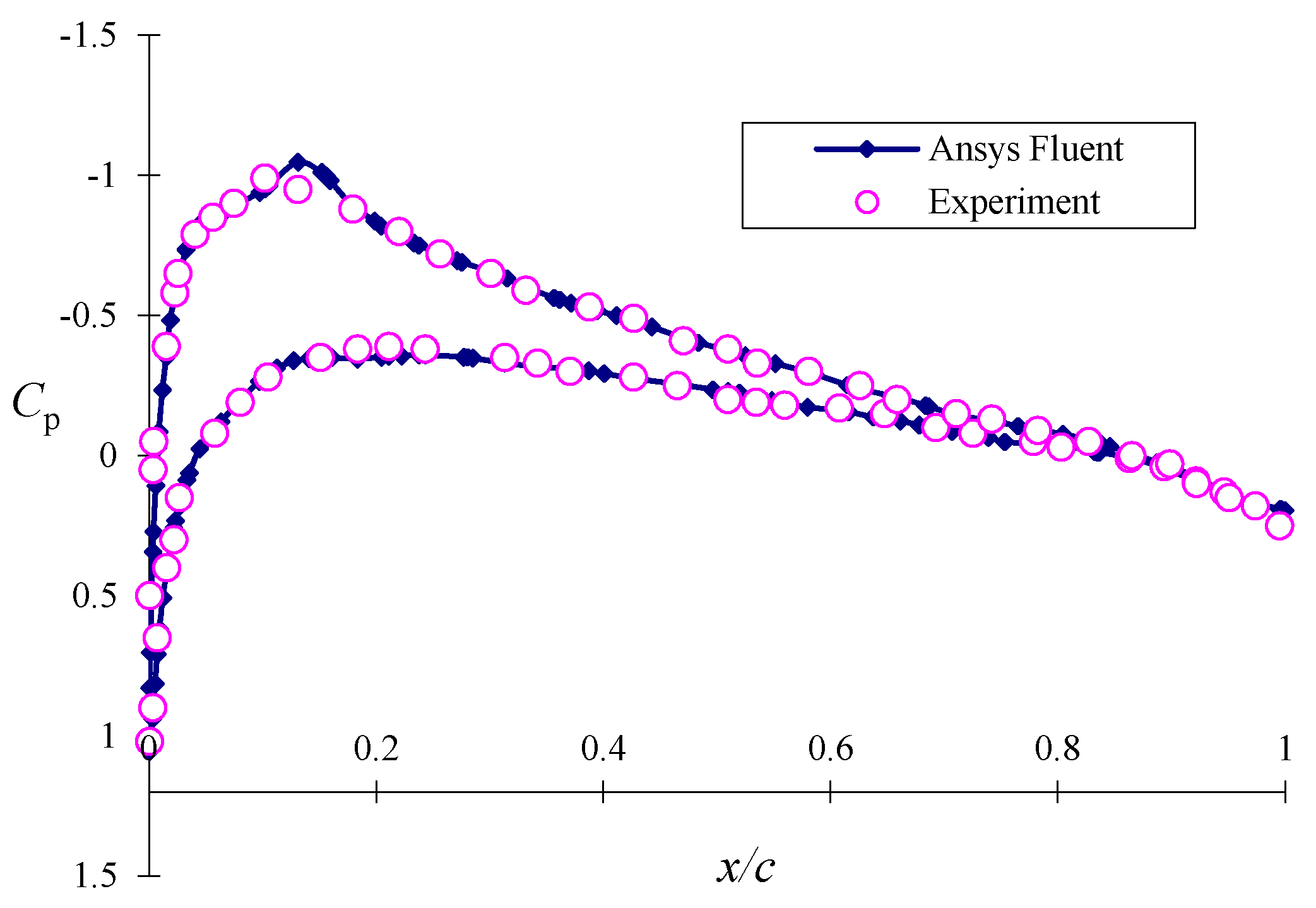
6.1. Annular-Ducted Fan Lift System in Hover Mode

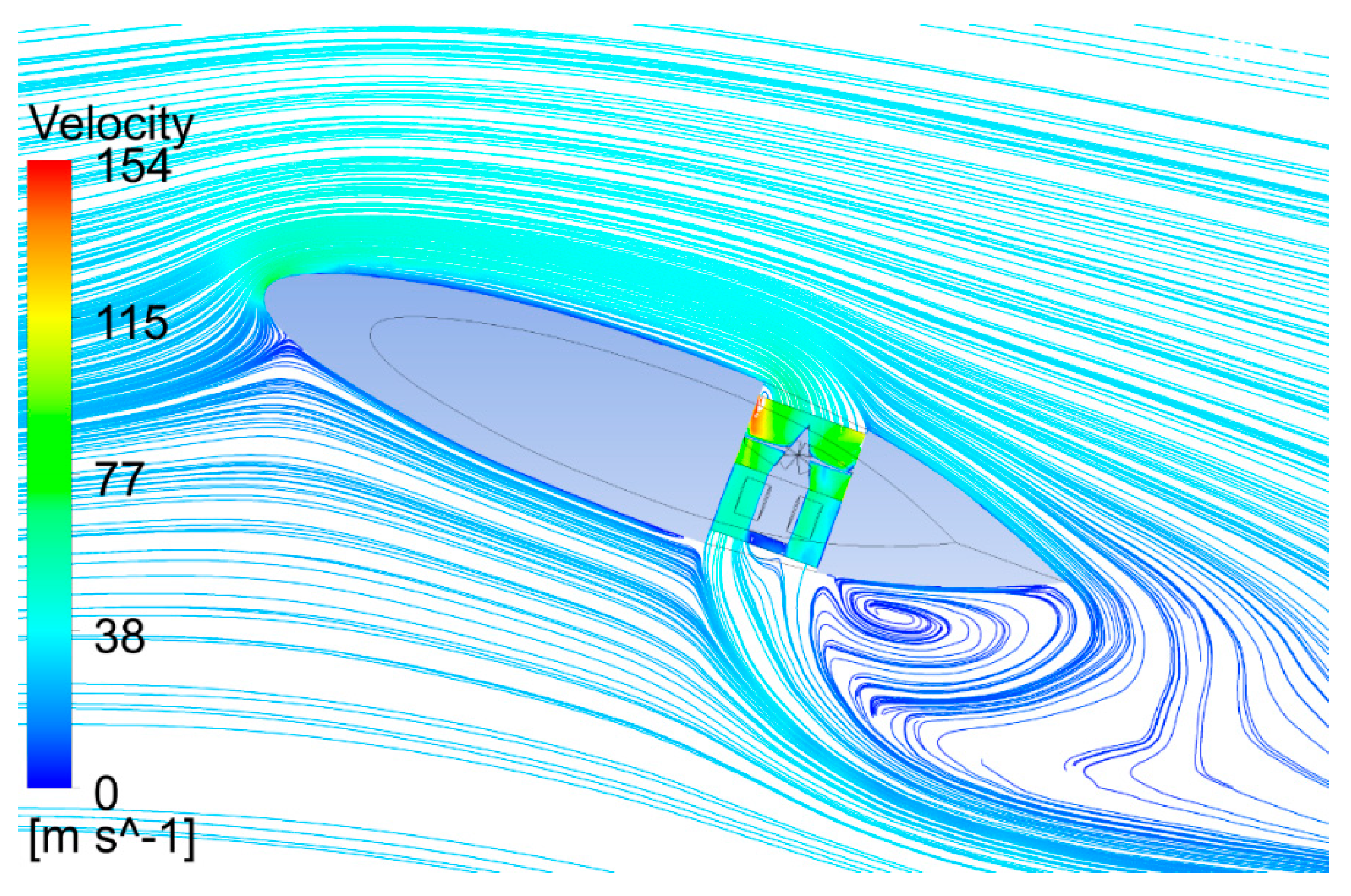
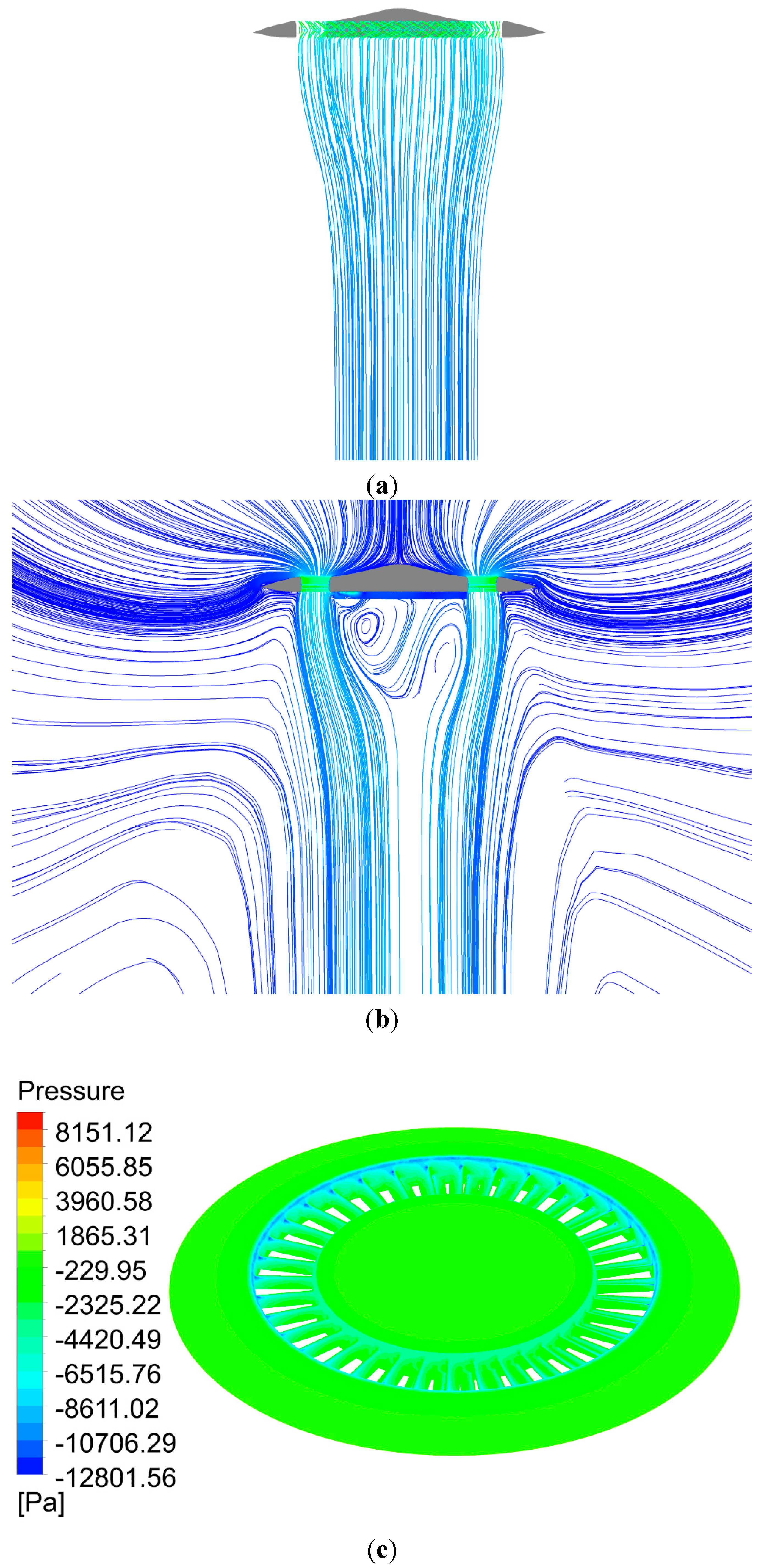
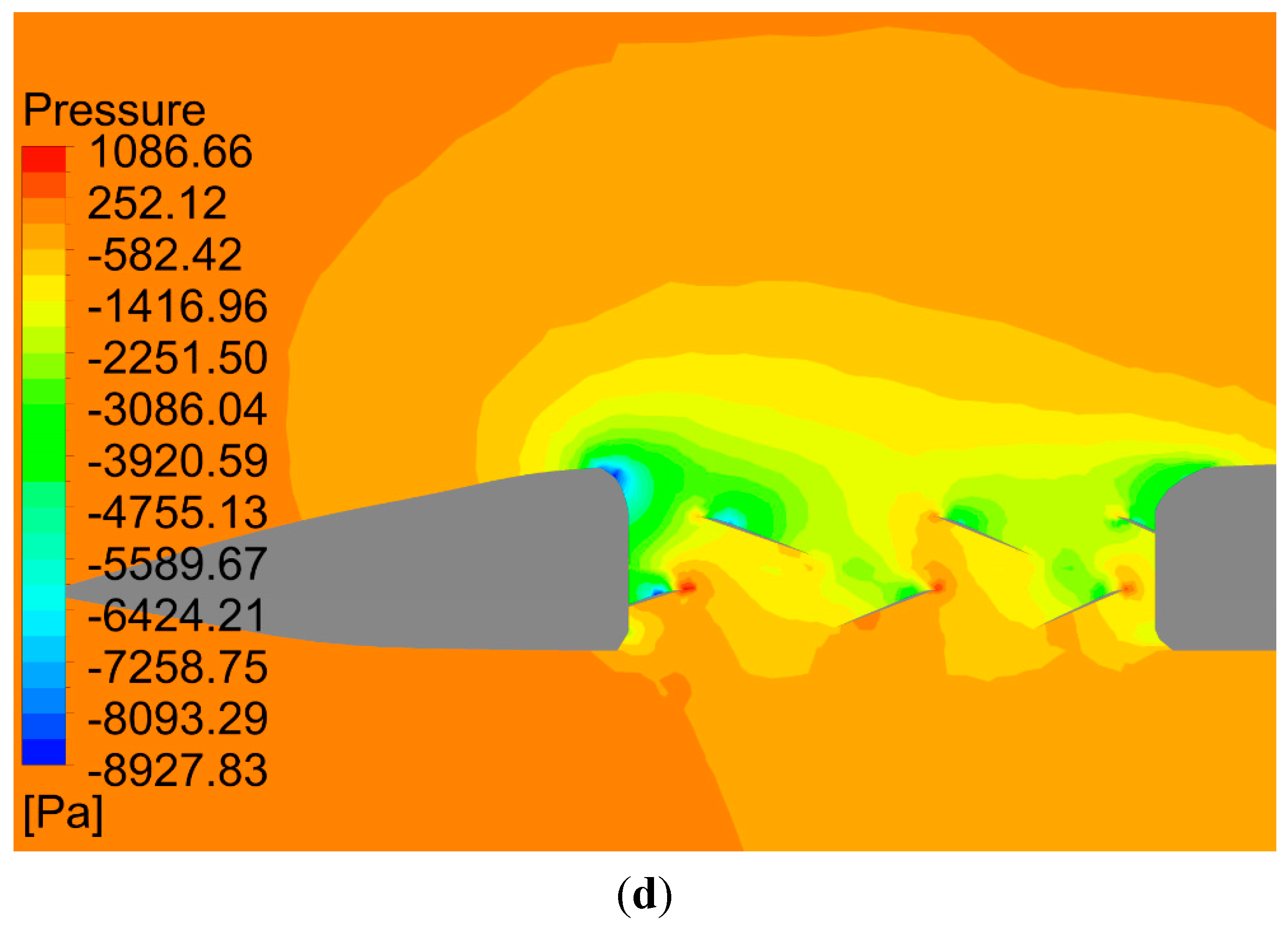
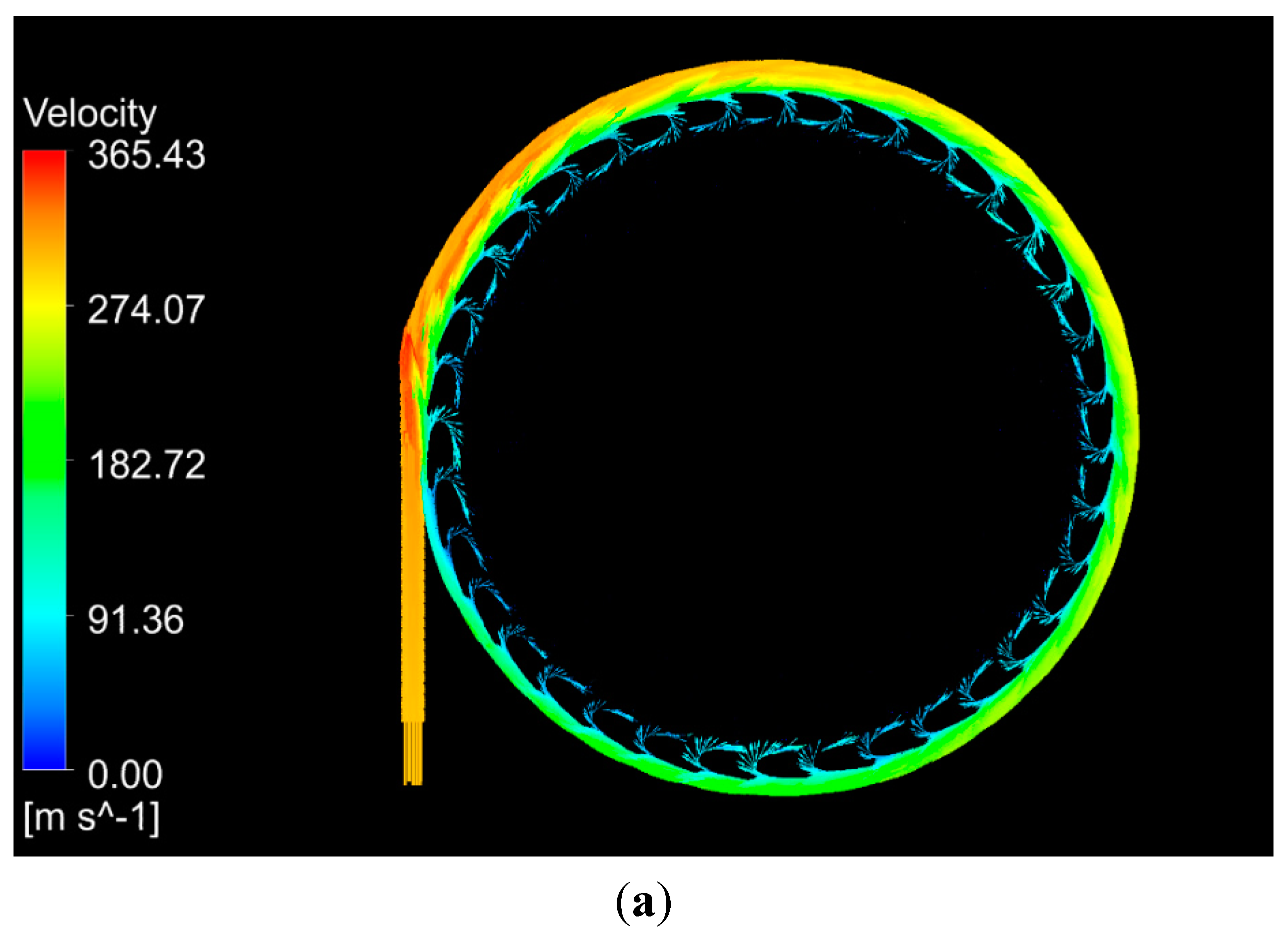
The annular-ducted fan lift system in hover mode was simulated. Figure 8 shows the streamlines and static pressure contour on the surface of the aircraft and inside the lift fan system in hover mode. The 3D streamlines through the annular duct show that the lift fan system generates a long wake in the flow field (Figure 8a). The wake is not swirling due to the counter rotation of the two fans; thus, there is no energy wasted on swirling air. The vortexes at the fan tips are also eliminated by the duct walls. The annular duct has a diffused outlet, which prevents the downstream flow from contraction and increases the duct lift. The wake streamlines still look a little contracted in Figure 8a because of the low pressure beneath the central fuselage, but the cross-sectional area of the flow is not decreased according to the surface streamlines in the central plane (Figure 8b). 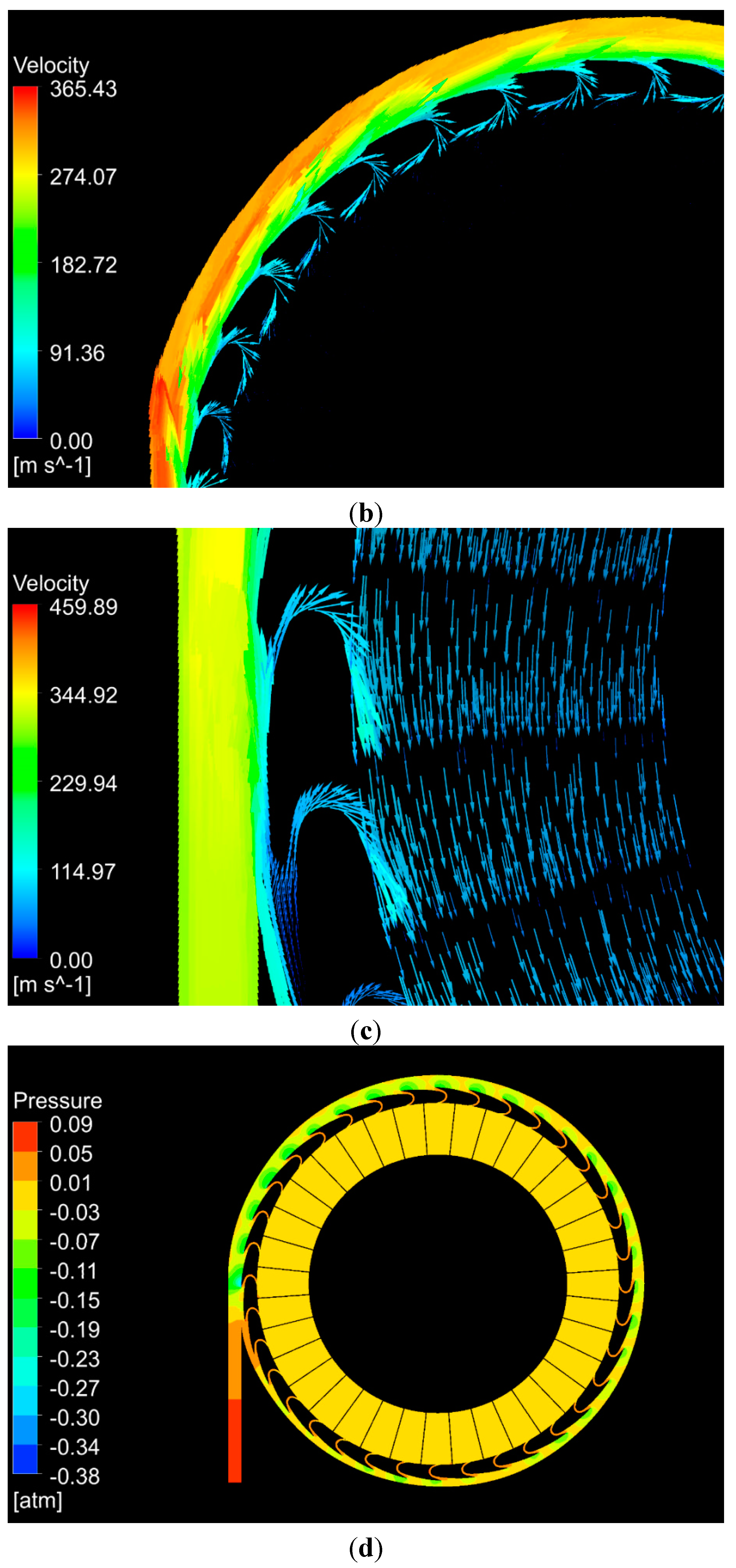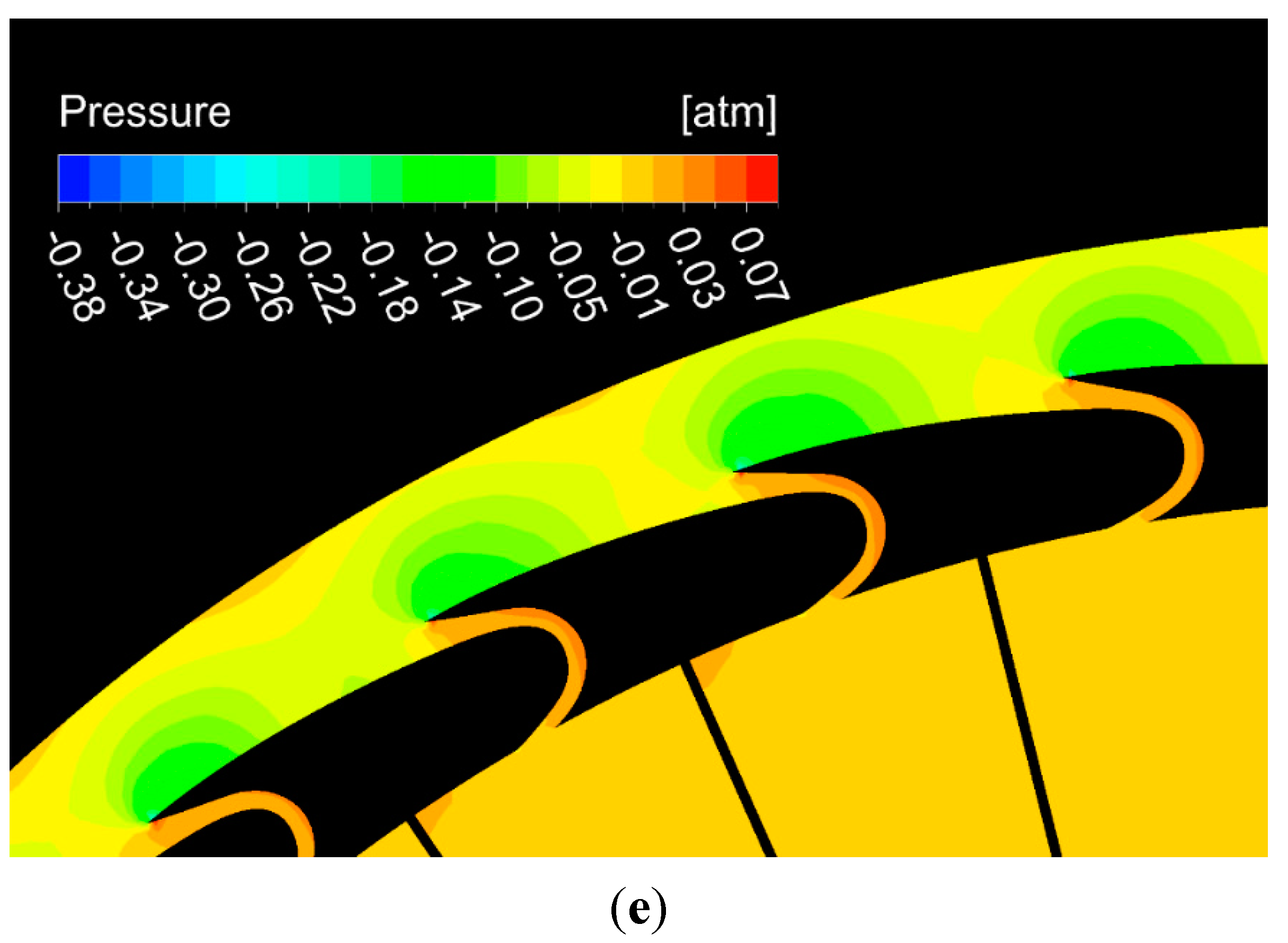The pressures on the upper surfaces of the duct walls and fan blades are low (Figure 8c,d). The low pressure caused by the induced flow on the inlet lips of the duct and upper surface of the peripheral wing generates duct lift (Figure 8b,d).

For the 3-m annular duct, when the two fans contra rotate at +103 and −99 rpm producing the same torque, the system lift is T = 102,408 N (10.433 tons, the maximum weight of the Apache helicopter), among which fan thrust is T_rotor = 58,361 N; thus, according to Equation (4) of the momentum theory:

$$\text{σ}=\frac{T}{2T_{rotor}}=0.88$$

(11)

Figure 8. (a) Three-dimensional streamlines in front of the central plane in hover mode; (b) surface streamlines in the central plane of the aircraft; (c) static pressure on the upper surface of the fans, duct, fuselage and peripheral wing; (d) pressure contour inside the annular-ducted lift fan system.

Figure 8. (a) Three-dimensional streamlines in front of the central plane in hover mode; (b) surface streamlines in the central plane of the aircraft; (c) static pressure on the upper surface of the fans, duct, fuselage and peripheral wing; (d) pressure contour inside the annular-ducted lift fan system.

The induced power according to Equation (5),

$$P=\frac{T^{3/2}}{\sqrt{4\text{σρ}A}}=1548\text{kW}$$

(12)

where fan area A = 103.62 m².

Compared to the Apache rotor, according to Equation (7):

$$\frac{P_{ducted}}{P_{unducted}}==\sqrt{\frac{A_{unducted}}{2\text{σ}{A}_{ducted}}}=0.95$$

(13)

where A_unducted = 167.33 m² for the rotor of the Apache helicopter.

It can be seen that, although the disk area of the Apache rotor (167.33 m²) is much larger than that of the lift fan system (103.62 m²), the induced power for the annular-ducted lift fan system to provide the same lift is even lower.

The moment of the upper fan is obtained as 98,925 N m, and the moment of the lower fan is 98,292 N m; thus, the mechanical shaft power of the lift fan system:

$$P_{shaft}=2\text{π}\frac{n}{60}rF=2085\text{kW}$$

(14)

Therefore, the fan efficiency is η = 1548/2085 = 0.74. The lift efficiency T/P_shaft = 10,433/2085 = 5.00 kg/kW.

For the AH-64E Apache helicopter, it is known that the maximum weight is T = 10.433 ton (102,243 N), power P = 2676 kW, A = 168.11 m², so the rotor efficiency η = P_induced/P = 0.603, and the lift efficiency T/P = 3.89 kg/kW. Therefore, compared to the Apache rotor, the 3-m lift fan system is more efficient and can save 22% of the power.

The reasons why the annular-ducted fan can save energy are two-fold [20]: (1) elimination of rotor tip vortex loss, wake swirling loss and wake coning loss: the duct not only eliminates fan tip vortex, but also prevents the downstream flow from contraction; and (2) additional duct lift. Beside the fan thrust, there is an additional duct lift caused by the low pressure on the duct inlet lips and the upper surfaces of fuselage and peripheral wing, which can be almost as much as the fan thrust. The additional duct lift helps reduce the required fan thrust, thus reducing the drag on fan blades and the corresponding power required to run the fan. According to the simulation results, about 1/4 of the lift comes from the upper fan, 1/4 from the lower fan, 1/4 from the annular duct lips and 1/4 from the peripheral wing due to the induced flow over the wing (Figure 8b,d).

It is known that a conventional circular ducted fan is more efficient than an unducted fan or propeller, so this result that the annular-ducted fan system is more efficient than a rotor is not surprising.

For a 2 m-wide annular duct, when the fans contra rotate at +118.5 and −116 rpm, the system lift is T = 102,270 N, among which fan thrust is T_rotor = 56,698 N and fan area A = 75.39; thus, σ = 0.902; the induced power P = 1791 kW; and P_ducted/P_unducted = 1.11.

The moment of the upper fan is 99,455 N m, and the moment of the lower fan is 100,603 N m; thus, the mechanical shaft power P_shaft = 2455 kW; the fan efficiency η = 0.73; and the lift efficiency T/P_shaft = 4.25 kg/kW. Therefore the 2-m annular-ducted lift fan system also needs less power and has higher lift efficiency than the Apache rotor to provide the same lift. Furthermore, if the ground effect is considered and the distance from the aircraft to the ground is 10 m, the shaft power will be only 1880 kW, much lower than the Apache’s power. The lift efficiency T/P = 5.55, which is much higher than the Apache rotor.

Although the 2-m annular duct system requires a little more power than the 3-m duct due to the reduced ducted fan area, the compact structure may reduce the dead space of the lift fan system during horizontal flight. After all, the VTOL process only occupies a short time of the flight.

6.2. Transition from VTOL to Horizontal Flight

The low disc loading ducted lift fan system can introduce tremendous momentum drag during transition from vertical takeoff mode to cruise mode. Momentum drag is generally caused by a directional change of the airflow going through the lift fan system. To achieve successful transition, the aircraft with the lift fan system must overcome the momentum drag and increase its speed to a certain level to gain sufficient aerodynamic lift. 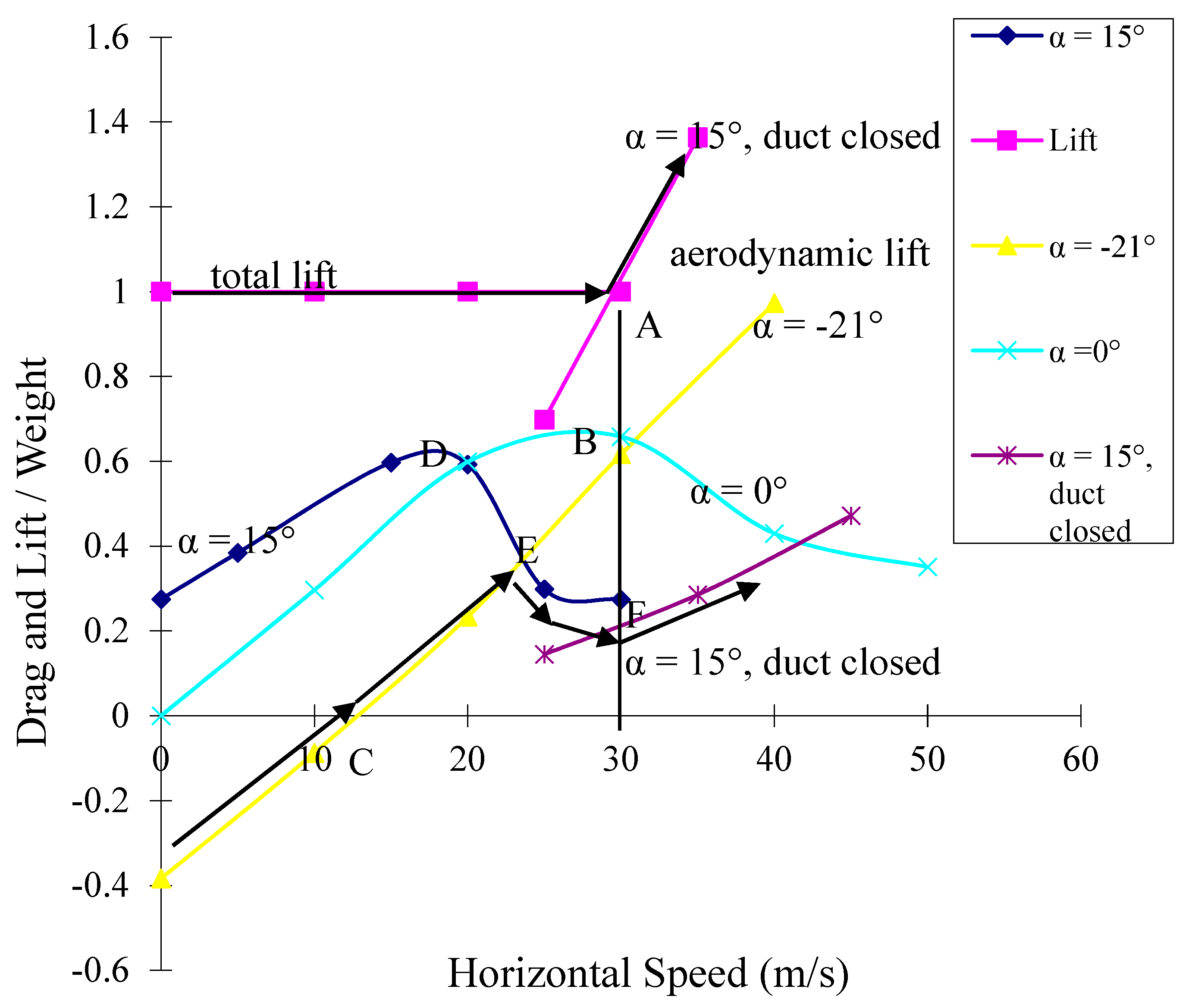As shown in Figure 9, the minimum speed for the aircraft to fly with the duct enclosed on aerodynamic lift is 30 m/s at an angle of attack of 15° (Spot A).

To approach this speed at an angle of attack of zero degrees (Figure 10a), the momentum drag forms a high peak at Spot B (Figure 9), which needs a forward jet thrust of 0.63 of the aircraft weight to be overcome. The peak exists because the momentum drag increases with the forward speed and the rotational speeds of the fans, while the rotational speeds of the fans needed to maintain the lift decrease with the forward speed. In the CFD simulation, the rotational speeds of fans were adjusted to keep the lift equal to the weight of the aircraft when the forward speed increased.

Figure 9. Computed time-averaged net drag and lift-to-aircraft weight ratio at different angles of attack in transition mode. The lift was maintained equal to the weight of the aircraft through the change of the rotational speed of the fans.

Figure 9. Computed time-averaged net drag and lift-to-aircraft weight ratio at different angles of attack in transition mode. The lift was maintained equal to the weight of the aircraft through the change of the rotational speed of the fans.

In Figure 9, the drag is not only aerodynamic drag, but net drag, including the horizontal force generated by the lift fan system. If the aircraft flies at a negative angle of attack, as shown in Figure 10b, there is a forward force produced by the lift fan system to offset aerodynamic drag, so the net drag can be negative. When the aircraft starts to fly at a −21° angle of attack (Figure 10b), the lift fan system generates a forward force to push the aircraft to fly forward without additional forward jet thrust. The aircraft can easily reach the speed of 13 m/s (Spot C) where the net drag is zero, which means that the forward force produced by the lift fan system equals the aerodynamic drag. After that point, the net drag increases rapidly with the increase of speed. The aircraft still needs additional forward thrust of 0.61 of the aircraft weight to reach the speed of 30 m/s.

If the aircraft starts at an angle of attack of 15° (Figure 10c), the lift fan system will produce a backward force, which is a positive net drag at a speed of 0 m/s. With the increase of the speed, there is also a high peak of drag at the speed of 18 m/s (Spot D), but after that point, the drag decreases rapidly.

Therefore, the best way to achieve efficient transition seems: (1) to rise at an angle of attack of zero degrees; (2) to change the angle of attack to −21° and fly forward without additional forward jet thrust (Figure 10b); (3) when the speed reaches about 13 m/s (Spot C), continue to fly with additional forward jet thrust; (4) when the speed reaches about 23 m/s (Spot E), change the angle of attack to 15° (Figure 10c), slow down the rotational speeds of the fans and continue to fly with additional forward jet thrust until the speed reaches 30 m/s (Spot F); (5) to stop the lift fan system and close off the duct; and (6) to continue to fly with aerodynamic lift and forward jet thrust. In this way, the peak of momentum drag is much lower (near Spot E), which only needs forward thrust of about 0.32 of the aircraft weight to overcome. The lift and net drag increase along the arrows in Figure 9.

Figure 10. The aircraft attitudes and streamlines in the central plane of the aircraft in transition mode. The lift was maintained equal to the weight of the aircraft by adjusting the fan rotational speeds. (a) Angle of attack α = 0°, freestream speed U = 20 m/s, fan speeds N = +108, −117 rpm; (b) angle of attack α = −21°, U = 10 m/s, fan speeds N = +122, −121 rpm; (c) angle of attack α = 15°, U = 20 m/s, fan speeds N = +91, −97 rpm.

Figure 10. The aircraft attitudes and streamlines in the central plane of the aircraft in transition mode. The lift was maintained equal to the weight of the aircraft by adjusting the fan rotational speeds. (a) Angle of attack α = 0°, freestream speed U = 20 m/s, fan speeds N = +108, −117 rpm; (b) angle of attack α = −21°, U = 10 m/s, fan speeds N = +122, −121 rpm; (c) angle of attack α = 15°, U = 20 m/s, fan speeds N = +91, −97 rpm.

For vertical landing, the aircraft can start to reduce the forward speed at an angle of attack of 15°, then open the duct and start the lift fan system (Figure 10c). When the forward speed slows down, then change the angle of attack to zero degrees to land (Figure 10a).

The aircraft attitudes and the streamlines in the central plane in transition mode are presented in Figure 10a–c. The incoming flow on the aircraft’s upper side is strongly entrained by the lift fan system, maintaining attached flow at the aircraft’s trailing edge.

The attitude control can be performed through changing the direction of the thrust from the two jet engines respectively. Thrust vectoring can also be used to offset the nose up pitching moment and rolling moment during the transition.

6.3. Aerodynamic Drag and Horizontal Cruise Speed Predictions

During cruise flight, the annular-ducted fan lift system will be shut off to reduce drag and provide aerodynamic lift, so the compressibility effects on the fan blade tips and fan drag will be eliminated and replaced by aerodynamic drag. With the lift fan system enclosed during horizontal flight, the aerodynamic drag of a specific size may be smaller than the rotor drag, so the aircraft may possibly fly faster than helicopters and tiltrotors.

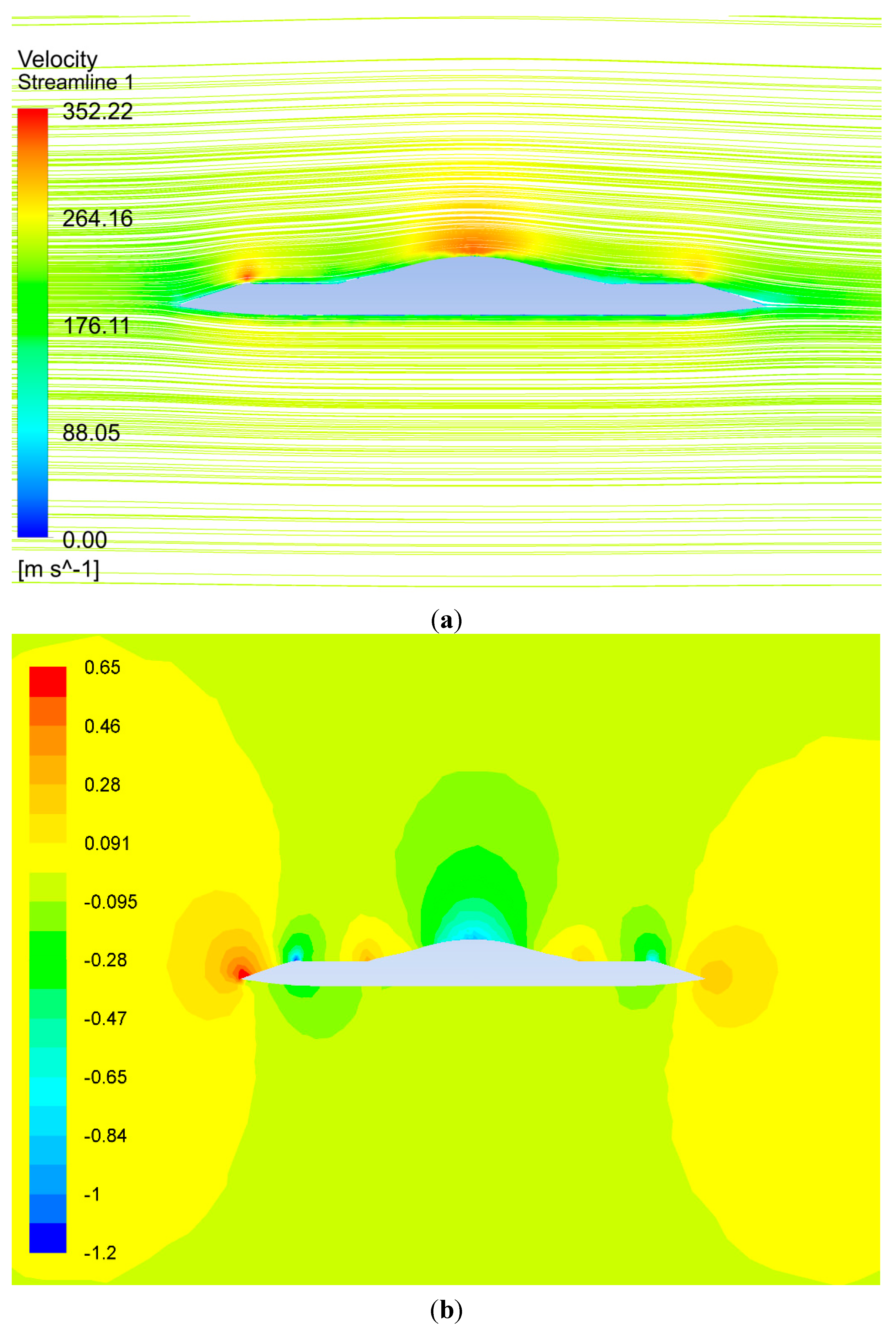
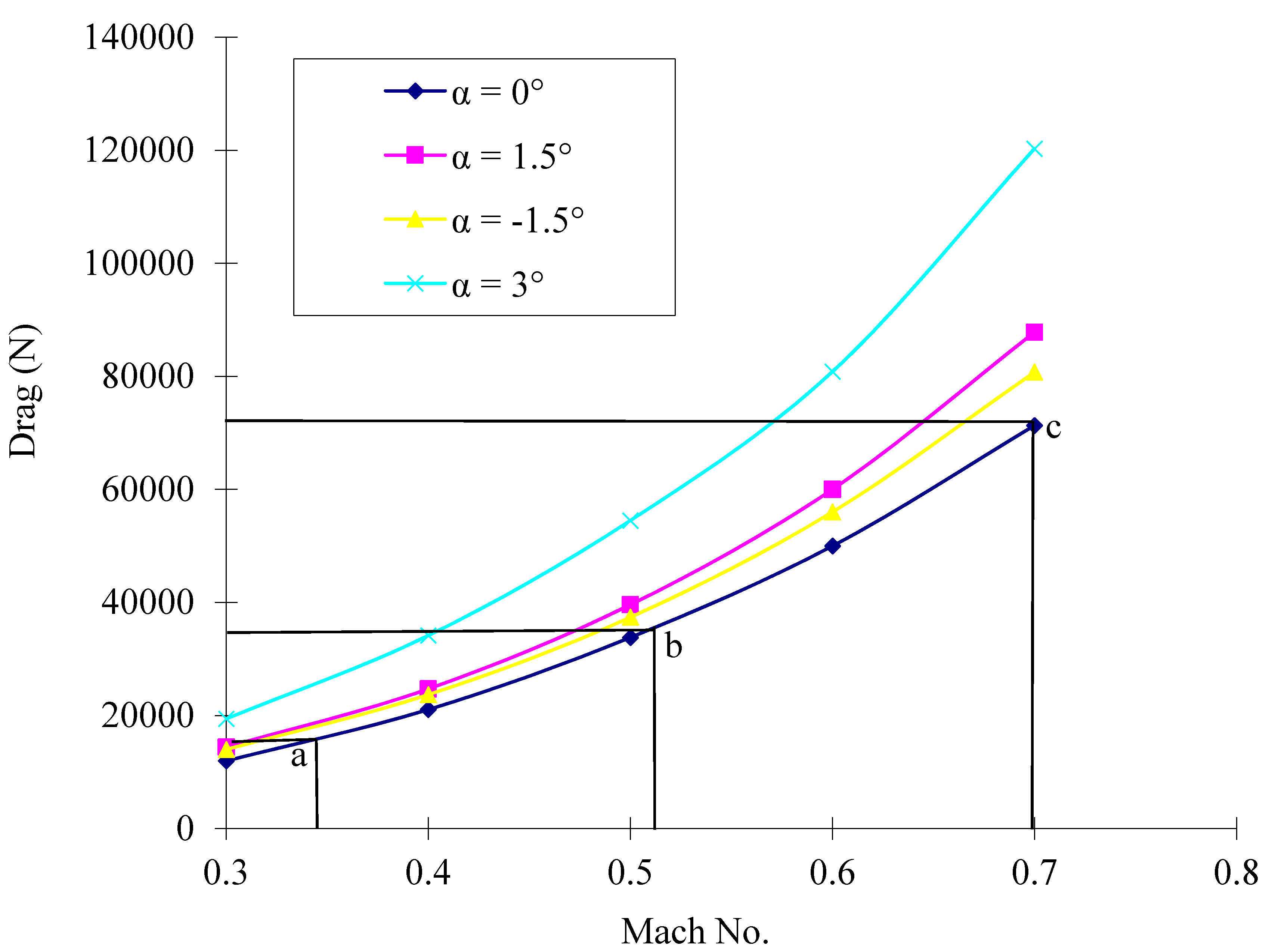
The drag and lift of the aircraft with the annular duct system enclosed during level flight were simulated. As shown in Figure 11, the airflow speed on the cambered upper surface of the aircraft increases (Figure 11a) and causes low pressure to generate lift (Figure 11b). The aerodynamic drag increases with flight speed (Figure 12).

Based on the balance of drag and jet thrust, when the drag equals the engine thrust, the maximum speed of the aircraft can be predicted. Therefore, when the flight speed increases to 0.35 Ma (428 km/h) at a zero degree angle of attack (Figure 12, Spot a), the drag is 15.7 kN. If the maximum jet thrust is just 15.7 kN, the maximum speed will be 428 km/h. Supposing the propulsive efficiency is 0.7, the jet power at this point is 2676 kW, which is the power of the Apache. While the maximum speed of the Apache is 293 km/h, the speed of 428 km/h is 46% faster than the Apache. At this point, the lift is 131 kN, enough to carry a weight of 102 kN. The configuration of the aircraft can be slightly modified (not so cambered) to reduce the lift to equal the weight without increasing the drag, so that the aircraft can fly in the minimum drag mode. The maximum speed is predicted here only based on drag prediction; some real-world effects, including engines, were not considered. The prediction of drag just gives some ideas about how fast the aircraft may theoretically fly without rotor drag.

If the jet thrust increases to 36.3 kN, the maximum speed will reach 0.52 Ma (625 km/h; Figure 12, Spot b). Supposing that the propulsive efficiency is 0.7, the jet engine power at this point is 9180 kW, which equals the power of the V-22 Osprey. The maximum speed of the Osprey is 509 km/h.

Without the constraints of rotor drag and the compressibility effects on the rotor blade tips, the speed of the aircraft can increase further if higher thrust turbofan jet engines are deployed. To reach the speed of 0.7 Ma (857 km/h), the aircraft will need jet thrust of 72.3 kN (Figure 12, Spot c). The lift at this point is 448 kN, much higher than the weight.

Figure 11. (a) Streamlines in the central plane of the aircraft in cruise mode; (b) pressure coefficient in the central plane of the aircraft at speed of 0.7 Ma.

Figure 11. (a) Streamlines in the central plane of the aircraft in cruise mode; (b) pressure coefficient in the central plane of the aircraft at speed of 0.7 Ma.

Figure 12. The computed drag (the engines were not considered) of the aircraft increases with cruise speed at different angles of attack.

Figure 12. The computed drag (the engines were not considered) of the aircraft increases with cruise speed at different angles of attack.

The annular-ducted lift fan aircraft can also be in other configurations, rather than the above circular flying saucer shape, to reduce drag. A triangular or rhombic configuration (Figure 13), like a blended wing body [21,22], may fly faster and is easier to deploy conventional aerodynamic control surfaces. Aerodynamic drag is determined by the shape and size of the aircraft. A thinner and streamlined shape has less drag and thus may fly faster.

Figure 13. Rhombic-shaped annular-ducted lift fan aircraft.

Figure 13. Rhombic-shaped annular-ducted lift fan aircraft.

6.4. Pneumatic Coupling of Tip Turbine and Engine Exhaust Gases

Shaft-driven and gas-driven annular-ducted lift fan systems are both feasible. The F-35 joint strike fighter finally adopted a shaft-driven lift fan [1], but a gas-driven annular-ducted lift fan system may be less expensive to develop than the shaft-driven system, because it does not require modifying the cruise engine. There are no gears or high power shafting required, and pneumatic coupling also provides balanced engine operation and engine out safety [2]. A preliminary gas-driven tip turbine CFD study was performed without validation due to a lack of experimental data.

As shown in Figure 14, the engine exhaust gases are ducted to the inlet of the gas chamber to spin the tip turbine. With a velocity inlet speed 300 m/s, a significant flow forms in the chamber (Figure 14a,b). The gas flow starts from the inlet, circulates in the chamber, passes through the turbine blades, exits from the outlets on the chamber and discharges itself to the annular duct. When the turbine and lift fan begin to rotate, the exiting gases mix with the rotating air (Figure 14c). The gas flows passing through the tip turbine blades cause a pressure difference on the two surfaces of a turbine blade (Figure 14d,e), which pushes the turbine to spin. A steady solution could not be achieved due to the strong unsteadiness on the turbine blade loading. Unsteady analysis showed that the forces on the blades slightly fluctuated with time, and time-averaged results could be obtained. With an inlet speed 300 m/s, when the turbine is still, the average moment of the gas flows on the turbine blades is about 156 kN m. When the turbine rotates at 120 rpm, the moment on the turbine blades is about 108 kN m, greater than the contra-moment on the lift fan of 100.6 kN m (see Section 6.1), thus enough to maintain the rotation of the lift fan. The gauge pressure inside the chamber is as low as about 0.1 atm (Figure 14d), making it easy to couple with the jet exhaust.

According to the lift fan experimental results with a fan diameter of 1.5 m, the fan augments the turbojet thrust by a factor of three to one for VTOL [2]. With the fan size increased to a diameter of 14 m, the fan may possibly augment jet thrust by more than five-fold.

Figure 14. (a) Velocity vector in the central plane of the gas chamber when the tip turbine was still; (b) enlarged view of velocity vectors; (c) enlarged view of velocity vectors when the tip turbine rotated at a speed n = 120 rpm; (d) pressure contour in the central plane of the chamber; (e) the enlarged view of pressure on the turbine blades to show the pressure difference on two sides of the blades.

Figure 14. (a) Velocity vector in the central plane of the gas chamber when the tip turbine was still; (b) enlarged view of velocity vectors; (c) enlarged view of velocity vectors when the tip turbine rotated at a speed n = 120 rpm; (d) pressure contour in the central plane of the chamber; (e) the enlarged view of pressure on the turbine blades to show the pressure difference on two sides of the blades.

7. Conclusions

The CFD study allows assessing the power and lift efficiency of the annular-ducted lift fan system in hover mode, the lift and drag of the system in transition mode, the drag and flight speed of the aircraft in cruise mode and the pneumatic coupling of the tip turbine and exhaust gases of the jet engine. The predicted data provide insight for future experimental study of annular-ducted lift fan aircraft.

The CFD simulation results show that the annular-ducted lift fan system has higher lift efficiency, compared to the rotor of a helicopter, due to the additional duct lift and the elimination of energy losses. Transition from VTOL to cruise flight needs some extra forward thrust to overcome a low peak of drag, primarily caused by the momentum drag of the low disc loading fan system. It may fly faster than helicopters and tiltrotors in cruise mode based on aerodynamic drag prediction, owing to the replacement of rotor drag by aerodynamic drag as the annular duct system is closed off. Pneumatic coupling of the tip turbine and jet exhaust of 300 m/s can provide enough moment to spin the lift fan system.