2.1. Layout Limitations
Wind tunnel engineers are used to working with models of reduced size, flown in conditions that are not the same as in the real world. Those problems do not arise when testing birds, because if you select a bird like a pigeon, you can fit the whole of it in the test section, and set the conditions as they are out of doors. That is a great convenience, because the pigeon does not have an anatomy in the way than an engineer can understand it. If you hold a pigeon in the hand, its wings are folded up, and if you unfold them, they can be set at dihedral angles from −60 to +90 degrees, and a span between one-third and the whole span, with all kinds of angles that can be set by muscles to a wide range of values. A pigeon wing cannot be set by hand into a position that is meaningful for flight. On the other hand, the whole pigeon can be trained to fly in a wind tunnel, and will set itself into a posture for whatever kind of flight it has to perform. You do not measure forces in a bird wind tunnel. You let the bird set itself up, and infer the forces from the geometry of its situation.
Bird wind tunnels are designed to achieve given levels of performance without being too expensive. Engineers, when consulted about this, often say that the best way is an open-circuit suction tunnel, with the fan at the downstream end. This type of design works very well when used in the wind tunnel laboratory, where the test section (containing air below ambient pressure) is carefully sealed. However, the ornithologist cannot leave his bird unattended. He needs access to it, and consequently leaves holes and doors open, which allows outside air to rush invisibly in, and disturb the flow in the test section. A suction tunnel does not work correctly, if air can get into the test section by routes not noticed in the design. In practice, blower and recirculating tunnels can be used [
1,
2] but suction tunnels are not practical for any form of quantitative work on live birds.
Figure 1 shows an open-circuit blower tunnel used in Bristol in the 1960s and later moved to Nairobi. The bird flies in the open air, at the exit from the contraction, which is at the current environmental static pressure, and allows the experimenter direct access to the bird or bat, without interfering with the air flow. This tunnel may have had some shortcomings, but it worked very well to get glide polars of pigeons, and allowed the range of lift and drag coefficients in the normal flight of birds to be determined. This tunnel was designed to allow forces and work to be scaled, in a set of similar animals in the manner pioneered by the physiologist A.V. Hill in the 1930s [
3], although his approach was not followed by later physiologists after the war.
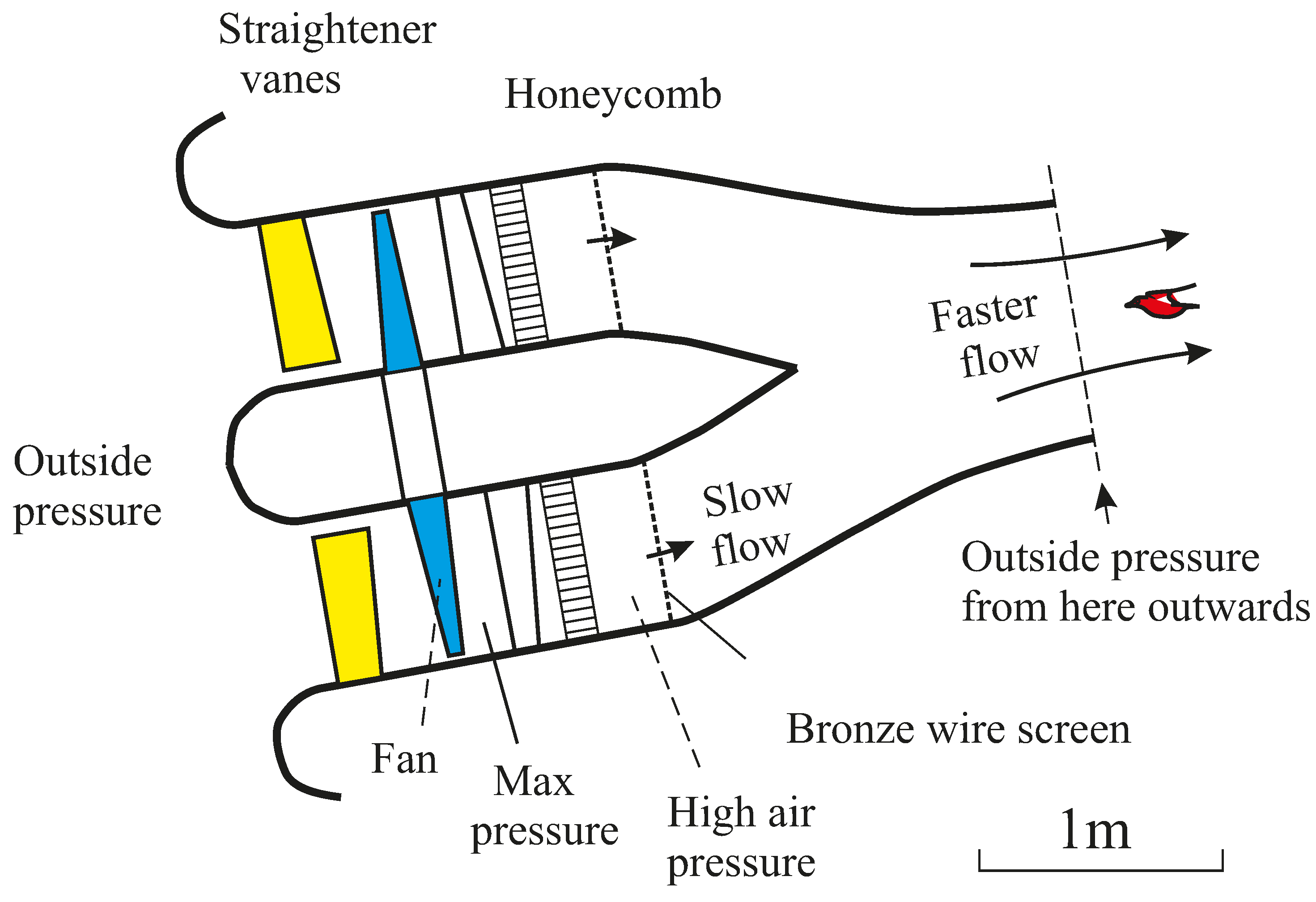
Figure 1.
Hydraulic-powered wind tunnel at Bristol in 1966, moved to Nairobi in 1970. This tunnel was powered by a Woods ventilating fan, with a contraction ratio of about 4. Fixed stator vanes before and after the fan straightened the flow, and there was a honeycomb and a fine mesh screen before the contraction. The pigeon flew outside the end of the contraction, where it could be photographed and measured at will. Maximum speed 22.1 m/s.
Figure 1.
Hydraulic-powered wind tunnel at Bristol in 1966, moved to Nairobi in 1970. This tunnel was powered by a Woods ventilating fan, with a contraction ratio of about 4. Fixed stator vanes before and after the fan straightened the flow, and there was a honeycomb and a fine mesh screen before the contraction. The pigeon flew outside the end of the contraction, where it could be photographed and measured at will. Maximum speed 22.1 m/s.
A better (but more expensive) solution was built by AB Rollab of Solna, Sweden, and installed in the Biology Department of Lund University in 1994 (
Figure 2) [
4]. This is a closed-circuit wind tunnel with a test section measuring 1.20 m across by 1.08 m vertically, and a contraction ratio of 12.25:1, rigged in such a way that the entire machine, return flow and all, can be tilted from 8° descent to 6° climb. The first 1.20 m of the test section is enclosed by walls, then there is an open 0.5 m gap before the line to the motor begins. The rest of the tunnel is entirely enclosed, so that the lowest pressure is at the test section, and air in the rest of the circuit is at higher pressure. This means that the experimenter can move equipment in and out of the gap in the test section, or reward the bird for its performance, without disturbing the flow where the bird is. Another version of this tunnel was installed by the same Swedish manufacturers later at the Max Planck Institute for Ornithology at Seewiesen in Germany, but this one has a horizontal circulation, and omits some of the original features, notably the tilting facility.
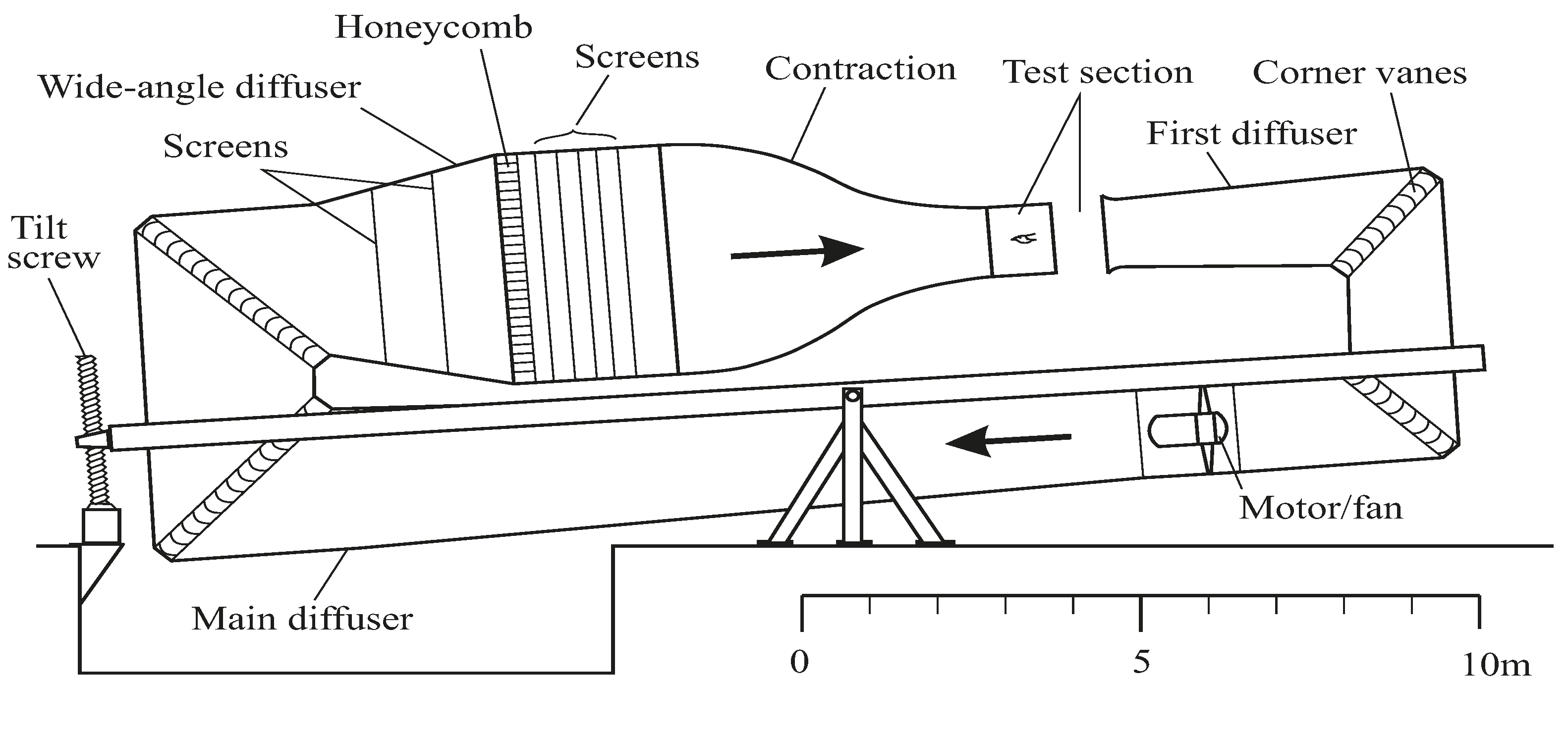
Figure 2.
The Lund wind tunnel, installed in 1994, has a test section measuring 1.20 × 1.08 m and a contraction ratio of 12.25. There is a honeycomb, 5 screens and a fine wire screen. The tilting arrangement allows for 8° climb to 6° descent. The closed-circuit arrangement is open at the test section, but closed everywhere else. Maximum speed 50 m/s.
Figure 2.
The Lund wind tunnel, installed in 1994, has a test section measuring 1.20 × 1.08 m and a contraction ratio of 12.25. There is a honeycomb, 5 screens and a fine wire screen. The tilting arrangement allows for 8° climb to 6° descent. The closed-circuit arrangement is open at the test section, but closed everywhere else. Maximum speed 50 m/s.
2.2. Gliding Flight
The simplest way to use a bird to make its own measurements is to train it to hold a constant position in a wind tunnel, in which the air flow has been set by the experimenter. For example, just about any bird can be trained to fly in a wind tunnel, in a body of air that is moving slightly upward relative to horizontal, at a speed that is within its normal range [
5]. By doing this over a range of speeds, and finding the minimum descent angle at which the bird can fly without flapping its wings, the basic “glide polar” can be found for the bird. This curve can be generalised, and used for gliding calculations in a wide range of birds. Unlike an engineer, you do not have to worry about small amounts of drag caused by poor wing-to-body junctions, because all birds are constantly modified by natural selection to deal with small performance defects, caused by minor variations of anatomy. Once the shape and size of wing are set to suit the bird’s life style (also by natural selection) the bird is optimised as well as it can be, to maximise performance. This type of optimisation only optimises species that already exist, and works over a period of many generations, but that is, of course, what biologists have to deal with.
Figure 3.
A pigeon gliding in the Bristol wind tunnel, showing planform variations with speed. There are no mechanical constraints with this in a bird wing, but there are in bat or pterosaur wings. The lift coefficient went from 1.3 to 0.3, not taking account of the tail area. It would have been much lower at high speeds, if the full span had been maintained.
Figure 3.
A pigeon gliding in the Bristol wind tunnel, showing planform variations with speed. There are no mechanical constraints with this in a bird wing, but there are in bat or pterosaur wings. The lift coefficient went from 1.3 to 0.3, not taking account of the tail area. It would have been much lower at high speeds, if the full span had been maintained.
A gliding pigeon (
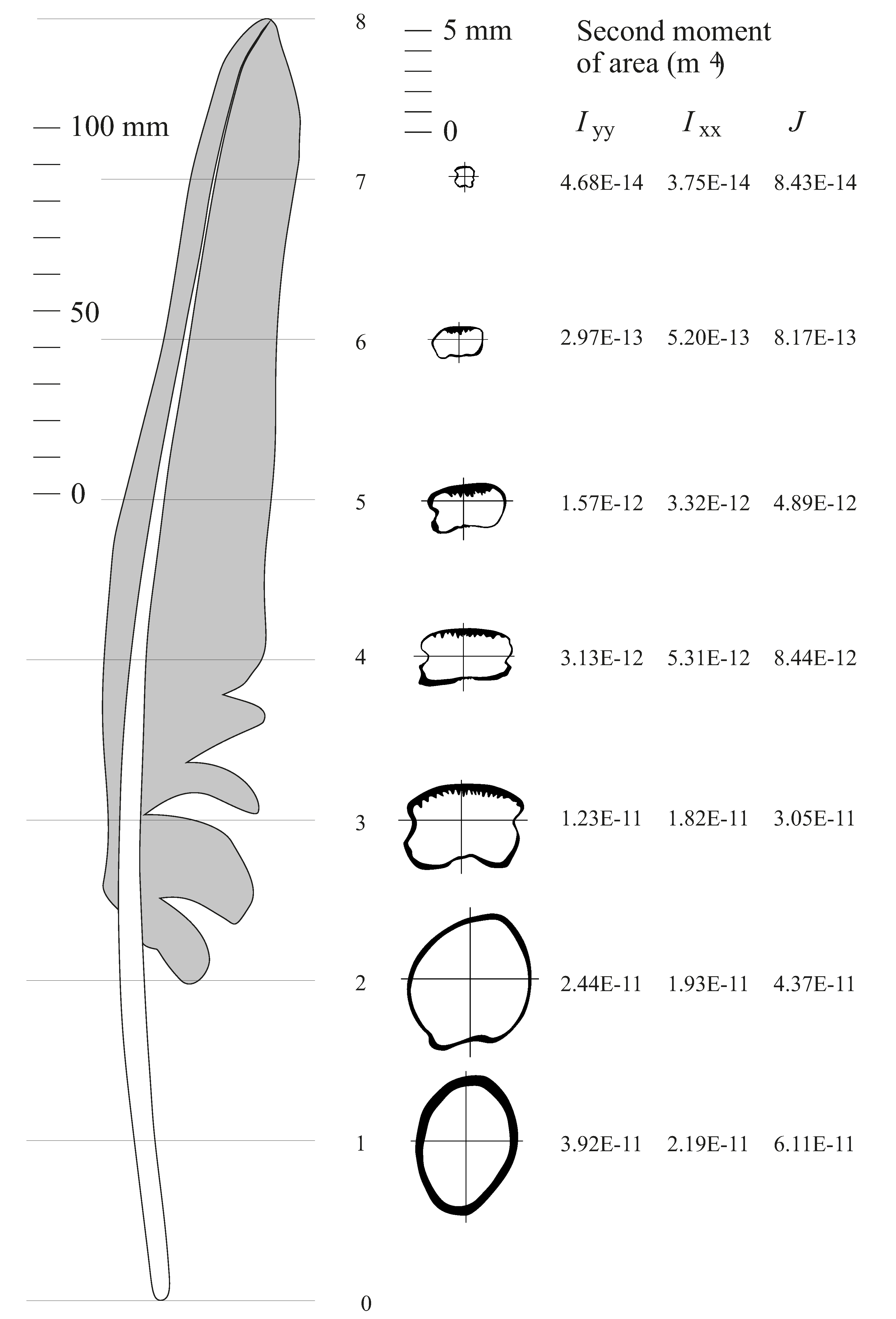
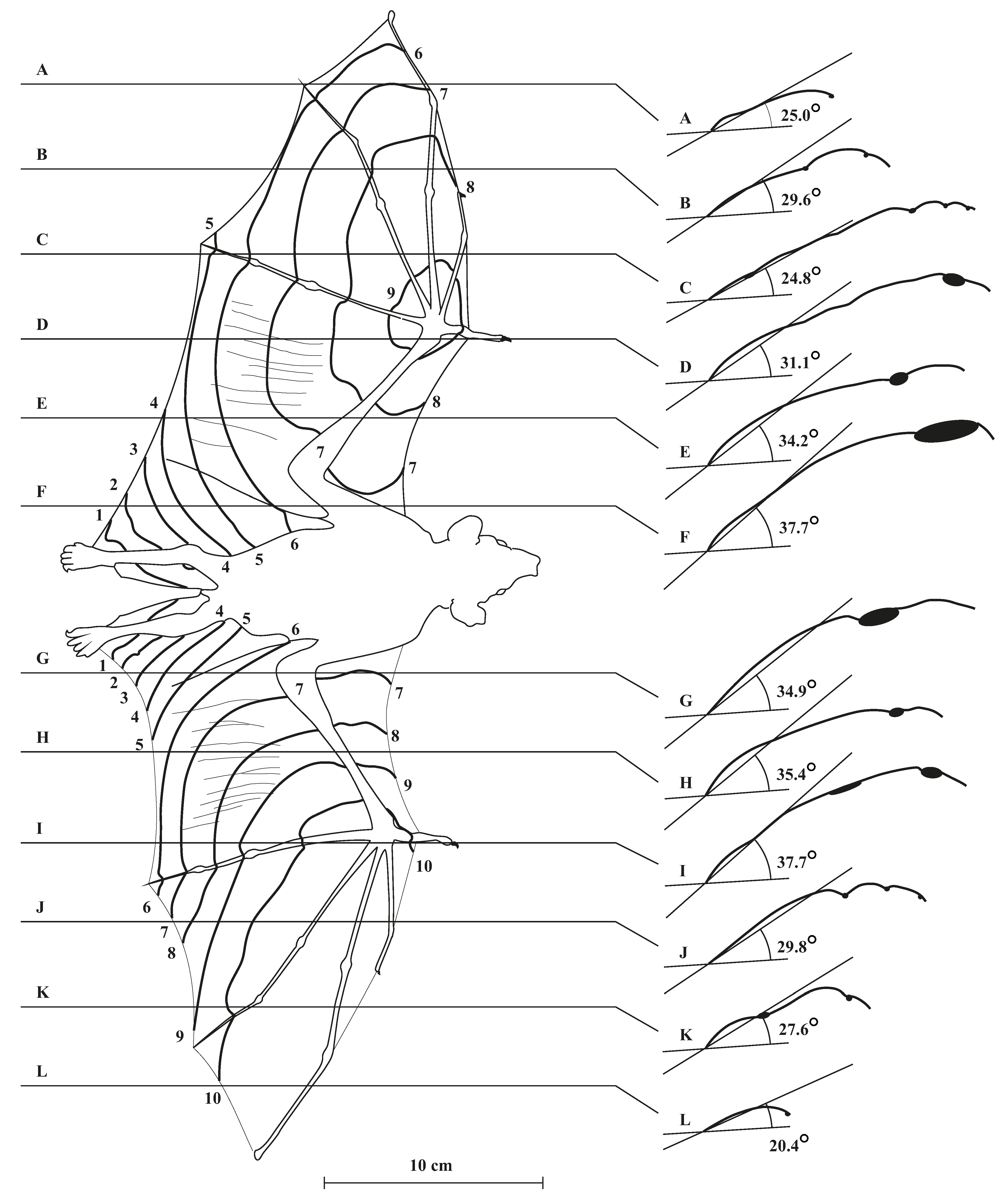
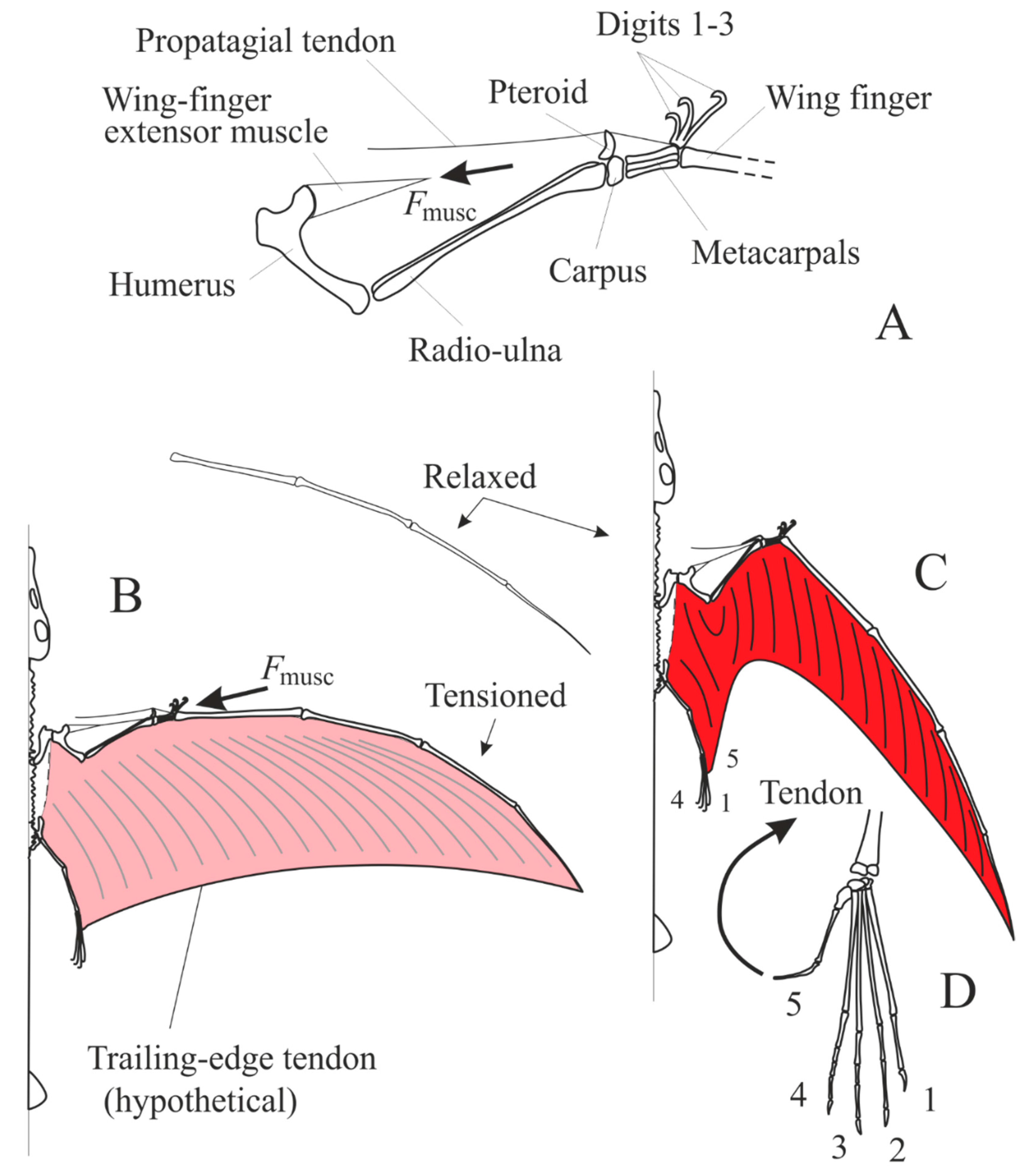
Figure 3) is quite a spectacle for a glider designer. In the first place, it gets unsteady at low speeds, but still flies nearly as well as before, if you put a rubber band around its tail to prevent it from spreading. How, then does it control its speed? The pigeon’s wings can move about the shoulder joints, forwards or back, upwards or down, and twisting nose-down or nose-up. To control speed, it moves them forward or back, like a hang-glider pilot. Moving the wings forward also spreads them to their greatest area, while moving them back allows the elbow and wrist joints to flex, so that the feathers of the wing slide inwards over one another, reducing the span and area of the wing. Fast-gliding birds can reduce their wing area and span to less than half the maximum values, without losing any strength whatsoever. This is possible because the bird wing is a multiple-spar design, with the shaft of each feather being a local spar for its own part of the wing. The same movement that adjusts the area of the wing also serves to control the area, by allowing the feathers to slide over one another. Varying the span is a better method of adjusting wing planform for speed than adjusting the chord, for instance by Fowler flaps. However, it involves a set of elbow and wrist joints, whose axes are out of line with each other, to allow various parts of the wing to be aligned, in a way that is unfamiliar in aircraft wings.
2.3. Measuring Drag
To generalise a measured glide polar, that is, adapt a measured polar to get new polars for other birds, you can add up sources of drag, starting with the drag of the feathered body, minus wings. If you try that, you get into trouble straightaway. If you take a dead bird, or stuffed or simulated one, no matter what you do, the air flow just separates from the body surface, and will not reattach. It gives a drag coefficient of 0.3 or more, like a football. As with all wind tunnel measurements on birds, trying to measure drag on parts of a dismembered bird is useless.
This problem was not solved until a way was found to measure a living bird’s body drag, without balances or any form of external measurement. It was noticed some years ago that this body drag coefficient is one of two morphological variables needed to calculate the speed (
Vmp) at which a particular bird requires minimum power to fly level. The other one is the dimensionless variable
k, which accounts for differences in lift distribution from the ideal ellipse.
k can be got at from field observations of wild birds and is a little below 1, because of splayed feathers at the wing tips. The other variables for the calculation are easily measured, like wing span, gravity, air density and so on. The experiment for the body drag coefficient is to fly the bird level, and measure its wing beat frequency, where it is easy to show that the small variations of frequency vary directly with the power. If the drag coefficient is high,
Vmp comes down, and if it is low
Vmp goes up. You take a few dozen of those frequency curves, from the minimum to the maximum speeds at which the bird will fly horizontally, and having measured
Vmp, you turn the equation round to get the body
CD. A bird with no back load has a value around 0.1 or a bit less, but adding even small bits of plastic on the bird’s back sends its
CD up sharply [
6]. That is a serious problem for those of us who use satellite tracking to follow long-distance migrants, as we do not have an easy way to check increases of body drag, caused by add-on equipment boxes.
2.4. Power in Biology
A bird flying horizontally overcomes drag by flapping its wings about the shoulder joint. The flapping motion results in a mean horizontal thrust force, and this force, multiplied by the speed, is the power required from the flight muscles [
6]. The power comes from the stress developed by the muscle, and the speed at which it can shorten, and these two variables set the power available for shortening in the muscles of birds of different size. Measuring a bird’s total drag is the starting point in any discussion of power requirements in level flight, but the drag itself is not a simple calculation, as in a fixed wing.
To measure the drag, you have to measure (or estimate) the rates of all processes in the living bird that require energy from fuel reserves. This begins with the basal metabolism, the power needed to keep the bird alive, which scales roughly with the 0.75 power of the body mass in birds of different mass. The mechanical power required to fly, neglecting comparisons, varies with about the 1.17 power of the mass. An African vulture requires less than 4% of its cruising power to stay alive, whereas a small passerine like a Goldcrest uses over 30% of its power for the same purpose. Also the small bird goes slower than the large one. Consequently small birds cannot afford any kind of migration strategy that wastes time, whereas large birds can use soaring procedures that cut their energy expenditure, at the expense of a lot of time spent soaring in thermals. The energy used in flapping the wings, and overcoming the drag of the wings also has to be expressed in terms of the fuel energy consumed, rather than of the work done. The task of calculating the power needed by a flapping wing is far beyond current experimenters, but can be handled by analogy methods, relating this work to the amount of work that would have to be done, without flapping the wings. The details of how that is done are in my book
Modelling the Flying Bird [
2].
Biologists know that using muscles to generate mechanical power results in the consumption of fuel, but they call this “metabolism”, and think of it as something that occurs during muscular activity, but not connected with other changes that occur in flight. They never measure the air density, or think about changing gravity. If the bird is “flying”, that is enough, and if it does manoeuvres like cyclical acceleration and deceleration, they are just ignored. Consequently, published measurements of the rate of fuel consumption when flying, which have been made by physiological methods, are not very helpful to the flight theorist. The key to using this approach for practical calculations is to define a speed Vmp, at which the bird requires less power to fly, than one flying faster or slower, and devise a practical way to measure it, which can be done by measuring wingbeat frequency in level flight.
Biologists like to do statistics on every kind of wing that is of interest to them, while those of us who study flight behave more like engineers, and define any bird by its mass, wing span and wing area, plus those environmental variables that affect the result,
i.e., gravity and the air density. Having defined these primary variables, we can define others that follow, and combine the whole thing into a programme called
Flight, which has been available from [
2] for many years, and is essentially a model of a flying bird. If we have a bird and we know its measurements and the air density, then we also have a power curve for it,
i.e., a curve that relates power required, and rate of loss of fuel, to the forward speed. The curve is severely constrained by natural selection, as we can see by thinking about birds that do not exist. If we extend our known measurements upwards to birds bigger than any that we know (20 kg and up), we find that the wingbeat frequency goes down, and the work done by each gram of muscle in each contraction goes up, until eventually the bird cannot fly at all, because the requirements for stress and strain are above the upper limit for flight muscles. There are no huge flapping birds. Beyond a certain size, there is no room for extra muscle to fly at
Vmp, and well before that, the bird cannot lift extra load in the form of fuel, or do sudden manoeuvers to change speed or avoid obstacles. Current birds fly up to a body mass around 16 kg, where they have obvious difficulties, and there are none at all above 20 kg.
There was once a group of very large flapping animals, the last known pterosaurs of the Cretaceous period. At the end, for a short time, they had wing spans approaching 12 m, far more than earlier pterosaurs. We do not know what happened, but most probably the earth changed, by changing minerals in the mantle into a less dense form, and moving them outwards. This would reduce the surface gravity without changing the Earth’s mass [
7]. If we extend the measurements down to miniature hummingbirds (3 g and down) the wingbeat frequency gets so high that the wing muscles do not have time to get ready for the next contraction, a problem that insects overcome with a different type of muscle, that develops low-amplitude contractions in the kilohertz range. Meanwhile, the regular-sized birds all have essentially the same anatomy, with adjustable mass, wing span and wing area. They obey the rules, and adjust everything together. The best combination of power and wingbeat frequency is found in medium-sized birds, especially waders of around 300 g, some of which fly over 10,000 km non-stop. Range performance fades to nothing in very small and very big birds.
2.5. Accuracy of Calculations
These arguments depend on calculating the power required in level flight, which we can do, but we can only check the accuracy of the results by looking at the performance of migrants. We got a chance to try this in 2008, when we were asked by the BBC to help tracking geese on their spring migrations [
8]. We joined in a BBC radio project by Julian Hector, called “World on the Move” in which a great variety of animals were tracked as they migrated, and our job was to work out each goose’s remaining fuel, and show it on the website. When the birds were airborne, we had the help of the BBC weather department to get the winds and the groundspeeds. The GPS tracks gave the ground speeds, which were sometimes so low that it was clear that the birds had stopped, although this was not visible from the GPS points. We could calculate the power the geese needed to fly at the measured air speed, or sit on the ground, and the mass of fuel consumed.
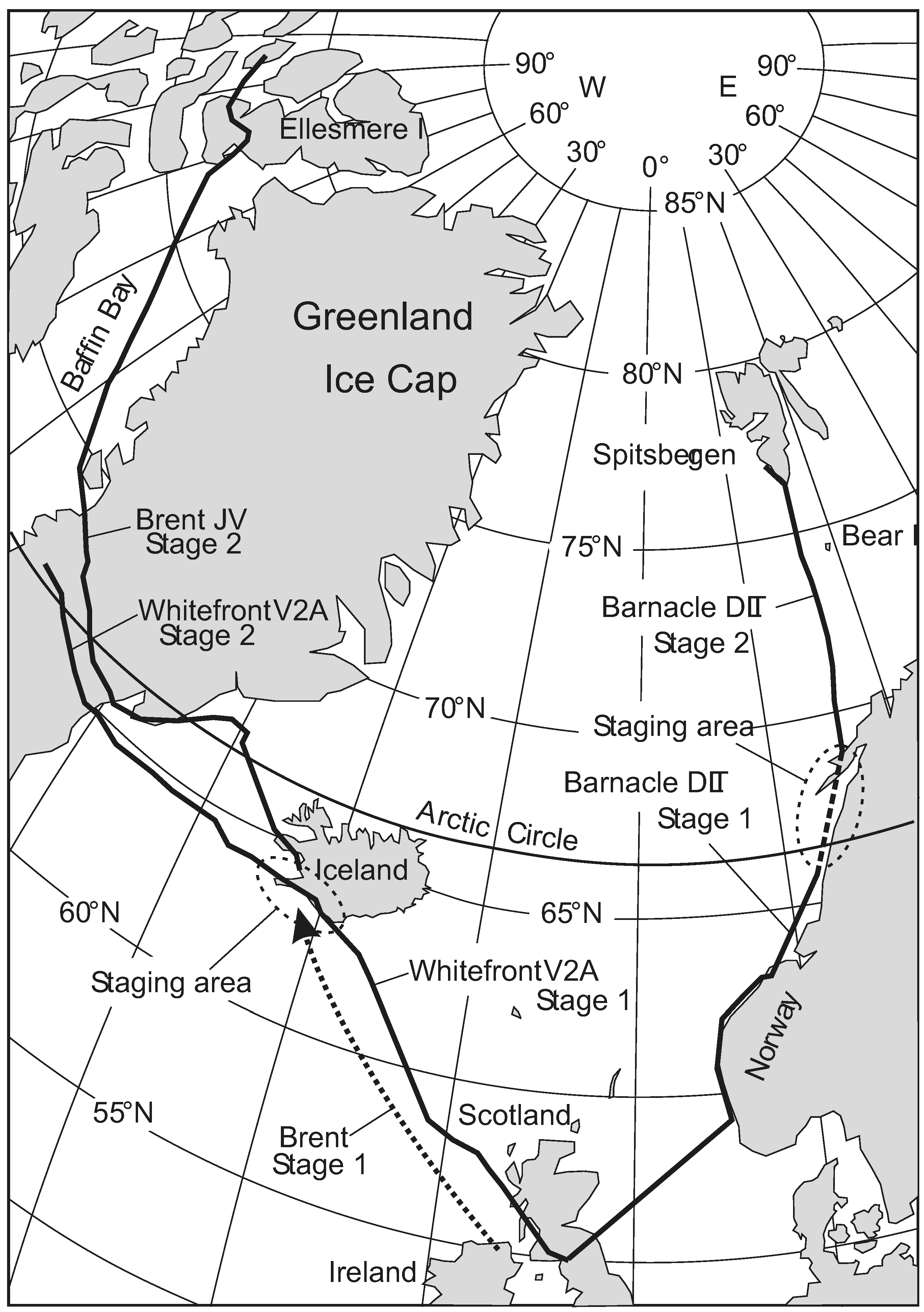
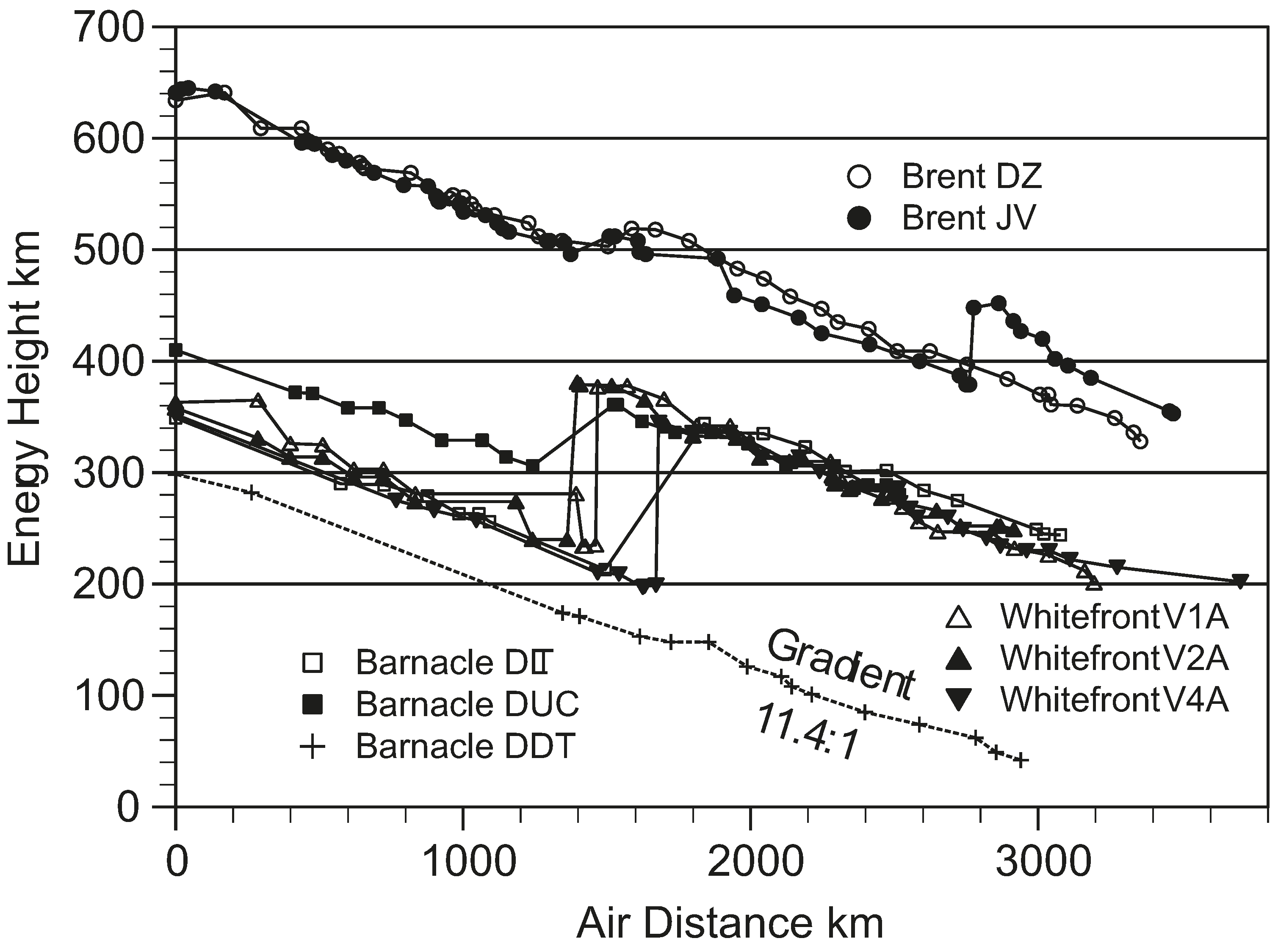
Figure 4 shows the routes that the different kinds of geese followed. We saw the climb up the Greenland ice cap, the increased speed at the top, and the fact that the big geese (Whitefronts) had trouble flying when they were up there and had to walk at times, while smaller geese (Brents) could fly over the top, and carry on up into Canada on the west side. We had estimates of starting fuel loads, and saw that these geese always arrive anywhere with at least 200 km of
energy height in hand (more later), except when going south in autumn, when they crept into the wintering area without much fuel in hand. In other words, the predicted fuel amounts from the
Flight programme gave quite a detailed idea of exactly how the geese set up their migratory flights, and showed that they did not stop for head winds, but just carried on, head wind or not. However, we had no direct way of checking whether our calculated fuel accounts were right, as we could not get at the birds when they were out in the wilds.
In its predictive format, the
Flight programme prints out a list of the current values of 30 variables that change as the bird goes along, starting with the mass, the speed and the power. If we were to catch the bird over the ocean, those figures say what we would expect to see, if we were to catch and inspect the geese. Actually, the Lund wind tunnel was originally designed to make those checks possible, during a long flight in the wind tunnel. To do that, you have to swing a balance into the test section every hour or so, and stop the wind for a minute or two so that the bird can weigh itself. You also have to make provision so that the bird can control its flight speed, using sensors that determine whether the bird is creeping to the upstream or downstream end of the test section, and adjusting the speed accordingly. This arrangement of sensors and speed control was included in the original design [
4], but it would require a lot of time to get all that working. The tunnel is all set up to monitor a flight lasting days, allowing the bird to set its speed, and keeping track of its weight, measuring fuel, speed and everything else as we go, but this has not yet been done.
Figure 4.
Migration routes of the three species of geese tracked during the spring migration of 2008. Positions were GPS recorded, usually every 2 h.
Figure 4.
Migration routes of the three species of geese tracked during the spring migration of 2008. Positions were GPS recorded, usually every 2 h.